第二章习题及答案.doc
2第二章 需求、供给与均衡价格(习题及答案)

第二章需求、供给与均衡价格思考与练习一、选择题1.当羽毛球拍的价格下降时,对羽毛球的需求将( )。
A.减少B.不变C.增加D.视具体情况而定2.假如生产某种商品所需原料的价格上升了,这种商品的( )。
A.需求曲线将向左移动B.供给曲线将向左移动C.供给曲线将向右移动D.需求曲线将向左移动3.均衡价格随着( )。
A.需求和供给的增加而上升B.需求的减少和供给的增加而上升C.需求和供给的减少而上升D.需求的增加和供给的减少而上升4.保持所有其他因素不变,某种商品的价格下降,将导致( )。
A.需求增加B.需求减少C.需求量增加D.需求量减少5.消费者预期某物品未来价格要上升,则对该物品当前需求会( )。
A.减少B.增加C.不变D.上述三种情况都可能6.所有下列因素中除哪一种以外都会使需求曲线移动( )。
A.消费者收入变化B.商品本身价格下降C.其他有关商品价格下降D.消费者偏好变化7.某种商品的供给曲线向右上方倾斜.如果该种商品的一种互补品的价格上升则会引起( )。
A.均衡数量增加,均衡价格上升B.均衡数量增加,均衡价格下降C.均衡数量减少,均衡价格上升D.均衡数量减少,均衡价格下降8.根据供求定理,供给的变动引起( )。
A.均衡价格和均衡数量同方向变动B.均衡价格和均衡数量反方向变动C.均衡价格反方向变动。
均衡数量同方向变动D.均衡价格同方向变动,均衡数量反方向变动9.下面哪一种情况表明存在着价格上限( )。
A.尽管现在供给短缺。
但生产者正在迅速增加供给B.供给短缺。
但生产者不愿意增加生产C.供求平衡D.消费者的需求得到了完全满足10.下面哪一种情况表明存在着价格下限( )。
A.尽管现在供给过剩,但生产者仍在增加供给B.由于供给过剩,消费者巳不愿意购买C.供求平衡D.生产者的产品全卖了出去参考答案:1.C;2.B;3.D;4.C;5.B;6.B;7.D;8.C;9.B;10.A二、判断题1.需求就是家庭在某一特定时期内,在每一价格水平时愿意购买的商品量。
第二章 习题答案

第二章 需求、供给和均衡价格2. 假定表2—1(即教材中第54页的表2—5)是需求函数Q d =500-100P 在一定价格范围内的需求表:表2—1某商品的需求表 价格(元) 1 2 3 4 5需求量 400 300 200 100 0(1)求出价格2元和4元之间的需求的价格弧弹性。
(2)根据给出的需求函数,求P =2元时的需求的价格点弹性。
(3)根据该需求函数或需求表作出几何图形,利用几何方法求出P =2元时的需求的价格点弹性。
它与(2)的结果相同吗?解答:(1)根据中点公式e d =-ΔQ ΔP ·P 1+P 22,Q 1+Q 22),有e d =2002·2+42,300+1002)=1.5(2)由于当P =2时,Q d =500-100×2=300,所以,有e d =-d Q d P ·P Q =-(-100)·2300=23(3)根据图2—4,在a 点即P =2时的需求的价格点弹性为e d =GB OG =200300=23或者 e d =FO AF =23图2—4显然,在此利用几何方法求出的P =2时的需求的价格点弹性系数和(2)中根据定义公式求出的结果是相同的,都是e d =23。
3. 假定表2—2(即教材中第54页的表2—6)是供给函数Q s =-2+2P 在一定价格范围内的供给表:表2—2某商品的供给表 价格(元) 2 3 4 5 6供给量 2 4 6 8 10(1)求出价格3元和5元之间的供给的价格弧弹性。
(2)根据给出的供给函数,求P =3元时的供给的价格点弹性。
(3)根据该供给函数或供给表作出几何图形,利用几何方法求出P =3元时的供给的价格点弹性。
它与(2)的结果相同吗?解答:(1)根据中点公式e s =ΔQ ΔP ·P 1+P 22,Q 1+Q 22),有e s =42·3+52,4+82)=43(2)由于当P =3时,Q s =-2+2×3=4,所以,e s =d Q d P ·P Q =2·34=1.5。
第二章练习题及参考答案

第二章练习题及参考答案《马克思主义基本原理概论》练习题及参考答案第二章认识世界和改造世界一、单项选择题1、唯物论认识论的基本原则和核心是(A )A反映论 B实践论 C先验论 D可知论2、人类认识发展的根本动力是(B )A科学兴趣 B社会实践 C求知欲望 D好奇心3、物质生产实践主要处理(A )A人与自然的关系 B人与人的关系 C对抗性矛盾的关系 D非对抗性矛盾的关系4、真理总是与谬误相比较而存在,相斗争而发展的,因而(A )A真理与谬误的对立是相对的 B真理中包含谬误的认识C谬误中包含一定的真理性认识 D谬误是真理不可摆脱的对立面5、认识的最终目的是(B )A发现真理 B改造世界 C创立科学理论 D改造客观规律6、人的认识能力是至上的,又是非至上的属于(D)观点A客观唯心论 B主观唯心论 C旧唯物论 D辩证唯物主义7、认识的本质在于( B )A主体创造 B能动反映 C社会实践 D客观存在8、人类认识运动的基本过程是(C)A概念——判断——推理 B感觉——知觉——表象C个别——一般——个别 D一般——个别——一般9、马克思认为“理论一经掌握群众,就会变成物质的力量”说明(B )A实践对理论有决定作用 B理论对实践有指导作用C理论比实践更为重要 D实践比理论重要10、真理是对客观事物和规律的(D )A本质认识 B深刻认识 C内在认识 D正确认识11、法国科学家路易·巴斯德说:“在观察事物之际,机遇偏爱有准备的头脑”。
这句话强调了(B )A人们对每一事物都要细心观察 B 人们在认识事物时要有理性指导C人们获得感性经验的重要性 D人们要充分发挥意识能动性12、人的认识是不是真理,要看(D)A能否满足人们的需要 B能否被大多数人认可C能否付诸实践 D能否在实践中取得预期效果13、“不唯上,不唯书,不唯师,只唯实”说明( B )A书本知识是不重要的 B一切从实际出发C上级的指示和决议不能成为行动的依据D没有直接经验就没有发言权14、从认识发展的规律看,“熟知”与“真知”的关系是(B )A熟知即真知 B熟知不等于真知 C熟知起源于真知 D熟知必然转化为真知15、唯心论与不可知论的关系是( B)A唯心论都是不可知论 B唯心论有可知论与不可知论之分C主观唯心论是可知论,客观唯心论是不可知论D客观唯心论是可知论,主观唯心论是不可知论16、认识的起点是感觉,这是( D )A唯物主义的观点 B唯心主义的观点C辩证唯物主义的观点 D唯物论和唯心论都可以承认的观点17、对不可知论最令人信服的驳斥是(C )A科学知识 B丰富的经验 C社会实践 D人类的认识能力18、判断对某一事物的认识是否完成的标志是( D)A占有的感性材料是否十分丰富真实B感性认识是否上升到理性认识C这一认识是否反复多次D理性认识是否运用于实践并取得预期效果19、唯物论和彻底的唯心论的认识论都是(B )A反映论 B可知论 C能动的革命的反映论 D先验论20、假象是(C )A人们认识中发生的错觉 B从正面反映本质的现象C从反面歪曲本质的现象 D不表现本质的现象21、实践作为检验认识真理性的标准具有不确定性的含义是(D)A实践标准是不可靠的 B科学理论也是检验真理的标准C除了实践标准还有其他标准D实践的历史局限性决定检验理论是一个过程22、辩证唯物主义认识论与唯心论认识论的区别是( C )A世界是可以被认识的 B认识发展是辩证的过程C客观事物是认识的对象 D社会实践是认识的基础23、人类活动的“两个尺度”是(C)A认识与实践 B真理与谬误 C真理与价值 D抽象与具体24、人们的下列活动中属于最基本的实践活动的是(C)A医生给病人做手术 B法官审理案件 C农民播种小麦 D科学家进行化学实验25、当代自然科学的发展日新月异,新的研究成果层出不穷,根本原因是(D)A科学家的聪明才智决定的正确的科技政策决定的C环境与资源的状况决定的 D生产实践的需要决定的26、“离开革命实践的理论是空洞的理论,不以革命的理论为指导的实践是盲目的实践”说明(C)A要重视实践对理论的决定作用 B要发挥理论对实践的指导作用C要坚持理论与实践相结合的原则 D要在实践中丰富和发展理论27、从本质上看,认识是( D)A主体心灵的主观创造 B主体心灵对客体的直觉C主体对客体的直接反映 D主体对客体的能动反映28、“从物到感觉和思想”与“从思想和感觉到物”的对立,属于(B)A辩证法与形而上学的对立B唯物主义反映论与唯心主义先验论的对立C经验论与唯理论的对立D能动的革命的反映论与消极的被动的反映论的对立29、“人的认识是主体对客体的直接反映”的观点属于(C )A主观唯心主义认识论B客观唯心主义认识论C形而上学唯物主义认识论 D辩证唯物主义认识论30、我们看到苹果的形状和颜色,嗅到它的气味,摸到它的光滑,尝到它的滋味,在意识中就形成对苹果的整体感性形象。
第二章 习题参考答案(修正)

第二章 需求、供给与均衡价格(题目及习题解答)一、判断题1.需求曲线描述了:其它条件不变,市场需求量与价格之间的关系。
解答:√。
知识点:课本第14页倒数第3行。
2.以纵轴代表价格,横轴代表数量,如果两条需求曲线通过同一点,则在那一点处,较陡的那条的弹性更大。
解答:×。
知识点:(考察弹性的几何意义)课本21页公式2.6和22页6-15行。
应该是“较陡的那条的弹性更小”。
理由:图中,直线AC 、BD 分别为需求曲线1和需求曲线2,AC 比BD 陡峭。
AC 之上的E 点弹性等于|AE|/|CE|,而BD 之上的E 点弹性等于|BE|/|DE|。
不难判定,|BE|>|AE|,而|DE|<|CE|,所以|AE|/|CE|<|BE|/|DE|,即“在那一点处,较陡的那条的弹性更小”。
3.如果需求是一条倾斜的直线,则价格水平越高,需求的价格弹性(绝对值)越大。
解答:√。
知识点:两种解法。
第一种是利用弹性的几何意义,课本22页6-7行。
如左下图所示:D 点价格大于B 点,D 点弹性=|AD|/|CD|>B 点弹性=|AB| /|BC|;第二种利用21页公式2.6。
因为B 点和D 点都在同一条直线上,所以dQ/dP 都相同,而P2<P 1,Q 2>Q1。
2121E E B D P P dQ dQ dP Q dP Q =⋅<=⋅ 4.如供给是一条直线,则供给的价格弹性为常数。
解答:×。
26页2.10b 。
“供给的价格弹性不确定”。
设供给函数为P=a+b ·Q s ,则dQ s /dP=-1/b 2,5.需求曲线越陡峭,则供给的变化对价格的影响越大。
P=a 1+b 1·Q s ,需求曲线P=a 2-b 2·Q d 。
令Q *=Q s =Q d ,得P *=(a 1b 2+b 1a 2)/(b 1+b 2)。
需求曲线a 1变化而b 1不变(平行移动)。
第二章课后习题答案

第二章课后习题答案第二章牛顿定律2-1如图(a)所示,质量为m的物体用平行于斜面的细线联结置于光滑的斜面上,若斜面向左方作加速运动,当物体刚脱离斜面时,它的加速度的大小为()(A)ginθ(B)gcoθ(C)gtanθ(D)gcotθ分析与解当物体离开斜面瞬间,斜面对物体的支持力消失为零,物体在绳子拉力FT(其方向仍可认为平行于斜面)和重力作用下产生平行水平面向左的加速度a,如图(b)所示,由其可解得合外力为mgcotθ,故选(D).求解的关键是正确分析物体刚离开斜面瞬间的物体受力情况和状态特征.2-2用水平力FN把一个物体压着靠在粗糙的竖直墙面上保持静止.当FN逐渐增大时,物体所受的静摩擦力Ff的大小()(A)不为零,但保持不变(B)随FN成正比地增大(C)开始随FN增大,达到某一最大值后,就保持不变(D)无法确定分析与解与滑动摩擦力不同的是,静摩擦力可在零与最大值μFN范围内取值.当FN增加时,静摩擦力可取的最大值成正比增加,但具体大小则取决于被作用物体的运动状态.由题意知,物体一直保持静止状态,故静摩擦力与重力大小相等,方向相反,并保持不变,故选(A).2-3一段路面水平的公路,转弯处轨道半径为R,汽车轮胎与路面间的摩擦因数为μ,要使汽车不至于发生侧向打滑,汽车在该处的行驶速率()μgR(B)必须等于μgR(C)不得大于μgR(D)还应由汽车的质量m决定(A)不得小于分析与解由题意知,汽车应在水平面内作匀速率圆周运动,为保证汽车转弯时不侧向打滑,所需向心力只能由路面与轮胎间的静摩擦力提供,能够提供的最大向心力应为μFN.由此可算得汽车转弯的最大速率应为v=μRg.因此只要汽车转弯时的实际速率不大于此值,均能保证不侧向打滑.应选(C).2-4一物体沿固定圆弧形光滑轨道由静止下滑,在下滑过程中,则()(A)它的加速度方向永远指向圆心,其速率保持不变(B)它受到的轨道的作用力的大小不断增加(C)它受到的合外力大小变化,方向永远指向圆心(D)它受到的合外力大小不变,其速率不断增加分析与解由图可知,物体在下滑过程中受到大小和方向不变的重力以及时刻指向圆轨道中心的轨道支持力FN作用,其合外力方向并非指向圆心,其大小和方向均与物体所在位置有关.重力的切向分量(mgcoθ)使物体的速率将会不断增加(由机械能守恒亦可判断),则物体作圆周运动的向心力(又称法向力)将不断增大,由轨道法向方向上的动力学方程v2FNmginθm可判断,随θ角的不断增大过程,轨道支持力FN也将不R断增大,由此可见应选(B).2-5图(a)示系统置于以a=1/4g的加速度上升的升降机内,A、B两物体质量相同均为m,A所在的桌面是水平的,绳子和定滑轮质量均不计,若忽略滑轮轴上和桌面上的摩擦,并不计空气阻力,则绳中张力为()(A)58mg(B)12mg(C)mg(D)2mg分析与解本题可考虑对A、B两物体加上惯性力后,以电梯这个非惯性参考系进行求解.此时A、B两物体受力情况如图(b)所示,图中a′为A、B两物体相对电梯的加速度,ma′为惯性力.对A、B两物体应用牛顿第二定律,可解得FT=5/8mg.故选(A).讨论对于习题2-5这种类型的物理问题,往往从非惯性参考系(本题为电梯)观察到的运动图像较为明确,但由于牛顿定律只适用于惯性参考系,故从非惯性参考系求解力学问题时,必须对物体加上一个虚拟的惯性力.如以地面为惯性参考系求解,则两物体的加速度aA和aB均应对地而言,本题中aA和aB的大小与方向均不相同.其中aA应斜向上.对aA、aB、a和a′之间还要用到相对运动规律,求解过程较繁.有兴趣的读者不妨自己尝试一下.2-6图示一斜面,倾角为α,底边AB长为l=2.1m,质量为m的物体从题2-6图斜面顶端由静止开始向下滑动,斜面的摩擦因数为μ=0.14.试问,当α为何值时,物体在斜面上下滑的时间最短?其数值为多少?解取沿斜面为坐标轴O某,原点O位于斜面顶点,则由牛顿第二定律有mginαmgμcoαma(1)又物体在斜面上作匀变速直线运动,故有l11at2ginαμcoαt2coα22则t2l(2)gcoαinαμcoα为使下滑的时间最短,可令dt0,由式(2)有dαinαinαμcoαcoαcoαμinα0则可得tan2α1o,49μ此时t2l0.99gcoαinαμcoα2-7工地上有一吊车,将甲、乙两块混凝土预制板吊起送至高空.甲块质量为m1=2.00某102kg,乙块质量为m2=1.00某102kg.设吊车、框架和钢丝绳的质量不计.试求下述两种情况下,钢丝绳所受的张力以及乙块对甲块的作用力:(1)两物块以10.0m·s-2的加速度上升;(2)两物块以1.0m·s-2的加速度上升.从本题的结果,你能体会到起吊重物时必须缓慢加速的道理吗?解按题意,可分别取吊车(含甲、乙)和乙作为隔离体,画示力图,并取竖直向上为Oy轴正方向(如图所示).当框架以加速度a上升时,有FT-(m1+m2)g=(m1+m2)a(1)FN2-m2g=m2a(2)解上述方程,得FT=(m1+m2)(g+a)(3)FN2=m2(g+a)(4)(1)当整个装置以加速度a=10m·s-2上升时,由式(3)可得绳所受张力的值为FT=5.94某103N乙对甲的作用力为F′N2=-FN2=-m2(g+a)=-1.98某103N(2)当整个装置以加速度a=1m·s-2上升时,得绳张力的值为FT=3.24某103N此时,乙对甲的作用力则为F′N2=-1.08某103N由上述计算可见,在起吊相同重量的物体时,由于起吊加速度不同,绳中所受张力也不同,加速度大,绳中张力也大.因此,起吊重物时必须缓慢加速,以确保起吊过程的安全.2-8如图(a)所示,已知两物体A、B的质量均为m=3.0kg物体A以加速度a=1.0m·s-2运动,求物体B与桌面间的摩擦力.(滑轮与连接绳的质量不计)分析该题为连接体问题,同样可用隔离体法求解.分析时应注意到绳中张力大小处处相等是有条件的,即必须在绳的质量和伸长可忽略、滑轮与绳之间的摩擦不计的前提下成立.同时也要注意到张力方向是不同的.解分别对物体和滑轮作受力分析[图(b)].由牛顿定律分别对物体A、B及滑轮列动力学方程,有mAg-FT=mAa(1)F′T1-Ff=mBa′(2)F′T-2FT1=0(3)考虑到mA=mB=m,FT=F′T,FT1=F′T1,a′=2a,可联立解得物体与桌面的摩擦力Ffmgm4ma7.2N2讨论动力学问题的一般解题步骤可分为:(1)分析题意,确定研究对象,分析受力,选定坐标;(2)根据物理的定理和定律列出原始方程组;(3)解方程组,得出文字结果;(4)核对量纲,再代入数据,计算出结果来.2-9质量为m′的长平板A以速度v′在光滑平面上作直线运动,现将质量为m的木块B轻轻平稳地放在长平板上,板与木块之间的动摩擦因数为μ,求木块在长平板上滑行多远才能与板取得共同速度?分析当木块B平稳地轻轻放至运动着的平板A上时,木块的初速度可视为零,由于它与平板之间速度的差异而存在滑动摩擦力,该力将改变它们的运动状态.根据牛顿定律可得到它们各自相对地面的加速度.换以平板为参考系来分析,此时,木块以初速度-v′(与平板运动速率大小相等、方向相反)作匀减速运动,其加速度为相对加速度,按运动学公式即可解得.该题也可应用第三章所讲述的系统的动能定理来解.将平板与木块作为系统,该系统的动能由平板原有的动能变为木块和平板一起运动的动能,而它们的共同速度可根据动量定理求得.又因为系统内只有摩擦力作功,根据系统的动能定理,摩擦力的功应等于系统动能的增量.木块相对平板移动的距离即可求出.解1以地面为参考系,在摩擦力Ff=μmg的作用下,根据牛顿定律分别对木块、平板列出动力学方程Ff=μmg=ma1F′f=-Ff=m′a2a1和a2分别是木块和木板相对地面参考系的加速度.若以木板为参考系,木块相对平板的加速度a=a1+a2,木块相对平板以初速度-v′作匀减速运动直至最终停止.由运动学规律有-v′2=2a由上述各式可得木块相对于平板所移动的距离为mv22μgmm解2以木块和平板为系统,它们之间一对摩擦力作的总功为W=Ff(+l)-Ffl=μmg式中l为平板相对地面移动的距离.由于系统在水平方向上不受外力,当木块放至平板上时,根据动量守恒定律,有m′v′=(m′+m)v″由系统的动能定理,有μmg由上述各式可得11mv2mmv222mv22μgmm2-10如图(a)所示,在一只半径为R的半球形碗内,有一粒质量为m的小钢球,当小球以角速度ω在水平面内沿碗内壁作匀速圆周运动时,它距碗底有多高?分析维持钢球在水平面内作匀角速度转动时,必须使钢球受到一与向心加速度相对应的力(向心力),而该力是由碗内壁对球的支持力FN的分力来提供的,由于支持力FN始终垂直于碗内壁,所以支持力的大小和方向是随ω而变的.取图示O某y坐标,列出动力学方程,即可求解钢球距碗底的高度.解取钢球为隔离体,其受力分析如图(b)所示.在图示坐标中列动力学方程FNinθmanmRω2inθ(1)Rh(3)且有coθR由上述各式可解得钢球距碗底的高度为hR可见,h随ω的变化而变化.gω22-11火车转弯时需要较大的向心力,如果两条铁轨都在同一水平面内(内轨、外轨等高),这个向心力只能由外轨提供,也就是说外轨会受到车轮对它很大的向外侧压力,这是很危险的.因此,对应于火车的速率及转弯处的曲率半径,必须使外轨适当地高出内轨,称为外轨超高.现有一质量为m的火车,以速率v沿半径为R的圆弧轨道转弯,已知路面倾角为θ,试求:(1)在此条件下,火车速率v0为多大时,才能使车轮对铁轨内外轨的侧压力均为零?(2)如果火车的速率v≠v0,则车轮对铁轨的侧压力为多少?分析如题所述,外轨超高的目的欲使火车转弯的所需向心力仅由轨道支持力的水平分量FNinθ提供(式中θ角为路面倾角).从而不会对内外轨产生挤压.与其对应的是火车转弯时必须以规定的速率v0行驶.当火车行驶速率v≠v0时,则会产生两种情况:如图所示,如v>v0时,外轨将会对车轮产生斜向内的侧压力F1,以补偿原向心力的不足,如v<v0时,则内轨对车轮产生斜向外的侧压力F2,以抵消多余的向心力,无论哪种情况火车都将对外轨或内轨产生挤压.由此可知,铁路部门为什么会在每个铁轨的转弯处规定时速,从而确保行车安全.解(1)以火车为研究对象,建立如图所示坐标系.据分析,由牛顿定律有v2FNinθm(1)解(1)(2)两式可得火车转弯时规定速率为v0gRtanθ(2)当v>v0时,根据分析有v2FNinθF1coθm(3)RFNcoθF1inθmg0(4)解(3)(4)两式,可得外轨侧压力为v2F1mcoθginθR当v<v0时,根据分析有v2FNinθF2coθm(5)RFNcoθF2inθmg0(6)解(5)(6)两式,可得内轨侧压力为v2F2mginθcoθR2-12一杂技演员在圆筒形建筑物内表演飞车走壁.设演员和摩托车的总质量为m,圆筒半径为R,演员骑摩托车在直壁上以速率v作匀速圆周螺旋运动,每绕一周上升距离为h,如图所示.求壁对演员和摩托车的作用力.分析杂技演员(连同摩托车)的运动可以看成一个水平面内的匀速率圆周运动和一个竖直向上匀速直线运动的叠加.其旋转一周所形成的旋线轨迹展开后,相当于如图(b)所示的斜面.把演员的运动速度分解为图示的v1和v2两个分量,显然v1是竖直向上作匀速直线运动的分速度,而v2则是绕圆筒壁作水平圆周运动的分速度,其中向心力由筒壁对演员的支持力FN的水平分量FN2提供,而竖直分量FN1则与重力相平衡.如图(c)所示,其中φ角为摩托车与筒壁所夹角.运用牛顿定律即可求得筒壁支持力的大小和方向解设杂技演员连同摩托车整体为研究对象,据(b)(c)两图应有FN1mg0(1)FN2v2m(2)Rv2vcoθv2πR2πR2h2(3)22FNFN1FN2(4)以式(3)代入式(2),得FN2m4π2R2v24π2Rmv222(5)2222R4πRh4πRh将式(1)和式(5)代入式(4),可求出圆筒壁对杂技演员的作用力(即支承力)大小为22FNFN1FN224π2Rv22mg4π2R2h2与壁的夹角φ为FN24π2Rv2arctanarctan222FN14πRhg讨论表演飞车走壁时,演员必须控制好运动速度,行车路线以及摩托车的方位,以确保三者之间满足解题用到的各个力学规律.2-13一质点沿某轴运动,其受力如图所示,设t=0时,v0=5m·s-1,某0=2m,质点质量m=1kg,试求该质点7s末的速度和位置坐标.分析首先应由题图求得两个时间段的F(t)函数,进而求得相应的加速度函数,运用积分方法求解题目所问,积分时应注意积分上下限的取值应与两时间段相应的时刻相对应.解由题图得0t52t,Ft5t7355t,由牛顿定律可得两时间段质点的加速度分别为a2t,0t5a355t,5t7对0<t<5s时间段,由adv得dtvtv00dvadt积分后得v5t再由v2d某得dtd某vdt某00某t积分后得某25tt将t=5s代入,得v5=30m·s-1和某5=68.7m对5s<t<7s时间段,用同样方法有133dvv0vt5a2dt得v35t2.5t82.5t再由得某=17.5t2-0.83t3-82.5t+147.87将t=7s代入分别得v7=40m·s-1和某7=142m2-14一质量为10kg的质点在力F的作用下沿某轴作直线运动,已知F =120t+40,式中F的单位为N,t的单位的s.在t=0时,质点位于某=5.0m处,其速度v0=6.0m·s-1.求质点在任意时刻的速度和位置.分析这是在变力作用下的动力学问题.由于力是时间的函数,而加速度a=dv/dt,这时,动力学方程就成为速度对时间的一阶微分方程,解此微分方程可得质点的速度v(t);由速度的定义v=d某/dt,用积分的方法可求出质点的位置.解因加速度a=dv/dt,在直线运动中,根据牛顿运动定律有2某某5d某vdt5t120t40mdvdt依据质点运动的初始条件,即t0=0时v0=6.0m·s-1,运用分离变量法对上式积分,得vv0dv12.0t4.0dt0tv=6.0+4.0t+6.0t2又因v=d某/dt,并由质点运动的初始条件:t0=0时某0=5.0m,对上式分离变量后积分,有d某6.04.0t6.0tdt某t2某00某=5.0+6.0t+2.0t2+2.0t32-15轻型飞机连同驾驶员总质量为1.0某103kg.飞机以55.0m·s-1的速率在水平跑道上着陆后,驾驶员开始制动,若阻力与时间成正比,比例系数α=5.0某102N·s-1,空气对飞机升力不计,求:(1)10s后飞机的速率;(2)飞机着陆后10s内滑行的距离.分析飞机连同驾驶员在水平跑道上运动可视为质点作直线运动.其水平方向所受制动力F为变力,且是时间的函数.在求速率和距离时,可根据动力学方程和运动学规律,采用分离变量法求解.解以地面飞机滑行方向为坐标正方向,由牛顿运动定律及初始条件,有dvαtdtvtαtdvv00mdtα2t得vv02mFmam因此,飞机着陆10s后的速率为v=30m·s-1又tα2d某vdt某0002mt某故飞机着陆后10s内所滑行的距离某某0v0tα3t467m6m2-16质量为m的跳水运动员,从10.0m高台上由静止跳下落入水中.高台距水面距离为h.把跳水运动员视为质点,并略去空气阻力.运动员入水后垂直下沉,水对其阻力为bv2,其中b为一常量.若以水面上一点为坐标原点O,竖直向下为Oy轴,求:(1)运动员在水中的速率v与y的函数关系;(2)如b/m=0.40m-1,跳水运动员在水中下沉多少距离才能使其速率v减少到落水速率v0的1/10?(假定跳水运动员在水中的浮力与所受的重力大小恰好相等)分析该题可以分为两个过程,入水前是自由落体运动,入水后,物体受重力P、浮力F和水的阻力Ff的作用,其合力是一变力,因此,物体作变加速运动.虽然物体的受力分析比较简单,但是,由于变力是速度的函数(在有些问题中变力是时间、位置的函数),对这类问题列出动力学方程并不复杂,但要从它计算出物体运动的位置和速度就比较困难了.通常需要采用积分的方法去解所列出的微分方程.这也成了解题过程中的难点.在解方程的过程中,特别需要注意到积分变量的统一和初始条件的确定.解(1)运动员入水前可视为自由落体运动,故入水时的速度为v02gh运动员入水后,由牛顿定律得P-Ff-F=ma由题意P=F、Ff=bv2,而a=dv/dt=v(dv/dy),代入上式后得-bv2=mv(dv/dy)考虑到初始条件y0=0时,v0t2gh,对上式积分,有vdvmdy0v0vbvv0eby/m2gheby/m(2)将已知条件b/m=0.4m-1,v=0.1v0代入上式,则得ymvln5.76mbv0某2-17直升飞机的螺旋桨由两个对称的叶片组成.每一叶片的质量m=136kg,长l=3.66m.求当它的转速n=320r/min 时,两个叶片根部的张力.(设叶片是宽度一定、厚度均匀的薄片)分析螺旋桨旋转时,叶片上各点的加速度不同,在其各部分两侧的张力也不同;由于叶片的质量是连续分布的,在求叶片根部的张力时,可选取叶片上一小段,分析其受力,列出动力学方程,然后采用积分的方法求解.解设叶片根部为原点O,沿叶片背离原点O的方向为正向,距原点O为r处的长为dr一小段叶片,其两侧对它的拉力分别为FT(r)与FT(r+dr).叶片转动时,该小段叶片作圆周运动,由牛顿定律有dFTFTrFTrdr由于r=l时外侧FT=0,所以有m2ωrdrltFTrdFTlrmω2rdrlmω2222πmn222FTrlrlr2ll上式中取r=0,即得叶片根部的张力FT0=-2.79某105N负号表示张力方向与坐标方向相反.2-18一质量为m的小球最初位于如图(a)所示的A点,然后沿半径为r 的光滑圆轨道ADCB下滑.试求小球到达点C时的角速度和对圆轨道的作用力.分析该题可由牛顿第二定律求解.在取自然坐标的情况下,沿圆弧方向的加速度就是切向加速度at,与其相对应的外力Ft是重力的切向分量mginα,而与法向加速度an相对应的外力是支持力FN和重力的法向分量mgcoα.由此,可分别列出切向和法向的动力学方程Ft=mdv/dt和Fn=man.由于小球在滑动过程中加速度不是恒定的,因此,需应用积分求解,为使运算简便,可转换积分变量.倡该题也能应用以小球、圆弧与地球为系统的机械能守恒定律求解小球的速度和角速度,方法比较简便.但它不能直接给出小球与圆弧表面之间的作用力.解小球在运动过程中受到重力P和圆轨道对它的支持力FN.取图(b)所示的自然坐标系,由牛顿定律得Ftmginαmdv(1)dtmv2FnFNmgcoαm(2)R由vdrdαrdα,得dt,代入式(1),并根据小球从点A运动到点Cdtdtv的始末条件,进行积分,有vv0vdvα90orginαdα得v则小球在点C的角速度为2rgcoαωv2gcoα/rrmv2mgcoα3mgcoα由式(2)得FNmr由此可得小球对圆轨道的作用力为FN3mgcoαFN负号表示F′N与en反向.2-19光滑的水平桌面上放置一半径为R的固定圆环,物体紧贴环的内侧作圆周运动,其摩擦因数为μ,开始时物体的速率为v0,求:(1)t时刻物体的速率;(2)当物体速率从v0减少到12v0时,物体所经历的时间及经过的路程.解(1)设物体质量为m,取图中所示的自然坐标,按牛顿定律,有mv2FNmanRFfmatdvdt由分析中可知,摩擦力的大小Ff=μFN,由上述各式可得v2dvμRdt取初始条件t=0时v=v0,并对上式进行积分,有t0dtRvdvμv0v2vRv0Rv0μt(2)当物体的速率从v0减少到1/2v0时,由上式可得所需的时间为t物体在这段时间内所经过的路程Rμv0vdt0tt0Rv0dtRv0μtRln2μ2-20质量为45.0kg的物体,由地面以初速60.0m·s-1竖直向上发射,物体受到空气的阻力为Fr=kv,且k=0.03N/(m·s-1).(1)求物体发射到最大高度所需的时间.(2)最大高度为多少?分析物体在发射过程中,同时受到重力和空气阻力的作用,其合力是速率v的一次函数,动力学方程是速率的一阶微分方程,求解时,只需采用分离变量的数学方法即可.但是,在求解高度时,则必须将时间变量通过速度定义式转换为位置变量后求解,并注意到物体上升至最大高度时,速率应为零.解(1)物体在空中受重力mg和空气阻力Fr=kv作用而减速.由牛顿定律得mgkvmdv(1)dt某2-25如图(a)所示,电梯相对地面以加速度a竖直向上运动.电梯中有一滑轮固定在电梯顶部,滑轮两侧用轻绳悬挂着质量分别为m1和m2的物体A和B.设滑轮的质量和滑轮与绳索间的摩擦均略去不计.已知m1>m2,如以加速运动的电梯为参考系,求物体相对地面的加速度和绳的张力.分析如以加速运动的电梯为参考系,则为非惯性系.在非惯性系中应用牛顿定律时必须引入惯性力.在通常受力分析的基础上,加以惯性力后,即可列出牛顿运动方程来.解取如图(b)所示的坐标,以电梯为参考系,分别对物体A、B作受力分析,其中F1=m1a,F2=m2a分别为作用在物体A、B上的惯性力.设ar为物体相对电梯的加速度,根据牛顿定律有m1gm1aFT1m1ar(1)m2gm2aFT2m2ar(2)FT2FT2(3)由上述各式可得arm1m2gam1m22m1m2gam1m2FT2FT2由相对加速度的矢量关系,可得物体A、B对地面的加速度值为a1aram1m2g2m2am1m22m1am1m2gm1m2a2araa2的方向向上,a1的方向由ar和a的大小决定.当ar<a,即m1g-m2g-2m2a>0时,a1的方向向下;反之,a1的方向向上.某2-26如图(a)所示,在光滑水平面上,放一质量为m′的三棱柱A,它的斜面的倾角为α.现把一质量为m的滑块B放在三棱柱的光滑斜面上.试求:(1)三棱柱相对于地面的加速度;(2)滑块相对于地面的加速度;(3)滑块与三棱柱之间的正压力.分析这类问题可应用牛顿定律并采用隔离体法求解.在解题的过程中必须注意:(1)参考系的选择.由于牛顿定律只适用于惯性系,可选择地面为参考系(惯性系).因地面和斜面都是光滑的,当滑块在斜面上下滑时,三棱柱受到滑块对它的作用,也将沿地面作加速度为aA的运动,这时,滑块沿斜面的加速度aBA,不再是它相对于地面的加速度aB了.必须注意到它们之间应满足相对加速度的矢量关系,即aB=aA+aBA.若以斜面为参考系(非惯性系),用它求解这类含有相对运动的力学问题是较为方便的.但在非惯性系中,若仍要应用牛顿定律,则必须增添一惯性力F,且有F=maA.(2)坐标系的选择.常取平面直角坐标,并使其中一坐标轴方向与运动方向一致,这样,可使解题简化.(3)在分析滑块与三棱柱之间的正压力时,要考虑运动状态的影响,切勿简单地把它视为滑块重力在垂直于斜面方向的分力mgcoα,事实上只有当aA=0时,正压力才等于mgcoα.解1取地面为参考系,以滑块B和三棱柱A为研究对象,分别作示力图,如图(b)所示.B受重力P1、A施加的支持力FN1;A受重力P2、B施加的压力FN1′、地面支持力FN2.A的运动方向为O某轴的正向,Oy轴的正向垂直地面向上.设aA为A对地的加速度,aB为B对的地加速度.由牛顿定律得FN1inαmaA(1)FN1inαmaB某(2)FN1coαmgmaBy(3)FN1FN1(4)设B相对A的加速度为aBA,则由题意aB、aBA、aA三者的矢量关系如图(c)所示.据此可得aB某aAaBAcoα(5)aByaBAinα(6)解上述方程组可得三棱柱对地面的加速度为aAmginαcoα2mminαmginαcoαmmin2α滑块相对地面的加速度aB在某、y轴上的分量分别为aB某aBymmgin2αmmin2α则滑块相对地面的加速度aB的大小为aBaa2B某2Bym22mmm2in2αginαmmin2α其方向与y轴负向的夹角为amcotαθarctanB某arctanaBymmA与B之间的正压力FN1mmgcoα2mminα解2若以A为参考系,O某轴沿斜面方向[图(d)].在非惯性系中运用牛顿定律,则滑块B的动力学方程分别为mginαmaAcoαmaBA(1)mgcoαFN1maAinα0(2)又因FN1inαmaA0(3)FN1FN1(4)由以上各式可解得aAaBAmginαcoαmmin2αmmginαmmin2α由aB、aBA、aA三者的矢量关系可得m22mmm2in2αaBginαmmin2α以aA代入式(3)可得FN1mmgcoαmmin2α。
第二章课后习题及答案

第二章心理辅导的理论基础一、理论测试题(一)单项选择题1.()是根据操作性条件反射原理,强调行为的改变是依据行为后果而定的。
A •强化法B •系统脱敏法C.代币法D •来访者中心疗法2•在对学生进行心理辅导时,常使用的“强化法”属于()。
A •行为改变技术B •认知改变法C.运动改变法D •精神分析法3•在心理辅导的行为演练中,系统脱敏法是由()首创。
A .皮亚杰B •沃尔帕C艾利斯D •罗杰斯4•心理辅导老师帮李晓明建立焦虑等级,让他想象引起焦虑的情境,然后逐渐减少焦虑等级,直至完全放松,以缓解其考试焦虑,这种方法是()。
A •强化法B •系统脱敏法C.理性一情绪疗法D •来访者中心疗法5 •行为塑造法是根据()的操作条件反射研究结果而设计的培育和养成新反应或行为模式的一项行为治疗技术,是操作条件作用法强化原则的有力应用之一。
A .皮亚杰B •斯金纳C.艾利斯D .奥苏贝尔6.()就是运用代币并编制一套相应的激励系统来对符合要求的目标行为的表现进行肯定和奖励。
A .强化法B .理性一情绪疗法C.代币法D .来访者中心疗法7.李老师通过奖励小红花来表扬学生的行为,这种心理辅导方法属于()。
A .系统脱敏法B •代币法C.行为塑造法D .来访者中心疗法8.晓红是韩老师班上的学生,她孤僻、羞涩,当她主动与同学交谈或请教老师时,韩老师就给予肯定或激励。
这种心理辅导方法是()。
A .强化法B •系统脱敏法C.来访者中心法D .理性一情绪疗法9.()不是行为改变的基本方法。
A .强化法B .代币法C.自我控制法D .演练法10.小伟过分害怕狗,通过让他看狗的照片,谈论狗,远看狗到近看狗、摸狗、抱狗,消除对狗的惧怕反应,这是行为训练的()。
A .全身松弛训练B .系统脱敏法C.行为塑造法D .肯定性训练11.当一位胆小的学生敢于主动向教师提问时,教师教师耐心解答并给予表扬和鼓励。
的这种做法属于行为改变方法中的()。
第二章习题答案参考

第二章 金属切削机床设计22. 什么是传动组的级比和级比指数?常规变速传动系的各传动组的级比指数有什么规律性? 传动组的级比是指主动轴上同一点传往被动轴相邻两传动线的比值,用ϕxi 表示。
级比ϕxi 中的指数X i 值称为级比指数,它相当于由上述相邻两传动线与被动轴交点之间相距的格数。
设计时要使主轴转速为连续的等比数列,必须有一个变速组的级比指数为1,此变速组称为基本组。
基本组的级比指数用X 0表示,即X 0 = 1,后面变速组因起变速扩大作用,所以统称为扩大组。
第一扩大组的级比指数X 1一般等于基本组的传动副数P 0,即X 1 = P 0。
第二扩大组的作用是将第一扩大组扩大的变速范围第二次扩大,其级比指数X 2等于基本组的传动副数和第一扩大组传动副数的乘积,即X 2 = P 0×P 1。
如有更多的变速组,则依次类推。
上述设计是传动顺序和扩大顺序相一致的情况,若将基本组和各扩大组采取不同的传动顺序,还有许多方案。
25. 某机床主轴转速n =100~1120 r/min ,转速级数z =8,电动机转速n 电=1440 r/min ,试设计该机床主传动系,包括拟定结构式和转速图,画出主传动系图。
解:2.111001120min max ===n n R n ===-712.11Z n R φ 1.41查表可获得8级转速为 100,140,200,280,400,560,800,1120拟定8级转速的结构式:根据级比规律和传动副前多后少、传动线前密后疏的的原则确定4212228⨯⨯=241.141.111max ≤===ϕ主u 符合要求4/182.2/141.133min ≥===--ϕ主u 符合要求最后扩大组的变速范围:8441.1)12(4)1(≤===--i i P x i R ϕ符合要求 绘制传动系统图如下:26. 试从ϕ=1.26,z =18级变速机构的各种传动方案中选出其最佳方案,并写出结构式,画出转速图和传动系图。
第二章 中华人民共和国安全生产法(习题及答案)

第二章中华人民共和国安全生产法第一节安全生产法立法目的、适用范围第二节安全生产法的基本规定第三节生产经营单位的安全生产保障第四节安全生产从业人员权利和义务第五节安全生产的监督管理第六节生产安全事故的应急救援与调查处理第七节安全生产法律责任4-06.依据《安全生产法》的规定,生产经营单位进行()等危险作业,应当安排专业人员进行现场安全管理,确保操作规程的遵守和安全措施的落实。
4-06 AA.爆破、吊装 B.高空施工、电力安装 C.采掘、架设 D.易燃易爆物品试验5-06.重视和保障从业人员的(),是贯穿《安全生产法》的主线。
5-06 B A.知情权 B.生命权 C.健康权 D.批评检举权6-06.依据《安全生产法》的规定,生产经营单位委托工程技术人员为本单位提供安全生产管理服务的,安全生产责任由()负责。
6-06 BA.被委托的工程技术人员B.生产经营单位C.被委托的工程技术人员所在中介机构D.所在地的安全生产监管部门7-06.《安全生产法》所称生产经营单位,是指从事生产经营活动的()。
7-06 C A.公司 B.工厂 C.基本生产经营单元 D.个体工商户8-06.《安全生产法》规定的安全生产违法行为的法律责任形式,包括()。
8-06 D A.行政责任和刑事责任B.宪法责任、行政责任和刑事责任C.司法责任和民事责任D.行政责任、民事责任和刑事责任9-06.依据《安全生产法》的规定,生产经营单位应当按照国家有关规定将本单位重大危险源及有关安全措施、应急措施报()备案。
9-06 CA.有关地方人民政府公安部门B.有关地方人民政府劳动管理部门C.有关地方人民政府负责安全生产监督管理的部门和有关部门D.有关地方人民政府公安部门和安全生产监督管理部门10-06.依据《安全生产法》的规定,从业人员的工伤保险费由()缴纳。
10-06 D A.从业人员B.生产经营单位和从业人员共同C.生产经营单位主要负责人D.生产经营单位11-06.依据《安全生产法》的规定,作业场所和工作岗位的危险因素、防范措施、事故应急措施由()如实告知从业人员。
第二章习题与答案

第二章会计科目、会计账户和借贷复式记账法一、单项选择题1.账户是根据()开设的,用来连续、系统地记载各项经济业务的一种手段。
A.会计凭证B.会计对象C.会计科目D.财务指标2.根据借贷记账法的原理,记录在账户贷方的是()。
A.费用的增加B.收入的增加C.负债的减少D.所有者权益的减少3.会计科目是()的名称。
A.会计账户B.会计等式C.会计对象D.会计要素4借贷记账法的记账规则是()。
A.同增、同减、有增、有减B.同收、同付、有收、有付C.有增必有减,增减必相等D.有借必有贷,借贷必相等5.在借贷记账法中,账户的哪一方记录增加,哪一方记录减少是由()决定的。
A.账户的性质B.记账规则C.账户的结构D.业务的性质6.复试记账法的基本理论依据是()的平衡原理。
A.资产=负债+所有者权益B.收入–费用=利润C.期初余额+本期增加数-本期减少数=期末余额D.借方发生额=贷方发生额8.按照借贷记账法的记录方法,下列四组账户中,增加额均记在贷方的是()。
A.资产类和负债类B.负债类和所有者权益类C.成本类和损益类D.损益类中的收入和支出类9.会计科目与账户之间的区别在于()。
A.反映经济内容不同B.账户有结构而会计科目无结构C.分类的对象不同D.反映的结果不同10.按照借贷记账法的记录方法,下列账户的贷方登记增加额的是()。
A.库存现金B.应收账款C.应付账款D.原材料11.按照借贷记账法的记录方法,下列账户中,账户的借方登记增加额的是()。
A.实收资本B.应付职工薪酬C.累计折旧D.所得税费用12.目前我国会计制度规定,企业会计采用的记账方法是()。
A.增减记账法B.现金收付记账法C.借贷记账法D.财产收付记账法13.账户的基本结构分为左右两方,其基本依据是()。
A.登记收支业务B.借贷原理C.收付原理D.资金在运动中量的增加和减少14.不属于损益类会计科目的是()。
A.投资收益B.管理费用C.主营业务成本D.生产成本15.下列属于资产类的会计科目是()。
高中物理教材第二章练习题及答案

高中物理教材第二章练习题及答案
本文档提供了高中物理教材第二章的练题及答案,旨在帮助高中物理学生巩固和复相关知识。
1. 第一节练题
1.1. 问题:描述牛顿第一定律的内容是什么?
答案:牛顿第一定律又称惯性定律,它指出一个物体如果没有外力作用,将保持匀速运动或静止状态。
1.2. 问题:如何判断一个物体是否处于平衡状态?
答案:一个物体处于平衡状态时,所有作用在它上面的力的合力为零。
1.3. 问题:什么是质量和重量?
答案:质量是一个物体所固有的特性,衡量了物体对于改变其运动状态所需要的力。
重量是物体受地球引力作用的结果,由质量乘以重力加速度计算得出。
...
2. 第二节练题
2.1. 问题:什么是力的合成?
答案:力的合成是将两个或多个力的作用效果用一个等效的单一力表示的方法。
2.2. 问题:如何计算力的合成?
答案:力的合成可以通过将各个力的大小和方向相加来计算。
2.3. 问题:什么是力的分解?
答案:力的分解是将一个力分解成多个分力的过程。
...
以上所列为部分练题及其答案,希望对学生们的物理研究有所帮助。
更多练题和答案请参考教材第二章。
(完整版)第二章习题解答
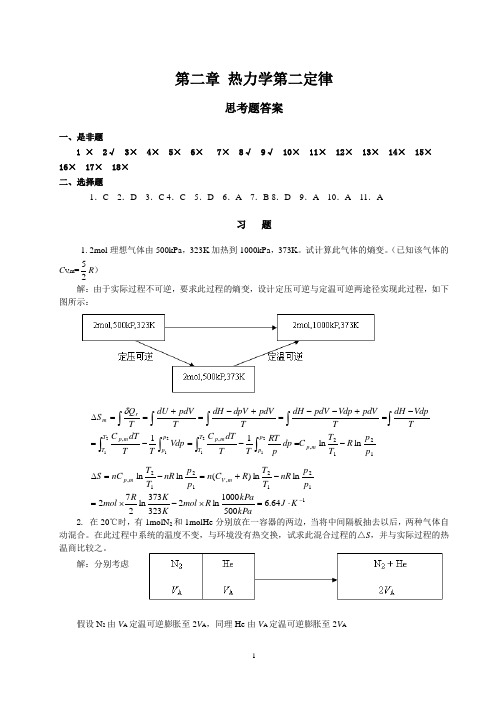
第二章 热力学第二定律思考题答案一、是非题1 × 2√ 3× 4× 5× 6× 7× 8√ 9√ 10× 11× 12× 13× 14× 15× 16× 17× 18× 二、选择题1.C 2.D 3.C 4.C 5.D 6.A 7.B 8.D 9.A 10.A 11.A习 题1. 2mol 理想气体由500kPa ,323K 加热到1000kPa ,373K 。
试计算此气体的熵变。
(已知该气体的C V ,m =25R ) 解:由于实际过程不可逆,要求此过程的熵变,设计定压可逆与定温可逆两途径实现此过程,如下图所示:1212,,,ln ln 1121212121p pR T T C dp p RT T T dT C Vdp TTdT C TVdpdH T pdV Vdp pdV dH T pdV dpV dH TpdVdU T Q S m p p p T T m p p p T T m p rm -=-=-=-=+--=+-=+==∆⎰⎰⎰⎰⎰⎰⎰⎰⎰δ11212,1212,64.65001000ln 2323373ln 272ln ln )(ln ln -⋅=⨯-⨯=-+=-=∆K J kPakPa R mol K K R mol p pnR T T R C n p p nR T T nC S m V m p2. 在20℃时,有1molN 2和1molHe 分别放在一容器的两边,当将中间隔板抽去以后,两种气体自动混合。
在此过程中系统的温度不变,与环境没有热交换,试求此混合过程的△S ,并与实际过程的热温商比较之。
解:分别考虑假设N 2由V A 定温可逆膨胀至2V A ,同理He 由V A 定温可逆膨胀至2V A△S 1 = n (N 2)R ln2 △S 2 = n (He)R ln2所以系统的 △S = △S 1+△S 2 = n (N 2) R ln2 + n (He) R ln2= 2×1mol×8.314 J ·mol -1·K -1×ln2 = 11.52J.K -1而实际过程系统没有与环境交换热和功,则 TQ= 0 即 △S >TQ 3. 1 mol 双原子理想气体,温度为298.15 K ,压强为p θ,分别进行:(1)绝热可逆膨胀至体积增加1倍;(2)绝热自由膨胀至体积增加1倍。
概率论与数理统计习题及答案第二章.doc

习题 2-21. 设 A 为任一随机事件 , 且 P ( A )= p (0< p <1). 定义随机变量1, 发生 ,XA0, 不发生 .A写出随机变量 X 的分布律 .解 { =1}= ,{ =0}=1- p .P X p P X或者X 0 1P1- pp2. 已知随机变量X 只能取 -1,0,1,2 四个值 , 且取这四个值的相应概率依次为1 , 3 , 5 , 7. 试确定常数 c ,并计算条件概率 P{ X1 | X0} .2c 4c 8c 16c解 由离散型随机变量的分布律的性质知,1 3 571,2c4c8c 16c37所以 c .161P{ X1}8所求概率为{ <1|X0 }=2c.P XP{ X 0}1 5 7252c 8c 16c3. 设随机变量 X 服从参数为 2, p 的二项分布 , 随机变量 Y 服从参数为 3, p 的二项分布 ,若P{X ≥1}5, 求P{Y ≥1}.9解 注意 p{x=k}=C n k p k q n k , 由题设 5P{ X ≥1}1 P{ X0} 1 q 2 ,9故 q1 p2 从而.3P{Y ≥1} 1 P{ Y 0}1 (2 )3 19 .3 274. 在三次独立 的重复试验中 , 每次试验成功的概率相同 , 已知至少成功一次的概率19为, 求每次试验成功的概率 .27解设每次试验成功的概率为p , 由题意知至少成功一次的概率是19,那么一次都27没有成功的概率是8 . 即 (1 p)38 ,故p = 1 .272735. 若 X 服从参数为的泊松分布 ,且P{X1} P{ X 3}, 求参数 .解 由泊松分布的分布律可知 6 .6. 一袋中装有 5 只球 , 编号为 1,2,3,4,5.在袋中同时取 3 只球, 以 X 表示取出的 3 只球中的最大号码 , 写出随机变量 X 的分布律 .解 从 1,2,3,4,5 中随机取 3 个,以 X 表示 3 个数中的最大值, X 的可能取值是 3,4,5,在 5 个数中取 3 个共有C 5310 种取法 .{ =3} 表示取出的 3 个数以 3 为最大值, P{=3}=C 22= 1;C 53 10{ =4} 表示取出的 3 个数以 4 为最大值, P{=4}=C 323 ;C 53 10 { =5} 表示取出的 3 个数以 5 为最大值, P{=5}=C 423 .5 C 53X 的分布律是X 3 45P13310105习题 2-31. 设 X 的分布律为X -11P求分布函数( ), 并计算概率 { <0},{ <2},{-2 ≤ <1}.F xPXPXPX0, x 1, 解 (1)0.15, 1≤ x 0,F ( x )=0≤ x 1,0.35, 1,x ≥1.(2) P { X <0}= P { X =-1}=; (3) P { X <2}= P { X =-1}+ P { X =0}+P { X =1}=1; (4) P {-2 ≤ x <1}= P { X =-1}+ P { X =0}=.2. 设随机变量 X 的分布 函数为( ) = + arctan x - ∞< <+∞.F xA Bx试求 : (1) 常数 A 与 B ; (2)X 落在 (-1, 1] 内的概率 .解 (1) 由于 (- ∞)=0,(+∞)=1, 可知F FA B()1 12A, B.A B( )122于是F ( x) 1 1arctan x, x .2(2) P{ 1X ≤1} F (1) F ( 1)1 1 1 1arctan( 1))( arctan1) (2 21 1 1 1 () 1 .2424 23. 设随机变量 X 的分布函数为F ( x )=0,x 0, x,0≤x 1,1,x ≥1,求 P { X ≤ -1}, P { < X <}, P {0< X ≤ 2}.解 P {X ≤ 1} F( 1) 0,P {< X <}= F - F {}- P { X =}=, P {0< X ≤2}= F (2)- F (0)=1.5.X 的绝对值不大于1;P{ X1}1 1}1 假设随机变量 ,P{X; 在事件{ 1 X 1} 出现的条件下 ,84X 在 (-1,1) 内任一子区间上取值的条件概率与该区间的长度成正比 . (1) 求 X 的分布函数 F ( x) P{ X ≤ x }; (2)求 X 取负值的概率 p .解 (1) 由条件可知 ,当 x1时,F ( x) 0 ;当 x 1 时 , F ( 1) 1;当 x 1时 , 8F (1)= P { X ≤ 1}= P ( S )=1.所以P{ 1 X1} F (1) F ( 1)P{X 1}1 1 514.88易见 , 在 X 的值属于 (1,1) 的条件下 , 事件 { 1 X x} 的条件概率为P{ 1 X ≤ x | 1X 1} k[ x( 1)],取 x =1 得到 1= k (1+1),所以 k = 1.2x 1 . 因此P{ 1 X ≤x | 1 X 1}于是 , 对于1 x 1 ,有2P{ 1X ≤ x} P{ 1X ≤ x, 1 X 1}P{ 1 X 1} P{ 1 X ≤ x | 1 X 1}5 x 1 5x 5 . 对于 x ≥1,8 2 16有 F ( x) 1. 从而0, x 1, F ( x)5x 7 , 1x 1,161, ≥x1.(2) X 取负值的概率p P{ X0} F(0) P{ X0} F (0) [F(0)F (0 )] F (0 )7 . 习题 2-4161. 选择题设 f ( x)2x, x [0, c],则 f ( x) 是某一随机变量的概率(1)0,x如果 c =(),[0, c].密度函数 .(A)1(B)1.(C) 1.(D)3.2.3c2f ( x)dx 11 ,于是 c 1解 由概率密度函数的性质可得2xdx, 故本题应选 (C ).(2) 设 X ~ N (0,1), 又常数 c 满足 P{ X ≥ c} P{ X c} , 则 c 等于 ( ).(A) 1.(B) 0.(C)1 (D) -1..2解因为P{ X ≥ c} P{ X c} ,所以 1 P{ X c} P{ X c} , 即2P{ Xc} 1, 从而 P{X c} 0.5 , 即 ( c) 0.5 , 得 c =0. 因此本题应选 (B).(3) 下列函数中可以作为某一随机变量的概率密度的是( ).cos x, x [0, ],1x2,(A)f (x)(B)f (x),0,其它 .20,其它 .1( x) 2x≥22e,≥ 0,e , x0, (C)f (x) (D)f ( x)20, x0.0,x 0.解 由概率密度函数的性质f ( x)dx 1 可知本题应选 (D).(4) 设随机变量X ~ N(,42) , Y~N(,52), P 1P{X ≤4 },P 2 PY ≥ 5 }, 则( ).(A) 对任意的实数 , P 1P 2 . (B) 对任意的实数 , P 1 P 2 .(C) 只对实数的个别值 ,有P 1 P 2 . (D) 对任意的实数 , P P .12解 由正态分布函数的性质可知对任意的实数, 有P 1( 1) 1 (1) P 2 .因此本题应选 (A).Xf xf (x)f ( x)F x(5) 设随机变量 的概率密度为 , 且 , 又( )为分布函数 , 则对任意实数 a , 有 ( ).a(A)F ( a) 1∫0 f (x)dx .(B)F ( a)(C) F ( a)F ( a) . (D) Fa解由分布函数的几何意义及概率密度的性质知答案为1 a2 ∫0f ( x)dx.2F ( a) 1 .(B).(6) 设随机变量X 服从正态分布N (1, 12 ) , Y 服从正态分布 N ( 2, 22) ,且P{ X11} P{ Y21},则下式中成立的是 (). (A) σ1 < σ2 .(B)σ 1 > σ 2 .(C)μ1 <μ2 .(D)μ1 >μ2 .解 答案是 (A). XN(0 1)u 满足(7) 设随机变量 服从正态分布对给定的正数, 数(0,1),P{ X u }, 若P{X x}, 则 x 等于 ().(A)u .(B)u.(C)u 1-.(D)u 1.2122解 答案是 (C).2. 设连续型随机变量 X 服从参数为的指数分布 ,要使P{ kX 2k}1成立 ,4应当怎样选择数 k ?解 因为随机变量 X 服从参数为的指数分布 , 其分布函数为F ( x)1 e x , x 0,0,x ≤ 0.由题意可知1 P{ k X 2k} F(2k) F ( k) (1 e2 k )(1 e k ) e k e 2 k .4于是kln 2.3. 设随机变量 X 有概率密度f ( x) 4 x 3 , 0 x 1, 0,其它 ,要使 P{ X ≥ a}P{ Xa} ( 其中 a >0) 成立 , 应当怎样选择数 a ?解由条件变形 , 得到 1P{ Xa} P{ Xa},可知P{ X a} 0.5 ,于是a3dx 0.5,因此 a14x.424. 设连续型随机变量 X 的分布函数为0,x 0,F ( x)x 2 , 0≤x ≤1,1,x 1,求: (1)X 的概率密度 ; (2) P{0.3 X 0.7} .解 (1)根据分布函数与概率密度的关系F ( x)f ( x) ,可得f (x)2x, 0 x 1,0, 其它 .(2)P{0.3 X0.7}F (0.7) F (0.3) 0.720.320.4 .5. 设随机变量 X 的概率密度为2x,0≤ x ≤1,f ( x ) =其它 ,0,求P {X ≤ 1}与P {1< X ≤2}.241}11 1解P{X ≤ 22xdx x 22 ;24P{ 1 X ≤2}1 2 xdx x 2 1 15 .1444 166. 设连续型随机变量 X 具有概率密度函数x,0 x ≤1,f ( x) Ax,1x ≤2,0,其它 .求 : (1) 常数 A ; (2) X 的分布函数 F ( x ).解 (1) 由概率密度的性质可得11 2( A x)dx1 x2xdx12于是A 2;(2) 由公式 F ( x) xf ( x)dx可得当 x ≤0 时 , F ( x) 0 ; 当 0x ≤1时 ,F( x)x1 x2 ;xdx2当 1x ≤2时 ,F ( x)1x(2xdx1当 x >2 时,F ( x) 1.0,1 x2 , 所以F ( x)2 x 22x1,2112[ Ax x 2]A 1,21x 2 x)dx 2x1;2x ≤ 0,0 x ≤ 1,1 x ≤ 2,1,x2.7. 设随机变量 X 的概率密度为1f ( x) 4( x 1), 0 x 2,0, 其它 ,对 X 独立观察 3 次, 求至少有 2 次的结果大于 1 的概率 . 解根据概率密度与分布函数的关系式P{ a X ≤ b} F (b) F ( a)b f ( x)dx ,a可得P{ X 1} 21 ( x 1)dx 54.1 8 所以 , 3 次观察中至少有2 次的结果大于 1 的概率为C 2(5)2(3) C 3 ( 5)3 175 .8 8 2568 4x 2 8. 设 X ~U(0,5) , 求关于 x 的方程 4 Xx 2 0 有实根的概率 .解 随机变量 X 的概率密度为1, ≤ x 5,f ( x)50, 其它 ,若方程有实根 , 则16 X 232≥0, 于是 X 2 ≥ 2. 故方程有实根的概率为P { X 2 ≥2}= 1P{ X 2 2}1 P{2 X2}1 21dx0 512 .59. 设随机变量 X ~ N(3,22) .(1)计算 P{2 X ≤5} , P{ 4 X ≤10}, P{| X | 2}, P{X 3};(2)确定 c 使得P{ X c} P{ X ≤ c}; (3) 设 d 满足 P{ X d}≥0.9 , 问 d 至多为多少?解 (1) 由 P { a <x ≤ b }= P { a3 X 3 ≤ b 3 } Φ( b 3 ) Φ( a 3)公式,得到2 2 2 22XΦ(1) Φ( 0.5) 0.5328P,{2< ≤5}=P {-4< X ≤10}= Φ(3.5) Φ( 3.5) 0.9996,P{|X|2}=P{X2} +P{X2}=1 2 32 3Φ() +Φ(2 ) =,2P{ X 3} =1 P{ X ≤3} 1Φ( 3 3 ) 1 Φ(0) = .2(2) 若P{Xc}P{ X ≤ c} , 得 1P{ X ≤ c}P{ x ≤ c} ,所以P{ X ≤ c} 0.5由 Φ(0) =0 推得c3 0, 于是 c =3.2 Φ(d3(3)P{ X d}≥ 0.9 即1)≥ 0.9 , 也就是2Φ( d 3 )≥ 0.9 Φ(1.282) ,2因分布函数是一个不减函数, 故(d 3)≥ 1.282,2解得d ≤ 3 2 ( 1.282) 0.436 .10. 设随机变量 X ~ N (2, 2) , 若 P{0 X4} 0.3 , 求 P{X 0} .解 因为X ~ N2,所以 ZX~ N(0,1). 由条件 P{0 X4} 0.3可知0.3 P{0 X4}0 2X 24 22(2P{}( )) ,于是 222 ( )10.3从而 ( )0.65 .,P{X 0}P{X202}(22 所以) 1( ) 0.35.习题 2-5 1. 选择题(1) 设 X 的分布函数为 F ( x ), 则 Y 3 X 1 的分布函数 G y 为( ).(A) F (1 1 (B)F (3 y 1) .y) .3311(C)3F ( y) 1.(D)F ( y).3 3解 由随机变量函数的分布可得 , 本题应选 (A).(2) 设X~N 01 ,令YX 2, 则Y ~().(A)N( 2, 1). (B)N(0,1) . (C) N( 2,1) . (D)N (2,1) .解 由正态分布函数的性质可知本题应选 (C).2. 设 X ~ N(1,2), Z 2X 3 , 求 Z 所服从的分布及概率密度 . 解 若随机变量 X ~ N(,2) , 则 X 的线性函数 YaX b 也服从正态分布 , 即Y aX b ~ N( a b,( a ) 2). 这里 1,2 , 所以 Z ~ N(5,8) .概率密度为1 ( x 5) 2f (z)16,x.e43. 已知随机变量 X 的分布律为X -1137P(1) 求 =2- X 的分布律; (2) 求 =3+ 2分布律 .YYX解 (1)2-X-5-1123P(2)3+X 23 41252P4. 已知随机变量 X 的概率密度为1, 1 x 4,f X ( x)=2 x ln 20,其它,且 Y =2- X , 试求 Y 的概率密度 .解 先求Y的分布函数F Y ( y):F Y ( y) = P{ Y ≤ y}P{2X ≤ y}P{X ≥2 y}2 y1 P{ X 2y} =1-f X ( x)dx.于是可得 Y 的概率密度为1, 1 2 y4,f Y ( y)f X (2y)(2 y)=2(2 y) ln 20,其它 .1, 2 y1,f Y ( y)即2(2 y) ln 20,其它 .5. 设随机变量 X 服从区间 (-2,2) 上的均匀分 布, 求随机变量 YX 2 的概率密度 .解 由题意可知随机变量 X 的概率密度为f X ( x)1 ,2 x2,40, 其它 .因为对于 0<y <4,F Y ( y) P{ Y ≤ y} P{ X 2 ≤ y} P{y ≤ X ≤ y }F X ( y ) F X ( y ) .于是随机变量YX 2 的概率密度函数为f Y ( y)1 f X ( y )11 , 0 y 4.f X ( y )y4 2 y2 yf ( y)1 , 0 y 4,即4 y0,其它 .总习题二1. 一批产品中有 20%的次品 , 现进行有放回抽样 , 共抽取 5 件样品 . 分别计算这 5 件样品中恰好有 3 件次品及至多有 3 件次品的概率 .解 以 X 表示抽取的 5 件样品中含有的次品数 . 依题意知 X ~ B(5,0.2) .(1) 恰好有 3 件次品的概率是 P X C 5 0.2 3 0.8 .{ =3}= 3 23(2) 至多有 3 件次品的概率是C 5k 0.2k 0.85 k .k 02. 一办公楼装有 5 个同类型的供水设备 . 调查表明 , 在任一时刻 t 每个设备被使用 的概率为 . 问在同一时刻(1) 恰有两个设备被使用的概率是多少? (2) 至少有 1 个设备被使用的概率是多少? (3) 至多有 3 个设备被使用的概率是多少?(4) 至少有 3 个设备被使用的概率是多少?解 以 X 表示同一时刻被使用的设备的个数,则X ~B (5,,{ = }=k k5 kP X kC 50.1 0.9, k =0,1, ,5.(1) 所求的概率是 P XC 50.1 0.90.0729 ;{ =2}=223(2)所求的概率是 P X(1 0.1)5 0.40951 ;{ ≥ 1}=1(3)所求的概率是{ ≤ 3}=1-P{ =4}- { =5}=;P XXP X(4) 所求的概率是 P { X ≥ 3}= P { X =3}+ P { X =4}+ P { X =5}=.3. 设随机变量 X 的概率密度为xkf ( x)e , x ≥0,0, x0,1且已知k θ, 求常数.,2k x解由概率密度的性质可知dx1得到 k =1.e1x1由已知条件1, 得.1 e dx2ln 24. 某产品的某一质量指标 X ~ N(160, 2 ) , 若要求 P{120 ≤X ≤ 200} ≥, 问允许最大是多少 ?解 由P{120 ≤ ≤ 200} P{ 120 160 X160 200 160X≤ ≤ }= ( 404040) (1( ))2 ( ) 1≥,( 40 ) ≥ , 40最大值为 .得到 查表得 ≥ , 由此可得允许5.设随机变量 X 的概率密度为( x ) = e -| x | , - ∞< <+∞.φX A x试求 : (1) 常数 ; (2) {0< <1}; (3)的分布函数 .AP X解 (1)由于(x)dxAe |x|dx 1, 即2 Ae x dx 1故 2A = 1, 得1到A = .2所以φ( x ) =1 e -|x |.2(2) P {0< X <1} = 11 xdx1 ( e x 11 e 10.316.e2 ) 220 (3)因为 F ( x)x1 e |x| 得到2 dx,11当 x <0 时 , F ( x)x x x ,2 e dx 2e当 x ≥0 时,F ( x)1 0x1 xe x1 x,2e dx2dx 1 e21e x ,x0,所以 X 的分布函数为F ( x)21 ex,1 x ≥ 0.2。
第二章 习题

第二章 化学反应的基本原理一、判断题(正确请画“√”,错误的画“×”)1.当温度接近0K 时,所有放热反应可以认为都是自发进行的反应。
解:对。
根据吉布斯赫姆赫磁公式ΔG = Δ H – T ΔS 判断。
2.△S>0的反应,必定是自发反应。
解:错,不能判断,因为△S 作判据只适用于孤立系统中。
3.对于一个定温反应,如果△H>△G ,则该反应必定是熵增的反应。
解:对。
根据吉布斯赫姆赫磁公式ΔG = Δ H – T ΔS 判断。
则ΔS = (Δ H –ΔG )/T4.△G θ值大,平衡常数K θ值就愈大。
解:错。
ln K θ (T ) = - Δ r G m θ (T )/RT 。
需要考虑温度。
5.平衡常数K 值越大,则反应速度越快。
解:错。
平衡常数K 值是热力学问题,而反应速度是动力学问题6.对于△H<0的反应,提高温度,速度常数k 值减小。
解 错7.对于△H θ>0的可逆反应,提高温度,平衡常数K θ值增大。
解:对。
ln K θ (T ) = - ΔH θ /RT +△S θ/R8.NO 的△f G θm (298.15K )>0,空气中的N 2和O 2在常温常压下稳定共存。
但在高温常压时能发生反应,说明该反应是△H θ>0, △S θ>0的反应。
RTE aAe k -=解:对。
低温稳定,即不反应,高温不稳定,说明反应是△H θ>0,△S θ>0的反应。
ΔG = Δ H – T ΔS9.反应CO (g )=C (s )+1/2O 2(g )的△G>0,正向非自发,加入催化剂后降低了活化能,则反应正向进行。
解:错,催化剂不能改变反应方向。
10.在一个封闭系统中进行的可逆反应达到平衡后,若平衡体积和温度不变,则系统中各组分的的浓度和分压不变。
解:对,平衡状态下各组分浓度不变。
11.一定温度下,△v g =0的可逆反应达到平衡后,改变系统中某组分的浓度或分压,平衡不移动。
生理学第二章细胞基本功能的习题及答案.doc

第一章细胞的基本功能【习题】一、名词解释1.易化扩散2.阈强度3.阈电位4.局部反应二、填空题1.物质跨越细胞膜被动转运的主要方式有_______和_______。
2.一些无机盐离子在细胞膜上_______的帮助下,顺电化学梯度进行跨膜转动。
3.单纯扩散时,随浓度差增加,扩散速度_______。
4.通过单纯扩散方式进行转动的物质可溶于_______。
5.影响离子通过细胞膜进行被动转运的因素有_______,_______和_______。
6.协同转运的特点是伴随_______的转运而转运其他物质,两者共同用同一个_______。
7.易化扩散必须依靠一个中间物即_______的帮助,它与主动转运的不同在于它只能浓度梯度扩散。
8.蛋白质、脂肪等大分子物质进出细胞的转动方式是_______和_______。
9.O2和CO2通过红细胞膜的方式是_______;神经末梢释放递质的过程属于。
10.正常状态下细胞内K+浓度_______细胞外,细胞外Na+浓度_______细胞内。
11.刺激作用可兴奋细胞,如神经纤维,使之细胞膜去极化达_______水平,继而出现细胞膜上_______的爆发性开放,形成动作电位的_______。
12.人为减少可兴奋细胞外液中_______的浓度,将导致动作电位上升幅度减少。
13.可兴奋细胞安静时细胞膜对_______的通透性较大,此时细胞膜上相关的_______处于开放状态。
14.单一细胞上动作电位的特点表现为_______和_______。
15.衡量组织兴奋性常用的指标是阈值,阈值越高则表示兴奋性_______。
16.细胞膜上的钠离子通道蛋白具有三种功能状态,即_______,_______和_______。
17.神经纤维上动作电位扩布的机制是通过_______实现的。
18.骨骼肌进行收缩和舒张的基本功能单位是_______。
当骨骼肌细胞收缩时,暗带长度,明带长度_______,H带_______。
第二章习题及答案

第⼆章习题及答案第⼆章习题及答案化⼯原理练习题五.计算题1. 密度为1200kg.m的盐⽔,以25m3.h-1的流量流过内径为75mm的⽆缝钢管。
两液⾯间的垂直距离为25m,钢管总长为120m,管件、阀门等的局部阻⼒为钢管阻⼒的25%。
试求泵的轴功率。
假设:(1)摩擦系数λ=0.03;(2)泵的效率η=0.61.答案*****Z1+u2/2g+P1/ρg+He=Z2+u2/2g+P2/ρg+∑H fZ=0,Z=25m,u≈0,u≈0,P=P∴H=Z+∑H=25+∑H∑H=(λ×l/d×u/2g)×1.25u=V/A=25/(3600×0.785×(0.07 5))=1.573m.s∑H=(0.03×120/0.075×1.573/(2×9.81)×1.25=7.567m盐⽔柱H=25+7.567=32.567mN=Q Hρ/102=25×32.567×120 0/(3600×102)=2.66kwN轴=N/η=2.66/0.6=4.43kw2.(16分)如图的输⽔系统。
已知管内径为d=50mm, 在阀门全开时输送系统的Σ(l+le ) =50m,摩擦系数可取λ=0.03,泵的性能曲线,在流量为6 m3.h-1⾄15 m3.h-1范围内可⽤下式描述: H=18.92-0.82Q2.,此处H为泵的扬程m,Q为泵的流量m3.h-1,问:(1)如要求流量为10 m3.h-1,单位质量的⽔所需外加功为多少? 单位重量的⽔所需外加功为多少?此泵能否完成任务? (2)如要求输送量减⾄8 m3.h-1 (通过关⼩阀门来达到),泵的轴功率减少百分之多少?(设泵的效率变化忽略不计)答案*****⑴u=10/(3600×0.785×0.05)=1.415[m.s-1]Σhf =λ[Σ(l+le )/d](u2/2)=0.03×(50/0.05)(1.4152/2)=30.03Pa/ρ+W=Pa/ρ+Z g+Σhf 1 - 2W=Z2g+Σhf 1 - 2 =10×9.81+30.03=128.13 [J.kg]H需要=W/g=128.13/9.81=13.06[m]⽽H泵=18.92-0.82(10)=13.746[m]H泵>H需故泵可⽤⑵N=H泵Q泵ρg/ηρg/η=常数∴N∝H泵Q泵N前∝13.746×10H泵后=18.92-0.82(8)0 . 8 =14.59N后∝14.59×8N后/N前=14.59×8/(13.746×10)=0.849(N前-N后)/N前=1-0.849≈15.1%3. 如图3B57离⼼泵将20℃的⽔由敞⼝⽔池送到⼀压⼒为2.5at的塔内,管径为φ108×4mm管路全长100m(包括局部阻⼒的当量长度,管的进、出⼝当量长度也包括在内)。
(完整版)第二章习题参考答案(5版)

第二章运算方法和运算器习题参考答案1. 写出下列各数的原码、反码、补码、移码表示(用8位二进制数)。
其中MSB是最高位(又是符号位)LSB是最低位。
如果是小数,小数点在MSB之后;如果是整数,小数点在LSB之后。
(1) -35 (2) 128 (3) -127 ( 4) -1解:(1)先把十进制数-35/64写成二进制小数:(注意位数为8位)x=(-35)10=(-100011)2[x]原=10100011 [x]反=11011100[x]补=11011101(2) 128写成二进制小数:x=(128)10=(10000000)2[x]原=10000000 [x]反=10000000[x]补=10000000(3) 先把十进制数-127写成二进制小数:x=(-127)10=(-1111111)2[x]原=11111111 [x]反=10000000 [x]补=10000001(4) 令Y=-1=-0000001B[Y]原=10000001 [Y]反=11111110[Y]补=111111112. 设[X]补= a7,a6,a5…a0 , 其中a i取0或1,若要x>-0.5,求a0,a1,a2,…,a6 的取值。
解:若a7= 0,则:x>0, 所以:a1= 0,a2,…,a6任意;若a7= 1,则:a1= 1,a2,…,a6 不全为0。
3. 有一个字长为32位的浮点数,符号位1位,阶码8位,用移码表示;尾数23位(包括1位尾符)用补码表示,基数R=2。
请写出:(1) 最大数的二进制表示;(2) 最小数的二进制表示;(3) 规格化数所能表示的数的范围;解:(1) 111111111 0 111111111111111111111(2)111111111 1000000000000000000000(3)111111111 0111111111111111111111~011111111 1000000000000000000000(4)000000000 00000000000000000000001~000000000 111111111111111111111114. 将下列十进制数表示成浮点规格化数,阶码3位,用补码表示;尾数9位,用补码表示。
第二章课后习题与答案

第2章人工智能与知识工程初步1. 设有如下语句,请用相应的谓词公式分别把他们表示出来:s(1)有的人喜欢梅花,有的人喜欢菊花,有的人既喜欢梅花又喜欢菊花。
解:定义谓词dP(x):x是人L(x,y):x喜欢y其中,y的个体域是{梅花,菊花}。
将知识用谓词表示为:(∃x )(P(x)→L(x, 梅花)∨L(x, 菊花)∨L(x, 梅花)∧L(x, 菊花))(2)有人每天下午都去打篮球。
解:定义谓词P(x):x是人B(x):x打篮球A(y):y是下午将知识用谓词表示为:a(∃x )(∀y) (A(y)→B(x)∧P(x))(3)新型计算机速度又快,存储容量又大。
解:定义谓词NC(x):x是新型计算机F(x):x速度快B(x):x容量大将知识用谓词表示为:(∀x) (NC(x)→F(x)∧B(x))(4)不是每个计算机系的学生都喜欢在计算机上编程序。
解:定义谓词S(x):x是计算机系学生L(x, pragramming):x喜欢编程序U(x,computer):x使用计算机将知识用谓词表示为:¬(∀x) (S(x)→L(x, pragramming)∧U(x,computer))(5)凡是喜欢编程序的人都喜欢计算机。
解:定义谓词P(x):x是人L(x, y):x喜欢y将知识用谓词表示为:(∀x) (P(x)∧L(x,pragramming)→L(x, computer))2请对下列命题分别写出它们的语义网络: (1) 每个学生都有一台计算机。
解:(2) 高老师从3月到7月给计算机系学生讲《计算机网络》课。
解:(3) 学习班的学员有男、有女、有研究生、有本科生。
解:参例2.14(4) 创新公司在科海大街56号,刘洋是该公司的经理,他32岁、硕士学位。
解:参例2.10(5) 红队与蓝队进行足球比赛,最后以3:2的比分结束。
解:2.19 请把下列命题用一个语义网络表示出来: (1) 树和草都是植物; 解:(2) 树和草都有叶和根; 解:(3) 水草是草,且生长在水中; 解:(4) 果树是树,且会结果; 解:(5) 梨树是果树中的一种,它会结梨。
试题库——教材课后习题及答案(第二章)

第二章一、填空1、在室温附近,温度每升高1°С,二极管导通正向压降on U 约 减小2~2.5 mV 。
温度每升高10°С,反向电流约 增大一倍 。
2、最大整流电流F I 定义为二极管 长期运行允许通过的最大正向平均 电流。
3、最高反向工作电压RM U 是允许施加在二极管两端的 最大反向电压 。
通常规定为反向击穿电压BR U 的 一半 。
4、理想二极管模型是将二极管看作一个 开关 ,加正向电压 导通 ,导通时正向压降为零 ;加反向电压 截止 ,截止时 电流 为零。
5、二极管正向电阻越 小 ,反向电阻越 大 ,表明 单向导电特性 好。
若正反向电阻均趋于0,表明二极管 击穿损坏 。
若正反向电阻均趋于无穷大,表明二极管 开路损坏 。
6、稳压管的反向击穿特性很 陡 ,反相击穿时,电流虽然在很大范围内变化,但稳压管的 电压 变化却很小。
7、稳压管处于稳压工作时电压特性应 反 偏,并应有合适的工作 电流 。
8、稳压管是通过自身的 电流 调节作用,并通过限流电阻R ,转化为 电压 调节作用,从而达到稳定电压的目的。
二、选择题1、反映二极管质量的参数是 C 。
A 、最大整流电流F IB 、最高反向工作电压RM UC 、反向饱和电流S ID 、最高工作频率M f2、温度升高后,二极管正向压降将 B ,反向电流将 A 。
A 、增大 B 、减小 C 、不变 D 、不定3、硅二极管与锗二极管相比,一般情况,反向电流较 B ,正向压降较 A 。
A 、大 B 、小 C 、不定 D 、相等4、稳压二极管构成的稳压电路,其接法是 。
A 、稳压二极管与负载电阻串联B 、稳压二极管与负载电阻并联C 、限流调整电阻与稳压二极管串联后,负载电阻再与稳压二极管并联。
5、单相半波整流电路中,负载电阻L R 上平均电压等于 B 。
A 、0.92V B 、0.452V C 、12V6、单相桥式或全波整流电路,电容滤波后,负载电阻L R 上平均电压等于 B 。
第二章练习题附答案

一、单项选择题1、( D )不是内部招募的优点。
P69(A )激励性强(B )适应较快(C )准确性高(D )费用较高2、布告法经常用于非管理层人员的招聘,特别适合于(C )的招聘。
(A)销售人员(B)技术人员(C)普通职员(D)高层人员3、经常用于非管理人员招聘的员工招募方法是(B )。
P74(A)推荐法(B)布告法(C)档案法(D)任命法4、关于发布广告,描述不正确的是(A )。
P75(A)广告是内部招募最常用的方法之一(B)有广泛的宣传效果.可以展示单位实力(C)发布广告要注重广告媒体的选择和广告内容的设计(D)工作空缺的信息发布迅速.能够在一两天内就传达给外界5、对于高级人才和尖端人才,比较适合的招聘渠道是(B )。
P76(A )人才交流中心(B )猎头公司(C )校园招聘(D )网络招聘P74 P746、在以下招聘方式中,成本最高的是(D )。
P76(A )发布广告(B )网络招聘(C )校园招聘(D )猎头推荐P76 7、企业招聘大批的初级技术人员,最适合的招聘渠道是(A )。
(A)校园招聘(B)猎头公司(C)熟人推荐(D)档案筛选8、可能在组织中形成裙带关系的员工招募方法是(D )。
P77(A )校园招募(B )借助中介(C)猎头公司(D)熟人推介9、筛选简历时,应更多地关注(D )。
P79(A)学习成绩(B)管理能力(C)主观内容(D)客观内容10、在费用和时间允许的情况下,对应聘者的初选工作应坚持(D )。
P81(A )细选原则(B )精选原则(C )重点原则(D )面广原则11、面试不能够考核应聘者的(D )。
P81(A )交流能力(B )风度气质(C )衣着外貌(D )科研能力12、在面试过程中,考官不应该(C )。
P82(A )创造融洽的气氛(B )让应聘者了解单位的现实状况(C )决定应聘者是否被录用(D )了解应聘者的知识技能和非智力素质13、面试的开始阶段应从(D )发问,从而营造和谐的面试气氛。
第二章 习题及答案

第二章 金属切削原理与刀具班级_____________ 学号____________姓名_____________ 成绩____________一、 选择题:1、车削细长轴时,车刀的主偏角应取[ D ]A 、30ºB 、45ºC 、60 ºD 、90 º2、粗车时,选择切削用量的顺序是[ B ]A 、f v a c p →→B 、c p v f a →→C 、c p v a f →→D 、f a v p c →→3、车细长轴时,为防止工件产生弯曲和振动,应尽量减少[ D ]A 、轴向力B 、前角C 、主偏角D 、径向力4、积屑瘤对粗加工有利的原因是[ A ]A 、保护刀具、增加实际前角B 、积屑瘤硬度高C 、提高加工表面质量D 、加大切削深度5、增加一般外圆粗车刀的刀刃的抗冲击能力的角度是[ B ]A 、大主偏角B 、负刃倾角C 、正刃倾角D 、大后角6、车削加工中影响已加工表面残留面积大小的主要因素是[ B ]A 、切削速度c vB 、进给量fC 、背吃刀量p aD 、工件转速n7、降低切削温度最有效的措施是[ A ]A 、浇注切削液B 、增大刀尖圆角半径C 、增大主偏角D 、适当增大前角8、与高速钢刀具的耐热性相比,硬质合金刀具的耐热性[ C ]A 、较低B 、相等C 、较高D 、不确定9、当刀尖是主切削刃上最低点时,刃倾角为[ A ]A 、负B 、零C 、正D 、不确定10、纵向走刀车外圆时消耗功率最大的力是[ A ]A 、切向力B 、径向力C 、轴向力D 、不确定11、车外圆时,若刀尖低于工件中心,则将增大的工作角度是[ B ]A 、前角B 、后角C 、主偏角D 、副偏角12、YG 类硬质合金刀具主要用于加工[ D ]A 、陶瓷B 、金刚石C 、钢D 、铸铁13、在切削平面中测量的主切削刃与基面之间的夹角是[ D ]A 、前角B 、后角C 、主偏角D 、刃倾角14、YT 类硬质合金刀具主要用于加工[ A ]A 、钢B 、铸铁C 、陶瓷D 、金刚石二、判断题1、积屑瘤使刀具的实际前角增大,并使切削轻快省力,所以对精加工有利。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章总论习题及答案一、单项选择题1、凡是当期已经实现的收入和已经发生的或应当负担的费用,无论款项是否收付,都应当作为当期的收入和费用,计入利润表的会计核算基础或要求的是()。
A、相关性B、收付实现制C、权责发生制D、及时性2、下列对会计基本假设的表述中恰当的是()。
A、在会计分期的前提下,会计确认、计量和报告应该以企业持续、正常的生产经营活动为前提B、一个会计主体必然是一个法律主体C、持续经营确定了会计核算的空间范围D、会计分期确立了会计核算的时间范围3、以下关于财务报告的说法中不正确的是()。
A、财务报告是企业对外提供的反映企业某一特定日期的财务状况和某一会计期间经营成果、现金流量等会计信息的文件B、财务报告是对外报告C、财务报告必须是一个系统的文件D、财务报告只提供给企业的投资者使用4、企业的资产按取得时的实际成本计价,这满足了()会计信息质量要求。
A、可靠性B、明晰性C、历史成本D、相关性5、从会计信息成本效益看,对所有会计事项应采取分轻重主次和繁简详略进行会计核算,而不应采用完全相同的会计程序和处理方法。
其体现的会计信息质量要求是()。
A、谨慎性B、可比性C、相关性D、重要性6、如果企业资产按照现在购买相同或者相似资产所需支付的现金或者现金等价物的金额计量,负债按照现在偿付该项债务所需支付的现金或者现金等价物的金额计量,则其所采用的会计计量属性为()。
A、可变现净值B、重置成本C、现值D、公允价值7、如果企业资产按照购买时所付出对价的公允价值计量,负债按照日常活动中为偿还负债预期需要支付的现金或者现金等价物的金额计量,则其所采用的会计计量属性为()。
A、公允价值B、历史成本C、现值D、可变现净值8、下列计价方法中,未采用历史成本计量属性的是()。
A、发出存货计价所使用的个别计价法B、期末存货计价所使用的可变现净值法(即成本与可变现净值孰低法)C、发出存货计价所使用的先进先出法D、发出存货计价所使用的移动加权平均法9、某公司的下列会计行为中,符合会计核算重要性原则的是()。
A、本期将购买办公用品的支出直接记入当期费用B、期末按照实际利率法确认持有至到期投资的应计利息C、每一中期末都要对外提供中期报告D、按固定期间对外提交财务报告10、下列各项中,不属于反映会计信息质量要求的是()。
A、会计核算方法一经确定不得随意变更B、会计核算应当注重交易或事项的实质C、会计核算应当以实际发生的交易或事项为依据D、会计核算应当以权责发生制为基础11、企业对于已经发生的交易或者事项,应当及时进行会计确认、计量和报告,不得提前或者延后,这体现的是()。
A、及时性B、相关性C、谨慎性D、重要性12、企业提供的会计信息应当清晰明了,便于财务会计报告使用者理解和使用。
这体现的是()。
A、相关性要求B、可靠性要求C、及时性要求D、可理解性要求13、企业提供的会计信息应有助于财务会计报告使用者对企业过去、现在或者未来的情况作出评价或者预测,这体现了会计核算质量要求的是()。
A、相关性B、可靠性C、可理解性D、可比性14、强调不同企业发生的相同或者相似的交易或者事项,应当采用规定的会计政策,确保会计信息口径一致的会计信息质量要求是()。
A、可靠性B、可理解性C、及时性D、可比性15、会计准则规定,上市公司的下列行为中,违反会计信息质量可比性要求的是()。
A、根据企业会计准则的要求,将所得税会计由应付税款法改为资产负债表债务法B、将已达到预定可使用状态的工程借款的利息支出予以费用化C、由于被投资方发生了重大亏损,将对该被投资方的股权投资由权益法改按成本法核算D、企业有确凿证据表明可以采用公允价值模式计量的投资性房地产,由按成本模式计量改为按公允价值模式计量16、非货币性资产交换的会计处理体现了()要求。
A、实质重于形式B、重要性C、相关性D、谨慎性17、下列说法中,体现了实质重于形式要求的是()。
A、对融资租入的固定资产视同自有固定资产核算B、发出存货的计价方法一经确定,不得随意改变,如有变更需在财务报告中说明C、对有的资产、负债采用公允价值计量D、期末对存货采用成本与可变现净值孰低法计价18、下列做法中,不符合会计实质重于形式要求的是()。
A、企业对售后租回固定资产收入的确认B、企业融资租入的固定资产作为企业自己的资产核算C、固定资产按期计提折旧D、关联方关系的确定19、期末存货采用成本与可变现净值孰低计价,其所体现的会计信息质量要求是()。
A、及时性B、相关性C、谨慎性D、重要性20、以下各项符合谨慎性要求的做法是()。
A、按照成本与可变现净值孰低法,应计提存货跌价准备400万元,实际计提400万元B、期末未决诉讼可能导致赔偿,将或有负债500万元列入资产负债表C、期末未决诉讼很可能导致赔偿200万元,确认预计负债100万元列入资产负债表D、按照成本与可变现净值孰低法,应计提存货跌价准备100万元,考虑当期利润较低实际计提跌价准备50万元21、甲公司对有关事项的会计处理如下:(1)2007年初因执行新企业会计准则,甲公司将发出存货成本的计价方法由后进先出法改为加权平均法,并采用成本与可变现净值孰低法对存货进行期末计量。
(2)因公允价值能够可靠计量,2009年初将作为投资性房地产核算的经营租出办公楼的后续计量由成本模式改为公允价值模式。
(3)2009年12月融资租入的一台大型生产设备,视为自有固定资产进行管理和核算,预计使用年限为10年,采用年限平均法计提折旧。
2011年由于市场上出现更先进的同类设备,因此,甲公司将该设备的折旧方法由年限平均法改为年数总和法。
(4)拥有C公司20%的有表决权股份,对C公司有重大影响,预计C公司2010年将发生重大亏损,2010年初甲公司将对C公司长期股权投资的后续计量由权益法改为成本法。
(5)2011年3月1日预收一笔购货款,由于甲公司预收账款业务不多,没有设置预收账款账户,所以将收到的预收款计入应收账款账户的贷方。
要求:根据上述资料,不考虑其他因素,回答下列各题。
<1>、下列关于甲公司会计处理说法中,不正确的是()。
A、对存货期末计价采用成本与可变现净值孰低法计量体现了会计信息质量谨慎性要求B、因C公司将发生重大亏损,将对C公司的长期股权投资由权益法改为成本法符合会计信息质量可比性要求C、对融资租入的固定资产采用年数总和法计提折旧符合会计信息质量谨慎性要求D、将预收款计入应收账款核算体现了会计信息质量重要性要求<2>、下列项目中,违背会计信息质量可比性要求的是()。
A、因预计发生年度亏损,将以前年度计提的坏账准备全部予以转回B、企业有确凿证据表明可以采用公允价值模式计量的投资性房地产,由成本模式计量改为公允价值模式计量C、对于无法合理分割土地使用权与地上建筑物的自用房地产,企业应统一在固定资产中核算D、由于固定资产购建完成并达到预定可使用状态,将借款费用由资本化变为费用化核算<3>、甲公司的下列会计处理中,符合会计信息质量实质重于形式要求的是()。
A、将发出存货成本的计价方法由后进先出法改为加权平均法B、将投资性房地产的后续计量由成本模式改为公允价值模式C、融资租入固定资产作为自有固定资产核算D、将固定资产的折旧方法由年限平均法改为年数总和法22、甲公司为一般纳税人,主要经营冬季羽绒服的生产和销售,2×10年9月份有关资料如下:(1)为应对即将到来的销售高峰,甲公司急需一批资金用于购置机器设备以扩大生产,但因资金不足,甲公司于9月15日与乙租赁公司签订一项融资租赁合同,并将该融资租入设备确认为一项固定资产,视同自有资产核算。
(2)对于上述融资租入的机器设备,甲公司从10月份开始采用直线法计提折旧,预计使用年限为5年。
2×12年的随着市场竞争的加剧,该设备预期能够带来的经济利益流入大幅下降。
甲公司期末对其计提了相应的减值准备。
要求:根据上述资料,不考虑其他因素,回答下列问题:<1>、根据资料(1),甲公司对融资租赁固定资产的会计处理,体现了()。
A、实质重于形式要求B、重要性要求C、谨慎性要求D、可靠性要求<2>、根据资料(2),甲公司对融资租入设备计提减值准备,体现了()。
A、实质重于形式要求B、重要性要求C、谨慎性要求D、可靠性要求23、下列各项中体现了相关性原则的是()。
A、投资性房地产采用公允价值模式进行后续计量B、企业对外提供年度财务报告时没有相应的披露日后期间发生的巨额亏损C、对于融资租入资产作为自有资产予以管理D、企业在年中(非资产负债表日)发生了重大的合并事项而对外提供财务报告24、以下没有体现可比性原则的是()。
A、对于会计政策变更采用追溯调整法B、对于重要的前期差错采用追溯重述法C、某企业因2009年发放股票股利而重新计算2008年的每股收益D、为了保持前后一致在投资性房地产满足了公允价值计量模式的情况下仍然采用成本模式进行后续计量25、以下体现谨慎性原则的是()。
A、会计小王为了给老总留下足够的招待费用而私设小金库B、会计小王根据以往的情况预计下半年为销售旺季为此提前确认了一部分收入C、公司在一项诉讼中认为很可能败诉赔偿100万元,会计小王认为虽然法院没有判决但是满足了预计负债的确认条件而确认了100万元的预计负债D、会计小王考虑谨慎性原则为了不高估资产将企业内部研发成功的无形资产发生所有支出予以费用化二、多项选择题1、下列有关会计主体的说法中正确的有()。
A、法律主体一定是会计主体B、基金管理公司管理的证券投资基金,也可以成为会计主体C、对于拥有子公司的母公司来说,企业集团应作为一个会计主体来编制财务报表D、会计主体一定是法律主体E、分公司和子公司一样都是法律主体,也是会计主体2、以下体现实质重于形式原则的有()。
A、附追索权的商业承兑汇票贴现B、合并报表中关于购买少数股权产生现金流量的说法C、合并报表的编制D、对赊销的商品,出于对方财务状况恶化的原因而没有确认收入3、按照企业会计准则的规定,上市公司的下列行为中,不违反会计信息质量可比性要求的有()。
A、应收某企业货款100万元,鉴于该企业财务状况恶化,有证据表明该货款全部无法收回,本期对应收该企业的账款改按100%提取坏账准备B、根据企业会计准则的要求,将所得税会计由应付税款法改为资产负债表债务法C、将已达到预定可使用状态的工程借款的利息支出予以费用化D、根据企业会计准则的要求,将对子公司的股权投资由权益法改按成本法核算E、企业有确凿证据表明可以采用公允价值模式计量的投资性房地产,由按成本模式计量改为按公允价值模式计量4、我国企业财务报告的目标是向()提供与企业财务状况、经营成果和现金流量等有关的会计信息,反映企业管理层受托责任履行情况,有助于财务报告使用者作出经营决策。
