2020 人教版 九年级 圆专题复习练习题(有部分答案)
人教版2020年中考数学一轮复习《与圆有关的证明和计算》大题专项练习含答案解析

中考专题——与圆有关的证明和计算纵观近几年全国各地中考题,圆的有关概念以及性质等一般以填空题,选择题的形式考查并占有一定的分值;圆的有关性质,如垂径定理,圆周角,切线的判定与性质等综合性问题的运用一般以计算证明的形式考查;一般在10分-15分左右,以后发展中利用圆的知识与其他知识点如函数,方程等相结合作为中考压轴题将会占有非常重要的地位。
考查的类型:(1)线段、角以及切线的证明;(2)利用勾股定理、相似以及锐角三角函数进行线段,比值和阴影面积的求解.例题精讲:1、如图,点O为Rt△ABC斜边AB上一点,以OA为半径的⊙O与BC切于点D,与AC 交于点E,连接AD.(1)求证:AD平分∠BAC;(2)若∠BAC=60°,OA=2,求阴影部分的面积(结果保留π).2、如图,A,P,B,C是圆上的四个点,∠APC=∠CPB=60°,AP,CB的延长线相交于点D.(1)求证:△ABC是等边三角形;(2)若∠PAC=90°,AB=2,求PD的长.3、如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E,(1)求证:DE=DB;(2)若∠BAC=90°,BD=4,求△ABC外接圆的半径.4、如图,△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于点D,OB与⊙O相交于点E.(1)求证:AC是⊙O的切线;(2)若BD=,BE=1.求阴影部分的面积.5、如图,AB是⊙O的直径,C是⊙O上一点,过点O作OD⊥AB,交BC的延长线于D,交AC于点E,F是DE的中点,连接CF.(1)求证:CF是⊙O的切线.(2)若∠A=22.5°,求证:AC=DC.补充练习:1、如图,在△ABC中,AB=AC,以AB为直径作⊙O,分别交BC,AC于点D,E,过点D作DF⊥AC于点F.(1)求证:DF是⊙O的切线;(2)若∠C=60°,⊙O的半径为2,求由弧DE,线段DF,EF围成的阴影部分的面积(结果保留根号和π)2、如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E.(1)求证:AD平分∠BAC;(2)若CD=1,求图中阴影部分的面积(结果保留π).3、如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为F,连接DE.(1)求证:直线DF与⊙O相切;(2)若AE=7,BC=6,求AC的长.4、如图,AB为半圆O的直径,AC是⊙O的一条弦,D为的中点,作DE⊥AC,交AB 的延长线于点F,连接DA.(1)求证:EF为半圆O的切线;(2)若DA=DF=6,求阴影区域的面积.(结果保留根号和π)5、如图所示,以△ABC的边AB为直径作⊙O,点C在⊙O上,BD是⊙O的弦,∠A=∠CBD,过点C作CF⊥AB于点F,交BD于点G,过C作CE∥BD交AB的延长线于点E.(1)判断CE与⊙O的位置关系,并说明理由;(2)若∠DBA=30°,CG=8,求BE的长.6、如图,AB为⊙O的直径,C,E为⊙O上的两点,若AC平分∠EAB,CD⊥AE于点D.(1)求证:DC是⊙O的切线;3,求DE的长;(2)若AO=6,DC=33,求图中阴影部分面积.(3)过点C作CF⊥AB于F,如图2,若AD-OA=1.5,AC=3答案解析例题精讲:1、(1)证明:∵⊙O切BC于D,∴OD⊥BC,∵AC⊥BC,∴AC∥OD,∴∠CAD=∠ADO,∵OA=OD,∴∠OAD=∠ADO,∴∠OAD=∠CAD,即AD平分∠CAB;(2)设EO与AD交于点M,连接ED.∵∠BAC=60°,OA=OE,∴∠AEO是等边三角形,∴AE=OA,∠AOE=60°,∴AE=A0=OD,又由(1)知,AC∥OD即AE∥OD,∴四边形AEDO是菱形,则△AEM≌△DMO,∠EOD=60°,∴S△AEM=S△DMO,∴S阴影=S扇形EOD==.2、(1)证明:∵∵ABC=∵APC,∵BAC=∵BPC,∵APC=∵CPB=60°,∵∵ABC=∵BAC=60°,∵∵ABC是等边三角形.(2)解:∵∵ABC是等边三角形,AB=2,∵AC=BC=AB=2,∵ACB=60°.在Rt∵PAC中,∵PAC=90°,∵APC=60°,AC=2,∵AP=AC•cot∵APC=2.在Rt∵DAC中,∵DAC=90°,AC=2,∵ACD=60°,∵AD=AC•tan∵ACD=6.∵PD=AD﹣AP=6﹣2=4.3、(1)证明:∵BE平分∠BAC,AD平分∠ABC,∴∠ABE=∠CBE,∠BAE=∠CAD,∴,∴∠DBC=∠CAD,∴∠DBC=∠BAE,∵∠DBE=∠CBE+∠DBC,∠DEB=∠ABE+∠BAE,∴∠DBE=∠DEB,∴DE=DB;(2)解:连接CD,如图所示:由(1)得:,∴CD=BD=4,∵∠BAC=90°,∴BC是直径,∴∠BDC=90°,∴BC==4,∴△ABC外接圆的半径=×4=2.4、(1)证明:连接OD,作OF⊥AC于F,如图,∵△ABC为等腰三角形,O是底边BC的中点,∴AO⊥BC,AO平分∠BAC,∵AB与⊙O相切于点D,∴OD⊥AB,∵OF⊥AC,∴OF=OD,∴AC是⊙O的切线;(2)解:在Rt△BOD中,设⊙O的半径为r,则OD=OE=r,∴r2+()2=(r+1)2,解得r=1,∴OD=1,OB=2,∴∠B=30°,∠BOD=60°,∴∠AOD=30°,在Rt△AOD中,AD=OD=,∴阴影部分的面积=2S△AOD﹣S扇形DOF=2××1×﹣=﹣.5、(1)证明:∵AB 是⊙O 的直径,∴∠ACB =∠ACD =90°,∵点F 是ED 的中点,∴CF =EF =DF ,∴∠AEO =∠FEC =∠FCE ,∵OA =OC ,∴∠OCA =∠OAC ,∵OD ⊥AB ,∴∠OAC+∠AEO =90°, ∴∠OCA+∠FCE =90°,即OC ⊥FC ,∴CF 与⊙O 相切;(2)解:∵OD ⊥AB ,AC ⊥BD ,∴∠AOE =∠ACD =90°,∵∠AEO =∠DEC ,∴∠OAE =∠CDE =22.5°, ∵AO =BO ,∴AD =BD ,∴∠ADO =∠BDO =22.5°,∴∠ADB =45°,∴∠CAD =∠ADC =45°,∴AC =CD .补充练习:1、(1)如图,连接OD ∵AB 为⊙O 的直径∴AD ⊥BC ∵AB=AC ∴BD=CD ,D 为BC 中点∵O 为AB 中点∴OD ∥AC ∵DF ⊥AC ∴DF ⊥OD ∴DF 为⊙O 的切线(2)如图,连接OE 、OD ∵AB=AC ,∠C=60°∴△ABC 为等边三角形∴∠B=∠A=60°,AB=AC=BC=2⨯2=4∵OA=OB=OD=OE ∴△OAE ,△OBD 都是等边三角形∴∠ODB=∠BOD=∠AOE -∠OEA=∠C=60° ∴∠DOE=180°-2⨯60°=60°,OD ∥AC ,OE ∥BC ∴四边形ODCE 是平行四边形∴OD=CE=BD=CD=2∴DF=CDsin60°=3232=⨯,CF=CDcos60°=1212=⨯ ∴ππ32-323360260-3121-32--2=⨯⨯⨯⨯==∆ODE CDF S S S S 扇形平行四边形阴影2、(1)证明:连接DE 、OD ∵BC 相切⊙O 于点D ∴∠CDA=∠AED ∵AE 为直径∴∠ADE=90°∵AC ⊥BC ∴∠ACD=90°∴∠DAO=∠CAD ∴AD 平分∠BAC(3)在Rt △ABC 中,∠C=90°,AC=BC ∴∠B=∠BAC=45°∵BC 相切⊙O 于点D ∴∠ODB=90°∴OD=BD ,∠BOD=45°设BD=x ,则OD=OA=x ,0B=3x ∴BC=AC=x+1∵AC 2+BC 2=AB 2∴22)2()12x x x +=+( 所以x=2∴BD=OD=2 ∴()4-1360245-22212ππ=⨯⨯=-∆=DOE S BOD S S 扇形阴影3、(1)证明:连接OD ,∵AB=AC ,∴∠B=∠C 。
2020年九年级中考数学复习专题训练:《圆的综合 》(含答案)

2020年九年级中考数学复习专题训练:《圆的综合》1.如图,在Rt△ACB中,∠ACB=90°,以AC为直径作⊙O,交AB于点D.(1)若AB=8,∠ABC=30°,求⊙O的半径;(2)若点E是边BC的中点,连结DE,求证:直线DE是⊙O的切线;(3)在(1)的条件下,保持Rt△ACB不动,将⊙O沿直线BC向右平移m个单位长度后得到⊙O′,当⊙O′与直线AB相切时,m=.2.如图,矩形ABCD中,AB=13,AD=6.点E是CD上的动点,以AE为直径的⊙O与AB交于点F,过点F作FG⊥BE于点G.(1)当E是CD的中点时:tan∠EAB的值为;(2)在(1)的条件下,证明:FG是⊙O的切线;(3)试探究:BE能否与⊙O相切?若能,求出此时BE的长;若不能,请说明理由.3.如图,已知正方形ABCD 的边长为1,正方形BEFG 中,点E 在AB 的延长线上,点G 在BC 上,点O 在线段AB 上,且AO ≥BO .以OF 为半径的⊙O 与直线AB 交于点M ,N . (1)如图1,若点O 为AB 中点,且点D ,点C 都在⊙O 上,求正方形BEFG 的边长. (2)如图2,若点C 在⊙O 上,求证:以线段OE 和EF 为邻边的矩形的面积为定值,并求出这个定值.(3)如图3,若点D 在⊙O 上,求证:DO ⊥FO .4.如图,四边形ABCD 内接于⊙O ,AC 为直径,AC 和BD 交于点E ,AB =BC . (1)求∠ADB 的度数;(2)过B 作AD 的平行线,交AC 于F ,试判断线段EA ,CF ,EF 之间满足的等量关系,并说明理由;(3)在(2)条件下过E ,F 分别作AB ,BC 的垂线,垂足分别为G ,H ,连接GH ,交BO 于M ,若AG =3,S 四边形AGMO :S 四边形CHMO =8:9,求⊙O 的半径.5.定义:当点P在射线OA上时,把的的值叫做点P在射线OA上的射影值;当点P不在射线OA上时,把射线OA上与点P最近点的射影值,叫做点P在射线OA上的射影值.例如:如图1,△OAB三个顶点均在格点上,BP是OA边上的高,则点P和点B在射线OA 上的射影值均为=.(1)在△OAB中,①点B在射线OA上的射影值小于1时,则△OAB是锐角三角形;②点B在射线OA上的射影值等于1时,则△OAB是直角三角形;③点B在射线OA上的射影值大于1时,则△OAB是钝角三角形.其中真命题有.A.①②B.①③C.②③D.①②③(2)已知:点C是射线OA上一点,CA=OA=1,以〇为圆心,OA为半径画圆,点B是⊙O 上任意点.①如图2,若点B在射线OA上的射影值为.求证:直线BC是⊙O的切线;②如图3,已知D为线段BC的中点,设点D在射线OA上的射影值为x,点D在射线OB上的射影值为y,直接写出y与x之间的函数关系式为.6.问题发现:(1)如图1,△ABC内接于半径为4的⊙O,若∠C=60°,则AB=;问题探究:(2)如图2,四边形ABCD内接于半径为6的⊙O,若∠B=120°,求四边形ABCD的面积最大值;解决问题:(3)如图3,一块空地由三条直路(线段AD、AB、BC)和一条弧形道路围成,点M 是AB道路上的一个地铁站口,已知AD=BM=1千米,AM=BC=2千米,∠A=∠B=60°,的半径为1千米,市政府准备将这块空地规划为一个公园,主入口在点M处,另外三个入口分别在点C、D、P处,其中点P在上,并在公园中修四条慢跑道,即图中的线段DM、MC、CP、PD,是否存在一种规划方案,使得四条慢跑道总长度(即四边形DMCP 的周长)最大?若存在,求其最大值;若不存在,说明理由.7.如图,AB是⊙O的直径,BM切⊙O于点B,点P是⊙O上的一个动点(点P不与A,B两点重合),连接AP,过点O作OQ∥AP交BM于点Q,过点P作PE⊥AB于点C,交QO的延长线于点E,连接PQ,OP,AE.(1)求证:直线PQ为⊙O的切线;(2)若直径AB的长为4.①当PE=时,四边形BOPQ为正方形;②当PE=时,四边形AEOP为菱形.8.已知AB是⊙O的直径,DA为⊙O的切线,切点为A,过⊙O上的点C作CD∥AB交AD于点D,连接BC、AC.(1)如图①,若DC为⊙O的切线,切点为C,求∠ACD和∠DAC的大小.(2)如图②,当CD为⊙O的割线且与⊙O交于点E时,连接AE,若∠EAD=30°,求∠ACD和∠DAC的大小.9.已知AB为⊙O的直径,点C为⊙O上一点,点D为AB延长线一点,连接AC.(Ⅰ)如图①,OB=BD,若DC与⊙O相切,求∠D和∠A的大小;(Ⅱ)如图②,CD与⊙O交于点E,AF⊥CD于点F连接AE,若∠EAB=18°,求∠FAC的大小.10.如图,AB为⊙O的直径,点P为AB延长线上的一点,过点P作⊙O的切线PE,切点为M,过A、B两点分别作PE的垂线AC,BD,垂足分别为C,D,连接AM.(1)求证:AM平分∠CAB;(2)若AB=4,∠APE=30°,求的长.11.如图,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于E,过点A作AF⊥AC于F,交⊙O于D,连接DE,BE,BD(1)求证:∠C=∠BED;(2)若AB=12,tan∠BED=,求CF的长.12.已知,点A为⊙O外一点,过A作⊙O的切线与⊙O相切于点P,连接PO并延长至圆上一点B连接AB交⊙O于点C,连接OA交⊙O于点D连接DP且∠OAP=∠DPA.(1)求证:PO=PD;(2)若AC=,求⊙O的半径.13.如图,AB是⊙O的直径,C为⊙O上一点,P是半径OB上一动点(不与O,B重合),过点P作射线l⊥AB,分别交弦BC,于D,E两点,过点C的切线交射线1于点F.(1)求证:FC=FD.(2)当E是的中点时,①若∠BAC=60°,判断以O,B,E,C为顶点的四边形是什么特殊四边形,并说明理由;②若=,且AB=30,则OP=.14.如图,在∠DAM内部做Rt△ABC,AB平分∠DAM,∠ACB=90°,AB=10,AC=8,点N 为BC的中点,动点E由A点出发,沿AB运动,速度为每秒5个单位,动点F由A点出发,沿AM运动,速度为每秒8个单位,当点E到达点B时,两点同时停止运动,过A、E、F作⊙O.(1)判断△AEF的形状为,并判断AD与⊙O的位置关系为;(2)求t为何值时,EN与⊙O相切?求出此时⊙O的半径,并比较半径与劣弧长度的大小;(3)直接写出△AEF的内心运动的路径长为;(注:当A、E、F重合时,内心就是A点)(4)直接写出线段EN与⊙O有两个公共点时,t的取值范围为.(参考数据:sin37°=,tan37°=,tan74°≈,sin74°≈,cos74°≈)15.如图1,CD是⊙O的直径,且CD过弦AB的中点H,连接BC,过弧AD上一点E作EF∥BC,交BA的延长线于点F,连接CE,其中CE交AB于点G,且FE=FG.(1)求证:EF是⊙O的切线;(2)如图2,连接BE,求证:BE2=BG•BF;(3)如图3,若CD的延长线与FE的延长线交于点M,tan F=,BC=5,求DM的值.16.如图,在Rt△ABC中,AB⊥BC,以AB为直径的圆交AC于点D,E是BC的中点,连接DE.(1)求证:DE是⊙O的切线;(2)设⊙O的半径为r,证明r2=AD•OE;(3)若DE=4,sin C=,求AD之长.17.定义:三角形一边上的点将该边分为两条线段,且这两条线段的积等于这个点到该边所对顶点连线的平方,则称这个点为三角形该边的“好点”.如图1,△ABC中,点D是BC 边上一点,连结AD,若AD2=BD•CD,则称点D是△ABC中BC边上的“好点”.(1)如图2,△ABC的顶点是4×3网格图的格点,请仅用直尺画出AB边上的一个“好点”.(2)△ABC中,BC=9,tan B=,tan C=,点D是BC边上的“好点”,求线段BD的长.(3)如图3,△ABC是⊙O的内接三角形,OH⊥AB于点H,连结CH并延长交⊙O于点D.①求证:点H是△BCD中CD边上的“好点”.②若⊙O的半径为9,∠ABD=90°,OH=6,请直接写出的值.18.如图,在等腰三角形ABC中,AB=AC,以AC为直径的⊙O分别交AB、BC于点M、N,过点C作⊙O的切线交AB的延长线于点P.(1)求证:∠CAB=2∠BCP;(2)若⊙O的直径为5,sin∠BCP=,求△ABC内切圆的半径;(3)在(2)的条件下,求△ACP的周长.19.已知四边形ABCD为⊙O的内接四边形,直径AC与对角线BD相交于点E,作CH⊥BD于H,CH与过A点的直线相交于点F,∠FAD=∠ABD.(1)求证:AF为⊙O的切线;(2)若BD平分∠ABC,求证:DA=DC;(3)在(2)的条件下,N为AF的中点,连接EN,若∠AED+∠AEN=135°,⊙O的半径为2,求EN的长.20.如图,在Rt△ABC中,∠ACB=90°,O是线段BC上一点,以O为圆心,OC为半径作⊙O,AB与⊙O相切于点F,直线AO交⊙O于点E,D.(1)求证:AO是△CAB的角平分线;(2)若tan∠D=,求的值;(3)如图2,在(2)条件下,连接CF交AD于点G,⊙O的半径为3,求CF的长.参考答案1.解:(1)在Rt△ABC中,∵AB=8,∠ABC=30°,∴AC=AB sin∠ABC=8sin30°=4,∴⊙O的半径为2;(2)证明:连接OD,CD,∵AC为⊙O的直径,∴CD⊥AB,∴∠CDB=90°,∵点E是边BC的中点,∴DE=CE=CB,∴∠DCE=∠CDE,∵OC=OD,∴∠OCD=∠ODC,∴∠ACE=∠ACD+∠DCE=90°,∴∠ODE=∠ODC+∠CDE=90°,∴OD⊥DE,∴直线DE是⊙O的切线;(3)连接OO′交AB于F,设⊙O′与AB相切于G,连接O′G,则∠O′GF=90°,∵将⊙O沿直线BC向右平移m个单位长度后得到⊙O′,∴OO′∥BC,AO=O′G,∴∠AOF=∠ACB=90°,∵∠AFO=∠O′FG,∴△AOF≌△O′GF(AAS),∴O′F=AF,∵在Rt△AOF中,∵∠A=60°,AO=2,∴AF=4,OF=2,∴O′F=AF=4,∴OO′=4+2,∴m=4+2.故答案为:4+2.2.(1)解:∵四边形ABCD是矩形,∴∠D=90°,CD∥AB,CD=AB=13,∴∠EAB=∠DEA,∵E是CD的中点,∴DE=CD=,∴tan∠DEA===.故答案为:.(2)证明:连接OF,在矩形ABCD中,AD=BC,∠ADE=∠BCE=90°,又CE=DE,∴△ADE≌△BCE(SAS),∴AE=BE,∴∠EAB=∠EBA.∵OF=OA,∴∠OAF=∠OFA,∴∠OFA=∠EBA.∴OF∥EB.∵FG⊥BE,∴FG⊥OF,∴FG是⊙O的切线.(3)解:若BE能与⊙O相切,由AE是⊙O的直径,则AE⊥BE,∠AEB=90°.设DE=x,则EC=13﹣x.由勾股定理得:AE2+EB2=AB2,即(36+x2)+[(13﹣x)2+36]=132,整理得x2﹣13x+36=0,解得:x1=4,x2=9,∴DE=4或9,当DE=4时,CE=9,BE===3,当DE=9时,CE=4,BE===2,∴BE能与⊙O相切,此时BE=2或3.3.解:(1)如图1,连接OC,∵四边形ABCD和四边形BEFG为正方形,∴AB=BC=1,BE=EF,∠OEF=∠ABC=90°,∵点O为AB中点,∴OB=AB=,设BE=EF=x,则OE=x+,在Rt△OEF中,∵OE2+EF2=OF2,∴,在Rt△OBC中,∵OB2+BC2=OC2,∴=OC2,∵OC,OF为⊙O的半径,∴OC=OF,∴,解得:x=,∴正方形BEFG的边长为;(2)证明:如图2,连接OC,设OB=y,BE=EF=x,同(1)可得,OE2+EF2=OF2,OB2+BC2=OC2,∴OF2=x2+(x+y)2,OC2=y2+12∵OC,OF为⊙O的半径,∴OC=OF,∴x2+(x+y)2=y2+12,∴2x2+2xy=1,∴x2+xy=,即x(x+y)=,∴EF×OE=,∴以线段OE和EF为邻边的矩形的面积为定值,这个定值为.(3)证明:连接OD,设OA=a,BE=EF=b,则OB=1﹣a,则OE=1﹣a+b,∵∠DAO=∠OEF=90°,∴DA2+OA2=OD2,OE2+EF2=OF2,∴12+a2=OD2,(1﹣a+b)2+b2=OF2,∵OD=OF,∴12+a2=(1﹣a+b)2+b2,∴(b+1)(a﹣b)=0,∵b+1≠0,∴a﹣b=0,∴a=b,∴OA=EF,在Rt△AOD和Rt△EFO中,,∴Rt△AOD≌Rt△EFO(HL),∴∠FOE=∠ODA,∵∠DAO=90°,∴∠ODA+∠AOD=90°,∴∠FOE+∠AOD=90°,∴∠DOF=90°,∴DO⊥FO.4.解:(1)如图1,∵AC为直径,∴∠ABC=90°,∴∠ACB+∠BAC=90°,∵AB=BC,∴∠ACB=∠BAC=45°,∴∠ADB=∠ACB=45°;(2)线段EA,CF,EF之间满足的等量关系为:EA2+CF2=EF2.理由如下:如图2,设∠ABE=α,∠CBF=β,∵AD∥BF,∴∠EBF=∠ADB=45°,又∠ABC=90°,∴α+β=45°,过B作BN⊥BE,使BN=BE,连接NC,∵AB=CB,∠ABE=∠CBN,BE=BN,∴△AEB≌△CNB(SAS),∴AE=CN,∠BCN=∠BAE=45°,∴∠FCN=90°.∵∠FBN=α+β=∠FBE,BE=BN,BF=BF,∴△BFE≌△BFN(SAS),∴EF=FN,∵在Rt△NFC中,CF2+CN2=NF2,∴EA2+CF2=EF2;(3)如图3,延长GE,HF交于K,由(2)知EA 2+CF 2=EF 2, ∴EA 2+CF 2=EF 2,∴S △AGE +S △CFH =S △EFK ,∴S △AGE +S △CFH +S 五边形BGEFH =S △EFK +S 五边形BGEFH ,即S △ABC =S 矩形BGKH , ∴S △ABC =S 矩形BGKH ,∴S △GBH =S △ABO =S △CBO ,∴S △BGM =S 四边形COMH ,S △BMH =S 四边形AGMO ,∵S 四边形AGMO :S 四边形CHMO =8:9,∴S △BMH :S △BGM =8:9,∵BM 平分∠GBH ,∴BG :BH =9:8,设BG =9k ,BH =8k ,∴CH =3+k ,∵AG =3,∴AE =3, ∴CF =(k +3),EF =(8k ﹣3),∵EA 2+CF 2=EF 2, ∴+=,整理得:7k 2﹣6k ﹣1=0,解得:k 1=﹣(舍去),k 2=1.∴AB =12,∴AO =AB =6,∴⊙O的半径为6.5.解:(1)①错误.点B在射线OA上的射影值小于1时,∠OBA可以是钝角,故△OAB 不一定是锐角三角形;②正确.点B在射线OA上的射影值等于1时,AB⊥OA,∠OAB=90°,△OAB是直角三角形;③正确.点B在射线OA上的射影值大于1时,∠OAB是钝角,故△OAB是钝角三角形;故答案为:B.(2)①如图2,作BH⊥OC于点H,∵点B在射线OA上的射影值为,∴=,=,CA=OA=OB=1,∴=,又∵∠BOH=∠COB,∴△BOH∽△COB,∴∠BHO=∠CBO=90°,∴BC⊥OB,∴直线BC是⊙O的切线;②图形是上下对称的,只考虑B在直线OC上及OC上方部分的情形.过点D作DM⊥OC,作DN⊥OB,当∠DOB<90°时,设DM=h,∵D为线段BC的中点,∴S△OBD =S△ODC,∴OB×DN=OC×DM,∴DN=2h,∵在Rt△DON和Rt△DOM中,OD2=DN2+ON2=DM2+OM2,∴4h2+y2=h2+x2,∴3h2=x2﹣y2①,∵BD2=CD2,∴4h2+(1﹣y)2=h2+(2﹣x)2②,①②消去h得:y=2x﹣.如图,当∠BOD=90°时,过点D作DM⊥OC于点M,∵D为线段BC的中点,∴S△OBD =S△ODC,∴OB×DO=OC×DM,∵CA=OA=OB=1,∴OD=2DM,∴sin∠DOM=,∴∠DOM=30°,设DM=h,则OD=2h,OM=h,∴h2+=1+4h2,∴h=,∴OM=,当点B在OC上时,OD=,综上所述,当≤x≤时,y=0;当<x≤时,y=2x﹣.故答案为:y=0(≤x≤)或y=2x﹣(<x≤).6.解:(1)如图1,连接OA、OB,过点O作OH⊥AB于点H,∵∠C=60°,∴∠AOB=120°,∵OA=OB,∴△OAB为等腰三角形,∵OH⊥AB,∴∠AOH=∠BOH=60°,∴AH=OA sin∠AOH=4×=2,则AB=2AH=4;故答案为4;(2)如图2,连接AC,过点D作DE⊥AC于点E,过点B作BF⊥AC于点F,∵四边形ABCD的面积S=AC×DE AC×BF=AC×(DE+BF),∴当D、E、F、B四点共线且为直径时,四边形ABCD的面积S最大;∵∠ABC=120°,∴∠ADC=60°,∴∠AOC=120°,在△AOC中,由(1)知,AC=2×OA sin60°=2×6×=6,∴四边形ABCD的面积S的最大值为:×AC×BD=6×12=36,故四边形ABCD的面积的最大值为36;(3)如图3,过点D作DK⊥AB于点K,连接CD,在△ADM中,DK=AD•sin A=1×=,同理AK=,则KM=AM﹣AK=2﹣=,则tan∠DMK==∴∠DMK=30°,故△ADM为直角三角形,同理△CMB为直角三角形,在Rt△ADM中,DM===,∴∠DMC=180°﹣∠DMA﹣∠CMB=60°∵AD=BM,AM=BC,∠A=∠B=60°,∴Rt△ADM≌Rt△BMC(SAS),∴DM=CM,∴△CDM为等边三角形;设所在的圆的圆心为R,连接DR、CR、MR,∵DM=CM,RM=RM,DR=CR,∴△DRM≌△CRM(SSS),∴∠DMR=∠CMR=∠DMC=30°,在△DMR中,DR=1,∠DMR=30°,DM==CM,过点R作RH⊥DM于点H,则RM===1=RD,故D、P、C、M四点共圆,∴∠DPC=120°,如图4,连接MP,在PM上取PP′=PC,∵△CDM为等边三角形,∴∠CDM=60°=∠CPM,∴△P′PC为等边三角形,则PP′=P′C=PC,∵∠PMC=∠PDC,∠CP′M=180°﹣∠PP′C=120°=∠DPC,CD=CM,∴△PDC≌△P′MC(AAS),∴PD=P′M,∴PD+PC=PP′+PD=PP′+P′M=PM,故当PM是直径时,PD+PC最大值为2;∵四边形DMCP的周长=DM+CM+PC+PD=2+PD+PC,而PD+PC最大值为2;故四边形DMCP的周长的最大值为:2+2,即四条慢跑道总长度(即四边形DMCP的周长)最大为2+2.7.(1)证明:∵OQ∥AP,∴∠EOC=∠OAP,∠POQ=∠APO,又∵OP=OA,∴∠APO=∠OAP,又∵∠BOQ=∠EOA=∠OAP,∴∠POQ=∠BOQ,在△BOQ与△POQ中,,∴△POQ≌△BOQ(SAS),∴∠OPQ=∠OBQ=90°,∵点P在⊙O上,∴PQ是⊙O的切线;(2)解:①∵△POQ≌△BOQ,∴∠OBQ=∠OPQ=90°,当∠BOP=90°,四边形OPQB为矩形,而OB=OP,则四边形OPQB为正方形,此时点C、点E与点O重合,PE=PO=AB=2;②∵PE⊥AB,∴当OC=AC,PC=EC,四边形AEOP为菱形,∵OC=OA=1,∴PC===,∴PE=2PC=2.故答案为:2;2.8.解:(1)∵AB是⊙O的直径,DA为⊙O的切线,切点为A,∴DA⊥AB,∴∠DAB=90°,∵DC为⊙O的切线,切点为C,∴DC=DA,∵CD∥AB,∴∠D+∠DAB=180°,∴∠D=90°,∴∠ACD=∠DAC=45°;(2)∵AB是⊙O的直径,DA为⊙O的切线,切点为A,∴DA⊥AB,∴∠DAB=90°,∠DEA=∠EAB,∴∠ADC=90°,∵∠EAD=30°,∴∠DEA=60°,∴∠EAB=60°,∴∠BCE=120°,∵AB是⊙O的直径,∴∠BCA=90°,∴∠ACD=30°,∴∠DAC=60°.9.解:(Ⅰ)如图①,连接OC,BC,∵AB为⊙O的直径,∴∠ACB=90°,∵DC与⊙O相切,∴∠OCD=90°,∵OB=BD,∴BC=OD=OB=BD,∴BC=OB=OC,∴△OBC是等边三角形,∴∠OBC=∠OCB=∠COB=60°,∴∠BCD=∠OCA=30°,∴∠D=∠A=30°;(Ⅱ)如图②,连接BE,∵AB为⊙O的直径,∴∠AEB=90°,∵AF⊥CD,∴∠AFC=90°,∵∠ACF是圆内接四边形ACEB的外角,∴∠ACF=∠ABE,∴∠FAC=∠EAB=18°,答:∠FAC的大小为18°.10.解:(1)连接OM,∵PE为⊙O的切线,∴OM⊥PC,∵AC⊥PC,∴OM∥AC,∴∠CAM=∠AMO,∵OA=OM,∠OAM=∠AMO,∴∠CAM=∠OAM,即AM平分∠CAB;(2)∵∠APE=30°,∴∠MOP=∠OMP﹣∠APE=90°﹣30°=60°,∵AB=4,∴OB=2,∴的长为=.11.(1)证明:∵AB是⊙O的直径,CA切⊙O于A,∴∠C+∠AOC=90°;又∵OC⊥AD,∴∠OFA=90°,∴∠AOC+∠BAD=90°,∴∠C=∠BAD.又∵∠BED=∠BAD,∴∠C=∠BED.(2)解:由(1)知∠C=∠BAD,tan∠BED=,∴tan∠C=,∴tan∠C==,且OA=AB=6,∴,解得AC=8,∴=10,∵OC•AF=OA•AC,∴.∴==.12.(1)证明:∵PA与⊙O相切于点P,∴BP⊥AP∴∠OPD+∠DPA=90°,∠OAP+∠AOP=90°∵∠OAP=∠DPA.∴∠OPD=∠AOP∴OD=PD∵PO=OD∴PO=PD.(2)连接PC,∵PB为⊙O的直径∴∠BCP=90°∵PO=PD=OD∴∠AOP=60°设⊙O的半径为x,则PB=2x,=tan60°∴PA=x∴AB==x∵∠BPA=∠BCP=90°,∠B=∠B∴△BAP∽△BPC∴=∵AC=∴=∴7x﹣=4x∴x=∴⊙O的半径为.13.证明:(1)连接OC,(1)证明:连接OC∵CF是⊙O的切线,∴OC⊥CF,∴∠OCF=90°,∴∠OCB+∠DCF=90°,∵OC=OB,∴∠OCB=∠OBC,∵PD⊥AB,∴∠BPD=90°,∴∠OBC+∠BDP=90°,∴∠BDP=∠DCF,∵∠BDP=∠CDF,∴∠DCF=∠CDF,∴FC=FD;(2)如图2,连接OC,OE,BE,CE,①以O,B,E,C为顶点的四边形是菱形.理由如下:∵AB是直径,∴∠ACB=90°,∵∠BAC=60°,∴∠BOC=120°,∵点E是的中点,∴∠BOE=∠COE=60°,∵OB=OE=OC,∴△BOE,△OCE均为等边三角形,∴OB=BE=CE=OC∴四边形BOCE是菱形;②∵,∴设AC=3k,BC=4k(k>0),由勾股定理得AC2+BC2=AB2,即(3k)2+(4k)2=302,解得k=6,∴AC=18,BC=24,∵点E是的中点,∴OE⊥BC,BH=CH=12,=OE×BH=OB×PE,即15×12=15PE,解得:PE=12,∴S△OBE由勾股定理得OP===9.故答案为:9.14.解:(1)过点E作EH⊥AF于H,连接OA、OE、OH,如图1所示:∵∠ACB=90°,AB=10,AC=8,∴BC===6,设运动时间为t,则AE=5t,AF=8t,∵∠AHE=∠ACB=90°,∠EAH=∠BAC,∴△EAH∽△BAC,∴=,即:=,∴AH=4t,∴FH=AF﹣AH=8t﹣4t=4t,∴AH=FH,∵EH⊥AF,∴△AEF是等腰三角形,∴E为的中点,∠EAF=∠EFA,∵AH=FH,∴OH⊥AC,∴E、H、O三点共线,∴∠OAF+∠AOE=90°,∵AB平分∠DAM,∴∠DAE=∠EAF=∠EFA,∵∠AOE=2∠EFA,∴∠AOE=∠DAE+∠EAF=∠DAF,∴∠DAF+∠OAF=90°=∠DAO,即OA⊥AD,∵OA为⊙O的半径,∴AD与⊙O相切;故答案为:等腰三角形,相切;(2)连接OA、OF、OE,OE于AC交于H,如图2所示:由(1)知:EH⊥AC,∵EN与⊙O相切,∴∠OEN=90°,∵∠ACB=90°,∴四边形EHCN为矩形,∴EH=NC,在Rt△AHE中,EH===3t,∴NC=3t,∵点N为BC的中点,∴BC=2NC=6t,∵BC=6,∴6t=6,∴t=1,∴AH=4,EH=3,设⊙O的半径为x,则OH=x﹣3,在Rt△AOH中,由勾股定理得:OA2=OH2+AH2,即x2=(x﹣3)2+42,解得:x=,∴⊙O的半径为,∴OH=,∴tan∠AOH==,∴∠AOH=74°,∵∠AOH=60°时,△AOE是等边三角形,AE=OA,74°>60°,∴AE>OA,∴劣弧长度的大于半径;(3)当点E运动到B点时,t=10÷5=2,∴AF=2×8=16,AE=EF=AB=10,此时△AEF的内心记为G,当A、E、F重合时,内心为A点,∴△AEF的内心运动的路径长为AG,作GP⊥AE于P,GQ⊥EF于Q,连接AG、GF,则CG=PG=NQ,如图3所示:S△AEF=AF•BC=×16×6=48,设CG=PG=NQ=a,则S△AEF =S△AGF+S△AEB+S△FEG=AF•CG+AE•PG+EF•NQ=×(16+10+10)a=48,解得:a=,在Rt△AGC中,AC2+CG2=AG2,即82+()2=AG,∴AG=,故答案为:;(4)分别讨论两种极限位置,①当EN与⊙O相切时,由(2)知,t=1;②当N在⊙O上,即ON为⊙O的半径,连接OA、ON、OE,OE交AC于H,过点O作OK⊥BC于K,如图4所示:则四边形OKCH为矩形,OA=OE=ON,∴OH=CK,AH=4t,EH=3t,设⊙O的半径为x,则在Rt△AOH中,AH2+OH2=OA2,即(4t)2+(x﹣3t)2=x2,解得:x=t,∴OH=CK=t﹣3t=t,在Rt△OKN中,OK2+KN2=ON2,即(8﹣4t)2+(3+t)2=(t)2,解得:t=,∴线段EN与⊙O有两个公共点时,t的取值范围为:1<t≤,故答案为:1<t≤.15.解:(1)连接OE,则∠OCE=∠OEC=α,∵FE=FG,∴∠FGE=∠FEG=β,∵H是AB的中点,∴CH⊥AB,∴∠GCH+∠CGH=α+β=90°,∴∠FEO=∠FEG+∠CEO=α+β=90°,∴EF是⊙O的切线;(2)∵CH⊥AB,∴=∴∠CBA=∠CEB,∵EF∥BC,∴∠CBA=∠F,故∠F=∠CEB,∴∠FBE=∠GBE,∴△FEB∽△EGB,∴BE2=BG•BF;(3)如图2,过点F作FR⊥CE于点R,设∠CBA=∠CEB=∠GFE=γ,则tanγ=,∵EF∥BC,∴∠FEC=∠BCG=β,故△BCG为等腰三角形,则BG=BC=5,在Rt△BCH中,BC=5,tan∠CBH=tanγ=,则sinγ=,cosγ=,CH=BC sinγ=5×=3,同理HB=4;设圆的半径为r,则OB2=OH2+BH2,即r2=(r﹣3)2+(4)2,解得:r=;GH=BG﹣BH=5﹣4=,tan∠GCH===,则cos∠GCH=,则tan∠CGH=3=tanβ,则cosβ=,连接DE,则∠CED=90°,在Rt△CDE中cos∠GCH===,解得:CE=,在△FEG中,cosβ===,解得:FG=;∵FH=FG+GH=,∴HM=FH tan∠F=×=;∵CM=HM+CH=,∴MD=CM﹣CD=CM﹣2r=.16.(1)证明:连接OD、BD,∵AB为圆O的直径,∴∠BDA=90°,∴∠BDC=180°﹣90°=90°,∵E为BC的中点,∴DE=BC=BE,∴∠EBD=∠EDB,∵OD=OB,∴∠OBD=∠ODB,∵∠EBD+∠DBO=90°,∴∠EDB+∠ODB=90°,∴∠ODE=90°,∴DE是圆O的切线.(2)证明:如图,连接BD.由(1)知,∠ODE=∠ADB=90°,BD⊥AC.∵E是BC的中点,O是AB的中点,∴OE是△ABC的中位线,∴OE∥AC,∴OE⊥BD.∴OE∥AC,∴∠1=∠2.又∵∠1=∠A,∴∠A=∠2.即在△ADB与△ODE中,∠ADB=∠ODE,∠A=∠2,∴△ADB∽△ODE.∴=,即=.∴r2=AD•OE;(3)∵AB为⊙O的直径,∴∠ADB=∠BDC=90°,∵点E为BC的中点,∴BC=2DE=8,∵sin C=,∴设AB=3x,AC=5x,根据勾股定理得:(3x)2+82=(5x)2,解得x=2.则AC=10.由切割线定理可知:82=(10﹣AD)×10,解得,AD=3.6.17.解:(1)如答图1,当CD⊥AB或点D是AB的中点是,CD2=AD•BD;(2)作AE⊥BC于点E,由,可设AE=4x,则BE=3x,CE=6x,∴BC=9x=9,∴x=1,∴BE=3,CE=6,AE=4,设DE=a,①如答图2,若点D在点E左侧,由点D是BC边上的“好点”知,AD2=BD•CD,∴a2+42=(3﹣a)(6+a),即2a2+3a﹣2=0,解得,a=﹣2(舍去),2∴.②如答图3,若点D在点E右侧,由点D是BC边上的“好点”知,AD2=BD•CD,∴a2+42=(3+a)(6﹣a),即2a2﹣3a﹣2=0,=2,(舍去)解得a1∴BD=3+a=3+2=5.∴或5.(5)①∵∠CHA=∠BHD,∠ACH=∠DBH∴△AHC∽△DHB,∴,即AH•BH=CH•DH,∵OH⊥AB,∴AH=BH,∴BH2=CH•DH∴点H是△BCD中CD边上的“好点”.②.理由如下:如答图4,连接AD,BD,∵∠ABD=90°,∴AD是直径,∴AD=18.又∵OH⊥AB,∴OH∥BD.∵点O是线段AD的中点,∴OH是△ABD的中位线,∴BD=2OH=12.在直角△ABD中,由勾股定理知:AB===6.∴由垂径定理得到:BH=AB=3.在直角△BDH中,由勾股定理知:DH===3.又由①知,BH2=CH•DH,即45=3CH,则CH=.∴==,即.18.解:(1)如图,连接AN,∵AC为直径,∴AN⊥BC,∵AB=AC,∴AN平分∠BAC,∵PC是圆的切线,∴∠ACP=90°,∵∠NAC+∠ACB=∠PCB+∠ACB=90°,∴∠NAC=∠BCP,即∠BAC=2∠BCP;(2)由(1)知,AN平分∠BAC,则∠NAC=∠BCP,故sin∠NAC=sin∠BCP=,则tan∠NAC=,在Rt△NAC中,AC=5,NC=AC•sin∠NAC=5×=,同理AN=2,则BC=2NC=2;S=×BC•AN=2×2=10,△ABC设△ABC内切圆的半径为r,则S=(AB+AC+BC)•r=×(5+5+2)=10,△ABC解得:r=;故△ABC内切圆的半径为;(3)在△ABC中,设AC边长的高为h,则S=AC•h=×5×h=10,解得:h=4,△ABCsin∠BAC==,在Rt△ACP中,∵sin∠BAC==,设PC=4m,则AP=5m,则AC=3m=5,解得m=,△ACP的周长=3m+4m+5m=12m=20.19.(1)证明:如图1,∵AC为⊙O的直径,∴∠ADC=90°,∴∠DAC+∠DCA=90°.∵=,∴∠ABD=∠DCA,∵∠FAD=∠ABD,∴∠FAD=∠DCA,∴∠FAD+∠DCA=90°,∴CA⊥AF,∴AF为⊙O的切线.(2)证明:如图2,连接OD,∵=,∴∠ABD=∠AOD,∵=,∴∠DBC=∠DOC,∵BD平分∠ABC,∴∠ABD=∠DBC,∴∠DOA=∠DOC,∴DA=DC.(3)如图3,连接OD交CF于M,作EP⊥AD于P,∵AC为⊙O的直径,∴∠ADC=90°.∵DA=DC,∴DO⊥AC,∴∠FAC=∠DOC=90°,∴AF∥OM,∵AO=OC,∴OM=AF.∵∠ODE+∠DEO=90°,∠OCM+∠DEO=90°.∴∠ODE=∠OCM.∵∠DOE=∠COM,OD=OC,∴∴△ODE≌△OCM,∴OE=OM,设OM=m,∴AE=2﹣m,AP=PE=2﹣m,DP=2+m,∵∠AED+∠AEN=135°,∠AED+∠ADE=135°,∴∠AEN=∠ADE,∵∠EAN=∠DPE,∴△EAN∽△DPE,∴=,∴=,∴m=,∴AN=,AE=,∴勾股定理得NE=.20.(1)证明:连接OF,∵AB与⊙O相切于点F,∴OF⊥AB,∵∠ACB=90°,OC=OF,∴∠OAF=∠OAC,即AO是△ABC的角平分线;(2)如图2,连接CE,∵ED是⊙O的直径,∴∠ECD=90°,∴∠ECO+∠OCD=90°,∵∠ACB=90°,∴∠ACE+∠ECO=90°,∴∠ACE=∠OCD,∵OC=OD,∴∠OCD=∠ODC,∴∠ACE=∠ODC,∵∠CAE=∠CAE,∴△ACE∽△ADC,∴,∵tan∠D=,∴,∴;(3)由(2)可知:=,∴设AE=x,AC=2x,∵△ACE∽△ADC,∴,∴AC2=AE•AD,∴(2x)2=x(x+6),解得:x=2或x=0(不合题意,舍去),∴AE=2,AC=4,∴AO=AE+OE=2+3=5,如图3,连接CF交AD于点G,∵AC,AF是⊙O的切线,∴AC=AF,∠CAO=∠OAF,∴CF⊥AO,∴∠ACO=∠CGO=90°,∵∠COG=∠AOC,∴△CGO∽△ACO,∴,∴OC2=OG•OA,∴OG=,∴CG===,∴CF=2CG=.。
2020年九年级数学中考《圆》综合专题复习试题(含答案)

1 ∵AH=2AC= 3,
AH ∴OA=sin60°=2. ∴⊙O 半径的长为 2. (2)证明:在 BM 上截取 BE=BC,连接 CE, ∵∠ABC=120°,BM 平分∠ABC, ∴∠MBA=∠MBC=60°. ∵BE=BC, ∴△EBC 是等边三角形.
∴CE=CB=BE,∠BCE=60°. ∴∠BCD+∠DCE=60°. ∵∠ACM=∠ABM=60°,∴∠ECM+∠DCE=60°. ∴∠ECM=∠BCD. ∵∠CAM=∠CBM=60°,∠ACM=∠ABM=60°. ∴△ACM 是等边三角形.∴AC=CM. ∴△ACB≌△MCE(SAS).∴AB=ME. ∵ME+EB=BM, ∴AB+BC=BM.
基础题组
1.(2019·保定一模)已知⊙O 的半径 OA 长为 2,若 OB= 3,则可以得到的正确图形可
能是(A)
2.(2019·广州)平面内,⊙O 的半径为 1,点 P 到 O 的距离为 2,过点 P 可作⊙O 的切线条
数为(C)
A.0 条
B.1 条
C.2 条
D.无数条
3.如图,在 Rt△ABC 中,∠C=90°,AC=3,BC=4,以点 A 为圆心作圆.如果⊙A 与线
则∠D=27°.
基础题组
1.(2019·柳州)如图,A,B,C,D 是⊙O 上的点,则图中与∠A 相等的角是(D)
A.∠B
B.∠C
C.∠DEB
D.∠D
A︵B
A︵B
2.(2019·吉林)如图,在⊙O 中, 所对的圆周角∠ACB=50°.若 P 为 上一点,
∠AOP=55°,则∠POB 的度数为(B)
A.30°
3 切,连接 OC,则 tan∠OCB= 5 .
2019-2020学年人教版九年级数学上学期同步测试专题24-1:圆的有关性质(含解析)
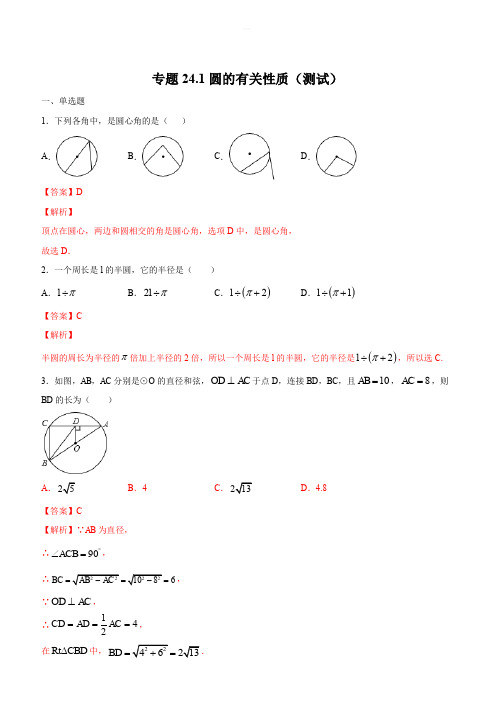
专题24.1圆的有关性质(测试)一、单选题1.下列各角中,是圆心角的是( )A .B .C .D .【答案】D 【解析】顶点在圆心,两边和圆相交的角是圆心角,选项D 中,是圆心角, 故选D .2.一个周长是l 的半圆,它的半径是( ) A .l π÷ B .2l π÷C .()2l π÷+D .()1l π÷+【答案】C 【解析】半圆的周长为半径的π倍加上半径的2倍,所以一个周长是l 的半圆,它的半径是()2l π÷+,所以选C. 3.如图,AB ,AC 分别是⊙O 的直径和弦,OD AC ⊥于点D ,连接BD ,BC ,且10AB =,8AC =,则BD 的长为( )A .B .4C .D .4.8【答案】C【解析】∵AB 为直径, ∴90ACB ︒∠=,∴6BC =, ∵OD AC ⊥, ∴142CD AD AC ===,故选C . 4.如图,AB 是O 的弦,OC AB ⊥交O 于点C ,点D 是O 上一点,30ADC ∠=︒,则BOC ∠的度数为( ).A .30°B .40°C .50°D .60°【答案】D【解析】解:如图,∵30ADC ∠=︒, ∴260AOC ADC ∠=∠=︒. ∵AB 是O 的弦,OC AB ⊥交O 于点C ,∴AC BC =.∴60AOC BOC ∠=∠=︒. 故选:D ..5.如图,有一圆形展厅,在其圆形边缘上的点A 处安装了一台监视器,它的监控角度是65°.为了监控整个展厅,最少需在圆形边缘上共安装这样的监视器( )台.A .3B .4C .5D .6【答案】A【解析】设需要安装n (n 是正整数)台同样的监控器,由题意,得:65°×2×n ≥360°, 解得n ≥3613,∴至少要安装3台这样的监控器,才能监控整个展厅.故选:A .且10CD m =,则这段弯路所在圆的半径为( )A .25mB .24mC .30mD .60m【答案】A 【解析】解:OC AB ⊥,20AD DB m ∴==,在Rt AOD ∆中,222OA OD AD =+, 设半径为r 得:()2221020r r =-+, 解得:25r m =,∴这段弯路的半径为25m故选:A .7.若AB 和CD 的度数相等,则下列命题中正确的是( ) A .AB =CDB .AB 和CD 的长度相等C .AB 所对的弦和CD 所对的弦相等D .AB 所对的圆心角与CD 所对的圆心角相等 【答案】D【解析】如图,AB 与CD 的度数相等,A 、根据度数相等,不能推出弧相等,故本选项错误;B 、根据度数相等,不能推出两弧的长度相等,故本选项错误;C 、根据度数相等,不能推出所对应的弦相等,故本选项错误;D 、根据度数相等,能推出弧所对的两个圆心角相等,故本选项正确;8.如图,C、D为半圆上三等分点,则下列说法:①AD=CD=BC;②∠AOD=∠DOC=∠BOC;③AD =CD=OC;④△AOD沿OD翻折与△COD重合.正确的有()A.4个B.3个C.2个D.1个【答案】A【解析】∵C、D为半圆上三等分点,∴»»»AD CD BC==,故①正确,∵在同圆或等圆中,等弧对的圆心角相等,等弧对的弦相,∴AD=CD=OC,∠AOD=∠DOC=∠BOC=60°,故②③正确,∵OA=OD=OC=OB,∴△AOD≌△COD≌△COB,且都是等边三角形,∴△AOD沿OD翻折与△COD重合.故④正确,∴正确的说法有:①②③④共4个,故选A.9.下列说法:①优弧一定比劣弧长;②面积相等的两个圆是等圆;③长度相等的弧是等弧;④经过圆内的一个定点可以作无数条弦;⑤经过圆内一定点可以作无数条直径.其中不正确的个数是()A.1个B.2个C.3个D.4个【答案】C【解析】解:在同圆或等圆中,优弧一定比劣弧长,所以①错误;面积相等的两个圆半径相等,则它们是等圆,所以②正确;能完全重合的弧是等弧,所以③错误;经过圆内一个定点可以作无数条弦,所以④正确;经过圆内一定点可以作无数条直径或一条直径,所以⑤错误.10.如图所示,AB 是半圆O 的直径。
人教版数学九年级2020年中考同步训练:《圆的选择题》(含答案)

人教版数学九年级2020年中考同步训练:《圆的选择题》1.将沿弦BC折叠,交直径AB于点D,若AD=4,DB=5,则BC的长是()A.3B.8 C.D.22.如图,已知圆O的圆心在原点,半径OA=1(单位圆),设∠AOP=∠α,其始边OA与x 轴重合,终边与圆O交于点P,设P点的坐标P(x,y),圆O的切线AT交OP于点T,且AT=m,则下列结论中错误的是()A.sinα=y B.cosα=xC.tanα=m D.x与y成反比例3.如图,Rt△ABC的斜边BC=4,∠ABC=30°,以AB、AC为直径分别作圆.则这两圆的公共部分面积为()A.+B.﹣C.﹣D.﹣4.如图,在圆O上依次有A.B,C三点,BO的延长线交圆O于E,=,点C作CD ∥AB交BE的延长线于D,AD交圆O于点F,连接OA,OF,若∠AOF=3∠FOE,且AF=2,劣弧CF的长是()A.πB.πC.πD.π5.如图,正方形ABCD中,⊙O过点A,B交边AD于点E,连结CE交⊙O于点F,连结AF,若tan∠AFE=,则的值为()A.1 B.C.D.6.如图,点O为正六边形的中心,P,Q分别从点A(1,0)同时出发,沿正六边形按图示方向运动,点P的速度为每秒1个单位长度,点Q的速度为每秒2个单位长度,则第2020次相遇地点的坐标为()A.B.(1,0)C.D.(﹣1,0)7.如图,在圆内接五边形ABCDE中,AB=AE,BC=CD=DE,且∠D=100°,连接AC和EC.则∠ACE的度数为()A.30°B.35°C.40°D.48°8.如图,四边形ABCD是菱形,⊙O经过点A、C、D,与BC相交于点E,连接AC、AE.若∠D=78°,则∠EAC的度数为()A.22°B.24°C.27°D.30°9.如图,在平面直角坐标系中.点A的坐标是(20,0),点B的坐标是(16,0),点C,D在以OA为直径的半圆M上,四边形OCDB是平行四边形.则点C的坐标为()A.(1,7)B.(2,6)C.(2,7)D.(1,6)10.如图,AB是⊙O的直径,点C,点D是半圆上两点,连结AC,BD相交于点P,连结AD,OD.已知OD⊥AC于点E,AB=2.下列结论:①AD2+BC2=4;②sin∠DAC=;③若AC=BD,则DE=OE;④若点P为BD的中点,则DE=2OE.其中确的是()A.①②③B.②③④C.③④D.②④11.如图,圆心为M的量角器的直径的两个端点A,B分别在x轴,y轴正半轴上(包括原点O),AB=4.点P,Q分别在量角器60°,120°刻度线外端,连结MP.量角器从点A 与点Q重合滑动至点Q与点O重合的过程中,线段MP扫过的面积为()A.π+B.πC.π+2D.312.如图,△ABC内接于⊙O,且AB=AC.直径AD交BC于点E,F是AE的中点,连结CF,若AD=6.则CF的最大值为()A.6 B.5 C.4 D.313.如图,△ABC内接于⊙O,将沿BC翻折,交AC于点D,连接BD,若∠BAC=66°,则∠ABD的度数是()A.66°B.44°C.46°D.48°14.如图,半径为3的⊙O与五边形ABCDE的边相切于点A,C,连接OA交BC于点H,连接OB,AB.若∠D+∠E=240°,HC=3BH,则△ABO的面积为()A.3B.C.D.215.如图,点A,B,C是⊙O上三点,AC=BC,点M为⊙O上一点,CE⊥AM,垂足为点E,AE=2,BM=,CM=,则的长为()A.πB.πC.πD.π16.如图,在△ABC中,∠C=40°,∠A=60°.以B为圆心,适当长度为半径作弧,分别交AB,BC于点D,E;分别以D,E为圆心,大于DE长度为半径作弧,两弧交于点F;作射线BP,交AC于点P,过点P作PM⊥AB于M;以P为圆心,PM的长为半径作⊙P.则下列结论中,错误的是()A.∠PBA=40°B.PC=PBC.PM=MB D.⊙P与△ABC有4个公共点17.如图,在△ABC中,∠A=60°,AB=4,以BC的中点O为圆心作圆,分别与AB、AC相切于D、E两点,则的长是()A.πB.πC.πD.318.如图,在边长为8的菱形ABCD中,∠DAB=60°,以点D为圆心,菱形的高DF为半径画弧,交AD于点E,交CD于点G,则图中阴影部分的面积是()A.18﹣3πB.18﹣πC.32﹣16πD.18﹣9π19.如图,5×3的网格图中,每个小正方形的边长均为1,设经过图中格点A,C,B三点的圆弧与AE交于H,则弧AH的弧长为()A.πB.πC.πD.π20.如图,△ACD内接于⊙O,AB是⊙O的切线,∠C=45°,∠B=30°.AD=4,则AB长为()A.4 B.C.D.参考答案1.解:连接CA、CD;根据折叠的性质,知所对的圆周角等于∠CBD,又∵所对的圆周角是∠CBA,∵∠CBD=∠CBA,∴AC=CD(相等的圆周角所对的弦相等);∴△CAD是等腰三角形;过C作CE⊥AB于E.∵AD=4,则AE=DE=2;∴BE=BD+DE=7;在Rt△ACB中,CE⊥AB,根据射影定理,得:BC2=BE•AB=7×9=63;故BC=3.故选:A.2.解:如图,过点P作PH⊥OA于H,由题意知,OA=OP=1,OH=x,PH=y,由切线的性质定理可知AT⊥OA,在Rt△POH中,∠AOP=∠α,∴sinα===y,cosα===x,故A,B正确;在Rt△TOA中,tanα===m,故C正确,在Rt△POH中,OH2+PH2=OP2,∴x2+y2=1,故D错误;故选:D.3.解:如图,设点E是两圆的公共点,连接AE,取AC,AB的中点G,H.在Rt△ABC中,∵∠CAB=90°,∠ABC=30°,BC=4,∴AC=2,AB=2,∠C=60°,∴∠AHE=60°,∠AGE=120°,∴S阴=S扇形HAE﹣S△AEH+S扇形GEA﹣S△AEG=﹣×()2+﹣×1×=﹣,故选:C.4.解:∵=,∴∠CBD=∠ABD,∵CD∥AB,∴∠ABD=∠CDB,∴∠CBD=∠CDB,∴CB=CD,∵BE是⊙O的直径,∴=,∴AB=BC=CD,∵CD∥AB,∴四边形ABCD是菱形,∴BC∥AD,∵∠AOF=3∠FOE,设∠FOE=x,则∠AOF=3x,∠AOD=∠FOE+∠AOF=4x,∵OA=OF,∴∠OAF=∠OFA=(180﹣3x)°,∵OA=OB,∴∠OAB=∠OBA=2x,∴∠ABC=4x,∵BC∥AD,∴∠ABC+∠BAD=180°,∴4x+2x+(180﹣3x)=180,解得:x=20°,∴∠AOF=3x=60°,∠AOE=80°,∴∠COF=80°×2﹣60°=100°,∵OA=OF,∴△AOF是等边三角形,∴OF=AF=2,∴的长==π,故选:C.5.解:如图,设⊙O交BC于J,连接AJ,JF,EJ,过点F作FM⊥AD于M交BC于N.设AB =3a.∵四边形ABCD是正方形,∴∠ABC=∠BAD=∠BCD=90°,AD∥BC,AD=AB=BC=CD=3a,∴AJ是⊙O的直径,∴∠AFJ=∠AEJ=90°,∵FM⊥AD,AD∥CB,∴MN⊥BC,∴∠MNC=∠BCD=∠D=90°,∴四边形MNCD是矩形,四边形ABJE是矩形,∴MN=CD=3a,AE=BJ,∴=,∴∠BAJ=∠AFE,∴tan∠BAJ=tan∠AFE=,∴BJ=AE=a,JC=2a,∵∠JAF=∠JEC,∴tan∠JAF=tan∠JEC,∴==,∵∠AFM+∠JFN=90°,∠JFN+∠FJN=90°,∴∠AFM=∠FJN,∵∠AMF=∠FNJ=90°,∴△AMF∽△FNJ,∴===,设JN=2x,则FM=3x,∵AM=AE+EM=a+2x,∴FN=AM=(a+2x),∵FM+FN=3a,∴3x+(a+2x)=3a,∴9x+2a+4x=9a,∴x=a,∴CN=2a﹣2x=2a﹣a=a,∵EM∥CN,∴===,故选:B.6.解:∵A(1,0),O为正六边形的中心,∴OA=AB=1,连接OB,作BG⊥OA于点G,则AG=OA=,BG=,∴B(,),∴C(﹣,),E(﹣,﹣),∵正六边形的边长=1,∴正六边形的周长=6,∵点P的速度为每秒1个单位长度,点Q的速度为每秒2个单位长度,∴第1次相遇需要的时间为:6÷(1+2)=2(秒),此时点P的路程为1×2=2,点的Q路程为2×2=4,此时P,Q相遇地点的坐标在点C(﹣,),以此类推:第二次相遇地点在点E(﹣,﹣),第三次相遇地点在点A(1,0),…如此下去,∵2020÷3=673…1,∴第2020次相遇地点在点C,C的坐标为(﹣,).故选:A.7.解:∵DE=DC,∴∠DEC=∠DCE=(180°﹣100°)=40°,∵BC=CD,∴=,∴∠BAC=∠CED=40°,∵∠EAC+∠EDC=180°,∴∠EAC=180°﹣100°=80°,∴∠EAB=∠EAC+∠BAC=120°,∴∠ECB=180°﹣∠EAB=60°,∵AE=AB,∴=,∴∠ACE=∠ACB=∠ECB=30°,故选:A.8.解:∵四边形ABCD是菱形,∴DA=DC,∴∠DAC=∠DCA=(180°﹣78°)=51°,∵AD∥BC,∴∠ACE=∠DAC=51°,∵四边形AECD是⊙O的内接四边形,∴∠AEC=180°﹣78°=102°,∴∠EAC=180°﹣102°﹣51°=27°,故选:C.9.解:如图,连接OD,AD,DM,作DF⊥OA于F.∵A(20,0),B(16,0),∴OA=20,OB=16,∴AB=20﹣16=4,∵四边形ABCD是平行四边形,∴CD∥OB,CD=OB=16,OC=BD,∴∠CDO=∠DOA,∴=,∴OC=AD=BD,∵DF⊥BA,∴BF=FA=2,∴OF=18,∴在Rt△DMF中.DF===6,∴D(18,6),C(2,6),故选:B.10.解:∵AB是直径,∴∠ACB=90°,∴AC2+BD2=AB2=4,∵AC>AD,∴AD2+BC2<4,故①错误,∵∠DAC=∠CBD,∴sin∠DAC=sin∠CBD=,故②正确,∵AE⊥OE,假设DE=EO,则AD=AO=OD,∴△ADO是等边三角形,显然不符合题意,故③错误,∵∠DEP=∠BCP=90°,DP=PB,∠DPE=∠BPC,∴△PDE≌△PBC(AAS),∴DE=BC,∵OE∥BC,AO=OB,∴AE=EC,∴BC=2OE,∴DE=2OE,故④正确.故选:D.11.解:由题意可知,点M的运动轨迹是以O为圆心,2为半径,圆心角为60°的扇形,点P在第四象限内时,∠AOB是弧AP所对的圆周角,所以∠AOP=30°,点P在第二象限内时,∠BOP是弧BP所对的圆周角,所以∠BOP=60°,所以点P的运动路径是一条线段,当量角器从点A与O重合滑动至点Q与点O重合时,MP扫过的图形是如图所示的阴影部分,它是由两个边长为2的等边三角形与一个扇形组成,所以PM扫过的面积为:+2××22=π+2,故选:C.12.解:∵F是AE的中点,∴设AF=EF=x,则AE=2x,∴DE=6﹣2x,∵AB=AC,∴=,∵AD为⊙O的直径,∴BC⊥AD,∠ABD=90°∴BE=CE,∠ABE+∠DBE=∠DBE+∠D=90°,∴∠ABE=∠D,∵∠AEB=∠DEB=90°,∴△ABE∽△BDE,∴,∴BE2=AE•DE=2x(6﹣x),∴CE2=2x(6﹣x),在Rt△CEF中,CF2=EF2+CE2=x2+2x(6﹣x)=﹣3(x﹣2)2+36,∴当x=2时,CF的最大值为6,故选:A.13.解:∵将沿BC翻折,交AC与点D,∴∠BAC+∠BDC=180°,∵∠BAC=66°,∴∠BDC=114°,∴∠ADB=180°﹣∠BDC=66°,∴∠ABD=180°﹣66°﹣66°=48°,故选:D.14.解:连接OC,过点C,B分别作AO的垂线,垂足分别为M,N,∵半径为3的⊙O与五边形ABCDE的边相切于点A,C,∴∠OAE=∠OCD=90°,∵∠AOC+∠OCD+∠D+∠E+∠OAE=540°,∠D+∠E=240°,∴∠AOC=120°,∴∠MOC=180°﹣∠AOC=60°,∵OC=3,∴,∵CM⊥AO,BN⊥AO,∴CM∥BN,∴△HCM∽△HBN,∴,∴,∴,故选:C.15.解:在AE上截取AG=BM,连接CG,∵AC=BC,∠A=∠B,∴△ACG≌△BCM(SAS),∴CG=CM=,∵AE=2,AG=BM=,∴GE=,∵CE⊥AM,∴CE===2,∴tan∠A==,∴∠A=30°,∴∠COM=60°,连接OM,CO,∵OC=OM,∴△COM是等边三角形,∴OC=,∴的长==,故选:A.16.解:∵∠C=40°,∠A=60°,∴∠ABC=80°,由题意得,BP平分∠ABC,∴∠ABP=ABC=40°,故选项A正确;∵∠PBC=∠PBA=ABC=40°,∴∠C=∠PBC,∴PC=PB,故选项B正确;∵PM⊥AB,∴∠BMP=90°,∴∠BPM=50°,∴∠BPM≠∠MBP,∴PM≠BM,故C选项错误;∵点P在∠ABC的角平分线上,∴P到AB和BC的距离=PM=⊙P的半径,∴AB,BC与⊙P相切,∵PA>PM,PC>PM,∴⊙P与AC相交,∴⊙P与△ABC有4个公共点,故D选项正确,故选:C.17.解:连接OA,OE,OD,∵AB、AC与⊙O相切于D、E两点,∴∠OEC=∠ODB=∠AEO=∠ADO=90°,∵∠BAC=60°,∴∠DOE=120°,∵点O为BC的中点,∴OB=OC,∵OE=OD,∴Rt△OEC≌RtODB(HL),∴∠C=∠B,∴AC=AB=4,AO⊥BC,∴∠CAO=,∴AO=AC=2,∴OE=AO=,∴的长是=π,故选:C.18.解:∵四边形ABCD是菱形,∠DAB=60°,∴AD=AB=8,∠ADC=180°﹣60°=120°,∵DF是菱形的高,∴DF⊥AB,∴DF=AD•sin60°=8×=4,∴图中阴影部分的面积=菱形ABCD的面积﹣扇形DEG的面积=8×4﹣=32﹣16π.故选:C.19.解:连接EB,BH,AB,∵BE=AB==,AE==,∴BE2+AB2=AE2,∴∠ABE=90°,∴△ABE是等腰直角三角形,∵∠ACB=90°,∴AB是圆的直径,∴∠AHB=90°,∴BH⊥AH,∴∠ABH=∠BAH=45°,∴弧AH所对的圆心角为90°,∴的长==.故选:B.20.解:如图,连接OA、OD,∵∠C=45°.∴∠AOD=2∠C=90°.又∵OA=OD,AD=4,∴AD2=2OA2=16,则OA=2.又∵AB是⊙O的切线,∴∠OAB=90°.∵∠B=30°,OA=2,∴AB=OA=2.故选:D.。
人教版数学九年级上册:24《圆》专题练习(附答案)

word版初中数学第二十四章《圆》专题练习目录专题1 与圆周角有关的辅助线作法 (1)专题2圆周角定理 (3)专题3 证明切线的两种常用方法 (4)专题4与切线长有关的教材变式 (5)专题5与圆的切线有关的计算与证明 (6)专题6 求阴影部分的面积 (8)专题1 与圆周角有关的辅助线作法类型1 构造同弧或等弧所对的圆周角或圆心角1.如图,点A ,B ,C ,D 在⊙O 上,∠AOC =140°,点B 是AC ︵的中点,则∠D 的度数是( )A .70°B .55°C .35.5°D .35°2.如图,点A ,B ,C ,D 分别是⊙O 上的四点,∠BAC =50°,BD 是直径,则∠DBC 的度数是( )A .40°B .50°C .20°D .35°3.如图,A ,B ,C ,D 四个点均在⊙O 上,∠AOD =50°,AO ∥DC ,则∠B 的度数为( ) A .50°B .55°C .60°D .65°4.如图,A ,B ,C 在⊙O 上,∠ACB =40°,点D 在ACB ︵上,M 为半径OD 上一点,则∠AMB 的度数不可能为( )A .45°B .60°C .75°D .85°类型2 利用直径构造直角三角形5.如图,在⊙O 中,∠OAB =20°,则∠C 的度数为 .6.如图,在⊙O 中,AB 为直径,∠ACB 的平分线交⊙O 于点D ,AB =6,则BD = .7.如图,⊙A 过点O ,C ,D ,点C 的坐标为(3,0),点B 是x 轴下方⊙A 上的一点,连接BO ,BD ,已知∠OBD =30°,则⊙A 的半径等于 .8.如图,△ABC 是⊙O 的内接三角形,AD ⊥BC 于点D ,AC =5,DC =3,AB =42,则⊙O 的半径为 .类型3 构造圆内接四边形9.如图,点B,C,D在⊙O上,若∠BCD=130°,则∠BOD的度数是()A.50° B.60°C.80° D.100°10.如图,已知A,B,C,D是⊙O上的四个点,⊙O的直径AB=2 3.若∠ACD=120°,则线段AD的长为.专题2 圆周角定理1.如图,四边形APBC 是圆内接四边形,延长BP 至E ,若∠EPA =∠CPA ,判断△ABC 的形状,并证明你的结论.2.如图,A ,P ,B ,C 是半径为8的⊙O 上的四点,且满足∠BAC =∠APC =60°. (1)求证:△ABC 是等边三角形; (2)求圆心O 到BC 的距离OD.3.如图,点A ,B ,C ,D 在同一个圆上,且C 点为一动点(点C 不在BAD ︵上,且不与点B ,D 重合),∠ACB =∠ABD =45°.(1)求证:BD 是该圆的直径; (2)连接CD ,求证:2AC =BC +CD.专题3 证明切线的两种常用方法类型1 直线与圆有交点:连半径,证垂直 (一)借助角度转换证垂直1.如图,△ABC 内接于⊙O ,CD 是⊙O 的直径,AB 与CD 交于点E ,点P 是CD 延长线上的一点,AP =AC ,且∠B =2∠P.求证:PA 是⊙O 的切线.(二)利用平行证垂直2.如图,AB 是⊙O 的直径,点F ,C 是⊙O 上两点,且点C 为BF ︵的中点,连接AC ,AF ,过点C 作CD ⊥AF 交AF 延长线于点D.求证:CD 是⊙O 的切线.(三)利用全等证垂直3.如图,AB 是⊙O 的直径,BC ⊥AB 于点B ,连接OC 交⊙O 于点E ,弦AD ∥OC.求证: (1)DE ︵=BE ︵; (2)CD 是⊙O 的切线.(四)利用勾股定理的逆定理证垂直4.(南充中考改编)如图,C 是⊙O 上一点,点P 在直径AB 的延长线上,⊙O 的半径为3,PB =2,PC =4.求证:PC 是⊙O 的切线.类型2 不确定直线与圆是否有交点:作垂直,证半径5.如图,△ABC 为等腰三角形,O 是底边BC 的中点,腰AB 与⊙O 相切于点D ,OB 与⊙O 相交于点E.求证:AC 是⊙O 的切线.专题4 与切线长有关的教材变式1.如图,AB ,BC ,CD 分别与⊙O 相切于点E ,F ,G ,若∠BOC =90°,求证:AB ∥CD.2.如图,⊙O的直径AB=12 cm,AM和BN是它的两条切线,DE与⊙O相切于点E,并与AM,BN分别相交于D,C 两点.设AD=x,BC=y,求y关于x的函数解析式.3.如图,Rt△ABC的内切圆⊙O与AB,BC,AC分别相切于点D,E,F,且AC=13,AB=12,∠ABC=90°,则⊙O 的半径为.4.如图,△ABC的周长为18,其内切圆⊙O分别切三边于D,E,F三点,AF=3,FC=4,则BE=.5.已知一个三角形的三边长分别为5,7,8,则其内切圆的半径为()A.32B.32C. 3 D.2 3专题5 与圆的切线有关的计算与证明1.如图,过⊙O 外一点P 引⊙O 的两条切线PA ,PB ,切点分别是A ,B ,OP 交⊙O 于点C ,点D 是优弧ABC ︵上不与点A ,点C 重合的一个动点,连接AD ,CD.若∠APB =80°,则∠ADC 的度数是( )A .15°B .20°C .25°D .30°2.如图,将正方形ABCD 绕点A 按逆时针方向旋转30°,得正方形AB 1C 1D 1,B 1C 1交CD 于点E ,AB =3,则四边形AB 1ED 的内切圆半径为( )A.3+12 B.3-32 C.3+13 D.3-333.如图,矩形ABCD 中,AB =4,BC =3,连接AC ,⊙P 和⊙Q 分别是△ABC 和△ADC 的内切圆,则PQ 的长是( )A.52B. 5C.52D .2 24.如图,⊙O 是△ABC 的外接圆,BC 为⊙O 的直径,点E 为△ABC 的内心,连接AE 并延长交⊙O 于点D ,连接BD 并延长至点F ,使得BD =DF ,连接CF ,BE.求证: (1)DB =DE ;(2)直线CF 为⊙O 的切线.5.如图,点O在∠APB的平分线上,⊙O与PA相切于点C.(1)求证:直线PB与⊙O相切;(2)PO的延长线与⊙O交于点E,若⊙O的半径为3,PC=4.求弦CE的长.6.如图,PA,PB是⊙O的切线,A,B为切点,∠APB=60°,连接PO并延长与⊙O交于C点,连接AC,BC.(1)求证:四边形ACBP是菱形;(2)若⊙O 的半径为1,求菱形ACBP 的面积.7.如图,⊙O 是边长为6的等边△ABC 的外接圆,点D 为BC ︵的中点,过点D 作DE ∥BC ,DE 交AC 的延长线于点E ,连接AD ,CD.(1)DE 与⊙O 的位置关系是相切; (2)求△ADC 的内切圆半径r.专题6 求阴影部分的面积类型1 直接利用公式求面积1.如图,从一块直径为2 m 的圆形铁皮上剪出一个圆心角为90°的扇形,则此扇形的面积为( ) A.π2 m 2 B.32π m 2 C .π m 2 D .2π m 2类型2 利用和差法求面积2.如图,在Rt △ABC 中,∠ACB =90°,AC =23,以点B 为圆心,BC 的长为半径作弧,交AB 于点D.若点D 为AB 的中点,则阴影部分的面积是( )A .23-23πB .43-23πC .23-43π D.23π3.如图,在扇形AOB 中,∠AOB =90°,正方形CDEF 的顶点C 是AB ︵的中点,点D 在OB 上,点E 在OB 的延长线上,当正方形CDEF 的边长为22时,则阴影部分的面积为( )A .2π-4B .4π-8C .2π-8D .4π-44.如图,分别以五边形ABCDE 的顶点为圆心,以1为半径作五个圆,则图中阴影部分的面积之和为( )A.32π B .3π C.72π D .2π5.如图,将半径为2,圆心角为120°的扇形OAB 绕点A 逆时针旋转60°,点O ,B 的对应点分别为O ′,B ′,连接BB ′,则图中阴影部分的面积是( )A.2π3 B .23-π3 C .23-2π3 D .43-2π36.如图,在正方形ABCD 中,AB =12,点E 为BC 的中点,以CD 为直径作半圆CFD ,点F 为半圆的中点,连接AF ,EF ,图中阴影部分的面积是( )A .18+36πB .24+18πC .18+18πD .12+18π7.如图,在平行四边形ABCD 中,AB <AD ,∠D =30°,CD =4,以AB 为直径的⊙O 交BC 于点E ,则阴影部分的面积为 .8.如图,在Rt △ABC ,∠B =90°,∠C =30°,O 为AC 上一点,OA =2,以O 为圆心,以OA 为半径的圆与CB 相切于点E ,与AB 相交于点F ,连接OE ,OF ,则图中阴影部分的面积是 .类型3 利用等积转化法求面积9.如图,AB 是⊙O 的直径,弦CD ⊥AB ,∠CDB =30°,CD =23,则阴影部分的面积为( )A .2πB .Π C.π3 D.2π310.如图,在正方形ABCD中,O为对角线交点,将扇形AOD绕点O顺时针旋转一定角度得到扇形EOF,则在旋转过程中图中阴影部分的面积()A.不变 B.由大变小C.由小变大 D.先由小变大,后由大变小11.如图是某商品的标志图案,AC与BD是⊙O的两条直径,首尾顺次连接点A,B,C,D,得到四边形ABCD.若AC =10 cm,∠BAC=36°,则图中阴影部分的面积为()A.5π cm2 B.10π cm2 C.15π cm2 D.20π cm212.运用图形变化的方法研究下列问题:如图,AB是⊙O的直径,CD,EF是⊙O的弦,且AB∥CD∥EF,AB=10,CD =6,EF=8.则图中阴影部分的面积是()A.252π B.10π C.24+4π D.24+5π13.如图,在△ACB中,∠BAC=90°,AC=2,AB=3,现将△ACB绕点A逆时针旋转90°得到△AC1B1,则阴影部分的面积为.参考答案:专题1 与圆周角有关的辅助线作法1.D2.A3.D4.D5.110°__.67.1.829.D11.3.专题2 圆周角定理——教材P90T14的变式与应用1.解:△ABC是等腰三角形,理由:∵四边形APBC是圆内接四边形,∴∠EPA=∠ACB.∵∠EPA=∠CPA,∠CPA=∠ABC,∴∠ACB=∠ABC.∴AB=AC.∴△ABC是等腰三角形.2.解:(1)证明:∵∠ABC=∠APC=60°,∠BAC=∠APC=60°,∴∠ABC=∠BAC=60°.∴△ABC是等边三角形.(2)连接OB ,OC.可得∠BOC =2∠BAC =2×60°=120°. ∵OB =OC ,∴∠OBD =∠OCD =12×(180°-120°)=30°.∵∠ODB =90°,∴OD =12OB =4.3.证明:(1)∵∠ACB =∠ADB =45°, ∠ABD =45°, ∴∠BAD =90°. ∴BD 是该圆的直径.(2)在CD 的延长线上截取DE =BC ,连接EA. ∵∠ABD =∠ADB ,∴AB =AD.∵∠ADE +∠ADC =180°,∠ABC +∠ADC =180°,∴∠ABC =∠ADE. 在△ABC 和△ADE 中, ⎩⎪⎨⎪⎧AB =AD ,∠ABC =∠ADE ,BC =DE ,∴△ABC ≌△ADE (SAS ). ∴∠BAC =∠DAE.∴∠BAC +∠CAD =∠DAE +∠CAD. ∴∠BAD =∠CAE =90°.∵∠ACD=∠ABD=45°,∴△CAE是等腰直角三角形.∴2AC=CE.∴2AC=DE+CD=BC+CD.专题3 证明切线的两种常用方法1.证明:连接OA,AD.∵∠B=2∠P,∠B=∠ADC.∴∠ADC=2∠P.又∵AP=AC,∴∠P=∠ACP.∴∠ADC=2∠ACP.∵CD为直径,∴∠DAC=90°.∴∠ADC=60°,∠ACD=30°.∴△ADO为等边三角形.∴∠AOP=60°.而∠P=∠ACP=30°,∴∠OAP=90°.∴OA⊥PA.又∵AO为⊙O的半径,∴PA是⊙O的切线.2.证明:连接OC,∵CF ︵=CB ︵,OA =OC , ∴∠DAC =∠BAC =∠ACO. ∴AD ∥OC. ∵CD ⊥AF 于点D , ∴∠DCO =90°. 又∵OC 为⊙O 的半径, ∴CD 为⊙O 的切线. 3.证明:(1)连接OD. ∵AD ∥OC ,∴∠DAO =∠COB ,∠ADO =∠DOC. 又∵OA =OD ,∴∠DAO =∠ADO. ∴∠COB =∠COD. ∴DE ︵=BE ︵.(2)由(1)知∠DOE =∠BOE , 在△COD 和△COB 中, ⎩⎪⎨⎪⎧CO =CO ,∠DOC =∠BOC ,OD =OB ,∴△COD ≌△COB (SAS ). ∴∠CDO =∠B.又∵BC ⊥AB ,∴∠CDO =∠B =90°.∵点D在⊙O上,∴CD是⊙O的切线.4.证明:连接OC.∵⊙O的半径为3,∴OC=OB=3.又∵BP=2,∴OP=5.在△OCP中,OC2+PC2=32+42=52=OP2,∴△OCP为直角三角形,∠OCP=90°.∴OC⊥PC.∵C是⊙O上一点,∴PC为⊙O的切线.5.证明:连接OA,OD,作OF⊥AC于点F,垂足为F. ∵△ABC为等腰三角形,O是底边BC的中点,∴AO⊥BC,AO平分∠BAC.∵AB与⊙O相切于点D,∴OD⊥AB.而OF⊥AC,∴OF=OD.∴AC是⊙O的切线.专题4 与切线长有关的教材变式1.证明:∵∠BOC=90°,∴∠OBC+∠OCB=90°.又∵BE与BF为⊙O的切线,∴BO为∠EBF的平分线.∴∠OBE=∠OBF.同理可得∠OCB=∠OCG.∴∠OBE+∠OCG=90°.∴∠OBC+∠OCB+∠OBE+∠OCG=180°,即∠ABF+∠DCF=180°.∴AB∥CD.2.解:过点D作DF⊥BC于点F.∵AD,BC分别是⊙O的切线,∴∠OAD=∠OBF=90°.又∵DF⊥BC,∴四边形ABFD为矩形.∴DF=AB=12 cm,BF=AD.∵AD,BC,DC分别为⊙O的切线,∴DE=DA=x,CE=CB=y.∴DC=x+y,CF=y-x.在Rt △DCF 中,由勾股定理,得DC 2=CF 2+DF 2,即(x +y )2=(y -x )2+122,整理,得xy =36.∴y =36x. ∴y 关于x 的函数解析式y =36x(x>0). 3.2.4.2.5.C专题5 与圆的切线有关的计算与证明1.C2.B3.B4.证明:(1)∵E 为△ABC 的内心,∴∠DAC =∠DAB ,∠CBE =∠EBA.又∵∠DBC =∠DAC ,∠DBE =∠DBC +∠CBE ,∠DEB =∠EAB +∠EBA ,∴∠DBE =∠DEB.∴DB =DE.(2)连接OD.∵BD =DF ,O 是BC 的中点,∴OD ∥CF.又∵BC 为⊙O 的直径,OB =OD ,∴∠ODB =∠DBO =∠DAC =45°.∴∠OCF =∠BOD =90°.∴OC ⊥CF.又∵OC 为⊙O 的半径,∴直线CF 为⊙O 的切线.5.解:(1)证明:过点O 作OD ⊥PB ,连接OC.∵AP 与⊙O 相切,∴OC ⊥AP.又∵OP 平分∠APB ,∴OD =OC.∴PB 是⊙O 的切线.(2)过点C 作CF ⊥PE 于点F.在Rt △OCP 中,OP =OC2+CP2=5.∵S △OCP =12OC ·CP =12OP ·CF ,∴CF =125. 在Rt △COF 中,OF =CO2-CF2=95. ∴FE =3+95=245.在Rt △CFE 中,CE =CF2+EF2=1255. 6.解:(1)证明:连接AO ,BO.∵PA ,PB 是⊙O 的切线,∴∠OAP =∠OBP =90°,PA =PB ,∠APO =∠BPO =12∠APB =30°. ∴∠AOP =60°.∵OA =OC ,∴∠OAC =∠OCA.∴∠AOP =∠CAO +∠ACO.∴∠ACO =30°.∴∠ACO =∠APO.∴AC =AP.同理BC =PB ,∴AC =BC =BP =AP.∴四边形ACBP 是菱形.(2)连接AB 交PC 于点D ,则AD ⊥PC.在Rt △AOD 中,∠AOD =60°,∴∠OAD =30°.∴OD =12OA =12. ∴AD =OA2-OD2=12-(12)2=32.∴PA =2AD =3,AB =2AD = 3.∴OP =OA2+PA2=2,PC =OP +OC =2+1=3.∴菱形ACBP 的面积为12AB ·PC =332. 7.解:∵D 为BC ︵的中点,∴BD ︵=DC ︵.∴∠BAD =∠DAC =30°.又∵AB =AC ,∴AD 垂直平分BC.∴AD 为⊙O 的直径.∴∠ACD =90°.在Rt △ACD 中,∠DAC =30°,设DC =x ,则AD =2x.由勾股定理,得AD 2=DC 2+AC 2,即(2x )2=x 2+62.解得x =2 3.∴DC =23,AD =4 3.作Rt △ADC 的内切圆⊙O ′,分别切AD ,AC ,DC 于点F ,G ,H ,易知CG =CH =r , ∴AG =AF =6-r ,DH =DF =23-r.∵AF +DF =AD ,∴6-r +23-r =4 3.∴r =3- 3.专题6 求阴影部分的面积1.A2.A3.A4.C5.C6.C73823 9.D10.A11.B12.A13.94π.。
2020年九年级数学 中考第二轮专题训练 圆 (含答案)

2020年九年级数学中考第二轮专题训练圆1、已知:如图,⊙O的直径A B与弦C D相交于E,=,⊙O的切线B F与弦A D的延长线相交于点F.(1)求证:C D∥B F.(2)连接B C,若⊙O 的半径为4,cos∠BCD =,求线段A D、C D的长.2、如图,在△ABC中,AB=AC,以AB为直径的半圆O交BC于点D,DE⊥AC,垂足为E.(1)判断D E与⊙O 的位置关系,并证明你的结论;(2)如果⊙O的直径为9,cos B=,求D E的长.3、如图,在Rt△ABC 中,∠ABC=90°,以A B为直径作⊙O,点D 为⊙O上一点,且C D=C B,连接D O并延长交C B的延长线于点E.(1)判断直线C D与⊙O 的位置关系,并说明理由;(2)若BE=2,DE=4,求圆的半径及A C的长.4、如图,BC 是⊙O的直径,CE 是⊙O的弦,过点E 作⊙O 的切线,交C B的延长线于点G,过点B作B F⊥G E于点F,交C E的延长线于点A.(1)求证:∠ABG=2∠C;(2)若G F=33,GB=6,求⊙O的半径.5、如图,点A、B、C分别是⊙O上的点,∠B=60°,CD是⊙O的直径,P是C D延长线上的点,且A P=A C.(1)求证:A P是⊙O的切线;(2)若A C=3,求P D 的长.6、如图,在矩形A B C D中,CD=2,AD =4,点P在B C上,将△A B P沿A P折叠,点B 恰好落在对角线A C上的E点,O为A C上一点,⊙O经过点A,P(1)求证:BC 是⊙O的切线;(2)在边C B上截取C F=C E,点F是线段B C的黄金分割点吗?请说明理由.7、已知:如图,在Rt△ABC 中,∠C=90°,点O在A B上,以O为圆心,O A 长为半径的圆与A C,A B分别交于点D,E,且∠CB D=∠A.(1)判断直线B D与⊙O的位置关系,并证明你的结论;(2)若B C=2,B D=,求的值.8、如图,AB是⊙O的直径,C是⊙O上一点,过点O作OD⊥AB,交BC的延长线于D,交AC于点E,F是DE的中点,连接CF.(1)求证:CF是⊙O的切线.(2)若∠A=22.5°,求证:AC=DC.9、如图,在△A B C中,A B=A C,以A B为直径的⊙O分别交B C、A C于点D、E,连接E B交O D于点F.(1)求证:O D⊥B E;(2)若D E=,A B=,求A E的长.10、如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC,垂足为点F.(1)求证:直线D F是⊙O的切线;(2)求证:B C2=4C F•A C;(3)若⊙O的半径为 4,∠CDF=15°,求阴影部分的面积.11、如图,A B是⊙O的直径,C是⊙O上一点,D是的中点,E为O D延长线上一点,且∠C A E=2∠C,AC 与B D交于点H,与O E交于点F.(1)求证:AE 是⊙O的切线;(2)若DH=9,tan C=,求直径A B的长.12、已知Rt△ABC 中,∠ABC=90°,以A B为直径作⊙O交A C于点D,连接B D.(1)如图 1,若BD :CD =3:4,AD =3,求⊙O的直径A B的长;(2)如图 2,若E是B C的中点,连接E D,请你判断直线E D与⊙O的位置关系,并证明你的结论.13、如图,△A B C内接于⊙O,A B为直径,作O D⊥A B交A C于点D,延长B C,O D交于点F,过点C作⊙O的切线C E,交O F于点E.(1)求证:E C=E D;(2)如果OA=4,EF=3,求弦A C的长.14、以坐标原点为圆心,1 为半径的圆分别交x,y轴的正半轴于点A,B.(1)如图一,动点P从点A处出发,沿x轴向右匀速运动,与此同时,动点Q从点B处出发,沿圆周按顺时针方向匀速运动.若点Q的运动速度比点P的运动速度慢,经过 1 秒后点P运动到点(2,0),此时P Q 恰好是⊙O的切线,连接O Q.求∠Q O P的大小;(2)若点Q按照(1)中的方向和速度继续运动,点P停留在点(2,0)处不动,求点Q 再经过 5 秒后直线PQ被⊙O截得的弦长.15、如图,已知半径为 1 的⊙O1 与x轴交于A,B两点,O M 为⊙O1 的切线,切点为M,圆心O1的坐标为(2,0),二次函数y=﹣x2+b x+c的图象经过A,B两点.(1)求二次函数的解析式;(2)求切线O M的函数解析式;(3)线段O M 上存在一点P,使得以P,O,A为顶点的三角形与△O O1M 相似.请问有几个符合条件的点P 并分别求出它们的坐标.16、(1)方法选择如图①,四边形A B C D是⊙O的内接四边形,连接A C,B D,A B=B C=A C.求证:B D=A D+C D.小颖认为可用截长法证明:在D B上截取D M=A D,连接A M…小军认为可用补短法证明:延长C D至点N,使得D N=A D…请你选择一种方法证明.(2)类比探究【探究 1】如图②,四边形A B C D是⊙O的内接四边形,连接A C,B D,B C是⊙O的直径,A B=A C.试用等式表示线段A D,B D,C D之间的数量关系,井证明你的结论.【探究 2】如图③,四边形A B C D是⊙O的内接四边形,连接A C,B D.若B C是⊙O的直径,∠ABC =30°,则线段A D,B D,C D之间的等量关系式是.(3)拓展猜想如图④,四边形A B C D是⊙O的内接四边形,连接A C,B D.若B C是⊙O的直径,B C:A C:A B=a:b:c,则线段A D,B D,C D之间的等量关系式是.17、如图,Rt△ABC 中,∠ACB=90°,以B C上一点O为圆心作圆与A B相切于点D,与B C分别交于点F、N,连接D F并延长交A C的延长线点E.(1)求证:A E=A D;(2)过点D作D H⊥B C于点B,连接A F并延长交⊙O于点G,连接D G,若D O平分∠G D H.求证:∠A F D=2∠D F N;(3)在(2)的条件下,延长D G交A E的延长线于点P,连接P F并延长交⊙O于点M,若FM=5,FH =9,求O H的长.参考答案1、(1)证明:∵直径A B平分,∴AB⊥CD.∵BF与⊙O相切,AB是⊙O的直径,∴A B⊥B F.∴C D∥B F.(2)解:连接BD,BC.∵AB是⊙O的直径,∴∠ADB=90°.在Rt△ADB中,∵cos∠BAF=c os∠BCD=,AB=4×2=8.∴AD=AB •c o s∠BAF=8×=6.∵AB⊥CD于E,在Rt△AED中,c os∠BAF=c os∠BCD=,sin∠BAF=.∴DE=AD •s i n∠BAF=6×.∵直径A B平分,∴C D=2D E=3.2、解:(1)答:D E是⊙O的切线.证明:连接O D,A D,∵AB是直径,∴∠ADB=90°,即A D⊥B C,∵O D=O A,∴∠O D A=∠O A D,∴∠O A D=∠C A D,∴∠O D A=∠C A D,又∵D E⊥A C,∴∠EDA+∠CAD=90°,∴∠EDA+∠ODA=90°,即:O D⊥D E,∴DE是⊙O的切线;(2)解:∵AB是⊙O的直径,∴∠ADB=90°,在Rt△ADB中,∵cos∠B==,AB=9,∴B D=C D=3,在Rt△CDE中,∵cos∠C=,∴CE=CD•cos∠C=3•cos∠B=3×=1,∴D E==2.3、(1)证明:连接O C.∵CB=CD,CO=CO,OB=OD,∴△O C B≌△O C D(S S S),∴∠ODC=∠OBC=90°,∴OD⊥DC,∴DC是⊙O的切线;(2)解:设⊙O的半径为r.在Rt△O B E中,∵O E2=E B2+O B2,∴(4﹣r)2=r2+22,∴r=1.5,∵tan∠E==,∴=,∴CD=BC=3,在Rt△ABC中,A C===3.∴圆的半径为1.5,AC 的长为3.4、(1)证明:连接O E,∵EG是⊙O的切线,∴O E⊥E G,∵B F⊥G E,∴O E∥A B,∴∠A=∠OEC,∵OE=OC,∴∠O E C=∠C,∴∠A=∠C,∵∠ABG=∠A+∠C,∴∠ABG=2∠C;(2)解:∵BF⊥GE,∴∠BFG=90°,∵GF=3,GB=6,∴B F==3,∵BF∥OE,∴△B G F∽△O G E,∴=,∴=,∴OE=6,∴⊙O的半径为 6.5、解:(1)证明:连接O A,∵∠B=60°,∴∠AOC=2∠B=120°,∵OA=OC,∴∠ACP=∠CAO=30°,∴∠AOP=60°,又∵A P=A C,∴∠P=∠ACP=30°,∴∠OAP=90°,即O A⊥A P,∵点A在⊙O上,∴AP是⊙O的切线.(2)解:连接A D,∵CD是⊙O的直径,∴∠CAD=90°,∴AD=AC∙tan30°=,C D=2A D=2,∴D O=A O=C D=,在Rt△P A O中,由勾股定理得:P A2+A O2=P O2,∴32+()2=(P D+)2,∵PD的值为正数,∴P D=.6、解:(1)连接O P,则∠P A O=∠A P O,而△A E P是由△A B P沿A P折叠而得:故A E=A B=4,∠O A P=∠P A B,∴∠BAP=∠OPA,∴AB∥OP,∴∠OPC=90°,∴BC是⊙O的切线;(2)C F=C E=A C﹣A E=﹣4=2﹣2,=,故:点F是线段B C的黄金分割点. 7、解:(1)直线B D与⊙O相切.证明:如图 1,连接O D.∵OA=OD,∴∠A=∠A D O.∵∠C=90°,∴∠CBD +∠CDB=90°.又∵∠C B D=∠A,∴∠ADO+∠CDB=90°.∴∠ODB=90°.∴直线BD与⊙O相切.(2)解法一:如图 1,连接DE.∵∠C=90°,BC=2,BD=∴.∵AE是⊙O的直径,∴∠ADE=90°.∴.∵∠CBD=∠A,∴==.∵AE=2AO,∴=.解法二:如图 2,过点O作OH⊥AD于点H.∴.∴∵∠C=90°,BC=2,BD=∴.∵∠CBD=∠A,∴==.∴=.8、(1)证明:∵AB是⊙O的直径,∴∠ACB=∠ACD=90°,∵点F是ED的中点,∴CF=EF=DF,∴∠AEO=∠FEC=∠FCE,∵OA=OC,∴∠OCA=∠OAC,∵OD⊥AB,∴∠OAC+∠AEO=90°,∴∠OCA+∠FCE=90°,即OC⊥FC,∴CF与⊙O相切;(2)解:∵OD⊥AB,AC⊥BD,∴∠AOE=∠ACD=90°,∵∠AEO=∠DEC,∴∠OAE=∠CDE=22.5°,∵A O=B O,∴A D=B D,∴∠ADO=∠BDO=22.5°,∴∠ADB=45°,∴∠CAD=∠ADC=45°,∴AC=CD.9、证明:(1)连接A D.∵AB是⊙O的直径,∴∠ADB=∠AEB=90°,∵A B=A C,∴D C=D B.∵O A=O B,∴O D∥A C.∴∠OFB=∠AEB=90°,∴OD⊥BE.(2)设AE=x,∵OD⊥BE,∴可得OD是BE的中垂线,∴DE=DB,∴∠1=∠2,∴B D=E D=,∵O D⊥E B,∴F E=F B.∴O F=A E=,D F=O D﹣O F=.在Rt△DFB 中,;在Rt△OFB 中,;∴=.解得,即.10、解:(1)如图所示,连接O D,∵AB=AC,∴∠ABC=∠C,而OB=OD,∴∠ODB=∠ABC=∠C,∵DF⊥AC,∴∠CDF+∠C=90°,∴∠CDF+∠ODB=90°,∴∠ODF=90°,∴直线DF是⊙O的切线;(2)连接A D,则A D⊥B C,则A B=A C,则D B=D C=,∵∠CDF+∠C=90°,∠C+∠DAC=90°,∴∠CDF=∠DCA,而∠D F C=∠A D C=90°,∴△C F D∽△C D A,∴C D2=C F•A C,即B C2=4C F•A C;(3)连接O E,∵∠CDF=15°,∠C=75°,∴∠OAE=30°=∠OEA,∴∠AOE=120°,S△O A E=A E×O E sin∠O E A=×2×O E×cos∠O E A×O E sin∠O E A=4,S =﹣S =×π×42﹣4 =﹣4 .阴影部分S扇形OAE △OAE11、解:(1)∵D是的中点,∴OE⊥AC,∴∠AFE=90°,∴∠E+∠EAF=90°,∵∠AOE=2∠C,∠CAE=2∠C,∴∠CAE=∠AOE,∴∠E+∠AOE=90°,∴∠EAO=90°,∴AE是⊙O的切线;(2)∵∠C=∠B,∵OD=OB,∴∠B=∠O D B,∴∠O D B=∠C,∴tan C=tan∠ODB==,∴设HF=3x,DF=4x,∴DH=5x=9,∴x=,∴D F=,H F=,∵∠C=∠FDH,∠DFH=∠CFD,∴△D F H∽△C F D,∴=,∴C F==,∴A F=C F=,设O A=O D=x,∴O F=x﹣,∵A F2+O F2=O A2,∴()2+(x﹣)2=x2,解得:x=10,∴OA=10,∴直径AB的长为 20.12、解:(1)如图,∵A B是⊙O的直径,∴∠ADB=90°.则∠CDB=∠ADB=90°.∴∠C+∠CBD=90°.∵∠ABC=90°,∴∠ABD+∠CBD=90°.∴∠C=∠A B D.∴△A D B∽△B D C.∴.∵BD:CD=3:4,AD=3,∴BD=4.在Rt△A B D中,A B=;(3 分)(2)直线E D与⊙O相切.证明:如图,连接O D.由(1)得∠BDC=90°.∵E是BC的中点,∴D E=B E=B C,∴∠E D B=∠E B D,∵OB=OD,∴∠ODB=∠OBD.∵∠OBD+∠EBD=90°,∴∠ODB+∠EDB=∠ODE=90°.∵点D在⊙O上,且OD⊥DE∴ED是⊙O的切线.(5 分)13、(1)证明:连接O C,∵CE与⊙O相切,为C是⊙O的半径,∴OC⊥CE,∴∠OCA+∠ACE=90°,∵OA=OC,∴∠A=∠OCA,∴∠ACE+∠A=90°,∵OD⊥AB,∴∠ODA+∠A=90°,∵∠ODA=∠CDE,∴∠CDE+∠A=90°,∴∠CDE=∠ACE,∴EC=ED;(2)解:∵AB为⊙O的直径,∴∠ACB=90°,在Rt△DCF中,∠DCE+∠ECF=90°,∠DCE=∠CDE,∴∠CDE +∠ECF=90°,∵∠CDE +∠F=90°,∴∠ECF=∠F,∴E C=E F,∵EF=3,∴EC=DE=3,∴O E==5,∴OD=OE﹣DE=2,在Rt△OAD中,A D==2,在Rt△AOD 和Rt△ACB 中,∵∠A=∠A,∠A C B=∠A O D,∴Rt△AOD∽Rt△ACB,∴,即,∵∴O C = = .. ∴A C = .14、解:(1)如图一,连接A Q .由题意可知:O Q =O A =1.∵OP =2,∴A 为 OP 的中点.∵PQ 与⊙O 相切于点 Q ,∴△O Q P 为直角三角形.∴.即△OAQ 为等边三角形.∴∠QOP =60°.(2)由(1)可知点 Q 运动 1 秒时经过的弧长所对的圆心角为 30°,若 Q 按照(1)中的方向和速度继续运动,那么再过 5 秒,则 Q 点落在⊙O 与 y 轴负半轴的交点处(如图二).设 直线 P Q 与⊙O 的另外一个交点为 D ,过 O 作 OC ⊥QD 于点 C ,则 C 为 QD 的中点.∵∠QOP =90°,OQ =1,OP =2,∴Q P =. , ∵O C ⊥Q D ,O Q =1,O C = ,∴Q C == .∴QD =15、解:(1)∵圆心的坐标为O1(2,0),⊙O1 半径为 1,∴A(1,0),B(3,0),∵二次函数y=﹣x2+b x+c的图象经过点A,B,∴可得方程组,解得:,∴二次函数解析式为y=﹣x2+4x﹣3.(2)过点M作M F⊥X轴,垂足为F.∵O M是⊙O1 的切线,M为切点,∴O1M⊥O M(圆的切线垂直于经过切点的半径).在R T△O O1M中,sin∠O1O M==,∵∠O1O M为锐角,∴∠O1O M=30°,∴O M=O O1•cos30°=,在R T△M O F中,OF=OM •cos30°=.MF=O M sin30°=.∴点M坐标为(),设切线O M的函数解析式为y=k x(k≠0),由题意可知=k,∴k=,∴切线O M的函数解析式为y=x(3)两个,①过点A作A P1⊥x轴,与O M交于点P1,可得 Rt△A P1O∽Rt△M O1O(两角对应相等两三角形相似),P1A=O A•tan∠A O P1=,∴P1(1,);②过点A作A P2⊥O M,垂足为,过P2 点作P2 H⊥O A,垂足为H.可得 Rt△O P2A∽Rt△O1 M O(两角对应相等两三角形相似),在Rt△O P2A中,∵OA=1,∴P2=O A•cos30°=,在Rt△O P2 H中,O H=O P2•cos∠A O P2=,P2H=O P2 •sin∠A O P2=,P2(,),∴符合条件的P点坐标有(1,),(,).16、解:(1)方法选择:∵A B=B C=A C,∴∠ACB=∠ABC=60°,如图①,在BD上截取DEMAD,连接AM,∵∠ADB=∠ACB=60°,∴△ADM是等边三角形,∴AM=AD,∵∠ABM=∠ACD,∵∠AMB=∠ADC=120°,∴△A B M≌△A C D(A A S),∴BM=CD,∴BD=BM+DM=CD+AD;(2)类比探究:如图②,∵BC是⊙O的直径,∴∠BAC=90°,∵AB=AC,∴∠ABC=∠ACB=45°,过A作A M⊥A D交B D于M,∵∠ADB=∠ACB=45°,∴△ADM是等腰直角三角形,∴AM=AD,∠AMD=45°,∴D M=A D,∴∠AMB=∠ADC=135°,∵∠ABM=∠ACD,∴△A B M≌△A C D(A A S),∴BM=CD,∴B D=B M+D M=C D+A D;【探究 2】如图③,∵若BC是⊙O的直径,∠ABC=30°,∴∠BAC=90°,∠ACB=60°,过A作A M⊥A D交B D于M,∵∠ADB=∠ACB=60°,∴∠AMD=30°,∴MD=2AD,∵∠ABD=∠ACD,∠AMB=∠ADC=150°,∴△ABM∽△ACD,∴=,∴B M=C D,∴B D=B M+D M=C D+2A D;故答案为:B D=C D+2A D;(3)拓展猜想:B D=B M+D M=C D+A D;理由:如图④,∵若B C是⊙O的直径,∴∠BAC=90°,过A作AM⊥AD交BD于M,∴∠MAD=90°,∴∠B A M=∠D A C,∴△A B M∽△A C D,∴=,∴B M=C D,∵∠ADB=∠ACB,∠BAC=∠NAD=90°,∴△ADM∽△ACB,∴==,∴D M=A D,∴B D=B M+D M=C D+A D.故答案为:B D=C D+A D17、解:(1)证明:∵∠A C B=90°∴∠E+∠CFE=∠ACB=90°∵∠CFE=∠OFD∴∠E+∠OFD=90°∵AB切⊙O于D∴OD⊥AB∴∠ODF+∠ADE=90°∵OD=OF∴∠OFD=∠ODF∴∠E=∠ADE∴AE=AD(2)证明:连接D N∵DO平分∠GDH∴设∠ODG=∠ODH=α,设∠FDG=β,则∠FDH=2α+β∵OF=OD∴∠DFN=∠ODF=α+β∵DH⊥FN∴∠DHF=90°∴∠DFN+∠FDH=90°,即α+β+2α+β=3α+2β=90°∵FN为⊙O直径∴∠FDN=90°∴∠DNF=90°﹣∠DFN=90°﹣(2α+β)=3α+2β﹣(α+β)=2α+β∴∠G=∠DNF=2α+β∵∠AFD=∠G+∠FDG=2α+β+β=2α+2β∴∠AFD=2∠DFN(3)过O作O Q∥A B交F M于点Q∵∠AEF+∠EFC=90°,∠DFN+∠FDH=90°,∠EFC=∠DFN∴∠AEF=∠FDH=2α+β∴∠ADE=∠AEF=2α+β∴∠FAD=180°﹣∠AFD﹣∠ADF=2(3α+2β)﹣(2α+2β)﹣(2α+β)=2α+β 即∠F A D=∠A D F∴AF=DF∴F在AD的垂直平分线上∵∠AEF=∠FGD=2α+β,∠AFE=∠DFG∴∠EAF=∠FDG=β∴∠PAD=∠PDA=β+(2α+β)=2α+2β∴PA=PD∴P在A D的垂直平分线上即P M垂直平分A D∴OQ⊥FM∴∠OQF=90°,FQ=F M=∵OQ∥AB∴∠FOQ=∠B∵∠B+∠DOH=∠DOH+∠ODH=90°∴∠B=∠ODH∴∠F O Q=∠O D H在△F O Q与△O D H中∴△FOQ≌△ODH(AAS)∴OH=FQ=。
2020 人教版 九年级 圆专题复习练习题(有部分答案)

圆一、单选题1.如图所示,MN 为⊙O 的弦,52N ∠=o ,则MON ∠的度数为( )A .38oB .52oC .76oD .104o2.如图,点A ,B ,C 是⊙O 上的三点,若∠BOC=50°,则∠A 的度数是( )A .25°B .20°C .80°D .100°3.如图,AB 是⊙O 的直径,AC 是⊙O 的切线,A 为切点,BC 与⊙O 交于点D ,连结OD .若50C ∠=︒,则∠AOD 的度数为( )A .40︒B .50︒C .80︒D .100︒4.如图,AB 为⊙O 的直径,点C 在⊙O 上,若∠OCA =40°,AB =6,则弧BC 的长为( )A .83πB .103πC .53πD .43π5.如果,AB 是⊙O 的切线,A 为切点,,AB=5,AC 是⊙O 的弦,OH ⊥AC ,垂足为H ,若OH=3,则弦AC 的长为( )A.5 B.6 C.8 D.106.如图,已知⊙O 是正方形ABCD 的外接圆,点E 是弧AD 上任意一点,则∠BEC 的度数为()A.30°B.45°C.60°D.90°7.以O为中心点的量角器与直角三角板ABC如图所示摆放,直角顶点B在零刻度线所在直线DE上,且量角器与三角板只有一个公共点P,若点P的读数为35°,则∠CBD的度数是()A.55°B.45°C.35°D.258.如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,AB长为25cm,贴纸部分的宽BD为15cm,若纸扇两面贴纸,则贴纸的面积为()A.175πcm2B.350πcm2C.8003πcm2D.150πcm29.下列说法正确的是( )A.等弧所对的圆心角相等B.平分弦的直径垂直于这条弦C.经过三点可以作一个圆D.相等的圆心角所对的弧相等10.如图,四边形ABCD内接于⊙O,连接OA,OC.若∠AOC=∠ABC,则∠D的大小为( )A.50°B.60°C.80°D.120°11.如图,从一张腰长为90cm,顶角为120︒的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的底面半径为()A.15cm B.12cm C.10cm D.20cm12.如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是()A.πB.54πC.3+πD.8﹣π二、填空题13.若圆锥的底面积为16π cm2,母线长为12 cm,则它的侧面展开图的圆心角为__________.14.已知扇形的圆心角100°,所对的弧长为53π,则此扇形的面积是_________.15.如图,AB是⊙O的直径,CD是⊙O的弦,AB⊥CD于点E,AE=CD,若⊙O的半径为5,则弦CD的长为_____.16.如图,∆ABC 是圆O 的内接三角形,连接OA 、OC ,若∠AOC =∠ABC ,弦AC =则圆O 的半径为__________.17.如图,直线y=-34x-3交x 轴于点A ,交y 轴于点B ,点P 是x 轴上一动点,以点P 为圆心,以1个单位长度为半径作⊙P ,当⊙P 与直线AB 相切时,点P 的坐标是_______.18.如图,菱形ABCD 中,2AB =,60C ∠=°,菱形ABCD 在直线L 上向右作无滑动的翻滚,每绕着一个顶点旋转60︒叫一次操作,则经过45次这样的操作菱形中心O 所经过的路径总长为______.(结果保留π)19.如图,四边形ABCD 内接于O e ,若四边形ABCO 是平行四边形,则ADC ∠的大小为_______.20.如图,在边长为4的正方形ABCD中,以点B为圆心,以AB为半径画弧,交对角线BD于点E,则图中阴影部分的面积是_____(结果保留π)三、解答题21.在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O 经过点E,且交BC于点F.(1)求证:AC是⊙O的切线;(2)若BF=6,⊙O的半径为5,求CE的长.22.如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,且AC=CD,∠ACD=120°. (1)求证:CD是⊙O的切线;e的半径为2,求图中阴影部分的面积.(2)若O23.如图,△ABC 内接于⊙O,∠B=60°,CD 是⊙O 的直径,点P 是CD 延长线上的一点且AP=AC.(1)求证:P A 是⊙O 的切线;(2)若2AB =+,4BC =,求⊙O 的半径24.如图,⊙O 是△ABC 的外接圆,AB 是直径,D 是AC 中点,直线OD 与⊙O 相交于E ,F 两点,P 是⊙O 外一点,P 在直线OD 上,连接P A ,PC ,AF ,且满足∠PCA =∠ABC .(1)证明:EF 2=4OD •OP ;(2)若tan ∠AFP =23,求DE BC的值. 25.已知如图,以Rt △ABC 的AC 边为直径作⊙O 交斜边AB 于点E ,连接EO 并延长交BC 的延长线于点D ,点F 为BC 的中点,连接EF(1)求证:EF 是⊙O 的切线;(2)若⊙O 的半径为3,∠EAC =60°,求AD 的长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3
B . 10π
A . 8π
3
D . 4π
5
圆
一、单选题
1.如图所示, MN 为⊙O 的弦, ∠N = 52o ,则 ∠MON 的度数为( )
A . 38o
B . 52o
C . 76o
D .104o
2.如图,点 A ,B ,C 是⊙O 上的三点,若∠BOC=50°,则∠A 的度数是(
)
A .25°
B .20°
C .80°
D .100°
3.如图,AB 是⊙ O 的直径,AC 是⊙ O 的切线,A 为切点,BC 与⊙ O 交于点 D ,连结 OD .若 ∠C = 50︒ ,则∠AOD 的度数为(
)
A . 40︒
B . 50︒
C . 80︒
D .100︒
4.如图,AB 为⊙O 的直径,点 C 在⊙O 上,若∠OCA =40°,AB =6,则弧 BC 的长为( )
3
C .
π
3
5.如果,AB 是⊙O 的切线,A 为切点,OB=5 2 ,AB=5,AC 是⊙O 的弦,OH ⊥AC ,
垂足为 H ,若 OH=3,则弦 AC 的长为( )
A.175πcm2B.350πcm2C.800
3D.150πcm2
A.5B.6C.8D.10
6.如图,已知⊙O是正方形ABCD的外接圆,点E是弧AD上任意一点,则∠BEC的度数为()
A.30°B.45°C.60°D.90°
7.以O为中心点的量角器与直角三角板ABC如图所示摆放,直角顶点B在零刻度线所在直线DE上,且量角器与三角板只有一个公共点P,若点P的读数为35°,则∠CBD的度数是()
A.55°B.45°C.35°D.25
8.如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,AB长为25cm,贴纸部分的宽BD为15cm,若纸扇两面贴纸,则贴纸的面积为()
πcm2
9.下列说法正确的是()
A.等弧所对的圆心角相等C.经过三点可以作一个圆B.平分弦的直径垂直于这条弦D.相等的圆心角所对的弧相等
10.如图,四边形ABCD内接于⊙O,连接OA,OC.若∠AOC=∠ABC,则∠D的大小
B . 5π 5
为(
)
A .50°
B .60°
C .80°
D .120°
11.如图,从一张腰长为 90cm ,顶角为120 ︒ 的等腰三角形铁皮 O AB 中剪出一个最大的扇
形 OCD ,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗) 则该圆锥的底面半径为
(
)
A .15cm
B .12cm
C .10cm
D . 20cm
12.如图,在 △Rt
AOB 中,∠AOB =90°,OA =3,OB =2,将 △Rt AOB 绕点 O 顺时针旋转 90°
后得 △Rt FOE ,将线段 EF 绕点 E 逆时针旋转 90°后得线段 ED ,分别以 O ,E 为圆心,OA 、
ED 长为半径画弧 AF 和弧 DF ,连接 AD ,则图中阴影部分面积是(
)
A .π
4 C .3+π
D .8﹣π
二、填空题
13.若圆锥的底面积为 16π cm 2,母线长为 12 cm ,则它的侧面展开图的圆心角为__________.
14.已知扇形的圆心角 100°,所对的弧长为 π
,则此扇形的面积是_________.
3
15.如图,AB 是⊙O 的直径,CD 是⊙O 的弦,AB ⊥CD 于点 E ,AE =CD ,若⊙O 的半径
为 5,则弦 CD 的长为_____.
16.如图,∆ABC是圆O的内接三角形,连接OA、OC,若∠AOC=∠ABC,弦AC=63则圆O的半径为__________.
17.如图,直线y=-
3
4
x-3交x轴于点A,交y轴于点B,点P是x轴上一动点,以点P为圆心,以1个单位长度为半径作⊙P,当⊙P与直线AB相切时,点P的坐标是_______.
18.如图,菱形ABCD中,AB=2,∠C=60°,菱形ABCD在直线L上向右作无滑动的翻滚,每绕着一个顶点旋转60︒叫一次操作,则经过45次这样的操作菱形中心O所经过的路径总长为______.(结果保留π)
19.如图,四边形ABCD内接于e O,若四边形ABCO是平行四边形,则∠ADC的大小为_______.
)
20.如图,在边长为4的正方形ABCD中,以点B为圆心,以AB为半径画弧,交对角线BD于点E,则图中阴影部分的面积是_____(结果保留π
三、解答题
21.在△Rt ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O 经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=6,⊙O的半径为5,求CE的长.
22.如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,且AC=CD,∠ACD=120°.(1)求证:C D是⊙O的切线;
(2)若e O的半径为2,求图中阴影部分的面积.
23.如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点且AP=AC.
(2)若tan∠AFP=
2
(1)求证:P A是⊙O的切线;
(2)若AB=2+15,BC=4,求⊙O的半径
24.如图,⊙O△是ABC的外接圆,AB是直径,D是AC中点,直线OD与⊙O相交于E,F两点,P是⊙O外一点,P在直线OD上,连接P A,PC,AF,且满足∠PCA=∠ABC.
(1)证明:EF2=4OD OP;
DE
,求的值.
3BC
25.已知如图,以△Rt ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为3,∠EAC=60°,求AD的长。
26.如图,⊙O△是ABC的外接圆,AB是直径,OD⊥AC,垂足为D点,直线OD与⊙O 相交于E,F两点,P是⊙O外一点,P在直线OD上,连接P A,PB,PC,且满足∠PCA
(3)若BC=8,
AB
3,0)或P(-
17
17.(-
7
=∠ABC
(1)求证:P A=PC;
(2)求证:P A是⊙O的切线;
3
=,求DE的长.
DF2
参考答案1.C
2.A
3.C
4.D
5.C
6.B
7.C
8.B
9.A
10.B
11.A
12.D
13.120°
5
14.π
2
15.8
16.6
3,0)
18.103π+5π19.600
20.8﹣2π21.(1)略;(2)CE=4.22.(1)略
(2)图中阴影部分的面积为23.(1)略;(2)32 3π.
24.(1)略;(2)4 5.
25.(2)37
26.(1)略;(2)略;(3)DE=8。
