数据结构C语言版 平衡二叉树
数据结构中平衡二叉树的教学探讨与研究

数据结构中平衡二叉树的教学探讨与研究作者:朱洪浩来源:《赤峰学院学报·自然科学版》 2012年第5期朱洪浩(蚌埠学院计算机科学与技术系,安徽蚌埠 233000)摘要:平衡二叉树是对二叉排序树的一种改进,又被称为AVL树,平衡二叉树的结构较好,可以提高查找运算的速度.本文分析了权威教材和相关论文中平衡二叉树的调整方法,这些方法学生普遍反映理解和掌握较困难.据此,本文依据平衡因子和二叉排序树的特性,设计出一种基于平衡因子和二叉排序树的平衡二叉树的调整方法,该方法易于理解和掌握.关键词:二叉排序树;平衡因子;平衡二叉树中图分类号:TP311.12 文献标识码:A 文章编号:1673-260X(2012)03-0019-031 引言数据结构课程是计算机及相关专业的核心课程,是程序设计的重要理论技术基础[1].在动态查找表中,平衡二叉树被广泛的应用,平衡二叉树又称AVL树,它是由Adel,son-Vel,skii和Landis两位数学家于1962年提出并用他们的名字来命名的.平衡二叉树或者是一棵空树,或者是满足下列条件的二叉排序树:二叉排序树的所有结点的平衡因子为-1、0和1.所谓平衡因子BF(Balance Factor)可定义为某结点左子树的深度减去右子树的深度[2].若二叉树中任一个结点的平衡因子的绝对值大于1,则该二叉树就不是平衡二叉树.平衡二叉树在插入结点和删除结点时候,会使其变得不平衡.为此,需要对二叉排序树进行调整,使之重新变为平衡二叉树.相关教材和论文中关于平衡二叉树的调整方法较难理解,学生难以接受.笔者通过阅读大量的相关资料,并且总结教学经验,提出了一种易于理解和实用的二叉排序树转换成平衡二叉树方法.2 平衡二叉树调整方法的文献综述由于平衡二叉树的重要性,以及学生在学习平衡二叉树调整的过程中,普遍反映对用于平衡二叉树调整的四种方法较难理解,算法复杂.为此,许多学者对平衡二叉树的调整进行了大量的研究.严蔚敏、吴伟民[1]在《数据结构》(C语言版)一书中二叉排序树调整为平衡二叉树采用左旋转(LL)、右旋转(LR)、先左旋转后右旋转(LR)、先右旋转后左旋转(RL)四种旋转方法.李春葆[2]在《数据结构教程》(第2版)一书中也是采用了LL、LR、RR、RL四种旋转方法.朱宇、张红彬[3]在《平衡二叉树的选择调整算法》一文中,提出利用“中为根、小为左、大为右”的调整策略,但本质上仍然是利用旋转的思想.胡云[4]在《快速构建AVL树》一文中采用“将二叉排序树中的数据进行排序,将中点数据作为根,大于中点的数据构成右子树,小于中点的数据构成左子树,然后采用同样的方法分别对左子树和右子树进行调整.”但从作者举出的实例可以看出,该方法与传统方法得到的平衡二叉树并不一致.杜薇薇[5]等在《基于平衡因子的AVL树设计实现》一文中则从平衡因子出发,并用数学公式进行了验证了插入和删除操作.刘绍翰[6]等在《一种简化的AVL树的实现方法》一文提出了高度平衡树(HAVL)它是一种新的AVL树的数学描述.以上文献中虽然提出了较好的调整方法,但在平衡二叉树的调整基本上仍然是采用旋转的方法进行调整,并没有从根本上解决学生的困惑.笔者在教学中发现学生对二叉排序树的建立普遍能熟练掌握,并且平衡二叉树的前提必须是一棵二叉排序树,为此,本文提出了一种利用平衡因子和构建二叉排序树的方法来实现平衡二叉树的调整,从而解决了学生的困惑.3 平衡二叉树的调整方法根据平衡二叉树的定义可知,插入和删除结点造成平衡二叉树不平衡的原因是产生2或者-2的平衡因子,其实,调整的方法只需将以平衡因子为2或者-2为根结点的子二叉排序树重新找一个根结点建立新的子二叉排序树.从而使二叉排序树中的平衡因子都为-1、0或者1,即调整成为平衡二叉树.问题的关键是如何找根结点,即序列中的第一个结点,具体方法如下文所示规则.3.1 插入结点的调整插入结点时,可以利用规则一、规则二进行:规则一某结点的平衡因子为2时,把以该结点为根的树采用中序遍历的方法进行遍历,即得到一个递增的子序列,同时看该结点的左孩子的平衡因子.(1)若左孩子的平衡因子为-1时,则取该左孩子的右孩子结点,并将其移动到序列的最前面,得到一个新的序列,对该序列构造二叉排序树.(2)若左孩子的平衡因子为1时,则取该左孩子结点,并将其移动到序列的最前面,得到一个新序列,对该序列构造二叉排序树.规则二某结点的平衡因子为-2时,把以该结点为根的树采用中序遍历的方法进行遍历,即得到一个递增的子序列,同时看该结点的右孩子的平衡因子.(1)若右孩子的平衡因子为-1时,则取该右孩子结点,并将其移动到序列的最前面,得到一个新的序列,对该序列构造二叉排序树.(2)若右孩子的平衡因子为1时,则取该右孩子的左孩子结点,并将其移动到序列的最前面,得到一个新序列,对该序列构造二叉排序树.3.2 删除结点的调整删除结点时,要确定删除的结点是否是叶子结点,具体方法见规则三.规则三(1)若删除的是叶子结点,直接删除,并且自底向下查看树中的平衡因子,若发现存在平衡因子为2时,采用规则一进行调整,若平衡因子为-2时,则采用规则二进行调整.(2)若不是叶子结点,首先按照二叉排序树非叶子结点的删除方法即用该结点左子树的最大值(或者右子树的最小值)代替该结点,然后在从二叉排序树中删去它的最大值(或者最小值),同样,自底向下查看树中的平衡因子,若发现存在平衡因子为2时,采用规则一进行调整,若平衡因子为-2时,则采用规则二进行调整.4 算法描述4.1 插入结点的算法平衡二叉树的插入实现算法步骤:(1)插入结点L(L总是作为新的叶子结点插入的),插入的方法同一般的二叉排序树插入结点一样.(2)沿着插入结点L的路线返回,逐层回溯.必要时修改L的祖先的平衡因子,发现平衡因子为2或-2时,则利用规则一、规则二找到结点R.(3)把该二叉排序树进行中序遍历,得到一递增序列,并把结点R移动到该序列的最前面,然后对新形成的序列构造二叉排序树.同时检查树中其它结点,若发现平衡因子为2或-2的结点,进行调整.重复(2)(3)直到所有的结点都保持平衡为止.(4)回到(1),继续插入新的结点,直到所有的结点都插入完为止.实例1:输入关键字序列{16,3,7,11,9,26,18, 14,15},构造一棵平衡二叉树[2].4.2 删除结点的算法平衡二叉树的删除实现算法步骤:(1)用二叉排序树的删除算法找到并删除结点L.(2)从被删除结点到根结点逐层向上回溯,必要时修改L的祖先结点的平衡因子,发现平衡因子为2或-2时,则利用规则一、规则二找到结点R.(3)把该二叉排序树进行中序遍历,得到一递增序列,并把结点R移动到该序列的最前面,然后对新形成的序列构造二叉排序树.(4)如果调整之后,子树的总高度比调整前降低了,仍然要继续回溯,直到所有结点平衡因子都为-1、0、1时,即都保持平衡为止.实例2:对实例1生成的AVL树,给出删除结点11,9,14的步骤[2].5 结束语平衡二叉树的调整是数据结构教学中的重点和难点,学生在学习的过程中对该部分内容难以理解和接受,为了打破这种局面,作者通过阅读大量的资料,总结了此方法,该方法“只需找到新的根结点,重新构造成二叉排序树”即可,通过教学实践发现,本文采用的方法容易被学生理解和掌握,在教学中得到了良好的效果,得到学生的认可.参考文献:〔1〕严蔚敏,吴伟民.数据结构(C语言版)[M].北京:清华大学出版社,2007.〔2〕李春葆.数据结构教程(第2版).北京:清华大学出版社,2007.〔3〕朱宇,张红彬.平衡二叉树的选择调整算法[J].中国科学院研究生院学报,2006,23(4):527-533.〔4〕胡云.快速构建AVL树[J].安阳师范学院学报,2007(6):61-63.〔5〕杜薇薇,张翼燕,瞿春柳.基于平衡因子的AVL树设计实现[J].计算机技术与发展,2010,20(3):24-27.〔6〕刘绍翰,高天行,黄志球.一种简化的AVL树的实现方法[J].三峡大学学报(自然科学版),2011,33(1):85-87.。
数据结构平衡二叉树的操作演示

平衡二叉树操作的演示1.需求分析本程序是利用平衡二叉树,实现动态查找表的基本功能:创建表,查找、插入、删除。
具体功能:(1)初始,平衡二叉树为空树,操作界面给出创建、查找、插入、删除、合并、分裂六种操作供选择。
每种操作均提示输入关键字。
每次插入或删除一个结点后,更新平衡二叉树的显示。
(2)平衡二叉树的显示采用凹入表现形式。
(3)合并两棵平衡二叉树。
(4)把一棵二叉树分裂为两棵平衡二叉树,使得在一棵树中的所有关键字都小于或等于x,另一棵树中的任一关键字都大于x。
如下图:2.概要设计平衡二叉树是在构造二叉排序树的过程中,每当插入一个新结点时,首先检查是否因插入新结点而破坏了二叉排序树的平衡性,若是则找出其中的最小不平衡子树,在保持二叉排序树特性的前提下,调整最小不平衡子树中各结点之间的链接关系,进行相应的旋转,使之成为新的平衡子树。
具体步骤:(1)每当插入一个新结点,从该结点开始向上计算各结点的平衡因子,即计算该结点的祖先结点的平衡因子,若该结点的祖先结点的平衡因子的绝对值不超过1,则平衡二叉树没有失去平衡,继续插入结点;(2)若插入结点的某祖先结点的平衡因子的绝对值大于1,则找出其中最小不平衡子树的根结点;(3)判断新插入的结点与最小不平衡子树的根结点个关系,确定是那种类型的调整;(4)如果是LL型或RR型,只需应用扁担原理旋转一次,在旋转过程中,如果出现冲突,应用旋转优先原则调整冲突;如果是LR型或RL型,则需应用扁担原理旋转两次,第一次最小不平衡子树的根结点先不动,调整插入结点所在子树,第二次再调整最小不平衡子树,在旋转过程中,如果出现冲突,应用旋转优先原则调整冲突;(5)计算调整后的平衡二叉树中各结点的平衡因子,检验是否因为旋转而破坏其他结点的平衡因子,以及调整后平衡二叉树中是否存在平衡因子大于1的结点。
流程图3.详细设计二叉树类型定义:typedef int Status;typedef int ElemType;typedef struct BSTNode{ElemType data;int bf;struct BSTNode *lchild ,*rchild;} BSTNode,* BSTree;Status SearchBST(BSTree T,ElemType e)//查找void R_Rotate(BSTree &p)//右旋void L_Rotate(BSTree &p)//左旋void LeftBalance(BSTree &T)//插入平衡调整void RightBalance(BSTree &T)//插入平衡调整Status InsertAVL(BSTree &T,ElemType e,int &taller)//插入void DELeftBalance(BSTree &T)//删除平衡调整void DERightBalance(BSTree &T)//删除平衡调整Status Delete(BSTree &T,int &shorter)//删除操作Status DeleteAVL(BSTree &T,ElemType e,int &shorter)//删除操作void merge(BSTree &T1,BSTree &T2)//合并操作void splitBSTree(BSTree T,ElemType e,BSTree &T1,BSTree &T2)//分裂操作void PrintBSTree(BSTree &T,int lev)//凹入表显示附录源代码:#include<stdio.h>#include<stdlib.h>//#define TRUE 1//#define FALSE 0//#define OK 1//#define ERROR 0#define LH +1#define EH 0#define RH -1//二叉类型树的类型定义typedef int Status;typedef int ElemType;typedef struct BSTNode{ElemType data;int bf;//结点的平衡因子struct BSTNode *lchild ,*rchild;//左、右孩子指针} BSTNode,* BSTree;/*查找算法*/Status SearchBST(BSTree T,ElemType e){if(!T){return 0; //查找失败}else if(e == T->data ){return 1; //查找成功}else if (e < T->data){return SearchBST(T->lchild,e);}else{return SearchBST(T->rchild,e);}}//右旋void R_Rotate(BSTree &p){BSTree lc; //处理之前的左子树根结点lc = p->lchild; //lc指向的*p的左子树根结点p->lchild = lc->rchild; //lc的右子树挂接为*P的左子树lc->rchild = p;p = lc; //p指向新的根结点}//左旋void L_Rotate(BSTree &p){BSTree rc;rc = p->rchild; //rc指向的*p的右子树根结点p->rchild = rc->lchild; //rc的左子树挂接为*p的右子树rc->lchild = p;p = rc; //p指向新的根结点}//对以指针T所指结点为根结点的二叉树作左平衡旋转处理,//本算法结束时指针T指向新的根结点void LeftBalance(BSTree &T){BSTree lc,rd;lc=T->lchild;//lc指向*T的左子树根结点switch(lc->bf){ //检查*T的左子树的平衡度,并做相应的平衡处理case LH: //新结点插入在*T的左孩子的左子树,要做单右旋处理T->bf = lc->bf=EH;R_Rotate(T);break;case RH: //新结点插入在*T的左孩子的右子树上,做双旋处理rd=lc->rchild; //rd指向*T的左孩子的右子树根switch(rd->bf){ //修改*T及其左孩子的平衡因子case LH: T->bf=RH; lc->bf=EH;break;case EH: T->bf=lc->bf=EH;break;case RH: T->bf=EH; lc->bf=LH;break;}rd->bf=EH;L_Rotate(T->lchild); //对*T的左子树作左旋平衡处理R_Rotate(T); //对*T作右旋平衡处理}}//右平衡旋转处理void RightBalance(BSTree &T){BSTree rc,ld;rc=T->rchild;switch(rc->bf){case RH:T->bf= rc->bf=EH;L_Rotate(T);break;case LH:ld=rc->lchild;switch(ld->bf){case LH: T->bf=RH; rc->bf=EH;break;case EH: T->bf=rc->bf=EH;break;case RH: T->bf = EH; rc->bf=LH;break;}ld->bf=EH;R_Rotate(T->rchild);L_Rotate(T);}}//插入结点Status InsertAVL(BSTree &T,ElemType e,int &taller){//taller反应T长高与否if(!T){//插入新结点,树长高,置taller为trueT= (BSTree) malloc (sizeof(BSTNode));T->data = e;T->lchild = T->rchild = NULL;T->bf = EH;taller = 1;}else{if(e == T->data){taller = 0;return 0;}if(e < T->data){if(!InsertAVL(T->lchild,e,taller))//未插入return 0;if(taller)//已插入到*T的左子树中且左子树长高switch(T->bf){//检查*T的平衡度,作相应的平衡处理case LH:LeftBalance(T);taller = 0;break;case EH:T->bf = LH;taller = 1;break;case RH:T->bf = EH;taller = 0;break;}}else{if (!InsertAVL(T->rchild,e,taller)){return 0;}if(taller)//插入到*T的右子树且右子树增高switch(T->bf){//检查*T的平衡度case LH:T->bf = EH;taller = 0;break;case EH:T->bf = RH;taller = 1;break;case RH:RightBalance(T);taller = 0;break;}}}return 1;}void DELeftBalance(BSTree &T){//删除平衡调整BSTree lc,rd;lc=T->lchild;switch(lc->bf){case LH:T->bf = EH;//lc->bf= EH;R_Rotate(T);break;case EH:T->bf = EH;lc->bf= EH;R_Rotate(T);break;case RH:rd=lc->rchild;switch(rd->bf){case LH: T->bf=RH; lc->bf=EH;break;case EH: T->bf=lc->bf=EH;break;case RH: T->bf=EH; lc->bf=LH;break;}rd->bf=EH;L_Rotate(T->lchild);R_Rotate(T);}}void DERightBalance(BSTree &T) //删除平衡调整{BSTree rc,ld;rc=T->rchild;switch(rc->bf){case RH:T->bf= EH;//rc->bf= EH;L_Rotate(T);break;case EH:T->bf= EH;//rc->bf= EH;L_Rotate(T);break;case LH:ld=rc->lchild;switch(ld->bf){case LH: T->bf=RH; rc->bf=EH;break;case EH: T->bf=rc->bf=EH;break;case RH: T->bf = EH; rc->bf=LH;break;}ld->bf=EH;R_Rotate(T->rchild);L_Rotate(T);}}void SDelete(BSTree &T,BSTree &q,BSTree &s,int &shorter){if(s->rchild){SDelete(T,s,s->rchild,shorter);if(shorter)switch(s->bf){case EH:s->bf = LH;shorter = 0;break;case RH:s->bf = EH;shorter = 1;break;case LH:DELeftBalance(s);shorter = 0;break;}return;}T->data = s->data;if(q != T)q->rchild = s->lchild;elseq->lchild = s->lchild;shorter = 1;}//删除结点Status Delete(BSTree &T,int &shorter){ BSTree q;if(!T->rchild){q = T;T = T->lchild;free(q);shorter = 1;}else if(!T->lchild){q = T;T= T->rchild;free(q);shorter = 1;}else{SDelete(T,T,T->lchild,shorter);if(shorter)switch(T->bf){case EH:T->bf = RH;shorter = 0;break;case LH:T->bf = EH;shorter = 1;break;case RH:DERightBalance(T);shorter = 0;break;}}return 1;}Status DeleteAVL(BSTree &T,ElemType e,int &shorter){ int sign = 0;if (!T){return sign;}else{if(e == T->data){sign = Delete(T,shorter);return sign;}else if(e < T->data){sign = DeleteAVL(T->lchild,e,shorter);if(shorter)switch(T->bf){case EH:T->bf = RH;shorter = 0;break;case LH:T->bf = EH;shorter = 1;break;case RH:DERightBalance(T);shorter = 0;break;}return sign;}else{sign = DeleteAVL(T->rchild,e,shorter);if(shorter)switch(T->bf){case EH:T->bf = LH;shorter = 0;break;case RH:T->bf = EH;break;case LH:DELeftBalance(T);shorter = 0;break;}return sign;}}}//合并void merge(BSTree &T1,BSTree &T2){int taller = 0;if(!T2)return;merge(T1,T2->lchild);InsertAVL(T1,T2->data,taller);merge(T1,T2->rchild);}//分裂void split(BSTree T,ElemType e,BSTree &T1,BSTree &T2){ int taller = 0;if(!T)return;split(T->lchild,e,T1,T2);if(T->data > e)InsertAVL(T2,T->data,taller);elseInsertAVL(T1,T->data,taller);split(T->rchild,e,T1,T2);}//分裂void splitBSTree(BSTree T,ElemType e,BSTree &T1,BSTree &T2){ BSTree t1 = NULL,t2 = NULL;split(T,e,t1,t2);T1 = t1;T2 = t2;return;}//构建void CreatBSTree(BSTree &T){int num,i,e,taller = 0;printf("输入结点个数:");scanf("%d",&num);printf("请顺序输入结点值\n");for(i = 0 ;i < num;i++){printf("第%d个结点的值",i+1);scanf("%d",&e);InsertAVL(T,e,taller) ;}printf("构建成功,输入任意字符返回\n");getchar();getchar();}//凹入表形式显示方法void PrintBSTree(BSTree &T,int lev){int i;if(T->rchild)PrintBSTree(T->rchild,lev+1);for(i = 0;i < lev;i++)printf(" ");printf("%d\n",T->data);if(T->lchild)PrintBSTree(T->lchild,lev+1);void Start(BSTree &T1,BSTree &T2){int cho,taller,e,k;taller = 0;k = 0;while(1){system("cls");printf(" 平衡二叉树操作的演示 \n\n");printf("********************************\n");printf(" 平衡二叉树显示区 \n");printf("T1树\n");if(!T1 )printf("\n 当前为空树\n");else{PrintBSTree(T1,1);}printf("T2树\n");if(!T2 )printf("\n 当前为空树\n");elsePrintBSTree(T2,1);printf("\n********************************************************************* *********\n");printf("T1操作:1.创建 2.插入 3.查找 4.删除 10.分裂\n");printf("T2操作:5.创建 6.插入 7.查找 8.删除 11.分裂\n");printf(" 9.合并 T1,T2 0.退出\n");printf("*********************************************************************** *******\n");printf("输入你要进行的操作:");scanf("%d",&cho);switch(cho){case 1:CreatBSTree(T1);break;case 2:printf("请输入要插入关键字的值");scanf("%d",&e);InsertAVL(T1,e,taller) ;break;case 3:printf("请输入要查找关键字的值");scanf("%d",&e);if(SearchBST(T1,e))printf("查找成功!\n");elseprintf("查找失败!\n");printf("按任意键返回87"); getchar();getchar();break;case 4:printf("请输入要删除关键字的值"); scanf("%d",&e);if(DeleteAVL(T1,e,k))printf("删除成功!\n");elseprintf("删除失败!\n");printf("按任意键返回");getchar();getchar();break;case 5:CreatBSTree(T2);break;case 6:printf("请输入要插入关键字的值"); scanf("%d",&e);InsertAVL(T2,e,taller) ;break;case 7:printf("请输入要查找关键字的值"); scanf("%d",&e);if(SearchBST(T2,e))printf("查找成功!\n");elseprintf("查找失败!\n");printf("按任意键返回");getchar();getchar();break;case 8:printf("请输入要删除关键字的值"); scanf("%d",&e);if(DeleteAVL(T2,e,k))printf("删除成功!\n");elseprintf("删除失败!\n");printf("按任意键返回");getchar();getchar();break;case 9:merge(T1,T2);T2 = NULL;printf("合并成功,按任意键返回"); getchar();getchar();break;case 10:printf("请输入要中间值字的值"); scanf("%d",&e);splitBSTree(T1,e,T1,T2) ;printf("分裂成功,按任意键返回"); getchar();getchar();break;case 11:printf("请输入要中间值字的值"); scanf("%d",&e);splitBSTree(T2,e,T1,T2) ;printf("分裂成功,按任意键返回"); getchar();getchar();break;case 0:system("cls");exit(0);}}}main(){BSTree T1 = NULL;BSTree T2 = NULL;Start(T1,T2);}。
数据结构c语言课设-二叉树排序

题目:二叉排序树的实现1 内容和要求1)编程实现二叉排序树,包括生成、插入,删除;2)对二叉排序树进展先根、中根、和后根非递归遍历;3)每次对树的修改操作和遍历操作的显示结果都需要在屏幕上用树的形状表示出来。
4)分别用二叉排序树和数组去存储一个班(50 人以上)的成员信息(至少包括学号、姓名、成绩3 项),比照查找效率,并说明在什么情况下二叉排序树效率高,为什么?2 解决方案和关键代码2.1 解决方案:先实现二叉排序树的生成、插入、删除,编写DisplayBST函数把遍历结果用树的形状表示出来。
前中后根遍历需要用到栈的数据构造,分模块编写栈与遍历代码。
要求比照二叉排序树和数组的查找效率,首先建立一个数组存储一个班的成员信息,分别用二叉树和数组查找,利用clock〔〕函数记录查找时间来比照查找效率。
2.2关键代码树的根本构造定义及根本函数typedef struct{KeyType key;} ElemType;typedef struct BiTNode//定义链表{ElemType data;struct BiTNode *lchild, *rchild;}BiTNode, *BiTree, *SElemType;//销毁树int DestroyBiTree(BiTree &T){if (T != NULL)free(T);return 0;}//清空树int ClearBiTree(BiTree &T){if (T != NULL){T->lchild = NULL;T->rchild = NULL;T = NULL;}return 0;}//查找关键字,指针p返回int SearchBST(BiTree T, KeyType key, BiTree f, BiTree &p) {if (!T){p = f;return FALSE;}else if EQ(key, T->data.key){p = T;return TRUE;}else if LT(key, T->data.key)return SearchBST(T->lchild, key, T, p);elsereturn SearchBST(T->rchild, key, T, p);}二叉树的生成、插入,删除生成void CreateBST(BiTree &BT, BiTree p){int i;ElemType k;printf("请输入元素值以创立排序二叉树:\n");scanf_s("%d", &k.key);for (i = 0; k.key != NULL; i++){//判断是否重复if (!SearchBST(BT, k.key, NULL, p)){InsertBST(BT, k);scanf_s("%d", &k.key);}else{printf("输入数据重复!\n");return;}}}插入int InsertBST(BiTree &T, ElemType e){BiTree s, p;if (!SearchBST(T, e.key, NULL, p)){s = (BiTree)malloc(sizeof(BiTNode));s->data = e;s->lchild = s->rchild = NULL;if (!p)T = s;else if LT(e.key, p->data.key)p->lchild = s;elsep->rchild = s;return TRUE;}else return FALSE;}删除//某个节点元素的删除int DeleteEle(BiTree &p){BiTree q, s;if (!p->rchild) //右子树为空{q = p;p = p->lchild;free(q);}else if (!p->lchild) //左子树为空{q = p;p = p->rchild;free(q);}else{q = p;s = p->lchild;while (s->rchild){q = s;s = s->rchild;}p->data = s->data;if (q != p)q->rchild = s->lchild;elseq->lchild = s->lchild;delete s;}return TRUE;}//整棵树的删除int DeleteBST(BiTree &T, KeyType key) //实现二叉排序树的删除操作{if (!T){return FALSE;}else{if (EQ(key, T->data.key)) //是否相等return DeleteEle(T);else if (LT(key, T->data.key)) //是否小于return DeleteBST(T->lchild, key);elsereturn DeleteBST(T->rchild, key);}return 0;}二叉树的前中后根遍历栈的定义typedef struct{SElemType *base;SElemType *top;int stacksize;}SqStack;int InitStack(SqStack &S) //构造空栈{S.base = (SElemType*)malloc(STACK_INIT_SIZE *sizeof(SElemType));if (!S.base) exit(OVERFLOW);S.top = S.base;S.stacksize = STACK_INIT_SIZE;return OK;}//InitStackint Push(SqStack &S, SElemType e) //插入元素e为新栈顶{if (S.top - S.base >= S.stacksize){S.base = (SElemType*)realloc(S.base, (S.stacksize + STACKINCREMENT)*sizeof(SElemType));if (!S.base) exit(OVERFLOW);S.top = S.base + S.stacksize;S.stacksize += STACKINCREMENT;}*S.top++ = e;return OK;}//Pushint Pop(SqStack &S, SElemType &e) //删除栈顶,应用e返回其值{if (S.top == S.base) return ERROR;e = *--S.top;return OK;}//Popint StackEmpty(SqStack S) //判断是否为空栈{if (S.base == S.top) return TRUE;return FALSE;}先根遍历int PreOrderTraverse(BiTree T, int(*Visit)(ElemType e)) {SqStack S;BiTree p;InitStack(S);p = T;while (p || !StackEmpty(S)){if (p){Push(S, p);if (!Visit(p->data)) return ERROR;p = p->lchild;}else{Pop(S, p);p = p->rchild;}}return OK;}中根遍历int InOrderTraverse(BiTree T, int(*Visit)(ElemType e)) {SqStack S;BiTree p;InitStack(S);p = T;while (p || !StackEmpty(S)){if (p){Push(S, p);p = p->lchild;}else{Pop(S, p);if (!Visit(p->data)) return ERROR;p = p->rchild;}}return OK;}后根遍历int PostOrderTraverse(BiTree T, int(*Visit)(ElemType e)) {SqStack S, SS;BiTree p;InitStack(S);InitStack(SS);p = T;while (p || !StackEmpty(S)){if (p){Push(S, p);Push(SS, p);p = p->rchild;}else{if (!StackEmpty(S)){Pop(S, p);p = p->lchild;}}}while (!StackEmpty(SS)){Pop(SS, p);if (!Visit(p->data)) return ERROR;}return OK;}利用数组存储一个班学生信息ElemType a[] = { 51, "陈继真", 88,82, "黄景元", 89,53, "贾成", 88,44, "呼颜", 90,25, "鲁修德", 88,56, "须成", 88,47, "孙祥", 87, 38, "柏有患", 89, 9, " 革高", 89, 10, "考鬲", 87, 31, "李燧", 86, 12, "夏祥", 89, 53, "余惠", 84, 4, "鲁芝", 90, 75, "黄丙庆", 88, 16, "李应", 89, 87, "杨志", 86, 18, "李逵", 89, 9, "阮小五", 85, 20, "史进", 88, 21, "秦明", 88, 82, "杨雄", 89, 23, "刘唐", 85, 64, "武松", 88, 25, "李俊", 88, 86, "卢俊义", 88, 27, "华荣", 87, 28, "杨胜", 88, 29, "林冲", 89, 70, "李跃", 85, 31, "蓝虎", 90, 32, "宋禄", 84, 73, "鲁智深", 89, 34, "关斌", 90, 55, "龚成", 87, 36, "黄乌", 87, 57, "孔道灵", 87, 38, "张焕", 84, 59, "李信", 88, 30, "徐山", 83, 41, "秦祥", 85, 42, "葛公", 85, 23, "武衍公", 87, 94, "范斌", 83, 45, "黄乌", 60, 67, "叶景昌", 99, 7, "焦龙", 89, 78, "星姚烨", 85, 49, "孙吉", 90, 60, "陈梦庚", 95,};数组查询函数void ArraySearch(ElemType a[], int key, int length){int i;for (i = 0; i <= length; i++){if (key == a[i].key){cout << "学号:" << a[i].key << " 姓名:" << a[i].name << " 成绩:" << a[i].grade << endl;break;}}}二叉树查询函数上文二叉树根本函数中的SearchBST()即为二叉树查询函数。
平衡二叉树调整教学探讨

平衡二叉树调整教学探讨在“数据结构与算法”课程教学中,许多教科书在介绍平衡二叉树调整这部分内容时,采用的都是旋转的方法,将不平衡二叉树用左右、顺逆时针旋转的方法使失去平衡的二叉排序树调整为平衡二叉树。
但是在实际教学过程中,笔者发现这样的方法不太容易被学生理解,许多学生尤其是专科学生搞不清楚怎么旋转、围绕谁旋转。
针对这一问题,笔者通过不断的教学实践摸索出一种更容易被学生接受和理解的平衡二叉树调整方法——填空法,这种方法充分利用了二叉排序树的特点,采用填空的方式对失衡的二叉排序树进行调整使之保持平衡。
1基本原理我们知道,二叉排序树具有这样一个特点:左子树上所有结点的值均小于它的根结点的值,右子树上所有结点的值均大于它的根结点的值。
即有这样一个关系:左根据二叉排序树的特点(左假定都在CL中插入一个结点使得A的平衡因子的绝对值变为2从而使得原平衡二叉树失去平衡,此时以A为根结点的子树就是最小不平衡子树,这棵最小不平衡子树可以分为7个部分。
沿着从根结点A到插入结点位置CL的路径方向依次取三个结点,假设为A、B、C,它们和剩下的AL、AR、BL、BR、CL、CR中的4个构成的二叉排序树要成为平衡二叉树,则由这7个部分组成的平衡二叉树的基本结构一定是如图5所示情形:其中,A、B、C三者中值最小的为左子树的根结点,值最大的为右子树的根结点,中间的为整个最小不平衡子树的根结点。
其余的AL、AR、BL、BR、CL、CR等按从小到大的顺序排列,将它们从左到右依次填在树的第三层即可,完成后的二叉树一定是平衡二叉树。
对上述四种复杂情形,平衡后如图6所示:2示例例:已知长度为12的表:{Jan,Feb,Mar,Apr,May,June, July,Aug,Sep,Oct,Nov,Dec},按照表中元素顺序构造一棵平衡二叉排序树。
解:构造过程如图7、图8所示。
教学实践证明,本文采用的填空法要比传统的旋转法更容易被学生接受和理解。
详解平衡二叉树
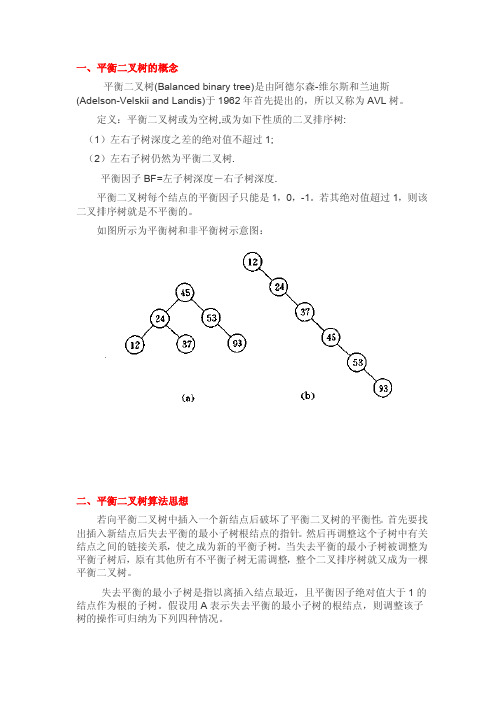
一、平衡二叉树的概念平衡二叉树(Balanced binary tree)是由阿德尔森-维尔斯和兰迪斯(Adelson-Velskii and Landis)于1962年首先提出的,所以又称为AVL树。
定义:平衡二叉树或为空树,或为如下性质的二叉排序树:(1)左右子树深度之差的绝对值不超过1;(2)左右子树仍然为平衡二叉树.平衡因子BF=左子树深度-右子树深度.平衡二叉树每个结点的平衡因子只能是1,0,-1。
若其绝对值超过1,则该二叉排序树就是不平衡的。
如图所示为平衡树和非平衡树示意图:二、平衡二叉树算法思想若向平衡二叉树中插入一个新结点后破坏了平衡二叉树的平衡性。
首先要找出插入新结点后失去平衡的最小子树根结点的指针。
然后再调整这个子树中有关结点之间的链接关系,使之成为新的平衡子树。
当失去平衡的最小子树被调整为平衡子树后,原有其他所有不平衡子树无需调整,整个二叉排序树就又成为一棵平衡二叉树。
失去平衡的最小子树是指以离插入结点最近,且平衡因子绝对值大于1的结点作为根的子树。
假设用A表示失去平衡的最小子树的根结点,则调整该子树的操作可归纳为下列四种情况。
1)LL型平衡旋转法由于在A的左孩子B的左子树上插入结点F,使A的平衡因子由1增至2而失去平衡。
故需进行一次顺时针旋转操作。
即将A的左孩子B向右上旋转代替A作为根结点,A向右下旋转成为B的右子树的根结点。
而原来B的右子树则变成A的左子树。
(2)RR型平衡旋转法由于在A的右孩子C 的右子树上插入结点F,使A的平衡因子由-1减至-2而失去平衡。
故需进行一次逆时针旋转操作。
即将A的右孩子C向左上旋转代替A作为根结点,A向左下旋转成为C的左子树的根结点。
而原来C的左子树则变成A的右子树。
(3)LR型平衡旋转法由于在A的左孩子B的右子数上插入结点F,使A的平衡因子由1增至2而失去平衡。
故需进行两次旋转操作(先逆时针,后顺时针)。
即先将A结点的左孩子B的右子树的根结点D向左上旋转提升到B结点的位置,然后再把该D结点向右上旋转提升到A结点的位置。
数据结构与算法系列研究五——树、二叉树、三叉树、平衡排序二叉树AVL

数据结构与算法系列研究五——树、⼆叉树、三叉树、平衡排序⼆叉树AVL树、⼆叉树、三叉树、平衡排序⼆叉树AVL⼀、树的定义树是计算机算法最重要的⾮线性结构。
树中每个数据元素⾄多有⼀个直接前驱,但可以有多个直接后继。
树是⼀种以分⽀关系定义的层次结构。
a.树是n(≥0)结点组成的有限集合。
{N.沃恩}(树是n(n≥1)个结点组成的有限集合。
{D.E.Knuth})在任意⼀棵⾮空树中:⑴有且仅有⼀个没有前驱的结点----根(root)。
⑵当n>1时,其余结点有且仅有⼀个直接前驱。
⑶所有结点都可以有0个或多个后继。
b. 树是n(n≥0)个结点组成的有限集合。
在任意⼀棵⾮空树中:⑴有⼀个特定的称为根(root)的结点。
⑵当n>1时,其余结点分为m(m≥0)个互不相交的⼦集T1,T2,…,Tm。
每个集合本⾝⼜是⼀棵树,并且称为根的⼦树(subtree)树的固有特性---递归性。
即⾮空树是由若⼲棵⼦树组成,⽽⼦树⼜可以由若⼲棵更⼩的⼦树组成。
树的基本操作1、InitTree(&T) 初始化2、DestroyTree(&T) 撤消树3、CreatTree(&T,F) 按F的定义⽣成树4、ClearTree(&T) 清除5、TreeEmpty(T) 判树空6、TreeDepth(T) 求树的深度7、Root(T) 返回根结点8、Parent(T,x) 返回结点 x 的双亲9、Child(T,x,i) 返回结点 x 的第i 个孩⼦10、InsertChild(&T,&p,i,x) 把 x 插⼊到 P的第i棵⼦树处11、DeleteChild(&T,&p,i) 删除结点P的第i棵⼦树12、traverse(T) 遍历树的结点:包含⼀个数据元素及若⼲指向⼦树的分⽀。
●结点的度: 结点拥有⼦树的数⽬●叶结点: 度为零的结点●分枝结点: 度⾮零的结点●树的度: 树中各结点度的最⼤值●孩⼦: 树中某个结点的⼦树的根●双亲: 结点的直接前驱●兄弟: 同⼀双亲的孩⼦互称兄弟●祖先: 从根结点到某结点j 路径上的所有结点(不包括指定结点)。
二叉排序树的c语言代码

二叉排序树(Binary Sort Tree)是一种特殊的二叉树,它或左子树或右子树为完全二叉树。
由于二叉排序树的特点,其每个节点的值均大于其左子树中的所有节点的值,且小于其右子树中的所有节点的值。
以下是一个简单的二叉排序树的C语言实现,包括插入、查找和删除操作。
```c#include <stdio.h>#include <stdlib.h>typedef struct Node {int data;struct Node *left;struct Node *right;} Node;// 创建一个新的节点Node* createNode(int data) {Node* newNode = (Node*)malloc(sizeof(Node));if (!newNode) {printf("内存分配失败\n");return NULL;}newNode->data = data;newNode->left = newNode->right = NULL;return newNode;}// 在二叉排序树中插入一个新的节点Node* insert(Node* root, int data) {if (!root) { // 如果树为空,创建新节点并返回根节点root = createNode(data);} else if (data <= root->data) { // 如果插入的数据小于当前节点的值,则在左子树中插入root->left = insert(root->left, data);} else { // 如果插入的数据大于当前节点的值,则在右子树中插入root->right = insert(root->right, data);}return root; // 返回插入后的根节点}// 在二叉排序树中查找一个值是否存在int search(Node* root, int data) {if (!root) { // 如果树为空,返回0表示未找到return 0;} else if (root->data == data) { // 如果找到,返回1表示找到return 1;} else if (data < root->data) { // 如果插入的数据小于当前节点的值,在左子树中查找return search(root->left, data);} else { // 如果插入的数据大于当前节点的值,在右子树中查找return search(root->right, data);}}// 在二叉排序树中删除一个节点,并返回被删除的节点指针(如果存在)Node* deleteNode(Node* root, int data) {if (!root) return NULL; // 如果树为空,直接返回NULL(空树)if (data < root->data) { // 如果要删除的值小于当前节点的值,则在左子树中查找并删除root->left = deleteNode(root->left, data);} else if (data > root->data) { // 如果要删除的值大于当前节点的值,则在右子树中查找并删除root->right = deleteNode(root->right, data);} else { // 如果要删除的节点就是当前节点,根据情况选择删除方式(左子树或右子树)if (root->left == NULL) { // 如果左子树为空,直接删除当前节点(只有根节点时)Node *temp = root; // 临时保存当前节点,用于释放内存后替换原节点指针为NULLfree(temp); // 释放内存空间后将原指针设为NULL} else if (root->right == NULL) { // 如果右子树为空,直接删除当前节点(只有一个节点时)Node *temp = root->left; // 临时保存左子树的根节点,用于替换原节点指针为左子树的根节点指针(此时原节点为空)free(root); // 释放原节点的内存空间后将原指针设为NULL(此时原节点为空)root = temp; // 将原指针设为新的根节点指针(此时原节点为空)} else { // 如果左右子树都存在,则找到右子树中的最小节点(即要被替换的节点),替换原节点指针为最小节点的指针(此时原节点为空)并删除最小节点(通过递归实现)Node *temp = root->right; // 临时保存右子树的根节点指针(即要被替换的节点)root->data = temp->data; // 将原节点的数据。
二叉树c语言实现完整代码

二叉树c语言实现完整代码二叉树是一种非常常见的数据结构,它由节点和边组成,每个节点最多有两个子节点,分别称为左子节点和右子节点。
在计算机科学中,二叉树被广泛应用于搜索、排序、编译器等领域。
本文将介绍如何使用C语言实现二叉树的完整代码。
我们需要定义二叉树的节点结构体。
每个节点包含三个成员变量:数据、左子节点和右子节点。
代码如下:```struct TreeNode {int val;struct TreeNode *left;struct TreeNode *right;};```接下来,我们需要实现二叉树的基本操作,包括创建节点、插入节点、删除节点、查找节点等。
这些操作可以通过递归实现。
代码如下:```// 创建节点struct TreeNode* createNode(int val) {struct TreeNode* node = (struct TreeNode*)malloc(sizeof(struct TreeNode));node->val = val;node->left = NULL;node->right = NULL;return node;}// 插入节点struct TreeNode* insertNode(struct TreeNode* root, int val) {if (root == NULL) {return createNode(val);}if (val < root->val) {root->left = insertNode(root->left, val);} else {root->right = insertNode(root->right, val);}return root;}// 删除节点struct TreeNode* deleteNode(struct TreeNode* root, int val) {if (root == NULL) {return NULL;}if (val < root->val) {root->left = deleteNode(root->left, val);} else if (val > root->val) {root->right = deleteNode(root->right, val);} else {if (root->left == NULL) {struct TreeNode* temp = root->right;free(root);return temp;} else if (root->right == NULL) {struct TreeNode* temp = root->left;free(root);return temp;}struct TreeNode* temp = findMin(root->right); root->val = temp->val;root->right = deleteNode(root->right, temp->val); }return root;}// 查找节点struct TreeNode* searchNode(struct TreeNode* root, int val) {if (root == NULL || root->val == val) {return root;}if (val < root->val) {return searchNode(root->left, val);} else {return searchNode(root->right, val);}}// 查找最小节点struct TreeNode* findMin(struct TreeNode* root) {while (root->left != NULL) {root = root->left;}return root;}```我们需要实现二叉树的遍历操作,包括前序遍历、中序遍历和后序遍历。
数据结构-C语言-树和二叉树

练习
一棵完全二叉树有5000个结点,可以计算出其
叶结点的个数是( 2500)。
二叉树的性质和存储结构
性质4: 具有n个结点的完全二叉树的深度必为[log2n]+1
k-1层 k层
2k−1−1<n≤2k−1 或 2k−1≤n<2k n k−1≤log2n<k,因为k是整数
所以k = log2n + 1
遍历二叉树和线索二叉树
遍历定义
指按某条搜索路线遍访每个结点且不重复(又称周游)。
遍历用途
它是树结构插入、删除、修改、查找和排序运算的前提, 是二叉树一切运算的基础和核心。
遍历规则 D
先左后右
L
R
DLR LDR LRD DRL RDL RLD
遍历规则
A BC DE
先序遍历:A B D E C 中序遍历:D B E A C 后序遍历:D E B C A
练习 具有3个结点的二叉树可能有几种不同形态?普通树呢?
5种/2种
目 录 导 航 Contents
5.1 树和二叉树的定义 5.2 案例引入 5.3 树和二叉树的抽象数据类型定义 5.4 二叉树的性质和存储结构 5.5 遍历二叉树和线索二叉树 5.6 树和森林 5.7 哈夫曼树及其应用 5.8 案例分析与实现
(a + b *(c-d)-e/f)的二叉树
目 录 导 航 Contents
5.1 树和二叉树的定义 5.2 案例引入 5.3 树和二叉树的抽象数据类型定义 5.4 二叉树的性质和存储结构 5.5 遍历二叉树和线索二叉树 5.6 树和森林 5.7 哈夫曼树及其应用 5.8 案例分析与实现
二叉树的抽象数据类型定义
特殊形态的二叉树
只有最后一层叶子不满,且全部集中在左边
数据结构 (C语言版) (第二版)(目录)

数据结构(C语言版)(第二版)(目录)第1章导论
1 算法和数据结构
2 什么是数据结构
3 符号,引理,定理与证明
4 说明文篇
5 C语言和程序设计
6 总结
第2章算法分析
1 算法的衡量标准
2 时间和空间复杂度分析
3 运行时复杂度分析
4 递归分析
第3章线性表
1 一维数组
2 线性表
3 顺序表
4 链表
5 循环链表
6 树表
7 双向链表
第4章栈
1 栈的定义
2 栈的抽象数据类型
3 栈的基本操作
4 栈的应用——后缀表达式的求算
第7章树
1 树的定义
2 树的抽象数据类型
3 树的存储
4 树的遍历
5 二叉树
6 二叉排序树(搜索树)
7 平衡二叉树
8 哈夫曼树
9 图的存储
第8章查找
1 静态查找
2 哈希表
3 动态单值查找
第10章数据结构综合应用
1 树的遍历
2 贪心法
3 回溯法
4 分析与评价
附录 A C语言库
1 算法入口及时区函数
2 内存处理函数
3 字符串处理函数
4 文件处理函数
附录 B 内存分配方式。
c语言将二叉树填充为完全二叉树的方法

c语言将二叉树填充为完全二叉树的方法要将二叉树填充为完全二叉树,需要按照层次遍历方式进行操作。
下面是使用C语言来实现这个过程的方法:#include <stdio.h>#include <stdlib.h>#define MAX_SIZE 100// 二叉树节点结构体typedef struct Node {int data; // 当前节点的数据struct Node* left; // 左子节点指针struct Node* right; // 右子节点指针} Node;// 辅助队列结构体typedef struct Queue {Node* data[MAX_SIZE];int front, rear;} Queue;// 创建新节点Node* createNode(int data) {Node* newNode = (Node*)malloc(sizeof(Node)); newNode->data = data;newNode->left = NULL;newNode->right = NULL;return newNode;}// 插入节点Node* insertNode(Node* root, int data) {if (root == NULL) {return createNode(data);}Queue queue;queue.front = -1;queue.rear = -1;queue.data[++queue.rear] = root;while (queue.front != queue.rear) {Node* temp = queue.data[++queue.front];if (temp->left) {queue.data[++queue.rear] = temp->left; } else {temp->left = createNode(data);return root;}if (temp->right) {queue.data[++queue.rear] = temp->right; } else {temp->right = createNode(data);return root;}}return root;}// 中序遍历打印二叉树void inorderTraversal(Node* root) {if (root == NULL) {return;}inorderTraversal(root->left);printf("%d ", root->data);inorderTraversal(root->right);}int main() {Node* root = createNode(1);// 假设以下数据为二叉树的节点数据int data[] = {2, 3, 4, 5, 6, 7};int dataSize = sizeof(data) / sizeof(data[0]);for (int i = 0; i < dataSize; i++) {root = insertNode(root, data[i]);}printf("填充完全二叉树后的中序遍历结果:");inorderTraversal(root);return 0;}通过以上代码,我们可以将给定的二叉树填充为完全二叉树,并通过中序遍历方式打印出填充完后的结果。
数据结构:第9章 查找2-二叉树和平衡二叉树

return(NULL); else
{if(t->data==x) return(t);
if(x<(t->data) return(search(t->lchild,x));
else return(search(t->lchild,x)); } }
——这种既查找又插入的过程称为动态查找。 二叉排序树既有类似于折半查找的特性,又采用了链表存储, 它是动态查找表的一种适宜表示。
注:若数据元素的输入顺序不同,则得到的二叉排序树形态 也不同!
讨论1:二叉排序树的插入和查找操作 例:输入待查找的关键字序列=(45,24,53,45,12,24,90)
二叉排序树的建立 对于已给定一待排序的数据序列,通常采用逐步插入结点的方 法来构造二叉排序树,即只要反复调用二叉排序树的插入算法 即可,算法描述为: BiTree *Creat (int n) //建立含有n个结点的二叉排序树 { BiTree *BST= NULL;
for ( int i=1; i<=n; i++) { scanf(“%d”,&x); //输入关键字序列
– 法2:令*s代替*p
将S的左子树成为S的双亲Q的右子树,用S取代p 。 若C无右子树,用C取代p。
例:请从下面的二叉排序树中删除结点P。
F P
法1:
F
P
C
PR
C
PR
CL Q
CL QL
Q SL
S PR
QL S
SL
法2:
F
PS
C
PR
CL Q
QL SL S SL
数据结构(C语言版)复习题

一、单项选择题:1、树形结构不具备这样的特点:()A. 每个节点可能有多个后继(子节点)B. 每个节点可能有多个前驱(父节点)C. 可能有多个内节点(非终端结点)D. 可能有多个叶子节点(终端节点)2、二叉树与度数为2的树相同之处包括()。
A. 每个节点都有1个或2个子节点B. 至少有一个根节点C. 至少有一个度数为2的节点D. 每个节点至多只有一个父节点3、一棵完全二叉树有999 个结点,它的深度为()。
A.9 B.10 C.11 D.124、在一个单链表中,若p所指结点不是最后结点,在p之后插入s所指结点,则执行()A. s->next=p;p->next=s;B. s->next=p->next;p->next=s;C. s->next=p->next;p=s;D. p->next=s;s->next=p;5、对于一棵具有n个结点、度为5的树来说,()A. 树的高度至多是n-3B. 树的高度至多是n-4C. 树的高度至多是nD. 树的高度至多是n-56、在顺序队列中,元素的排列顺序()。
A. 由元素插入队列的先后顺序决定B. 与元素值的大小有关C. 与队首指针和队尾指针的取值有关D. 与数组大小有关7、串是一种特殊的线性表,其特殊性体现在()。
A.可以顺序存储 B.数据元素是一个字符C.可以链式存储 D.数据元素可以是多个字符若8、顺序循环队列中(数组的大小为 6),队头指示 front 和队尾指示 rear 的值分别为 3和 0,当从队列中删除1个元素,再插入2 个元素后,front和 rear的值分别为()。
A.5 和1 B.2和4 C.1和5 D.4 和29、一棵完全二叉树上有1001 个结点,其中叶子结点的个数为()。
A.250 B.500 C.254 D.50110、已知一个有向图如下图所示,则从顶点a出发进行深度优先遍历,不可能得到的DFS序列为()。
平衡二叉树的实现c语言

平衡二叉树的实现c语言平衡二叉树(AVL树)是一种自平衡的二叉查找树,其中任何节点的两个子树的高度差最多为1。
下面是一个简单的AVL树的C语言实现:```cinclude <>include <>typedef struct AVLNode {int key;int height;struct AVLNode left, right;} AVLNode;typedef struct {AVLNode root;} AVLTree;int getHeight(AVLNode node) {if (node == NULL)return 0;return node->height;}int getBalance(AVLNode node) {if (node == NULL)return 0;return getHeight(node->left) - getHeight(node->right);}AVLNode rotateRight(AVLNode y) {AVLNode x = y->left;AVLNode T2 = x->right;x->right = y;y->left = T2;y->height = max(getHeight(y->left), getHeight(y->right)) + 1; x->height = max(getHeight(x->left), getHeight(x->right)) + 1; return x; // new root is x}AVLNode rotateLeft(AVLNode x) {AVLNode y = x->right;AVLNode T2 = y->left;y->left = x;x->right = T2;x->height = max(getHeight(x->left), getHeight(x->right)) + 1; y->height = max(getHeight(y->left), getHeight(y->right)) + 1; return y; // new root is y}AVLNode insert(AVLTree tree, int key) {AVLNode root = tree->root;if (root == NULL) { // tree is empty, create a new node as root. tree->root = (AVLNode)malloc(sizeof(AVLNode));root = tree->root;root->key = key;root->height = 1;return root;} else if (key < root->key) { // insert into left subtree.root->left = insert(root->left, key);} else if (key > root->key) { // insert into right subtree.root->right = insert(root->right, key);} else { // duplicate keys not allowed.return root; // don't insert duplicate key.}root->height = 1 + max(getHeight(root->left), getHeight(root->right)); // adjust height of current node.int balance = getBalance(root);if (balance > 1 && key < root->left->key) { // left left case.return rotateRight(root); // rotate right.} else if (balance < -1 && key > root->right->key) { // right right case.return rotateLeft(root); // rotate left.} else if (balance > 1 && key > root->left->key) { // left right case. root->left = rotateLeft(root->left); // rotate left first.return rotateRight(root); // then rotate right.} else if (balance < -1 && key < root->right->key) { // right left case.root->right = rotateRight(root->right); // rotate right first.return rotateLeft(root); // then rotate left.} // keep balance.return root; // already balanced.} ```。
二叉树 c语言

二叉树 c语言在计算机科学领域中,树型数据结构是一种非常重要的数据结构,在实际开发中也得到了广泛的应用。
其中,二叉树又是一种非常常见的树型结构。
二叉树在很多情况下都能够提供更好的算法效率,同时也易于理解和实现,因此我们可以通过通过学习和掌握二叉树的特点以及优点,来更好的应用到实际开发中。
一、二叉树的定义二叉树是一种树型结构,树型结构是由节点构成的。
二叉树与一般的树型结构不同,它的每个节点最多只有两个子节点,分别称为左子树和右子树。
它们可以为空或者不为空,其子节点的数量时不固定且没有任何限制的。
二叉树的定义如下:(1)空树是树的一种特殊的状态。
我们可以把它称为二叉树;(2)若不是空树,那么它就是由一个称为根节点(root)的元素和左右两棵分别称为左子树(left subtree)和右子树(right subtree)的二叉树组成。
二、二叉树的特性(1)每个节点最多只有两个子节点,分别称为左子节点和右子节点;(2)左子树和右子树是二叉树;(3)二叉树没有重复的节点。
三、二叉树的应用二叉树是一种非常实用的数据结构,因为它可以模拟很多实际生活中的情况。
例如,我们可以利用二叉树来对某些数据进行分类和排序。
在二叉树的基础上,我们还可以构造二叉堆、哈夫曼树等更高级的数据结构。
除此之外,二叉树还可以应用到程序设计中。
例如,我们可以构造一个二叉树来表示某个程序的控制流,这个程序在执行时可以沿着二叉树的各个节点进行分支和选择,实现不同的功能。
此外,我们还可以利用二叉树来加快某些算法的执行效率,比如二分查找算法等。
四、二叉树的遍历方式对于二叉树的遍历,有三种基本方式,即前序遍历、中序遍历、后序遍历。
它们的遍历顺序不同,因此也得到了不同的称呼。
下面我们来简要介绍一下这三种遍历方式的特点和应用。
(1)前序遍历前序遍历是指首先访问树的根节点,然后按照从左到右的顺序依次遍历左子树和右子树。
前序遍历的应用非常广泛,可以用于生成表达式树、构造二叉树等等。
C语言数据结构系列篇二叉树的概念及满二叉树与完全二叉树
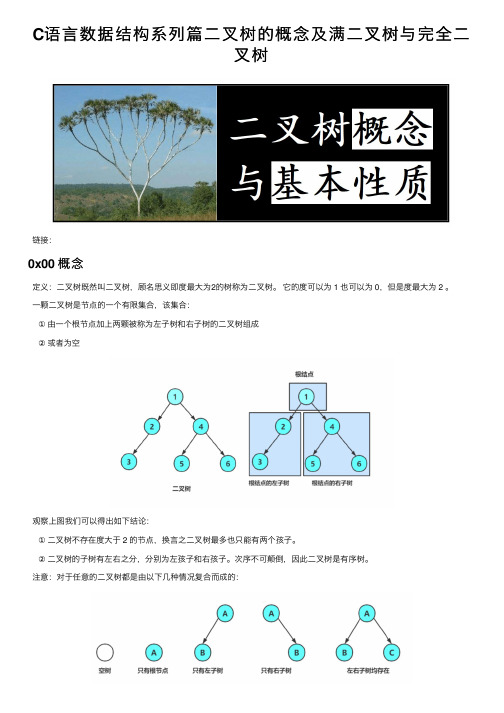
C语⾔数据结构系列篇⼆叉树的概念及满⼆叉树与完全⼆叉树链接:0x00 概念定义:⼆叉树既然叫⼆叉树,顾名思义即度最⼤为2的树称为⼆叉树。
它的度可以为 1 也可以为 0,但是度最⼤为 2 。
⼀颗⼆叉树是节点的⼀个有限集合,该集合:①由⼀个根节点加上两颗被称为左⼦树和右⼦树的⼆叉树组成②或者为空观察上图我们可以得出如下结论:①⼆叉树不存在度⼤于 2 的节点,换⾔之⼆叉树最多也只能有两个孩⼦。
②⼆叉树的⼦树有左右之分,分别为左孩⼦和右孩⼦。
次序不可颠倒,因此⼆叉树是有序树。
注意:对于任意的⼆叉树都是由以下⼏种情况复合⽽成的:0x01 满⼆叉树定义:⼀个⼆叉树,如果每⼀层的节点数都达到了最⼤值(均为2),则这个⼆叉树就可以被称作为 "满⼆叉树" 。
换⾔之,如果⼀个⼆叉树的层数为,且节点总数是,则他就是⼀个满⼆叉树。
计算公式:①已知层数求总数:②已知总数求层数:⼗亿个节点,满⼆叉树是多少层?≈ 10亿多0x02 完全⼆叉树定义:对于深度为的,有个结点的⼆叉树,当且仅当其每⼀个结点都与深度为的满⼆叉树中编号从 1 ⾄的结点⼀⼀对应时称之为完全⼆叉树。
前层是满的,最后⼀层不满,但是最后⼀层从左到右是连续的。
完全⼆叉树是效率很⾼的数据结构,完全⼆叉树是由满⼆叉树⽽引出来的。
所以,满⼆叉树是⼀种特殊的完全⼆叉树(每⼀层节点均为2)。
常识:①完全⼆叉树中,度为 1 的最多只有 1 个。
②⾼度为的完全⼆叉树节点范围是0x03 ⼆叉树的性质①若规定根节点的层数为 1 ,则⼀颗⾮空⼆叉树的第层上最多有个节点。
②若规定根节点的层数为 1 ,则深度为的⼆叉树最⼤节点数是 .③对任何⼀颗⼆叉树,如果度为 0 其叶⼦结点个数为,度为 2 的分⽀节点个数为,则有。
换⾔之,度为 0 的永远⽐度为 2 的多⼀个叶⼦结点。
④若规定根节点的层数为 1 ,具有个节点的满⼆叉树的深度(log是以2为底,n+1的对数)。
对于有个节点的完全⼆叉树,如果按照从上⾄下从左⾄右的数组顺序对所有节点从 0 开始编号,则对于序号为的节点有:(⾮完全⼆叉树,也可以⽤数组存放,但会浪费很多空间)假设是⽗节点在数组中的下标,此公式仅适⽤于完全⼆叉树:①求左孩⼦:②求右孩⼦:③求⽗亲(假设不关注是左孩⼦还是右孩⼦):④判断是否有左孩⼦:⑤判断是否由右孩⼦:PS:⼆叉树不⼀定要标准,⽐如这个其实也是⼆叉树:课后练习:1. 某⼆叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该⼆叉树中的叶⼦结点数为()A. 不存在这样的⼆叉树B. 200C. 1982. 在具有 2n 个结点的完全⼆叉树中,叶⼦结点个数为()A. nB. n+1C. n-1D. n/23. ⼀棵完全⼆叉树的节点数位为531个,那么这棵树的⾼度为()A. 11B. 10C. 8D. 125. ⼀个具有767个节点的完全⼆叉树,其叶⼦节点个数为()A. 383B. 384C. 385D. 386参考资料:Microsoft. MSDN(Microsoft Developer Network)[EB/OL]. []. .笔者:王亦优更新: 2021.11.24勘误:⽆声明:由于作者⽔平有限,本⽂有错误和不准确之处在所难免,本⼈也很想知道这些错误,恳望读者批评指正!本篇完。
数据结构_第9章_查找2-二叉树和平衡二叉树

F
PS
C
PR
CL Q
QL SL S SL
10
3
18
2
6 12
6 删除10
3
18
2
4 12
4
15
15
三、二叉排序树的查找分析
1) 二叉排序树上查找某关键字等于给定值的结点过程,其实 就是走了一条从根到该结点的路径。 比较的关键字次数=此结点的层次数; 最多的比较次数=树的深度(或高度),即 log2 n+1
-0 1 24
0 37
0 37
-0 1
需要RL平衡旋转 (绕C先顺后逆)
24
0
-012
13
3573
0
01
37
90
0 53 0 53
0 90
作业
已知如下所示长度为12的表:
(Jan, Feb, Mar, Apr, May, June, July, Aug, Sep, Oct, Nov, Dec)
(1) 试按表中元素的顺序依次插入一棵初始为空的二叉 排序树,画出插入完成之后的二叉排序树,并求其在 等概率的情况下查找成功的平均查找长度。
2) 一棵二叉排序树的平均查找长度为:
n i1
ASL 1
ni Ci
m
其中:
ni 是每层结点个数; Ci 是结点所在层次数; m 为树深。
最坏情况:即插入的n个元素从一开始就有序, ——变成单支树的形态!
此时树的深度为n ; ASL= (n+1)/2 此时查找效率与顺序查找情况相同。
最好情况:即:与折半查找中的判ห้องสมุดไป่ตู้树相同(形态比较均衡) 树的深度为:log 2n +1 ; ASL=log 2(n+1) –1 ;与折半查找相同。
《数据结构(c语言版)》重点知识汇总

数据结构(C语言版)重点知识汇总1. 线性结构数组•数组是一种线性结构,它的每个元素占据一段连续的内存空间;•数组的下标是从0开始的;•数组可以存储同类型的元素,支持随机访问和修改。
链表•链表也是一种线性结构,其元素是以节点的方式逐个存储在内存中;•节点包含元素和指向下一个节点的指针;•链表优点是可以动态增加或删除元素,缺点是访问和修改元素比较麻烦,需要遍历链表。
栈和队列•栈和队列是两种特殊的线性结构;•栈和队列都是通过数组或者链表实现的;•栈的特点是先进后出,可以用于进行函数调用、表达式求值等;•队列的特点是先进先出,可以用于模拟排队、网络数据传输等。
2. 树形结构二叉树•二叉树是一种特殊的树形结构,树中的每个节点最多有两个孩子节点;•二叉树可以是满二叉树、完全二叉树或者普通的二叉树;•遍历二叉树的方法有前序遍历、中序遍历和后序遍历。
二叉搜索树•二叉搜索树也是一种二叉树,具有以下性质:–左子树上的元素都小于根节点的元素;–右子树上的元素都大于根节点的元素;–左右子树也是二叉搜索树。
•二叉搜索树可以用于搜索、排序等算法。
平衡二叉树•平衡二叉树是一种强制性要求左右子树高度差不超过1的二叉树;•平衡二叉树可以在保持搜索树特性的同时,提高搜索效率。
堆•堆也是一种树形结构,常用于实现优先队列;•堆分为最大堆和最小堆,最大堆的根节点最大,最小堆的根节点最小;•堆的插入和删除操作能够始终保证堆的性质。
3. 图形结构图的基本概念•图由节点和边两个基本元素组成;•节点也被称为顶点,边连接两个顶点;•图分为有向图和无向图,有向图中的边是有方向性的;•图还有一些特殊的概念,如权重、连通性、环等。
图的存储结构•图的存储结构有邻接矩阵、邻接表和十字链表三种常见的形式;•邻接矩阵利用二维数组来表示节点之间的关系;•邻接表利用链表来存储节点和其邻居节点的关系;•十字链表进一步扩展了邻接表的概念,可以处理有向图和无向图的情况。
平衡二叉树构造方法

平衡二叉树构造方法构造平衡二叉树的方法有很多,其中一种绝妙的方法是通过AVL树进行构造。
AVL树是一种平衡二叉树,它的左子树和右子树的高度差不超过1、利用这种特性,我们可以通过以下步骤构造平衡二叉树:1.将需要构造平衡二叉树的数据按照升序或者降序排列。
2.选择数据的中间元素作为根节点。
3.将数据分成左右两个部分,分别作为根节点的左子树和右子树的数据。
4.递归地对左子树和右子树进行构造。
下面我们通过一个例子来具体说明这个方法:假设我们需要构造一个平衡二叉树,并且数据为1,2,3,4,5,6,7,8,9首先,我们将数据按照升序排列得到1,2,3,4,5,6,7,8,9、选择中间的元素5作为根节点。
然后,我们将数据分成两部分:1,2,3,4和6,7,8,9、递归地对这两个部分进行构造。
对于左子树,我们选择中间元素2作为根节点,将数据分成两部分:1和3,4、递归地构造这两个部分。
对于右子树,我们选择中间元素8作为根节点,将数据分成两部分:6,7和9、递归地构造这两个部分。
重复这个过程,直到所有的数据都被构造为节点。
最后得到的树就是一个平衡二叉树。
这个构造方法的时间复杂度是O(nlogn),其中n是数据的数量。
虽然它的时间复杂度比较高,但是它保证了构造的树是一个平衡二叉树,从而提高了数据的查找、插入和删除等操作的效率。
总结起来,通过AVL树进行构造是一种有效的方法来构造平衡二叉树。
它将数据按照升序或者降序排列,选择中间元素作为根节点,然后递归地对左子树和右子树进行构造。
这种方法保证了构造的树是一个平衡二叉树,从而提高了数据的查找、插入和删除等操作的效率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
// 构造一个空的动态查找表DT
int InitDSTable(BSTree *DT)
{
*DT=NULL;
return 1;
}
// 销毁动态查找表DT
void DestroyDSTable(BSTree *DT)
{
if(*DT) // 非空树
{
if((*DT)->lchild) // 有左孩子
printf("\n请输入待查找的关键字: ");
scanf("%d",&j);
p=SearchBST(dt,j); // 查找给定关键字的记录
if(p)
print(p->data);
else
printf("表中不存在此值");
printf("\n");
DestroyDSTable(&dt);
rc->bf=EH;
break;
case EH: (*T)->bf=rc->bf=EH;
break;
case LH: (*T)->bf=EH;
rc->bf=RH;
}
rd->bf=EH;
R_Rotate(&(*T)->rchild); // 对*T的右子树作右旋平衡处理
#define RH -1 // 右高
#define N 5 // 数据元素个数
typedef char KeyType; // 设关键字域为字符型
typedef struct
{
KeyType key;
int order;
}ElemType; // 数据元素类型
// 平衡二叉树的类型
L_Rotate(T); // 对*T作左旋平衡处理
}
}
// 算法9.11
// 若在平衡的二叉排序树T中不存在和e有相同关键字的结点,则插入一个
// 数据元素为e的新结点,并返回1,否则返回0。若因插入而使二叉排序树
// 失去平衡,则作平衡旋转处理,布尔变量taller反映T长高与否。
L_Rotate(&(*T)->lchild); // 对*T的左子树作左旋平衡处理
R_Rotate(T); // 对*T作右旋平衡处理
}
}
// 对以指针T所指结点为根的二叉树作右平衡旋转处理,本算法结束时,
// 指针T指向新的根结点
void RightBalance(BSTree *T)
system("pause");
return 0;
{ // 应继续在*T的左子树中进行搜索
if(!InsertAVL(&(*T)->lchild,e,taller)) // 未插入
return 0;
if(*taller)
// 已插入到*T的左子树中且左子树“长高”
switch((*T)->bf) // 检查*T的平衡度
}
}
void print(ElemType c)
{
printf("(%d,%d)",c.key,c.order);
}
int main()
{
BSTree dt,p;
int k;
int i;
KeyType j;
ElemType r[N]={
{13,1},{24,2},{37,3},{90,4},{53,5}
数据结构C语言版 平衡二叉树.txt
/*
数据结构C语言版 平衡二叉树
P236
编译环境:Dev-C++ 4.9.9.2
日期:2011年2月15日
*/
#include <stdio.h>
#include <malloc.h>
#define LH +1 // 左高
#define EH 0 // DT)->lchild); // 销毁左孩子子树
if((*DT)->rchild) // 有右孩子
DestroyDSTable(&(*DT)->rchild); // 销毁右孩子子树
free(*DT); // 释放根结点
*DT=NULL; // 空指针赋0
return T; // 查找结束
else if(key < T->data.key) // 在左子树中继续查找
return SearchBST(T->lchild,key);
else
return SearchBST(T->rchild,key); // 在右子树中继续查找
{
// 应继续在*T的右子树中进行搜索
if(!InsertAVL(&(*T)->rchild,e,taller)) // 未插入
return 0;
if(*taller) // 已插入到T的右子树且右子树“长高”
switch((*T)->bf) // 检查T的平衡度
{
BSTree rc,rd;
rc=(*T)->rchild; // rc指向*T的右子树根结点
switch(rc->bf)
{ // 检查*T的右子树的平衡度,并作相应平衡处理
case RH: // 新结点插入在*T的右孩子的右子树上,要作单左旋处理
(*T)->bf=rc->bf=EH;
case LH:
(*T)->bf=RH;
lc->bf=EH;
break;
case EH:
(*T)->bf=lc->bf=EH;
break;
case RH:
(*T)->bf=EH;
lc->bf=LH;
}
rd->bf=EH;
}
// 算法9.9 P236
// 对以*p为根的二叉排序树作右旋处理,处理之后p指向新的树根结点,即旋转
// 处理之前的左子树的根结点。
void R_Rotate(BSTree *p)
{
BSTree lc;
lc=(*p)->lchild; // lc指向p的左子树根结点
(*p)->lchild=lc->rchild; // lc的右子树挂接为p的左子树
(*T)->bf=EH;
*taller=1;
}
else
{
if(e.key == (*T)->data.key)
{ // 树中已存在和e有相同关键字的结点则不再插入
*taller=0;
return 0;
}
if(e.key < (*T)->data.key)
}
}
// 算法9.5(a)
// 在根指针T所指二叉排序树中递归地查找某关键字等于key的数据元素,
// 若查找成功,则返回指向该数据元素结点的指针,否则返回空指针。
BSTree SearchBST(BSTree T,KeyType key)
{
if((!T)|| (key == T->data.key))
*taller=1;
break;
case RH: // 原本右子树比左子树高,需要作右平衡处理
RightBalance(T);
*taller=0;
}
}
}
return 1;
}
// 按关键字的顺序对DT的每个结点调用函数Visit()一次
// 指针T指向新的根结点。
void LeftBalance(BSTree *T)
{
BSTree lc,rd;
lc=(*T)->lchild; // lc指向*T的左子树根结点
switch(lc->bf)
{ // 检查*T的左子树的平衡度,并作相应平衡处理
case LH: // 新结点插入在*T的左孩子的左子树上,要作单右旋处理
}; // (以教科书P234图9.12为例)
InitDSTable(&dt); // 初始化空树
for(i=0;i<N;i++)
InsertAVL(&dt,r[i],&k); // 建平衡二叉树
TraverseDSTable(dt,print); // 按关键字顺序遍历二叉树
{
case LH:
(*T)->bf=EH; // 原本左子树比右子树高,现左、右子树等高
*taller=0;
break;
case EH: // 原本左、右子树等高,现因右子树增高而使树增高
(*T)->bf=RH;
void TraverseDSTable(BSTree DT,void(*Visit)(ElemType))
{
if(DT)
{
TraverseDSTable(DT->lchild,Visit); // 先中序遍历左子树
Visit(DT->data); // 再访问根结点
TraverseDSTable(DT->rchild,Visit); // 最后中序遍历右子树
(*T)->bf=LH;
*taller=1; //标志长高
break;
