磁矩剩磁表磁Pc计算
剩磁和磁通量的关系

剩磁和磁通量的关系磁场是物质中由电荷运动而产生的力场,其特征之一是具有磁感应强度,即磁场的强度。
磁感应强度的大小与物质中的磁通量有着密切的关系。
而在磁场中,当磁场的强度发生变化时,会产生剩磁效应,即磁场消失后物体仍然保留一定强度的磁性。
本文将探讨剩磁和磁通量的关系。
我们需要了解磁通量的概念。
磁通量是指磁场线通过一个平面的数量,用Φ表示。
磁通量的大小与磁感应强度和面积有关,可用下式表示:Φ = B * A,其中B为磁感应强度,A为面积。
磁通量的单位是韦伯(Wb)。
剩磁是指磁场消失后,物体仍然保留的一定强度的磁性。
在物体受到外界磁场的作用时,磁场中的磁矩会发生定向排列,形成一个较强的磁性。
当外界磁场消失后,物体仍然保持一定的磁性,这就是剩磁效应。
剩磁和磁通量之间存在着紧密的关系。
当物体受到外界磁场的作用时,磁感应强度会增加,从而磁通量也会增加。
当外界磁场消失后,物体保留了一定的磁通量,即剩磁。
因此,剩磁的大小与磁通量的大小密切相关。
在实际应用中,剩磁效应被广泛应用于磁存储领域。
例如,磁盘驱动器中的磁性材料在受到外界磁场的作用时,磁颗粒会发生定向排列,形成磁区。
当外界磁场消失后,磁区仍然保留一定的磁性,这就是剩磁效应。
通过对磁区的磁通量进行读取和写入操作,可以实现数据的存储和读取。
剩磁效应还可以应用于磁性材料的制备和磁记录的保护。
通过控制磁性材料中的剩磁大小,可以调节材料的磁性能,以满足不同的应用需求。
同时,剩磁也起到了保护磁记录的作用,当外界磁场发生变化时,磁性材料中的剩磁可以减少磁记录的损坏,确保数据的安全性。
总结起来,剩磁和磁通量之间存在着紧密的关系。
剩磁是指磁场消失后物体仍然保留的一定强度的磁性,而磁通量是磁场线通过一个平面的数量。
剩磁的大小与磁通量的大小密切相关,当外界磁场作用于物体时,磁通量增加,剩磁效应产生。
剩磁效应在磁存储领域和磁性材料制备中有重要应用,能够实现数据的存储和读取,以及调节材料的磁性能。
永磁体磁矩剩磁体积之间的关系

永磁体磁矩剩磁体积之间的关系The relationship between the magnetic moment and the remanent magnetization in permanent magnets is a complex and interesting topic. Permanent magnets, also known as ferromagnetic materials, have the ability to retain their magnetization once they have been magnetized. This property is crucial for their widespread applications in various technologies and industries.永磁体的磁矩是指一个永磁体单位磁极矩大小的一个向量,它受永磁体内部微观磁矩的影响。
而剩磁则是永磁体去除外磁场后仍然具有残余磁场的能力。
磁矩和剩磁之间的关系可以通过永磁体的磁化曲线来描述。
永磁体磁矩与剩磁体积之间的关系是复杂的,需要综合考虑永磁体的材料、形状、制备工艺等因素。
The relationship between the magnetic moment and the remanent magnetization can be understood through the hysteresis curve of a permanent magnet. When a permanent magnet is subjected to an external magnetic field, it becomes magnetized and the magnetic moments align in a particular direction. When the external magnetic field is removed, some of the magnetic moments in the material mayremain aligned, leading to remanent magnetization. The magnitudeof the remanent magnetization is directly related to the magnetic moment of the material.磁矩和剩磁之间的关系也受到永磁体的晶粒大小、磁畴结构以及化学成分等因素的影响。
磁性材料术语解释及计算公式

磁性材料术语解释及计算公式起始磁导率μi初始磁导率是磁性材料的磁导率(B/H )在磁化曲线始端的极限值,即μi =01μ× H B ∆∆ ()0→∆H式中μ0为真空磁导率(m H /7104-⨯π) ∆H 为磁场强度的变化率(A/m )∆B 为磁感应强度的变化率(T )有效磁导率μe在闭合磁路中,如果漏磁可忽略,可以用有效磁导率来表示磁芯的性能。
e μ =AeLe N L 20⋅μ 式中 L 为装有磁芯的线圈的电感量(H )N 为线圈匝数Le 为有效磁路长度(m )Ae 为有效截面积 (m 2)饱和磁通密度Bs (T )磁化到饱和状态的磁通密度。
见图1。
HcH图 1剩余磁通密度Br(T)从饱和状态去除磁场后,剩余的磁通密度。
见图1。
矫顽力Hc(A/m)从饱和状态去除磁场后,磁芯继续被反向磁场磁化,直至磁感应强度减为零,此时的磁场强度称为矫顽力。
见图1。
损耗因子tanδ损耗系数是磁滞损耗、涡流损耗和剩余损耗三者之和。
tanδ= tanδh + tanδe + tanδr式中tanδh为磁滞损耗系数tanδe为涡流损耗系数tanδr为剩余损耗系数相对损耗因子 tanδ/μi比损耗因子是损耗系数与与磁导率之比:tanδ/μi(适用于材料)tanδ/μe(适用于磁路中含有气隙的磁芯)品质因数 Q品质因数为损耗因子的倒数: Q = 1/ tan δ温度系数αμ( 1/K)温度系数为T1和T2范围内变化时,每变化1K 相应的磁导率的相对变化量:αμ=112μμ-μ.12T T 1- 式中μ1为温度为T1时的磁导率μ2为温度为T2时的磁导率 相对温度系数αμr(1/K)温度系数和磁导率之比,即αμr = 2112μμ-μ.12T T 1- 减落系数 DF在恒温条件下,完全退磁的磁芯的磁导率随时间的衰减变化,即 DF = 212121μ1T T log μμ⨯- (T2>T1) μ1为退磁后T1分钟的磁导率μ2为退磁后T2分钟的磁导率居里温度Tc (℃)在该温度时材料由铁磁性(或亚铁磁)转变为顺磁性,见图2。
亥姆霍兹测量永磁体的Pc值

亥姆霍兹线圈测量永磁体的Pc 值 实验目的利用亥姆霍兹线圈测量永磁体的Pc 值。
实验仪器永磁特性测量仪 亥姆霍兹线圈 磁通计实验原理亥姆霍兹线圈是一对绕线匝数相同平行且薄的线圈组成,两个线圈之间等于线圈的半径,两个线圈是串联顺接的。
当测量样品在亥姆霍兹线圈轴线方向从线圈中央移至线圈外某一位置时,则在线圈内产生一个磁通量的变化,根据法拉第电磁感应定律,产生的感应生电动势E 为dtd E φ-= (1) 故产生磁通的变化量φ∆可写成:⎰-=∆Edt φ (2)放置在线圈中央的样品与线圈直径相比是很小的,可以近似把它看成磁偶极子势的时间积分正比于样品的磁偶极矩Pm ,即⎰=Edt C P m (3)C 为常数 ,根据磁极化强度J 的定义 :VP J m = 式中V 为磁偶极子的体积。
磁极化强度J 与磁化强度M 存在如下关系: M J 0μ=故样品的开路磁化强度d M 表示为:⎰=Edt V C M d 0μ (4) (4)式即是利用亥姆霍兹线圈测量永磁体开路磁化强度的基本原理,⎰Edt 由磁通计读出,又有C 和Pc 的计算公式为:N R C 855= (5) dd c H B P 0μ= 如果把永磁体的B ~ H 曲线近似地看成直线,并已测得永磁体的r B 和CB H ,则永磁体的开路磁化强度d M 可写成:CBr c r c d H B P B P M 00/)1(μμ++= (6) 由(4)式和(6)式可以求得Pc 值:110--=⎰⎰Edt VB C Edt VH C P r CB c μ (7) (7)式即是利用亥姆霍兹线圈测定永磁体Pc 值的原理,式中V 为永磁体的体积,可计算求得也可用排水法求得。
实验内容及步骤线圈的骨架应是非金属材料的,线圈的半径应至少是被测磁体最大尺寸2 .5倍 。
这一限制条件是保证所测磁体在线圈的均匀敏感区内。
为了能保证测量小磁体时有适当的灵敏度,又同时避免测量大磁体时不超过测量仪器的量程,每个线圈的匝数通常选用100匝或更多一些,所选线径应使整个线圈的阻抗与仪器的输入阻抗一致。
磁力和磁力矩的计算

第6章磁力的计算由理论力学可知,体系在某一方向的力和力矩等于在该方向的能量梯度,可表达为:ii i WT q W F θ∂∂=∂∂=,(6-1) 式中,W —为体系的能量,i q —在i 方向的坐标,i F —i 方向的力,T —作用在θ方向的力矩,θ—旋转角。
1.吸引力的计算1)气隙能量有解的表达式:22μgg g L A B W =或π82gg g L A B W =(6-2)由上式得吸引力:22μgg A B F =(6-3)式中,F —吸引力()N ,g B —气隙磁密()2mWb,g A —板面积()2m,0μ—真空磁导率()mH7104-⨯π2)如果气隙较大,g B 不均匀,能量表达式由(3)得引力应为:π82gg A B F =(6-4)式中,F —吸引力()yn d ,g B —G ,g A —2cm 。
为了计算方便,将上式化为:g g A B F 24965⎪⎪⎭⎫⎝⎛=(6-5)式中,F —kgf ,g B —G ,g A —2cm 。
dV B W g ⎰⎰⎰=0221μ(6-6)dV 为气隙体积元,积分在全部气隙中进行,如果1≠r μ时,0μ应改为0μ0r μ,此式由计算机求出W ,再由iq W∂∂求出i F 。
3)也可不先求W ,直接按下式求出磁吸引力F:⎰⎰∇=s d p F(6-7)F——作用于磁体上的磁吸引力;s——包围该物体的任意表面; p——作用于该表面上的应力; p的表达式为:()n B B B n p 200211μμ-⋅=(6-8) n——沿积分表面s 法线方向的单位矢量; B——磁感应强度矢量4)下面介绍05RC 与铁氧体之间的磁吸引力。
试验证明,在永磁体直径D 等于高度m L 时,吸引力最大。
故假定1=≠D L m ,此时,气隙磁密g B 可用下列公式(注:此法由磁核积分法导出)。
在磁力试验中发现永磁体的C B H 也起作用,故将上式改为:⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+-=211D L D L H B B g g C B r g (6-9) 例,求两个铁氧圆环之间的吸引力。
磁学量经常使用单位换算

磁学量经常使用单位换算1Oe=103/4 A/m1Gs=103 A/m4M1MGOe=102/4 kJ/m34•10-7H/m-磁概念永磁材料:永磁材料被外加磁场磁化后磁性不消失,可对外部空间提供稳固磁场。
钕铁硼永磁体经常使用的衡量指标有以下四种:剩磁(Br)单位为特斯拉(T)和高斯(Gs) 1Gs =将一个磁体在闭路环境下被外磁场充磁到技术饱和后撤消外磁场,现在磁体表现的磁感应强度咱们称之为剩磁。
它表示磁体所能提供的最大的磁通值。
从退磁曲线上可见,它对应于气隙为零时的情形,故在实际磁路中磁体的磁感应强度都小于剩磁。
钕铁硼是现今发觉的Br最高的有效永磁材料。
磁感矫顽力(Hcb)单位是安/米(A/m)和奥斯特(Oe)或1 Oe≈m处于技术饱和磁化后的磁体在被反向充磁时,使磁感应强度降为零所需反向磁场强度的值称之为磁感矫顽力(Hcb)。
但现在磁体的磁化强度并非为零,只是所加的反向磁场与磁体的磁化强度作用彼此抵消。
(对外磁感应强度表现为零)现在假设撤消外磁场,磁体仍具有必然的磁性能。
钕铁硼的矫顽力一样是11000Oe以上。
内禀矫顽力(Hcj)单位是安/米(A/m)和奥斯特(Oe)1 Oe≈m使磁体的磁化强度降为零所需施加的反向磁场强度,咱们称之为内禀矫顽力。
内禀矫顽力是衡量磁体抗退磁能力的一个物理量,若是外加的磁场等于磁体的内禀矫顽力,磁体的磁性将会大体排除。
钕铁硼的Hcj会随着温度的升高而降低因此需要工作在高温环境下时应该选择高Hcj的牌号。
磁能积(BH)单位为焦/米3(J/m3)或高•奥(GOe) 1 MGOe≈7. 96k J/m3退磁曲线上任何一点的B和H的乘积既BH咱们称为磁能积,而B×H的最大值称之为最大磁能积(BH)max。
磁能积是恒量磁体所贮存能量大小的重要参数之一,(BH)max越大说明磁体包括的磁能量越大。
设计磁路时要尽可能使磁体的工作点处在最大磁能积所对应的B和H周围。
磁矩的计算

一 纯自旋磁矩 在多数情况下, 分子磁矩主要是由电子的自旋产生的, 纯的 自旋磁矩可根据总自旋量子数进行计算。 s=g S(S + 1) 其中S为总自旋量子数, 等于未成对电子数的一半, g为朗德 因子。对于自由电子, g=2.0023, 通常取g=2, 于是上式变为: s= n ( n + 2) 式中n为未成对电子数。这个式子表明, 如果忽略轨道角动 量对磁矩的贡献, 可由磁矩直接计算出某种离子的未成对电子 数。 按这个公式算出来的磁矩, 在少数情况下与实验值不一致, 这正是由于忽略了未成对电子的轨道运动对磁矩的贡献之故。
(1)单分子亲核取代机理 SNI 单分子亲核取代机理(SNI)也称为离解机理, 或D机理。 MLn MLn-1+L (慢) MLn-1+Y MLn-1Y (快) 离解机理的特点:首先是旧键断裂, 腾出配位空位, 然 后Y占据空位, 形成新键。 其中, 决定速率的步骤是离解, 即M-L键的断裂, 总 反应速率只取决于MLn的浓度, 与配体Y的浓度无关, 因此, 此类反应为一级反应, υ=k[MLn] 其中,k为反应的速率常数。
二 轨道磁性对磁矩的贡献
如果加上轨道磁性对磁矩的贡献,则磁矩的计算公式变为:
S+L= 4S(S + 1) + L(L + 1)
按照这个公式计算出来的磁矩在大多数情况下也与实验值 , 不一致。表明在多数情况下, 轨道角动量对分子磁矩的贡献很小 或没有贡献。
取决 于外磁场改变时电子能否自旋平行地在不同轨道之间 再分配。这种分配必须在对称性相同的能级之间进行。 再分配。
应当指出, 实际反应进行时, 通常并非仅按上述两种极端情况 发生, 在大多数的取代反应中, 进入配体的结合与离去配体的解离 几乎是同时进行的, 因此在现代的文献中又提出了第三种机理。 (3)交换机理或I机理
PC值-永磁体Pc值

Design Guide ContentsIntroduction Manufacturing Methods Modern Magnet Materials CoatingsUnits Of Measure Assembly Considerations Design Considerations MagnetizationPermanent Magnet Stability Measurement And TestingPhysical Characteristics And Machining Of Permanent Magnets Handling And StorageQuick Reference Specification Checklist1.0 IntroductionMagnets are an important part of our daily lives, serving as essential components in everything from electric motors, loudspeakers, computers, compact disc players, microwave ovens and the family car, to instrumentation, production equipment, and research. Their contribution is often overlooked because they are built into devices and are usually out of sight.Magnets function as transducers, transforming energy from one form to another, without any permanent loss of their own energy. General categories of permanent magnet functions are: Mechanical to mechanical - such as attraction and repulsion.Mechanical to electrical - such as generators and microphones.Electrical to mechanical - such as motors, loudspeakers, charged particle deflection.Mechanical to heat - such as eddy current and hysteresis torque devices.Special effects - such as magneto resistance, Hall effect devices, and magnetic resonance. The following sections will provide a brief insight into the design and application of permanent magnets. The Design Engineering team at Magnet Sales & Manufacturing will be happy to assist you further in your applications.2.0 Modern Magnet MaterialsThere are four classes of modern commercialized magnets, each based on their material composition. Within each class is a family of grades with their own magnetic properties. Thesegeneral classes are:Neodymium Iron BoronSamarium CobaltCeramicAlnicoNdFeB and SmCo are collectively known as Rare Earth magnets because they are both composed of materials from the Rare Earth group of elements. Neodymium Iron Boron (general composition Nd2Fe14B, often abbreviated to NdFeB) is the most recent commercial addition to the family of modern magnet materials. At room temperatures, NdFeB magnets exhibit the highest properties of all magnet materials. Samarium Cobalt is manufactured in two compositions: Sm1Co5 and Sm2Co17 - often referred to as the SmCo 1:5 or SmCo 2:17 types. 2:17 types, with higher H ci values, offer greater inherent stability than the 1:5 types. Ceramic, also known as Ferrite, magnets (general composition BaFe2O3 or SrFe2O3) have been commercialized since the 1950s and continue to be extensively used today due to their low cost. A special form of Ceramic magnet is "Flexible" material, made by bonding Ceramic powder in a flexible binder. Alnico magnets (general composition Al-Ni-Co) were commercialized in the 1930s and are still extensively used today.These materials span a range of properties that accommodate a wide variety of application requirements. The following is intended to give a broad but practical overview of factors that must be considered in selecting the proper material, grade, shape, and size of magnet for a specific application. The chart below shows typical values of the key characteristics for selected grades of various materials for comparison. These values will be discussed in detail in the following sections. Table 2.1 Magnet Material ComparisonsMaterial Grade Br Hc Hci BHmax T max (Deg C)* NdFeB39H12,80012,30021,00040150SmCo2610,5009,20010,00026300NdFeB B10N6,8005,78010,30010150Alnico512,500640640 5.5540Ceramic83,9003,2003,250 3.5300Flexible11,6001,3701,3800.6100* T max (maximum practical operating temperature)is for reference only. The maximum practical operating temperature of any magnet is dependent on the circuit the magnet is operating in.3.0 Units of MeasureThree systems of units of measure are common: the cgs (centimeter, gram, second), SI (meter, kilogram, second), and English (inch, pound, second) systems. This catalog uses the cgs system for magnetic units, unless otherwise specified.Table 3.1 Units of Measure SystemsFluxømaxwell weber maxwell Flux Density B gauss tesla lines/in2 Magnetomotive Force F gilbert ampere turn ampere turn Magnetizing Force H oersted ampere turns/m ampere turns/in Length L cm m in Permeability of a vacuum?sub>v10.4x 10-6 3.192 Table 3.2Conversion Factorsinches 2.54 centimeterslines/in20.155 Gausslines/in2 1.55 x 10-5TeslaGauss 6.45lines/in2Gauss 0-4TeslaGilberts 0.79577 ampere turns4.0 Design ConsiderationsBasic problems of permanent magnet design revolve around estimating the distribution of magnetic flux in a magnetic circuit, which may include permanent magnets, air gaps, high permeability conduction elements, and electrical currents. Exact solutions of magnetic fields require complex analysis of many factors, although approximate solutions are possible based on certain simplifying assumptions. Obtaining an optimum magnet design often involves experience and tradeoffs.4.1 Finite Element AnalysisFinite Element Analysis (FEA) modeling programs are used to analyze magnetic problems in order to arrive at more exact solutions, which can then be tested and fine tuned against a prototype of the magnet structure. Using FEA models flux densities, torques, and forces may be calculated. Results can be output in various forms, including plots of vector magnetic potentials, flux density maps, and flux path plots. The Design Engineering team at Magnet Sales & Manufacturing has extensive experience in many types of magnetic designs and is able to assist in the design and execution of FEA models.4.2 The B-H CurveThe basis of magnet design is the B-H curve, or hysteresis loop, which characterizes each magnet material. This curve describes the cycling of a magnet in a closed circuit as it is brought to saturation, demagnetized, saturated in the opposite direction, and then demagnetized again under the influence of an external magnetic field.The second quadrant of the B-H curve, commonly referred to as the "Demagnetization Curve", describes the conditions under which permanent magnets are used in practice. A permanent magnet will have a unique, static operating point if air-gap dimensions are fixed and if any adjacent fields are held constant. Otherwise, the operating point will move about the demagnetization curve, the manner of which must be accounted for in the design of the device.The three most important characteristics of the B-H curve are the points at which it intersects the B and H axes (at B r - the residual induction - and H c - the coercive force - respectively), and the point at which the product of B and H are at a maximum (BH max - the maximum energy product).B r represents the maximum flux the magnet is able to produce under closed circuit conditions. In actual useful operation permanent magnets can only approach this point. H c represents the point at which the magnet becomes demagnetized under the influence of an externally applied magnetic field. BH max represents the point at which the product of B and H, and the energy density of the magnetic field into the air gap surrounding the magnet, is at a maximum. The higher this product, the smaller need be the volume of the magnet. Designs should also account for the variation of the B-H curve with temperature. This effect is more closely examined in the section entitled"Permanent Magnet Stability".When plotting a B-H curve, the value of B is obtained by measuring the total flux in the magnet (?/font>)and then dividing this by the magnet pole area (A) to obtain the flux density (B=?/font>/A). The total flux is composed of the flux produced in the magnet by the magnetizing field (H), and the intrinsic ability of the magnet material to produce more flux due to the orientation of the domains. The flux density of the magnet is therefore composed of two components, one equal to the applied H, and the other created by the intrinsic ability of ferromagnetic materials to produce flux. The intrinsic flux density is given the symbol B i where total flux B = H + B i, or, B i = B - H. In normal operating conditions, no external magnetizing field is present, and the magnet operates in the second quadrant, where H has a negative value. Although strictly negative, H is usually referred to as a positive number, and therefore, in normal practice, B i = B + H. It is possible to plot an intrinsic as well as a normal B-H curve. The point at which the intrinsic curve crosses the H axis is the intrinsic coercive force, and is given the symbol H ci. High H ci values are an indicator of inherent stability of the magnet material. The normal curve can be derived from the intrinsic curve and vice versa. In practice, if a magnet is operated in a static manner with no external fields present, the normal curve is sufficient for design purposes. When external fields are present, the normal and intrinsic curves are used to determine the changes in the intrinsic properties of the material.4.3 Magnet CalculationsIn the absence of any coil excitation, the magnet length and pole area may be determined by the following equations:Equation 1andEquation 2where B m = the flux density at the operating point,H m = the magnetizing force at the operating point,A g, = the air-gap area,L g = the air-gap length,B g = the gap flux density,A m = the magnet pole area,and L m = the magnet length.Combining the two equations, the permeance coefficient P c may be determined as follows:Equation 3Strictly,where ?is the permeability of the medium, and k is a factor which takes account of leakage and reluctance that are functions of the geometry and composition of the magnetic circuit.Click here to calculate Permeance Coefficients of Disc, Rectangle, Ring(The intrinsic permeance coefficient P ci = B i/H. Since the normal permeance coefficient P c = B/H, and B = H + B i,P c =(H + B i)/H or P c = 1 + B i /H. Even though the value of H in the second quadrant is actually negative, H is conventionally referred to as a positive number. Taking account of this convention, P c = 1 - B i /H, or B i /H = P ci = P c + 1. In other words, the intrinsic permeance coefficientis equal to the normal permeance coefficient plus 1. This is a useful relationship when working on magnet systems that involve the presence of external fields.)The permeance coefficient is a useful first order relationship, helpful in pointing towards the appropriate magnet material, and to the approximate dimensions of the magnet. The objective of good magnet design is usually to minimize the required volume of magnet material by operating the magnet at BH max. The permeance coefficient at which BH max occurs is given in the material properties tables .We can compare the varios magnet materials for general characteristics using equation 3 above.Consider that a particular field is required in a given air-gap, so that the parameters B g, H g (air-gap magnetizing force), A g, and L g are known.Alnico 5 has the ability to provide very high levels of flux density B m, which is often desirable in high performance electromechanical devices. This is accompanied, however, by a low coercivity H m, and so some considerable magnet length will be required.Alnico 8 operates at a higher magnetizing force, H m, needing a smaller length L m, but will yield a lower B m, and would therefore require a larger magnet area A m.Rare Earth materials offer reasonable to high values of flux density at very high values of magnetizing force. Consequently, very short magnet lengths are needed, and the required volume of this material will be small.Ceramic operates at relatively low flux densities, and will therefore need a correspondingly greater pole face area, A m.The permeance coefficient method using the demagnetization curves allows for initial selection of magnet material, based upon the space available in the device, this determining allowable magnet dimensions.4.3.1 Calculation Of Flux Density On A Magnet's Central LineClick here to calculate flux density of rectangular or cylindrical magnets in various configurations(equations 4 through 8).For magnet materials with straight-line normal demagnetization curves such as Rare Earths and Ceramics, it is possible to calculate with reasonable accuracy the flux density at a distance X from the pole surface (where X>0) on the magnet centerline under a variety of conditions.a. Cylindrical MagnetsEquation 4Table 4.1 shows flux density calculations for a magnet 0.500" in diameter by 0.250" long at a distance of 0.050" from the pole surface, for various materials. Note that you may use any unit of measure for dimensions; since the equation is a ratio of dimensions, the result is the same using any unit system. The resultant flux density is in units of gauss.Table 4.1 Flux Density vs. MaterialMaterial and Grade Residual Flux Density,BrFlux at distance of 0.050" from surface ofmagnetCeramic 12,200629 Ceramic 53,9501,130 SmCo 188,6002,460 SmCo 2610,5003,004 NdFeB 3512,3003,518 NdFeB 42H13,3003,804b. Rectangular MagnetsEquation 5(where all angles are in radians)c. For a Magnet on a Steel Back plateEquation 6 Substitute 2L for L in the above formulae.d. For Identical Magnets Facing Each Other in Attracting PositionsEquation 7 The value of B x at the gap center is double the value of B x in case 3. At a point P, B p is the sum of B(x-p) and B(x-p), where (X+P) and (X-P) substitute for X in case 3.e. For Identical, Yoked Magnets Facing Each Other in Attracting PositionsEquation 8 Substitute 2L for L in case 4, and adopt the same procedure to calculate B p.4.3.2 Force CalculationsThe attractive force exerted by a magnet to a ferromagnetic material may be calculated by:Equation 9where F is the force in pounds, B is the flux density in Kilogauss, and A is the pole area in square inches. Calculating B is a complicated task if it is to be done in a rigorous manner. However, it is possible to approximate the holding force of certain magnets in contact with a piece of steel using the relationship:Equation 10where B r is the residual flux density of the material, A is the pole area in square inches, and L m isthe magnetic length.Click here to calculate approximate pull of a rectangular or disc magnet.This formula is only intended to give an order of magnitude for the holding force that is available from a magnet with one pole in direct contact with a flat, machined, steel surface. The formula can only be used with straight-line demagnetization curve materials - i.e. for rare earth and ceramic materials - and where the magnet length, L m, is kept within the bounds of normal, standard magnet configurations.5.0 Permanent Magnet StabilityThe ability of a permanent magnet to support an external magnetic field results from small magnetic domains "locked" in position by crystal anisotropy within the magnet material. Once established by initial magnetization, these positions are held until acted upon by forces exceeding those that lock the domains. The energy required to disturb the magnetic field produced by a magnet varies for each type of material. Permanent magnets can be produced with extremely high coercive forces (H c) that will maintain domain alignment in the presence of high external magnetic fields. Stability can be described as the repeated magnetic performance of a material under specific conditions over the life of the magnet.Factors affecting magnet stability include time, temperature, reluctance changes, adverse fields, radiation, shock, stress, and vibration.5.1 TimeThe effect of time on modern permanent magnets is minimal. Studies have shown that permanent magnets will see changes immediately after magnetization. These changes, known as "magnetic creep", occur as less stable domains are affected by fluctuations in thermal or magnetic energy, even in a thermally stable environment. This variation is reduced as the number of unstable domains decreases. Rare Earth magnets are not as likely to experience this effect because of theirextremely high coercivities. Long-term time versus flux studies have shown that a newly magnetized magnet will lose a minor percent of its flux as a function of age. Over 100,000 hours, these losses are in the range of essentially zero for Samarium Cobalt materials to less than 3% for Alnico 5 materials at low permeance coefficients.5.2 TemperatureTemperature effects fall into three categories:Reversible losses.Irreversible but recoverable losses.Irreversible and unrecoverable losses.5.2.1. Reversible losses.These are losses that are recovered when the magnet returns to its original temperature. Reversible losses cannot be eliminated by magnet stabilization. Reversible losses are described by the Reversible Temperature Coefficients (T c), shown in table 5.1. T c is expressed as % per degree Centigrade. These figures vary for specific grades of each material but are representative of the class of material as a whole. It is because the temperature coefficients of B r and H c are significantly different that the demagnetization curve develops a "knee" at elevated temperatures. Table 5.1 Reversible Temperature Coefficients of B r and H cMaterial T c of B r T c of H cNdFeB-0.12-0.6SmCo-0.04-0.3Alnico-0.020.01Ceramic-0.20.35.2.2. Irreversible but recoverable losses.These losses are defined as partial demagnetization of the magnet from exposure to high or lowtemperatures. These losses are only recoverable by remagnetization, and are not recovered when the temperature returns to its original value. These losses occur when the operating point of the magnet falls below the knee of the demagnetization curve. An efficient permanent magnet design should have a magnetic circuit in which the magnet operates at a permeance coefficient above the knee of the demagnetization curve at expected elevated temperatures. This will prevent performance variations at elevated temperatures.5.2.3. Irreversible and unrecoverable losses.Metallurgical changes occur in magnets exposed to very high temperatures and are not recoverable by remagnetization. Table 5.2 shows critical temperatures for the various materials, whereT Curie is the Curie temperature at which the elementary magnetic moments are randomized and the material is demagnetized; andT max is the maximum practical operating temperatures for general classes of major materials. Different grades of each material exhibit values differing slightly from the values shown here. Table 5.2 Critical Temperatures for Various MaterialsMaterial T Curie T max*Neodymium Iron Boron310 (590)150 (302)Samarium Cobalt750 (1382)300 (572)Alnico860 (1580)540 (1004)Ceramic460 (860)300 (572)(Temperatures are shown in degrees Centigrade with the Fahrenheit equivalent in parentheses.) *Note that the maximum practical operating temperature is dependent on the operating point of the magnet in the circuit. The higher the operating point on the Demagnetization Curve, the higher the temperature at which the magnet may operate.Flexible materials are not included in this table since the binders that are used to render the magnet flexible break down before metallurgical changes occur in the magnetic ferrite powder thatprovides flexible magnets with their magnetic properties.Partially demagnetizing a magnet by exposure to elevated temperatures in a controlled manner stabilizes the magnet with respect to temperature. The slight reduction in flux density improves a magnetís stability because domains with low commitment to orientation are the first to lose their orientation. A magnet thus stabilized will exhibit constant flux when exposed to equivalent or lesser temperatures. Moreover, a batch of stabilized magnets will exhibit lower variation of flux when compared to each other since the high end of the bell curve which characterizes normal variation will be brought in closer to the rest of the batch.5.3 Reluctance ChangesThese changes occur when a magnet is subjected to permeance changes such as changes in air gap dimensions during operation. These changes will change the reluctance of the circuit, and may cause the magnet's operating point to fall below the knee of the curve, causing partial and/or irreversible losses. The extents of these losses depend upon the material properties and the extent of the permeance change. Stabilization may be achieved by pre-exposure of the magnet to the expected reluctance changes.5.4 Adverse FieldsExternal magnetic fields in repulsion modes will produce a demagnetizing effect on permanent magnets. Rare Earth magnets with coercive forces exceeding 15 KOe are difficult to affect in this manner. However, Alnico 5, with a coercive force of 640 Oe will encounter magnetic losses in the presence of any magnetic repelling force, including similar magnets. Applications involving Ceramic magnets with coercive forces of approximately 4KOe should be carefully evaluated in order to assess the effect of external magnetic fields.5.5 RadiationRare Earth materials are commonly used in charged particle beam deflection applications, and it is necessary to account for possible radiation effects on magnetic properties. Studies (A.F. Zeller andJ.A. Nolen, National Superconducting Cyclotron Laboratory, 09/87, and E.W. Blackmore, TRIUMF, 1985) have shown that SmCo and especially Sm2Co17 withstand radiation 2 to 40 times better than NdFeB materials. SmCo exhibits significant demagnetization when irradiated with a proton beam of 109 to 1010 rads. NdFeB test samples were shown to lose all of their magnetization at a dose of 7 x 107 rads, and 50% at a dose of 4 x 106 rads. In general, it is recommended that magnet materials with high H ci values be used in radiation environments, that they be operated at high permeance coefficients, P c, and that they be shielded from direct heavy particle irradiation. Stabilization can be achieved by pre-exposure to expected radiation levels.5.6 Shock, Stress, and VibrationBelow destructive limits, these effects are very minor on modern magnet materials. However, rigid magnet materials are brittle in nature, and can easily be damaged or chipped by improper handling. Samarium Cobalt in particular is a fragile material and special handling precautions must be taken to avoid damage. Thermal shock when Ceramics and Samarium Cobalt magnets are exposed to high temperature gradients can cause fractures within the material and should be avoided.6.0 Manufacturing MethodsPermanent magnets are manufactured by one of the following methods:Sintering, (Rare Earths, Ceramics, and Alnicos)Pressure Bonding or Injection Molding, (Rare Earths and Ceramics)Casting, (Alnicos)Extruding, (Bonded Neodymium and Ceramics)Calendering (Neodymium and Ceramics)The sintering process involves compacting fine powders at high pressure in an aligning magnetic field, then sintering to fuse into a solid shape. After sintering, the magnet shape is rough, and will need to be machined to achieve close tolerances. The intricacy of shapes that can be thus pressedis limited.Rare Earth magnets may be die pressed (with pressure being applied in one direction) or isostatically pressed (with equal pressure being applied in all directions). Isostatically pressed magnets achieve higher magnetic properties than die pressed magnets. The aligning magnetic field for die pressed magnets can be either parallel or perpendicular to the pressing direction. Magnets pressed with the aligning field perpendicular to the pressing direction achieve higher magnetic properties than the parallel pressed form.Both Rare Earth and Ceramic magnets can also be manufactured by pressure bonding or injection molding the magnet powders in a carrier matrix. The density of magnet material in this form is lower than the pure sintered form, yielding lower magnetic properties. However, bonded or injection molded magnets may be made with close tolerances "off-tool" and in relatively intricate shapes.Alnico is manufactured in a cast or sintered form. Alnicos may be cast in large or complex shapes (such as the common horseshoe), while sintered Alnico magnets are made in relatively small sizes (normally one ounce or less) and in simple shapes.Flexible Rare Earth or Ceramic magnets are made by calendering or extruding magnet powders in a flexible carrier matrix such as vinyl. Magnet powder densities and therefore magnetic properties in this form of manufacture are even lower than the bonded or injection molded form. Flexible magnets are easily cut or punched to shape.7.0 Physical Characteristics and Machining of Permanent MagnetsSintered Samarium Cobalt and Ceramic magnets exhibit small cracks within the material that occur during the sintering process. Provided that cracks do not extend more than halfway through a section, they do not normally affect the operation of the magnet. This is also true for small chips that may occur during machining and handling of these magnets, especially on sharp edges. Magnets may be tumbled to break edges: this is done to avoid "feathering" of sharp edges due to the brittle nature of the materials. Tumbling can achieve edge breaks of 0.003" to 0.010". Although Neodymium Iron Boron is relatively tough as compared to Samarium Cobalt and Ceramic, it is still brittle and care must be taken in handling. Because of these inherent material characteristics, it is not advisable to use any permanent magnet material as a structural component of an assembly.Rare Earth, Alnico, and Ceramic magnets are machined by grinding, which may considerably affect the magnet cost. Maintaining simple geometries and wide tolerances is therefore desirable from an economic point of view. Rectangular or round sections are preferable to complex shapes. Square holes (even with large radii), and very small holes are difficult to machine and should be avoided. Magnets may be ground to virtually any specified tolerance. However, to reduce costs, tolerances of less than +0.001" should be avoided if possible.Cast Alnico materials exhibit porosity as a natural consequence of the casting process. This may become a problem with small shapes, which are machined out of larger castings. The voids occupy a small portion of the larger casting, but can account for a large portion of the smaller fabricated magnets. This may cause a problem where uniformity or low variation is critical, and it may be advisable either to use a sintered Alnico, or another material. In spite of its slightly lower magnetic properties, sintered Alnico may yield a higher or more uniform net density, resulting in equal or higher net magnetic output.In applications where the cosmetic qualities of the magnet are of a concern, special attention should be placed on selecting the appropriate material, since cracks, chips, pores, and voids are common in rigid magnet materials.Magnet Sales & Manufacturing has extensive experience in the machining and handling of all permanent magnet materials. In house machining facilities allow the ability to deliver prototype to production quantities with short lead times.8.0 CoatingsSamarium Cobalt, Alnico, and Ceramic materials are corrosion resistant, and do not require to be coated against corrosion. Alnico is easily plated for cosmetic qualities, and Ceramics may be coated to seal the surface, which will otherwise be covered by a thin film of ferrite powder (although not a problem for most applications).Neodymium Iron Boron magnets are susceptible to corrosion and consideration should be given to the operating environment to determine if coating is necessary. Nickel or tin plating may be used for Neodymium Iron Boron magnets, however, the material must be properly prepared and the plating process properly controlled for successful plating. Plating houses experienced in the plating of NdFeB materials are difficult to locate, and must be furnished with the necessary information for proper preparation and control of the process. Aluminum chromate or cadmium chromate vacuum deposition has been successfully tested, with coating thickness as low as 0.0005". Teflon and other organic coatings are relatively inexpensive and have also been successfully tested. A further option for critical applications is to apply two types of protective coatings or to encase the magnet in a stainless steel or other housing to reduce the chances of corrosion.9.0 Assembly ConsiderationsMagnet Sales & Manufacturing Inc. has manufacturing capabilities to manufacture complex magnet pole pieces and housings to provide a complete magnet assembly. The following points should be considered when designing magnet assemblies.9.1 Affixing Magnets to HousingsMagnets can be successfully affixed to housings using adhesives. Cyanoacrylate adhesives that are rated to temperatures up to 350 F with fast cure times are most commonly used. Fast cure。
磁矩_
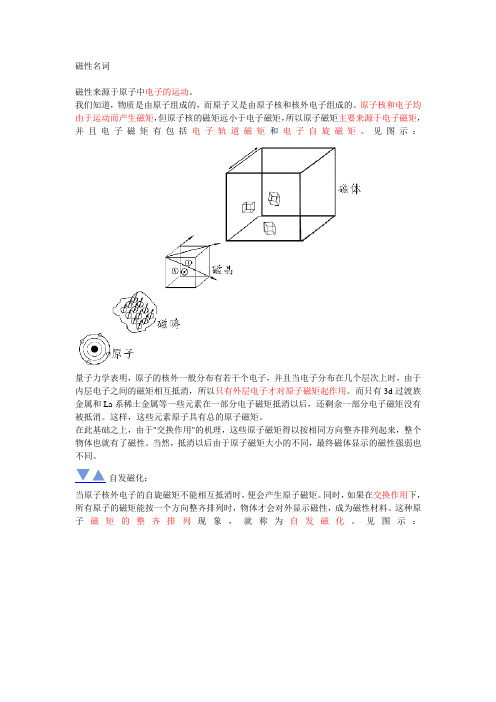
磁性名词磁性来源于原子中电子的运动。
我们知道,物质是由原子组成的,而原子又是由原子核和核外电子组成的。
原子核和电子均由于运动而产生磁矩,但原子核的磁矩远小于电子磁矩,所以原子磁矩主要来源于电子磁矩,并且电子磁矩有包括电子轨道磁矩和电子自旋磁矩。
见图示:量子力学表明,原子的核外一般分布有若干个电子,并且当电子分布在几个层次上时,由于内层电子之间的磁矩相互抵消,所以只有外层电子才对原子磁矩起作用。
而只有3d过渡族金属和La系稀土金属等一些元素在一部分电子磁矩抵消以后,还剩余一部分电子磁矩没有被抵消。
这样,这些元素原子具有总的原子磁矩。
在此基础之上,由于"交换作用"的机理,这些原子磁矩得以按相同方向整齐排列起来,整个物体也就有了磁性。
当然,抵消以后由于原子磁矩大小的不同,最终磁体显示的磁性强弱也不同。
·自发磁化:当原子核外电子的自旋磁矩不能相互抵消时,便会产生原子磁矩。
同时,如果在交换作用下,所有原子的磁矩能按一个方向整齐排列时,物体才会对外显示磁性,成为磁性材料。
这种原子磁矩的整齐排列现象,就称为自发磁化。
见图示:·磁畴:所谓磁畴,是指磁性材料内部的一个个小区域。
各个磁畴之间的交界面称为磁畴壁。
磁畴内原子磁矩一致整齐排列。
在材料未被磁化时,磁畴之间原子磁矩方向各不相同。
只有当磁性材料被磁化以后,它才能对外显示出磁性。
实际的磁性材料中,磁畴形貌五花八门,如条形畴、树枝状畴等。
既然磁畴内部的磁矩排列是整齐的,那么在磁畴壁处原子磁矩又是怎样排列的呢?在畴壁的一侧,原子磁矩指向某个方向,假设在畴壁的另一侧原子磁矩方向相反。
那么,在畴壁内部,原子磁矩必须成某种形式的过渡状态。
实际上,畴壁由很多层原子组成。
为了实现磁矩的转向,从一侧开始,每一层原子的磁矩都相对于磁畴中的磁矩方向偏转了一个角度,并且每一层的原子磁矩偏转角度逐渐增大,到另一侧时,磁矩已经完全转到和这一侧磁畴的磁矩相同的方向。
磁矩的计算方法

二 轨道磁性对磁矩的贡献
如果加上轨道磁性对磁矩的贡献,则磁矩的计算公式变为:
µ S+L= 4S(S + 1) + L(L + 1)
按照这个公式计算出来的磁矩在大多数情况下也与实验值 , 不一致。表明在多数情况下, 轨道角动量对分子磁矩的贡献很小 或没有贡献。
取决 于外磁场改变时电子能否自旋平行地在不同轨道之间 再分配。这种分配必须在对称性相同的能级之间进行。 再分配。
研究表明:轨道角动量对分子磁矩是否有贡献,
在八面体场中,d轨道分裂为t2g和eg, 由于eg轨道是 由形状不相同的两个简并轨道组成的,两条轨道的对 称性不同,电子不能在这两条轨道中进行自旋平行的 再分配,所以对磁矩不能作出贡献;但t2g 轨道是由对 称性和形状都完全相同的dxy、dxz、dyz所组成,电子可 以在这三条轨道中进行自旋平行的再分配,因而能对 磁矩作出贡献。但是当三条轨道各被一个或两个电子 占据时,这种再分配不能进行,所以半满和全满的t2g 轨道的磁矩也被冻结。相反, t2g1、t2g2、t2g4、t2g5, 由于 对同一自旋方向的电子来说,还存在有空轨道,因而 能进行自旋平行的再分配,所以可对磁矩作出贡献。
过渡态 过渡态 过渡态
右图示出反应体系的能量 Ea 中间体 变化, 其中(a)为具有交换机理 反应物 的能量曲线, 反应物分子吸收活 反应物 △ H H △ 产物 产物 化能后互相缔合成为一种活化 (b) (a) 配合物, 然后离解出离去配 体放出能量。而(b)为具有A机理或D机理取代反应的能量曲线, 图 上有两个过渡态和一个能量高于反应物和产物的中间体。 对于A机理, 第一过渡态是通过缔合模式而得到的活化配合 物, 这时形成了一个新键, 生成一个配位数增加的中间体, 接着经 过第二个过渡态即离解活化模式的活化配合物之后变成产物。 对于D机理, 能量曲线与A机理相同, 只是刚好与A机理相反, 第一个过渡态是通过离解模式而第二过渡态是通过缔合模式所产 生, 而中间体是配位数比反应物少的物种。
磁性材料术语解释及计算公式

磁性材料术语解释及计算公式起始磁导率“i初始磁导率是磁性材料的磁导率(B/H)在磁化曲线始端的极限值,即式中“o为真空磁导率(4TTX\0~7 H/m)△H为磁场强度的变化率(A/m)△B为磁感应强度的变化率(T)有效磁导率“e在闭合磁路中,如果漏磁可忽略,可以用有效磁导率来表示磁芯的性能0式中L为装有磁芯的线圈的电感量(H)N为线圈匝数Le为有效磁路长度5)Ae为有效截面积(卅)饱和磁通密度Bs (T)磁化到饱和状态的磁通密度。
见图1。
・ 1a 1 =—x ——(AH T O)图1剩余磁通密度Br (T)从饱和状态去除磁场后,剩余的磁通密度。
见图1。
矫顽力He (A/m)从饱和状态去除磁场后,磁芯继续被反向磁场磁化,直至磁感应强度减为零,此时的磁场强度称为矫顽力。
见图1。
损耗因子tan5损耗系数是磁滞损耗、涡流损耗和剩余损耗三者之和。
tan^= tan d h + t an del tan dr式中tan o i.为磁滞损耗系数tan o e为涡流损耗系数tan d r为剩余损耗系数相对损耗因子t an6//I i比损耗因子是损耗系数与与磁导率之比:tano /i (it用于材料)tano/zze (适用于磁路中含有气隙的磁芯)品质因数Q品质因数为损耗因子的倒数:Q = 1/ tan5温度系数a“( 1/K)温度系数为T1和T2范围内变化时,每变化1K 相应的磁导率的相对变化量: a 口 =卩2_卩1 1Pl T 2 _T ] 式中“1为温度为T1时的磁导率“2为温度为T2时的磁导率相对温度系数a “r(l/K)温度系数和磁导率之比,即在恒温条件下,完全退磁的磁芯的磁导率随时间的衰减变化,即DF =x 丄(T2>T1)“1为退磁后T1分钟的磁导率“2为退磁后T2分钟的磁导率居里温度Tc (°C)在该温度时材料由铁磁性(或亚铁磁)转变为顺磁性,见图2。
a //r = 减落系数DFGT电阻率p(Q.m)具有单位截面积和单位长度的磁性材料的电阻。
高频变压器磁损计算!

高频变压器磁损计算!一、引言磁性元件是开关电源设备中的重要元件,它对开关电源设备的体积、效率有很大影响。
在高频下,磁性元件损耗占整机的比重很大。
因此对磁性元件的损耗进行相关研究是十分重要的。
磁芯损耗与磁性材料特性和工作频率等密切相关。
在交流磁化过程中,磁芯损耗功率(Pv)由磁滞损耗(Ph)、涡流损耗(Pe)和剩余损耗(Pc)组成。
磁滞损耗(Ph)是磁性材料在磁化过程中,磁畴要克服磁畴壁的摩擦而损失的能量,这部分损失最终使磁芯发热而消耗掉。
单位体积磁芯损耗的能量正比于磁滞回线包围的面积。
每磁化一个周期,就要损耗与磁滞回线包围面积成正比的能量,所以可以得出:磁滞曲线面积越小,磁滞损耗就越小;频率越高,损耗功率越大。
涡流损耗(Pe)是因磁芯材料的电阻率不是无限大,有一定的电阻值,在高频时还是会由于激磁磁场在磁芯中产生涡流而导致损耗。
剩余损耗(Pc)是由于磁化弛豫效应或磁性滞后效应引起的损耗。
所谓弛豫是指在磁化或反磁化的过程中,磁化状态并不是随磁化强度的变化而立即变化到它的最终状态,而是需要一个过程,这个‘时间效应’便是引起剩余损耗的原因。
本文对高频下磁芯损耗的计算进行了研讨。
二、磁芯损耗的经典计算方法前面对磁芯损耗的构成进行了分析,磁芯损耗功率(Pv)由磁滞损耗(Ph)、涡流损耗(Pe)和剩余损耗(Pc)组成:对于软磁铁氧体,文献[1]分别给出了正弦波形激励下Ph,Pe,Pc 的计算模型,但并不适合工程上的应用。
在一个世纪以前Steinmetz 总结出一个实用于工程计算磁芯损耗的经验公式:这个公式表明单位体积的损耗Pv 是重复磁化频率和磁通密度的指数函数。
Cm ,α 和β 是经验参数,两个指数都可以不为整数,一般的1<α<3 和2<β<3。
对于不同的材质,生产厂家一般会给出其相应的一套参数,但公式和参数仅仅适用于正弦的磁化情况,这是该经验公式应用于开关电源领域的一个主要缺陷。
三、Steinmetz 经验公式的应用与调整3.1 频率和温度的影响借助Steinmetz 模型计算磁损在工程上的应用十分广泛,然而该模型的参数随频率变化,也就是说用来反映频率和最大磁感应强度与磁损关系的幂指数α 和β 的拟合值在不同频率时是不同的,同时温度对磁芯损耗的影响也很大。
(参考资料)烧结钕铁硼基础知识培训教材

二、烧结钕铁硼永磁材料产品生产工序
包 装:
三、烧结钕铁硼磁体的主要性能参数
剩磁(Br):将磁体在外磁场的作用下充磁到技术饱和后撤消外 磁场,此时磁体表现的磁感应强度称之为剩磁 磁感矫顽力(Hcb):磁体在反向充磁时,使磁体内部磁感应强 度降为零所需的反向磁场强度。但此时磁体的磁化强度并不为 零,只是所加的反向磁场与磁体的磁化强度作用相互抵消 内禀矫顽力(Hcj):使磁体的磁化强度降为零所需施加的反向 磁场强度 磁能积(BH)max:退磁曲线上任何一点的B和H的乘积,而 B×H的最大值称之为最大磁能积 膝点矫顽力(Hk):使磁体的磁化强度降低10%(或5%)所 需施加的反向磁场强度 方形度:Hk与Hcj的比值,理论极限为1,我司标准大于0.9
磁性能参数转换关系
中文名称 英文简称
剩磁
Br
感应矫顽力 Hcb
内禀矫顽力 Hcj, Hic
磁能积
BH max
表磁
H
单位SI
T kA/m kA/m kJ/m3 kA/m
单位CGS
kGs kOe kOe MGOe kOe
CGS / SI
10 4π/103 4π/103 4π/102 4π/103
磁通
Φ
烧结钕铁硼永磁材料基本知识
技术研发中心
二零一一年三月
内容
烧结钕铁硼永磁材料简介 烧结钕铁硼永磁材料产品生产工序 烧结钕铁硼磁体的主要性能参数 企业标准介绍 了解潜在要求,满足潜在需求
一、烧结钕铁硼永磁材料简介
磁性材料:三大基础功能材料之一
软磁材料:钢、铁
软磁铁氧体
俗称钕铁硼
多铁非晶材料 硬磁(永磁)材料:
抗弯强度/MPa,根据客户需要,采用三点弯曲方 法进行测试
什么是剩磁?如何计算剩磁大小?

什么是剩磁?如何计算剩磁大小?展开全文常用的磁测仪器有:磁通计、特斯拉计(又称为高斯计)、磁测仪。
磁通计用于测量磁感应通量,特斯拉计用于测量表面磁场强度或气隙磁场强度,磁测仪用于测量综合磁性能。
所有仪器使用之前应仔细阅读说明书,根据说明书的要求预热,预热之后按照说明书的要求进行操作。
二、应用特斯拉计(高斯计)测量特斯拉计一般可用于测量磁性材料的表面磁场强度,具体而言就是测量表面中心部位的场强。
测量之前应根据说明书的要求进行预热,然后检查、调整零点,使得非测量状态下的示值为"0"。
注意:在使用过程中一般不应调整霍尔电流。
更换探头时应根据探头的说明在仪器热态下调整霍尔电流,并在适当的部位标识霍尔电流参数值。
可以经常检查电流值,应为规定的数值。
测量表场的方法无法准确获得全面的磁参数(如剩磁、矫顽力、磁能积),通常以上下限标样的中心场资料作为参考资料来进行合格判别。
此种方法对n、m系列可用,对h以上系列准确度要差一些。
一般而言可以按照下述公式计算不同尺寸(圆柱或圆片)的中心场:h=br*k/√(1+5.28*k*k)(gs)式中:br--标称剩磁k--圆柱、圆片的长径比或方块磁化方向与另二个方向中较短边长之比。
对于长宽相差较大的产品k=取向长度/sqr(长*宽)更准确的计算公式:h=br*k/√(1+(4+32/l)*k*k)(gs)l--方块磁化方向的长度32--探头的测试系数参数(0.5*64)特斯拉计探头内霍尔片位置的确定:一般而言,霍尔片只有大约1*1~2*3平方毫米左右大小的面积,厚度约0.3~0.5毫米,且不在探头的最前部,有时需要确定霍尔片的位置,可以采用如下的方法来判断霍尔片的位置:将探头在充磁产品的表面,此时特斯拉计示值不为零,探头一直向外侧延伸探出,当特斯拉计示值为零时即为霍尔片的前边部,用铅笔或记号笔沿产品的外边界线标记记号;将探头向相反方向延伸(此时探头只有一小部分接触在磁体上),当特斯拉计示值为零时在做记号,两个记号的中位置即为霍尔片的实际位置。
永磁体基本性能参数

永磁体基本性能参数永磁体基本性能参数永磁材料:永磁材料被外加磁场磁化后磁性不消失,可对外部空间提供稳定磁场。
钕铁硼永磁体常用的衡量指标有以下四种:剩磁(Br)单位为特斯拉(T)和高斯(Gs)1Gs =0.0001T将一个磁体在闭路环境下被外磁场充磁到技术饱和后撤消外磁场,此时磁体表现的磁感应强度我们称之为剩磁。
它表示磁体所能提供的最大的磁通值。
从退磁曲线上可见,它对应于气隙为零时的情况,故在实际磁路中磁体的磁感应强度都小于剩磁。
钕铁硼是现今发现的Br 最高的实用永磁材料。
磁感矫顽力(Hcb )单位是安/米(A/m )和奥斯特(Oe)或1 0e〜79.6A/m处于技术饱和磁化后的磁体在被反向充磁时,使磁感应强度降为零所需反向磁场强度的值称之为磁感矫顽力(Hcb)。
但此时磁体的磁化强度并不为零,只是所加的反向磁场与磁体的磁化强度作用相互抵消。
(对外磁感应强度表现为零)此时若撤消外磁场,磁体仍具有一定的磁性能。
钕铁硼的矫顽力一般是llOOOOe以上。
内禀矫顽力(Hcj)单位是安/米(A/m)和奥斯特(Oe) 1 Oe〜79.6A/m 使磁体的磁化强度降为零所需施加的反向磁场强度,我们称之为内禀矫顽力。
内禀矫顽力是衡量磁体抗退磁能力的一个物理量,如果外加的磁场等于磁体的内禀矫顽力,磁体的磁性将会基本消除。
钕铁硼的Hcj 会随着温度的升高而降低所以需要工作在高温环境下时应该选择高Hcj的牌号。
磁能积(BH)单位为焦/米 3 (J/m3 )或高?奥(GOe) 1 MGOe〜7. 96k J/m3退磁曲线上任何一点的B和H的乘积既BH我们称为磁能积,而B X H 的最大值称之为最大磁能积(BH)max。
磁能积是恒量磁体所储存能量大小的重要参数之一,(BH)max越大说明磁体蕴含的磁能量越大。
设计磁路时要尽可能使磁体的工作点处在最大磁能积所对应的B和H附近。
各向同性磁体:任何方向磁性能都相同的磁体。
各向异性磁体:不同方向上磁性能会有不同;且存在一个方向,在该方向取向时所得磁性能最高的磁体。
钕铁硼永磁体磁特性参数的快速测量方法

Copyright©2000–2015Linkjoin
5
图一是计算公式的图示:
图一:第二象限退磁曲线
内禀磁通密度
内禀磁通密度定义为单位体积的磁体磁矩,知道了磁体的体积和磁矩,内 禀磁通密度可依下式计算。
为计算方便,把韦伯/平方厘米 转换为 高斯
Copyright©2000–2015Linkjoin
2
磁测量设备制造与工业磁测量系统集成解决方案服务商
计算磁体最大磁能积
从上面的计算公式中,我们可以看出,在测量磁体磁矩后,必须知道磁体
的回复磁导率和磁导系数PC值才能依据以上公式得出材料的剩磁,矫顽力和磁
能积。但材料的回复磁导率1.02——1.1之间的一个值,同一厂家不同批次的产
Copyright©2000–2015Linkjoin
3
磁测量设备制造与工业磁测量系统集成解决方案服务商
Magnetic measuringequipmentmanufacturer andsystemintegrationprojectprovider
测量方法:采用亥姆霍兹线圈进行开路测量,不需要外部励磁。 工作模式:分选功能,声光报警模式。 数据存储:大容量数据存储,可保存10万组数据。
为计算方便把韦伯平方厘米转换为高斯计算开路时的工作点磁场强度计算开路时的工作点磁通量密度measurementequipmentwwwlinkjoincomlinkjoin计算剩余磁通量密度剩磁计算矫顽力退磁曲线近似直线这种计算方法是将材料的退磁曲线假定为直线的前提下提出的如果磁材料在第2象限有拐点矫顽力计算值就不准确
1
磁测量设备制造与工业磁测量系统集成解决方案服务商
Magnetic measuringequipmentmanufacturer andsystemintegrationprojectprovider
