过程设备设计第三版课后答案及重点
过程设备设计第三版课后答案及重点

过程设备设计题解1.压力容器导言习题1. 试应用无力矩理论的基本方程,求解圆柱壳中的应力(壳体承受气体内压p ,壳体中面半径为R ,壳体厚度为t )。
若壳体材料由20R (MPa MPa s b 245,400==σσ)改为16MnR(MPa MPa s b 345,510==σσ)时,圆柱壳中的应力如何变化?为什么?解:○1求解圆柱壳中的应力 应力分量表示的微体和区域平衡方程式:δσσθφzp R R -=+21φσππφsin 220t r dr rp F k r z k=-=⎰圆筒壳体:R 1=∞,R 2=R ,p z =-p ,r k =R ,φ=π/2tpRpr tpR k 2sin 2===φδσσφθ○2壳体材料由20R 改为16MnR ,圆柱壳中的应力不变化。
因为无力矩理论是力学上的静定问题,其基本方程是平衡方程,而且仅通过求解平衡方程就能得到应力解,不受材料性能常数的影响,所以圆柱壳中的应力分布和大小不受材料变化的影响。
2. 对一标准椭圆形封头(如图所示)进行应力测试。
该封头中面处的长轴D=1000mm ,厚度t=10mm ,测得E 点(x=0)处的周向应力为50MPa 。
此时,压力表A 指示数为1MPa ,压力表B 的指示数为2MPa ,试问哪一个压力表已失灵,为什么?解:○1根据标准椭圆形封头的应力计算式计算E 的内压力: 标准椭圆形封头的长轴与短轴半径之比为2,即a/b=2,a=D/2=500mm 。
在x=0处的应力式为:MPa abt p btpa 15002501022222=⨯⨯⨯===θθσσ ○2从上面计算结果可见,容器内压力与压力表A 的一致,压力表B 已失灵。
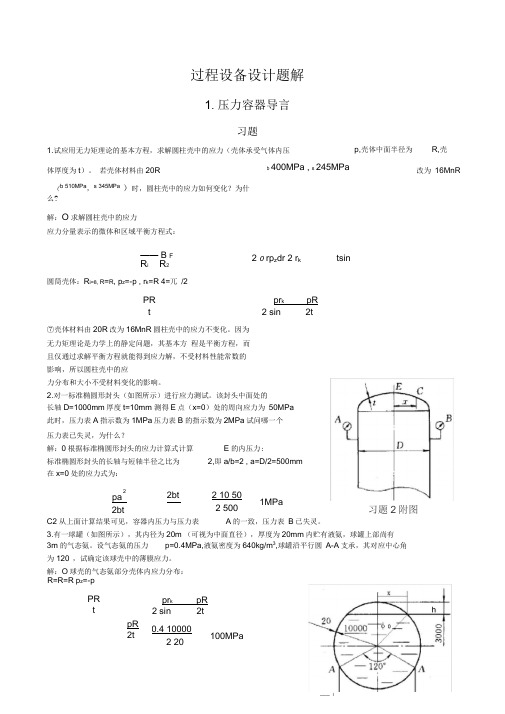
3. 有一球罐(如图所示),其内径为20m (可视为中面直径),厚度为20mm 。
内贮有液氨,球罐上部尚有3m 的气态氨。
设气态氨的压力p=0.4MPa ,液氨密度为640kg/m 3,球罐沿平行圆A-A 支承,其对应中心角为120°,试确定该球壳中的薄膜应力。
过程设备设计(郑津洋第三版)终极版思考题答案

过程设备设计(郑津洋第三版)终极版思考题答案第1章压力容器导言思考题1.1介质的毒性程度和易燃特性对压力容器的设计、制造、使用和管理有何影响?答:我国《压力容器安全技术监察规程》根据整体危害水平对压力容器进行分类。
压力容器破裂爆炸时产生的危害愈大,对压力容器的设计、制造、检验、使用和管理的要求也愈高。
设计压力容器时,依据化学介质的最高容许浓度,我国将化学介质分为极度危害(Ⅰ级)、高度危害(Ⅱ级)、中度危害(Ⅲ级)、轻度危害(Ⅳ级)等四个级别。
介质毒性程度愈高,压力容器爆炸或泄漏所造成的危害愈严重。
压力容器盛装的易燃介质主要指易燃气体或液化气体,盛装易燃介质的压力容器发生泄漏或爆炸时,往往会引起火灾或二次爆炸,造成更为严重的财产损失和人员伤亡。
因此,品种相同、压力与乘积大小相等的压力容器,其盛装介质的易燃特性和毒性程度愈高,则其潜在的危害也愈大,相应地,对其设计、制造、使用和管理也提出了更加严格的要求。
例如,Q235-B钢板不得用于制造毒性程度为极度或高度危害介质的压力容器;盛装毒性程度为极度或高度危害介质的压力容器制造时,碳素钢和低合金板应逐进行超声检测,整体必须进行焊后热处理,容器上的A、B类焊接接头还应进行100%射线或超声检测,且液压试验合格后还应进行气密性试验。
而制造毒性程度为中度或轻度的容器,其要求要低得多。
又如,易燃介质压力容器的所有焊缝均应采用全熔透结构思考题1.2 压力容器主要由哪几部分组成?分别起什么作用?答:筒体:压力容器用以储存物料或完成化学反应所需要的主要压力空间,是压力容器的最主要的受压元件之一;封头:有效保证密封,节省材料和减少加工制造的工作量;密封装置:密封装置的可靠性很大程度上决定了压力容器能否正常、安全地运行;开孔与接管:在压力容器的筒体或者封头上开设各种大小的孔或者安装接管,以及安装压力表、液面计、安全阀、测温仪等接管开孔,是为了工艺要求和检修的需要。
支座:压力容器靠支座支承并固定在基础上。
过程设备设计第三版课后答案及重点
过程设备设计题解1.压力容器导言习题1.试应用无力矩理论的基本方程,求解圆柱壳中的应力(壳体承受气体内压(b 510MPa ,s 345MPa )时,圆柱壳中的应力如何变化?为什么?解:O 求解圆柱壳中的应力应力分量表示的微体和区域平衡方程式:—— B FR i R 2圆筒壳体:R i=8, R =R , p z =-p , r k =R 4=兀 /2PR t⑦壳体材料由20R 改为16MnR 圆柱壳中的应力不变化。
因为无力矩理论是力学上的静定问题,其基本方 程是平衡方程,而且仅通过求解平衡方程就能得到应力解,不受材料性能常数的影响,所以圆柱壳中的应C2从上面计算结果可见,容器内压力与压力表A 的一致,压力表B 已失灵。
3.有一球罐(如图所示),其内径为20m (可视为中面直径),厚度为20mm 内贮有液氨,球罐上部尚有 3m 的气态氨。
设气态氨的压力 p=0.4MPa,液氨密度为640kg/m 3,球罐沿平行圆 A-A 支承,其对应中心角为120°,试确定该球壳中的薄膜应力。
解:O 球壳的气态氨部分壳体内应力分布:体厚度为t )。
若壳体材料由20Rb400MPa , s 245MPa改为 16MnR力分布和大小不受材料变化的影响。
2.对一标准椭圆形封头(如图所示)进行应力测试。
该封头中面处的 长轴D=1000mm 厚度t=10mm 测得E 点(x=0)处的周向应力为 50MPa 此时,压力表A 指示数为1MPa 压力表B 的指示数为2MPa 试问哪一个 压力表已失灵,为什么? 解:0根据标准椭圆形封头的应力计算式计算 E 的内压力:标准椭圆形封头的长轴与短轴半径之比为 2,即a/b=2 , a=D/2=500mm在x=0处的应力式为: 2pa 2bt 2bt2 10 502 5001MPa习题2附图p,壳体中面半径为 R,壳2 0 rp z dr 2 r k tsinpr k pR 2 sin 2tR=R=R p z =-pPRtpR 2tpr k pR 2 sin 2t0.4 100002 20100MPa—-」习题3附图世支承以上部分,任一 4角处的应力: d 4R=R=R, pz=-[p+ p g R (cos 4 0-cos 4 )] r=Rsin()),dr=Rcos ())sin 0 .102 72 10517Qcos 0.7由区域平衡方程和拉普拉斯方程: 2 R tsin 2 2coscos R g rdr 2 p R gcos rrdrr 。
过程设备设计(郑津洋第三版)终极版思考题答案_extract

第1章压力容器导言思考题 1.1 介质的毒性程度和易燃特性对压力容器的设计、制造、使用和管理有何影响?答:我国?压力容器平安技术监察规程? 根据整体危害水平对压力容器进展分类。
压力容器破裂爆炸时产生的危害愈大,对压力容器的设计、制造、检验、使用和管理的要求也愈高。
设计压力容器时,依据化学介质的最高容许浓度,我国将化学介质分为极度危害〔Ⅰ级〕、高度危害〔Ⅱ级〕、中度危害〔Ⅲ级〕、轻度危害〔Ⅳ级〕等四个级别。
介质毒性程度愈高,压力容器爆炸或泄漏所造成的危害愈严重。
压力容器盛装的易燃介质主要指易燃气体或液化气体,盛装易燃介质的压力容器发生泄漏或爆炸时,往往会引起火灾或二次爆炸,造成更为严重的财产损失和人员伤亡。
因此,品种一样、压力与乘积大小相等的压力容器,其盛装介质的易燃特性和毒性程度愈高,那么其潜在的危害也愈大,相应地,对其设计、制造、使用和管理也提出了更加严格的要求。
例如, Q235-B 钢板不得用于制造毒性程度为极度或高度危害介质的压力容器;盛装毒性程度为极度或高度危害介质的压力容器制造时,碳素钢和低合金板应逐X进展超声检测,整体必须进展焊后热处理,容器上的A、B 类焊接接头还应进展 100%射线或超声检测,且液压试验合格后还应进展气密性试验。
而制造毒性程度为中度或轻度的容器,其要求要低得多。
又如,易燃介质压力容器的所有焊缝均应采用全熔透构造思考题 1.2压力容器主要由哪几局部组成?分别起什么作用?答:筒体:压力容器用以储存物料或完成化学反响所需要的主要压力空间,是压力容器的最主要的受压元件之一;封头:有效保证密封,节省材料和减少加工制造的工作量;密封装置:密封装置的可靠性很大程度上决定了压力容器能否正常、平安地运行;开孔与接收:在压力容器的筒体或者封头上开设各种大小的孔或者安装接收,以及安装压力表、液面计、平安阀、测温仪等接收开孔,是为了工艺要求和检修的需要。
支座:压力容器靠支座支承并固定在根底上。
过程设备设计(郑津洋第三版)终极版思考题答案之欧阳与创编

第1章压力容器导言思考题1.1介质的毒性程度和易燃特性对压力容器的设计、制造、使用和管理有何影响?答:我国《压力容器安全技术监察规程》根据整体危害水平对压力容器进行分类。
压力容器破裂爆炸时产生的危害愈大,对压力容器的设计、制造、检验、使用和管理的要求也愈高。
设计压力容器时,依据化学介质的最高容许浓度,我国将化学介质分为极度危害(Ⅰ级)、高度危害(Ⅱ级)、中度危害(Ⅲ级)、轻度危害(Ⅳ级)等四个级别。
介质毒性程度愈高,压力容器爆炸或泄漏所造成的危害愈严重。
压力容器盛装的易燃介质主要指易燃气体或液化气体,盛装易燃介质的压力容器发生泄漏或爆炸时,往往会引起火灾或二次爆炸,造成更为严重的财产损失和人员伤亡。
因此,品种相同、压力与乘积大小相等的压力容器,其盛装介质的易燃特性和毒性程度愈高,则其潜在的危害也愈大,相应地,对其设计、制造、使用和管理也提出了更加严格的要求。
例如,Q235B钢板不得用于制造毒性程度为极度或高度危害介质的压力容器;盛装毒性程度为极度或高度危害介质的压力容器制造时,碳素钢和低合金板应逐张进行超声检测,整体必须进行焊后热处理,容器上的A、B类焊接接头还应进行100%射线或超声检测,且液压试验合格后还应进行气密性试验。
而制造毒性程度为中度或轻度的容器,其要求要低得多。
又如,易燃介质压力容器的所有焊缝均应采用全熔透结构思考题1.2 压力容器主要由哪几部分组成?分别起什么作用?答:筒体:压力容器用以储存物料或完成化学反应所需要的主要压力空间,是压力容器的最主要的受压元件之一;封头:有效保证密封,节省材料和减少加工制造的工作量;密封装置:密封装置的可靠性很大程度上决定了压力容器能否正常、安全地运行;开孔与接管:在压力容器的筒体或者封头上开设各种大小的孔或者安装接管,以及安装压力表、液面计、安全阀、测温仪等接管开孔,是为了工艺要求和检修的需要。
支座:压力容器靠支座支承并固定在基础上。
安全附件:保证压力容器的安全使用和工艺过程的正常进行。
过程设备设计(郑津洋第三版)终极版思考题答案之欧阳歌谷创作

第1章压力容器导言欧阳歌谷(2021.02.01)思考题 1.1介质的毒性程度和易燃特性对压力容器的设计、制造、使用和管理有何影响?答:我国《压力容器安全技术监察规程》根据整体危害水平对压力容器进行分类。
压力容器破裂爆炸时产生的危害愈大,对压力容器的设计、制造、检验、使用和管理的要求也愈高。
设计压力容器时,依据化学介质的最高容许浓度,我国将化学介质分为极度危害(Ⅰ级)、高度危害(Ⅱ级)、中度危害(Ⅲ级)、轻度危害(Ⅳ级)等四个级别。
介质毒性程度愈高,压力容器爆炸或泄漏所造成的危害愈严重。
压力容器盛装的易燃介质主要指易燃气体或液化气体,盛装易燃介质的压力容器发生泄漏或爆炸时,往往会引起火灾或二次爆炸,造成更为严重的财产损失和人员伤亡。
因此,品种相同、压力与乘积大小相等的压力容器,其盛装介质的易燃特性和毒性程度愈高,则其潜在的危害也愈大,相应地,对其设计、制造、使用和管理也提出了更加严格的要求。
例如,Q235B钢板不得用于制造毒性程度为极度或高度危害介质的压力容器;盛装毒性程度为极度或高度危害介质的压力容器制造时,碳素钢和低合金板应逐张进行超声检测,整体必须进行焊后热处理,容器上的A、B类焊接接头还应进行100%射线或超声检测,且液压试验合格后还应进行气密性试验。
而制造毒性程度为中度或轻度的容器,其要求要低得多。
又如,易燃介质压力容器的所有焊缝均应采用全熔透结构思考题 1.2 压力容器主要由哪几部分组成?分别起什么作用?答:筒体:压力容器用以储存物料或完成化学反应所需要的主要压力空间,是压力容器的最主要的受压元件之一;封头:有效保证密封,节省材料和减少加工制造的工作量;密封装置:密封装置的可靠性很大程度上决定了压力容器能否正常、安全地运行;开孔与接管:在压力容器的筒体或者封头上开设各种大小的孔或者安装接管,以及安装压力表、液面计、安全阀、测温仪等接管开孔,是为了工艺要求和检修的需要。
支座:压力容器靠支座支承并固定在基础上。
过程设备设计(郑津洋第三版)终极版思考题答案之欧阳歌谷创作

第1章压力容器导言欧阳歌谷(2021.02.01)思考题 1.1介质的毒性程度和易燃特性对压力容器的设计、制造、使用和管理有何影响?答:我国《压力容器安全技术监察规程》根据整体危害水平对压力容器进行分类。
压力容器破裂爆炸时产生的危害愈大,对压力容器的设计、制造、检验、使用和管理的要求也愈高。
设计压力容器时,依据化学介质的最高容许浓度,我国将化学介质分为极度危害(Ⅰ级)、高度危害(Ⅱ级)、中度危害(Ⅲ级)、轻度危害(Ⅳ级)等四个级别。
介质毒性程度愈高,压力容器爆炸或泄漏所造成的危害愈严重。
压力容器盛装的易燃介质主要指易燃气体或液化气体,盛装易燃介质的压力容器发生泄漏或爆炸时,往往会引起火灾或二次爆炸,造成更为严重的财产损失和人员伤亡。
因此,品种相同、压力与乘积大小相等的压力容器,其盛装介质的易燃特性和毒性程度愈高,则其潜在的危害也愈大,相应地,对其设计、制造、使用和管理也提出了更加严格的要求。
例如,Q235-B钢板不得用于制造毒性程度为极度或高度危害介质的压力容器;盛装毒性程度为极度或高度危害介质的压力容器制造时,碳素钢和低合金板应逐张进行超声检测,整体必须进行焊后热处理,容器上的A、B类焊接接头还应进行100%射线或超声检测,且液压试验合格后还应进行气密性试验。
而制造毒性程度为中度或轻度的容器,其要求要低得多。
又如,易燃介质压力容器的所有焊缝均应采用全熔透结构思考题 1.2 压力容器主要由哪几部分组成?分别起什么作用?答:筒体:压力容器用以储存物料或完成化学反应所需要的主要压力空间,是压力容器的最主要的受压元件之一;封头:有效保证密封,节省材料和减少加工制造的工作量;密封装置:密封装置的可靠性很大程度上决定了压力容器能否正常、安全地运行;开孔与接管:在压力容器的筒体或者封头上开设各种大小的孔或者安装接管,以及安装压力表、液面计、安全阀、测温仪等接管开孔,是为了工艺要求和检修的需要。
支座:压力容器靠支座支承并固定在基础上。
过程设备设计第三版(郑津洋)习题题解

过程设备设计题解1.压力容器导言思考题1.压力容器主要由哪几部分组成?分别起什么作用?答:压力容器由筒体、封头、密封装置、开孔接管、支座、安全附件六大部件组成。
筒体的作用:用以储存物料或完成化学反应所需要的主要压力空间。
封头的作用:与筒体直接焊在一起,起到构成完整容器压力空间的作用。
密封装置的作用:保证承压容器不泄漏。
开孔接管的作用:满足工艺要求和检修需要。
支座的作用:支承并把压力容器固定在基础上。
安全附件的作用:保证压力容器的使用安全和测量、控制工作介质的参数,保证压力容器的使用安全和工艺过程的正常进行。
2.介质的毒性程度和易燃特性对压力容器的设计、制造、使用和管理有何影响?答:介质毒性程度越高,压力容器爆炸或泄漏所造成的危害愈严重,对材料选用、制造、检验和管理的要求愈高。
如Q235-A或Q235-B钢板不得用于制造毒性程度为极度或高度危害介质的压力容器;盛装毒性程度为极度或高度危害介质的容器制造时,碳素钢和低合金钢板应力逐张进行超声检测,整体必须进行焊后热处理,容器上的A、B类焊接接头还应进行100%射线或超声检测,且液压试验合格后还得进行气密性试验。
而制造毒性程度为中度或轻度的容器,其要求要低得多。
毒性程度对法兰的选用影响也甚大,主要体现在法兰的公称压力等级上,如内部介质为中度毒性危害,选用的管法兰的公称压力应不小于1.0MPa;内部介质为高度或极度毒性危害,选用的管法兰的公称压力应不小于1.6MPa,且还应尽量选用带颈对焊法兰等。
易燃介质对压力容器的选材、设计、制造和管理等提出了较高的要求。
如Q235-A·F不得用于易燃介质容器;Q235-A不得用于制造液化石油气容器;易燃介质压力容器的所有焊缝(包括角焊缝)均应采用全焊透结构等。
《压力容器安全技术监察规程》在确定压力容器类别时,为什么不仅要根据压力高低,还要视压力与容积的乘积pV大小进行分类?答:因为pV乘积值越大,则容器破裂时爆炸能量愈大,危害性也愈大,对容器的设计、制造、检验、使用和管理的要求愈高。
过程设备设计(第三版,郑津洋_董其伍)化工工业出版社答案

5.储存设备5.1 设计双鞍座卧式容器时,支座位置应该按照那些原则确定?试说明理由。
根据JB4731规定,取A小于等于0.2L,最大不得超过0.25L,否则容器外伸端将使支座界面的应力过大。
因为当A=0.207L时,双支座跨距中间截面的最大弯距和支座截面处的弯距绝对值相等,使两个截面保持等强度。
考虑到除弯距以外的载荷,所以常取外圆筒的弯距较小。
所以取A小于等于0.2L。
当A满足小于等于0.2L时,最好使A小于等于0.5Rm(Rm为圆筒的平均半径)。
这是因为支座靠近封头可充分利用封头对支座处圆筒的加强作用。
5.2 双鞍座卧式容器受力分析与外伸梁承受均布载荷有何相同何不同,试用剪力图和弯距图比较。
外伸梁的剪力和弯矩图与此图类似,只是在两端没有剪力和弯矩作用,两端的剪力和弯矩均为零5.3 “扁塌”现象的原因是什么?如何防止这一现象出现?由于支座处截面受剪力作用而产生周向弯距,在周向弯距的作用下,导致支座处圆筒的上半部发生变形,产生所谓“扁塌”现象。
可以设置加强圈,或者使支座靠近封头布置,利用加强圈或封头的加强作用。
5.4 双鞍座卧式容器设计中应计算那些应力?如何产生的?①圆筒上的轴向应力。
由轴向弯矩引起。
②支座截面处圆筒和封头上的切向切应力和封头的附加拉伸应力。
由横向剪力引起。
③支座截面处圆筒的周向弯曲应力。
由截面上切向切应力引起。
④支座截面处圆筒的周向压缩应力。
通过鞍座作用于圆筒上的载荷所导致的。
5.5 鞍座包角对卧式容器筒体应力和鞍座自身强度有何影响?鞍座包角的大小不仅影响鞍座处圆筒截面上的应力分布,而且也影响卧式储罐的稳定性和储罐-支座系统的重心高低。
包角小,鞍座重量轻,但重心高,且鞍座处圆筒上的应力较大。
5.6 在什么情况下应对卧式容器进行加强圈加强?如卧式储罐支座因结构原因不能设置在靠近封头处(A>0.5Ri),且圆筒不足以承受周向弯距时,就需在支座截面处的圆筒上设置加强圈,以便与圆筒一起承载。
(设备管理)过程设备设计(郑津洋第三版)终极版思考题答案

第1章压力容器导言思考题1.1介质的毒性程度和易燃特性对压力容器的设计、制造、使用和管理有何影响?答:我国《压力容器安全技术监察规程》根据整体危害水平对压力容器进行分类。
压力容器破裂爆炸时产生的危害愈大,对压力容器的设计、制造、检验、使用和管理的要求也愈高。
设计压力容器时,依据化学介质的最高容许浓度,我国将化学介质分为极度危害(Ⅰ级)、高度危害(Ⅱ级)、中度危害(Ⅲ级)、轻度危害(Ⅳ级)等四个级别。
介质毒性程度愈高,压力容器爆炸或泄漏所造成的危害愈严重。
压力容器盛装的易燃介质主要指易燃气体或液化气体,盛装易燃介质的压力容器发生泄漏或爆炸时,往往会引起火灾或二次爆炸,造成更为严重的财产损失和人员伤亡。
因此,品种相同、压力与乘积大小相等的压力容器,其盛装介质的易燃特性和毒性程度愈高,则其潜在的危害也愈大,相应地,对其设计、制造、使用和管理也提出了更加严格的要求。
例如,Q235-B钢板不得用于制造毒性程度为极度或高度危害介质的压力容器;盛装毒性程度为极度或高度危害介质的压力容器制造时,碳素钢和低合金板应逐张进行超声检测,整体必须进行焊后热处理,容器上的A、B类焊接接头还应进行100%射线或超声检测,且液压试验合格后还应进行气密性试验。
而制造毒性程度为中度或轻度的容器,其要求要低得多。
又如,易燃介质压力容器的所有焊缝均应采用全熔透结构思考题1.2 压力容器主要由哪几部分组成?分别起什么作用?答:筒体:压力容器用以储存物料或完成化学反应所需要的主要压力空间,是压力容器的最主要的受压元件之一;封头:有效保证密封,节省材料和减少加工制造的工作量;密封装置:密封装置的可靠性很大程度上决定了压力容器能否正常、安全地运行;开孔与接管:在压力容器的筒体或者封头上开设各种大小的孔或者安装接管,以及安装压力表、液面计、安全阀、测温仪等接管开孔,是为了工艺要求和检修的需要。
支座:压力容器靠支座支承并固定在基础上。
安全附件:保证压力容器的安全使用和工艺过程的正常进行。
过程设备设计(郑津洋第三版)终极版思考题答案之欧阳道创编

第1章压力容器导言思考题 1.1介质的毒性程度和易燃特性对压力容器的设计、制造、使用和管理有何影响?答:我国《压力容器安全技术监察规程》根据整体危害水平对压力容器进行分类。
压力容器破裂爆炸时产生的危害愈大,对压力容器的设计、制造、检验、使用和管理的要求也愈高。
设计压力容器时,依据化学介质的最高容许浓度,我国将化学介质分为极度危害(Ⅰ级)、高度危害(Ⅱ级)、中度危害(Ⅲ级)、轻度危害(Ⅳ级)等四个级别。
介质毒性程度愈高,压力容器爆炸或泄漏所造成的危害愈严重。
压力容器盛装的易燃介质主要指易燃气体或液化气体,盛装易燃介质的压力容器发生泄漏或爆炸时,往往会引起火灾或二次爆炸,造成更为严重的财产损失和人员伤亡。
因此,品种相同、压力与乘积大小相等的压力容器,其盛装介质的易燃特性和毒性程度愈高,则其潜在的危害也愈大,相应地,对其设计、制造、使用和管理也提出了更加严格的要求。
例如,Q235B钢板不得用于制造毒性程度为极度或高度危害介质的压力容器;盛装毒性程度为极度或高度危害介质的压力容器制造时,碳素钢和低合金板应逐张进行超声检测,整体必须进行焊后热处理,容器上的A、B类焊接接头还应进行100%射线或超声检测,且液压试验合格后还应进行气密性试验。
而制造毒性程度为中度或轻度的容器,其要求要低得多。
又如,易燃介质压力容器的所有焊缝均应采用全熔透结构思考题 1.2 压力容器主要由哪几部分组成?分别起什么作用?答:筒体:压力容器用以储存物料或完成化学反应所需要的主要压力空间,是压力容器的最主要的受压元件之一;封头:有效保证密封,节省材料和减少加工制造的工作量;密封装置:密封装置的可靠性很大程度上决定了压力容器能否正常、安全地运行;开孔与接管:在压力容器的筒体或者封头上开设各种大小的孔或者安装接管,以及安装压力表、液面计、安全阀、测温仪等接管开孔,是为了工艺要求和检修的需要。
支座:压力容器靠支座支承并固定在基础上。
安全附件:保证压力容器的安全使用和工艺过程的正常进行。
过程设备设计(第三版郑津洋)答案

过程设备设计(第三版郑津洋)答案思考题1.压⼒容器导⾔1.1 介质的毒性程度和易燃特性对压⼒容器的设计、制造、使⽤和管理有何影响?我国《压⼒容器安全技术监察规程》根据整体危害⽔平对压⼒容器进⾏分类。
压⼒容器破裂爆炸时产⽣的危害愈⼤,对压⼒容器的设计、制造、检验、使⽤和管理的要求也愈⾼。
设计压⼒容器时,依据化学介质的最⾼容许浓度,我国将化学介质分为极度危害(Ⅰ级)、⾼度危害(Ⅱ级)、中度危害(Ⅲ级)、轻度危害(Ⅳ级)等四个级别。
介质毒性程度愈⾼,压⼒容器爆炸或泄漏所造成的危害愈严重。
压⼒容器盛装的易燃介质主要指易燃⽓体或液化⽓体,盛装易燃介质的压⼒容器发⽣泄漏或爆炸时,往往会引起⽕灾或⼆次爆炸,造成更为严重的财产损失和⼈员伤亡。
因此,品种相同、压⼒与乘积⼤⼩相等的压⼒容器,其盛装介质的易燃特性和毒性程度愈⾼,则其潜在的危害也愈⼤,相应地,对其设计、制造、使⽤和管理也提出了更加严格的要求。
例如,Q235-B钢板不得⽤于制造毒性程度为极度或⾼度危害介质的压⼒容器;盛装毒性程度为极度或⾼度危害介质的压⼒容器制造时,碳素钢和低合⾦板应逐张进⾏超声检测,整体必须进⾏焊后热处理,容器上的A、B类焊接接头还应进⾏100%射线或超声检测,且液压试验合格后还应进⾏⽓密性试验。
⽽制造毒性程度为中度或轻度的容器,其要求要低得多。
⼜如,易燃介质压⼒容器的所有焊缝均应采⽤全熔透结构1.2 压⼒容器主要由哪⼏部分组成?分别起什么作⽤?筒体:压⼒容器⽤以储存物料或完成化学反应所需要的主要压⼒空间,是压⼒容器的最主要的受压元件之⼀;封头:有效保证密封,节省材料和减少加⼯制造的⼯作量;密封装置:密封装置的可靠性很⼤程度上决定了压⼒容器能否正常、安全地运⾏;开孔与接管:在压⼒容器的筒体或者封头上开设各种⼤⼩的孔或者安装接管,以及安装压⼒表、液⾯计、安全阀、测温仪等接管开孔,是为了⼯艺要求和检修的需要。
⽀座:压⼒容器靠⽀座⽀承并固定在基础上。
(设备管理)过程设备设计(郑津洋第三版)终极版思考题答案

第1章压力容器导言思考题介质的毒性程度和易燃特性对压力容器的设计、制造、使用和管理有何影响答:我国《压力容器安全技术监察规程》根据整体危害水平对压力容器进行分类。
压力容器破裂爆炸时产生的危害愈大,对压力容器的设计、制造、检验、使用和管理的要求也愈高。
设计压力容器时,依据化学介质的最高容许浓度,我国将化学介质分为极度危害(Ⅰ级)、高度危害(Ⅱ级)、中度危害(Ⅲ级)、轻度危害(Ⅳ级)等四个级别。
介质毒性程度愈高,压力容器爆炸或泄漏所造成的危害愈严重。
压力容器盛装的易燃介质主要指易燃气体或液化气体,盛装易燃介质的压力容器发生泄漏或爆炸时,往往会引起火灾或二次爆炸,造成更为严重的财产损失和人员伤亡。
因此,品种相同、压力与乘积大小相等的压力容器,其盛装介质的易燃特性和毒性程度愈高,则其潜在的危害也愈大,相应地,对其设计、制造、使用和管理也提出了更加严格的要求。
例如,Q235-B钢板不得用于制造毒性程度为极度或高度危害介质的压力容器;盛装毒性程度为极度或高度危害介质的压力容器制造时,碳素钢和低合金板应逐张进行超声检测,整体必须进行焊后热处理,容器上的A、B类焊接接头还应进行100%射线或超声检测,且液压试验合格后还应进行气密性试验。
而制造毒性程度为中度或轻度的容器,其要求要低得多。
又如,易燃介质压力容器的所有焊缝均应采用全熔透结构思考题压力容器主要由哪几部分组成分别起什么作用?答:筒体:压力容器用以储存物料或完成化学反应所需要的主要压力空间,是压力容器的最主要的受压元件之一;封头:有效保证密封,节省材料和减少加工制造的工作量;密封装置:密封装置的可靠性很大程度上决定了压力容器能否正常、安全地运行;开孔与接管:在压力容器的筒体或者封头上开设各种大小的孔或者安装接管,以及安装压力表、液面计、安全阀、测温仪等接管开孔,是为了工艺要求和检修的需要。
支座:压力容器靠支座支承并固定在基础上。
安全附件:保证压力容器的安全使用和工艺过程的正常进行。
过程设备设计(郑津洋第三版)终极版思考题答案

过程设备设计(郑津洋第三版)终极版思考题答案第1章压⼒容器导⾔思考题1.1介质的毒性程度和易燃特性对压⼒容器的设计、制造、使⽤和管理有何影响?答:我国《压⼒容器安全技术监察规程》根据整体危害⽔平对压⼒容器进⾏分类。
压⼒容器破裂爆炸时产⽣的危害愈⼤,对压⼒容器的设计、制造、检验、使⽤和管理的要求也愈⾼。
设计压⼒容器时,依据化学介质的最⾼容许浓度,我国将化学介质分为极度危害(Ⅰ级)、⾼度危害(Ⅱ级)、中度危害(Ⅲ级)、轻度危害(Ⅳ级)等四个级别。
介质毒性程度愈⾼,压⼒容器爆炸或泄漏所造成的危害愈严重。
压⼒容器盛装的易燃介质主要指易燃⽓体或液化⽓体,盛装易燃介质的压⼒容器发⽣泄漏或爆炸时,往往会引起⽕灾或⼆次爆炸,造成更为严重的财产损失和⼈员伤亡。
因此,品种相同、压⼒与乘积⼤⼩相等的压⼒容器,其盛装介质的易燃特性和毒性程度愈⾼,则其潜在的危害也愈⼤,相应地,对其设计、制造、使⽤和管理也提出了更加严格的要求。
例如,Q235-B钢板不得⽤于制造毒性程度为极度或⾼度危害介质的压⼒容器;盛装毒性程度为极度或⾼度危害介质的压⼒容器制造时,碳素钢和低合⾦板应逐张进⾏超声检测,整体必须进⾏焊后热处理,容器上的A、B类焊接接头还应进⾏100%射线或超声检测,且液压试验合格后还应进⾏⽓密性试验。
⽽制造毒性程度为中度或轻度的容器,其要求要低得多。
⼜如,易燃介质压⼒容器的所有焊缝均应采⽤全熔透结构思考题1.2 压⼒容器主要由哪⼏部分组成?分别起什么作⽤?答:筒体:压⼒容器⽤以储存物料或完成化学反应所需要的主要压⼒空间,是压⼒容器的最主要的受压元件之⼀;封头:有效保证密封,节省材料和减少加⼯制造的⼯作量;密封装置:密封装置的可靠性很⼤程度上决定了压⼒容器能否正常、安全地运⾏;开孔与接管:在压⼒容器的筒体或者封头上开设各种⼤⼩的孔或者安装接管,以及安装压⼒表、液⾯计、安全阀、测温仪等接管开孔,是为了⼯艺要求和检修的需要。
⽀座:压⼒容器靠⽀座⽀承并固定在基础上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
过程设备设计题解1.压力容器导言习题1. 试应用无力矩理论的基本方程,求解圆柱壳中的应力(壳体承受气体内压p ,壳体中面半径为R ,壳体厚度为t )。
若壳体材料由20R (MPa MPa s b 245,400==σσ)改为16MnR(MPa MPa s b 345,510==σσ)时,圆柱壳中的应力如何变化?为什么?解:○1求解圆柱壳中的应力 应力分量表示的微体和区域平衡方程式:δσσθφzp R R -=+21φσππφsin 220t r dr rp F k r z k=-=⎰圆筒壳体:R 1=∞,R 2=R ,p z =-p ,r k =R ,φ=π/2tpRpr tpR k 2sin 2===φδσσφθ○2壳体材料由20R 改为16MnR ,圆柱壳中的应力不变化。
因为无力矩理论是力学上的静定问题,其基本方程是平衡方程,而且仅通过求解平衡方程就能得到应力解,不受材料性能常数的影响,所以圆柱壳中的应力分布和大小不受材料变化的影响。
2. 对一标准椭圆形封头(如图所示)进行应力测试。
该封头中面处的长轴D=1000mm ,厚度t=10mm ,测得E 点(x=0)处的周向应力为50MPa 。
此时,压力表A 指示数为1MPa ,压力表B 的指示数为2MPa ,试问哪一个压力表已失灵,为什么?解:○1根据标准椭圆形封头的应力计算式计算E 的内压力: 标准椭圆形封头的长轴与短轴半径之比为2,即a/b=2,a=D/2=500mm 。
在x=0处的应力式为:MPa a bt p btpa 15002501022222=⨯⨯⨯===θθσσ○2从上面计算结果可见,容器内压力与压力表A 的一致,压力表B 已失灵。
3. 有一球罐(如图所示),其内径为20m (可视为中面直径),厚度为20mm 。
内贮有液氨,球罐上部尚有3m 的气态氨。
设气态氨的压力p=,液氨密度为640kg/m 3,球罐沿平行圆A-A 支承,其对应中心角为120°,试确定该球壳中的薄膜应力。
解:○1球壳的气态氨部分壳体内应力分布: R 1=R 2=R ,p z =-pMPat pR tpRpr tpR k 100202100004.022sin 2=⨯⨯===⇒===+θφφθφσσφδσσσ○2支承以上部分,任一φ角处的应力:R 1=R 2=R ,p z =-[p+ ρg R (cos φ0-cos φ)],r=Rsin φ,dr=Rcos φd φφ0h7.0cos 105110710sin 0220==-=φφ由区域平衡方程和拉普拉斯方程:()[]()()()()()()()()()()()()()()()⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡-+-+---+=--+=-=+⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡-+-+-=-+-+=-+-+=-+=-+=⎰⎰⎰033022002220003302200222203322022003330220223002cos cos 31sin sin 2cos sin sin 2sin cos cos cos cos cos cos 31sin sin 2cos sin sin 2sin sin 3cos cos sin 2sin sin cos cos cos 32sin sin cos sin cos 2cos 2cos cos 2sin 20φφφφφρφφφρφφσρφφσσσφφφφφρφφφφφφρφφφφρσφφρπφφφρπφφφρπφρπρφφπφσπφθφθφφφφg R p t R R tg R p R tg R p tRp g R p t R t g R t g R p R g R g R p R d g R rdr g R p rdrg R p t R zr r rr ()()()(){()()()(){}()(){}[]MPa g R p t R 042.12cos 1.2sin 2.22sin 50.343cos 2.151.0sin 22.2sin 50.343cos 2092851.0sin 221974.4sin 5007.0cos 3151.0sin 35.081.94060151.0sin 102.0sin 02.010cos cos 31sin sin 2cos sin sin 2sin 32232232233226203302200222-+=-⨯+-⨯≈-⨯+-⨯=⎭⎬⎫⎥⎦⎤⎢⎣⎡-+-⨯⨯⨯⨯+-⨯⨯⨯=⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡-+-+-=φφφφφφφφφφφφφφφφφφρφφφσφ()()()()[]MPag R p t R R tgR p 042.12cos 1.2sin 2.22sin 5cos 392.31974.221cos cos 31sin sin 2cos sin sin 2sin cos cos 322033022002220-+-⨯-=⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡-+-+---+=φφφφφφφφφρφφφρφφσθ ○3支承以下部分,任一φ角处的应力 (φ>120°) :R 1=R 2=R ,p z =-[p+ ρg R (cos φ0-cos φ)],r=Rsin φ,dr=Rcos φd φ()[]()()()[]()()()()[]()()()()()()()()()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛---⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡-+-+---+=--+=-=+⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--+⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡-+-+-=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--+-+-+==--+-+-+=--+-+=--+-+=⎰⎰⎰R h h R t gg R p t R R tg R p R tg R p tRp R h h R t gg R p t R R h h R t gt g R t g R p R t R V h R h R g g R g R p R h R h R gd g R rdr g R p gh R h g R rdr g R p V zr r r r 34sin 6cos cos 31sin sin 2cos sin sin 2sin cos cos cos cos 34sin 6cos cos 31sin sin 2cos sin sin 2sin 34sin 6sin 3cos cos sin 2sin sin cos sin 2343cos cos 32sin sin cos 343sin cos 2cos 233134cos cos 2222033022002220022203302200222222203322022022303330220223230230000φρφφφφφρφφφρφφσρφφσσσφρφφφφφρφφφφρφφφρφφφφρσφσππρφφρπφφφρππρφφφρπφρπρπρπρφφπφθφθφφφφ()()()(){()()()(){}()(){}[]()()()()()()(){}()[][]MPag R p t R R h h R t gR t g R p MPa R h h R t gg R p t R 14.8cos 1.2sin 2.22sin 5cos 31.392-221.97414.8cos 1.2sin 2.22sin 5cos 7.0392.31200sin 19.6566240.343cos 2.151.0sin 22.2sin 5cos 7.0392.31200cos cos 31sin sin 2cos sin sin 2sin 34sin 6cos cos 14.8cos 1.2sin 2.22sin 5 3.90.343cos 2.151.0sin 22.2sin 539313.2480.343cos 2092851.0sin 221974.4sin 500sin 196566247.0cos 3151.0sin 35.081.94060151.0sin 102.0sin 02.01034sin 6cos cos 31sin sin 2cos sin sin 2sin 3223222322033022002222220322322322233226222203302200222-⨯+⨯-⨯=-⨯+⨯--⨯+=--⨯+-⨯--⨯+=⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡-+-+--⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛----+=-⨯+⨯=+-⨯+-⨯≈+-⨯+-⨯=+⎭⎬⎫⎥⎦⎤⎢⎣⎡-+-⨯⨯⨯⨯+-⨯⨯⨯=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--+⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡-+-+-=φφφφφφφφφφφφφφφφφφρφφφφρρφφσφφφφφφφφφφφφφφφρφφφφφρφφφσθφ 4. 有一锥形底的圆筒形密闭容器,如图所示,试用无力矩理论求出锥形底壳中的最大薄膜应力σθ与σφ的值及相应位置。
已知圆筒形容器中面半径R ,厚度t ;锥形底的半锥角α,厚度t ,内装有密度为ρ的液体,液面高度为H ,液面上承受气体压力p c 。
解:圆锥壳体:R 1=∞,R 2=r/cos α(α半锥顶角),p z =-[p c +ρg(H+x)],φ=π/2-α,αxtg R r -=()()()()()()ααρααραρρσασπρπρπφφcos 23cos 231cos 232222222222t xtg R g tg x xRtg R x g H p R rt gRr r R x g H p R t r g Rr r R x g H p R F c c c -⎪⎪⎭⎫ ⎝⎛+-++=++++==++++=()[]()()()[]{}()αρααρρασσσααρσρααασαραρασααρσσσθφθθθθθθφcos 2210cos 2210cos 1cos max2221t g tg p Htg R g g p H tg R H p 。
,。
x t gtg dx d g tg p Htg R tg x dx d :tg g x H p xtg R g t dx d t xtg R g x H p t p R R c c c c c c z ⎪⎪⎭⎫ ⎝⎛++⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡-⎪⎪⎭⎫ ⎝⎛-++=∞<-=⎥⎦⎤⎢⎣⎡--==++--=-++=-=+其值为的最大值在锥顶有最大值处在令 5. 试用圆柱壳有力矩理论,求解列管式换热器管子与管板连接边缘处(如图所示)管子的不连续应力表达式(管板刚度很大,管子两端是开口的,不承受轴向拉力)。
设管内压力为p ,管外压力为零,管子中面半径为r ,厚度为t 。
