7.5-7.7 惠菲原理、单缝衍射、光学仪器分辨率
光的衍射现象、惠更斯-菲涅耳原理

S
*
光 源
衍 射
观 察
夫琅和费衍射
屏
屏
5
3. 惠更斯—菲涅耳原理
波传到的任何一点都是子波的波 源,各子波在空间某点的相干叠加, 就决定了该点波的强度。
惠更斯
菲涅耳
dE CK( ) d S cos(t - 2r )
r
K( ) :倾斜因子
0,K Kmax 1,
沿原波传播方向 的子波振幅最大
-1
0
1
2 sin(a / )
25
2光栅衍射光强曲线 (振幅矢量法)
明纹条件: d sin k
(k = 0, 1, 2, 3…) -- 光栅方程
设每个缝发的光在对应衍射角
方向P点的光振动的振幅为Ep
P 点为主极大时
EP
NEP
暗纹条件:
2k
IP
N
2
E
有限的情况下才能积分出来。
积分计算相当复杂(超出了本课范围),下节将介绍 菲涅耳提出的一种简便的分析方法——半波带法.
它在处理一些有对称性的问题时,既方便, 物理图象又清晰。
7
§2 夫琅和费单缝衍射 夫琅和费衍射:障碍物距光源、屏均为无限远。
缝平面 透镜L
透镜L
B
S
*
a
Aδ f
f
观察屏
·p
2
λ 2
λ 2
所以任何两个相邻波带所发出 的光线在P点相互抵消.
当BC是/2的偶数倍,所有波带成对抵消,P点暗,
当BC是/2的奇数倍,所有波带成对抵消后留下一个波带,P点明。
13
第二级明纹
P
第二级暗纹
单缝衍射
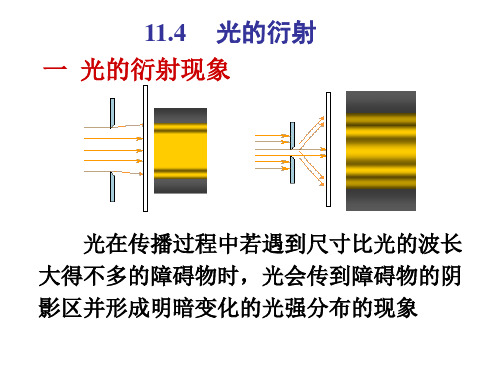
(2) d l0 25 cm 2.2 10
4
0.005 5 cm 0.055 mm
11.5
一 光栅
光栅衍射
光栅: 利用多缝衍射原理使光发生色散的元件
衍射光栅参数:
光栅常数
总缝数
d a b
d
a
光栅宽度为 l mm, 每毫米缝 数为 m , 总缝数 N m l
s2 s s1 d (cot 2 cot1 )
d[cot( 15 ) cot( 15 )] 153 m
四
圆孔衍射
H
L
P
艾 里 斑
d
L
D
f
P
d
d
:艾里斑直径
d 2 1.22 f D
五
瑞利判据
0.8I 0
对于两个强度相等的不相干的点光源 (物点),一个点光源的衍射图样的主极 大刚好和另一点光源衍射图样的第一极小 相重合,这时两个点光源(或物点)恰为 这一光学仪器所分辨.
b增大, 1减小
1增大 b减小,
0, 1 0 b 光直线传播 π b , 1 2 衍射最大
1越大,衍射效应越明显. b一定, 越大,
(2)中央明纹
( k 1 的两暗纹间)
角范围 sin b b
线范围 f x f b b
b
R
A
衍射角
L
f
P
Q
o
B C
b sin
(k 1,2,3,)
(衍射角
:向上为正,向下为负)
2
菲涅耳波带法 BC b sin k
1. 半波带法
单缝衍射的原理

单缝衍射的原理单缝衍射是一种波动现象,当一束光通过一个很窄的单缝时,光线会发生弯曲和散射,形成一系列交替出现的明暗条纹。
这一现象可以通过单缝衍射的原理来解释。
单缝衍射的原理可以用惠更斯-菲涅尔原理来解释。
根据该原理,光波在传播过程中会沿着各个方向传播,当遇到障碍物或缝隙时,会发生弯曲和散射。
在单缝衍射实验中,光波经过一个很窄的缝隙后,会形成一系列交替出现的明暗条纹,这是因为光波在通过缝隙后会发生干涉现象。
在单缝衍射实验中,光波通过缝隙后会形成一个圆形的波前,这个波前可以看作是由无数个波源发出的球面波。
当这些球面波重叠时,会发生干涉现象。
在某些区域,波峰与波峰相遇,波峰与波谷相遇,会发生叠加增强,形成明亮的区域;而在其他区域,波峰与波谷相遇,会发生叠加抵消,形成暗淡的区域。
这样就形成了一系列交替出现的明暗条纹。
根据单缝衍射的原理,可以得出一些结论。
首先,当缝隙越窄时,明暗条纹越清晰和密集。
缝隙越宽时,条纹越模糊和稀疏。
其次,当光的波长越短时,条纹越密集;波长越长时,条纹越稀疏。
这是因为波长与条纹间距之间存在一定的关系。
最后,当观察屏幕距离缝隙越远时,条纹越密集;距离越近时,条纹越稀疏。
这是因为观察距离与条纹间距之间存在一定的关系。
单缝衍射不仅仅是光学现象,类似的现象也可以在其他波动现象中观察到。
例如,水波通过一个狭缝时也会发生类似的现象。
这说明单缝衍射的原理是普适的,并不局限于光波。
单缝衍射在科学研究和工程应用中有着广泛的应用。
在科学研究方面,单缝衍射可以用来研究光的性质和波动理论。
通过观察单缝衍射的条纹模式,可以精确测量光的波长和光源的亮度。
在工程应用方面,单缝衍射可以用来设计光学仪器,如衍射光栅和光波导等。
衍射光栅可以用来分光和光谱分析,光波导可以用来实现光通信和光学传感。
单缝衍射是一种波动现象,通过窄缝可以观察到一系列交替出现的明暗条纹。
这一现象可以通过惠更斯-菲涅尔原理来解释,即光波在传播过程中会发生干涉现象。
高中物理 光的衍射和惠菲定理
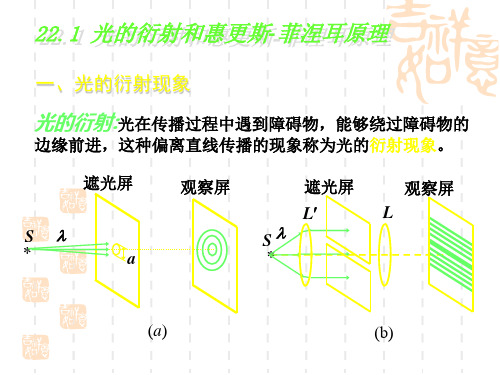
O
f
d sin
Ap NAi
I p N 2 Ii
•主极大
暗纹位置:
A
G
P
N 2 n
O f
n 0,N ,2 N ,3 N
0 级 主 极 大 1 级 主 极 大 2 级 主 极 大 3 级 主 极 大
n 有N-1个取值
次极大:
相邻主极大之间有N-1个暗条纹 相邻主极大之间有N-2个次极大
主极大条 纹细锐的 原因
P
d sin
d sin N
Nd
2 2 Nd
1 sin 1= d
衍射图样光强分布特点
因此,光栅衍射图样是多缝干涉光强 分布受单缝衍射光强分布调制的结果。
缺
级
# 缺极时衍射角同时满足:
a ·sin = ± k' d· sin = ± k k = ± d /a·k'
22.1 光的衍射和惠更斯-菲涅耳原理
一、光的衍射现象
光的衍射:光在传播过程中遇到障碍物,能够绕过障碍物的
边缘前进,这种偏离直线传播的现象称为光的衍射现象。
遮光屏
S
观察屏
S
遮光屏
观察屏
L
L
*
a
*
( a)
(b)
二、衍射的分类
菲涅耳衍射:
光源--观察屏--衍射屏,距离有限远。(近场衍射)
E
A
a sin 2k 2
P
k 1
0
f
x0
E
a sin 0 2 2
大学物理 菲涅耳原理-单缝衍射

半波带法
R
A
a
A
A1
C
L
P
Q
B
缝长
o
L
B
A
R
/2
a
A
A1 A2
C
P
Q
B
o
/2
B
a
A . .. . C A1.
A 2. θ B
θ
缝边缘两条光线之 间的光程差为
AC a sin
x P
.
f
半波带的条数为 a sin N 2
三个半波带
平 面 波
二、惠更斯—菲涅耳原理
• 同一波前上的各点发出的都是相干次波;
• 各次波在空间某点的相干叠加,就决定了该点波的强度。 设波面 Q 初相为0 ,其上面元ds 在P 点引起的振动为
n
Q
ds
——倾斜因子
1
r
P
s k ( )
π2
0
P 点的振动
三、衍射的分类 菲涅尔衍射 夫琅禾费 衍射 缝
1.4㎜ O f
b sin k 分析:b sin (2k 1) 2
(k 1,2,) 暗纹 (k 1,2,) 明纹
解: )依题意,P点符合 (1 2 OP 且 sin tg f b sin ( 2k 1)
1.4㎜ O
f
可见光在真空中的波 长约为760~400nm
薄膜干涉
2 2 2d n2 n1 s in2 i
反 2 射 光
垂 直 入 射
2dn2
2
n2 n1
单缝和圆孔的夫琅禾费衍射介绍

明纹在屏上的位置
x f sin f (2k 1)
2a
k ax 1 3.5 0.5 3
f 2
第3级明 纹
(2)对应于 p点缝可分成多少个半波带?
asin (2k 1)
2
(23 1) 7
22
7个半波带
(3)将缝宽增加1倍,p 点将变为什么条纹?
y2 = u
-2 - o
··
··
2 u
-2.46π -1.43π
+1.43π +2.46π
u 1.43, 2.46, 3.47,…
相应 asin 1.43, 2.46, 3.47,…
三、入射光非垂直入射时光程差的计算
DB BC
b(sin sin)
“半波带”发的光在 P处干涉相消形成暗纹。
当asin=3/2时,可将缝分为3个半波带.
a
AA
A1
p
B
A2 C
o
B /2
相邻半波带的相对应点光程差均是/2,两个
“半波带”发的光在 P处干涉相消形成暗纹。第 3个“半波带”发的光在 P形成明纹。
一般情况下,可将缝分为k个半波带,当k为偶数 时,p点为暗纹,当k为奇数时,p点为明纹。
例3 在单缝衍射中,若使单缝和透镜分别 稍向上移,则衍射条纹将如何变化? 解:
o
⑴单缝上移衍射光束向上平移经透镜聚焦后, 位置不变条纹不变 ⑵透镜上移衍射光束经透镜聚焦后,位置随之 上移条纹向上平移
例4 在单缝夫琅和费衍射实验中,缝宽a=10,缝 后透镜焦距 f =40cm , 试求第一级明纹的角宽度,线 宽度以及中央明纹的线宽度。
大学物理光的衍射单缝衍射光学仪器分辨率PPT精选文档
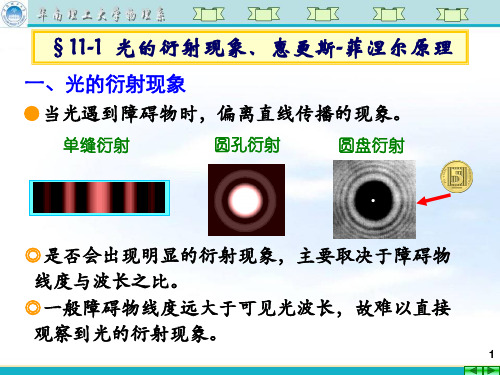
0
a sin k
(2k
1)
2
k 1,2,L k 1,2,L
中央明纹 k级暗纹 k级明纹
说明:
由半波带法得出的明纹中心位置是近似的。其精确
位置可由单缝衍射光强分布公式求出。
8
三、单缝衍射光强分布
1.光强公式
I
I0
sin
2
asin
◎中央亮纹强度最大。
I I0
中心处: 0 II0
o
c
o
注:对近轴光线,薄透
镜不附加程差。
15
例:用平行光垂直照射单缝而在屏上形成衍射条纹。若
第4级明纹距中央明纹中心1.6mm,求:1. 入射光波长;
2. 狭缝处的波面可分成的半波带数目。设单缝宽
a = 0.4mm,透镜焦距 f =30cm。
P
解:1. 单缝衍射明纹条件
a
y
asin(2k1) k 4
§11-1 光的衍射现象、惠更斯-菲涅尔原理
一、光的衍射现象
●当光遇到障碍物时,偏离直线传播的现象。
单缝衍射
圆孔衍射
圆盘衍射
◎是否会出现明显的衍射现象,主要取决于障碍物 线度与波长之比。
◎一般障碍物线度远大于可见光波长,故难以直接 观察到光的衍射现象。
1
二、惠更斯-菲涅尔原理
●基本思想:同一波面上的子波之间也可以产生干涉,其
一、夫朗和费单缝衍射
装置和现象
E
L2 L1
o
S
单缝衍射条纹
o
单缝
f DD
:衍射角(衍射光与入射光方向的夹角)
中央 明纹
4
用菲涅尔波带法求明暗纹位置
沿方向衍射的光的最大光程差为 BCasin
7.5 光的衍射现象 惠更斯-菲涅耳原理

S
θ dS r
v n
P
K(θ ) t r dE = C cos 2π ( − )dS r T λ
K(θ ) t r dE = C cos 2π ( − )dS r T λ
C----比例常数 K(θ )----倾斜因子 倾斜因子
θ ↑⇒ K(θ ) ↓ θ = 0 ⇒ K(θ )最大 π θ ≥ , K(θ ) = 0 ⇒ dE = 0
2 惠更斯-菲涅耳原理解释了波为什么不向后传 惠更斯 菲涅耳原理解释了波为什么不向后传 的问题,这是惠更斯原理所无法解释的。 的问题,这是惠更斯原理所无法解释的。
P点的光振动(惠更斯原理的数学表达)为: 点的光振动(惠更斯原理的数学表达) 点的光振动
K(θ ) t r E = ∫ dE = ∫ C cos 2π ( − )dS r T λ
7.5 光的衍射 惠更斯-菲涅耳原理 惠更斯一、 光的衍射现象及其分类 屏幕 屏幕
阴 影
缝较大时, 缝较大时,光是直线传播的
缝很小时, 缝很小时,衍射现象明显
衍射系统由光源、衍射屏、接收屏组成。 衍射系统由光源、衍射屏、接收屏组成。 衍射的分类 菲涅耳衍射 光源—障碍物 光源 障碍物 —接收屏 接收屏 距离为有限远。 距离为有限远。 夫琅禾费衍射
S 光源—障碍物 光源 障碍物 —接收屏 接收屏 距离为无限远。 距离为无限远。光源
障碍物
接收屏
E A
B
障碍物
接收屏
二、惠更斯-费涅耳原理 惠更斯 费涅耳原理 从同一波阵面上各点所发出的子波, 从同一波阵面上各点所发出的子波,在传播过程 中相遇时,也可相互叠加产生干涉现象, 中相遇时,也可相互叠加产生干涉现象,空间各点波 的强度,由各子波在该点的相干叠加所决定。 的强度,由各子波在该点的相干叠加所决定。 若取时刻t=0波阵面上各点发 若取时刻 波阵面上各点发 出的子波初相为零, 出的子波初相为零,则面元 dS在P点引起的光振动为: 在 点引起的光振动为 点引起的光振动为:
大学物理 单缝衍射

o
f
2 f 中央明纹 x a
其余明纹
x
a
f
中央明纹线宽度为其余明纹线宽度的两倍
⑤条纹亮度分布是否均匀,为什么?
中央明纹中心:
全部光线干涉相长
一级明纹中心:
屏幕
二级明纹中心: 1/5部分光线干涉相长
中央明纹集中大部分能量,明条纹级次越高亮度越弱。
I
1/3部分光线干涉相长
⑥条纹随、a 的变化
③条纹角宽度
f
0
中央明纹中心
sin
k
a
2a
暗纹 明纹
k 1、、 2
a
( 2k 1)
中央明纹
2 a
其余明纹
中央明纹角宽度为其余明纹角宽度的两倍
I
a
④条纹线宽度
L2
x
x f tg
x f (tg 2 tg1 )
x f ( 2 1 ) f
确定 a a , 衍射不明显
若 a ,则为直线传播
a , 衍射显著
, a 确定 a ,
若用白光照射:
单缝夫琅禾费衍射
单缝夫琅禾费衍射
⑦单缝衍射的动态变化
单缝上下移动,根据透镜成像原理衍射图不变 .
0
0
衍射光线汇集于 焦点F L2
0
中央明纹中心
衍射光线汇集于2焦平面上某点 L P
0
P处光强可由菲涅耳公式计算
介绍确定P光强的两种简便方法
2. 半波带法(半定量方法) 衍射角为 的一束平 行光线的最大光程差:
单缝衍射

d
r
0.610
r
sin
L
D
f
P
d
d
:艾里斑直径
sin 0.61 / R 1.22 / D
爱里斑对透镜中心的张角为:
2 2sin 2.44 / D
式中D 2 R 为圆孔的直径, f 为透镜 L 的焦距。 爱里斑的半径为: sin
/a
sin
屏幕
-2/a -3/a
例1、若有一波长为 =600nm 的单色平行光,垂直入 射到缝宽 a =0.6mm 的单缝上,缝后有一焦距 f = 40 cm 透镜。试求:(1)屏上中央明纹的宽度;(2)若在屏 上 P 点观察到一明纹,op=1.4mm 问 P 点处是第几级明 纹,对 P 点而言狭缝处波面可分成几个半波带? 解: (1) 两个第一级暗纹中心间的距离即为中央明纹的宽度 6 107 x 2 f 2 0.4 0.8 103 m 0.6 103 a
(中央明纹向下移动)
a
A
D
C
B A
BC DA
a(sin sin )
(中央明纹向上移动)
D
a
C
B
6、单缝衍射的动态变化 单缝上下移动,根据透镜成像原理衍射图不变 .
R
f
o
单缝上移,零级明 纹仍在透镜光轴上.
单缝宽度变化,条纹宽度如何变化? 中央明纹的角宽度
0 2
Ai A0
sin
a sin
相邻两缝间的光程差:
衍射角
(a b)sin d sin
大学物理第7章第7节-圆孔缝夫琅禾费衍射及光学仪器的分辨率

a
b
(a) 可分辨
b
a a
b
0
(b) 恰能分辨
(c) 不能分辨
光学仪器分辨率 (瑞利判据): 其中一个 艾里斑的极大处刚好落在另一个艾里斑的 极小处时, 光学仪器恰好能够分辨出是两个 点.
b
a
0
(b) 恰能分辨
光学仪器的最小分辨角: 在满足瑞利判 据的条件下两物点对透镜光心的张角
0 1.22
7.7 圆孔夫琅禾费衍射 及光学仪器的分辨率
一. 圆孔衍射 将单缝夫琅禾费单缝衍 射中的狭缝换成圆孔, 在屏 上观察到明暗相间的同心圆 环形衍射条纹, 即圆孔夫琅禾 费衍射图样. 在中央处为一个圆形亮斑, 称 为艾里斑.
圆孔夫琅禾费衍射图样的强度分布 当 0 时为中央极大, 以中央极大对称分布的艾 里斑的光强最大, 占入射光 I I 强度的 83.78%.
f N D f 200103 0.05m D N 4
镜头的最小分辨角
0 1.22
9
D
55010 5 1 . 34 10 rad 1.22 0.05
镜头能分辨出前方10m处的两物点最 小距离
0
l
r
l r 0 10 1.34 105
1.34 104 m 0.134mm
对人眼, 最小分辨角为
55010 4 1 . 34 10 rad 0 1.22 1.22 3 D 5 10
9
眼睛能分辨出前方10m处的两物点最 小距离
0
l
r
l r 0 10 1.34 104 1.34 103 m 1.34mm
1
D
大学物理-第四节单缝衍射

50
70
a
a
a
a
中央明纹的宽度
l0
2x1
2 a
f
单缝宽度变化,中央明纹宽度如何变化?
入射波长变化,衍射效应如何变化 ?
越大,越1 大,衍射效应越明显.
(3)条纹宽度(相邻条纹间距)
a sin 2k k 干涉相消(暗纹)
2
a sin (2k 1)
干涉加强(明纹)
2
l
k1 f
k
f
f
a
除了中央明纹外的其 它明纹、暗纹的宽度
三、 单缝夫琅和费衍射
单
缝 衍夫 射琅
禾
R
L
A 衍射角
a C
B a sin
fP
Q
o
费
(衍射角 :向上为正,向下为负 .)
当衍射角=0时,所有衍射光线从缝面AB到会聚点0
都经历了相同的光程,因而它是同位相的振动。
在O点合振动的振幅等于所有这些衍射线在该点引 起的振动振幅之和,振幅最大,强度最大。
O点呈现明纹,因处于屏中央,称为中央明纹。
当k=2时,λ=3000 A0
x 2 f
a 5000 1010 2 1 0.5 103
在可见光范围内,入射光波长为λ=5000A0。 2 103 m
例3、在夫琅和费单缝实验中,垂直入射的平行单色光波长为 =605.8nm,缝宽a=0.3mm,透镜焦距f=1m。求: (1)中央明纹宽度;(2)第二级明纹中心至中央明纹中 心的距离;(3)相应于第二级和第三级明纹,可将单缝 分出多少个半波带,每个半波带占据的宽度是多少?
菲涅尔数:单缝波面被分成完整的波带数目。它满足:
a sin m
2
单缝、圆孔衍射

解: 两个第一级暗纹中心间的距离即为中央明纹宽度,对 第一级暗条纹(k=1)求出其衍射角
a sin 1 a sin 1
1 sin 1
a
式中 1 很小
λ
Δ x0
中央明纹的角宽度 2 1 2
a
f
透镜焦面上出现中央明纹的宽度
0
1' 2'
解:
0 1.22
D
问题:波长是真空中的波长还是介质中的波长?
由瑞利判据得:
0 1.22
D
y
2 1
n=1
n'=1.336
L
n=1
0
折射定律:n sin n ' sin '
n n ' '
'
n' n 1 .2 2
在实验中的夫琅禾费衍射
缝平面 透镜L
观察屏
透镜L
*
f
S
B Aδ
p · 0 f
a
S: 单色线光源
a:缝宽 : 衍射角
三、惠更斯—菲涅耳原理
惠更斯原理指出波前上各点都可以看成是子波源, 这一原理虽然能解释波的衍射现象,但不能解释 光强分布。 菲涅耳指出:不仅波前的各点可以看成子波源, 而且这些子波都是相干波,子波的叠加是相干叠 加。
2
θ B 半波带 a
半波带
A
1 2 1′ 2′ 1 2 1′ 2′
半波带 半波带
λ /2
菲涅耳半波带法
2
a
a sin
两相邻半波带上对应点发的 光在P 处干涉相消。
单缝衍射及惠更斯—菲涅尔原理.ppt

x ftg f sin , 角很小
A C a
f
o
x
k f (k 1,2) 暗纹
a
(2k
1)f
2a
(k 1,2)
B L
明纹
x P
10
(1)暗纹位置
x k f
a
3 2 1
2 1
x1
f
a
两条,对称分布屏幕中央两侧。
1
其它各级暗纹也两条,对称分布。
波面AB
分割成奇数个半波带, P 点为明纹。
9
分割成偶数个半波带, P 点为暗纹。
波面AB
分割成奇数个半波带, P 点为明纹。
讨论:
a sin m
1.加强减弱条件 2k (k 1,2) 减弱
2
a sin
2
(2k 1)
2.明纹、暗纹位置
2
(k
1,2) 加强
sin tg x (2)
f
联立(1)和(2)式得:
k ax / f 1
2 0.6 10 3 1.4 10 3 / 0.4 6 10 7 1 / 2
3
所以p点所在的位置为第三级 明纹,
由a sin (2k 1) / 2可知
在O点合振动的振幅等于所有这些衍射线在该点 引起的振动振幅之和,振幅最大,强度最大。
O点呈现明纹,因处于屏中央,称为中央明纹。
5
在其它位置:
设一束衍射光 会聚在在屏幕上某
点 P ,它距屏幕中 心 o 点为 x,对应
A C a
f
该点的衍射角为 。
o x
过B点作这束
单元六 牛顿环(续)单缝衍射, 光学仪器的分辨率
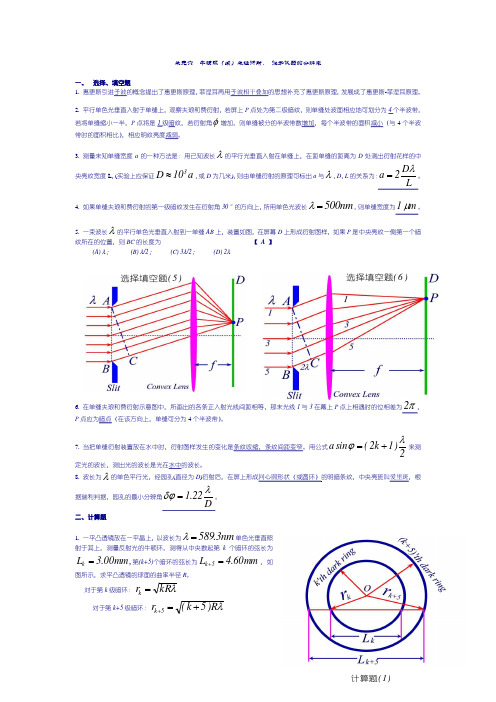
)1(计算题单元六 牛顿环(续)单缝衍射, 光学仪器的分辨率一、 选择、填空题1. 惠更斯引进子波的概念提出了惠更斯原理,菲涅耳再用子波相干叠加的思想补充了惠更斯原理,发展成了惠更斯-菲涅耳原理。
2. 平行单色光垂直入射于单缝上,观察夫琅和费衍射,若屏上P 点处为第二级暗纹,则单缝处波面相应地可划分为4个半波带,若将单缝缩小一半,P 点将是1级暗纹,若衍射角φ增加,则单缝被分的半波带数增加,每个半波带的面积减小(与4个半波带时的面积相比),相应明纹亮度减弱。
3. 测量未知单缝宽度a 的一种方法是:用已知波长λ的平行光垂直入射在单缝上,在距单缝的距离为D 处测出衍射花样的中央亮纹宽度L ,(实验上应保证a 10D 3≈,或D 为几米),则由单缝衍射的原理可标出a 与λ,D ,L 的关系为:LD 2a λ=。
4. 如果单缝夫琅和费衍射的第一级暗纹发生在衍射角30°的方向上,所用单色光波长nm 500=λ,则单缝宽度为m 1μ。
5. 一束波长λ的平行单色光垂直入射到一单缝AB 上,装置如图,在屏幕D 上形成衍射图样,如果P 是中央亮纹一侧第一个暗纹所在的位置,则BC 的长度为 【 A 】 (A) λ; (B) λ/2; (C) 3λ/2; (D) 2λ6. 在单缝夫琅和费衍射示意图中,所画出的各条正入射光线间距相等,那末光线1与3在幕上P 点上相遇时的位相差为π2,P 点应为暗点(在该方向上,单缝可分为4个半波带)。
7. 当把单缝衍射装置放在水中时,衍射图样发生的变化是条纹收缩,条纹间距变窄。
用公式2)1k 2(sin a λϕ+=来测定光的波长,测出光的波长是光在水中的波长。
8. 波长为λ的单色平行光,经园孔(直径为D )衍射后,在屏上形成同心圆形状(或圆环)的明暗条纹,中央亮班叫爱里斑,根据瑞利判据,园孔的最小分辨角D22.1λδϕ=。
二、计算题1. 一平凸透镜放在一平晶上,以波长为nm 3.589=λ单色光垂直照射于其上,测量反射光的牛顿环,测得从中央数起第k 个暗环的弦长为,mm 00.3L k =第(k+5)个暗环的弦长为mm 60.4L 5k =+,如图所示,求平凸透镜的球面的曲率半径R 。
大学物理第十七讲 光的衍射 单缝衍射 光学仪器分辨率
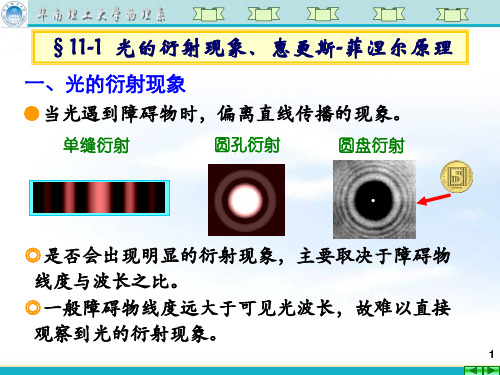
思考:如图,若屏(透镜焦平面)上的o和o 点分别是透镜 中心和狭缝中心的对应点,则单缝衍射的中央明纹中心 应位于其中的哪一点? 答案:位于o点。 分析:单缝衍射干涉条纹在 屏上的分布与缝的纵向位置 (上下移动)无关,但同一方 向的衍射光会聚于透镜焦平 面上的同一位置,形成同一 级干涉条纹。光程差为零的 各光将会聚于o点,故对应 中央明纹。说明干涉条纹随 透镜上下移动而移动。
十四米远以后的同学将把等号看成减号.
25
(b)
a 10
15
10
5
0
5
10
15 (度)
I / I0
(c)
a 100
15
0
15 (度)
13
2.当单缝上下移动,干涉条纹在屏上的位置分布不变.
P
c
o
E
沿同一方向衍射的平行光会聚于焦平面上的同一点, 并且形成同一级次的干涉条纹。
因此,无论单缝上移或下移,同一级次的干涉条纹必定在同一个位置。14
反之,当 a
即
a
1
sin 0
此时观察不到衍射现象,光沿直线传播。 ●几何光学是波动光学在 /a 0情况下的近似。
12
缝 宽 与 波 长 之 比 为 不 同 值 时 的 衍 射 光 强 分 布
I / I0
屏上衍射条纹
a
(a)
15
0
I / I0
15 (度)
2
B
N
C
2
o
(N个半波带)
a sin 0
a sin 2k
中央明纹中心
2
0
N 2k
惠更斯菲涅尔原理 单缝衍射打印稿PPT课件
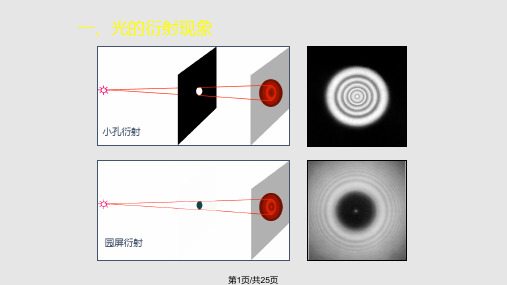
解
1
a
中央明纹角宽度:
中央明纹线宽度:
2x1 f 21
a
0.1cm
明纹条件:
21
2
a
5 103
rad
L
21
o 2x1
f
第14页/共25页
a sin (2k 1) 第一明纹:
2
k= 1
a
sin1
3
2
a
3
2
1
3
2a
,
x1
f
1
3f 2a
两种单色光第一明纹间距:
x x21 x11
1 2
L
-----中央明纹中心
θ ≠0时,用半波带 方法讨论:
o L
第8页/共25页
四、单缝Fraunhofer衍射的半波带分析方法
θ = 0时,干涉相长 -----中央明纹中心
θ ≠0时,用半波带 方法讨论:
m、n在 p 点引起的 光振动之和:
Emp Enp 0
L A a A1
B
p
Ao
m A1
n B
▲衍射:无限个波的迭加。
r p
第4页/共25页
三、衍射的分类
█ 当光源及观察屏到衍射物的距离为有限远时: 近场衍射(near-field diffraction)----Fresnel 衍射
第5页/共25页
█ 当光源及观察屏到衍射物的距离为无限远时
远场衍射(far-field diffraction)
----Fraunhofer 衍射
第6页/共25页
单缝的衍射:
D →0 时 :
投影像(几何像)D → 来自限大时:带条纹的投入 射
影像(近场衍射)
单缝衍射

在恰能分辨时, 在恰能分辨时,两个点光源在透镜前所 张的角度, 张的角度,称为最小分辨角 δ ϕ 。 圆孔衍射的第一级极小值由下式给出: 圆孔衍射的第一级极小值由下式给出: λ sin 1 =1.22 d θ ϕ = 1 ~ sinθ 1 = 1.22 λ δ 最小分辨角为: 最小分辨角为: θ d 1 d = 1.22 λ 分辨本领为: 分辨本领为: R = θ 结束 返回
在迎面驶来的汽车上, 例2: 在迎面驶来的汽车上,两盏前灯相距 1.2m。试问汽车离人多远的地方,眼睛才 。试问汽车离人多远的地方, 可能分辨这两盏前灯? 可能分辨这两盏前灯?假设夜间人眼瞳孔直 径为5.0mm,而入射光波长λ =550.0nm。 径为 , 。 Δx λ λ 解: δϕ =1.22 δϕ = l = 1.22 d d dΔx 5×10-3×1.2 l= = 1.22×550×10-9 1.22 λ =8.94×103 (m)
2. 望远镜的分辨本领 1 = d R= θ 1 1.22 λ
物镜的直径 d 3. 显微镜的最小分辨距离 0.61λ ∆ y= n sin u 孔径对物点的半张角 u 物方的折射率 n 显微镜的数值孔径 n sin u
本节要求: 本节要求: 1、了解惠更斯 菲涅耳原理。 菲涅耳原理。 、了解惠更斯—菲涅耳原理 2、熟记单缝衍射的明、暗纹公式。 、熟记单缝衍射的明、暗纹公式。 3、熟记单缝衍射的中央明纹宽度公式。 、熟记单缝衍射的中央明纹宽度公式。 4、熟记最大衍射级数和最多明纹条数公式。 、熟记最大衍射级数和最多明纹条数公式。 5、理解瑞利判据,知道望远镜的分辨本领。 、理解瑞利判据,知道望远镜的分辨本领。
ϕ
d
结束
返回
瑞利判据: 瑞利判据:如果一个点光源的衍射图象的中 央最亮处刚好与另一个点光源的衍射图象第 一个最暗处相重合, 一个最暗处相重合,认为这两个点光源恰好 能为这一光学仪器所分辨。 能为这一光学仪器所分辨。
第 4 章光的衍射

条数为n,则光栅常数 如 每 厘 米 刻 5000 条栅痕的衍
1 d n
射光栅常数
1 d cm 2 10 6 m 5000
普通光栅刻线为数十条/mm ─ 数千条/mm 用电子束刻制可达数万条/mm(d 101 μ m )。
3. 光栅衍射的实验装置
光栅衍射的实验装置
D为光学仪器的透光孔径
提高光学仪器分辨本领的途径: 增大仪器的孔径。如望远镜 采用波长短的波入射。如光学显微镜采用紫光 入射。电子:0.1 Å~1 Å,电子显微镜R很大, 可观察物质结构
射电望远镜
波多黎各射电望远镜
三、光学仪器的分辨本领
如 人 眼 的 瞳 孔 基 本 为 圆 孔 , 直 径 d 一 般 在
k 2, 2 600nm (符合) (符合)
可允许在屏上 x=1.5mm 处的明纹为波长 600nm 的第二 级衍射和波长为 420nm 的第三级衍射
光的衍射习题课
(2)此时单缝可分成的波带数分别是
k 2, 时 为 2k 1 5 k 3, 时 为 2k 1 7
讨论:当单缝平行于透镜(屏)上下微小平移时,屏上 的条纹位置是否也随之移动. 答案:位置不变!
2、光学仪器的分辨本领 爱里斑
S1 * S2 *
D
点光源经过光学仪器的小圆孔后,由于衍射的影响, 所成的象不是一个点而是一个明暗相间的圆形光斑。
若两物点距离很近,对应的两个爱里斑可能部分 重叠而不易分辨
能 分 辨
不 能 分 辨
恰 能 分 辨
瑞利判据:如果一个点光源的衍射图象的中央最亮处 刚好与另一个点光源的衍射图象第一个最暗处相重合, 认为这两个点光源恰好能为这一光学仪器所分辨。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7.5 光的衍射现象 惠更斯-菲涅耳原理
一、 光的衍射现象及其分类 屏幕 屏幕
阴 影
缝较大时,光是直线传播的
缝很小时,衍射现象明显
衍射:光在传播过程中绕过障碍物的边缘而偏离直线 传播的现象
圆孔衍射
亮纹 解:(3) (a) a sin (2k 1) 2 x sin tan f
ax 1 k 3 f 2
(3)如果在屏幕上离中央亮纹中心为x=3.5mm处的 P点为一亮纹,试求(a)该P处亮纹的级数;(b)从P处 看,对该光波而言,狭缝处的波阵面可分割成几个 半波带?
(b)当k=3时,光程差
a sin ( 2k 1 )
2
7
2
狭缝处波阵面可分成7个半波带。
例2.在复色光垂直照射下的某个单缝衍射图样中,其 中某一波长的第3级明纹位置恰好与波长为600nm的 单色光的第2级衍射明纹相重合,求此光波的波长 P202习题7.22 解:对单缝衍射明纹,由公式: a sin (2k 1)
二、光学仪器的分辨率 点光源经过光学仪器的小圆孔后, 由于衍射的影响,所成的象不是一 个点而是一个明暗相间的圆形光斑 。若两物点距离很近,对应的两个 爱里斑可能部分重叠而不易分辨。
3 3
而第1级明纹在屏上的宽度为第2级暗纹与第1级暗纹 在屏上的间距, 则 2 x x2 x1 f tan 2 f tan1 f a a
600109 f 0.5 1.5 103 m a 0.2 103
(3)由于第k级明纹对应单缝处的波面可划分的半 波带数为2k+1, 因此, 对第1级明纹, 单缝处的波面 可划分的半波带数为
2
由题意知
71 a sin 1 (2 3 1) 2 2
600 3000 a sin 2 (2 2 1) (2 2 1) 2 2 2
1
2
,
1 2
代入可得
3000 1 428.6nm 7
例3: 用波长为λ=600nm的单色光垂直照射到缝宽为 a=0.2mm的单缝上, 缝后用焦距为f=0.5m的凸透镜将衍 射光汇聚到屏上. 求: (1)中央明纹的角宽度和线宽度; (2) 第1级明纹中心在屏上的位置和宽度; (3)对第1级明纹, 单缝处的波面可划分为几个半波带. P177例题7.8 解:(1)中央明纹的角宽度为 0 , 0 为第1级暗纹的衍射角
一、单缝夫琅禾费衍射
单缝衍射实验装置E屏幕L2L1KS*
用菲涅耳半波带法解释单缝衍射现象
将衍射光束分成一组一组的平行光,每组平行光的 衍射角(与原入射方向的夹角)相同
AC a sin
衍射角不同, 最大光程差也 不同,P点位 置不同。光的 强度分布取决 于最大光程差
A
a
B
C (2) (1 ) (2)
解:由单缝衍射明纹所满足的条件 a sin (2k 1)
2
第1级明纹所对应的衍射角满足
600 109 sin (2k 1) (2 1 1) 4.5 103 2a 2 0.2 103
x f tan f sin 0.5 4.5 10 2.25 10 m
2. 中央明纹
中央两侧第一暗条纹之间的区域,称做零极 (或中央)明条纹,它满足条件:
I
a
a sin
a 3 2a 5 sin 2a
5 3 2a 2a
0
0
a sin k
x
f
a
x a sin 0 a tan 0 a f f
x (2k 1) f / 2a
明纹中心
条纹在屏幕上的位置与波长成正比,如果用白光 做光源,中央为白色明条纹,其两侧各级都为彩色条 纹。该衍射图样称为衍射光谱。 由微分式 x k f / a 看出,λ 一定时,缝越窄 ( a 越小),条纹分散的越开,衍射现象越明显;反 之,当a一定时,λ 越长,衍射现象越明显 当缝宽比波长大很多时,形成单一的明条纹,这就是 透镜所形成线光源的象。显示了光的直线传播的性质。
I
5 3 2a 2a
0
3 2a
5 sin 2a
当 角增加时,半波带数增加,未被抵消的半 波带面积减少,所以光强变小; 另外,当:
k ( ) I
单缝夫琅禾费衍射光强分布图
这是在观察屏上所见的光强分布图,中央明纹区域 集中了光能的大部分,而次极大迅速减小,因此中 央明纹比其他明纹都更加明亮,而且宽。
•缝宽对衍射条纹的影响:
宽度变窄。
2 f x 2 x a
中央亮纹线宽度
缝宽增加,中央亮纹
•光源位置对衍射条纹的影响:光源上移,中央
亮纹位置向下移动,宽度不变。
2 f x 2 x a
中央亮纹线宽度
例1、一束波长为 =5000Å的平行光垂直照射在一个 单缝上。(1)已知单缝衍射的第一暗纹的衍射角1=300, 求该单缝的宽度a=? (2)如果所用的单缝的宽度 a=0.5mm,缝后紧挨着的薄透镜焦距f=1m,求:(a) 中央明条纹的角宽度;(b)中央亮纹的线宽度;(c) 第 一级与第二级暗纹的距离;(3)如果在屏幕上离中 央亮纹中心为x=3.5mm处的P点为一亮纹,试求(a)该 P处亮纹的级数;(b)从P处看,对该光波而言,狭缝 处的波阵面可分割成几个半波带? 解: (1)
(2)(a)
a
sin
a
2 5000 107 mm 3 0 2 2 10 rad a 0.5mm
(b) (c)
2f x0 f 0 2 103 m 2mm a
2 5000 107 x21 f f f 1103 1mm a a a 0.5
a sin 2k
则
2
k
k 1
a sin0
2 2 600 109 0 6 103 rad a 0.2 103
中央明纹的线宽度由
2 x0 f f 0 0.5 6 103 3 103 m a
(2)第1级明纹中心在屏上的位置和宽度
(1 ) (2)
(1 )
P0
x P
f
菲涅耳半波带法
A
A1 A2 A3
C
相邻平面间的距离是入射 单色光的半波长。 任何两个相邻波带上对应 点所发出的光线到达AC平 面的光程差均为半波长 (即位相差为) ,在P点 会聚时将一一抵消。
B
AB面分成奇数个半波带,出现亮纹
AC a sin 3
A
E
障碍物
B
接收屏
二、惠更斯-费涅耳原理
从同一波阵面上各点所发出的子波,在传播过程 中相遇时,也可相互叠加产生干涉现象,空间各点波 的强度,由各子波在该点的相干叠加所决定。
若取时刻t=0波阵面上各点发 出的子波初相为零,则子波
S
dS在P点引起的光振动为:
dS r
v n
dS 2 r dE Fk ( ) cos(t ) r F----比例常数
a sin k (k 1, 2,3L )
5000 1010 a 1.0 106 m o sin 1 sin 30
第一级暗纹 k=1,1=300
(2)如果所用的单缝的宽度a=0.5mm,缝后紧挨着的薄 透镜焦距f=1m,求:(a)中央明条纹的角宽度;(b)中 央亮纹的线宽度;(c) 第一级与第二级暗纹的距离.
x
2 f x0 2 f tan 0 a
(k 1, 2, L ) 暗纹
一级暗纹条件
a
一级暗纹坐标
中央亮纹线宽度
0
a
中央亮纹半角宽度
2 0 a
中央亮纹角宽度
2 f x 2 x a
中央亮纹线宽度
当缝宽a
条纹在接收 屏上的位置
中央亮纹线宽度 x
S
*
H
P
G
单缝衍射
S
*
正三边形孔
正四边形孔
正六边形孔
正八边形孔
单缝
衍射系统由光源、衍射屏、接收屏组成。
衍射的分类 菲涅耳衍射 (近场衍射) 光源和接收屏(或二 者之一)到障碍物的 距离为有限远。
A
E
S
光源 障碍物
B
接收屏
夫琅禾费衍射 (远场衍射) 光源、接收屏到 障碍物的距离均 为无限远。
S
光源
2k 1 2 1 1 3 个
作业P203: 7.23、7.24、
7.7 圆孔夫琅和费衍射及光学仪器的分辨本领 一、圆孔夫琅和费衍射
S
D
d
第一暗环所围成的中央光斑称为爱里斑。
爱里斑半径d/2 对透镜光心的张角称为爱里斑的半角宽度
d 2 0 sin 0 1.22 / D f
k( )----倾斜因子,随 的增大而减小
P
dS 2 r dE Fk ( ) cos(t ) r
F----比例常数 k( )----倾斜因子
2 惠更斯-菲涅耳原理解释了波为什么在屏上会出 现明暗条纹且不能向后传播的问题,这是惠更斯原理 所无法解释的。
P点的光振动(惠更斯原理的数学表达)为:
二、单缝衍射的动态变化
单缝上下移动,根据透镜成像原理衍射图不变 .
R
f
o
单缝上移,零级明 纹仍在透镜光轴上.
•单缝位置对衍射条纹的影响:单缝位置变化,
中央亮纹位置不变,宽度不变。
