第四讲 数数与计数(二)
六年级下册数学讲义-培优专题讲练:第4讲:枚举法(教师版)

第四讲枚举法1.计数问题分为两个大类,一类是“计次序”的问题,一类是“不计次序”的问题。
2.枚举需要按照一定的顺序和一定的规律来进行分类,这样可以做到不重复和不遗漏。
3.枚举法的根本思想在于分类,通过分类可以将原本复杂的问题拆分成若干个比较简单的问题,然后再逐一进行分析。
分类的思想可以化繁为简,化复杂为简单。
4.可以利用“树形图”来方便的记录枚举的过程,有几类问题就分出几个分枝,逐层按照顺序不断分叉再一一筛选,留下符合条件的,去掉不符合条件的。
注意在枚举“不计次序”的问题时,只需考虑从小到大(或从大到小)排列的分枝,而不用理会其他情况。
5.计次序:不但要挑选出来,而且还需要排列顺序,不同的排列顺序认为是不同的情况或方法。
这类问题通常是“排列”的题目。
6.不计次序:只要挑选出来即可,不需要排列顺序,不同的排列顺序认为是相同的情况或方法。
这类问题通常是“选取”的题目。
1.理解“枚举法”的含义。
2.能在题目中熟练运用枚举法解题。
例1:小明和小红玩掷骰子的游戏,共有两枚骰子,一起掷出。
若两枚骰子的点数和为7,则小明胜;若点数和为8,则小红胜。
试判断他们两人谁获胜的可能性大。
分析与解:将两枚骰子的点数和分别为7与8的各种情况都列举出来,就可得到问题的结论。
用a+b表示第一枚骰子的点数为a,第二枚骰子的点数是b的情况。
出现7的情况共有6种,它们是:1+6,2+5,3+4,4+3,5+2,6+1。
出现8的情况共有5种,它们是:2+6,3+5,4+4,5+3,6+2。
所以,小明获胜的可能性大。
注意,本题中若认为出现7的情况有1+6,2+5,3+4三种,出现8的情况有2+6,3+5,4+4也是三种,从而得“两人获胜的可能性一样大”,那就错了。
例2:数一数,右图中有多少个三角形。
分析与解:图中的三角形形状、大小都不相同,位置也很凌乱,不好数清楚。
为了避免数数过程中的遗漏或重复,我们将图形的各部分编上号(见右图),然后按照图形的组成规律,把三角形分成单个的、由两部分组成的、由3部分组成的……再一类一类地列举出来。
二年级华数
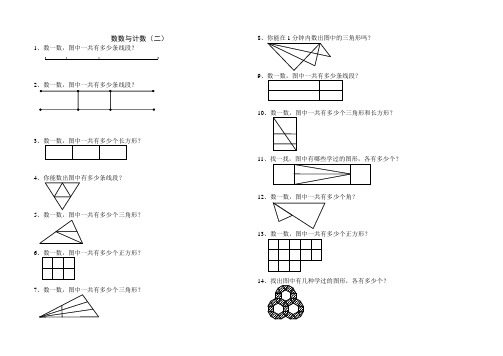
数数与计数(二)1、数一数,图中一共有多少条线段?2、数一数,图中一共有多少条线段?345、数一数,图中一共有多少个三角形?67、数一数,图中一共有多少个三角形?8、你能在1分钟内数出图中的三角形吗?9101112、数一数,图中一共有多少个角?1314找规律填图1、根据前面几幅图的规律,接下去该怎样画?234(1)(2)5、请你根据前面几幅图的规律,接着画。
67911、按顺序仔细观察图,第三幅图“?”出怎么填?121314、仔细观察图,回答下面的问题:(1)在第四幅图中应画什么图形?(2)在第十幅图中应画什么图形?第一组 第二组 第三组 第四组数数与计数(一)1、数一数,图中有多少个黑方格和白方格?23、在1~100中,数字“0”共出现了多少次?4、一本书共有200页,页码依次为1、2、3、…、200,数字“2”在页码中出现了多少次?5 6、数一数,图中有多少个小方块?7、数一数,图中一共有多少个正方体?(每一层的中间是空心) 89、数一数,图中一共有多少个正方体?10、将10个小正方体组成一个“I ”字形,如图,再将表面涂成红色,然后把小正方体分开。
问:(1)3面涂成红色的小正方体有多少块?( )块(2)4面涂成红色的小正方体有多少块?( )块(3)5面涂成红色的小正方体有多少块?( )块11、图中这堆木方块共有多少块?12、图中一共有多少个○?13、如图所示,这是由12个小方块组成的,如果在它的表面涂上蓝色,再分成12个小方块。
问:(1)5面涂成蓝色的有几个块小方块?( )块 (2)4面涂成蓝色的有几个块小方块?( )块 (3)3面涂成蓝色的有几个块小方块?( )块 (4)2面涂成蓝色的有几个块小方块?( )块第1题 第5题第7题第11题 第13题综合练习一、找规律填数。
(1)1、2、4、5、7、8、10、()、()(2)1、1、2、3、5、8、()、()(3)1、2、4、7、11、()、()(4)18、9、10、5、6、()、()(5)1、2、3、6、7、()、()(6)19、9、17、8、15、7、()、()(7)2、5、6、9、10、13、14、()、()二、填空。
小学数学西师大版二年级下册《数数》课件

数数
你还记得我们学过哪些 计数单位吗?
百 十个
一个一个地数,十个一是( 十)。 十个十个地数,十个十是(一百 )
聪明的你能一百一 百往下数吗?
一百,两百,三百,四百,五百, 六百,七百,八百,九百, 一千。
当数到第十个一百时,出
现了一个新的计数单位, 那就是千。
在这里, 我们可以发现:
10个一百是(一千 )。
我来考考你
(10)个一百是一千。
一千里面有(10)个一百。
百与千的关系是:
十个一百是一千。
你们真棒!
我们来试试一千一千地数。
一千,二千,三千,四千, 五千,
六千, 十个一千是一万。
满(10 )向前面进一。
数位顺序表
…… 万 千 百 十位 个 位位 位位
左
右
从一百起,一个一个地数,数 到一百二十五。
从一百九十六起,一个一个地数, 数到二百零四。
从一百八十起,十个十个地数,数 到二百六十。
从三千七百起,一百一百地 数,数到四千三百。
同桌合作: 按照要求一个人拨计数器,一个人数。
从六千九百九十五起,一个一个地数,数到七千零二。 从九千四百起,一百一百地数,数到一万。
这节课你有什么收获?
谢谢大家
六年级下数学思维训练教程(尖子生)

六年级下期第一讲 图形题例1 一个长方形(左下图)被分为9个面积不相等的小长方形。
其中A 、B 、C 、D 、E 的面积分别是A =160,B =172,C =215,D =240,E =300(单位:㎝2)。
原来大长方形的面积是多少平方厘米?(北京市第十一届迎春杯数学竞赛题)解:给大长方形宽上的四个点标上字母(右上图),NP MN =C B =215172=54, PQ MN =D A =240160=64,所以MN ∶NP ∶PQ =4∶5∶6。
设MN 、NP 、PQ 分别为4a 、5b 、6c ,那么原长方形的长=a A 4+a C 5+a E 6=a 1(4A +5C +6E )=a 133。
所以原长方形的面积是a 133×(4+5+6)a =1995(㎝2)。
例2 如图,阴影部分小正六角星形的面积是16㎝2。
问:大正六角形的面积是多少平方厘米?(第五届“华杯赛”决赛题)解:小正六角星形可以分成12个相等的小正三角形,每个小正三角形的面积是16÷12=131(㎝2)。
围绕小正六角星形的正六边形比小六角星形大了6个小等边三角形,每个小等边三角形的面积等于一个小正三角形的面积,所以正六边形的面积是16+131×6=24(㎝2),而大正六角星形面积等于正六边形面积的2倍,是24×2=48(㎝2)。
例3 如左下图,将三角形ABC 的BA 边延长1倍到D ,CB 边延长2倍到E ,AC 边延长3倍到F 。
如果三角形ABC 的面积等于1,那么三角形DEF 的面积是多少?(北京市第一届“迎春杯”数学竞赛题)D DA AC CB BE F E F解:连结CD 、AE 、BF 如右上图,那么△ACD =△ABC =1,△ADE =△ABE =2,A B CD E M N P Q A B C D E△CDF =△CBF =3,△BEF =6,所以,△DEF =1×2+2×2+3×2+6=18。
数数与计数教案

个性化辅导教案授课时间:2014年7月日年级:小二科目:数学课时:2课时课题: 数数与计数数数与计数(一)数学需要观察.大数学家欧拉就特别强调观察对于数学发现的重要作用,认为“观察是一件极为重要的事”.本讲数数与计数的学习有助于培养同学们的观察能力.在这里请大家记住,观察不只是用眼睛看,还要用脑子想,要充分发挥想像力.例1数一数,图2-1和图2-2中各有多少黑方块和白方块?解:仔细观察图2-1,可发现黑方块和白方块同样多.因为每一行中有4个黑方块和4个白方块,共有8行,所以:黑方块是:4×8=32(个)白方块是:4×8=32(个)再仔细观察图2-2,从上往下看:第一行白方块5个,黑方块4个;第二行白方块4个,黑方块5个;第三、五、七行同第一行,第四、六、八行同第二行;但最后的第九行是白方块5个,黑方块4个.可见白方块总数比黑方块总数多1个.白方块总数:5+4+5+4+5+4+5+4+5=41(个)黑方块总数:4+5+4+5+4+5+4+5+4=40(个)再一种方法是:每一行的白方块和黑方块共9个.共有9行,所以,白、黑方块的总数是: 9×9=81(个).1由于白方块比黑方块多1个,所以白方块是41个,黑方块是40个.例2图2-3所示砖墙是由正六边形的特型砖砌成,中间有个“雪花”状的墙洞,问需要几块正六边形的砖(图2-4)才能把它补好?解:仔细观察,并发挥想象力可得出答案,用七块正六边形的砖可把这个墙洞补好.如果动手画一画,就会看得更清楚了.例3将8个小立方块组成如图2-5所示的“丁”字型,再将表面都涂成红色,然后就把小立方块分开,问:(1)3面被涂成红色的小立方块有多少个?(2)4面被涂成红色的小立方块有多少个?(3)5面被涂成红色的小立方块有多少个?解:如图2-6所示,看着图,想像涂色情况.当把整个表面都涂成红色后,只有那些“粘在一起”的面(又叫互相接触的面),没有被涂色.每个小立方体都有6个面,减去没涂色的面数,就得涂色的面数.每个小立方体涂色面数都写在了它的上面,参看图2-6所示.(1)3面涂色的小立方体共有1个;(2)4面涂色的小立方体共有4个;(3)5面涂色的小立方体共有3个.例4如图2-7所示,一个大长方体的表面上都涂上红色,然后切成18个小立方体(切线如图中虚线所示).在这些切成的小立方体中,问:(1)1面涂成红色的有几个?2(2)2面涂成红色的有几个?(3)3面涂成红色的有几个?解:仔细观察图形,并发挥想像力,可知:(1)上下两层中间的2块只有一面涂色;(2)每层四边中间的1块有两面涂色,上下两层共8块;(3)每层四角的4块有三面涂色,上下两层共有8块.最后检验一下小立体总块数:2+8+8=18(个).能力训练1.如图2-8所示,数一数,需要多少块砖才能把坏了的墙补好?2.图2-9所示的墙洞,用1号和2号两种特型砖能补好吗?若能补好,共需几块?3.图2-10所示为一块地板,它是由1号、2号和3号三种不同图案的瓷砖拼成.问这三种瓷砖各用了多少块?34.如图2-11所示,一个木制的正方体,棱长为3寸,它的六个面都被涂成了红色.如果沿着图中.画出的线切成棱长为1寸的小正方体求:(1)3面涂成红色的有多少块?(2)2面涂成红色的有多少块?(3)1面涂成红色的有多少块?(4)各面都没有涂色的有多少块?4数数与计数(二)第一层 1个第二层 2个第三层 3个第四层 4个第五层 5个第六层 6个第七层 7个5第九层 9个第十层 10个第十一层 9个第十二层 8个第十三层 7个第十四层 6个第十五层 5个第十六层 4个第十七层 3个第十八层 2个第十九层 1个总数1+2+3+4+5+6+7+8+9+10+9+8+7+6+5+4+3+2+1=(1+2+3+4+5+6+7+8+9+10)+(9+8+7+6+5+4+3+2+1)=55+45=100(利用已学过的知识计算).6第二层 3个第三层 5个第四层 7个第五层 9个第六层 11个第七层 13个第八层 15个第九层 17个第十层 19个总数:1+3+5+7+9+11+13+15+17+19=100(利用已学过的知识计算).71+2+3+4+5+6+7+8+9+10+9+8+7+6+5+4+3+2+1=10×10即等号左边这样的一串数之和等于中间数的自乘积.由此我们猜想:1=1×11+2+1=2×21+2+3+2+1=3×31+2+3+4+3+2+1=4×41+2+3+4+5+4+3+2+1=5×51+2+3+4+5+6+5+4+3+2+1=6×61+2+3+4+5+6+7+6+5+4+3+2+1=7×71+2+3+4+5+6+7+8+7+6+5+4+3+2+1=8×81+2+3+4+5+6+7+8+9+8+7+6+5+4+3+2+1=9×981+2+3+4+5+6+7+8+9+10+9+8+7+6+5+4+3+2+1=10×10这样的等式还可以一直写下去,能写出很多很多.同学们可以自己检验一下,看是否正确,如果正确我们就发现了一条规律.③由方法2和方法3也可以得出下式:1+3+5+7+9+11+13+15+17+19=10×10.即从1开始的连续奇数的和等于奇数个数的自乘积.由此我们猜想:1+3=2×21+3+5=3×31+3+5+7=4×41+3+5+7+9=5×51+3+5+7+9+11=6×61+3+5+7+9+11+13=7×71+3+5+7+9+11+13+15=8×81+3+5+7+9+11+13+15+17=9×91+3+5+7+9+11+13+15+17+19=10×10还可往下一直写下去,同学们自己检验一下,看是否正确,如果正确,我们就又发现了一条规律.9解:(1)我们已知,两点间的直线部分是一条线段.以A点为共同端点的线段有:AB AC AD AE AF 5条.以B点为共同左端点的线段有:BC BD BE BF 4条.以C点为共同左端点的线段有:CD CE CF 3条.以D点为共同左端点的线段有:DE DF 2条.以E点为共同左端点的线段有:EF1条.总数5+4+3+2+1=15条.10习题数数与计数(三)数数与计数习题1.学生排成一队,在小进的前面有6人,后面有8人,问这队共有多少人?2.12辆汽车组成一列车队向前行进。
四下第四讲——小数的意义和性质

第四讲小数的性质和意义例题精讲例1、小数的意义、组成和数位顺序表:例2、小数的性质:例3、小数的大小比较:例4、小数点的移动:例5、名数的改写:(单位换算)例6、小数的近似数:例7、把较大的数改写成以“亿”或“万”做单位的数:例8、解答题:【课堂练习】【课后习题一】1、填空题:2、判断题:3、把下面各数的小数点都移到最高位的左边,小数的大小有什么变化?【课后习题二】一、填空:1、5.25是由()个1,()个0。
1和()个0.01组成的。
2、0.01平方米扩大到它的100倍是(),1平方米缩小到它的1/1000是( )。
3、4.06千米=()米 6.24公顷=()平方米6.005吨=( )千克 70平方分米=( )平方米4、0.6里面有()个0.01;0。
42里面有( )个0。
01。
5、()扩大到它的1000倍是96;( )缩小到它的1/100是0。
089.6、求5.3645的近似数,精确到千分位是(),精确到百分位是(),精确到十分位是()。
7、960米=()千米 360平方米=()公顷1。
4平方米=()平方分米 8.56吨=( )吨( )千克8、2。
65是由 ( )个1,()个0。
1和()个0.01组成的。
9、把0。
03扩大到它的100倍是( );缩小到它的1/10是()。
10、把235780000改写成用“亿”做单位的数是(),精确到0.01是( )。
11、一个末尾有若干个零的多位数,把它末尾的零去掉三个。
原数是新数的( )倍。
12、十分之一是小数的();十分位上的3个单位相当于()个千分位上的单位。
13、把0。
96的小数点向左移动两位后,缩小为原数的( )。
14、0.2的小数点向右移动三位后,在向左移动两位是()。
15、一个数的十位上是1,百分位上是5,个位和十分位上都是0,这个数是(),读作(),精确到十分位是()。
16、5个0。
1是(),8个()是0.08,()里有3个百分之一,0。
16里有( )个( )。
高斯小学奥数六年级上册含答案第04讲对应计数

第四讲对应计数有9个球排成一行:OOOO OO O传说电尤利曲斯在界眩了独韻的波吕輩1®塘后,离幵了独眼巨人的丄地一血那个可怜的戶人毎入早展都坐在詞穴人口的附近,帚让一只博羊从洞里出来,就从一堆卵石中捡趾哄来一等到了黄昏爲羊回兀的时慎.他每放进一只羊*就放下一块卵石” 就这样・如果早晨捲起的弟石都放完了,他就知道他所冇的羊状回来了.我们往其中插入两块(相同的)木板,就能够把这9个球分成三堆,例如:O ODO O O ODO O O O OOQO ODO O O O OOOOOOODODO可以看到,插入两块木板把9个球分成三堆的方法很多,那么到底有多少种插入木板的方法呢?每相邻两个小球之间有一个空隙,一共有8个空隙.插入的两块木板要把小球分成三堆,说明两块木板要放在两个不同的空隙之中. 8个空隙选两个,共有2C s 28种方法.如果要把三堆小球分别装入颜色为红、 黄、蓝的三个袋子里,又有多少种装法呢?其实,所谓装入红、黄、蓝三个袋子,就是把球分成三堆,因此答案也是28 •这样我们就把“小球装袋”问题转化成“小球插板”问题来求解了,这种方法我们称之为“插 “插板法”是一种特殊的对应技巧,能够帮我们解决很多计数问题.例1. 把20个苹果分给3个小朋友,每个小朋友至少分1个,共有多少种分苹果的方法?第二问允许有的“小朋友没有分到苹果” ,还能不能用“插板法”呢? 练习1、龟丞相把7个顶级乌龟壳分给4只小乌龟.如果每只小乌龟至少分一 个,共有多少种分法?如果可以有的小乌龟没有分到乌龟壳,共有多少种方 法?例2.某班40名学生参加了一项关于“超市是否应该提供免费塑料袋”的调查,每人均在“应该提供”、“不应该提供”和“无所谓”三个选项中做出了选择•请问:三个选项的统计数字共有多少种不同的可能?「分析」题目只关心三个选项的统计数字,需要具体考虑每个学生所作的选择吗?练习2、8名同学做同一道单选题,它有 A 、B 、C 、D 四个选项,每个同学都选了其中如何用“插板法”求解呢?放入红色放入黄色 放入蓝色如果可以有小朋友没有分到苹果,共有多少种分法?一个选项.老师为了调查同学们的做题情况,把选择各个选项的人数都做了统计,则有多少种可能的统计结果?最早的计数方法一一对应法] 我们这一讲学习对应的计数方法,这种计数方法有很强的技巧性,很考验思维能力. 也/::许你觉得这种对应法不是那么容易掌握,但它其实是非常有用,而且历史悠久的.人类最早使用的计数方法不是枚举,不是排列组合,也不是递推,而是对应!y!■对应法最早的应用是结绳计数. 最早期的时候,人类还没有发明数字. 因而用枚举等其他方法来记录数量的多少是不可能办到的. 这时,人们的计数方法是在绳子上打结或者在树;;上刻痕•用绳子上的结的数目或者树上划痕的道数来记录补获了多少猎物,采集了多少花:果.这个时期持续了很长时间,因为人类的历史已经有几百万年,而数字的发明距今还不到::1万年,在人类历史上的大部分时间,使用的计数方法是对应法一一结绳计数.i; 结绳记数这种方法,不但在远古时候使用,而且一直在某些民族中沿用下来•宋朝:人在一本书中说:“鞑靼无文字,每调发军马,即结草为约,使人传达,急于星火.”这是用结草来调发军马,传达要调的人数呢!其他如藏族、彝族等,虽都有文字,但在一般不识字的人中间都还长期使用这种方法•中央民族大学就收藏着一副高山族的结:绳,由两条绳组成:每条上有两个结,再把两条绳结在一起.「:有趣的是,结绳计数不止在我们中国古代用过,在国外也有很多结绳计数的记载. 传说古波斯王有一次打仗,命令手下兵马守一座桥,要守60天.为了让将士们不少守一天:也不多守一天,波斯王用一根长长的皮条,把上面系了60个扣.他对守桥的官兵们说:\“我走后你们一天解一个扣,什么时候解完了,你们就可以回家了.”: 对应是最原始的计数方法,充分蕴含着人类的智慧.例3.在8 8的方格棋盘中,一共可以数出多少个如下图所示的由4个单位小正方形组成的“L ” 型? ”型放入8 8的方格棋盘的方格盘中,按照放的方向分,可以有情形,那么是不是需要对每一个方向的“ L ”型分别进行计数呢?例4. ( 1) 一只青蛙沿着一条直线跳跃 4次后回到起点•如果它每一次跳跃的长度都是 1分米,那么这只青蛙共有多少种可能的跳法?(2)如果这只青蛙在一个方格边长为 1分米的方格纸上沿格线跳跃 4次后回到起点,每次跳跃的长度仍是 1分米,那么这只青蛙共有多少种可能的跳法?「分析」(1)青蛙在直线上跳跃 4次后要回到起点,如果一直往一个方向跳,显然是不 行的•那么青蛙应该怎么跳呢?( 2)青蛙在方格表上跳跃 4 次后要回到起点,现在青蛙有哪些跳跃的方向,每个方向 上各应该跳跃多少次呢?练习3、在6 6的方格棋盘中, 一共可以数出多少个如下图所示的由 3个单位小正方形练习4、一只青蛙沿着一条直线跳跃6 次后回到起点.如果它每一次跳跃的长度都是1分米,那么这只青蛙共有多少种可能的跳法?对应法是一种很巧的计数方法,但如何建立对应关系,是其中的难点.之前几道题,对应关系的建立相对比较直接,而有些问题,则需要通过大量的分析,才能找出隐藏的对应关系.例5.常昊与古力两人进行围棋“棋圣”冠军争霸赛,谁先胜4 局即获得比赛的胜利. 请问: 比赛过程一共有多少种不同的方式?「分析」由对称性,只需求出常昊获胜的比赛过程有多少种.比赛最多进行7 场,其中常昊一定胜4场.如果我们按比赛先后顺序给每场比赛编号,那么常昊胜的4 场比赛编号,就决定了整个比赛流程.而常昊获胜的比赛可以是哪 4 场呢?例6.海淀大街上一共有18 盏路灯,区政府为了节约用电,打算熄灭其中的7 盏.但为了行路安全,任意相邻的两盏灯不能同时被熄灭,请问:一共有多少种熄灯方案?分析」你能用插板法求解这道题吗?课堂内外 -------------------------------------------------最早的密码战公元前405年,雅典和斯巴达之间的伯罗奔尼撒战争已进入尾声. 斯巴达军队逐渐占据了优势地位,准备对雅典发动最后一击.这时,原来站在斯巴达一边的波斯帝国突然改变态度,停止了对斯巴达的援助,意图是使雅典和斯巴达在持续的战争中两败俱伤,以便从中渔禾U.在这种情况下,斯巴达急需摸清波斯帝国的具体行动计划,以便采取新的战略方针•正在这时,斯巴达军队捕获了一名从波斯帝国回雅典送信的雅典信使. 斯巴达士兵仔细搜查这名信使,可搜查了好大一阵,除了从他身上搜出一条布满杂乱无章的希腊字母的普通腰带外,别无他获.情报究竟藏在什么地方呢?斯巴达军队统帅莱桑德把注意力集中到了那条腰带上,情报一定就在那些杂乱的字母之中. 他反复琢磨研究这些天书似的文字,把腰带上的字母用各种方法重新排列组合,怎么也解不出来.最后,莱桑德失去了信心,他一边摆弄着那条腰带,一边思考着弄到情报的其他途径. 当他无意中把腰带呈螺旋形缠绕在手中的剑鞘上时,奇迹出现了.原来腰带上那些杂乱无章的字母,竟组成了一段文字.这便是雅典间谍送回的一份情报,它告诉雅典,波斯军队准备在斯巴达军队发起最后攻击时,突然对斯巴达军队进行袭击.斯巴达军队根据这份情报马上改变了作战计划,先以迅雷不及掩耳之势攻击毫无防备的波斯军队,并一举将它击溃,解除了后顾之忧.随后,斯巴达军队回师征伐雅典,终于取得了战争的最后胜利.公元前405年,雅典和斯巴达之间的伯罗奔尼撒战争已进入尾声. 斯巴达军队逐渐占据了优势地位,准备对雅典发动最后一击.这时,原来站在斯巴达一边的波斯帝国突然改变态度,停止了对斯巴达的援助,意图是使雅典和斯巴达在持续的战争中两败俱伤,以便从中渔禾U.在这种情况下,斯巴达急需摸清波斯帝国的具体行动计划,以便采取新的战略方针.正在这时,斯巴达军队捕获了一名从波斯帝国回雅典送信的雅典信使. 斯巴达士兵仔细搜查这名信使,可搜查了好大一阵,除了从他身上搜出一条布满杂乱无章的希腊字母的普通腰带外,别无他获.情报究竟藏在什么地方呢?斯巴达军队统帅莱桑德把注意力集中到了那条腰带5. 作业1. 一部电视连续剧共 8集,电视台要在周一到周四这 4天内按顺序播完,其中可以有若干 天不播,共有多少种安排播出的方法?2. 现在有12道竞赛题,卡莉娅要在今天、明天、后天这三天内按顺序做完,但每一天可以做很多道题也可以一道不做•共有多少种安排做题的方案?3. 阿呆在玩PSP 格斗游戏,游戏采用的是五局三胜制(阿呆VS 电脑),谁先胜三场谁就 获得胜利.如果最后阿呆获胜,那么一共有多少种可能的比赛过程?(只考虑每场比赛的胜负) 4. 在6 6的方格棋盘中,一共可以数出多少个如图所示的由5个单位小正方形组成的“凹”字形?(注:这8个鸡蛋看作完全相同)(1)有8个鸡蛋,每天至少吃 1个,一共吃了 5天,有多少种不同的吃法?(2)有8个鸡蛋,每天至少吃2个,一共吃了 3天,有多少种不同的吃法?例题:例题1.答案:171 ; 231详解:第一问用课文里所说的“插板法”即可解决.20个苹果,共有19个空隙,分给3个小朋友需要3 1 2块隔板,将2块隔板插入19个空隙中的某两个中,就是从2 19个空隙中挑出两个用来插板子,方法有C 19 171 ;第二问同样用插板法,仍然是 20个苹果和2块隔板•但此时隔板不一定要放在 19个空隙中,也可以放在所有苹果 的最左端或者最右端,而且它们也不一定插入两个不同的空隙,插入同一个空隙也是可以的.因此,我们只要把20个苹果和2块隔板随意排成一行即可. 这20 2 22个 对象排成一行会占 22个位置,从这22个位置中挑出2个来放隔板,剩余的 20个位 置自然就是放苹果,因此共有 C ;2 231种不同的方法.例题2.答案:861详解:本题相当于把 40个苹果放入3个盘子里,每个盘子都允许为空•因此共有 40 个苹果和2块隔板.方法数等于 C 42 861 .可以分为两类情形:第一类,1、2、3、4各一个,共有A 4种方法;第二类,只有21、2或者只有3、4,共有2 C 4种方法.两者相加共 36种. 例题5.答案:70 详解:由对称性,只需求出常昊获胜的比赛过程有多少种,再乘以 2即可.比赛最多进行7场,其中常昊一定胜 4场,而且比赛一定是在常昊获得第 4场胜利时结束的, 因此常昊获胜的那 4场比赛的编号就决定了整个比赛流程. 第四讲对应计数例题4.答案: (1)(1) 6; (2) 36详解:青蛙要能够回到起点, 必须向左跳两次, 右,右),(左,右,右,左)等.不难看出,只要从 外两步自然向右,所以只要确定哪两步是向左跳,就确定了哪两步是向右跳.因 此跳跃的方法数为C : 6种;(2) 详解:现在青蛙需要朝四个方向跳,我们记四个方向为 示).如果想要跳回原地,必须保证四步之内向右跳两次. 4步中挑出1、2、3、4 (如图所1和2 一样多,3和4 一样多.于是 例题3.答案:336个 详解:如右图所示,每个2 此只要求出图中有几个 册第 2 6 29讲)的知识不难得知,7 84个,所以共有“例如(左,左,2步来向左,另例题6.答案:C:792详解:本题从题面上看,是要从18盏灯中选出7盏来熄灭•但实际解决的时候,需要换一个角度:如何把灭掉的7盏灯,插入另外11盏亮着的灯之间.如下图所示,在11盏亮灯之间插入熄灭的灯时,每个空隙最多插1盏,否则灭灯就相邻了,因此必须挑7个空隙,每个空隙插一盏,而可供插入的空隙有12个(两端也可),因此答案为C:792 •d’A ifhJLxr w. A<> <> <> <> <> <> <> <> <> <>A A A R* * r* 八练习:1. 答案:C B 20 ;C;o 120简答:用插板法即可解决,具体过程略.32. 答案:C11 165简答:相当于把8个球放入4个篮子,每个篮子都可以为空.3. 答案:100简答:每个田字格都可以找到4个“L”型•共有5 5 25个田字格,所以共4 25 100 个“L”型.4. 答案:20简答:6次跳远中,一定3次向左,3次向右,因此共有C;20种不同的跳法.作业1.答案:165简答: 4 1 3C8 4 1 C111652.答案:91简答:C1^3 1 G4913.答案:10简答:C s 10 •4.答案:80简答:每个2 3的方格内都有2个“凹”字形,一共有40个2 3的方格,因此共有80 个“凹”字形.5. 答案:(1)35;(2)6简答:(1)用插板法,8个鸡蛋之间有7个“空”,用4个“板”隔成5部分,有C; 35种方法;(2)每天预先吃掉一个鸡蛋,问题相当于是3天吃8 3 5个鸡蛋,每天至少2吃一个,有C42 6 种吃法.。
中班数学《数数》教案

中班数学《数数》教案教案标题:小班数学《数数》教学目标:1.能够按照指定的顺序数数,掌握1-30的数的顺序。
2.能够正确地念出并标示1—10的基本数词。
3.能够根据实物和图形进行数数,并能通过手指、计数棒或计数器等进行实际操作。
4.能够从一组物品中选出指定的数量。
教学重点:1.数的顺序和数词的正确念法。
2.实物和图形的对应。
3.使用物品进行实际操作。
教学准备:1.教学图片或卡片,上面标有数字1-30。
2.数字卡片。
3.实物数数道具,如小球、计数棒、手指等。
教学步骤:Step 1: 导入新课 (10分钟)1.通过展示数字图片或卡片,引导学生回忆1-30的数的顺序。
2.利用数字卡片,教授1-10的基本数词及数的顺序。
Step 2: 通过实物进行数数 (15分钟)1.准备一些实物,如小球或计数棒,并将它们摆放在学生面前。
2.教师先数一遍实物,然后请学生模仿教师的数数方式进行数数。
3.引导学生观察实物数量的变化,并理解相应的数词。
Step 3: 用手指进行数数 (15分钟)1.教师引导学生使用手指进行数数,从1开始数到10。
2.随后,教师提出一个数,要求学生用手指显示出该数。
3.继续进行,逐渐增加数的范围,直到30。
Step 4:利用计数器进行数数 (15分钟)1.准备一些计数器,如计数棒或小球,并将它们分发给学生。
2.教师先数一遍计数器,然后请学生模仿教师的数数方式进行数数。
3.引导学生理解计数器的作用,即通过计数器记录数量。
Step 5:数和实物的对应 (15分钟)1.准备一些具有不同数量的物品,如纸小人、玩具等,在教室中分散放置。
2.教师口头提出一个数,要求学生根据该数,在教室中找出相应的数量物品。
3.学生通过实践操作,增强了数和实物之间的对应关系。
Step 6:练习和巩固 (15分钟)1.教师给学生分发一些与数有关的练习题,要求学生完成。
2.教师检查和纠正学生的练习,并解答学生的疑问。
3.引导学生通过练习,巩固和运用所学知识。
红棉杯冲刺讲义第四讲---计数综合

HM 冲刺讲义第四讲——计数综合知识汇编:1.加法原理和分类计数法加法原理:做一件事,完成它可以有n 类办法,在第一类办法中有1M 种不同的方法,在第二类办法中有2M 种不同的方法,……,在第n 类办法中有n M 种不同的方法,那么完成这件事共有N=n M M M M ++++ 321种不同方法。
分类计数法:第一类办法的方法属于集合1A ,第二类办法的方法属于集合2A ,……,第n 类办法的方法属于集合n A ,那么完成这件事的方法属于集合n A A A A ++++ 321。
分类的要求:每一类中的每一种方法都可以独立地完成此任务;两类不同办法中的具体方法,互不相同(即分类不重);完成此任务的任何一种方法,都属于某一类(即分类不漏)。
加法原理的常用方法:(1)枚举法:数出来的种类分类枚举找规律(2)树形图:“树形图法”实际上是枚举的一种,但是它借助于图形,可以使枚举过程不仅形象直观,而且有条理又不重复遗漏,使人一目了然。
(3)标数法:平面图形标数法立体图形标数法适用于最短路线问题,需要一步一步标出所有相关点的线路数量,最终得到到达终点的方法总数.标数法是加法原理与递推思想的结合。
2.乘法原理乘法原理:做一件事,完成它需要分成n 个步骤,做第一步有m 1种不同的方法,做第二步有m 2种不同的方法,……,做第n 步有m n 种不同的方法,那么完成这件事共有N=m 1×m 2×m 3×…×m n 种不同的方法。
合理分步的要求:任何一步的一种方法都不能完成此任务,必须且只须连续完成这n 步才能完成此任务;各步计数相互独立;只要有一步中所采取的方法不同,则对应的完成此事的方法也不同。
3.排列组合(1)排列就是指从给定个数的元素中取出指定个数的元素进行排序。
排列的定义:从n 个不同元素中,任取m(m≤n,m 与n 均为自然数,下同)个元素按照一定的顺序排成一列,叫做从n 个不同元素中取出m 个元素的一个排列;从n 个不同元素中取出m(m≤n)个元素的所有排列的个数,叫做从n 个不同元素中取出m 个元素的排列数,用符号m nA 表示。
奥数讲座(2年级-下)(15讲)

二年级奥数讲座(二)目录第一讲机智与顿悟第二讲数数与计数第三讲速算与巧算第四讲数与形相映第五讲一笔画问题第六讲七座桥问题第七讲数字游戏问题(一)第八讲数字游戏问题(二)第九讲整数的分拆第十讲枚举法第十一讲找规律法第十二讲逆序推理法第十三讲画图显示法第十四讲等量代换法第十五讲等式加减法第一讲机智与顿悟数学需要踏实与严谨,也含有机智与顿悟.例1 在美国把5月2日写成5/2,而在英国把5月2日写成2/5.问在一年之中,在两国的写法中,符号相同的有多少天?解:一年中两国符号相同的日子共有12天.它们是:一月一日 1/1 七月七日 7/7二月二日 2/2 八月八日 8/8三月三日 3/3 九月九日 9/9四月四日 4/4 十月十日 10/10五月五日 5/5 十一月十一日 11/11六月六日 6/6 十二月十二日 12/12注意由差异应当想到统一,有差异就必须有统一,仔细想一想这道题就会有所领悟.例2 有一个老妈妈,她有三个男孩,每个男孩又都有一个妹妹,问这一家共有几口人?解:全家共有5口人.妹妹的年龄最小,她是每一个男孩的妹妹.如果你列出算式:1个妈妈+3个男孩+3个妹妹=7口人那就错了.为什么呢?请你想一想.例3 小明给了小刚2支铅笔,他们俩的铅笔数就一样多了,问小明比小刚多几支铅笔?解:小明比小刚多4支铅笔.注意,可不是多2支;如果只多2支的话,小明给小刚后,小刚就反而比小明多2支,不会一样多了.例4 小公共汽车正向前跑着,售票员对车内的人数数了一遍,便说道,车里没买票的人数是买票的人数的2倍.你知道车上买了票的乘客最少有几人吗?解:最少1人.因为售票员和司机是永远不必买票的,这是题目的“隐含条件”.有时发现“隐含条件”会使解题形势豁然开朗.例5 大家都知道:一般说来,几个数的和要比它们的积小,如2+3+4比2×3×4小.那么请你回答:0、1、2、3、4、5、6、7、8、9这几个数相加的和大还是相乘的积大?解:和大.注意:“0”是个很有特点的数.①0加到任何数上仍等于这个数本身;②0乘以任何数时积都等于0;把它们写出来就是:0+1+2+3+4+5+6+7+8+9=450×1×2×3×4×5×6×7×8×9=0所以,应当重视特例.例6 两个数的和比其中一个数大17,比另一个数大15,你知道这两个数都是几?你由此想到一般关系式吗?解:这两个数就是17和15.因为它们的和比15大17,又比17大15.由一个特例联想、推广到一般,是数学思维的特点之一.此题可能引起你如下联想:和-15=17,那么和=15+17.一般和=一个数+另一个加数,或写成:和-一个加数=另一个加数,或写成:被减数-减数=差,也可写成:被减数-差=减数.以上这些都是你从课本上学过的内容,这里不过是把它们联想到一起罢了.学数学要注意联想,学会联想才能融会贯通.例7 小明和小英一同去买本,小明买的是作文本,小英买的是数学本.已知小英买的数学本的本数是小明买的作文本的2倍.又知一本作文本的价钱却是一本数学本的价钱的2倍,请问他俩谁用的钱多?解:他俩花的钱一样多.可以这样想:因为作文本的价钱是数学本的2倍,所以把买作文本的钱用来买数学本,同样多的钱所买到的本数应该是作文本的2倍,这刚好与题意相符.可见两人花的钱一样多.结论是隐含着的,推理就是要把它明明白白地想通,写出来的推理过程就叫“证明”,这是同学们现在就可以知道的.例8 中午放学的时候,还在下雨,大家都盼着晴天.小明对小英说:“已经连续三天下雨了,你说再过36小时会出太阳吗?”小朋友你说呢?解:不会出太阳.因为从中午起再过36个小时正好是半夜.而阴雨天和夜里是不会出太阳的.注意:解题的第一要义是首先明确“问什么”,而且要紧紧抓住“问什么”?“问什么”是思考目标,这就好比小朋友走着来上学,学校是你走路的目的,试想,如果你走路没有目标,结果会怎样?本题迷惑人的地方就是想用阴天下雨把你的注意力从应当思考的目标引开,给你的思维活动造成干扰.学会删繁就简,抓住目标,将会大大地提高你的解题效率.例9 一位画家想订做一个像框,用来装进他的立体画.他画了一张像框的尺寸图拿给你看(右图),请你帮他算算,需要多长的材料才能做好?(画家说,材料粗细要求一样,形状尺寸一定要按图示加工,拐角部分都要做成直角).解:不管多长的材料,像框也无法做成.从每一部分来说,这个图看来是合理的,但从整体上看,这个图是“荒谬的”、“失调的”.用一句普通的话说,就是“有点不对劲的”.请你注意,对现实生活觉得有点不对劲的感觉是创造性的起因.习题一1.如右图所示,若每个圆圈里都有五只蚂蚁,问右图中一共应有多少只蚂蚁?2.一个课外小组活动日,老师进教室一看,来参加活动的学生只占教室里全体人数的一半.老师很生气.你知道这天共来了多少学生吗?3.小林和小蓉两人口袋里各有10元钱.两人去书店买书.买完书后发现,小林花去的钱正好和小蓉剩下的钱数一样多.请问,现在他们两人一共还有多少钱?4.满满一杯牛奶,小明先喝了半杯;然后添水加满,之后再喝去半杯;再一次添水加满,最后把它全部喝完.请问小明一共喝了多少杯牛奶多少杯水?5.小黄和小兰想买同一本书.小黄缺一分钱,小兰缺4角2分钱.若用他俩的钱合买这本书,钱还是不够.请问这本书的价钱是多少?他俩各有多少钱?6.一个骑自行车的人以每小时10公里的速度从一个城镇出发去一个村庄;与此同时,另一个人步行,以每小时5公里的速度从那个村庄出发去那个城镇.经过一小时后他们相遇.问这时谁离城镇较远,是骑车的人还是步行的人?7.有人去买葱,他问多少钱一斤.卖葱的说:“1角钱1斤.”买葱的说:“我要都买了.不过要切开称.从中间切断,葱叶那段每斤2分,葱白那部分每斤8分.你卖不卖?”卖葱的一想:“8分+2分就是1角”.他就同意全部卖了.但是卖后一算账,发现赔了不少钱.小朋友,你知道为什么吗?8.一天鲍勃用赛车送海伦回家.汽车在快车道上急驶.鲍勃看到前面有辆大卡车.灵机一动,突然向海伦提出了一个巧妙的问题.鲍勃说:“海伦,你看!前面那辆大卡车开得多快!但是我们可以超过它.假定现在我们在它后面正好是1500米,它以每分钟1000米的速度前进,而我用每分钟1100米的速度追赶它,我们这样一直开下去,到时候肯定会从后面撞上它.但是,海伦,请你告诉我,在相撞前一分钟,我们与它相距多少米?”聪明的海伦略加思考立刻回答了鲍勃的问题.小朋友,你也能回答吗?9.小明家附近有个梯形公园,公园中有4棵树排成了一行,如图所示.小明每天放学回家都要到公园里去玩一会儿.有一天,他玩着玩着突然想出了一个问题:“能不能把公园分成大小和形状都相同的4块,而且每一块上保留一棵树?”回到家以后,他又和爸爸妈妈一块儿讨论,终于像小明想的那样分好了,小明非常高兴.小朋友,你也回家与爸爸妈妈讨论讨论,看能不能分好?10.小莉在少年宫学画油画.一天,他找到了一块中间有个圆孔的纸板.他想把这块板分成两块,重新组合成一块调色板,如下图,小朋友看该怎么切才好呢?注意:回顾由第9题到第10题的解题思路,这里有一个克服“思维定势”的问题.在做第9题时,你可能费了很大劲,把大梯形这样划分,那样划分,试来试去,最终得到了满意的结果.做完了第9题后这种思考问题的方式方法就可能深深地在你的头脑中扎根了.当你着手解第10题时,你可能还是沿着原来的思路,按原来的思维方式处理面临的新问题,这种情况心理学上就叫做“思维定势”.思维定势不利于创造性的发挥,从这个意义上讲,有人说学习的最大障碍是头脑中已有的东西,是有一定道理的,你在做第10题时,对此大概也有体会了吧!今后要以此为训.对本讲其它各题,在你做完以后也希望你做一些回顾和总结,以便发现些更有价值的东西,使自己变得更聪明起来.习题一解答1.解:一共只有5只蚂蚁.如右图所示,每一个圆圈里都有五只蚂蚁.2.解:只来了一名学生.教室里共有两人,另一个人是老师,所以说学生占教室里全体人数的一半.3.解:他们两人此时一共还有10元.如下图所示.4.解:小明共喝了一杯牛奶和一杯水.因为原来就有一杯牛奶,最后喝光了;后来又加了两次水,每次半杯,合起来是一杯水,最后也喝光了.5.解:这本书的价钱就是4角2分钱.小黄有4角1分钱(所以买书还差1分),小兰1分钱都没有,所以他若买这本书,还差4角2分钱;小兰若是有1分钱的话,他俩的钱合起来也就够买这本书了.6.解:相遇后,两人就在一处了,此时二人离城自然一样远.7.解:按照买葱人的说法,葱叶那段每斤2分,葱白那段每斤8分,合起来确是1角.但是这样合起来后是2斤卖1角,不再是一斤1角钱,所以卖葱的人赔了钱.8.解:相撞前一分钟赛车落后卡车100米.海伦思考的窍门是倒着想.鲍勃的赛车比卡车每分钟快100米(即1100米-1000米=100米),所以碰车前的1分钟它们相距100米.9.解:划分方法如右图所示.每一块都是个小梯形,四个小梯形大小相等,形状相同.小梯形和大梯形之间是大小不等、形状相似.10.解:方法不止一种.①从中切下一条,倒换个位置放进去.(见图)②在需要开孔的位上开一个小圆孔,把切下的部分填到中间的孔中去.(见图)第二讲数数与计数从数数与计数中,可以发现重要的算术运算定律.例1 数一数,下面图形中有多少个点?解:方法1:从上到下一行一行地数,见下图.点的总数是:5+5+5+5=5×4.方法2:从左至右一列一列地数,见下图.点的总数是:4+4+4+4+4=4×5.因为不论人们怎样数,点数的多少都是一定的,不会因为数数的方法不同而变化.所以应有下列等式成立:5×4=4×5从这个等式中,我们不难发现这样的事实:两个数相乘,乘数和被乘数互相交换,积不变.这就是乘法交换律.正因为这样,在两个数相乘时,以后我们也可以不再区分哪个是乘数,哪个是被乘数,把两个数都叫做“因数”,因此,乘法交换律也可以换个说法:两个数相乘,交换因数的位置,积不变.如果用字母a、b表示两个因数,那么乘法交换律可以表示成下面的形式:a×b=b×a.方法3:分成两块数,见右图.前一块4行,每行3个点,共3×4个点.后一块4行,每行2个点,共2×4个点.两块的总点数=3×4+2×4.因为不论人们怎样数,原图中总的点数的多少都是一定的,不会因为数数的方法不同而变化.所以应有下列等式成立:3×4+2×4=5×4.仔细观察图和等式,不难发现其中三个数的关系:3+2=5所以上面的等式可以写成:3×4+2×4=(3+2)×4也可以把这个等式调过头来写成:(3+2)×4=3×4+2×4.这就是乘法对加法的分配律.如果用字母a、b、c代表三个数,那么乘法对加法的分配律可以表示成下面的形式:(a+b)×c=a×c+b×c分配律的意思是说:两个数相加之和再乘以第三数的积等于第一个数与第三个数的积加上第二个数与第三个数的积之和.进一步再看,分配律是否也适用于括号中是减法运算的情况呢?请看下面的例子:计算(3-2)×4和3×4-2×4.解:(3-2)×4=1×4=43×4-2×4=12-8=4.两式的计算结果都是4,从而可知:(3-2)×4=3×4-2×4这就是说,这个分配律也适用于一个数与另一个数的差与第三个数相乘的情况.如果用字母a、b、c(假设a>b)表示三个数,那么上述事实可以表示如下:(a-b)×c=a×c-b×c.正因为这个分配律对括号中的“+”和“-”号都成立,于是,通常人们就简称它为乘法分配律.例2 数一数,下左图中的大长方体是由多少个小长方体组成的?解:方法1:从上至下一层一层地数,见上右图.第一层4×2个第二层4×2个第三层4×2个三层小长方体的总个数(4×2)×3个.方法2:从左至右一排一排地数,见下图.第一排2×3个第二排2×3个第三排2×3个第四排2×3个四排小长方体的总个数为(2×3)×4.若把括号中的2×3看成是一个因数,就可以运用乘法交换律,写成下面的形式:4×(2×3).因为不论人们怎样数,原图中小长方体的总个数是一定的,不会因为数数的方法不同而变化.把两种方法连起来看,应有下列等式成立:(4×2)×3=4×(2×3).这就是说在三个数相乘的运算中,改变相乘的顺序,所得的积相同.或是说,三个数相乘,先把前两个数相乘再乘以第三个数,或者先把后两个数相乘,再去乘第一个数,积不变,这就是乘法结合律.如果用字母a、b、c表示三个数,那么乘法结合律可以表示如下:(a×b)×c=a×(b×c).巧妙地运用乘法交换律、分配律和结合律,可使得运算变得简洁、迅速.从数数与计数中,还可以发现巧妙的计算公式.例3 数一数,下图中有多少个点?解:方法1:从上至下一层一层地数,见下图.总点数=1+2+3+4+5+6+7+8+9=45.方法2:补上一个同样的三角形点群(但要上下颠倒放置)和原有的那个三角形点群共同拼成一个长方形点群,则显然有下式成立(见下图):三角形点数=长方形点数÷2因三角形点数=1+2+3+4+5+6+7+8+9而长方形点数=10×9=(1+9)×9代入上面的文字公式可得:1+2+3+4+5+6+7+8+9=(1+9)×9÷2=45.进一步把两种方法联系起来看:方法1是老老实实地直接数数.方法2可以叫做“拼补法”.经拼补后,三角形点群变成了长方形点群,而长方形点群的点数就可以用乘法算式计算出来了.即1+2+3+4+5+6+7+8+9=(1+9)×9÷2.这样从算法方面讲,拼补法的作用是把一个较复杂的连加算式变成了一个较简单的乘除算式了.这种方法在700多年前的中国的古算书上就出现了.习题二下列各题至少用两种方法数数与计数.1.数一数,下图中有多少个点?2.数一数,下图中的三角形点群有多少个点?3.数一数,下图中有多少个小正方形?4.数一数,下图中共有多少个小三角形?习题二解答1.解:方法1:从上至下一行一行地数,共4行每行5个点,得5×4=20.方法2:分成两个三角形后再数,见下图.得:(1+2+3+4)×2=20.发现一个等式:1+2+3+4=(1+4)×4÷2.2.解:方法1:从上至下一行一行地数,再相加,得:1+2+3+4+5+6+7+8+9+10=55.方法2:用拼补法,如图所示:11×10÷2=55.发现一个等式:1+2+3+4+5+6+7+8+9+10=(1+10)×10÷2.3.解:方法1:从上至下一层一层地数,得:5×4=20.方法2:做阶梯形切割,分两部分数,见右图.(1+2+3+4)×2=20.发现一个等式:1+2+3+4=(1+4)×4÷2.4:解:方法1:从上至下一层一层地数(图略)得:20×10=200.方法2:分成两个三角形来数:(1+3+5+7+9+11+13+15+17+19)×2=200.发现一个等式:1+3+5+7+9+11+13+15+17+19第三讲速算与巧算利用上一讲得到的乘法运算定律和等差数列求和公式,可以使计算变得巧妙而迅速.例1 2×4×5×25×54=(2×5)×(4×25)×54 (利用了交换=10×100×54 律和结合律)=54000例2 54×125×16×8×625=54×(125×8)×(625×16)(利用了=54×1000×10000 交换律和结合律)=540000000例3 5×64×25×125 将64分解为2、4、8=5×(2×4×8)×25×125 的连乘积是关键一=(5×2)×(4×25)×(8×125)步.=10×100×1000=1000000例5 37×48×625=37×(3×16)×625 注意37×3=111=(37×3)×(16×625)=111×10000=1110000例6 27×25+13×25 逆用乘法分配律,=(27+13)×25 这样做叫提公因数=40×25=1000例7 123×23+123+123×76 注意123=123×1;再=123×23+123×1+123×76 提公因数123=123×(23×1+76)=123×100=12300例8 81+991×9 把81改写(叫分解因=9×9+991×9 数)为9×9是为了下=(9+991)×9 一步提出公因数9=1000×9=9000例9 111×99=111×(100-1)=111×100-111=11100-111=10989例10 23×57-48×23+23=23×(57-48+1)=23×10=230例11 求1+2+3+…+24+25的和.解:此题是求自然数列前25项的和.方法1:利用上一讲得出的公式和=(首项+末项)×项数÷21+2+3+…+24+25=(1+25)×25÷2=26×25÷2=325方法2:把两个和式头尾相加(注意此法多么巧妙!)想一想,这种头尾相加的巧妙求和方法和前面的“拼补法”有联系吗?例12 求8+16+24+32+…+792+800的和.解:可先提公因数8+16+24+32+…+792+800=8×(1+2+3+4+…+99+100)=8×(1+100)×100÷2=8×5050=40400例13 某剧院有25排座位,后一排都比前一排多2个座位,最后一排有70个座位,问这个剧院一共有多少个座位?解:由题意可知,若把剧院座位数按第1排、第2排、第3排、…、第25排的顺序写出来,必是一个等差数列.那么第1排有多少个座位呢?因为:第2排比第1排多2个座位,2=2×1第3排就比第1排多4个座位,4=2×2第4排就比第1排多6个座位,6=2×3这样,第25排就比第1排多48个座位,48=2×24.所以第1排的座位数是:70-48=22.再按等差数列求和公式计算剧院的总座位数:和=(22+70)×25÷2=92×25÷2=1150.习题三计算下列各题:1.4×135×252.38×25×63.124×254.132476×1115.35×53+47×356.53×46+71×54+82×547.①11×11 ②111×111③1111×1111 ④11111×11111⑤111111111×1111111118.①12×14 ②13×17③15×17 ④17×18⑤19×15 ⑥16×129.①11×11 ②12×12③13×13 ④14×14⑤15×15 ⑥16×16⑦17×17 ⑧18×18⑨19×1910.计算下列各题,并牢记答案,以备后用.①15×15 ②25×25③35×35 ④45×45⑤55×55 ⑥65×65⑦75×75 ⑧85×85⑨95×9511.求1+2+3+…+(n-1)+n之和,并牢记结果.12.求下列各题之和.把四道题联系起来看,你能发现具有规律性的东西吗?①1+2+3+…+10②1+2+3+…+100③1+2+3+…+1000④1+2+3+…+1000013.求下表中所有数的和.你能想出多少种不同的计算方法?习题三解答1.解:4×135×25=(4×25)×135=100×135=13500.2.解:38×25×6=19×2×25×2×3=19×(2×25×2)×3=19×100×3=1900×3=5700.3.解:124×25=(124÷4)×(25×4)=31×100=3100.4.解:132476×111=132476×(100+10+1)=13247600+1324760+132476=14704836.或用错位相加的方法:5.解:35×53+47×35=35×(53+47)=35×100=3500.6.解:53×46+71×54+82×54=(54-1)×46+71×54+82×54=54×46-46+71×54+82×54=54×(46+71+82)-46=54×199-46=54×(200-1)-46=54×200-54-46=10800-100=10700.7.解:①11×11=121②111×111=12321③1111×1111=1234321④11111×11111=123454321⑤111111111×111111111=12345678987654321.8.解:①12×14=12×(10+4)=12×10+12×4=12×10+(10+2)×4=12×10+10×4+2×4 多次运用乘法分配=(12+4)×10+2×4 律(或提公因数)=160+8=168②13×17=13×(10+7)=13×10+13×7 多次运用乘法分配=13×10+(10+3)×7 律(或提公因数)=13×10+10×7+3×7=(13+7)×10+3×7=200+21=221发现规律:求十几乘以十几的积的速算方法是:用一个数加上另一个数的个位数,乘以10(即接着添个“0”),再加上它们个位数字的积.用这个方法计算下列各题:③15×17=(15+7)×10+5×7=220+35=255④17×18=(17+8)×10+7×8=250+56=306⑤19×15=240+45=285⑥16×12=180+12=192.9.解:作为十几乘以十几的特例,以下各小题的结果请牢牢记住:10.解:①15×15 注意矩形框中=15×(10+5)式子=15×10+15×5=15×10+(10+5)×5=15×10+10×5+5×5=(15+5)×10+5×5==225②25×25=25×(20+5)=25×20+25×5=25×20+(20+5)×5=25×20+20×5+5×5=(25+5)×20+5×5 注意矩形框中= 式子=625发现规律:几十五的自乘积就是十位数字和十位数字加1的积,再在其后写上25.如15×15的积就是1×2再写上25得225.25×25的积就是2×3再写上25得625.用这个方法写出其他各题的答案如下:③35×35=3×4×100+25=1225④45×45=4×5×100+25=2025⑤55×55=5×6×100+25=3025⑥65×65=6×7×100+25=4225⑦75×75=7×8×100+25=5625⑧85×85=8×9×100+25=7225⑨95×95=9×10×100+25=9025要牢记以上方法和结果.要知道,孤立的一道题不好记,但有规律的一整套的东西反而容易记住!11.解:有的同学问:“n是几?”老师告诉你:“n就是末项,你说是几就是几”.用头尾相加法求,自然数列的前n项之和.12.解:请注意规律性的东西.①1+2+3+…+10=(1+10)×10÷2=55②1+2+3+…+100=(1+100)×100÷2=5050③1+2+3+…+1000=(1+1000)×1000÷2=500500④1+2+3+…+10000=(1+10000)×10000÷2=50005000.13.解:方法1:仔细观察不难发现把每列(或每行)的10个数相加之和按顺序排列起来构成一个等差数列,它就是:55,65,75,85,95,105,115,125,135,145∴总和=(55+145)×10÷2=1000.方法2:首先各行都按第一行计数,得10行10列数字方阵的所有数之和为55×10=550.但第二行比第一行多10,第三行比第一行多20,…,第十行比第一行多90.总计共多:10+20+30+40+50+60+70+80+90=450.所以原题数字方阵的所有数相加之和为:550+450=1000.方法3:仔细观察可发现,若以数字10所在的对角线为分界线,将该数字方阵折叠之后,它就变成下述的三角形阵(多么巧妙!)20 20 20 20 20 20 20 20 20 1020 20 20 20 20 20 20 20 1020 20 20 20 20 20 20 1020 20 20 20 20 20 1020 20 20 20 20 1020 20 20 20 1020 20 20 1020 20 1020 1010总和=20×(1+2+3+4+5+6+7+8+9+10)-100=20×55-100=1000.方法4:找规律,先从简单情况开始可见原来数字方阵的所有数的和=10×10×10=1000.看!方法多么简捷;数学多么微妙!第四讲数与形相映形和数的密切关系,在古代就被人们注意到了.古希腊人发现的形数就是非常有趣的例子.例1 最初的数和最简的图相对应.这是古希腊人的观点,他们说一切几何图形都是由数产生的.例2 我国在春秋战国时代就有了“洛图”(见下图).图中也是用“圆点”表示数,而且还区分了偶数和奇数,偶数用实心点表示,奇数用空心点表示.你能把这张图用自然数写出来吗?见下图所示,这个图又叫九宫图.例3 古希腊数学家毕达哥拉斯发现了“形数”的奥秘.比如他把1,3,6,10,15,…叫做三角形数.因为用圆点按这些数可以堆垒成三角形,见下图.毕达哥拉斯还从圆点的堆垒规律,发现每一个三角形数,都可以写成从1开始的n 个自然数之和,最大的自然数就是三角形底边圆点的个数.第一个数:1=1第二个数:3=1+2第三个数:6=1+2+3第四个数:10=1+2+3+4第五个数:15=1+2+3+4+5…第n个数:1+2+3+4+5+…+n指定的三角形数.比如第100个三角形数是:例4 毕达哥拉斯还发现了四角形数,见下图.因为用圆点按四角形数可以堆垒成正方形,因此它们最受毕达哥拉斯及其弟子推崇.第一个数:1=12=1第二个数:4=22=1+3第三个数:9=32=1+3+5第四个数:16=42=1+3+5+7第五个数:25=52=1+3+5+7+9…第n个数:n2=1+3+5+9+…+(2n-1).四角形数(又叫正方形数)可以表示成自然数的平方,也可以表示成从1开始的几个连续奇数之和.奇数的个数就等于正方形的一条边上的点数.例5 类似地,还有四面体数见下图.仔细观察可发现,四面体的每一层的圆点个数都是三角形数.因此四面体数可由几个三角形数相加得到:第一个数:1第二个数:4=1+3第三个数:10=1+3+6第四个数:20=1+3+6+10第五个数:35=1+3+6+10+15.例6 五面体数,见下图.仔细观察可以发现,五面体的每一层的圆点个数都是四角形数,因此五面体数可由几个四角形数相加得到:第一个数:1=1第二个数:5=1+4第三个数:14=1+4+9第四个数:30=1+4+9+16第五个数:55=1+4+9+16+25.例7 按不同的方法对图中的点进行数数与计数,可以得出一系列等式,进而可猜想到一个重要的公式.由此可以使人体会到数与形之间的耐人导味的微妙关系.方法1:先算空心点,再算实心点:22+2×2+1.方法2:把点图看作一个整体来算32.因为点数不会因计数方法不同而变,所以得出:22+2×2+1=32.方法1:先算空心点,再算实心点:32+2×3+1.方法2:把点图看成一个整体来算:42.因为点数不会因计数方法不同而变,所以得出:32+2×3+1=42.方法1:先算空心点,再算实心点:42+2×4+1.方法2:把点图看成一个整体来算52.因为点数不会因计数方法不同而变,所以得出:42+2×4+1=52.把上面的几个等式连起来看,进一步联想下去,可以猜到一个一般的公式:22+2×2+1=3232+2×3+1=4242+2×4+1=52…n2+2×n+1=(n+1)2.利用这个公式,也可用于速算与巧算.如:92+2×9+1=(9+1)2=102=100992+2×99+1=(99+1)2=1002=10000.习题四1.第25个三角形数是几?2.第50个三角形数是几?3.第1000个三角形数是几?4.三角形数的奇偶性是很有规律的,想一想,这是为什么?5.观察下列图形,你能发现什么?6.第99个与第100个三角形数的和等于多少?7.每一个四角形数(或叫正方形数)(除1外)都能拆成两个三角形数吗?比如,100是哪两个三角形数的和?8.第8个三角形数恰是第6个四角形数,因为你还能试着找到一个这样的例子吗?(这事比较困难)9.请你试着画一画五角形数和六角形数的图形.并试着把第n个五(六)角形数拆成以1为首页、有n项的等差数列之和的形式.10.写出前10个四面体数.11.写出前10个五面体数.12.按不同的方法对下图中的点进行数数与计数,得出一系列等式,进而猜想出一个公式来,从中体会数与形之间的微妙关系.如:因为点数不会因计数方法不同而变,所以得出:请你照此继续做下去.(可参考本讲例7)13.模仿例7,用不同的方法分别对下两图中的点进行数数与计数,先得出一系列等式,进而猜想出一个重要的公式.习题四解答1.解:1+2+3+…+25=(1+25)×25÷2=325.2.解:1+2+3+…+50=(1+50)×50÷2=1275.3.解:1+2+3+…+1000=(1+1000)×1000÷2=500500.4.解:观察前几个三角形数的构成,就可以发现其中的规律:第1个数=1…奇数;第2个数=第1个数+2…奇数+偶数=奇数;第3个数=第2个数+3…奇数+奇数=偶数;第4个数=第3个数+4…偶数+偶数=偶数;第5个数=第4个数+5…偶数+奇数=奇数.5.解:相邻的两个三角形之和是一个四角形数(或叫正方形数),或是说,一个四角形数,可以拆成两个三角形数之和.或者根据第6题,=第100个四角形数=100×100=10000.7.解:能拆.100=55+45.8.解:寻找这样的例子比较困难.有人找到第49个三角形数是第35个四角形数,因为:(49+1)×49÷2=1225=352.9.解:五角形数如下图所示:第一个数:1=l第二个数:5=1+4第三个数:12=1+4+7第四个数:22=1+4+7+10第五个数:35=1+4+7+10+13 六角形数如下图所示:第一个数 1=1第二个数 6=1+5第三个数 15=1+5+9第四个数 28=1+5+9+13第五个数 45=1+5+9+13+17.第五讲一笔画问题一天,小明做完作业正在休息,收音机中播放着轻松、悦耳的音乐.他拿了支笔,信手在纸上写了“中”、“日”、“田”几个字.突然,他脑子里闪出一个念头,这几个字都能一笔写出来吗?他试着写了写,“中”和“日”可以一笔写成(没有重复的笔划),但写到“田”字,试来试去也没有成功.下面是他写的字样.(见下图)这可真有意思!由此他又联想到一些简单的图形,哪个能一笔画成,哪个不能一笔画成呢?下面是他试着画的图样.(见下图)经过反复试画,小明得到了初步结论:图中的(1)、(3)、(5)能一笔画成;(2)、(4)、(6)不能一笔画成.真奇怪!小明发现,简单的笔画少的图不一定能一笔画得出来.而复杂的笔画多的图有时反倒能够一笔画出来,这其中隐藏着什么奥秘呢?小明进一步又提出了如下问题:如果说一个图形是否能一笔画出不决定于图的复杂程度,那么这事又决定于什么呢?能不能找到一条判定法则,依据这条法则,对于一个图形,不论复杂与否,也不用试画,就能知道是不是能一笔画成?。
小学 奥数 数学课本 二年级 打印版

99+98+97+96+95=97×5=485
(2)9+99+999=10+100+1000-3
=1110-3=1107
5.解:(1)5+6+7+8&5+10+15+20+25+30+35
=20×7=140
(3)9+18+27+36+45+54
=(9+54)×3=63×3=189
第一讲速算与巧算 一、“凑整”先算
1.计算:(1)24+44+56 (2)53+36+47 解:(1)24+44+56=24+(44+56) =24+100=124 这样想:因为44+56=100是个整百的数,所以先把它们的 和算出来. (2)53+36+47=53+47+36 =(53+47)+36=100+36=136 这样想:因为53+47=100是个整百的数,所以先把+47带 着符号搬家,搬到+36前面;然后再把53+47的和算出来. 2.计算:(1)96+15 (2)52+69 解:(1)96+15=96+(4+11) =(96+4)+11=100+11=111 这样想:把15分拆成15=4+11,这是因为96+4=100,可凑 整先算. (2)52+69=(21+31)+69 =21+(31+69)=21+100=121 这样想:因为69+31=100,所以把52分拆成21与31之和, 再把31+69=100凑整先算. 3.计算:(1)63+18+19 (2)28+28+28 解:(1)63+18+19 =60+2+1+18+19 =60+(2+18)+(1+19) =60+20+20=100 这样想:将63分拆成63=60+2+1就是因为2+18和1+19可以 凑整先算. (2)28+28+28 =(28+2)+(28+2)+(28+2)-6 =30+30+30-6=90-6=84 这样想:因为28+2=30可凑整,但最后要把多加的三个2 减去. 二、改变运算顺序:在只有“+”、“-”号的混合算式中,运 算顺序可改变 计算:(1)45-18+19 (2)45+18-19 解:(1)45-18+19=45+19-18 =45+(19-18)=45+1=46 这样想:把+19带着符号搬家,搬到-18的前面.然后先算 19-18=1. (2)45+18-19=45+(18-19) =45-1=44 这样想:加18减19的结果就等于减1.
奥数讲座(1年级-上)(16讲)

一年级奥数讲座(一)目录第一讲速算与巧算(一)第二讲速算与巧算(二)第三讲数数与计数(一)第四讲数数与计数(二)第五讲数数与计数(三)第六讲数数与计数(四)第七讲填图与拆数(一)第八讲填图与拆数(二)第九讲分组与组式第十讲自然数串趣题第十一讲不等与排序第十二讲奇与偶第十三讲是与非第十四讲火柴棍游戏(一)第十五讲火柴棍游戏(二)第十六讲火柴棍游戏(三)附录一点、线、角附录二长方形、正方形、三角形和圆附录三多边形和扇形附录四立体图形的认识第一讲速算与巧算(一)一、凑十法:同学们已经知道,下面的五组成对的数相加之和都等于10:1+9=102+8=103+7=104+6=105+5=10巧用这些结果,可以使计算又快又准。
例1 计算1+2+3+4+5+6+7+8+9+10解:对于这道题,当然可以从左往右逐步相加:1+2=3 3+3=66+4=10 10+5=1515+6=21 21+7=2828+8=36 36+9=4545+10=55这种逐步相加的方法,好处是可以得到每一步的结果,但缺点是麻烦、容易出错;而且一步出错,以后步步都错。
若是利用凑十法,就能克服这种缺点。
二、凑整法同学们还知道,有些数相加之和是整十、整百的数,如:1+19=20 11+9=302+18=20 12+28=403+17=20 13+37=504+16=20 14+46=605+15=20 15+55=706+14=20 16+64=807+13=20 17+73=908+12=20 18+82=1009+11=20又如:15+85=100 14+86=10025+75=100 24+76=10035+65=100 34+66=10045+55=100 44+56=100等等巧用这些结果,可以使那些较大的数相加又快又准。
像10、20、 30、40、50、60、70、80、90、100等等这些整十、整百的数就是凑整的目标。
例2 计算1+3+5+7+9+11+13+15+17+19解:这是求1到19共10个单数之和,用凑整法做:例3 计算2+4+6+8+10+12+14+16+18+20解:这是求2到20共10个双数之和,用凑整法做:例4 计算2+13+25+44+18+37+56+75解:用凑整法:三、用已知求未知利用已经获得较简单的知识来解决面临的更复杂的难题这是人们认识事物的一般过程,凑十法、凑整法的实质就是这个道理,可见把这种认识规律用于计算方面,可使计算更快更准。
一年级下册奥数举一反三数学拓展思维(全20讲含讲义习题)

第三讲 数数和计数(一)
一年级数学奥数举一反三下册
一年级数学奥数举一反三下册
一年级数学奥数举一反三下册
一年级数学奥数举一反三下册
一年级数学奥数举一反三下册
一年级数学奥数举一反三下册
一年级数学奥数举一反三下册
一年级数学奥数举一反三下册
一年级数学奥数举一反三下册
一年级数学奥数举一反三下册
一年级数学奥数举一反三下册
一年级数学奥数举一反三下册
第二讲 速算与巧算 习题二
一年级数学奥数举一反三下册
第二讲 速算与巧算 习题二
一年级数学奥数举一反三下册
第二讲 速算与巧算 习题二
一年级数学奥数举一反三下册
第二讲 速算与巧算 习题二
一年级数学奥数举一反三下册
一年级数学奥数举一反三下册
一年级数学奥数举一反三下册
一年级数学奥数举一反三下册
一年级数学奥数举一反三下册
一年级数学奥数举一反三下册
一年级数学奥数举一反三下册
一年级数学奥数举一反三下册
一年级数学奥数举一反三下册
一年级数学奥数举一反三下册 三、用已知量求未知
一年级数学奥数举一反三下册
一年级数学奥数举一反三下册
思路分析:如图看一看,数一数可知:5个 手指间有4个“空”,空又叫做间隔,也就 是说,人的一只手有五个指头4个间隔。
一年级数学奥数举一反三下册
一年级数学奥数举一反三下册
一年级数学奥数举一反三下册
一年级数学奥数举一反三下册
练习题
1.一队男生8人,老师要求在2名男生中间插进1名女生,问可插进 多少女生?
一年级数学奥数举一反三下册
31.一年级奥数下册:第四讲 数数与计数 习题3 32.一年级奥数下册:第四讲 数数与计数 习题解答 33.一年级奥数下册:第五讲 数数与计数(三) 34.一年级奥数下册:第五讲 数数与计数(三)习题 35.一年级奥数下册:第五讲 数数与计数(三)习题解答 36.一年级奥数下册:第六讲 数数与计数(四) 37.一年级奥数下册:第六讲 数数与计数(四)习题 38.一年级奥数下册:第六讲 数数与计数(四)习题解答 39.一年级奥数下册:第七讲 填图与拆数(一) 40. 一年级奥数下册:第七讲 填图与拆数(一)习题 41. 一年级奥数下册:第七讲 填图与拆数(一)习题解答
高斯小学奥数六年级上册含答案第04讲 对应计数

3.阿呆在玩PSP格斗游戏,游戏采用的是五局三胜制(阿呆VS电脑),谁先胜三场谁就获得胜利.如果最后阿呆获胜,那么一共有多少种可能的比赛过程?(只考虑每场比赛的胜负)10
练习:
1.答案: ;
简答:用插板法即可解决,具体过程略.
2.答案:
简答:相当于把8个球放入4个篮子,每个篮子都可以为空.
3.答案:100
简答:每个田字格都可以找到4个“L”型.共有 个田字格,所以共 个“L”型.
4.答案:20
简答:6次跳远中,一定3次向左,3次向右,因此共有 种不同的跳法.
作业
1.答案:165
例3.在 的方格棋盘中,一共可以数出多少个如下图所示的由4个单位小正方形组成的“L”型?
「分析」要把“L”型放入 的方格棋盘的方格盘中,按照放的方向分,可以有8种情形,那么是不是需要对每一个方向的“L”型分别进行计数呢?
练习3、在 的方格棋盘中,一共可以数出多少个如下图所示的由3个单位小正方形组成的图形?
对应法最早的应用是结绳计数.最早期的时候,人类还没有发明数字.因而用枚举等其他方法来记录数量的多少是不可能办到的.这时,人们的计数方法是在绳子上打结或者在树上刻痕.用绳子上的结的数目或者树上划痕的道数来记录补获了多少猎物,采集了多少花果.这个时期持续了很长时间,因为人类的历史已经有几百万年,而数字的发明距今还不到1万年,在人类历史上的大部分时间,使用的计数方法是对应法——结绳计数.
详解:第一问用课文里所说的“插板法”即可解决.20个苹果,共有19个空隙,分给3个小朋友需要 块隔板,将2块隔板插入19个空隙中的某两个中,就是从19个空隙中挑出两个用来插板子,方法有 ;第二问同样用插板法,仍然是20个苹果和2块隔板.但此时隔板不一定要放在19个空隙中,也可以放在所有苹果的最左端或者最右端,而且它们也不一定插入两个不同的空隙,插入同一个空隙也是可以的.因此,我们只要把20个苹果和2块隔板随意排成一行即可.这 个对象排成一行会占22个位置,从这22个位置中挑出2个来放隔板,剩余的20个位置自然就是放苹果,因此共有 种不同的方法.
人大附中分班考试班部分答案

人大附中分班考试班第四讲部分答案第四讲计数问题一. 加法原理与乘法原理例1.满足下面性质的数称为好数,它的个位比十位大,十位比百位大,百位比千位大,并且相邻两位数字差不超过2.例如1346为好数,3579为好数,但1456就不是好数.那么有四位好数.答案:36 .例2.用3种颜色把一个3´3的方格表染色,要求相同行和相同列的3个格所染的颜色互不相同,一共有________种不同的染色法例3.□□□+□□=□□+□□,把数字1~9填入上面的方框中,使等式成立.每个数字只能填1次,一共有多少种不同的填法?例4.如图,把A、B、C、D、E这5个部分用4种不同的颜色着色,且相邻的部分不能使用同一种颜色,不相邻的部分可以使用同一种颜色。
那么,这幅图共有多少种不同的着色方法?解析:4×3×2×2×2=96。
例5.有一种四位数,它与它的逆序四位数和为9999.例如7812+2187=9999,3636+6363=9999等.那么这样的四位数一共有多少个?二. 排列组合例6.3个男生,3个女生排成一排,要求男生不能相邻,求一共有多少种排法?如果女生也不能相邻,求一共有多少种排法?解析:72。
只可能是“男女男女男女”和“女男女男女男”。
例7.从10个人中挑出5人,求满足下列条件的选法有多少种。
(1)A,B必须入选;(2)A,B 至少有一个人入选;(3)A,B,C中恰好有一个人入选;(4)A,B,C不能同时入选。
例8.用数字1,2组成一个8位数,其中至少有连续4位都是数字1的有多少个?例9.从1、2、3、…、9中选取若干互不相同的数字(至少一个),使得其和是3的倍数,共有多少种选法?解析:按取出数的个数分类,总共有175种取法。
例10.老师要将20个相同的苹果分给3个小朋友,要求每个小朋友至少分得3个苹果,那么共有_____种分配方法.三. 计数综合例11.各位数字之和为33,而且能够被33整除的五位数有多少个?解析:288个。
一年级奥数教材

一年级奥数教材Pleasure Group Office【T985AB-B866SYT-B182C-BS682T-STT18】一年级奥数本教材形象而且易懂,方便家长和老师下载和理解,希望为了孩子多多下载,给孩子多多讲解。
一年级奥数教材目录1.小学一年级奥数:速算与巧算2.一年级奥数题:找规律巧填空3. 一年级奥数题:如何巧分苹果4.一年级单数与双数例题讲解(一)5.一年级单数与双数例题讲解(二)6.一年级重叠问题例题讲解(一)7.一年级重叠问题例题讲解(二)8.一年级重叠问题例题讲解(三)9.一年级重叠问题例题讲解(四)10.一年级认识图形例题讲解(一)11.一年级认识图形例题讲解(二)12.一年级认识图形例题讲解(三)13.一年级数学应用题1 13.一年级数学应用题114.一年级数学应用题2 15.一年级数学应用题316.一年级数学应用题4 17.一年级数学应用题518.一年级数学应用题6 19.一年级数学应用题720.一年级数学应用题8 21.一年级数学应用题922.一年级数学应用题1023.一年级奥数下册:第一讲速算与巧算(一)24.一年级奥数下册:第一讲速算与巧算习题一25.一年级奥数下册:第一讲速算与巧算习题解答26.一年级奥数下册:第二讲速算与巧算(二)27.一年级奥数下册:第二讲速算与巧算习题二28.一年级奥数下册:第二讲速算与巧算习题二解答29.一年级奥数下册:第三讲数数与计数(一)30.一年级奥数下册:第三讲数数与计数习题31.一年级奥数下册:第三讲数数与计数习题解答32.一年级奥数下册:第四讲数数与计数(二)33.一年级奥数下册:第四讲数数与计数习题34.一年级奥数下册:第四讲数数与计数习题解答35.一年级奥数下册:第五讲数数与计数(三)36.一年级奥数下册:第五讲数数与计数(三)习题37.一年级奥数下册:第五讲数数与计数(三)习题解答38.一年级奥数下册:第六讲数数与计数(四)39.一年级奥数下册:第六讲数数与计数(四)习题40.一年级奥数下册:第六讲数数与计数(四)习题解答41.一年级奥数下册:第七讲填图与拆数(一)42.一年级奥数下册:第七讲填图与拆数(一)习题43.一年级奥数下册:第七讲填图与拆数(一)习题解答44.一年级奥数下册:第八讲填图与拆数(二)45.一年级奥数下册:第八讲填图与拆数(二)习题46.一年级奥数下册:第八讲填图与拆数(二)习题解答47.一年级奥数下册:第九讲分组与组式48.一年级奥数下册:第九讲分组与组式习题49.一年级奥数下册:第九讲分组与组式习题解答50.一年级奥数下册:第十讲自然数串趣题51.一年级奥数下册:第十讲自然数串趣题习题52.一年级奥数下册:第十讲自然数串趣题习题解答53.一年级奥数下册:第十一讲不等与排序54.一年级奥数下册:第十一讲不等与排序习题55.一年级奥数下册:第十一讲不等与排序习题解答56.一年级奥数下册:第十二讲奇与偶57.一年级奥数下册:第十二讲奇与偶习题58.一年级奥数下册:第十二讲奇与偶习题解答59.一年级奥数下册:第十三讲是与非60.一年级奥数下册:第十三讲是与非习题61.一年级奥数下册:第十三讲是与非习题解答62.一年级奥数下册:第十四讲火柴棍游戏(一)63.一年级奥数下册:第十四讲火柴棍游戏(一)习题64.一年级奥数下册:第十四讲火柴棍游戏(一)习题解答65.一年级奥数下册:第十五讲火柴棍游戏(二)66.一年级奥数下册:第十五讲火柴棍游戏(二)习题67.一年级奥数下册:第十五讲火柴棍游戏(二)习题解答68.一年级奥数下册:第十六讲火柴棍游戏(三)69.一年级奥数下册:第十六讲火柴棍游戏(三)习题70.一年级奥数下册:第十六讲火柴棍游戏(三)习题解答1.小学一年级奥数:速算与巧算计算:21+22+23+24+25+26+27+28+29的和等于多少解答:21+22+23+24+25+26+27+28+29=21+29+22+28+23+27+24+26+25=50+50+50+50+25=225【小结】对于这类题目要注意观察数字的规律和符号的规律。
小学二年级奥数第三讲 数数与计数(二)练习+答案

第三讲数数与计数(二)例1 数一数,图3-1中共有多少点?解:(1)方法1:如图3-2所示从上往下一层一层数:第一层 1个第二层 2个第三层 3个第四层 4个第五层 5个第六层 6个第七层 7个第八层 8个第九层 9个第十一层 9个第十二层 8个第十三层 7个第十四层 6个第十五层 5个第十六层 4个第十七层 3个第十八层 2个第十九层 1个总数1+2+3+4+5+6+7+8+9+10+9+8+7+6+5+4+3+2+1=(1+2+3+4+5+6+7+8+9+10)+(9+8+7+6+5+4+3+2+1)=55+45=100(利用已学过的知识计算).(2)方法2:如图3-3所示:从上往下,沿折线数第一层 1个第二层 3个第三层 5个第五层 9个第六层 11个第七层 13个第八层 15个第九层 17个第十层 19个总数:1+3+5+7+9+11+13+15+17+19=100(利用已学过的知识计算).(3)方法3:把点群的整体转个角度,成为如图3-4所示的样子,变成为10行10列的点阵.显然点的总数为10×10=100(个).想一想:①数数与计数,有时有不同的方法,需要多动脑筋.②由方法1和方法3得出下式:1+2+3+4+5+6+7+8+9+10+9+8+7+6+5+4+3+2+1=10×10即等号左边这样的一串数之和等于中间数的自乘积.由此我们猜想:1=1×11+2+1=2×21+2+3+2+1=3×31+2+3+4+3+2+1=4×41+2+3+4+5+4+3+2+1=5×51+2+3+4+5+6+5+4+3+2+1=6×61+2+3+4+5+6+7+6+5+4+3+2+1=7×71+2+3+4+5+6+7+8+7+6+5+4+3+2+1=8×81+2+3+4+5+6+7+8+9+8+7+6+5+4+3+2+1=9×91+2+3+4+5+6+7+8+9+10+9+8+7+6+5+4+3+2+1=10×10这样的等式还可以一直写下去,能写出很多很多.同学们可以自己检验一下,看是否正确,如果正确我们就发现了一条规律.③由方法2和方法3也可以得出下式:1+3+5+7+9+11+13+15+17+19=10×10.即从1开始的连续奇数的和等于奇数个数的自乘积.由此我们猜想:1+3=2×21+3+5=3×31+3+5+7=4×41+3+5+7+9=5×51+3+5+7+9+11=6×61+3+5+7+9+11+13=7×71+3+5+7+9+11+13+15=8×81+3+5+7+9+11+13+15+17=9×91+3+5+7+9+11+13+15+17+19=10×10还可往下一直写下去,同学们自己检验一下,看是否正确,如果正确,我们就又发现了一条规律.例2 数一数,图3-5中有多少条线段?解:(1)我们已知,两点间的直线部分是一条线段.以A点为共同端点的线段有:AB AC AD AE AF 5条.以B点为共同左端点的线段有:BC BD BE BF 4条.以C点为共同左端点的线段有:CD CE CF 3条.以D点为共同左端点的线段有:DE DF 2条.以E点为共同左端点的线段有:EF1条.总数5+4+3+2+1=15条.(2)用图示法更为直观明了.见图3-6.总数5+4+3+2+1=15(条).想一想:①由例2可知,一条大线段上有六个点,就有:总数=5+4+3+2+1条线段.由此猜想如下规律(见图3-7):还可以一直做下去.总之,线段总条线是从1开始的一串连续自然数之和,其中最大的自然数比总数小1.我们又发现了一条规律.它说明了点数与线段总数之间的关系.②上面的事实也可以这样说:如果把相邻两点间的线段叫做基本线段,那么一条大线段上的基本线段数和线段总条数之间的关系是:线段总条数是从1开始的一串连续自然数之和,其中最大的自然数等于基本线段的条数(见图3-8).基本线段数线段总条数还可以一直写下去,同学们可以自己试试看.例3 数一数,图3-9中共有多少个锐角?解:(1)我们知道,图中任意两条从O点发出的射线都组成一个锐角.所以,以OA边为公共边的锐角有:∠LAOB,∠AOC,∠AOD,∠AOE,∠AOF共5个.以OB边为公共边的锐角有:∠BOC,∠BOD,∠BOE,∠BOF共4个.以OC边为公共边的锐角有:∠COD,∠COE,∠COF共3个.以OD边为公共边的锐角有:∠DOE,∠DOF共2个.以OE边为一边的锐角有:∠EOF只1个.锐角总数5+4+3+2+1=15(个).②用图示法更为直观明了:如图3-10所示,锐角总数为:5+4+3+2+1=15(个).想一想:①由例3可知:由一点发出的六条射线,组成的锐角的总数=5+4+3+2+1(个),由此猜想出如下规律:(见图3-11~15)两条射线1个角(见图3-11)三条射线2+1个角(见图3-12)四条射线3+2+1个角(见图3-13)五条射线4+3+2+1个角(见图3-14)六条射线5+4+3+2+1个角(见图3-15)总之,角的总数是从1开始的一串连续自然数之和,其中最大的自然数比射线数小1.②同样,也可以这样想:如果把相邻两条射线构成的角叫做基本角,那么有共同顶点的基本角和角的总数之间的关系是:角的总数是从1开始的一串连续自然数之和,其中最大的自然数等于基本角个数.③注意,例2和例3的情况极其相似.虽然例2是关于线段的,例3是关于角的,但求总数时,它们有同样的数学表达式.同学们可以看出,一个数学式子可以表达表面上完全不同的事物中的数量关系,这就是数学的魔力.习题1.书库里把书如图3-16所示的那样沿墙堆放起来.请你数一数这些书共有多少本?2.图3-17所示是一个跳棋盘,请你数一数,这个跳棋盘上共有多少个棋孔?3.数一数,图3-18中有多少条线段?4.数一数,图3-19中有多少锐角?5.数一数,图3-20中有多少个三角形?6.数一数,图3-21中有多少正方形?习题解答1.解:方法1:从左往右一摞一摞地数,再相加求和:10+11+12+13+14+15+14+13+12+11+10=135(本).方法2:把这摞书形成的图形看成是由一个长方形和一个三角形“尖顶”组成.长方形中的书 10×11=110三角形中的书 1+2+3+4+5+4+3+2+1=25总数:110+25=135(本).2.解:因为棋孔较多,应找出排列规律,以便于计数.仔细观察可知,图中大三角形ABC上的棋孔的排列规律是(从上往下数):1,2,3,4,5,6,7,8,9,10,11,12,13,另外还有三个小三角形中的棋孔的排列规律是1,2,3,4,所以棋孔总数是:(1+2+3+4+5+6+7+8+9+10+11+12+13)+(1+2+3+4)×3=91+10×3=121(个).3.解:方法1:按图3-22所示方法数(图中只画出了一部分)线段总数:7+6+5+4+3+2+1=28(条).方法2:基本线段共7条,所以线段总数是:7+6+5+4+3+2+1=28(条).4.解:按图3-23的方法数:角的总数:7+6+5+4+3+2+1=28(个).5.解:方法1:(1)三角形是由三条边构成的图形.以OA边为左公共边构成的三角形有:△OAB,△OAC,△OAD,△OAE,△OAF,△OAG,△OAH,共7个;以OB边为左公共边构成的三角形有:△OBC,△OBD,△OBE,△OBF,△OBG,△OBH,共6个;以OC边为左公共边构成的三角形有:△OCD,△OCE,△OCF,△OCG,△OCH,共5个;以OD边为左公共边构成的三角形有:△ODE,△ODF,△ODG,△ODH,共4个;以OE边为左公共边构成的三角形有:△OEF,△OEG,△OEH,共3个;以OF边为左公共边构成的三角形有:△OFG,△OFH,共2个;以OG边和OH,GH两边构成的三角形仅有:△OGH1个;三角形总数:7+6+5+4+3+2+1=28(个).(2)方法2:显然底边AH上的每一条线段对应着一个三角形,而基本线段是7条,所以三角形总数为:7+6+5+4+3+2+1=28(个).6.解:最小的正方形有25个,由4个小正方形组成的正方形 16个;由9个小正方形组成的正方形 9个;由16个小正方形组成的正方形 4个;由25个小正方形组成的正方形 1个;正方形总数:25+16+9+4+1=55个.。
华罗庚学校数学课本∶二年级

华罗庚学校数学课本:二年级上册第一讲速算与巧算习题一习题一解答第二讲数数与计数(一)习题二习题二解答第三讲数数与计数(二)习题三习题三解答第四讲认识简单数列习题四习题四解答第五讲自然数列趣题习题五习题五解答第六讲找规律(一)习题六习题六解答第七讲找规律(二)习题七习题七解答第八讲找规律(三)习题八习题八解答第九讲填图与拆数习题九习题九解答第十讲考虑所有可能情况(一)习题十习题十解答第十一讲考虑所有可能情况(二)习题十一习题十一解答第十二讲仔细审题习题十二习题十二解答第十三讲猜猜凑凑习题十三习题十三解答第十四讲列表尝试法习题十四习题十四解答第十五讲画图凑数法习题十五习题十五解答下册第一讲机智与顿悟习题一习题一解答第二讲数数与计数习题二习题二解答第三讲速算与巧算习题三习题三解答第四讲数与形相映习题四习题四解答第五讲一笔画问题习题五习题五解答第六讲七座桥问题习题六习题六解答第七讲数字游戏问题(一)习题七习题七解答第八讲数字游戏问题(二)习题八习题八解答第九讲整数的分拆习题九习题九题答第十讲枚举法习题十习题十解答第十一讲找规律法习题十一习题十一解答第十二讲逆序推理法习题十二习题十二解答第十三讲画图显示法习题十三习题十三解答第十四讲等量代换法习题十四习题十四解答第十五讲等式加减法习题十五习题十五解答附录第一讲重量的认识习题一习题一解答第二讲长度的认识习题二习题二解答第三讲时间的认识(上)习题三习题三解答第四讲时间的认识(下)习题四习题四解答。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四讲数数与计数(二)
数数与计数时,注意不应漏掉,不应重复。
如果漏掉了,要加上;如果重复了,要减掉。
例1 小朋友排队,小红前面4个人,后面3个人,问这队共有几个人?
解:
这队的总人数要数上小红,所以是4+3+1=8(人)。
例2 排好队,来报数,
正着报数我报七,
倒着报数我报九,
一共多少小朋友?
解:见下图
正着报数“我”报了一次,倒着报数“我”又报了一次,所以把两次报数加起来时,“我”被加了两次。
因此算这队的总人数时,应从两次报数之和减1。
7+9-1=15(人)。
也可以这样想:正着报数报到我为止,倒着报数时,我就不报了,只报到我的后面相邻的那个人他应该报8,所以全队总人数是:
7+(9-1)=15(人)。
例3少先队员排成队去参观科技馆。
从排头数起刘平是第20个;从排尾数起,张英是第23个。
已知刘平的前一个是张英。
问这队少先队员共有多少人?
解:画示意图,用点代表少先队员。
由图可见,从排头数起时,把张英和刘平数了一次。
由排尾数起时,又把刘平和张英数了一次,可见把他两人多数了一次,所以点总人数时,应减去多数的那一次才对。
20+23-2=41(人)。
例4 45个小朋友排成一队去春游。
从排头往后数,小刚是第19个;从排尾往前数,小莉是第12个,问小刚和小莉中间有几个人?
解:画示意图。
用点“·”代表人
由图可见,小刚和小莉中间的人数是:
45-(19+12)=14(人)。
例5一班同学做花,做红花的有38人,做黄花的有39人,没有做花的有3人。
如果全班55人,那么既做红花又做黄花的有多少人?
解:画图如下:
由图可见,做花的人:55-3=52(人)。
图中阴影部分表示两色花都做的人:
38+39-52=25(人)。
习题四
1.学生排成一队,在小进的前面有6人,后面有8人,问这队共有多少人?
2.12辆汽车组成一列车队向前行进。
从前面数起,红色的小轿车是第7辆。
问从后面数它是第几辆?
3.游泳池里男生都戴蓝帽,女生都戴红帽。
池中一个男生小强边看边数,他看见蓝帽4个,红帽5个。
问池中男女生共多少人?
4.说稀奇、道稀奇,鸭子队里有只鸡。
正着数它第六,倒着数它第七。
请你帮助算一算,小鸭一共有几只?
5.一个小组的小学生共有5人,已知他们都做了语文作业或数学作业。
又知做完语文作业的有3人,做完数学作业的有4人。
问语文和数学作业都做完的有几人?
6.在100名学生中统计,有65人会骑自行车,有73人会游泳,有10人既不会骑自行车又不会游泳。
问既会骑自行车又会游泳的人有多少?
7.某班有学生45人,订阅《中国少年报》的有29人,订阅《小朋友》的有28人,其中两种都订阅的有16人,问两种刊物都没有订阅的人有多少?
习题四解答
1.解
由图可知:总人数是
6+8+1=15人。
2.解:方法1:数一数;先画示意图如下,用●代表红色小轿车,用○代表其他车。
从后面往前数一数,红色小轿车是第6辆。
方法2:算一算;这队车共有12辆,从前面往后数,红色小轿车是第7辆,所以红色小轿车前面有7-1=6辆车,因此从后面往前数,红色小轿车是第12-6=6辆。
3.解:画示意图如下:
因为男生小强边看边数时,没有看见自己的蓝帽,他把自己漏数了。
所以算总人数时,要把他加上,即
4+5+1=10(人)。
4.解:画示意图,用○代表小鸭,用●代表小鸡。
由图可见,正数算上了小鸡,倒数也算上了小鸡。
这样两数之和
6+7=13中,把小鸡计算了两次。
所以求小鸭的数目时就要减去两个小鸡。
6+7-2=11(只)。
5.解:画示意图如下:
两种作业都做完的人既算在了做完语文作业的3人中,又算在了做完数学作业的4人中,因此这部分人被多算了一次,(如图中阴影部分所示)所以两种作业都做完的人数是:
3+4-5=2(人)。
6.解:画图如下:
由图可知:会骑车或是会游泳的总人数是
100-10=90(人)。
两种都会的人数是65+73-90=48(人)。
(图中阴影部分所示)
7.解:画示意图如下:
因为至少订1份刊物的人:
28+29-16=41(人)。
两种刊物都没有订的人:
45-41=4(人)。
