和倍应用题的数量关系
小学数学应用题类型讲解——和倍问题

和倍问题含义:已知两个数的和,以及它们的倍数关系,求这两个数各是多少,这样的问题叫做和倍问题。
数量关系:和÷(倍数+1)=较小数较小数×倍数=较大数和-较小数=较大数和倍问题类型一:基本型【例1】工厂有职工480人,其中男职工人数是女职工人数的3倍,工厂的男、女职工各有多少人?解题思路1:已知男、女职工的人数和是480,两者的倍数关系是3。
由公式直接求解。
列式:女职工480÷(3+1)=120(人)男职工120×3=360(人)或 480-120=360(人)答:女职工有120人,男职工有360人。
解题思路2:画线段图分析由图可知,将女职工的人数看作1份,男职工的人数是女职工的3倍,男职工的人数就是3份,总共是4份,总人数是480人,先求出1份的人数,再求出几份的人数。
列式:女职工480÷(3+1)=120(人)男职工120×3=360(人)或 480-120=360(人)答:女职工有120人,男职工有360人。
【例2】在一道除法算式中,已知被除数和除数的和为360,商是5,被除数和除数各是多少?解题思路1:在除法算式中,被除数÷除数=商,此题中商是5,说明被除数是除数的5倍,已知被除数和除数的和是360,由公式直接求解。
列式:除数 360÷(5+1)=60被除数 60×5=300 或 360-60=300答:被除数是300,除数是60。
解题思路2:画线段图分析由图可知,被除数是除数的5倍,除数和被除数的和为360,直接用公式求解。
列式:除数 360÷(5+1)=60被除数 60×5=300 或 360-60=300答:被除数是300,除数是60。
总结:基本的和倍问题是题目中直接给出两个数的和与倍数关系,那么我们可以直接利用数量关系式求出这两个数各是多少,同时也可以利用画线段图的方式去理解分析。
小学五年级奥数第一讲和倍问题

第一讲:和倍问题【知识点】已知两个数的和与它们之间的倍数关系,求这两个数各是多少的应用题,叫做和倍应用题。
基本数量关系:和÷倍数和=较小数【例1】学校有科技书和故事书共480本,科技书是故事书的3倍,两种书各有多少本?【思路导航】把故事书的本数看作1份,那么科技书的本数就是这样的3份,两种书的本数就是1+3=4份。
把480本书平均分成4份,1份就是故事书的本数,3份就是科技书的本数。
【练习1】用锡和铝制成的合金是720千克,其中铝的质量是锡的5倍,铝和锡各用了多少千克?【练习2】一块长方形黑板的周长是96分米,长是宽的3倍,这块长方形黑板的长和宽各是多少分米?【例2】果园里有梨树、桃树和苹果树共1200棵,其中梨树的棵树是苹果树的3倍,桃树的棵树是苹果树的4倍。
求梨树、桃树和苹果树各有多少棵?【思路导航】如果把苹果树的棵树看作1份,三种树的总棵树是1+3+4=8份。
所以,苹果树有1200÷8=150(棵),梨树有150×3=450(棵),桃树有150×4=600(棵)【练习1】专业户李大伯养鸭、鸡、鹅共960只,养鸡的只数是鹅的3倍,养鸭的只数是鹅的4倍。
鸡、鸭、鹅各养了多少只?【练习2】商店有铅笔、钢笔、圆珠笔共560支,圆珠笔的支数是钢笔的3倍,铅笔的支数和圆珠笔的支数同样多。
铅笔、钢笔、圆珠笔各有多少支?【例3】少先队员种柳树和杨树共216棵,杨树的棵树比柳树的棵树的3倍多20棵,两种树各种了多少棵?【思路导航】如果杨树少种20棵,那么杨树和柳树的总棵树是216-20=196棵,这时杨树的棵树恰好是柳树的3倍,柳树的棵树是196÷(3+1)=49棵,杨树的棵树是216-49=167(棵)。
【练习1】小华和小明两人参加数学竞赛,两人共得168分,小华的得分比小明的2倍少42分,两人各得了多少分?【练习2】学校购买了720本图书分给高、中、低三个年级段,高年级段分得的比低年级段的3倍多8本,中年级段分得的比低年级段的2倍多4本。
第13讲:和差倍问题

第13讲:和差倍问题知识梳理:1、已知两个数的和与它们之间的倍数关系,求这两个数是多少的应用题,叫做和倍问题。
解答和倍应用题的基本数量关系是:和÷(倍数+1)=小数2、解答差倍问题时,先要求出与两个数的差对应的倍数差。
解答差倍应用题的基本数量关系是:差÷(倍数-1)=小数3、已知两个数的和与差,求出这两个数各是多少的应用题,叫和差应用题。
解答和差应用题的基本数量关系是:(和-差)÷2=小数或:(和+差)÷2=大数典型例题:题型一:和倍问题例1:学校有科技书和故事书共480本,科技书的本数是故事书的3倍。
两种书各有多少本?练习:用锡和铝制成的合金是720千克,其中铝的重量是锡的5倍。
铝和锡各用了多少千克?例2:果园里有梨树、桃树和苹果树共1200棵,其中梨树的棵数是苹果树的3倍,桃树的棵数是苹果树的4倍。
求梨树、桃树和苹果树各有多少棵?练习:李大伯养鸡、鸭、鹅共960只,养鸡的只数是鹅的3倍,养鸭的只数是鹅的4倍。
鸡、鸭、鹅各养了多少只?例3:有三个书橱共放了330本书,第二个书橱里的书是第一个的2倍,第三个书橱里的书是第二个的4倍。
每个书橱里各放了多少本书?练习:甲、乙、丙三个数之和是400,已知甲是乙的3倍,丙是甲的4倍。
求甲、乙、丙各是多少。
例4:少先队员种柳树和杨树共216棵,杨树的棵数比柳树的3倍多20棵,两种树各种了多少棵?练习:粮站有大米和面粉共6300千克,大米的重量比面粉的4倍还多300千克,大米和面粉各有多少千克?例5:三个筑路队共筑路1360米,甲队筑的米数是乙队的2倍,乙队比丙队多240米。
三个队各筑多少米?练习:三个植树队共植树1900棵,甲队植树的棵数是乙队的2倍,乙队比丙队少植300棵。
三个队各植树多少棵?题型二:差倍问题例6:光明小学开展冬季体育比赛,参加跳绳比赛的人数是踺子人数的3倍,比踢踺子的多36人。
参加跳绳和踢踺子比赛的各有多少人?练习:城南小学三年级的人数是一年级人数的2倍,三年级的人数比一年级多130人。
和倍问题差倍问题和差问题

和倍问题学法指导已知两个数的和及它们之间的倍数关系,求这两个数各是多少的应用题叫做和倍应用题,简称和倍问题。
首先我们要并清几个问题:两个数相比,以被比的数为标准,这个被比的数称为一倍数,比的数里有几个这样的一倍数,就是几倍数,我们就说一个数是另一个数的几倍。
它们之间的数量关系式是: 一倍数×倍数=几倍数t几倍数÷一倍数=倍数几倍数÷倍数=一倍数在解决和倍问题时,先要确定一个数为标准(通常以较小的数为标准),即一倍数,再根据较大的数与较小的数之间的倍数关系,确定总和相当于一倍数(较小的数)的多少倍,然后求出一倍数(较小的数),再算出其他各数量。
和倍问题的数量关系式是:和÷(倍数+1)=一倍数即较小的数和一较小的数=较大的数,或较小的数×倍数=较大的数甲、乙两车间共有工人664人,甲车间的人数是乙的3倍,甲、乙两车间各有工人多少人?【分析与解答】我们可以用线段图表示题中的已知条件与问题:乙车间:甲车间:从上图看出,甲车间的人数是乙的3倍,那么把乙车间的人数看作1份,甲就有这样的3份,总人数664人占了1+3 =4份,把664人平均分成4份,l份就是乙车间的人数,3份就是甲车间的人数。
664÷(1+3) =166(人)166 x3 =498(人)或664 —166= 498(人)答:甲车间有工人498人,乙车间有166人.试一试1华强和建军共有图书84本,华强的图书本数是建军的3倍。
华强和建军各有图书多少本?果园里有梨树、苹果树、桃树共207棵,其中梨树的棵数是苹果树的3倍,苹果树的棵数是桃树的2倍。
三种果树各多少棵?【分析与解答】我们把桃树的棵数看作1份,苹果树的棵数就是这样的2份,梨树的棵数就是桃树的2 x3 =6倍,三种果树的总棵数就是桃树的6 +2 +1 =9倍。
可以先求出桃树有207÷9=23(棵),苹果树有23×2 =46(棵),梨树就是46 x3 =138(棵)。
和倍问题的基本数量关系

和倍问题的基本数量关系:(小数)1倍数=和÷(倍数+1)。
大数=和-小数,或大数=小数×倍数。
1、甲、乙两仓库共存粮264吨,甲仓库存粮是乙仓库存粮的10倍。
甲、乙两仓库各存粮多少吨?2、图书馆有故事书和科技书共1080本,故事书是科技书的3倍,故事书和科技书各有多少本?3、王叔叔的果园今年收苹果核桔子共3510千克,其中苹果是桔子的2倍,苹果和桔子各重多少千克?差倍问题的基本数量关系式是:两数差÷(倍数-1)=1倍数(小数)1倍数×倍数=几倍数(大数)小红买的兰花比月季多12朵,已知兰花的朵数是月季的3倍。
小红买了兰花和月季各多少朵?甲队有45人,乙队有75人。
甲队要调入乙队多少人,乙队人数才是甲队人数的3倍?妹妹有书24本,哥哥有书53本。
要使哥哥的书是妹妹的书的6倍,妹妹应给哥哥多少本书?差倍问题的基本数量关系式是:两数差÷(倍数-1)=1倍数(小数)1倍数×倍数=几倍数(大数)1、甲存款数是乙的4倍,甲比乙多存600元。
甲、乙两人各存款多少元?2、饲养场里养的白兔比灰兔多32只,已知白兔的只数是灰兔的5倍。
白兔、灰兔各养了多少只?3、舞蹈队里女生人数是男生人数的3倍。
女生比男生多18人,舞蹈队有男生和女生各多少人?4、小丽有科技书比故事书少16本,故事书的本数是科技书的3倍,小丽有科技书、故事书各多少本?5、一台彩电的价钱是一台冰箱的3倍,买一台彩电比一台冰箱多用2800元,一台彩电和一台冰箱各多少元?6、果园里苹果树的棵数是梨树的3倍,其中苹果树比梨树多262棵,苹果树和梨树各有多少棵?甲、乙两个粮仓各存粮若干吨,甲仓存粮的吨数是乙的3倍。
如果甲仓中取出260吨,乙仓中取出60吨,则甲、乙两个粮仓存粮的吨数相等。
甲、乙两个粮仓各存粮多少吨?1、小明的存款数是小刚的3倍,现在小明取出8500元,小刚取出500元,两人的存款数变得同样多。
五年级奥数十类问题的举一反三剖析

倍数问题专题简析:解决倍数问题的关键是,必须确定一个数作为标准数,并根据题中的已知条件,找出其它几个数与这个标准数的倍数关系,再用除法求出这个标准数。
由于倍数应用题中数量关系的变化,要求同学们在解题过程中注意解题技巧,灵活解题。
和倍问题的数量关系是:和数÷(倍数+1)=较小数较小数×倍数=较大数差倍问题的数量关系是:差数÷(倍数-1)=较小数较小数×倍数=较大数例1,养鸡场的母鸡只数是公鸡的6倍,后来公鸡和母鸡各增加60只,结果母鸡只数就是公鸡的4倍。
原来养鸡场一共养了多少只鸡?分析养鸡场原来母鸡的只数是公鸡的6倍,如果公鸡增加60只,母鸡增加60×6=360只,那么,后来的母鸡只数还是公鸡的6倍。
可实际母鸡只增加了60只,比360只少300只。
因此,现在母鸡只数只有公鸡的4倍,少了2倍。
所以,现在公鸡的只数是300÷2=150只,原来有公鸡150-60=90只,一共养了90×(1+6)=630只鸡。
练习一1,今年,爸爸的年龄是小明的6倍,再过4年,爸爸的年龄就是小明的4倍。
今年小明多少岁?2,原来食堂里存的大米是面粉的4倍,大米和面粉各吃掉80千克,大米的重量是面粉的2倍。
食堂里原来存有大米、面粉各多少千克?3,饲养场的白兔只数是黑兔的5倍,后来卖掉了10只黑兔,买回来20只白兔,现在白兔的只数是黑兔的7倍。
饲养场原来养白兔和黑兔各多少只?组合图形面积1专题简析:组合图形是由两个或两个以上的简单的几何图形组合而成的。
组合的形式分为两种:一是拼合组合,二是重叠组合。
由于组合图形具有条件相等的特点,往往使得问题的解决无从下手。
要正确解答组合图形的面积,应该注意以下几点:1,切实掌握有关简单图形的概念、公式,牢固建立空间观念;2,仔细观察,认真思考,看清所求图形是由哪几个基本图形组合而成的;3,适当采用增加辅助线等方法帮助解题;4,采用割、补、分解、代换等方法,可将复杂问题变得简单。
(完整)六年级奥数_和倍、差倍、和差问题

第二十三讲和倍问题【知识概述】:已知两个数的和与它们之间的倍数关系,求这两个数各是多少的应用题,叫做和倍应用题。
要想顺利解决和倍应用题,最好的方法就是根据题意,画出线段图,使数量关系一目了然,从而正确的列式计算。
解答和倍应用题的关键是找出两数的和以及与其对应的倍数和。
解答和倍应用题的基本数量关系是:和÷(倍数+1)=小数;小数×倍数=大数(几倍数)或者:两数和-小数=大数如果遇到三个或三个以上的数的倍数关系,也可用这个公式。
(首先找最小的一个数,再找出另几个数是最小数的倍数即可)【经典例题】:例1.幼儿园的老师和小朋友共有81人在做游戏,小朋友们总是跟着自己的老师转,每位老师身边都有8个小朋友,问:小朋友有多少个?老师有多少人?练习1:1、学校有科技书和故事书共480本科技书的本数是故事书的3倍,两种书各多少本?2、一个养鸡场有675只鸡,其中母鸡是公鸡的4倍,这个养鸡场有公鸡、母鸡各多少只?3、学校将360本图书分给二、三年级,已知三年级所得的本书比二年级的2倍还多60本,二、三年级各得图书多少本?4、爸爸要把140张邮票分给弟弟和妹妹,已知弟弟分得的邮票张数比妹妹的4倍少10张,弟弟和妹妹各分得邮票多少张?例2、甲、乙、丙3数和是183,乙比丙的2倍少4,甲比丙的3倍多7,求甲、乙、丙三数各是多少?解析:乙数加上4就是丙数的2倍,甲数减少7就是丙数的3倍。
而总数也就应该加上4,再减去7。
丙数1倍数,乙是2倍数。
甲是3倍数,先求丙。
丙数=(183+4-7)÷(1+2+3)=30,乙数=30×2-4=56,甲数=30×3+7=97。
练习2、1、三堆糖果共有105颗,其中第一堆糖果的数量是第二堆的3倍,而第三堆糖果的数量又比第二堆的2倍少3颗.第三堆糖果有多少颗?2. 甲、乙、丙三个粮仓一共存有109吨粮食.其中甲粮仓的粮食总量比乙粮仓的3倍多1吨,而乙粮仓的粮食总量则是丙粮仓的2倍.问:甲粮仓比丙粮仓多存粮多少吨?5.果园里有桃树、、苹果树共552棵.桃树比梨树的2倍多12棵,苹果树比梨树少20棵,求桃树、梨树和苹果树各有多少棵?(☆☆☆)6.某驻军有三个坦克连,共有115辆坦克,一连坦克数量比二连的2倍多2,而二连的坦克数量比三连的3倍多1.请问:一连比三连多几辆坦克?(★★★)【重难点例题】:甲组的图书是乙组的3倍,若乙组给甲组6本,则甲组的图书是乙组的5倍,甲组原来有图书多少本?解析:甲组的图书是乙组的3倍,若乙组拿出6本,甲组相应的也拿出6×3=18(本),则甲组仍是乙组的3倍。
三年级思维拓展-和倍问题

和倍问题☜知识要点和倍应用题:已知大小两个数的和,与大小两个数的倍数关系,求这两个数各是多少,这一类的应用题叫做和倍问题。
解决和倍问题的关键就是学会画线段图,这样可以帮助我们更好的弄清各个数量之间的关系。
和倍问题中的4个关键量:和,倍数,大数,小数和倍问题的数量关系式:和÷(倍数+1)=小数小数×倍数=大数或和-小数=大数☜精选例题【例1】:甲班和乙班共有图书160本,甲班的图书是乙班的3倍,甲班和乙班各有图书多少本?思路点拨:甲班的图书本数加上乙班的图书本数,和是160本;甲班是乙班的3倍,即乙班是1份,甲班是3份,两班的图书加起来一共为4份,通过:和÷(倍数+1)=小数,可求出乙班1份数,再用过关系式求出甲班3份的数量即可。
☝标准答案:乙班:160÷(3+1)=40(本)甲班:160-40=120(本)或40×3=120(本)答:甲班有图书120本,乙班有图书40本。
✌活学巧用1、小明和小红共贴花15张,其中小明帖的张数是小红的2倍,问小明和小红各贴花多少张?2、图书馆有故事书和科技书共120本,故事书是科技书的3倍,图书馆有故事书和科技书各多少本?3、小华和爷爷今年共72岁,爷爷的岁数是小华的7倍,爷爷比小华大多少岁?4、一个长方形的周长是30厘米,长是宽的2倍,求这个长方形的面积的多少平方厘米?【例2】:小淘气和妈妈比身高,妈妈说:我的身高是你的2倍还多8厘米,我们两个的身高加起来和是236厘米,妈妈和小淘气的身高各是多少厘米?☝思路点拨:小淘气的身高是1倍数,而妈妈的身高比小淘气的2倍还多8厘米,如果减少8厘米,妈妈的身高就刚好是小淘气的2倍,那么总数也相应减少8厘米,即:236-8=228(厘米),这时228对应的就是2+1=3(倍),即可求出小数与大数。
☝标准答案:小淘气:(236-8)÷(2+1)=76(厘米)妈妈:236-76=160(厘米)答:妈妈身高为160厘米,小淘气身高为76厘米。
和倍问题讲义与练习题

和倍问题【知识了解】已知两个数的和与它们之间的倍数关系,求这两个数是多少的应用题,叫做和倍问题。
解答和倍应用题的基本数量关系是:和÷(倍数+1)=小数小数×倍数=大数(和-小数=大数)【例题讲解及思维拓展训练题】例1:学校有科技书和故事书共480本,科技书的本数是故事书的3倍。
两种书各有多少本?【思维点睛】为了便于理解题意,我们画图来分析:由图可知,如果把故事书的本数看作一份,那么科技书的本数就是这样的3份,两种书的总本数就是这样的1+3=4份。
把480本书平均分成4份,1份是故事书的本数,3份是科技书的本数。
480÷(1+3)=120(本)120×3=360(本).思维拓展训练一:1、用锡和铝制成的合金是720千克,其中铝的重量是锡的5倍。
铝和锡各用了多少千克?2、甲、乙两数的和是112.甲数除以乙数的商是6,甲、乙两数各是多少?3、一块长方形黑板的周长是96分米,长是宽的3倍。
这块长方形黑板的长和宽各是多少分米?例2:果园里有梨树、桃树和苹果树共1200棵,其中梨树的棵数是苹果树的3倍,桃树的棵数是苹果树的4倍。
求梨树、桃树和苹果树各有多少棵?【思维点睛】如果把苹果树的棵数看作1份,三种树的总棵数是这样的1+3+4=8份。
所以,苹果树有1200÷8=150(棵),梨树有150×3=450(棵),桃树有150×4=600(棵).思维拓展训练二:1、李大伯养鸡、鸭、鹅共960只,养鸡的只数是鹅的3倍,养鸭的只数是鹅的4倍。
鸡、鸭、鹅各养了多少只?2、甲、乙、丙三数之和是360,已知甲是乙的3倍,丙是乙的2倍。
求甲、乙、丙各是多少。
3、商店有铅笔、钢笔、圆珠笔共560支,圆珠笔的支数是钢笔的3倍,铅笔的支数与圆珠笔的支数同样多。
铅笔、钢笔和圆珠笔各有多少支?例3:有三个书橱共放了330本书,第二个书橱里的书是第一个的2倍,第三个书橱里的书是第二个的4倍。
年龄和倍问题的公式及例题!

小学数学典型应用题年龄问题小学数学中把含有数量关系的实际问题用语言或文字叙述出来,这样所形成的题目叫做应用题。
任何一道应用题都由两部分构成,第一部分是已知条件(简称条件),第二部分是所求问题(简称问题)。
和倍问题【含义】已知两个或多个人年龄关系,求各自年龄或年龄关系,这类应用题叫做和倍问题。
【数量关系】大数=(和+差)÷2小数=(和-差)÷2总和÷(几倍+1)=较小的数总和-较小的数=较大的数较小的数×几倍=较大的数两个数的差÷(几倍-1)=较小的数较小的数×几倍=较大的数【解题思路和方法】年龄问题具有年龄同增同减,年龄差不变的特性。
年龄问题都可以转化为和差、和倍、差倍问题。
简单的题目直接利用公式,复杂的题目变通后利用公式。
例1:爸爸今年38岁,妈妈今年36岁,当爸爸42岁时,妈妈_____ 岁。
1、本题考查的年龄差不变(简单),不管过了多少年年龄差是不变的。
2、爸爸比妈妈大2岁,根据不管过了多少年年龄差是不变的,当爸爸42岁时,妈妈是40岁。
例2:姐姐今年15岁,妹妹今年12岁,当她们的年龄和是39岁时,那时妹妹_____ 岁。
解:方法一:1、利用年龄同增同减的思路。
2、姐妹俩今年的年龄之和是:15+12=27(岁),年龄之和到达39岁时需要的年限是:(39-27)÷2=6(年)。
3、那是妹妹的年龄是12+6=18(岁)。
方法二:1、利用年龄差不变的思路。
2、两姐妹的年龄差为15-12=3(岁),再根据小数=(和-差)÷2的公式,可以求出妹妹的年龄为(39-3)÷2=18(岁)。
例3:爸爸今年50岁,哥哥今年14岁,_____ 年前,爸爸的年龄是哥哥的5倍。
解:1、不管过了多少年,年龄差是不变的,当爸爸的年龄是哥哥的5倍时,年龄差仍是50-14=36(岁)。
2、问什么时候爸爸的年龄是哥哥的5倍,实际上年龄差就是哥哥的5-1=4倍。
小学数学知识点:和倍问题

小学数学知识点:和倍问题01知识要点已知两个数的和与它们之间的倍数关系,求这两个数是多少的应用题,叫做和倍问题。
解答和倍应用题的基本数量关系是:和÷(倍数+1)=小数小数×倍数=大数(和-小数=大数)02精讲精练【例题1】学校有科技书和故事书共480本,科技书的本数是故事书的3倍。
两种书各有多少本?【思路导航】为了便于理解题意,我们画图来分析:由图可知,如果把故事书的本数看作一份,那么科技书的本数就是这样的3份,两种书的总本数就是这样的1+3=4份。
把480本书平均分成4份,1份是故事书的本数,3份是科技书的本数。
480÷(1+3)=120(本)120×3=360(本)练习1:1.用锡和铝制成的合金是720千克,其中铝的重量是锡的5倍。
铝和锡各用了多少千克?2.甲、乙两数的和是112.甲数除以乙数的商是6,甲、乙两数各是多少?3.一块长方形黑板的周长是96分米,长是宽的3倍。
这块长方形黑板的长和宽各是多少分米?【答案】1.铝的质量是600千克,锡的质量是120千克2.甲是96,乙是163.长是36分米,宽是12分米【例题2】果园里有梨树、桃树和苹果树共1200棵,其中梨树的棵数是苹果树的3倍,桃树的棵数是苹果树的4倍。
求梨树、桃树和苹果树各有多少棵?【思路导航】如果把苹果树的棵数看作1份,三种树的总棵数是这样的1+3+4=8份。
所以,苹果树有1200÷8=150(棵),梨树有150×3=450(棵),桃树有150×4=600(棵)练习2:1.李大伯养鸡、鸭、鹅共960只,养鸡的只数是鹅的3倍,养鸭的只数是鹅的4倍。
鸡、鸭、鹅各养了多少只?2.甲、乙、丙三数之和是360,已知甲是乙的3倍,丙是乙的2倍。
求甲、乙、丙各是多少。
3.商店有铅笔、钢笔、圆珠笔共560支,圆珠笔的支数是钢笔的3倍,铅笔的支数与圆珠笔的支数同样多。
铅笔、钢笔和圆珠笔各有多少支?【答案】1.鸡360只,鸭480只,鹅120只2.甲是180,乙是60,丙是1203.铅笔240支,钢笔80支,圆珠笔240支【例题3】有三个书橱共放了330本书,第二个书橱里的书是第一个的2倍,第三个书橱里的书是第二个的4倍。
和倍问题

和倍问题已知两个数的和与它们之间的倍数关系,求这两个数是多少的应用题,叫做和倍问题。
解答和倍应用题的基本数量关系是:和÷(倍数+1)=小数小数×倍数=大数和-小数=大数例1:学校有科技书和故事书共480本,科技书的本数是故事书的3倍。
两种书各有多少本?分析与解答:为了便于理解题意,我们画图来分析:由图可知,如果把故事书的本数看作一份,那么科技书的本数就是这样的3份,两种书的总本数就是这样的1+3=4份。
把480本书平均分成4份,1份是故事书的本数,3份是科技书的本数。
480÷(1+3)=120(本) 120×3=360(本)练习:1,用锡和铝制成的合金是720千克,其中铝的重量是锡的5倍。
铝和锡各用了多少千克?2,甲、乙两数的和是112,甲数除以乙数的商是6,甲、乙两数各是多少?3,一块长方形黑板的周长是96分米,长是宽的3倍。
这块长方形黑板的长和宽各是多少分米?和倍问题(二)例2:果园里有梨树、桃树和苹果树共1200棵,其中梨树的棵数是苹果树的3倍,桃树的棵数是苹果树的4倍。
求梨树、桃树和苹果树各有多少棵?分析与解答:如果把苹果树的棵数看作1份,三种树的总棵数是这样的1+3+4=8份。
所以,苹果树有1200÷8=150(棵),梨树有150×3=450(棵),桃树有150×4=600(棵)练习二1,李大伯养鸡、鸭、鹅共960只,养鸡的只数是鹅的3倍,养鸭的只数是鹅的4倍。
鸡、鸭、鹅各养了多少只?2,甲、乙、丙三数之和是360,已知甲是乙的3倍,丙是乙的2倍。
求甲、乙、丙各是多少。
3,商店有铅笔、钢笔、圆珠笔共560支,圆珠笔的支数是钢笔的3倍,铅笔的支数与圆珠笔的支数同样多。
铅笔、钢笔和圆珠笔各有多少支?例3:有三个书橱共放了330本书,第二个书橱里的书是第一个的2倍,第三个书橱里的书是第二个的4倍。
每个书橱里各放了多少本书?分析与解答:把第一个书橱里的本数看作1份,那么第二个书橱里的本数是这样的2份,第三个就是这样的2×4=8份,三个书橱里的总本数就是这样的1+2+8=11份。
和倍问题

和倍问题【含义】已知两个数的和及大数是小数的几倍(或小数是大数的几分之几),要求这两个数各是多少,这类应用题叫做和倍问题。
【数量关系】总和÷(几倍+1)=较小的数总和-较小的数=较大的数较小的数×几倍=较大的数【解题思路和方法】简单的题目直接利用公式,复杂的题目变通后利用公式。
例1、果园里有杏树和桃树共248棵,桃树的棵数是杏树的3倍,求杏树、桃树各多少棵?解:(1)杏树有多少棵?248÷(3+1)=62(棵)(2)桃树有多少棵?62×3=186(棵)答:杏树有62棵,桃树有186棵。
例2东西两个仓库共存粮480吨,东库存粮数是西库存粮数的1.4倍,求两库各存粮多少吨?解:(1)西库存粮数=480÷(1.4+1)=200(吨)(2)东库存粮数=480-200=280(吨)(3)答:东库存粮280吨,西库存粮200吨。
例3 、甲站原有车52辆,乙站原有车32辆,若每天从甲站开往乙站28辆,从乙站开往甲站24辆,几天后乙站车辆数是甲站的2倍?解:每天从甲站开往乙站28辆,从乙站开往甲站24辆,相当于每天从甲站开往乙站(28-24)辆。
把几天以后甲站的车辆数当作1倍量,这时乙站的车辆数就是2倍量,两站的车辆总数(52+32)就相当于(2+1)倍,那么,几天以后甲站的车辆数减少为(52+32)÷(2+1)=28(辆)所求天数为(52-28)÷(28-24)=6(天)答:6天以后乙站车辆数是甲站的2倍。
例4、甲乙丙三数之和是170,乙比甲的2倍少4,丙比甲的3倍多6,求三数各是多少?解:乙丙两数都与甲数有直接关系,因此把甲数作为1倍量。
因为乙比甲的2倍少4,所以给乙加上4,乙数就变成甲数的2倍;又因为丙比甲的3倍多6,所以丙数减去6就变为甲数的3倍;这时(170+4-6)就相当于(1+2+3)倍。
那么,甲数=(170+4-6)÷(1+2+3)=28乙数=28×2-4=52 丙数=28×3+6=901、小敏与爸爸的年龄之和是64岁,爸爸的年龄是小敏的3倍。
1、倍的问题(一)
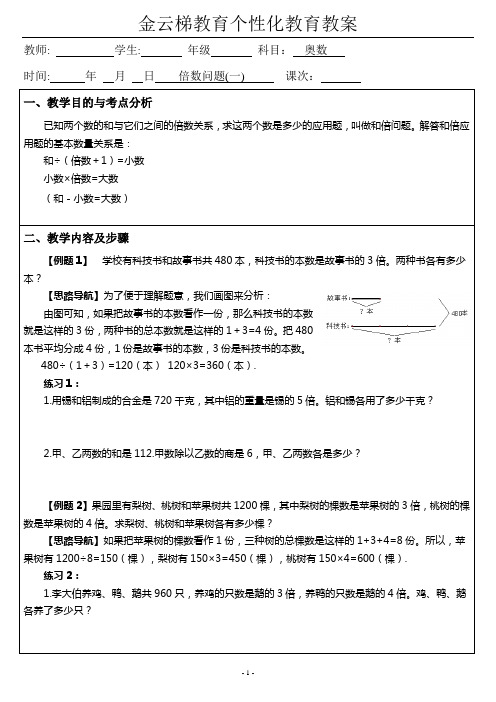
2.小华和小明两人参加数学竞赛,两人共得168分,小华的得分比小明的2倍少42分。两人各得多少分?
【例题5】三个筑路队共筑路1360米,甲队筑的米数是乙队的2倍,乙队比丙队多240米。三个队各筑多少米?
练习2:
1.李大伯养鸡、鸭、鹅共960只,养鸡的只数是鹅的3倍,养鸭的只数是鹅的4倍。鸡、鸭、鹅各养了多少只?
2.甲、乙、丙三数之和是360,已知甲是乙的3倍,丙是乙的2倍。求甲、乙、丙各是多少。
【例题3】有三个书橱共放了330本书,第二个书橱里的书是第一个的2倍,第三个书橱里的书是第二个的4倍。每个书橱里各放了多少本书?
【思路导航】把第一个书橱里的本数看作1份,那么第二个书橱里的本数是这样的2份,第三个就是这样的2×4=8份,三个书橱里的总本数就是这样的1+2+8=11份。所以,第一个书橱里放了
330÷11=30(本),第二个书橱里放了30×2=60(本),第三个书橱里放了60×4=240(本)。
练习3:
1.甲、乙、丙三个数之和是400,已知甲是乙的3倍,丙是甲的4倍。求甲、乙、丙各是多少。
2.三个数的和是1540,甲数是丙数的7倍,乙数比甲数多40。三个数各是多少?
三、本次课后作业
1.一块长方形黑板的周长是96分米,长是宽的3倍。这块长方形黑板的长和宽各是多少分米?
2.商店有铅笔、钢笔、圆珠笔共560支,圆珠笔的支数是钢笔的3倍,铅笔的支数与圆珠笔的支数同样多。铅笔、钢笔和圆珠笔各有多少支?
四、学生对于本次课的评价:
○特别满意○满意○一般○差
学生签字:
3.甲、乙、丙三个修路队共修路1200米,甲队修的米数是乙队的2倍,乙队修的数数是丙队的3倍。三个队各修了多少米?
和倍问题(经典)

【知识梳理】知识点1、和倍和倍问题就是已知两个数的和以及它们之间的倍数关系,求这两个数各是多少的问题.解答此类应用题时要根据题目中所给的条件和问题,画出线段图,使数量关系一目了然,从而找出解题规律,正确迅速地列式解答。
和倍问题的特点是已知两个数的和与大数是小数的几倍,要求两个数,一般是把较小数看作倍数,大数就是几倍数,这样就可知总和相当于小数的几倍了,可求出小数,再求大数.和倍问题的数量关系式是:和÷(倍数+)=小数小数×倍数=大数或和一小数=大数如果要求两个数的差,要先求份数:份数×(倍数-)=两数差.解决和倍问题,关键是学会画线段图,这样可以帮助我们更好的弄清各数量之间的关系。
【例题精讲】例1、两个数的和为 27, 其中一个数是另一个数的 2 倍, 求这两个数。
【举一反三】练习1、纺织厂有职工 480 人, 其中女职工人数是男职工人数的 3 倍. 请问:男、女职工各有几人?练习2、小敏有元,小花有元,小花给小敏几元,小敏的钱数就是小花的倍?【例题精讲】例2、师、徒两人共加工个零件,师傅加工的个数比徒弟的倍还多个,师傅和徒弟各加工零件多少个?【举一反三】练习1、光明小学有学生760人,其中男生比女生的3倍少40人,男、女生各有多少人?练习2、常州市某小学的同学为幼儿园的小朋友做红花和黄花共300朵。
已知红花的朵数比黄花的2倍少30朵。
问两种花各有多少朵?【例题精讲】例3、果园里有桃树、梨树、苹果树共552棵.桃树比梨树的2倍多12棵,苹果树比梨树少20棵,求桃树、梨树和苹果树各有多少棵?【举一反三】练习1、一家三口人,三人年龄之和是岁,妈妈和爸爸同岁,妈妈的年龄是孩子的倍,三人各是多少岁?练习2、有100块糖,分给甲乙丙三位小朋友,甲比乙多分了3块,乙比丙多分了5块,三位小朋友各分得多少块糖?【例题精讲】例4、甲、乙、丙三所小学的学生人数的总和为1999。
已知甲校学生人数的2倍和乙校学生人数减去3人与丙校学生人数加上4人都相等。
小学五年级奥数第17讲 倍数问题(二)(含答案分析)

第17讲倍数问题(二)一、知识要点解决倍数问题的关键是,必须确定一个数作为标准数,并根据题中的已知条件,找出其它几个数与这个标准数的倍数关系,再用除法求出这个标准数。
由于倍数应用题中数量关系的变化,要求同学们在解题过程中注意解题技巧,灵活解题。
和倍问题的数量关系是:和数÷(倍数+1)=较小数较小数×倍数=较大数差倍问题的数量关系是:差数÷(倍数-1)=较小数较小数×倍数=较大数二、精讲精练【例题1】养鸡场的母鸡只数是公鸡的6倍,后来公鸡和母鸡各增加60只,结果母鸡只数就是公鸡的4倍。
原来养鸡场一共养了多少只鸡?练习1:1.今年,爸爸的年龄是小明的6倍,再过4年,爸爸的年龄就是小明的4倍。
今年小明多少岁?2.原来食堂里存的大米是面粉的4倍,大米和面粉各吃掉80千克,大米的重量是面粉的2倍。
食堂里原来存有大米、面粉各多少千克?3.饲养场的白兔只数是黑兔的5倍,后来卖掉了10只黑兔,买回来20只白兔,现在白兔的只数是黑兔的7倍。
饲养场原来养白兔和黑兔各多少只?【例题2】有1800千克的货物,分装在甲、乙、丙三辆车上。
已知甲车装的千克数正好是乙车的2倍,乙车比丙车多装200千克。
甲、乙、丙三辆车各装货物多少千克?练习2:1.三堆货物共1800箱,甲堆的箱数是乙堆的2倍,乙堆的箱数比丙堆少200箱。
三堆货物各多少箱?2.甲、乙、丙三数的和是224,如果甲是乙的3倍,丙是甲的4倍,求甲、乙、丙三数各是多少。
3.把840本书放在书架的三层里,下层放的本数比上层的3倍多5本,中层放的本数是上层的2倍多1本。
问:上、中、下三层各放书多少本?【例题3】甲、乙两个书架,已知甲书架有书600本,从甲书架借出三分之一,从乙书架借出四分之三后,甲书架的书是乙书架的2倍还多150本。
乙书架原来有书多少本?练习3:1.某校有男生630人,选出男生人数的三分之一和女生人数的四分之三去排练团体操,剩下的男生人数是女生人数的2倍。
五年级奥数-和倍问题

和倍问题姓名:知识点拨和倍问题就是已知两个数的和以及它们之间的倍数关系,求这两个数各是多少的问题.解答此类应用题时要根据题目中所给的条件和问题,画出线段图,使数量关系一目了然,从而找出解题规律,正确迅速地列式解答。
和倍问题的特点是已知两个数的和与大数是小数的几倍,要求两个数,一般是把较小数看作1倍数,大数就是几倍数,这样就可知总和相当于小数的几倍了,可求出小数,再求大数。
和倍问题的数量关系式是:和÷(倍数+1)=小数小数×倍数=大数或和一小数=大数如果要求两个数的差,要先求1份数:l份数×(倍数-1)=两数差解决和倍问题,关键是学会画线段图,这样可以帮助我们更好的弄清各数量之间的关系。
教学目标:1、学会分析题意并且熟练的利用线段图法能够分析和倍问题。
2、掌握寻找和倍的方法解决问题。
经典例题【例1】根据线段图列式:【巩固】一家三口人,三人年龄之和是72岁,妈妈和爸爸同岁,妈妈的年龄是孩子的4倍,三人各是多少岁?【巩固】实验小学三、四年级的同学们一共制作了318件航模,四年级同学制作的航模件数是三年级的2倍,三、四年级的同学各制作了多少件航模?【巩固】5箱苹果和5箱葡萄共重75千克,每箱苹果是每箱葡萄重量的2倍。
每箱苹果和每箱葡萄各重多少千克?【巩固】红、黄、蓝三个纸盒里共有彩票56张.其中红色纸盒里的彩票是黄色纸盒的2倍,蓝色纸盒里的彩票是红色纸盒的2倍,红、黄、蓝三个纸盒里各有多少张彩票?【巩固】一个长方形的周长是36厘米,长是宽的2倍,这个长方形的面积是多少平方厘米?【例2】小敏有14元,小花有10元,小花给小敏几元,小敏的钱数就是小花的2倍?【例3】小华和爷爷今年共72岁,爷爷的岁数是小华的7倍.爷爷比小华大多少岁?【巩固】果园里有梨树和苹果树共54棵,苹果树的棵数是梨树的5倍,苹果树比梨树多多少棵?【例4】两个书架,甲书架存书相当于乙书架存书量的5倍,甲书架比乙书架存书多120本,则乙书架存书多少本?【例5】师、徒两人共加工105个零件,师傅加工的个数比徒弟的3倍还多5个,师傅和徒弟各加工零件多少个?【巩固】光明小学有学生760人,其中男生比女生的3倍少40人,男、女生各有多少人?【巩固】实验小学共有学生956人,男生比女生2倍少4人.问:实验小学男学生和女学生各有多少人?【巩固】两组学生参加义务劳动,甲组学生人数是乙组的3倍,而乙组的学生人数比甲组的3倍少40人,求参加义务劳动的学生共有多少人?【巩固】商店运来橘子、苹果、香蕉共53千克,橘子的重量是苹果的3倍少3千克,香蕉的重量是苹果的2倍多2千克,橘子重多少千克?【例6】甲、乙、丙三个小朋友共有73块巧克力,如果丙吃掉3块,那么乙和丙的巧克力就一样多;如果乙给甲2块巧克力,那么甲的巧克力就是乙的2倍,丙原有多少块巧克力?过手训练一、填空题。
三年级数学思维能力提升--和倍问题1

三年级数学思维能力提升和倍问题知识与方法归纳1、已知两个数的和与它们之间的倍数关系,求这两个数是多少的应用题,叫做和倍问题。
2、和倍问题的数量关系:小数(1倍数)= 和÷(倍数 +1)大数 = 小数×倍数 = 和 - 小数3、方法指引:(1)用图形来理解题意;其中画图的规律性方法是先画出倍数关系即1倍和几倍,再画多少关系。
(2)找出数字之间的联系与倍数之间的联系;(3)通过找出整倍数的和求出1倍数,再求出几倍数。
典型题讲解例1、(1)笑笑和妈妈的年龄加在一起是40岁,妈妈年龄是笑笑年龄的3倍,笑笑和妈妈各多少岁?(2)笑笑和妈妈的年龄加在一起是40岁,妈妈年龄比笑笑年龄多3倍,笑笑和妈妈各多少岁?例2、一块长方形木板,长是宽的4倍,周长是20厘米,长和宽各是多少厘米?练习1、学校买来两种粉笔共48盒,已知白色粉笔的盒数是彩色粉笔的5倍。
两种粉笔各买了多少盒?例3、杨树和柳树共24棵,其中杨树的棵数比柳树棵数的2倍还多3棵,杨树和柳树各多少棵?例4、动物园的猴山上共有40只猴。
大猴子的只数比小猴子的5倍少8只。
猴山上大小猴子各有多少只?思维训练2、三年级一班共有学生27人,其中男生比女生的2倍少3人,男、女生各有多少人?例5、甲乙两个数相除,商3,甲乙的和是16,甲和乙分别是多少?例6、养殖场养鸡、鸭、鹅共90只,鸡的只数是鸭的3倍,鸭的只数是鹅的2倍,鸡、鸭、鹅各几只?巩固提升1、填空题(1)一个长方形,长是宽的5倍,周长是108厘米,长方形的长是()厘米,宽是()厘米。
(2)大小两个桶共有油16千克,其中大桶的油是小桶的3倍,大桶有()千克油。
(3)舞蹈队共有队员21人,其中女队员比男队员的2倍多3人,求男队员有()人。
(4)生产队养公鸡、母鸡共24只,公鸡是母鸡的3倍,公鸡养了()只,母鸡养了()只。
(5)小明从家到学校要走100米长的路,如果他来回走2趟共行()米。
(6)甲书架有图书18本,乙书架有图书8本,班级图书管理员又买来图书16本,分给甲()本,乙()本才能使甲书架图书的本书是乙书架的2倍。
和倍应用题的数量关系

和倍应用题的数量关系:小数=两数和÷(倍数+1)大数=小数×倍数或者大数=两数和—小数1、有一个书架,上层有故事书160本,下层有故事书40本,上层给下层()本故事书以后,下层故事书就比上层的3倍还多20本。
2、在一道减法算式里,被减数、减数与差的和是360,而差比减数的4倍还多20, 被减数是(),减数是(),差是()。
3、饲养场养鸡、鸭、鹅共518只,其中养鸡的只数比鸭的3倍多18只,养鸭的只数比鹅的2倍少10只,饲养场养鸡()只,鸭()只,鹅()只。
4、甲、乙、丙、丁四个数的和是180,如果甲数加上2,乙数减去2,丙数乘2,丁数除以2以后,四个数就相等,则甲数是( ),乙数是( ),丙数是(),丁数是()。
5、两数相除,商3余4,如果被除数、除数、商及余数相加,和是43,被除数是(),除数是()。
6、两箱茶叶共176千克,从甲箱取出30千克放乙箱,乙箱的千克数就是甲箱的3倍。
甲箱原有茶叶()千克,乙箱原有茶叶()千克。
7、甲数是乙数的3倍,丙数是乙数的4倍,丁数是丙数的一半,四个数的和是1040,丁数是()。
8、两个数相除商9,无余数,被除数、除数与商的和是89,除数是()。
9、两个数的和是682,其中一个加数的个位是0,若把0去掉,则与另一个数相同,这两个数分别是()和()。
10、在一个减法算式里,被减数、减数与差的和等于120,而差是减数的3倍,那么差等于()。
数量关系式:小数=两数差÷(倍数-1)大数=小数×倍数或者大数=小数+数量差1、育才小学参加科技小组的同学比参加合唱队的4倍少45人,参加科技小组的同学比合唱队的人数多105人,求参加科技小组同学和参加合唱队的人数各有()人和()人。
2、甲仓库存大米500袋,乙仓库存大米200袋,现从两个仓库里运走同样袋数的大米,结果甲仓库剩下大米正好是乙仓库剩下大米的3倍。
甲仓库里运走()袋大米,乙仓库里运走()袋大米。
和倍问题

和倍问题已知两个数的和与两个数之间的倍数关系,求这两个数分别是多少,像这样的应用题通常叫做“和倍问题”根据题意画出线段图,使数量关系一目了然,从而正确解答。
解答和倍问题,关键是找出两个数的和以及与其对应的倍数和,从而先求出一倍量,再求出几倍量。
数量关系式:两数和÷(倍数+1)=小数(1倍数)小数×倍数=大数(几倍数)两数和-小数=大数典型例题:例1. 在一道除法算式里,被除数与除数的和是320,商是7,被除数和除数各是几?分析:“商是7”,可知被除数是除数的7倍,把除数看做1倍量,被除数是它的7倍。
线段图如下:除数:被除数:列式:除数:320÷(1+7)=40 被除数:40×7=280答:被除数是280,除数是40.基础练习:1、被除数和除数的和是95,商是4,求被除数和除数。
2、被除数、除数、商的和是79,商是4,求被除数和除数。
例2 。
师徒两人共加工零件318个。
已知师傅加工的零件个数比徒弟的2倍还多18个,师徒两人各加工零件多少个?画线段图理解题意:徒弟:师傅:由图可知,徒弟加工的零件数看做1倍数,师傅加工的个数比徒弟的2倍还多18个,如果师傅少加工18个就的徒弟的2倍,那么总数也少18个。
所以(318-18)÷(2+1)=100(个),就是徒弟加工的理解数,师傅加工的理解数:100×2+18=218(个)答:师傅加工零件218个,徒弟加工零件100个。
基础练习:1、甲乙两数的和是108,其中甲数比乙数的2倍少36,甲乙两数各是多少?2、果园里有桃树和杏树一共460棵,其中桃树的棵树比杏树的3倍多20棵。
两种树各有多少棵?例3、小明有邮票80张,小丽有邮票60张,小丽必须给小明多少张邮票才能使小明的邮票张数是小丽的4倍?怎样分析这道题的数量关系?基础练习:1、甲仓库存粮54吨,乙仓库存粮82吨,从乙仓库运出多少到甲仓库,甲仓库存粮是乙仓库的3倍?2、甲书架有书18本,乙书架有书8本,又买来16本,怎样分配才能使甲书架的书是乙书架的2倍?例4、幼儿园买来60个皮球,其中红皮球的个数是花皮球的3倍,黄皮球比红皮球多4个。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
和倍应用题的数量关系:小数=两数和÷(倍数+1)大数=小数×倍数或者大数=两数和—小数1、有一个书架,上层有故事书160本,下层有故事书40本,上层给下层()本故事书以后,下层故事书就比上层的3倍还多20本。
2、在一道减法算式里,被减数、减数与差的和是360,而差比减数的4倍还多20, 被减数是(),减数是(),差是()。
3、饲养场养鸡、鸭、鹅共518只,其中养鸡的只数比鸭的3倍多18只,养鸭的只数比鹅的2倍少10只,饲养场养鸡()只,鸭()只,鹅()只。
4、甲、乙、丙、丁四个数的和是180,如果甲数加上2,乙数减去2,丙数乘2,丁数除以2以后,四个数就相等,则甲数是( ),乙数是( ),丙数是(),丁数是()。
5、两数相除,商3余4,如果被除数、除数、商及余数相加,和是43,被除数是(),除数是()。
6、两箱茶叶共176千克,从甲箱取出30千克放乙箱,乙箱的千克数就是甲箱的3倍。
甲箱原有茶叶()千克,乙箱原有茶叶()千克。
7、甲数是乙数的3倍,丙数是乙数的4倍,丁数是丙数的一半,四个数的和是1040,丁数是()。
8、两个数相除商9,无余数,被除数、除数与商的和是89,除数是()。
9、两个数的和是682,其中一个加数的个位是0,若把0去掉,则与另一个数相同,这两个数分别是()和()。
10、在一个减法算式里,被减数、减数与差的和等于120,而差是减数的3倍,那么差等于()。
数量关系式:小数=两数差÷(倍数-1)大数=小数×倍数或者大数=小数+数量差1、育才小学参加科技小组的同学比参加合唱队的4倍少45人,参加科技小组的同学比合唱队的人数多105人,求参加科技小组同学和参加合唱队的人数各有()人和()人。
2、甲仓库存大米500袋,乙仓库存大米200袋,现从两个仓库里运走同样袋数的大米,结果甲仓库剩下大米正好是乙仓库剩下大米的3倍。
甲仓库里运走()袋大米,乙仓库里运走()袋大米。
3、一个车间,女工比男工少35人,男女工各调出17人后,男工人数是女工人数的2倍。
原有男工()人,女工()人。
4、两筐重量相等的苹果,甲筐卖出7千克,乙筐卖出19千克以后,甲筐余下的千克数是乙筐的3倍,甲筐苹果有()千克,乙筐有苹果()千克。
5、一天,A、B、C三个钓鱼协会的会员去郊外钓鱼,已知A比B多钓6条,C钓的鱼是A的2倍,比B多钓22条,他们一共钓了()条鱼。
6、已知两个数的商是4,这两个数的差是39,那么这两个数中较小的一个数是()。
7、有两堆沙子,第一堆有98吨,第二堆有154吨,每天各运走5吨,()天后第二堆剩下沙子的重量是第一堆剩下的3倍。
8、班级里有图书,科技书的本数比故事书多40本,故事书的本数比连环画少4本,科技书的本数比连环画的2倍还多6本,故事书有()本,科技书有()本,连环画有()本。
9、有两筐梨,如果从第一筐拿出18个梨放入第二筐,两筐梨的个数就相等。
如果从第二筐拿出24个梨放入第一筐,则第一筐梨的个数是第二筐的3倍。
原来第一筐有梨()个,第二筐原来有梨()个。
10、小华做加法算式,他把其中一个加数个位的零漏掉,结果和变成了403,老师指出了他的错误,并告诉他正确得数是628。
你能帮助他吗?这个加数是()。
一、计算(直接写出得数,每小题1分,共10分)90-90÷(25+5)=25×2÷25×2=25×4×0÷100= 1000-875-125=25×32×125= 1234+5678+8766+4322=58×12+12×41+12=1996×56+1996×45-1996=(125×99+125)×16= 7777×6+1111×58=二、填空(每题4分,共40分)1、已知△+○=24,○=△+△+△,△=(),○=()2、△÷○=9……6,○最小可以是(),这时△应该是()3、在一个减法算式里,被减数、减数与差的和等于90,而差是减数的2倍,那么差是()4、一根木料,截成3段要12分钟,如果每截一段的时间相等,那么截成6段要()分钟。
5、小强把(4+△)×15错算成4+△×15,他算出的结果与正确的得数相差年龄问题应用题班级姓名数量关系:几年后年龄=大小年龄差÷倍数差-小年龄几年前年龄=小年龄-大小年龄差÷倍数差1、妈妈今年35岁,恰好是女儿年龄的7倍。
()年后,妈妈的年龄恰好是女儿的3倍。
2、小明今年8岁,他与爸爸、妈妈的年龄和是81岁,()年后他们的平均年龄是34岁。
这时小明()岁。
3、小冬今年12岁,五年前爷爷的年龄是小冬年龄的9倍,爷爷今年()岁。
4、妈妈今年40岁,恰好是小红年龄的4倍,()年后,妈妈的年龄是小红的2倍。
5、一家三口人,三人的年龄和是72岁。
妈妈和爸爸同岁,妈妈的年龄是孩子的4倍,妈妈和爸爸都是()岁,孩子是()岁。
6、今年,祖父的年龄是小明年龄的6倍,几年后,祖父的年龄将是小明年龄的5倍。
又过了几年后,祖父的年龄将是小明年龄的4倍,祖父今年()岁。
7、三年前爸爸的年龄正好是儿子小刚年龄的6倍,今年父子年龄和是55岁,小刚今年()岁。
8、爸爸15年前的年龄相当于儿子12年后的年龄,当爸爸的年龄是儿子的4倍时,爸爸()岁。
9、甲的年龄数字颠倒过来恰好是乙的年龄,两人年龄和为99岁,甲比乙大9岁,甲的年龄是()岁。
10、祖孙三人的年龄加在一起正好是100岁,祖父过的年数正好等于孙子过的月数,儿子过的星期数正好等于孙子过的天数。
祖父()岁、儿子()岁、孙子()岁。
11、已知祖父和父亲、父亲和孙子的年龄的差是一样的。
又知祖父和孙子的年龄之和为84岁,这个岁数再加上孙子的年龄,正好是100岁,祖父()岁,父亲()岁,孙子()岁。
12、小英一家由小英和她的父母组成。
小英的父亲比母亲大3岁。
今年全家年龄的总和是71岁,8年前这个家庭成员的年龄总和是49岁。
今年小英()岁,父亲()岁,母亲()岁。
例1、一列货车早晨8时从甲地开往乙地,平均每小时行40千米,一列客车从乙地开往甲地,平均每小时行60千米。
已知客车在货车开出后2小时才出发,下午2时两车同时经过途中某站,然后仍继续前进。
那么,当客车到达甲地时,货车离乙地还有多少千米?练一练:1、甲乙两站相距360千米。
客车和货车同时从甲站出发驶向乙站,客车每小时行60千米,货车每小时行40千米,客车到乙站后停留0.5小时,又以原速返回甲站,两车对面相遇的地点离乙站多少千米?2、甲乙两地间的路程是600千米,上午8点客车以平均每小时60千米的速度从甲地开往乙地。
货车以平均每小时50千米的速度从乙地开往甲地。
要使两车在全程的中点相遇,货车必须在上午几点出发?例2、小军和小琴两人同时从相距2千米的两地相向而行。
小军每分钟行120米,小琴每分钟行80米,如果一只狗与小军同时出发,同向而行,它每分钟行400米,当它遇到小琴后,立即回头向小军跑去,遇到小军后又立即回头向小琴跑去。
这样来回不断,直到小军和小琴相遇为止,这时狗行了多少千米?练一练:甲乙两地相距352千米。
甲乙两汽车从甲、乙两地对开,甲车每小时行36千米,乙车每小时行44千米。
乙车因事,在甲车开出32千米后才出发。
两车从各自出发起到相遇时,哪辆车走的路程多?多多少千米?1、甲乙两辆汽车同时从东西两地相向开出,甲车每小时行56千米,乙车每小时行48千米,两车在离中点32千米处相遇,求东西两地的距离是多少千米?2、兄妹两人同时离家去上学。
哥哥每分钟走90米,妹妹每分钟走60米,哥哥到校门时,发现忘带课本,立即沿原路回家去取,行至离校180米处和妹妹相遇。
问他们家离学校多远?3、东、西两镇相距240千米,一辆客车在上午8时从东镇开往西镇,一辆货车在上午9时从西镇开往东镇,到正午12时,两车恰好在两镇间的中点相遇。
如果两车都从上午8时由两镇相向开行,速度不变,到上午10时,两车还相距多少千米?4、客车和货车同时从甲乙两站相对开出,客车每小时行54千米,货车每小时行48千米,两车相遇后又以原来的速度继续前进,客车到乙站后立即返回,货车到甲站后也立即返回,两车再次相遇时,客车比货车多行216千米。
求甲乙两站间的路程是多少千米?5、“八一”节那天,某少先队以每小时4千米的速度从学校往相距17千米的解放军营房去慰问,出发0.5小时后,解放军闻讯前往迎接,每小时比少先队员快2千米,再过几小时,他们在途中相遇?6、甲、乙两站相距440千米,一辆大车和一辆小车从两站相对开出,大车每小时行35千米,小车每小时行45千米。
一只燕子以每小时50千米的速度和大车同时出发,向小车飞去,遇到小车后又折回向大车飞去,遇到大车又往回飞向小车,这样一直飞下去,燕子飞了多少千米,两车才能相遇?求平均应用题的基本数量关系:总数量÷总份数=平均数总数量÷平均数=总份数平均数×总份数=总数量1、从小到大有5个连续的双数,它们的和是70,在这5个数中最大的是(),最小的是()。
2、有4筐水果,平均每筐有56个苹果,甲筐和乙筐的平均数是30个,丙筐和丁筐的平均数是()个。
3、有5个数排成一列,它们的平均数是72,其中前3个数的平均数是70,后3个数的平均数是80,第三个数是()。
4、甲、乙两人的平均年龄是22岁,乙、丙两人的平均年龄是25岁,甲、丙两人的平均年龄是27岁,则甲、乙、丙三人的年龄分别是()岁、()岁、()岁。
5、有7个数,它们的平均数是18,去掉一个数后,剩下6个数的平均数是19;再去掉一个数后,剩下的5个数的平均数是20。
去掉的两个数的积是()。
