离散信源题与答案
信息论习题——精选推荐

选择题1、离散有记忆信源],[21x x X =,12()()0.5P x P x ==,其极限熵H ∞ 。
A 、1bit >B 、1bit <C 、1bit =D 、不能确定2、任意离散随机变量X 、Y 、Z , 必定成立A 、)|()|(XZ Y H YZ X H =B 、)()()()(Z H Y H X H XYZ H ++=C 、)|()|(Y X H YZ X H ≤D 、0)|;(=Z Y X I3、|Y X P 给定时,(;)I X Y 是X P 的 函数。
A 、上凸B 、下凸C 、上升D 、下降4、使(;)I X Y 达到最大的 称为最佳分布。
A 、联合分布B 、后验分布C 、输出分布D 、输入分布5、离散平稳无记忆信源],[21x x X =,且bit X H 1)(=,则=)(1x P 。
A 、41B 、2C 、1D 、216、=);(Y X I 。
A 、)|()(X Y H X H -B 、)|()(Y X H Y H +C 、)|()(X Y H Y H -D 、)()(X H XY H -7、通常所说的“连续信源”是指 信源。
A 、时间连续且取值连续的B 、取值连续C 、时间离散且取值连续的D 、时间连续8、已知信道,意味着已知 。
A 、 先验分布B 、转移概率分布C 、 输入输出联合概率分布D 、输出概率分布9、已知X Y P |,可求出A 、)(XY HB 、 )|(X Y HC 、);(Y X ID 、)|(i j x y I10、连续信源的输出可用 来描述A 、常量B 、变量C 、离散随机变量D 、连续随机变量11、101)(=i x P ,则=)(i x I 。
A 、bit 10lnB 、dit 10lnC 、dit 1D 、dit 10log12、信道容量表征信道的 。
A 、最大通过能力B 、最大尺寸C 、最小通过能力D 、最小尺寸13、DMS 的信息含量效率等于信源的实际熵 信源的最大熵。
2024年国家电网招聘之通信类真题精选附答案

2024年国家电网招聘之通信类真题精选附答案单选题(共45题)1、离散信源输出5个不同符号,若各符号概率分别为1/2,1/4,1/8,1/16,1/16,则该信源的熵为()。
A.1.5bit/signB.1.875bit/signC.2bit/signD.1bit/sign【答案】 B2、()是在接收端逐个统计不相关的分集支路,经过相位校正,并按适当的可变增益加权再相加后送入检测器进行相干检测。
此方法合并效果最好,但实现较复杂。
A.收发合并B.最大比合并C.等增益合并D.选择性合并【答案】 B3、IPPON的上层是(),这种方式可更加充分地利用网络资源,容易实现系统带宽的动态分配,简化中间层的复杂设备。
A.数据链路层B.物理层C.IP层D.网络层【答案】 C4、某省游泳队进行了为期一个月的高原集训,集训最后一日所有队员进行了一次队内测试,几位教练預测了一下队员的成绩:张教练说:这次集训时间短,没人会达标。
孙教练说:有队员会达标。
王教练说:省运会冠军或国家队队员可达标。
测试结束后,只有一位教练的预测是正确的。
由此可以推出( )A.没有人达标B.全队都达标了C.省运会冠军达标D.国家队队员未达标【答案】 D5、用于连接数字程控交换系统和数字用户终端设备之间的接口电路是()接口。
A.模拟用户B.数字用户C.模拟中继D.数字中继【答案】 B6、下列描述中,不属于 IP 层实现的功能是()A.尽力而为的不可靠传输服务B.数据报的分段与重组C.确定主机进程间的接口D.报文交换、TAM 交换【答案】 D7、连续信道的信道容量将受到“三要素”的限制,其“三要素”是()。
A.带宽、信号功率、信息量B.带宽、信号功率、噪声功率谱密度C.带宽、信号功率、噪声功率D.信息量、带宽、噪声功率谱密度【答案】 B8、当电磁波和障碍物符合()条件时,比较容易发生绕射现象。
A.障碍物为金属表面B.障碍物尺寸与波长相似或者更小C.障碍物尺寸远远大于波长D.障碍物表面粗糙【答案】 B9、根据《建设项目环境影响评价资质管理办法》,评价机构每年须填写“建设项目环境影响评价机构年度业绩报告表”,于()前报国家环境保护总局。
第3章 离散信源

时间长度为bi,则该信源的时间熵定义为:Ht(X)=H(X)/b. 其中b为信源符号的
平均时间长度。
M
b p( xi ) bi
i 1
s / 符号
离散信源的时间熵(续)
K重符号序列离散无记忆信源的时间熵:
K K Ht (X ) H(X ) / B
bit / s 其中B Kb
为K重符号序列消息的平均时间长度。由于信源无记忆,上式也可以写成:
bit / s
由于信源有记忆,所以有:
K ( H t X ) KH ( X ) (Kb) KH ( X ) /(Kb) H ( X ) / b
bit / s
有记忆信源与无记忆信源相比,对外提供信息量的速度下降了。
离散信源的时间熵(续)
马尔可夫信源的时间熵: 若信源从状态Si转移到状态Sj,发出的符号是xij,它的时间长度设为bij,则 信源从状态Si发生转移并发出一个符号时,符号的平均长度为:
信源分类
若离散信源输出符号彼此间相互独立,而且所有符号服从同一种概率分布,则称之 为简单无记忆信源;
若输出符号间彼此相关,且每个符号只与它前面的一个符号相关,而这种相关性可 以用符号间的转移概率来描述,则称之为马尔可夫信源。
离散信源的熵
单符号离散无记忆信源熵: 若信源X含有M个符号,而且每个符号相互独立,则当信源每次发送一个 符号代表一条消息时,其信源熵可以表示为:
H(X ) 100% H ( X )max
信源符号的相关性越大,信源效率越低,要提高信源效率,要设法降 低符号之间的相关性。
信源的效率与冗余度(续)
(2)信源冗余度:
H ( X )max H ( X ) H(X ) R 1 1 100% H ( X )max H ( X )max
信息论与纠错编码题库 (1)

第三章 离散信源无失真编码3.2离散无记忆信源,熵为H[x],对信源的L 长序列进行等长编码,码字是长为n 的D 进制符号串,问:(1)满足什么条件,可实现无失真编码。
(2)L 增大,编码效率 也会增大吗? 解:(1)当log ()n D LH X ≥时,可实现无失真编码;(2)等长编码时,从总的趋势来说,增加L 可提高编码效率,且当L →∞时,1η→。
但不一定L 的每次增加都一定会使编码效率提高。
3.3变长编码定理指明,对信源进行变长编码,总可以找到一种惟一可译码,使码长n 满足D X H log )(≤n <D X H log )(+L 1,试问在n >D X H log )(+L1时,能否也找到惟一可译码? 解:在n >D X H log )(+L1时,不能找到惟一可译码。
证明:假设在n >D X H log )(+L1时,能否也找到惟一可译码,则由变长编码定理当n 满足D X H log )(≤n <D X H log )(+L 1,总可以找到一种惟一可译码知:在n ≥DX H log )( ① 时,总可以找到一种惟一可译码。
由①式有:Ln ≥L X H )(logD ② 对于离散无记忆信源,有H(x)=LX H )( 代入式②得:n L≥ D x H log )(即在nL≥Dx H log )(时,总可以找到一种惟一可译码;而由定理给定熵H (X )及有D 个元素的码符号集,构成惟一可译码,其平均码长满足D X H log )(≤n L <DX H log )(+1 两者矛盾,故假设不存在。
所以,在n >D X H log )(+L1时,不能找到惟一可译码。
3.7对一信源提供6种不同的编码方案:码1~码6,如表3-10所示信源消息 消息概率 码1 码2 码3 码4 码5 码6 u1 1/4 0 001 1 1 00 000 u2 1/4 10 010 10 01 01 001 U3 1/8 00 011 100 001 100 011 u4 1/8 11 100 1000 0001 101 100 u5 1/8 01 101 10000 00001 110 101 u6 1/16 001 110 100000 000001 1110 1110 u71/161111111000000000000111111111(1) 这些码中哪些是惟一可译码? (2) 这些码中哪些是即时码?(3) 对所有唯一可译码求出其平均码长。
信息论与编码习题参考答案(全)
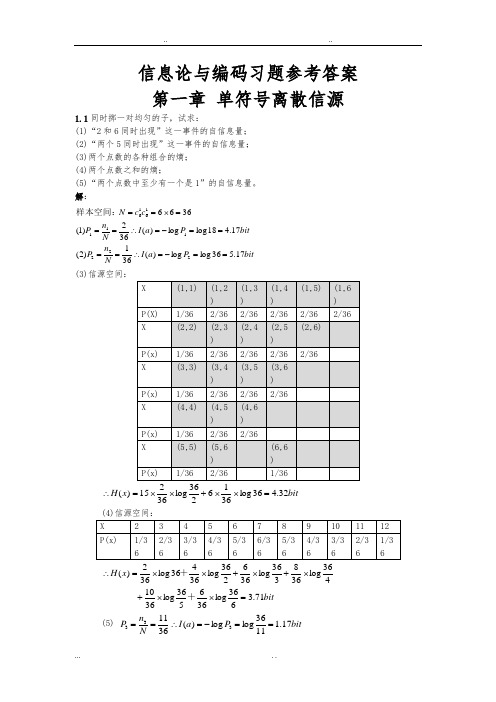
信息论与编码习题参考答案 第一章 单符号离散信源1.1同时掷一对均匀的子,试求:(1)“2和6同时出现”这一事件的自信息量; (2)“两个5同时出现”这一事件的自信息量; (3)两个点数的各种组合的熵; (4)两个点数之和的熵;(5)“两个点数中至少有一个是1”的自信息量。
解:bitP a I N n P bit P a I N n P c c N 17.536log log )(361)2(17.418log log )(362)1(36662221111616==-=∴====-=∴===⨯==样本空间:(3)信源空间:bit x H 32.436log 3662log 3615)(=⨯⨯+⨯⨯=∴ (4)信源空间: bitx H 71.3636log 366536log 3610 436log 368336log 366236log 36436log 362)(=⨯⨯+⨯+⨯+⨯⨯=∴++ (5) bit P a I N n P 17.11136log log )(3611333==-=∴==1.2如有6行、8列的棋型方格,若有两个质点A 和B ,分别以等概落入任一方格,且它们的坐标分别为(Xa ,Ya ), (Xb ,Yb ),但A ,B 不能同时落入同一方格。
(1) 若仅有质点A ,求A 落入任一方格的平均信息量; (2) 若已知A 已落入,求B 落入的平均信息量; (3) 若A ,B 是可辨认的,求A ,B 落入的平均信息量。
解:bita P a P a a P a I a P A i 58.548log )(log )()(H 48log )(log )(481)(:)1(481i i i i i ==-=∴=-=∴=∑=落入任一格的概率bitb P b P b b P b I b P A i 55.547log )(log )()(H 47log )(log )(471)(:B ,)2(481i i i i i ==-=∴=-=∴=∑=落入任一格的概率是落入任一格的情况下在已知 bitAB P AB P AB H AB P AB I AB P AB i i i i i i i 14.11)4748log()(log )()()(log )(471481)()3(47481=⨯=-=-=∴⨯=∑⨯=是同时落入某两格的概率1.3从大量统计资料知道,男性中红绿色盲的发病率为7%,女性发病率为0.5%.如果你问一位男士:“你是否是红绿色盲?”他的回答可能是:“是”,也可能“不是”。
信息论基础第2章离散信源及其信息度量

第2章 离散信源及其信息度量
本章内容
2.1 离散信源的分类 2.2 离散信源的统计特性 2.3 离散随机变量的信息度量 2.4 离散信源的N次扩展信源 2.5 离散平稳信源 2.6 马尔可夫信源 2.7 离散信源的相关性和剩余度
《信息论基础》
2.1 离散信源的分类
离散信源的分类
按照离散信源输出的是一个消息符号还是消息符 号序列,可分为单符号离散信源和多符号离散信 源。
,
q2 pn
,
qm ) pn
n
m
其中, pi 1, qj pn 。
i1
j 1
可见,由于划分而产生的不确定性而导致熵的增加量为
pnHm (
q1 pn
,
q2 pn
, qm pn
)
6、上凸性
熵函数 H (p) 是概率矢量 p ( p1, p2 ,
pq ) 的严格∩型凸函数
( 或 称 上 凸 函 数 )。 即 对 任 意 概 率 矢 量 p1 ( p1, p2 , pq ) 和
成 H ( p1) 或 H ( p2 ) 。
和自信息相似,信息熵 H ( X ) 有两种物理含义:
① 信源输出前,信源的信息熵表示信源的平均 不确定度。
② 信源输出后,信源的信息熵表示信源输出一 个离散消息符号所提供的平均信息量。如果信道无噪 声干扰,信宿获得的平均信息量就等于信源的平均信 息量,即信息熵。需要注意的是,若信道中存在噪声, 信宿获得的平均信息量不再是信息熵,而是 2.5 节介 绍的平均互信息。
联合熵 H (XY ) 的物理含义表示联合离散符号集 XY 上
的每个元素对平均提供的信息量或平均不确定性。 单位为“bit/符号对”。 需要注意的是,两个随机变量 X 和 Y 既可以表示两个
2015秋.信息论.第2章离散信源与信息熵

第2章离散信源与信息熵信号 信号+干扰 消息干扰消息 信源 编码器 信道 译码器 信宿 噪声源通信系统模型信息2.1 信源的分类和描述信源是信息的发源地,可以是人、生物、机器或其他事物。
信源的输出是包含信息的消息。
消息的形式可以是离散的或连续的。
信源输出为连续信号形式(如语音),可用连续随机变量描述。
连续信源←→模拟通信系统信源输出是离散的消息符号(如书信),可用离散随机变量描述。
离散信源←→数字通信系统离散信源…X i…X j…离散无记忆信源:输出符号Xi Xj之间相互无影响;离散有记忆信源:输出符号Xi Xj之间彼此依存。
3离散信源无记忆有记忆发出单个符号发出符号序列马尔可夫信源非马尔可夫信源y j将一粒棋子随意地放在棋盘中的某列;棋子放置的位置是一个随机事件;可看做一个发出单个符号的离散信源。
x i1212,,...,(),(),...,()m m x x x X P p x p x p x ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦就数学意义来讲,信源就是一个概率场,可用概率空间来描述信源。
由离散随机变量X 表示棋子位置:10()1,()1m i ii p x p x =≤≤=∑i x 其中,代表随机事件的某一结果。
2.2离散信源的信息熵信息的可度量性是信息论建立的基础;香农的信息论用事件发生概率的对数来描述事件的不确定性,得到消息的信息量,建立熵的概念。
2.2.1自信息量–定义2.1 任意随机事件x i 的自信息量定义为:i i i 1(x )log log (x )(x )I P P ==-小概率事件所包含的不确定性大,自信息量大。
大概率事件所包含的不确定性小,自信息量小。
概率为1的确定性事件,自信息量为零。
i i i 1(x )log log (x )(x )I P P ==-信息量的单位与公式中的对数取底有关。
以2为底,单位比特(bit );以e 为底,单位奈特(nat );()22log log ,log log ln log c a c b b x e x a==⋅–例:棋盘共8列,甲随手一放,将一枚棋子放在了第3列。
第3章-离散信源(1)题与答案

3.1 设有一离散无记忆信源,其概率空间为⎭⎬⎫⎩⎨⎧=====⎥⎦⎤⎢⎣⎡8/14/1324/18/310)(4321x x x x X P X 该信源发出的信息序列为(202 120 130 213 001 203 210 110 321 010 021 032 011 223 210)。
求:(1) 此消息的自信息量是多少?(2) 此消息中平均每符号携带的信息量是多少?解: (1)此消息总共有14个0、13个1、12个2、6个3,因此消息发出的概率是:62514814183⎪⎭⎫ ⎝⎛⨯⎪⎭⎫ ⎝⎛⨯⎪⎭⎫ ⎝⎛=p此消息的信息量是:bit p I 811.87log =-=(2)此消息中平均每符号携带的信息量是:bit n I 951.145/811.87/==3.2 某一无记忆信源的符号集为{0, 1},已知信源的概率空间为⎭⎬⎫⎩⎨⎧=⎥⎦⎤⎢⎣⎡4/34/110)(X P X(1) 求信息符号的平均熵;(2) 由100个符号构成的序列,求某一特定序列(例如有m 个“0”和(100 - m )个“1”)的自信息量的表达式; (3) 计算(2)中序列的熵。
解: (1)bit x p x p X H ii i 811.043log 4341log 41)(log )()(=⎪⎭⎫ ⎝⎛+-=-=∑(2)bit m x p x I x p mi i m mm i 585.15.4143log)(log )(434341)(100100100100100+=-=-==⎪⎭⎫ ⎝⎛⨯⎪⎭⎫ ⎝⎛=---(3)bit X H X H 1.81811.0100)(100)(100=⨯==3.5 某信源的消息符号集的概率分布和二进制代码如题表3.2所列。
题表 3.2(1) (2) 求每个消息符号所需要的平均二进制码的个数或平均代码长度。
进而用这一结果求码序列中的一个二进制码的熵;(3) 当消息是由符号序列组成时,各符号之间若相互独立,求其对应的二进制码序列中出现0和1的无条件概率0p 和1p ,求相邻码间的条件概率1/0p 、0/1p 、1/1p 、0/0p 。
第三章离散信源

p(xi )
? 熵函数的自变量是X,表示信源整体,实质上是无
记忆信源平均不确定度的度量。试验后平均信息
量为熵
不确定性=携载的信息
? 单位:以2为底,比特/符号
? 为什么要用熵这个词与热熵的区别?
例3.2.1二元熵函数是对0-1分布的随机变量所求的熵:
X
0
1
=
P(x)
p
1-p
则: H(X) = -plogp-(1-p)log(1-p)=H(p)
? ?X
??P( X
? )??
?
? x1,
? ?
p(
x1
),
x2,? , p(x2 ),?
xi ,? , , p(xi
),?
,
p(
xn ? xn )??
,
n i?1
p(xi )
?
1
则信源X的N次扩展信源用 X N来表示,该新信源有 nN个元素(消息序列)
取值于同一集合
,且分量之间
统计{ 独x1 ,立x 2,, ? 则, x由n }随机矢量 X 组成的新信源称为
离散无记忆信源 X的N次扩展信源。
离散无记忆信源 X的N次扩展信源 (或称序列信 源)的熵就是离散信源 X的熵的N倍。
H ( X N ) ? NH ( X )
理解
若单符号离散信源的数 学模型为 :
qN
qN q
? P(? i ) ? ?? P(aik ) ? 1
i?1
i? 1 ik ? 1
有记忆信源:输出的随机序列 X中各随机变量 之间有依赖关系,但记忆长度有限。 m阶马尔可夫信源:信源每次发出的符号只与 前m个符号有关,与更前面的符号无关。
P(xi |? xi?2xi?1xi?1xi?2xi?3 ? xi?m ? xi?1)
信息论与编码(第三版) 第4章 离散信源编码理论-0525

1
1
N log p(x1x2...xN ) N i log p(xi )
-E log p(x) 以概率
H(X)
定义4.1 关于p(x)的典型集合 A( N ) 是序列 (x1x2...xN ) X 的集合,具有下列性质 2N (H ( X ) ) p(x1x2...xN ) 2N (H ( X ) )
)
H(X
)
|
}
1
得到性质2
性质(3) 2 | A | 1 p(X)
p(X)
2N (H ( X ) )
XxN
XA ( N )
XA( N )
N (H ( X ) ) (N )
渐近等同 分割含义
典型序列 定义
相同数据 相加
性质(4) 对于充分大的N p{A (N)} 1
2 | A | 1 p{A(N)}
前
缀
典型序列数量不大于2N(H(X)+ε)
编码:0+序列编号
码
码长 N(H ) 2
非典型序列
编码:1+序列编号
码长: N log | X | 1
这是一种无失 真编码方法
❖ 上述的编码方案具有下列性质:
码与序列之间是一一对应的,第一位是前缀码,表示码的长 度或者类型。
非典型序列采用的是枚举法,尽管没有考虑非典型序列的长
X p(x)
0 p(0)
p
1 p(1) q
主要关心典型序 列,典型序列的 任何特性都是以 大概率成立的, 而且决定了样点
值的主要特性
如果随机变量 X1, X2,..., X N 都服从独立同一分布
那么序列 (x1x2...xN ) 的概率为
第3章离散信源习题与答案

3.1 设有一离散无记忆信源,其概率空间为⎭⎬⎫⎩⎨⎧=====⎥⎦⎤⎢⎣⎡8/14/1324/18/310)(4321x x x x X P X 该信源发出的信息序列为(202 120 130 213 001 203 210 110 321 010 021 032 011 223 210)。
求:(1) 此消息的自信息量是多少?(2) 此消息中平均每符号携带的信息量是多少?解: (1)此消息总共有14个0、13个1、12个2、6个3,因此消息发出的概率是:62514814183⎪⎭⎫ ⎝⎛⨯⎪⎭⎫ ⎝⎛⨯⎪⎭⎫ ⎝⎛=p此消息的信息量是:bit p I 811.87log =-=(2)此消息中平均每符号携带的信息量是:bit n I 951.145/811.87/==3.2 某一无记忆信源的符号集为{0, 1},已知信源的概率空间为⎭⎬⎫⎩⎨⎧=⎥⎦⎤⎢⎣⎡4/34/110)(X P X(1) 求信息符号的平均熵;(2) 由100个符号构成的序列,求某一特定序列(例如有m 个“0”和(100 - m )个“1”)的自信息量的表达式; (3) 计算(2)中序列的熵。
解: (1)bit x p x p X H ii i 811.043log 4341log 41)(log )()(=⎪⎭⎫ ⎝⎛+-=-=∑(2)bit m x p x I x p mi i m mm i 585.15.4143log)(log )(434341)(100100100100100+=-=-==⎪⎭⎫ ⎝⎛⨯⎪⎭⎫ ⎝⎛=---(3)bit X H X H 1.81811.0100)(100)(100=⨯==3.5 某信源的消息符号集的概率分布和二进制代码如题表3.2所列。
题表 3.2(1) (2) 求每个消息符号所需要的平均二进制码的个数或平均代码长度。
进而用这一结果求码序列中的一个二进制码的熵;(3) 当消息是由符号序列组成时,各符号之间若相互独立,求其对应的二进制码序列中出现0和1的无条件概率0p 和1p ,求相邻码间的条件概率1/0p 、0/1p 、1/1p 、0/0p 。
信息论习题

信息论部分:1. 已经两个离散信源X 和Y ,其联合概率P(X,Y)为:P(0,0)=1/8,P(0,1)=3/8,P(1,0)=3/8,P(1,1)=1/8,现定义另一个随机变量:Z=XY(一般乘积),试求H(X),H(Y),H(Z)及H(X,Y)。
2. 有一个一阶马尔柯夫信源X={A,B,C},已知:p(A)=1/2,p(B)=p(C)=1/4,信源状态之间的转移概率p(j/i)分别为:p(A/A)=1/2, p(B/A)=1/4, p(C/A)=1/4, p(A/B)=2/3, p(B/B)=0, p(C/B)=1/3, p(A/C)=2/3, p(B/C)=1/3, p(C/C)=0。
求:信源的熵和剩余度?3. 设一个连续随机变量X 的概率密度函数为p x bx x ()=≤⎧⎨⎪⎩⎪202 π其它 求信源X 的熵H(X)。
4. 设一个连续随机变量X 的概率密度函数为 p x e ()=-12λλX -∞<X <∞ 求信源X 的熵H(X)。
5.掷一枚均匀的硬币,直到出现“正面”为止。
令X 表示所需掷出的次数,求熵H(X)。
6.设有噪声二元对称信道(BSC)的信道误码率为p e =1/8,码速率为n=1000/s,(1)若p(0)=1/3, p(1)=2/3, 求信道熵速率, (2)求信道容量。
7.某无线电厂可生产A ,B ,C ,D 四种产品,其中,A 占10%,B 占20% ,C 占30% ,D 占40%。
有两种消息:“现完成一台B 种产品”,“现完成一台C 种产品”,试问哪一种消息提供的信息量大? 8.设每帧电视图象是由3×105个象素组成,所有象素是相互独立的,且每个象素可取128个不同的亮度电平,并假设各种亮度电平是等概出现的。
问每帧电视图象含有多少信息量?9.设电话信号的信息速率为5.6×104bit/s ,在一个噪声功率谱密度为N 0=5×10-6mW/Hz ,频带为F ,限输入功率为P 的高斯信道中传送,若F=4KHz ,问无差错传输所需的最小功率是多少?若F 趋于无穷,则P 是多少瓦。
信息论编码模拟试题8及参考答案

模拟试题一一、概念简答题(共10题,每题5分)1.简述离散信源和连续信源的最大熵定理。
2.什么是平均自信息(信息熵)?什么是平均互信息?比较一下两个概念的异同之处。
3.解释等长信源编码定理和无失真变长信源编码定理,说明对于等长码和变长码,最佳码的每符号平均码长最小为多少?编码效率最高可达多少?4.解释最小错误概率译码准则,最大似然译码准则和最小距离译码准则,说明三者的关系。
5.设某二元码字C={111000,001011,010110,101110},①假设码字等概率分布,计算此码的编码效率?②采用最小距离译码准则,当接收序列为110110时,应译成什么码字?6.一平稳二元信源,它在任意时间,不论以前发出过什么符号,都按发出符号,求和平均符号熵7.分别说明信源的概率分布和信道转移概率对平均互信息的影响,说明平均互信息与信道容量的关系。
8.二元无记忆信源,有求:(1)某一信源序列由100个二元符号组成,其中有m个“1”,求其自信息量?(2)求100个符号构成的信源序列的熵。
9.求以下三个信道的信道容量:,,10.已知一(3,1,3)卷积码编码器,输入输出关系为:试给出其编码原理框图。
二、综合题(共5题,每题10分)1.二元平稳马氏链,已知P(0/0)=,P(1/1)=,求:(1)求该马氏信源的符号熵。
(2)每三个符号合成一个来编二进制Huffman码,试建立新信源的模型,给出编码结果。
(3)求每符号对应的平均码长和编码效率。
2.设有一离散信道,其信道矩阵为,求:(1)最佳概率分布?(2)当,时,求平均互信息信道疑义度(3)输入为等概率分布时,试写出一译码规则,使平均译码错误率最小,并求此3.设线性分组码的生成矩阵为,求:(1)此(n,k)码的n=? k=?,写出此(n,k)码的所有码字。
(2)求其对应的一致校验矩阵H。
(3)确定最小码距,问此码能纠几位错?列出其能纠错的所有错误图样和对应的伴随式。
信息论习提答案

1、 熵 是香农信息论最基本最重要的概念。
2、 单符号离散信源一般用随机变量描述,而多符号离散信源一般用 随机矢量 描述。
3、 两个相互独立的随机变量的联合自信息量等于 两个自信息量之和 。
4、 离散平稳无记忆信源X 的N 次扩展信源的熵等于离散信源X 的熵的 N 倍 。
5、 对于n 元m 阶马尔可夫信源,其状态空间共有 n m 个不同的状态。
6、 若一离散无记忆信源的信源熵H (X )等于4.2,对信源进行等长的无失真二进制编码,则编码长度至少为 5 。
7、 同时掷两个正常的骰子,各面呈现的概率都为1/6,则“3和6同时出现”这件事的自信息量是 log 218或(1+2 log 23)。
8、 一副充分洗乱的扑克牌(52张),从中任意抽取1张,然后放回,若把这一过程看作离散无记忆信源,则其信源熵为 52log 2 。
9、 具有一一对应关系的无噪信道的信道容量C= log 2n 。
10、 信道编码定理是一个理想编码的存在性定理,即:信道无失真传递信息的条件是 信息率小于信道容量 。
11、 信源的消息通过信道传输后的误差或失真越大,信宿收到消息后对信源存在的不确定性就 越大 ,获得的信息量就越小12、 平均失真度的下限取0的条件是失真矩阵的 每一行至少有一个零元素 。
13、 率失真函数对允许的平均失真度是 单调递减和连续的 。
14、 对于离散无记忆信源的率失真函数的最大值是 log 2n 。
15、 信源编码的目的是: 提高通信的有效性 。
16、 对具有8个消息的单符号离散无记忆信源进行4进制哈夫曼编码时,为使平均码长最短,应增加 2 个概率为0的消息。
17、 对于香农编码、费诺编码和哈夫曼编码,编码方法惟一的是 香农编码 。
18、 游程序列的熵 等于 原二元序列的熵。
19、 n 位重复码的编码效率是 1/n 。
20、 若纠错码的最小距离为d min ,则可以纠正任意小于等于t= ⎥⎦⎥⎢⎣⎢-21min d 个差错。
3.3离散平稳信源

信息论与编码技术电子信息工程专业主讲:孙静机械电子工程系3.3 离散平稳信源3.3.1 离散有记忆信源1.实际情况中,离散信源输出的是在空间或时间的离散符号序列,而且在序列中符号之间有依赖关系。
让我们来看两个例子!中文自然语言:字符集A={所有汉字,标点符号}根据中文的语法、习惯用语、修辞制约和表达实际意义的制约所构成的中文序列才是有意义的中文句子或文章在汉字序列中前后文字的出现是有依赖的,不能认为是彼此不相关的其他自然语言都一样,如英文、德文等离散化平面灰度图像:从XY平面空间上看,每幅画面是一系列空间离散的灰度值符号(像素点)空间每一点的符号取值是随机的可以形成不同的图像信息【分析】这类信源具有如下特点:信源输出的消息是按一定概率选取的符号序列→可用随机矢量或随机变量序列来描述这类消息输出序列的符号之间存在或强或弱的相关性→有记忆信源→研究信源的多维联合概率分布和条件概率分布3.3.1 离散有记忆信源2.离散有记忆信源是指发出的各个符号之间具有统计关联关系的一类信源。
3.【研究对象】在一般情况下,信源的前后消息之间有前后依赖关系,可以用随机矢量描述:X=X1X2…X N其中,任一X都是离散随机变量,它表i示t=i 时刻所输出的符号。
3.3.1 离散有记忆信源4.信源在t =i 时刻将要输出的符号取决于两个方面:①与信源在t =i 时刻随机变量X i 取值的概率分布p (x i )有关➢一般t 不同,p (x i ) ≠p (x j ) ②与t =i 时刻以前信源输出的符号有关➢与条件概率p (x i |x i -1x i -2…)有关➢一般情况下,p (x i |x i -1x i -2…) ≠p (x j |x j -1x j -2…)一般来说,离散信源输出序列的统计特性可能会随时间而变化,在不同时刻,其输出序列的概率分布可能不同。
3.3.2 离散平稳信源1.【问题】有时离散信源其消息出现的概率,与消息出现的时间无关,即为平稳信源。
《通信原理》试题及答案

一、填空题1、某四进制信源,其中一个信号出现的概率为1/2,且各符号出现的概率是相对独立的,则要使该符号集的平均信息量最大,其余三个符号出现的概率分别为_________2、某二进制信息代码为100000000001100000,其对应的HDB3码为__________3、在数字基带传输系统中,减小码间串扰的措施有_________4、若信道传输带宽为3KHz,信噪比为30dB,该信道的最高信息传输速率理论值为__________5、某FM信号为S FM(t)=10cos(2π×106t+8sin2π×103t),该调频波的带宽为_______Hz6、在 2ASK、2FSK、 2PSK这三种调制方式中,_______的误码率最小,______的频带利用率最低。
7、狭义平稳过程,其一维分布与____________无关;二维分布仅与____________有关。
8、若4PSK系统中的四个符号独立等概出现,信息速率为1Mb/s,抽样判决器的位定时信号的频率为________9、13折线A率编码器,其最小量化级为1个单位,已知抽样脉冲值为-718单位,则编码器输出码组为____________(段内码采用折叠二进制码)10、在模拟脉冲调制中,PDM称为____________调制11、为了提高频带利用率,并使冲击响应尾巴震荡衰减加快,而有控制地在某些码元的抽样时刻引入码间干扰,这种技术称为___________12、衡量均衡器效果的两个准则是:____________准则和____________准则13、2DSK , 2ASK , 2PSK , 2FSK, 采用相干解调时,抗信道加性高斯白噪声性能从好到坏排列顺序_________________________________14、码元速率相同,八进制的信息速率是二进制的________________倍(等概时)15、AM调制在__________________情况下会出现门限效应。
信息论与编码理论-习题答案-姜楠-王健-编著-清华大学

可得 ,3种状态等概率分布。
一阶马尔可夫信源熵为
信源剩余度为
(2)二阶马尔可夫信源有9种状态(状态转移图略),同样列方程组求得状态的平稳分布为
二阶马尔可夫信源熵为
信源剩余度为
由于在上述两种情况下,3个符号均为等概率分布,所以信源剩余度都等于0。
总的概率
所需要的信息量
2.6设 表示“大学生”这一事件, 表示“身高1.60m以上”这一事件,则
故
2.7四进制波形所含的信息量为 ,八进制波形所含信息量为 ,故四进制波形所含信息量为二进制的2倍,八进制波形所含信息量为二进制的3倍。
2.8
故以3为底的信息单位是比特的1.585倍。
2.9(1)J、Z(2)E(3)X
(2)三元对称强噪声信道模型如图所示。
4.7由图可知信道1、2的信道矩阵分别为
它们串联后构成一个马尔科夫链,根据马氏链的性质,串联后总的信道矩阵为
4.8传递矩阵为
输入信源符号的概率分布可以写成行向量形式,即
由信道传递矩阵和输入信源符号概率向量,求得输出符号概率分布为
输入符号和输出符号的联合概率分布为
由冗余度计算公式得
3.18(1)由一步转移概率矩阵与二步转移概率矩阵的公式 得
(2)设平稳状态 ,马尔可夫信源性质知 ,即
求解得稳态后的概率分布
3.19设状态空间S= ,符号空间
且
一步转移概率矩阵
状态转移图
设平稳状态 ,由马尔可夫信源性质有
即
可得
马尔可夫链只与前一个符号有关,则有
3.20消息元的联合概率是
平均信息传输速率
信息论与编码填空题

信息论与编码填空题1. 在无失真的信源中,信源输出由H (X )来度量;在有失真的信源中,信源输出由 R (D ) 来度量。
2. 要使通信系统做到传输信息有效、可靠和保密,必须首先信源编码,然后_加密_编码,再_信道编码,最后送入信道。
3. 带限AWGN 波形信道在平均功率受限条件下信道容量的基本公式,也就是有名的香农公式是log(1)C W SNR =+;当归一化信道容量C/W 趋近于零时,也即信道完全丧失了通信能力,此时E b /N 0为dB ,我们将它称作香农限,是一切编码方式所能达到的理论极限。
4. 保密系统的密钥量越小,密钥熵H (K )就越小,其密文中含有的关于明文的信息量I (M ;C )就越大。
5. 已知n =7的循环码42()1g x x x x =+++,则信息位长度k 为 3 ,校验多项式h(x)= 31x x ++ 。
6. 设输入符号表为X ={0,1},输出符号表为Y ={0,1}。
输入信号的概率分布为p =(1/2,1/2),失真函数为d (0,0) = d (1,1) = 0,d (0,1) =2,d (1,0) = 1,则D min = 0 ,R (D min )= 1bit/symbol ,相应的编码器转移概率矩阵[p(y/x )]=1001;D max =,R (D max )=0 ,相应的编码器转移概率矩阵[p(y/x )]=1010。
7. 已知用户A 的RSA 公开密钥(e,n )=(3,55),5,11p q ==,则()φn = 40 ,他的秘密密钥(d,n )=(27,55) 。
若用户B 向用户A 发送m =2的加密消息,则该加密后的消息为 8 。
1.设X的取值受限于有限区间[a,b ],则X 服从均匀分布时,其熵达到最大;如X 的均值为μ,方差受限为2σ,则X 服从高斯分布时,其熵达到最大。
2.信息论不等式:对于任意实数0>z ,有1ln -≤z z ,当且仅当1=z 时等式成立。
第二章 信源习题

1、设英文字母E出现的概率为0.105,X出现的概率为0.002,试求E和X 的信息量。
2、某离散信源输出x1、x2、…、x8共8个不同的消息,符号速率为2400B,其中四个消息出现的概率为P(x1)=P(x2)=1/16,P(x3)=1/8,P(x4)=1/4,其他消息等概率出现。
①求该信源的平均信息速率;②求传送一小时的信息量。
3、设一离散信源分别以概率P A、P B、P C、P D发送四个消息A、B、C、D,每个消息的出现是相互独立的,试根据条件完成以下计算:①如果P A=1/4,P B =1/8,P C =1/8,P D=1/2,试计算该信源的熵;②对于传输的每一消息用二进制脉冲编码,00代表A,01代表B,11代表C,10代表D,每个脉冲宽度为5ms,如果不同的消息等可能出现,试计算传输的平均信息速率;③如果P A=1/5,P B =1/4,P C =1/4,P D=3/10,试用Huffman编码算法对该信源进行编码,并计算编码效率。
4、设A系统以2000bps的比特率传输2PSK调制信号的带宽为2000Hz,B 系统以2000bps的比特率传输4PSK调制信号的带宽为1000Hz。
试问:哪个系统更有效?5、设某四进制数字传输系统的每个码元的持续时间(宽度)为833×10-6s,连续工作1h后,接收端收到6个错码,且错误码元中仅发生1bit的错码。
①求该系统的码元速率和信息速率;②求该系统的误码率和误信率。
6、设某数字传输系统传送二进制码元的速率为1200B,试求该系统的信息速率;若该系统改为传送八进制信号码元,码元速率不变,则这时系统的信息速率为多少?7、设输入抽样器的信号为门函数G(t),宽度为τ=20ms,若忽略其频谱第10个零点以外的频率分量,试求其最小抽样频率。
8、已知信号f(t)=6.4×sin(800πt),按Nyquist速率进行抽样后,进行64个电平均匀量化编码,采用自然二进制码。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
设有一离散无记忆信源,其概率空间为⎭⎬⎫⎩⎨⎧=====⎥⎦⎤⎢⎣⎡8/14/1324/18/310)(4321x x x x X P X 该信源发出的信息序列为(202 120 130 213 001 203 210 110 321 010 021 032 011 223 210)。
求:(1) 此消息的自信息量是多少?(2) 此消息中平均每符号携带的信息量是多少?解: (1)此消息总共有14个0、13个1、12个2、6个3,因此消息发出的概率是:62514814183⎪⎭⎫ ⎝⎛⨯⎪⎭⎫ ⎝⎛⨯⎪⎭⎫ ⎝⎛=p此消息的信息量是:bit p I 811.87log =-=(2)此消息中平均每符号携带的信息量是:bit n I 951.145/811.87/==某一无记忆信源的符号集为{0, 1},已知信源的概率空间为⎭⎬⎫⎩⎨⎧=⎥⎦⎤⎢⎣⎡4/34/110)(X P X(1) 求信息符号的平均熵;(2) 由100个符号构成的序列,求某一特定序列(例如有m 个“0”和(100 - m )个“1”)的自信息量的表达式; (3) 计算(2)中序列的熵。
解: (1)bit x p x p X H ii i 811.043log 4341log 41)(log )()(=⎪⎭⎫ ⎝⎛+-=-=∑(2)bit m x p x I x p mi i m mm i 585.15.4143log)(log )(434341)(100100100100100+=-=-==⎪⎭⎫ ⎝⎛⨯⎪⎭⎫ ⎝⎛=---(3)bit X H X H 1.81811.0100)(100)(100=⨯==某信源的消息符号集的概率分布和二进制代码如题表所列。
题表(1) (2) 求每个消息符号所需要的平均二进制码的个数或平均代码长度。
进而用这一结果求码序列中的一个二进制码的熵;(3) 当消息是由符号序列组成时,各符号之间若相互独立,求其对应的二进制码序列中出现0和1的无条件概率0p 和1p ,求相邻码间的条件概率1/0p 、0/1p 、1/1p 、0/0p 。
解: (1)bit x p x p X H ii i 75.181log 8181log 8141log 4121log 21)(log )()(=⎪⎭⎫ ⎝⎛+++-=-=∑(2)bit X H LX H N X H l x p l E L N ii i i 1)(1)(1)(75.1381381241121)()(====⨯+⨯+⨯+⨯===∑(3)设消息序列长为N ,则0u 、1u 、2u 、3u 的个数分别为8/ ,8/ ,4/ ,2/N N N N 个。
则0的个数为8708181412NN N N N =⨯+⨯+⨯+⨯ 而1的个数为8738281402NN N N N =⨯+⨯+⨯+⨯因而5.010==p p212141/ 21212121/21212121/ 212141/1111/11010/10000/01101/0====⨯===⨯=====p p p p p p p p p p p p设有一个信源,它产生0,1序列的信息。
该信源在任意时间而且不论以前发生过什么消息符号,均按P(0) = ,P(1) = 的概率发出符号。
(1) 试问这个信源是否是平稳的;(2) 试计算H(X 2), H(X 3/X 1X 2)及H ∞;(3) 试计算H(X 4)并写出X 4信源中可能有的所有符号。
解: (1)这个信源是平稳无记忆信源。
因为有这些词语:“它在任意时间....而且不论以前发生过什么符号...........……” (2)bitX H X X X X H H bit x p x p X H X X X H bitX H X H N N N N ii i 971.0)().../(lim 971.0)6.0log 6.04.0log 4.0()(log )()()/( 942.1)6.0log 6.04.0log 4.0(2)(2)(12132132====+-=-===+⨯-==-∞>-∞∑(3)1111111011011100101110101001100001110110010101000011001000010000的所有符号: 884.3)6.0log 6.04.0log 4.0(4)(4)(44X bit X H X H =+⨯-==有一马尔可夫信源,已知转移概率为3/2)/(11=S S p ,3/1)/(12=S S p ,1)/(21=S S p ,0)/(22=S S p 。
试画出状态转移图,并求出信源熵。
解:bitS S p S S p S p H S p S p S p S p S p S p S p S p S p S p S p S S p S p S S p S p S p S S p S p S S p S p S p iji j i j i 689.0 31log 314332log 3243 )/(log )/()(4/1)(4/3)(1)()()(31)()(31)()()(32)()/()()/()()()/()()/()()(2121121221112122222121111=⎪⎭⎫ ⎝⎛⨯+⨯-=-=⎩⎨⎧==⎪⎩⎪⎨⎧=+=⎪⎪⎩⎪⎪⎨⎧=+=⎩⎨⎧+=+=∑∑∞2/3黑白传真机的信息元只有黑色和白色两种X ={黑,白},一般气象图上黑色出现的概率为P(黑) = ,白色出现的概率为P(白) = ,黑白消息前后没有关联,其转移概率为P(白/白) = ,P(黑/白) = ,P(白/黑) = ,P(黑/黑) = 。
求该一阶马尔可夫信源的不确定性H(X/X),并画出该信源的状态转移图。
解:bitS S p S S p S p H S p S p S p S p S p S p S p S p S p S p S p S p S S p S p S S p S p S p S S p S p S S p S p S p iji j i j i 553.0 9.0log 9.0321.0log 1.0322.0log 2.0318.0log 8.031 )/(log )/()(3/2)(3/1)(1)()()(2)()(2.0)(9.0)()(1.0)(8.0)()/()()/()()()/()()/()()(21211212221112122222121111=⎪⎭⎫⎝⎛⨯+⨯+⨯+⨯-=-=⎩⎨⎧==⎩⎨⎧=+=⎩⎨⎧+=+=⎩⎨⎧+=+=∑∑∞设信源产生A, B, C 三种符号2/1)/(=B B p ,4/1)/()/(==B C p B A p ,8/5)/(=A A p ,4/1)/(=A B p ,8/1)/(=A C p ,8/5)/(=C C p ,4/1)/(=C B p ,8/1)/(=C A p 。
试计算冗余度。
解:⎪⎪⎪⎩⎪⎪⎪⎨⎧++=++=++=)(85)(41)(81)()(41)(21)(41)()(81)(41)(85)(C B A C C B A B C B A A s p s p sp s p s p s p s p s p s p s p s p s pp(黑/黑)=0.8S 1S 2p(白/白)=0.9138.03log 366.111 366.1 85log 853141log 413181log 8131 41log413121log 213141log 4131 81log813141log 413185log 8531 )/(log )/()(3/1)(3/1)(3/1)(1)()()()()()(0333=-=-==⎥⎦⎤⨯+⨯+⨯+⨯+⨯+⨯+⎢⎣⎡⨯+⨯+⨯-=-=⎪⎩⎪⎨⎧===⎩⎨⎧=++==∞∞∑∑∑H H R bit p e e p e e p e p H s p s p s p s p s p s p s p s p s p ijki j i j i CB AC B A C B A一阶马尔可夫信源的状态图如下图所示。
信源X 的符号集为{0, 1, 2}。
(1) 求平稳后信源的概率分布; (2) 求信源的熵H ∞。
解: (1)⎪⎪⎪⎩⎪⎪⎪⎨⎧+=+=+=)(43)(31)()(41)(32)()(41)(43)(323122311s p s p s p s p s p s p s p s p s p⎪⎩⎪⎨⎧===⎪⎩⎪⎨⎧==11/4)(11/3)(11/4)()(43)()()(3211231s p s p s p s p s p s p s p(2)bite e p e e p e p H ijki j i j i 840.0 43log 4311441log 41114 31log3111332log 32113 41log4111443log 43114 )/(log )/()(333=⎥⎦⎤⨯+⨯+⨯+⨯+⎢⎣⎡⨯+⨯-=-=∑∑∑∞。
