原子具有线状光谱ppt
合集下载
原子光谱与分子光谱ppt课件

2024/7/28
“雪亮工程"是以区(县)、乡(镇) 、村( 社区) 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
一、 原子光谱
1.光谱项符号
原子外层有一个电子时,其能级可由四个量子数决定: 主量子数 n;角量子数 l;磁量子数 m;自旋量子数 s; 原子外层有多个电子时,其运动状态用总角量子数L;总 自旋量子数S;内量子数J 描述;
例:钠原子,一个外层电子, S =1/2;因此: M =2( S ) +1 = 2;双重线; 碱土金属:两个外层电子, 自旋方向相同时, S =1/2 + 1/2 =1, M = 3;三重线; 自旋方向相反时, S =1/2 - 1/2 =0, M = 1;单重线;
2024/7/28
“雪亮工程"是以区(县)、乡(镇) 、村( 社区) 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
元素由基态到第一激发 态的跃迁最易发生,需要的 能量最低,产生的谱线也最 强,该谱线称为共振线 ,也 称为该元素的特征谱线;
2024/7/28
“雪亮工程"是以区(县)、乡(镇) 、村( 社区) 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
2024/7/28
“雪亮工程"是以区(县)、乡(镇) 、村( 社区) 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
“雪亮工程"是以区(县)、乡(镇) 、村( 社区) 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
一、 原子光谱
1.光谱项符号
原子外层有一个电子时,其能级可由四个量子数决定: 主量子数 n;角量子数 l;磁量子数 m;自旋量子数 s; 原子外层有多个电子时,其运动状态用总角量子数L;总 自旋量子数S;内量子数J 描述;
例:钠原子,一个外层电子, S =1/2;因此: M =2( S ) +1 = 2;双重线; 碱土金属:两个外层电子, 自旋方向相同时, S =1/2 + 1/2 =1, M = 3;三重线; 自旋方向相反时, S =1/2 - 1/2 =0, M = 1;单重线;
2024/7/28
“雪亮工程"是以区(县)、乡(镇) 、村( 社区) 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
元素由基态到第一激发 态的跃迁最易发生,需要的 能量最低,产生的谱线也最 强,该谱线称为共振线 ,也 称为该元素的特征谱线;
2024/7/28
“雪亮工程"是以区(县)、乡(镇) 、村( 社区) 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
2024/7/28
“雪亮工程"是以区(县)、乡(镇) 、村( 社区) 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
PPT原子吸收光谱法分析原理和方法PPT课件PPT54页

AAS 分析时,待测物浓度很低,该变宽可勿略。
❖ 外界压力增加——谱线中心频率0位移、形状和宽度发生变化—— 发射线与吸收线产生错位——影响测定灵敏度;
❖ 温度在1500-30000C之间,压力为1.01310-5Pa ——热变宽和压变宽 有相同的变宽程度;
❖ 火焰原子化器——压变宽为主要;石墨炉原子化器——热变宽为主 要。
第6页,共54页。
根据吸收定律的表达式,以 I~ 和 K- 分别作图得吸收强度与频 率的关系及谱线轮廓。可见谱线是有宽度的。
K0
K0/2 I0
I K
0
I~ (吸收强度与频率的关系)
0
K~ (谱线轮廓)
图中:
K—吸收系数;K0—最大吸收系数; 0,0—中心频率或波长(由原子能级决定); ,—谱线轮廓半宽度(K0/2处的宽度);
电流越大,光强越大,但过大则谱线变宽且强度不稳定;充入低压惰性气 体可防止与元素反应并减小碰撞变宽。 问题:为什么HCL会产生低背景的锐线光源? 答:低压-原子密度低,Lorentz Broadening小;小电流-温度低Doppler Broadening 小,故产生锐线光源!惰性气体难于激发且谱线相对简单——低背景。
K0
1
D
ln 2 e2 mc
N0 f
1
D
ln 2 e2 (c) f mc
A KcL
上式表明,当用锐线光源作原子吸收测定时,所得A与原子蒸气中待测元素的基态 原子数成正比。
第15页,共54页。
3. 锐线光源 根据Walsh的两点假设,发射线必须是“锐线”(半宽度很小的谱线)。
发射线
吸收线
I
形式,其高度和角度可调(让光通过火焰适宜的部位并有最
❖ 外界压力增加——谱线中心频率0位移、形状和宽度发生变化—— 发射线与吸收线产生错位——影响测定灵敏度;
❖ 温度在1500-30000C之间,压力为1.01310-5Pa ——热变宽和压变宽 有相同的变宽程度;
❖ 火焰原子化器——压变宽为主要;石墨炉原子化器——热变宽为主 要。
第6页,共54页。
根据吸收定律的表达式,以 I~ 和 K- 分别作图得吸收强度与频 率的关系及谱线轮廓。可见谱线是有宽度的。
K0
K0/2 I0
I K
0
I~ (吸收强度与频率的关系)
0
K~ (谱线轮廓)
图中:
K—吸收系数;K0—最大吸收系数; 0,0—中心频率或波长(由原子能级决定); ,—谱线轮廓半宽度(K0/2处的宽度);
电流越大,光强越大,但过大则谱线变宽且强度不稳定;充入低压惰性气 体可防止与元素反应并减小碰撞变宽。 问题:为什么HCL会产生低背景的锐线光源? 答:低压-原子密度低,Lorentz Broadening小;小电流-温度低Doppler Broadening 小,故产生锐线光源!惰性气体难于激发且谱线相对简单——低背景。
K0
1
D
ln 2 e2 mc
N0 f
1
D
ln 2 e2 (c) f mc
A KcL
上式表明,当用锐线光源作原子吸收测定时,所得A与原子蒸气中待测元素的基态 原子数成正比。
第15页,共54页。
3. 锐线光源 根据Walsh的两点假设,发射线必须是“锐线”(半宽度很小的谱线)。
发射线
吸收线
I
形式,其高度和角度可调(让光通过火焰适宜的部位并有最
原子发射光谱详解PPT课件

2020年9月28日
9
直流电弧特点:
优点:样品蒸发能力强(阳极斑)---进入电弧的待测物多--绝对灵敏度高---适于定性分析及低含量杂质的测定,以及部 分矿物、岩石等难熔样品及稀土难熔元素定量; 缺点: 1)电弧不稳----分析重现性差; 2)弧层厚,自吸严重; 3)安全性差; 4)电极头温度比较高 因此不宜用于定量分析及低熔点元素测定
过程:接触短路引燃(或高频引燃);阴极发出电子流,冲击阳极,产生 高热,使试样蒸发,又与电子碰撞,电离成离子,再冲击阴极,引起二次电子 发射……电子再撞击阳极,产生高温阳极斑(4000 K);产生的电弧温度: 4000~7000K,因此在分析间隙各种电子原子粒子相互碰撞,能量交换,引起试 样激发,发射出一定波长的谱线。
而对难熔盐分析的灵敏度略差于直流电弧。
2020年9月28日
12
高压火花:高频高压引燃并放电。
B
L
R1
220V
V~
D C
D
G 分析间隙
220V 10~25kV (B) C充电 击穿分析隙 G 放电;
回路 L-C-G 中高压高频振荡电流, G 放电中断; 下一回合充放电开始 火花不灭。 火花特点: 1)放电稳定,分析重现性好; 2)放电间隙长,电极温度(蒸发温度)低,检出现低,多适于分析易熔金
2. 历史:
• 1859年,基尔霍夫(Kirchhoff G R)、本生(Bunsen R W)
研
制第一台用于光谱分析的分光镜,实现了光谱检验;
• 随后30年——定性分析;
• 1930年以后,建立了光谱定量分析方法;
2020年9月28日
2
10.2 基本原理
一. 原子发射光谱的产生
原子光谱和分子光谱PPT讲稿

(3)化学发光光谱:化学反应物或反应产物受反应释放的 化学能激发而产生的光辐射。(用于化学发光光谱分析法: 发光总强度与分析物浓度成正比。)
光致发光示意图.swf
10:36:46
10:36:46
I f kC
2、分子发光光谱
(1)分子荧光光谱:光致发光,用于分子荧光光谱分析法 (MFS) 定性:荧光光谱 定量:对于一给定的物质,当激发光波长和强度一定时, 发射荧光的强度与物质浓度成正比。
(2)分子磷光光谱:光致发光,用于分子磷光光谱分析 (MPS) 在一定条件下,发射磷光的强度与物质浓度成正比。 荧光与磷光的比较:二者均为光致发光,但发光机理不同 荧光:入射光停止照射,荧光几乎立即停止; 磷光:入射光停止照射,磷光还可持续~10秒。
发射光谱
10:36:46
二、分子光谱
•分子光谱(带光谱):
基于分子中电子能级、振转能级跃迁而产生的光谱。
10:36:46
分子光谱(带状光谱)
原子光谱为线状光谱, 分子光谱为带状光谱; 为什么分子光谱为带状光谱?
10:36:46
原子光谱图 分子光谱图
(一)分子的能级与跃迁 1.分子的能量
E=Ee+ Ev + Er + En + Et + Ei 分子中原子的核能: En 分子的平移能:Et 电子运动能: Ee 原子间相对振动能: Ev 分子转动能: Er 基团间的内旋能: Ei
在一般化学反应中, En不变; Et 、 Ei较小; E=Ee+ Ev + Er
10:36:46
2. 分子的能级:电子能级、振动能级、转动能级
10:36:46
(二)分子吸收光谱和分子发光光谱
1、分子吸收光谱:分子对辐射能的选择吸收 由基态或较低能级跃迁到较高能级产生的分 子光谱。
光致发光示意图.swf
10:36:46
10:36:46
I f kC
2、分子发光光谱
(1)分子荧光光谱:光致发光,用于分子荧光光谱分析法 (MFS) 定性:荧光光谱 定量:对于一给定的物质,当激发光波长和强度一定时, 发射荧光的强度与物质浓度成正比。
(2)分子磷光光谱:光致发光,用于分子磷光光谱分析 (MPS) 在一定条件下,发射磷光的强度与物质浓度成正比。 荧光与磷光的比较:二者均为光致发光,但发光机理不同 荧光:入射光停止照射,荧光几乎立即停止; 磷光:入射光停止照射,磷光还可持续~10秒。
发射光谱
10:36:46
二、分子光谱
•分子光谱(带光谱):
基于分子中电子能级、振转能级跃迁而产生的光谱。
10:36:46
分子光谱(带状光谱)
原子光谱为线状光谱, 分子光谱为带状光谱; 为什么分子光谱为带状光谱?
10:36:46
原子光谱图 分子光谱图
(一)分子的能级与跃迁 1.分子的能量
E=Ee+ Ev + Er + En + Et + Ei 分子中原子的核能: En 分子的平移能:Et 电子运动能: Ee 原子间相对振动能: Ev 分子转动能: Er 基团间的内旋能: Ei
在一般化学反应中, En不变; Et 、 Ei较小; E=Ee+ Ev + Er
10:36:46
2. 分子的能级:电子能级、振动能级、转动能级
10:36:46
(二)分子吸收光谱和分子发光光谱
1、分子吸收光谱:分子对辐射能的选择吸收 由基态或较低能级跃迁到较高能级产生的分 子光谱。
第五章、原子发射光谱(共24张PPT)

交变感应磁场; 2)火花 氩气 气体电离 少量电荷 相互碰
撞 “雪崩”现象 大量载流子;
3)数百安极高感应电流(涡电流,Eddy current) 瞬
间加热 到10000K 等离子体 趋肤效应 内管通入Ar 形成环状结构样品通道 样品蒸发、原 子化、激发。
ICP光源特点
1)低检测限:蒸发和激发温度高;
测量电压(电容电压)为
3)基体效应小(matrix effect): 样品处于化学隋性环境(Ar)的高温分析区
已知光信号产生的电流 i 与谱线强度I成正比,即
内管—载气,样品引入(使用
待测物发出的光谱经分光得一系列谱线,这些不同波长的光在感光板上曝光,经显影、定影后于相板上得到平行排列的谱线(黑线),这些谱线“变
火花特点: 1)放电稳定,分析重现性好; 2)放电间隙长,电极温度(蒸发温度)低,检出现低,多适于分析易熔金
属、合金样品及高含量元素分析;
3)激发温度高(瞬间可达10000K)适于难激发元素分析。
电感耦合等离子体
组成:ICP 高频发生器+ 炬管
+ 样品引入系统
炬管包括:
外管—冷却气,沿切线引入
中管—辅助气,点燃 ICP (点燃
LTE 定性、难熔样品及元素定量、 导体、矿物纯物质
LTE 矿物、低含量金属定量分析
~10000
好 LTE 难激发元素、高含量金属定量
分析
ICP ~10000
6000~8000 很好 非LTE 溶液、难激发元素、大多数元
素
火焰 2000~3000 激光 ~10000
2000~3000 很好 LTE 溶液、碱金属、碱土金属 ~10000 很好 LTE 固体、液体
E0tIijdtK 1 0ti
撞 “雪崩”现象 大量载流子;
3)数百安极高感应电流(涡电流,Eddy current) 瞬
间加热 到10000K 等离子体 趋肤效应 内管通入Ar 形成环状结构样品通道 样品蒸发、原 子化、激发。
ICP光源特点
1)低检测限:蒸发和激发温度高;
测量电压(电容电压)为
3)基体效应小(matrix effect): 样品处于化学隋性环境(Ar)的高温分析区
已知光信号产生的电流 i 与谱线强度I成正比,即
内管—载气,样品引入(使用
待测物发出的光谱经分光得一系列谱线,这些不同波长的光在感光板上曝光,经显影、定影后于相板上得到平行排列的谱线(黑线),这些谱线“变
火花特点: 1)放电稳定,分析重现性好; 2)放电间隙长,电极温度(蒸发温度)低,检出现低,多适于分析易熔金
属、合金样品及高含量元素分析;
3)激发温度高(瞬间可达10000K)适于难激发元素分析。
电感耦合等离子体
组成:ICP 高频发生器+ 炬管
+ 样品引入系统
炬管包括:
外管—冷却气,沿切线引入
中管—辅助气,点燃 ICP (点燃
LTE 定性、难熔样品及元素定量、 导体、矿物纯物质
LTE 矿物、低含量金属定量分析
~10000
好 LTE 难激发元素、高含量金属定量
分析
ICP ~10000
6000~8000 很好 非LTE 溶液、难激发元素、大多数元
素
火焰 2000~3000 激光 ~10000
2000~3000 很好 LTE 溶液、碱金属、碱土金属 ~10000 很好 LTE 固体、液体
E0tIijdtK 1 0ti
《原子发射光谱》课件

不同的样品类型和测量方法对样品制备的要求也不同,因此需要根据实际情况选择 合适的样品制备方法。
样品溶解
样品溶解是原子发射光谱分析 中的重要环节,其目的是将待 测样品中的目标元素充分溶解
在合适的溶剂中。
常用的溶剂有酸、碱、盐等 ,根据待测元素和样品的性
质选择合适的溶剂。
在溶解过程中,需要控制温度 、压力、搅拌速度等条件,以 保证目标元素能够充分溶解在
归一化法
通过比较不同元素谱线强度的比例,消除基体效 应和物理干扰的影响。
Part
06
原子发射光谱的未来发展与挑 战
新技术应用
01
02
03
激光技术
利用激光的高能量和高精 度特性,提高原子发射光 谱的检测灵敏度和分辨率 。
微纳加工技术
将原子发射光谱仪器小型 化、集成化,便于携带和 移动检测。
人工智能技术
利用人工智能算法对原子 发射光谱数据进行处理和 解析,提高分析准确性和 效率。
仪器改进与优化
高性能探测器
研发更灵敏、更快速响应的探测器,提高光谱信号的采集和解析能 力。
高效能光源
优化光源的稳定性和寿命,提高光谱信号的强度和可靠性。
自动化与智能化
实现原子发射光谱仪器的自动化和智能化操作,降低人为误差和操作 复杂度。
高温条件下可实现元素的完全蒸发和激发 ,具有较高的灵敏度和准确度。
需要使用高温电热丝,设备成本较高,且 对某些元素的分析效果不佳。
火花/电弧原子发射光谱法
原理 通过电火花或电弧产生的高温使 待测元素激发为光谱状态,通过 测量光谱线的波长和强度,进行 定性和定量分析。
缺点 分析速度较慢,设备成本较高, 且对某些元素的分析效果不佳。
应用范围
样品溶解
样品溶解是原子发射光谱分析 中的重要环节,其目的是将待 测样品中的目标元素充分溶解
在合适的溶剂中。
常用的溶剂有酸、碱、盐等 ,根据待测元素和样品的性
质选择合适的溶剂。
在溶解过程中,需要控制温度 、压力、搅拌速度等条件,以 保证目标元素能够充分溶解在
归一化法
通过比较不同元素谱线强度的比例,消除基体效 应和物理干扰的影响。
Part
06
原子发射光谱的未来发展与挑 战
新技术应用
01
02
03
激光技术
利用激光的高能量和高精 度特性,提高原子发射光 谱的检测灵敏度和分辨率 。
微纳加工技术
将原子发射光谱仪器小型 化、集成化,便于携带和 移动检测。
人工智能技术
利用人工智能算法对原子 发射光谱数据进行处理和 解析,提高分析准确性和 效率。
仪器改进与优化
高性能探测器
研发更灵敏、更快速响应的探测器,提高光谱信号的采集和解析能 力。
高效能光源
优化光源的稳定性和寿命,提高光谱信号的强度和可靠性。
自动化与智能化
实现原子发射光谱仪器的自动化和智能化操作,降低人为误差和操作 复杂度。
高温条件下可实现元素的完全蒸发和激发 ,具有较高的灵敏度和准确度。
需要使用高温电热丝,设备成本较高,且 对某些元素的分析效果不佳。
火花/电弧原子发射光谱法
原理 通过电火花或电弧产生的高温使 待测元素激发为光谱状态,通过 测量光谱线的波长和强度,进行 定性和定量分析。
缺点 分析速度较慢,设备成本较高, 且对某些元素的分析效果不佳。
应用范围
原子发射光谱法.pptx

9
第一节 基本原理
一般将低能级光谱项符号写在前,高能级写在后。 根据量子力学的原理,电子的跃迁不能在任意两个能 级之间进行,而必须遵循一定的“选择定则”,这个定 则是: 1, △n=0或任意正整数; 2, △ L= 1跃迁只允许在S项和P项, P项和S项或D
项之间,D项和P项 或F项之间,等; 3, △ S=0,即单重项只能跃迁到单重项,三重项只能
在原子谱线表中,罗马数Ⅰ表示中性原子发射光谱的 谱线,Ⅱ表示一次电离离子发射的谱线,Ⅲ表示二次电 离离子发射的谱线例如Mg Ⅰ285.21nm为原子线,MgⅡ
3
第一节 基本原理
280.27nm为一次电离离子线。
二、原子能级与能级图
原子光谱是原子的外层电子(或称价电子)在两个 能级之间跃迁而产生。原子的能级通常用光谱项符号表 示:
式中Ni为单位体积内处于高能级i的原子数,Aij为i、j两能 级间的跃迁几率,h为普朗克常数, ij为发射谱线的频率。
若激发是处于热力学平衡的状态下,分配在各激发态 和基态的原子数目Ni 、N0 ,应遵循统计力学中麦克斯韦-
11
第一节 基本原理
玻兹曼分布定律。 Ni = N0 gi/g0e (-E / kT)
1
第一节 基本能级向低能级跃迁,能量以电 磁辐射的形式发射出去,这样就得到发射光谱。原子发 射光谱是线状光谱。
一般情况下,原子处于基态,通过电致激发、热致 激发或光致激发等激发光源作用下,原子获得能量,外 层电子从基态跃迁到较高能态变为激发态 ,约经10-8 s, 外层电子就从高能级向较低能级或基态跃迁,多余的能 量的发射可得到一条光谱线。
第二章 原子发射光谱法
原子发射光谱法是一种成分分析方法,可对约70种 元素(金属元素及磷、硅、砷、碳、硼等非金属元素) 进行分析。这种方法常用于定性、半定量和定量分析。
第一节 基本原理
一般将低能级光谱项符号写在前,高能级写在后。 根据量子力学的原理,电子的跃迁不能在任意两个能 级之间进行,而必须遵循一定的“选择定则”,这个定 则是: 1, △n=0或任意正整数; 2, △ L= 1跃迁只允许在S项和P项, P项和S项或D
项之间,D项和P项 或F项之间,等; 3, △ S=0,即单重项只能跃迁到单重项,三重项只能
在原子谱线表中,罗马数Ⅰ表示中性原子发射光谱的 谱线,Ⅱ表示一次电离离子发射的谱线,Ⅲ表示二次电 离离子发射的谱线例如Mg Ⅰ285.21nm为原子线,MgⅡ
3
第一节 基本原理
280.27nm为一次电离离子线。
二、原子能级与能级图
原子光谱是原子的外层电子(或称价电子)在两个 能级之间跃迁而产生。原子的能级通常用光谱项符号表 示:
式中Ni为单位体积内处于高能级i的原子数,Aij为i、j两能 级间的跃迁几率,h为普朗克常数, ij为发射谱线的频率。
若激发是处于热力学平衡的状态下,分配在各激发态 和基态的原子数目Ni 、N0 ,应遵循统计力学中麦克斯韦-
11
第一节 基本原理
玻兹曼分布定律。 Ni = N0 gi/g0e (-E / kT)
1
第一节 基本能级向低能级跃迁,能量以电 磁辐射的形式发射出去,这样就得到发射光谱。原子发 射光谱是线状光谱。
一般情况下,原子处于基态,通过电致激发、热致 激发或光致激发等激发光源作用下,原子获得能量,外 层电子从基态跃迁到较高能态变为激发态 ,约经10-8 s, 外层电子就从高能级向较低能级或基态跃迁,多余的能 量的发射可得到一条光谱线。
第二章 原子发射光谱法
原子发射光谱法是一种成分分析方法,可对约70种 元素(金属元素及磷、硅、砷、碳、硼等非金属元素) 进行分析。这种方法常用于定性、半定量和定量分析。
原子光谱项ppt课件
h
ML
L(L1)
2
h
(ML)Z mL 2
MS
S (S 1) h
2
h
(MS)Z mS 2
h
MJ
J(J1)
2
(M J )Z
可编辑课件
mJ
h
2
8
多电子原子的状态及量子数
多电子原子中,电子之间的相互作用是非常复杂的,但大 致可以归纳为以下几种相互作用:
电子轨道运动间的相互作用; 电子自旋运动间的相互作用; 轨道运动与自旋运动间的相互作用;
如, 对于d2, 壳层电子数少于半充满,故 3F4 > 3F3 > 3F2
可编辑课件
29
互补组态具有相同的谱项
所谓互补组态是指满足: (nl)x与 (nl)2(2l+1)-x关系的组态, 如p1与p5, p2与p4,
d1与d9,d3与d7等组态.因为前者的电子数与后者的空穴数 相等(反之亦然),光谱项必然相同。但应注意,基谱 支项并不相同。
原子光谱中的任何一条谱线都可以写成两项之差,每一
项与一能级对应,其大小相当于该能级的能量除以hc,通
常称这些项为光谱项。
可编辑课件
3
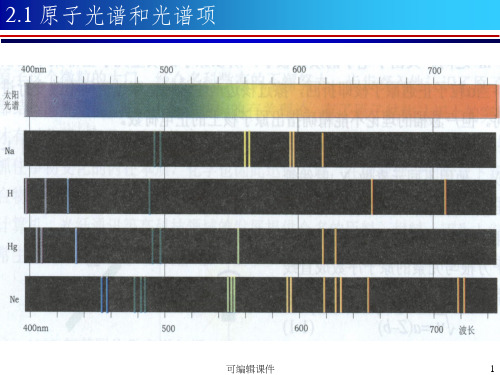
原子光谱
可编辑课件
氢原子光谱可对 氢原子结构进行解释
4
原子光谱
可编辑课件
氢原子光谱可对 氢原子结构进行解释
5
2.1.2 原子光谱项——描述原子的整体运动状态
原子的光谱(光谱实验)是与原子所处的能级有关, 而原子的能级与原子的整体运动状态有关。
(2S+1)个不同的mS值。
可编辑课件
18
(3)单电子的光谱项
例:p1 组态(l = 1; m= -1、0、+1;s = 1/2; ms=+1/2,-1/2)
原子吸收光谱分析ppt课件

原子吸收分光光度法 Atomic Absorption Spectrophotometry,
(AAS)
1.简述 2.方法原理 3.仪器设备 4.火焰原子化法测试的任务参数选择 5.石墨炉原子化法测试的任务参数选择 6.干扰及消除
第一节.简述
1.原子吸收的发现
1802年,伍朗斯顿(W. H. Wollaston)在进展太 阳察看时,发现太阳光谱中存在一些暗线。 夫郎霍费(J. Fraunhofer)在1814~1817年,布鲁 斯特(D. Brewster) 在1820年相继对这些暗线 进展仔细的察看,以为是由于太阳外围较 冷 的气体吸收了太阳光所引起的。
1964年,黄本立等将蔡司Ⅲ型滤光片式 火焰光度计改装为一台简易原子吸收光谱安装, 测定了溶液中的钠,发表了最早的原子吸收光谱 分析的研讨论文。
1965年吴庭照等利用自制的同心型气动 玻璃雾化器、预混合金属层流熄灭器、镁空心阴 极灯,英国Hilger的H-700火焰分光光度计的单色 器、10 cm长不锈钢平头水冷熄灭器的预混合型火 焰原子化器组装了原子吸收光谱仪器。完成了鋰 中微量镁的测定。
4.原子吸收光谱分析的特点
优点: ⑴ 检出限低 火焰原子吸收法的检出限可到达 ng/mL量级,石墨炉原子吸收光谱法的检出限可到 达10-13~10-14g。 ⑵ 选择性好 由于原子吸收是线状吸收,又采用 待测元素特征谱线作为光源,即使在溶液中有多 个元素共存,只需它们不与待测元素产生难原子 化的化合物,就不会产生较大的谱线干扰。加上 吸收谱线比发射谱线少的多,各元素谱线的重叠
鉴于沃尔什在建立和开展原子吸收光谱分析方 面的历史功勋,1991年在挪威卑尔根召开的第27 届国际光谱学大会(CSI)上授予他第一届CSI奖。
Alan Walsh(1916-1998)和他的原子吸收光谱仪
(AAS)
1.简述 2.方法原理 3.仪器设备 4.火焰原子化法测试的任务参数选择 5.石墨炉原子化法测试的任务参数选择 6.干扰及消除
第一节.简述
1.原子吸收的发现
1802年,伍朗斯顿(W. H. Wollaston)在进展太 阳察看时,发现太阳光谱中存在一些暗线。 夫郎霍费(J. Fraunhofer)在1814~1817年,布鲁 斯特(D. Brewster) 在1820年相继对这些暗线 进展仔细的察看,以为是由于太阳外围较 冷 的气体吸收了太阳光所引起的。
1964年,黄本立等将蔡司Ⅲ型滤光片式 火焰光度计改装为一台简易原子吸收光谱安装, 测定了溶液中的钠,发表了最早的原子吸收光谱 分析的研讨论文。
1965年吴庭照等利用自制的同心型气动 玻璃雾化器、预混合金属层流熄灭器、镁空心阴 极灯,英国Hilger的H-700火焰分光光度计的单色 器、10 cm长不锈钢平头水冷熄灭器的预混合型火 焰原子化器组装了原子吸收光谱仪器。完成了鋰 中微量镁的测定。
4.原子吸收光谱分析的特点
优点: ⑴ 检出限低 火焰原子吸收法的检出限可到达 ng/mL量级,石墨炉原子吸收光谱法的检出限可到 达10-13~10-14g。 ⑵ 选择性好 由于原子吸收是线状吸收,又采用 待测元素特征谱线作为光源,即使在溶液中有多 个元素共存,只需它们不与待测元素产生难原子 化的化合物,就不会产生较大的谱线干扰。加上 吸收谱线比发射谱线少的多,各元素谱线的重叠
鉴于沃尔什在建立和开展原子吸收光谱分析方 面的历史功勋,1991年在挪威卑尔根召开的第27 届国际光谱学大会(CSI)上授予他第一届CSI奖。
Alan Walsh(1916-1998)和他的原子吸收光谱仪
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2π
③频率公式:原子由一个定态到另一个定态,吸收或发出 频率公式:原子由一个定态到另一个定态, 单色辐射, 单色辐射,其频率 En Ek − hνkn = En − Ek 或 νkn = h h
2. 氢原子轨道半径和能量的计算 mv 2 e2 根据库仑定律和牛顿定律 = r 4 πε o r 2 将动量矩的量子化条件 L = mvr = n h 带入上式, 带入上式,得
带入上式, 将n=1带入上式,得氢原子的最低能级 带入上式
1 me 4 me 4 基态能级 E1 = − 2 ( ) =− = − 13 .6 eV ——基态能级 2 n 8ε o 2 h 2 n =1 8ε o h 2
氢原子的能级公式 13 .6 E n = − 2 eV n
n = 1, 2,3, L
§22-2 原子光谱的实验规律 原子具有线状光谱; 原子具有线状光谱; 谱线的波数由两个谱项的差值决定; 谱线的波数由两个谱项的差值决定; 第一个谱项的变量决定不同的谱系, 第一个谱项的变量决定不同的谱系,第二个谱项的变量 决定同一谱系中的不同谱线。 决定同一谱系中的不同谱线。 卢瑟福的原子的核型结构( 二、卢瑟福的原子的核型结构(1911年) 年 α 1911年 卢瑟福在α 1911年,卢瑟福在α粒子散射 实验的基础上提出了原子的核 型结构: 型结构:原子中的全部正电荷 和几乎全部质量都集中在原子 中央一个很小的体积内, 中央一个很小的体积内,称为 原子核, 原子核,原子中的电子在核的 α 周围绕核转动。 周围绕核转动。
εoh 2 rn = n 2 ( ) 2 πme
n = 1, 2,3, L
带入上式, 将n=1带入上式,得核外电子的最小轨道半径 带入上式
εoh 2 εoh 2 r1 = n 2 ( ) = = 0 .529 × 10 −10 m — —玻尔半径 πme 2 n =1 πme 2
电子轨道半径 rn Rc ( 2 − 2 ) 比较, 比较, 2 n 得里德伯常数的理论值
me 4 7 −1 R = 2 3 = 1.097373 × 10 m 8ε o h c
很吻合。 与实验值 R = 1 .0967758 × 10 7 m − 1 很吻合。
T=R/n2 ∞ 6 4387cm-1 5 6855cm-1 4
E∞ = 0
氢原子被电离 , E 电离 = E ∞ − E 1 = − E 1 = 13 .6 eV
3. 里德伯恒量的计算
将能级公式E 将能级公式 n和E2带入玻尔频率公式 ν kn
En Ek = − h h
中,
ν 2n
En − E2 me 1 1 = = 2 3 ( 2 − 2) h 8ε o h 2 n
玻尔-索末菲理论是经典与量子的混合物, 玻尔 索末菲理论是经典与量子的混合物,它一方面保留 索末菲理论是经典与量子的混合物 了经典的确定性轨道, 了经典的确定性轨道,另一方面又假定量子化条件来限制 电子的运动,但对这些条件却提不出适当的理论解释, 电子的运动,但对这些条件却提不出适当的理论解释,不 是一个自洽的理论系统。 是一个自洽的理论系统。 “定态能级”和“能级跃迁决定谱线频率”的假设,仍是量 定态能级” 定态能级 能级跃迁决定谱线频率”的假设, 子力学中的重要概念。 子力学中的重要概念。 作业: 作业:21-9,12,22-6,9 , , ,
按照经典电磁理论, 按照经典电磁理论,原子核型结构与原子光谱的实验规律 之间存在矛盾: 之间存在矛盾: 原子光谱应是连续的; 原子光谱应是连续的; 电子辐射电磁波,能量会逐渐减少, 电子辐射电磁波,能量会逐渐减少,最后电子会落到原 子核上,核型结构不稳定。 子核上,核型结构不稳定。 原子结构的玻尔理论( 三、原子结构的玻尔理论(1913年) 年 1. 三个基本假设 ①定态假设:能量状态不连续,电子只能在相应轨道上 定态假设:能量状态不连续, 运动,不辐射能量,这些状态称为原子的定态 定态; 运动,不辐射能量,这些状态称为原子的定态; 量子化条件: ②量子化条件: nh ≡ nh n — 量子数 电子轨道运动动量矩 L =
n = 1, 2,3, L
以电子在无穷远处的静电势能为零, 以电子在无穷远处的静电势能为零,则氢原子系统的能量 1 e2 E n = E k + E p = mv 2 − n 2 4 πε 0 rn
e2 1 me 4 En = − =− 2( ), 2 2 8 πε 0 rn n 8ε o h
n = 1, 2,3, L ——能级 能级
12186cm-13 2741cm-1
En=−hcR/n2 − 布喇开系 −hcR/25=-0.544eV −hcR/16=-0.85eV 帕邢系 −hcR/9=-1.51eV 巴耳末系 −hcR/4=-3.39eV
2
赖曼系
109677cm-11
−hcR=-13.6eV 氢原子能级图
四、玻尔理论的进步性与局限性 1. 玻尔理论的进步性 成功地解释了原子的稳定性 原子的稳定性、大小以及氢原子和一价 ①成功地解释 原子的稳定性 大小以及氢原子和一价 类氢离子( 光谱的规律性; 类氢离子(He+、Li2+、Be3+等)光谱的规律性; 提出了对应原理,即当量子数n趋于无限大时 趋于无限大时, ②提出了对应原理,即当量子数 趋于无限大时,量子理 论得出的结果与经典理论的结果相一致。 论得出的结果与经典理论的结果相一致。 证明当n很大时 氢原子中的电子从n态跃迁到 很大时, 态跃迁到n-1态 例1. 证明当 很大时,氢原子中的电子从 态跃迁到 态 所发射的谱线频率,等于电子在n态轨道上绕转的频率 态轨道上绕转的频率。 所发射的谱线频率,等于电子在 态轨道上绕转的频率。 2. 玻尔理论的局限性 玻尔理论无法解释复杂碱金属光谱、光谱的精细结构、 玻尔理论无法解释复杂碱金属光谱、光谱的精细结构、 塞曼效应等实验事实。 塞曼效应等实验事实。 3. 玻尔理论的改进 索末菲、威尔逊各自独立对玻尔理论进行了改进,考虑 索末菲、威尔逊各自独立对玻尔理论进行了改进, 了椭圆轨道、相对论效应、磁场中轨道平面的取向, 了椭圆轨道、相对论效应、磁场中轨道平面的取向,提 出更一般的量子化条件,对上述现象作出了初步解释。 出更一般的量子化条件,对上述现象作出了初步解释。
