教育与心理统计学的习题与解答
高校教育与心理统计学试卷附答案.

某高校成教学院教育与心理统计学结业试卷20XX、X、X姓名▁▁▁▁▁▁班级▁▁▁▁▁▁学号▁▁▁▁任职单位▁▁▁▁▁▁(说明:以下题目的答案数据一律保留2位小数)一、4个数据分别为70、60、70、90。
填出下表中所缺的统计指标名称、统计学符号、EXCEL函数及计算值。
(28分)注:差异系数以总体标准差为基准。
二、36个学生在一次测验中的得分如下:606265687071717374757576767777777879808080808182828283858586868888888995请以5分为一组制作简单次数分布表及次数分布多边图。
(12分)三、某年级甲、乙、丙三个班级学生人数分别为50人、55人、55人。
期末数学考试各班的平均成绩分别为90分、90分、85分,使用加权平均数求全年级学生的平均成绩,并指出丙班的权数和权重。
(10分)四、在一次测验中,全班学生的成绩平均分为90分,标准差为4分。
得94分的学生,他的标准分数为多少?另一个标准分数为-2 的学生,他的原始分数为多少?(6分)六、分)1、标准分数的平均数与标准差之和为▁▁▁▁:A、0B、1C、2D、不是一个确定值2、教育统计学与教育学科其它分支学科相比,其特点之一是通过对教育领域中大量数据进行分析以▁▁▁▁:A、发现其变化规律B、预测其结局C、描述相关D、揭示其原因3、在统计学书籍中,小写希腊字母一般用来表示▁▁▁▁。
A、集中量数B、总体参数C、 差异量数D、样本统计量4、下面哪一句话是错误的?A、称名数据即类别数据B、计数数据是根据称名数据统计出来的C、比率数据必然是等距数据D、称名数据是测量水平最高的数据5、在▁▁▁▁时,中数肯定与某一个原始数据的值相等。
A、原始数据按升序排列B、原始数据为连续数据C、原始数据个数为奇数D、原始数据为顺序数据6、相关系数的量纲单位▁▁▁▁。
A、与原始数据单位一致B、无测度单位C、是原始数据单位的平方D、以占原始数据总和的百分比来表示7、在统计分析中应用最为广泛的统计指标是▁▁▁▁。
教育与心理统计学考试试题及答案

第二学期《教育与心理统计学》期末考试试题A注:t0.05/2(60)=2.00 Z0.05/2=1.96一、单项选择题(本大题共15小题,每小题2分,共30分)1.当我们按性别差异,将男性指定用数字“1”来代表,女性指定用数字“2”来代表,这里所得到的数据是( )A.称名数据B.顺序数据C.等距数据D.比率数据2.比较不同单位资料的差异程度,可以采用的统计量是( )A.差异系数B.方差C.全距D.标准差3..中数的优点是( )A.不受极端值影响B.灵敏C.适于代数运算D.全部数据都参与运算4.一班32名学生的平均分为72.6,二班40人的平均分为80.2,三班36人的平均分为75,则三个班级总平均分为()A.75.93 B.76.21 C.80.2 D.735.用平面直角坐标系上点的散布图来表示两种事物之间的相关性及联系模式,这种统计图是()A.散点图 B.线形图 C.条形图 D.圆形图6.一组数据中任何两个相邻数据之比接近于常数,表示其集中量数应使用()A.算术平均数 B.几何平均数 C.中位数 D.加权平均数7.随机现象中出现的各种可能的结果称为()A.随机事件 B.必然事件 C.独立事件 D.不可能事件8.进行多个总体平均数差异显著性检验时,一般采用()A.Z检验 B.t检验 C.χ2检验 D.方差分析9.已知P(Z>1)=0.158,P(Z>1.96)=0.025,则P(1<Z<1.96)等于( )A.0.133B.0.183C.1.58D.3.5810.统计学中最常见,应用最广的一种分布是( )A.概率分布B.t分布C.正态分布D.F分布11.如果相互关联的两变量的变化方向一致(同时增大或同时减小),这表明两变量之间有( )A.完全相关B.负相关C.正相关D.零相关12.假设检验中的犯“取伪”错误的概率是( )A.αB.βC.1-αD.1-β13.某实验选取了4个样本,其容量分别是n1=8,n2=9,n3=10,n4=8,用方差分析检验平均数间差异时,其组间自由度是( )A.3B.8C.31D.3514.PR=80所表示的含义是( )A.该生考试成绩为80分B.该生考试成绩为20分C.80%的学生成绩高于该生D.80%的学生成绩低于该生15.若将某班每个人的语文考试分数都加上10分,那么与原来相比其平均数和标准差的变化是()A.平均数减少,标准差不变 B.平均数增加,标准差增加C.平均数增加,标准差不变 D.平均数增加,标准差减少二、填空题(本大题共10小题,每小题1分,共10分)1.已求得算术平均数,中位数Mdn=71,则众数为_______。
心理与教育统计学课后题答案

张厚粲现代心理与教育统计学第一章答案1名词概念(1)随机变量答:在统计学上把取值之前,不能准确预料取到什么值的变量,称为随机变量。
(2)总体答:总体(population)又称为母全体或全域,是具有某种特征的一类事物的总体,是研究对象的全体.(3)样本答:样本是从总体中抽取的一部分个体.(4)个体答:构成总体的每个基本单元。
(5)次数是指某一事件在某一类别中出现的数目,又称作频数,用f表示。
(6)频率答:又称相对次数,即某一事件发生的次数除以总的事件数目,通常用比例或百分数来表示. (7)概率答:概率(probability),概率论术语,指随机事件发生的可能性大小度量指标。
其描述性定义。
随机事件A在所有试验中发生的可能性大小的量值,称为事件A的概率,记为P(A)。
(8)统计量答:样本的特征值叫做统计量,又称作特征值。
(9)参数答:又称总体参数,是描述一个总体情况的统计指标。
(10)观测值答:随机变量的取值,一个随机变量可以有多个观测值。
2何谓心理与教育统计学?学习它有何意义?答:(1)心理与教育统计学是专门研究如何运用统计学原理和方法,搜集、整理、分析心理与教育科学研究中获得的随机性数据资料,并根据这些数据资料传递的信息,进行科学推论找出心理与教育统计活动规律的一门学科.具体讲,就是在心理与教育研究中,通过调查、实验、测量等手段有意地获取一些数据,并将得到的数据按统计学原理和步骤加以整理、计算、绘制图表、分析、判断、推理,最后得出结论的一种研究方法。
(2)学习心理与教育统计学有重要的意义。
①统计学为科学研究提供了一种科学方法。
科学是一种知识体系。
它的研究对象存在于现实世界各个领域的客观事实之中.它的主要任务是对客观事实进行预测和分类,从而揭示蕴藏于其中的种种因果关系。
要提高对客观事实观测及分析研究的能力,就必须运用科学的方法。
统计学正是提供了这样一种科学方法。
统计方法是从事科学研究的一种必不可少的工具。
心理与教育统计学课后题答案心理统计学试题及答案

心理与教育统计学课后题答案心理统计学试题及答案张厚粲现代心理与教育统计学第一章答案张厚粲现代心理与教育统计学第一章答案第一章1 名词概念(1)随机变量)答:在统计学上把取值之前,不能准确预料取到什么值的变量,称为随机变量。
(2)总体)答:总体(population)又称为母全体或全域,是具有某种特征的一类事物的总体,是研究对象的全体。
(3)样本)答:样本是从总体中抽取的一部分个体。
(4)个体)答:构成总体的每个基本单元。
(5)次数)是指某一事件在某一类别中出现的数目,又称作频数,用 f 表示。
(6)频率)答:又称相对次数,即某一事件发生的次数除以总的事件数目,通常用比例或百分数来表示。
(7)概率)答:概率(probability),概率论术语,指随机事件发生的可能性大小度量指标。
其描述性定义。
随机事件 A 在所有试验中发生的可能性大小的量值,称为事件 A 的概率,记为P(A)。
(8)统计量)答:样本的特征值叫做统计量,又称作特征值。
(9)参数)答:又称总体参数,是描述一个总体情况的统计指标。
(10)观测值)答:随机变量的取值,一个随机变量可以有多个观测值。
2 何谓心理与教育统计学?学习它有何意义?何谓心理与教育统计学?学习它有何意义?答:(1)心理与教育统计学是专门研究如何运用统计学原理和方法,搜集、整理、分析心理与教育科学研究中获得的随机性数据资料,并根据这些数据资料传递的信息,进行科学推论找出心理与教育统计活动规律的一门学科。
具体讲,就是在心理与教育研究中,通过调查、实验、测量等手段有意地获取一些数据,并将得到的数据按统计学原理和步骤加以整理、计算、绘制图表、分析、判断、推理,最后得出结论的一种研究方法。
(2)学习心理与教育统计学有重要的意义。
①统计学为科学研究提供了一种科学方法。
科学是一种知识体系。
它的研究对象存在于现实世界各个领域的客观事实之中。
它的主要任务是对客观事实进行预测和分类,从而揭示蕴藏于其中的种种因果关系。
心理与教育统计学课后题答案

张厚粲现代心理与教育统计学第一章答案1名词概念(1)随机变量答:在统计学上把取值之前,不能准确预料取到什么值的变量,称为随机变量。
(2)总体答:总体(population)又称为母全体或全域,是具有某种特征的一类事物的总体,是研究对象的全体。
(3)样本答:样本是从总体中抽取的一部分个体。
(4)个体答:构成总体的每个基本单元。
(5)次数是指某一事件在某一类别中出现的数目,又称作频数,用f表示。
(6)频率答:又称相对次数,即某一事件发生的次数除以总的事件数目,通常用比例或百分数来表示。
(7)概率答:概率(probability),概率论术语,指随机事件发生的可能性大小度量指标。
其描述性定义。
随机事件A在所有试验中发生的可能性大小的量值,称为事件A的概率,记为P(A)。
(8)统计量答:样本的特征值叫做统计量,又称作特征值。
(9)参数答:又称总体参数,是描述一个总体情况的统计指标。
(10)观测值答:随机变量的取值,一个随机变量可以有多个观测值。
2何谓心理与教育统计学?学习它有何意义?答:(1)心理与教育统计学是专门研究如何运用统计学原理和方法,搜集、整理、分析心理与教育科学研究中获得的随机性数据资料,并根据这些数据资料传递的信息,进行科学推论找出心理与教育统计活动规律的一门学科。
具体讲,就是在心理与教育研究中,通过调查、实验、测量等手段有意地获取一些数据,并将得到的数据按统计学原理和步骤加以整理、计算、绘制图表、分析、判断、推理,最后得出结论的一种研究方法。
(2)学习心理与教育统计学有重要的意义。
①统计学为科学研究提供了一种科学方法。
科学是一种知识体系。
它的研究对象存在于现实世界各个领域的客观事实之中。
它的主要任务是对客观事实进行预测和分类,从而揭示蕴藏于其中的种种因果关系。
要提高对客观事实观测及分析研究的能力,就必须运用科学的方法。
统计学正是提供了这样一种科学方法。
统计方法是从事科学研究的一种必不可少的工具。
《教育与心理统计学》复习思考题答案

《教育与心理统计学》复习思考题1简答题(第一部分)1. 简述条形图、直方图、圆形图、线图以及散点图的用途2. 简述正态分布的主要应用3. 简述T检验和方差分析法在进行组间比较上的区别和联系4. 简述Z分数的主要应用5. 简述卡方配合度检验和卡方独立性检验的区别6. 简述方差分析法的步骤7. 简述方差和差异系数在反映数据离散程度上的区别和联系8. 简述回归分析法最小二乘法的思路9. 简述完全随机化设计和随机区组设计进行方差分析的区别10. 简述假设检验中两类错误的区别和联系11. 简述多重比较和简单效应检验的区别12. 简述卡方检验的主要用途13. 简述平均数显著性检验和平均数差异显著性检验的区别和联系14. 简述假设检验中零假设和研究假设的作用15. 简述条图、饼图和直方图用法的区别和联系16. 简述什么是抽样分布17. 简述统计量和参数的区别和联系18. 简述相关分析和回归分析的区别和联系19. 简述积差相关系数、等级相关系数、二列、点二列相关系数间的区别20. 简述非参数检验的主要特点(第二部分)简要回答下面的问题应当用何种统计方法进行分析(不需计算)1.某研究者欲研究学习动机和学习成绩之间的关系,2.用动机量表测得学生的学习动机,3.再用标4.准化学绩考试测得成绩,5.两组数据均可视为连续等距数据。
如果学生的成绩是教师的等级评定分,6.又应如何分析?7.为研究职业类型(工人、农民、教师、公务员、商人)对生活满意度(满意、不8.满意)是否有影响,9.应选用什么样的统计方法?3.两考生的高考成绩五科如下表,已知所有考生各科成绩的平均数和标准差,如何判断两考生高考成绩哪一个更好?475,10,现欲选出40%高分者录用,问分数线应当定成多少?5.某校长根据自己的经验预测今年高考全区的平均分为530分,全区随机抽取100名毕业生高考平均成绩为520分,标准差42。
问该校长的预测是否准确?6.某研究者想考查教师教学效能感和教师教学效果之间的数量关系,分别用量表测得两组数据均可视为连续正态数据。
教育与心理统计学习题

《教育与心理统计学》复习思考题一一、简答题1. 简述正态分布的基本性质。
2. 二列相关适用于哪种资料?3.简述点二列相关系数的应用条件。
4.简述t 分布与标准正态分布的关系。
5.简述判断估计量优劣的标准。
6.什么是相关样本?请列举相关样本显著性检验的各种情况。
7. 有人说:“t 检验适用于样本容量小于30的情况。
Z 检验适用于大样本检验” ,谈谈你对此的看法8.什么是标准分数?使用标准分数有什么好处? 9. 简答标准Z 分数的用途。
10. 简答χ2分布具有哪些特点。
11. 简述区间估计的涵义。
12.学业考试成绩为x ,智力测验分数为y ,已知这两者的rxy=0.5,IQ=100+15z ,某学校根据学业考试成绩录取学生,录取率为15%,若一个智商为115的学生问你他被录取的可能性为多少,你如何回答他?二、计算题1.某年级200名学生在一次数学测验中的成绩如下表: 已知数据如下表:(1)求其平均数 (2)试计算70X,80X 。
(3)已知某考生的成绩为66分,试计算该考生的百分位。
3.已知在某年高考数学中,平均成绩为70分,标准差15S分,甲乙两考生的成绩分=别为65分和80分,试计算他们的标准分数,如果该年的考试成绩服从正态分布)N,(21570,试计算甲乙考生的百分位?4.已知在一次测验中数学平均成绩为75分,语文的平均成绩是数学平均成绩的2.1倍,语文成绩的标准差是数学成绩标准差的5.1倍,语文成绩Y与数学成绩X之间的相关系数为r,=.075(1)试求语文成绩Y与数学成绩X之间的回归方程。
(2)如果考生的数学成绩为60,试估计他的语文成绩Y,并计算估计的标准误(设S?=10)Y5.某校高一年级共150人,高一上学期由甲教师任教,在统考中平均成绩为75分,标准差12=S分,S分,高一下则由乙教师任教,期末统考中平均成绩为72分,标准差为10 =假设该校所在城市两次考试成绩均服从正态分布,且总体平均成绩,总体标准差相同。
现代心理与教育统计学答案

第一章1名词概念(1)随机变量答:在统计学上把取值之前,不能准确预料取到什么值的变量,称为随机变量。
(2)总体答:总体(population)又称为母全体或全域,是具有某种特征的一类事物的总体,是研究对象的全体。
(3)样本答:样本是从总体中抽取的一部分个体。
(4)个体答:构成总体的每个基本单元。
(5)次数是指某一事件在某一类别中出现的数目,又称作频数,用f表示。
(6)频率答:又称相对次数,即某一事件发生的次数除以总的事件数目,通常用比例或百分数来表示。
(7)概率答:概率(probability),概率论术语,指随机事件发生的可能性大小度量指标。
其描述性定义。
随机事件A在所有试验中发生的可能性大小的量值,称为事件A 的概率,记为P(A)。
(8)统计量答:样本的特征值叫做统计量,又称作特征值。
(9)参数答:又称总体参数,是描述一个总体情况的统计指标。
(10)观测值答:随机变量的取值,一个随机变量可以有多个观测值。
2何谓心理与教育统计学?学习它有何意义?答:(1)心理与教育统计学是专门研究如何运用统计学原理和方法,搜集、整理、分析心理与教育科学研究中获得的随机性数据资料,并根据这些数据资料传递的信息,进行科学推论找出心理与教育统计活动规律的一门学科。
具体讲,就是在心理与教育研究中,通过调查、实验、测量等手段有意地获取一些数据,并将得到的数据按统计学原理和步骤加以整理、计算、绘制图表、分析、判断、推理,最后得出结论的一种研究方法。
(2)学习心理与教育统计学有重要的意义。
①统计学为科学研究提供了一种科学方法。
科学是一种知识体系。
它的研究对象存在于现实世界各个领域的客观事实之中。
它的主要任务是对客观事实进行预测和分类,从而揭示蕴藏于其中的种种因果关系。
要提高对客观事实观测及分析研究的能力,就必须运用科学的方法。
统计学正是提供了这样一种科学方法。
统计方法是从事科学研究的一种必不可少的工具。
②心理与教育统计学是心理与教育科研定量分析的重要工具。
张敏强《教育与心理统计学》课后习题集详解(1-5章)【圣才出品】
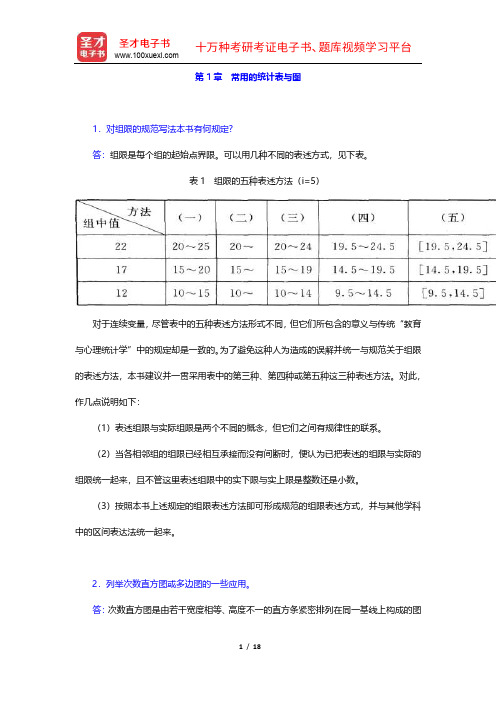
第1章常用的统计表与图1.对组限的规范写法本书有何规定?答:组限是每个组的起始点界限。
可以用几种不同的表述方式,见下表。
表1 组限的五种表述方法(i=5)对于连续变量,尽管表中的五种表述方法形式不同,但它们所包含的意义与传统“教育与心理统计学”中的规定却是一致的。
为了避免这种人为造成的误解并统一与规范关于组限的表述方法,本书建议并一贯采用表中的第三种、第四种或第五种这三种表述方法。
对此,作几点说明如下:(1)表述组限与实际组限是两个不同的概念,但它们之间有规律性的联系。
(2)当各相邻组的组限已经相互承接而没有间断时,便认为已把表述的组限与实际的组限统一起来,且不管这里表述组限中的实下限与实上限是整数还是小数。
(3)按照本书上述规定的组限表述方法即可形成规范的组限表述方式,并与其他学科中的区间表达法统一起来。
2.列举次数直方图或多边图的一些应用。
答:次数直方图是由若干宽度相等、高度不一的直方条紧密排列在同一基线上构成的图形,而次数多边图是利用闭合的折线构成多边形以反映次数变化的情况的一种图示方法。
他们都适合连续性的数据。
应用举例:如学生考试成绩的分布,商场一年12个月的销售额情况,学生去学校所花费的时间,某班学生的身高情况,某班学生的体重情况,体育课上学生一分钟内跳绳的次数,居民月平均用水量的情况等。
3.试比较简单条形图与简单次数直方图在制作和应用方面的异同点。
答:简单条形图是以若干平行而等宽的长条来表示离散型数据的对比关系的图形;次数直方图是指由若干宽度相等、高度不一的直方条紧密排列在同一基线上构成的图形。
(1)相同点①简单条形图与简单次数直方图都是统计学中常用的分布图。
②简单条形图与简单次数直方图都含有长条。
(2)不同点①简单条形图的长条是紧密相连的,而简单次数直方图的长条是分开的。
②简单条形图适合用来描述离散型变量(如属性变量)的统计数据,而简单次数直方图则是用来刻划连续性变量的观测数据。
4.简述散点图、折线图、条形图和圆形图这四种统计分析图的应用特点。
心理与教育统计学课后题答案

张厚粲现代心理与教育统计学第一章答案1名词概念(1)随机变量答:在统计学上把取值之前,不能准确预料取到什么值的变量,称为随机变量。
(2)总体答:总体(population)又称为母全体或全域,是具有某种特征的一类事物的总体,是研究对象的全体。
(3)样本答:样本是从总体中抽取的一部分个体。
(4)个体答:构成总体的每个基本单元。
(5)次数是指某一事件在某一类别中出现的数目,又称作频数,用f表示。
(6)频率答:又称相对次数,即某一事件发生的次数除以总的事件数目,通常用比例或百分数来表示。
(7)概率答:概率(probability),概率论术语,指随机事件发生的可能性大小度量指标。
其描述性定义。
随机事件A在所有试验中发生的可能性大小的量值,称为事件A的概率,记为P(A)。
(8)统计量答:样本的特征值叫做统计量,又称作特征值。
(9)参数答:又称总体参数,是描述一个总体情况的统计指标。
(10)观测值答:随机变量的取值,一个随机变量可以有多个观测值。
2何谓心理与教育统计学?学习它有何意义?答:(1)心理与教育统计学是专门研究如何运用统计学原理和方法,搜集、整理、分析心理与教育科学研究中获得的随机性数据资料,并根据这些数据资料传递的信息,进行科学推论找出心理与教育统计活动规律的一门学科。
具体讲,就是在心理与教育研究中,通过调查、实验、测量等手段有意地获取一些数据,并将得到的数据按统计学原理和步骤加以整理、计算、绘制图表、分析、判断、推理,最后得出结论的一种研究方法。
(2)学习心理与教育统计学有重要的意义。
①统计学为科学研究提供了一种科学方法。
科学是一种知识体系。
它的研究对象存在于现实世界各个领域的客观事实之中。
它的主要任务是对客观事实进行预测和分类,从而揭示蕴藏于其中的种种因果关系。
要提高对客观事实观测及分析研究的能力,就必须运用科学的方法。
统计学正是提供了这样一种科学方法。
统计方法是从事科学研究的一种必不可少的工具。
《心理与教育统计学》习题答案
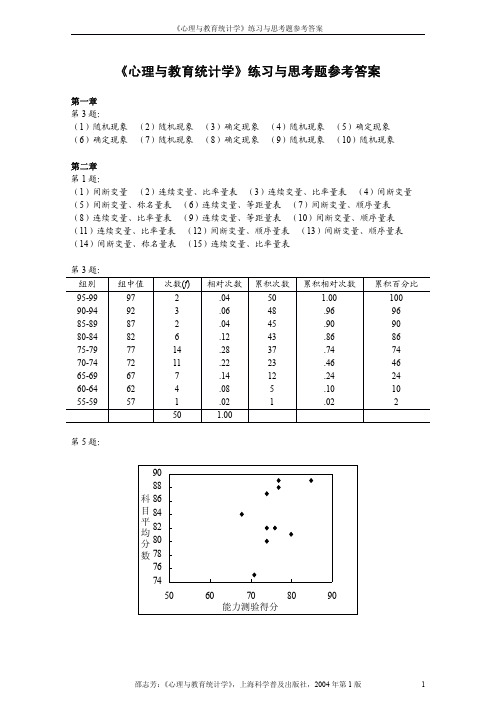
邵志芳: 《心理与教育统计学》 ,上海科学普及出版社,2004 年目 84 平 82 均 分 80 数 78 76 74 50 60 70 80 能力测验得分 90
邵志芳: 《心理与教育统计学》 ,上海科学普及出版社,2004 年第 1 版
1
《心理与教育统计学》练习与思考题参考答案
第三章 第 1 题: (1)84 (2)89 (3)420 (4)略 第 2 题: (1)13.5 (2)12 第 3 题:S2 = 8.5 S = 2.915 第 4 题:3159 第 5 题:男生 CV = 10%,女生 CV = 9.17%,男生成绩离散程度较高 第四章 第 2 题: (1)0.077 (2)0.25 (3)0.50 (4)0.25 (5)0.192 第 3 题: (1)0.0625 (2)0.0625 (3)0.25 (4)0.004 第 4 题: (1)0.008 (2)0.128 第五章 第 1 题: (1)1 (2)0.866 (3)0.0469 第 2 题: (1) 0.38493 (2) 0.30598 (3) 0.41924 (4) 0.89726 (5) 0.66141 (6) 0.78193 第 3 题:34.134 人;68.268% 第 4 题:A、B、C、D、E 等级人数分别为 18、119、226、119、18 第七章 第 1 题:95%的置信区间(66.08,73.92) ,99%的置信区间(64.84,75.16) 第 2 题: (67.30,75.70) 第 3 题: (73.27, 86.73) 第 4 题:Z = 9.09 > Z0.005 = 2.58 第 5 题:Z = – 2.68 < – Z0.01 = – 2.33 第八章 第 1 题: (– 8.573,9.538) 第 2 题:t = 0 第 3 题:|t| = | –1.033| < t0.025, 9=2.262 第 4 题:|t| = | –3.4| > t0.01, 7 = 2.998 第九章 第 1 题: (5.30,14.06) 第 2 题:F = 186.67 > F0.01, 4, 6 = 9.15 第 3 题:Z = 4.187 > Z0.005 = 2.58 第十章 第 1 题:F = 25.70 < F0.05, 2, 9 = 4.26 第 2 题:F = 2.854 < F0.05, 2, 9 = 4.26 第 3 题:F = 4.495 > F0.05, 3, 21 = 3.07 第 4 题:FA =1.692,FB =0.884,FA*B =0.617,均小于 F0.05,1, 16 = 4.49 第 5 题: 差异来源 平方和 SS 自由度 df A 因素 B 因素 A*B 组内 180 300 3000 100 2 3 6 12 方差 MS 90 100 500 8.33
心理和教育统计学课后题答案解析

张厚粲现代心理与教育统计学第一章答案1名词概念(1)随机变量答:在统计学上把取值之前,不能准确预料取到什么值的变量,称为随机变量。
(2)总体答:总体(population)又称为母全体或全域,就是具有某种特征的一类事物的总体,就是研究对象的全体。
(3)样本答:样本就是从总体中抽取的一部分个体。
(4)个体答:构成总体的每个基本单元。
(5)次数就是指某一事件在某一类别中出现的数目,又称作频数,用f表示。
(6)频率答:又称相对次数,即某一事件发生的次数除以总的事件数目,通常用比例或百分数来表示。
(7)概率答:概率(probability),概率论术语,指随机事件发生的可能性大小度量指标。
其描述性定义。
随机事件A在所有试验中发生的可能性大小的量值,称为事件A的概率,记为P(A)。
(8)统计量答:样本的特征值叫做统计量,又称作特征值。
(9)参数答:又称总体参数,就是描述一个总体情况的统计指标。
(10)观测值答:随机变量的取值,一个随机变量可以有多个观测值。
2何谓心理与教育统计学?学习它有何意义?答:(1)心理与教育统计学就是专门研究如何运用统计学原理与方法,搜集、整理、分析心理与教育科学研究中获得的随机性数据资料,并根据这些数据资料传递的信息,进行科学推论找出心理与教育统计活动规律的一门学科。
具体讲,就就是在心理与教育研究中,通过调查、实验、测量等手段有意地获取一些数据,并将得到的数据按统计学原理与步骤加以整理、计算、绘制图表、分析、判断、推理,最后得出结论的一种研究方法。
(2)学习心理与教育统计学有重要的意义。
①统计学为科学研究提供了一种科学方法。
科学就是一种知识体系。
它的研究对象存在于现实世界各个领域的客观事实之中。
它的主要任务就是对客观事实进行预测与分类,从而揭示蕴藏于其中的种种因果关系。
要提高对客观事实观测及分析研究的能力,就必须运用科学的方法。
统计学正就是提供了这样一种科学方法。
统计方法就是从事科学研究的一种必不可少的工具。
心理和教育统计学课后题答案解析

张厚粲现代心理与教育统计学第一章答案1名词概念(1)随机变量答:在统计学上把取值之前,不能准确预料取到什么值的变量,称为随机变量.(2)总体答:总体(population)又称为母全体或全域,是具有某种特征的一类事物的总体,是研究对象的全体.(3)样本答:样本是从总体中抽取的一部分个体。
(4)个体答:构成总体的每个基本单元。
(5)次数是指某一事件在某一类别中出现的数目,又称作频数,用f表示。
(6)频率答:又称相对次数,即某一事件发生的次数除以总的事件数目,通常用比例或百分数来表示. (7)概率答:概率(probability),概率论术语,指随机事件发生的可能性大小度量指标.其描述性定义。
随机事件A在所有试验中发生的可能性大小的量值,称为事件A的概率,记为P(A)。
(8)统计量答:样本的特征值叫做统计量,又称作特征值。
(9)参数答:又称总体参数,是描述一个总体情况的统计指标。
(10)观测值答:随机变量的取值,一个随机变量可以有多个观测值.2何谓心理与教育统计学?学习它有何意义?答:(1)心理与教育统计学是专门研究如何运用统计学原理和方法,搜集、整理、分析心理与教育科学研究中获得的随机性数据资料,并根据这些数据资料传递的信息,进行科学推论找出心理与教育统计活动规律的一门学科。
具体讲,就是在心理与教育研究中,通过调查、实验、测量等手段有意地获取一些数据,并将得到的数据按统计学原理和步骤加以整理、计算、绘制图表、分析、判断、推理,最后得出结论的一种研究方法.(2)学习心理与教育统计学有重要的意义。
①统计学为科学研究提供了一种科学方法.科学是一种知识体系.它的研究对象存在于现实世界各个领域的客观事实之中.它的主要任务是对客观事实进行预测和分类,从而揭示蕴藏于其中的种种因果关系。
要提高对客观事实观测及分析研究的能力,就必须运用科学的方法.统计学正是提供了这样一种科学方法.统计方法是从事科学研究的一种必不可少的工具。
心理与教育统计学课后题答案

张厚粲现代心理与教育统计学第一章答案1名词概念(1)随机变量答:在统计学上把取值之前,不能准确预料取到什么值的变量,称为随机变量。
(2)总体答:总体(population)又称为母全体或全域,是具有某种特征的一类事物的总体,是研究对象的全体。
(3)样本答:样本是从总体中抽取的一部分个体。
(4)个体答:构成总体的每个基本单元。
(5)次数是指某一事件在某一类别中出现的数目,又称作频数,用f表示。
(6)频率答:又称相对次数,即某一事件发生的次数除以总的事件数目,通常用比例或百分数来表示。
(7)概率答:概率(probability),概率论术语,指随机事件发生的可能性大小度量指标。
其描述性定义。
随机事件A在所有试验中发生的可能性大小的量值,称为事件A的概率,记为P(A)。
(8)统计量答:样本的特征值叫做统计量,又称作特征值。
(9)参数答:又称总体参数,是描述一个总体情况的统计指标。
(10)观测值答:随机变量的取值,一个随机变量可以有多个观测值。
2何谓心理与教育统计学?学习它有何意义?答:(1)心理与教育统计学是专门研究如何运用统计学原理和方法,搜集、整理、分析心理与教育科学研究中获得的随机性数据资料,并根据这些数据资料传递的信息,进行科学推论找出心理与教育统计活动规律的一门学科。
具体讲,就是在心理与教育研究中,通过调查、实验、测量等手段有意地获取一些数据,并将得到的数据按统计学原理和步骤加以整理、计算、绘制图表、分析、判断、推理,最后得出结论的一种研究方法。
(2)学习心理与教育统计学有重要的意义。
①统计学为科学研究提供了一种科学方法。
科学是一种知识体系。
它的研究对象存在于现实世界各个领域的客观事实之中。
它的主要任务是对客观事实进行预测和分类,从而揭示蕴藏于其中的种种因果关系。
要提高对客观事实观测及分析研究的能力,就必须运用科学的方法。
统计学正是提供了这样一种科学方法。
统计方法是从事科学研究的一种必不可少的工具。
教育与心理统计学复习试题及答案

一、单项选择题(本大题共15小题,每小题3分,共45分)1.下列被认为是世界上第一本有关教育与心理统计学专著的是()A.桑代克的《心理与社会测量导论》B.瑟斯顿的《统计学纲要》C.加勒特的《心理与教育统计法》D.吉尔福德等人的《心理与教育中的统计学》2 .单向秩次方差分析检验,相当于对多组数据的哪种统计量进行参数的方差分析?()A.方差B.标准差C.平均数D.相关系数3 .随机化区组实验设计的基本要求是()A.区组内可以有异质性,区组间要有同质性B.区组内和区组间均要有同质性C.区组内和区组间均可以有异质性D.区组内要有同质性,区组间可以有异质性4 .连加号的符号为()A.++B.+,+C.nD.285 .一批数据在量尺上各等距区组内所出现的次数情况是()A.概率B.概率密度函数C.累积概率密度函数D.次数分布6 .相关系数(r)的取值范围为()A.-1.00<r<0,00B,0.00<r卡1.00C.-1.00wr卡1.00D,-0.50wr卡0.507 .把对随机现象的一次观察叫做一次()A,随机实验B,随机试验C.教育与心理实验D,教育与心理试验8,总体的平均数称为符号为()A.XB.YC.(TD…9 .假设检验的第二类错误是()A.弃真第一类错误B.弃伪C.取真D.取伪10 .假设检验中的两类假设称为(C)A.I型假设和II型假设B.a假设和B假设C.原假设和备择假设D.正假设和负假设11 .符号秩次检验法不仅考虑差值的符号,还同时考虑差值的()A.大小B.分布C.方向D,显著性12 .在一元线性回归中,决定系数R2是因变量和自变量积差相关系数的()A.2倍B,平方C.立方D.2倍的平方13 .方差齐性检验的意义是(A.两正态总体的方差是否相等等C.两正态总体的方差是否整齐齐14 .F 分布主要用于比较数据的(A.离散程度B,符合正态分布的程度C.符合t 分布的程度D.偏移程度15 .把被实验或进行科学研究对象的全体称之为()A.总体B.个体C.样本D.元素二、填空题(每空3分,共45分)16 .随机变量的特点:()、()和()17 .中数又称中位数,符号记为()。
现代心理与教育统计学练习卷2附答案(共八套)

现代心理与教育统计学练习卷2附答案(共八套)-CAL-FENGHAI.-(YICAI)-Company One1练习21.一组数据44,45,48,52,60,64,65,89,83,66,67,81,80,68,79,72, 79,73的四分差为()A.8.15 B.8.75 C.79.5 D.622.若考查两变量的相关程度,其中一列变量是连续变量,另一列变量是二分变量时,应使用:()A.积差相关B.等级相关C.点二列相关D.∮相关3.总体为正态,总体方差已知时,平均数的抽样分布为:()A.t分布B.正态C.渐近正态D.F分布4.在正态分布中,标准差反映了:()A.随机变量的波动性B.正态曲线的对称位置C.随机变量的平均水平D.正态曲线的陡峭程度5.假如某班成绩服从正态分布,在按优、良、中、及格、不及格评定学生成绩时,良等成绩z分数应取值在哪个区间?()A.-0.6--0.6B.-1--1C.0.6--1.8D.0.5--2.56.欲从某重点中学720名高一学生中随机抽取120名调查其视力情况。
首先按原有视力记录,将他们的视力情况分为上、中、下三等,各等人数分别为108人、360人、252人。
若用分层按比例抽样法,则中等视力水平的学生中应抽取()A.18人B.60人C.42人D. 72人7.下列数据14,2,17,9,22,13,1,7,11的中位数是:()A.11B.9C.13D.14238.某县教师人数1990年为2000人,1994年为2880人,若照此速度增长,试估计2002年该县的教师人数为多少?( )A.5960人B.5970人C.5980人D.5990人9.方差分析的条件之一是:( )A.总体分布形态已知B.各总体方差齐性C.样本小于30D.样本容量相等 10. 我期望的月工资收入是3000元,该数据类型是( )A.计数数据B.称名数据C.定序数据D.测量数据11.当一组数据以平均数为其集中量数的代表值时,常以四分差为其差异量数的代表值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、全国大学英语四级考试结束后,随机抽取广州市考生21 名,长沙市考生
16名,得到数据如下表所示,试确定两市考生该次考试成绩是否有显著差异?(α=0.05)
x477539629483
频数261237
y38926580
频数3265
解:X 4 727 56 3 9 6 229 438 37
21
74.86
Y
3 839 22 6 568 05
16
68 2
121
( X i X ) 2236.6
S 1
n 11i1
2
116
(Y i Y ) 2308.4
S 2n
2
1i1
( 1)由于总体方差未知,所以先做方差的齐性检验
H0:
1=σ2H1: σ1≠2σσ2
F S 大308.4
2
= 1 . 3 S 小236.6
当0.0时5,查表F 2.57F 1 . 3
0.05(15,20)
所以接受零假设H0,即方差齐性 ,即认为两个总体方差相等
( 2)对两个样本进行显著性检验
H0:μ 1=μ 2H1: μ1≠μ2
t
X Y74.8668
1.3
2220236.615308.411
(n
1
1)S
1
(n
2
2)S
2
11
)()
(
21162
n n2n n2116 1212
对于给定的0 . 0 ,5 且 d f21 16 2 查3表5知,t0 .0 5t 1 . 3
2( 1 5,20)
所以接受零假设H0
答:两市考生该次考试成绩没有显著差异。
2、《教育统计学》考试成绩的σ=5,某班49名学生,该班这门课程考试成绩平均分为85分,试推论这门课程学习的真实成绩。
(α
=0 .05 )
解:已知 X
85,
2
2 =1.96,设实际成绩为 x ,
=25,查表得 Z
0 .05
X
X ~N (0,1 )与P Z
Z
0.得05
则由Z=
n
0.05
2
X -1.96·
≤ x ≤ X 1 .96 ·
n
n
代入数据计算得 83.6
X
86.4
故该班这门课程学习的真实成绩在 83.6 和 86.4 之间。
3、已知某能力测验由三个分测验组成,各分测验在标准化样组上的
平均数和标准差如下表所示:
分 测 验 一 二 三 平 均 数 65 58 111 标 准 差
7
5
15
①、 甲生在分测验一、二、三上的成绩依次为
82,70,110,
比较他在各分测验上成绩的高低。
②、
第一个分测验用公式计算: T=10Z+50,求甲生在第一个分 测验上的 T 分数。
③、
乙生在第一个分测验上的 T 分数为 75 分,求他在该测验
上的原始分数。
解:(1)由公式Z=
X
1
得
S
Z
82-65
=
= 2.43
1
7 70
58
Z
2
2.4
5
110
111
Z
3
0.067
15
显 然 有
Z
Z Z
1
2
3
所以甲在第一个测验上的分数最高, 其次是第二个测验, 最后是第三个测验 。
(2)由( 1)知 Z 1 =2.43,再由 T=10Z+50得
T=10 ×2.43+50=74.3
所以甲生在第一个分测验上的T 分数为 74.3
(3)由T=10Z+50,得Z=2.5
X
由公式Z=
S
X65
得 2.5=,推出X=82 .5
7
所以乙在第一个测验上的原始分数为82.5
4、某研究者估计,对于10 岁儿童而言,比奈智力测验与韦氏儿童智力测验的
相关为 0.70 ,现随机抽取 10 岁儿童 50 名进行上述两种智力测验,结果相关系数为 r=0.54 ,试问实测结果是否支持研究者的估计?(α=0.05 )解:检验零假设 H0 : P=0.70 H 1 :P ≠0.70
查附表 8,r=0.54 时, Zr=0.604 ,ρ=0.70 时, Zρ=0.867
z r z p
由公式Z
1
n3
0.6040.8670.263
得 Z 1.80
10.146
5 03
当α =0.05 时,查表得Z2=1.96
0.05
Z=-1.80<Z2
,即 p>0.05, 即接受零假设
0 .05=1.96
答:实得 r 值与理论估计值差异不显著,这位研究者的估计不能推翻。
补充说明:
(1)原假设为 P=0 时(即假设总体相关系数为 0),检验由实际观测值求得的样
本相关系数 r 与假设的总体相关系数 P=0间差异是否显著,或者说检验样本相关系数 r 是否来自零相关的总体。
则假设检验公式为:
r n2
t
2
r
1
(2)如果已知总体相关系数不为零,而是某一数值,即H0: P=c (c 为某一常数 ),这时样本相关系数 r 的分布是偏态的,但 r 值经过一定转换后可得到Zr 值,Zr 值服从正态分布,因此检验样本相关系数与总体相关系数间差异时采用Z 检验。
Z r Z p
Z
1
n 3
5、某班40名学生测验成绩如表1—1 所示(课本 P13 中的中间 40
名),
①、试做出此次测验的成绩分布表;
②、某考生得 35 分,试求他的百分等级分数。
解:表如下:
3838383737373737
3636363636353535
3535353434343434
3333323232323231
3131303030292929
(1)全距 R=38-29=9
22
定组数K 1.87
(N 1)5 1.87 (401) 58
定组距R9
1.1,故可以把组距定为1 .5 K8
所以此次测验的成绩分布表为:
组别组中值次数( f)相对次数累积次数累积相对次数累积百分数[39~40.5)39.750040 1.00100 [37.5~39)38.2530.07540 1.00100
[36~37.5)36.75100.25370.92592.5 [34.5~36)35.2560.15270.67567.5
[33~34.5)33.7560.15210.52552.5 [31.5~33)32.2550.125150.37537.5
[30~31.5)30.7570.175100.2525
[28.5~30)29.2530.07530.0757.5 (2) 由上表知,当 x35时, F b21, f6, L 34.5, i 1.5, N 40
( x L ) f
F b i
(2)由公式PR100
N
(35 34.5) 6
21
1.5
100 57.5
得 PR
40
答:考生得35 分,他的百分等级数为57.5。
