通信原理(陈启兴版)第10章课后习题答案
通信原理(陈启兴版)第9章课后习题答案

第9章差错控制编码9.1 学习指导9.1.1 要点差错控制编码常称为纠错编码,或信道编码,其基本思想是在发送端根据一定的规律在待发送的信息码元中加入监督码元,接收端就可以利用监督码元与信息码元的关系来发现或纠正错误,其实质就是通过牺牲有效性来换取可靠性的提高。
本章的要点有差错控制技术和编码分类;最小码距与纠检错能力;线性分组码的生成、监督和纠错;循环码的生成多项式、生成矩阵、编码和译码;卷积码的矩阵、多项式和图形描述方法。
1. 差错控制技术对于不同类型的信道,应该采用不同的差错控制技术。
差错控制技术主要有以下四种。
(1) 检错(error detection)重发(retransmission):在发送码元序列中加入差错控制码元,接收端利用这些码元检测到有错码时,利用反向信道通知发送端,要求发送端重发,直到正确接收为止。
所谓检测到有错码,是指在一组接收码元中知道有一个或一些错码,但是不知道该错码应该如何纠正。
在二进制系统中,这种情况发生在不知道一组接收码元中哪个码元错了。
因为若知道哪个码元错了,将该码元取反即能纠正,即将错码“0”改为“1”或将错码“1”改为“0”就可以了,不需要重发。
在多进制系统中,即使知道了错码的位置,也无法确定其正确取值。
采用检错重发技术时,通信系统需要有双向信道传送重发指令。
(2)前向纠错(Forward Error Correction):这时接收端利用发送端在发送码元序列中加入的差错控制码元,不但能够发现错码,还能将错码恢复其正确取值。
在二进制码元情况下,能够确定错码的位置,就相当于能够纠正错码。
采用FEC时,不需要反向信道传送重发指令,也没有因反复重发而产生的时延,故实时性好。
但是为了能够纠正错码,而不是仅仅检测到错码,和检错重发相比,需要加入更多的差错控制码元。
故设备要比检测重发设备复杂。
(3)反馈(feedback)校验(check out):这时不需要在发送序列中加入差错控制码元。
现代通信原理教程10章部分习题解答

(2)均采用想干解调时,各系统的输出信噪比
(3)当输入信号功率Si相同时,各系统的输出信噪比。
解:(1)
AM
DSB
SSB
(2)
AM相干解调器输出信号
DSB相干解调器输出信号
DSB相干解调器输出信号
(3)当输入信号功率Si相同时,各系统的输出信噪比
AM相干解调器输出信号
解:
⑴设DSB已调信号 ,则接收机的输入信号功率
⑵相干解调之后,接收机的输出信号 ,因此输出信号功率
⑶解调器的输出信噪功率比
13某线性调制系统的输出信噪比为20dB,输出噪声功率为 W,由发射机输出端到解调器输入之间总的传输损耗为100dB,试求:
(1)DSB时的发射机输出功率;
(2)SSB时的发射机输出功率。
表2-14维特比算法译码第一步计算结果
序号
路径
对应序列
码距
幸存否
1
000 000 000
6
否
2
111 110 111
4
是
3
000 000 111
5
是
4
111 110 000
5
否
5
000 111 110
7
否
6
111 001 001
1
是
7
000 111 001
6
否
8
111 001 110
2
是
②继续考察接收序列中后继 位,计算出新增路径段的码组与接收序列中后继3位之间的新增码距,总码距(原幸存路径的码距+新增码距),选出幸存路径,分别如图(b)、(c)、(d)和图(e)所示。由图(e)可见,幸存路径 上的序列“111 001 001 000 110 000”与接收序列码距最小(概率最大),故对应发送信息为110101。
通信原理(陈启兴版)第10章课后习题答案

第10章 正交编码与伪随机序列10.1 学习指导 10.1.1 要点正交编码与伪随机序列的要点主要包括正交编码的概念、常见的正交编码和伪随机序列。
1. 正交编码的概念对于二进制信号,用一个数字序列表示一个码组。
这里,我们只讨论二进制且码长相同的编码。
两个码组的正交性可用它们的互相关系数来表述。
设码长为n 的编码中码元只取值+1和-1。
如果x 和y 是其中的两个码组:x = (x 1, x 2, …, x n ),y = (y 1, y 2, …, y n ),其中,x i , y i ∈ {+1, -1},i = 1, 2, …, n ,则码组x 和y 的互相关系数被定义为2. i i 11(, ) (10-1)==∑ni x y x y n ρ如果码组x 和y 正交,则ρ(x , y ) = 0。
两两正交的编码称为正交编码。
类似地,我们还可以定义一个码组的自相关系数。
一个长为n 的码组x 的自相关系数被定义为x i i + j 11(),0, 1, , 1 (10-2)===-∑ni j x x j n n ρ其中,x 的下标按模n 运算,即x n +k ≡ x k 。
在二进制编码理论中,常采用二进制数字“0”和“1”表示码元的可能取值。
若规定用二进制数字“0”代替上述码组中的“-1”,用二进制数字“1”代替“+1”,则码组x 和y 的互相关系数被定义为(, ) (10-3)a bx y a bρ-=+ 其中,a 表示码组 x 和y 中对应码元相同的个数,b 表示码组x 和y 中对应码元不同的个数。
例如,对于4个码组:x 1 = (1,1, 1, 1),x 2 = (1, 1, 0,0),x 3 = (1, 0, 0, 1),x 4 = (1, 0, 1, 0),它们任意两者之间的相关系数都为0。
对于采用二进制数字“0”和“1”表示的码元,若用x 的j 次循环移位代替y ,就得到x 的自相关系数ρx (j )。
通信原理课后答案精选版

通信原理课后答案 Document serial number【KKGB-LBS98YT-BS8CB-BSUT-BST108】第一章习题习题 在英文字母中E 出现的概率最大,等于,试求其信息量。
解:E 的信息量:()()b 25.3105.0log E log E 1log 222E =-=-==P P I 习题 某信息源由A ,B ,C ,D 四个符号组成,设每个符号独立出现,其出现的概率分别为1/4,1/4,3/16,5/16。
试求该信息源中每个符号的信息量。
解:习题 某信息源由A ,B ,C ,D 四个符号组成,这些符号分别用二进制码组00,01,10,11表示。
若每个二进制码元用宽度为5ms 的脉冲传输,试分别求出在下列条件下的平均信息速率。
(1) 这四个符号等概率出现; (2)这四个符号出现概率如习题所示。
解:(1)一个字母对应两个二进制脉冲,属于四进制符号,故一个字母的持续时间为2×5ms。
传送字母的符号速率为等概时的平均信息速率为 (2)平均信息量为则平均信息速率为 s b 7.197977.1100B b =⨯==H R R习题 试问上题中的码元速率是多少解:311200 Bd 5*10B B R T -=== 习题 设一个信息源由64个不同的符号组成,其中16个符号的出现概率均为1/32,其余48个符号出现的概率为1/96,若此信息源每秒发出1000个独立的符号,试求该信息源的平均信息速率。
解:该信息源的熵为 =比特/符号因此,该信息源的平均信息速率 1000*5.795790 b/s b R mH === 。
习题 设一个信息源输出四进制等概率信号,其码元宽度为125 us 。
试求码元速率和信息速率。
解:B 6B 118000 Bd 125*10R T -=== 等概时,s kb M R R B b /164log *8000log 22=== 习题 设一台接收机输入电路的等效电阻为600欧姆,输入电路的带宽为6 MHZ ,环境温度为23摄氏度,试求该电路产生的热噪声电压的有效值。
通信原理陈启兴版课后习题答案分解

第四章 模拟调制4.1 学习指导4.1.1 要点模拟调制的要点主要包括幅度调制、频率调制和相位调制的工作原理。
1. 幅度调制幅度调制是用调制信号去控制载波信号的幅度,使之随调制信号作线性变化的过程。
在时域上,已调信号的振幅随基带信号的规律成正比变化;在频谱结构上,它的频谱是基带信号频谱在频域内的简单平移。
由于这种平移是线性的,因此,振幅调制通常又被称为线性调制。
但是,这里的“线性”并不是已调信号与调制信号之间符合线性变换关系。
事实上,任何调制过程都是一种非线性的变换过程。
幅度调制包括标准调幅(简称调幅)、双边带调幅、单边带调幅和残留边带调幅。
如果调制信号m (t )的直流分量为0,则将其与一个直流量A 0相叠加后,再与载波信号相乘,就得到了调幅信号,其时域表达式为[]()()()AM 0c 0c c ()()cos cos ()cos (4 - 1)s t A m t t A t m t t ωωω=+=+ 如果调制信号m (t )的频谱为M (ω),则调幅信号的频谱为[][]AM 0c c c c 1()π()()()() (4 - 2)2S A M M ωδωωδωωωωωω=++-+++- 调幅信号的频谱包括载波份量和上下两个边带。
上边带的频谱结构与原调制信号的频谱结构相同,下边带是上边带的镜像。
由波形可以看出,当满足条件|m (t )| ≤ A 0 (4-3)时,其包络与调制信号波形相同,因此可以用包络检波法很容易恢复出原始调制信号。
否则,出现“过调幅”现象。
这时用包络检波将发生失真,可以采用其他的解调方法,如同步检波。
调幅信号的一个重要参数是调幅度m ,其定义为[][][][]00max min 00max min()() (4 - 4)()()A m t A m t m A m t A m t +-+=+++ AM 信号带宽B AM 是基带信号最高频率分量f H 的两倍。
AM 信号可以采用相干解调方法实现解调。
通信原理课后答案

第一章习题习题1.1 在英文字母中E 出现的概率最大,等于0.105,试求其信息量。
解:E 的信息量:()()b 25.3105.0log E log E 1log 222E =-=-==P P I习题1.2 某信息源由A ,B ,C ,D 四个符号组成,设每个符号独立出现,其出现的概率分别为1/4,1/4,3/16,5/16。
试求该信息源中每个符号的信息量。
解:b A P A P I A 241log )(log )(1log 222=-=-==b I B 415.2163log 2=-= b I C 415.2163log 2=-= b I D 678.1165log 2=-=习题1.3 某信息源由A ,B ,C ,D 四个符号组成,这些符号分别用二进制码组00,01,10,11表示。
若每个二进制码元用宽度为5ms 的脉冲传输,试分别求出在下列条件下的平均信息速率。
(1) 这四个符号等概率出现; (2)这四个符号出现概率如习题1.2所示。
解:(1)一个字母对应两个二进制脉冲,属于四进制符号,故一个字母的持续时间为2×5ms 。
传送字母的符号速率为Bd 100105213B =⨯⨯=-R等概时的平均信息速率为s b 2004log log 2B 2B b ===R M R R(2)平均信息量为比特977.1516log 165316log 1634log 414log 412222=+++=H则平均信息速率为 s b 7.197977.1100B b =⨯==H R R习题1.4 试问上题中的码元速率是多少? 解:311200 Bd 5*10B B R T -===习题1.5 设一个信息源由64个不同的符号组成,其中16个符号的出现概率均为1/32,其余48个符号出现的概率为1/96,若此信息源每秒发出1000个独立的符号,试求该信息源的平均信息速率。
解:该信息源的熵为96log 961*4832log 321*16)(log )()(log )()(22264121+=-=-=∑∑==i i i i Mi i x P x P x P x P X H=5.79比特/符号因此,该信息源的平均信息速率 1000*5.795790 b/s b R mH === 。
通信原理(陈启兴版)作业和思考题参考答案

通信原理(陈启兴版)作业和思考题参考答案————————————————————————————————作者:————————————————————————————————日期:5-1 设二进制符号序列为1 0 0 1 0 0 1 ,试求矩形脉冲为例,分别画出相应的单极性、双极性、单极性归零、双极性归零、二进制差分波形和四电平波形。
解 单极性、双极性、单极性归零、双极性归零、二进制差分、四电平波形分别如下图5-6(a)、(b)、(c)、(d)、(e)、(f)所示。
图5-6 波形图5-2 设二进制随机脉冲序列中的“0”和“1”分别由g (t )和-g (t )表示,它们的出现概率分别为2/5及3/5:(1) 求其功率谱密度;(2) 若g (t )为如图题5-2(a)所示波形,T s 为码元宽度,问该序列是否存在位定时分量f s = 1/T s ? (3) 若g (t )改为图题5-2(b),重新回答题(1)和(2)所问。
图题5-2g (t )0.5T sO -0.5T st(a)g (t )0.25T sO -0.25T st(b)11解 (1)随机二进制序列的功率谱密度212()(1)()()s S P f f P P G f G f =--+212[()(1)()]()S S S S m f PG mf P G mf f mf δ∞=-∞+--∑由题意知g 1(t ) = - g 2(t ) = g (t ),因此双极性波形序列的功率谱密度为1 0 0 1 0 0 1 +E -E(e1 0 0 1 0 0 1(a+E 01 0 0 1 0 0 1+E(c 1 0 0 1 0 0 1 +E-E(d 1 0 0 1 0 0 1+E-E(b 1100 0110(f()2222()4(1)()12()()S S S SS P f f P P G f f P G mff mf δ+∞-∞=-+--∑222241()()()2525S S S S f G f f G mf f mf δ+∞-∞=+-∑式中,G (f )⇔g (t );等式右端第一项是连续谱成分,第二项是离散谱成分。
通信原理(陈启兴版)第9章课后习题答案(DOC)

第9章差错控制编码9.1 学习指导9.1.1 要点差错控制编码常称为纠错编码,或信道编码,其基本思想是在发送端根据一定的规律在待发送的信息码元中加入监督码元,接收端就可以利用监督码元与信息码元的关系来发现或纠正错误,其实质就是通过牺牲有效性来换取可靠性的提高。
本章的要点有差错控制技术和编码分类;最小码距与纠检错能力;线性分组码的生成、监督和纠错;循环码的生成多项式、生成矩阵、编码和译码;卷积码的矩阵、多项式和图形描述方法。
1. 差错控制技术对于不同类型的信道,应该采用不同的差错控制技术。
差错控制技术主要有以下四种。
(1) 检错(error detection)重发(retransmission):在发送码元序列中加入差错控制码元,接收端利用这些码元检测到有错码时,利用反向信道通知发送端,要求发送端重发,直到正确接收为止。
所谓检测到有错码,是指在一组接收码元中知道有一个或一些错码,但是不知道该错码应该如何纠正。
在二进制系统中,这种情况发生在不知道一组接收码元中哪个码元错了。
因为若知道哪个码元错了,将该码元取反即能纠正,即将错码“0”改为“1”或将错码“1”改为“0”就可以了,不需要重发。
在多进制系统中,即使知道了错码的位置,也无法确定其正确取值。
采用检错重发技术时,通信系统需要有双向信道传送重发指令。
(2)前向纠错(Forward Error Correction):这时接收端利用发送端在发送码元序列中加入的差错控制码元,不但能够发现错码,还能将错码恢复其正确取值。
在二进制码元情况下,能够确定错码的位置,就相当于能够纠正错码。
采用FEC时,不需要反向信道传送重发指令,也没有因反复重发而产生的时延,故实时性好。
但是为了能够纠正错码,而不是仅仅检测到错码,和检错重发相比,需要加入更多的差错控制码元。
故设备要比检测重发设备复杂。
(3)反馈(feedback)校验(check out):这时不需要在发送序列中加入差错控制码元。
通信原理教程(第2版)课后答案12-10
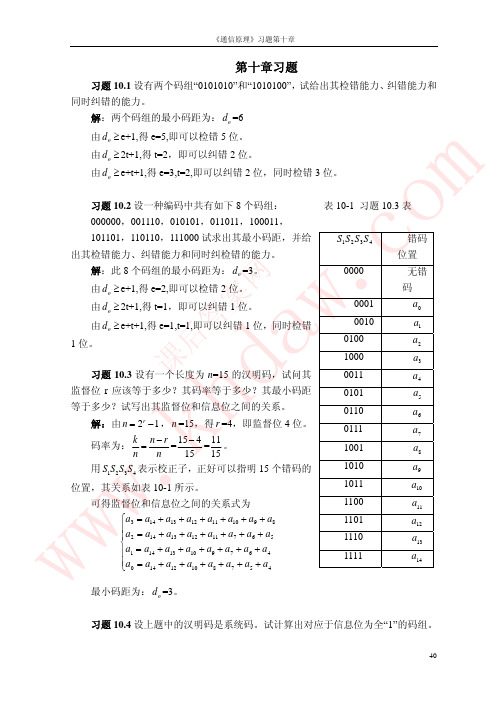
h 试问由它可以构成多少种码长为 15 的循环码?并列出它们的生成多项式。
解:因为 2r 1 n ,而 n =15,所以 4 r 13 。因为
生成多项式 g(x) x3 x 1 ,从而生成矩阵为
42
《通信原理》习题第十章
x3 g ( x)
1 0 0 1 0 0
G(
x
)=
x
2
g
(
x)
xg ( x)
g(x)
,或
G=
0 0 0
1 0 0
0 1 0
1 0 1
0 1 1
0 ,
x7 g(x)
0 0 0 1 1 0 0 1 0 0 0 0 0 0 0
x6 g(x)
0 0 0 0 1 1 0 0 1 0 0 0 0 0 0
G(x)
=
x5
g(x)
,或
G=
0
0
0
0
0
1
1
0
01
0
0
0
0
0
x4 g(x)
0 0 0 0 0 0 1 1 0 0 1 0 0 0 0
d 习题 10.11 已知一个(15,11)汉明码的生成多项式为 hg(x) x4 x3 1
试求出其生成矩阵和监督矩阵。
www.k 解:由g(x) x4 x3 1得
43
《通信原理》习题第十章
x10 g(x)
通信原理(陈启兴版)第9章课后习题答案

a.监督子仅与错误图样有关,而与发送的具体码字无关; b.若S =0,则判断没有错码出现,它表明接收的码字是一个许用码字,当然如果错码超过了纠错能力,也无法检测出错码。若S≠0,判断有错码出现; c.在纠错能力范围内,不同的错误图样具有不同的监督子,监督子是H 阵中“与错误码元相对应”的各列之和。对于纠一位错码的监督矩阵,监督子就是H 阵中与错误码元位置对应的各列。 (3) 汉明码 汉明码是能够纠正单个错误而且编码效率高的线性分组码。关于线性分组码的分析方法全部适用于汉明码。 一般说来,如果希望用r 个监督码元构造的(n ,k )线性分组码能够纠正一位错码,则要求 21r n -≥ (9-7) 汉明码满足条件 21r n -= (9-8) 汉明码的监督矩阵H 的列是由所有非零的互不相同的(n-k )重二元序列组成。如果码字中哪一位发生错误,其伴随式就是H 中该列的列矢量。 5. 循环码 在线性分组码中,有一种重要的码称为循环码(cyclic code)。它是在严密的代数学理论基础上建立起来的。这种码的编码和解码设备都不太复杂,而且检纠错的能力较强。循环码除了具有线性码的一般性 质外,还具有循环性。循环性是指任一码组循环一位(即将最右端的一个码元移至左端,或反之)以后,仍为该码中的一个码组。 (1) 码多项式 在代数编码理论中,为了便于计算,通常用多项式去描述循环码,它把码组 中各码元当作是一个多项式(poly-nomial)的系数,即把一个长度为n 的码组表示成 121210()n n n n T x a x a x a x a ----=++++ (9-9) 在循环码中,若T (x )是一个长为n 的许用码组,则x i ﹒T (x )在按模x n +1运算下,也是该编码中的一个许用码组,即若 ) (模)1()()(+'≡?n i x x T x T x (9-10) 则T '(x )也是该编码中的一个许用码组。 (2) 生成多项式 在一个(n , k )循环码中,有一个且仅有一个次数为(n-k )的多项式: 111()11n k n k n k g x x a x a x -----=?+++ (9-11) 称此g (x )为该循环码的生成多项式。g (x )表示该循环码的前(k -1)位皆为“0”的码组。g (x )有如下性质: a. g (x )是一个常数项为1,最高次数为(n -k )次,且是x n +1的一个因式。 b. 所有码多项式T (x )都可被g (x )整除,而且任意一个次数不大于(k -1)的多项式乘g (x )都是码多项式。 (3) 生成矩阵G 在循环码中,一个(n , k )码有2k 个不同的码组。若用g (x )表示其中前(k -1)位皆为“0”的码组,则g (x ),xg (x ),x 2g (x ),?,x k-1g (x )都是码组,而且这k 个码组是线性无关的。因此它们可以用来构成此 循环码的生成矩阵G 。一旦确定了g (x ),则整个(n , k )循环码就被确定了。 因此,循环码的生成矩阵G 可以写成 12()()()()()k k x g x x g x x xg x g x --?????? ? ?=???????? G (9-12) 由于上面的生成矩阵不是标准阵,这样编码得到的码字一般不是系统码。 (4) 系统循环码的编码思路 a. 用信息码元的多项式m (x )表示信息码元。 b. 用x n - k 乘m (x ),得到 x n - k m (x )。 c. 用g (x )除x n - k m (x ),得到商Q (x )和余式r (x ),即 ()()()()() n k x m x r x Q x g x g x -=+ (9-13) d. 编出的码组()T x 为 ()()()n k T x x m x r x -=+ (9-14) (5) 循环码的译码 接收端可以将接收码组R (x )用原生成多项式g (x )去除。当传输中未发生错误 时,接收码组与发送码组相同,即R (x ) = T (x ),故接收码组R (x )必定能被g (x )整除;若码组在传输中发生错误,则R (x ) ≠ T (x ),R (x )被g (x )除时可能除不尽而有余项,从而发现错误。 纠正错码相对复杂。因此,原则上纠错可按下述步骤进行: a. 用生成多项式g (x )除接收码组R (x ),得出余式r (x )。 b. 按余式r (x ),用查表的方法或通过某种计算得到错误图样E (x );例如,通过计算校正子S 和表中的关系,就可以确定错码的位置。 c. 从R(x )中减去E (x ),便得到已经纠正错码的原发送码组T (x )。 6. 卷积码 卷积码是指把信源输出的信息序列,以k 个信息码元划分为一组,通过编码器输出长为n (≥k )的码段。与线性分组码不同的是:卷积码的子码中(n -k )个监督码不仅与本组的信息码元有关,而且也与其前 m 组的信息码元有关。一般用(n ,k ,m )表示,其中m 为编码存储器,它表示输入信息在编码器中需存储的单位时间。编码效率R =k /n 。 类似于线性分组码,卷积码的输入序列A =[…a k-2 a k-1 a k a k+1…],输出序列0:10:20:31:11:21:32:12:22:3[,,,,,,,,,]C c c c c c c c c c =,监督矩阵H ∞和生成矩阵G ∞具有下列关系 ,0,0T T T C MG H C G H ∞∞∞∞==?= (9-15) 卷积码可以采用解析表示法,即采用码的生成矩阵、监督矩阵和码的多项式 来计算分析。此外,由于卷积码的特点,还可以采用图形表示法来研究,即从树状图、网格图和状态图的观点进行研究。 卷积码的译码方法主要有三种:序列译码、大数逻辑解码(门限译码)和概率解码(最大似然译码)。 9.1.2 难点 本章的难点主要有汉明码的特点及检验接收码组B 是否出错的方法。
通信原理课后练习答案

1/ 2
Rz ( )
1
1 / 2
⑶ 试求功率谱密度 Pz ( f ) 及功率S。
平稳随机过程的功率谱密度是其自相关函数的傅里 1 叶变换,即 Pz ( f ) Rm ( ) cos c t
2 1 1 Pz ( f ) Pm ( f ) * ( f f c ) ( f f c ) 2 2
j 2 fT 2 2
H ( f ) 2(1 cos 2 fT )
n0 输入噪声的功率谱密度: Pn ( f ) , 2
f 第3章课后作业解答
3-8 一个中心频率为fc、带宽为B的理想带通滤波器如 下图所示。假设输入是 均值为零、功率谱密度 为n0/2 的高斯白噪声,试求:
H( f )
B B
0
fc
fc
f
⑴ 滤波器输出噪声的自相关函数;
⑵ 滤波器输出噪声的平均功率;
⑶ 输出噪声的一维概率密度函数。
第3章课后作业解答
⑴ 滤波器输出噪声的自相关函数;
可以很容易得到滤波器输出噪声的功率谱密度:
ì n0 B ï ï fc - # f Pn ( f ) = ï 2 í 2 ï ï ï î 0 其他 B fc + 2
第3章课后作业解答
P Y ( f ) RY ( )
j 2 fT j 2 fT P ( f ) 2 P ( f ) P ( f ) e P ( f ) e Y X X X
2(1 cos 2 fT ) PX ( f )
或者:
PY ( f ) PX ( f ) H ( f ) H( f ) 1 e
1-10 已知某四进制数字传输系统的传信率为2400b/s, 接收端在 0.5h 内共收到 216 个错误码元,试计算该系 统的误码率 Pe。
通信原理课后习题参考答案

++++++++++++++++++++++++++第一章习题答案1-1解:1-2解:1-3解:1-4 解:1-5 解:1-6 解:1-7 解:1-8 解:第二章习题答案2-1 解:群延迟特性曲线略2-2 解:2-3 解:2-4 解:二径传播时选择性衰落特性图略。
2-5 解:2-6 解:2-7 解:2-8 解:第三章习题答案3-4 解:3-5 解:3-6 解:3-7 解:3-8 解:3-9 解:3-10 解:3-11 解:第四章习题答案4-2 解:4-3 解:4-4 解:4-6 解:4-8 解:4-9 解:4-10 解:4-11 解:4-12 解:4-13 解:4-15 解:4-16 解:4-17 解:第五章习题答案5-1 解:,,,(1)波形(2)5-2 解:,,(1)(2)相干接收时5-3 解:,,(1)相干解调时(2)非相干解调时5-4 解:,,,(1)最佳门限:而:所以:(2)包检:5-5 解:系统,,5-6 解:(1)信号与信号的区别与联系:一路可视为两路(2)解调系统与解调系统的区别与联系:一路信号的解调,可利用分路为两路信号,而后可采用解调信号的相干或包检法解调,再进行比较判决。
前提:信号可分路为两路信号谱不重叠。
5-7 解:系统,,,(1)(2)5-8 解:系统,,,,(1)(2)所以,相干解调时:非相干解调时:5-9 解:5-10 解:(1)信号时1 0 0 1 0(2)1 0 1 0 0,5-12 解:时:相干解调码变换:差分相干解调:,,(1):a:相干解调时解得:b:非相干解调时解得:(2):(同上)a:相干解调时,b:非相干解调时,(3)相干解调时即在保证同等误码率条件下,所需输入信号功率为时得1/4,即(4)a:差分相干解调时即在保证同等误码率条件下,所需输入信号功率为时得1/4,即b:相干解调的码变换后解得:5-16 解:(A方式)0 1 1 0 0 1 1 1 0 1 0 0 ,5-17 解:(1)时所以(2)时所以5-18 解:5-19 解:,::一个码元持续时间,含:个周波个周波。
通信原理(陈启兴版) 第10章作业和思考题参考答案
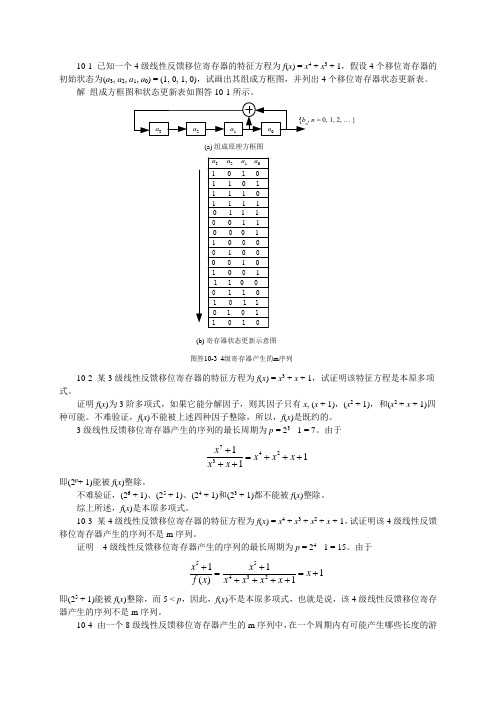
10-1 已知一个4级线性反馈移位寄存器的特征方程为f (x ) = x 4 + x 3 + 1,假设4个移位寄存器的初始状态为(a 3, a 2, a 1, a 0) = (1, 0, 1, 0),试画出其组成方框图,并列出4个移位寄存器状态更新表。
解 组成方框图和状态更新表如图答10-1所示。
图答10-3 4级寄存器产生的m 序列, n = 0, 1, 2, … }(a) 组成原理方框图(b) 寄存器状态更新示意图1 0 1 0a 3 a 2 a 1 a 01 1 0 11 1 1 01 1 1 10 1 1 10 0 1 10 0 0 11 0 0 00 1 0 00 0 1 01 0 0 11 1 0 00 1 1 01 0 1 10 1 0 11 0 1 010-2 某3级线性反馈移位寄存器的特征方程为f (x ) = x 3+ x + 1,试证明该特征方程是本原多项式。
证明f (x )为3阶多项式,如果它能分解因子,则其因子只有x , (x + 1),(x 2 + 1),和(x 2 + x + 1)四种可能。
不难验证,f (x )不能被上述四种因子整除,所以,f (x )是既约的。
3级线性反馈移位寄存器产生的序列的最长周期为p = 23 - 1 = 7。
由于 7423111x x x x x x +=+++++ 即(2p + 1)能被f (x )整除。
不难验证,(26 + 1)、(25 + 1)、(24 + 1)和(23 + 1)都不能被f (x )整除。
综上所述,f (x )是本原多项式。
10-3 某4级线性反馈移位寄存器的特征方程为f (x ) = x 4 + x 3 + x 2 + x + 1,试证明该4级线性反馈移位寄存器产生的序列不是m 序列。
证明 4级线性反馈移位寄存器产生的序列的最长周期为p = 24 - 1 = 15。
由于55432111()1x x x f x x x x x ++==+++++即(25 + 1)能被f (x )整除,而5 < p ,因此,f (x )不是本原多项式,也就是说,该4级线性反馈移位寄存器产生的序列不是m 序列。
通信原理课后习题和作业答案40页PPT

11、获得的成功越大,就越令人高兴 。野心 是使人 勤奋的 原因, 节制使 人枯萎 。 12、不问收获,只问耕耘。如同种树 ,先有 根茎, 再有枝 叶,尔 后花实 ,好好 劳动, 不要想 太多, 那样只 会使人 胆孝懒 惰,因 为不实 践,甚 至不接 触社会 ,难道 你是野 人。(名 言网) 13、不怕,不悔(虽然只有四个字,但 常看常 新。 14、我在心里默默地为每一个人祝福 。我爱 自己, 我用清 洁与节 制来珍 惜我的 身体, 我用智 慧和知 识充实 我的头 脑。 15、这世上的一切都借希望而完成。 农夫不 会播下 一粒玉 米,如 果他不 曾希望 它长成 种籽; 单身汉 不会娶 妻,如 果他不 曾希望 有小孩 ;商人 或手艺 人不会 工作, 如果他 不曾希 望因此 而有收 益。-- 马钉路 德。
25、学习是劳动,是充满思想的劳。——乌申斯基
谢谢!
21、要知道对好事的称颂过于夸大,也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤,荒于嬉;行成于思,毁于随。——韩愈
23、一切节省,归根到底都归结为时间的节省。——马克思 24、意志命运往往背道而驰,决心到最后会全部推倒。——莎士比亚
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第10章 正交编码与伪随机序列10.1 学习指导 10.1.1 要点正交编码与伪随机序列的要点主要包括正交编码的概念、常见的正交编码和伪随机序列。
1. 正交编码的概念对于二进制信号,用一个数字序列表示一个码组。
这里,我们只讨论二进制且码长相同的编码。
两个码组的正交性可用它们的互相关系数来表述。
设码长为n 的编码中码元只取值+1和-1。
如果x 和y 是其中的两个码组:x = (x 1, x 2, …, x n ),y = (y 1, y 2, …, y n ),其中,x i , y i ∈ {+1, -1},i = 1, 2, …, n ,则码组x 和y 的互相关系数被定义为2. i i 11(, ) (10-1)==∑ni x y x y n ρ如果码组x 和y 正交,则ρ(x , y ) = 0。
两两正交的编码称为正交编码。
类似地,我们还可以定义一个码组的自相关系数。
一个长为n 的码组x 的自相关系数被定义为x i i + j 11(),0, 1, , 1 (10-2)===-∑ni j x x j n n ρ其中,x 的下标按模n 运算,即x n +k ≡ x k 。
在二进制编码理论中,常采用二进制数字“0”和“1”表示码元的可能取值。
若规定用二进制数字“0”代替上述码组中的“-1”,用二进制数字“1”代替“+1”,则码组x 和y 的互相关系数被定义为(, ) (10-3)a bx y a bρ-=+ 其中,a 表示码组 x 和y 中对应码元相同的个数,b 表示码组x 和y 中对应码元不同的个数。
例如,对于4个码组:x 1 = (1,1, 1, 1),x 2 = (1, 1, 0,0),x 3 = (1, 0, 0, 1),x 4 = (1, 0, 1, 0),它们任意两者之间的相关系数都为0。
对于采用二进制数字“0”和“1”表示的码元,若用x 的j 次循环移位代替y ,就得到x 的自相关系数ρx (j )。
比如,如果一个长为n 的码组x = (x 1, x 2, …, x n ),则y = (x 1 + j , x 2 + j , …, x n , x 1, x 2, …, x j )。
根据上式计算出码组x 和y 的互相关系数就是码组x 的自相关系数。
显然,无论是采用二进制数字“0”和“1”表示的码元,还是采用二进制数字“+1”和“-1”表示的码元,互相关系数和自相关系数都是在1与-1之间取值。
若两个码组间的互相关系数ρ < 0,则称这两个码组互相超正交。
如果一种编码中任意两码组之间均超正交,则称这种编码为超正交码。
例如,对于3个码组:x 1 = (+1, +1, +1),x 2 = (+1, -1, -1),x 3 = (-1, -1, +1),由它们构成的编码是超正交码。
由正交编码和其反码构成的编码就是双正交编码。
例如,4个码组:x 1 = (+1, +1, +1, +1),x 2 = (+1, +1, -1, -1),x 3 = (+1, -1, -1, +1),x 4 = (+1, -1, +1, -1),其反码为:y 1 = (-1, -1, -1, -1),x 2 = (-1, -1, +1, +1),x 3 = (-1, +1, +1, -1),x 4 = (-1, +1, -1, +1)。
这8个码组构成的编码就是双正交编码,任意两个码组之间的互相关系数ρ为0或-1。
2.常见的正交编码 常见的正交编码有Hadamard 码矩阵、Walsh 矩阵和伪随机序列等。
Hadamard 码矩阵是法国数学家M. J. Hadamard 于1893年首先构造出来的一种方阵,仅由元素+1和-1构成,而且其任意两行(列)之间是互相正交的,简记为H 矩阵。
H 矩阵的最低阶数为2,即211 (10-4)11++⎡⎤=⎢⎥+-⎣⎦H 为了简便起见,把上式中的+1和-1简写为+和-,上式就表示为2 (10-5)++⎡⎤=⎢⎥+-⎣⎦H阶数为2k 的高阶H 矩阵从下列递推关系得出k k/22 (10-6)⊗H =H H其中,k 为正整数,⊗是直积运算。
上式的直积运算是指将矩阵H k / 2中的每一个元素用矩阵H 2代替,比如,2242222 ++++⎡⎤⎢⎥+-+-⎡⎤⎢⎥=⊗==⎢⎥⎢⎥-++--⎣⎦⎢⎥+--+⎣⎦HH H H H H H 4484244 ++++++++⎡⎤⎢⎥+-+-+-+-⎢⎥⎢⎥++--++--⎢⎥+--++--+⎡⎤⎢⎥=⊗==⎢⎥⎢⎥-++++----⎣⎦⎢⎥+-+--+-+⎢⎥⎢⎥++----++⎢⎥+--+-++-⎢⎥⎣⎦H H H H H H H H 2矩阵、H 4矩阵和H 8矩阵都是对称矩阵,而且第一行和第一列的元素全为“+”,我们把这样的H 矩阵称为Hadamard 码矩阵的正规形式,或称为正规Hadamard 码矩阵。
在H 矩阵中,交换任意两行或两列,或改变任一行或列中每个元素的符号,都不会影响矩阵的正交性质。
因此,正规H 矩阵经过上述各种交换或改变后仍为H 矩阵,但不一定是正规的了。
按照递推关系式可以构造出所有2k 阶的H 矩阵。
可以证明,高于2阶的H 矩阵的阶数一定是4的倍数。
不过,以4的倍数作为阶数是否一定存在H 矩阵,这一问题并未解决。
H 矩阵是正交方阵。
如果把其中每一行看作是一个码组,则这些码组也是互相正交的,而整个H 矩阵就是一种码长为n 的正交编码,它包含n 个码组。
因为长度为n 的编码共有2n 个不同码组,如果只将这n 个码组作为许用码组,其余(2n - n )个为禁用码组,则可以将其多余度用来纠错。
这种编码在纠错编码理论中称为Reed-Muller 码。
Walsh 函数的定义常用三角函数法、拉德马赫函数乘积表示法、Hadamard 矩阵表示法和递推公式法等。
这里介绍Walsh 函数的递推公式形式,其定义为[]/2111 wal(0, )22Others wal(, )=wal(2, )11 (1)wal ,2(1)wal ,2 (10-7)44++⎧-≤<⎪=⎨⎪⎩+⎧⎫⎡⎤⎡⎤⎛⎫⎛⎫=-++--⎨⎬ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦⎩⎭q j j qt t k t j q t j t j θ其中,j = 0,1,2, …, q = 0或1,[j /2]表示j /2的整数部分。
为了便于理解,做以下几点说明:(1) 当把Wal(j , t )改成Wal(j , 2t )时,表示保持波形相对形状不变,只是将时基从-1/2 ≤ t ≤ 1/2压缩到-1/4 ≤ t ≤ 1/4;(2) 当把Wal(j , 2t )改成Wal[j , 2(t ± 1/4)]时,表示保持波形相对形状不变,只是将波形向左(对应“+”号)或向右(对应“-”号)平移 1/4。
例如,Wal(5, t )应该根据Wal(2, t )递推出来,此时,k = 5, j = 2, q = 1, [j /2] = 1。
1121Wal(5, )Wal(221, )11 (1)Wal 2, 2(1)Wal 2, 24411 Wal 2, 2Wal 2, 244t t t t t t ++=⨯+⎧⎫⎡⎤⎡⎤⎛⎫⎛⎫=-++--⎨⎬ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦⎩⎭⎧⎫⎡⎤⎡⎤⎛⎫⎛⎫=+--⎨⎬⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦⎩⎭其中,()0010Wal(2, )Wal 210, 11 (1)Wal 1, 2(1)Wal 1, 24411 Wal 1, 2Wal 1, 244t t t t t t ++=⨯+⎧⎫⎡⎤⎡⎤⎛⎫⎛⎫=-++--⎨⎬ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦⎩⎭⎧⎫⎡⎤⎡⎤⎛⎫⎛⎫=+--⎨⎬⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦⎩⎭()0110Wal(1, )Wal 201, 11 (1)Wal 0, 2(1)Wal 0, 24411 Wal 0, 2Wal 0, 244t t t t t t ++=⨯+⎧⎫⎡⎤⎡⎤⎛⎫⎛⎫=-++--⎨⎬ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦⎩⎭⎧⎫⎡⎤⎡⎤⎛⎫⎛⎫=-+--⎨⎬⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦⎩⎭前八个Walsh 函数中的任意两个函数都是正交的。
将前N 个Walsh 函数在等距的N 个点抽样,再将抽样值写成矩阵形式,即得N × N 矩阵。
例如,N = 8时,可以得到8 × 8矩阵:(10-8)++++++++⎡⎤⎢⎥----++++⎢⎥⎢⎥--++++--⎢⎥++--++--⎢⎥=⎢⎥+--++--+⎢⎥-++-+--+⎢⎥⎢⎥-+-++-+-⎢⎥+-+-+-+-⎢⎥⎣⎦W如果把Walsh 矩阵的每一行作为一个码组,就得到Walsh 编码。
3. 伪随机序列一方面,由于随机噪声的存在,通信系统的性能会变坏;另一方面,有时为了达到特殊的目的,通信系统中又需要噪声,比如保密通信中,让有用信号隐藏在随机噪声之中,以达到防止有用信号被截获。
相同的随机噪声难以重复产生,这给通信接收方造成了困难,因为难以从隐藏在随机噪声之中提取出有用信号。
后来,人们发明了伪随机序列,才使得这个难题得以解决。
伪随机序列具有类似于随机噪声的某些统计特性,同时又能够重复产生。
目前广泛应用的伪随机噪声都是由周期性数字序列经过滤波等处理后得出的。
我们将这种周期性数字序列称为伪随机序列,它有时又被称为伪随机信号和伪随机码。
常用的伪随机序列有m 序列、M 序列、二次剩余序列和双素数序列。
10.1.2 难点正交编码与伪随机序列的难点主要是m 序列的产生。
m 序列是最长线性反馈移位寄存器序列的简称,它是由带线性反馈移存器产生的周期最长的一种序列。
一般来说,希望用尽可能少的级数产生尽可能长的序列。
一个n 级线性反馈移存器可能产生的最长周期等于(2n - 1)。
这种最长的序列称为最长线性反馈移存器序列就是m 序列。
反馈电路连接方法不同,移存器产生的序列的周期长度也会不同。
一般的线性反馈移存器原理方框图如图10-1所示,其中,各级移存器的状态用a i 表示,a i = 0或1,i 为非负整数。
反馈线的连接状态用c i 表示,c i =1表示此线接通,c i =0表示此线断开。
反馈线的连接状态不同,输出序列的周期就可能不同。
图10-1 n 级线性反馈移位寄存器原理框图}根据上图,可以得到寄存器a n-1的新状态为()()()()()()()n 1n 12n-2n 11n 01n 12n 2n-110i n-i 1 = (10-9)----==⊕⊕⊕⊕=⊕⊕⊕⊕∑ni a c a c a c a c a c a c a c a a c a事实上,上式是一个递推公式。
显然,其它寄存器的新状态等于前一级寄存器的旧状态。
