钢结构之钢柱与钢压杆ppt课件
合集下载
钢结构讲义4

一. 弯曲屈曲
静力法:据曲线平衡状态求解微分 求临界力的方法 方程。属于精确法。 z 能量法:属于近似法。 P 列平衡方程 Py M 静力法: P M 即: EIy Py 0 V y 注意:对实心截面,可以不考虑剪力 y 影响,薄壁截面不能忽略。 能量法稳定准则:杆件从直杆平衡状态转变为无限 临近的曲杆平衡状态时,外荷势能的变化和杆件中应变 能的变化总量不变。 即: V U 0 应变能的变化 外荷势能的变化
曲杆平衡
N
cr
受压构件的承载力常决定于稳定
2
EI
2
因而为了提高临界力,应采用较为开展的截面型式 即提高回转半径 i 。 通常采用实腹式截面和格构式截面。 实腹式:沿构件全长都是连续分布的。 格构式:由柱肢和缀材组成截面,缀材沿构件全长 是间隔分布的。
(d)格构式构件截面 1
l
I i A
2
§4.3 轴心受压构件的临界力 理想轴心受压构件丧失稳定,或者称屈曲,有三种 情况: 弯曲屈曲:杆件纵轴线发生弯曲变形 扭转屈曲:杆件各截面绕纵轴线扭转变形 弯扭屈曲:既有各截面绕纵轴线的扭转,又有纵 轴线的弯曲变形 需算出三种屈曲情况的屈曲临界力,然后取小值, 作为轴压构件的临界力。 确定轴心受压构件的临界力时,采用下列假设: ① 杆件为两端铰接的理想直杆; ② 轴心压力作用于杆件两端,且为保向力(即弯 曲时,轴心压力方向不变)。 ③ 屈曲时变形很小,忽略杆长的变化。 ④ 屈曲时轴线挠曲成正弦半波曲线,截面仍保持 平面。
V M 应变能为:U dz dz 2 EI 2 l l
2
N y2 Vg 1 y
式中:M N cr y
2 cr
N N 故: U y dz 2 y dz 2 EI
钢结构基本原理ppt课件

N1Vy V/n
N1Tx
N1T
y1 r1
T1y xi2yi2
N1Ty
N1T
x1 r1
T1x xi2yi2
验算公式:
N 1N 1 T x2N 1 T yN 1 T y2N m b in
注意: y1≤3x时,N1T=N1XT=Ty1/Σyi2
x1≤3y时,N1T=N1yT=T. x1/Σxi2
应力集中:应力集中越严重,出现同号三相应力场的应力水平越接近,
钢材越趋于脆性。
温度:高温热塑性变形,低温冷脆(脆性温度转变区)
荷载类型:加载速度:低温脆性破坏
循环荷载 高周疲劳—— n514 0 fy
低周疲劳—— n= 120 ~ 5140 fy
疲劳:钢材在连续交变荷载作用下,会逐渐累积损伤、产生裂纹及裂纹
30
受拉螺栓连接:
1、受力:沿杆轴方向受拉。 破坏:栓杆被拉断。
2、单个螺栓受拉承载力设计值
Ntb Ae ftb
de2 4
ftb
f tb 值的由来:考虑橇杠作用,并对其进行简化,从 而采如用 ftb 0.8f 来考虑。
3、螺栓群受拉连拉计算。
1>轴心力:
n
N
N
b t
.
31
2>偏心力作用下
a.小偏心情况:螺栓群全部受拉。
逐渐扩展,直到最后破坏,这种现象称为疲劳。
疲劳破坏具有突然性,破坏前没有明显的宏观塑性变形,属于脆性断裂。 其破坏过程经历裂纹的产生、裂纹的缓慢扩展和最后迅速断裂三个阶段, 是延时断裂。
.
9
钢 柱 上 焊 接 牛 腿 ( 腹 板 和 翼 缘 )
.
10
梁柱节点:梁分别连接在柱的腹板和翼缘(连接角钢与
钢结构案例分析.ppt

Sx1 260 16 198 8.24 10 5 mm 3
2
2.受力情况
V=F=550KN, M=Fe=550×0.3=165KN·m
3.焊缝强度验算
h
max
M 2
Iw
165106 206 3.81108
89.2N/mm2
ftw
185N/mm2
max
VSx lxt
550103 1.04106 3.81108 12
150.1N / mm2
f
f
w f
195N / mm2
腹板焊缝的强度:
f
V (he2lw2 )
365103 127.8N / mm2 2 0.7 6 340
f
w f
160N / mm2
7
【例3.5】支托板与柱的角焊缝连接(图3.44),板厚t=12mm,Q235钢材,采用
三面围焊,在焊缝群重心上作用有轴力N=50kN,剪力V=200kN,扭矩T=
所以
1.1 l1 0.976 0.7
150 d0
每一个螺栓平均分担剪力V:
NV
V n
250 10
25KN
N
b c
122KN
剪力和拉力联合作用下:
NV NVb
2
Nt Ntb
2
25
2
20
2
0.79 1
40.84 0.976 41.62
14
【例3.9】将例3.6中的连接改为摩擦型高强度螺栓拼接,d=20mm,接触面 喷砂处理,8.8级。 【解】:单栓抗剪承载力设计值:
5.6 202 .82
4 95 5.6 172 .82
1.88 108 mm 4
《钢结构格构柱》PPT课件
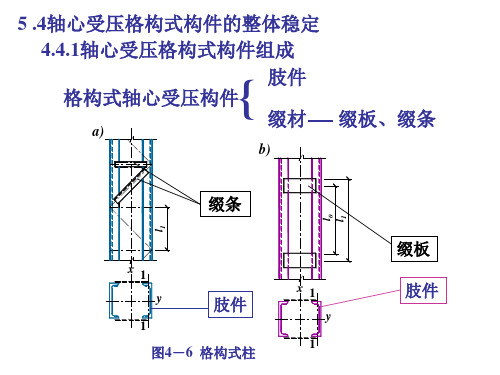
5 .4轴心受压格构式构件的整体稳定 4.4.1轴心受压格构式构件组成 肢件 格构式轴心受压构件 缀材 缀板、缀条
{
a)
b)
缀条
l1 l0 l1
缀板
x 1 y 1
肢件
x 1
y
肢件
图4-6 格构式柱
1
肢件:受力件。 由 2 肢(工字钢或槽钢)、 4 肢(角钢)、 3 肢 (园管)组成。
a)
x y
b)
2 EI y
l
2 y
(4-10)
(4-12)
y ,cr
2 E 2 y
2、绕虚轴屈曲 绕虚轴屈曲时,不能忽略剪切变形影响,这时,
N x ,cr
EI x EI x 2 ( l x ) lx
2 2
N b,cr
2 EI
l2
x ,cr
式中
2 E 2 E 2 ( x ) x2
I1 A i
2 1
② 计算
引入单肢节间段长细比1,且 1= l1 /i1 代入式:
1 2 EI x
l
2 x
2 1
12 EA
因为 Ix=Aix2, x= lx /ix ,代入得:
2 2 2 1 1 1 2 1 2 12 x x
③ 计算 x
x
y
c)
x y
d)
x y
图4-7 格构式柱的截面型 式
4.4.2整体稳定临界力
公式(4-9)仍然是适用的。
N b,cr
2 EI
l
2
1 2 EI 1 2 1 l
( 4- 9)
1、绕实轴屈曲 绕实轴屈曲时,与实腹截面一样,可忽略剪切变形 的影响,并写成弹性与非弹性通式,得
{
a)
b)
缀条
l1 l0 l1
缀板
x 1 y 1
肢件
x 1
y
肢件
图4-6 格构式柱
1
肢件:受力件。 由 2 肢(工字钢或槽钢)、 4 肢(角钢)、 3 肢 (园管)组成。
a)
x y
b)
2 EI y
l
2 y
(4-10)
(4-12)
y ,cr
2 E 2 y
2、绕虚轴屈曲 绕虚轴屈曲时,不能忽略剪切变形影响,这时,
N x ,cr
EI x EI x 2 ( l x ) lx
2 2
N b,cr
2 EI
l2
x ,cr
式中
2 E 2 E 2 ( x ) x2
I1 A i
2 1
② 计算
引入单肢节间段长细比1,且 1= l1 /i1 代入式:
1 2 EI x
l
2 x
2 1
12 EA
因为 Ix=Aix2, x= lx /ix ,代入得:
2 2 2 1 1 1 2 1 2 12 x x
③ 计算 x
x
y
c)
x y
d)
x y
图4-7 格构式柱的截面型 式
4.4.2整体稳定临界力
公式(4-9)仍然是适用的。
N b,cr
2 EI
l
2
1 2 EI 1 2 1 l
( 4- 9)
1、绕实轴屈曲 绕实轴屈曲时,与实腹截面一样,可忽略剪切变形 的影响,并写成弹性与非弹性通式,得
钢结构第五章_轴心受力构件详解

得欧拉临界力和临界应力:
Ncr
NE
2 EI l2
2 EA
2
cr
E
2E 2
(4 7) (4 8)
上式中,假定材料满足虎克定律,E为常量,因此当
截面应力超过钢材的比例极限 fp 后,欧拉临界力公式不 再适用。
第五章 钢柱与钢压杆
3、初始缺陷、加工条件和截面形式对压杆稳定都有影响
初
力学缺陷:残余应力、材料不均匀等
钢结构中理想的轴心受压构件的失稳,也叫发生屈 曲。理想的轴心受压构件有三种屈曲形式,即:弯曲屈 曲,扭转屈曲,弯扭屈曲。
第五章 钢柱与钢压杆
(1)弯曲屈曲——只发生弯曲变形,截面只绕一个 主轴旋转,杆纵轴由直线变为曲线,是双轴对称截面常 见的失稳形式。
图14
第五章 钢柱与钢压杆
图15整体弯曲屈曲实例
图1桁架
第五章 钢柱与钢压杆
图2 网架
图3 塔架
第五章 钢柱与钢压杆
图4 临时天桥
第五章 钢柱与钢压杆
图5 固定天桥
第五章 钢柱与钢压杆
图6 脚手架
第五章 钢柱与钢压杆
图7 桥
第五章 钢柱与钢压杆
5.1.2 轴心受力构件类型 轴心受力构件包括轴心受压杆和轴心受拉杆。 轴心受拉 :桁架、拉杆、网架、塔架(二力杆) 轴心受压 :桁架压杆、工作平台柱、各种结构柱
第五章 钢柱与钢压杆
5.1钢柱与钢压杆的应用和构造形式
本节目录
1. 轴心受力构件的应用 2. 轴心受力构件类型 3. 轴心受力构件的截面形式 4. 轴心受力构件的计算内容
基本要求
了解轴心受力构件的类型、应用。
掌握计算内容
第五章 钢柱与钢压杆
5.1.1 轴心受力构件的应用
钢结构轴心受力构件

t<80mm t≥80mm
焊接工字 形形截面
翼缘为焰切边 翼缘为轧制或剪切边
y x
板件宽厚比大于20 焊接箱形截面
板件宽厚比小于等于20
对x轴 b类 c类 b类 c类 b类
c类
对y轴 c类 d类 b类 d类 b类 c类
钢柱与钢压杆
(2)构件长细比的确定
①截面为双轴对称或极对称构件:
y
y
x lox ix
f
(2)求两主轴方向的回转半径:
ix
l0 x
;
iy
l0 y
钢柱与钢压杆
(3)由截面面积A和两主轴方向的回转半径ix,iy,优先
选用轧制型钢,如工字钢、H型钢等。型钢截面不能满足 时,选用组合截面,组合截面的尺寸可由回转半径确定。
h ix ;
1
b iy
2
α1、α2为系数,表示h、b和回转半径之间的近似数值关系。
钢柱与钢压杆
表2 各种截面回转半径的近似值
截面
y
y
y
y
b
b
b
x
hx
hx
hx
hx
hx
hx
h
b
b
b
b=h
y
y
y
ix 1h 0.43h
iy 2b 0.24b
0.38h 0.44b
0.38h 0.60b
0.40h 0.30h 0.28h 0.40b 0.215b 0.24b
0.32h 0.20b
(4)由求得的A、h、b,综合考虑构造、局部稳定、钢 材规格等,确定截面尺寸。
钢柱与钢压杆
(5)构件验算:
①截面有削弱时,需进行强度验算。 N f
中南大学《钢结构原理》课件第五章 轴心受力构件

☆措施(确保长细比不是很小,不扭转失稳)
y (x ) 5.07b / t
☆长细较大时,弯曲失稳起控制作用,作弯曲失稳验算。
中南大学桥梁工程系
第五章 轴心受力构件
5.5 轴心受压构件局部稳定性
1、局部稳定的概念
轴心受压柱局部屈曲变形
轴心受压构件翼缘的凸曲现象
中南大学桥梁工程系
第五章 轴心受力构件
1916年因施工问题又发生一次倒塌事故。
前苏联在1951~1977年间共发生59起重大钢结构事故,有17起 属稳定问题。
(设计、制作、安装或使用不当都可能引发稳定事故)
例如:
1957年前苏联古比雪夫列宁冶金厂锻压车间,7榀1200m2屋盖塌落。 起因是一对尺寸相同的拉压杆装配颠倒。 1974年,苏联一个俱乐部观众厅24×39m钢屋盖倒塌。起因是受力 较大的钢屋架端斜杆失稳。
中南大学桥梁工程系
第五章 轴心受力构件
•荷载初始偏心降低稳定承载力
vm e0 (sec
2
N 1) NE
中南大学桥梁工程系
第五章 轴心受力构件
•残余应力降低稳定承载力
中南大学桥梁工程系
第五章 轴心受力构件
(1)使部分截面提前进入塑性状态,截面的弹性区域减少, 干扰后只有弹性区产生抗力增量,故降低了稳定承载力。
N 1 fy A Ry
N 1 fu An Ru
偏安全简化处理
N 1 fy f An Ry
中南大学桥梁工程系
第五章 轴心受力构件
2、刚度计算
•刚度计算的目的:保证在安装、使用过程中正常使用要求
•实例1:九江桥主拱吊杆涡振现象
中南大学桥梁工程系
第五章 轴心受力构件
y (x ) 5.07b / t
☆长细较大时,弯曲失稳起控制作用,作弯曲失稳验算。
中南大学桥梁工程系
第五章 轴心受力构件
5.5 轴心受压构件局部稳定性
1、局部稳定的概念
轴心受压柱局部屈曲变形
轴心受压构件翼缘的凸曲现象
中南大学桥梁工程系
第五章 轴心受力构件
1916年因施工问题又发生一次倒塌事故。
前苏联在1951~1977年间共发生59起重大钢结构事故,有17起 属稳定问题。
(设计、制作、安装或使用不当都可能引发稳定事故)
例如:
1957年前苏联古比雪夫列宁冶金厂锻压车间,7榀1200m2屋盖塌落。 起因是一对尺寸相同的拉压杆装配颠倒。 1974年,苏联一个俱乐部观众厅24×39m钢屋盖倒塌。起因是受力 较大的钢屋架端斜杆失稳。
中南大学桥梁工程系
第五章 轴心受力构件
•荷载初始偏心降低稳定承载力
vm e0 (sec
2
N 1) NE
中南大学桥梁工程系
第五章 轴心受力构件
•残余应力降低稳定承载力
中南大学桥梁工程系
第五章 轴心受力构件
(1)使部分截面提前进入塑性状态,截面的弹性区域减少, 干扰后只有弹性区产生抗力增量,故降低了稳定承载力。
N 1 fy A Ry
N 1 fu An Ru
偏安全简化处理
N 1 fy f An Ry
中南大学桥梁工程系
第五章 轴心受力构件
2、刚度计算
•刚度计算的目的:保证在安装、使用过程中正常使用要求
•实例1:九江桥主拱吊杆涡振现象
中南大学桥梁工程系
第五章 轴心受力构件
钢结构教学课件PPT轴心受力构件

第六章 轴心受力构件
§6.1 轴心受力构件的应用及截面形式
6.1.1 轴心受力构件的应用
a)
轴心受力构件是指承受通过截面形 心轴线的轴向力作用的构件。包括 轴心受拉构件(轴心拉杆)和轴心 受压构件(轴心压杆)。
在钢结构中应用广泛,如桁架、网 架中的杆件,工业厂房及高层钢结 构的支撑,操作平台和其它结构的 支柱等。
1、弹性弯曲屈曲
欧拉(Euler)早在1744年通过对理想轴心压杆的整体稳定问题进 行的研究,当轴心力达到临界值时,压杆处于屈曲的微弯状态。 在弹性微弯状态下,根据外力矩平衡条件,可建立平衡微分方程, 求解后得到了著名的欧拉临界力和欧拉临界应力。
钢结构设计原理 Design Principles of Steel Structure
其临界力。
钢结构设计原理 Design Principles of Steel Structure
第六章 轴心受力构件
2、弹塑性弯曲屈曲
1889年恩格塞尔,用应力-应变曲线的切线模量代替欧拉公式中 的弹性模量E,将欧拉公式推广应用于非弹性范围,即:
Ncr
2Et I
l02
2 Et
2
A
(6.3.5)
钢结构设计原理 Design Principles of Steel Structure
第六章 轴心受力构件
对于高强螺栓的摩擦型连接,可以认为连接传力所依靠的摩擦力 均匀分布于螺孔四周,故在孔前接触面已传递一半的力,因此最 外列螺栓处危险截面的净截面强度应按下式计算:
N f
An,1
其中:An,1 b n1 d0 t;
+
+
+
+
b)
++
§6.1 轴心受力构件的应用及截面形式
6.1.1 轴心受力构件的应用
a)
轴心受力构件是指承受通过截面形 心轴线的轴向力作用的构件。包括 轴心受拉构件(轴心拉杆)和轴心 受压构件(轴心压杆)。
在钢结构中应用广泛,如桁架、网 架中的杆件,工业厂房及高层钢结 构的支撑,操作平台和其它结构的 支柱等。
1、弹性弯曲屈曲
欧拉(Euler)早在1744年通过对理想轴心压杆的整体稳定问题进 行的研究,当轴心力达到临界值时,压杆处于屈曲的微弯状态。 在弹性微弯状态下,根据外力矩平衡条件,可建立平衡微分方程, 求解后得到了著名的欧拉临界力和欧拉临界应力。
钢结构设计原理 Design Principles of Steel Structure
其临界力。
钢结构设计原理 Design Principles of Steel Structure
第六章 轴心受力构件
2、弹塑性弯曲屈曲
1889年恩格塞尔,用应力-应变曲线的切线模量代替欧拉公式中 的弹性模量E,将欧拉公式推广应用于非弹性范围,即:
Ncr
2Et I
l02
2 Et
2
A
(6.3.5)
钢结构设计原理 Design Principles of Steel Structure
第六章 轴心受力构件
对于高强螺栓的摩擦型连接,可以认为连接传力所依靠的摩擦力 均匀分布于螺孔四周,故在孔前接触面已传递一半的力,因此最 外列螺栓处危险截面的净截面强度应按下式计算:
N f
An,1
其中:An,1 b n1 d0 t;
+
+
+
+
b)
++
钢结构A-钢柱与钢压杆

[ ]
N f A
轴心受压构件的整体稳定 Buckling of Rolled or welded Section Column
轴心受压构件的三种整体失稳状态
无缺陷的轴心受压构件(双轴对称的 工型截面)通常发生弯曲失稳,构件 的变形发生了性质上的变化,即构件 由直线形式改变为弯曲形式,且这种 变化带有突然性。
规范在制定轴心受压构件的柱子曲线时,根据不同截面形状和尺寸、 不同加工条件和相应的残余应力分布和大小、不同的弯曲屈曲方向以 及l/1000的初弯曲,按照极限承载力理论,采用数值积分法,对多种 实腹式轴心受压构件弯曲屈曲算出了近200条柱子曲线。
规范将这些曲线分成四组,也就是将分布带分成四个窄带,取每组的 平均值曲线作为该组代表曲线,给出a、b、c、d四条柱子曲线,如图
柱子曲线(
曲线
)
规范根据截 面分类查表 格。
轴心受压实腹式构件的整体稳定计算 Buckling of Rolled or welded Section Column
N cr cr f y f A R fy R N 即: f A
欧拉公式:
EId2 y / dz2 Ny 0
k 2 N / EI
N A
z
y k y 0
2
方程通解: 临界力:
y A sin kz B coskz
N cr 2 EI / l 2 2 EA /(l / i) 2 EA /
2 2
y
屈曲弯曲 状态
理想轴心受压构件 (1)杆件为等截面理想直杆; (2)压力作用线与杆件形心轴重合; (3)材料为匀质,各项同性且无限弹性,符合虎克定律; (4)构件无初应力,节点铰支。
同济大学课件-钢结构设计原理

钢结构基本原理及设计
6.3.3 力学缺陷对弯曲屈曲的影响
1.残余应力的产生与分布规律
(1)残余应力产生 热轧H型钢 (2)
火焰切割边钢板焊
接H型钢 (3)量测残余应力 分割法、钻孔法
钢结构基本原理及设计
热轧的宽翼缘工字钢(H型 钢),翼缘宽度较大,热轧后冷 却过程中,翼缘两端由于其暴露 于空气中的面积较翼缘与腹板交 接部分为多而冷却较快, 腹板中间部位则因厚度较薄 而冷却较快,翼缘与腹板交接部 位冷却收缩变形受到先冷却部分 的约束而出现残余拉应力,先冷 却部分则出现残余压应力。
钢结构基本原理及设计
欧拉公式
N cr E I cr 2 A l A 2 2 2 E E E 2 2 2 i 2 l l i2
其中,
2 EI 2 EI 2 EA N cr 2 2 2 (l ) l0 2
考虑剪切影响?
i
分岔屈曲后,结构只能在比临界荷载低的荷载下才能维 持平衡位形。承受轴向荷载的圆柱壳,承受均匀外压的球壳都 呈不定分岔屈曲形式。长细比不大的圆管压杆与圆柱壳很相似, 薄壁方管压杆亦有指表现为不稳定分岔屈曲。 P
v
钢结构基本原理及设计
(3)跃越屈曲
结构以大幅度的变形从一个平衡位形跳到另一个平衡 位形。 铰接坦拱和油罐的扁球壳顶盖都属于这种失稳情形。 在发生跃越后,荷载一般还可以显著增加,但是其变形大 大超出了正常使用极限状态,显然不宜以此为承载能力的 极限状态。
钢结构基本原理及设计
第6章 轴心受力构件
§6-1 §6-2 §6-3 §6-4 §6-5 §6-6 §6-7 §6-8 构件的应用和截面形式 构件的强度和刚度 轴心受压构件的整体稳定 实际轴心受压构件整体稳定的计算 轴心受压构件的局部稳定 实腹式轴心受压构件的截面设计 格构式轴心受压构件 柱头、柱脚
钢结构 柱和支撑的设计

5.其他
强:梁与柱刚性连接时,柱在梁翼缘上 下各500mm的范围内,柱翼缘与柱腹板 间或箱形柱壁板间的连接焊缝应采用全 熔透坡口焊缝。
整理课件
29
6.改进节点
改进的节点构造-1 (骨形连接)
Dogbone Moment Connection
❖梁翼缘局部削弱, 形成骨形连接;
❖塑性铰自梁端外移。
塑性铰所在截面
54
* 地震区的工字形截面中心支撑 宜采用轧制宽翼缘H型钢;
* 如果采用焊接工字形截面,则 其腹板和翼缘的连接焊缝应设 计成焊透的对接焊缝;
* 与支撑相连接的柱通常加工成 带悬臂梁段的形式,以避免梁 柱节点处的工地焊缝。
整理课件
55
4.3.4.2 偏心支撑
1. 偏心支撑的性能与特点
(a) 门架式 (b) 单斜杆式 (c) 人字形 (d) V形
K1,K2 :交于柱上下端的横梁线刚度之和与柱线刚度之和的比值
整理课件
13
柱节点域设计
N c1
M c1 V c1
M b1
V b1
Vb2 hb hb1
M b2
V c2
M c2 N c2
hc
h c 1 整理课件
14
1. 节点域厚度要求
(hb hc 90
)
tw
2. 节点域抗剪强度
Mb1Mb2 Vc1Vc2
(Aw A)0.3
(Aw A)0.3
a1.6Mlp Vl
a [ 1 .1 0 5 .5(A wA )1 .] 6 M lp V l
N V
N、V —— 耗能梁段的轴力、剪力设计值
Aw——
耗能梁段腹板面积 整理课件
60
6. 耗能梁段强度验算
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ix
l0x
ix 1h
h0
h ix
1
求对 y 轴弯曲所需的回转半径 iy
iy
l0y
iy 2b1
b1
iy
2
系数值根据 所选的截面 形式由附录 八查得。
.
轧
焊
制
接
.
(二)确定型钢型号或组合截面的其它尺寸 1、型钢
根据 A、ix、iy 查型钢表选型号
2、组合截面 根据 A、h、b1,考虑制造工艺,并结合钢 材规格选择板件尺寸
t
fy
max[x,y], 30 ~100
.
5.4 轴心受压实腹柱的设计
一、截面形式
工字形、圆管 (1)等稳性 x≈ y,或λx ≈ λy (2)宽肢薄壁 (3)制造省工 (4)连接简便
.
截面形式、计算长度l0和钢材钢号确定的前提下
二、截面选择
(一)确定截面尺寸A、ix、iy、b1 、 h
.
A. 假定长细比λ查附录七查出相应的
λ=l/i≤[λ]
主要结构的压杆的容许长细比为150,支撑 中的压杆的容许长细比为200,闸门构件的容 许长细比见表5-2。
.
5.3 轴心受压实腹式构件的局部稳定
1、翼缘板
b (10 0.1) 235
t
fy
max[x,y ], 30 ~ 100
b—翼缘外伸宽度,即翼缘半宽
.
2、腹板
h0 (250.5)235
b kb
x
t
h
I ex Ix
2kbt(h / 2)2 2bt(h / 2)2
k
Iey 2 t(kb )3 /1 2 k 3 I y 2tb 3 /1 2
残余应力对弱轴的影响
t
y
比对强轴的影响严重的多
.
三、实际轴心压杆的稳定极限承载力
1、实际压杆的工作性能
存在初始缺陷:初偏心、初弯矩、残余应力、 材质不均匀
影响降低压杆稳定承载能力的主要因素之一是 由于残余应力的存在。
.
1、不同加工方法的残余应力分布情况
轧制翼缘板
焰切翼缘板
.
2、残余应力与作用平均应力的叠加
0.3f y 0.7f y
fy
.
3、非弹性范围的压杆的临界应力
(1)
当c
N A
f
,
y
截
面
为
弹
性
阶
用 段
欧 ,
拉
公
式
计 算Ncr、cr
EI
Ncr l02
第五章 钢柱与钢压杆
.
5.1 应用与构造
一、应用
桁架、网架、塔架与框架中存在着大量的 承受轴心压力的轴心受压构件以及同时承受 轴心压力和弯矩的压弯构件。
.
.
F
基础
.
二、种类
实腹式、格构式
.
5.2 轴心受压实腹式构件的整体稳定
轴心受压实腹式构件的截面设计需要 满足强度、刚度、整体稳定性和局部稳 定性的要求,其中整体稳定性是主要决 定因素。
.
2、非弹性范围的压杆的临界应力
cr f P
cr
2E t 2
切线模量
E t 的确定
比较困难,实际运用
时常用经验公式计算
.
Q235钢
柱 子 曲 线
.
二、残余应力的影响
实际结构中,理想的轴心压杆是不存在的,由 于种种原因,经常出现一些不利的因素,例如杆 件的初弯曲、荷载的初偏心等,都在不同程度上 使压杆的稳定承载能力降低。
.
① 截面高度 h 和翼缘宽度 b1 A. 焊接工字形截面 ix = 0.43h,iy = 0.24b1
l0x ≈ l0y ,λx = λy
l0x l0y 0.43h 0.24b1
b1 1.8h
此 时取h
b1, 在l0x
l0
时
y
,y
x
y 轴 方向 的 稳定 性 较, 差
截 面稳 定 由y 轴 的稳 定 条件 决 定
cr
2E 2
.
(2)
当 c
N A
f
,
y
而
截
面
还
未
全
部
屈
服 时
,
截
面
由
弹 性 区 和 塑 性 区 组 成 , 只 考 虑 弹 性 区 为 有 效 区 来
计算压杆稳定
y
Ncr
EIe
l02
EI(Ie
l02 I
)
x
cr
2E(Ie) 2 I
x y
.
由于残余应力的存在,使压杆截面提前出现塑性区, 从而降低了压杆临界应力,降低多少取决于Ie/I比值 的大小,而Ie/I比值又与残余应力的分布与大小、杆 件截面的形状以及屈曲时的弯曲方向有关。
N f
A
所需截面面积 A N
f
假定λ值时,可参考经验数据:当l0=5~6m, N<1500kN时,可假定λ=70~100;N=1500~ 3500kN时,可假定λ=50~70。
.
B.根据假定的λ值和等稳定条件(一般取 x y ),求 得截面所需的回转半径,继而确定所需截面的宽度 和高度。
求对 x 轴弯曲所需的回转半径 ix
.
l0=l
l0=2l
l0=0.5l
.
l0=0.7l
N cr
2 EI
l
2 0
N
与弯曲刚度成正比,与计算长度
cr
l0
成反比,而与材料强度无关,可通过
增大 I 和减小 l0 的方法来提高压杆的整 体稳定性
.
cr
N cr A
2E 2
cr与 2 成反比, 越大, cr 越低, 稳定性越差,由此可用 来反映 压杆的刚度 []
.
B. 焊接工字形截面 ix = 0.43h,iy = 0.24b1 l0x ≈2 l0y ,λx = λy
0.l4 0xh 30.l2 0yb4 1 b10.9h,取 hb1
.
稳定系数:=cr fy
.
.
.
(3)实腹式轴心受压构件的整体稳定计算公式 N cr cr fy f A R fy R —轴心受压构件整体稳定系数,根据
表5-1的截面分类,由钢号和长细比 查附录7 确定
在长细比的计算中: 注意构件对截面主轴x和y得计算长
度可能相等或不相. 等。
.
为了减小构件在制造、运输和安装过程中 因偶然碰撞而产生变形,或在使用中因自重 引起得弯曲以及因动载引起的振动而影响正 常使用,要保证构件有足够的刚度,对轴心 受力构件应按照下式验算刚度:
2、压溃理论
考虑初偏心和残余应力的影响,将压杆作为一 根有小偏心压力作用的偏心压杆,由此求其稳 定承载能力的理论方法
.
.
3、验算方法 (1)根据截面形式、尺寸、加工条件、残余
应力的大小和分布等因素,按压溃理论计 算出 96 条无量纲的柱子线 (2)采用数理统计和可靠度分析方法,将承 载能力相近的按截面形式、屈曲方向和加 工条件归纳为a、b、c三类曲线
.
一、理想轴心压杆的临界力
理想轴心压杆: (1)等截面直杆 (2)压力线与形心线重合 (3)材质均匀,各向同性,且无限弹性,符合
虎克定律
E
.
1、理想等直细长轴心压杆的稳定问题
欧拉公式
2EI
Ncr l02
长细比 l0 / i
cr
Ncr A
2E 2
回转半径i I / A
压杆自由长度 l0 l
