三角形四大模型
八年级上册数学三角形模型

八年级上册数学的三角形模型包括以下几种:
1. 直角三角形模型:直角三角形是指其中一个角度为90度的三角形。
可以用两条直线表示斜边和直角边,另一条边则由勾股定理得出。
2. 等腰三角形模型:等腰三角形是指其中两边相等的三角形。
可以用两条等长的线段表示等腰边,另一条边则由勾股定理得出。
3. 等边三角形模型:等边三角形是指三条边都相等的三角形。
可以用三条等长的线段表示三边。
4. 直角坐标系中的三角形模型:可以用坐标轴上的点表示三角形的顶点,用计算坐标点之间距离的方法计算三边长度,然后用勾股定理判断是否为直角三角形或者等腰三角形。
5. 正弦定理、余弦定理和正切定理模型:这些定理是求解任意三角形的边长和角度的重要工具,在解决实际问题时经常应用。
以上是八年级上册数学三角形模型的介绍,希望对你有所帮助。
八年级上册数学三角形模型大全

八年级上册数学三角形模型大全
八年级上册数学三角形模型包括以下几种:
1. A字模型:∠1 + ∠2 = ∠c + 180°。
2. 高分角模型:高分角等于底角差的一半。
3. 八字模型:两翼和相等。
4. 飞镖模型:∠d = ∠a + ∠b + ∠c。
5. 镖分分模型:上下之和等于中间两倍。
6. 八字加角分线模型:上下之和等于中间两倍。
7. 双角平分线模型—内内:内内90°+1/2。
8. 双角平分线模型—外外:外外90°-1/2。
9. 双角平分线模型—内外:本质上有某些关联。
10. 一内一外模型:由三角形的一个内角平分线和一个外角平分线产生夹角。
11. 两内模型:两个内角平分线的夹角。
12. 两外模型:两个外角平分线的夹角。
以上内容仅供参考,可以请教数学老师或查看教辅资料,以获取更多有关三角形模型的解题技巧和方法。
三角形五大模型及证明过程

三角形五大模型及证明过程嘿,咱今儿就来聊聊三角形的五大模型!这可都是几何世界里的宝贝呀!先来说说第一个模型,那就是等底等高模型。
就好像你有两个一模一样的大面包,底一样长,高也一样高,那它们的大小肯定是一样的呗!在三角形里也是这个道理呀,等底等高的三角形,面积肯定相等呀!这多简单易懂呀!再看看第二个模型,鸟头模型。
这名字是不是挺有意思?想象一下,三角形就像一只小鸟的头,有着特别的比例关系呢。
它可神奇了,通过一些角度和边长的关系,能让我们找到好多隐藏的规律。
接着是第三个模型,蝴蝶模型。
哇,是不是感觉像美丽的蝴蝶在三角形里翩翩起舞呀!这个模型里有着好多对称和相等的关系呢,就像蝴蝶的翅膀一样美妙。
然后是第四个模型,燕尾模型。
嘿,就像燕子的尾巴一样有着独特的形状和特点。
通过它,我们能发现好多线段之间的奇妙联系。
最后一个模型,沙漏模型。
时间就像沙漏一样慢慢流逝,而这个模型里也有着时间般的规律呢。
它能帮我们理解好多三角形里关于比例和相似的问题。
那怎么证明这些模型呢?咱就拿等底等高模型来说吧。
你看呀,假如有两个三角形,底都是那条直直的线,高呢,都从顶点直直地垂下来到那条底边上。
那我们可以通过把其中一个三角形剪下来,放到另一个上面,是不是严丝合缝呀!这不就证明了它们面积相等嘛!其他模型的证明也是各有各的巧妙之处呢。
这些三角形模型就像我们几何世界里的秘密武器,掌握了它们,我们就能在三角形的海洋里畅游啦!是不是很有趣呀?它们就像是一个个小宝藏,等着我们去发掘,去探索。
学习这些模型的过程就像是一场冒险,每一个模型都是一道关卡,我们要勇敢地去挑战,去理解,去证明。
当我们真正掌握了它们,那种成就感,哎呀,别提多棒啦!所以呀,别小看这小小的三角形,它里面蕴含着大大的智慧呢!大家都快来一起探索三角形的奥秘吧!让我们在几何的天空中自由翱翔!。
三角形的四大模型

三角形的四大模型三角形是几何学中最基本的形状之一,它具有许多重要的性质和特点。
在研究三角形时,我们可以采用不同的模型来帮助我们理解和解决问题。
下面将介绍三角形的四大模型:欧拉模型、特里希亚特中心模型、边-角模型和向量模型。
一、欧拉模型欧拉模型通过研究三角形的顶点、边和面之间的关系来理解三角形的性质。
欧拉公式是欧拉模型中的重要定理之一,它表达了三角形的顶点数、边数和面数之间的关系。
根据欧拉公式,三角形的顶点数加上面数减去边数等于2。
这个定理可以用来验证三角形是否构成一个封闭的几何图形。
欧拉模型还可以帮助我们研究三角形的垂心、重心、外心和内心等特殊点的性质。
这些特殊点有助于我们理解三角形的对称性、平衡性和内切性质。
二、特里希亚特中心模型特里希亚特中心模型是通过研究三角形的三个特殊点来理解三角形的性质。
特里希亚特中心包括三角形的重心、外心和内心。
重心是三角形三条中线的交点,外心是三角形三条外接圆的交点,内心是三角形三条内切圆的交点。
特里希亚特中心模型可以帮助我们研究三角形的平衡性、外接性和内切性质。
例如,通过研究重心,我们可以了解三角形的平衡点和质心的性质;通过研究外心,我们可以了解三角形的外接圆和外心角的性质;通过研究内心,我们可以了解三角形的内切圆和内心角的性质。
三、边-角模型边-角模型是通过研究三角形的边和角之间的关系来理解三角形的性质。
边-角模型可以帮助我们研究三角形的角度关系、边长关系和面积关系。
在边-角模型中,我们可以利用三角函数来计算三角形的角度、边长和面积。
例如,正弦定理可以用来计算三角形的边长,余弦定理可以用来计算三角形的角度,海伦公式可以用来计算三角形的面积。
四、向量模型向量模型是通过利用向量的特性来理解三角形的性质。
向量模型可以帮助我们研究三角形的平行性、共线性和向量运算等。
在向量模型中,我们可以用向量的减法来计算两个向量之间的夹角,用向量的叉乘来计算两个向量构成的平行四边形的面积。
全等三角形八大基本模型

全等三角形八大基本模型
(原创实用版)
目录
1.全等三角形的定义与性质
2.全等三角形的八大基本模型
1.手拉手模型
2.一线三垂直模型
3.一线三等角模型
4.等腰三角形中边边角模型
5.背对背模型
6.半角旋转模型
7.角分线模型
8.正方形手拉手模型
正文
全等三角形是指两个三角形的对应边和对应角分别相等的三角形。
在解决全等三角形问题时,我们需要了解全等三角形的定义和性质,以及掌握一些常用的模型。
本文将介绍全等三角形的八大基本模型,希望能帮助大家更好地理解和解决全等三角形问题。
1.手拉手模型:两个三角形通过一个公共边,并且这个公共边的两个端点分别与另外两个三角形的顶点相连。
2.一线三垂直模型:两个三角形的一组对应边互相平行,且另外两组对应边互相垂直。
3.一线三等角模型:两个三角形的一组对应边互相平行,且另外两组对应角相等。
4.等腰三角形中边边角模型:两个等腰三角形,其中一个等腰三角形的底边与另一个等腰三角形的腰相等,且两个等腰三角形的底角相等。
5.背对背模型:两个三角形的一组对应边互相垂直,且另外一组对应边互相平行。
6.半角旋转模型:一个三角形通过某个顶点旋转 180 度后与另一个三角形重合。
7.角分线模型:两个三角形的一组对应角相等,且另一组对应边的延长线相交于一点,这个点将延长线分成的两段长度相等。
8.正方形手拉手模型:两个正方形,其中一个正方形的一边与另一个正方形的一边相连,另外两个正方形的边也分别相连。
以上就是全等三角形的八大基本模型,这些模型在解决全等三角形问题时非常实用。
数学全等三角形五大模型及必要步骤

数学全等三角形五大模型及必要步骤
一、等积变换模型
1、等底等高的两个三角形面积相等.
2、两个三角形高相等,面积比等于它们的底之比.
3、两个三角形底相等,面积比等于它的的高之比.
二、共角定理模型
两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形.
共角三角形的面积比等到于对应角(相等角或互补角)两夹边的乘积之比.
三、蝴蝶定理模型
(说明:任意四边形与四边形、长方形、梯形,连接对角线所成四部的比例关系是一样的.)四、相似三角形模型
相似三角形:是形状相同,但大小不同的三角形叫相似三角形.
相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比.
相似三角形的面积比等于它们相似比的平方.
五、燕尾定理模型
不多说了,应该知道吧。
三角形的四大模型培训课件

三角形的四大模型一、三角形的重要概念和性质1、三角形的内角和定理:三角形的内角和等于180°2、三角形的外角和定理:三角形的一个外角等于和它不相邻的两个内角的和3、三角形角平分线(角分线)中线(分面积等)高(直角三角形两锐角互余)二、八字模型:证明结论:∠A+∠B=∠C+∠D三、飞镖模型:证明结论:1.∠BOC=∠A+∠B+∠C四、角分线模型:如图,BD、CD分别是∠ABC和∠ACB的角平分线,BD、CD相交于点D,试探索∠A与∠D之间的数量关系,并证明你的结论.如图,△ABC两个外角(∠CAD、∠ACE)的平分线相交于点P.探索∠P与∠B有怎样的数量关系,并证明你的结论.题型一、三角形性质等应用1.如图,小亮从A点出发前进10m,向右转15°,再前进10m,又向右转15°,这样一直走下去,他第一次回到出发点A时,一共走了米数是()A.120 B.150 C.240 D.3602.如图所示是重叠的两个直角三角形.将其中一个直角三角形沿BC方向平移得到△DEF.如果AB=8cm,BE=4cm,DH=3cm,则图中阴影部分面积为cm2.3.如图,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且S△ABC=4cm2,则S阴影= cm2.4.A、B、C是线段A1B,B1C,C1A的中点,S△ABC的面积是1,则S△A1B1C1的面积.5.一个四边形截去一个角后,剩下的部分可能是什么图形?画出所有可能的图形,并分别说出内角和和外角和变化情况.6.如图,直线AC∥BD,连接AB,直线AC,BD及线段AB把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分.当动点P落在某个部分时,连接PA,PB,构成∠PAC,∠APB,∠PBD三个角.(提示:有公共端点的两条重合的射线所组成的角是0°角)(1)当动点P落在第①部分时,求证:∠APB=∠PAC+∠PBD;(2)当动点P落在第②部分时,∠APB=∠PAC+∠PBD是否成立?(直接回答)(3)当动点P在第③部分时,全面探究∠PAC,∠APB,∠PBD之间的关系,并写出动点P的具体位置和相应的结论.选择其中一种结论加以证明.题型二、八字模型应用7.(1)如图1的图形我们把它称为“8字形”,请说明∠A+∠B=∠C+∠D;(2)如图2,AB∥CD,AP、CP分别平分∠BAD、∠BCD,①图2中共有个“8字形”;②若∠ABC=80°,∠ADC=38°,求∠P的度数;(提醒:解决此问题你可以利用图1的结论或用其他方法)③猜想图2中∠P与∠B+∠D的数量关系,并说明理由.8.(1)求五角星的五个角之和;(2)求这六个角之和题型三、飞镖模型应用9.如图,已知AB∥DE,BF,EF分别平分∠ABC与∠CED交于点F,探索∠BFE与∠BCE 之间的数量关系,并证明你的结论.10.如图1,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.(1)探究猜想:①若∠A=30°,∠D=40°,则∠AED等于多少度?②若∠A=20°,∠D=60°,则∠AED等于多少度?③猜想图1中∠AED,∠EAB,∠EDC的关系并证明你的结论.(2)拓展应用:如图2,射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的4个区域(不含边界,其中区域③、④位于直线AB上方,P是位于以上四个区域上的点,猜想:∠PEB,∠PFC,∠EPF的关系(不要求证明).题型四、角分线模型应用11.如图,∠A=65°,∠ABD=30°,∠ACB=72°,且CE平分∠ACB,求∠BEC的度数.12.如图,在△ABC中,∠A=42°,∠ABC和∠ACB的三等分线分别交于点D,E,则∠BDC的度数是()A.67°B.84°C.88°D.110°第11题第12题第13题13.如图,若∠DBC=∠D,BD平分∠ABC,∠ABC=50°,则∠BCD的大小为()A.50°B.100°C.130°D.150°14.如图,∠ACD是△ABC的外角,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC 的平分线与∠A1CD的平分线交于点A2,…,∠A n﹣1BC的平分线与∠A n﹣1CD的平分线交于点A n.设∠A=θ.则:(1)∠A1= ;(2)∠A2= ;(3)∠A n= .题型五、其他应用15.已知△ABC中,∠A=60°.(1)如图①,∠ABC、∠ACB的角平分线交于点D,则∠BOC= °.(2)如图②,∠ABC、∠ACB的三等分线分别对应交于O1、O2,则∠BO2C= °.(3)如图③,∠ABC、∠ACB的n等分线分别对应于O1、O2…O n﹣1(内部有n﹣1个点),求∠BO n﹣1C(用n的代数式表示).(4)如图③,已知∠ABC、∠ACB的n等分线对应于O1、O2…O n﹣1,若∠BO n﹣1C=90°,求n的值.16.我们知道,任何一个三角形的三条内角平分线相交于一点,如图,若△ABC 的三条内角平分线相交于点I,过I作DE⊥AI分别交AB、AC于点D、E.(1)请你通过画图、度量,填写右上表(图画在草稿纸上,并尽量画准确)(2)从上表中你发现了∠BIC与∠BDI之间有何数量关系,写出并说明其中的道理.∠BAC的度数40°60°90°120°∠BIC的度数∠BDI的度数(备用图)。
三角形计算四大模型

三角形计算四大模型三角形是数学中的一种基本几何形状,拥有三边和三个内角。
在数学中,有四种常见的三角形计算模型:余弦定理、正弦定理、海伦公式和面积公式。
这些模型可以用于计算三角形的各种属性,例如边长、角度和面积。
下面将详细介绍这四个模型。
1.余弦定理:余弦定理表达了一个三角形的任意一条边的平方与其余两条边的平方之间的关系。
设三角形的三边长度分别为a、b、c,内角对应的顶点分别为A、B、C,那么余弦定理可以表达为:a^2 = b^2 + c^2 - 2bc*cosAb^2 = a^2 + c^2 - 2ac*cosBc^2 = a^2 + b^2 - 2ab*cosC2.正弦定理:正弦定理利用了角度和边长之间的关系。
设三角形的三边长度分别为a、b、c,内角对应的顶点分别为A、B、C,那么正弦定理可以表达为:a/sinA = b/sinB = c/sinC3.海伦公式:海伦公式可以用来计算三角形的面积。
设三角形的三边长度分别为a、b、c,令s为半周长(即s=(a+b+c)/2),那么海伦公式可以表达为:面积 = sqrt(s*(s-a)*(s-b)*(s-c))4.面积公式:面积公式也可以用来计算三角形的面积。
面积=(1/2)*b*h这四大模型都能够为我们提供计算三角形属性的方法。
余弦定理和正弦定理适用于计算三角形边长和角度的情况,而海伦公式和面积公式则适用于计算三角形的面积。
根据具体的问题,我们可以选择合适的模型来计算三角形的属性。
除了上述四大模型之外,三角形的属性还可以通过其他方法来计算,例如勾股定理、角平分线定理等。
每个模型在不同的问题中都有其特定的适用场景,因此了解并掌握这些模型可以帮助我们更好地解决各种三角形计算问题。
专题11 三角形常见模型(热考模型)(解析版)
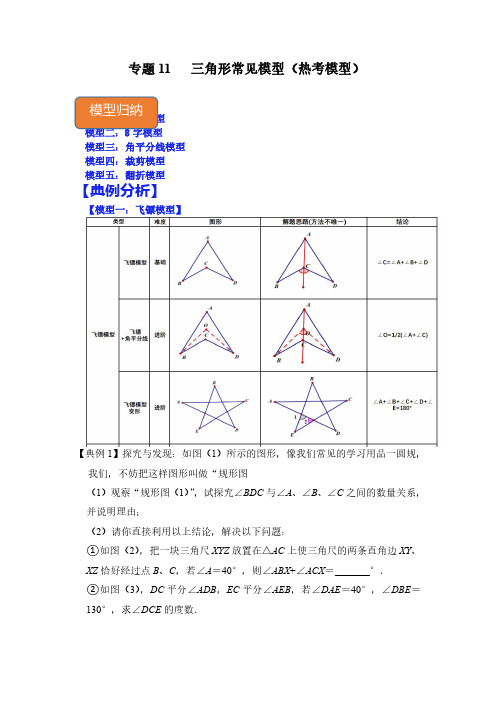
专题11三角形常见模型(热考模型)模型一:飞镖模型模型二:8字模型模型三:角平分线模型模型四:裁剪模型模型五:翻折模型【典例分析】【模型一:飞镖模型】【典例1】探究与发现:如图(1)所示的图形,像我们常见的学习用品一圆规,我们,不妨把这样图形叫做“规形图(1)观察“规形图(1)”,试探究∠BDC与∠A、∠B、∠C之间的数量关系,并说明理由;(2)请你直接利用以上结论,解决以下问题:①如图(2),把一块三角尺XYZ放置在△AC上使三角尺的两条直角边XY、XZ恰好经过点B、C,若∠A=40°,则∠ABX+∠ACX=°.②如图(3),DC平分∠ADB,EC平分∠AEB,若∠DAE=40°,∠DBE=130°,求∠DCE的度数.【解答】解:(1)如图(1),∠BDC=∠BAC+∠B+∠C,理由是:过点A、D作射线AF,∵∠FDC=∠DAC+∠C,∠BDF=∠B+∠BAD,∴∠FDC+∠BDF=∠DAC+∠BAD+∠C+∠B,即∠BDC=∠BAC+∠B+∠C;(2)①如图(2),∵∠X=90°,由(1)知:∠A+∠ABX+∠ACX=∠X=90°,∵∠A=40°,∴∠ABX+∠ACX=50°,故答案为:50;②如图(3),∵∠A=40°,∠DBE=130°,∴∠ADE+∠AEB=130°﹣40°=90°,∵DC平分∠ADB,EC平分∠AEB,∴∠ADC=∠ADB,∠AEC=∠AEB,∴∠ADC+∠AEC==45°,∴∠DCE=∠A+∠ADC+∠AEC=40°+45°=85°.【变式1-1】(2020春•沙坪坝区校级期中)如图,△ABC中,∠A=30°,D为CB延长线上的一点,DE⊥AB于点E,∠D=40°,则∠C为()A.20°B.15°C.30°D.25°【答案】A【解答】解:∵DE⊥AB,∴∠DEB=90°,∵∠D=40°,∴∠ABD=180°﹣∠D﹣∠DEB=50°,∵∠ABD=∠A+∠C,∠A=30°,∴∠C=∠ABD﹣∠A=50°﹣30°=20°.故选:A.【变式1-2】(2017•东昌府区一模)如图,∠BDC=98°,∠C=38°,∠A=37°,∠B的度数是()A.33°B.23°C.27°D.37°【答案】B【解答】解:如图,延长CD交AB于E,∵∠C=38°,∠A=37°,∴∠1=∠C+∠A=38°+37°=75°,∵∠BDC=98°,∴∠B=∠BDC﹣∠1=98°﹣75°=23°.故选:B.【变式1-3】(2021春•工业园区校级月考)如图,点C是∠BAD内一点,连CB、CD,∠A=80°,∠B=10°,∠D=40°,则∠BCD的度数是()A.110°B.120°C.130°D.150°【答案】C【解答】解:延长BC交AD于E,∵∠BED是△ABE的一个外角,∠A=80°,∠B=10°,∴∠BED=∠A+∠B=90°,∵∠BCD是△CDE的一个外角∴∠BCD=∠BED+∠D=130°,故选:C.【变式1-4】(2021•碑林区校级二模)如图,BE是∠ABD的平分线,CF是∠ACD 的平分线,BE与CF交于G,如果∠BDC=140°,∠BGC=110°,则∠A =.【答案】80°【解答】解:连接BC,∵∠BDC=140°,∴∠DBC+∠DCB=180°﹣140°=40°,∵∠BGC=110°,∴∠GBC+∠GCB=180°﹣110°=70°,∴∠GBD+∠GCD=70°﹣40°=30°,∵BE是∠ABD的平分线,CF是∠ACD的平分线,∴∠ABG+∠ACG=∠GBD+∠GCD=30°,在△ABC中,∠A=180°﹣40°﹣30°﹣30°=80°.故答案为:80°.【模型二:8字模型】【典例2】图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系:;(2)仔细观察,在图2中“8字形”的个数:个;(3)图2中,当∠D=50度,∠B=40度时,求∠P的度数.(4)图2中∠D和∠B为任意角时,其他条件不变,试问∠P与∠D、∠B之间存在着怎样的数量关系.(直接写出结果,不必证明).【答案】见试题解答内容【解答】解:(1)∵∠A+∠D+∠AOD=∠C+∠B+∠BOC=180°,∠AOD=∠BOC,∴∠A+∠D=∠C+∠B,故答案为:∠A+∠D=∠C+∠B;(2)①线段AB、CD相交于点O,形成“8字形”;②线段AN、CM相交于点O,形成“8字形”;③线段AB、CP相交于点N,形成“8字形”;④线段AB、CM相交于点O,形成“8字形”;⑤线段AP、CD相交于点M,形成“8字形”;⑥线段AN、CD相交于点O,形成“8字形”;故“8字形”共有6个,故答案为:6;(3)∠DAP+∠D=∠P+∠DCP,①∠PCB+∠B=∠PAB+∠P,②∵∠DAB和∠BCD的平分线AP和CP相交于点P,∴∠DAP=∠PAB,∠DCP=∠PCB,①+②得:∠DAP+∠D+∠PCB+∠B=∠P+∠DCP+∠PAB+∠P,即2∠P=∠D+∠B,又∵∠D=50度,∠B=40度,∴2∠P=50°+40°,∴∠P=45°;(4)关系:2∠P=∠D+∠B.∠D+∠1=∠P+∠3①∠B+∠4=∠P+∠2②①+②得:∠D+∠1+∠4+∠B=∠P+∠3+∠2+∠P,∵∠DAB和∠DCB的平分线AP和CP相交于点P,∴∠1=∠2,∠3=∠4∴2∠P=∠D+∠B.【变式2-1】(2020•柯桥区模拟)如图所示,∠α的度数是()A.10°B.20°C.30°D.40°【答案】A【解答】解:∵∠A+∠B+∠AOB=∠C+∠D+∠COD,∠AOB=∠COD,∴∠A+∠B=∠C+∠D∴30°+20°=40°+α,∴α=10°故选:A.【变式2-2】如图,BP平分∠ABC交CD于点F,DP平分∠ADC交AB于点E,若∠A=45°,∠P=40°,则∠C的度数为()A.30°B.35°C.40°D.45°【答案】B【解答】解:∵∠A+∠ADG+∠AGD=180°,∠ABC+∠C+∠BGC=180°,∴∠A+∠ADG+∠AGD=∠ABC+∠C+∠BGC.又∵∠AGD=∠BGC,∴∠A+∠ADG=∠C+∠GBC.∴∠A﹣∠C=∠GBC﹣∠ADG.同理可得,∠A+∠ADE=∠P+∠PBE.∴∠A﹣∠P=∠PBE﹣∠ADE.∵BP平分∠ABC交CD于点F,DP平分∠ADC交AB于点E,∴∠GBC=2∠PBE,∠ADG=2∠ADE.∴∠A﹣∠C=2(∠A﹣∠P).∴∠A+∠C=2∠P.又∵∠A=45°,∠P=40°,∴∠C=35°.故选:B【变式2-3】已知,如图,线段AD、CB相交于点O,连结AB、CD,∠DAB和∠BCD的平分线AP和CP相交于点P.试问∠P与∠D、∠B之间存在着怎样的数量关系,请说明理由.【答案】2∠P=∠B+∠D.【解答】解:2∠P=∠B+∠D,理由如下:如图,在△AOB和△COD中,∵∠AOB=∠COD,∴∠OAB+∠B=∠OCD+∠D,在△AEP和△CED中,∵∠AEP=∠CED,∴∠1+∠P=∠2+∠D,∵AP、CP分别是∠DAB和∠BCD的角平分线,∴∠OAB=2∠1,∠OCD=2∠2,∴2∠P﹣∠B=2∠D﹣∠D,整理得,2∠P=∠B+∠D.【变式2-4】在学习并掌握了平行线的性质和判定内容后,数学老师安排了自主探究内容一利用平行线有关知识探究并证明:三角形的内角和等于180°.小颖通过探究发现:可以将三角形的三个内角之和转化为一个平角来解决,也就是可以过三角形的一个顶点作其对边的平行线来证明.请将下面(1)中的证明补充完整:(1)已知:如图1,三角形ABC,求证:∠BAC+∠B+∠C=180°,证明:过点A作EF∥BC.(2)如图2,线段AB、CD相交于点O,连接AD、CB,我们把形如图2这样的图形称之为“8字形”.请利用小颖探究的结论直接写出∠A、∠B、∠C、∠D之间的数量关系:;(3)在图2的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N,得到图3,请判断∠P与∠D、∠B之间存在的数量关系,并说明理由.【答案】(1)证明见解析;(2)∠A+∠D=∠C+∠B,证明见解析;(3)2∠P=∠D+∠B,证明见解析.【解答】(1)证明:过A作EF∥BC,∴∠EAB=∠B,∠FAC=∠C,又∠EAB+∠BAC+∠FAC=180°,∴∠B+∠C+∠BAC=180°;(2)解:根据(1)得∠A+∠D+∠AOD=∠C+∠B+∠COB=180°,又∠AOD=∠BOC,∴∠A+∠D=∠C+∠B;故答案为:∠A+∠D=∠C+∠B;(3)解:2∠P=∠D+∠B.根据(2)∠D+∠DAP=∠P+∠DCP①,∠P AB+∠P=∠B+∠PCB②,∵∠DAB和∠BCD的平分线AP和CP相交于点P,∴∠DAP=∠PAB,∠DCP=∠PCB,∴①﹣②得:∠D﹣∠P=∠P﹣∠B,∴2∠P=∠D+∠B.【典例3】如图,五角星的五个角之和,即:∠A+∠B+∠C+∠D+∠E=()A.180°B.90°C.270°D.240°【答案】A【解答】解:连接CD,设BD与CE交于点O,由∠BOE=∠COD得:∠B+∠E=∠OCD+∠ODC,在△ACD中,∠A+∠ACD+∠ADC=180°,即∠A+∠ACE+∠OCD+∠ODC+∠ADB=180°,∴∠A+∠ACE+∠B+∠E+ADB=180°,即五角星的五个内角之和为180°.故选:A.【变式3-1】如图所示,∠A+∠B+∠C+∠D+∠E+∠F=度.【答案】360.【解答】解:∵∠B+∠C=∠1,∠A+∠F=∠2,∴∠A+∠B+∠C+∠D+∠E+∠F=∠1+∠2+∠E+∠D=360°.故答案为:360.【变式3-2】如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为【答案】见试题解答内容【解答】解:如图,∵∠1=∠2+∠F=∠B+∠E+∠F,∠1+∠A+∠C+∠D=360°,∴∠A+∠B+∠C+∠D+∠E+∠F=360°,故答案为:360°.【模型三:角平分线模型】【典例4】在△ABC中,∠A=40°:(1)如图(1)BO、CO是△ABC的内角角平分线,且相交于点O,求∠BOC;(2)如图(2)BO、CO是△ABC的外角角平分线,且相交于点O,求∠BOC;(3)如图(3)BO、CO分别是△ABC的一内角和一外角角平分线,且相交于点O,求∠BOC;(4)根据上述三问的结果,当∠A=n时,分别可以得出∠BOC与∠A有怎样的数量关系(只需写出结论).【答案】见试题解答内容【解答】解:(1)∵∠BOC=180°﹣∠OBC﹣∠OCB,∴2∠BOC=360°﹣2∠OBC﹣2∠OCB,而BO平分∠ABC,CO平分∠ACB,∴∠ABC=2∠OBC,∠ACB=2∠OCB,∴2∠BOC=360°﹣(∠ABC+∠ACB),∵∠ABC+∠ACB=180°﹣∠A,∴2∠BOC=180°+∠A,∴∠BOC=90°+∠A.当∠A=40°,∠BOC=110°;(2)∠OBC=(∠A+∠ACB),∠OCB=(∠A+∠ABC),∠BOC=180°﹣∠0BC﹣∠OCB,=180°﹣(∠A+∠ACB)﹣(∠A+∠ABC),=180°﹣∠A﹣(∠A+∠ABC+∠ACB),结论∠BOC=90°﹣∠A.∠BOC=90°﹣∠A.当∠A=40°,∠BOC=70°.(3)∵∠OCD=∠BOC+∠OBC,∠ACD=∠ABC+∠A,而BO平分∠ABC,CO平分∠ACD,∴∠ACD=2∠OCD,∠ABC=2∠OBC,∴2∠BOC+2∠OBC=∠ABC+∠A,∴2∠BOC=∠A,即∠BOC=∠A.当∠A=40°,∠BOC=20°;(4)∠BOC=90°+n;∠BOC=90°﹣n;∠BOC=n.【变式4-1】(1)如图1,在△ABC中,BP平分∠ABC,CP平分∠ACB,求证:∠P=90°+∠A;(2)如图2,在△ABC中,BP平分∠ABC,CP平分外角∠ACE,猜想∠P 和∠A有何数量关系,并证明你的结论.【答案】(1)证明过程见解答;(2)∠P=A.【解答】(1)证明:∵A+∠ABC+∠ACB=180°,∴∠ABC+∠ACB=180°﹣∠A,∵BP平分∠ABC,CP平分∠ACB,∴∠PCB=ACB,∠PBC=ABC,∴∠P=180°﹣(∠PCB+∠PBC)=180°﹣(∠ACB+∠ABC)=180°﹣(180°﹣∠A)=90°+A;(2)猜想:证明:∵∠ACE=∠A+∠ABC,∴∠A=∠ACE﹣∠ABC,∵∠PCE=∠P+∠PBC,∴∠P=∠PCE﹣∠PBC,又∵BP平分∠ABC,CP平分∠ACE,∴,∴∠P=ACE﹣ABC=(∠ACE﹣∠ABC)=A.【变式4-2】在△ABC中,∠ABC与∠ACB的平分线相交于点P.(1)如图①,若∠BPC=α,则∠A=;(用α的代数式表示,请直接写出结论)(2)如图②,作△ABC外角∠MBC、∠NCB的角平分线交于点Q,试探究∠Q与∠BPC之间的数量关系,并说明理由.【答案】(1)2α﹣180°;(2)∠BPC+∠Q=180°,证明见解析.【解答】(1)解:如图①∵BP,CP分别平分∠ABC与∠ACB,∴∠PBC=∠ABC,∠PCB=ACB,∵∠BPC=180°﹣(∠PBC+∠PCB)∴∠BPC=180°(∠ABC+∠ACB)∴∠BPC=180°(180°﹣∠A),∴∠BPC=90°∠A,∵∠BPC=α,∴∠A=2α﹣180°.故答案为2α﹣180°.(2)∠BPC+∠Q=180°.证明:如图②∵BQ,CQ分别平分∠MBC,∠NCB,∴∠QBC=∠CBM,∠BCQ=∠BCN,∴∠QBC+∠QCB=(∠CBM+∠BCN)∴∠QBC+∠QCB=(∠A+∠ACB+∠A+∠ABC)=(180°+∠A)∴∠QBC+∠QCB=90°∠A,∴∠Q=180°﹣(90°∠A)=90°∠A,∵∠BPC=90°∠A,∴∠BPC+∠Q=180°.【模型四:裁剪模型】【典例5】如图,将一个三角形剪去一个角后,∠1+∠2=240°,则∠A等于()A.45°B.60°C.75°D.80°【答案】B【解答】解:∵∠1+∠2=240°,∴∠B+∠C=360°﹣(∠1+∠2)=120°,∴∠A=180°﹣(∠B+∠C)=60°,故选:B.【变式5-1】如图,一个直角三角形纸片,剪去直角后,得到一个四边形,则∠1+∠2=()°.A.90B.135C.180D.270【答案】D【解答】解:∠1+∠2=360°﹣(180°﹣90°)=270°,故选:D.【变式5-2】如图,△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于()A.90°B.135°C.150°D.270°【答案】D【解答】解:∠CDE=180°﹣∠1,∠CED=180°﹣∠2,在△CDE中,∠CDE+∠CED+∠C=180°,所以,180°﹣∠1+180°﹣∠2+90°=180°,所以,∠1+∠2=270°.故选:D.【变式5-3】如图,在△ABC中,∠C=50°,按图中虚线将∠C剪去后,∠1+∠2等于.【答案】见试题解答内容【解答】解:∵△ABC中,∠C=50°,∴∠A+∠B=180°﹣∠C=130°,∵∠A+∠B+∠1+∠2=360°,∴∠1+∠2=360°﹣130°=230°,故答案为:230°.【模型五:翻折模型】【典例6】我们在小学已经学习了“三角形内角和等于180°”.在三角形纸片中,点D,E分别在边AC,BC上,将∠C沿DE折叠,点C落在点C'的位置.(1)如图1,当点C落在边BC上时,若∠ADC'=58°,则∠C=,可以发现∠ADC'与∠C的数量关系是;(2)如图2,当点C落在△ABC内部时,且∠BEC'=42°,∠ADC'=20°,求∠C的度数;(3)如图3,当点C落在△ABC外部时,若设∠BEC'的度数为x,∠ADC'的度数为y,请求出∠C与x,y之间的数量关系.【答案】(1)29°,∠ADC'=2∠C;(2)31°;(3)∠C=x﹣y.【解答】解:(1)∵∠ADC′=58°,∴∠CDC′=180°﹣∠ADC′=122°,由折叠得:∠CDE=∠C′DE=∠CDC′=61°,∠DEC=∠DEC′=×180°=90°,∴∠C=180°﹣∠EDC﹣∠DEC=29°,∴∠ADC'与∠C的数量关系:∠ADC'=2∠C.故答案为:29°,∠ADC'=2∠C;(2)∵∠BEC′=42°,∠ADC′=20°,∴∠CEC′=180°﹣∠BEC′=138°,∠CDC′=180°﹣∠ADC′=160°,由折叠得:∠CDE=∠C′DE=∠CDC′=80°,∠DEC=∠DEC′=∠CEC′=69°,∴∠C=180°﹣∠EDC﹣∠DEC=31°,∴∠C的度数为31°;(3)如图:∵∠BEC′=x,∠ADC′=y,∴∠CEC′=180°﹣x,∠1=180°+∠ADC′=180°+y,由折叠得:∠CDE=∠C′DE=∠1=90°+y,∠DEC=∠DEC′=∠CEC′=90°﹣x,∴∠C=180°﹣∠EDC﹣∠DEC=180°﹣(90°+y)﹣(90°﹣x)=x﹣y,∴∠C与x,y之间的数量关系:∠C=x﹣y.【变式6-1】如图,在△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在边AC上点E处,若∠B=65°,则∠ADE的大小为()A.40°B.50°C.65°D.75°【答案】A【解答】解:在△ABC中,∠ACB=90°,∠B=65°,∴∠A=90°﹣65°=25°,根据折叠可得∠CED=∠B=65°,∴∠ADE=65°﹣25°=40°,故选:A.【变式6-2】如图,将△ABC沿着平行于BC的直线DE折叠,点A落在点A'处,若∠B=44°,则∠A'DB的度数是()A.108°B.104°C.96°D.92°【答案】D【解答】解:∵△ABC沿着平行于BC的直线折叠,点A落到点A′,∴∠ADE=∠B=44°,∴∠A′DE=∠ADE=44°,∴∠A′DB=180°﹣44°﹣44°=92°,故选:D.【变式6-3】如图,将△ABC一角折叠,若∠1+∠2=80°,则∠B+∠C=()A.40°B.100°C.140°D.160°【答案】C【解答】解:连接AA′.∵∠1=∠3+∠4,∠2=∠5+∠6,∴∠1+∠2=∠3+∠4+∠5+∠6=∠EAD+∠EA′D,∵∠EAD=∠EA′D,∴∠1+∠2=2∠EAD=160°,∴∠EAD=40°,∴∠B+∠C=180°﹣40°=140°,故选:C.【夯实基础】1.如图,在△ABC中,BF平分∠ABC,CF平分∠ACB,∠BFC=125°,则∠A的度数为()A.60°B.80°C.70°D.45°【答案】C【解答】解:在△FBC中,∠BFC=125°.∴∠FBC+∠FCB=180°﹣∠BFC=55°.∵BF平分∠ABC,CF平分∠ACB.∴∠ABC=2∠FBC,∠ACB=2∠FCB.∴∠ABC+∠ACB=2(∠FBC+∠FCB)=110°.∴在△ABC中,∠A=180°﹣(∠ABC+∠ACB)=70°.故选:C.2.如图,点B是△ADC的边AD的延长线上一点,DE平分∠CDB,若∠C=50°,∠BDE=60°,则∠A的度数等于()A.70°B.100°C.110°D.120°【答案】A【解答】解:∵DE平分∠CDB,∴∠CDE=∠BDE,∵∠BDE=60°,∴∠CDE=60°,∴∠ADC=180°﹣∠BDE﹣∠CDE=180°﹣60°﹣60°=60°,∵∠C=50°,∴∠A=180°﹣∠C﹣∠ADC=180°﹣50°﹣60°=70°,故选:A.3.如图,在△ABC中,∠ABC与∠ACB的平分线交于点D,∠A=40°,则∠BDC的度数是()A.110°B.120°C.130°D.140°第6题图【答案】A【解答】解:在△ABC中,∵∠A=40°,∠A+∠ABC+∠ACB=180°,∴∠ABC+∠ACB=180°﹣∠A=180°﹣40°=140°,∵∠ABC、∠ACB的平分线交于点D,∴∠DBC=∠ABC,∠DCB=∠ACB,∴∠DBC+∠DCB=(∠ABC+∠ACB)=×140°=70°,在△DBC中,∵∠DBC+∠DCB+∠BDC=180°,∴∠BDC=180°﹣(∠DBC+∠DCB)=180°﹣70°=110°.故选:A.4.如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC 边上的点E处.若∠A=24°,则∠EDC等于()A.69°B.67°C.66°D.42°【答案】A【解答】解:在△ABC中,∠ACB=90°,∠A=24°,∴∠B=90°﹣∠A=66°.由折叠的性质可得:∠BCD=∠ACB=45°,∴∠BDC=∠EDC=180°﹣∠BCD﹣∠B=69°.故选:A.5.如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC 边上的点E处.若∠A=22°,则∠EDA等于()A.46°B.56°C.36°D.77°【答案】A【解答】解:△ABC中,∠ACB=90°,∠A=22°,∴∠B=90°﹣∠A=68°,由折叠的性质可得:∠CED=∠B=68°,∴∠EDA=∠CED﹣∠A=46°,故选:A.6.如图,把△ABC纸片沿DE折叠,点A落在四边形DEBC内部A',当∠A=30°时,∠1+∠2=()A.30°B.40°C.50°D.60°【答案】D【解答】解:在△ADE中,∠A=30°,∠ADE+∠AED=180°﹣∠A=180°﹣30°=150°,由折叠可知:∠A'DE=∠ADE,∠A'ED=∠AED,∴∠1+∠2=360°﹣∠A'DE﹣∠ADE﹣∠A'ED﹣∠AED=360°﹣2(∠ADE+∠AED)=360°﹣2×150°=60°.故选:D.7.在直角△ABC中,∠C=90°,沿图中虚线剪去∠C,则∠1+∠2=.【答案】见试题解答内容【解答】解:∵∠A+∠B+∠C=180°,∴∠A+∠B=180°﹣∠C=90°,∵∠1+∠2+∠A+∠B=360°,∴∠1+∠2=360°﹣90°=270°.故答案是:270°.8.如图,在△ABC中,∠C=40°,按图中虚线将∠C剪去后,∠1+∠2等于.【答案】见试题解答内容【解答】解:∵△ABC中,∠C=40°,∴∠A+∠B=180°﹣∠C=140°,∵∠A+∠B+∠1+∠2=360°,∴∠1+∠2=360°﹣140°=220°,故答案为:220°.9.有一张直角三角形纸片,记作△ABC,其中∠B=90°.按如图方式剪去它的一个角(虚线部分),在剩下的四边形ADEC中,若∠1=165°,则∠2的度数为°.【答案】见试题解答内容【解答】解:∵∠B=90°,∴∠BDE+∠BED=180°﹣∠B=90°,又∵∠BDE+∠2=180°,∠BED+∠1=180°,∴∠1+∠2=360°﹣(∠BDE+∠BED)=270°.∵∠1=165°,∴∠2=105°.故答案为:105.10.将纸片△ABC沿DE折叠使点A落在点A'处,若∠1=80°,∠2=28°,则∠A的度数为.【答案】26°.【解答】解:如图,由折叠的性质可知∠A'=∠A,∵∠1=∠A+∠AFD,∠AFD=∠2+∠A',∴2∠A+∠2=∠1,∵∠1=80°,∠2=28°,∴∠A=26°,故答案为:26°.11.如图,将△ABC纸片沿DE折叠,使点A落在点A′处,且BA′平分∠ABC,CA′平分∠ACB,若∠BA′C=115°,则∠1+∠2的度数为.【答案】100°.【解答】解:如图,连接AA',∵A'B平分∠ABC,A'C平分∠ACB,∴∠A'BC=∠ABC,∠A'CB=∠ACB,∵∠BA'C=115°,∴∠A'BC+∠A'CB=180°﹣115°=65°,∴∠ABC+∠ACB=130°,∴∠BAC=180°﹣130°=50°,∵沿DE折叠,∴∠DAA'=∠DA'A,∠EAA'=∠EA'A,∵∠1=∠DAA'+∠DA'A=2∠DAA',∠2=∠EAA'+∠EA'A=2∠EAA',∴∠1+∠2=2∠DAA'+2∠EAA'=2∠BAC=2×50°=100°,故答案为:100°.12.如图所示,求∠A+∠B+∠C+∠D+∠E的度数.【答案】见试题解答内容【解答】解:由图可知:∵∠2是三角形的外角,∴∠2=∠A+∠1,同理∠1也是三角形的外角,∴∠1=∠E+∠C,在△BDF中,∠B+∠D+∠2=180°,即∠A+∠B+∠C+∠D+∠E=180°.13.如图1,已知线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.试解答下列问题:(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系:;(2)如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.请直接利用(1)中的结论,完成下列各题:①仔细观察,在图2中“8字形”的个数:个;②若∠D=40°,∠B=50°,试求∠P的度数;③若∠D和∠B为任意角,其他条件不变,试问∠P与∠D、∠B之间是否存在一定的数量关系?若存在,请写出推理过程;若不存在,请说明理由;④若∠D和∠B为任意角,∠DAB=3∠2,∠DCB=3∠4,试问∠P与∠D、∠B之间是否存在一定的数量关系?若存在,请直接写出结论;若不存在,请说明理由.【答案】(1)∠A+∠D=∠B+∠C;(2)①6;②45°;③∠B+∠D=2∠P;④2∠B+∠D=3∠P.【解答】解:(1)∵∠A+∠D=180°﹣∠AOD,∠B+∠C=180°﹣∠COB,且∠AOD=∠COB,∴∠A+∠D=∠B+∠C;故答案为∠A+∠D=∠B+∠C;(2)①以M为交点的有1个,为△AMD和△CMP,以O为交点的有4个,为△AOD和△BOC,△AOD和△CON,△AOM和△BOC,△AOM和△CON,以N为交点的有1个,为△ANP和△BNC,故答案为6个;②∵AP平分∠DAB,CP平分∠BCD,∴2∠1=∠OAD,2∠3=∠OCB,由(1)中的结论得:∠1+∠D=∠3+∠P,2∠1+∠D=2∠3+∠B,整理得:∠B+∠D=2∠P,∴∠P==45°;③:∠B+∠D=2∠P,理由如下:∵AP平分∠DAB,CP平分∠BCD,∴2∠1=∠OAD,2∠3=∠OCB,由(1)中的结论得:∠1+∠D=∠3+∠P,2∠1+∠D=2∠3+∠B,整理得:∠B+∠D=2∠P;④2∠B+∠D=3∠P,理由如下:由(1)中结论得:∠2+∠P=∠4+∠B,3∠2+∠D=3∠4+∠B,整理得:2∠B+∠D=3∠P.14.“8字”的性质及应用:(1)如图①,AD、BC相交于点O,得到一个“8字”ABCD,求证:∠A+∠B=∠C+∠D.(2)图②中共有多少个“8字”?(3)如图②,∠ABC和∠ADC的平分线相交于点E,利用(1)中的结论证明∠E=(∠A+∠C).【答案】见试题解答内容【解答】解:(1)∵∠A+∠B+∠AOB=180°,∠C+∠D+∠COD=180°,又∠AOB=∠COD,∴∠A+∠B=∠C+∠D;(2)图②中有:ABCD、BECD、ABED,BFDC、BFDH、ABHD6个“8字”;(3)∵BE平分∠ABC,DE平分∠ADC,∴∠ABE=∠CBE=ABC,∠CDE=∠ADE=∠ADC,∵∠A+∠ABE=∠E+∠ADE,∠C+∠CDE=∠E+∠CBE,∴∠E=(∠A+∠C).15.(1)如图1,在△ABC中,∠ABC,∠ACB的平分线交于点O,过点O作EF∥BC分别交AB,AC于点E,F.直接写出线段EF与BE,CF之间的数量关系:.(2)如图2,若△ABC中∠ABC的平分线BO与三角形外角平分线CO交于点O,过O点作OE∥BC交AB于点E,交AC于点F.则EF与BE,CF之间的数量关系又如何?说明你的理由.【答案】(1)EF=EB+FC;(2)EF=BE﹣CF.【解答】解:(1)∵BO平分∠ABC,CO平分∠ACB,∴∠ABO=∠OBC,∠ACO=∠OCB,∵EF∥BC,∴∠EOB=∠OBC,∠FOC=∠OCB,∴∠EBO=∠EOB,∠FOC=∠FCO,∴EB=EO,FC=FO,∵EF=EO+FO,∴EF=EB+FC,故答案为:EF=EB+FC;(2)EF=BE﹣CF,理由是:∵BO平分∠ABC,∴∠ABO=∠OBC,∵EF∥BC,∴∠EOB=∠OBC,∴∠EBO=∠EOB,∴EB=EO,同理可得:FO=CF,∵EF=EO﹣FO,∴EF=BE﹣CF【能力提升】16.如图,在△ABC中,∠A=α,∠ABC的平分线与∠ACD的平分线交于点A1,得∠A1,则∠A1=.∠A1BC的平分线与∠A1CD的平分线交于点A2,得∠A2,…,∠A2009BC的平分线与∠A2009CD的平分线交于点A2010,得∠A2010,则∠A2010=.【答案】见试题解答内容【解答】解:∵∠ACD=∠A+∠ABC,∠A1CD=∠A1+∠A1BC,∠ACD=2∠A1CD,∠ABC=2∠A1BC,∴2∠A1CD=∠A+2∠A1BC,即∠A1CD=∠A+∠A1BC,∴∠A1==,由此可得∠A2010=.故答案为:,.17.如图1,已知线段AB、CD相交于点O,连接AC、BD,则我们把形如这样的图形称为“8字型”.(1)求证:∠A+∠C=∠B+∠D.利用以上结论解决下列问题:(2)如图2所示,∠1=130°,则∠A+∠B+∠C+∠D+∠E+∠F的度数为.(3)如图3,若∠CAB和∠BDC的平分线AP和DP相交于点P,且与CD,AB分别相交于点M,N.①若∠B=100°,∠C=120°,求∠P的度数.②若角平分线中角的关系改成“∠CAP=∠CAB,∠CDP=∠CDB”,试直接写出∠P与∠B,∠C之间存在的数量关系,并证明理由.【答案】(1)证明见解析过程;(2)260°;(3)①110°,②4∠P=∠B+3∠C,理由见解析过程.【解答】解:(1)证明:在图1中,有∠A+∠C=180°﹣∠AOC,∠B+∠D =180°﹣∠BOD,∵∠AOC=∠BOD,∴∠A+∠C=∠B+∠D;(2)如图2所示,∵∠DME=∠A+∠E,∠3=∠DME+∠D,∴∠A+∠E+∠D=∠3,∵∠2=∠3+∠F,∠1=130°,∴∠3+∠F=∠2=∠1=130°,∴∠A+∠E+∠D+∠F=130°,∵∠B+∠C=∠1=130°,∴∠A+∠B+∠C+∠D+∠E+∠F=260°.故答案为:260°.(3)①以M为交点“8字型”中,有∠P+∠CDP=∠C+∠CAP,以N为交点“8字型”中,有∠P+∠BAP=∠B+∠BDP∴2∠P+∠BAP+∠CDP=∠B+∠C+∠CAP+∠BDP,∵AP、DP分别平分∠CAB和∠BDC,∴∠BAP=∠CAP,∠CDP=∠BDP,∴2∠P=∠B+∠C,∵∠B=100°,∠C=120°,∴∠P=(∠B+∠C)=(100°+120°)=110°;②3∠P=∠B+2∠C,其理由是:∵∠CAP=∠CAB,∠CDP=∠CDB,∴∠BAP=∠CAB,∠BDP=∠CDB,以M为交点“8字型”中,有∠P+∠CDP=∠C+∠CAP,以N为交点“8字型”中,有∠P+∠BAP=∠B+∠BDP∴∠C﹣∠P=∠CDP﹣∠CAP=(∠CDB﹣∠CAB),∠P﹣∠B=∠BDP﹣∠BAP=(∠CDB﹣∠CAB).∴3(∠C﹣∠P)=∠P﹣∠B,∴4∠P=∠B+3∠C.18.如图①,在△ABC中,∠ABC、∠ACB的平分线相交于点O.(1)若∠A=40°,则∠BOC=.若∠A=60°,则∠BOC =.若∠BOC=3∠A,则∠BOC=.(2)如图②,在△A′B′C′中的外角平分线相交于点O′,∠A=40°,则∠B′O′C′=(3)上面(1)、(2)两题中的∠BOC与∠B′O′C′有怎样的数量关系?若∠A=∠A′=n°,∠BOC与∠B′O′C′是否有这样的关系?这个结论你是怎样得到的?(4)如图③,△A″B″C″的内角∠ACB的外角平分线与∠ABC的内角平分线相交于点O″,∠BOC与∠B″O″C″有怎样的数量关系?若∠A=∠A′=n°,∠BOC与∠B″O″C″是否有这样的关系?这个结论你是怎样得到的?【答案】(1)110°,60°,108°;(2)70°;(3)∠BOC+∠B′O′C′=180°;(4)∠BOC﹣∠B″O″C″=90°.【解答】解:(1)∵∠A=40°,∴∠ABC+∠ACB=180°﹣40°=140°,∵∠ABC、∠ACB的平分线相交于点O,∴∠1+∠2=∠ABC+∠ACB=×140°=70°,∴∠BOC=180°﹣(∠1+∠2)=110°,∵∠A=60°,∴∠ABC+∠ACB=180°﹣60°=120°,∵∠ABC、∠ACB的平分线相交于点O,∴∠1+∠2=∠ABC+∠ACB=×120°=60°,∴∠BOC=180°﹣120°=60°;∵设∠A=x°,则∠1+∠2=(∠ABC+∠ACB)=×(180°﹣x°)=90°﹣x°,∴∠BOC=180°﹣(∠1+∠2)=180°﹣(90°﹣x°)=90°+x°,∵∠BOC=3∠A,∴3x=90+x,x=36,即∠BCO=3x°=108°;故答案为:110°,60°,108°;(2)如图2,∵∠A′=40°,∴∠A′B′C′+∠A′C′B′=180°﹣40°=140°,∴∠MB′C′+NC′B′=360°﹣140°=220°,∵B′O′、C′O′分别平分∠MB′C′,∠NC′B′,∴∠1=∠MB′C′,∠2=∠NC′B′,∴∠1+∠2=110°,∴∠B′O′C′=180°﹣110°=70°,故答案为:70°;(3)图1和图2的∠BOC+∠B′O′′=180°(当∠A=∠A′时);图1中∠BOC=180°﹣(∠1+∠2)=180°﹣(∠ABC+∠ACB)=180°﹣(180°﹣∠A)=90°+∠A,图2中∠B′O′′=180°﹣(∠1+∠2)=180°﹣(∠MB′C′+∠NC′B′)=180°﹣[360°﹣(∠A′B′C′+∠A′C′B′)]=(180°﹣∠A′)=90°﹣∠A′,∵∠A=∠A′=n°,∴∠BOC+∠B′O′C′=180°(4)∵∠A″C″M=2∠2=∠A″+∠A″B″C″,∠2=∠O″+∠1,∵C″D″平分∠A″C″M,B″O″平分∠A″B″C″∴∠A″C″M=2∠2,∠A″B″C″=2∠1,∴∠A″=2∠O″=n°,∴∠B″O″C″=∠A″,∵∠BOC=90°+∠A,∠A=∠A′=n°∴∠BOC﹣∠B″O″C″=90°.19.已知△ABC中,∠A=x°(1)如图1,若∠ABC和∠ACB的角平分线相交于点O,则用x表示∠BOC =°(2)如图2,若∠ABC和∠ACB的三等分线相交于点O1、O2,则用x表示∠BO1C=°(3)如图3,若∠ABC和∠ACB的n等分线相交于点O1、O2、…、O n﹣1,则用x表示∠BO1C=°【答案】见试题解答内容【解答】解:(1)∵∠ABC和∠ACB的角平分线相交于点O,∴2∠OBC=∠ABC,2∠OCB=∠ACB,∵∠A+∠ABC+∠ACB=180°,∴∠A+2∠OBC+2∠OCB=180°,∴∠OBC+∠OCB=90°﹣∠A,∵∠BOC=180°﹣(∠OBC+∠OCB)=90°+∠A,∵∠A=x°,∴∠BOC=(90+x)°;。
微专题 三角形四大常考全等模型

基本模型
图示
模型总结
有三个直角,常利用同角(等角)的余角相等证明角相等
针对训练 3.在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D, BE⊥MN于E. 求证:DE=AD+BE.
第3题图
证明:∵∠ACB=90°,AC=BC, ∴∠ACD+∠BCE=90°, 又∵AD⊥MN,BE⊥MN,∴∠ADC=∠CEB=90°, ∴∠ACD+∠DAC=90°, ∴∠BCE=∠CAD. 在△ADC和△CEB中,
ቤተ መጻሕፍቲ ባይዱ
第4题图
∠A=∠ACF AD=CF , ∠A DF =∠F ∴△ADE≌△CFE(ASA).
W
点击链接至综合提升
例2题图
解:全等.
理由如下:∵∠1=∠2,∴DB=DC.
∵AB=AC,∴∠ABC=∠ACB.
∴∠ABC-∠1=∠ACB-∠2,
∴∠ABD=∠ACD,
在△ABD和△ACD中, AB=AC ∠ABD=∠ACD, BD=CD ∴△ABD≌△ACD(SAS).
基本模型
图示
所给图形可沿某一直线折叠,直线两旁的部分能完全重合,重合的顶 模型总结 点就是全等三角形的对应顶点,解题时要注意其隐含条件,即公共边
【思维教练】要证△ABC≌△DEC, 题干已知BC=CE,AB=DE,∠BAE =∠BCE=90°,只需证明∠B= ∠CED即可.
例4题图
证明:∵∠BAE=∠BCE=90°, ∴∠ABC+∠AEC=180°. ∵∠AEC+∠DEC=180°, ∴∠DEC=∠B. 在△ABC和△DEC中, AB=DE ∠B=∠DEC, BC=EC ∴△ABC≌△DEC(SAS).
微专题 四大常考全等模型
(必考,均在几何图形的证明与计算中涉及考查) 模型一 平移模型 例1 如图,已知BC∥EF,∠B=∠DGC,点D、C在AF上,且AB=DE. 求证:AD=CF. 【找一找】
专题13 全等三角形重难点模型(五大模型)(解析版)

专题13全等三角形重难点模型(五大模型)模型一:一线三等角型模型二:手拉手模型模型三:半角模型模型四:对角互补模型模型五:平行+线段中点构造全等模型【典例分析】【模型一:一线三等角型】如图一,∠D=∠BCA=∠E=90°,BC=AC。
结论:Rt△BDC≌Rt△CEA模型二一线三等角全等模型如图二,∠D=∠BCA=∠E,BC=AC。
结论:△BEC≌△CDA图一图二应用:①通过证明全等实现边角关系的转化,便于解决对应的几何问题;②与函数综合应用中有利于点的坐标的求解。
【典例1】如图,平面直角坐标系中有点A(﹣1,0)和y轴上一动点B(0,a),其中a>0,以B点为直角顶点在第二象限内作等腰直角△ABC,设点C的坐标为(c,d).(1)当a=2时,则C点的坐标为;(2)动点B在运动的过程中,试判断c+d的值是否发生变化?若不变,请求出其值;若发生变化,请说明理由.【解答】解:(1)如图1中,过点C作CE⊥y轴于E,则∠CEB=∠AOB.∵△ABC是等腰直角三角形,∴BC=BA,∠ABC=90°,∴∠BCE+∠CBE=90°=∠BAO+∠CBE,∴∠BCE=∠ABO,在△BCE和△BAO中,,∴△CBE≌△BAO(AAS),∵A(﹣1,0),B(0,2),∴AO=BE=1,OB=CE=2,∴OE=1+2=3,∴C(﹣2,3),故答案为:(﹣2,3);(2)动点A在运动的过程中,c+d的值不变.理由:过点C作CE⊥y轴于E,则∠CEA=∠AOB,∵△ABC是等腰直角三角形,∴BC=BA,∠ABC=90°,∴∠BCE+∠CBE=90°=∠ABO+∠CBE,∴∠BCE=∠ABO,在△BCE和△BAO中,,∴△CBE≌△BAO(AAS),∵B(﹣1,0),A(0,a),∴BO=AE=1,AO=CE=a,∴OE=1+a,∴C(﹣a,1+a),又∵点C的坐标为(c,d),∴c+d=﹣a+1+a=1,即c+d的值不变.【变式1】点A的坐标为(4,0),点B为y轴负半轴上的一个动点,分别以OB、AB为直角边在第三象限和第四象限作等腰Rt△OBC和等腰Rt△ABD.(1)如图一,若点B坐标为(0,﹣3),连接AC、OD.①求证:AC=OD;②求D点坐标.(2)如图二,连接CD,与y轴交于点E,试求BE长度.【解答】(1)①证明:∵△OBC和△ABD是等腰直角三角形,∴OB=CB,BD=AB,∠ABD=∠OBC=90°,∴∠ABD+ABO=∠OBC+∠A∠O,∴∠OBD=∠CBA,∴△OBD≌△CBA(SAS),∴AC=OD;②如图一、∵A(4,0),B(0,﹣3),∴OA=4,OB=3,过点D作DF⊥y轴于F,∴∠BOA=∠DFB=90°,∴∠ABO+∠OAB=90°,∵∠ABD=90°,∴∠ABO+∠FBD=90°,∴∠OAB=∠FBD,∵AB=BD,∴△AOB≌△BFD(AAS),∴DF=OB=3,BF=OA=4,∴OF=OB+BF=7,∴D(3,﹣7);(2)如图二、过点D作DF⊥y轴于F,则∠DFB=90°=∠CBF,同(1)②的方法得,△AOB≌△BFD(AAS),∴DF=OB,BF=OA=4,∵OB=BC,∴BC=DF,∵∠DEF=∠CEB,∴△DEF≌△CEB(AAS),∴BE=EF,∴BF=BE+EF=2BE=4,∴BE=2.【典例2】(1)猜想:如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.试猜想DE、BD、CE有怎样的数量关系,请直接写出;(2)探究:如果三个角不是直角,那结论是否会成立呢?如图2,将(1)中的条件改为:在△ABC中,AB=AC,D,A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α(其中α为任意锐角或钝角)如果成立,请你给出证明;若不成立,请说明理由;(3)解决问题:如图3,F是角平分线上的一点,且△ABF和△ACF均为等边三角形,D、E分别是直线m上A点左右两侧的动点,D、E、A互不重合,在运动过程中线段DE的长度始终为n,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状,并说明理由.【解答】解:(1)DE=BD+CE,理由如下:∵∠BAC=90°,∴∠BAD+∠CAE=90°,∵BD⊥m,CE⊥m,∴∠ADB=∠CEA=90°,∴∠BAD+∠ABD=90°,∴∠ABD=∠CAE,在△ADB和△CEA中,,∴△ADB≌△CEA(AAS),∴BD=AE,AD=CE,∴DE=AD+AE=BD+CE;(2)结论DE=BD+CE成立,理由如下:∵∠BAD+∠CAE=180°﹣∠BAC,∠BAD+∠ABD=180°﹣∠ADB,∠ADB=∠BAC,∴∠ABD=∠CAE,在△BAD和△ACE中,,∴△BAD≌△ACE(AAS),∴BD=AE,AD=CE,∴DE=DA+AE=BD+CE;(3)△DFE为等边三角形,理由如下:由(2)得,△BAD≌△ACE,∴BD=AE,∠ABD=∠CAE,∴∠ABD+∠FBA=∠CAE+FAC,即∠FBD=∠FAE,在△FBD和△FAE中,,∴△FBD≌△FAE(SAS),∴FD=FE,∠BFD=∠AFE,∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°,∴△DFE为等边三角形.【变式2】已知,在△ABC中,AB=AC,D,A,E三点都在直线m上,且DE =9cm,∠BDA=∠AEC=∠BAC(1)如图①,若AB⊥AC,则BD与AE的数量关系为,CE与AD 的数量关系为;(2)如图②,判断并说明线段BD,CE与DE的数量关系;(3)如图③,若只保持∠BDA=∠AEC,BD=EF=7cm,点A在线段DE上以2cm/s的速度由点D向点E运动,同时,点C在线段EF上以xcm/s的速度由点E向点F运动,它们运动的时间为t(s).是否存在x,使得△ABD与△EAC全等?若存在,求出相应的t的值;若不存在,请说明理由.【解答】解:(1)∵∠BDA=∠AEC=∠BAC,∴∠BAD+∠CAE=∠BAD+∠ABD,∴∠CAE=∠ABD,∵∠BDA=∠AEC,BA=CA,∴△ABD≌△CAE(AAS),∴BD=AE,CE=AD,故答案为:BD=AE,CE=AD;(2)DE=BD+CE,由(1)同理可得△ABD≌△CAE(AAS),∴BD=AE,CE=AD,∴DE=BD+CE;(3)存在,当△DAB≌△ECA时,∴AD=CE=2cm,BD=AE=7cm,∴t=1,此时x=2;当△DAB≌△EAC时,∴AD=AE=4.5cm,DB=EC=7cm,∴t=,x=7÷=,综上:t=1,x=2或t=,x=.【模型二:手拉手模型】应用:①利用手拉手模型证明三角形全等,便于解决对应的几何问题;②作辅助线构造手拉手模型,难度比较大。
三角形中的几个重要几何模型(知识梳理与考点分类讲解)(人教版)(教师版)24-25学年八年级数学上册
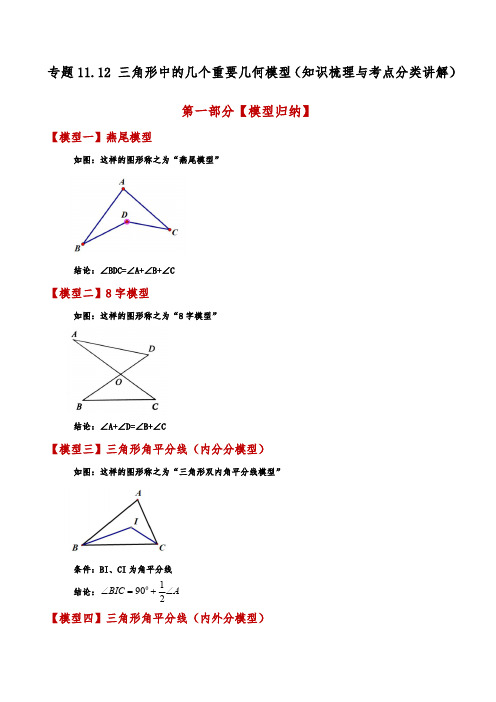
专题11.12三角形中的几个重要几何模型(知识梳理与考点分类讲解)第一部分【模型归纳】【模型一】燕尾模型如图:这样的图形称之为“燕尾模型”结论:∠BDC=∠A+∠B+∠C【模型二】8字模型如图:这样的图形称之为“8字模型”结论:∠A+∠D=∠B+∠C【模型三】三角形角平分线(内分分模型)如图:这样的图形称之为“三角形双内角平分线模型”条件:BI、CI 为角平分线结论:01902BIC A ∠=+∠【模型四】三角形角平分线(内外分模型)如图:这样的图形称之为“三角形内外角平分线模型”条件:BP、CP 为角平分线结论:12P A ∠=∠【模型五】三角形角平分线(外外分模型)如图:这样的图形称之为“三角形双外角平分线模型”条件:BP、CP 为角平分线结论:01902P A ∠=-∠【模型六】角平分线+平行线模型条件:CP 平分∠ACB,DE 平行于BC结论:ED=EC第二部分【题型展示与方法点拨】【题型1】燕尾模型【例1】如图所示,已知四边形ABDC ,求证BDC A B C ∠=∠+∠+∠.【答案】见解析【分析】方法1连接BC ,根据三角形内角和定理可得结果;方法2作射线AD ,根据三角形的外角性质得到31B ∠=∠+∠,42C ∠=∠+∠,两式相加即可得到结论;方法3延长BD ,交AC 于点E ,两次运用三角形外角的性质即可得出结论.解:方法1如图所示,连接BC .在ABC 中,180A ABC ACB ∠+∠+∠= ,即12180A ABD ACD ∠+∠+∠+∠+∠= .在BCD △中,12180BDC ∠+∠+∠= ,++BDC A ABD ACD ∴∠=∠∠∠;方法2如图所示,连接AD 并延长.3∠ 是ABD △的外角,31+ABD ∴∠=∠∠.同理,42ACD ∠=∠+∠.3412ABD ACD ∴∠+∠=∠+∠+∠+∠.即BDC A ABD ACD ∠=∠+∠+∠.方法3如图所示,延长BD ,交AC 于点E .DEC ∠ 是ABE 的外角,DEC A ABD ∴∠=∠+∠.BDC ∠ 是DEC 的外角,BDC DEC ACD ∴∠=∠+∠.BDC A ABD ACD ∴∠=∠+∠+∠.【点拨】本题考查了三角形的外角性质:解题的关键是知道三角形的任一外角等于与之不相邻的两内角的和.也考查了三角形内角和定理.【变式1】(2021九年级·全国·专题练习)在社会实践手工课上,小茗同学设计了一个形状如图所示的零件,如果52,25A B ︒︒∠=∠=,30,35,72C D E ︒︒︒∠=∠=∠=,那么F ∠的度数是().A .72︒B .70︒C .65︒D .60︒【答案】B 【分析】延长BE 交CF 的延长线于O ,连接AO ,根据三角形内角和定理求出,BOC ∠再利用邻补角的性质求出DEO ∠,再根据四边形的内角和求出DFO ∠,根据邻补角的性质即可求出DFC ∠的度数.解:延长BE 交CF 的延长线于O ,连接AO ,如图,∵180,OAB B AOB ∠+∠+∠=︒∴180,AOB B OAB ∠=︒-∠-∠同理得180,AOC OAC C ∠=︒-∠-∠∵360,AOB AOC BOC ∠+∠+∠=︒∴360BOC AOB AOC∠=︒-∠-∠360(180)(180)B OAB OAC C =︒-︒-∠-∠-︒-∠-∠107,B C BAC =∠+∠+∠=︒∵72,BED ∠=︒∴180108,DEO BED ∠=︒-∠=︒∴360DFO D DEO EOF∠=︒-∠-∠-∠36035108107110,=︒-︒-︒-︒=︒∴180********DFC DFO ∠=︒-∠=︒-︒=︒,故选:B .【点拨】本题考查三角形内角和定理,多边形内角和,三角形的外角的性质,邻补角的性质,解题关键是会添加辅助线,将已知条件联系起来进行求解.三角形外角的性质:三角形的一个外角等于与它不相邻的两个内角的和;邻补角性质:邻补角互补;多边形内角和:180(2)n ︒-.【变式2】如图,A B C D E ∠+∠+∠+∠+∠=.【答案】180︒/180度【分析】连接CE ,根据三角形内角和定理得到A B OEC OCE ∠+∠=∠+∠,然后根据三角形内角和定理求解.解:如图所示,连接CE ,∵180A B AOB ∠+∠+∠=︒,180OEC OCE COE ∠+∠+∠=︒,AOB COE∠=∠∴A B OEC OCE ∠+∠=∠+∠,∵DEC DEO OEC ∠=∠+∠,DCE DCO OCE ∠=∠+∠,∴A B ACD D DEB∠+∠+∠+∠+∠OCE OEC ACD D DEB=∠+∠+∠+∠+∠()()OCE ACD OEC DEB D=∠+∠+∠+∠+∠DCE DEC D=∠+∠+∠180=︒.故答案为:180︒.【点拨】此题考查了三角形内角和定理,解题的关键是熟练掌握三角形内角和定理.【题型2】8字模型【例2】如图,求A B C D E F ∠+∠+∠+∠+∠+∠的度数.【答案】360A B C D E F ∠+∠+∠+∠+∠+∠=︒.【分析】连接CD ,将A B C D E F ∠+∠+∠+∠+∠+∠转化为四边形CDEF 的内角和即可求出答案.解:如图所示,连接CD .由对顶三角形得,A B ACD BDC ∠+∠=∠+∠,∴A B C D E F ∠+∠+∠+∠+∠+∠360CDE DCF E F =∠+∠+∠+∠=︒.【点拨】本题考查了三角形、四边形的内角和定理、对顶角的性质等知识.将所求角的度数和转化为四边形内角和是解题的关键.【变式1】如图,AB 和CD 相交于点O ,∠A =∠C ,则下列结论中不能完全确定正确的是()A .∠B =∠DB .∠1=∠A +∠DC .∠2>∠D D .∠C =∠D【答案】D 【分析】利用三角形的外角性质,对顶角相等逐一判断即可.解:∵∠A +∠AOD +∠D =180°,∠C +∠COB +∠B =180°,∠A =∠C ,∠AOD =∠BOC ,∴∠B =∠D ,∵∠1=∠2=∠A +∠D ,∴∠2>∠D ,故选项A ,B ,C 正确,故选D .【点拨】本题考查了对顶角的性质,三角形外角的性质,熟练掌握并运用两条性质是解题的关键.【变式2】下图是可调躺椅示意图(数据如图),AE 与BD 的交点为C ,且A ∠,B ∠,E ∠保持不变.为了舒适,需调整D ∠的大小,使110EFD ∠=︒,则图中D ∠应(填“增加”或“减少”)度.【答案】减少10【分析】先通过作辅助线利用三角形外角的性质得到∠EDF与∠D、∠E、∠DCE之间的关系,进行计算即可判断.解:∵∠A+∠B=50°+60°=110°,∴∠ACB=180°-110°=70°,∴∠DCE=70°,如图,连接CF并延长,∴∠DFM=∠D+∠DCF=20°+∠DCF,∠EFM=∠E+∠ECF=30°+∠ECF,∴∠EFD=∠DFM+∠EFM=20°+∠DCF+30°+∠ECF=50°+∠DCE=50°+70°=120°,要使∠EFD=110°,则∠EFD减少了10°,若只调整∠D的大小,由∠EFD=∠DFM+∠EFM=∠D+∠DCF+∠E+∠ECF=∠D+∠E+∠ECD=∠D+30°+70°=∠D+100°,因此应将∠D减少10度;故答案为:①减少;②10.【点拨】本题考查了三角形外角的性质,同时涉及到了三角形的内角和与对顶角相等的知识;解决本题的关键是理解题意,读懂图形,找出图形中各角之间的关系以及牢记公式建立等式求出所需的角,本题蕴含了数形结合的思想方法.【题型3】三角形的角平分线(内内分模型)【例3】(22-23八年级上·江西赣州·期中)如图,在△ABC中,(1)如果AB=4cm,AC=3cm,BC是能被3整除的的偶数,求这个三角形的周长.(2)如果BP、CP分别是∠ABC和∠ACB的角平分线.a、当∠A=45°时,求∠BPC的度数.b、当∠A=x°时,求∠BPC的度数.【答案】(1)13cm(2)a、112.5°;b、90°+12 x°【分析】(1)利用三角形的三边关系:两边之和大于第三边,两之差小于第三边,得出BC的取值范围为1<BC<7,再根据BC是能被3整除的偶数,得到BC=6cm,再求出周长为13cm.(2)利用三角形的内角和等于180°,先求出∠ABC+∠ACB,再利用角平分线平分角的知识,求出∠PBC+∠PCB,然后再一次用三角形内角和等于180°,求出∠BPC.解:(1)∵AB=4cm,AC=3cm∴1<BC<7∴BC=6cm∴三角形的周长为:C△ABC=AB+AC+BC=4+3+6=13cm(2)a、当∠A=45°时,由三角形的内角和可知:∠ABC+∠ACB=180°−∠A=180°−45°=135°∵BP、CP分别是∠ABC和∠ACB的角平分线∴∠PBC=12∠ABC ,∠PCB=12∠ACB∴∠PBC+∠PCB=12∠ABC+12∠ACB =12(∠ABC+∠ACB)=12×135°=67.5°∴∠BPC=180°−(∠PBC+∠PCB)=180°−67.5°=112.5°b 、当∠A =x °时,由三角形的内角和可知:∠ABC +∠ACB =180°−∠A =180°−x °∵BP 、CP 分别是∠ABC 和∠ACB 的角平分线∴∠PBC =12∠ABC ,∠PCB =12∠ACB∴∠PBC +∠PCB =12∠ABC +12∠ACB =12(∠ABC +∠ACB )=12×(180°−x °)=90°−12x °∴∠BPC =180°−(∠PBC +∠PCB )=180°−(90°−12x °)=90°+12x °【点拨】本题考查有关三角形的知识.第一小问的解题关键是运用三角形的三边关系:两边之和大于第三边,两之差小于第三边进行解答;第二小问的解题关键是运用三角形的内角和等于180°,以及角平分线平分角的知识结合一起解答,在求角度时,有时不一定需要每个角都求出来,可以利用整体思想.【变式1】如图,ABC 中,ABC ∠与ACB ∠的平分线交于点F ,过点F 作//DE BC 交AB 于点D ,交AC 于点E ,那么下列结论:①BDFV和CEF△都是等腰三角形②DE BD CE=+;③BF CF>;④若80ABFC∠=︒.∠=︒,则130其中正确的有()个A.1B.2C.3D.4【答案】C【分析】根据等腰三角形的判断与性质和平行线的性质及三角形三边的关系即可求解.解:①∵BF是∠ABC的角平分线,CF是∠ACB的角平分线,∴∠ABF=∠CBF,∠ACF=∠BCF,∵DE∥BC,∴∠CBF=∠BFD,∠BCF=∠EFC(两直线平行,内错角相等),∴∠ABF=∠BFD,∠ACF=∠EFC,∴DB=DF,EF=EC,∴△BDF和△CEF都是等腰三角形,∴①选项正确,符合题意;②∵DE=DF+FE,∴DB=DF,EF=EC,∴DE=DB+CE,∴②选项正确,符合题意;③根据题意不能得出BF>CF,∴④选项不正确,不符合题意;④∵若∠A=80°,∴∠ABC+∠ACB=180°-∠A=180°-80°=100°,∵∠ABF=∠CBF,∠ACF=∠BCF,∴∠CBF+∠BCF=12×100°=50°,∴∠BFC=180°-∠CBF-∠BCF=180°-50°=130°,∴④选项正确,符合题意;故①②④正确.故选C【点拨】等腰三角形的判断与性质和平行线的性质及三角形三边的关系,解题关键是逐个判断选项即可得出正确答案.【变式2】如图,在ABC 中,已知70A ∠=︒,ABC ∠、ACB ∠的平分线OB 、OC 相交于点O ,则BOC ∠的度数为.【答案】125︒【分析】根据三角形的内角和定理求出ABC ACB ∠+∠,再根据角平分线的定义求出OBC OCB ∠+∠,然后利用三角形的内角和定理列式计算即可得解.解:在ABC 中,180 ********ABC ACB A ∠+∠=︒-∠=︒-︒=︒,∵ABC ∠与ACB ∠的角平分线,BO CO 相交于点O ,∴()111105522OBC OCB ABC ACB ∠+∠=∠+∠=⨯︒=︒,在BOC 中,()1 801 80 55 1 25BOC OBC OCB ∠=︒-∠+∠=︒-︒=︒,故答案为:125︒.【点拨】本题考查了三角形的内角和定理,角平分线的定义,整体思想的利用是解题的关键.【题型4】三角形的角平分线(内外分模型)【例4】如图,在△ABD 中,∠ABD 的平分线与∠ACD 的外角平分线交于点E ,∠A=80°,求∠E 的度数【答案】40°【分析】由题意:设∠ABE=∠EBC=x ,∠ACE=∠ECD=y ,利用三角形的外角的性质构建方程组解决问题即可.解:由题意:设∠ABE=∠EBC=x ,∠ACE=∠ECD=y ,则有2=2=y x A y x E +∠⎧⎨+∠⎩①②,①-2×②可得∠A=2∠E ,∴∠E=12∠A=40°.【点拨】本题考查三角形的外角的性质,角平分线的定义等知识,解题的关键是学会利用参数构建方程组解决问题.【变式1】如图,BA 1和CA 1分别是△ABC 的内角平分线和外角平分线,BA 2是∠A 1BD 的角平分线CA 2是∠A 1CD 的角平分线,BA 3是A 2BD ∠的角平分线,CA 3是∠A 2CD 的角平分线,若∠A 1=α,则∠A 2013为()A .2013αB .20132αC .2012αD .20122α【答案】D解:∵BA 1和CA 1分别是△ABC 的内角平分线和外角平分线,∴∠A 1BC=12∠ABC ,∠A 1CD=12∠ACD ,又∵∠ACD=∠A+∠ABC ,∠A 1CD=∠A 1BC+∠A 1,∴∠A 1BC+∠A 1=12(∠A+∠ABC)=12∠A+12∠ABC=12∠A+∠A 1BC ,∴∠A 1=12∠A ;,同理可得:∠A 2=12∠A 1=2α,∠A 3=12∠A 2=4α,L ,∠A n =12∠A n-1=12n α-,∴∠A 2013=20122α.故选D .点拨:利用三角形外角的性质和三角形内角和定理结合角平分线的定义推导得到∠A 1和∠A 的关系是解这道题的关键,由此可推导出∠A 2与∠A 1的关系,进一步推广到∠A n 和∠A n-1的关系就可找到规律求得∠A 2013.【变式2】如图,1BA 和1CA 分别是ABC 的内角平分线和外角平分线,2BA 是1A BD ∠的平分线,2CA 是1A CD ∠的平分线,3BA 是2A BD ∠的平分线,3CA 是2A CD ∠的平分线,……以此类推,若A α∠=,则2020A ∠=.【答案】20202α【分析】根据角平分线的定义可得∠A 1BC =12∠ABC ,∠A 1CD =12∠ACD ,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACD =∠A +∠ABC ,∠A 1CD =∠A 1BC +∠A 1,整理即可得解112A A ∠=∠,同理求出∠A 2,∠A 3,可以发现后一个角等于前一个角的12,根据此规律即可得解.解:∵A 1B 是∠ABC 的平分线,A 1C 是∠ACD 的平分线,∴∠A 1BC =12∠ABC ,∠A 1CD =12∠ACD ,又∵∠ACD =∠A +∠ABC ,∠A 1CD =∠A 1BC +∠A 1,∴12(∠A+∠ABC )=12∠ABC+∠A1,∴∠A1=12∠A ,∵∠A=α.∠A1=12∠A=12α,同理可得∠A2=12∠A1=212α,根据规律推导,∴2020A ∠=20202α,故答案为20202α.【点拨】本题主要考查的是三角形外角性质,角平分线定理,熟知三角形的一个外角等于与它不相邻的两个内角的和的性质,角平分线的定义是解题的关键.【题型5】三角形的角平分线(外外分模型)【例5】如图,已知在ABC ∆中,B ∠、C ∠的外角平分线相交于点G ,若ABC m ∠=︒,ACB n ∠=︒,求BGC ∠的度数.【答案】()12BGC m n ∠=+ 【分析】运用角平分线的知识列出等式求解即可.解答过程中要注意代入与之有关的等量关系.解:∠B 、∠C 的外角平分线相交于点G ,在BCG ∆中,∠BGC=180°-(12∠EBC+12∠BCF )=180°-12(∠EBC+∠BCF )=180°-12(180°-∠ABC+180°-∠ACB )=180°-12(180°-m°+180°-n°);=()12+ m n 【点拨】本题考查的是三角形内角和定理以及角平分线的知识.此类题的关键是找出与之相关的等量关系简化计算得出.【变式1】如图,在△ABC 中,∠ABC 和∠ACB 的外角平分线交于点O ,设∠A =m ,则∠BOC =()A.B.C.D.【答案】B【分析】根据三角形的内角和,可得∠ABC+∠ACB,根据角的和差,可得∠DBC+∠BCE,根据角平分线的定义,可得∠OBC+∠OCB,根据三角形的内角和,可得答案.解:如图:,由三角形内角和定理,得∠ABC+∠ACB=180°-∠A=180°-m,由角的和差,得∠DBC+∠BCE=360°-(∠ABC+∠ACB)=180°+m,由∠ABC和∠ACB的外角平分线交于点O,得∠OBC+∠OCB=12(∠DBC+∠BCE)=90°+12m,由三角形的内角和,得∠O=180°-(∠OBC+∠OCB)=90°-12 m.故选:B.【点拨】本题考查了三角形内角和定理,利用三角形内角和定理,角的和差,角平分线的定义是解题关键.【变式2】如图,△ABC中,分别延长△ABC的边AB、AC到D、E,∠CBD与∠BCE的平分线相交于点P,爱动脑筋的小明在写作业的时发现如下规律:(1)若∠A=60°,则∠P=°;(2)若∠A=40°,则∠P=°;(3)若∠A=100°,则∠P=°;(4)请你用数学表达式归纳∠A与∠P的关系.【答案】(1)65;(2)45;(3)40;(4)∠P =90°-12∠A【分析】(1)若∠A =50°,则有∠ABC +∠ACB =130°,∠DBC +∠BCE =360°-130°=230°,根据角平分线的定义可以求得∠PBC +∠PCB 的度数,再利用三角形的内角和定理即可求得∠P 的度数;(2)、(3)和(1)的解题步骤类似.解:(1)∵∠A =50°,∴∠ABC +∠ACB =180°-50°=130°,∴∠DBC +∠BCE =360°-130°=230°,∵BP ,CP 分别为∠CBD 与∠BCE 的平分线,∴12CBP CBD ∠=∠,12BCP BCE ∠=∠,∴()11152CBP BCP CBD BCE ∠+∠=∠+∠=︒,∴()18065P CBP BCP ∠=︒-∠+∠=︒;(2)∵∠A =40°,∴∠ABC +∠ACB =180°-40°=140°,∴∠DBC +∠BCE =360°-140°=220°,∵BP ,CP 分别为∠CBD 与∠BCE 的平分线,∴12CBP CBD ∠=∠,12BCP BCE ∠=∠,∴()11102CBP BCP CBD BCE ∠+∠=∠+∠=︒,∴()18070P CBP BCP ∠=︒-∠+∠=︒;(3)∵∠A =100°,∴∠ABC +∠ACB =180°-100°=80°,∴∠DBC +∠BCE =360°-80°=280°,∵BP ,CP 分别为∠CBD 与∠BCE 的平分线,∴12CBP CBD ∠=∠,12BCP BCE ∠=∠,∴()11402CBP BCP CBD BCE ∠+∠=∠+∠=︒,∴()18040P CBP BCP ∠=︒-∠+∠=︒;(4)∠ABC +∠ACB =180°-∠A ,∴()360180DBC BCE ABC ACB A ∠+∠=︒-∠+∠=︒+∠,∵BP ,CP 分别为∠CBD 与∠BCE 的平分线,∴12CBP CBD ∠=∠,12BCP BCE ∠=∠,∴()119022CBP BCP DBC BCE A ∠+∠=∠+∠=︒+∠,∴()1180902P CBP BCP A ∠=︒-∠+∠=︒-∠.故答案为:∠P =90°-12∠A .【点拨】本题主要考查三角形内角和定理,三角形的外角性质.关键是熟练掌握三角形的一个外角等于和它不相邻的两个内角的和的性质以及角平分线的定义.【题型6】角平分线+平行线模型【例6】(23-24八年级上·四川泸州·期末)如图,在ABC 中,84A BO ∠=︒,平分ABC CO ∠,平分ACB ∠,过点O 作BC 的平行线与,AB AC 分别相交于点M N ,.若6,8AB AC ==.(1)求BOC ∠的度数;(2)求AMN 的周长.【答案】(1)132︒(2)14【分析】本题考查了三角形内角和定理及角平分线定义,平行线的性质,熟练掌握知识点是解题的关键.(1)先利用三角形内角和定理及角平分线定义得出1902OBC OCB A ∠+∠=︒-∠,再根据内角和定理求解即可;(2)根据角平分线的定义和平行线的性质可证明MO BM =,NO NC =,进而求解即可.(1)解:180A ABC ACB ,Ð+Ð+Ð=°180ABC ACB A ∴∠+∠=︒-∠,BO 平分ABC ∠,CO 平分ACB ∠,()()111111809022222OBC OCB ABC ACB ABC ACB A A \�����窗-��,()11809090421322BOC OBC OCB A \Ð=°-Ð+Ð=°+Ð=°+°=°;(2)解:BO 平分ABC ∠,ABO CBO ∴∠=∠,MN BC ∥ ,MOB CBO ∴∠=∠,ABO MOB ∴∠=∠,MO BM ∴=,同理可得:NO NC =,AM MN AN AM MO ON AN AM BM AN NC AB AC ∴++=+++=+++=+,6,8AB AC == ,AMN ∴ 的周长=14AB AC +=.【变式1】如图,△EFG 的三个顶点E ,G 和F 分别在平行线AB ,CD 上,FH 平分∠EFG ,交线段EG 于点H ,若∠AEF =36°,∠BEG =57°,则∠EHF 的大小为()A .105°B .75°C .90°D .95°【答案】B 【分析】首先根据∠AEF =36°,∠BEG =57°,求出∠FEH 的大小;然后根据AB ∥CD ,求出∠EFG 的大小,再根据FH 平分∠EFG ,求出∠EFH 的大小;最后根据三角形内角和定理,求出∠EHF 的大小为多少即可.解:∵∠AEF =36°,∠BEG =57°,∴∠FEH=180°-36°-57°=87°;∵AB ∥CD ,∴∠EFG=∠AEF=36°,∵FH 平分∠EFG ,∴∠EFH =12∠EFG =12×36°=18°,∴∠EHF =180°-∠FEH -∠EFH =180°-87°-18°=75°.故选:B .【点拨】此题主要考查了三角形内角和定理的应用,角平分线的性质和应用,以及平行线的性质和应用,要熟练掌握.【变式2】如图,EFG 的三个顶点E ,G 和F 分别在平行线AB ,CD 上,FH 平分EFG ∠,交线段EG 于点H ,若36AEF ∠=︒,57BEG ∠=︒,则EHF ∠的大小为.【答案】75°.【分析】首先根据∠AEF =36°,∠BEG =57°,求出∠FEH 的大小;然后根据AB ∥CD ,求出∠EFG 的大小,再根据FH 平分∠EFG ,求出∠EFH 的大小;最后根据三角形内角和定理,求出∠EHF 的大小为多少即可.解:∵∠AEF =36°,∠BEG =57°∴∠FEH=180°-∠AEF-∠BEG=87°∵//AB CD∴∠EFG=∠AEF=36°∵FH 平分∠EFG∴∠EFH=12∠EFG=18°∴∠EHF=180°-∠FEH-∠EFH=75°故答案为:75.︒【点拨】此题主要考查了三角形内角和定理的应用,角平分线的性质和应用,以及平行线的性质和应用,要熟练掌握.第三部分【中考链接与拓展延伸】1、直通中考【例1】(2024·四川达州·中考真题)如图,在ABC 中,1AE ,1BE 分别是内角CAB ∠、外角CBD ∠的三等分线,且113E AD CAB ∠=∠,113E BD CBD ∠=∠,在1ABE 中,2AE ,2BE 分别是内角1E AB ∠,外角1E BD ∠的三等分线.且2113E AD E AB ∠=∠,2113E BD E BD ∠=∠,…,以此规律作下去.若C m ∠=︒.则n E ∠=度.【答案】13nm 【分析】本题考查了三角形的外角定理,等式性质,熟练掌握知识点是解题的关键.先分别对1,ABC E AB △△运用三角形的外角定理,设1E AD α∠=,则3CAB α∠=,1E BD β∠=,则3CBD β∠=,得到1E βα=+∠,33C βα=+∠,同理可求:2211133E E C ⎛⎫∠=∠=∠ ⎪⎝⎭,所以可得13n n E C ⎛⎫∠=∠ ⎪⎝⎭.解:如图:∵113E AD CAB ∠=∠,113E BD CBD ∠=∠,∴设1E AD α∠=,1E BD β∠=,则3CAB α∠=,3CBD β∠=,由三角形的外角的性质得:1E βα=+∠,33C βα=+∠,∴113E C ∠=∠,如图:同理可求:2113E E ∠=∠,∴2213E C ⎛⎫∠=∠ ⎪⎝⎭,……,∴13nn E C ⎛⎫∠=∠ ⎪⎝⎭,即13n nE m ∠=︒,故答案为:13n m .【例2】(2019·辽宁铁岭·中考真题)如图,在CEF △中,80E ∠=︒,50F ∠=︒,AB CF ,AD CE ,连接BC ,CD ,则A ∠的度数是()A .45°B .50°C .55°D .80°【答案】B 【分析】连接AC 并延长交EF 于点M .由平行线的性质得31∠=∠,24∠∠=,再由等量代换得3412BAD FCE ∠=∠+∠=∠+∠=∠,先求出FCE ∠即可求出A ∠.解:连接AC 并延长交EF 于点M .AB CF ,31∴∠=∠,AD CE ,24∴∠=∠,3412BAD FCE ∴∠=∠+∠=∠+∠=∠,180180805050FCE E F ∠=︒-∠-∠=︒-︒-︒=︒ ,50BAD FCE ∴∠=∠=︒,故选B .【点拨】本题主要考查了平行线的性质以及三角形的内角和定理,属于基础题型.【例3】(2020·北京·中考真题)如图,AB 和CD 相交于点O ,则下列结论正确的是()A .∠1=∠2B .∠2=∠3C .∠1>∠4+∠5D .∠2<∠5【答案】A 【分析】根据对顶角性质、三角形外角性质分别进行判断,即可得到答案.解:由两直线相交,对顶角相等可知A 正确;由三角形的一个外角等于它不相邻的两个内角的和可知B 选项为∠2>∠3,C 选项为∠1=∠4+∠5,D 选项为∠2>∠5.故选:A .【点拨】本题考查了三角形的外角性质,对顶角性质,解题的关键是熟练掌握三角形的外角性质进行判断.2、拓展延伸【例1】如图1所示的图形,像我们常见的学习用品——圆规.我们不妨把这样图形叫做“规形图”,请发挥你的聪明才智,解决以下问题:(1)观察“规形图”,试探究BDC ∠与A B C ∠∠∠、、之间的关系,并说明理由;(2)请你直接利用以上结论,解决以下三个问题:①如图2,把一块三角尺XYZ 放置在ABC 上,使三角尺的两条直角边XY XZ 、恰好经过点B 、C ,若50A ∠=︒,直接写出ABX ACX ∠+∠的结果;②如图3,DC 平分ADB ∠,EC 平分AEB ∠,若50,130DAE DBE ∠=︒∠=︒,求DCE ∠的度数;③如图4,,ABD ACD ∠∠的10等分线相交于点291G G G 、、、 ,若1140,77BDC BG C ∠=︒∠=︒,求A ∠的度数.【答案】(1)BDC A B C ∠=∠+∠+∠,见解析(2)①40︒;②90︒;③70︒【分析】(1)首先连接AD 并延长,然后根据外角的性质,即可判断出BDC A B C ∠=∠+∠+∠;(2)①由(1)可得ABX ACX A BXC ∠+∠+∠=∠,然后根据40A ∠=︒,90BXC ∠=︒,即可求出ABX ACX ∠+∠的值;②由(1)可得DBE DAE ADB AEB ∠=∠+∠+∠,再根据50,130DAE DBE ∠=︒∠=︒,求出ADB AEB ∠+∠的值;然后根据()12DCE ADB AEB DAE ∠=∠+∠+∠,即可求出DCE ∠的度数;③设1ABG x ∠=︒,1ACG y ∠=︒,结合已知可得10ABD x ∠=︒,10ACD y ∠=︒,再根据(1)可得77A x y ∠+︒+︒=︒,1010140A x y ∠+︒+︒=︒,即可判断出A ∠的度数.解:(1)解:BDC A B C ∠=∠+∠+∠,理由如下:如图,连接AD 并延长.根据外角的性质,可得BDF BAD B ∠=∠+∠,CDF C CAD ∠=∠+∠,又∵BDC BDF CDF ∠=∠+∠,BAC BAD CAD ∠=∠+∠,∴BDC A B C ∠=∠+∠+∠,故答案为:BDC A B C ∠=∠+∠+∠;(2)①由(1)可得ABX ACX A BXC ∠+∠+∠=∠,∵50A ∠=︒,90BXC ∠=︒,∴905040ABX ACX ∠+∠=︒-︒=︒;②由(1)可得DBE DAE ADB AEB ∠=∠+∠+∠,∴1305080ADB AEB DBE DAE ∠+∠=∠-∠=︒-︒=︒,∴()8024120ADB AEB ∠+∠=︒÷=︒,∴()50490120DCE ADB AEB DAE ∠=∠+∠+∠=︒+︒=︒;③设1ABG x ∠=︒,1ACG y ∠=︒,则10ABD x ∠=︒,10ACD y ∠=︒,则77A x y ∠+︒+︒=︒,1010140A x y ∠+︒+︒=︒,解得7x y +=︒,所以77770A ∠=︒-︒=︒,即A ∠的度数为70︒.【点拨】此题还考查了三角形的外角的性质,要熟练掌握,解答此题的关键是要明确:三角形的外角等于和它不相邻的两个内角的和.【例2】如图①,在△ABC 中,∠ABC 与∠ACB 的平分线相交于点P .(1)如果∠A =70°,求∠BPC 的度数;(2)如图②,作△ABC 外角∠MBC ,∠NCB 的角平分线交于点Q ,试探索∠Q ,∠A 之间的数量关系.(3)如图③,延长线段BP ,QC 交于点E ,在△BQE 中,存在一个内角等于另一个内角的3倍,求∠A 的度数.【答案】(1)125︒(2)1902Q A ∠=︒-∠(3)∠A 的度数是45︒或60︒或120︒或135︒【分析】(1)在△ABC 中,根据三角形内角和定理求出∠ABC +∠ACB =110°,根据角平分线的定义得出∠PBC =12∠ABC ,∠PCB =12∠ACB ,求出∠PBC +∠PCB =55°,再在△BPC 中,根据三角形内角和定理求出即可;(2)根据三角形外角性质得出∠MBC =∠ACB +∠A ,∠NCB =∠ABC +∠A ,求出∠MBC +∠NCB =∠ACB +∠A +∠ABC +∠A =180°+∠A ,根据角平分线的定义得出QBC =12∠MBC ,∠QCB =12∠NCB ,求出∠QBC+∠QCB=90°+12∠A,根据三角形内角和定理求出即可;(3)根据角平分线的定义得出∠ACF=2∠BCF,∠ABC=2∠EBC,根据三角形外角性质得出∠ECF=∠EBC+∠E,求出∠A=2∠E,求出∠EBQ=90°,分为四种情况:①∠EBQ=3∠E=90°,②∠EBQ=3∠Q,③∠Q=3∠E,④∠E=3∠Q,再求出答案即可解:(1)∵∠A=70°,∴∠ABC+∠ACB=180°﹣∠A=110°,∵点P是∠ABC和∠ACB的角平分线的交点,∴∠PBC=12∠ABC,∠PCB=12∠ACB,∴∠PBC+∠PCB=55°,∴∠BPC=180°﹣(∠PBC+∠PCB)=125°;(2)∵∠MBC=∠ACB+∠A,∠NCB=∠ABC+∠A,∴∠MBC+∠NCB=∠ACB+∠A+∠ABC+∠A=180°+∠A,∵点Q是∠MBC和∠NCB的角平分线的交点,∴∠QBC=12∠MBC,∠QCB=12∠NCB,∴∠QBC+∠QCB=12(∠MBC+∠NCB)=12(180°+∠A)=90°+12∠A,∴∠Q=180°﹣(∠QBC+∠QCB)=180°﹣(90°+12∠A)=90°﹣12∠A;(3)∵CQ为△ABC的外角∠NCB的角平分线,∴CE是△ABC的外角∠ACF的平分线,∴∠ACF=2∠BCF,∵BE平分∠ABC,∴∠ABC=2∠EBC,∵∠ECF=∠EBC+∠E,∴2∠ECF=2∠EBC+2∠E,即∠ACF=∠BC+2∠E,∵∠ACF=∠ABC+∠A,∴∠A=2∠E,即∠E=12∠A,∵∠EBQ=∠EBC+∠CBQ=12∠ABC+12 MBC=12(∠ABC+∠A+∠ACB)=90°,如果△BQE中,存在一个内角等于另一个内角的3倍,那么分为四种情况:①∠EBQ=3∠E=90°,则∠E=30°,∠A=2∠E=60°;②∠EBQ=3∠Q,则∠Q=30°,∠E=60°,∠A=2∠E=120°;③∠Q=3∠E,则∠E=22.5°,∠A=2∠E=45°;④∠E=3∠Q,则∠E=67.5°,∠A=2∠E=135°,综合上述,∠A的度数是45°或60°或120°或135°.【点拨】本题考查了三角形的外角性质,三角形内角和定理,角平分线的定义等知识点,熟练掌握知识点及运用分类讨论思想是解题的关键.。
三角形 数学建模 四大常考相似模型

(1)证明:∵∠B=∠C=∠AMN=90°,
∴∠AMB+∠CMN=90°,∠CMN+∠MNC=90°,
∴∠AMB=∠MNC,
∴△ABM∽△MCN.
2.结论: (1)
一线三垂直型 已知:∠B=∠ACE=∠D=90° 结论:(1)△ABC∽△CDE (2)AB·DE=BC·CD (3)当C为BD中点时,△ABC∽△CDE∽△ACE
(2)
一线三等角型 已知:∠B=∠ACE=∠D=α 结论:(1)△ABC∽△CDE (2) AB·DE=BC·CD (3)当C为BD中点时,△ABC∽△CDE∽△ACE
BC
1 3
.
2.如图,在△ABC中,P为边AB上一点,且∠ACP=∠B,若 AP=2,BP=3,则AC的长为 10.
3.如图,在△ABC中,AB=8,AC=6,点D在边AC上,AD=2,若点E在
边AB上,以A,D,E为顶点的三角形与△ABC相似,则AE的长
为
8或3
32
.
模型解读
模型二 8字型 特征:有一组隐含的等角(即对顶角相等). (1)
第四章 三角形
数学建模 四大常考相似模型
模型解读
特征:有一个公共角. (1)
模型一 A字型
A 字型 已知:DE∥BC 结论:AD = AE = DE
AB AC BC
反 A 字型 (2)
已知:∠AED=∠C 结论:AD = AE = DE
AB AC BC
(3)
反 A 字型(共边共角)
已知:∠ABD=∠C
8 字型 已知:AB∥CD 结论:AO = BO = AB
六年级数学【小升初】三角形五大模型

三角形五大模型模型一:等积模型①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比;两个三角形底相等,面积比等于它们的高之比;如图12::S S a b =; ③夹在一组平行线之间的等积变形,如图ACD BCD S S =△△;反之,如果ACD BCD S S =△△,则可知直平行于CD ;④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比。
模型二:等分点结论(“鸟头定理”) 如图,三角形AED 占三角形ABC 面积的23×14=16模型三:任意四边形中的比例关系 (“蝴蝶定理”) ① S 1︰S 2=S 4︰S 3 或者S 1×S 3=S 2×S 4 ② ②AO ︰OC=(S 1+S 2)︰(S 4+S 3)梯形中比例关系(“梯形蝴蝶定理”) ① S 1︰S 3=a 2︰b2②S 1︰S 3︰S 2︰S 4= a 2︰b 2︰ab ︰ab ③S 的对应份数为(a+b )2模型四:相似三角形性质D CBAbs 2s 1S 4S 3s 2s 1O DCBA S 4S 3s 2s 1ba如何判断相似(1)相似的基本概念:两个三角形对应边城比例,对应角相等。
(2)判断相似的方法:①两个三角形若有两个角对应相等则这两个三角形相似;②两个三角形若有两条边对应成比例,且这两组对应边所夹的角相等则两个三角形相似。
①a b c h A B C H === ② S 1︰S 2=a 2︰A 2模型五:燕尾定理S △ABG :S △AGC =S △BGE :S △GEC =BE :EC ; S △BGA :S △BGC =S △AGF :S △GFC =AF :FC ; S △AGC :S △BCG =S △ADG :S △DGB =AD :DB ;【重点难点解析】1. 模型一与其他知识混杂的各种复杂变形2. 在纷繁复杂的图形中如何辨识“鸟头” 【考点挖掘】1. 三角形面积等高成比2. “鸟头定理”3. “蝴蝶定理”【例1】(难度等级 ※)如图,长方形ABCD 的面积是56平方厘米,点E 、F 、G 分别是长方形ABCD 边上的中点,H 为AD 边上的任意一点,求阴影部分的面积。
相似三角形的八大基本模型

相似三角形的八大基本模型1、等腰三角形:等腰三角形是一种三角形,它的两条边长相等,称为等腰三角形。
它的三个角也是等角,每个角度都是60度,是一个等边三角形。
它也有着金字塔形状。
2、等边三角形:等边三角形是三角形中最常见的一种,它的三个边长都是相等的,因此得名等边三角形。
由于边长是相等的,因此三个角也是等角,每个角度都是60度。
此外,它也有着正三角形的特性。
3、直角三角形:直角三角形是一种三角形,它的一个角是90度,成为直角三角形。
直角三角形一般分为狭角三角形和钝角三角形两种,其中,狭角三角形的两个直角边都要大于第三条斜边,而钝角三角形则相反,其两个直角边都要小于第三条斜边。
4、相似三角形:相似三角形是指三角形中,由一条射线形成的两个三角形,三条边长的比值相等的三角形。
它的内角和外角相似,但是边长和面积都不同。
由此可以知道,如果两个三角形边长比值相同,则该两个三角形为相似三角形。
5、等分直角三角形:等分直角三角形是指一个直角三角形中,由底边一个端点引分出来的两条斜边上的各个点,连接起来后形成的直角三角形。
由于它的特点,两个边长和底边的面积比例也是相同的,每个等分点也和其他两个等分点是相等的。
6、正交三角形:正交三角形是指两个直角三角形中的一类,由其相似的三条边构成,两个斜边互相垂直相交,而三条边长分别是直角三角形中底边和邻边之和。
正交三角形属于相似三角形,具有和相似三角形一样的特性。
7、正三角形:正三角形是一种特殊的三角形,它的三个角都是60度,每个角度都相同,其三条边长也相等,为了符合这种特性,它也有其称之为正三角形的原因。
它有着明显的金字塔形状,但是每个角度都是60度,因此可以说它的金字塔形状是平行的。
8、稜角三角形:稜角三角形是一种特殊的三角形,它的其中一个角是60度,另外两个角都小于60度,一般不会大于60度,这种三角形因此也有着金字塔形状,但是由于角度上的不同,边长也不同。
其中,由三角形的垂足作为原点,内角和外角大小关系也要满足,且两个内角和一个外角和要等于180度。
奥数几何-三角形五大模型带解析

奥数几何-三角形五大模型带解析三角形是几何学中的基本图形之一,具有丰富的性质和应用。
在奥数竞赛中,常常会涉及到三角形的题目。
为了更好地应对这类题目,我们需要掌握三角形的五大模型,即:全等模型、相似模型、正弦定理模型、余弦定理模型和面积模型。
下面将对这五大模型进行详细解析。
一、全等模型全等模型是指两个三角形的对应边长和对应角度都相等。
利用全等模型,我们可以简化一些繁杂的计算,直接得到结论。
例如,已知三角形ABC和三角形DEF的对应边长和对应角度分别相等,我们就可以得出它们全等的结论,即△ABC≌△DEF。
利用全等模型,我们可以将问题简化为求解另一个已知三角形的性质,从而得到答案。
二、相似模型相似模型是指两个三角形的对应角度相等,但对应边长不一定相等。
相似模型在解决一些比例问题时非常有用。
例如,已知△ABC和△DEF的对应角度分别相等,我们可以推出它们相似的结论,即△ABC∽△DEF。
利用相似模型,我们可以通过已知比例关系,求解未知的边长或角度。
三、正弦定理模型正弦定理是指在一个三角形中,三个角的正弦值与对应边的长度之间存在着一定的比例关系。
正弦定理模型在求解三角形的边长和角度时非常有用。
正弦定理的公式为:sinA/a = sinB/b = sinC/c,其中A、B、C为三角形的角度,a、b、c为对应边的长度。
利用正弦定理模型,我们可以通过已知的角度和边长,求解未知的边长或角度。
四、余弦定理模型余弦定理是指在一个三角形中,三个角的余弦值与对应边的长度之间存在着一定的比例关系。
余弦定理模型在求解三角形的边长和角度时非常有用。
余弦定理的公式为:c² = a² + b² - 2abcosC,其中a、b、c为三角形的边长,C为对应的角度。
利用余弦定理模型,我们可以通过已知的边长和角度,求解未知的边长或角度。
五、面积模型面积模型是指通过三角形的面积关系求解三角形的边长或角度。
在面积模型中,我们常常使用海伦公式或高度公式来求解三角形的面积。
相似专题四相似三角形的四大模型初中数学

【证明】∵∠ACD=∠BCA,∠DAC=∠B, ∴△ACD∽△BCA,∴CADD=AACB. ∵CD=CE,∴∠CDE=∠CED,∴∠ADB=∠CEA. ∵∠DAC=∠B,∴△ADB∽△CEA, ∴AACB=BADE,∴CADD=BADE,∴CD·BD=AD·AE.
模型展示
结论
条件:∠C=∠ABD=∠E=90°. 结论:△ABC∽△BDE.
条件:∠C=∠AGD=∠F=90°. 结论:△ABC∽△EDF.
3 【2023·济南市中区期末】如图,在矩形ABCD中,点 E是BC的中点,EF⊥AE交CD于点F.
(1)求证:△ABE∽△ECF. 【证明】∵四边形ABCD是矩形, ∴∠B=∠C=90°,∴∠=90°, ∴∠AEB+∠CEF=90°,∴∠BAE=∠CEF, ∴△ABE∽△ECF.
模型2 8字型 【模型解读】两个三角形若有“一对对顶角+一对等角”, 则出现“8”字型相似.没有说明对应角的关系时,需分 ∠B=∠C或∠B=∠D两种情况讨论.
模型展示
结论
条件:AB∥CD. 结论:△AOB∽△DOC.
条件:∠A=∠C或∠B=∠D. 结论:△AOB∽△COD.
2 【2023·济南期末】如图,AD,BC相交于点P,连接 AC,BD,且∠1=∠2,AC=3,CP=2,DP=1,求 BD的长.
第九章 图形的相似
专题(四) 相似三角形的四大 模型
模型1 A字型 【模型解读】两个三角形若有“一个公共角+一对等角”, 则出现“A”字型相似,没有说明对应角的关系时,需分 ∠AED=∠B或∠AED=∠C两种情况讨论.
模型展示
结论
条件:DE∥BC. 结论:△AED∽△ACB.
模型展示
结论 条件:∠AED=∠B 或AADC=AAEB. 结论:△ AED∽△ABC.
初中数学几何模型系列之(三)三角形四大模型

初中几何模型系列之(三)三角形四大模型
全面完整版+例题解析
第一部分模型展示
一、八字模型:二、飞镖模型:
证明的过程很简单,请同学们思考一下吧!
模型展示
三、角平分线模型
角平分线模型包含三种类型,1.两内角的角平分线相交于一点;2.两外角的角平分线相交于一点;3.一条内角和一个外
模型展示
四、角平分线&高线模型
注意:此模型要注意,在此结论三个角的关
系中,∠ B和∠ C之间永远是大角-小角。
第二部分例题解析
点评:此题既可用
8字模型又可用飞
镖模型,同学们一
定要仔细观察!
点评:此题既可用8字模型又可用飞镖模型,同学们
点评:此题用到8字模型的一种特殊情况,大家要体会这种情况!
点评:此题用到两次飞镖模型,大家在做题时要注意构造模型
点评:此题用到两次飞镖模型,大家在做题时要注意观察
点评:此题属于角平分线中两外角平分线相交于一点的情况
例题解析
点评:此题标准的角平分线
+高线模型,第一问的计算
过程实际上就是对第二问的
铺垫
Network Optimization Expert Team
第三部分课后练习
Network Optimization Expert Team。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形的四大模型
、三角形的重要概念和性质
1、 三角形的内角和定理:三角形的内角和等于 180°
2、三角形的外角和定理:三角形的一个外角等于和它不相邻的两个内角的和
3、三角形角平分线 (角分线) 中线 (分面积等) 高(直角三角形两锐角互余)
、八字模型:
三、飞镖模型:
证明结论: 1.∠BOC =∠ A +∠B +∠ C
四、角分线模型:
如图, BD 、CD 分别是∠ ABC 和∠ ACB 的角平分线, BD 、CD 相交于点 D , 试探索∠ A 与∠D
之间的数量关系,并证明你的结论.
如图,△ ABC 两个外角(∠ CAD 、∠ ACE )的平分线相交于点 P . 探索∠ P 与∠B 有怎样的数量关系,并证明你的结论.
题型一、三角形性质等应用
5.一个四边形截去一个角后,剩下的部分可能是什么图形?画出所有可能的图形,并分别 说出
内角和和外角和变化情况.
6.如图,直线 AC ∥ BD ,连接 AB ,直线 AC ,BD 及线段 AB 把平面分成①、②、③、④ 四
个部分,规定:线上各点不属于任何部分.当动点 P 落在某个部分时,连接 PA ,PB ,
构成∠ PAC ,∠APB ,∠PBD 三个角.(提示:有公共端点的两条重合的射线所组成的角 是 0°角)
( 1)当动点 P 落在第①部分时,求证:∠ APB= ∠PAC+∠ PBD ;
( 2)当动点 P 落在第②部分时,∠ APB= ∠ PAC+∠PBD 是否成立?(直接回答) ( 3)当动点 P 在第③部分时,全面探究∠ PAC ,∠ APB ,∠ PBD 之间的关系,并写出
动点 P 的具体位置和相应的结论.选择其中一种结论加以证明.
1.如图,小亮从 A 点出发前进 下去,他第一次回到出发点 A .120
B . 150
2.如图所示是重叠的两个直角三角形.将其中一个直角三角形沿 如果 AB=8cm , BE=4cm , DH=3cm ,
10m , A 时, C . 向右转 15°,再前进10m ,又向右转 15°,这样一直
走 一共走了米数是( )
240 D .360
则图中阴影部分面积为
BC 方向平移得到 △
DEF .
2
3. 如图,在 △ ABC 中,已知点 D , 且 S △ABC =4cm 2,则 S 阴影=
4. A 、B 、C 是线段 A 1B ,B 1C ,C 1A 的中点, E , F 分别为边 BC ,AD , 2 cm .
S △ABC 的面积是 1,则 S △ A 1B 1C 1 的面积
CE 的中点,
题型二、八字模型应用
① 图 2中共有 个“8字形 ”;
② 若∠ ABC=80° ,∠ ADC=3°8 ,求∠ P 的度数; (提醒:解决此问题你可以利用图 1 的结论或用其他方法) ③ 猜想图 2中∠P 与∠B+∠D 的数量关系,并说明理由.
8.( 1)求五角星的五个角之和; ( 2
)求这六个角之和
7.( 1)如图 1 的图形我们把它
称为
8字形 ”,请说明∠
A+∠ B=∠C+∠D ;
题型三、飞镖模型应用
9.如图,已知 AB ∥DE ,BF ,EF 分别平分∠ ABC 与∠CED 交于点 F ,探索∠ BFE 与∠ BCE
之间的数量关系,并证明你的结论.
10.如图 1,E 是直线 AB ,CD 内部一点, AB ∥CD ,连接 EA ,ED .
(1)探究猜想:①若∠ A=30°,∠ D=40°,则∠ AED 等于多少度?
②若∠ A=20°,∠ D=60°,则∠ AED 等于多少度?
③猜想图 1中∠ AED ,∠ EAB ,∠ EDC 的关系并证明你的结论.
( 2)拓展应用:
如图 2,射线 FE 与矩形 ABCD 的边 AB 交于点 E ,与边 CD 交于点 F ,①②③④分 别是被射线 FE 隔开的 4 个区域(不含边界,其中区域③、④位于直线 AB 上方, P 是位于以上四个区域上的点,猜想:∠ PEB ,∠PFC ,∠EPF 的关系(不要求证明) .
题型四、角分线模型应用
11.如图,∠ A=65 °,∠ ABD=30 °,∠ ACB=72 °,且 CE 平分∠ ACB ,求∠ BEC 的度数. 12.如图,在 △ABC 中,∠ A=42 °,∠ ABC 和∠ ACB 的三等分线分别交于点 D ,E ,
14.如图,∠ ACD 是△ABC 的外角,∠ABC 的平分线与∠ ACD 的平分线交于点 A 1,∠A 1BC
的平分线与∠ A 1CD 的平分线交于点 A 2,⋯,∠ A n ﹣1BC 的平分线与∠ A n ﹣1CD 的平分线 交于点 A n .设∠ A= θ.则:( 1)∠ A 1= ;( 2)∠ A 2= ;( 3)∠A n = .
题型五、其他应用
15.已知△ ABC 中,∠ A=60°.
(1)如图①,∠ ABC 、∠ ACB 的角平分线交于点 D ,则∠ BOC=
°.
(2)如图②,∠ ABC 、∠ ACB 的三等分线分别对应交于 O 1、O 2,则∠BO 2C=
°.
(3)如图③,∠ ABC 、∠ ACB 的 n 等分线分别对应于 O 1、O 2⋯O n ﹣1(内部有 n ﹣ 1个点), 求∠ BO n ﹣1C (用 n 的代数式表示) .
(4)如图③,已知∠ ABC 、∠ ACB 的 n 等分线对应于 O 1、O 2⋯O n ﹣1,若∠ BO n ﹣1C=90°,
求 n 的值.
C .88
D .
110 第 13 题
,则∠ BCD 的大小为( )
B . 100°
C . 130°
D . 150°
A . 50
°
则∠BDC 的度数是(
教育之通病是教用脑的人不用手,不教用手的人用脑,所以一无所能。
教育革命的对策是手脑联盟,结果是手与脑的力量都可以大到不可思议。
16. 我们知道,任何一个三角形的三条内角平分线相交于一点,如图,若 △ABC 的三条内
角平分线相交于点 I ,过 I 作 DE ⊥AI 分别交 AB 、AC 于点 D 、E .
(1)请你通过画图、度量,填写右上表(图画在草稿纸上,并尽量画准确)
( 2
)从上表中你发现了∠ BIC
与∠
BDI 之间有何数量关系,写出并说明其中的道理.
∠BAC 的度数 40° 60° 90° 120°
∠BIC 的度数
∠ BDI 的度数
单纯的课本内容,并不能满足学生的需要,通过补充,达到内容的完善。
