四相移相键控(QPSK)调制及解调实验

合集下载

四相移相键控(QPSK)调制及解调实验

通信对抗原理实验报告实验名称:四相移相键控（QPSK）调制及解调实验学生姓名：学生学号：学生班级:所学专业：实验日期：1. 实验目的1. 掌握QPSK 调制解调原理及特性.2。

. 熟悉Matlab 仿真软件的使用。

2. 实验内容1、编写Matlab 程序仿真QPSK 调制及相干解调。

2、观察IQ 两路基带信号的特征及与输入NRZ 码的关系。

3、观察IQ 调制解调过程中各信号变化。

4、观察功率谱的变化。

5、分析仿真中观察的数据，撰写实验报告。

3. 实验原理1、QPSK 调制原理QPSK 又叫四相绝对相移调制,它是一种正交相移键控。

QPSK 利用载波的四种不同相位来表征数字信息。

由于每一种载波相位代表两个比特信息，因此，对于输入的二进制数字序列应该先进行分组，将每两个比特编为一组,然后用四种不同的载波相位来表征。

我们把组成双比特码元的前一信息比特用a 代表,后一信息比特用b 代表。

双比特码元中两个信息比特ab 通常是按格雷码排列的,它与载波相位的关系如表1-1所示，矢量关系如图1—1所示。

图1-1（a)表示A 方式时QPSK 信号矢量图,图1—1（b)表示B 方式时QPSK 信号的矢量图。

由于正弦和余弦的互补特性,对于载波相位的四种取值,在A 方式中：45°、135°、225°、315°，则数据k I、k Q 通过处理后输出的成形波形幅度有两种取值±2/2;B 方式中:0°、90°、180°、270°,则数据k I、k Q 通过处理后输出的成形波形幅度有三种取值±1、0。

表(0,1)(1,1)(0,0)参考相位参考相位(a)(b)图1-1 QPSK 信号的矢量图下面以A 方式的QPSK 为例说明QPSK 信号相位的合成方法。

串/并变换器将输入的二进制序列依次分为两个并行序列,然后通过基带成形得到的双极性序列(从D/A 转换器输出，幅度为±2/2）。

四相移相键控调制解调

太原理工大学现代科技学院实验报告一、实验目的1、了解QPSK 调制解调原理及特性。

2、了解载波在QPSK 相干及非相干时的解调特性。

二、实验内容1、观察I 、Q 两路基带信号的特征及与输入NRZ 码的关系。

2、观察IQ 调制解调过程中各信号变化。

3、观察解调载波相干时和非相干时各信号的区别。

三、基本原理1、QPSK 调制原理 QPSK 又叫四相绝对相移调制，它是一种正交相移键控。

QPSK 利用载波的四种不同相位来表征数字信息。

由于每一种载波相位代表两个比特信息，因此，对于输入的二进制数字序列应该先进行分组，将每两个比特编为一组，然后用四种不同的载波相位来表征。

我们把组成双比特码元的前一信息比特用a 代表，后一信息比特用b 代表。

双比特码元中两个信息比特ab 通常是按格雷码排列的，它与载波相位的关系如表1-1所示，矢量关系如图1-1所示。

图1-1（a ）表示A 方式时QPSK 信号矢量图，图1-1（b ）表示B 方式时QPSK 信号的矢量图。

由于正弦和余弦的互补特性，对于载波相位的四种取值，在A 方式中：45°、135°、225°、315°，则数据k I 、k Q 通过处理后输出的成形波形幅度有三种取值±1、0。

表1-1 双比特码元与载波相位关系太原理工大学现代科技学院实验报告(0,1)(1,1)(0,0)参考相位参考相位(a)(b)图1-1 QPSK 信号的矢量图下面以A 方式的QPSK 为例说明QPSK 信号相位的合成方法。

串/并变换器将输入的二进制序列依次分为两个并行序列，然后通过基带成形得到的双极性序列（从D/A 转码元。

双极性的a 和b 脉冲通过两个平衡调制器分别对同相载波及正交载波进行二相调制，得到图1-2中虚线矢量，将两路输出叠加，即得到QPSK 调制信号，其相位编码关系如表1-2所示。

a(1)b(1)b(0)a(0)图1-2 矢量图表1-2 QPSK 信号相位编码逻辑关系用调相法产生QPSK 调制器框图如图1-3所示。

QPSK、DQPSK系统调制与解调

实验四QPSK与DQPSK调制实验一、实验目的在2PSK，2DPSK的学习基础上，掌握QPSK，以及以其为基础的DQPSK，OQPSK， /4—DQPSK等若干种相关的重要调制方式的原理，从而对多进制调相有一定了解。

二、实验设备1、“移动通信技术应用综合实训系统” 实验仪一台。

2、50MHz示波器一台。

3、实验模块：信源模块，QPSK-调制模块。

三、实验原理一）基本理论(A)四相绝对移相键控（QPSK）的调制四相绝对移相键控利用载波的四种不同相位来表征数字信息。

由于每一种载波相位代表两个比特信息，故每个四进制码元又被称为双比特码元。

我们把组成双比特码元的前一信息比特用a代表，后一信息比特用b代表。

双比特码元中两个信息比特ab通常是按格雷码（即反射码）排列的，它与载波相位的关系如表所列。

表4-1 双比特码元与载波相位的关系由于四相绝对移相调制可以看作两个正交的二相绝对移相调制的合成，故两者的功率谱密度分布规律相同。

下面我们来讨论QPSK 信号的产生与解调。

QPSK 信号的产生方法与2PSK 信号一样，也可以分为调相法和相位选择法。

(1) 调相法用调相法产生QPSK 信号的组成方框图如下所示。

图4-1 QPSK 信号的组成方框图设两个序列中的二进制数字分别为a 和b ，每一对ab 称为一个双比特码元。

并设经过串并变换后上支路为a,下支路为b 。

双极性的a 和b 脉冲通过两个平衡调制器分别对同相载波及正交载波进行二相调制。

a(1)(1,0)b(0)(0,0)a(0)b(1)(0,1)(1,1)表4-2 QPSK 信号相位编码逻辑关系(2)相位选择法用相位选择法产生QPSK信号的组成方框图如下所示。

图4-2 相位选择法产生QPSK信号方框图(B)四相相对移相键控（DQPSK）的调制所谓四相相对移相键控也是利用前后码元之间的相对相位变化来表示数字信息。

若以前一码元相位作为参考，并令△φ为本码元与前一码元的初相差。

四相移相键控调制解调

武夷学院实验报
课程名称：移动通信原理与技术
项目名称：四相移相键控（QPSK）调制及解调实验
姓名：陈真灼专业：通信工程班级： 3班学号：20114173004
1注：1、实验预习部分包括实验环境准备和实验所需知识点准备。

2、若是单人单组实验，同组成员填无。

c、对比观测解调前后的I路信号
示波器探头分别接IQ模块的“
解调正确，若不一致可能是载波相位不对，可按下
复位。

）
2注：实验过程记录要包含实验目的、实验原理、实验步骤，页码不够可自行添加。

六
实验报告成绩（百分制）__________ 实验指导教师签字：__________。

四相移相键控(QPSK)调制及解调实验

实验二四相移相键控（QPSK ）调制及解调实验一、实验目的1、了解QPSK 调制解调原理及特性。

2、了解载波在QPSK 相干及非相干时的解调特性。

二、实验内容1、观察I 、Q 两路基带信号的特征及与输入NRZ 码的关系。

2、观察IQ 调制解调过程中各信号变化。

3、观察解调载波相干时和非相干时各信号的区别。

三、基本原理（说明：原理部分需简要介绍）1、QPSK 调制原理QPSK 的调制有两种产生方法相乘电路法和选择法。

相乘法：输入信号是二进制不归零的双极性码元，它通过“串并变换”电路变成了两路码元。

变成并行码元后，每个码元的持续时间是输入码元的两倍。

用两路正交载波去调制并行码元。

发射信号定义为：⎪⎩⎪⎨⎧≤≤-+=其他,00],4)12(2cos[/2)(b t T t i ft t E t S ππ其中，i ＝1，2，3，4；E 是发射信号的每个符号的能量，T 为符号的持续时间，载波频率f 等于nc/T ，nc 为固定整数选择法输入基带信号经过串并变换后用于控制一个相位选择电路，按照当时的输入双比特ab ，决定选择哪个相位的载波输出2、QPSK 解调原理QPSK 接收机由一对共输入地相关器组成。

这两个相关器分别提供本地产生地相干参考信号()t 1φ和()t 2φ。

四、实验步骤（说明：要详细）（1）QPSK 调制程序close all% x1是类似[1 1 -1 -1 -1 -1 1 1]的分布,作用是控制相位的180°反转。

%由于仿真中载波的频率是f=1Hz，所以1s的间隔内有一个完整周期的正弦波。

t=[-1:0.01:7-0.01]; % t共800个数据，-1~7st1=[0:0.01:8-0.01]; %t1也是800个数据点，0 ~8stt=length(t); % tt=800x1=ones(1,800);for i=1:ttif (t(i)>=-1 & t(i)<=1) | (t(i)>=5& t(i)<=7);x1(i)=1;else x1(i)=-1;endendt2 = 0:0.01:7-0.01; %t2是700个数据点，是QPSK_rc绘图的下标t3 = -1:0.01:7.1-0.01; %t3有810个数据点，是i_rc的时间变量t4 = 0:0.01:8.1-0.01; %t4有810个数据点，是q_rc的时间变量tt1=length(t1);x2=ones(1,800); %x2是类似于[1 1 -1 -1 1 1 1 1]的分布,作用是控制相位的180°反转for i=1:tt1if (t1(i)>=0 & t1(i)<=2) | (t1(i)>=4& t1(i)<=8);x2(i)=1;else x2(i)=-1;endendf=0:0.1:1;xrc=0.5+0.5*cos(pi*f); %xrc是一个低通特性的传输函数y1=conv(x1,xrc)/5.5; %y1和x1 实际上没什么区别，仅仅是上升沿、下降沿有点过渡带y2=conv(x2,xrc)/5.5; % y2和x2 实际上没什么区别，仅仅是上升沿、下降沿有点过渡带n0=randn(size(t2));f1=1;i=x1.*cos(2*pi*f1*t); % x1就是I dataq=x2.*sin(2*pi*f1*t1); %x2就是Q dataI=i(101:800);Q=q(1:700);QPSK=sqrt(1/2).*I+sqrt(1/2).*Q;QPSK_n=(sqrt(1/2).*I+sqrt(1/2).*Q)+n0;n1=randn(size(t2));i_rc=y1.*cos(2*pi*f1*t3); % y1就是I data，i_rc可能是贴近实际的波形,i则是理想波形q_rc=y2.*sin(2*pi*f1*t4); %y2就是Q data，q_rc可能是贴近实际的波形,q则是理想波形I_rc=i_rc(101:800);Q_rc=q_rc(1:700);QPSK_rc=(sqrt(1/2).*I_rc+sqrt(1/2).*Q_rc);QPSK_rc_n1=QPSK_rc+n1;subplot(3,1,1);plot(t3,i_rc);axis([-1 8 -1 1]);ylabel('a序列');subplot(3,1,2);plot(t4,q_rc);axis([-1 8 -1 1]);ylabel('b序列');subplot(3,1,3);plot(t2,QPSK_rc);axis([-1 8 -1 1]);ylabel('合成序列');（2）QPSK解调程序clear allclose allbit_in = randint(1e3, 1, [0 1]);bit_I = bit_in(1:2:1e3); %bit_I为”奇数序列”，奇数序列是同相分量，以cos为载波bit_Q = bit_in(2:2:1e3); %bit_Q是bit_in的所有偶数下标组成的”偶数序列”，以sin为载波data_I = -2*bit_I+1; % 将bit_I中的1变成-1，0变成1; 注意data_I是500点data_Q = -2*bit_Q+1; %将bit_Q中的1变成-1，0变成1data_I1=repmat(data_I',20,1); %将500行的列向量data_I的共轭转置data_I’复制为20*500的矩阵，20行数据是相同的。

实验二__交错四相移相键控(OQPSK)调制及解调实验

实验二交错四相移相键控（OQPSK ）调制及解调实验一、实验目的1、了解OQPSK 调制解调原理及特性2、了解载波在QPSK 相干及非相干时的解调特性3、与QPSK 调制对比，掌握它们的差别二、实验内容1、观察I 、Q 两路基带信号的特征及与输入NRZ 码的关系。

2、观察IQ 调制解调过程中各信号变化。

3、观察QPSK 调制及OQPSK 调制各信号的区别。

4、观察解调载波相干时和非相干时各信号的区别。

三、基本原理OQPSK 又叫偏移四相相移键控，它是基于QPSK 的一类改进型，为了克服QPSK 中过零点的相位跃变特性，以及由此带来的幅度起伏不恒定和频带的展宽（通过带限系统后）等一系列问题。

若将QPSK 中并行的I ，Q 两路码元错开时间（如半个码元），称这类QPSK 为偏移QPSK 或OQPSK 。

通过I 、Q 两路码元错开半个码元调制之后的波形，其载波相位跃变由180°降至90°，避免了过零点，从而大大降低了峰平比和频带的展宽。

下面通过一个具体的例子说明某个带宽波形序列的I 路，Q 路波形，以及经载波调制以后相位变化情况。

若给定基带信号序列为`1 －1 －1 1 1 1 1 －1 －1 1 1 －1对应的QPSK 与OQPSK 发送波形如图2-1所示。

1-1-11111-1-111-1111-11-111-11-1-111-11-1基带波形I 信道QPSK,OQPSKQ 信道QPSK Q 信道OQPSK-1图2-1 QPSK,OQPSK 发送信号波形图2-1中，I 信道为奇数数据单元，Q 信道为偶数数据单元，而OQPSK 的Q 信道与其I 信道错开（延时）半个码元。

QPSK ，OQPSK 载波相位变化公式为{}()33arctan ,,,()4444j i ji Q t I t ππϕππ⎡⎤⎛⎫⎧⎫=--⎢⎥⎨⎬ ⎪⎩⎭⎢⎥⎝⎭⎣⎦ (2-1)QPSK 数据码元对应的相位变化如图2-2所示，OQPSK 数据码元对应相位变化如图2-3所示1)图2-2 QPSK 相位变化图图2-3 OQPSK 相位变化图对于QPSK 数据码元对的相位变换由图2-1和2-2求得为：(1,-1)(1,1)(1,-1)(1,-1)(-1,1)()4-()34()4()4-()34()4-2π-2π-πππ码元对相位及相位变化：可见，在QPSK中存在过零点的180°跃变。

QPSK调制解调实验

实验一QPSK 调制实验一、实验目的1、掌握QPSK 的调制解调原理。

2、掌握QPSK 的软件仿真方法。

3、掌握QPSK 的硬件设计方法。

二、预习要求1、掌握QPSK 的编解码原理和方法。

2、熟悉matlab 的应用和仿真方法。

3、熟悉DSP 和FPGA 的开发方法。

三、实验原理1、QPSK 调制的工作原理多相相移键控（MPSK ），特别是四相相移键控（QPSK ）是目前移动通信、微波通信和卫星通信中最常用的载波传输方式。

四相相移键控（QPSK ）信号的正弦载波有4个可能的离散相位状态，每个载波相位携带2个二进制符号，其信号表达式为：)cos()(i c i t A t S θω+= i ＝1，2，3，4 0≤t ≤TsTs 为四进制符号间隔，{i θ:i=1,2,3,4}为正弦波载波的相位，有四种可能状态。

如以下矢量图所示：如图为QPSK 的相位图，QPSK 的相位为（－3π/4，－π/4，π/4，3π/4）。

对于QPSK ：)sin cos cos (sin )sin()(i c i c i c i t t A t A t S θωθωθω+=+= 0≤t ≤Ts由于21cos ±=i θ 21s i n ±=i θ所以：)cos )(sin )((2)(t t Q t t I A t S c c i ωω+=21cos )(±==i t I θ21s i n )(±==i t Q θQPSK 正交调制器方框图如图所示：I图QPSK 正交调制器方框图在kTs ≤t ≤(k+1) Ts(Ts=2Tb)的区间，QPSK 产生器的输出为：⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧--=-+-=--+=+++=+=----11),43cos(11),4cos(11),43cos(11),4cos()(1111n n c n n c n n c n n c a a t A a a t A a a t A a a t A t s πωπωπωπω2、QPSK 的相干解调的基本工作原理 QPSK 的相干解调方框图如图所示：图QPSK 的相干解调方框图当调制信号为I ＝1，Q ＝1时，由调制原理，调制输出信号为t t t S c c i ωωcos sin )(+=，在没有噪声和延时的理想状态时，解调器的输入t t t S t r c c i ωωcos sin )()(+==，则I 检测器的输出为：t t t t t t r c c c c c ωωωωωsin cos sin sin sin )(+=t t t t c c c c ωωωω2sin 212cos 21212sin 21)2cos 1(21+-=+-=则Q 检测器的输出为：t t t t t t r c c c c c ωωωωωcos cos cos sin cos )(+=t t t t c c c c ωωωω2sin 212cos 21212sin 21)2cos 1(21++=++=用截止频率小于2c ω的低通滤波器对I 检测器的输出滤波后得到1/2,即为逻辑1；对Q 检测器的输出滤波后得到1/2,即为逻辑1。

0QPSK调制解调实验报告

0QPSK调制解调实验报告一、实验目的1．掌握0QPSK调制解调原理。

2．理解0QPSK的优缺点。

二、实验内容1．观察0QPSK调制过程各信号波形。

2．观察0QPSK解调过程各信号波形。

三、预备知识1．0QPSK调制解调的基本原理。

2. 0QPSK调制解调模块的工作原理及电路说明。

四、实验器材1. 移动通信原理实验箱。

2．20M数字双踪示波器。

五、实验原理0QPSK调制解调原理0QPSK又叫四相相移键控，它通QPSK的不同之处是在正交支路引入了一个码元（Ts）的延时，这使得两个支路的数据错开了一个码元时间，不会同时发生变化，而不像QPSK那样产生±π的相位跳变，而仅能产生±π/2的相位跳变，如图4-1所示。

从图4-1星座图和相位转移图中看出对于1QPSK，±π相位的跳变消除了，所以1QPSK 信号的带限不会导致信号包络经过零点。

0QPSK包络的变化小多了，因此对1QPSK的硬限幅或非线性放大不会再产生严重的频带扩展，0QPSK即使在非线性放大后仍能保持其带限的性质。

0QPSK的调制方法和QPSK一样。

图4-1 QPSK和0QPSK的星座图和相位转移图1)六、实验步骤1.A 方式的0QPSK 调制实验（1）将“调制类型选择”拨码开关拨为00001000、0001，则调制类型选择为A 方式的0QPSK 调制。

（2）分别观察并说明NRZ 码经串并转换得到的‘DI ’、‘DQ ’两路的一个周期的数据波形。

CH1:NRZCH2:DI CH1:NRZ CH2:DQ（3）双踪观察并分析说明‘DI ’与‘I 路成形’信号波形；‘DQ ’与‘Q 路成形’信号波形；CH1:DI CH2: I路成形CH1:DQ CH2: Q路成形（4）双踪观察并分析说明‘I路成形’信号波形与‘I路调制’同相调制信号波形；‘Q路成形’信号与‘Q路调制’正交调制信号波形。

CH1: I路成形CH2: I路调制CH1: Q路成形CH2: Q路调制（5）用示波器观察并说明‘I路成形’信号与‘Q路成形信号的X-Y波形。

QPSK、DQPSK系统调制与解调

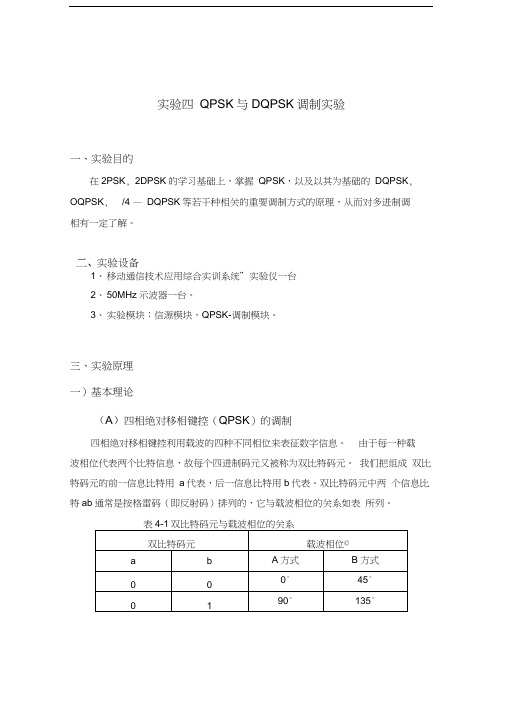
实验四QPSK与DQPSK调制实验一、实验目的在2PSK, 2DPSK的学习基础上，掌握QPSK，以及以其为基础的DQPSK, OQPSK, /4 —DQPSK等若干种相关的重要调制方式的原理，从而对多进制调相有一定了解。

1、移动通信技术应用综合实训系统”实验仪一台2、50MHz示波器一台。

3、实验模块：信源模块，QPSK-调制模块。

三、实验原理一）基本理论（A）四相绝对移相键控（QPSK）的调制四相绝对移相键控利用载波的四种不同相位来表征数字信息。

由于每一种载波相位代表两个比特信息，故每个四进制码元又被称为双比特码元。

我们把组成双比特码元的前一信息比特用a代表，后一信息比特用b代表。

双比特码元中两个信息比特ab通常是按格雷码（即反射码）排列的，它与载波相位的关系如表所列。

双比特码元载波相位©a b A方式B方式000°45°0190°135°实验设备由于四相绝对移相调制可以看作两个正交的二相绝对移相调制的合成，故两者的功率谱密度分布规律相同。

下面我们来讨论QPSK信号的产生与解调。

QPSK信号的产生方法与2PSK 信号一样，也可以分为调相法和相位选择法。

(1) 调相法用调相法产生QPSK信号的组成方框图如下所示图4-1 QPSK信号的组成方框图设两个序列中的二进制数字分别为a和b,每一对ab称为一个双比特码元。

并设经过串并变换后上支路为a,下支路为b。

双极性的a和b脉冲通过两个平衡调制器分别对同相载波及正交载波进行二相调制。

表4-2 QPSK信号相位编码逻辑关系(2) 相位选择法用相位选择法产生QPSK信号的组成方框图如下所示图4-2相位选择法产生QPSK信号方框图(B)四相相对移相键控(DQPSK)的调制所谓四相相对移相键控也是利用前后码元之间的相对相位变化来表示数字信息。

若以前一码元相位作为参考，并令△©为本码元与前一码元的初相差。

MATLAB_QPSK调制与解调

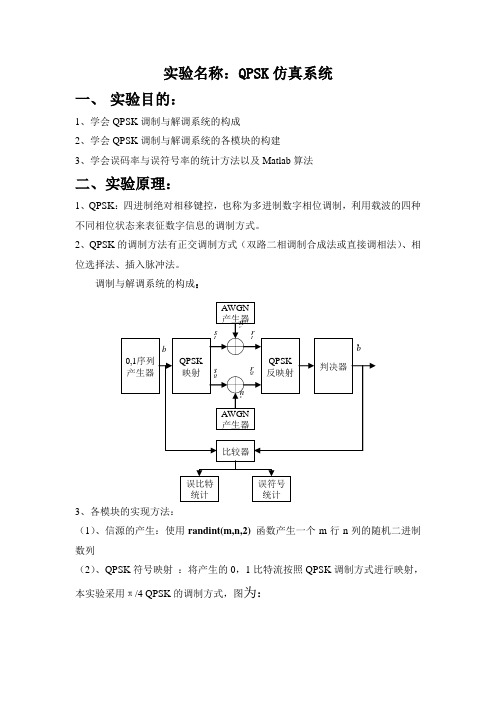
实验名称：QPSK仿真系统一、实验目的：1、学会QPSK调制与解调系统的构成2、学会QPSK调制与解调系统的各模块的构建3、学会误码率与误符号率的统计方法以及Matlab算法二、实验原理：1、QPSK：四进制绝对相移键控，也称为多进制数字相位调制，利用载波的四种不同相位状态来表征数字信息的调制方式。

2、QPSK的调制方法有正交调制方式（双路二相调制合成法或直接调相法）、相位选择法、插入脉冲法。

调制与解调系统的构成：3、各模块的实现方法：（1）、信源的产生：使用randint(m,n,2)函数产生一个m行n列的随机二进制数列（2）、QPSK符号映射：将产生的0，1比特流按照QPSK调制方式进行映射，本实验采用π/4 QPSK的调制方式，图为：（3）、AWGN 信号产生：AWGN 产生器就是产生满足均值为0，方差为1的高斯白噪声。

实验中使用randn(m,n)函数产生一个m 行n 列的高斯噪声序列。

（4）、信号幅度控制：根据AWGN 信道模型，接收信号可以分别表示为α就是当噪声功率归一化为1（0均值，方差为1）时，根据信噪比关系而计算出来的信号平均幅度（5）、QPSK 反映射及判决：对接收到的信号在4种可能的四种信号向量[(1,0), (0,1), (-1,0), (0,-1)]上投影(即进行点积)。

投影最大的值所对应的信号向量就是所发送信号的符号值，然后恢复出比特流（6）、误码率及误符号率统计：误码率：将检测出来的比特流和发送的原始比特流进行比较，统计出出现错误的比特数误符号率：将检测出来的比特流变成两组，构成符号，和发送端符号映射后的符号流进行比较，只要符号中任错一bit ，就算该符号出错。

统计出现错误的符号数三、实验内容：1、调制与解调I I Ir s n α=+Q Q Qr s n α=+22210log 10^10s s n n v SNR SNR v sqrt v v ⎛⎫⎛⎫⎛⎫=⇒=* ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭s v α=clear allclose all% 调制bit_in = randint(1e3, 1, [0 1]);bit_I = bit_in(1:2:1e3);bit_Q = bit_in(2:2:1e3);data_I = -2*bit_I+1;data_Q = -2*bit_Q+1;data_I1=repmat(data_I',20,1);data_Q1=repmat(data_Q',20,1);for i=1:1e4data_I2(i)=data_I1(i);data_Q2(i)=data_Q1(i);end;f=0:0.1:1;xrc=0.5+0.5*cos(pi*f);data_I2_rc=conv(data_I2,xrc)/5.5;data_Q2_rc=conv(data_Q2,xrc)/5.5;f1=1;t1=0:0.1:1e3+0.9;n0=rand(size(t1));I_rc=data_I2_rc.*cos(2*pi*f1*t1);Q_rc=data_Q2_rc.*sin(2*pi*f1*t1); QPSK_rc=(sqrt(1/2).*I_rc+sqrt(1/2).*Q_rc); QPSK_rc_n0=QPSK_rc+n0;% 解调I_demo=QPSK_rc_n0.*cos(2*pi*f1*t1);Q_demo=QPSK_rc_n0.*sin(2*pi*f1*t1);% 低通滤波I_recover=conv(I_demo,xrc);Q_recover=conv(Q_demo,xrc);I=I_recover(11:10010);Q=Q_recover(11:10010);t2=0:0.05:1e3-0.05;t3=0:0.1:1e3-0.1;% 抽样判决data_recover=[];for i=1:20:10000data_recover=[data_recover I(i:1:i+19) Q(i:1:i+19)];end;bit_recover=[];for i=1:20:20000if sum(data_recover(i:i+19))>0data_recover_a(i:i+19)=1;bit_recover=[bit_recover 1];elsedata_recover_a(i:i+19)=-1;bit_recover=[bit_recover -1];endenderror=0;dd = -2*bit_in+1;ddd=[dd'];ddd1=repmat(ddd,20,1);for i=1:2e4ddd2(i)=ddd1(i);endfor i=1:1e3if bit_recover(i)~=ddd(i)error=error+1;endendp=error/1000;figure(1)subplot(2,1,1);plot(t2,ddd2);axis([0 100 -2 2]);title('原序列');subplot(2,1,2);plot(t2,data_recover_a);axis([0 100 -2 2]);title('解调后序列');2、误码率仿真% QPSK误码率分析SNRindB1=0:2:10;SNRindB2=0:0.1:10;for i=1:length(SNRindB1)[pb,ps]=cm_sm32(SNRindB1(i));smld_bit_err_prb(i)=pb;smld_symbol_err_prb(i)=ps;end;for i=1:length(SNRindB2)SNR=exp(SNRindB2(i)*log(10)/10);theo_err_prb(i)=Qfunct(sqrt(2*SNR)); end;title('QPSK误码率分析');semilogy(SNRindB1,smld_bit_err_prb,'*');axis([0 10 10e-8 1]);hold on;% semilogy(SNRindB1,smld_symbol_err_prb,'o'); semilogy(SNRindB2,theo_err_prb);legend('仿真比特误码率','理论比特误码率'); hold off;function[y]=Qfunct(x)y=(1/2)*erfc(x/sqrt(2));function[pb,ps]=cm_sm32(SNRindB)N=10000;E=1;SNR=10^(SNRindB/10);sgma=sqrt(E/SNR)/2;s00=[1 0];s01=[0 1];s11=[-1 0];s10=[0 -1];for i=1:Ntemp=rand;if (temp<0.25)dsource1(i)=0;dsource2(i)=0;elseif (temp<0.5)dsource1(i)=0;dsource2(i)=1;elseif (temp<0.75)dsource1(i)=1;dsource2(i)=0;elsedsource1(i)=1;dsource2(i)=1;end;end;numofsymbolerror=0;numofbiterror=0;for i=1:Nn=sgma*randn(size(s00));if((dsource1(i)==0)&(dsource2(i)==0))r=s00+n;elseif((dsource1(i)==0)&(dsource2(i)==1)) r=s01+n;elseif((dsource1(i)==1)&(dsource2(i)==0)) r=s10+n;elser=s11+n;end;c00=dot(r,s00);c01=dot(r,s01);c10=dot(r,s10);c11=dot(r,s11);c_max=max([c00 c01 c10 c11]);if (c00==c_max)decis1=0;decis2=0;elseif(c01==c_max)decis1=0;decis2=1;elseif(c10==c_max)decis1=1;decis2=0;elsedecis1=1;decis2=1;end;symbolerror=0;if(decis1~=dsource1(i))numofbiterror=numofbiterror+1;symbolerror=1;end;if(decis2~=dsource2(i))numofbiterror=numofbiterror+1;symbolerror=1;end;if(symbolerror==1)numofsymbolerror=numofsymbolerror+1;end;end;ps=numofsymbolerror/N;pb=numofbiterror/(2*N);3、QPSK在AWGN信道下的仿真close allclcclear allSNR_DB=[0:1:12];sum=1000000;data= randsrc(sum,2,[0 1]);[a1,b1]=find(data(:,1)==0&data(:,2)==0);message(a1)=-1-j;[a2,b2]=find(data(:,1)==0&data(:,2)==1);message(a2)=-1+j;[a3,b3]=find(data(:,1)==1&data(:,2)==0);message(a3)=1-j;[a4,b4]=find(data(:,1)==1&data(:,2)==1);message(a4)=1+j;scatterplot(message)title('B点信号的星座图')A=1;Tb=1;Eb=A*A*Tb;P_signal=Eb/Tb;NO=Eb./(10.^(SNR_DB/10));P_noise=P_signal*NO;sigma=sqrt(P_noise);for Eb_NO_id=1:length(sigma)noise1=sigma(Eb_NO_id)*randn(1,sum);noise2=sigma(Eb_NO_id)*randn(1,sum);receive=message+noise1+noise2*j;resum=0;total=0;m1=find(angle(receive)<=pi/2&angle(receive)>0);remessage(1,m1)=1+j;redata(m1,1)=1;redata(m1,2)=1;m2= find( angle(receive)>pi/2&angle(receive)<=pi);remessage(1,m2)=-1+j;redata(m2,1)=0;redata(m2,2)=1;m3=find( angle(receive)>-pi&angle(receive)<=-pi/2);remessage(1,m3)=-1-j;redata(m3,1)=0;redata(m3,2)=0;m4=find( angle(receive)>-pi/2&angle(receive)<=0);remessage(1,m4)=1-j;redata(m4,1)=1;redata(m4,2)=0;[resum,ratio1]=symerr(data,redata);pbit(Eb_NO_id)=resum/(sum*2);[total,ratio2]=symerr(message,remessage);pe(Eb_NO_id)=total/sum;endscatterplot(receive)title('C点信号的星座图')Pe=1-(1-1/2*erfc(sqrt(10.^(SNR_DB/10)/2))).^2;Pbit=1/2*erfc(sqrt(10.^(SNR_DB/10)/2));figure(3)semilogy(SNR_DB,pe,':s',SNR_DB,Pe,'-*',SNR_DB,pbit,'-o',SNR_DB,Pbit,':+')legend('QPSK仿真误码率','QPSK理论误码率','QPSK仿真误比特率','QPSK理论误比特率',1) xlabel('信噪比/dB')ylabel('概率P')gird on结果：4、QPSK在AWGN信道下的性能检测clear all;%对随机序列产生的方法初始化s = RandStream('mt19937ar','Seed', 5489);RandStream.setDefaultStream(s);s = RandStream('mcg16807', 'Seed',0);RandStream.setDefaultStream(s);N = 10^5; %码元数Eb_N0 = -4:20; %Eb/N0比特信噪比s_data = zeros(1,N);ErrorCount=zeros(1,length(Eb_N0)); %预先分配内存，用于记录错误的码元数for j = 1:length(Eb_N0)p = (2*(rand(1,N)>0.5)-1) + 1i*(2*(rand(1,N)>0.5)-1);s = (1/sqrt(2))*p; %归一化n = 10^(-Eb_N0(j)/40)*1/sqrt(2)*(randn(1,N) + 1i*randn(1,N)); %加性高斯白噪声r = s + n;%解调r_re = real(r); %实部r_im = imag(r); %虚部s_data(r_re < 0 & r_im < 0) = -1 + -1*1i;s_data(r_re >= 0 & r_im > 0) = 1 + 1*1i;s_data(r_re < 0 & r_im >= 0) = -1 + 1*1i;s_data(r_re >= 0 & r_im < 0) = 1 - 1*1i;ErrorCount(j) = size(find(p- s_data),2); %错误的码元数endsim_QPSK = ErrorCount/N;theory_QPSK = erfc(sqrt(0.5*(10.^(Eb_N0/20)))) -(1/4)*(erfc(sqrt(0.5*(10.^(Eb_N0/20))))).^2;close allfiguresemilogy(Eb_N0,theory_QPSK,'b.-');hold onsemilogy(Eb_N0,sim_QPSK,'mx-');axis([-4 20 10^-3 1])grid on。

移动通信原理实验 OQPSK调制解调实验

课程名称移动通信原理
实验序号实验二
实验项目OQPSK调制解调实验实验地点
实验学时实验类型验证性专业班级
学号姓名
年月日
五、测试/调试及实验结果分析
图中从上到下四种颜色分别表示：测试点TP201测试输入的基带数据波形，测试点TP202测试发送的I路数据，在测试点TP203测试发送的Q路数据，测试点TP308测试的OQPSK调制波形。

可以得出输入的基带信号、I路信号和Q路信号一周期的码元序列如下：
基带：0 0 1 1 0 1 0 1 0 0 1 0 1 0 1 1
I路：0 1 0 0 0 1 1 1
Q路：0 1 1 1 0 0 0 1
I路数据是基带数据的奇数码元，Q路数据是基带数据的偶数码元，经验证数据无误。

但从图1的波形可以看到Q路信号没有发生错位偏移TS/2。

由上图，可以清晰看到OQPSK调制波形。

从波形可以看到正交支路信号偏移TS/2后，调制波形在每个TS/2信号只发生±/2的变化。

图中从上到下两种颜色分别表示：TP204测试接收的I路解调波形，TP205测试接收的Q路解调波形，I路的码元序列为：01000111
Q路解调不出波形。

解调后的I路和输入的I路一周期数据一致，但是Q路解调失败。

实验一 QPSK调制解调实验

实验一 QPSK 调制解调实验一、实验目的1. 了解QPSK 调制和解调的基本原理； 2．熟悉软件完成QPSK 的过程。

二、实验内容1．熟悉QPSK 调制和解调过程； 2．通过示波器测试QPSK 各点的波形；3*.设计一个通过DSP 程序完成QPSK 的程序，加强对QPSK 的理解。

三、实验原理BPSK 是用两种相位(0, π)来表示两种信息，而四相移相键控（QPSK ）是利用载波的四个不同相位来表征数字信息，每一个载波相位代表两个比特的信息。

因此对于输入的二进制数字序列应该先进行分组。

将每两个比特编为一组，采用相应的相位来表示。

当初始相位取0时，四种不同的相位为：0,π/2,π,3π/2 分别表示数字信息：11、01、00、10；当初始相位为4/π时，四种不同的相位为：4/π、4/3π、4/5π、4/7π分别表示11、01、00、10。

这两种QPSK 信号可以通过图4-9-1的矢量图来表征。

(a) 初始相位为0(b) 初始相位为л/4图4-9-1 QPSK 信号的矢量图表示QPSK 信号可以表示为：t T Q t t I t e ωωsin )(cos )()(0-=，其中I (t )称为同相分量，Q (t )称为正交分量。

根据上式可以得到QPSK 正交调制器的方框图，如图4-9-2所示。

图4-9-2 QPSK 系统调制器原理框图从图4-9-2可以看出，QPSK 调制器可以看作为两个BPSK 调制器构成，输入的二进制信息序列经过串并转换，分成两路速率减半的序列I (t )和Q (t )，然后对t ωcos 和t ωsin 进行调制，相加后即可得到QPSK 信号。

经过串并变换之后的两个支路，一路为单数码元，另一路是偶数码元，这两个支路为正交，一个称为同相支路，即I 支路，另一个称为正交支路，即Q 支路。

QPSK 信号可以采用两个正交的载波信号实现相干解调。

通过载波恢复电路，产生相干载波，分别将同相载波和正交载波提供给同相支路和正交支路的相关器，经过积分、判决和并串转换，即可恢复原来的二进制信息。

QPSK调制解调实验报告

QPSK调制解调实验报告一、实验目的1．把握QPSK调制解调原理。

2．明白得QPSK的优缺点。

二、实验内容1．观看QPSK调制进程各信号波形。

2．观看QPSK解调进程各信号波形。

三、预备知识1．QPSK调制解调的大体原理。

2. QPSK调制解调模块的工作原理及电路说明。

四、实验器材1. 移动通信原理实验箱。

2．20M数字双踪示波器。

五、实验原理1.QPSK调制原理QPSK又叫四相绝对相移调制，QPSK利用载波的四种不同相位来表征数字信息。

由于每一种载波相位代表两个比特信息，故每一个四进制码元又被称为双比特吗元。

咱们把组成双比特码元的前一信息比特用a代表，后一信息比特用b代表。

双比特码元中两个信息比特ab一般是依照格雷码排列的，它与载波相位的关系如表3-1所示，矢量关系如图3-1所示。

图（a）表示A方式的QPSK信号矢量图，图（b）表示B方式的QPSK信号矢量图。

用调相发产生QPSK调制原理框图如下图：解调原理由于QPSK能够看做诗两个正交2PSK信号的合成，故它能够采纳与2PSK信号类似的解调方式进行解调，即由两个2PSK信号相干解调器组成，其原理框图如下图：六．实验步骤方式的QPSK调制实验（1）将“调制类型选择”拨码开关拨为00010000、0001，那么调制类型选择为A方式的QPSK 调制。

（2）别离观看并说明NRZ码经串并转换取得的‘DI’、‘DQ’两路的一个周期的数据波形。

CH1:NRZ CH2:DI CH1:NRZ CH2:DQ（3）双踪观看并分析说明‘DI’与‘I路成型’信号波形；‘DQ’与‘Q路成型’信号波形；CH1:DI CH2:I路成形 CH1:DQ CH2:Q路成形（4）双踪观看并分析说明‘I路成形’信号波形与‘I路调制’同相调制信号波形；‘Q路成形’信号与‘Q路调制’正交调制信号波形。

CH1: I路成形 CH2: I路调制CH1: Q路成形 CH2: Q路调制（5）用示波器观看并说明‘I路成形’信号与‘Q路成形信号的X-Y波形。

交错四相移相键控调制解调实验结果分析

交错四相移相键控调制解调实验结果分析
交错四相移相键控调制（QPSK）是数字调制技术中的一种常见形式，它可以在同样的带宽和信噪比条件下传输比二进制相移键控调制（BPSK）更多的信息。

QPSK调制器将两个BPSK 调制器的输出信号进行交错，并通过四相移相器将I、Q分量同时进行相移，从而生成QPSK 信号。

QPSK解调器则是将接收到的QPSK信号分别进行相移，从而分离出两个BPSK信号，再进行解调。

在实验室中，可以通过对QPSK信号进行采样和解调来验证QPSK调制器和解调器的性能。

实验需要使用信号发生器来生成QPSK信号，并通过传输信道将其发送到接收端。

接收端需要使用混频器将接收到的信号与本地载波进行混频，再进行低通滤波和采样，最后通过解调器进行解调。

实验结果的分析可以从以下几个方面入手：
1. BER性能：通过不同信噪比下的误码率测试，可以分析QPSK调制器和解调器的BER性能，了解其在不同信噪比下的性能表现。

2. 符号误差率：通过对采样点进行比较，可以分析符号误差率，了解QPSK调制器和解调器在发送和接收过程中可能存在的误差。

3. 误码分析：通过对接收到的信号进行解调和解码，可以分析误码率及误码类型，了解误码率高发生错误的原因，有利于调整技术参数。

4. 相位误差分析：通过比较接收信号的相位与本地载波的相位，可以分析QPSK调制器和解调器的相位误差，从而确定误差源并加以改进。

5. 传输速率：通过计算QPSK信号的传输速率，了解该技术对传输速率的影响和局限。

QPSK 调制解调

四相绝对相移键控 QPSK是属于多进制数字相位调制，它是利用载波的四种不同相位来表征输入的数字信息。目前广泛应用于数字微波通信系统，数字卫星通信系统，宽带接入与移动通信，以及有线电视的上行传输。但四相相移键控信号，在码元交替处的载波相位往往是突变的，当相邻的两个码元同时转换时，会出现±π的相位跳变，这会使调相波的包络上出现零（交）点，其信号功率谱上将产生很强的旁瓣分量。因此从 QPSK方式派生出一种新的相位调制方式，交错四相相移键控（OQPSK）。即在 QPSK调制的正交支路上引入一个比特（半个码元）的时延，使得两个支路的数据不会同时发生变化，从而不可能产生±π的相位跳变，仅产±π/2的相位跳变。
关键词: 相移键控四相移键控 QPSK调制相干解调
I
×××大学本科毕业设计
QPSK Demodulation Experimental Design
Abstract：Indigitalcommunication，weoftenmodulatanddemodulat digital
signalbyFSKandPSKtotransmitdigitalinformation。 Nowadays，PSKoftenuse QPSK and NPSK. Any digital modulation scheme uses a finite number of distinct signals to represent digital data. PSK uses a finite number of phases, each assigned a unique pattern of binary digits. Usually, each phase encodes an equal number of bits. Each pattern of bits forms the symbol that is represented by the particular phase. The demodulator, which is designed specifically for the symbol-set used by the modulator, determines the phase of the received signal and maps it back to the symbol it represents, thus recovering the original data. This requires the receiver to be able to compare the phase of the received signal toareferencesignal— suchasystemistermedcoherent(andreferredtoas CPSK). This text is detailed on the concept,implement and principle of QPSK. It also detailed introduces the designedand realize of QPSK.

QPSK调制解调实验.doc

实验一QPSK 调制实验一、实验目的1、掌握QPSK 的调制解调原理。

2、掌握QPSK 的软件仿真方法。

3、掌握QPSK 的硬件设计方法。

二、预习要求1、掌握QPSK 的编解码原理和方法。

2、熟悉matlab 的应用和仿真方法。

3、熟悉DSP 和FPGA 的开发方法。

如以下矢量图所示：如图为QPSK 的相位图，QPSK 的相位为（－3π/4，－π/4，π/4，3π/4）。

对于QPSK ：)sin cos cos (sin )sin()(i c i c i c i t t A t A t S θωθωθω+=+= 0≤t ≤Ts由于21cos ±=i θ 21sin ±=i θ所以：)cos )(sin )((2)(t t Q t t I A t S c c i ωω+=21cos )(±==i t I θ21sin )(±==i t Q θQPSK 正交调制器方框图如图所示：I图QPSK 正交调制器方框图在kTs ≤t ≤(k+1) Ts(Ts=2Tb)的区间，QPSK 产生器的输出为：⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧--=-+-=--+=+++=+=----11),43c os(11),4c os(11),43c os(11),4c os()(1111n n c n n c n n c n n c a a t A a a t A a a t A a a t A t s πωπωπωπω2、QPSK 的相干解调的基本工作原理 QPSK 的相干解调方框图如图所示：图QPSK 的相干解调方框图当调制信号为I ＝1，Q ＝1时，由调制原理，调制输出信号为tt t S c c i ωωcos sin )(+=，在没有噪声和延时的理想状态时，解调器的输入tt t S t r c c i ωωcos sin )()(+==，则I 检测器的输出为：tt t t t t r c c c c c ωωωωωsin cos sin sin sin )(+=t t t t c c c c ωωωω2sin 212cos 21212sin 21)2cos 1(21+-=+-=则Q 检测器的输出为：tt t t t t r c c c c c ωωωωωcos cos cos sin cos )(+=t t t t c c c c ωωωω2sin 212cos 21212sin 21)2cos 1(21++=++=用截止频率小于2c ω的低通滤波器对I 检测器的输出滤波后得到1/2,即为逻辑1；对Q 检测器的输出滤波后得到1/2,即为逻辑1。

QPSK调制解调试验报告

QPSK调制解调试验报告0QPSK调制解调实验报告一、实验目的1.掌握0QPSK调制解调原理。

2.理解0QPSK的优缺点。

二、实验内容1.观察0QPSK调制过程各信号波形。

2.观察0QPSKB调过程各信号波形。

三、预备知识1..0QPSK调制解调的基本原理。

2.0QPSK调制解调模块的工作原理及电路说明。

四、实验器材1,移动通信原理实验箱。

3字双踪示波器。

五、实验原理0QPSK调制解调原理0QPSK又叫四相相移键控，它通QPSK的不同之处是在正交支路引入了一个码元（TS）的延时，这使得两个支路的数据错开了一个码元时间，不会同时发生变化，而不像QPSK那样产生土兀的相位跳变，而仅能产生土兀/2的相位跳变，如图41星座图和相位转移图中看出对1QPSK兀相位的跳变消除了，所以1QPSK信号的带限不会导致信号包络经过零点。

0QPSK包络的变化小多了，因此对1QPSK的硬限幅或非线性放大不会再产生严重的频带扩展，0QPSK即使在非线性放大后仍能保持其带限的性质。

0QPSK 的调制方法和QPSK一样。

图41+100信道六、实验步骤1.A方式的0QPS颁制实验(1)将“调制类型选择”拨码开关拨为000XXXX1000、0001,则调制类型选择为A方式的0QPSK调制。

(2)分别观察并说明NRZ码经串并转换得到的D、DQ两路的一个周期的数据波形。

CH1:NRZCH2:DCH1:NRZCH2:DQ(3)双踪观察并分析说明D与路成形信号波形；DQ与Q路成形信号波形;CH1:DCH2:路成形CH1:DQCH2:Q路成形(4)双踪观察并分析说明路成形信号波形与路调制同相调制信号波形；Q路成形信号与Q路调制正交调制信号波形。

CH1:路成形CH2:路调制(5)用示波器观察并说明路成形信号与图进行比较说明。

CH1:Q路成形CH2:Q路调制Q路成形t号的_Y波形，分析并说明与A方式的星座图有什么不同。

3.A方式的0QPSKB调实验(1)将“调制类型选择”拨码开关拨为000XXXX1000、0100,“解调类型选择”拨码开关拨为000XXXX1000、0100,则解调类型选择为A方式的0QPSK解调。