常用符号的英文名称
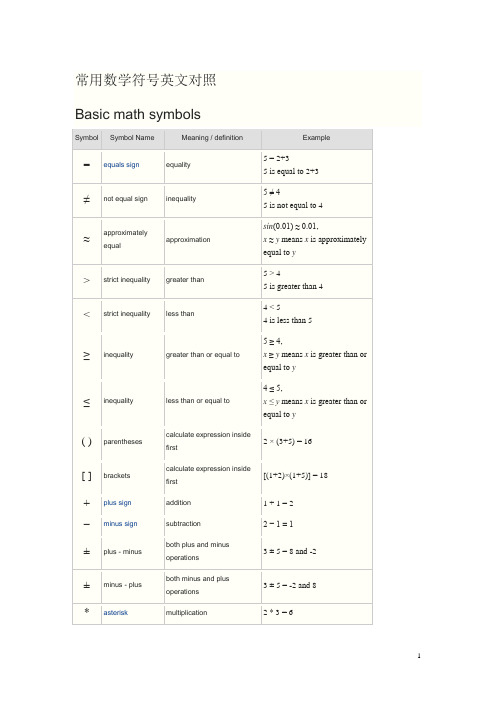
常用数学符号英文对照

常用数学符号英文对照Basic math symbolsSymbol Symbol Name Meaning / definition Example= equals sign equality 5 = 2+35 is equal to 2+3≠not equal sign inequality 5 ≠ 45 is not equal to 4≈approximatelyequal approximationsin(0.01) ≈ 0.01,x≈y means x isapproximately equal to y> strictinequality greater than5 > 45 is greater than 4< strictinequality less than4 < 54 is less than 5≥inequality greater than or equal to 5 ≥ 4,x≥y means x is greater than or equal to y≤inequality less than or equal to 4 ≤ 5,x ≤ y means x is greater than or equal to y( ) parentheses calculate expressioninside first2 × (3+5) = 16[ ] brackets calculate expressioninside first[(1+2)×(1+5)] = 18 + plus sign addition 1 + 1 = 2−minus sign subtraction 2 − 1 = 1±plus - minus both plus and minusoperations3 ± 5 = 8 and -2±minus - plus both minus and plusoperations3 ± 5 = -2 and 8* asterisk multiplication 2 * 3 = 6×times sign multiplication 2 × 3 = 6·multiplicationdotmultiplication 2 · 3 = 6÷division sign /obelusdivision 6 ÷ 2 = 3/ division slash division 6 / 2 = 3–horizontal line division / fractionmod modulo remainder calculation 7 mod 2 = 1. period decimal point, decimalseparator2.56 = 2+56/100a b power exponent 23= 8a^b caret exponent 2 ^ 3= 8√a square root √a ·√a = a√9 = ±33√a cube root 3√a ·3√a ·3√a = a3√8 = 24√a fourth root 4√a ·4√a ·4√a ·4√a =a4√16 = ±2n√a n-th root(radical)for n=3, n√8 = 2 % percent1% = 1/100 10% × 30 = 3‰per-mille1‰ = 1/1000 = 0.1% 10‰× 30 = 0.3 ppm per-million1ppm = 1/1000000 10ppm × 30 = 0.0003 ppb per-billion 1ppb = 1/1000000000 10ppb × 30 = 3×10-7Geometry symbolsSymbolSymbol NameMeaning / definitionExample∠angle formed by two rays ∠ABC = 30°measured angle ABC = 30°sphericalangleAOB = 30°∟ right angle = 90° α = 90°°degree 1 turn = 360° α = 60° degdegree1 turn = 360degα = 60deg ′ primearcminute, 1° = 60′α = 60°59′″double prime arcsecond, 1′ = 60″ α = 60°59′59″line infinite lineABline segment line from point A to point Bray line that start from point Aarc arc from point A to point B= 60°⊥ perpendicular perpendicular lines (90° angle) AC ⊥ BC| | parallel parallel lines AB | | CD≅ congruent toequivalence of geometric shapes and size∆ABC ≅ ∆XYZ~similarity same shapes, not same size ∆ABC~ ∆XYZΔtriangle triangle shape ΔABC≅ΔBCD |x-y| distance distance between points x and y | x-y| = 5πpi constant π= 3.141592654...is the ratio between the circumferenceand diameter of a circlec= π·d=2·π·rrad radians radians angle unit 360° = 2π rad c radians radians angle unit 360° = 2πcgrad gradians /gonsgrads angle unit 360° = 400 gradggradians /gonsgrads angle unit 360° = 400 gAlgebra symbolsSymbol Symbol Name Meaning / definition Examplex x variable unknown value to find when 2x= 4, then x= 2 ≡equivalence identical to≜equal by definition equal by definition:= equal by definition equal by definition~ approximately equal weak approximation 11 ~ 10≈approximately equal approximation sin(0.01) ≈ 0.01∝proportional to proportional to y∝x when y= kx,k constant ∞lemniscate infinity symbol≪much less than much less than 1 ≪ 1000000≫much greater than much greater than 1000000 ≫ 1( ) parentheses calculate expressioninside first2 * (3+5) = 16[ ] brackets calculate expressioninside first[(1+2)*(1+5)] = 18 { } braces set⌊x⌋floor brackets rounds number to lowerinteger⌊ 4.3⌋ = 4⌈x⌉ceiling brackets rounds number to upperinteger⌈ 4.3⌉ = 5x! exclamation mark factorial4! = 1*2*3*4 = 24 | x|single vertical bar absolute value | -5 | = 5f (x) function of x maps values of x to f(x) f (x) = 3x+5(f∘g) function composition(f∘g) (x)= f (g(x))f (x)=3x,g(x)=x-1 ⇒(f∘g)(x)=3(x-1)(a,b) open interval (a,b) ={x| a< x< b}x∈ (2,6)[a,b] closed interval [a,b] ={x| a≤x≤b}x∈ [2,6]∆delta change / difference ∆t= t1 -t0∆discriminant Δ = b2- 4ac∑sigma summation - sum of allvalues in range of series∑x i= x1+x2+...+x n∑∑sigma double summation∏capital piproduct - product of all values in range of series∏ x i =x 1∙x 2∙...∙x nee constant / Euler's numbere = 2.718281828... e = lim (1+1/x )x , x →∞γ Euler-Mascheroni const antγ = 0.527721566...φgolden ratio golden ratio constantπpi constantπ = 3.141592654...is the ratio between the circumference and diameter of a circlec = π·d = 2·π·rLinear Algebra SymbolsSymbolSymbol NameMeaning / definitionExample· dot scalar producta ·b ×cross vector producta ×b A ⊗Btensor product tensor product of A and BA ⊗ Binner product[ ] brackets matrix of numbers( ) parentheses matrix of numbers| A | determinant determinant of matrix Adet(A )determinant determinant of matrix A|| x || double vertical bars normA Ttranspose matrix transpose(A T)ij = (A )jiProbability and statistics symbols Symbol Symbol Name Meaning / definition Example P(A) probabilityfunctionprobability of event A P(A) = 0.5P(A∩B) probability ofeventsintersectionprobability that of events Aand BP(A∩B) = 0.5P(A∪B) probability ofevents union probability that of events Aor BP(A∪B) = 0.5P(A| B) conditionalprobabilityfunctionprobability of event A givenevent B occuredP(A | B) = 0.3f (x) probabilitydensityfunction (pdf)P(a ≤x ≤b)= ∫ f (x)dxF(x) cumulativedistributionfunction (cdf)F(x) = P(X≤x)μpopulation mean mean of population values μ= 10E(X) expectationvalue expected value of randomvariable XE(X) = 10E(X | Y) conditionalexpectation expected value of randomvariable X given YE(X | Y=2) = 5var (X )variancevariance of random variable Xvar (X ) = 4σ2variance variance of population valuesσ2 = 4std (X )standard deviation standard deviation of random variable Xstd (X ) = 2σX standard deviationstandard deviation value of random variable X σX = 2medianmiddle value of random variable xcov (X ,Y ) covariancecovariance of random variables X and Y cov (X,Y ) = 4corr (X ,Y ) correlationcorrelation of random variables X and Y corr (X,Y ) = 0.6ρX ,Ycorrelationcorrelation of random variables X and YρX ,Y= 0.6∑summationsummation - sum of all values in range of series∑∑double summationdouble summationMo mode value that occurs most frequently in populationMR mid-rangeMR = (x max +x min )/2Mdsample median half the population is below this valueQ 1lower / first quartile25% of population are below this valueQ 2median / second quartile50% of population are below this value = median of samplesQ3upper / thirdquartile 75% of population are below this valuex sample mean average / arithmetic mean x= (2+5+9) / 3 = 5.333s2sample variance population samples varianceestimators2= 4s sample standarddeviation population samples standard deviation estimators= 2z x standard score z x= (x-x) /s xX ~ distribution of X distribution of randomvariable XX ~N(0,3)N(μ,σ2) normaldistributiongaussian distribution X ~N(0,3)U(a,b) uniformdistributionequal probability in rangea,bX ~U(0,3)exp(λ) exponentialdistributionf (x)= λe-λx, x≥0gamma(c, λ) gammadistributionf (x)= λ c x c-1e-λx/ Γ(c), x≥0χ2(k) chi-squaredistributionf (x)= x k/2-1e-x/2/( 2k/2 Γ(k/2) )F (k1, k2) F distributionBin(n,p) binomialdistributionf (k)= n C k p k(1-p)n-kPoisson(λ) Poissondistributionf (k)= λk e-λ/ k!Geom(p) geometricdistributionf (k)= p(1-p)kHG(N,K,n) hyper-geometric distributionBern(p) Bernoulli distributionSet theory symbolsSymbol Symbol Name Meaning / definition Example{ } set a collection of elements A = {3,7,9,14},B = {9,14,28}A ∩B intersection objects that belong to set A and setBA ∩B = {9,14}A ∪B union objects that belong to set A or setBA ∪B ={3,7,9,14,28}A ⊆B subset subset has fewer elements or equal tothe set{9,14,28} ⊆{9,14,28}A ⊂B proper subset /strict subsetsubset has fewer elements than theset{9,14} ⊂{9,14,28}A ⊄B not subset left set not a subset of right set {9,66} ⊄{9,14,28}A ⊇B superset set A has more elements or equal tothe set B{9,14,28} ⊇{9,14,28}A ⊃B proper superset /strict supersetset A has more elements than set B{9,14,28} ⊃{9,14}A ⊅B not superset set A is not a superset of set B {9,14,28} ⊅{9,66}2Apower set all subsets of Apower set all subsets of AA =B equalityboth sets have the same membersA={3,9,14},B={3,9,14}, A=BA ccomplementall the objects that do not belong to set AA \B relative complementobjects that belong to A and not to BA = {3,9,14},B = {1,2,3}, A-B = {9,14} A - B relative complementobjects that belong to A and not to BA = {3,9,14},B = {1,2,3}, A-B = {9,14} A ∆ Bsymmetric differenceobjects that belong to A or B but not to their intersectionA = {3,9,14},B = {1,2,3}, A ∆ B = {1,2,9,14} A ⊖ Bsymmetric differenceobjects that belong to A or B but not to their intersectionA = {3,9,14},B = {1,2,3}, A ⊖ B = {1,2,9,14}a ∈Aelement of set membershipA={3,9,14}, 3 ∈ Ax ∉ A not element ofno set membershipA={3,9,14}, 1 ∉ A(a ,b ) ordered pair collection of 2 elementsA ×B cartesian product set of all ordered pairs from A and B|A| cardinalitythe number of elements of set AA={3,9,14}, |A|=3 #Acardinality the number of elements of set AA={3,9,14}, #A=3aleph-nullinfinite cardinality of natural numbers setaleph-one cardinality of countable ordinal numbers setØ empty set Ø = { }C = {Ø}universal set set of all possible valuesnatural numbers /whole numbers set (with zero) 0= {0,1,2,3,4,...} 0 ∈1natural numbers /whole numbers set (without zero)1= {1,2,3,4,5,...} 6 ∈1integer numbers set={...-3,-2,-1,0,1,2,3,...}-6 ∈rational numbers set= {x | x =a /b , a ,b ∈}2/6 ∈real numbers set= {x | -∞ < x <∞} 6.343434∈complex numbers set= {z | z=a +bi , -∞<a <∞, -∞<b <∞}6+2i ∈∨reversed caret or x∨y | vertical line or x| y x' single quote not - negation x'x bar not - negation x¬not not - negation ¬x ! exclamation mark not - negation ! x⊕circled plus / oplus exclusive or - xor x⊕y ~ tilde negation ~ x⇒implies⇔equivalent if and only if (iff)↔equivalent if and only if (iff)∀for all∃there exists∄there does not exists∴therefore∵because / sinceCalculus & analysis symbolsSymbol Symbol Name Meaning / definition Examplelimit limit value of a functionεepsilonrepresents a very small number, near zeroε → 0eeconstant / Euler's numbere = 2.718281828...e = lim(1+1/x )x,x →∞y ' derivativederivative - Lagrange's notation (3x 3)' = 9x 2y '' second derivative derivative of derivative(3x 3)'' = 18xy (n )nth derivativen times derivation(3x 3)(3)= 18derivativederivative - Leibniz's notation d (3x 3)/dx = 9x 2secondderivativederivative of derivatived 2(3x 3)/dx 2 = 18xnthderivativen times derivationtime derivative derivative by time - Newton's notationtime second derivativederivative of derivativeD x y derivative derivative - Euler's notationD x 2ysecond derivativederivative of derivativepartialderivative∂(x 2+y 2)/∂x = 2x∫ integral opposite to derivation∫ f(x)dx∫∫ double integral integration of function of 2 variables∫∫ f(x,y)dxdy ∫∫∫triple integral integration of function of 3 variables∫∫∫ f(x,y,z)dxdydz∮closedcontour / line integral∯closedsurface integral∰closedvolume integral[a ,b ] closed interval [a ,b ] ={x | a ≤ x ≤ b }(a ,b )open interval (a ,b ) ={x | a < x < b }i imaginary unit i ≡ √-1 z = 3 + 2iz * complex conjugate z = a +bi → z *=a -bi z* = 3 - 2izcomplex conjugatez = a +bi → z = a -bi z = 3 - 2i∇ nabla / del gradient / divergence operator ∇f (x ,y ,z )vectorunit vectorx * y convolutiony (t ) = x (t ) * h (t )) = {{。
常用数学符号英文对照
×times sign multiplication 2 × 3 = 6 ·multiplication dot multiplication 2 · 3 = 6÷division sign /division 6 ÷ 2 = 3obelus/ division slash division 6 / 2 = 3–horizontal line division / fractionmod modulo remainder calculation 7 mod 2 = 1. period decimal point, decimal2.56 = 2+56/100separatora b power exponent 23= 8a^b caret exponent 2 ^ 3= 8√a square root √a ·√a = a√9 = ±33√a cube root 3√a ·3√a ·3√a = a3√8 = 24√a fourth root 4√a ·4√a ·4√a ·4√a = a4√16 = ±2n√a n-th root (radical) for n=3, n√8 = 2% percent1% = 1/100 10% × 30 = 3‰per-mille1‰ = 1/1000 = 0.1%10‰ × 30 = 0.3ppm per-million1ppm = 1/1000000 10ppm × 30 = 0.0003ppb per-billion 1ppb = 1/1000000000 10ppb × 30 = 3×10-7ppt per-trillion 1ppt = 10-1210ppt × 30 = 3×10-10Geometry symbolsSymbol Symbol Name Meaning / definition Example ∠angle formed by two rays ∠ABC = 30°measuredABC = 30°anglespherical angle AOB = 30°∟right angle = 90°α = 90°°degree 1 turn = 360°α = 60°deg degree 1 turn = 360deg α = 60deg′prime arcminute, 1° = 60′α = 60°59′″double prime arcsecond, 1′ = 60″α = 60°59′59″line infinite lineAB line segment line from point A to point Bray line that start from point Aarc arc from point A to point B= 60°⊥perpendicular perpendicular lines (90° angle) AC ⊥ BC| | parallel parallel lines AB | | CD≅congruent to equivalence of geometric shapes and size ∆ABC≅∆XYZ ~ similarity same shapes, not same size ∆ABC~ ∆XYZ Δtriangle triangle shape ΔABC≅ΔBCD |x-y| distance distance between points x and y | x-y | = 5πpi constant π = 3.141592654...is the ratio between the circumference and diameter of acirclec = π·d = 2·π·rrad radians radians angle unit 360° = 2π rad c radians radians angle unit 360° = 2πcgrad gradians / gons grads angle unit 360° = 400 gradg gradians / gons grads angle unit 360° = 400 g Algebra symbolsSymbol Symbol Name Meaning /definitionExample[a,b] closed interval [a,b] ={x | a≤x≤b}x∈[2,6]∆delta change /difference∆t = t1 - t0∆discriminant Δ =b2 - 4ac∑sigma summation -sum of allvalues in rangeof series∑ x i= x1+x2+...+x n∑∑sigma doublesummation∏capital pi product -product of allvalues in rangeof series∏ x i=x1∙x2∙...∙x ne e constant / Euler's number e =2.718281828...e = lim (1+1/x)x , x→∞γEuler-Mascheroni constantγ =0.527721566...φgolden ratio golden ratioconstantπpi constant π =3.141592654...is the ratiobetween thecircumference anddiameter of acirclec = π·d = 2·π·rLinear Algebra SymbolsSymbol Symbol Name Meaning / definition Example ·dot scalar product a · b×cross vector product a × bA⊗B tensor product tensor product of A and B A⊗B inner product[ ] brackets matrix of numbers( ) parentheses matrix of numbers| A | determinant determinant of matrix Adet(A) determinant determinant of matrix A|| x || double vertical bars normA T transpose matrix transpose (A T)ij = (A)jiA†Hermitian matrix matrix conjugate transpose (A†)ij = (A)ji A*Hermitian matrix matrix conjugate transpose (A*)ij = (A)ji A-1inverse matrix A A-1 = Irank(A) matrix rank rank of matrix A rank(A) = 3 dim(U) dimension dimension of matrix A rank(U) = 3 Probability and statistics symbolsSymbol Symbol Name Meaning / definition ExampleP(A) probabilityfunctionprobability of event A P(A) = 0.5P(A∩B) probability ofeventsintersectionprobability that ofevents A and BP(A∩B) = 0.5P(A∪B) probability ofevents union probability that ofevents A or BP(A∪B) = 0.5P(A | B) conditionalprobabilityfunctionprobability of event Agiven event BoccuredP(A | B) = 0.3f (x) probabilitydensity function(pdf)P(a ≤ x ≤ b) = ∫f (x) dxF(x) cumulative F(x) = P(X≤ x)distribution function (cdf)μpopulationmean mean of populationvaluesμ = 10E(X) expectationvalue expected value ofrandom variable XE(X) = 10E(X | Y) conditionalexpectation expected value ofrandom variable Xgiven YE(X | Y=2) = 5var(X) variance variance of randomvariable Xvar(X) = 4σ2variance variance ofpopulation valuesσ2 = 4std(X) standarddeviation standard deviation ofrandom variable Xstd(X) = 2σX standarddeviation standard deviationvalue of randomvariable XσX=2median middle value of random variable xcov(X,Y) covariance covariance ofrandom variables Xand Ycov(X,Y) = 4corr(X,Y) correlation correlation ofrandom variables Xand Ycorr(X,Y) = 0.6ρX,Y correlation correlation ofrandom variables Xand YρX,Y = 0.6∑summation summation - sum of all values in range of series∑∑doublesummationdouble summationBin(n,p) binomialdistributionf (k) = n C k p k(1-p)n-kPoisson(λ)Poissondistributionf (k)= λk e-λ / k!Geom(p) geometricdistributionf (k) = p(1-p) kHG(N,K,n) hyper-geometric distributionBern(p) Bernoulli distributionCombinatorics SymbolsSymbol Symbol Name Meaning / definition Examplen! factorial n! = 1·2·3·...·n5! = 1·2·3·4·5 = 120 n P k permutation 5P3 = 5! / (5-3)! = 60 n C kcombination 5C3 = 5!/[3!(5-3)!]=10Set theory symbolsSymbol Symbol Name Meaning / definition Example{ } set a collection of elements A = {3,7,9,14},B = {9,14,28}A ∩B intersection objects that belong to set A and setBA ∩B = {9,14}A ∪B union objects that belong to set A or setBA ∪B ={3,7,9,14,28}A ⊆B subset subset has fewer elements orequal to the set{9,14,28} ⊆{9,14,28}A ⊂B proper subset / strict subset has fewer elements than {9,14} ⊂subset the set {9,14,28}A ⊄B not subset left set not a subset of right set {9,66} ⊄{9,14,28}A ⊇B superset set A has more elements or equalto the set B{9,14,28} ⊇{9,14,28}A ⊃B proper superset / strictsupersetset A has more elements than setB{9,14,28} ⊃{9,14}A ⊅B not superset set A is not a superset of set B {9,14,28} ⊅{9,66}2A power set all subsets of A power set all subsets of AA =B equality both sets have the same members A={3,9,14}, B={3,9,14}, A=BA c complement all the objects that do not belong to set AA \B relative complement objects that belong to A and not toBA = {3,9,14},B = {1,2,3},A-B = {9,14}A -B relative complement objects that belong to A and not toBA = {3,9,14},B = {1,2,3},A-B = {9,14}A ∆B symmetric difference objects that belong to A or B butnot to their intersectionA = {3,9,14},B = {1,2,3},A ∆B ={1,2,9,14}A ⊖B symmetric difference objects that belong to A or B butnot to their intersectionA = {3,9,14},B = {1,2,3},A ⊖B ={1,2,9,14}a∈A element of set membership A={3,9,14}, 3 ∈Ax∉A not element of no set membership A={3,9,14}, 1 ∉A(a,b) ordered pair collection of 2 elementsA×B cartesian product set of all ordered pairs from A andB|A| cardinality the number of elements of set A A={3,9,14},|A|=3#A cardinality the number of elements of set A A={3,9,14},#A=3aleph-null infinite cardinality of natural numbers setaleph-one cardinality of countable ordinal numbers setØ empty set Ø = { } C = {Ø} universal set set of all possible values0natural numbers / wholenumbers set (with zero) 0= {0,1,2,3,4,...} 0 ∈01natural numbers / wholenumbers set (withoutzero)1= {1,2,3,4,5,...} 6 ∈1 integer numbers set = {...-3,-2,-1,0,1,2,3,...} -6 ∈rational numbers set = {x | x=a/b, a,b∈} 2/6 ∈real numbers set = {x | -∞ < x <∞} 6.343434∈complex numbers set= {z | z=a+bi,-∞<a<∞,-∞<b<∞}6+2i∈Logic symbolsSymbol Symbol Name Meaning / definition Example ·and and x·y^ caret / circumflex and x ^ y& ampersand and x & y+ plus or x + y∨reversed caret or x∨y | vertical line or x | yx' single quote not - negation x'x bar not - negation x¬not not - negation ¬x! exclamation mark not - negation ! x⊕circled plus / oplus exclusive or - xor x⊕y ~ tilde negation ~ x⇒implies⇔equivalent if and only if (iff)↔equivalent if and only if (iff)∀for all∃there exists∄there does not exists∴therefore∵because / sinceCalculus & analysis symbolsSymbol Symbol Name Meaning / definition Example limit limit value of a functionεepsilon represents a very small number,ε→0near zeroe e constant / Euler'snumber e = 2.718281828...e = lim(1+1/x)x ,x→∞y ' derivative derivative - Lagrange's notation (3x3)' = 9x2y '' second derivative derivative of derivative (3x3)'' = 18xy(n)nth derivative n times derivation (3x3)(3) = 18 derivative derivative - Leibniz's notation d(3x3)/dx = 9x2second derivative derivative of derivative d2(3x3)/dx2 = 18xnth derivative n times derivationtime derivative derivative by time - Newton's notationtime secondderivativederivative of derivativeD x y derivative derivative - Euler's notationD x2y second derivative derivative of derivativepartial derivative ∂(x2+y2)/∂x = 2x ∫integral opposite to derivation ∫f(x)dx∫∫double integral integration of function of 2variables∫∫f(x,y)dxdy∫∫∫triple integral integration of function of 3variables∫∫∫f(x,y,z)dxdydz∮closed contour / lineintegral∯closed surfaceintegral∰closed volumeintegral[a,b] closed interval [a,b] = {x | a ≤ x ≤ b}(a,b) open interval (a,b) = {x | a < x < b}i imaginary unit i≡ √-1 z = 3 + 2i z* complex conjugate z = a+bi→z*=a-bi z* = 3 - 2i z complex conjugate z = a+bi→z = a-bi z = 3 - 2i ∇nabla / del gradient / divergence operator ∇f (x,y,z) vectorunit vectorx * y convolution y(t) = x(t) * h(t)Laplace transform F(s) = {f (t)}Fourier transform X(ω) = {f (t)}δdelta function∞lemniscate infinity symbol。
西方经济学中常用的符号

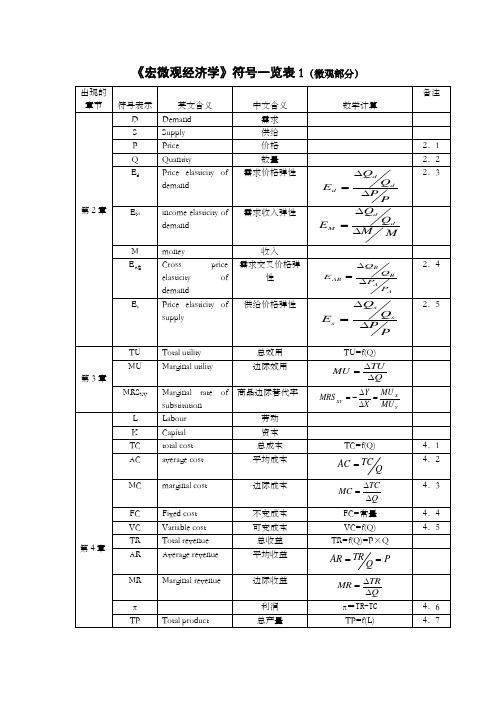
《宏微观经济学》符号一览表1(微观部分)注:2.1 不同商品或要素的价格,表现为不同的下标,如X、Y、L、K。
2.2 有时是需求量Q d,有时是供给量Q s,有时就表示产量或其他的数量。
2.3 有时又表示为e p,有时又简称为需求弹性或价格弹性。
2.4 有时就简称为交叉弹性。
2.5 有时就简称为供给弹性。
4.1 既可能是短期总成本,也可能是长期总成本,有时又写作C。
4.2 既可能是短期平均成本,也可能是长期平均成本。
4.3 既可能是短期边际成本,也可能是长期边际成本。
4.4 也就是后面的短期总不变成本,又称为固定成本。
4.5 也就是后面的短期总可变成本,又称为变动成本。
4.6 又称为经济利润,或超额利润。
4.7 有时也用Q表示。
4.8 如可变的投入是其他要素,可加上不同的下标。
《宏微观经济学》符号一览表2(宏观部分)注:9.1 其中,C 0是自发性消费;cY 是引致性消费。
9.2 与GDP 的区别在于前者是以生产者的国籍作为标准;而后者是以生产地作为标准。
10.1 经常用来表示国民收入,亦可表示总需求和总供给。
10.2 在上述的消费函数中,边际消费倾向即是b 。
10.3 两部门经济时,Y=C+S 。
10.4 两部门经济时,MPC+MPS=1,APC+APS=1。
10.5 这儿的乘数应是指投资乘数,两部门时,bK -=11。
14.1 这仍是两部门经济下(不考虑税收)的乘数。
14.2 这是三部门经济下(考虑税收)的乘数。
15.1 M 0—流通中现金;RE -存款准备金。
15.2 D -派生存款;MR -原始存款;rd-法定准备金率。
15.3 M 1-货币供给;M h —基础货币。
17.1 s -储蓄率,s=S/Y ;J -资本产出比率,J=K/Y 。
因时间仓促,如有遗漏或错误,希望大家及时指正,多谢。
Welcome !!! 欢迎您的下载,资料仅供参考!。
(英文)标点符号用法总结.doc

(英文)标点符号用法总结(英文)标点符号用法英文中常用的标点符号:.period句号,comma逗号:colon冒号;semicolon分号!exclamation惊叹号?questionmark问号 ̄hyphen连字符apostrophe省略号;所有格符号—dash破折号‘’singlequotationmarks单引号“”doublequotationmarks双引号()parentheses圆括号[]squarebrackets方括号《》Frenchquotes法文引号;书名号.ellipsis 省略号¨tandemcolon双点号“ditto同上‖parallel双线号/virgule斜线号&ampersand=and~swungdash代字号§section;division分节号→arrow箭号;参见号+plus加号;正号-minus减号;负号±plusorminus正负号×ismultipliedby乘号÷isdividedby除号=isequalto等于号≠isnotequalto不等于号≡isequivalentto全等于号≌isequaltoorapproximatelyequalto等于或约等于号≈isapproximatelyequalto约等于号<islessthan小于号>ismorethan 大于号≮isnotlessthan不小于号≯isnotmorethan不大于号≤islessthanorequalto小于或等于号≥ismorethanorequalto大于或等于号%percent百分之…‰permill千分之…∞infinity无限大号∝variesas与…成比例√(square)root平方根∵since;because因为∴hence所以∷equalsas(proportion)等于,成比例∠angle角⌒semicircle半圆⊙circle圆○circumference圆周πpi圆周率△triangle 三角形⊥perpendicularto垂直于∪unionof并,合集∩intersectionof 交,通集∫theintegralof…的积分∑(sigma)summationof总和°degree度′minute分″second秒#number…号℃Celsiussystem摄氏度@at 单价以下是具体使用方法(一)逗号的用法 1.在并列连词(and,but,for,nor,or,yet)前使用,用来连接句中的各分句。
常用数学符号英文对照
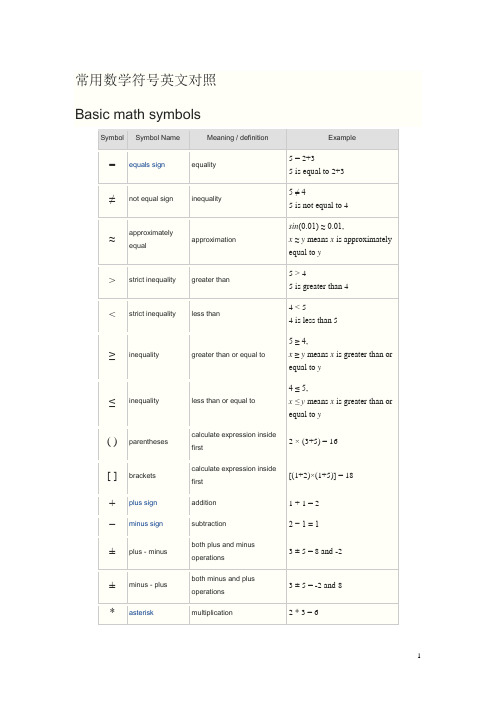
常用数学符号英文对照Basic math symbolsSymbol Symbol Name Meaning / definition Example= equals sign equality 5 = 2+35 is equal to 2+3≠not equal sign inequality 5 ≠ 45 is not equal to 4≈approximatelyequal approximationsin(0.01) ≈ 0.01,x≈y means x is approximatelyequal to y> strict inequality greater than 5 > 45 is greater than 4< strict inequality less than 4 < 54 is less than 5≥inequality greater than or equal to 5 ≥ 4,x≥y means x is greater than or equal to y≤inequality less than or equal to 4 ≤ 5,x ≤ y means x is greater than or equal to y( ) parentheses calculate expression insidefirst2 × (3+5) = 16[ ] brackets calculate expression insidefirst[(1+2)×(1+5)] = 18 + plus sign addition 1 + 1 = 2−minus sign subtraction 2 − 1 = 1±plus - minus both plus and minusoperations3 ± 5 = 8 and -2±minus - plus both minus and plusoperations3 ± 5 = -2 and 8 * asterisk multiplication 2 * 3 = 6×times sign multiplication 2 × 3 = 6 ·multiplication dot multiplication 2 · 3 = 6÷division sign /division 6 ÷ 2 = 3obelus/ division slash division 6 / 2 = 3–horizontal line division / fractionmod modulo remainder calculation 7 mod 2 = 1. period decimal point, decimal2.56 = 2+56/100separatora b power exponent 23= 8a^b caret exponent 2 ^ 3= 8√a square root √a ·√a = a√9 = ±33√a cube root 3√a ·3√a ·3√a = a3√8 = 24√a fourth root 4√a ·4√a ·4√a ·4√a = a4√16 = ±2n√a n-th root (radical) for n=3, n√8 = 2% percent1% = 1/100 10% × 30 = 3‰per-mille1‰ = 1/1000 = 0.1%10‰ × 30 = 0.3ppm per-million1ppm = 1/1000000 10ppm × 30 = 0.0003ppb per-billion 1ppb = 1/1000000000 10ppb × 30 = 3×10-7ppt per-trillion 1ppt = 10-1210ppt × 30 = 3×10-10ABC = 30°AOB = 30°°degree 1 turn = 360°α = 60°deg degree 1 turn = 360deg α = 60deg′prime arcminute, 1° = 60′α = 60°59′″double prime arcsecond, 1′ = 60″α = 60°59′59″line infinite lineAB line segment line from point A to point Bray line that start from point Aarc arc from point A to point B= 60°⊥perpendicular perpendicular lines (90° angle) AC ⊥ BC| | parallel parallel lines AB | | CD≅congruent to equivalence of geometric shapes and size ∆ABC≅∆XYZ ~ similarity same shapes, not same size ∆ABC~ ∆XYZ Δtriangle triangle shape ΔABC≅ΔBCD |x-y| distance distance between points x and y | x-y | = 5πpi constant π = 3.141592654...is the ratio between the circumference and diameter of acirclec = π·d = 2·π·rrad radians radians angle unit 360° = 2π rad c radians radians angle unit 360° = 2πcgrad gradians / gons grads angle unit 360° = 400 gradg gradians / gons grads angle unit 360° = 400 gx x variableto findwhen 2x = 4, then x = 2≡equivalence identical to≜equal by definition equal bydefinition:= equal by definition equal bydefinition~ approximately equal weakapproximation11 ~ 10≈approximately equal approximation sin(0.01) ≈ 0.01∝proportional to proportional to y∝x when y = kx, k constant ∞lemniscate infinity symbol≪much less than much less than 1 ≪1000000≫much greater than much greaterthan1000000 ≫1( ) parentheses calculateexpressioninside first2 * (3+5) = 16[ ] brackets calculateexpressioninside first[(1+2)*(1+5)] = 18{ } braces set⌊x⌋floor brackets rounds numberto lower integer⌊4.3⌋ = 4⌈x⌉ceiling brackets rounds numberto upper integer⌈4.3⌉ = 5x! exclamation mark factorial4! = 1*2*3*4 = 24 | x | single vertical bar absolute value | -5 | = 5f (x) function of x maps values ofx to f(x)f (x) = 3x+5(f∘g) function composition (f∘g) (x)= f (g(x))f (x)=3x,g(x)=x-1 ⇒(f∘g)(x)=3(x-1)(a,b) open interval (a,b) = x∈(2,6)[a ,b ] closed interval[a ,b ] = {x | a ≤ x ≤ b }x ∈ [2,6]∆ delta change / difference∆t = t 1 - t 0∆ discriminantΔ = b 2 - 4ac∑sigmasummation -sum of all values in range of series ∑ x i = x 1+x 2+...+x n∑∑sigmadouble summation∏capital piproduct -product of all values in range of series∏ x i =x 1∙x 2∙...∙x ne e constant / Euler's numbere =2.718281828... e = lim (1+1/x )x , x →∞γ Euler-Mascheroni constant γ =0.527721566...φgolden ratio golden ratio constantπpi constant π =3.141592654...is the ratiobetween the circumference and diameter of a circlec = π·d = 2·π·rA ⊗Btensor product tensor product of A and BA ⊗ Binner product[ ] brackets matrix of numbers ( ) parentheses matrix of numbers| A | determinant determinant of matrix A det(A ) determinant determinant of matrix A|| x || double vertical bars normA T transpose matrix transpose(A T )ij = (A )ji A † Hermitian matrix matrix conjugate transpose (A †)ij = (A )ji A * Hermitian matrix matrix conjugate transpose(A *)ij = (A )jiA -1inverse matrixA A -1 = Irank(A ) matrix rank rank of matrix A rank(A ) = 3 dim(U )dimensiondimension of matrix Arank(U ) = 3Probability and statistics symbolsSymbolSymbol Name Meaning / definitionExampleP (A )probability function probability of event A P (A ) = 0.5P (A ∩ B ) probability ofeventsintersection probability that of events A and BP (A ∩B ) = 0.5P (A ∪B ) probability ofevents unionprobability that of events A or B P (A ∪B ) = 0.5P (A | B )conditionalprobability function probability of event A given event B occuredP (A | B ) = 0.3f (x ) probabilitydensity function (pdf) P (a ≤ x ≤ b ) = ∫ f (x ) dxF (x )cumulativeF (x ) = P (X ≤ x )distribution function (cdf)μ population mean mean of population valuesμ = 10E (X )expectation valueexpected value of random variable X E (X ) = 10E (X | Y )conditional expectationexpected value of random variable X given YE (X | Y=2) = 5var (X ) variance variance of random variable X var (X ) = 4σ2variancevariance of population values σ2 = 4std (X ) standard deviationstandard deviation of random variable X std (X ) = 2σXstandard deviationstandard deviation value of random variable X σX = 2medianmiddle value of random variable xcov (X ,Y )covariance covariance ofrandom variables X and Y cov (X,Y ) = 4corr (X ,Y ) correlationcorrelation ofrandom variables X and Y corr (X,Y ) = 0.6ρX ,Ycorrelation correlation ofrandom variables X and YρX ,Y = 0.6∑summation summation - sum ofall values in range of series∑∑double summationdouble summationMo mode value that occurs most frequently in populationMR mid-range MR = (x max+x min)/2 Md sample median half the population isbelow this valueQ1lower / firstquartile 25% of population are below this valueQ2median /second quartile 50% of population are below this value = median of samplesQ3upper / thirdquartile 75% of population are below this valuex sample mean average / arithmeticmeanx = (2+5+9) / 3 = 5.333s2samplevariance population samples variance estimators2 = 4s samplestandarddeviationpopulation samplesstandard deviationestimators = 2z x standard score z x = (x-x) / s xX ~ distribution of X distribution ofrandom variable XX ~ N(0,3)N(μ,σ2) normaldistributiongaussian distribution X ~ N(0,3)U(a,b) uniformdistributionequal probability inrange a,bX ~ U(0,3)exp(λ)exponentialdistributionf (x) = λe-λx , x≥0gamma(c, λ)gammadistributionf (x) = λ c x c-1e-λx /Γ(c), x≥0χ 2(k) chi-squaredistributionf (x) = x k/2-1e-x/2 /( 2k/2 Γ(k/2) )F (k1, k2) F distributionBin (n ,p )binomial distribution f (k ) = n C k p k (1-p )n-kPoisson (λ)Poisson distribution f (k ) = λk e -λ / k !Geom (p )geometric distribution f (k ) = p (1-p ) kHG (N ,K ,n ) hyper-geometric distributionBern (p ) Bernoulli distributionsubset the set {9,14,28} A ⊄ B not subset left set not a subset of right set{9,66} ⊄{9,14,28} A ⊇B supersetset A has more elements or equalto the set B{9,14,28} ⊇{9,14,28} A ⊃Bproper superset / strictsupersetset A has more elements than setB{9,14,28} ⊃{9,14}A ⊅B not superset set A is not a superset of set B{9,14,28} ⊅{9,66} 2A power set all subsets of Apower set all subsets of AA =B equalityboth sets have the samemembersA={3,9,14},B={3,9,14},A=BA c complementall the objects that do not belongto set AA \B relative complementobjects that belong to A and notto BA = {3,9,14},B = {1,2,3},A-B = {9,14} A - B relative complementobjects that belong to A and notto BA = {3,9,14},B = {1,2,3},A-B = {9,14} A ∆ B symmetric differenceobjects that belong to A or B butnot to their intersectionA = {3,9,14},B = {1,2,3},A ∆B ={1,2,9,14} A ⊖ B symmetric differenceobjects that belong to A or B butnot to their intersectionA = {3,9,14},B = {1,2,3},A ⊖B ={1,2,9,14}a∈A element of set membership A={3,9,14}, 3 ∈Ax∉A not element of no set membership A={3,9,14}, 1 ∉A(a ,b ) ordered pair collection of 2 elementsA×B cartesian product set of all ordered pairs from Aand B|A| cardinality the number of elements of set AA={3,9,14}, |A|=3 #A cardinality the number of elements of set AA={3,9,14}, #A=3aleph-nullinfinite cardinality of naturalnumbers setaleph-one cardinality of countable ordinalnumbers setØ empty set Ø = { }C = {Ø}universal set set of all possible valuesnatural numbers / whole numbers set (with zero) 0 = {0,1,2,3,4,...}0 ∈ 01natural numbers / wholenumbers set (withoutzero)1 = {1,2,3,4,5,...}6 ∈ 1integer numbers set= {...-3,-2,-1,0,1,2,3,...} -6 ∈rational numbers set= {x | x =a /b , a ,b ∈}2/6 ∈real numbers set= {x | -∞ < x <∞} 6.343434∈complex numbers set= {z | z=a +bi ,-∞<a <∞, -∞<b <∞}6+2i ∈∨reversed caret or x∨y | vertical line or x | y x' single quote not - negation x'x bar not - negation x¬not not - negation ¬x ! exclamation mark not - negation ! x ⊕circled plus / oplus exclusive or - xor x⊕y ~ tilde negation ~ x ⇒implies⇔equivalent if and only if (iff)↔equivalent if and only if (iff)∀for all∃there exists∄there does not exists∴therefore∵because / sincee e constant / Euler'snumber e = 2.718281828...e = lim(1+1/x)x ,x→∞y ' derivative derivative - Lagrange's notation (3x3)' = 9x2y '' second derivative derivative of derivative (3x3)'' = 18xy(n)nth derivative n times derivation (3x3)(3) = 18derivative derivative - Leibniz's notation d(3x3)/dx = 9x2second derivative derivative of derivative d2(3x3)/dx2 = 18xnth derivative n times derivationtime derivative derivative by time - Newton's notationtime secondderivativederivative of derivativeD x y derivative derivative - Euler's notationD x2y second derivative derivative of derivativepartial derivative ∂(x2+y2)/∂x = 2x ∫integral opposite to derivation ∫f(x)dx∫∫double integral integration of function of 2variables∫∫f(x,y)dxdy∫∫∫triple integral integration of function of 3variables∫∫∫f(x,y,z)dxdydz∮closed contour / lineintegral∯closed surfaceintegral∰closed volumeintegral[a,b] closed interval [a,b] = {x | a ≤ x ≤ b}(a,b) open interval (a,b) = {x | a < x < b}i imaginary unit i≡ √-1 z = 3 + 2i z* complex conjugate z = a+bi→z*=a-bi z* = 3 - 2i z complex conjugate z = a+bi→z = a-bi z = 3 - 2i ∇nabla / del gradient / divergence operator ∇f (x,y,z)vectorunit vectorx * y convolution y(t) = x(t) * h(t)Laplace transform F(s) = {f (t)}Fourier transform X(ω) = {f (t)}δdelta function∞lemniscate infinity symbol。
常用的希腊字母、符号、特殊字符的读法和英文发音

希腊字母1、Ααalpha a:lf 阿尔法角度;系数Αα:阿尔法Alpha2、Ββbeta bet 贝塔磁通系数;角度;系数Ββ:贝塔Beta3、Γγgamma ga:m 伽马电导系数(小写)Γγ:伽玛Gamma4、Γδdelta delt 德尔塔变动;密度;屈光度Γδ:德尔塔Delte5、Δεepsilon ep`silon 伊普西龙对数之基数Δε:艾普西龙Epsilon6、Εδzeta zat 截塔系数;方位角;阻抗;相对粘度;原子序数δ:捷塔Zeta7、Ζεeta eit 艾塔磁滞系数;效率(小写)ε:依塔Eta8、Θζthet ζit 西塔温度;相位角Θζ:西塔Theta9、Ηηiot aiot 约塔微小,一点儿Ηη:艾欧塔Iota10 、Κθkappa kap 卡帕介质常数Κθ:喀帕Kappa11 、∧ιlambda lambd 兰布达波长(小写);体积Λι:拉姆达Lambda12 、Μκmu mju 缪磁导系数;微(千分之一);放大因数(小写)Μκ:缪Mu13 、Νλnu nju 纽磁阻系数Νλ:拗Nu14 、Ξμxi ksi 克西Ξμ:克西Xi15 、Ονomicron omik`ron 奥密克戎Ον:欧麦克轮Omicron16 、∏πpi pai 派圆周率=圆周÷直径=3.1416 Ππ:派Pi17 、Ρξrho rou 肉电阻系数(小写)Ρξ:柔Rho18 、∑ζsigma `sigma 西格马总和(大写),表面密度;跨导(小写)ζ:西格玛Sigma19 、Σηtau tau 套时间常数Ση:套Tau20 、Τυupsilon jup`silon 宇普西龙位移Τυ:宇普西龙Upsilon21 、Φθphi fai 佛爱磁通;角Φθ:fai Phi22 、Υχchi phai 西Υχ:器Chi23 、Φψpsi psai 普西角速;介质电通量(静电力线);角Φψ:普赛Psi24 、Χωomega o`miga 欧米伽欧姆(大写);角速(小写);角Χω:欧米伽Omega键盘符号的英文读法` backquote 反引号~ tilde! exclam@ at# numbersign,英语国家是hash,美语是pound,音乐里作sharp,如C# $ dollar% percent^ caret& ampersand* asterisk,star(美语),数学公式中作multiply( parenleft,opening parentheses) parenright,closing paretheses- minus;hyphen连字符,不读_ underscore+ plus= equal[ bracketleft,opening bracket] bracketright,closing bracket{ braceleft} braceright; semicolon: colon' quote" doublequote/ slash\ backslash 反斜杠| bar, comma< less> greater. period? questionspace 空格下面是一些特殊符号的英文读法,主要是数学符号<is less than>is more than≤is not less than≥is not more than≢is less than or equal to 小于或等于号- hyphen 连字符≣is more than or equal to 大于或等于号' apostrophe 省略号,英文中省略字符用的撇号;所有格符号%percent-dash 破折号‰per mille∞infinity 无限大号∝varies as 与…成比例( ) parentheses 圆括号√(square) root 平方根[ ] square brackets 方括号∵since; because 因为《》French quotes 法文引号;书名号∴hence 所以…ellipsis 省略号∷equals, as (proportion) 等于,成比例¨tandem colon 双点号∟angle 角∶ditto 双点号≨semicircle 半圆‖parallel 双线号≦circle 圆/virgule 斜线号○circumference 圆周~swung dash 代字号△triangle 三角形§section; division 分节号≧perpendicular to 垂直于→arrow 箭号;参见号∪union of 并,合集∩intersection of 交,通集∫the integral of …的积分ªplus or minus 正负号∑summation of 总和×is multiplied by 乘号©degree 度÷is divided by 除号′minute 分″second 秒≠is not equal to 不等于号≡is equivalent to 全等于号℃Celsius degree 摄氏度≌is equal to or approximately equal to 等于或约等于号一些符号的读法+ plus 加号;正号- minus 减号;负号ªplus or minus 正负号×is multiplied by 乘号÷is divided by 除号=is equal to 等于号≠is not equal to 不等于号≡is equivalent to 全等于号≌is equal to or approximately equal to 等于或约等于号≈is approximately equal to 约等于号<is less than 小于号>is more than 大于号≤is not less than 不小于号≥is not more than 不大于号≢is less than or equal to 小于或等于号≣is more than or equal to 大于或等于号% per cent 百分之…‰per mill 千分之…∞infinity 无限大号∝varies as 与…成比例√(square) root 平方根∵since; because 因为∴hence 所以∷equals, as (proportion) 等于,成比例∟angle 角≨semicircle 半圆≦circle 圆○circumference 圆周πpi 圆周率△triangle 三角形≧perpendicular to 垂直于∪union of 并,合集∩intersection of 交,通集∫the integral of …的积分∑(sigma) summation of 总和©degree 度′minute 分〃second 秒℃Celsius system 摄氏度{ open brace, open curly 左花括号} close brace, close curly 右花括号( open parenthesis, open paren 左圆括号) close parenthesis, close paren 右圆括号() brakets/ parentheses 括号[ open bracket 左方括号] close bracket 右方括号[] square brackets 方括号. period, dot 句号,点| vertical bar, vertical virgule 竖线& ampersand, and, reference, ref 和,引用/ slash, divide, oblique 斜线,斜杠,除号// slash-slash, comment 双斜线,注释符# pound 井号\ backslash, sometimes escape 反斜线转义符,有时表示转义符或续行符~ tilde 波浪符. full stop 句号, comma 逗号: colon 冒号; semicolon 分号? question mark 问号! exclamation mark (英式英语) exclamation point (美式英语)' apostrophe 撇号- hyphen 连字号-- dash 破折号... dots/ ellipsis 省略号" single quotation marks 单引号"" double quotation marks 双引号‖parallel 双线号& ampersand = and~swung dash 代字号§section; division 分节号→arrow 箭号;参见号_ underscore 下划线。
字母符号大全花样符号

字母符号大全花样符号在日常生活和工作中,我们经常会用到各种各样的字母符号,它们不仅可以丰富文本内容,还可以起到装饰和强调的作用。
本文将为大家介绍一些常见的花样符号,希望能够给大家带来一些灵感和帮助。
1. 希腊字母。
希腊字母是指古希腊语所使用的字母,它们常常被用于数学、物理、化学等领域。
例如,α(alpha)、β(beta)、γ(gamma)等字母常常用于表示角度、速度、波长等物理量。
这些希腊字母不仅可以让文本看起来更加专业和规范,还可以凸显特定的概念和含义。
2. 数学符号。
数学符号在科学技术领域中被广泛应用,它们不仅可以表示数字和运算符号,还可以表示各种数学关系和函数。
例如,加减乘除符号(+、-、×、÷)、等于号(=)、大于小于号(>、<)等,它们可以帮助我们清晰地表达数学运算和关系,提高文本的准确性和可读性。
3. 特殊符号。
除了常见的字母和数学符号外,还有一些特殊的花样符号可以用来装饰文本和表达情感。
例如,❤️(心形符号)、❤️(太阳符号)、❤️(胜利手势符号)等,它们可以为文本增添一些趣味和活力,让读者眼前一亮。
4. 货币符号。
货币符号用于表示不同国家和地区的货币单位,它们在国际贸易和金融交易中扮演着重要的角色。
例如,$(美元符号)、€(欧元符号)、¥(人民币符号)等,它们可以帮助我们清晰地表达货币金额和单位,避免歧义和误解。
5. 表情符号。
表情符号是一种用图形符号表示情感和心情的符号,它们在网络聊天和社交媒体中被广泛使用。
例如, (微笑符号)、 (大笑符号)、 (哭泣符号)等,它们可以让我们更加生动地表达情感,增强沟通的效果和趣味性。
6. 特殊符号。
除了上述提到的符号外,还有一些特殊的符号可以用来装饰文本和表达特定含义。
例如,★(星号符号)、♫(音符符号)、♡(爱心符号)等,它们可以让文本看起来更加美观和有趣,吸引读者的注意力。
总结。
通过本文的介绍,我们可以看到字母符号在文本中的重要作用,它们不仅可以丰富文本内容,还可以起到装饰和强调的作用。
西方经济学中常用的符号
《宏微观经济学》符号一览表1(微观部分)2.1 不同商品或要素的价格,表现为不同的下标,如X、Y、L、K。
2.2 有时是需求量Q d,有时是供给量Q s,有时就表示产量或其他的数量。
2.3 有时又表示为e p,有时又简称为需求弹性或价格弹性。
2.4 有时就简称为交叉弹性。
2.5 有时就简称为供给弹性。
4.1 既可能是短期总成本,也可能是长期总成本,有时又写作C。
4.2 既可能是短期平均成本,也可能是长期平均成本。
4.3 既可能是短期边际成本,也可能是长期边际成本。
4.4 也就是后面的短期总不变成本,又称为固定成本。
4.5 也就是后面的短期总可变成本,又称为变动成本。
4.6 又称为经济利润,或超额利润。
4.7 有时也用Q表示。
4.8 如可变的投入是其他要素,可加上不同的下标。
《宏微观经济学》符号一览表2(宏观部分)9.1 其中,C 0是自发性消费;cY 是引致性消费。
9.2 与GDP 的区别在于前者是以生产者的国籍作为标准;而后者是以生产地作为标准。
10.1 经常用来表示国民收入,亦可表示总需求和总供给。
10.2 在上述的消费函数中,边际消费倾向即是b 。
10.3 两部门经济时,Y=C+S 。
10.4 两部门经济时,MPC+MPS=1,APC+APS=1。
10.5 这儿的乘数应是指投资乘数,两部门时,bK -=11。
14.1 这仍是两部门经济下(不考虑税收)的乘数。
14.2 这是三部门经济下(考虑税收)的乘数。
15.1 M 0—流通中现金;RE -存款准备金。
15.2 D -派生存款;MR -原始存款;rd-法定准备金率。
15.3 M 1-货币供给;M h —基础货币。
17.1 s -储蓄率,s=S/Y ;J -资本产出比率,J=K/Y 。
因时间仓促,如有遗漏或错误,希望大家及时指正,多谢。
最常用单位及符号中英文对照

基数词0 nought;zero;O1 one2 two3 three4 four5 five6 six7 seven8 eight9 nine10 ten11 eleven12 twelve13 thirteen14 fourteen15 fifteen16 sixteen17 seventeen18 eighteen19 nineteen20 twenty21 twenty-one22 twenty-two23 twenty-three30 thirty32 thirty-two40 forty50 fifty60 sixty70 seventy80 eighty90 ninety100 one hundred101 one hundred and one156 one hundred and fifty-six 192 one hundred and ninety-two 200 two hundred300 three hundred400 four hundred500 five hundred600 six hundred700 seven hundred800 eight hundred900 nine hundred1,000 one thousand1,001 one thousand and one 1,300 thirteen hundred;one thousand and threehundred2,000 two thousand2,034 two thousand and thirty-four6,502 six thousand five hundred and two38,000 thirty-eight thousand45,672 forty-five thousand six hundred andseventy-two500,000 five hundred thousand1,000,000 one million3,123,400 three million,one hundred and twenty-three thousand and four hundred8,000,000 eight million47,000,000 forty-seven million900,000,000 nine hundred million1,000,000,000 a milliard,one milliard(美作:a billion,one billion)1,050,000,000 one billion and fifty million10,000,000,000 ten billion200,000,000,000 two hundred billion1,000,000,000,000 a billion,one billion(美作:a trillion,one trillion)6,000,000,000,000 six million million序数词first第一second第二third第三fourth第四fifth第五sixth第六seventh第七eighth第八ninth第九tenth第十eleventh第十一twelfth第十二thirteenth第十三fourteenth第十四fifteenth第十五sixteenth第十六seventeenth第十七eighteenth第十八nineteenth第十九twentieth第二十twenty-first第二十一twenty-second第二十二twenty-third第二十三thirtieth第三十thirty-first第三十一fortieth第四十fiftieth第五十sixtieth第六十seventieth第七十eightieth第八十ninetieth第九十(one)hundredth第一百(one)hundred and first第一百零一hundred and thirty-fourth第一百三十四two-hundredth第二百three-hundredth第三百four-hundredth第四百five-hundredth第五百six-hundredth第六百seven-hundredth第七百eight-hundredth第八百nine-hundredth第九百(one)thousandth第一千thousand and first第一千零一two thousand and thirty-fourth第二千零三十四ten thousandth第一万(one)millionth第一百万(美作:billionth)billionth第十亿(美作:trillionth)分数1/2 : one-half;a half1/3 : one-third3/4 : three-fourths1/5 : one-fifth2/5 : two-fifths7/8 : seven-eighths1/10 : one-tenth;a tenth1/100 : one-hundredth;one per cent1/1000 : one-thousandth1/10000 : one ten-thousandth21/2 : two and one half;two and a half42/3 : four and two-thirds百分比100% : one hundred per cent0.5% : point five per cent0.46% : point four six per cent小数2.05 : two point nought five;two point O five6.003 : six point nought nought three;six point O O three 78.12 : seventy-eight point one two电话号码119 : one one nine120 : one two oh688 : six double-eight5337 : five double-three seven6512 : six five one two97868 : nine seven eight six eight893493 : eight nine three four nine three737964 : seven three seven nine six four62374881 : six two three seven four double-eight one时间同一个时间可以有几种表达方法。
常用标点符号的中英文对照

_ underscore, underline, underbar下划线@ at, accent sign¯overline, overscore, overbar 上划线(例如0,1)~ tilde 波浪线\ reverse solidus or back slash/ slash- dash 破折号,hyphen 连字符,minus (sign), opposite sign, negative sign, break sign# 电话键盘上念pound 乐谱上念sharp (升半音) 号码sharp (后跟数字) 或number| pipe, vertical bar^ caret* asterisk, star (sign)§section; division 分节号→ arrow 箭号;参见号. period, dot, full stop? question mark... ellipsis, etc! exclamation mark(感叹号), caution sign(警示标志), factorial sign阶乘符号(数), comma: colon; semicolon( ) brackets, round brackets, parentheses, left bracket, right bracket[] brackets, square brackets, left square bracket, right square bracket{} brackets, curly brackets, left curly bracket, right curly bracket<> angle brackets 尖括号+ plus (sign), cross sign, positive sign$ dollar (sign), currency sign% percent (sign)& and= equals, sign of equality' quotation marks, single quotation mark, single quotes, apostrophe " quotation marks, quotation mark, quot(es)> greater than< less than∑ (sigma) summation of 总和。
各种符号、数字英语读法

常用的数学符号英文读法一、一般符号对应的英文单词. period 句号, comma 逗号: colon 冒号; semicolon 分号! exclamation 惊叹号? question mark 问号─ hyphen 连字符’ apostrophe 省略号;所有格符号— dash 破折号‘’single quotation marks 单引号“”double quotation marks 双引号( ) parentheses 圆括号[ ] square brackets 方括号《》French quotes 法文引号;书名号... ellipsis 省略号¨ tandem colon 双点号" ditto 同上‖ parallel 平行双线号/ virgule 斜线号& ampersand = and~ swung dash 代字号§ section; division 分节号→ arrow 箭号;参见号+ plus 加号;正号- minus 减号;负号± plus or minus 正负号× is multiplied by or cross 叉乘÷ is divided by 除号= is equal to 等于号≠ is not equal to 不等于号≡ is equivalent to 全等于号≌ is equal to or approximately equal to 等于或约等于号≈ is approximately equal to 约等于号< is less than 小于号> is more than (is greater than在数学中更常用)大于号≮ is not less than不小于号≯ is not more than不大于号≤ is less than or equal to 小于或等于号≥ is more than or equal to 大于或等于号% per cent 百分之…‰ per mill 千分之…∞ infinity 无限大号∝ varies as 与…成比例√ (square) root 平方根∵ since; because 因为∴ hence 所以∷ equals, as (proportion) 等于,成比例∠ angle 角⌒ semicircle 半圆⊙ circle 圆○ circumference 圆周π pi 圆周率△ triangle 三角形⊥ perpendicular to 垂直于;另外normal to,right to也都有垂直的意思。
常用数学符号的英文表达

常用数学符号的英文表达English Expression of the Mathematical Symbol in Common Use第一部分英汉微积分词汇Part1 English-Chinese Calculus V ocabulary第一章函数与极限Chapter1 Function and Limit集合set元素element子集subset空集empty set并集union交集intersection差集difference of set基本集basic set补集complement set直积direct product笛卡儿积Cartesian product开区间open interval闭区间closed interval半开区间half open interval有限区间finite interval区间的长度length of an interval无限区间infinite interval领域neighborhood领域的中心centre of a neighborhood领域的半径radius of a neighborhood左领域left neighborhood右领域right neighborhood映射mappingX到Y的映射mapping of X ontoY满射surjection单射injection一一映射one-to-one mapping双射bijection算子operator变化transformation函数function 逆映射inverse mapping复合映射composite mapping自变量independent variable因变量dependent variable定义域domain函数值value of function函数关系function relation值域range自然定义域natural domain单值函数single valued function多值函数multiple valued function单值分支one-valued branch函数图形graph of a function绝对值函数absolute value符号函数sigh function整数部分integral part阶梯曲线step curve当且仅当if and only if(iff)分段函数piecewise function上界upper bound下界lower bound有界boundedness无界unbounded函数的单调性monotonicity of a function 单调增加的increasing单调减少的decreasing单调函数monotone function函数的奇偶性parity(odevity) of a function对称symmetry偶函数even function奇函数odd function函数的周期性periodicity of a function周期period反函数inverse function直接函数direct function复合函数composite function中间变量intermediate variable函数的运算operation of function基本初等函数basic elementary function初等函数elementary function幂函数power function指数函数exponential function对数函数logarithmic function三角函数 trigonometric function反三角函数 inverse trigonometric function 常数函数 constant function 双曲函数 hyperbolic function 双曲正弦 hyperbolic sine 双曲余弦 hyperbolic cosine 双曲正切 hyperbolic tangent反双曲正弦 inverse hyperbolic sine 反双曲余弦 inverse hyperbolic cosine 反双曲正切 inverse hyperbolic tangent 极限 limit数列 sequence of number 收敛 convergence 收敛于 a converge to a 发散 divergent极限的唯一性 uniqueness of limits收敛数列的有界性 boundedness of aconvergent sequence子列 subsequence函数的极限 limits of functions函数()f x 当x 趋于x 0时的极限 limit of functions ()f x as x approaches x 0 左极限 left limit 右极限 right limit单侧极限 one-sided limits水平渐近线 horizontal asymptote 无穷小 infinitesimal 无穷大 infinity铅直渐近线 vertical asymptote 夹逼准则 squeeze rule单调数列 monotonic sequence高阶无穷小 infinitesimal of higher order 低阶无穷小 infinitesimal of lower order 同阶无穷小 infinitesimal of the same order 等阶无穷小 equivalent infinitesimal 函数的连续性 continuity of a function 增量 increment函数()f x 在x 0连续 the function ()f x is continuous at x 0左连续 left continuous 右连续 right continuous区间上的连续函数 continuous function 函数()f x 在该区间上连续 function ()f x is continuous on an interval 不连续点 discontinuity point第一类间断点 discontinuity point of the first kind第二类间断点 discontinuity point of the second kind初等函数的连续性 continuity of the elementary functions定义区间 defined interval最大值 global maximum value (absolute maximum)最小值 global minimum value (absolute minimum)零点定理 the zero point theorem 介值定理 intermediate value theorem第二章 导数与微分Chapter2 Derivative and Differential 速度 velocity匀速运动 uniform motion 平均速度 average velocity瞬时速度 instantaneous velocity 圆的切线 tangent line of a circle 切线 tangent line切线的斜率 slope of the tangent line 位置函数 position function 导数 derivative 可导 derivable函数的变化率问题 problem of the change rate of a function导函数 derived function 左导数 left-hand derivative 右导数 right-hand derivative 单侧导数 one-sided derivatives()f x 在闭区间【a,b 】上可导 ()f x isderivable on the closed interval [a,b] 切线方程 tangent equation 角速度 angular velocity 成本函数 cost function 边际成本 marginal cost 链式法则 chain rule隐函数implicit function显函数explicit function二阶函数second derivative三阶导数third derivative高阶导数nth derivative莱布尼茨公式Leibniz formula对数求导法log- derivative参数方程parametric equation相关变化率correlative change rata微分differential可微的differentiable函数的微分differential of function自变量的微分differential of independent variable微商differential quotient间接测量误差indirect measurement error 绝对误差absolute error相对误差relative error第三章微分中值定理与导数的应用Chapter3 MeanValue Theorem of Differentials and the Application of Derivatives罗马定理Rolle’s theorem费马引理Fermat’s lemma拉格朗日中值定理Lagrange’s mean value theorem驻点stationary point稳定点stable point临界点critical point辅助函数auxiliary function拉格朗日中值公式Lagrange’s mean value formula柯西中值定理Cauchy’s mean value theorem洛必达法则L’Hospital’s Rule0/0型不定式indeterminate form of type 0/0不定式indeterminate form泰勒中值定理Taylor’s mean value theorem泰勒公式Taylor formula余项remainder term拉格朗日余项Lagrange remainder term 麦克劳林公式Maclaurin’s formula佩亚诺公式Peano remainder term 凹凸性concavity凹向上的concave upward, cancave up凹向下的,向上凸的concave downward’concave down拐点inflection point函数的极值extremum of function极大值local(relative) maximum最大值global(absolute) mximum极小值local(relative) minimum最小值global(absolute) minimum目标函数objective function曲率curvature弧微分arc differential平均曲率average curvature曲率园circle of curvature曲率中心center of curvature曲率半径radius of curvature渐屈线evolute渐伸线involute根的隔离isolation of root隔离区间isolation interval切线法tangent line method第四章不定积分Chapter4 Indefinite Integrals原函数primitive function(antiderivative) 积分号sign of integration被积函数integrand积分变量integral variable积分曲线integral curve积分表table of integrals换元积分法integration by substitution分部积分法integration by parts分部积分公式formula of integration by parts有理函数rational function真分式proper fraction假分式improper fraction第五章定积分Chapter5 Definite Integrals曲边梯形trapezoid with曲边curve edge窄矩形narrow rectangle曲边梯形的面积area of trapezoid with curved edge积分下限lower limit of integral积分上限upper limit of integral积分区间integral interval分割partition积分和integral sum可积integrable矩形法rectangle method积分中值定理mean value theorem of integrals函数在区间上的平均值average value of a function on an integvals牛顿-莱布尼茨公式Newton-Leibniz formula微积分基本公式fundamental formula of calculus换元公式formula for integration by substitution递推公式recurrence formula反常积分improper integral反常积分发散the improper integral is divergent反常积分收敛the improper integral is convergent无穷限的反常积分improper integral on an infinite interval无界函数的反常积分improper integral of unbounded functions绝对收敛absolutely convergent第六章定积分的应用Chapter6 Applications of the Definite Integrals元素法the element method面积元素element of area平面图形的面积area of a luane figure直角坐标又称“笛卡儿坐标(Cartesian coordinates)”极坐标polar coordinates抛物线parabola椭圆ellipse旋转体的面积volume of a solid of rotation旋转椭球体ellipsoid of revolution, ellipsoid of rotation曲线的弧长arc length of acurve 可求长的rectifiable光滑smooth功work水压力water pressure引力gravitation变力variable force第七章空间解析几何与向量代数Chapter7 Space Analytic Geometry and Vector Algebra向量vector自由向量free vector单位向量unit vector零向量zero vector相等equal平行parallel向量的线性运算linear poeration of vector 三角法则triangle rule平行四边形法则parallelogram rule交换律commutative law结合律associative law负向量negative vector差difference分配律distributive law空间直角坐标系space rectangular coordinates坐标面coordinate plane卦限octant向量的模modulus of vector向量a与b的夹角angle between vector a and b方向余弦direction cosine方向角direction angle向量在轴上的投影projection of a vector onto an axis数量积,外积,叉积scalar product,dot product,inner product曲面方程equation for a surface球面sphere旋转曲面surface of revolution母线generating line轴axis圆锥面cone顶点vertex旋转单叶双曲面revolution hyperboloidsof one sheet旋转双叶双曲面revolution hyperboloids of two sheets柱面cylindrical surface ,cylinder圆柱面cylindrical surface准线directrix抛物柱面parabolic cylinder二次曲面quadric surface椭圆锥面dlliptic cone椭球面ellipsoid单叶双曲面hyperboloid of one sheet双叶双曲面hyperboloid of two sheets旋转椭球面ellipsoid of revolution椭圆抛物面elliptic paraboloid旋转抛物面paraboloid of revolution双曲抛物面hyperbolic paraboloid马鞍面saddle surface椭圆柱面elliptic cylinder双曲柱面hyperbolic cylinder抛物柱面parabolic cylinder空间曲线space curve空间曲线的一般方程general form equations of a space curve空间曲线的参数方程parametric equations of a space curve螺转线spiral螺矩pitch投影柱面projecting cylinder投影projection平面的点法式方程pointnorm form eqyation of a plane法向量normal vector平面的一般方程general form equation of a plane两平面的夹角angle between two planes 点到平面的距离distance from a point to a plane空间直线的一般方程general equation of a line in space方向向量direction vector直线的点向式方程pointdirection form equations of a line方向数direction number直线的参数方程parametric equations of a line两直线的夹角angle between two lines垂直perpendicular直线与平面的夹角angle between a line and a planes平面束pencil of planes平面束的方程equation of a pencil of planes行列式determinant系数行列式coefficient determinant第八章多元函数微分法及其应用Chapter8 Differentiation of Functions of Several Variables and Its Application一元函数function of one variable多元函数function of several variables内点interior point外点exterior point边界点frontier point,boundary point聚点point of accumulation开集openset闭集closed set连通集connected set开区域open region闭区域closed region有界集bounded set无界集unbounded setn维空间n-dimentional space二重极限double limit多元函数的连续性continuity of function of seveal连续函数continuous function不连续点discontinuity point一致连续uniformly continuous偏导数partial derivative对自变量x的偏导数partial derivative with respect to independent variable x高阶偏导数partial derivative of higher order二阶偏导数second order partial derivative 混合偏导数hybrid partial derivative全微分total differential偏增量oartial increment偏微分partial differential全增量total increment可微分differentiable必要条件necessary condition充分条件sufficient condition叠加原理superpostition principle全导数total derivative中间变量intermediate variable隐函数存在定理theorem of the existence of implicit function曲线的切向量tangent vector of a curve法平面normal plane向量方程vector equation向量值函数vector-valued function切平面tangent plane法线normal line方向导数directional derivative梯度gradient数量场scalar field梯度场gradient field向量场vector field势场potential field引力场gravitational field引力势gravitational potential曲面在一点的切平面tangent plane to a surface at a point曲线在一点的法线normal line to a surface at a point无条件极值unconditional extreme values 条件极值conditional extreme values拉格朗日乘数法Lagrange multiplier method拉格朗日乘子Lagrange multiplier经验公式empirical formula最小二乘法method of least squares均方误差mean square error第九章重积分Chapter9 Multiple Integrals二重积分double integral可加性additivity累次积分iterated integral体积元素volume element三重积分triple integral直角坐标系中的体积元素volume element in rectangular coordinate system 柱面坐标cylindrical coordinates柱面坐标系中的体积元素volume element in cylindrical coordinate system球面坐标spherical coordinates球面坐标系中的体积元素volume element in spherical coordinate system反常二重积分improper double integral曲面的面积area of a surface质心centre of mass静矩static moment密度density形心centroid转动惯量moment of inertia参变量parametric variable第十章曲线积分与曲面积分Chapter10 Line(Curve)Integrals and Surface Integrals对弧长的曲线积分line integrals with respect to arc hength第一类曲线积分line integrals of the first type对坐标的曲线积分line integrals with respect to x,y,and z第二类曲线积分line integrals of the second type有向曲线弧directed arc单连通区域simple connected region复连通区域complex connected region格林公式Green formula第一类曲面积分surface integrals of the first type对面的曲面积分surface integrals with respect to area有向曲面directed surface对坐标的曲面积分surface integrals with respect to coordinate elements第二类曲面积分surface integrals of the second type有向曲面元element of directed surface高斯公式gauss formula拉普拉斯算子Laplace operator格林第一公式Green’s first formula通量flux散度divergence斯托克斯公式Stokes formula环流量circulation旋度rotation,curl第十一章无穷级数Chapter11 Infinite Series一般项general term部分和partial sum余项remainder term等比级数geometric series几何级数geometric series公比common ratio调和级数harmonic series柯西收敛准则Cauchy convergence criteria, Cauchy criteria for convergence正项级数series of positive terms达朗贝尔判别法D’Alembert test柯西判别法Cauchy test交错级数alternating series绝对收敛absolutely convergent条件收敛conditionally convergent柯西乘积Cauchy product函数项级数series of functions发散点point of divergence收敛点point of convergence收敛域convergence domain和函数sum function幂级数power series幂级数的系数coeffcients of power series 阿贝尔定理Abel Theorem收敛半径radius of convergence收敛区间interval of convergence泰勒级数Taylor series麦克劳林级数Maclaurin series二项展开式binomial expansion近似计算approximate calculation舍入误差round-off error,rounding error欧拉公式Euler’s formula魏尔斯特拉丝判别法Weierstrass test三角级数trigonometric series振幅amplitude角频率angular frequency初相initial phase矩形波square wave谐波分析harmonic analysis 直流分量direct component基波fundamental wave二次谐波second harmonic三角函数系trigonometric function system 傅立叶系数Fourier coefficient傅立叶级数Forrier series周期延拓periodic prolongation正弦级数sine series余弦级数cosine series奇延拓odd prolongation偶延拓even prolongation傅立叶级数的复数形式complex form of Fourier series第十二章微分方程Chapter12 Differential Equation解微分方程solve a dirrerential equation 常微分方程ordinary differential equation 偏微分方程partial differential equation,PDE微分方程的阶order of a differential equation微分方程的解solution of a differential equation微分方程的通解general solution of a differential equation初始条件initial condition微分方程的特解particular solution of a differential equation初值问题initial value problem微分方程的积分曲线integral curve of a differential equation可分离变量的微分方程variable separable differential equation隐式解implicit solution隐式通解inplicit general solution衰变系数decay coefficient衰变decay齐次方程homogeneous equation一阶线性方程linear differential equation of first order非齐次non-homogeneous齐次线性方程homogeneous linear equation非齐次线性方程non-homogeneous linearequation常数变易法method of variation of constant暂态电流transient stata current稳态电流steady state current伯努利方程Bernoulli equation全微分方程total differential equation积分因子integrating factor高阶微分方程differential equation of higher order悬链线catenary高阶线性微分方程linera differential equation of higher order自由振动的微分方程differential equation of free vibration强迫振动的微分方程differential equation of forced oscillation串联电路的振荡方程oscillation equation of series circuit二阶线性微分方程second order linera differential equation线性相关linearly dependence线性无关linearly independce二阶常系数齐次线性微分方程second order homogeneour linear differential equation with constant coefficient二阶变系数齐次线性微分方程second order homogeneous linear differential equation with variable coefficient特征方程characteristic equation无阻尼自由振动的微分方程differential equation of free vibration with zero damping 固有频率natural frequency简谐振动simple harmonic oscillation,simple harmonic vibration微分算子differential operator待定系数法method of undetermined coefficient共振现象resonance phenomenon欧拉方程Euler equation幂级数解法power series solution数值解法numerial solution勒让德方程Legendre equation微分方程组system of differential equations常系数线性微分方程组system of linera differential equations with constant c。
常用数学符号英文对照

×times sign multiplication 2 × 3 = 6 ·multiplication dot multiplication 2 · 3 = 6÷division sign /division 6 ÷ 2 = 3obelus/ division slash division 6 / 2 = 3–horizontal line division / fractionmod modulo remainder calculation 7 mod 2 = 1. period decimal point, decimal2.56 = 2+56/100separatora b power exponent 23= 8a^b caret exponent 2 ^ 3= 8√a square root √a ·√a = a√9 = ±33√a cube root 3√a ·3√a ·3√a = a3√8 = 24√a fourth root 4√a ·4√a ·4√a ·4√a = a4√16 = ±2n√a n-th root (radical) for n=3, n√8 = 2% percent1% = 1/100 10% × 30 = 3‰per-mille1‰ = 1/1000 = 0.1%ppm per-million1ppm = 1/1000000ppb per-billion 1ppb = 1/1000000000 10ppb × 30 = 3×10-7ppt per-trillion 1ppt = 10-1210ppt × 30 = 3×10-10Geometry symbolsSymbol Symbol Name Meaning / definition Example ∠angle formed by two rays ∠ABC = 30°measuredABC = 30°anglespherical angle AOB = 30°∟right angle = 90°α = 90°°degree 1 turn = 360°α = 60°deg degree 1 turn = 360deg α = 60deg′prime arcminute, 1° = 60′α = 60°59′″double prime arcsecond, 1′ = 60″α = 60°59′59″line infinite lineAB line segment line from point A to point Bray line that start from point Aarc arc from point A to point B= 60°⊥perpendicular perpendicular lines (90° angle) AC ⊥ BC| | parallel parallel lines AB | | CD≅congruent to equivalence of geometric shapes and size ∆ABC≅∆XYZ ~ similarity same shapes, not same size ∆ABC~ ∆XYZ Δtriangle triangle shape ΔABC≅ΔBCD |x-y| distance distance between points x and y | x-y | = 5πpi constant π = 3.141592654...is the ratio between the circumference and diameter of acirclec = π·d = 2·π·rrad radians radians angle unit 360° = 2π rad c radians radians angle unit 360° = 2πcgrad gradians / gons grads angle unit 360° = 400 gradg gradians / gons grads angle unit 360° = 400 g Algebra symbolsSymbol Symbol Name Meaning /definitionExample[a,b] closed interval [a,b] ={x | a≤x≤b}x∈[2,6]∆delta change /difference∆t = t1 - t0∆discriminant Δ =b2 - 4ac∑sigma summation -sum of allvalues in rangeof series∑ x i= x1+x2+...+x n∑∑sigma doublesummation∏capital pi product -product of allvalues in rangeof series∏ x i=x1∙x2∙...∙x ne e constant / Euler's number e =2.718281828...e = lim (1+1/x)x , x→∞γEuler-Mascheroni constantγ =0.527721566...φgolden ratio golden ratioconstantπpi constant π =3.141592654...is the ratiobetween thecircumference anddiameter of acirclec = π·d = 2·π·rLinear Algebra SymbolsSymbol Symbol Name Meaning / definition Example ·dot scalar product a · b×cross vector product a × bA⊗B tensor product tensor product of A and B A⊗B inner product[ ] brackets matrix of numbers( ) parentheses matrix of numbers| A | determinant determinant of matrix Adet(A) determinant determinant of matrix A|| x || double vertical bars normA T transpose matrix transpose (A T)ij = (A)jiA†Hermitian matrix matrix conjugate transpose (A†)ij = (A)ji A*Hermitian matrix matrix conjugate transpose (A*)ij = (A)ji A-1inverse matrix A A-1 = Irank(A) matrix rank rank of matrix A rank(A) = 3 dim(U) dimension dimension of matrix A rank(U) = 3 Probability and statistics symbolsSymbol Symbol Name Meaning / definition ExampleP(A) probabilityfunctionprobability of event A P(AP(A∩B) probability ofeventsintersectionprobability that ofevents A and BP(A∩BP(A∪B) probability ofevents union probability that ofevents A or BP(A∪BP(A | B) conditionalprobabilityfunctionprobability of event Agiven event BoccuredP(A | Bf (x) probabilitydensity function(pdf)P(a ≤ x ≤ b) = ∫f (x) dxF(x) cumulative F(x) = P(X≤ x)distribution function (cdf)μpopulationmean mean of populationvaluesμ = 10E(X) expectationvalue expected value ofrandom variable XE(X) = 10E(X | Y) conditionalexpectation expected value ofrandom variable Xgiven YE(X | Y=2) = 5var(X) variance variance of randomvariable Xvar(X) = 4σ2variance variance ofpopulation valuesσ2 = 4std(X) standarddeviation standard deviation ofrandom variable Xstd(X) = 2σX standarddeviation standard deviationvalue of randomvariable XσX=2median middle value of random variable xcov(X,Y) covariance covariance ofrandom variables Xand Ycov(X,Y) = 4corr(X,Y) correlation correlation ofrandom variables Xand Ycorr(X,YρX,Y correlation correlation ofrandom variables Xand YρX,Y∑summation summation - sum of all values in range of series∑∑doublesummationdouble summationBin (n,p) binomialdistributionf (k) = n C k p k(1-p)n-kPoisson(λ)Poissondistributionf (k)= λk e-λ / k!Geom(p) geometricdistributionf (k) = p(1-p) kHG(N,K,n) hyper-geometric distributionBern(p) Bernoulli distributionCombinatorics SymbolsSymbol Symbol Name Meaning / definition Examplen! factorial n! = 1·2·3·...·n5! = 1·2·3·4·5 = 120 n P k permutation 5P3 = 5! / (5-3)! = 60 n C kcombination 5C3 = 5!/[3!(5-3)!]=10Set theory symbolsSymbol Symbol Name Meaning / definition Example{ } set a collection of elements A = {3,7,9,14},B = {9,14,28}A ∩B intersection objects that belong to set A and setBA ∩B = {9,14}A ∪B union objects that belong to set A or setBA ∪B ={3,7,9,14,28}A ⊆B subset subset has fewer elements orequal to the set{9,14,28} ⊆{9,14,28}A ⊂B proper subset / strict subset has fewer elements than {9,14} ⊂subset the set {9,14,28}A ⊄B not subset left set not a subset of right set {9,66} ⊄{9,14,28}A ⊇B superset set A has more elements or equalto the set B{9,14,28} ⊇{9,14,28}A ⊃B proper superset / strictsupersetset A has more elements than setB{9,14,28} ⊃{9,14}A ⊅B not superset set A is not a superset of set B {9,14,28} ⊅{9,66}2A power set all subsets of A power set all subsets of AA =B equality both sets have the same members A={3,9,14}, B={3,9,14}, A=BA c complement all the objects that do not belong to set AA \B relative complement objects that belong to A and not toBA = {3,9,14},B = {1,2,3},A-B = {9,14}A -B relative complement objects that belong to A and not toBA = {3,9,14},B = {1,2,3},A-B = {9,14}A ∆B symmetric difference objects that belong to A or B butnot to their intersectionA = {3,9,14},B = {1,2,3},A ∆B ={1,2,9,14}A ⊖B symmetric difference objects that belong to A or B butnot to their intersectionA = {3,9,14},B = {1,2,3},A ⊖B ={1,2,9,14}a∈A element of set membership A={3,9,14}, 3 ∈Ax∉A not element of no set membership A={3,9,14}, 1 ∉A(a,b) ordered pair collection of 2 elementsA×B cartesian product set of all ordered pairs from A andB|A| cardinality the number of elements of set A A={3,9,14},|A|=3#A cardinality the number of elements of set A A={3,9,14},#A=3aleph-null infinite cardinality of natural numbers setaleph-one cardinality of countable ordinal numbers setØ empty set Ø = { } C = {Ø} universal set set of all possible values0natural numbers / wholenumbers set (with zero) 0= {0,1,2,3,4,...} 0 ∈01natural numbers / wholenumbers set (withoutzero)1= {1,2,3,4,5,...} 6 ∈1 integer numbers set = {...-3,-2,-1,0,1,2,3,...} -6 ∈rational numbers set = {x | x=a/b, a,b∈} 2/6 ∈real numbers set = {x | -∞ < x <∞}∈complex numbers set= {z | z=a+bi,-∞<a<∞,-∞<b<∞}6+2i∈Logic symbolsSymbol Symbol Name Meaning / definition Example ·and and x·y^ caret / circumflex and x ^ y& ampersand and x & y+ plus or x + y∨reversed caret or x∨y | vertical line or x | yx' single quote not - negation x'x bar not - negation x¬not not - negation ¬x! exclamation mark not - negation ! x⊕circled plus / oplus exclusive or - xor x⊕y ~ tilde negation ~ x⇒implies⇔equivalent if and only if (iff)↔equivalent if and only if (iff)∀for all∃there exists∄there does not exists∴therefore∵because / sinceCalculus & analysis symbolsSymbol Symbol Name Meaning / definition Example limit limit value of a functionεepsilon represents a very small number,ε→0near zeroe e constant / Euler'snumber e = 2.718281828...e = lim(1+1/x)x ,x→∞y ' derivative derivative - Lagrange's notation (3x3)' = 9x2y '' second derivative derivative of derivative (3x3)'' = 18xy(n)nth derivative n times derivation (3x3)(3) = 18 derivative derivative - Leibniz's notation d(3x3)/dx = 9x2second derivative derivative of derivative d2(3x3)/dx2 = 18xnth derivative n times derivationtime derivative derivative by time - Newton's notationtime secondderivativederivative of derivativeD x y derivative derivative - Euler's notationD x2y second derivative derivative of derivativepartial derivative ∂(x2+y2)/∂x = 2x ∫integral opposite to derivation ∫f(x)dx∫∫double integral integration of function of 2variables∫∫f(x,y)dxdy∫∫∫triple integral integration of function of 3variables∫∫∫f(x,y,z)dxdydz∮closed contour / lineintegral∯closed surfaceintegral∰closed volumeintegral[a,b] closed interval [a,b] = {x | a ≤ x ≤ b}(a,b) open interval (a,b) = {x | a < x < b}i imaginary unit i≡ √-1 z = 3 + 2i z* complex conjugate z = a+bi→z*=a-bi z* = 3 - 2i z complex conjugate z = a+bi→z = a-bi z = 3 - 2i ∇nabla / del gradient / divergence operator ∇f (x,y,z) vectorunit vectorx * y convolution y(t) = x(t) * h(t)Laplace transform F(s) = {f (t)}Fourier transform X(ω) = {f (t)}δdelta function∞lemniscate infinity symbol。
英文标点符号的使用

英文标点符号的使用英文标点符号的使用句点(full stop / period,“.”)问号(question mark,“?”)感叹号(exclamation mark,“!”)逗点(comma,“,”)冒号(colon,“:”)分号(semicolon,“;”)连字符(hyphen,“-”)连接号(en dash,“C”)破折号(em dash,“―”)括号(parentheses,小括号“( )”;中括号“[]”;大括号“{}”)引号(quotation marks,双引号““”;单引号“‘”)缩写及所有格符号(apostrophe,“‘”)一、.句点1.句点用于当一句话完全结束时。
2.句点也可以用于英文单词的缩写,如mrs., dr., p.s. 等。
但要注意的是当缩写的字母形成了一个单词的时候就不要使用句点。
如ibm, dna 等。
二、?问号问号要用在一个直接的问句,而不是间接的。
如how will you solve the problem?是正确的用法,但用在i wonder how you will solve the problem?就不对了,应该使用句点而不是问号。
另外,在客气的用语中,也是用句点而不是问号.如will you please give me a call tomorrow. 三、! 感叹号感叹号用于感叹和惊叹的陈述中,在商业写作中要注意感叹号的应用,因为不恰当的使用会显得突兀及不稳重。
四、;分号1.与中文一样,分号用于分隔地位平等的独立子句。
在某些情况下,使用分号比使用句点更显出子句之间的紧密联系,另外分号也经常与连接副词thus, however, therefore一起使用(放在这些词语之前)。
如i realize i need exerci se; however, i’ll lie down first to think about it. 2.在句子中如果已经使用过逗点,为了避免歧义的产生,就用分号来分隔相似的内容。
常用标点的英文表达和用法

℃ Celsius system摄氏度{ open brace, opencurly左花括号} close brace, close curly右花括号( open parenthesis, open paren左圆括号) close parenthesis, close paren右圆括号() brakets/ parentheses括号[ open bracket 左方括号] close bracket 右方括号[] square brackets方括号. period, dot句号,点| vertical bar, vertical virgule竖线& ampersand, and, reference, ref和,引用* asterisk, multiply, star, pointer星号,乘号,星,指针/ slash, divide, oblique 斜线,斜杠,除号// slash-slash, comment 双斜线,注释符# pound井号\ backslash, sometimes escape反斜线转义符,有时表示转义符或续行符~ tilde波浪符. full stop句号, comma逗号: colon冒号; semicolon分号? question mark问号! exclamation mark (英式英语) exclamation point (美式英语) ' apostrophe撇号- hyphen连字号-- dash 破折号... dots/ ellipsis省略号" single quotation marks 单引号"" double quotation marks 双引号‖ parallel 双线号& ampersand = and~swung dash 代字号§ section; division 分节号→arrow 箭号;参见号英文标点符号的使用方法一、.句点1.句点用于当一句话完全结束时。
常用数学符号英文对照
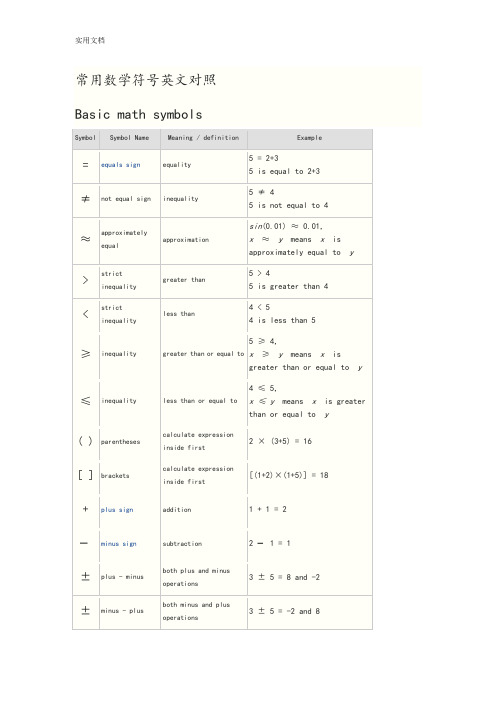
常用数学符号英文对照Basic math symbolsSymbol Symbol Name Meaning / definition Example= equals sign equality 5 = 2+35 is equal to 2+3≠not equal sign inequality 5 ≠ 45 is not equal to 4≈approximatelyequal approximationsin(0.01) ≈ 0.01,x≈y means x isapproximately equal to y> strictinequality greater than5 > 45 is greater than 4< strictinequality less than4 < 54 is less than 5≥inequality greater than or equal to 5 ≥ 4,x≥y means x is greater than or equal to y≤inequality less than or equal to 4 ≤ 5,x ≤ y means x is greater than or equal to y( ) parentheses calculate expressioninside first2 × (3+5) = 16[ ] brackets calculate expressioninside first[(1+2)×(1+5)] = 18 + plus sign addition 1 + 1 = 2−minus sign subtraction 2 − 1 = 1±plus - minus both plus and minusoperations3 ± 5 = 8 and -2±minus - plus both minus and plusoperations3 ± 5 = -2 and 8* asterisk multiplication 2 * 3 = 6×times sign multiplication 2 × 3 = 6·multiplicationdotmultiplication 2 · 3 = 6÷division sign /obelusdivision 6 ÷ 2 = 3/ division slash division 6 / 2 = 3–horizontal line division / fractionmod modulo remainder calculation 7 mod 2 = 1. period decimal point, decimalseparator2.56 = 2+56/100a b power exponent 23= 8a^b caret exponent 2 ^ 3= 8√a square root √a ·√a = a√9 = ±33√a cube root 3√a ·3√a ·3√a = a3√8 = 24√a fourth root 4√a ·4√a ·4√a ·4√a =a4√16 = ±2n√a n-th root(radical)for n=3, n√8 = 2 % percent1% = 1/100 10% × 30 = 3‰per-mille1‰ = 1/1000 = 0.1% 10‰× 30 = 0.3 ppm per-million1ppm = 1/1000000 10ppm × 30 = 0.0003 ppb per-billion 1ppb = 1/1000000000 10ppb × 30 = 3×10-7Geometry symbolsSymbolSymbol NameMeaning / definitionExample∠angle formed by two rays ∠ABC = 30°measured angle ABC = 30°sphericalangleAOB = 30°∟ right angle = 90° α = 90°°degree 1 turn = 360° α = 60° degdegree1 turn = 360degα = 60deg ′ primearcminute, 1° = 60′α = 60°59′″double prime arcsecond, 1′ = 60″ α = 60°59′59″line infinite lineABline segment line from point A to point Bray line that start from point Aarc arc from point A to point B= 60°⊥ perpendicular perpendicular lines (90° angle) AC ⊥ BC| | parallel parallel lines AB | | CD≅ congruent toequivalence of geometric shapes and size∆ABC ≅ ∆XYZ~similarity same shapes, not same size ∆ABC~ ∆XYZΔtriangle triangle shape ΔABC≅ΔBCD |x-y| distance distance between points x and y | x-y| = 5πpi constant π= 3.141592654...is the ratio between the circumferenceand diameter of a circlec= π·d=2·π·rrad radians radians angle unit 360° = 2π rad c radians radians angle unit 360° = 2πcgrad gradians /gonsgrads angle unit 360° = 400 gradggradians /gonsgrads angle unit 360° = 400 gAlgebra symbolsSymbol Symbol Name Meaning / definition Examplex x variable unknown value to find when 2x= 4, then x= 2 ≡equivalence identical to≜equal by definition equal by definition:= equal by definition equal by definition~ approximately equal weak approximation 11 ~ 10≈approximately equal approximation sin(0.01) ≈ 0.01∝proportional to proportional to y∝x when y= kx,k constant ∞lemniscate infinity symbol≪much less than much less than 1 ≪ 1000000≫much greater than much greater than 1000000 ≫ 1( ) parentheses calculate expressioninside first2 * (3+5) = 16[ ] brackets calculate expressioninside first[(1+2)*(1+5)] = 18 { } braces set⌊x⌋floor brackets rounds number to lowerinteger⌊ 4.3⌋ = 4⌈x⌉ceiling brackets rounds number to upperinteger⌈ 4.3⌉ = 5x! exclamation mark factorial4! = 1*2*3*4 = 24 | x|single vertical bar absolute value | -5 | = 5f (x) function of x maps values of x to f(x) f (x) = 3x+5(f∘g) function composition(f∘g) (x)= f (g(x))f (x)=3x,g(x)=x-1 ⇒(f∘g)(x)=3(x-1)(a,b) open interval (a,b) ={x| a< x< b}x∈ (2,6)[a,b] closed interval [a,b] ={x| a≤x≤b}x∈ [2,6]∆delta change / difference ∆t= t1 -t0∆discriminant Δ = b2- 4ac∑sigma summation - sum of allvalues in range of series∑x i= x1+x2+...+x n∑∑sigma double summation∏capital piproduct - product of all values in range of series∏ x i =x 1∙x 2∙...∙x nee constant / Euler's numbere = 2.718281828... e = lim (1+1/x )x , x →∞γ Euler-Mascheroni const antγ = 0.527721566...φgolden ratio golden ratio constantπpi constantπ = 3.141592654...is the ratio between the circumference and diameter of a circlec = π·d = 2·π·rLinear Algebra SymbolsSymbolSymbol NameMeaning / definitionExample· dot scalar producta ·b ×cross vector producta ×b A ⊗Btensor product tensor product of A and BA ⊗ Binner product[ ] brackets matrix of numbers( ) parentheses matrix of numbers| A | determinant determinant of matrix Adet(A )determinant determinant of matrix A|| x || double vertical bars normA Ttranspose matrix transpose(A T)ij = (A )jiProbability and statistics symbols Symbol Symbol Name Meaning / definition Example P(A) probabilityfunctionprobability of event A P(A) = 0.5P(A∩B) probability ofeventsintersectionprobability that of events Aand BP(A∩B) = 0.5P(A∪B) probability ofevents union probability that of events Aor BP(A∪B) = 0.5P(A| B) conditionalprobabilityfunctionprobability of event A givenevent B occuredP(A | B) = 0.3f (x) probabilitydensityfunction (pdf)P(a ≤x ≤b)= ∫ f (x)dxF(x) cumulativedistributionfunction (cdf)F(x) = P(X≤x)μpopulation mean mean of population values μ= 10E(X) expectationvalue expected value of randomvariable XE(X) = 10E(X | Y) conditionalexpectation expected value of randomvariable X given YE(X | Y=2) = 5var (X )variancevariance of random variable Xvar (X ) = 4σ2variance variance of population valuesσ2 = 4std (X )standard deviation standard deviation of random variable Xstd (X ) = 2σX standard deviationstandard deviation value of random variable X σX = 2medianmiddle value of random variable xcov (X ,Y ) covariancecovariance of random variables X and Y cov (X,Y ) = 4corr (X ,Y ) correlationcorrelation of random variables X and Y corr (X,Y ) = 0.6ρX ,Ycorrelationcorrelation of random variables X and YρX ,Y= 0.6∑summationsummation - sum of all values in range of series∑∑double summationdouble summationMo mode value that occurs most frequently in populationMR mid-rangeMR = (x max +x min )/2Mdsample median half the population is below this valueQ 1lower / first quartile25% of population are below this valueQ 2median / second quartile50% of population are below this value = median of samplesQ3upper / thirdquartile 75% of population are below this valuex sample mean average / arithmetic mean x= (2+5+9) / 3 = 5.333s2sample variance population samples varianceestimators2= 4s sample standarddeviation population samples standard deviation estimators= 2z x standard score z x= (x-x) /s xX ~ distribution of X distribution of randomvariable XX ~N(0,3)N(μ,σ2) normaldistributiongaussian distribution X ~N(0,3)U(a,b) uniformdistributionequal probability in rangea,bX ~U(0,3)exp(λ) exponentialdistributionf (x)= λe-λx, x≥0gamma(c, λ) gammadistributionf (x)= λ c x c-1e-λx/ Γ(c), x≥0χ2(k) chi-squaredistributionf (x)= x k/2-1e-x/2/( 2k/2 Γ(k/2) )F (k1, k2) F distributionBin(n,p) binomialdistributionf (k)= n C k p k(1-p)n-kPoisson(λ) Poissondistributionf (k)= λk e-λ/ k!Geom(p) geometricdistributionf (k)= p(1-p)kHG(N,K,n) hyper-geometric distributionBern(p) Bernoulli distributionSet theory symbolsSymbol Symbol Name Meaning / definition Example{ } set a collection of elements A = {3,7,9,14},B = {9,14,28}A ∩B intersection objects that belong to set A and setBA ∩B = {9,14}A ∪B union objects that belong to set A or setBA ∪B ={3,7,9,14,28}A ⊆B subset subset has fewer elements or equal tothe set{9,14,28} ⊆{9,14,28}A ⊂B proper subset /strict subsetsubset has fewer elements than theset{9,14} ⊂{9,14,28}A ⊄B not subset left set not a subset of right set {9,66} ⊄{9,14,28}A ⊇B superset set A has more elements or equal tothe set B{9,14,28} ⊇{9,14,28}A ⊃B proper superset /strict supersetset A has more elements than set B{9,14,28} ⊃{9,14}A ⊅B not superset set A is not a superset of set B {9,14,28} ⊅{9,66}2Apower set all subsets of Apower set all subsets of AA =B equalityboth sets have the same membersA={3,9,14},B={3,9,14}, A=BA ccomplementall the objects that do not belong to set AA \B relative complementobjects that belong to A and not to BA = {3,9,14},B = {1,2,3}, A-B = {9,14} A - B relative complementobjects that belong to A and not to BA = {3,9,14},B = {1,2,3}, A-B = {9,14} A ∆ Bsymmetric differenceobjects that belong to A or B but not to their intersectionA = {3,9,14},B = {1,2,3}, A ∆ B = {1,2,9,14} A ⊖ Bsymmetric differenceobjects that belong to A or B but not to their intersectionA = {3,9,14},B = {1,2,3}, A ⊖ B = {1,2,9,14}a ∈Aelement of set membershipA={3,9,14}, 3 ∈ Ax ∉ A not element ofno set membershipA={3,9,14}, 1 ∉ A(a ,b ) ordered pair collection of 2 elementsA ×B cartesian product set of all ordered pairs from A and B|A| cardinalitythe number of elements of set AA={3,9,14}, |A|=3 #Acardinality the number of elements of set AA={3,9,14}, #A=3aleph-nullinfinite cardinality of natural numbers setaleph-one cardinality of countable ordinal numbers setØ empty set Ø = { }C = {Ø}universal set set of all possible valuesnatural numbers /whole numbers set (with zero) 0= {0,1,2,3,4,...} 0 ∈1natural numbers /whole numbers set (without zero)1= {1,2,3,4,5,...} 6 ∈1integer numbers set={...-3,-2,-1,0,1,2,3,...}-6 ∈rational numbers set= {x | x =a /b , a ,b ∈}2/6 ∈real numbers set= {x | -∞ < x <∞} 6.343434∈complex numbers set= {z | z=a +bi , -∞<a <∞, -∞<b <∞}6+2i ∈∨reversed caret or x∨y | vertical line or x| y x' single quote not - negation x'x bar not - negation x¬not not - negation ¬x ! exclamation mark not - negation ! x⊕circled plus / oplus exclusive or - xor x⊕y ~ tilde negation ~ x⇒implies⇔equivalent if and only if (iff)↔equivalent if and only if (iff)∀for all∃there exists∄there does not exists∴therefore∵because / sinceCalculus & analysis symbolsSymbol Symbol Name Meaning / definition Examplelimit limit value of a functionεepsilonrepresents a very small number, near zeroε → 0eeconstant / Euler's numbere = 2.718281828...e = lim(1+1/x )x,x →∞y ' derivativederivative - Lagrange's notation (3x 3)' = 9x 2y '' second derivative derivative of derivative(3x 3)'' = 18xy (n )nth derivativen times derivation(3x 3)(3)= 18derivativederivative - Leibniz's notation d (3x 3)/dx = 9x 2secondderivativederivative of derivatived 2(3x 3)/dx 2 = 18xnthderivativen times derivationtime derivative derivative by time - Newton's notationtime second derivativederivative of derivativeD x y derivative derivative - Euler's notationD x 2ysecond derivativederivative of derivativepartialderivative∂(x 2+y 2)/∂x = 2x∫ integral opposite to derivation∫ f(x)dx∫∫ double integral integration of function of 2 variables∫∫ f(x,y)dxdy ∫∫∫triple integral integration of function of 3 variables∫∫∫ f(x,y,z)dxdydz∮closedcontour / line integral∯closedsurface integral∰closedvolume integral[a ,b ] closed interval [a ,b ] ={x | a ≤ x ≤ b }(a ,b )open interval (a ,b ) ={x | a < x < b }i imaginary unit i ≡ √-1 z = 3 + 2iz * complex conjugate z = a +bi → z *=a -bi z* = 3 - 2izcomplex conjugatez = a +bi → z = a -bi z = 3 - 2i∇ nabla / del gradient / divergence operator ∇f (x ,y ,z )vectorunit vectorx * y convolutiony (t ) = x (t ) * h (t )) = {{。
英文,常用数学符号、公式和等式的读法

一、常用数学符号、公式和等式的读法+ 加号,加 plus+ 正号 positive- 减号,减 minus- 负号,负 negetive± 加或减 plus or minus± 正或负 plus or minus· 乘 multiplied by times into÷ 除 divided by: 比 proportional to= 等号 equal sign= 等于 to equal,to equals> 大于 greater than< 小于 less than≥ 大于等于 greater than or equal≤ 小于等于less than or equal≡ 恒等于 identical with≈ 约等于 approximately equal≌ 全等于 congruent~等价于 equivalent to;相似于 similar to→ 趋近于 approaches( ) 括号,括弧 1) parentheses;parenthesis;sign parenthesis圆括号,圆括弧 2) round brackets[ ] 方括号1) squre [angular] brackets括号2) brackets{ } 花括号 braces∑ 求和summstion of;sigma从1到n的和 the sum form i equalsone to n;sigma从1到n的积 the product form i equalsone to nx1 +x2+x3+ΛΛ x one x two plus x three,etc(et cetera)a=b 1) a equals to b2) a is equal to b3) a is ba≠b a is not equal to b;a is not ba>b a is greater than baa≥b a is greater than or equal to ba≤b a is less than or equal to ba≈b a approximately equal (s) ba∝b a varies directly as b;a is (directly) proportional to ba∈A a is member of set AA⊂B A is contained in B;A is a proper subset of B AIB A intersection BAYB A union{ }或φ empty set⇒implies⇔is equivalent to xRy x is in the relation R to y a±b a plus or minus b(a+b)(a-b) a plus b,a minus b(a+b)2 a plus b all squared(a÷b)2 a over b all squaredn! n factorial;factorial na% a persent|a| mod a;modulus ax→∞ x approaches infinity0< x0≤x≤a zero is less than or equal to x is less than or equal to ac=a.b 1)c equals (is equal to) a multiplied by b2) c equals a times b1:2 the ratio of one to two1/2 a half;one half1/3 a third;one third1/100 a[one] hundredth1/1000 a[one] thousandth0.1(.1) zero point one;nought point one0.01(.01) zero point zero one;nought point nought one3.1416 three point one four one six14. one four point one four,one four recurringa:b the ratio of a to ba:b=c 1) a devided by b equals c2) a devided by b is c3)the ratio of a to b is ca:b=c:d 1) the ratio of a to b equals the ratio of c to d2) a is to b as c is to da+b>c a plus b is greater then ca+b< then b plus>a+b=c a plus b is (are;equals;is equal to) ca-b=c a minus b(b from a) is(equals;is equal to;leaves) c (a,b) a<X[a,b]a≤x≤b the closed interval from a to b(a,b) the interval a<X≤B< td>[a,b] the interval a≤x<B< td>a<Xa≤x≤b a is less then or equal to x is less then or equal to blogax logarithm (base) of xlnx natural logarithm of xx2 1)x square;x squured2) x to the second power3) x raised to the second power4) the square of x5) the second power of x6) x to the secondx3 1)x cube;x cubed2) x to the third power3) x raised to the third power4) the cube of x5) the third power of x6) x to the thirdx n 1)x to the n-th power2) x raised to the n-th power3) the n-th power of x4) x to the n-thx-n 1) x to the minus n-th2) x to the minus n-th powerradical=b 1) the square root of a is(equals) b 2) the square root out of a is(equals) bthe square root of athe cube root of athe cube rootthe n-th roota′ a primea n 1) a second prime2) a double prime3) a twice dashed;a m 1) a triple prime2) a third primea1) a sub one12) a firsta2 1) a sub two2) a second1) a sub mam2) a m-tha'1) a prime,sub mm2) a sub m,primea first primea'12 a second, second primeany first derivative of ysecond derivative of ydy/dx first derivative of y with respect to xd2y/dx2 second derivative of y with respect to xy=f(x) y is a function of x∫ integral of1) integral of……from a to b2) integral of……between limits a and bcapital L equals the square root of (out of ) capital R squareplus minus x squarea to the m by n-th power equals the n-th root of (out of) a tothe m-th powerP=∞ p is equal to infinity∠ angle⊥ perpendicular;is perpendicular to∥ parallel;is parallel to△ABC triangje ABCvector Fa bar≌ is congruent to~ is similar tA-1 inverse of matrix A % percent二、英语缩写词abs absolute 绝对的absolutely 绝对地A.D Anno Domini 公元ad inf ad infinitum 趋于无限ads address 地址agg aggregate 总数、共计al algebra 代数alt altitude 高度alternate 交错,交替a.m above-mentioned 上述的a.m. arithmetic mean 算术平均amt amount 数量ans answer 答案、解答、回答AoI and-or-inverter 与或非等差数列A.P arithmeticprogressionappl application 应用appr approximate 近似、约计appx appendix 附录arg argument 自变数,幅角arith arithmetic 算术aut automatic 自动的aux,auxil auxiliary 辅助的av,avg average 平均Ax Axiom 公理B.C Before Christ 公元前二进制编码的十进制BCD Binary CodedDecimalBC.O Binary Coded Octal 二进制编码的八进制℃(c)centigrate 摄氏度C cubic 立方的cycle 周centi 厘,百分之一ca circa 大约CAD Computer-Aided计算机辅助设计Design计算机辅助教学CAI Computer-AidedInstructioncalcd calculated 计算的cat catalog (ue) 目录,一览表C.C.W Counter-Clockwise 逆时针方向c.d centre distance 中心距离cf. confer 参看、见、比较cg center of gravity 重心厘米·克·秒(单位)制C.G.S Centimetre GrammeSecondCh. Chapter 章chap chapter 章char character 字符cir circular 圆形的circum circumference 圆周cit cited 引用ckt circuit 电路C.l. center-line 中心线算术平均法,平均高度法C.L.A center lineaverage methodcm centimetre 厘米coeff. coefficient 系数com common 公,公共col column 行,纵行,栏,项目,柱comp. compare 比较con contra 相反conclusion 结论con.sec conic sections 圆锥曲线const constant 常数construction 作图contcontinued 续,接(contd)Contr. Contracted 省略的Contraction 省略Cor corollary 推论,系cp compare 比较ct constant 常数circuit 电路,线路ctr (s) center (s) 中心cu (cub) cubic 立方C.W. clockwise 顺时针方向CY cycle 周期,周d degree 度D density 密度diameter 直径date 日期D.C. digital computer 数字计算机微分方程D.E differentialequationdef(def’n)definition 定义deg degree 度demon demonstrative 求证den density 密度der derivative 导数,微商det detail 详细,细节,详图DF decimal fraction (十进)小数dia (m) diameter 直径diag diagram 图,图解diff difference 差,不同DIV divide 除Do (d°)ditto 同上,同前,如前所述doub double 加倍,二倍,成双的,成倍的DP data processing 数据处理E east 东edit edition 版,版本e.e error expected 允许的误差例如e.g exempligratia=forexampleeq. equal 相等eq (eq’n)equation 等式,方程esp. especially 特别et al et alii 及其他et alibi 及别处etc et cetera 等等et seq et sequentia 及以下等等ex (s) example(s) 例exercise 练习,习题extra 特别的ext external 外部的exterior 在外f frequency 频率fig figure 图,图形fn function 函数,功能FQCY frequency 频率fxd fixed 固定的,不变的g(gm) gramme 克GA general average 平均值最大公约数G.C.D greatest commondivisor最大公因子G.C.F greatest commonfactor最大公约数G.C.M greatest commonmeasuregeom. geometry 几何学G.P geometrical等比数列,几何数列progressiongr(grm) gram 克h hour 小时height 高,高度H.C.F. highest common最高公因式,最大公约数factorhf half 半hor horizontal 水平的hr hour 小时hyp hypothesis 假设ib (ibid) ibidem 在同处(书,文献等出处) id idem 同前,同上,同作者,同样iden identical 恒等,全等i.e id est=that is 即,就是,换言之ig idem quod 如同ih inverted hour 逆(反)时针的im image 图像inc increase 增加ind index 索引,指标,刻度indef indefinite 无限,不定in.ex in extenso 全部inf infinity 无穷大,无限大infra 上、下限inh inverted hour 逆(反)时针的int interior 内部的,在内int.al inter alia 尤其I/O input/output 输入/输出信息技术IT informationtechnologyinformation信息论theory独立变数IV independentvariableJ journal 期刊,杂志jour journal 期刊,杂志kg kilogram 千克km kilometer 千克l length 长度l.c loco citato 上述引文中最小公倍数(式)L.C.M. least commonmultipleLowest common multiple 最低公倍式Lgth length 长度l.h left hand 左方,左侧lim limit 极限lin linear 直线的,一次的,线性的lit liter (公)升loc location 位置loc.cit loco citato 上述引文中最低(数)位,最右(数)位ISD least significantdigitM mega 兆(106)mille 千M(m) medium 中间,中等m metre 米milli 毫(10-3)million 兆(106)minute 分钟μ(mu)micro 微(10-6)平均绝对误差mae mean absoluteerrormag magnitude 量,大小math mathematical 数学的mathematics 数学max maximum 最大,最大值min minimum 最小,最小值minute 分钟mo (s) month(s) 月mon monthly 月刊MS mean square 均方n net 净N number 数,编号,第…号North 北Northern 北方的n.a.s.c necessary andsufficient condition 充要条件,充分且必要的条件N.B nota bene= note注意wellneg negative 负的Net network 网络No(s) number(s) 数,编号,第…号nr near 在…附近常微分方程O.D.E. ordinarydifferentialequationopp opposed 相反的,对面ord ordinary 普通的,通常的p page 页PAR parallel 平行的,平行线,并联的par paragraph 节,段P.C. per cent 百分比pcs pieces 个,件,份偏微分方程P.D.E partialdifferentialequationPERT programevaluation andreview techniques 计划评审技术(统筹方法)ph phase 相位,相pos positive 正的pp pages 负(复数)p.p proportional part 比例部分Pr pair 偶,对pr(pri,pry) primary 初级,最初的prep perpendicular 垂直,正交proc proceeding 学报,会刊ps pseudo 伪,假pt(s) part(s) 部分p.t.o please turn over 请见(本页的)反面,请翻到下页q question 问题q.e quod est 这就是,即Q.E D quod erat证毕,证完,这就是所要证的,所求证者demonstrandumw.r.t with respect to 关于,相对于。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
"" double quotation marks 双引号
‖ parallel 双线号
& ampersand = and
~ swung dash 代字号
§ section; division 分节号
→ arrow 箭号;参见号
常用符号的英文名称
+ plus 加号;正号
- minus 减号;负号
± plus or minus 正负号
× is multiplied by 乘号
÷ is divided by 除号
= is equal to 等于号
≠ is not equal to 不等于号
≡ is equivalent to 全等于号
/ slash, divide, oblique 斜线,斜杠,除号
// slash-slash, comment 双斜线,注释符
# pound 井号
\ backslash, sometimes escape 反斜线转义符,有时表示转义符或续行符
~ tilde 波浪符
. full stop 句号
≤ is less than or equal to 小于或等于号
≥ is more than or equal to 大于或等于号
% per cent 百分之…
‰ per mill 千分之…
∞ infinity 无限大号
∝ varies as 与…成比例
√ (square) root 平方根
∪ union of 并,合集
∩ intersection of 交,通集
∫ the integral of …的积分
∑ (sigma) summation of 总和
° degree 度
′ minute 分
″ second 秒
℃ Celsius system 摄氏度
{ open brace, open curly 左花括号
∵ since; because 因为
∴ hence 所以
∷ equals, as (proportion) 等于,成比例
∠ angle 角
⌒ semicircle 半圆
⊙ circle 圆
○ circumference 圆周
π pi 圆周率
△ triangle 三角形
⊥ perpendicular to 垂直于
≌ is equal to or approximately equal to 等于或约等于号
≈ is approximately equal to 约等于号
< is less than 小于号
> is greater than 大于号
≮ is not less than 不小于号
≯ is not more than 不大于号
, comma 逗号
:colon 冒号
; semicolon 分号
? question mark 问号
! exclamation mark (英式英语) exclamation point (美式英语)
' apostrophe 撇号
- hyphen 连字号
-- dash 破折号
... dots/ ellipsis 省略号
} close brace, close curly 右花括号
( open parenthesis, open paren 左圆括号
) close parenthesis, close paren 右圆括号
() brakets/ parentheses 括号
[ open bracket 左方括号
] close bracket 右方括号
[] square brackets 方括号
. period, dot 句号,点
| vertical bar, vertical virgule 竖线
& ampersand, and, reference, ref 和,引用
* asterisk, multiply, star, pointer 星号,乘号,星,指针
