高一平面向量复习专题
高一平面向量的知识点归纳总结

高一平面向量的知识点归纳总结平面向量是高中数学中一个重要的概念,也是数学建模中常用的工具。
在高一阶段,学生首次接触平面向量,并需要掌握其相关的计算方法和性质。
本文将对高一平面向量的知识点进行归纳总结,以帮助学生更好地理解和掌握这一概念。
一、平面向量的定义与表示方法平面向量是有大小和方向的量,可以用有向线段表示,用一个点与另一个点之间的坐标差表示。
一般用字母加箭头表示,如AB→表示从点A指向点B的向量。
二、平面向量的运算1. 平面向量的相加减:向量的相加是指将一个向量的终点与另一个向量的起点相连,并以此线段为新向量的长度和方向。
向量的相减可以转换为向量的相加:A - B = A + (-B)。
2. 向量的数量乘法:向量的数量乘法是指将向量的长度与一个实数相乘,得到一个新的向量,其方向与原向量相同(若实数为正)或相反(若实数为负)。
3. 向量的数量积:向量的数量积等于向量的长度乘积与两向量夹角的余弦值的乘积。
数量积具有交换律和分配律。
三、平面向量的基本性质1. 平移性质:可以将一个向量平移至另一个点,其大小和方向不变。
2. 平面向量的共线性:如果两个向量的方向相同或相反,那么它们是共线的;如果两个向量的方向互相垂直,那么它们是互相垂直的;如果两个向量不共线且不垂直,那么它们是不共线也不垂直的。
3. 向量共点性质:三个向量共点的充分必要条件是其中一个向量等于另外两个向量的和。
四、平面向量的几何应用平面向量在几何中具有广泛的应用。
其中,平面向量的模表示向量的长度,平面向量的方向角表示向量与坐标轴的夹角,平面向量的端点坐标可以确定向量在平面直角坐标系中的位置。
通过对平面向量的几何运算,可以解决平面上的定位、距离和角度等问题。
五、平面向量的坐标表示在平面直角坐标系中,一个向量可以用其横坐标和纵坐标来表示。
具体地说,如果向量的起点在原点O(0, 0),终点在A(x₁, y₁),那么这个向量可以用[x₁, y₁]来表示。
(word完整版)高一数学数学必修4平面向量复习题

1•设a 、b 、c 是单位向量,且 a -b = o ,贝U a c ? b c 的最小值为(D )2A.1B.2C. 2A. 2B. 2 2C. 1D.12r r rr r r r r r uu r r r 2解析Q a,b,c 是单位向量a c ?bc ago (a b)gs crr r _ r r r1 |ab|gc| 1 <2cos ab,c 1.2.2.已知向量a 2,1 ,ab 10,|ab| 5J2,则 |b|(C )A. .5B. .10C.5D. 25r r 宀 r 宀 r r r 宀“ r2 2 2 2解析 Q50 |a b| |a | 2a gD |b| 5 20 | b ||b| 5 故选 C.3.平面向量a 与b 的夹角为600, a (2,0) , b 1则a 2b ( B )A.、3B. 2 3C. 4D.2解析 由已知 |a|= 2,|a + 2b|2= a 2 + 4a b + 4b 2= 4+ 4X2X1 Xcos60° + 4= 12A a 2b2^3LUIUuiuuuu uiPC) = 2AP PM=2 AP PM cosO 2 -5.已知a 3,2 , b1,0,向量a b 与a2b 垂直,则实数的值为()1 A.—1 B.-1 C.—D.17766uuruur uuu UUJ uujruuu6.设 D 、E 、 F 分别是△ ABC 的三边 BC 、CA 、AB 上的点,且DC2BD,CE2EA, AF 2FB,UJLT 则ADUUU uuu uuu BE CF 与 BC(A)A.反向平行B.同向平行C.互相垂直D.既不平行也不垂直(A )4444A.B.c.D.9339uu 由APUuu UJ uuuu 解析 2PM 知,p 为 ABC 的重心,根据向量的加法 ,PB P C2PM则 uur 4.在 ABC 中,M 是BC 的中点,AM=1,点P 在AM 上且满足学PALunn uur uuu uuu2PM ,则 PA (PB PC)等于uuruuu uiuuu uuu AP (PB1•设a 、b 、c 是单位向量,且 a -b = o ,贝U a c ? b c 的最小值为( D )27.已知a , b 是平面内两个互相垂直的单位向量,右向量 c 满足(ac) (b c)0,则 c 的最大值是(C )3 4uuu uuu uuur8.已知O 是厶ABC 所在平面内一点,D 为BC 边中点,且2OA OB OC 0,那么( A )则—的取值范围是mA .、3B . 2.3C .6 D . 2、616.在平行四边形 ABCD 中, uuu AE 1 uuu unr-AB, AF1 UULT一AD , CE 与BF 相交于G 点.的最小值为(B ) A. uuir unr AO ODunr uuir B. AO 2ODuuir uuirC. AO 3ODuur unr D. 2AO OD 9•设a5 ^2(4,3) , a 在b 上的投影为 ,b 在x 轴上的投影为2,且 | b |< 14,则 b 为(B ) (2,4)2,C .D . (2,) 10.设a, b 是非零向量,若函数f(x)(xa b) (a xb )的图象是一条直线, 则必有( A )11.设两个向量a ( 2,a//2cos C . |a|)和b|b|D . |a| |b|mm,—2 sin ,其中,m, 为实数.若a 2b ,A . [-6, 1]B. [4,]C. (-6, 1] D . [-1 , 6]12.已知向量a(1, n),(1, n ),若2a b 与b 垂直,则|a(C13•如图,已知正六边形 RP 2P 3P 4P 5P 6 ,F 列向量的数量积中最大的是(A. RP2 ,R F 3B. P 1P 2, P 1P4C. P 1P 2 , P 1 P 5D.P 1P 2 ,P 1P614.已知向量a 尢,|e |= 1,对任意t € R , 恒有|a - t e | 冷一e |,贝y ( B )A. a 丄 eB. e 丄(a - e )C.a 丄(a - e )D.(a + e )丄(a - e )15.已知向量 unr unr n uurOA , OB 的夹角为一,|OA| 4 ,3luu r|OB| 1,若点 M 在直线 OB 上,贝U |&A OM |uuu r uur r uuur AB a, AD b,则AG342 r 1 r 2 rA. a bB. a7 7 7 17.设向量a与b的夹角为A」10 B. 3b 73.10 10C.(2,1),C.1 r r 4 rb D. a7 72b (4,5),则cosD.18.已知向量a , b的夹角为3,且|a||b| 1 ,19.20.21.22.23.24.中,25.7等于D 则向量a与向量a 2b的夹角等于(5A .6已知向量A. [0, .2]已知单位向量A . 2.3在厶ABC 已知向量已知向量中,arOib-r-|b|其中b均为非零向量, 则| p |的取值范围是(B )B.[0,1]C.(0,2]D.[0,2]a,b的夹角为一,那么a2bAR 2RB,CP 2PR,若AP mAB nAC,贝U mC.a和b的夹角为120 ,B. 7|a| 2,且(2aOAA. [0,4]b) a,则|b |(0,2),OB (2,0),BCB .[冷C 2 cos ,2 sinC. [4,3T]),贝UOA与OC夹角的取值范围是(上海)直角坐标系xOy中,i, j分别是与x, y轴正方向同向的单位向量. 在直角三角形ABC若AB 2i A. 1 j, AC 3i k j,则k的可能值个数是(B. 2若四边形ABCD满足AB CDc.「uuu0 , (AB3uiur uuirAD) ACD. 4则该四边形一定是BA.直角梯形B.菱形C.矩形D.正方形ir r ir 26.已知向量m,n的夹角为一,且|m |6uuir D为BC边的中点,贝U | AD |(乜,订| 2 ,在△ABC中,uuuABir r uuur ir r2m 2n,AC 2m 6n,112427. A . 2 uuu|OA|已知A.3 B . uuu,|OB| .3 ,OA?O B =0 , AOCD . 8uuur 30o ,设OC uuu uuu mOA nOB (m, nR),则D. 28.如图, 其中45°直角三角板的斜边与 所对的直角边重合.若 x , y 等于B x 3, y 1B. 345°直角三角板和 30°直角三角板拼在一起, 直角三角板的 30°角 uuur y DA , uu u DB 30° uuu r DC 则A. C. x 2, y . 3 二、填空题 1. 若向量 a , b 满足 2. 3. 4. 5. 6. 7.8. 答案 .7 设向量 答案 1 3,y 3 3,y 1 3 1,b 2且a 与b 的夹角为—, 3 a (1,2), (2,3),若向量 a b 与向量c (4, 7)共线,则已知向量a 与b 的夹角为120°,且a b 4,那么 b (2a b)的值为答案 0 已知平面向量a (2,4) , b ( 1,2).答案 8,2b 的夹角为120 ,答案设向量 答案若向量 答案若向量 答案uuuAB60若 c a (a 则5a bb)b , 则|C|uu ur 2, ACuuu uur3, AB AC | J 19,则r r aba 与b 的夹角为60 , 1,则 a? a bCABa,b 满足2,(a b) a ,则向量a 与b 的夹角等于uuu UULT LUU LUT UJU9. O 为平面上定点,A, B, C 是平面上不共线的三若 (OB OC ) •OB OC 2OA)=0,贝U ABC 的形状是 __________________________ .等腰三角形答案 -2510.不共线的向量m^ , m 2的模都为2,若a3m i2m 2 , b 2mi 3m 2 ,则两向量a b 与a b 的夹角为 _________________ 90 ° 11 •定义一种运算 S a b ,在框图所表达的算法中揭示了这种运算“”的含义•那么,按照运算 “”的含义,计算 tan 15o tan300 tan300 tan 15o _________ 1 ___r r12、 已知向量 a (cos15o ,sin150), b ( sin 150, cos1S),贝y a b 的值为 ________ . 答案113、 已知 Rt △ ABC 的斜边BC=5 ,则 AB BC BC CA CA AB 的值等于y 轴平行的单位向量,若直角三角形ABC 中,uur r AB ir uuur r rj , AC 2i mj ,则实数 m=答案 —2或0三、解答题rr r r r r1、已知ia 4,|b| 3,(2a — 3b) (2a b) 61 ,r rr r(1 )求 a b 的值;求a 与b 的夹(3)求b 的值;r r r r 心解:(1)由(2a —3b) (2a b) 61 得4a r r 「2「2又由 k 4,|b| 3得 a 16, 9代入上式得64 4a b 2761 a br rr3b14.在直角坐标系xOy 中,i[j 分别是与x 轴,艸(13|fr!=4・得卜2・{妨=』_虛讪一&r5 52’uuuruur uur(2, 4),在向量OC 上是否存在点P ,使得PA PB ,若存在,求出点P 的坐标,若不存在,请说明理由。
《高一数学平面向量复习》.doc

x =P2(X2, V2),则<y = X] +Xx 2 1 +九 y 】+入y?设 P (x,y), P )(xi, yi), 高一数学复习——平面向量班级 _______ 姓名 ___________一、 复习要点1・向量的三种线性运算及运算的三种形式。
向量的加减法,实数与向量的乘积,两个向量的数量积都称为向量的线性运算,前两者的 结果是向量,两个向量数量积的结果是数屋。
每一种运算都可以有三种表现形式:图形、符 号、坐标语言。
主要内容列表如下:匝要定理、公式(1)向疑共线定理:如果有一个实数几使b = Xa(a 6),那么忌与方是共线向量;反之,如果bHaQi 6)是共线向量,那么有且只有一个实数2,使为=加。
―> ―>(2)平面向量基本定理;如果ei ,e2是同一平而内的两个不共线向量,那么对于该平面内—> —► —► —► 任一向量a,有且只有一对数数入1,入2,满足a 二入iei +入2。
2。
-> ——―> —* —•两个向量平行:设 a = (xi, yi), b=(x2, y2),则 a 〃bo 方=2a <=> xiy 2-x 2yi=0 两个向量垂直:设 a =(x b yi), b 二(X2, y?),贝9 a 丄 b o a ・b = O oxiXz+yy 二0—> —> —> 1 —> 2 —>线段定比分点公式:设P,P = XPP 9/则OP 二—— 0£+ —— OR 1 + 2 1 + 2 (3) (4)二、例题讲解1> 平面向量a = (3, ,-4), = (2, x), c = (2, y),已知a //b , d 丄c,求 &、c 及A与c 夹角。
2、已知向量m = (cossin )^11 n =( V2 - sin 0,cos0), 兀,一_ 2(1)求| m + n I的最大值;(2)若|示+剂=出⑪,求sin2^的值.TT 3TT3、己知A、B、C 三点的他标分别为A(3,0)、B(0,3)、C(cosa,sin a), ),2 2(1)^|AC|=|BC|,求角Q的值;“、卄r;. 2sin2 6Z + sin2(7(2)若AC BC = -l ,求---------------- 的值。
高一数学必修4知识点梳理:平面向量

2、零向量:长度为0第二章平面向量1、向量定义:既有大小又有方向的量叫做向量,向量都可用同一平面内的有向线段表示.的向量叫零向量,记作0;零向量的方向是任意的.3、单位向量:长度等于1个单位长度的向量叫单位向量;与向量a 平行的单位向量:e =±a a ||4、平行向量(共线向量):方向相同或相反的非零向量叫平行向量也叫共线向量,记作//ab ;规定0与任何向量平行.5、相等向量:长度相同且方向相同的向量叫相等向量,零向量与零向量相等.注意:任意两个相等的非零向量,都可以用同一条有向线段来表示,并且与有向线段的起点无关。
6、向量加法运算:⑴三角形法则的特点:首尾相接⑵平行四边形法则的特点:起点相同baCBA -=A -AB =B a bC Cc高一数学必修4知识点梳理:平面向量⑶运算性质:①交换律:+=+a b b a ;②结合律:++=++a b c a b c ()();③+=+=a a a 00.⑷坐标运算:设=a x y ,11(),=b x y ,22(),则+=++a b x x y y ,1212)(. 7、向量减法运算:⑴三角形法则的特点:共起点,连终点,方向指向被减向量. ⑵坐标运算:设=a x y ,11(),=b x y ,22(),则-=--a b x x y y ,1212)(.设A 、B 两点的坐标分别为x y ,11(),x y ,22(),则AB =--x x y y ,2121)(.8、向量数乘运算:⑴实数λ与向量a 的积是一个向量的运算叫做向量的数乘,记作λa . ①=λλa a ;②当>λ0时,λa 的方向与a 的方向相同;当<λ0时,λa 的方向与a 的方向相反; 当=λ0时,=λa 0.⑵运算律:①=λμλμa a ()();②+=+λμλμa a a ();③+=+λλλa b a b (). ⑶坐标运算:设=a x y ,(),则==λλλλa x y x y ,,()().9、向量共线定理:向量≠a a 0()与b 共线,当且仅当有唯一一个实数λ,使=λb a . 设=a x y ,11(),=b x y ,22(),其中≠b 0,则当且仅当-=x y x y 01221时,向量a 、≠b b 0()共线.10、平面向量基本定理:如果e 1、e 2是同一平面内的两个不共线向量,那么对于这一平面内的任意向量a ,有且只有一对实数λ1、λ2,使=+λλa e e 1122.(不共线的向量e 1、e 2作为这一平面内所有向量的一组基底)11、分点坐标公式:设点P 是线段P P 12上的一点,P 1、P 2的坐标分别是x y ,11(),x y ,22(),当P P =PP λ12时,点P 的坐标是⎝⎭++ ⎪⎛⎫++λλλλx x y y 11,1212. 12、平面向量的数量积:⑴定义:≠≠≤≤⋅=θθa b a b a b cos 0,0,0180)(.零向量与任一向量的数量积为0. ⑵性质:设a 和b 都是非零向量,则①⊥⇔⋅=a b a b 0.②当a 与b 同向时,⋅=a b a b ;当a 与b 反向时,⋅=-a b a b ;⋅==a a a a 22或=⋅a a a .③⋅≤a b a b .⑶运算律:①⋅=⋅a b b a ;②⋅=⋅=⋅λλλa b a b a b ()()();③+⋅=⋅+⋅a b c a c b c ().⑷坐标运算:设两个非零向量=a x y ,11(),=b x y ,22(),则⋅=+a b x x y y 1212. 若=a x y ,(),则=+a x y 222,或=+a x y 22.设=a x y ,11(),=b x y ,22(),则⊥⇔+=a b x x y y 01212.设a 、b 都是非零向量,=a x y ,11(),=b x y ,22(),θ是a 与b 的夹角,则++==⋅+θx yx ya ba b x x y y cos 112222221212.第三章 三角恒等变形1、同角三角函数基本关系式(1)平方关系:αα=+221cos sin (2)商数关系:=tan sin cos ααα(3)倒数关系:αα=1cot tan=+sin tan tan 1222ααα ; =+co s 1t an 122αα注意: tan ,cos ,sin ααα 按照以上公式可以“知一求二”2、两角和与差的正弦、余弦、正切S +βα)(:=++sin cos cos sin )sin(βαβαβα S -βα)(:=--sin cos cos sin )sin(βαβαβα C +βα)(:a =+-sin sin cos cos )cos(βαβαβ C -βα)(:a =-+sin sin cos cos )cos(βαβαβ T +βα)(: =++-)tan(tan tan tan tan 1βαβαβαT -βα)(: =--+)tan(tan tan tan tan 1βαβαβα正切和公式:-⋅+=+βαβαβα)tan tan 1()tan(tan tan3、辅助角公式:222222cos sin sin cos b a x b x a a b a x b b a x +=++++⎛⎝⎫⎭⎪⎪ x b a x x b a +⋅+=⋅+⋅+=ϕϕϕ2222)sin cos cos (sin )sin((其中ϕ称为辅助角,ϕ的终边过点b a ),(,tan ϕ=b a)4、二倍角的正弦、余弦和正切公式: S 2α: =cos sin 22sin αααC 2α: -=sin cos 2cos 22ααααα-=-=221cos 2sin 21 T 2α: =-2tan tan 2tan 12ααα*二倍角公式的常用变形:①、=-αα|sin |22cos 1,=+αα|cos |22cos 1;②、=-αα1212|sin |2cos , =+αα1212|cos |2cos③-=+-=ααααα442221cos sin 21cos sin 2sin 2;=-442cos sin cos ααα;*降次公式:=cos sin 122sin ααα ααα=-+-=2sin 2cos 12122cos 12 ααα=++=2cos 2cos 12122cos 125、*半角的正弦、余弦和正切公式:±=-ααsin2cos 12 ; ±=+ααcos 2cos 12, ±=-+tan2cos 1cos 1ααα=-=+cos 1sin sin cos 1αααα6、同角三角函数的常见变形:(活用“1”)① -=cos 1sin 22αα; -±=cos 1sin 2αα;-=sin 1cos 22αα; -±=sin 1cos 2αα; ②=++=22cot tan sin cos cos sin 22sin θθθθθθθ,αααααααθθ2cot 22sin 2cos 2cos sin sin cos tan cot 22==-=-③ααααα2sin 1cos sin 21)cos (sin 2±=±=±; |cos sin |2sin 1ααα±=± 7、补充公式:*①万能公式2tan12tan2sin 2ααα+=; 2t a n12t a n1c o s 22ααα+-=; 2t a n12t a n2t a n 2ααα-=*②积化和差公式)]sin()[sin(21cos sin βαβαβα-++=)]sin()[sin(21sin cos βαβαβα--+=)]cos()[cos(21cos cos βαβαβα-++=)]cos()[cos(21sin sin βαβαβα--+-=*③和差化积公式2cos 2sin 2sin sin βαβαβα-+=+; 2sin2cos 2sin sin βαβαβα-+=- 2co s 2co s 2co s co s βαβαβα-+=+;2sin2sin 2cos cos βαβαβα-+-=- 注:带*号的公式表示了解,没带*公式为必记公式。
高中数学平面向量知识点总结及常见题型

平面向量一.向量的基本概念与基本运算 1向量的概念:①向量:既有大小又有方向的量向量一般用c b a,,……来表示,或用有向线段的起点与终点的大写字母表示,如:AB 几何表示法 AB ,a;坐标表示法),(y x yj xi a =+=向量的大小即向量的模长度,记作|AB |即向量的大小,记作|a|向量不能比较大小,但向量的模可以比较大小.②零向量:长度为0的向量,记为0 ,其方向是任意的,0 与任意向量平行零向量a=0⇔|a|= 由于0的方向是任意的,且规定0平行于任何向量,故在有关向量平行共线的问题中务必看清楚是否有“非零向量”这个条件.注意与0的区别 ③单位向量:模为1个单位长度的向量向量0a 为单位向量⇔|0a|=1④平行向量共线向量:方向相同或相反的非零向量任意一组平行向量都可以移到同一直线上方向相同或相反的向量,称为平行向量记作a ∥b行任意的平移即自由向量,平行向量总可以平移到同一直线上,故平行向量也称为共线向量⑤相等向量:长度相等且方向相同的向量相等向量经过平移后总可以重合,记为b a=大小相等,方向相同),(),(2211y x y x =⎩⎨⎧==⇔2121y y x x2向量加法求两个向量和的运算叫做向量的加法设,AB a BC b ==,则a+b =AB BC +=AC1a a a=+=+00;2向量加法满足交换律与结合律; 向量加法有“三角形法则”与“平行四边形法则”:1用平行四边形法则时,两个已知向量是要共始点的,和向量是始点与已知向量的始点重合的那条对角线,而差向量是另一条对角线,方向是从减向量指向被减向量2 三角形法则的特点是“首尾相接”,由第一个向量的起点指向最后一个向量的终点的有向线段就表示这些向量的和;差向量是从减向量的终点指向被减向量的终点当两个向量的起点公共时,用平行四边形法则;当两向量是首尾连接时,用三角形法则.向量加法的三角形法则可推广至多个向量相加:AB BC CD PQ QR AR +++++=,但这时必须“首尾相连”.3向量的减法① 相反向量:与a 长度相等、方向相反的向量,叫做a的相反向量记作a-,零向量的相反向量仍是零向量关于相反向量有: i )(a --=a; ii a +a -=a -+a =0 ; iii 若a 、b是互为相反向量,则a =b -,b =a -,a +b =0②向量减法:向量a 加上b 的相反向量叫做a 与b的差,记作:)(b a b a-+=-求两个向量差的运算,叫做向量的减法③作图法:b a -可以表示为从b 的终点指向a 的终点的向量a 、b有共同起点 4实数与向量的积:①实数λ与向量a 的积是一个向量,记作λa,它的长度与方向规定如下:Ⅰa a⋅=λλ;Ⅱ当0>λ时,λa 的方向与a 的方向相同;当0<λ时,λa 的方向与a的方向相反;当0=λ时,0=a λ,方向是任意的②数乘向量满足交换律、结合律与分配律 5两个向量共线定理:向量b 与非零向量a共线⇔有且只有一个实数λ,使得b =a λ 6平面向量的基本定理:如果21,e e 是一个平面内的两个不共线向量,那么对这一平面内的任一向量a ,有且只有一对实数21,λλ使:2211e e a λλ+=,其中不共线的向量21,e e叫做表示这一平面内所有向量的一组基底 7 特别注意:1向量的加法与减法是互逆运算2相等向量与平行向量有区别,向量平行是向量相等的必要条件3向量平行与直线平行有区别,直线平行不包括共线即重合,而向量平行则包括共线重合的情况4向量的坐标与表示该向量的有向线条的始点、终点的具体位置无关,只与其相对位置有关二.平面向量的坐标表示 1平面向量的坐标表示:在直角坐标系中,分别取与x 轴、y 轴方向相同的两个单位向量,i j 作为基底由平面向量的基本定理知,该平面内的任一向量a 可表示成a xi yj =+,由于a 与数对x,y 是一一对应的,因此把x,y 叫做向量a 的坐标,记作a =x,y,其中x 叫作a 在x 轴上的坐标,y 叫做在y 轴上的坐标1相等的向量坐标相同,坐标相同的向量是相等的向量2向量的坐标与表示该向量的有向线段的始点、终点的具体位置无关,只与其相对位置有关2平面向量的坐标运算:(1)若()()1122,,,a x y b x y ==,则()1212,a b x x y y ±=±± (2)若()()2211,,,y x B y x A ,则()2121,AB x x y y =-- (3)若a =x,y,则λa =λx, λy(4)若()()1122,,,a x y b x y ==,则1221//0a b x y x y ⇔-= (5)若()()1122,,,a x y b x y ==,则1212a b x x y y ⋅=⋅+⋅若a b ⊥,则02121=⋅+⋅y y x x3,数与向量的乘积,向量的数量内积及其各运算的坐标表示和性质12(a b x x +=+AB BC AC +=12(a b x x -=-)(b a b a-+=- AB BA =-OB OA AB -=a a)()(λμμλ=12a b x x •=+三.平面向量的数量积 1两个向量的数量积:已知两个非零向量a 与b ,它们的夹角为θ,则a ·b =︱a ︱·︱b ︱cos θ叫做a 与b 的数量积或内积 规定00a ⋅=2向量的投影:︱b ︱cos θ=||a ba ⋅∈R,称为向量b 在a 方向上的投影投影的绝对值称为射影3数量积的几何意义:a ·b 等于a 的长度与b 在a 方向上的投影的乘积 4向量的模与平方的关系:22||a a a a ⋅== 5乘法公式成立:()()2222a b a b a b a b +⋅-=-=-;()2222a ba ab b ±=±⋅+222a a b b =±⋅+6平面向量数量积的运算律: ①交换律成立:a b b a ⋅=⋅②对实数的结合律成立:()()()()a b a b a b R λλλλ⋅=⋅=⋅∈ ③分配律成立:()a b c a c b c ±⋅=⋅±⋅()c a b =⋅± 特别注意:1结合律不成立:()()a b c a b c ⋅⋅≠⋅⋅; 2消去律不成立a b a c⋅=⋅不能得到b c =⋅3a b ⋅=0不能得到a =0或b =0 7两个向量的数量积的坐标运算:已知两个向量1122(,),(,)a x y b x y ==,则a ·b =1212x x y y +8向量的夹角:已知两个非零向量a 与b ,作OA =a , OB =b ,则∠AOB=θ001800≤≤θ叫做向量a 与b 的夹角cos θ=cos ,a b a b a b•<>=•=222221212121y x y x y y x x +⋅++当且仅当两个非零向量a 与b 同方向时,θ=00,当且仅当a 与b 反方向时θ=1800,同时0与其它任何非零向量之间不谈夹角这一问题9垂直:如果a 与b 的夹角为900则称a 与b 垂直,记作a ⊥b 10两个非零向量垂直的充要条件:a ⊥b ⇔a ·b=O ⇔2121=+y y x x 平面向量数量积的性质题型1.基本概念判断正误:1共线向量就是在同一条直线上的向量.2若两个向量不相等,则它们的终点不可能是同一点. 3与已知向量共线的单位向量是唯一的. 4四边形ABCD 是平行四边形的条件是AB CD =. 5若AB CD =,则A 、B 、C 、D 四点构成平行四边形. 6因为向量就是有向线段,所以数轴是向量. 7若a 与b 共线, b 与c 共线,则a 与c 共线. 8若ma mb =,则a b =. 9若ma na =,则m n =.10若a 与b 不共线,则a 与b 都不是零向量. 11若||||a b a b ⋅=⋅,则//a b . 12若||||a b a b +=-,则a b ⊥. 题型2.向量的加减运算1.设a 表示“向东走8km ”, b 表示“向北走6km ”,则||a b += .2.化简()()AB MB BO BC OM ++++= .3.已知||5OA =,||3OB =,则||AB 的最大值和最小值分别为 、 .4.已知AC AB AD为与的和向量,且,AC a BD b ==,则AB = ,AD = .5.已知点C 在线段AB 上,且35AC AB =,则AC = BC ,AB = BC . 题型3.向量的数乘运算1.计算:13()2()a b a b +-+= 22(253)3(232)a b c a b c +---+-=2.已知(1,4),(3,8)a b =-=-,则132a b -= .题型4.作图法球向量的和已知向量,a b ,如下图,请做出向量132a b +和322a b -.a b题型5.根据图形由已知向量求未知向量1.已知在ABC ∆中,D 是BC 的中点,请用向量AB AC ,表示AD . 2.在平行四边形ABCD 中,已知,AC a BD b ==,求AB AD 和.题型6.向量的坐标运算1.已知(4,5)AB =,(2,3)A ,则点B 的坐标是 .2.已知(3,5)PQ =--,(3,7)P ,则点Q 的坐标是 .3.若物体受三个力1(1,2)F =,2(2,3)F =-,3(1,4)F =--,则合力的坐标为 .4.已知(3,4)a =-,(5,2)b =,求a b +,a b -,32a b -.5.已知(1,2),(3,2)A B ,向量(2,32)a x x y =+--与AB 相等,求,x y 的值.6.已知(2,3)AB =,(,)BC m n =,(1,4)CD =-,则DA = .7.已知O 是坐标原点,(2,1),(4,8)A B --,且30AB BC +=,求OC 的坐标.题型7.判断两个向量能否作为一组基底1.已知12,e e 是平面内的一组基底,判断下列每组向量是否能构成一组基底: A.1212e e e e +-和 B.1221326e e e e --和4 C.122133e e e e +-和 D.221e e e -和2.已知(3,4)a =,能与a 构成基底的是A.34(,)55B.43(,)55C.34(,)55--D.4(1,)3--题型8.结合三角函数求向量坐标1.已知O 是坐标原点,点A 在第二象限,||2OA =,150xOA ∠=,求OA 的坐标.2.已知O 是原点,点A 在第一象限,||43OA =60xOA ∠=,求OA 的坐标.题型9.求数量积1.已知||3,||4a b ==,且a 与b 的夹角为60,求1a b ⋅,2()a a b ⋅+,31()2a b b -⋅,4(2)(3)a b a b -⋅+.2.已知(2,6),(8,10)a b =-=-,求1||,||a b ,2a b ⋅,3(2)a a b ⋅+, 4(2)(3)a b a b -⋅+.题型10.求向量的夹角1.已知||8,||3a b ==,12a b ⋅=,求a 与b 的夹角.2.已知(3,1),(23,2)a b ==-,求a 与b 的夹角.3.已知(1,0)A ,(0,1)B ,(2,5)C ,求cos BAC ∠. 题型11.求向量的模1.已知||3,||4a b ==,且a 与b 的夹角为60,求1||a b +,2|23|a b -.2.已知(2,6),(8,10)a b =-=-,求1||,||a b ,5||a b +,61||2a b -.3.已知||1||2a b ==,,|32|3a b -=,求|3|a b +.题型12.求单位向量 与a 平行的单位向量:||a e a =± 1.与(12,5)a =平行的单位向量是 .2.与1(1,)2m =-平行的单位向量是 . 题型13.向量的平行与垂直1.已知(6,2)a =,(3,)b m =-,当m 为何值时,1//a b 2a b ⊥2.已知(1,2)a =,(3,2)b =-,1k 为何值时,向量ka b +与3a b -垂直 2k 为何值时,向量ka b +与3a b -平行3.已知a 是非零向量,a b a c ⋅=⋅,且b c ≠,求证:()a b c ⊥-.题型14.三点共线问题1.已知(0,2)A -,(2,2)B ,(3,4)C ,求证:,,A B C 三点共线.2.设2(5),28,3()2AB a b BC a b CD a b =+=-+=-,求证:A B D 、、三点共线. 3.已知2,56,72AB a b BC a b CD a b =+=-+=-,则一定共线的三点是 .4.已知(1,3)A -,(8,1)B -,若点(21,2)C a a -+在直线AB 上,求a 的值.5.已知四个点的坐标(0,0)O ,(3,4)A ,(1,2)B -,(1,1)C ,是否存在常数t ,使OA tOB OC +=成立题型15.判断多边形的形状1.若3AB e =,5CD e =-,且||||AD BC =,则四边形的形状是 .2.已知(1,0)A ,(4,3)B ,(2,4)C ,(0,2)D ,证明四边形ABCD 是梯形.3.已知(2,1)A -,(6,3)B -,(0,5)C ,求证:ABC ∆是直角三角形.4.在平面直角坐标系内,(1,8),(4,1),(1,3)OA OB OC =-=-=,求证:ABC ∆是等腰直角三角形.题型16.平面向量的综合应用1.已知(1,0)a =,(2,1)b =,当k 为何值时,向量ka b -与3a b +平行2.已知(3,5)a =,且a b ⊥,||2b =,求b 的坐标.3.已知a b 与同向,(1,2)b =,则10a b ⋅=,求a 的坐标.3.已知(1,2)a =,(3,1)b =,(5,4)c =,则c = a + b .4.已知(5,10)a =,(3,4)b =--,(5,0)c =,请将用向量,a b 表示向量c .5.已知(,3)a m =,(2,1)b =-,1若a 与b 的夹角为钝角,求m 的范围; 2若a 与b 的夹角为锐角,求m 的范围.6.已知(6,2)a =,(3,)b m =-,当m 为何值时,1a 与b 的夹角为钝角 2a 与b 的夹角为锐角7.已知梯形ABCD 的顶点坐标分别为(1,2)A -,(3,4)B ,(2,1)D ,且//AB DC ,2AB CD =,求点C 的坐标.8.已知平行四边形ABCD 的三个顶点的坐标分别为(2,1)A ,(1,3)B -,(3,4)C ,求第四个顶点D 的坐标.9.一航船以5km/h 的速度向垂直于对岸方向行驶,航船实际航行方向与水流方向成30角,求水流速度与船的实际速度.10.已知ABC ∆三个顶点的坐标分别为(3,4)A ,(0,0)B ,(,0)C c ,1若0AB AC ⋅=,求c 的值;2若5c =,求sin A 的值.备用1.已知||3,||4,||5a b a b ==+=,求||a b -和向量,a b 的夹角.2.已知x a b =+,2y a b =+,且||||1a b ==,a b ⊥,求,x y 的夹角的余弦.1.已知(1,3),(2,1)a b ==--,则(32)(25)a b a b +⋅-= .4.已知两向量(3,4),(2,1)a b ==-,求当a xb a b +-与垂直时的x 的值.5.已知两向量(1,3),(2,)a b λ==,a b 与的夹角θ为锐角,求λ的范围. 变式:若(,2),(3,5)a b λ==-,a b 与的夹角θ为钝角,求λ的取值范围. 选择、填空题的特殊方法:1.代入验证法例:已知向量(1,1),(1,1),(1,2)a b c ==-=--,则c = A.1322a b -- B.1322a b -+ C.3122a b - D.3122a b -+ 2.排除法例:已知M 是ABC ∆的重心,则下列向量与AB 共线的是A.AM MB BC ++B.3AM AC +C.AB BC AC ++D.AM BM CM ++。
高一数学平面向量复习课件

2、数量积的几何意义:
B
b
a b a b cos
a
a b b a cos
A
O
| b | cos
a b b a
数量积a b等于a的长度a 与b在a的方向上的投影数量 b cos的乘积 .
3、数量积的物理意义:F
F cos
S
如果一个物体在力 F的作用下产生位移 s, 那么力F所做的功W 可用公式计算:
其实质就是向量的伸长或缩短!
坐标运算: 若a = (x , y), 则λa = λ (x , y)
= (λ x , λ y)
平面向量 复习 非零向量平行(共线)的充要条件 向量表示: a∥b
a=λb (λБайду номын сангаасR且b≠0)
坐标表示: 设a = ( x1, y1 ) , b = ( x2, y2 ),则
例2
思考: 此题还有没有其它解法?
平面向量小 复习
n为何值时, 向量a=(n,1)与b=(4,n) 共线且方向相同?
答案:
n= 2 ?
思考: 何时 n=±2
平面向量复习
例3 分析 设AB=2(a+5b),BC= 2a + 8b,CD=3(a b), 求证:A、B、D 三点共线。
要证A、B、D三点共线,可证 AB=λBD关键是找到λ
2
2
平面向量小 复习
已知向量a=(5,m)的长度是13,求m.
答案: m = ± 12
平面向量复习
1.向量的加法运算 三角形法则 AB+BC= AC
A
C
平行四边形法则
B
C
OA+OB= OC
高一数学平面向量知识点复习ppt公开课获奖课件

∴ λ= 5 ,μ=-12 2
第8页
三、两个重要定理
1、向量共线充要条件
向量b 与非零向量 a 共线充要条件是有且只有
一个实数λ,使得 b a
注意:这是判断两个向量共线(平行)重要措施。
2、平面向量基本定理
假如 e1, e2 是同一个平面内两个不共线向量,
(2)函数 y cos(x ) 2图象通过怎样
平移,可以得到函数 y 3cos x图象?
第14页
六、正弦定理及其变形公式
a b c 2R sin A sin B sin C
S ABC
1 bc sin 2
A
1 ca sin 2
B
1 2
ab sin C
a 2R sin A,b 2R sin B, c 2R sin C
使 k a b=λ (a 3b,) 由(k-3,2k+2)= λ(10,-4)
k 3 10 2k 2 4
解得 k 1 , 1
3
3
反向
第12页
五、两个重要公式
1、定比分点坐标公式
设P(x,y),P1(x1,y1),P2(x2,y2),且
P1P PP2,则
x
x1 x2 1
(3)(a b) a b
2、平面向量数量积运算律
思索:你能将此 运算律用坐标表 达出来吗?
(1)a b b a
(2)(a) b (a b) a ( b)
(3)(a b) c a c b c
第6页
例1 判断如下命题及其逆命题真假:
1、若| a|= | b| ,则 a 与 b是共线向量; 2、若 a∥b ,则 a在 b方向上投影是 ;a 3、若 | a || b | 1 ,则 a b 1 ; 4、若a 0,则 0且a 0
高一数学平面向量知识点及典型例题解析

高一数学 第八章 平面向量第一讲 向量的概念与线性运算 一.【要点精讲】 1.向量的概念①向量:既有大小又有方向的量。
几何表示法AB ,a ;坐标表示法),(y x j y i x a =+= 。
向量的模(长度),记作|AB |.即向量的大小,记作|a|。
向量不能比较大小,但向量的模可以比较大小.②零向量:长度为0的向量,记为0,其方向是任意的,规定0平行于任何向量。
(与0的区别) ③单位向量|a|=1。
④平行向量(共线向量)方向相同或相反的非零向量,记作a ∥b⑤相等向量记为b a=。
大小相等,方向相同),(),(2211y x y x =⎩⎨⎧==⇔2121y y x x 2.向量的运算(1)向量加法:求两个向量和的运算叫做向量的加法.如图,已知向量a ,b ,在平面内任取一点A ,作AB =a ,BC =b ,则向量叫做a 与b的和,记作a+b ,即 a+b AB BC AC =+=特殊情况:(1)BBabba +AABC C)2()3(向量加法的三角形法则可推广至多个向量相加:AB BC CD PQ QR AR +++++=,但这时必须“首尾相连”。
②向量减法: 同一个图中画出a b a b +-、要点:向量加法的“三角形法则”与“平行四边形法则”(1)用平行四边形法则时,两个已知向量是要共始点的,和向量是始点与已知向量的始点重合的那条对角线,而差向量是另一条对角线,方向是从减向量指向被减向量。
(2) 三角形法则的特点是“首尾相接”,由第一个向量的起点指向最后一个向量的终点的有向线段就表示这些向量的和;差向量是从减向量的终点指向被减向量的终点. (3)实数与向量的积3.两个向量共线定理:向量b 与非零向量a共线⇔有且只有一个实数λ,使得b =a λ。
二.【典例解析】题型一: 向量及与向量相关的基本概念概念 例1判断下列各命题是否正确(1)零向量没有方向 (2)ba ==则 (3)单位向量都相等 (4) 向量就是有向线段(5)两相等向量若共起点,则终点也相同 (6)若b a =,c b =,则c a =;(7)若b a //,c b //,则c a// (8) b a =的充要条件是||||b a =且b a //;(9) 若四边形ABCD 是平行四边形,则DA BC CD B ==,A练习. (四川省成都市一诊)在四边形ABCD 中,“AB →=2DC →”是“四边形ABCD 为梯形”的 A 、充分不必要条件B 、必要不充分条件C 、充要条件D 、既不充分也不必要条件题型二: 考查加法、减法运算及相关运算律 例2 化简)()(BD AC CD AB ---=练习1.下列命题中正确的是 A .OA OB AB -= B .0AB BA +=C .00AB ⋅=D .AB BC CD AD ++=2.化简AC -BD +CD -AB 得 A .AB B .DA C . D .03.如图,D 、E 、F 分别是△ABC 的边AB 、BC 、CA 的中点,则( )A.AD →+BE →+CF →=0B.BD →-CF →+DF →=0C.AD →+CE →-CF →=0D.BD →-BE →-FC →=0题型三: 结合图型考查向量加、减法例3在ABC ∆所在的平面上有一点P ,满足PA PB PC AB ++=,则PBC ∆与ABC ∆的面积之比是( )A .13B .12C .23D .34例4重心、垂心、外心性质练习: 1.如图,在ΔABC 中,D 、E 为边AB 的两个三等分点,CA →=3a ,CB → =2b ,求CD → ,CE → . 2已知a b a b+-=求证a b ⊥3若O 为ABC ∆的内心,且满足()(2)0OB OC OB OC OA -⋅+-=,则ABC ∆的形状为( )A.等腰三角形B.正三角形C.直角三角形D.钝角三角形4.已知O 、A 、B 是平面上的三个点,直线AB 上有一点C ,满足2AC →+CB →=0,则OC →=( ) A .2OA →-OB → B .-OA →+2OB →C.23OA →-13OB → D .-13OA →+23OB → 5.已知平面上不共线的四点O ,A ,B ,C .若OA →-3OB →+2OC →=0,则|AB →||BC →|等于________.6.已知平面内有一点P 及一个△ABC ,若PA →+PB →+PC →=AB →,则( )A .点P 在△ABC 外部B .点P 在线段AB 上C .点P 在线段BC 上D .点P 在线段AC 上ABDE7.在△ABC 中,已知D 是AB 边上一点,若AD →=2DB →,CD →=13CA →+λCB →,则λ等于( ) A.23 B.13 C .-13 D .-23 题型四: 三点共线问题例 4 设21,e e 是不共线的向量,已知向量2121212,3,2e e e e e k e -=+=+=,若A,B,D 三点共线,求k 的值例5已知A 、B 、C 、P 为平面内四点, A 、B 、C 三点在一条直线上 PC → =mPA → +nPB →,求证: m+n=1.练习:1.已知:2121212 ,B),(3e e e +=-=+=,则下列关系一定成立的是( )A 、A ,B ,C 三点共线 B 、A ,B ,D 三点共线 C 、C ,A ,D 三点共线 D 、B ,C ,D 三点共线2.(原创题)设a ,b 是两个不共线的向量,若AB →=2a +k b ,CB →=a +b ,CD →=2a -b ,且A ,B ,D 三点共线,则实数k 的值等于________.第2讲 平面向量的基本定理与坐标表示 一.【要点精讲】1.平面向量的基本定理如果21,e e 是一个平面内的两个不共线向量,那么对这一平面内的任一向量a ,有且只有一对实数21,λλ使:2211e e a λλ+=其中不共线的向量21,e e 叫做表示这一平面内所有向量的一组基底. 2.平面向量的坐标表示如图,在直角坐标系内,我们分别取与x 轴、y 轴方向相同的_单位向量_ i 、j 作为基底a ,有且只有一对实数x 、y ,BC AOM D使得a xi yj =+…………○1,把),(y x 叫做向量a 的(直角)坐标,记作(,)a x y =…………○2其中x 叫做a 在x 轴上的坐标,y 叫做a 在y 轴上的坐标,○2式叫做向量的坐标表示与a 相等的向量的坐标也为,(y x 特别地,(1,0)i =,(0,1)j =,0(0,0)=特别提醒:设yj xi +=,则向量的坐标),(y x 就是点A 的坐标;反过来,点A 的坐标),(y x 也就是向量的坐标在平面直角坐标系内,每一个平面向量都是可以用一对实数唯一表示3.平面向量的坐标运算(1)若11(,)a x y =,22(,)b x y =,则a b +=1212(,)x x y y ++,a b -= 1212(,)x x y y --(2) 若),(11y x A ,),(22y x B ,则AB = (3)若(,)a x y =和实数λ,则a λ=(,)x y λλ4.向量平行的充要条件的坐标表示:设a=(x 1, y 1) ,b =(x 2, y 2) 其中b ≠aa ∥b (b≠)的充要条件是12210x y x y -=二.【典例解析】题型一. 利用一组基底表示平面内的任一向量[例1] 在△OAB 中,21,41==,AD 与BC 交于点M ,设OA =a ,OB =b ,用a ,b 表示OM .练习:1.若已知1e 、2e 是平面上的一组基底,则下列各组向量中不能作为基底的一组是 ( ) A .1e 与—2e B .31e 与22e C .1e +2e 与1e —2e D .1e 与21e 2.在平行四边形ABCD 中,E 和F 分别是边CD 和BC 的中点,若AC →=λAE →+μAF →,其中λ、μ∈R ,则λ+μ=________.题型二: 向量加、减、数乘的坐标运算 例 3 已知A (—2,4)、B (3,—1)、C (—3,—4)且3=,2=,求点M 、N 的坐标及向量的坐标.练习:1. (2008年高考辽宁卷)已知四边形ABCD 的三个顶点A (0,2),B (-1,-2),C (3,1),且BC →=2AD →,则顶点D 的坐标为( )A .(2,72)B .(2,-12) C .(3,2) D .(1,3)2.若M(3, -2) N(-5, -1) 且 12MP =MN , 求P 点的坐标;3.若M(3, -2) N(-5, -1),点P 在MN 的延长线上,且 12MP MN =,求P 点的坐标;4.(2009年广东卷文)已知平面向量a =,1x () ,b =2,x x (-), 则向量+a b ( )A 平行于x 轴B.平行于第一、三象限的角平分线C.平行于y 轴D.平行于第二、四象限的角平分线5.在三角形ABC 中,已知A (2,3),B (8,-4),点G (2,-1)在中线AD 上,且AG →=2GD →, 则点C 的坐标是( )A .(-4,2)B .(-4,-2)C .(4,-2)D .(4,2)6.设向量a =(1,-3),b =(-2,4),c =(-1,-2),若表示向量4a 、4b -2c 、2(a -c )、d 的有向线段首尾相接能构成四边形,则向量d 为( )A .(2,6)B .(-2,6)C .(2,-6)D .(-2,-6)7.已知A (7,1)、B (1,4),直线y =12ax 与线段AB 交于C ,且AC →=2CB →,则实数a 等于( ) A .2 B .1 C.45 D.53 题型三: 平行、共线问题例4已知向量(1sin ,1)θ=-a ,1(,1sin )2θ=+b ,若a ∥b ,则锐角θ等于( )A .30︒B . 45︒C .60︒D .75︒例5.(2009北京卷文)已知向量(1,0),(0,1),(),a b c ka b k R d a b ===+∈=-, 如果//c d 那么( )A .1k =且c 与d 同向B .1k =且c 与d 反向C .1k =-且c 与d 同向D .1k =-且c 与d 反向练习:1.若向量a=(-1,x)与b =(-x, 2)共线且方向相同,求x2.已知点O(0,0),A(1,2),B(4,5)及AB t OA OP +=,求(1)t 为何值时,P 在x 轴上?P 在y 轴上?P 在第二象限。
专题01 平面向量的概念(解析版)

专题01 平面向量的概念一、单选题1.下列说法正确的是A .单位向量都相等B .若a b ≠,则a b ≠C .若a b =,则//a bD .若a b ≠,则a b ≠ 【试题来源】山西省忻州市第一中学北校2019-2020学年高一下学期3月月考【答案】D【分析】根据向量的概念,向量的两个要素:大小和方向性,即可判断各选项.【解析】对于A ,单位向量的大小都相等,但方向不一定相同,所以单位向量不一定都相等,所以A 错误;对于B ,两个向量不相等,可以大小相等,方向不同,因而当a b ≠时可能a b =,所以B 错误; 对于C ,两个向量的模相等,但方向可以不同,因而当a b =时a 和b 不一定平行,所以C 错误;对于D ,若两个向量的模不相等,则两个向量一定不相同,所以若a b ≠,则a b ≠成立,所以D 正确.综上可知,D 为正确选项,故选D 【名师点睛】本题考查了向量的概念,向量的两个要素:大小和方向性,属于基础题. 2.给出下列四个说法:①若||0a =,则0a =;②若||||a b =,则a b =或a b =-;③若//a b ,则||||a b =;④若//a b ,//b c ,则//a c .其中错误的说法有A .1B .2C .3D .4【试题来源】安徽省六安市第一中学2019-2020学年高一上学期期末(文)【答案】D【解析】①只有零向量的模是0,因此应有0a =,不是0,错;②模相等的向量方向不确定,不一定相同或相反,错;③两向量平行,只要方向相同或相反或有一个为零向量,模不作要求,错;④当0b =时,,a c 不一定共线,错.故选D .【名师点睛】本题考查向量的概念,掌握向量的定义是解题关键.3.下列关于向量的命题正确的是A .若||||a b =,则a b =B .若||||a b =,则//a bC .若a b =,b c =,则a c =D .若//a b ,//b c ,则//a c【试题来源】2020-2021学年高一数学十分钟同步课堂专练(人教A 版必修4)【答案】C【分析】利用向量的知识对每一个选项逐一分析判断得解.【解析】A . 若||||a b =,则,a b 不一定相等,因为向量是既有大小,又有方向的,||||a b =只能说明向量的大小相等,不能说明方向相同,所以该选项错误;B . 若||||a b =,则,a b 不一定平行,所以该选项错误;C . 若a b =,b c =,则a c =,所以该选项是正确的;D . 若//a b ,//b c ,则//a c 错误,如:=0b ,,a c 都是非零向量,显然满足已知,但是不一定满足//a c ,所以该选项错误.故选C【名师点睛】本题主要考查平面向量的概念,意在考查学生对这些知识的理解掌握水平,属于基础题.4.下列命题正确的是A .若||0a =,则0a =B .若||||a b =,则a b =C .若||||a b =,则//a bD .若//a b ,则a b =【试题来源】2020-2021学年【补习教材寒假作业】高一数学(人教A 版2019)【答案】A【分析】根据零向量的定义,可判断A 项正确;根据共线向量和相等向量的定义,可判断B ,C ,D 项均错.【解析】模为零的向量是零向量,所以A 项正确;||||=时,只说明向,a b的长度相等,无法确定方向,a b所以B,C均错;a b 时,只说明,a b方向相同或相反,没有长度关系,不能确定相等,所以D错.故选A.【名师点睛】本题考查有关向量的基本概念的辨析,属于基础题.5.下列说法中,正确的个数是①时间、摩擦力、重力都是向量;②向量的模是一个正实数;③相等向量一定是平行向量;④向量a→与b→不共线,则a→与b→都是非零向量A.1B.2C.3D.4【试题来源】湖北省武汉市第六中学2018-2019学年高一下学期2月月考【答案】B【分析】根据向量的相关概念,逐项判定,即可得出结果.【解析】①时间没有方向,不是向量,摩擦力,重力都是向量,故①错误;②零向量的模为零,故②错;③相等向量的方向相同,模相等,所以一定是平行向量,故③正确;④零向量与任意向量都共线,因此若向量a→与b→不共线,则a→与b→都是非零向量,即④正确.故选B.【名师点睛】本题主要考查向量有关命题的判定,熟记向量的相关概念即可,属于基础题型.6.下列说法中正确的是A.平行向量就是向量所在的直线平行的向量B.长度相等的向量叫相等向量C.零向量的长度为零D.共线向量是在一条直线上的向量【试题来源】吉林省长春市第二十九中学2019-2020学年高一下学期线上检测数学试卷【答案】C【分析】直接根据共线向量、相等向量、零向量的概念判断即可.【解析】平行向量也叫共线向量,是指方向相同或相反的两个向量,另外规定零向量与任意向量平行,故A,D错;相等向量是指长度相等、方向相同的向量,故B错;长度为零的向量叫零向量,故C对;故选C.【名师点睛】本题主要考查平面向量的有关概念,属于基础题.7.下列命题正确的是A.若,a b都是单位向量,则a b=B.两个向量相等的充要条件是它们的起点和终点都相同C.向量AB与BA是两个平行向量A B C D四点是平行四边形的四个顶点D.若AB DC=,则,,,【试题来源】2021年新高考数学一轮复习讲练测【答案】C【分析】利用单位向量的定义可判断A;利用向量相等的定义可判断B;利用平行向量的定义可判断C;利用向量相等的定义可判断D.【解析】对于A,单位长度为1的向量为单位向量,,a b都是单位向量,但方向可能不同,故A不正确;对于B,模相等,方向相同的向量为相等向量,故B不正确;对于C,向量AB与BA为相反向量,所以两个为平行向量,故C正确;A B C D四点在同一条直线上,对于D,AB DC=,若,,,A B C D 不能构成平行四边形,故D不正确;故选C,,,【名师点睛】本题考查了向量的基本概念,需理解单位向量、相等向量、共线向量的概念,属于基础题.8.下列说法错误的是A.向量OA的长度与向量AO的长度相等B.零向量与任意非零向量平行C.长度相等方向相反的向量共线D.方向相反的向量可能相等【试题来源】2021年新高考数学一轮复习讲练测【答案】D【分析】向量有方向、有大小,平行包含同向与反向两种情况.向量相等意味着模相等且方向相同,根据定义判断选项.【解析】A.向量OA与向量AO的方向相反,长度相等,故A正确;B .规定零向量与任意非零向量平行,故B 正确;C .能平移到同一条直线的向量是共线向量,所以长度相等,方向相反的向量是共线向量,故C 正确;D .长度相等,方向相同的向量才是相等向量,所以方向相反的向量不可能相等,故D 不正确.【名师点睛】本题主要考查向量的基本概念及共线(平行)向量和相等向量的概念,属于基础概念题型.9.有下列命题:①若向量a 与b 同向,且||||a b >,则a b >;②若四边形ABCD 是平行四边形,则AB CD =;③若m n =,n k =,则m k =;④零向量都相等.其中假命题的个数是A .1B .2C .3D .4【试题来源】2021年高考数学复习一轮复习笔记【答案】C【分析】分别根据每个命题的条件推论即可判断.【解析】对于①,因为向量是既有大小又有方向的量,不能比较大小,故①是假命题; 对于②,在平行四边形ABCD 中,,C AB D 是大小相等,方向相反的向量,即AB CD =-,故②是假命题;对于③,显然若m n =,n k =,则m k =,故③是真命题;对于④,因为大小相等,方向相同的向量是相等向量,而零向量的方向任意,故④是假命题.故选C .【名师点睛】本题主要考查平面向量的概念,意在考查学生对这些知识的理解掌握水平,属于基础题.10.下列说法中正确的是.A .零向量没有方向B .平行向量不一定是共线向量C .若向量a 与b 同向且a b =,则a b =D .若向量a ,b 满足a b >且a 与b 同向,则a b >【试题来源】吉林省松原市扶余市第一中学2019-2020学年高一下学期期中考试【答案】C【分析】由零向量,平行向量,相等向量的定义逐一判断可得选项.【解析】对于A ,零向量的方向是任意的,故A 错误;对于B ,平行向量就是共线向量,故B 错误;对于C ,由相等向量的定义:两向量的方向相同,大小相等可知,C 正确;对于D ,两个向量不能比较大小,故D 错误.故选C .【名师点睛】本题考查向量的基本定义,在判断关于向量的命题时注意向量的方向,属于基础题.11.以下说法正确的是A .若两个向量相等,则它们的起点和终点分别重合B .零向量没有方向C .共线向量又叫平行向量D .若a 和b 都是单位向量,则a b =【试题来源】2020-2021学年高一数学十分钟同步课堂专练(人教A 版必修4)【答案】C【分析】根据向量的基本概念逐一判断即可.【解析】只要两个向量的方向相同,模长相等,这两个向量就是相等向量,故A 错误, 零向量是没有方向的向量,B 错误; 共线向量是方向相同或相反的向量,也叫平行向量,C 正确;若a ,b 都是单位向量,两向量的方向不定,D 错误;故选C .12.给出下列命题:①零向量的长度为零,方向是任意的;②若,a b 都是单位向量,则a b =;③向量AB 与BA 相等.则所有正确命题的序号是A .①B .③C .①③D .①②【试题来源】2020-2021学年高一数学单元测试定心卷(人教B 版2019必修第二册)【答案】A【分析】根据零向量和单位向量的概念可以判定①②,注意相等向量不仅要长度相等,方向要相同,可否定③.【解析】根据零向量的定义可知①正确;根据单位向量的定义可知,单位向量的模相等,但方向不一定相同,故两个单位向量不一定相等,故②错误;向AB 与BA 互为相反向量,故③错误.故选A .【名师点睛】本题考查零向量和单位向量的概念,相等向量的概念,属概念辨析,正确掌握概念即可.13.下列关于平面向量的命题中,正确命题的个数是(1)长度相等、方向相同的两个向量是相等向量;(2)平行且模相等的两个向量是相等向量;(3)若a b ≠,则a b →→≠;(4)两个向量相等,则它们的起点与终点相同.A .0B .1C .2D .3 【答案】B【分析】根据相等向量的有关概念判断.【解析】由相等向量的定义知(1)正确;平行且模相等的两个向量也可能是相反向量,(2)错;方向不相同且长度相等的两个是不相等向量,(3)错;相等向量只要求长度相等、方向相同,而表示两个向量的有向线段的起点不要求相同,(4)错,所以正确答案只有一个.故选B .14.下列命题中,正确命题的个数是①单位向量都共线;②长度相等的向量都相等;③共线的单位向量必相等;④与非零向量a 共线的单位向量是||a a .A .0B .1C .2D .3【试题来源】天津市和平区耀华中学2019-2020学年高一下学期期中【答案】A【分析】根据单位向量,相等向量,共线向量的定义进行判断即可.【解析】因为不同的单位向量的方向可能不相同,所以①错误;相反向量的长度相等,但方向相反,则②错误;因为共线的单位向量方向可能相反,所以它们不一定相等,则③错误;与非零向量a 共线的单位向量是||a a 或||a a -,则④错误;故选A 【名师点睛】本题主要考查了对单位向量,相等向量,共线向量的辨析,属于基础题. 15.有下列命题:①若a b →→=,则a b →→=;②若AB DC →→=,则四边形ABCD 是平行四边形;③若m n →→=,n k →→=,则m k →→=;④若//a b →→,//b c →→,则//a c →→.其中,假命题的个数是A .1B .2C .3D .4 【试题来源】宁夏育才中学2019-2020学年高一5月教学质量检测 【答案】C 【分析】根据平面向量的概念及向量平行的相关知识逐个判断即可.【解析】a b →→=,则a b →→,的方向不确定,则a b →→,不一定相等, ①错误;若AB DC →→=,则,AB DC →→的方向不一定相同,所以四边形ABCD 不一定是平行四边形,②错误;若m n →→=,n k →→=,则m k →→=,③正确;若//a b →→,//b c →→,则0b →→=时,//a c →→不一定成立,所以④错误.综上,假命题的是①②④,共3个.故选C .【名师点睛】本题主要考查平面向量的概念,意在考查学生对这些知识的理解掌握水平,属于基础题.16.下列说法不正确的是A .平行向量也叫共线向量B .两非零向量平行,则它们所在的直线平行或重合C .若a 为非零向量,则a a是一个与a 同向的单位向量 D .两个有共同起点且模相等的向量,其终点必相同【试题来源】安徽省六安市第一中学2019-2020学年高一上学期期末(理)【答案】D【分析】根据共线向量的定义判断AB ;由a a 的模长为1,10a >得出a a是一个与a 同向的单位向量;举例排除D .【解析】由于任一组平行向量都可以平移到一条直线上,则平行向量也叫共线向量,A 正确; 两非零向量平行,则它们所在的直线平行或重合,由共线向量的定义可知,B 正确; a a 的模长为1,10a >,则a a是一个与a 同向的单位向量,C 正确; 从同一点出发的两个相反向量,有共同的起点且模长相等,但终点不同,D 错误;故选D【名师点睛】本题主要考查了共线向量概念的辨析,属于基础题.17.下列四个命题正确的是A .两个单位向量一定相等B .若a 与b 不共线,则a 与b 都是非零向量C .共线的单位向量必相等D .两个相等的向量起点、方向、长度必须都相同【试题来源】辽宁省阜新市第二高级中学2019-2020学年高一下学期第一次学考【答案】B【分析】由相等向量、共线向量的概念逐一核对四个选项得答案.【解析】两个单位向量一定相等错误,可能方向不同;若a与b不共线,则a与b都是非零向量正确,原因是零向量与任意向量共线;共线的单位向量必相等错误,可能是相反向量;两个相等的向量的起点、方向、长度必须相同错误,原因是向量可以平移.故选B.【名师点睛】本题考查命题的真假判断与运用,考查了平行向量、向量相等的概念,属于基础题.18.有下列说法:①若两个向量不相等,则它们一定不共线;②若四边形ABCD是平行四边形,则AB CD=;③若//a c;b c,则//a b,//AB CD.④若AB CD=,则AB CD且//其中正确说法的个数是A.0B.1C.2D.3【试题来源】2021年新高考数学一轮专题复习(新高考专版)【答案】A【分析】对于①,根据向量相等的定义以及向量共线的定义可知结论不正确;对于②,根据向量相等的定义可知结论不正确;对于③,找特殊向量,当0b=时,可知结论不正确;对于④,AB与CD不一定平行,AB与CD可能在一条直线上,可知结论不正确.【解析】对于①,当两个向量不相等时,可能方向相反,所以可能共线,故①不正确;对于②,若四边形ABCD是平行四边形,则AB DC=,故②不正确;对于③,当0b=时,a与c可以不共线,故③不正确;AB CD或AB与CD在一条直线上”,故④不对于④,“若AB CD=,则AB CD且//正确.故选A.【名师点睛】本题考查了向量相等的定义,考查了向量共线的定义,属于基础题.19.下列说法正确的是A .单位向量都相等B .若//a b ,则a b =C .若a b =,则a b =D .若λa b ,(0b ≠),则a 与b 是平行向量 【试题来源】山西省大同市灵丘县豪洋中学2019-2020学年高一下学期期中 【答案】D 【分析】根据相等向量,共线向量的定义判断可得;【解析】对于A ,单位向量的模长相等,但方向不一定相同,所以A 错误;对于B ,当//a b 时,其模长a 与b 可能相等或a b λ=0λ≥,或b a λ=0λ≥,所以B 错误;对于C ,当a b =时,不一定有a b =,因为a b =要a b =且a 与b 同向,所以C 错误; 对于D ,λa b ,(0b ≠),则a 与b 是平行向量,D 正确.故选D . 【名师点睛】本题考查了平面向量的基本概念应用问题,属于基础题.20.如图所示,在正ABC 中,D ,E ,F 均为所在边的中点,则以下向量中与ED 相等的是A .EFB .BEC .FBD .FC【试题来源】2020-2021学年【补习教材寒假作业】高一数学(人教A 版2019)【答案】D【分析】由题意先证明//DE CB 且12DE CB =,再利用中点找出所有与向量ED 相等的向量【解析】DE 是ABC 的中位线,//DE CB ∴且12DE CB =, 则与向量ED 相等的有BF ,FC .故选D .【名师点睛】本题考查了相等向量的定义,利用中点和中位线找出符合条件的所求的向量,属于基础题.21.已知a 、b 是平面向量,下列命题正确的是A .若||||1a b ==,则a b =B .若||||a b <,则a b <C .若0a b +=,则//a bD .零向量与任何非零向量都不共线【试题来源】备战2021年新高考数学一轮复习考点微专题【答案】C【分析】A ,根据向量的定义判断;B .向量不能比较大小判断;C ,若0a b +=,则b a =-,由共线向量定理判断;D ,由零向量与任一向量共线判断.【解析】对于A ,向量方向不相同则向量不相等,选项A 错误;对于B .向量不能比较大小,选项B 错误;对于C ,若0a b +=,则b a =-,//b a ∴,选项C 正确;对于D ,零向量与任一向量共线,选项D 错误.故选C .【名师点睛】本题主要考查平面向量的概念及线性运算,还考查了理解辨析的能力,属于基础题.22.下列命题中正确的是A .若||a b |=|,则a b =B .若a b ≠,则a b ≠C .若||a b |=|,则a 与b 可能共线D .若a b ≠,则a 一定不与b 共线【试题来源】考点18 平面向量的概念及其线性运算-备战2021年高考数学(理)一轮复习考点一遍过【答案】C【分析】利用共线向量、模的计算公式,即可得出.【解析】因为向量既有大小又有方向,所以只有方向相同、大小(长度)相等的两个向量才相等,因此A 错误;两个向量不相等,但它们的模可以相等,故B 错误;无论两个向量的模是否相等,这两个向量都可能共线,故C正确,D错误.故选C【名师点睛】本题考查了共线向量、模的计算公式,考查了理解能力,属于基础题.23.下列关于向量的概念叙述正确的是A.方向相同或相反的向量是共线向量B.若//a ca b,//b c,则//C.若a和b都是单位向量,则a b=D.若两个向量相等,则它们的起点和终点分别重合【试题来源】山西省2019-2020学年高一下学期期末(理)【答案】A【分析】由向量共线的定义,可知A正确;当0b=时,可知B不正确;单位向量,方向不定,不相等;向量相等即大小和方向相同即可.【解析】由向量共线的定义可知,A正确;当0b=时,可知B不正确;单位向量,方向不确定,故C不正确;向量是自由的,向量相等,只需大小和方向相同即可,不需起点终点重合,故D不正确.故选A【名师点睛】本题考查了向量的定义和基本性质,考查了理解辨析能力,属于基础题目.24.已知向量a与b共线,下列说法正确的是A.a b=或a b=-B.a与b平行C.a与b方向相同或相反D.存在实数λ,使得λa b【试题来源】安徽省合肥市庐江县2019-2020学年高一下学期期末【答案】B【分析】根据向量共线的概念,以及向量共线定理,逐项判断,即可得出结果.【解析】向量a与b共线,不能判定向量模之间的关系,故A错;向量a与b共线,则a与b平行,故B正确;a为零向量,则满足a与b共线,方向不一定相同或相反;故C错;当0a ≠,0b =时,满足a 与b 共线,但不存在实数λ,使得λa b ,故D 错.故选B .【名师点睛】本题主要考查向量共线的有关判定,属于基础题型.25.下列关于平面向量的命题中,正确命题的个数是①任一向量与它的相反向量都不相等;②长度相等、方向相同的两个向量是相等向量;③平行且模相等的两个向量是相等向量;④若a b ≠,则||||a b ≠;⑤两个向量相等,则它们的起点与终点相同.A .0B .1C .2D .3【答案】B【分析】根据平面向量的基本概念,对选项中的命题进行分析、判断正误即可.【解析】零向量与它的相反向量相等,①错;由相等向量的定义知,②正确;两个向量平行且模相等,方向不一定相同,故不一定是相等向量,例如,在平行四边形ABCD 中,//AB CD ,且=AB CD ,但AB CD ≠,故③错; a b ≠,可能两个向量模相等而方向不同,④错;两个向量相等,是指它们方向相同,大小相等,向量可以自由移动,故起点和终点不一定相同,⑤错.故选B .26.判断下列命题:①两个有共同起点而且相等的非零向量,其终点必相同; ②若//a b ,则a 与b 的方向相同或相反; ③若//a b 且//b c ,则//a c ; ④若a b =,则2a b >.其中正确的命题个数为A .0B .1C .2D .3【试题来源】四川省凉山州2019-2020学年高一下学期期末考试(文)【答案】B【分析】根据相等向量、共线向量、零向量等知识确定正确命题的个数.【解析】①,两个有共同起点而且相等的非零向量,其终点必相同,根据相等向量的知识可知①是正确的.②,若//a b ,则可能b 为零向量,方向任意,所以②错误.③,若//a b 且//b c ,则可能b 为零向量,此时,a c 不一定平行,所以③错误.④,向量既有长度又有方向,所以向量不能比较大小,所以④错误.故正确的命题有1个.故选B【名师点睛】本题主要考查相等向量、共线向量、零向量等知识,属于基础题. 27.设,a b 是非零向量,则“2a b =”是“a a b b =” 成立的 A .充要条件B .充分不必要条件C .必要不充分条件D .既不充分也不必要条件【试题来源】山东省济南市莱芜第一中学2020-2021学年高三上学期11月月考【答案】B 【分析】结合共线向量、单位向量的知识,以及充分、必要条件的概念,判断出正确选项.【解析】依题意,a b 是非零向量,a a 表示与a 同向的单位向量,b b 表示与b 同向的单位向量,当2a b =时,,a b 的方向相同,所以a a b b =, 当a a b b =时,,a b 的方向相同,但不一定有2a b =,如3a b =也符合, 所以“2a b =”是“a a b b=” 成立的充分不必要条件.故选B【名师点睛】本题主要考查共线向量的知识、单位向量的知识,考查充分、必要条件的判断,属于基础题.28.若四边形ABCD 是矩形,则下列说法不正确的是A .AB →与CD →共线B .AC →与BD →共线 C .AD →与CB →模相等,方向相反 D .AB →与CD →模相等【试题来源】2020-2021学年【补习教材寒假作业】高一数学(苏教版)【答案】B【分析】根据向量的共线及模的概念即可求解.【解析】因为四边形ABCD 是矩形,所以AB →与CD →共线,AD →与CB →模相等,方向相反,AB →与CD →模相等正确, AC →与BD →共线错误,故选B29.设,a b →→是两个平面向量,则“a b →→=”是“||||a b →→=”的A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件 【试题来源】浙江省金华市曙光学校2020-2021学年高二上学期期中【答案】A【分析】根据充分条件、必要条件的定义及向量的概念判断即可.【解析】因为a b →→=,则一定有||||a b →→=,而||||a b →→=推不出a b →→=,所以“a b →→=”是“||||a b →→=”的充分不必要条件,故选A30.下列关于向量的结论:(1)若||||a b =,则a b =或a b =-;(2)向量a 与b 平行,则a 与b 的方向相同或相反;(3)起点不同,但方向相同且模相等的向量是相等向量;(4)若向量a 与b 同向,且||||a b >,则a b >.其中正确的序号为A .(1)(2)B .(2)(3)C .(4)D .(3) 【试题来源】专题07 平面向量的实际背景及基本概念(重点练)-2020-2021学年高一数学十分钟同步课堂专练(人教A 版必修4)【答案】D【分析】根据向量的定义可判断(1)(4)错误,向量,a b 都是零向量时,由向量,a b 平行得不出方向相同或相反,从而判断(2)错误,根据相等向量的定义可判断(3)正确.【解析】(1)若||||a b =,由于,a b 的方向不清楚,故不能得出a b =或a b =-,故(1)不正确.(2)由零向量与任何向量平行,当向量a 与b 平行时,不能得出a 与b 的方向相同或相反,故(2)不正确.(3)由向量的相等的定义,起点不同,但方向相同且模相等的向量是相等向量;故(3)正确.(4)向量不能比较大小,故(4)不正确.故选D .二、多选题1.下面的命题正确的有.A .方向相反的两个非零向量一定共线B .单位向量都相等C .若a ,b 满足a b >且a 与b 同向,则a b >D .“若A 、B 、C 、D 是不共线的四点,且AB DC =”⇔“四边形ABCD 是平行四边形”【试题来源】备战2021年新高考数学一轮复习考点一遍过【答案】AD【分析】根据向量的概念:方向相反或相同的非零向量共线,模相等且方向相同的向量相等,向量除了相等的情况不能比较大小,即可判断选项正误;【解析】方向相反的两个非零向量必定平行,所以方向相反的两个非零向量一定共线,故A 正确;单位向量的大小相等,但方向不一定相同,故B 错误;向量是有方向的量,不能比较大小,故C 错误;A 、B 、C 、D 是不共线的点,AB DC =,即模相等且方向相同,即平行四边形ABCD 对边平行且相等,反之也成立,故D 正确.故选AD【名师点睛】本题考查了向量的基本概念,需要理解向量共线、相等的条件,属于简单题;2.若四边形ABCD 是矩形,则下列命题中正确的是A .,AD CB 共线B .,AC BD 相等 C .,AD CB 模相等,方向相反 D .,AC BD 模相等【试题来源】2020-2021学年高一数学单元测试定心卷(人教B 版2019必修第二册)【答案】ACD【分析】根据向量的加法和减法的几何意义(平行四边形法则),结合矩形的判定与性质进行分析可解.【解析】因为四边形ABCD 是矩形,,ADBC AC BD ∴=‖, 所以,AD CB 共线,,AC BD 模相等,故A 、D 正确;因为矩形的对角线相等,所以|AC|=|BD|,,AC BD 模相等,但的方向不同,故B 不正确;|AD|=|CB|且AD ∥CB ,所以,AD CB 的模相等,方向相反,故C 正确.【名师点睛】本题考查向量的共线,相等,模,向量的加减法的几何意义,属基础题,根据向量的加减法的平行四边形法则和矩形的性质综合判定是关键.3.在下列结论中,正确的有A .若两个向量相等,则它们的起点和终点分别重合B .平行向量又称为共线向量C .两个相等向量的模相等D .两个相反向量的模相等【试题来源】江苏省淮安市涟水县第一中学2019-2020学年高一上学期第二次月考【答案】BCD【分析】根据向量的定义和性质依次判断每个选项得到答案.【解析】A . 若两个向量相等,它们的起点和终点不一定不重合,故错误; B . 平行向量又称为共线向量,根据平行向量定义知正确;C . 相等向量方向相同,模相等,正确;。
高一数学平面向量复习1

典例解读
7、平面直角坐标系中,O为坐标原点,已知两点 A(3,1),B(-1,3),若点C满足OC=αOA+βOB, 其中α 、β∈R,且α+β=1,则点C的轨迹方程 为( ) (A)3x+2y-11=0 (B)(x-1)2+(y-2)2=5 (C)2x-y=0 (D)x+2y-5=0 8、已知A(5,-1)、B(-1,7)、C(1,2),求△ABC 中∠A平分线长 9 、设 P 、 Q 是四边形 ABCD 对角线 AC 、 BD 中点, BC=a,DA=b,则 PQ=_________
2、已知a,b方向相同,且|a|=3,|b|=7,则 |2a-b|=___________
3、若将向量a=(2,1)绕原点按逆时针方向旋 转 得到向量b,则向量b的坐标为_____
4
典例解读
4、下列算式中不正确的是( (A) AB+BC+CA=0 ) (B) AB-AC=BC
(C) 0· AB=0
知识提要
一、向量的概念
既有____又有____的量叫做向量。用有向线段 表示向量时,有向线段的长度表示向量的____, 有向线段的箭头所指的方向表示向量的____ __________叫零向量
__________叫做单位向量 ____的____向量叫做平行向量,因为任一组平 行向量都可以平移到同一条直线上,所以平行 向量也叫做_____ 。零向量与任一向量平行
(D)λ(μa)=(λμ)a
5、若向量a=(1,1),b=(1,-1),c=(-1,2),则c=( )
1 3 1 3 3 1 3 1 A. a b B . a b C . a b D . a b 2 2 2 2 2 2 2 2
高一第二学期期末复习资料-家长打印版(共48页)

18. 已知在 ABC 中,角 A ,B ,C 的对边分别为 a ,b ,c ,且 b sin A 3a cos B 3c .
(1)求角 A 的大小; (2)若 a 4 , D 为 BC 的中点, ABC 的面积为 3 3 ,求 AD 的长.
2
12
必修二 第 7 章 复数 期末考试复习
概念
3
5
题型五: 平面向量的应用
13. O 是△ABC 所在平面内的一定点,P 是△ABC 所在平面内的一动点,若(―P→B -―P→C )·(―O→B ―→ ―→ ―→ ―→ ―→
+ OC )=( PC - PA )·( OA + OC )=0,则 O 为△ABC 的( )
A.内心
B.外心
C.重心
D.垂心
2.(多选)下列命题中正确的是( )
A.向量 a 与 b 不共线,则 a 与 b 都是非零向量 ―→ ―→ ―→
B.已知 A,B,C 是平面内任意三点,则 AB + BC + CA =0 ―→ ―→ ―→ ―→ ―→
C.若 O 为△ABC 所在平面内任一点,且满足( OB - OC )·( OB + OC -2 OA )=0,则
ABC 的面积.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
10
15.在△ABC 中,角 A,B,C 的对边分别为 a,b,c,且(2a﹣c)(a2﹣b2+c2)=2abccosC. (1)求角 B 的大小; (2)若 sin A 3 cos C 1 ,求 b 的值.
2a
16.如图,在 ABC 中, B 60 , AB 8 , AD 7 ,点 D 在 BC 上,且 cos ADC 1 . 7
,且 a + b = 5,
高一必修四第二章《平面向量》重要知识点及重要题型

高一必修四第二章《平面向量》重要知识点及重要题型1、向量加法运算:⑴三角形法则的特点:首尾相连、⑵平行四边形法则的特点:共起点2、向量减法运算:⑴三角形法则的特点:共起点,连终点,方向是减向量终点指向被减向量终点、如图:其中是减向量,是被减向量3、向量加减坐标运算:设,,,,⑷运算性质:①交换律:;②结合律:;③、若,则,(终点坐标减去起点坐标)①;②;③、,①、②当与同向时,;当与反向时,;或、③、,、则、①;②;③、、向量共线定理:1、向量与共线(),当且仅当有唯一一个实数,使、2、若,,向量共线判断方法:2设,,以上两种方法都可以判断两向量平行、两向量垂直:,,即⑶三角形不等式:(以下)(其中当)例:中,若,则是矩形。
特别注意的点:对角线相等的平行四边形是矩形投影:中点坐标公式:典型例题集1、以下说法错误的是()A、零向量与任一非零向量平行B、零向量与单位向量的模不相等C、平行向量方向相同D、平行向量一定是共线向量2、下列四式不能化简为的是()A、B、C、D、3、已知=(3,4),=(5,12),与则夹角的余弦为()A、B、C、D、4、已知、均为单位向量,它们的夹角为60,那么|+3| =()A、B、C、D、45、已知ABCDEF是正六边形,且=,=,则=()(A)(B)(C)+(D)6、设,为不共线向量,=+2,=-4-,=-5-3,则下列关系式中正确的是()(A)=(B)=2 (C)=-(D)=-27、设与是不共线的非零向量,且k+与+k共线,则k的值是()(A)1 (B)-1 (C)(D)任意不为零的实数8、已知向量=(3,4),=(sinα,cosα),且∥,则tanα等于( )A、B、C、D、9、已知且与平行,则( )(A)(B)(C)1 (D)210、若是非零向量,且=1),=(,k),且∥,则实数k的值为( )13、在四边形ABCD中,=,且=0,则四边形ABCD是()(A)矩形(B)菱形(C)直角梯形(D)等腰梯形14、已知M(-2,7)、N(10,-2),点P是线段MN上的点,且=-2,则P点的坐标为()(A)(-14,16)(B)(22,-11)(C)(6,1)(D)(2,4)15、已知=(1,2),=(-2,3),且k+与-k垂直,则k =()(A)(B)(C)(D)16、若平面向量和互相平行,其中、则()A、或0;B、;C、2或;D、或、17、下面给出的关系式中正确的个数是()① ②③④⑤(A)0 (B)1 (C)2 (D)318、已知向量若时,∥;时,,则A、B、C、D、二、填空题(5分5=25分):1、若A点的坐标为(-2,-1),则B点的坐标为、2、已知,则、3、已知向量,且,则的坐标是_________________、4、ΔABC中,A(1,2),B(3,1),重心G(3,2),则C点坐标为________________5、若有以下命题:① 两个相等向量的模相等;② 若和都是单位向量,则;③ 相等的两个向量一定是共线向量;④ ,,则;⑤ ②;⑥ 两个非零向量的和可以是零。
高中的数学平面向量专题复习(含例题练习)

标准实用平面向量专题复习一.向量有关概念:1. 向量的概念:既有大小又有方向的量,注意向量和数量的区别。
向量常用有向线段来表示,注意 不能说向量就是有向线段,为什么?(向量可以平移) 。
如:2•零向量:长度为0的向量叫零向量,记作:0,注意零向量的方向是任意的;3 .单位向量:长度为一个单位长度的向量叫做单位向量(与AB 共线的单位向量是-AB ); 一|AB|4 •相等向量:长度相等且方向相同的两个向量叫相等向量,相等向量有传递性; 5.平行向量(也叫共线向量):方向相同或相反的非零向量 a 、b 叫做平行向量,记作: a // b ,规定零向量和任何向量平行。
提醒:① 相等向量一定是共线向量,但共线向量不一定相等;② 两个向量平行与与两条直线平行是不同的两个概念:两个向量平行包含两个向量共线 平行不包含两条直线重合; *③ 平行向量无传递性!(因为有0)$ ④ 三点A B C 共线 AB AC 共线;a 的相反向量是一a 。
女口 =b ,则a =b 。
(2)两个向量相等的充要条件是它们的起点相同,终点相同。
(4)若ABCD 是平行四边形,则 AB = DC 。
( 5)若a = b,b= c ,则、向量的表示1•几何表示法:用带箭头的有向线段表示,如 AB ,注意起点在前,终点在后;2 •符号表示法:用一个小写的英文字母来表示,如 a , b , c 等;坐标表示。
如果向量的起点在原点,那么向量的坐标与向量的终点坐标相同。
三. 平面向量的基本定理:如果 e 1和e 2是同一平面内的两个不共线向量,那么对该平面内的任一向量a ,有且只有一对实数 ■ 1、 ’2,使a= \ 8+ '2e 2。
女口卄片 片 ■+4例 2 (1)若 a =(1,1)b =(1,-1),c=(—1,2),则 c= _________(2) 下列向量组中,能作为平面内所有向量基底的是A. 2 =(0,0),e 2 =(1,-2)B. e =(-1,2)© =(5,7)13 C. e = (3,5)6 =(6,10) D. e =(2,-3)© =(—,-—)24(3) 已知AD,BE 分别是 ABC 的边BC,AC 上的中线,且AD =a,BE =b ,则BC 可用向量a,b 表示为 _____但两条直线6 .相反向量:长度相等方向相反的向量叫做相反向量。
高一数学(平面向量问题专题练习)含答案

平面向量专题复习二答案班级_________姓名_________1.已知向量a ,b 满足2(1,2)a b m += ,(1,)b m =,且a 在b 方向上的投影是5,则实数m =()A B .C .2D .2±【解析】向量a ,b满足()21,2a b m += ,()1,b m = ,所以0,2m a ⎛⎫= ⎪⎝⎭ ,22m a b ⋅= ,()2cos 2m b a θ==,所以42516160m m --=,即()()225440m m+-=,解得2m =±.2.在平行四边形ABCD 中,,AB a AD b == ,则当22()()a b a b +=-时,该平行四边形为()A .菱形B .矩形C .正方形D .以上都不正确【解析】由题意知,向量,a b 满足22()()a b a b +=-,即222222a b a b a b a b++⋅=+-⋅ ,解得0a b ⋅= ,所以a b ⊥,即AB AD ⊥,所以平行四边形ABCD 为矩形,故选B 。
3.ABC ∆中,·0AB BC>,则ABC ∆一定是()A .锐角三角形B .直角三角形C .钝角三角形D .不确定【解析】因为ABC ∆中,·0AB BC>,则()··cos 0AB BC B π-> ,即()cos 0B π->,cos 0B <,角B 为钝角,所以三角形为钝角三角形,故选C 。
4.在ABC ∆中,若=OA OB OB OC OC OA ⋅=⋅⋅,则O 是ABC ∆的()A .外心B .内心C .重心D .垂心【解析】∵OA OB OB OC ⋅=⋅ ∴()0OB OA OC ⋅-=;∴0OB CA ⋅=;∴OB ⊥AC ,同理由OA OB OC OA ⋅=⋅,得到OA ⊥BC ∴点O 是△ABC 的三条高的交点,故选D 。
高一数学平面向量复习课件

向量数量积的几何意义在于它表示了两个向量的长度和它们之间的夹角之间的关系。具体来说,当两个非零向量 的夹角为锐角时,它们的数量积为正;当夹角为直角时,数量积为零;当夹角为钝角时,数量积为负。
向量数量积的运算律
总结词
掌握向量数量积的运算律,包括 交换律、结合律和分配律。
详细描述
向量数量积满足交换律,即 a·b=b·a;结合律,即 (a+b)·c=a·c+b·c;分配律,即 (λa)·b=λ(a·b),其中λ是标量。
向量积的性质
向量积的性质
1. 向量积的方向与两个向量的夹角和大小有 关,其方向垂直于两个给定向量所确定的平 面;2. 向量积的模长为|a×b|=|a||b|sinθ; 3. 向量积满足结合律但不满足交换律;4. 向量积可以用来表示向量的旋转关系。
性质的应用
在解析几何中,向量积可以用来解决与旋转 、速度和加速度有关的问题;在物理中,向 量积可以用来描述力矩、角速度等物理量。 通过理解这些性质和应用,学生可以更好地
向量积的运算律
向量积的运算律
交换律a×b=-b×a,分配律 (a+b)×c=a×c+b×c。这些运算律与标量积 的运算律类似,但要注意向量积不满足结合 律。
运算律的理解
交换律表明向量积的方向与夹角有关,而分 配律表明向量积与向量的线性组合是可分配 的。这些运算律对于理解向量积的性质和计 算非常重要。
混合积的性质
非负性
向量a、b、c的混合积为非负数,当且仅当a、b、c三个 向量共面时取值为0。
线性性质
混合积满足线性性质,即对于任意标量m和n,有 $(mvec{a} + nvec{b}) cdot vec{c} = mvec{a} cdot vec{c} + nvec{b} cdot vec{c}$。
高一平面向量知识点+例题+练习 含答案
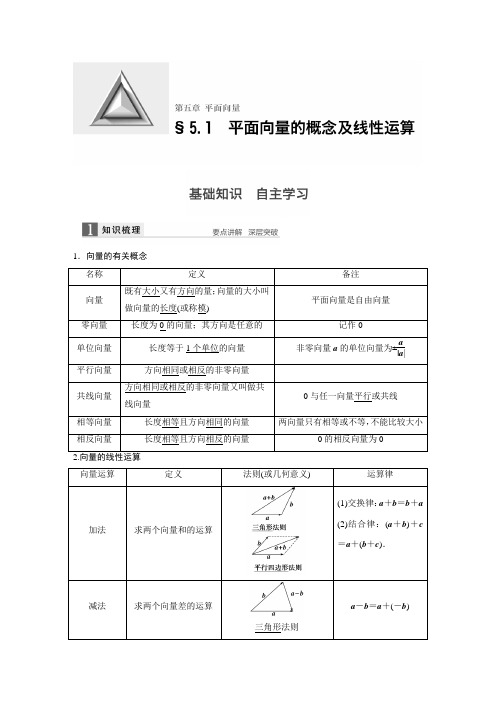
1.向量的有关概念 名称 定义备注向量 既有大小又有方向的量;向量的大小叫做向量的长度(或称模)平面向量是自由向量零向量 长度为0的向量;其方向是任意的记作0单位向量 长度等于1个单位的向量 非零向量a 的单位向量为±a|a |平行向量 方向相同或相反的非零向量共线向量 方向相同或相反的非零向量又叫做共线向量0与任一向量平行或共线 相等向量 长度相等且方向相同的向量 两向量只有相等或不等,不能比较大小相反向量 长度相等且方向相反的向量0的相反向量为02.向量的线性运算 向量运算定义法则(或几何意义)运算律加法求两个向量和的运算(1)交换律:a +b =b +a(2)结合律:(a +b )+c =a +(b +c ).减法 求两个向量差的运算三角形法则a -b =a +(-b )数乘求实数λ与向量a 的积的运算(1)|λa |=|λ||a |;(2)当λ>0时,λa 的方向与a 的方向相同;当λ<0时,λa 的方向与a 的方向相反;当λ=0时,λa=0(1)λ(μa )=(λμ)a ;(2)(λ+μ)a =λa +μa ; (3)λ(a +b )=λa +λb3.共线向量定理对空间任意两个向量a ,b (a ≠0),a 与b 共线的充要条件是存在实数λ,使得b =λa . 【思考辨析】判断下面结论是否正确(请在括号中打“√”或“×”)(1)向量与有向线段是一样的,因此可以用有向线段来表示向量.( × ) (2)|a |与|b |是否相等与a ,b 的方向无关.( √ ) (3)若a ∥b ,b ∥c ,则a ∥c .( × )(4)向量AB →与向量CD →是共线向量,则A ,B ,C ,D 四点在一条直线上.( × ) (5)当两个非零向量a ,b 共线时,一定有b =λa ,反之成立.( √ ) (6)△ABC 中,D 是BC 中点,则AD →=12(AC →+AB →).( √ )1.给出下列命题:①零向量的长度为零,方向是任意的;②若a ,b 都是单位向量,则a =b ;③向量AB →与BA →相等 .则所有正确命题的序号是________. 答案 ①解析 根据零向量的定义可知①正确;根据单位向量的定义可知,单位向量的模相等,但方向不一定相同,故两个单位向量不一定相等,故②错误;向量AB →与BA →互为相反向量,故③错误.2.如图所示,向量a -b =________(用e 1,e 2表示).答案 e 1-3e 2解析 由题图可得a -b =BA →=e 1-3e 2.3.(2015·课标全国Ⅰ改编)设D 为△ABC 所在平面内一点,BC →=3CD →,则AD →=______________(用AB →,AC →表示). 答案 -13AB →+43AC →解析 ∵BC →=3CD →,∴AC →-AB →=3(AD →-AC →), 即4AC →-AB →=3AD →,∴AD →=-13AB →+43AC →.4.(教材改编)已知▱ABCD 的对角线AC 和BD 相交于O ,且OA →=a ,OB →=b ,则DC →=________,BC →=________(用a ,b 表示). 答案 b -a -a -b解析 如图,DC →=AB →=OB →-OA →=b -a ,BC →=OC →-OB →=-OA →-OB →=-a -b .5.已知a 与b 是两个不共线向量,且向量a +λb 与-(b -3a )共线,则λ=________. 答案 -13解析 由已知得a +λb =-k (b -3a ),∴⎩⎪⎨⎪⎧λ=-k ,3k =1.解得⎩⎨⎧λ=-13,k =13.题型一 平面向量的概念例1 下列命题中,正确的是________.(填序号) ①有向线段就是向量,向量就是有向线段;②向量a 与向量b 平行,则a 与b 的方向相同或相反; ③向量AB →与向量CD →共线,则A 、B 、C 、D 四点共线; ④两个向量不能比较大小,但它们的模能比较大小.答案 ④解析 ①不正确,向量可以用有向线段表示,但向量不是有向线段,有向线段也不是向量; ②不正确,若a 与b 中有一个为零向量,零向量的方向是不确定的,故两向量方向不一定相同或相反;③不正确,共线向量所在的直线可以重合,也可以平行;④正确,向量既有大小,又有方向,不能比较大小;向量的模均为实数,可以比较大小. 思维升华 (1)相等向量具有传递性,非零向量的平行也具有传递性.(2)共线向量即为平行向量,它们均与起点无关.(3)向量可以平移,平移后的向量与原向量是相等向量.解题时,不要把它与函数图象的移动混为一谈.(4)非零向量a 与a |a |的关系:a|a |是与a 同方向的单位向量.设a 0为单位向量,①若a 为平面内的某个向量,则a =|a |a 0;②若a 与a 0平行,则a =|a |a 0;③若a 与a 0平行且|a |=1,则a =a 0.上述命题中,假命题的个数是________. 答案 3解析 向量是既有大小又有方向的量,a 与|a |a 0的模相同,但方向不一定相同,故①是假命题;若a 与a 0平行,则a 与a 0的方向有两种情况:一是同向,二是反向,反向时a =-|a |a 0,故②③也是假命题.综上所述,假命题的个数是3.题型二 平面向量的线性运算命题点1 向量的线性运算例2 (1)设D ,E ,F 分别为△ABC 的三边BC ,CA ,AB 的中点,则EB →+FC →=________. (2)在△ABC 中,AB →=c ,AC →=b ,若点D 满足BD →=2DC →,则AD →=______________(用b ,c 表示).答案 (1)AD →(2)23b +13c解析 (1)EB →+FC →=12(AB →+CB →)+12(AC →+BC →)=12(AB →+AC →)=AD →. (2)∵BD →=2DC →,∴AD →-AB →=BD →=2DC →=2(AC →-AD →), ∴3AD →=2AC →+AB →,∴AD →=23AC →+13AB →=23b +13c .命题点2 根据向量线性运算求参数例3 (1)在△ABC 中,已知D 是AB 边上的一点,若AD →=2DB →,CD →=13CA →+λCB →,则λ=____________.(2)在△ABC 中,点D 在线段BC 的延长线上,且BC →=3CD →,点O 在线段CD 上(与点C ,D 不重合),若AO →=xAB →+(1-x )AC →,则x 的取值范围是______________. 答案 (1)23(2)⎝⎛⎭⎫-13,0 解析 (1)∵AD →=2DB →,即CD →-CA →=2(CB →-CD →), ∴CD →=13CA →+23CB →,∴λ=23.(2)设CO →=yBC →, ∵AO →=AC →+CO →=AC →+yBC →=AC →+y (AC →-AB →) =-yAB →+(1+y )AC →.∵BC →=3CD →,点O 在线段CD 上(与点C ,D 不重合), ∴y ∈⎝⎛⎭⎫0,13, ∵AO →=xAB →+(1-x )AC →, ∴x =-y ,∴x ∈⎝⎛⎭⎫-13,0. 思维升华 平面向量线性运算问题的常见类型及解题策略(1)向量加法或减法的几何意义.向量加法和减法均适合三角形法则.(2)求已知向量的和.一般共起点的向量求和用平行四边形法则;求差用三角形法则;求首尾相连向量的和用三角形法则.(3)求参数问题可以通过研究向量间的关系,通过向量的运算将向量表示出来,进行比较求参数的值.如图,一直线EF 与平行四边形ABCD 的两边AB ,AD 分别交于E ,F 两点,且交对角线AC 于K ,其中,AE →=25AB →,AF →=12AD →,AK →=λAC →,则λ的值为________. 答案 29解析 ∵AE →=25AB →,AF →=12AD →,∴AB →=52AE →,AD →=2AF →.由向量加法的平行四边形法则可知, AC →=AB →+AD →, ∴AK →=λAC →=λ(AB →+AD →) =λ⎝⎛⎭⎫52AE →+2AF → =52λAE →+2λAF →, 由E ,F ,K 三点共线,可得λ=29.题型三 共线定理的应用例4 设两个非零向量a 与b 不共线,(1)若AB →=a +b ,BC →=2a +8b ,CD →=3(a -b ),求证:A 、B 、D 三点共线; (2)试确定实数k ,使k a +b 和a +k b 共线.(1)证明 ∵AB →=a +b ,BC →=2a +8b ,CD →=3(a -b ), ∴BD →=BC →+CD →=2a +8b +3(a -b ) =2a +8b +3a -3b =5(a +b )=5AB →. ∴AB →、BD →共线,又∵它们有公共点B , ∴A 、B 、D 三点共线. (2)解 ∵k a +b 和a +k b 共线, ∴存在实数λ,使k a +b =λ(a +k b ), 即k a +b =λa +λk b .∴(k -λ)a =(λk -1)b . ∵a 、b 是两个不共线的非零向量,∴k -λ=λk -1=0,∴k 2-1=0.∴k =±1.思维升华 (1)证明三点共线问题,可用向量共线解决,但应注意向量共线与三点共线的区别与联系.当两向量共线且有公共点时,才能得出三点共线.(2)向量a 、b 共线是指存在不全为零的实数λ1,λ2,使λ1a +λ2b =0成立,若λ1a +λ2b =0,当且仅当λ1=λ2=0时成立,则向量a 、b 不共线.设D ,E 分别是△ABC 的边AB ,BC 上的点,AD =12AB ,BE =23BC .若DE →=λ1AB→+λ2AC →(λ1,λ2为实数),则λ1+λ2的值为________. 答案 12解析 DE →=DB →+BE →=12AB →+23BC →=12AB →+23(AC →-AB →) =-16AB →+23AC →,∵DE →=λ1AB →+λ2AC →,∴λ1=-16,λ2=23,故λ1+λ2=12.10.方程思想在平面向量线性运算中的应用典例 (14分)如图所示,在△ABO 中,OC →=14OA →,OD →=12OB →,AD 与BC 相交于点M ,设OA →=a ,OB →=b .试用a 和b 表示向量OM →.思维点拨 (1)用已知向量来表示另外一些向量是用向量解题的基本要领,要尽可能地转化到平行四边形或三角形中去求解.(2)既然OM →能用a 、b 表示,那我们不妨设出OM →=m a +n b . (3)利用向量共线建立方程,用方程的思想求解. 规范解答解 设OM →=m a +n b ,则AM →=OM →-OA →=m a +n b -a =(m -1)a +n b .AD →=OD →-OA →=12OB →-OA →=-a +12b .[3分]又∵A 、M 、D 三点共线,∴AM →与AD →共线. ∴存在实数t ,使得AM →=tAD →, 即(m -1)a +n b =t ⎝⎛⎭⎫-a +12b .[5分] ∴(m -1)a +n b =-t a +12t b .∴⎩⎪⎨⎪⎧m -1=-t ,n =t 2,消去t 得,m -1=-2n , 即m +2n =1.① [8分]又∵CM →=OM →-OC →=m a +n b -14a =⎝⎛⎭⎫m -14a +n b , CB →=OB →-OC →=b -14a =-14a +b .又∵C 、M 、B 三点共线,∴CM →与CB →共线.[11分] ∴存在实数t 1,使得CM →=t 1CB →, ∴⎝⎛⎭⎫m -14a +n b =t 1⎝⎛⎭⎫-14a +b , ∴⎩⎪⎨⎪⎧m -14=-14t 1,n =t 1. 消去t 1得,4m +n =1. ②由①②得m =17,n =37,∴OM →=17a +37b .[14分]温馨提醒 (1)本题考查了向量的线性运算,知识要点清楚,但解题过程复杂,有一定的难度.(2)易错点是找不到问题的切入口,想不到利用待定系数法求解.(3)数形结合思想是向量加法、减法运算的核心,向量是一个几何量,是有“形”的量,因此在解决向量有关问题时,多数习题要结合图形进行分析、判断、求解,这是研究平面向量最重要的方法与技巧.如本题易忽视A 、M 、D 三点共线和B 、M 、C 三点共线这个几何特征.(4)方程思想是解决本题的关键,要注意体会.[方法与技巧]1.向量的线性运算要满足三角形法则和平行四边形法则,做题时,要注意三角形法则与平行四边形法则的要素.向量加法的三角形法则要素是“首尾相接,指向终点”;向量减法的三角形法则要素是“起点重合,指向被减向量”;平行四边形法则要素是“起点重合”. 2.证明三点共线问题,可用向量共线来解决,但应注意向量共线与三点共线的区别与联系,当两向量共线且有公共点时,才能得出三点共线.3.对于三点共线有以下结论:对于平面上的任一点O ,OA →,OB →不共线,满足OP →=xOA →+yOB →(x ,y ∈R ),则P ,A ,B 共线⇔x +y =1. [失误与防范]1.解决向量的概念问题要注意两点:一是不仅要考虑向量的大小,更重要的是要考虑向量的方向;二是考虑零向量是否也满足条件.要特别注意零向量的特殊性.2.在利用向量减法时,易弄错两向量的顺序,从而求得所求向量的相反向量,导致错误.A 组 专项基础训练 (时间:40分钟)1.给出下列四个命题,其中所有正确命题的序号是___________________.①a 与b 共线,b 与c 共线,则a 与c 也共线;②任意两个相等的非零向量的始点与终点是一个平行四边形的四顶点;③向量a 与b 不共线,则a 与b 都是非零向量;④有相同起点的两个非零向量不平行. 答案 ③解析 由于零向量与任一向量都共线,所以命题①中的b 可能为零向量,从而不正确;由于数学中研究的向量是自由向量,所以两个相等的非零向量可以在同一直线上,而此时就构不成四边形,更不可能是一个平行四边形的四个顶点,所以命题②不正确;向量的平行只要方向相同或相反即可,与起点是否相同无关,所以命题④不正确;对于命题③,其条件以否定形式给出,所以可从其逆否命题入手考虑,假若a 与b 不都是非零向量,即a 与b 至少有一个是零向量,而由零向量与任一向量都共线,可有a 与b 共线,其逆否命题正确,故命题③正确.综上所述,正确命题的序号是③.2.在△ABC 中,CA →=a ,CB →=b ,M 是CB 的中点,N 是AB 的中点,且CN 、AM 交于点P ,则AP →可用a 、b 表示为______________. 答案 -23a +13b解析 如图所示,AP →=AC →+CP →=-CA →+23CN →=-CA →+23×12(CA →+CB →)=-CA →+13CA →+13CB →=-23CA →+13CB →=-23a +13b . 3.如图,在四边形ABCD 中,AB ∥CD ,AB =3DC ,E 为BC 的中点,则AE →=________(用AB →,AD →表示). 答案 23AB →+12AD →解析 BC →=BA →+AD →+DC →=-23AB →+AD →,AE →=AB →+BE →=AB →+12BC →=AB →+12⎝⎛⎭⎫AD →-23AB → =23AB →+12AD →. 4.已知平面内一点P 及△ABC ,若P A →+PB →+PC →=AB →,则有关点P 与△ABC 的位置关系判断正确的是________(填序号).①点P 在线段AB 上; ②点P 在线段BC 上; ③点P 在线段AC 上; ④点P 在△ABC 外部. 答案 ③解析 由P A →+PB →+PC →=AB →得P A →+PC →=AB →-PB →=AP →,即PC →=AP →-P A →=2AP →,所以点P 在线段AC 上.5.已知点O 为△ABC 外接圆的圆心,且OA →+OB →+OC →=0,则△ABC 的内角A 等于________. 答案 60°解析 由OA →+OB →+OC →=0,知点O 为△ABC 的重心,又∵O 为△ABC 外接圆的圆心,∴△ABC 为等边三角形,A =60°.6.已知O 为四边形ABCD 所在平面内一点,且向量OA →,OB →,OC →,OD →满足等式OA →+OC →=OB →+OD →,则四边形ABCD 的形状为________. 答案 平行四边形解析 由OA →+OC →=OB →+OD →得OA →-OB →=OD →-OC →,所以BA →=CD →.所以四边形ABCD 为平行四边形.7.设点M 是线段BC 的中点,点A 在直线BC 外,BC →2=16,|AB →+AC →|=|AB →-AC →|,则|AM →|=________.答案 2解析 由|AB →+AC →|=|AB →-AC →|可知,AB →⊥AC →,则AM 为Rt △ABC 斜边BC 上的中线,因此,|AM →|=12|BC →|=2. 8.(2015·北京)在△ABC 中,点M ,N 满足AM →=2MC →,BN →=NC →.若MN →=xAB →+yAC →,则x =________;y =________.答案 12 -16解析 如图,MN →=MC →+CN →=13AC →+12CB → =13AC →+12(AB →-AC →) =12AB →-16AC →,∴x =12,y =-16. 9.如图,在△ABC 中,D 、E 分别为BC 、AC 边上的中点,G 为BE 上一点,且GB =2GE ,设AB →=a ,AC →=b ,试用a ,b 表示AD →,AG →.解 AD →=12(AB →+AC →)=12a +12b . AG →=AB →+BG →=AB →+23BE →=AB →+13(BA →+BC →) =23AB →+13(AC →-AB →)=13AB →+13AC →=13a +13b . 10.设两个非零向量e 1和e 2不共线.(1)如果AB →=e 1-e 2,BC →=3e 1+2e 2,CD →=-8e 1-2e 2,求证:A 、C 、D 三点共线;(2)如果AB →=e 1+e 2,BC →=2e 1-3e 2,CD →=2e 1-k e 2,且A 、C 、D 三点共线,求k 的值.(1)证明 ∵AB →=e 1-e 2,BC →=3e 1+2e 2,CD →=-8e 1-2e 2,∴AC →=AB →+BC →=4e 1+e 2=-12(-8e 1-2e 2)=-12CD →,∴AC →与CD →共线. 又∵AC →与CD →有公共点C ,∴A 、C 、D 三点共线.(2)解 AC →=AB →+BC →=(e 1+e 2)+(2e 1-3e 2)=3e 1-2e 2,∵A 、C 、D 三点共线,∴AC →与CD →共线,从而存在实数λ使得AC →=λCD →,即3e 1-2e 2=λ(2e 1-k e 2),得⎩⎪⎨⎪⎧3=2λ,-2=-λk ,解得λ=32,k =43. B 组 专项能力提升(时间:15分钟)11.设a ,b 不共线,AB →=2a +p b ,BC →=a +b ,CD →=a -2b ,若A ,B ,D 三点共线,则实数p 的值是________.答案 -1解析 ∵BC →=a +b ,CD →=a -2b ,∴BD →=BC →+CD →=2a -b .又∵A ,B ,D 三点共线,∴AB →,BD →共线.设AB →=λBD →,∴2a +p b =λ(2a -b ),∴2=2λ,p =-λ,∴λ=1,p =-1.12.如图,已知AB 是圆O 的直径,点C ,D 是半圆弧的两个三等分点,AB →=a ,AC →=b ,则AD →=____________(用a ,b 表示).答案 12a +b 解析 连结CD ,由点C ,D 是半圆弧的三等分点,得CD ∥AB 且CD →=12AB →=12a ,所以AD →=AC →+CD →=b +12a . 13.设G 为△ABC 的重心,且sin A ·GA →+sin B ·GB →+sin C ·GC →=0,则B 的大小为________.答案 60°解析 ∵G 是△ABC 的重心,∴GA →+GB →+GC →=0,GA →=-(GB →+GC →),将其代入sin A ·GA →+sin B ·GB →+sin C ·GC →=0,得(sin B -sin A )GB →+(sin C -sin A )GC →=0.又GB →,GC →不共线,∴sin B -sin A =0,sin C -sin A =0,则sin B =sin A =sin C .根据正弦定理知b =a =c , ∴△ABC 是等边三角形,则角B =60°.14.在▱ABCD 中,AB →=a ,AD →=b ,AN →=3NC →,M 为BC 的中点,则MN →=____________.(用a ,b 表示)答案 -14a +14b 解析 由AN →=3NC →得AN →=34AC →=34(a +b ), AM →=a +12b ,所以MN →=AN →-AM → =34(a +b )-⎝⎛⎭⎫a +12b =-14a +14b . 15.如图,经过△OAB 的重心G 的直线与OA ,OB 分别交于点P ,Q ,设OP →=mOA →,OQ →=nOB →,m ,n ∈R ,则1n +1m的值为________. 答案 3解析 设OA →=a ,OB →=b ,由题意知OG →=23×12(OA →+OB →)=13(a +b ),PQ →=OQ →-OP →=n b -m a ,PG →=OG →-OP →=⎝⎛⎭⎫13-m a +13b ,由P ,G ,Q 三点共线得,存在实数λ,使得PQ →=λPG →,即n b -m a =λ⎝⎛⎭⎫13-m a +13λb , 从而⎩⎨⎧ -m =λ⎝⎛⎭⎫13-m ,n =13λ,消去λ得1n +1m =3.。
高一数学第2讲 平面向量(知识点串讲)(解析版)

第2讲 平面向量(知识点串讲)知识整合1.向量的有关概念(1)向量:既有大小又有方向的量叫做向量,向量的大小叫做向量的长度(或模). (2)零向量:长度为0的向量,其方向是任意的. (3)单位向量:长度等于1个单位的向量.(4)平行向量:方向相同或相反的非零向量.平行向量又叫共线向量.规定:0与任一向量平行. (5)相等向量:长度相等且方向相同的向量. (6)相反向量:长度相等且方向相反的向量.例1、判断下列结论的正误(正确的打“√”,错误的打“×”) (1)向量不能比较大小,但向量的模可以比较大小.( ) (2)BA →=OA →-OB →.( )(3)向量AB →与向量CD →是共线向量,则A ,B ,C ,D 四点在一条直线上.( )(4)已知a ,b 是两个非零向量,当a ,b 共线时,一定有b =λa (λ为常数),反之也成立.( ) 【答案】 (1)√ (2)√ (3)× (4)√ [跟踪训练]1、有下列命题:①两个相等向量,它们的起点相同,终点也相同;②若|a |=|b |,则a =b ;③若|AB →|=|DC →|,则四边形ABCD 是平行四边形;④若m =n ,n =k ,则m =k ;⑤若a ∥b ,b ∥c ,则a ∥c ;⑥有向线段就是向量,向量就是有向线段.其中,假命题的个数是( )A .2B .3C .4D .5【答案】C [对于①,两个相等向量,它们的起点相同,终点也相同,①正确;对于②,若|a |=|b |,方向不确定,则a ,b 不一定相等,∴②错误;对于③,若|AB →|=|DC →|,AB →,DC →不一定相等,∴四边形ABCD 不一定是平行四边形,③错误;对于④,若m =n ,n =k ,则m =k ,④正确;对于⑤,若a ∥b ,b ∥c ,当b =0时,a ∥c 不一定成立,∴⑤错误;对于⑥,有向线段不是向量,向量可以用有向线段表示,∴⑥错误.综上,假命题是②③⑤⑥,共4个.] 知识整合2.向量的线性运算如果e 1,e 2是同一平面内的两个不共线向量,那么对于这一平面内的任意向量a ,有且只有一对实数λ1,λ2,使a =λ1e 1+λ2e 2.其中,不共线的向量e 1,e 2叫做表示这一平面内所有向量的一组基底.例2、(2019·山东东营检测)如图所示,BC →=3CD →,O 在线段CD 上,且O 不与端点C ,D 重合,若AO →=mAB →+(1-m )AC →,则实数m 的取值范围为________.【答案】⎝⎛⎭⎫-13,0 [设CO →=kBC →,则k ∈⎝⎛⎭⎫0,13, ∴AO →=AC →+CO →=AC →+kBC →=AC →+k (AC →-AB →)=(1+k )AC →-kAB →. 又AO →=mAB →+(1-m )AC →,∴m =-k . ∵k ∈⎝⎛⎭⎫0,13,∴m ∈⎝⎛⎭⎫-13,0.] [跟踪训练]2、(2019·山东潍坊调研)如图,在平行四边形ABCD 中,AC ,BD 相交于点O ,E 为线段AO 的中点.若BE →=λBA →+μBD →(λ,μ∈R ),则λ+μ等于( )A .1B .34C .23D .12【答案】B [∵E 为线段AO 的中点,∴BE →=12BA →+12BO →=12BA →+12⎝⎛⎭⎫12BD →=12BA →+14BD →=λBA →+μBD →,∴λ+μ=12+14=34.] 知识整合4.共线向量定理向量a (a ≠0)与b 共线,当且仅当有唯一一个实数λ,使b =λa .(1)一般地,首尾顺次相接的多个向量的和等于从第一个向量起点指向最后一个向量终点的向量,即A 1A 2→+A 2A 3→+A 3A 4→+…+A n -1A n =A 1A n →,特别地,一个封闭图形,首尾连接而成的向量和为零向量.(2)若P 为线段AB 的中点,O 为平面内任一点,则OP →=12(OA →+OB →).(3)OA →=λOB →+μOC →(λ,μ为实数),若点A ,B ,C 共线,则λ+μ=1.例3、(2019·山东青州月考)已知O 为△ABC 内一点,且2AO →=OB →+OC →,AD →=tAC →,若B ,O ,D 三点共线,则t 的值为( )A .14B .13C .12D .23【答案】B [设线段BC 的中点为M , 则OB →+OC →=2OM →.因为2AO →=OB →+OC →,所以AO →=OM →, 则AO →=12AM →=14(AB →+AC →)=14⎝⎛⎭⎫AB →+1t AD →=14AB →+14tAD →. 由B ,O ,D 三点共线,得14+14t =1,解得t =13.][跟踪训练]3、设两个非零向量a 与b 不共线.(1)若AB →=a +b ,BC →=2a +8b ,CD →=3(a -b ), 求证:A ,B ,D 三点共线;(2)试确定实数k ,使k a +b 和a +k b 共线.【答案】(1)证明 ∵AB →=a +b ,BC →=2a +8b ,CD →=3(a -b ), ∴BD →=BC →+CD →=2a +8b +3(a -b ) =2a +8b +3a -3b =5(a +b )=5AB →,∴AB →,BD →共线.又∵它们有公共点B ,∴A ,B ,D 三点共线. (2)解 假设k a +b 与a +k b 共线, 则存在实数λ,使k a +b =λ(a +k b ), 即(k -λ)a =(λk -1)b .又a ,b 是两个不共线的非零向量, ∴k -λ=λk -1=0.消去λ,得k 2-1=0,∴k =±1. 知识整合5.平面向量的坐标运算(1)向量的加法、减法、数乘向量及向量的模: 设a =(x 1,y 1),b =(x 2,y 2),则a +b =(x 1+x 2,y 1+y 2),a -b =(x 1-x 2,y 1-y 2),λa =(λx 1,λy 1),|a |=x 21+y 21. (2)向量坐标的求法:①若向量的起点是坐标原点,则终点坐标即为向量的坐标. ②设A (x 1,y 1),B (x 2,y 2),则AB →=(x 2-x 1,y 2-y 1), |AB →|=x 2-x 12y 2-y 12.6.平面向量共线的坐标表示设a =(x 1,y 1),b =(x 2,y 2),其中b ≠0,则a ∥b ⇔x 1x 2=y 1y 2.⇔x 1y 2-x 2y 1=0.例4、(2019·山东潍坊检测)如图,正方形ABCD 中,E 为DC 的中点,若AE →=λAB →+μAC →,则λ+μ的值为( )A . 12B .-12C .1D .-1【答案】A [法一:由题意得AE →=AD →+12AB →=BC →+AB →-12AB →=AC →-12AB →,∴λ=-12,μ=1,∴λ+μ=12.法二:利用坐标法,以A 为坐标原点,AB 、AD 所在直线分别为x 轴,y 轴建立平面直角坐标系(图略), 设正方形的边长为1,则A (0,0),B (1,0),C (1,1),E ⎝⎛⎭⎫12, 1,∴AE →=⎝⎛⎭⎫12, 1,AB →=(1,0),AC →=(1,1),则⎝⎛⎭⎫12, 1=λ(1,0)+μ(1,1),∴λ+μ=12.][跟踪训练]4、(2019·山东青岛调研)已知向量a =(-1,1),b =(3,m ),若a ∥(a +b ),则m =( ) A .-2 B .2 C .3D .-3【答案】D [向量a =(-1,1),b =(3,m ),则a +b =(2,m +1),a ∥(a +b ),则-(m +1)=2,解得m =-3.] 知识整合7.向量的夹角已知两个非零向量a 和b ,作OA →=a ,OB →=b ,则∠AOB 就是向量a 与b 的夹角,向量夹角的范围是:[0,π].8.平面向量的数量积9.①交换律:a ·b =b ·a ;②数乘结合律:(λa )·b =λ(a ·b )=a ·(λb ); ③分配律:a ·(b +c )=a ·b +a ·c . (2)平面向量数量积运算的常用公式①(a +b )·(a -b )=a 2-b 2. ②(a +b )2=a 2+2a ·b +b 2. ③(a -b )2=a 2-2a ·b +b 2. 10.平面向量数量积的性质及其坐标表示设非零向量a =(x 1,y 1),b =(x 2,y 2),θ=〈a ,b 〉.注:两个向量a ,b 的夹角为锐角⇔a ·b >0且a ,b 不共线;两个向量a ,b 的夹角为钝角⇔a ·b <0且a ,b 不共线.例5、(2018·天津卷)如图,在平面四边形ABCD 中,AB ⊥BC ,AD ⊥CD ,∠BAD =120°,AB =AD =1.若点E 为边CD 上的动点,则AE →·BE →的最小值为( )A .2116B .32C .2516D .3【答案】A [如图,以D 为坐标原点建立直角坐标系.连接AC ,由题意知∠CAD =∠CAB =60°,∠ACD =∠ACB =30°,则D (0,0),A (1,0),B ⎝⎛⎭⎫32,32,C (0,3).设E (0,y )(0≤y ≤3),则AE →=(-1,y ),BE →=⎝⎛⎭⎫-32,y -32,∴AE →·BE →=32+y 2-32y =⎝⎛⎭⎫y -342+2116,∴当y =34时,AE →·BE →有最小值2116.] [跟踪训练]5、(2018·天津卷)在如图所示的平面图形中,已知OM =1,ON =2,∠MON =120°,BM →=2MA →,CN →=2NA →,则BC →·OM →的值为( )A .-15B .-9C .-6D .0【答案】C [如图,连接MN .∵BM →=2MA →,CN →=2NA →,∴AM AB =13=AN AC ,∴MN ∥BC ,且MN BC =13,∴BC →=3MN →=3(ON →-OM →), ∴BC →·OM →=3(ON →·OM →-OM →2) =3(2×1×cos 120°-12)=-6.]。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高一平面向量复习专题
、选择题
uu un r r
2.设a D ,b 0分别是与a,b 向的单位向量,则下列结论中正确的是(
)
(3)若不平行的两个非零向量
a,b ,满足|a| |b|,则(a b ) (a b ) 0
_ — r r — -
(4 )若a 与b 平行,则adp |a| |b|其中真命题的个数是(
)
o
A . 0
B . 1
C . 2
D . 3
4 .下列命题中正确的是(
)
A .若 a b = 0 ,贝V a = 0 或 b = 0
B .若 a b = 0 ,贝 U a // b
C .若a // b ,则a 在b 上的投影为|a|
D .若a 丄b ,贝
U
a b = (a b)2
r
r
r r
5 .已知平面向量a
(3,1) ,b (x, 3),且
a b ,则
x (
)
A .
3 B .
1
C . 1
D . 3
6.已知向量a (cos ,sin ),向量b ( 3,
1)则 12a b|的最大值,最小值分别是(
)
A . 4 2,0
B . 4,4.2
C . 16,0
D . 4,0
7 .下列命题中正确的是(
)
uu uun UJU A . OA OB AB r mu r
C . 0 AB 0
3 .已知卜列命题中:
r r
(1 )若 k R ,且 kb 0 ,则k r r
r (2 )若 a b
0,则 a r r r
0或b 0
r
o uuu uur
B . AB BA 0
uuu uuu uuu uu
u D . AB BC CD AD
uuur 1 .化简AC uuu uuu uur BD CD AB 得(
r --
D
Be
c
函
B
出
UU UD A . a 0 b ° un ur
a 。
b ° 1
uu ur C . |a °| |P D I 2 uu ur
D
. I a 。
b 。
| 2
UUIT
8.设点A(2,0) , B(4,2),若点P 在直线AB 上,且AB uur
A P ,则点P 的坐标为(
)
A . (3,1)
B . (1, 1)
C . (3,1)或(1, 1)
D .无数多个
9.右 平面向量b 与向量a
(1, 2)的夹角是180o ,且|b| 3 5,则b (
A . ( 3,6)
B . (3, 6)
C . (6, 3)
D . ( 6,3)
10 .向量a
(2,3) , b ( 1,2),若 ma b 与 a 2b 平行,则 m 等于(
A .
2 B . 2
D .
1
r r r r r
r (a 2b) a , (b 2a)
b
,则a 与b 的夹角是( A .—
B
6
r
3 .
12 .设 a (c,sin
2
2
5
C .——
D .——
3 6
1 r 〃
(cos ,—),且all b ,则锐角
为( )
3
13 .若三点 A(2,3), B(3,a),C(4,b)共线,则有(
)
A . a 3,b 5
B . a b 1 0
C . 2a b 3
D . a 2b 0
14 .设 0
2 ,已知两个向量OR
cos , sin , OP 2
2 sin ,2 cos
则向量RP 2长度的最大值是( )
A. 2
B. 3
C. 3 2 D2 3 15 .下列命题正确的是(
)
A .单位向量都相等
B .若a 与b 是共线向量,b 与c 是共线向量,则a 与c 是共线向量(
)
、
-
- -
r r
C . | a b | | a b |,则 a b 0
D .若a 。
与b 。
是单位向量,则a 。
b 。
1
r
| r r
16 .已知a,b 均为单位向量,它们的夹角为
600,那么a 3b (
)
7 B . 10 C . 13 D . 4
11 •若a,b 是非零向量且满足
r b
3 ,
、填空题
I .若 OA = (2,8) , OB = ( 7,2),则-AB =
3 r r r
_
r r -
2. 平面向量a,b 中,若a (4, 3), b
=1,且a b 5,则向量b = _________
3. 若間3,|b| 2,且a 与b 的夹角为60°,则* b | ______
4. 把平面上一切单位向量归结到共同的始点,
那么这些向量的终点所构成的图形是 __________
5 .已知a (2,1)与b (1,2),要使|a tb|最小,则实数t 的值为 ___________________ 6. 若| a | 1,|b| 2,c a b ,且c a ,则向量a 与b 的夹角为 _____________________
7. 已知向量a (1,2) , b ( 2,3) , c (4,1),若用a 和b 表示c ,则c = ___________________
r r r - 0 r r r r
8. 若a 1, b 2 , a 与b 的夹角为60 ,若(3a 5b) (ma b),则m 的值为 _______________________
|ULU 9. 若菱形ABCD 的边长为2,贝U AB
10 .若a = (2,3) , b = ( 4,7),则a 在b 上的投影为 ____________ II .已知向量 a (cos ,sin ),向量b
1),则12a b|的最大值是 ____________
12 .若 A(1,2),B(2,3),C( 2,5),试判断则△ ABC 的形状 ____________
r r
一
13 .若a (2, 2),则与a 垂直的单位向量的坐标为 _______________
14 .若向量 |;| 1,|b| 2,|; b| 2,则 |; b| ____________
17 .已知向量a , b 满足a 1,b 4,且a b 2 ,则a 与b 的夹角为()
18 .若平面向量 b 与向量a
(2,1)平行,且 |b| 25,则 b () A . (4,2)
B . ( 4,
2) C . (6, 3) D . (4,2)或(4, 2)
UJU UUUTi CB CD
-- r r r r -*
15 .平面向量a, b中,已知a (4, 3), b 1,且a b 5,则向量b _________________
三、解答题
uuu r
如图,平行四边形 ABCD 中,E,F 分别是BC,DC 的中点,G 为交点,若AB = a ,
一..r r r ,一: uuu uuu AD = b ,试以a , b 为基底表示 DE 、BF 、CG .
a (1,2),
b (2,1)夹角相等的单位向量
c 的坐标.
设非零向量 a,b, c, d ,满足d (a c)b (a b)c ,求证:a d 7 .已知 a (cos ,sin ), b (cos ,sin ),其中 0
r
r
已知向量a 与b 的夹角为60°, |b | 4, (a 2b) (a 3b) 72 ,求向量a 的模。
已知点B(2, 1),且原点O 分AB 的比为 3,又b (1,3), 求b 在AB 上的投影。
已知a (1,2), b (3,2),当k 为何值时,
(1) ka 3b 垂直?
(2) ka
3 b 平行?平行时它们是同向还是反向?
求与向量
(i)求证:a b与a b互相垂直;
r r
⑵若ka b与a kb的长度相等,求的值(k为非零的常数).
r
8 .已知a,b,c是三个向量,试判断下列各命题的真假.
r r rr r r r r
(1 )若a b a c 且a 0,则b c
r r r (2)向量a在b的方向上的投影是一模等于|a cos (是a与b的夹角),方向与a在b 相同或相反的一个向量.
r r- r 1 73 一一
9 •平面向量a (、3, 1),b (―,),若存在不同时为0的实数k和t,满足条件:
2 2
r r 2 r r r r r r
x a (t23)b , y ka tb,且x y,试求函数关系式k f(t)。
10 .如图,在直角厶ABC中,已知BC a,若长为2a的线段PQ以点A为中点,问
PQ与BC的夹角取何值时BP CQ的值最大?并求出这个最大值。
