最新九年级数学高频考点核心考点复习提纲完整版总复习材料
完整版)初三数学总复习知识点

完整版)初三数学总复习知识点Chapter 1: Quadratic Radical1.A quadratic radical is an n of the form a (a≥0).Property: a (a≥0) is a non-negative number;a^2=a (a≥0);a^2=a (a≥0).2.n and n of quadratic radicals: a•b=ab (a≥0.b≥0);a/a (a≥0.b>0)=√a/b.3.n and n of quadratic radicals: when adding or subtracting quadratic radicals。
XXX form first。
then combine the quadratic radicals with the same radicand.4.Heron's formula: S=p(p-a)(p-b)(p-c)。
where S is the area ofa triangle。
and p=(a+b+c)/2.Chapter 2: XXX1.XXX that has only one unknown variable。
and the highest degree of the variable is2.2.XXX:Completing the square method: transform one side of the ninto a perfect square。
then take the square root of both sides;Quadratic formula: x=(-b±√(b^2-4ac))/2a;Factoring method: factor the left side of the n into two factors。
and set each factor equal to zero.3.ns of XXX life problems.4.Vieta's formulas: let x1 and x2 be the roots of the nax^2+bx+c=0.then we have b=-a(x1+x2) and c=a(x1x2).Chapter 3: XXX1.n of a figure: XXX it around a fixed point by a XXX.Properties: the distance from each point of the figure to the center of n remains the same;the angle een the line segment connecting each point and the center of n is equal to the angle of n;the original figure and the XXX.2.XXX to a point if the figure coincides with itself after a180-degree XXX point.A figure is XXX its image under a 180-degree n around apoint is identical to the original figure.3.Coordinates of points XXX to the origin.Chapter 4: Circle1.ns of circle。
九年级数学知识点提纲

九年级数学知识点提纲一、有理数及其运算1. 有理数概念2. 有理数的加减乘除3. 有理数的大小比较4. 有理数的绝对值二、代数式与分式1. 代数式的基本概念2. 代数式的运算法则3. 分式的概念与运算法则4. 分式方程的解法三、二次根式与无理数1. 二次根式的定义与性质2. 二次根式的化简与计算3. 无理数的概念与性质4. 无理数的运算法则四、平面图形的性质与计算1. 平面图形的基本概念2. 三角形的性质与分类3. 四边形的性质与分类4. 平行四边形与梯形的性质与计算五、三角形的性质与分类1. 三角形角度的性质2. 三角形边长的关系3. 三角形的分类与判定4. 三角形的面积计算与相似性质六、数列与函数1. 数列的概念与表示2. 等差数列与等比数列3. 函数的概念与性质4. 一次函数与二次函数七、方程与不等式1. 一元一次方程与二元一次方程2. 一元二次方程的解法3. 线性不等式的解法与图形表示4. 绝对值方程与不等式八、统计与概率1. 数据的收集与整理2. 统计图表的表示与分析3. 概率的基本概念与计算4. 事件的排列与组合计算九、几何变换与相似1. 平移、旋转、翻转的概念与性质2. 相似三角形的判定与性质3. 相似三角形的计算与应用4. 黄金分割与相似十、立体图形的认识与计算1. 空间图形的基本概念与性质2. 球体、圆锥、圆台的性质与计算3. 容积的计算与应用4. 空间立体图形的投影与展开图以上是九年级数学知识点提纲,包含了九年级数学的主要知识点。
通过学习这些知识点,可以帮助学生全面掌握九年级数学的基础概念、方法与技巧,为进一步学习高中数学奠定坚实的基础。
掌握了这些知识点,学生可以更好地解决数学问题,提高数学思维能力,并为将来的学习与应用打下坚实的数学基础。
最新九年级数学高频考点核心考点复习提纲完整版 圆

最新九年级数学高频考点核心考点复习提纲完整版圆24.1 圆24.1.1 圆·连接圆上任意两点的线段叫做弦。
圆上任意两点之间的部分叫做圆弧,简称弧。
24.1.2 垂直于弦的直径·垂径定理:垂直于弦的直径平分弦且平分弦所对的两条弧。
推论:平分弦的直径垂直于弦且平分弦所对的两条弧。
24.1.3 弧、弦、圆心角1、顶点在圆心的角叫做圆心角。
2、定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等。
推论1:相等的弧所对的弦相等,所对的圆心角也相等。
推论2:相等的弦所对的弧相等,所对的圆心角也相等。
24.1.4 圆周角1、顶点在圆上,且两边都与圆相交的角叫做圆周角。
2、圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,且都等于这条弧所对的圆心角的一半。
推论1:在同圆或等圆中,如果两个圆周角相等,那么它们所对的弧也一定相等。
推论2:半圆或直径所对的圆周角是直角,90°的圆周角所对的弦是直径。
3、如果一个多边形的所有顶点都在同一个圆上,那么这个多边形就叫做圆内接多边形,这个圆就叫做多边形的外接圆。
4、圆内接四边形的对角互补。
24.2 点、直线、圆和圆的位置关系24.2.1 点和圆的位置关系1、若⊙O的半径为r,点P到圆心的距离为d,则有:点P在圆外⇔d>r;点P在圆上⇔d=r;点P在圆内⇔d<r。
(“⇔”读作“等价于”,表示可以从符号“⇔”的一端得到另一端)2、经过已知的两个点的圆的圆心在这两个点的连线段的垂直平分线上。
3、不在同一直线上的三个点确定一个圆,确定方法:作三点的连线段的其中两条的垂直平分线,交点即为圆心,以圆心到其中一点的距离作为半径画圆即可。
4、若三角形的三个顶点在同一个圆上,那么这个圆叫做三角形的外接圆,外接圆的圆心是三角形三条边的垂直平分线的交点,叫做三角形的外心。
5、假设命题的结论不成立,经过推理得出矛盾,则假设不正确,故原命题成立,这种证明方法叫做反证法。
(2020年整理)九年级数学总复习提纲-人教新课标版.pptx

⑵符号法则: b b b a a a
⑶繁分式:①定义;②化简方法(两种) 3.整式运算法则(去括号、添括号法则)
4.幂 的 运 算 性 质 :① am · an = amn ;② am ÷ an = amn ; ③ (am )n = amn ; ④
一、基本概念
1. 方程、方程的解(根)、方程组的解、解方程(组) 2. 分类:
方程
有理方程 无理方程
整式方程 分式方程
一次方程 二次方程 高次方程
二、解方程的依据—等式性质 1.a=b←→a+c=b+c 2. a=b←→ac=bc (c≠0) 三、解 法
1. 一元一次方程的解法:去分母→去括号→移项→合并同类项→ 系数化成 1→解。
三、四边形 分类表: 1.一般性质(角) ⑴内角和:360° ⑵顺次连结各边中点得平行四边形。 推论 1:顺次连结对角线相等的四边形各边中点得菱形。 推论 2:顺次连结对角线互相垂直的四边形各边中点得矩形。 ⑶外角和:360°
2.特殊四边形 ⑴研究它们的一般方法:
学海无 涯
定义→性质→判定
边角对面 角积
x 2 =x, x 2=│x│等。 x
4.系数与指数 区别与联系:①从位置上看;②从表示的意义上看 5.同类项及其合并
条件:①字母相同;②相同字母的指数相同 合并依据:乘法分配律 6.根式 表示方根的代数式叫做根式。 含有关于字母开方运算的代数式叫做无理式。
注意:①从外形上判断;②区别: 3 、 7 是根式,但不是无理式(是无理数)。
对 称 性
线
轴中 对心 称对
称
⑵平行四边形、矩形、菱形、正方形;梯形、等腰梯形的定义、性质和判定 ⑶判定步骤:四边形→平行四边形→矩形→正方形
九年级数学知识点复习提纲

九年级数学知识点复习提纲数学这门学科在九年级是学生们需要重点复习的科目之一。
九年级的数学涉及到许多重要的知识点,掌握好这些知识点对于提高数学水平和取得好成绩至关重要。
在本文中,我将为大家总结九年级数学的主要知识点,帮助大家了解需要重点复习和掌握的内容。
代数是九年级数学的重点之一。
首先,需要掌握一元一次方程的解法和应用。
例如,如果给出一个方程2x + 3 = 7,我们可以用逆运算将它的解计算出来。
同时,要了解方程的解的性质,例如当方程有无穷多解时,或者无解时会出现什么情况。
在代数的基础之上,我们还需要学习一元一次不等式的解法和应用。
对于不等式3x - 5 > 7,我们需要找到解的范围,并且要注意在解的过程中是否需要改变不等号的方向。
因式分解也是九年级数学的重要内容。
在因式分解中,我们要掌握提公因式法、分组分解法以及差平方公式等常用方法。
例如,在因式分解中,我们可以将多项式15x^2 + 10x分解为5x(3x + 2)。
同时,了解因式分解的应用,例如可以通过因式分解来求解方程或者简化计算。
绝对值是九年级数学中的一个重要知识点。
绝对值是表示一个数值的正距离,它永远是非负的。
因此,在解绝对值不等式时,我们要根据绝对值的性质来得出解的范围。
例如,对于不等式|2x+ 3| < 5,我们可以通过分情况讨论来求解。
二次函数是九年级数学的一个重要内容。
在学习二次函数时,我们需要掌握二次函数的基本性质以及二次函数图像的特点。
例如,对于二次函数y = ax^2 + bx + c,我们可以通过抛物线的开口方向、顶点坐标以及对称轴等特征来确定二次函数的图像。
几何是九年级数学中另一个重要的知识点。
在几何中,我们需要学习平面几何和立体几何的相关内容。
平面几何的内容包括平行线、相交线、相似三角形等。
立体几何的内容包括平行四边形、三角形的面积计算、体积计算等。
同时,要了解几何定理和推理方法,例如垂直平分线定理、勾股定理等。
九年级数学知识点复习提纲

九年级数学知识点复习提纲九年级数学知识点复习提纲在年少学习的日子里,大家对知识点应该都不陌生吧?知识点就是一些常考的内容,或者考试经常出题的地方。
掌握知识点是我们提高成绩的关键!下面是店铺帮大家整理的九年级数学知识点复习提纲,供大家参考借鉴,希望可以帮助到有需要的朋友。
一、数与代数A、数与式:1、有理数:①整数→正整数/0/负整数②分数→正分数/负分数数轴:①画一条水平直线,在直线上取一点表示0(原点),选取某一长度作为单位长度,规定直线上向右的方向为正方向,就得到数轴。
②任何一个有理数都可以用数轴上的一个点来表示。
③如果两个数只有符号不同,那么我们称其中一个数为另外一个数的相反数,也称这两个数互为相反数。
在数轴上,表示互为相反数的两个点,位于原点的两侧,并且与原点距离相等。
④数轴上两个点表示的数,右边的总比左边的大。
正数大于0,负数小于0,正数大于负数。
绝对值:①在数轴上,一个数所对应的点与原点的距离叫做该数的绝对值。
②正数的绝对值是他的本身、负数的绝对值是他的相反数、0的绝对值是0。
两个负数比较大小,绝对值大的反而小。
有理数的运算:加法:①同号相加,取相同的符号,把绝对值相加。
②异号相加,绝对值相等时和为0;绝对值不等时,取绝对值较大的数的符号,并用较大的绝对值减去较小的绝对值。
③一个数与0相加不变。
减法:减去一个数,等于加上这个数的相反数。
乘法:①两数相乘,同号得正,异号得负,绝对值相乘。
②任何数与0相乘得0。
③乘积为1的两个有理数互为倒数。
除法:①除以一个数等于乘以一个数的倒数。
②0不能作除数。
乘方:求N个相同因数A的积的运算叫做乘方,乘方的结果叫幂,A叫底数,N叫次数。
混合顺序:先算乘法,再算乘除,最后算加减,有括号要先算括号里的。
2、实数无理数:无限不循环小数叫无理数平方根:①如果一个正数X的平方等于A,那么这个正数X就叫做A的算术平方根。
②如果一个数X的平方等于A,那么这个数X就叫做A的平方根。
最新九年级数学高频考点核心考点圆专题复习 (6)

2、如图2,在以O为圆心的两个同心圆
中,大圆的弦AB是小圆的切线,P为切点, 设AB=12,则两圆构成圆环面积为_____;
A
P O
B
3、下列四个命题中正确的是(
).
①与圆有公共点的直线是该圆的切线 ; ②垂直于圆的半径的直 线是该圆的切线 ; ③到圆心的距离等于半径的直线是该圆的切 线 ;④过圆直径的端点,垂直于此直径的直线是该圆的切线.
最新九年级数学高频考点核心考点 圆专题复习
--点、直线与圆有关的位置关系
四、点和圆的位置关系
.o .p r
Op<r Op=r Op>r
.o
.p
.o .p
点p在⊙o内 点p在⊙o上 点p在⊙o外
1、⊙O的半径为R,圆心到点A的距离为d,且R、d分别 是方程x2-6x+8=0的两根,则点A与⊙O的位置关系是 ( D) A.点A在⊙O内部 C.点A在⊙O外部 B.点A在⊙O上 D.点A不在⊙O上
6.如图:AB是圆O的直径,BD是圆O的弦, BD到C,AC=AB,BD与CD的大小有什么关系?
为什么?
A
补充:
若∠B=70 °,则 40 ° ∠DOE=___.
E
O
C
D
B
7、如图,AB是圆O的直径,圆O过 AC的中点D,DE⊥BC于E. 证明:DE是圆O的切线.
C D E B
A
. O
2、M是⊙O内一点,已知过点M的⊙O最长的弦为10 cm, 最短的弦长为8 cm,则OM= _____ cm. 3
练:有两个同心圆,半径分别为R和r, P是圆环内一点,则OP的取值 r<OP<R . 范围是_____
O
P
五.直线与圆的位置关系
初三数学知识点复习资料(精选3篇)

初三数学知识点复习资料〔精选3篇〕篇1:初三数学知识点分类复习资料代数局部:有理数、无理数、实数整式、分式、二次根式一元一次方程、一元二次方程、二(三)元一次方程组、二元二次方程组、分式方程、一元一次不等式函数(一次函数、二次函数、反比例函数) 几何局部:线段、角相交线、平行线三角形、四边形、相似形、圆。
1、实数的分类有理数:整数(包括:正整数、0、负整数)和分数(包括:有限小数和无限环循小数)都是有理数。
如:-3,,0.231,0.737373...无理数:无限不环循小数叫做无理数如:π,-,0.0010001...(两个1之间依次多1个0)。
实数:有理数和无理数统称为实数。
2、无理数在理解无理数时,要抓住“无限不循环”这一时之,它包含两层意思:一是无限小数;二是不循环.二者缺一不可.归纳起来有四类:(1)开方开不尽的数,如等;(2)有特定意义的数,如圆周率π,或化简后含有π的数,如+8等;(3)有特定构造的数,如0.0010001...等;(4)某些三角函数,如sin60o等。
注意:判断一个实数的属性(如有理数、无理数),应遵循:一化简,二辨析,三判断.要注意:“神似”或“形似”都不能作为判断的标准.3、非负数:正实数与零的统称。
(表为:x≥0)常见的非负数有:性质:假设干个非负数的和为0,那么每个非负担数均为0。
4、数轴:规定了原点、正方向和单位长度的直线叫做数轴(画数轴时,要注意上述规定的三要素缺一不可)。
解题时要真正掌握数形结合的思想,理解实数与数轴的点是一一对应的,并能灵敏运用。
①画一条程度直线,在直线上取一点表示0(原点),选取某一长度作为单位长度,规定直线上向右的方向为正方向,就得到数轴(“三要素”)。
②任何一个有理数都可以用数轴上的一个点来表示。
③假如两个数只有符号不同,那么我们称其中一个数为另外一个数的相反数,也称这两个数互为相反数。
作用:A.直观地比拟实数的大小;B.明确表达绝对值意义;C.建立点与实数的一一对应关系。
人教部编版九年级下数学复习提纲

人教部编版九年级下数学复习提纲一、知识点回顾1. 数的性质和分类- 有理数和无理数- 整数、分数和小数- 常见无理数及其性质2. 几何图形与计算- 点、线、面的性质和关系- 直角三角形和直角三角函数- 平行线和比例3. 线性方程与不等式- 一次函数及其图像- 一元一次不等式及其解法- 一次函数与线性方程的关系4. 几何变换- 平移、旋转、翻折和对称- 平移、旋转和翻折的性质和规律- 图形变换的几何意义5. 数据分析和统计- 数据的收集和整理- 数据的分析和统计指标- 概率和统计的应用二、考点梳理1. 几何图形的性质和计算- 判断线段、角的性质- 计算直角三角形的边长和角度- 用比例解决问题2. 线性方程与不等式- 解一元一次方程和不等式- 判断等式和不等式的解集关系- 用一次函数解决实际问题3. 几何变换- 判断图形的变换形式- 进行平移、旋转、翻折和对称操作- 利用变换的性质解决问题4. 数据分析和统计- 分析数据的特征和规律- 计算统计指标,如均值、中位数、众数- 应用概率和统计解决问题三、备考指导1. 适时进行知识点的复- 着重复易错知识点和考点- 多做题巩固基本知识2. 积累解题经验和技巧- 熟练掌握解题方法和步骤- 多思考和分析不同类型题目3. 举一反三,灵活运用知识- 将知识应用于实际问题解决中- 培养灵活思维和综合分析能力4. 合理安排备考时间- 制定复计划并坚持执行- 合理安排复时间和休息时间以上提纲是对人教部编版九年级下数学复习内容的总结和归纳,希望能帮助同学们复习备考,取得好成绩!。
最新九年级数学高频考点核心考点分类复习完整版
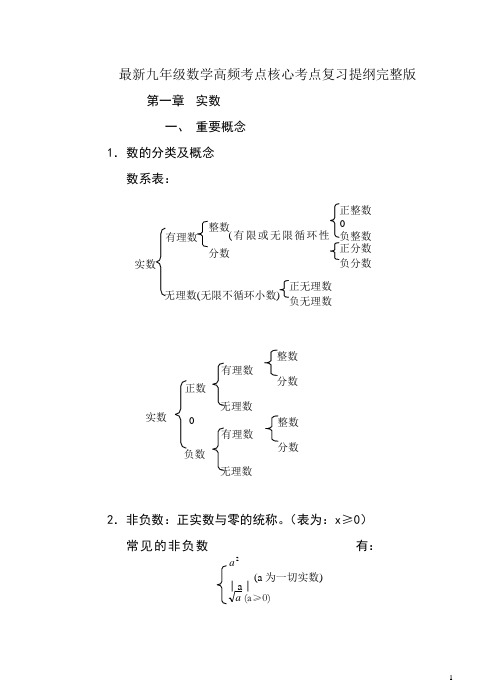
最新九年级数学高频考点核心考点复习提纲完整版第一章 实数一、 重要概念1.数的分类及概念数系表:2.非负数:正实数与零的统称。
(表为:x ≥0)常见的非负数有:实数 无理数(无限不循环小数) 有理数 正分数负分数正整数0 负整数(有限或无限循环性整数 分数 正无理数负无理数0 实数 负数 整数分数无理数有理数正数 整数分数无理数有理数│a │ 2aa (a ≥0)(a 为一切实数)性质:若干个非负数的和为0,则每个非负担数均为0。
3.倒数: ①定义及表示法②性质:A.a≠1/a (a≠±1);B.1/a 中,a≠0;C.0<a <1时1/a >1;a >1时,1/a <1;D.积为1。
4.相反数: ①定义及表示法②性质:A.a≠0时,a≠-a;B.a 与-a 在数轴上的位置;C.和为0,商为-1。
5.数轴:①定义(“三要素”)②作用:A.直观地比较实数的大小;B.明确体现绝对值意义;C.建立点与实数的一一对应关系。
6.奇数、偶数、质数、合数(正整数—自然数)定义及表示:奇数:2n-1偶数:2n (n 为自然数)7.绝对值:①定义(两种): 代数定义:几何定义:数a 的绝对值顶的几何意义是实数a 在数轴上所对应的点到原点的距离。
②│a │≥0,符号“││”是“非负数”的标志;③数a 的绝对值只有一个;④处理任何类型的题目,只要其中有“││”出现,其关键一步是去掉“││”符号。
二、实数的运算a(a ≥0) -a(a<0) │a │=运算法则(加、减、乘、除、乘方、开方)运算定律(五个—加法[乘法]交换律、结合律;[乘法对加法的分配律)运算顺序:A.高级运算到低级运算;B.(同级运算)从“左”到“右”(如5÷ ³5);C.(有括号时)由“小”到“中”到“大”。
第二章 代数式1.代数式与有理式用运算符号把数或表示数的字母连结而成的式子,叫做代数式。
单独的一个数或字母也是代数式。
最新九年级数学高频考点核心考点专题 三角形

最新九年级数学高频考点核心考点专题三角形一.三角形1.三角形的边:不在同一条直线上的三条线段首尾顺次相连所组成的图形叫做三角形。
*三角形三边之间的关系:两边之和大于第三边,两边之差小于第三边:如图:当△ ABC中的边c+b>a的时候,能够组成三角形,当c+b逐渐减小,直到c +b=a的时候,你会发现,线段a,b,c在同一条直线上,此时无法组成三角形。
既然三角形中的两边之和必然大于第三边,即c+b>a;那么,两边之差必然小于第三边,由c+b>a推出,c>a-b。
例题:(1)下列给出的各组线段中,能构成三角形的是()(A)5,12,13 (B)5,12,7 (C)8,18,7 (D)3,4,8(2)两条边长分别为2和8,第三边长是整数的三角形一共有()(A)3个(B)4个 (C)5个(D)无数个(3)在△ABC中,AB=9,BC=2,并且AC第为奇数,则△ABC的周长是_________*三角形与其他多边形(如四边形)相比,具有稳定性,即只要三遍的长度确定,期形状就不会发生改变;现实生活中也经常用到三角形的稳定性这一特点。
例子:自行车的三角架2.三角形的高、中线和角平分线:(1)高:画一个锐角△ABC,过A点向它所对的边BC所在的直线画垂线,垂足为D;你能画出其他两边上的高吗?通过画图你发现什么?想一想,如何画钝角三角形较小两边上的高?直角三角形的一条直角边是另一条直角边上的高。
直角三角形中,设∠C为直角,则边长有如下公式:AB2=BC2+AC2(勾股定理)例题:(1)一个直角三角形的三边长分别是15,20和25,则它的最大边上的高为()(A)12 (B)10 (C) 8 (D) 5(2)如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是()A. 锐角三角形B. 直角三角形C. 钝角三角形D. 锐角三角形(3)下列各阴影部分的面积有何关系?*三角形的三条高线交于一点(2)中线:连结ΔABC的顶点A和它所对的边BC的中点D,线段AD叫做ΔABC的边BC上的中线。
最新九年级数学高频考点核心考点分类复习完整版

最新九年级数学高频考点核心考点分类复习完整版知识点分类总结相应练习题一、二次函数与反比例函数1、二次函数1.下列函数中,二次函数是( )A .y =(m 2+1)x 2B .y =x 2-x (x -2)C .y =a x 2+b x +cD .y =x +1 2.若21(1)3m y m x mx +=-++是二次函数,则m 的值是( )A .1B .-1C .±1D .2 3.有长24m 的篱笆,一面利用围墙围城如图中间隔有一道篱笆的矩形花圃,设花圃的垂直于墙的一边长为x m ,面积是sm 2,则S 与x 的关系式是( ) A .S =-3x 2+24x B .S =-2x 2+24x C .S =-3x 2-24x D .S =-2x 2+24x 4.某公司的生产利润原来是a 元,经过连续两年的增长达到了y 万元,如果每年增长的百分数都是x ,那么y 与x 的函数关系是( )A .y =x 2+aB .y =a (x -1)2C .y =a (1-x )2D .y =a (1+x )2 2、二次函数2y ax =的图像5.如图,四个二次函数的图像中,分别对应的是①y = a 2x ;②y = b 2x ;③y = c 2x ; ④y =d 2x .则a 、b 、c 、d 的大小关系为( ) A.a>b>c>d B. a>b>d>c C.b>a>c>d D.b>a>d>c 3、二次函数2y ax bx c =++的图像和性质6.(中招•泰安)在同一坐标系内,一次函数y =a x +b 与二次函数y =a x 2+8x +b 的图象可能是( )A .B .C .D .7.(中招•呼和浩特)在同一直角坐标系中,函数y =m x +m 和y =-m x 2+2x +2(m 是常数,且m ≠0)的图象可能是( )A. B. C. D.8.(中招•台湾)坐标平面上有一函数y=-3x2+12x-7的图形,其顶点坐标为()A.(2,5) B.(2,-19) C.(-2,5) D.(-2,-43)9.(中招•徐州)二次函数y=a x2+b x+c图象上部分点的坐标满足下表:x…-3 -2 -1 0 1 …y…-3 -2 -3 -6 -11 …则该函数图象的顶点坐标为()A.(-3,-3) B.(-2,-2) C.(-1,-3) D.(0,-6)10.(中招•昭通)已知二次函数y=a x2+b x+c(a≠0)的图象如图所示,则下列结论中正确的是()A.a>0 B.3是方程a x2+b x+c=0的一个根C.a+b+c=0 D.当x<1时,y随x的增大而减小第10题第11题第12题11.(中招•平凉)已知二次函数y=a x2+b x+c(a≠0)的图象如图所示,在下列五个结论中:①2a-b<0;②abc<0;③a+b+c<0;④a-b+c>0;⑤4a+2b+c>0,错误的个数有()A.1个 B.2个 C.3个 D.4个12.(中招•襄阳)二次函数y =-x 2+b x +c 的图象如图所示:若点A (x 1,y 1),B (x 2,y 2)在此函数图象上,x 1<x 2<1,y 1与y 2的大小关系是( )A .y 1≤y 2B .y 1<y 2C .y 1≥y 2D .y 1>y 2 13.(中招•衢州)已知二次函数y =-12x 2-7x +152,若自变量x 分别取x 1,x 2,x 3,且0<x 1<x 2<x 3,则对应的函数值y 1,y 2,y 3的大小关系正确的是( )A .y 1>y 2>y 3B .y 1<y 2<y 3C .y 2>y 3>y 1D .y 2<y 3<y 114.(中招•衢州)抛物线y =x 2+b x +c 的图象先向右平移2个单位,再向下平移3个单位,所得图象的函数解析式为y =(x -1)2-4,则b 、c 的值为( )A .b=2,c=-6B .b=2,c=0C .b=-6,c=8D .b=-6,c=215.(中招•枣庄)将抛物线y =3x 2向左平移2个单位,再向下平移1个单位,所得抛物线为( )A .y =3(x -2)2-1B .y =3(x -2)2+1C .y =3(x +2)2-1 D .y =3(x +2)2+116.(中招•镇江)二次函数y =x 2-4x +5的最小值是( ) A .-1 B .1 C .3 D .517.(中招•贵阳)已知二次函数y =a x 2+b x +c (a <0)的图象如图所示,当-5≤x ≤0时,下列说法正确的是( )A .有最小值-5、最大值0B .有最小值-3、最大值6C .有最小值0、最大值6D .有最小值2、最大值618.(中招•泰安)若二次函数y =a x 2+b x +c 的x 与y 的部分对应值如下表:x -7 -6 -5 -4 -3 -2y-27-13-3353则当x =1时,y 的值为( )A .5B .-3C .-1D .-2719.(黔东南州)抛物线的图象如图所示,根据图象可知,抛物线的解析式可能是( )A .y =x 2-x -2 B .211222y x x =--+C .211122y x x =--+D .y =-x 2+x +220.(安徽)若二次函数y =x 2+bx x +5配方后为y =(x -2)2+k ,则b 、k 的值分别为( ) A .0,5 B .0,1 C .-4,5 D .-4,121.(泰安)将y =(2x -1)(x +2)化成y =a (x +m )2+n 的形式为( )A .23252()416y x =+-B .23172()48y x =--C .23252()48y x =+-D .23172()48y x =++4、二次函数与一元二次方程22.(长春)二次函数y =k x 2-6x +3的图象与x 轴有交点,则k 的取值范围是( ) A .k <3 B .k <3且k ≠0 C .k ≤3 D .k ≤3且k ≠023.(中招•襄阳)已知函数y =(k-3)x 2+2x +1的图象与x 轴有交点,则k 的取值范围是( ) A .k <4 B .k ≤4 C .k <4且k ≠3 D .k ≤4且k ≠324.(徐汇区一模)已知二次函数y =a x 2+b x +c 的y 与x 的部分对应值如下表:则下列判断中正确的是( )A .抛物线开口向上B .抛物线与y 轴交于负半轴C .当x =3时,y <0D .方程a x 2+b x +c=0有两个相等实数根25.根据下列表格中的对应值:判断方程a x 2+b x +c=0(a ≠0,a 、b 、c 为常数)一个解x 的范围最可能是( )x 0.75 0.8 0.85 0.9a x 2+b x +c-0.25 -0.04 0.190.44A .x <0.75B .0.75<x <0.8C .0.8<x <0.85D .0.85<x <0.926.(中招•牡丹江)抛物线y =a x 2+b x +c (a <0)如图所示,则关于x 的不等式a x 2+b x +c >0的解集是( )A .x <2B .x >-3C .-3<x <1D .x <-3或x >127.(淮北模拟)已知抛物线y =2(x -3)(x +1),当y >0时,对应的x 的范围是( )A .x >3B .x <-1C .x <-1,或x >3D .-1<x <35、二次函数的应用28.(中招•株洲)某广场有一喷水池,水从地面喷出,如图,以水平地面为x 轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y =-x 2+4x (单位:米)的一部分,则水喷出的最大高度是( )A .4米B .3米C .2米D .1米29.(日照)某民俗旅游村为接待游客住宿需要,开设了有100张床位的旅馆,当每张床位每天收费100元时,床位可全部租出.若每张床位每天收费提高20元,则相应的减少了10张床位租出.如果每张床位每天以20元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天最合适的收费是( )A .140元B .150元C .160元D .180元30.(河北)如图,二次函数y =x 2-4x +3的图象交x 轴于A ,B 两点,交y 轴于C ,则△ABC 的面积为( )A .6B .4C .3D .1 6、反比例函数31.(中招•安顺)若y =(a +1)22ax -是反比例函数,则a 的取值为( )A .1B .-1C .±1D .任意实数 32.下列关系中,两个量之间为反比例函数关系的是( ) A .正方形的面积S 与边长a 的关系 B .正方形的周长l 与边长a 的关系C .矩形的长为a ,宽为20,其面积S 与a 的关系D .矩形的面积为40,长a 与宽b 之间的关系33.(中招•随州)正比例函数y =k x 和反比例函数21k y x+=-(k 是常数且k ≠0)在同一平面直角坐标系中的图象可能是( )A .B .C .D .34.(中招•攀枝花)二次函数y =a x 2+b x +c (a ≠0)的图象如图所示,则函数ay x=与y =b x +c 在同一直角坐标系内的大致图象是( )A .B .C .D .35.(中招•三明)如图,已知直线y =m x 与双曲线ky x=的一个交点坐标为(3,4),则它们的另一个交点坐标是( )A .(-3,4)B .(-4,-3)C .(-3,-4)D .(4,3)第35题 第36题 第38题 第39题 36.(中招•南通)如图,设直线y =k x (k <0)与双曲线5y x=-相交于A (x 1,y 1)B (x 2,y 2)两点,则x 1y 2-3x 2y 1的值为( )A .-10B .-5C .5D .10 37.(中招•黑龙江)反比例函数2k y x-=的图象,当x >0时,y 随x 的值增大而增大,则k 的取值范围是( )A .k <2B .k ≤2C .k >2D .k ≥2 38.(中招•新疆)如图,l 1是反比例函数ky x=在第一象限内的图象,且经过点A (1,2).l 1关于x 轴对称的图象为l 2,那么l 2的函数表达式为( )A .2y x =(x <0) B .2y x =(x >0) C .2y x =-(x <0) D .2y x=-(x >0) 39.(中招•铜仁地区)如图,正方形ABOC 的边长为2,反比例函数ky x=的图象过点A ,则k 的值是( )A.2 B.-2 C.4 D.-440.(中招•株洲)已知点A(1,y1)、B(2,y2)、C(-3,y3)都在反比例函数6yx=的图象上,则y1、y2、y3的大小关系是()A.y3<y1<y2 B.y1<y2<y3 C.y2<y1<y3 D.y3<y2<y141.(中招•兰州)已知A(-1,y1),B(2,y2)两点在双曲线32myx+=上,且y1>y2,则m的取值范围是()A.m<0 B.m>0 C.m>32-D.m<32-42.(中招•娄底)已知反比例函数的图象经过点(-1,2),则它的解析式是()A.2y x=-B.2yx=-C.2yx=D.12yx=-43.(中招•天水)函数y1=x和y2=1x的图象如图所示,则y1>y2的x取值范围是()A.x<-1或x>1 B.x<-1或0<x<1C.-1<x<0或x>1 D.-1<x<0或0<x<1第43题第45题44.(中招•大庆)已知梯形的面积一定,它的高为h,中位线的长为x,则h与x的函数关系大致是()A. B. C. D.45.(中招•苏州)如图,菱形OABC的顶点C的坐标为(3,4).顶点A在x轴的正半轴上,反比例函数kyx=(x>0)的图象经过顶点B,则k的值为()A.12 B.20 C.24 D.32。
(完整版)初三数学总复习知识点

2b ab aa 0,b 0 。
x 1 x 2b,x 1 ?x 2 a第三章 旋转1图形的旋转 旋转:一个图形绕某一点转动一个角度的图形变换 性质:对应点到旋转中心的距离相等; 对应点与旋转中心所连的线段的夹角等于旋转角 旋转前后的图形全等。
中心对称:一个图形绕一个点旋转 180 度,和另一个图形重合,则两个图形关 于这个点中心对称;中心对称图形:一个图形绕某一点旋转 180 度后得到的图形能够和原来的图形初三数学知识点 第一章 二次根式 二次根式:形如a (a 0) 的式子为二次根式;性质: a是一个非负数;二次根式的乘除:aaaa 0;0。
a ? bab a 0,b 0 ;二次根式的加减: 3数相同的二次根式进行合并。
二次根式加减时,先将二次根式华为最简二次根式,再将被开方4 海伦-秦九韶公式: S p(p )(p b)(p c) ,S 是三角形的面积,p 为abc p 。
第二章1 程。
2元二次方程元二次方程:等号两边都是整式,且只有一个未知数,未知数的最高次是2的方一元二次方程的解法配方法:将方程的一边配成完全平方式,然后两边开方;公式法: xb b 2 4ac2a左边是两个因式的乘积,右边为零。
因式分解法: 一元二次方程在实际问题中的应用 韦达定理:设 x 1 , x 2是方程2 ax 2bx c 0 的两个根,那么有重合,则说这个图形是中心对称图形;3 关于原点对称的点的坐标第四章圆1 圆、圆心、半径、直径、圆弧、弦、半圆的定义2 垂直于弦的直径圆是轴对称图形,任何一条直径所在的直线都是它的对称轴;垂直于弦的直径平分弦,并且平方弦所对的两条弧;平分弦的直径垂直弦,并且平分弦所对的两条弧。
3 弧、弦、圆心角在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等。
4 圆周角在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半;半圆(或直径)所对的圆周角是直角,90 度的圆周角所对的弦是直径。
初三数学知识点归纳总结(通用5篇)

初三数学知识点归纳总结第1篇1、矩形的概念有一个角是直角的平行四边形叫做矩形。
2、矩形的性质(1)具有平行四边形的一切性质。
(2)矩形的四个角都是直角。
(3)矩形的对角线相等。
(4)矩形是轴对称图形。
3、矩形的判定(1)定义:有一个角是直角的平行四边形是矩形。
(2)定理1:有三个角是直角的四边形是矩形。
(3)定理2:对角线相等的平行四边形是矩形。
4、矩形的面积:S矩形=长×宽=ab初三数学重点知识点(四)1、正方形的概念有一组邻边相等并且有一个角是直角的平行四边形叫做正方形。
2、正方形的性质(1)具有平行四边形、矩形、菱形的一切性质;(2)正方形的四个角都是直角,四条边都相等;(3)正方形的两条对角线相等,并且互相垂直平分,每一条对角线平分一组对角;(4)正方形是轴对称图形,有4条对称轴;(5)正方形的一条对角线把正方形分成两个全等的.等腰直角三角形,两条对角线把正方形分成四个全等的小等腰直角三角形;(6)正方形的一条对角线上的一点到另一条对角线的两端点的距离相等。
3、正方形的判定(1)判定一个四边形是正方形的主要依据是定义,途径有两种:先证它是矩形,再证有一组邻边相等。
先证它是菱形,再证有一个角是直角。
(2)判定一个四边形为正方形的一般顺序如下:先证明它是平行四边形;再证明它是菱形(或矩形);最后证明它是矩形(或菱形)。
初三数学知识点归纳总结第2篇第一轮数学复习主要知识点总结1第一:高考数学中有函数、数列、三角函数、平面向量、不等式、立体几何等九大章节。
主要是考函数和导数,这是我们整个高中阶段里最核心的板块,在这个板块里,重点考察两个方面:第一个函数的性质,包括函数的单调性、奇偶性;第二是函数的解答题,重点考察的是二次函数和高次函数,分函数和它的一些分布问题,但是这个分布重点还包含两个分析就是二次方程的分布的问题,这是第一个板块。
第二:平面向量和三角函数。
重点考察三个方面:一个是划减与求值,第一,重点掌握公式,重点掌握五组基本公式。
初三数学知识点及复习提纲

初三数学知识点及复习提纲初三数学学问点邻补角:两条直线相交所构成的四个角中,有公共顶点且有一条公共边的两个角是邻补角。
对顶角:一个角的两边分别是另一个叫的两边的反向延长线,像这样的两个角互为对顶角。
垂线:两条直线相交成直角时,叫做相互垂直,其中一条叫做另一条的垂线。
平行线:在同一平面内,不相交的两条直线叫做平行线。
同位角、内错角、同旁内角:同位角:∠1与∠5像这样具有相同位置关系的一对角叫做同位角。
内错角:∠2与∠6像这样的一对角叫做内错角。
同旁内角:∠2与∠5像这样的一对角叫做同旁内角。
命题:推断一件事情的语句叫命题。
平移:在平面内,将一个图形沿某个方向移动肯定的距离,图形的这种移动叫做平移平移变换,简称平移。
对应点:平移后得到的新图形中每一点,都是由原图形中的某一点移动后得到的,这样的两个点叫做对应点。
初三数学学问点复习提纲1垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的2条弧。
逆定理:平分弦不是直径的直径垂直于弦,并且平分弦所对的2条弧。
2有关圆周角和圆心角的性质和定理①在同圆或等圆中,假如两个圆心角,两个圆周角,两组弧,两条弦,两条弦心距中有一组量相等,那么他们所对应的其余各组量都分别相等。
②一条弧所对的圆周角等于它所对的圆心角的一半。
直径所对的圆周角是直角。
90度的圆周角所对的弦是直径。
圆心角计算公式:θ=L/2πr×360°=180°L/πr=L/r弧度即圆心角的度数等于它所对的弧的度数;圆周角的度数等于它所对的弧的度数的一半。
③假如一条弧的长是另一条弧的2倍,那么其所对的圆周角和圆心角是另一条弧的2倍。
3有关外接圆和内切圆的性质和定理①一个三角形有唯一确定的外接圆和内?a href=// target=_blank性病M饨釉苍残氖侨?切胃鞅叽怪逼椒窒叩慕坏悖?饺?切稳?龆サ憔嗬胂嗟?②内切圆的圆心是三角形各内角平分线的交点,到三角形三边距离相等。
最新九年级数学高频考点核心考点 圆专题复习 (22)

最新九年级数学高频考点核心考点圆专题复习一知识点(一)圆的有关概念和性质1.圆是的所有点组成的图形.2.圆是轴对称图形,它的的直线都是对称轴;又时中心对称图形,它的中心是.3.垂直于弦的直径弦,并且弦所对的弧.4.平分弦(不是直径)的直径弦,并且弦所对的弧.5.在中,相等的圆心角所对的相等,所对的弦;如果两个圆心角、两条弦、两条弧中有一组量相等,那么其余各组量都分别.6.顶点在,并且两边都和圆的角叫做圆周角.7.在同圆或等圆中,一条弧所的圆周角等于它所对圆心角的.8在同圆或等圆中,同弧或等弧所对的圆周角.90的圆周角所对的弦是.9 .所对的圆周角是直角;︒(二)与圆有关的位置关系10.的三点确定一个圆.11.设圆的半径为r,点到圆心的距离为d,则点在圆外⇔;点在圆上⇔;点在圆内⇔.12.如果的半径为,圆心到直线的距离为,那么(1)直线和相交⇔;(2)直线和相切⇔;(3)直线和相离⇔.13.经过半径的,并且于这条半径的直线是圆的切线14圆的切线于切点的.15.经过圆的外一点作圆的切线,的长叫做这点到圆的切线长.16.从圆外一点可以引圆的条切线,它们的切线长.17.三角形的三个顶点可以确定一个圆,这个圆叫做,外接圆的圆心叫做三角形的,它到三角形都相等,是的交点.18.和三角形三边都的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的;它到三角形都相等,是的交点.19.设两圆的半径分别为R和r,圆心距为d,那么(1)两圆外离⇔;(2)两圆外切⇔;(3)两圆相交⇔;(4)两圆内切⇔;(5)两圆内切⇔.(三)圆的有关算20.正边形的一个内角的都数是;中心角为.l,扇形的面21.扇形的半径为R,扇形的圆心角为︒n,那么扇形的弧长=S.积=S.22.如果扇形的弧长为l,半径为R,那么扇形的面积=23.圆锥的侧面展开图是一个,如果底面半径为R,母线长为l,则圆锥的高为,侧面积为.二圆易错点1.注意考虑点的位置在解决点与圆的有关问题时,应注意对点的位置进行分类,如点在圆内圆外、点在优弧劣弧等.例1.点P 到⊙O 上的最近距离为cm 3,最远距离为cm 5,则⊙O 的半径为 cm .例2.BC 是⊙O 的一条弦, ︒=∠120BOC ,点A 是⊙O 上的一点(不与B 、C 重合),则BAC ∠的度数为 .2.注意考虑弦的位置在解决与弦有关的问题时,应对两条的位置进行分类,即注意位于圆心同侧和异侧的分类.例3.在半径cm 5为的圆中,有两条平行的弦,一条为cm 8,另一条为cm 6,则这两条平行弦的距离是 .例4.AB 是⊙O 的直径,AC 、AD 是⊙O 的两条弦,且︒=∠30BAC ,︒=∠45BAD ,则CAD ∠的度数为 .3.注意公共点的个数在涉及直线与圆的位置关系时,应注意有公共点和有唯一公共点的区别.例5.⊙O 的半径为cm 3,点P 在直线l 上,且cm OP 3=,则⊙O 和直线l 的位置关系为 .4.注意两圆相切中的分类在解决两圆相切的有关问题时,应注意对内切、外切以及两圆大小进行分类,如下面的例题.例6.已知⊙O 1和⊙O 2相切,两圆的圆心距为9cm ,⊙O 1的半径为4cm ,则⊙O 2的半径为( ).A .cm 5B .cm 13C .cm 9或cm 13D .cm 5 或cm 13 例7.⊙O 1和⊙O 2相内切,圆心距为cm 2,其一个圆的半径为cm 5,则另一圆的半径为 cm . 三 考点考点1:基本概念和性质考查形式:主要考查圆的对称性、直径与弦的关系、等弧等有关命题,常以选择题的形式出现.例1.(2010兰州)有下列四个命题:①直径是弦;②经过三个点一定可以作圆;③三角形的外心到三角形各顶点的距离都相等;④半径相等的两个半圆是等弧.其中正确的有( ).A .4个B .3个C . 2个D . 1个 考点2:圆心角与圆周角的关系例2.(2010年连云港)如图,点A 、B 、C 在⊙O 上,AB ∥CD ,∠B =22°, 则∠A =________°.图1A图2AD图3图4考点3:垂径定理考查形式:主要考查借助垂径定理的解决半径、弧、弦、弦心距之间的计算和证明,填空题、选择题或解答题中都经常出现它的身影.解决是应注意作出垂直于弦的半径或弦心距,构造直角三角形进行解决.例3.(2010芜湖)如图,在⊙O 中,有折线OABC ,其中8=OA ,12=AB ,︒=∠=∠60B A ,则弦BC 的长为( )。
最新九年级数学高频考点核心考点复习提纲完整版 三角函数

最新九年级数学高频考点核心考点复习提纲完整版三角函数锐角三角函数1.锐角三角函数的概念: 在Rt△ABC中(1)锐角∠A的对边与斜边的比值是∠A的正弦,记作sinA=∠A的对边斜边;(2)(2)锐角∠A的邻边与斜边的比值是∠A的余弦,记作cosA=∠A的邻边斜边;(3)(3)锐角∠A的对边与邻边的比值是∠A的正切,记作tanA=∠A的对边∠A的邻边;(4)锐角∠A的邻边与对边的比值是∠A的余切,记作cota=∠A的邻边∠A的对边;(5)坡面与水平面的夹角(α)称为坡角,坡面的铅直高度与水平面宽度的比称为坡度i(或坡比),既坡度等于坡角的正切,记做;(6)锐角A的正弦,余弦,正切和余切都叫做∠A的锐角三角函数;注:sinA,cosA,tanA,cotA 是在直角三角形中定义的(注意数形结合,构造直角三角形).她的实质是一个比值其大小只与∠A的大小有关。
2.互余两角之间的三角函数关系:(1)一个锐角的正弦等于它的余角的余弦,既sinA=cosB,或sinB=cosA;(2)一个锐角的余弦等于它的余角的正弦,既cosA=sinB,或cosB=sinA;(3)一个锐角的正切等于它的余角的余切,既tanA=cotB,或tanB=cotB;(4)一个锐角的余切等于它的余角的正切,既cotA=tanB,或cotB=tanA;3.同角之间的三角函数关系:(1)平方和关系:;(2)倒数关系: ;(3)商的关系:。
4.特殊角的三角函数值:α sin cos tan cot 30°45° 1 160°解直角三角形1、明确解直角三角形的依据和思路在直角三角形中,我们是用三条边的比来表述锐角三角函数定义的。
因此,锐角三角函数的定义本质揭示了直角三角形中边角之间的关系,是解直角三角形的基础。
如图1,在Rt△ABC中,∠C=90°,设三个内角A、B、C所对的边分别为a、b、c (以下字母同),则解直角三角形的主要依据是(1)边角之间的关系:sinA=cosB=,cosA =sinB=,tanA=cotB=,cotA=tanB=;(2)两锐角之间的关系:A+B=90°;(3)三条边之间的关系:。
最新九年级数学高频考点核心考点复习完整版 知识点大全

最新九年级数学高频考点核心考点复习完整版初中数学知识点大全1、一元一次方程根的情况△=b2-4ac当△>0时,一元二次方程有2个不相等的实数根;当△=0时,一元二次方程有2个相同的实数根;当△<0时,一元二次方程没有实数根2、平行四边形的性质:①两组对边分别平行的四边形叫做平行四边形。
②平行四边形不相邻的两个顶点连成的线段叫他的对角线。
③平行四边形的对边/对角相等。
④平行四边形的对角线互相平分。
菱形:①一组邻边相等的平行四边形是菱形②领心的四条边相等,两条对角线互相垂直平分,每一组对角线平分一组对角。
③判定条件:定义/对角线互相垂直的平行四边形/四条边都相等的四边形。
矩形与正方形:①有一个内角是直角的平行四边形叫做矩形。
②矩形的对角线相等,四个角都是直角。
③对角线相等的平行四边形是矩形。
④正方形具有平行四边形,矩形,菱形的一切性质。
⑤一组邻边相等的矩形是正方形。
多边形:①N边形的内角和等于(N-2)180度②多边心内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角,在每个顶点处取这个多边形的一个外角,他们的和叫做这个多边形的内角和(都等于360度)平均数:对于N个数X1,X2…XN,我们把(X1+X2+…+XN)/N叫做这个N个数的算术平均数,记为X加权平均数:一组数据里各个数据的重要程度未必相同,因而,在计算这组数据的平均数时往往给每个数据加一个权,这就是加权平均数。
二、基本定理1、过两点有且只有一条直线2、两点之间线段最短3、同角或等角的补角相等4、同角或等角的余角相等5、过一点有且只有一条直线和已知直线垂直6、直线外一点与直线上各点连接的所有线段中,垂线段最短7、平行公理经过直线外一点,有且只有一条直线与这条直线平行8、如果两条直线都和第三条直线平行,这两条直线也互相平行9、同位角相等,两直线平行10、内错角相等,两直线平行11、同旁内角互补,两直线平行12、两直线平行,同位角相等13、两直线平行,内错角相等14、两直线平行,同旁内角互补15、定理三角形两边的和大于第三边16、推论三角形两边的差小于第三边17、三角形内角和定理三角形三个内角的和等于180°18、推论1 直角三角形的两个锐角互余19、推论2 三角形的一个外角等于和它不相邻的两个内角的和20、推论3 三角形的一个外角大于任何一个和它不相邻的内角21、全等三角形的对应边、对应角相等22、边角边公理(SAS) 有两边和它们的夹角对应相等的两个三角形全等23、角边角公理( ASA)有两角和它们的夹边对应相等的两个三角形全等24、推论(AAS) 有两角和其中一角的对边对应相等的两个三角形全等25、边边边公理(SSS) 有三边对应相等的两个三角形全等26、斜边、直角边公理(HL) 有斜边和一条直角边对应相等的两个直角三角形全等27、定理1 在角的平分线上的点到这个角的两边的距离相等28、定理2 到一个角的两边的距离相同的点,在这个角的平分线上29、角的平分线是到角的两边距离相等的所有点的集合30、等腰三角形的性质定理等腰三角形的两个底角相等(即等边对等角)31、推论1 等腰三角形顶角的平分线平分底边并且垂直于底边32、等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合33、推论3 等边三角形的各角都相等,并且每一个角都等于60°34、等腰三角形的判定定理如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边)35、推论1 三个角都相等的三角形是等边三角形36、推论2 有一个角等于60°的等腰三角形是等边三角形37、在直角三角形中,如果一个锐角等于30°那么它所对的直角边等于斜边的一半38、直角三角形斜边上的中线等于斜边上的一半39、定理线段垂直平分线上的点和这条线段两个端点的距离相等40、逆定理和一条线段两个端点距离相等的点,在这条线段的垂直平分线上41、线段的垂直平分线可看作和线段两端点距离相等的所有点的集合42、定理1 关于某条直线对称的两个图形是全等形43、定理2 如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线44、定理3 两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上45、逆定理如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称46、勾股定理直角三角形两直角边a、b的平方和、等于斜边c的平方,即a2+b2=c247、勾股定理的逆定理如果三角形的三边长a、b、c有关系a2+b2=c2,那么这个三角形是直角三角形48、定理四边形的内角和等于360°49、四边形的外角和等于360°50、多边形内角和定理n边形的内角的和等于(n-2)×180°51、推论任意多边的外角和等于360°52、平行四边形性质定理1 平行四边形的对角相等53、平行四边形性质定理2 平行四边形的对边相等54、推论夹在两条平行线间的平行线段相等55、平行四边形性质定理3 平行四边形的对角线互相平分56、平行四边形判定定理1 两组对角分别相等的四边形是平行四边形57、平行四边形判定定理2 两组对边分别相等的四边形是平行四边形58、平行四边形判定定理3 对角线互相平分的四边形是平行四边形59、平行四边形判定定理4 一组对边平行相等的四边形是平行四边形60、矩形性质定理1 矩形的四个角都是直角61、矩形性质定理2 矩形的对角线相等62、矩形判定定理1 有三个角是直角的四边形是矩形63、矩形判定定理2 对角线相等的平行四边形是矩形64、菱形性质定理1 菱形的四条边都相等65、菱形性质定理2 菱形的对角线互相垂直,并且每一条对角线平分一组对角66、菱形面积=对角线乘积的一半,即S=(a×b)÷267、菱形判定定理1 四边都相等的四边形是菱形68、菱形判定定理2 对角线互相垂直的平行四边形是菱形69、正方形性质定理1 正方形的四个角都是直角,四条边都相等70、正方形性质定理2正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角71、定理1 关于中心对称的两个图形是全等的72、定理2 关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分73、逆定理如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点对称74、等腰梯形性质定理等腰梯形在同一底上的两个角相等75、等腰梯形的两条对角线相等76、等腰梯形判定定理在同一底上的两个角相等的梯形是等腰梯形77、对角线相等的梯形是等腰梯形78、平行线等分线段定理如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等79、推论1 经过梯形一腰的中点与底平行的直线,必平分另一腰80、推论2 经过三角形一边的中点与另一边平行的直线,必平分第三边81、三角形中位线定理三角形的中位线平行于第三边,并且等于它的一半82、梯形中位线定理梯形的中位线平行于两底,并且等于两底和的一半L=(a+b)÷2 S=L×h83、(1)比例的基本性质:如果a:b=c:d,那么ad=bc如果ad=bc ,那么a:b=c:d84、(2)合比性质:如果a/b=c/d,那么(a±b)/b=(c±d)/d85、(3)等比性质:如果a/b=c/d=…=m/n(b+d+…+n≠0),那么(a+c+…+m)/(b+d+…+n)=a/b86、平行线分线段成比例定理三条平行线截两条直线,所得的对应线段成比例87、推论平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例88、定理如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边89、平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形的三边与原三角形三边对应成比例90、定理平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似91、相似三角形判定定理1 两角对应相等,两三角形相似(ASA)92、直角三角形被斜边上的高分成的两个直角三角形和原三角形相似93、判定定理2 两边对应成比例且夹角相等,两三角形相似(SAS)94、判定定理3 三边对应成比例,两三角形相似(SSS)95、定理如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似96、性质定理1 相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比97、性质定理2 相似三角形周长的比等于相似比98、性质定理3 相似三角形面积的比等于相似比的平方99、任意锐角的正弦值等于它的余角的余弦值,任意锐角的余弦值等于它的余角的正弦值100、任意锐角的正切值等于它的余角的余切值,任意锐角的余切值等于它的余角的正切值101、圆是定点的距离等于定长的点的集合102、圆的内部可以看作是圆心的距离小于半径的点的集合103、圆的外部可以看作是圆心的距离大于半径的点的集合104、同圆或等圆的半径相等105、到定点的距离等于定长的点的轨迹,是以定点为圆心,定长为半径的圆106、和已知线段两个端点的距离相等的点的轨迹,是着条线段的垂直平分线107、到已知角的两边距离相等的点的轨迹,是这个角的平分线108、到两条平行线距离相等的点的轨迹,是和这两条平行线平行且距离相等的一条直线109、定理不在同一直线上的三点确定一个圆。
最新九年级数学高频考点核心考点分类复习完整版 中考数学常用公式定理

最新九年级数学高频考点核心考点分类复习完整版中考数学常用公式定理1、整数(包括:正整数、0、负整数)和分数(包括:有限小数和无限环循小数)都是有理数.如:-3,,0.231,0.737373…,,.无限不环循小数叫做无理数.如:π,-,0.1010010001…(两个1之间依次多1个0).有理数和无理数统称为实数.2、绝对值:a ≥0丨a 丨=a ;a ≤0丨a 丨=-a .如:丨-丨=;丨3.14-π丨=π-3.14.3、一个近似数,从左边笫一个不是0的数字起,到最末一个数字止,所有的数字,都叫做这个近似数的有效数字.如:0.05972精确到0.001得0.060,结果有两个有效数字6,0.4、把一个数写成±a ×10n的形式(其中1≤a <10,n 是整数),这种记数法叫做科学记数法.如:-40700=-4.07×105,0.000043=4.3×10-5. 5、乘法公式(反过来就是因式分解的公式):①(a +b )(a -b )=a 2-b 2.②(a ±b )2=a 2±2ab +b 2.③(a +b )(a 2-ab +b 2)=a 3+b 3.④(a -b )(a 2+ab +b 2)=a 3-b 3;a 2+b 2=(a +b )2-2ab ,(a -b )2=(a +b )2-4ab . 6、幂的运算性质:①a m ×a n =a m +n .②a m ÷a n =a m -n .③(a m )n =a mn .④(ab )n =a n b n .⑤()n=n .⑥a -n=1n a,特别:()-n =()n .⑦a 0=1(a ≠0).如:a 3×a 2=a 5,a 6÷a 2=a 4,(a 3)2=a 6,(3a 3)3=27a 9,(-3)-1=-,5-2==,()-2=()2=,(-3.14)º=1,(-)0=1.7、二次根式:①()2=a (a ≥0),②=丨a 丨,③=×,④=(a >0,b ≥0).如:①(3)2=45.②=6.③a <0时,=-a.④的平方根=4的平方根=±2.(平方根、立方根、算术平方根的概念)8、一元二次方程:对于方程:ax 2+bx +c =0:①求根公式是x =2b a-±,其中△=b 2-4ac 叫做根的判别式.当△>0时,方程有两个不相等的实数根; 当△=0时,方程有两个相等的实数根;当△<0时,方程没有实数根.注意:当△≥0时,方程有实数根.②若方程有两个实数根x 1和x 2,并且二次三项式ax 2+bx +c 可分解为a (x -x 1)(x -x 2). ③以a 和b 为根的一元二次方程是x 2-(a +b )x +ab =0.9、一次函数y =kx +b (k ≠0)的图象是一条直线(b 是直线与y 轴的交点的纵坐标即一次函数在y 轴上的截距).当k >0时,y 随x 的增大而增大(直线从左向右上升);当k <0时,y 随x 的增大而减小(直线从左向右下降).特别:当b =0时,y =kx (k ≠0)又叫做正比例函数(y 与x 成正比例),图象必过原点.10、反比例函数y =(k ≠0)的图象叫做双曲线.当k >0时,双曲线在一、三象限(在每一象限内,从左向右降);当k <0时,双曲线在二、四象限(在每一象限内,从左向右上升).因此,它的增减性与一次函数相反.11、统计初步:(1)概念:①所要考察的对象的全体叫做总体,其中每一个考察对象叫做个体.从总体中抽取的一部份个体叫做总体的一个样本,样本中个体的数目叫做样本容量.②在一组数据中,出现次数最多的数(有时不止一个),叫做这组数据的众数.③将一组数据按大小顺序排列,把处在最中间的一个数(或两个数的平均数)叫做这组数据的中位数. (2)公式:设有n 个数x 1,x 2,…,x n ,那么: ①平均数为:12......nx x x x n+++=;②极差:用一组数据的最大值减去最小值所得的差来反映这组数据的变化范围,用这种方法得到的差称为极差,即:极差=最大值-最小值; ③方差:数据1x 、2x ……, n x 的方差为2s ,则2s =()()()222121.....n x x x x x x n 轾-+-++-犏臌标准差:方差的算术平方根.数据1x 、2x ……, n x 的标准差s ,则s =一组数据的方差越大,这组数据的波动越大,越不稳定。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
最新九年级数学高频考点核心考点复习提纲完整版九年级数学总复习资料代数部分第一节实数[知识要点]1.实数的分类2.数轴:(1)定义:规定了原点、正方向和单位长度的直线叫做数轴。
(2)实数和数轴上的点一一对应。
3.相反数:只有符号不同的两个数互为相反数。
a的相反数为-a若a、b互为相反数,则a+b=0 或a=-b4.倒数:乘积为1的两个数互为倒数。
a(a≠0)的倒数为.5.绝对值6.实数的大小比较(1)正数>0;负数<0;正数>负数;两个正数,绝对值大的正数大;两个负数,绝对值大的反而小。
(2)用数轴比较:右边的数大于左边的数。
7.科学记数法、近似数和有效数字。
(1)科学记数法:把一个数记成±a³10n的形式(其中1≤a<10,n是整数)(2)近似数(3)有效数字:从左边第一个不是0的数字起,到精确到的数位止,所有的数字,都叫做这个数字的有效数字。
8.实数的运算(1)运算法则(2)运算律(3)运算顺序第二节二次根式[知识要点]1.平方根(1)定义:若x2=a,则x是a的平方根,记作:x=±(2)性质:1)正数的平方根有2个,它们互为相反数2)0的平方根是03)负数没有平方根2.算术平方根(1)定义:正数a的正的平方根,记作(2)性质:1)正数的算术根是一个正数。
2)0的算术平方根是03)负数没有算术平方根3.立方根4.二次根式的有关概念(1)二次根式:型如√a(a≥0)的式子叫二次根式。
(2)最简二次根式:1)被开方数的因数是整数 2)被开方数中不含能开得尽方得因数.(3)同类二次根式:化成同类二次根式以后,被开方数相同得二次根式,叫做同类二次根式.(4)二次根式的性质(5)分母有理化:把分母中得根号化去,叫做分母有理化.(6)二次根式得运算.第三节整式和因式分解[知识要点]1.代数式2.整式(1)同类项:所含字母相同,且相同字母的次数也相同的项叫同类项。
(2)添括号,去括号法则(3)指数运算3.因式分解(1)定义:把一个多项式化成几个整式积的形式,叫做因式分解。
(2)因式分解方法:1)提公因式法 2)公式法 3)十字相乘法 4)分组分解法第四节分式[知识要点]1.分式(1)定义:分母中含有字母的式子。
(2)分式有意义的条件:分母≠0(3)分式值=0的条件:分子=0且分母≠02.分式的性质(1)基本性质:(2)变号法则:分子、分母和分式本身的符号,改变其中任意两个,分式的值不变。
3.分式运算:加、减、乘、除、乘方、开方第五节一元一次方程一元二次方程和不等式[知识要点]1.方程的有关概念:方程、方程的解2.一元一次方程:(1)定义:只含有一个未知数,并且未知数的次数是一次的方程。
(ax=b,a ≠0)(2)解法:去分母、去括号、移项、合并同类项、系数化13.一元二次方程(1)定义:只含有一个未知数,并且未知数的最高次数是2的方程。
一般形式:ax2+bx+c=0 (a≠0)(2)解法:1)直接开平方法2)因式分解法3)公式法:4.一元一次不等式:ax+b>0 或 ax+b<0 (a≠0)5.一元一次不等式组解法:1)求出各个不等式的解集2)利用数轴确定不等式组的解集。
例题分析练习一、选择题1. 火星和地球之间的距离为34,000,000千米,用科学记数法表示为(D)A、0.34³108千米B、3.4³106千米C、34³106千米D、3.4³107千米2.把1949按四舍五入取近似数,保留两个有效数字表示为(C)A、1.9³104B、2.0³104C、1.9³103D、2.0³1033.如果在数轴上表示a,b两个实数的点的位置如图所示,那么|a-b|+|a+b|化简的结果等于(B)A、2aB、-2aC、0D、2b4.若|a|=-a,则a的取值范围是(A)A、正数B、非正数C、负数D、非负数12.已知x=-2是方程2x+m-4=0的一个根,则m的值是()A、8B、-8C、0D、213.方程(x-3)2=3-x的根是()A、x=2B、x=3C、x=4D、x=2或x=314.已知一个矩形的周长是30,宽的长度不超过3,则长的取值范围是()A、27≤a<30B、12<a<15C、12≤a<15D、0<a≤12二、计算题三、解方程四、解不等式或组答案一、选择题1.D2.C3.B4.B5.B6.A7.A8.C 9.A 10.D 11.A 12.A 13.D 14.C二、计算题几何部分第一节相交线、平行线[知识要点]一、相交线1.线段的垂直平分线:(1)定义:垂直且平分一条线段的直线,叫做线段的垂直平分线。
(2)性质:线段垂直平分线上的点,到线段两端点的距离相等。
2.角(1)定义(2)角的分类:平角、周角、直角、锐角、钝角(3)角的度量:1°=60' 1'=60"(4)相关的角:对顶角、余角、补角、邻补角(5)角的平分线1)定义2)性质:角平分线上的点到角两边的距离相等。
二、平行线1.定义:在同一平面内不相交的两条直线,叫平行线。
2.性质:(1)两直线平行,同位角相等。
(2)两直线平行,内错角相等(3)两直线平行,同旁内角互补(4)平行线间的距离相等(5)平行线截相交两条直线,对应线段成比例。
3.判定:(1)同位角相等,两直线平行(2)内错角相等,两直线平行(3)同旁内角互补,两直线平行(4)平行于同一直线的两直线平行。
(5)垂直于同一直线的两直线平行。
第二节三角形[知识要点]一、三角形的分类二、三角形的边角关系1.边与边的关系(1)△两边之和大于第三边(2)△两边之差小于第三边2.角与角关系(1)△三个内角的和等于180°(2)△的一个外角等于和它不相邻的两个内角的和(3)△的一个外角大于任何一个和它不相邻的内角三、△的主要线段(1)角平分线(2)中线(3)高线(4)中位线四、△的重要的点(1)内心:内心到三边距离相等。
(2)重心:重心到顶点的距离等于到对边中点距离的2倍(3)垂心(4)外心:外心到三个顶点的距离相等。
五、特殊三角形1.等腰△(1)性质:1)两腰相等2)两个底角相等3)底边上“三线合一”4)轴对称图形(1条对称轴)(2)判定:1)两边相等的三角形是等腰△2)两个角相等的三角形是等腰△2.等边△性质:1)三边相等2)三个角相等,都等于60°3)三边上都有“三线合一”4)轴对称图形(3条对称轴)3.Rt△(1)性质:1)两个锐角互余2)勾股定理3)斜边上中线等于斜边的一半4)30°角所对的直角边等于斜边的一半(2)判定:1)有一个角是直角的三角形2)勾股定理逆定理第三节全等三角形[知识要点]一、定义:二、性质:1.对应边相等2.对应角相等3.对应线段(高线、中线、角平分线)相等4.全等三角形面积相等三、判定:(SAS)(AAS)(ASA)(SSS)(HL)第四节四边形[知识要点]一、特殊四边形二、平行四边形(1)性质:1)边:对边平行且相等2)角:对角相等,邻角互补3)对角线:互相平分4)对称性:中心对称图形(2)判定:1)边:两组对边分别平行两组对边分别相等一组对边平行且相等2)对角线:对角线互相平分3)角:两组对角分别相等。
三、矩形1.性质:(1)具有平行四边形的一切性质(2)4个角都是直角(3)对角线相等(4)既是中心对称图形,又是轴对称图形2.判定:(1)有一个角是直角的平行四边形是矩形(2)有三个角是直角的四边形是矩形(3)对角线相等的平行四边形是矩形四、菱形1. 性质:(1)具有平行四边形的一切性质(2)四条边都相等(3)对角线互相垂直,且平分内对角2.判定:(1)邻边相等的平行四边形是菱形(2)四边都相等的四边形是菱形(3)对角线互相垂直的平行四边形是菱形。
五、正方形:(1)具有平行四边形、矩形、菱形的一切性质。
(2)判定:利用定义六、梯形1.等腰梯形的性质:(1)两腰相等(2)两底角相等(3)两条对角线相等(4)轴对称图形2.直角梯形的性质:一腰与底垂直3.梯形中常用辅助线七、多边形1. n边形内角和(n-2)²180°2.n边形外角和为360°3.n边形对角线条数例题分析例1已知直线AB和CD相交于O点,射线OE⊥AB于O,射线OF⊥CD 于O,且∠BOF=25°,求:∠AOC与∠EOD的度数。
(画出图形,结合图形计算)例3一张宽为3,长为4的矩形纸片ABCD,先沿对角线BD对折,点C落在点C'的位置(如图1),BC'交AD于G,再折叠一次,使点D与点A重合,得折痕EN(如图2),EN交AD于点M,求ME的长。
练习一、选择题1.如果线段AB=5cm,C在直线AB上,且BC=3cm,则A,C两点的距离是()A、8cmB、2cmC、8cm和2cmD、无法确定2.已知:OA⊥OC,∠AOB:∠AOC=2:3,则∠BOC的度数为()A、30°B、60°C、150°D、30°或150°3.如图:DH//EG//BC,且DC//EF,则图中与∠1相等的角(不包括∠1)A、2B、4C、5D、64.在等腰△ ABC中,AB=AC,BD平分∠ABC交AC于D,如果∠CDB=150°,则∠A等于()A、130°B、140 °C、150°D、160°5.等腰三角形一腰中线分周长为15cm,12cm两部分,则底边和腰长为()A、7和10B、11和8C、7和10或11和8D、不能确定6.等腰三角形的一个外角为140°,则它的一个底角为()度A、70°B、40°C、70°或40°D、不能确定8.下列命题中不成立的是()A、对角线相等的平行四边形是矩形B、对角线互相垂直的平行四边形是菱形C、对角线互相垂直且相等的四边形是正方形D、对角线相等的梯形是等腰梯形9.在(1)线段(2)等腰直角三角形(3)等边三角形(4)平行四边形(5)菱形中,既是轴对称图形,又是中心对称图形的是()个A、(3)(4)(5)B、(3)(5)C、(1)(3)(5)D、(1)(5)10.如图:若OA=OB,点C在OA上,点D在OB上,OC=OD,AD和BC相交于E,那么图中全等三角形共有()A、2对B、3对C、4对D、5对二、解答题1.如图:在□ABCD中,M和N分别为AD、BC的中点,AE⊥BD于E,CF⊥BD 于F。
求证:四边形ENFM是平行四边形2.如图:在正方形ABCD中,AB=3,过边AB上的一个三等分点N作NE//AD,交CD于E,以过A的一条直线为折痕,将点B折至NE上,这个落点为P,折痕与BC交于F,求:BF的长。
