热力学第一定律
热力学第一定律

举例2:门窗紧闭房间用空调降温
以房间为系统 闭口系能量方程
Q U W Q0 W 0 U Q W
if Q W
T
闭口系
Air-
conditioner
Q
空 调
§ 2-4 开口系能量方程
mout
out
•
•
u pv c2 / 2 gz min W net
in
开口系能量方程微分式(续)
当有多条进出口:
•
•
Q dEcv / W net
•
u pv c2 / 2 gz mout out
•
u pv c2 / 2 gz min in
流动时,总一起存在
焓Enthalpy的引入
1、焓是状态量 state property
2、H为广延参数 H=U+pV= m(u+pv)= mh h为比参数
3、对流动工质,焓代表能量(内能+推进功) 对静止工质,焓不代表能量
4、物理意义:开口系中随工质流动而携带的、 取决于热力状态的能量。
§2-5 稳定流动能量方程
Energy balance for steady-flow systems
可理解为:由于工质的进出,外界与系统
之间所传递的一种机械功,表现为流动工质 进出系统使所携带或所传递的一种能量。
开口系能量方程的推导
uin pvin
min
1 2
ci2n
gzin
Wnet
Q
Q + min(u + c2/2 + gz)in
热力学第一定律

热力学第一定律功:δW =δW e +δW f(1)膨胀功 δW e =p 外dV 膨胀功为正,压缩功为负。
(2)非膨胀功δW f =xdy非膨胀功为广义力乘以广义位移。
如δW (机械功)=fdL ,δW (电功)=EdQ ,δW (表面功)=rdA 。
热 Q :体系吸热为正,放热为负。
热力学第一定律: △U =Q —W 焓 H =U +pV 理想气体的内能和焓只是温度的单值函数。
热容 C =δQ/dT(1)等压热容:C p =δQ p /dT = (∂H/∂T )p (2)等容热容:C v =δQ v /dT = (∂U/∂T )v 常温下单原子分子:C v ,m =C v ,m t =3R/2常温下双原子分子:C v ,m =C v ,m t +C v ,m r =5R/2 等压热容与等容热容之差:(1)任意体系 C p —C v =[p +(∂U/∂V )T ](∂V/∂T )p (2)理想气体 C p —C v =nR 理想气体绝热可逆过程方程:pV γ=常数 TV γ-1=常数 p 1-γT γ=常数 γ=C p / C v 理想气体绝热功:W =C v (T 1—T 2)=11-γ(p 1V 1—p 2V 2) 理想气体多方可逆过程:W =1nR-δ(T 1—T 2) 热机效率:η=212T T T - 冷冻系数:β=-Q 1/W 可逆制冷机冷冻系数:β=121T T T -焦汤系数: μJ -T =H p T ⎪⎪⎭⎫⎝⎛∂∂=-()pT C p H ∂∂ 实际气体的ΔH 和ΔU :ΔU =dT T U V ⎪⎭⎫ ⎝⎛∂∂+dV V U T ⎪⎭⎫ ⎝⎛∂∂ ΔH =dT T H P ⎪⎭⎫ ⎝⎛∂∂+dp p H T⎪⎪⎭⎫ ⎝⎛∂∂ 化学反应的等压热效应与等容热效应的关系:Q p =Q V +ΔnRT 当反应进度 ξ=1mol 时, Δr H m =Δr U m +∑BB γRT化学反应热效应与温度的关系:()()()dT B C T H T H 21T T m p B1m r 2m r ⎰∑∆∆,+=γ热力学第二定律Clausius 不等式:0TQS BAB A ≥∆∑→δ—熵函数的定义:dS =δQ R /T Boltzman 熵定理:S =kln Ω Helmbolz 自由能定义:F =U —TS Gibbs 自由能定义:G =H -TS 热力学基本公式:(1)组成恒定、不作非膨胀功的封闭体系的热力学基本方程:dU =TdS -pdV dH =TdS +Vdp dF =-SdT -pdV dG =-SdT +Vdp (2)Maxwell 关系:T V S ⎪⎭⎫⎝⎛∂∂=V T p ⎪⎭⎫ ⎝⎛∂∂Tp S ⎪⎪⎭⎫ ⎝⎛∂∂=-p T V ⎪⎭⎫ ⎝⎛∂∂ (3)热容与T 、S 、p 、V 的关系:C V =T VT S ⎪⎭⎫⎝⎛∂∂ C p =T p T S ⎪⎭⎫ ⎝⎛∂∂Gibbs 自由能与温度的关系:Gibbs -Helmholtz 公式 ()pT /G ⎥⎦⎤⎢⎣⎡∂∆∂T =-2T H ∆ 单组分体系的两相平衡: (1)Clapeyron 方程式:dT dp=mX m X V T H ∆∆ 式中x 代表vap ,fus ,sub 。
热力学第一定律
21
例1: 一定量的理想气体从体积V1 膨胀到体积V2 ,经历 以下几个过程: AB等压过程; AC等温过程; AD绝热 过程。问:从P-V图上,(1) 哪一个过程做功较多?哪 一个过程做功较少?(2) 经历哪一个过程内能增加?经 历哪一个过程内能减少?(3) 经历哪一个过程吸热最多? P 解: (1) 等压过程做功最多 A A A P A B p T Q 绝热过程做功最少 P C
例2:图示两卡诺循环,S1 = S2 P (1) 吸热和放热差值是否相同? (2) 对外所做净功是否相同? (3) 效率是否相同? 答案:(1)相同;(2)相同;(3)不相同
讨论
T2 1 )卡诺热机效率C 1 T1
只与T1和T2有关
与物质种类、膨胀的体积无关
2 ) 理论指导作用
T1 提高 c T2
提高高温热源的温度现实些
31
3)理论说明低温热源温度T2 0
说明热机效率 且只能 进一步说明 •热机循环不向低温热源放热是不可能的
T
(2) 等压膨胀:系统吸热 O V1 V2 V 系统内能增加,且对外做功; 等温膨胀:系统吸热,全部用来对外做功,内能不变; 绝热膨胀:系统不吸收热量,靠减少系统的内能对外做功
PQ
D
等压:内能增加;等温:内能不变;绝热:内能减少。
(3) 等压膨胀过程吸热最多。(4)绝热线比等温线陡 22
例2: 一mol单原子理想气体在汽缸中,设汽缸与活塞无 摩擦,开始时,P1=1.013*105Pa, V1=1.0*10 –2m3 ,将 此气体在等压下加热,使其体积增大一倍,然后在等体 下加热至压强增大一倍,最后绝热 膨胀为起始温度。 (1)画P-V图(2)求内能的增量(3)过程中的功 解: (1)图示 (2)0 (3) P2
热力学第一定律

假定控制容积形状、大小、空间位置均不随时间改变。
——因而统计系统的总能时,不考虑系统整体的外观能量,但要计及 流体的流动动能,重力位能以及热力学能。
假定系统除与外界有物质流交换,在没有质量流穿越的边界
上还可以有传热和作功的相互作用。
假定进、出口截面上存在局部平衡。 假定流动为一元流动
——仅在沿流动的方向上才有参数的变化。
热能工程教研室
§2-2 热力学能和总能
一、热力学能
物质内部拥有的能量称为热力学能,其组成是: 内动能(分子平移,旋转,振动)
内位能(分子间作用力)
化学能(维持一定的分子结构) 原子能(原子核内部)
如果无化学反应,无核反应, 热力学能 U = 内动能 + 内位能 1kg物质的热力学能称比热力学能 u,单位是J / kg 。 热力学能是热力状态的单值函数,它与路径无关,是状态参数。 u = f(T,v); u = f(T,p); u = f(p,v) (2 - 1)
进入系统的能量 - 离开系统的能量 =系统中贮存能量的增加 它适用于任何过程和任何工质的热力系统。 闭口系的能量方程 Q - W = U = U2 – U1 Q = U + W ( 输入) (贮增)(输出) 对于一个微元过程,第一定律的解析式的微分形式: Q = dU + W 对于1kg工质,有 q = u + w q = du + w (2-9)
– p1 u
)
(2-19)
由式(2-18)并考虑q -△u = w,则
wt = w -△(p u)= w -(p2 u
热能工程教研室
2
1
(2-20)
技术功在示功图上的表示
对可逆过程:wt =
热力学三大定律分别是什么

热力学三大定律分别是什么
第一定律:能量守恒定律
第一定律,也称为能量守恒定律,是热力学中最基本的定律之一。
它表明能量在自然界中不能被创造或者毁灭,只能从一种形式转换为另一种形式。
这意味着一个封闭系统中的能量总量是恒定的,即能量的变化等于能量的转移。
换句话说,系统内的能量增加必须等于从系统中输出的能量减少。
第一定律的数学表达为:
$$\\Delta U = Q - W$$
其中,U为系统内能的变化,Q为系统吸收的热量,W为系统对外做的功。
第二定律:熵增定律
第二定律,又称为熵增定律,描述了自然系统朝着更高熵状态演化的方向。
熵是一个描述系统无序程度的物理量,熵增定律表明在一个孤立系统中,熵永远不会减少,只能增加或保持不变。
换句话说,热力学第二定律阐明了自然中不可逆的过程。
数学表达式为:
$$\\Delta S \\geq 0$$
其中,$\\Delta S$为系统熵的变化。
第三定律:绝对零度不可达性原理
热力学第三定律是与系统的绝对零度状态有关的定律,也称为绝对零度不可达性原理。
根据这一定律,在有限的步骤内无法将任何系统冷却到绝对零度。
绝对零度是温度的最低可能值,达到这个温度时物质的热运动会停止。
这一定律的提出主要是为了指出温度接近绝对零度时系统的行为,以及随着温度趋近于零熵也趋近于零。
具体表述为:
不可能通过有限的步骤将任何物质冷却到绝对零度。
热力学第一定律

23
本章学习要求
• 掌握能量、热力系统储存能、热力学能、热量和功量 的概念,理解热量和功量是过程量而非状态参数。 • 理解热力学第一定律的实质能量守恒定律。 • 掌握稳定流动能量方程,能熟练运用稳定流动能量方 程对简单的工程问题进行能量交换的分析和计算。 • 掌握膨胀功、轴功、流动功和技术功的概念、计算及 它们之间的关系。 • 理解焓的定义式及其物理意义。 • 了解常用热工设备主要交换的能量及稳定流动能量方 程的简化形式。
2. 宏观位能: Ep ,单位为 J 或 kJ
Ep mgz
5
热力系总储存能:E ,单位为 J 或 kJ
E U Ek Ep
比储存能:e ,单位为 J/kg 或 kJ /kg
1 2 e u ek ep u cf gz 2
6
内动能-温度 热力学能 (内能U、u) 外储存能 内位能-比体积
∴流动功是一种特殊的功,其数值取决于
控制体进、出口界面上工质的热力状态。
14
根据热力学第一定律, 有 :
1 2 1 2 u1 cf 1 gz1 p1v1 q u2 cf 2 gz2 p2v2 ws 0 2 2
令 upv h,由于u、p、v都是状态参数,所以h也是 状态参数,称为比焓。
对一切热力系统和热力过程,有:
进入系统的能量-离开系统的能量 = 系统储存能量的变化
8
二、闭口热力系的能量方程
如图: Q=△U+W 对微元过程: Q QdUW 或 qduw 即: 热力系获得热量= 增加的热力学能+膨胀做功 对于可逆过程 : qdupdv 或
ΔU
W
qu pdv
热力学第一定律

= PdV
A=
∫
V2
V1
pdV
7
A =
∫ dA = ∫
V2
V1
pdV
dV > 0, dA > 0, 系统对外作正功;
dV < 0,dA < 0, 系统对外作负功;
dV = 0,dA = 0, 系统不作功。
A = ∫ pdV
V1
V2
由积分意义可知,功的大小等于p—V 图上过程 曲线p(V)下的面积。功的数值不仅与初态和末 态有关,而且还依赖于所经历的中间状态,功 8 与过程的路径有关.
QT 热源 Q V
等容过程
热源 QP
等压过程
T 恒温大 V
6
三、功 热量 内能 dx 1功 如图示的热力学系统: P S 若过程为无摩擦的准静 态过程 活塞迎着气体一侧的面积为S气体膨胀推动活塞对 外作功:
dA =
当系统体积从 V1→ V2,系统对外界作功:
F Fdx = S Sdx
在等温过程中,理想气体吸热全部用于对外作 功,或外界对气体作功全转换为气体放出的热。 22
四、绝热过程
系统在状态变化过程中始终与外界没有热交换。
绝热膨胀过程中,系统对外作的功,是靠内能减少实 现的,故温度降低;绝热压缩过程中,外界对气体作 功全部用于增加气体内能,故温度上升。 绝热过程方程: 气体绝热自由膨胀 Q=0, A=0,△E=0
14
Q=∫
V2
V1
i pdV + νR(T2 − T1 ) 2
Q = ( E 2 − E 1) + A = ∆ E + A
热力学第一定律,是包含热量在内的能量守恒定律。
Q>0 Q<0
热力学第一定律

3. 摩尔恒压热容与摩尔恒容热容的关系
C p,m CV ,m
H m T
p
U m T
V
(Um pVm ) T
p
U m T
V
Um Um p Vm
T p T V
C p,m Cv,m
Um Vm
p
T
Vm T
p
2.4.8
C p,m
CV ,m
Um V
T
p
Vm T
p
对理想气体
(0
p)
(R / p)T T
p
R
C p,m CV ,m R
状态函数法举例
§2.2 热力学第一定律
热力学第一定律的本质是能量守恒原理,即隔离系统 无论经历何种变化,其能量守恒。
热Q
U U2 U1 Q W dU U2 U1 Q W 途径函数
(2.2.1a) (2.2.1b)
符号规定: 若系统从环境吸热+,若系统向环境放热-
第二章 热力学第一定律
热力学是自然科学中建立最早的学科之一 1. 第一定律:能量守恒,解决过程的能量衡算问题 (功、热、热力学能等) 2. 第二定律:过程进行的方向判据 3. 第三定律:解决物质熵的计算
经典热力学 1 . 研究含有大量质点的宏观系统 2. 只考虑平衡问题
§2.1 基本概念和术语
1. 系统与环境 系统:作为研究对象的那部分物质 环境:系统以外与之相联系的那部分物质(与系统密切 相关、有相互作用或影响所能及的部分)
热力学第一定律

R=8.314 J/mol.K.
• 由理想气体的模型, 无论分子间的距离大或小,其分 子间均无作用势能,故理想气体的内能与体系的体积 无关,因而与体系的压力也无关.
• 对于理想气体体系,其内能不含分子间作用势能这一 项,所以, 内能与体系的体积无关, 只与体系的温度有 关. 在体系的物质的量已确定的条件下,理想气体体 系的内能只是温度的函数,即:
第四节
可逆过程和不可逆过程
• 热力学函数中的过程量(Q,W)的数值与体系经 历的途径密切相关。 • 体系从一始态到一末态,理论上可以通过无 数条途径,所有这些途径,按其性质可分为 两大类:
•
可逆过程和不可逆过程
• 当体系的状态发生变化时,环境的状态也多少有所 变化,若将体系的状态还原为始态,环境的状态可 能还原,也可能未还原,正是根据环境是否能完全 还原,将过程分为可逆过程和不可逆过程。
CV,m=5/2R
• 多原子分子理想气体: 分子具有3个平动自由度和3个 转动自由度, 每个分子对内能的贡献为3kT, 多原子分 子理想气体的摩尔等容热容为(不考虑振动): •
CV,m=3R
• 2. 理想气体等压热容与等容热容之差 Cp,m﹣CV,m=(H/T)p﹣ (U/T)V =((U+pV)/T)p﹣ (U/T)V
A
•
E=U
B
因为宇宙的总能量是不变的,故体系能量的变化必 来自于周围环境。
若体系的能量增加,则环境的能量减少; 若体系的能量减少;则环境的能量增加。
体系与环境之间的能量交换形式只有热与功两种,故有:
U =Q+W
其物理意义是:
(体系对外做功为负)
上式即为热力学第一定律的数学表达式。
自然界的能量是恒定的,若体系的内能 发生了变化 (U),其值必定等于体系与环 境之间能量交换量(Q、W)的总和。
热力学第一定律

热力学第一定律科技名词定义中文名称:热力学第一定律英文名称:first law of thermodynamics其他名称:能量守恒和转换定律定义:热力系内物质的能量可以传递,其形式可以转换,在转换和传递过程中各种形式能源的总量保持不变。
概述热力学第一定律热力学第一定律:△U=Q+W。
系统在过程中能量的变化关系英文翻译:the first law of thermodynamics简单解释在热力学中,系统发生变化时,设与环境之间交换的热为Q(吸热为正,放热为负),与环境交换的功为W(对外做功为负,外界对物体做功为正),可得热力学能(亦称内能)的变化为ΔU = Q+ W或ΔU=Q-W物理中普遍使用第一种,而化学中通常是说系统对外做功,故会用后一种。
定义自然界一切物体都具有能量,能量有各种不同形式,它能从一种形式转化为另一种形式,从一个物体传递给另一个物体,在转化和传递过程中能量的总和不变。
英文翻译:The first explicit statement of the first law of thermodynamics, byRudolf Clausiusin 1850, referred to cyclic thermodynamic processes "In all cases in which work is produced by the agency of heat, a quantity of heat is consumed which is proportional to the work done; and conversely, by the expenditure of an equal quantity of work an equal quantity of heat is produced."基本内容能量是永恒的,不会被制造出来,也不会被消灭。
热力学第一定律

W>0 对系统作功
闭口系统的热力学第一定律表达式
一般式 Q = ∆U + W dQ = dU + dW q = ∆u + w dq = du + dw 适用条件: ) 适用条件: 1)任何工质 2) 任何过程 Q
微分形式 单位质量工质
W
闭口系统的热力学第一定律表达式
对于可逆过程 对于可逆过程
δw = pdv
实质:能量转换和守恒定律在热力学系统中的应用。 实质:能量转换和守恒定律在热力学系统中的应用。 可表述为: 可表述为:在孤立系统内能量的总量保持不变
能量守恒与转换定律:能量不可能被创造, 能量守恒与转换定律 能量不可能被创造,也不可能被消 能量不可能被创造 只能相互转换,且在孤立系统中总量保持不变。 灭,只能相互转换,且在孤立系统中总量保持不变。
• 18世纪初,工业革命,热效率只有 。 世纪初, 世纪初 工业革命,热效率只有1%。 • 1842年,J.R.Mayer阐述热力学第一定律, 年 阐述热力学第一定律, 阐述热力学第一定律 但没有引起重视。 但没有引起重视。 • 1840-1849年,Joule用多种实验的一致性证 1840-1849年 Joule用多种实验的一致性证 明热力学第一定律, 明热力学第一定律,于1850年发表并得到公 年发表并得到公 认。
• 第一 什么是热力学第一定律? 什么是热力学第一定律? 热力系内物质的能量可以传递,其形式可以转换,在转 热力系内物质的能量可以传递,其形式可以转换, 换和传递过程中各种形式能源的总量保持不变。 换和传递过程中各种形式能源的总量保持不变。 • 第二 为什么要学习热力学第一定律? 为什么要学习热力学第一定律? 物质和能量既不能被消灭也不能被创造。 物质和能量既不能被消灭也不能被创造。 • 第三 热力学第一定律的应用? 热力学第一定律的应用? 第一类永动机是不可能造成的
热力学第一定律
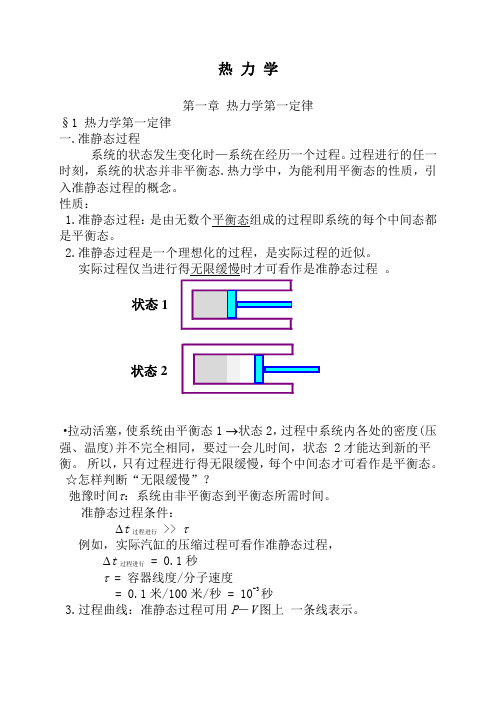
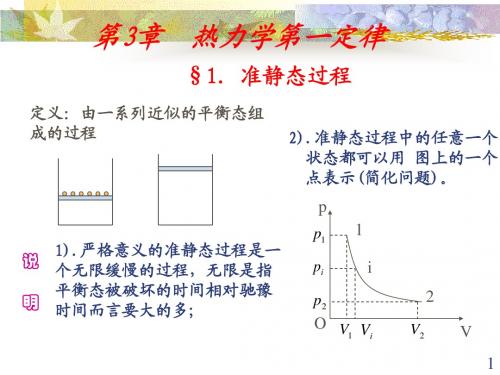
热 力 学第一章 热力学第一定律§1 热力学第一定律 一.准静态过程系统的状态发生变化时—系统在经历一个过程。
过程进行的任一时刻,系统的状态并非平衡态.热力学中,为能利用平衡态的性质,引入准静态过程的概念。
性质:1.准静态过程:是由无数个平衡态组成的过程即系统的每个中间态都是平衡态。
2.准静态过程是一个理想化的过程,是实际过程的近似。
实际过程仅当进行得无限缓慢时才可看作是准静态过程 。
·拉动活塞,使系统由平衡态1 →状态2,过程中系统内各处的密度(压强、温度)并不完全相同,要过一会儿时间,状态 2才能达到新的平衡。
所以,只有过程进行得无限缓慢,每个中间态才可看作是平衡态。
☆怎样判断“无限缓慢”?弛豫时间τ:系统由非平衡态到平衡态所需时间。
准静态过程条件: ∆t 过程进行 >> τ例如,实际汽缸的压缩过程可看作准静态过程, ∆t 过程进行 = 0.1秒τ = 容器线度/分子速度= 0.1米/100米/秒 = 10-3秒3.过程曲线:准静态过程可用P -V 图上 一条线表示。
状态1状态2二.功、内能、热量1.功 ·通过作功可以改变系统的状态。
·机械功(摩擦功、体积功)2.内能·内能包含系统内:(1)分子热运动的能量;(2)分子间势能和分子内的势能;(3)分子内部、原子内部运动的能量; (4)电场能、磁场能等。
·内能是状态的函数*对于一定质量的某种气体,内能一般是T 、V 或P 的函数; *对于理想气体,内能只是温度的函数 E = E (T )*对于刚性理想气体分子, i :自由度; ν :摩尔数 ·通过作功改变系统内能的实质是:分子的有规则运动能量和分子的无规则运动能量的转化和传递。
3.热量·传热也可改变系统的状态,其条件是系统和外界的温度不同。
·传热的微观本质:是分子的无规则运动能量从高温物体向低温物体传递。
热力学第一定律

∂U ∂U dU = dT + dV ∂T V ∂V T
在焦耳实验中,dV>0,dT=0,dU=0,故有:
∂U =0 ∂V T
以T,p作为内能的独立变量,同理有:
∂U ∂p = 0 T
微观解释: 理想气体分子间无相互作用力,分子 间相互作用的势能为零。体积改变导致的 分子间距离的改变不影响内能的数值。理 想气体的内能只是指分子的动能,而动能 仅是温度的函数,所以理想气体的内能仅 是温度的函数。
积分表达式
Q=?
W=?
二、体积功、最大功与可逆过程
物理化学中,常见的功有: 体积功、电功、表面功等。 各种功的具体表达式可概括为两个因 子的乘积: 强度因子×容量性质的改变量
功的形式 机械功 体积功 电 功 表面功
强度因素 f(力)
容量性质的 改变量 dl(位移)
p(外压力) dV(体积改变) E(电位差) dQ(电量改变) σ(表面张力) dA(表面积改变)
→ δQ p = dU + d ( pV ) = d (U + pV ), Q p = ∆(U + pV )
δW '= 0 , p = pamb
说明: 热虽然不是状态函数,然而由上述两 式表明,当不同的途径均满足恒容非体积 功为零或恒压非体积功为零的特定条件 时,不同途径的热已经分别与过程的热力 学函数相等,因此不同途径的恒容热相 等,不同途径的恒压热相等,而不再与途 径有关。。
1.2热力学第一定律
一、热力学第一定律的表述 蒸汽机的广泛使用 如何少消耗燃料而获得更多能量? 热与机械功的关系
焦耳定律:1cal=4.184J(热功当量)
第一类永动机提出
热力学第一定律

dV =
p1 m V2 m = RT ln RT ln p2 M V1 M
等温压缩 等温压缩
等温膨胀 等温膨胀
p p1
1 ( p1 , V1 , T )
p p1
2
1 ( p1 , V1 , T )
p2
( p2 ,V2 ,T )
A
V1
p2
( p2 ,V2 ,T )
A
V1
2
o
V2 V
o
V2 V
QT
p
p2
p1
2 ( p ,V , T ) 2 2 1 V
( p1 ,V , T1 )
p2
o
V
o
2 V
V
QV
E1
E2
QV
E1
E2
2.等压过程
特性 过程方程 热一律 对外作功
p = 常量
d Q p = d E + pd V
A = p(V2 − V1 )
V1 V2 = = 常量 T1 T2
p
p
( p,V1,T1) ( p,V2,T2 ) 1 2
绝热膨胀
绝热压缩
p
p1
1( p1 ,V1 , T1 )
p
p2
2( p2,V2,T2 )
p2
A
( p2,V2,T2 ) 2
( p1 ,V1 , T1 )
p1
A
1
o V1
V2 V
o V2
V1 V
E1
A
E2
E2
E1
A
2. 绝热线和等温线
p
pA
∆pT ∆pa
A C B
T =常量
Q=0
热力学第一定律

1.2 热 力 学 第 一 定 律1.2.1 热功当量热力学第一定律的数学表达式设有任一个物系做一个任意循环(如图),吸热为Q ',做功为W ,我们发现0=+'W Q J(1)由于Q '的单位为卡,功的单位为焦耳,二者 不能直接相加,Q '前必须乘以热功转换系数或称热功当量J (焦耳/卡)。
Joule (焦耳)和 Mayer (迈耶尔)自1840年起,历经20多年,用各种实验求证热和功的转换关系,得到的结果是一致的。
即: 1 cal = 4.1840 J这就是著名的热功当量,为能量守恒原理提供了科学的实验证明。
1.2.2 能量守恒定律自然界的一切物质都具有能量,能量有各种不同形式,能够从一种形式转化为另一种形式,但在转化过程中,能量的总值不变。
到1850年,科学界公认能量守恒定律是自然界的普遍规律之一。
1.2.3 热力学能(Internal energy)系统总能量通常有三部分组成: 1)系统整体运动的动能 2)系统在外力场中的位能 3)热力学能,也称为内能 1.2.3.1 定义热力学能是指系统内部能量的总和,包括分子运动的平动能、分子内的转动能、振动能、电子能、核能以及各种粒子之间的相互作用位能等。
p V热力学中一般只考虑静止的系统,无整体运动,不考虑外力场的作用,所以只注意热力学能1.2.3.2 热力学能的特点1) 内能是体系内部能量的总和 U ,单位J ,kJ ,包括:• 对于组成一定的均匀体系,只要体系的量确定, U 由体系的两个性质确定。
2)3)4) 5) 6) 热力学能是状态函数。
∆U=U 2-U 1,, 微小变化d U 。
1.2.4 热力学第一定律的数学表达式W Q dU δδ+=或 W Q U +=∆这就是热力学第一定律的数学表达式。
对于非循环过程,状态函数的变化值只与初末态有关,与具体的历程无关:w ad =U f -U i =△Uh =A f -A i =△A △U = Q + W (宏观过程)—the First Law of thermodynamics无穷小过程)process( mal infinitesi -+=W Q dU δδ热力学第一定律是能量转化和守恒定律的特殊形式。
热力学第一定律

P2V2
ln
V2 V1
7
又 ∵ 等温过程有
V2 P1 V1 P2
有
AT
P1V1 M
ln P1 P2 RT
ln
P2V2 P1
ln
P1 P2
M mol
P2
(3)强调QT=AT
即在等温过程中,系统的热交换不能直接计算,但可用等 温过程中的功值AT来间接计算。
8
※三种过程中气体做的功
等体过程
(1)特征:dT=0, ∴dE=0 热一律为 QT=AT
在等温过程中,理想气体所吸收 的热量全部转化为对外界做功,系 统内能保持不变。
(2)等温过程的功
PI
P1
P2
o
V1
II
V2 V
∵T=C(常数),
P RT 1
V
dAT PdV
AT
V2 RTdV RT ln V2
V V1
V1
P1V1
ln
V2 V1
T1)
M M mol R(T2 T1)
5
C p
C V
R i2R 2
──此即迈耶公式
(3)比热容比:
定义
Cp
Cv
i 2
RR iR
i2 i
2
对理想气体刚性分子有:
单原子分子:
双原子分子:
5 3 7 5
1.67 1.4
*: 经典理论的缺陷
多原子分子:
8 6
1.33
6
3、等温过程
1
符号规定
Q
吸热为正, 放热为负.
系统对外做功为正, A 外界对系统做功为负.
各物理量的单位统一用国际单位制。
第二章 热力学第一定律

第二章热力学第一定律基本公式功: δW = -P外dV热力学第一定律: dU =δQ + δW ΔU = Q + W焓的定义: H ≡ U + PV热容的定义: C=limΔT→0δQ/ ΔT等压热容的定义: C P =δQ P /dT =(∂H/∂T)P等容热容的定义: C V =δQ V /dT =(∂U/∂T)V任意体系的等压热容与等容热容之差: C P - C V = [P + (∂U/∂V)T] (∂V/∂T)P 理想气体的等压热容与等容热容之差: C P - C V = nR理想气体绝热可逆过程方程: γ = C P / C VPVγ-1 =常数T Vγ-1 =常数P1-γTγ=常数理想气体绝热功: W =C V(T1 – T2 ) W = P1V1 – P2V2 /γ-1热机效率: η = W/Q2可逆热机效率: η = T2 – T1 / T2冷冻系数: β= Q1′/W可逆制冷机冷冻系数: β = T1 / T2 – T1焦汤系数: μ = ( ∂T/ ∂P)H = - (∂H/∂P)/C P反应进度: ξ= n B – n B0 / νB化学反应的等压热效应与等容热效应的关系: Q P = Q V + ΔnRT当反应进度ξ= 1 mol 时Δr H m= Δr U m +ΣBνB RT化学反应等压热效应的几种计算方法:Δr H m⊖=ΣBνBΔf H m⊖(B)Δr H m⊖=ΣB (єB )反应物 - ΣB(єB )产物Δr H m⊖= -ΣBνBΔC H m⊖(B)反应热与温度的关系: Δr H m(T2) =Δr H m(T1) + ∫21T TΔr C P dT表 1-1 一些基本过程的W 、Q、△U 、△H 的运算过程W Q △U △H 理想气体自由膨胀0 0 0 0 理想气体等温可逆 -nRTLnV2/V1 -nRTLnV2/V10 0任意物质等容可逆理想气体0∫C V dT∫C V dTQ v∫C V dT△U + V△P∫C P dT任意物质等压可逆理想气体-P外△V-P外△V∫C P dT∫C p dTQ P - P△V∫C V dTQ P∫C P dT理想气体绝热过程C V(T2 – T1)1/γ-1(P2V2-P1V1) 0 ∫C V dT ∫C P dT理想气体多方可逆过程PVδ=常数n R/1-δ(T2-T1) △U + W ∫C V dT ∫C P dT 可逆相变(等温等压) -P外△V Q P Q P -W Q P化学反应(等温等压) -P外△VQ PQ P – WΔr H m=Δr U m+ΣBνB RTQ PΔr H m⊖=ΣBνBΔf H m⊖(B) 例题例1 0.02Kg 乙醇在其沸点时蒸发为气体。
热力学第一定律

解: A = P (V2 − V1 ) = ν R(T2 − T1 ), i+2 Q = ν C p (T2 − T1 ) = ν ( ) R(T2 − T1 ) 2 A 2 A 2 单原子分子i=3 , 单原子分子 = = Q i+2 Q 5 A 2 = 双原子分子i=5 双原子分子i=5 Q 7 [例 2] P.55.5.一定量的理想气体在等压过程中对 例 一定量的理想气体在等压过程中对 外作功40J,内能增加 外作功 ,内能增加100J,则该气体是 B ) ,则该气体是:( (A)单原子气体 (B)双原子气体 (C)多原子气体 单原子气体 双原子气体 多原子气体 解: A = P (V2 − V1 ) = ν R(T2 − T1 ) i ∆E = ν CV (T2 − T1 ) = ν R(T2 − T1 ) 2
ν=
M
i 理想气体的内能 E = ν RT 2
µ
是气体物质的量i , . 是气体物质的量 是气体分子的自由度
从热力学观点来看,改变系统的状态(内能) 从热力学观点来看,改变系统的状态(内能)有 两个途径: )向系统传递热量; )对系统做功。 两个途径:1)向系统传递热量;2)对系统做功。 1)当外界向系统传递热量时,系统的内能就 )当外界向系统传递热量时, 增加,从而使系统的温度升高; 增加,从而使系统的温度升高;当系统向外界放 出热量时,系统的内能就减少,温度降低。 出热量时,系统的内能就减少,温度降低。 2)当外界对系统做功时,系统的内能就增加, 2)当外界对系统做功时,系统的内能就增加, 温度升高;当系统对外界做功时, 温度升高;当系统对外界做功时,系统的内能就 减少,系统的温度降低。 减少,系统的温度降低。 功和热量的相同点和不同点 (1)不同点 ) 做功是通过物体在力的作用下产生宏观位移来
热力学第一定律

22
2.2.3 热力学第一定律的文字表述
第一类永动机:一种既不靠外界提供能量,本 身也不减少能量,却可以不断对外作功的机器称为 第一类永动机,它显然与能量守恒定律矛盾。 历史上曾一度热衷于制造这种机器,均以失败 告终,也就证明了能量守恒定律的正确性。
23
2.2.4 热力学第一定律的数学表达式
2.2.4 热力学第一定律的数学表达式
为:
自然界中一切物质均有能量,能量有各种不 同形式,能够从一种形式转化为另一种形式,但
在转化过程中能量的总值保持不变。
21
2.2.3 热力学第一定律的文字表述
2.2.3
热力学第一定律的文字表述
热力学第一定律是能量守恒与转化定律在热
现象领域内所具有的特殊形式,说明热力学能、
热和功之间可以相互转化,但总的能量不变。 也可以表述为:第一类永动机是不可能制成 的。第一定律是人类经验的总结。
活塞与汽缸无摩擦,当气体作 P 准静态压缩或膨胀时,外界的压强 Pe必等于此时气体的压强P ,否则 系统在有限压差作用下,将失去平衡,是一个非静 态过程。若有摩擦力存在,虽然也可使过程进行得 无限缓慢,成为准静态过程,但它不是可逆过程。
10
2.1.2 功
只考虑无摩擦准静态过程(可 逆过程)的功。
P
, 而
5
2.1.1 热
例:1mol,0℃,l00kPa的氢气可以用两种方式膨 胀到0℃、50kPa的状态,一种方式是在膨胀过程中,外
压始终维持在50kPa;另一种方式是使外压突然消失
为零(称为自由膨胀或向真空膨胀)。 实验证明,尽管两种膨胀方式的初末态相同,但
由于途径不同所传递的热量也不同,前者系统要从
由热力学第一定律: dU Q W
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.热力学第一定律热力学第一定律的主要内容,就是能量守恒原理。
能量可以在一物体与其他物体之间传递,可以从一种形式转化成另一种形式,但是不能无中生有,也不能自行消失。
而不同形式的能量在相互转化时永远是数量相当的。
这一原理,在现在看来似乎是顺理成章的,但他的建立却经历了许多失败和教训。
一百多年前西方工业革命,发明了蒸汽机,人们对改进蒸汽机产生了浓厚的兴趣。
总想造成不供能量或者少供能量而多做功的机器,曾兴起过制造“第一类永动机”的热潮。
所谓第一类永动机就是不需供给热量,不需消耗燃料而能不断循环做工的机器。
设计方案之多,但是成千上万份的设计中,没有一个能实现的。
人们从这类经验中逐渐认识到,能量是不能无中生有的,自生自灭的。
第一类永动机是不可能制成的,这就是能量守恒原理。
到了1840年,由焦耳和迈尔作了大量试验,测量了热和功转换过程中,消耗多少功会得到多少热,证明了热和机械功的转换具有严格的不变的当量关系。
想得到1J的机械功,一定要消耗0.239卡热,得到1卡热,一定要消耗4.184J的功,这就是著名的热功当量。
1cal = 4.1840J热功当量的测定试验,给能量守恒原理提供了科学依据,使这一原理得到了更为普遍的承认,牢牢的确立起来。
至今,无论是微观世界中物质的运动,还是宏观世界中的物质变化都无一例外的符合能量守恒原理。
把这一原理运用到宏观的热力学体系,就形成了热力学第一定律。
2.热力学第二定律能量守恒和转化定律就是热力学第一定律,或者说热力学第一定律是能量守恒和转化定律在热力学上的表现。
它指明热是物质运动的一种形式,物质系统从外界吸收的热量等于这个能的增加量和它对外所作的功的总和。
也就是说想制造一种不消耗任何能量就能永远作功的机器,即“第一种永动机”,是不可能的。
人们继续研究热机效率问题,试图从单一热源吸取能量去制作会永远作功的机器,这种机器并不违背能量守恒定律,只需将热源降温而利用其能量推动机器不断运转。
这种机器就是“第二类永动机”。
然而这种机器屡遭失败,不能成功,这就需要从理论上进一步探索。
前面说过,卡诺已经接近发现了热力学第一定律和热力学第二定律,但他受热质说的影响,不能把它们表述出来。
1850年,德国物理学家克劳胥斯在研究卡诺理论的基础上,提出“一个自行动作的机器,不可能把热从低温物体传到高温物体中去”。
这就是热力学第二定律的“克劳胥斯表述”。
1851年,英国物理学家威廉·汤姆生,即凯尔文勋爵也独立地从卡诺的工作中发现了热力学第二定律。
汤姆生,1824年生于英国贝尔发斯特城。
父亲是皇家学院的数学教授,治学勤奋,对子女要求也很严格,1832年被聘到母校格拉斯哥大学任教,全家也迁往该城。
当这位新来的教授开始上第一堂课时,同学们发现教室多了两个漂亮的小男孩,也在津津有味地听着,他们就是8岁的汤姆生和他10岁的哥哥。
汤姆生10岁时,和哥哥正式进格拉斯哥大学预科学习,这可能是当时最小的大学生。
汤姆生天资聪明,学习勤奋,表现出杰出的才能。
15岁,他获得学校的物理学奖,第二年获天文学奖。
17岁时,他在剑桥大学的数学杂志上发表了一篇论文,名震全校。
此后几年中,汤姆生发表了一连串的研究论文,内容包括数学、热力学和电学。
1846年,年仅22岁的汤姆生击败30多位教师候选人,获得了格拉斯哥大学的教授职位。
1847年6月,焦耳在牛津大学举行的学术会议上,阐明机械能可以定量地转化为热能,各种形式的能都可以相互转化。
汤姆生出席了这次会议,他也是传统的热质说的拥护者,认为能量不可能转化,准备反驳焦耳的观点。
当焦耳用实验证明自己的观点后,汤姆生逐渐明白焦耳学说里包含的真理。
汤姆生改变初衷,不但不反驳,而且在会后和焦耳亲切地交谈起来,大有相见恨晚之意。
克劳塞在汤姆生传记中写道:“说来也怪有趣的,就是汤姆生在年青时就碰到了两个大名鼎鼎的实验家:法拉第和焦耳,可是后来却只同其中之一的焦耳,成了最投机的同志。
”当时,汤姆生正在电磁理论边缘徘徊,和焦耳的一席交谈,使他把注意力转向了热力学研究,从而在物理学的另一个领域大放光彩。
1848年,汤姆生创立了绝对温标。
这种温标以—273℃作为0°,用于热力学计算,故称热力学温标。
现在公认的绝对0°是—273.15℃。
因为威廉·汤姆生在1892年被封为凯尔文勋爵,所以他创立的温标被称为开氏温标,简称K(因为凯尔文又译为开耳芬)。
1815年,汤姆生提出了一条新的普通原理:不可从单一热源吸取热量,使之完全变成有用的功而不产生其他影响。
这就是热力学第二定律的凯尔文表述。
凯尔文表述揭示了热运动的自然过程是不可逆的,制造第二种永动机也是不可能的。
1852年,汤姆生和焦耳合作,发现了著名的汤姆生——焦耳效应:气体从高气压的空间经过多孔性物质流向低气压空间时,温度要降低,但氢气除外。
这个效应被广泛地用于获得低温的技术上。
1853年,汤姆生对能量守恒和转化定律做了完整的表述。
汤姆生还把热力学第一定律和热力学第二定律具体应用到热学、电学和弹性现象等方面,对热力学的发展起了很大作用。
热力学第二定律后来被归纳为三种表述形式:1.热量总是从高温物体自动传到低温物体,不能作相反传递而不带来其他变化。
2.功可以全部转化为热,但任何热机不能全部地、连续不断地把所受的热量转变为功,人们无法制造第二种永动机。
3.在孤立系统中,实际发生的过程总是使整个系统的熵值增加,所以热力学第二定律又称“熵增加原理”。
3.热力学第三定律是否存在降低温度的极限?1702年,法国物理学家阿蒙顿已经提到了“绝对零度”的概念。
他从空气受热时体积和压强都随温度的增加而增加设想在某个温度下空气的压力将等于零。
根据他的计算,这个温度即后来提出的摄氏温标约为-239°C,后来,兰伯特更精确地重复了阿蒙顿实验,计算出这个温度为-270.3°C。
他说,在这个“绝对的冷”的情况下,空气将紧密地挤在一起。
他们的这个看法没有得到人们的重视。
直到盖-吕萨克定律提出之后,存在绝对零度的思想才得到物理学界的普遍承认。
1848年,英国物理学家汤姆逊在确立热力温标时,重新提出了绝对零度是温度的下限的。
1906年,德国物理学家能斯特在研究低温条件下物质的变化时,把热力学的原理应用到低温现象和化学反应过程中,发现了一个新的规律,这个规律被表述为:“当绝对温度赵于零时,凝聚系(固体和液体)的熵(即热量被温度除的商)在等温过程中的改变趋于零。
”德国著名物理学家普朗克把这一定律改述为:“当绝对温度趋于零时,固体和液体的熵也趋于零。
”这就消除了熵常数取值的任意性。
1912年,能斯特又这一规律表为绝对零度不可能达到原理:“不可能使一个物体冷却到绝对温度的零度。
”这就是热力学第三定律。
在统计物理学上,热力学第三定律反映了微观运动的量子化。
在实际意义上,第三定律并不像第一、二定律那样明白地告诫人们放弃制造第一种永动机和第二种永动机的个图。
而是鼓励人们想方高法尽可能接近绝对零度。
目前使用绝热去磁的方法已达到10 6K,但永远达不到0K。
永动机和热力学基本定律在19世纪早期,不少人沉迷于一种神秘机械——第一类永动机的制造,因为这种设想中的机械只需要一个初始的力量就可使其运转起来,之后不再需要任何动力和燃料,却能自动不断地做功。
在热力学第一定律提出之前,人们一直围绕着制造永动机的可能性问题展开激烈的讨论。
直至热力学第一定律发现后,第一类永动机的神话才不攻自破。
热力学第一定律是能量守恒和转化定律在热力学上的具体表现,它指明:热是物质运动的一种形式。
这说明外界传给物质系统的能量(热量),等于系统内能的增加和系统对外所作功的总和。
它否认了能量的无中生有,所以不需要动力和燃料就能做功的第一类永动机就成了天方夜谭式的设想。
热力学第一定律的产生是这样的:在18世纪末19世纪初,随着蒸汽机在生产中的广泛应用,人们越来越关注热和功的转化问题。
于是,热力学应运而生。
1798年,汤普生通过实验否定了热质的存在。
德国医生、物理学家迈尔在1841?843年间提出了热与机械运动之间相互转化的观点,这是热力学第一定律的第一次提出。
焦耳设计了实验测定了电热当量和热功当量,用实验确定了热力学第一定律,补充了迈尔的论证。
在热力学第一定律之后,人们开始考虑热能转化为功的效率问题。
这时,又有人设计这样一种机械——它可以从一个热源无限地取热从而做功。
这被称为第二类永动机。
1824年,法国陆军工程师卡诺设想了一个既不向外做工又没有摩擦的理想热机。
通过对热和功在这个热机内两个温度不同的热源之间的简单循环(即卡诺循环)的研究,得出结论:热机必须在两个热源之间工作,热机的效率只取决与热源的温差,热机效率即使在理想状态下也不可能的达到100%。
即热量不能完全转化为功。
1850年,克劳修斯在卡诺的基础上统一了能量守恒和转化定律与卡诺原理,指出:一个自动运作的机器,不可能把热从低温物体移到高温物体而不发生任何变化,这就是热力学第二定律。
不久,开尔文又提出:不可能从单一热源取热,使之完全变为有用功而不产生其他影响;或不可能用无生命的机器把物质的任何部分冷至比周围最低温度还低,从而获得机械功。
这就是热力学第二定律的“开尔文表述”。
奥斯特瓦尔德则表述为:第二类永动机不可能制造成功。
在提出第二定律的同时,克劳修斯还提出了熵的概念S=Q/T,并将热力学第二定律表述为:在孤立系统中,实际发生的过程总是使整个系统的熵增加。
但在这之后,克劳修斯错误地把孤立体系中的熵增定律扩展到了整个宇宙中,认为在整个宇宙中热量不断地从高温转向低温,直至一个时刻不再有温差,宇宙总熵值达到极大。
这时将不再会有任何力量能够使热量发生转移,此即“热寂论”。
为了批驳“热寂论”,麦克斯韦设想了一个无影无形的精灵(麦克斯韦妖),它处在一个盒子中的一道闸门边,它允许速度快的微粒通过闸门到达盒子的一边,而允许速度慢的微粒通过闸门到达盒子的另一边。
这样,一段时间后,盒子两边产生温差。
麦克斯韦妖其实就是耗散结构的一个雏形。
1877年,玻尔兹曼发现了宏观的熵与体系的热力学几率的关系S=KlnQ,其中 K为玻尔兹曼常数。
1906年,能斯特提出当温度趋近于绝对零度T→0时,△S / O = 0 ,即“能斯特热原理”。
普朗克在能斯特研究的基础上,利用统计理论指出,各种物质的完美晶体,在绝对零度时,熵为零(S 0 = 0 ),这就是热力学第三定律。
热力学三定律统称为热力学基本定律,从此,热力学的基础基本得以完备。
永动机是什么在一永久磁铁的上面有一电磁线圈,那么电磁线圈用定量的功所产生的势能与永久磁铁的磁力大小成正比。
永动机是指违反热力学基本定律的不能实现的发动机。
不消耗能量而能永远对外做功的机器,它违反了热力学第一定律,故称为“第一类永动机”。
