第十一章 无序分类资料的统计分析Stata实现
使用Stata进行统计数据分析教程

使用Stata进行统计数据分析教程章节一:Stata简介与安装Stata是一款广泛使用的统计软件,由StataCorp开发,并提供了强大的数据分析和数据管理功能。
首先,我们需要了解Stata的基本特点和优势,并学习如何安装Stata软件及其组件包。
为了顺利进行数据分析,安装正确的版本和组件是必不可少的。
章节二:数据导入与数据管理在开始数据分析之前,我们首先需要将数据导入Stata软件中,这涉及到数据的格式转换和读取,包括常见的Excel、CSV等格式。
然后,我们会学习如何对数据进行清洗,删除无效数据、处理缺失数据和异常值等。
此外,我们还会介绍如何创建和修改变量、合并数据集以及数据筛选等高级数据管理功能。
章节三:描述性统计分析描述性统计是最基本的统计方法之一,用于描述数据的分布和性质。
在这一章节中,我们会学习如何使用Stata进行描述性统计分析,包括计算平均数、中位数、标准差、最大值和最小值等统计指标。
同时,我们还会学习如何绘制直方图、箱线图和散点图等图形工具,以更直观地展示数据的分布特征。
章节四:推断统计分析推断统计分析用于从样本数据中推断总体的性质,常用的方法包括假设检验和置信区间估计。
在这一章节中,我们会学习如何使用Stata进行常见的假设检验,如单样本t检验、独立样本t检验和相关样本t检验等。
同时,我们还会介绍如何计算置信区间和进行方差分析等高级统计方法。
章节五:回归分析回归分析是统计学中常用的建模和预测方法,用于描述自变量与因变量之间的关系。
在这一章节中,我们会学习如何使用Stata 进行简单线性回归和多元线性回归分析,包括模型拟合、参数估计和模型诊断。
此外,我们还会介绍如何解决共线性和异方差等常见问题,并讨论如何进行交互效应和非线性回归分析。
章节六:多元统计分析除了回归分析,Stata还提供了丰富的多元统计分析方法,如主成分分析、因子分析和聚类分析等。
在这一章节中,我们会学习如何使用Stata进行多元统计分析,包括降维与因子提取、聚类分析和判别分析等。
使用Stata进行统计分析的方法与实例

使用Stata进行统计分析的方法与实例第一章:导言统计分析是一种基于数据的科学方法,主要用于搜集、整理、分析和解释数据,以便更好地理解和描述现象、随机事件或人类行为。
Stata是一款功能强大且广泛应用于统计学和经济学领域的统计分析软件。
本文将介绍使用Stata进行统计分析的方法和实例,并按以下章节进行详细说明。
第二章:数据导入与清洗在使用Stata进行统计分析之前,首先需要导入和清洗数据。
Stata支持多种数据导入格式,如文本文件、Excel表格和数据库等。
通过使用Stata的数据管理命令,我们可以对数据进行清洗和预处理,包括删除缺失值、处理离群值和进行变量转换等。
第三章:描述性统计分析描述性统计分析是研究对象的基本特征和总体分布的方法。
在Stata中,我们可以使用各种命令来计算和展示数据的描述性统计量,如平均值、标准差、中位数和频数分布等。
此外,可以使用图表工具来可视化数据的分布和特征,如直方图、箱线图和散点图等。
第四章:推断统计分析推断统计分析是通过抽样来推断总体参数的方法。
Stata提供了一系列统计模型和命令,用于进行参数估计、假设检验和置信区间估计等推断统计分析。
常见的推断统计方法包括回归分析、方差分析和非参数检验等。
通过Stata的命令和函数,我们可以轻松地应用这些方法,从而得出关于总体的推断结论。
第五章:多元统计分析多元统计分析是研究多个变量之间关系的方法。
Stata提供了多元统计模型和命令,用于探索和解释多个变量之间的关系。
其中包括多元线性回归分析、主成分分析和因子分析等。
通过使用Stata的多元统计分析功能,我们可以深入研究变量之间的相关性和潜在结构等。
第六章:时间序列分析时间序列分析是研究时间变化规律的方法。
在Stata中,我们可以使用时间序列模型和命令,对时间序列数据进行建模和预测分析。
其中包括平稳性检验、自回归移动平均模型和差分自回归移动平均模型等。
通过利用Stata的时间序列分析功能,我们可以分析和预测各种经济和社会现象的发展趋势。
Stata统计分析命令.doc

Stata统计分析常用命令汇总一、winsorize极端值处理范围:一般在1%和99%分位做极端值处理,对于小于1%的数用1%的值赋值,对于大于99%的数用99%的值赋值。
1、Stata中的单变量极端值处理:stata 11.0,在命令窗口输入“findit winsor”后,系统弹出一个窗口,安装winsor模块安装好模块之后,就可以调用winsor命令,命令格式:winsor var1, gen(new var) p(0.01) 或者在命令窗口中输入:ssc install winsor安装winsor命令。
winsor命令不能进行批量处理。
2、批量进行winsorize极端值处理:打开链接:/judson.caskey/data.html,找到winsorizeJ,点击右键,另存为到stata中的ado/plus/目录下即可。
命令格式:winsorizeJ var1var2var3,suffix(w)即可,这样会生成三个新变量,var1w var2w var3w,而且默认的是上下1%winsorize。
如果要修改分位点,则写成如下格式:winsorizeJ var 1 var2 var3,suffix(w) cuts(5 95)。
3、Excel中的极端值处理:(略)winsor2 命令使用说明简介:winsor2 winsorize or trim (if trim option is specified) the variables in varlist at particular percentiles specified by option cuts(# #). In defult, new variables will be generated with a suffix "_w" or "_tr", which can be changed by specifying suffix() option. The replace option replaces the variables with their winsorized or trimmed ones.相比于winsor命令的改进:(1) 可以批量处理多个变量;(2) 不仅可以winsor,也可以trimming;(3) 附加了by() 选项,可以分组winsor 或trimming;(4) 增加了replace 选项,可以不必生成新变量,直接替换原变量。
无序分类资料统计分析

验只能说明效应指标定性反应类别的构成 比是否相同,而各组效应的比较宜采用秩 和检验
注意的问题
3.行列表卡方检验的适用条件
–理论频数不宜太小,一般认为不宜有1/5以上 格子的理论频数小于5或有一个格子的理论频 数小于1 –不太理想的办法
• 与邻近行或列中的实际频数合并 • 删去理论频数太小的格子所对应的行或列
一、两独立样本四格表资料卡方检验
例11-2 某研究小组为研究慢支口服液II号对慢性支气管炎治疗效果,以口服消咳喘为对 照进行了临床试验,试验组120人、对照组117人(两组受试者病程、病情等均衡),疗程 2周,两组治疗后有效的患者分别为116人、82人。问慢支口服液II号与消咳喘治疗慢性支 气管炎的疗效是否相同?
组别 正常胃粘膜 不典型增生 胃癌组织 合计 观测例数 25 25 50 100 阳性例数 7(15.250) 11(15.250) 43(30.500) 61 阴性例数 18(9.750) 14(9.750) 7(19.500) 39 阳性率(%) 28.0 44.0 86.0 61.0
注 :括号内为理论频数
组别 中西医结合组 西医组 有效 92(88.973) 85(88.027) 无效 2(5.027) 8(4.973) 合计 94 93 有效率(%) 97.87 91.40
注 :括号内为理论频数
连续性校正公式:
( A − T − 0.5) 2 T
χ2 = ∑
;
n 2 ( ad − bc − ) n 2 χ2 = (a + b)(c + d )(a + c)(b + d )
–本例即28、8、22、14保持不变的条件下,若 H0成立,计算出现各种四格表的概率
STATA软件操作(四)分类与等级资料的统计分析

tab sex
tab group sex
| sex group | 0 1| Total ------------+----------------------+---------1| 8 4| 12 2| 4 7| 11 3| 3 4| 7 ------------+----------------------+---------Total | 15 15 | 30
tab sex,sum(x)
| Summary of x sex | Mean Std. Dev. Freq. ------------+-----------------------------------0 | 4.1266667 .8224238 15 1| 4.26 .9627342 15 ------------+-----------------------------------Total | 4.1933333 .88236879 30
-- Poisson Exact -Variable | Exposure Mean Std. Err. [95% Conf. Interval] -------------+------------------------------------------------------------| 1 8 2.828427 3.454 15.76225
x group 3.9 1 4.2 1 3.7 1 4 1 4.4 1 ……
sex 0 0 0 0 0
tab group
group | Freq. Percent Cum. ------------+----------------------------------1| 12 40.00 40.00 2| 11 36.67 76.67 3| 7 23.33 100.00 ------------+----------------------------------Total | 30 100.00 sex | Freq. Percent Cum. ------------+----------------------------------0| 15 50.00 50.00 1| 15 50.00 100.00 ------------+----------------------------------Total | 30 100.00
如何使用Stata进行统计学分析

如何使用Stata进行统计学分析Stata是一种流行的统计学软件,广泛应用于各个领域的数据分析和统计学研究。
本文将介绍如何使用Stata进行统计学分析,并按照不同的主题进行划分章节。
第一章:Stata基础操作在开始使用Stata进行统计学分析之前,首先需要了解一些基础操作。
包括数据导入和导出、数据清洗、变量定义等。
Stata支持各种数据文件格式的导入,例如Excel、CSV等,通过使用`import`命令可以将数据导入到Stata中。
此外,Stata还提供了丰富的数据清洗功能,如缺失值处理、异常值处理等。
在数据准备工作完成后,可以使用`generate`命令定义变量,并使用`list`命令查看数据集的内容。
第二章:描述性统计分析描述性统计分析是了解数据的基本特征和分布情况的重要手段。
在Stata中,可以使用`summarize`命令计算变量的均值、方差、最大值、最小值等统计量。
此外,还可以使用`tabulate`命令生成频数表和列联表,用以统计分类变量的分布情况和不同变量之间的关联。
第三章:统计图形绘制统计图形是数据可视化的重要工具,有助于更直观地理解数据的特点和模式。
Stata提供了多种绘图命令,例如`histogram`命令用于绘制直方图、`scatter`命令用于绘制散点图、`boxplot`命令用于绘制箱线图等。
通过适当选择和组合这些绘图命令,可以呈现出丰富的数据图形,有助于揭示数据背后的规律。
第四章:参数估计与假设检验参数估计和假设检验是统计学分析的核心内容。
Stata提供了多种统计分析命令,如`ttest`命令用于独立样本t检验、`regress`命令用于回归分析、`anova`命令用于方差分析等。
这些命令可以根据用户提供的数据和分析需求,进行相应的估计和检验,并输出相应的统计结果和解释。
第五章:相关分析和回归分析相关分析和回归分析是统计学中常用的分析方法,用于探究变量之间的关系和预测模型的建立。
应用stata做统计分析

1)Describe 数据的简要描述d2)List 将所有数据列在result里面l3)Summarize 分析统计指标su4)correlate 统计各个变量之间的相关系数cor5)graph twoway connected math score,yaxis(1)||connected english score,yaxis(2) title(“”)横坐标表示score 左y轴表示数学右y轴表示英语6)browse chinese math if score>640只显示总分大于640的数学和语文的成绩7)edit math ability score 只显示数学基本能力和总分,可以进行编辑8)gen any=uniform() 新建一个随机变量,从0-19)list math chinese english in 60/70 列出其中60-70个观测值的数学语文和英语10)replace any=100*any 将ANY这个变量的值*100,然后取代原来的变量11)sample 10 仅剩下随即的10%,sample 30,count随机的剩下30个观测值12)gsort –math 按数学从高到低排序13)gsort name 将观测值的姓名顺序排序14)gsort –name 姓名逆序排序15)help gesort 排序的帮助16)tabulate math if score>600 在result窗口中显示总分600以上的数学得频数百分比及累计百分比17)edit math score 在编辑器窗口中只显示数学和总分18)list in 4在result窗口中只显示第4个观测值19)list in 10/20列出第10-20个观测值20)sum if score>660 只对总分大于660的观测值进行统计分析21)sun if place !=”canada”对字符串的除外统计22)sum if score>600&score<65023)list if score>620|(math>=140&english>=135)列出其中的总分大于620 或者数学大于140和英语大于135 的观测值24)help datafun寻找日期的命令25)help strfun字符串函数26)dispay 作为统计显示的计算器使用27)sum math ,display r(mean),gen mathdev=math-r(menn),sum math mathdev28)help egen生成函数的扩展29)tabulate class,gen (class) 在编辑窗口新生成16个变量,class26-41,并且以0-1 表示30)list class class10-class14 在result 中只显示10-14班的内容31)sum math if class!=28 对数学进行求统计量,然后排出28班32)replace score2=1 if score >=600&score<.主要针对缺失值的运算因为缺失值.被认为是非常大的数。
教你如何使用Stata进行统计分析和建模

教你如何使用Stata进行统计分析和建模Stata是一款广泛使用的统计软件,它在数据处理、统计分析和建模等方面具有强大的功能。
本文将介绍如何使用Stata进行统计分析和建模,包括数据导入、数据整理和清洗、描述性统计分析、假设检验、回归分析等内容。
一、数据导入在使用Stata进行统计分析和建模之前,首先需要将数据导入Stata软件中。
Stata支持多种数据格式,包括Excel、CSV、SPSS等格式。
通过点击菜单栏中的"File"选项,选择"Import Data"命令,可以将数据导入Stata软件中。
二、数据整理和清洗当数据导入Stata之后,需要对数据进行整理和清洗,以便进行后续的统计分析和建模。
数据整理包括选择所需变量、变量重命名、变量标签设置等操作。
数据清洗则包括缺失值处理、异常值处理等。
三、描述性统计分析描述性统计分析是对数据进行概括的过程,可以使用Stata的各种命令来完成。
常用的描述性统计分析包括计算均值、中位数、标准差、最小值、最大值以及绘制直方图、散点图等。
四、假设检验在进行统计分析和建模时,常常需要进行假设检验,以验证研究假设的合理性。
Stata提供了多种假设检验的方法,如t检验、方差分析、卡方检验等。
通过运用这些方法,可以对不同群体之间的差异进行检验。
五、回归分析回归分析是一种通过建立数学模型来研究因变量与自变量之间关系的统计方法。
在Stata软件中,可以使用regress命令进行普通最小二乘回归分析。
此外,Stata还支持逐步回归、多元回归分析等其他回归分析方法。
六、模型诊断与验证在进行回归分析时,需要对模型进行诊断和验证,以确保模型的有效性和可靠性。
Stata提供了多个命令,如estat命令用于检验模型的方差齐性和正态性假设,predict命令用于保存残差和拟合值,以供进一步的分析和验证。
七、模型应用和预测通过回归分析建立的模型,可以应用于实际问题的预测和决策。
STATA软件操作(四)分类与等级资料的统计分析

STATA软件操作(四)分类与等级资料的统计分析STATA软件操作(四)分类与等级资料的统计分析在统计学中,数据可分为分类数据和等级数据。
分类数据是指事物被划分为不同的类别或类型,每个类别之间没有顺序或大小的关系。
而等级数据则是指事物按照某种特定的顺序或大小排列。
STATA是一款功能强大的统计分析软件,它提供了丰富的工具和函数,可以进行分类数据和等级数据的统计分析。
本文将介绍如何使用STATA软件进行分类与等级资料的统计分析。
一、分类数据的统计分析分类数据的统计分析主要包括频数和比例统计、列联表分析和卡方检验等。
下面以一个简单的示例说明如何用STATA软件进行分类数据的分析。
假设我们有一份调查问卷数据,其中包含了100个受访者的性别(男、女)和喜好的水果(苹果、香蕉、橙子)信息。
我们想要了解男女受访者喜好的水果分布是否存在差异。
首先,我们需要将数据导入STATA软件。
在STATA命令窗口中输入以下命令:```use "文件路径/文件名.dta"```接着,我们可以使用`tab`命令来计算频数和比例。
输入以下命令:```tab sex fruit```这样,STATA会输出一个包含性别和水果的频数表和比例表。
通过观察这些表,我们可以得到男女受访者对不同水果的喜好情况。
如果我们还想了解性别和喜好水果的关系是否显著,可以进行列联表分析和卡方检验。
输入以下命令:```tab sex fruit, chi2```STATA会输出一个包含列联表和卡方检验结果的表格。
通过观察卡方检验的p值,我们可以判断性别和喜好水果之间是否存在显著差异。
二、等级数据的统计分析等级数据的统计分析主要包括描述统计分析和推断统计分析。
下面以一个实例介绍如何使用STATA软件进行等级数据的分析。
假设我们有一份学生数学考试成绩数据,其中包含了100个学生的分数信息。
我们想要了解这些学生成绩的分布情况。
首先,我们需要将数据导入STATA软件。
使用Stata进行统计分析和数据可视化的教程

使用Stata进行统计分析和数据可视化的教程Stata是一种常用的统计分析软件,广泛应用于社会科学、经济学和健康科学等领域的数据分析和可视化。
本文将为大家提供一个使用Stata进行统计分析和数据可视化的教程,包括数据导入、数据处理、统计分析和数据可视化等内容。
首先,我们需要了解Stata软件的基本操作。
一、Stata软件的基本操作1. 安装与启动:将Stata软件下载并安装在电脑上,然后双击桌面上的图标启动程序。
2. 导入数据:在Stata中,可以通过多种方式导入数据,如Excel表格、文本文件和数据库等。
使用命令“import excel”导入Excel表格数据,命令“import delimited”导入文本文件数据。
导入数据后,可以使用“describe”命令查看数据的结构和变量的属性。
3. 数据浏览与修改:使用“browse”命令可以打开数据集的浏览窗口,查看数据的内容。
要对数据进行修改,可以使用“generate”或“replace”命令创建或修改变量的值。
4. 数据子集选择:使用“keep”和“drop”命令选择需要分析的变量或观测。
5. 数据排序:使用“sort”命令可以按照指定的变量对数据进行排序。
二、数据处理与统计分析1. 描述统计分析:使用“summarize”命令计算变量的均值、方差、最大值、最小值等统计指标。
可以使用“tabulate”命令生成频数表和交叉表。
使用“histogram”命令生成直方图,“scatter”命令生成散点图。
2. t检验与方差分析:使用“ttest”命令进行两样本t检验,使用“oneway”命令进行方差分析。
3. 回归分析:使用“regress”命令进行线性回归分析。
可以使用“predict”命令创建预测值,并使用“estat”命令计算回归结果的统计量。
4. 面板数据分析:对于面板数据,使用“xtset”命令设置面板数据的结构,然后使用面板数据专用的命令进行分析,如“xtreg”进行面板数据的固定效应模型分析。
上机实习 复习

2 数据输入,保存在Data editor中直接输入由word,excel复制粘贴至data editor注意:数字型变量中不允许输入文本内容3 基本命令◆输入数据Input x1 x2 y◆查看数据List◆排序Sort x1Sort x1 y◆堆砌列数据Stack x1 x2 , into(x)◆生成新变量Gen xx=1Gen xx=1 if x<10if语句Replace xx=2 if x>=10改写数据统计描述的Stata实现为制作频数表,键入Stata命令:所有数据频数表概率分布累积函数标准正态分布累积函数norm(X) :X服从N(0,1),计算概率P(X<1.96) df norm (x<1.96) X服从N(0,1),计算概率P(X>1.96) 1-上面的X服从N(μ,σ2),则~(0,1)XY Nμσ-=,因此对其他正态分布只要在函数括号中插入一个上述表达式就可以得到相应概率。
1.t分布右侧累积函数ttail(df,X) ,其中df是自由度(小于的用1-)例如:设t服从自由度为10的t分布,计算概率P(t<-2),操作如下. di 1-ttail(10,-2).03669402 概率P(t<-2)=0.036694022.χ2分布累积函数chi2(df,X) ,其中df是自由度3.χ2分布右侧累积函数chi2tail(df,X) ,其中df是自由度4.F分布累积函数F(df1,df2,X),df1为分子自由度,df2为分母自由度5.F分布右侧累积函数Ftail(df1,df2,X),df1为分子自由度,df2为分母自由度(F小于的用1-)产生随机数clear 清除内存set seed 100 设置种子数为100set obs 20 设置样本量为20gen r=uniform()产生20个在(0,1)区间上均匀分布的随机数。
list 显示这些随机数某实验要把20只大鼠随机分为2组,每组10只,请制定随机分组方案和措施。
Stata的统计分析功能介绍
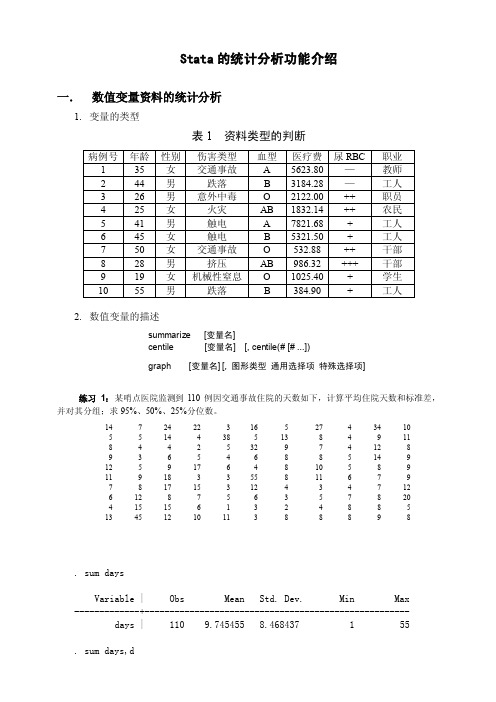
Stata的统计分析功能介绍一.数值变量资料的统计分析1.变量的类型表1 资料类型的判断2.数值变量的描述summarize [变量名]centile [变量名] [, centile(# [# ...])graph [变量名] [, 图形类型通用选择项特殊选择项]练习1:某哨点医院监测到110例因交通事故住院的天数如下,计算平均住院天数和标准差,并对其分组;求95%、50%、25%分位数。
14 7 24 22 3 16 5 27 4 34 105 5 14 4 38 5 13 8 4 9 118 4 4 2 5 32 9 7 4 12 89 3 6 5 4 6 8 8 5 14 912 5 9 17 6 4 8 10 5 8 911 9 18 3 3 55 8 11 6 7 97 8 17 15 3 12 4 3 4 7 126 12 87 5 6 3 5 78 204 15 156 1 3 2 4 8 8 513 45 12 10 11 3 8 8 8 9 8. sum daysVariable | Obs Mean Std. Dev. Min Max-------------+-----------------------------------------------------days | 110 9.745455 8.468437 1 55. sum days,ddays-------------------------------------------------------------Percentiles Smallest1% 2 15% 3 210% 3 2 Obs 11025% 5 3 Sum of Wgt. 11050% 8 Mean 9.745455Largest Std. Dev. 8.46843775% 11 3490% 17 38 Variance 71.7144395% 27 45 Skewness 2.87051799% 45 55 Kurtosis 12.96038gra days,bin(11) ylab(0,0.1,0.2,0.3,0.4,0.5) xlab(0,5,10,15,20,25,30,35,40,45,50,55). gen g=int((days-0)/5)+1. tab gg | Freq. Percent Cum.------------+-----------------------------------1 | 24 21.82 21.822 | 52 47.27 69.093 | 18 16.36 85.454 | 7 6.36 91.825 | 3 2.73 94.556 | 1 0.91 95.457 | 2 1.82 97.278 | 1 0.91 98.1810 | 1 0.91 99.0912 | 1 0.91 100.00------------+-----------------------------------Total | 110 100.00. centile days,centile(2.5,50,97.5)-- Binom. Interp. --Variable | Obs Percentile Centile [95% Conf. Interval]-------------+-------------------------------------------------------------days | 110 2.5 2 1 3*| 50 8 7 8| 97.5 39.575 24.32943 55*Lower (upper) confidence limit held at minimum (maximum) of sample3.t检验用于三种情况:样本均数与总体均数比较;配对数值变量资料的比较;两样本均数的比较;命令格式(ttest命令容许使用[if 表达式]和[in 范围]条件限制):(1)样本均数与总体均数比较的t检验的命令是ttest:ttest 变量名= #valttesti #obs #mean #sd #val练习2:某区10例犬伤患者的治疗费用如下,另一区的平均费用为680元,问两区是否在费用上有区别?病例号: 1 2 3 4 5 6 7 8 9 10 治疗费用(元)730 650 580 550 680 620 600 510 630 590. ttest a=680One-sample t test------------------------------------------------------------------------------Variable | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]---------+--------------------------------------------------------------------a | 10 614 20.06656 63.45602 568.6063 659.3937 ------------------------------------------------------------------------------ Degrees of freedom: 9Ho: mean(a) = 680Ha: mean < 680 Ha: mean ~= 680 Ha: mean > 680t = -3.2891 t = -3.2891 t = -3.2891P < t = 0.0047 P > |t| = 0.0094 P > t = 0.9953. ttesti 10 614 63.456 680结果同上(2)配对样本t检验的命令是ttest:ttest 变量1=变量2练习3:某类别伤害两个医院治疗时间(天)配对研究病例号: 1 2 3 4 5 6 7 8 9 10 甲医院(x0): 7.3 6.8 7.0 6.9 7.1 7.2 6.7 6.5 6.9 7.1 乙医院(x1): 7.1 7.0 6.2 6.0 6.1 7.4 6.5 7.0 6.0 6.9. ttest x0=x1Paired t test------------------------------------------------------------------------------ Variable | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval] ---------+-------------------------------------------------------------------- x0 | 10 6.95 .0763763 .2415229 6.777225 7.122775 x1 | 10 6.62 .1645195 .5202564 6.247831 6.992169 ---------+-------------------------------------------------------------------- diff | 10 .33 .1706524 .5396501 -.0560424 .7160425 ------------------------------------------------------------------------------ Ho: mean(x0 - x1) = mean(diff) = 0Ha: mean(diff) < 0 Ha: mean(diff) ~= 0 Ha: mean(diff) > 0t = 1.9338 t = 1.9338 t = 1.9338P < t = 0.9574 P > |t| = 0.0852 P > t = 0.0426(3)两样本均数比较的t检验ttest 变量1=变量2, unpairedttest 变量, by(分组变量)ttesti #obs1 #mean1 #sd1 #obs2 #mean2 #sd2练习4:两个区对犬伤治疗费用的比较?730 650 580 550 680 620 600 510 630 590 730 650 580 550 甲区:乙区:710 600 740 650 670 660 590 670 770 690 580. ttest v1=v2,unpTwo-sample t test with equal variances------------------------------------------------------------------------------Variable | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]---------+--------------------------------------------------------------------v1 | 14 617.8571 17.54675 65.65394 579.9497 655.7646v2 | 11 666.3636 18.2544 60.543 625.6903 707.037---------+-------------------------------------------------------------------- combined | 25 639.2 13.36563 66.82814 611.6147 666.7853---------+--------------------------------------------------------------------diff | -48.50649 25.57778 -101.4182 4.405167------------------------------------------------------------------------------Degrees of freedom: 23Ho: mean(v1) - mean(v2) = diff = 0Ha: diff < 0 Ha: diff ~= 0 Ha: diff > 0t = -1.8964 t = -1.8964 t = -1.8964P < t = 0.0353 P > |t| = 0.0705 P > t = 0.9647二.分类变量资料的χ2检验tabulate var1 var2 [fw=频数变量] [,选择项]tabi其中var1,var2分别表示行变量和列变量,[fw=频数变量]只在变量以频数形式存放时选用。
统计描述的Stata实现

为制作频数表,键入 Stata 命令:
.gen f=int((x-160)/2)*2+160 .tab f 产生用以作频数表的新变量“f” 对变量“f”作频数表
“gen”命令产生新变量“f”,将各观察值转换成相应该组的下限值。 int 为取整函数,结果为括号内函数值的整数部分,如 int(3.24)=3。“160”为第 一 组 的 下 限 , “ 2 ” 为 组 距 。 以 第 一 例 观 察 值 160.1cm 为 例 , f=int((160.1-160)/2)*2+160=160,则它应归入“160~”组。 结果如下:
49 28 14 12 10 8 5 3 230
21.30 12.17 6.09 5.22 4.35 3.48 2.17 1.30
100.00
150 178 192 204 214 222 227 230 —
65.2 77.4 83.5 88.7 93.0 96.5 98.7 100.0 —
Stata 数据格式如下: x 1 2 3 4 5 6 7 8 9 10
数据格式如下:
x 1 2 3 4 5 6 7 8
164.4 175.5 171.7 171.8 172.2 176.4 164.3 169.9
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51
结果如下:
.1 Density .02 0
160
.04
.06
.08
165
170 f
175
如何使用Stata进行统计分析和数据管理

如何使用Stata进行统计分析和数据管理第一章:Stata软件介绍Stata是一款功能强大的统计分析和数据管理软件,被广泛应用于学术研究、商业分析和政府决策等领域。
它提供了丰富的统计分析工具和数据操作功能,可以帮助用户进行各种数据处理、可视化和模型建立等工作。
第二章:数据导入和管理在使用Stata进行统计分析之前,首先需要将数据导入到软件中进行管理。
Stata支持多种数据格式的导入,比如Excel、CSV、SPSS等。
用户可以使用import命令将外部数据导入到Stata的数据集中,并可以使用rename、label等命令对数据集进行重命名和备注,提高数据管理的效率和准确性。
第三章:数据清洗和变量转换在进行统计分析之前,常常需要对原始数据进行清洗和变量转换。
Stata提供了丰富的数据清洗命令,如drop、replace、gen等,可以帮助用户处理缺失值、异常值和重复观测等问题。
同时,Stata还支持对变量进行变换,如计算新变量、重编码变量和生成虚拟变量等,以满足不同的分析需求。
第四章:描述性统计分析描述性统计是了解数据特征和总体情况的基本手段,Stata提供了多种描述性统计命令,如mean、median、sum、tab等。
这些命令可以计算数据的均值、中位数、总和、频数等统计量,并可以按照变量和组别进行分析,帮助用户发现数据的分布、集中趋势和离散程度等信息。
第五章:推断性统计分析推断性统计分析是基于样本数据对总体进行推断的方法,Stata 提供了丰富的推断性统计命令,如ttest、regress、anova等。
这些命令可以进行单样本和双样本假设检验、回归分析、方差分析等统计计算,从而帮助用户验证研究假设、探究变量之间的关系和差异。
第六章:多元统计分析多元统计分析是研究多个变量之间的关系和模式的方法,Stata 提供了多种多元统计分析命令,如因子分析、聚类分析和多元回归等。
用户可以使用这些命令对数据进行降维、分类、预测和解释,挖掘变量之间的潜在结构和相互作用关系,为研究提供更深入的认识和解释。
第十一章无序分类资料的统计分析的Stata实现
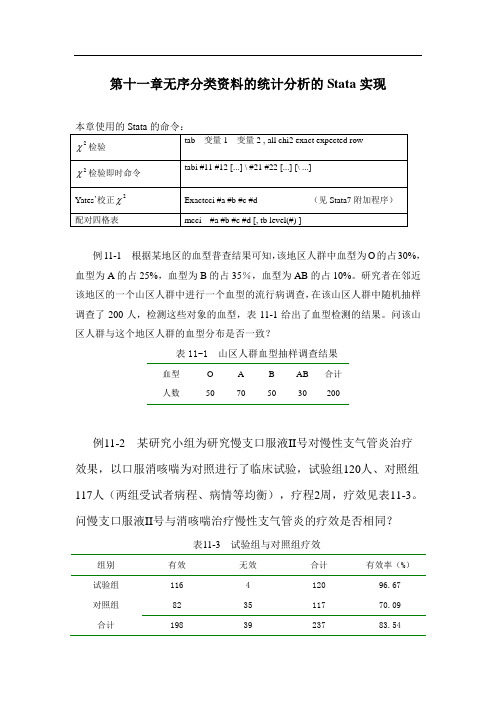
第十一章无序分类资料的统计分析的Stata实现例11-1 根据某地区的血型普查结果可知,该地区人群中血型为O的占30%,血型为A的占25%,血型为B的占35%,血型为AB的占10%。
研究者在邻近该地区的一个山区人群中进行一个血型的流行病调查,在该山区人群中随机抽样调查了200人,检测这些对象的血型,表11-1给出了血型检测的结果。
问该山区人群与这个地区人群的血型分布是否一致?表11-1 山区人群血型抽样调查结果血型O A B AB 合计人数50 70 50 30 200例11-2 某研究小组为研究慢支口服液II号对慢性支气管炎治疗效果,以口服消咳喘为对照进行了临床试验,试验组120人、对照组117人(两组受试者病程、病情等均衡),疗程2周,疗效见表11-3。
问慢支口服液II号与消咳喘治疗慢性支气管炎的疗效是否相同?表11-3 试验组与对照组疗效组别有效无效合计有效率(%)试验组116 4 120 96.67对照组82 35 117 70.09合计198 39 237 83.541.建立检验假设,确定检验水准0H :21ππ=,即两种药物治疗慢性支气管炎的疗效相同1H :21ππ≠,即两种药物治疗慢性支气管炎的疗效不同05.0=αStata 命令:结果:Pearson chi2(1) = 30.4463 Pr = 0.000,05.0<P ,按α=0.05水准拒绝0H ,差别有统计学意义,可认为慢支口服液II 号治疗慢性支气管炎有效率高于消咳喘。
例11-3 为评价中西结合治疗抑郁发作的疗效。
将187例患者随机分为2组,两组患者均选用阿咪替林西医综合治疗,中西医结合组在上述治疗的同时,再配合中医辨证治疗,根据中医辨证分型采用不同的方剂,治疗结果见表11-5,问两种治疗方案的疗效有无差别?表11-5 试验组与对照组疗效组别 有效 无效 合计 有效率(%)中西医结合组 92(88.973) 2(5.027) 94 97.87 西医组85(88.027)8(4.973)9391.40注 ;括号内为理论频数 例11-3 假设检验步骤1.建立检验假设,确定检验水准0H :21ππ=,即两种治疗方案疗效相同1H :21ππ≠,即两种治疗方案疗效不同05.0=αStata 命令:结果:本例需要用校正卡方,p=0.1005,两种治疗方案疗效的差异无统计学意义。
第八讲有序分类资料的统计分析Stata实现

第⼋讲有序分类资料的统计分析Stata实现第⼗⼆章有序分类资料的统计分析的 Stata 实现本章使⽤的 STATA 命令:列变量有序时的分类资料 CMH 卡⽅分析双向有序时的 Spearman 相关 opartchi ⾏变量 [weight], by(列变量) (见 Stata7 附加程序) spearman 变量 1 变量 2例 12-2某研究欲观察⼈参的镇静作⽤,选取 32 只同批次的⼩⽩⿏,将其中 20 只随机分配到⼈参组:以 5%⼈参浸液对其做腹腔注射,12 只分配到对照组:以等量蒸馏⽔对其做同样注射。
实验结果如表 12-2 所⽰。
能否说明⼈参有镇静作⽤?表 12-2镇静等级 ± + ++ +++⼈参镇静作⽤的实验结果对照组 11 0 1 0 0⼈参组 4 1 2 1 121.建⽴检验假设,确定检验⽔准。
H 0 :⼈参没有镇静作⽤(样本来⾃两个相同总体)H 1 :⼈参有镇静作⽤(样本来⾃两个不同总体)0.05Stata 数据为:a 1 1 1 1 1 2 2 2 2 2Stata 命令为:b 1 2 3 4 5 1 2 3 4 5x4 1 2 1 12 11 0 1 0 0opartchi b [weight=x],by(a) 结果为: Chi-square tests df Chi-square P-value Independence 4 16.64 0.0023 ------------------------------------------------------Components of independence test Location 1 15.29 0.0001 Dispersion 1 .3496 0.5543在 ? ? 0.05 的⽔平上,拒绝 H 0 ,接受 H1,认为两总体之间的差别有统计学意义,可以认为⼈参组和对照组镇静等级的差别有统计学意义,⼈参有镇静作⽤。
12无序分类资料的统计分析
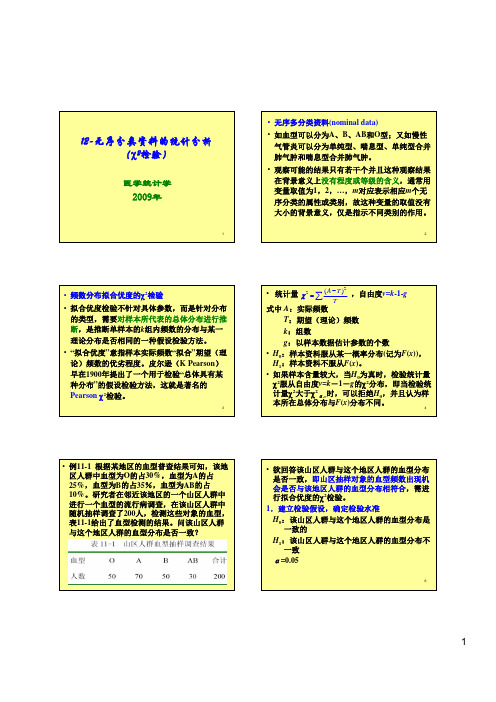
与这个地区人群的血型分布是否一致?53.计算χ统计量及自由度22()20.38A T Tχ−==∑10与消咳喘治疗慢性支气管炎的疗效是否相同?11数据,其余数据均由此派生。
13•一般地,R 行C 列的理论频数n :总频数n R :第R 行频数合计n C :第C 列频数合计•两个独立样本率的比较可用基本公式•亦可用上述基本公式的展开式n n n T CR =∑−=TT A 22)(χ)1(22−=∑CR n n A n χ14•四格表专用公式•在此,式(11-1)、(11-3)及(11-4)等价。
•由于受到“行频数合计等于n ,且列频数合计等于n ”条件的约束,自由度为•对于两独立样本四格表资料,自由度22()()()()()ad bc na b c d a c b d χ−=++++)(列数)行数11(−×−=ν11212(=−×−=)()ν151.建立检验假设,确定检验水准H 0:π1=π2,即两种药物治疗慢性支气管炎的疗效相同H 1:π1≠π2,即两种药物治疗慢性支气管炎的疗效不同α=0.05162.求检验统计量χ2值和自由度v•首先,计算a 、b 、c 、d 对应的理论频数。
•当然,在计算T 11基础上,其余三个理论数也可以按以下方式计算。
253.100237/19812011=×=T 747.19237/3912012=×=T 747.97237/19811721=×=T 253.19237/3911722=×=T 747.19253.10012012=−=T 747.97253.10019821=−=T 253.19747.9711722=−=T 17然后,计算检验统计量χ2值和自由度v•四个表专用公式:45.30 253.19)253.1935(747.97)747.9782(747.19)747.194(253.100)253.100116( )(222222=−+−+−+−=−=∑TT A χ1ν=×(2-1)(2-1)=222()()()()()(11635482)23730.44631(1164)(8235)(11682)(435)ad bc na b c d a c b d −=++++×−××==+×+×+×+χ183.确定P 值,下结论•查附表8,χ20.05,1=3.84,χ2=30.45>χ20.05,1,P<0.05,按α=0.05水准拒绝H 0,差别有统计学意义,可认为慢支口服液II 号治疗慢性支气管炎有效率高于消咳喘。
stata分类计算

stata分类计算在Stata中,分类计算通常涉及对数据进行分组,并在每个组内执行某种计算。
Stata中有几种方法可以实现这一目标,具体取决于您的数据结构和所需的计算。
以下是一些在Stata中进行分类计算的常见方法:1. egen命令:`egen`命令用于生成新的变量,可以通过对观测值进行分类来计算统计量。
例如,可以使用`egen`计算每个组内的平均值、总和等。
```stata// 以变量group为基准计算var的平均值egen mean_var = mean(var), by(group)```2. bysort命令:`bysort`命令用于排序数据并按照某些变量进行分组。
然后,您可以在每个组内执行计算。
```stata// 先按照group排序,然后计算每个组内var的平均值bysort group: egen mean_var = mean(var)```3. collapse命令:`collapse`命令可用于对数据进行汇总,并在汇总期间执行计算。
这通常与`by`子句结合使用。
```stata// 按照group分组,计算每个组内var的平均值collapse (mean) var, by(group)```4. tabstat命令:`tabstat`命令用于计算汇总统计量,包括平均值、总和等。
您可以使用`by`子句对数据进行分组。
```stata// 按照group分组,计算每个组内var的平均值和标准差tabstat var, by(group) stat(mean sd)```5. egen group()函数:`egen`命令的`group()`函数允许您创建一个新的变量,其中包含每个唯一组的标识符。
```stata// 为每个唯一的group创建一个标识符egen group_id = group(group)```这只是一些Stata中进行分类计算的方法的简要介绍。
具体的方法取决于您的数据和所需的计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十一章无序分类资料的统计分析的Stata实现
例11-1 根据某地区的血型普查结果可知,该地区人群中血型为O的占30%,血型为A的占25%,血型为B的占35%,血型为AB的占10%。
研究者在邻近该地区的一个山区人群中进行一个血型的流行病调查,在该山区人群中随机抽样调查了200人,检测这些对象的血型,表11-1给出了血型检测的结果。
问该山区人群与这个地区人群的血型分布是否一致?
表11-1 山区人群血型抽样调查结果
血型O A B AB 合计
人数50 70 50 30 200
例11-2 某研究小组为研究慢支口服液II号对慢性支气管炎治疗效果,以口服消咳喘为对照进行了临床试验,试验组120人、对照组117人(两组受试者病程、病情等均衡),疗程2周,疗效见表11-3。
问慢支口服液II号与消咳喘治疗慢性支气管炎的疗效是否相同?
表11-3 试验组与对照组疗效
组别有效无效合计有效率(%)试验组116 4 120 96.67
对照组82 35 117 70.09
合计198 39 237 83.54
1.建立检验假设,确定检验水准
0H :21ππ=,即两种药物治疗慢性支气管炎的疗效相同
1H :21ππ≠,即两种药物治疗慢性支气管炎的疗效不同
05.0=α
结果:
Pearson chi2(1) = 30.4463 Pr = 0.000,05.0<P ,按α=0.05水准拒
绝0H ,差别有统计学意义,可认为慢支口服液II 号治疗慢性支气管炎有效率高于消咳喘。
例11-3 为评价中西结合治疗抑郁发作的疗效。
将187例患者随机分为2组,两组患者均选用阿咪替林西医综合治疗,中西医结合组在上述治疗的同时,再配合中医辨证治疗,根据中医辨证分型采用不同的方剂,治疗结果见表11-5,问两种治疗方案的疗效有无差别?
表11-5 试验组与对照组疗效
组别 有效 无效 合计 有效率(%)
中西医结合组 92(88.973) 2(5.027) 94 97.87 西医组
85(88.027)
8(4.973)
93
91.40
注 ;括号内为理论频数 例11-3 假设检验步骤
1.建立检验假设,确定检验水准
0H :21ππ=,即两种治疗方案疗效相同
1H :21ππ≠,即两种治疗方案疗效不同
05.0=α
Stata 命令:
结果:
本例需要用校正卡方,p=0.1005,两种治疗方案疗效的差异无统计学意义。
例11-4 为了解国产紫外线瞬间消毒器与进口高压蒸汽消毒机对牙科手机消毒灭菌的效果,将刚去腐揭卡过垢等待处理的牙科手机29个随机分为A 、B 两组,A 组为紫外线消毒组,B 组为高压蒸汽组。
消毒前细菌培养均为阳性,消毒后细菌培养结果见下表。
问两种消毒法消毒后细菌培养阳性率有无差别?
表11-6 两种方法消毒后细菌培养结果
组别 阳性 阴性 合计 A 10 5 15 B 1 13 14 合计 11
18
29
由于总频数29小于40,对两组阳性率的比较宜采用Fisher 精确概率检验,假设检验步骤如下:
1.建立检验假设,确定检验水准
0H :21ππ=,即两种方法消毒后细菌培养阳性率相同
1H :21ππ≠,即两种方法消毒后细菌培养阳性率不同
05.0=α
本例需要用Fisher's 确切概率法,p=0.002,两种方法消毒后细菌培养阳性率不同。
例11-5 为探讨埃兹蛋白(Ezrin )在胃癌组织中的表达情况,采用免疫组化法检测50
例胃癌组织、25例胃粘膜不典型增生和25例正常胃粘膜中Ezrin 的表达,结果见表11-9。
问不同胃组织Ezrin 表达阳性率是否相同?
表11-9 Ezrin 在不同胃组织中的表达
组别 观测例数 阳性例数 阴性例数 阳性率(%)
正常胃粘膜 25 7(15.250) 18(9.750) 28.0 不典型增生 25 11(15.250) 14(9.750) 44.0 胃癌组织 50 43(30.500)
7(19.500)
86.0 合计
100
61
39
61.0
注 :括号内为理论频数
这是一个3个样本率的比较问题,假设检验步骤为: 1.建立检验假设,确定检验水准
0H :321πππ==,即3种不同胃组织Ezrin 表达阳性率相等
1H :1π、2π、3π不全相等,即3种不同胃组织Ezrin 表达阳性率不全相等
05.0=α
结果:
05.0<P ,按α=0.05水准拒绝0H ,差别有统计学意义,可认为3种不同胃组织Ezrin 表
达阳性率不全相等。
例11-6 为评价国产注射用头孢美唑钠(A )治疗中、重度呼吸系统细菌性感染性疾病的临床有效性及安全性,以先锋美他醇(B )为对照进行临床试验,入组受试者疾病类型构成情况见表11-10。
问A 、B 两组受试者疾病类型总体构成有无差别?
表11-10 两组受试者疾病类型
组别 急性扁桃体炎 肺炎
急支炎
慢支炎急发
支扩伴感染 A 5(6.042) 21(19.636) 21(21.650) 20(20.643) 5(4.028) B
7(5.958)
18(19.364) 22(21.350) 21(20.357)
3(3.972)
注 :括号内为理论频数
这是一个2组构成比比较的问题,其假设检验步骤为: 1.建立检验假设,确定检验水准
0H :A 、B 受试者疾病类型总体构成相同
1H :A 、B 受试者疾病类型总体构成不同
05.0=α
例11-7 将100份样品一分为二,分别用含血培养基与无血培养基接种培养,观察弯曲菌检出情况,结果如表11-12所示。
试问:两种培养基接种培养弯曲菌的阳性率是否相等?两种培养基培养结果间是否有关联性?
将表11-12整理为表11-13形式
表11-13 两种培养基弯曲菌检出结果
无血培养基
含血培养基
合计+ -
+ 52 17 69
- 8 23 31
合计60 40 100 0
H:两种培养基接种培养弯曲菌的阳性率相同
1
H:两种培养基接种培养弯曲菌的阳性率不同
05
.0
=
α
利用Stata的即时命令
结果为:
H,尚不能认为两种培养基接种培养弯曲菌的阳性率不05
.0
P,按α=0.05水准不拒绝
>
相同。
H:两种培养基培养结果之间无关联性
H:两种培养基培养结果之间有关联性
1
α
=
.0
05
Stata命令为:
结果为:
H,可认为两种培养基接种培养弯曲菌结果之间存在关联P,按α=0.05水准拒绝
05
<
.0
性。
