运筹学期中考试试卷(含答案)
运筹学期中试卷
期中试卷某市是一个人口不到15万人的小城市，根据该市的蔬菜种植情况分别在A 、B 和C 设三个批发市场。
清晨5点前菜农将蔬菜送至各批发市场，再由各批发市场分送到全市的8个菜市场。
该市道路情况、各路段距离（单位：100m ）及各批发市场、菜市场的具体位置如图：74 75 8 3 7 664 85 7 54 117 75 66 3 56 6 10 810 511按常年情况，A 、B 、C 三个批发市场每天供应量分别为200、170和160（单位：100kg ），各菜市场的每天需求量及发生供应短缺时带来的损失（元/100kg ）见下表。
设从批发市场至各菜市场蔬菜调运费用为1元/（100kg*100m ）。
12 634587 BA C菜市场每天需求（100kg）短缺损失（元/100kg）1 75 102 60 83 80 54 70 105 100 106 55 87 90 58 80 8（1）求A、B、C三个批发市场分别到8个市场的最短路径是多少？（2）为该市设计一个从各批发市场至各菜市场的定点供应方案，使用于蔬菜调运的运费和预期的短缺损失之和的总成本最小。
（3）若规定各菜市场短缺量一律不超过需求量的20%，重新设计定点供应方案。
要求：1、运用运筹学所学习的知识对上述实际问题进行分析和求解。
要求建立相应的数学模型，并用软件进行求解，最终形成一份课程论文（用WORD进行排版并打印），电子版的课程论文于5月15日之前通过网络平台提交，每组只要组长提交就行。
2、以小组的形式完成，一个小组最多3人，小组自由组合，并民主推选一个组长。
3、成绩构成：（1）课程论文（占70%）：任课教师根据课程论文排版的美观性、分析的逻辑性、结果的正确进行评分。
（2）完成任务表现（占30%）：组长根据组员在任务完成过程中的团队合作精神、对任务完成的贡献进行评分；任课教师根据组长的任务完成过程中的协调能力、团队的整体表现进行评分。
4、不要抄袭，如发现，当作1份答卷，共享最终成绩，每组只能得平均分，如发现2份答卷是相互抄袭的，成绩为80分，那2份答卷最终成绩分别为40分。
运筹学 期中测试题(答案)
答案：一、解：化为标准型123max 20z x x x -+-=s.t. 1234123512363621220,1,2,,6i x x x x x x x x x x x x x i +++=⎧⎪-++=⎪⎨+-+=⎪⎪≥=⎩单纯形表如下：故最优解为(1.5,0.5,0)x =，最优值为 2.5z =.二、解：设其对偶问题的变量为12,y y ，则其对偶线性规划为12min 43y y ω=+s.t. 12121212121222;3;2352;33;,0y y y y y y y y y y y y +≤-≤+≤⎧⎨+≤+≤≥⎩因**124/50,3/50y y =>=>，由互补松弛性条件知原问题的两个约束条件应取等式,即1234512345234233x x x x x x x x x x ++++=⎧⎨-+++=⎩；将**124/5,3/5y y ==代入约束条件得,**124322255y y +=+⨯=, 2**143355y y -=-<,12**431723235555y y +=⨯+⨯=<,12**43255y y +=+<, 12**4333355y y +=⨯+=. 第二至四个约束条件为严格不等式,由互补松弛性条件,必有234***0,0,0x x x ===．从而1515****3423x x x x ⎧+=⎪⎨+=⎪⎩.故15**1,1x x ==.因此,原问题的最优解为()*1,0,0,0,1Tx =.最优值为*5z =.三、解：用最小元素法确定初始调运方案用沃格尔法确定初始调运方案五、解：六、解：用逆序法.全过程分四个阶段，从最后一个阶段开始. （1）4k =.第四阶段.有两种状态12,D D .41()1f D =，42()5f D =；**4142()()u D u D ==E. （2）3k =.第三阶段.有三种状态123,,C C C .3131141()(,)()415f C d C D f D =+=+=，即由1C E -的最短路径为11C D E --,最短距离为5,相应决策为*311()u C D =.同理,有 321413232242(,)()31()min min 4(,)()25d C D f D f C d C D f D +⎧⎫+⎧⎫===⎨⎬⎨⎬++⎩⎭⎩⎭即由2C E -的最短路径为21C D E --,最短距离为4,相应决策为*321()u C D = 3333242()(,)()156f C d C D f D =+=+=即由3C E -的最短路径为32C D E --,最短距离为6,相应决策为*332()u C D = （3）2k =，第二阶段.有两种初始状态12,B B .同理,有211312121232(,)()75()min min 10(,)()64d B C f C f B d B C f C +⎧⎫+⎧⎫===⎨⎬⎨⎬++⎩⎭⎩⎭222322222333(,)()24()min min 6(,)()46d B C f C f B d B C f C +⎧⎫+⎧⎫===⎨⎬⎨⎬++⎩⎭⎩⎭即由1B E -的最短路径为1B -21C D E --,最短距离为10,相应决策为*212()u B C =由2B E -的最短路径为221B C D E ---,最短距离为6,相应决策为*222()u B C =（4）1k =，第一阶段.只有一种状态A112111222(,)()110()min min 9(,)()36d A B f B f A d A B f B +⎧⎫+⎧⎫===⎨⎬⎨⎬++⎩⎭⎩⎭，相应决策为*12()u A B =即从A E -全过程的最短路径为221A B C D E ----,最短距离为9。
运筹学期中考试试卷
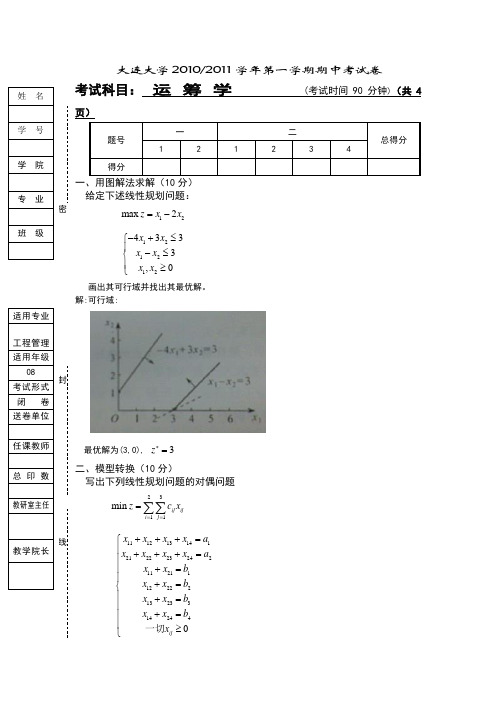
大连大学2010/2011学年第一学期期中考试卷考试科目： 运 筹 学 (考试时间90分钟)（共4页）题号 一二总得分 1 2 1 2 3 4 得分给定下述线性规划问题：12max 2z x x =-1212124333,0x x x x x x -+≤⎧⎪-≤⎨⎪≥⎩ 画出其可行域并找出其最优解。
解:可行域:最优解为(3,0), 3z *=二、模型转换（10分）写出下列线性规划问题的对偶问题 2311min ij ij i j z c x ===∑∑111213141212223242112111222213233142440ij x x x x a x x x x ax x b x x b x x b x x b x +++=⎧⎪+++=⎪⎪+=⎪+=⎨⎪+=⎪+=⎪⎪≥⎩一切姓 名 学 号 学 院 专 业 班 级密封线适用专业 工程管理 适用年级08 考试形式 闭卷送卷单位任课教师总印数教研室主任教学院长解：112211223344max w a u a u b v b v b v b v =+++++111112121313142121222223232412123400,,,,,u v c u v c u v c u v u v c u v c u v c u v u u v v v v +≤⎧⎪+≤⎪⎪+≤⎪+≤⎪⎪+≤⎨⎪+≤⎪+≤⎪⎪+≤⎪⎪⎩无符号限制三、计算题（每小题20分，共80分）1. 用单纯形法求解下列线性规划问题(列出计算过程)。
12min 35z x x =--12121282123436,0x x x x x x -≥-⎧⎪≤⎪⎨+≤⎪⎪≤⎩ 解：标准化：123451324125123453500082123436,,,,0MaxW x x x x x x x x x x x x x x x x x ''=--+++'-+=⎧⎪'-+=⎪⎨''--+=⎪⎪''≥⎩(标准化可分两段，第一步把决策变量变量，第二步标准化)最优解2. 用单纯形法中两阶段法求解下述线性规划问题(列出计算过程)。
《管理运筹学》期中复习题答案
《管理运筹学》期中复习题答案标准化文件发布号：（9312-EUATWW-MWUB-WUNN-INNUL-DQQTY-《管理运筹学》期中测试题 第一部分 线性规划 一、填空题 1．线性规划问题是求一个 目标函数 在一组 约束条件 下的最值问题。
2．图解法适用于含有 两个 _ 变量的线性规划问题。
3．线性规划问题的可行解是指满足 所有约束条件_ 的解。
4．在线性规划问题的基本解中，所有的非基变量等于 零 。
5．在线性规划问题中，基本可行解的非零分量所对应的列向量线性 无 关 6．若线性规划问题有最优解，则最优解一定可以在可行域的 顶点_ 达到。
7．若线性规划问题有可行解，则 一定 _ 有基本可行解。
8．如果线性规划问题存在目标函数为有限值的最优解，求解时只需在其 可行解 的集合中进行搜索即可得到最优解。
9．满足 非负 _ 条件的基本解称为基本可行解。
10．在将线性规划问题的一般形式转化为标准形式时，引入的松驰变量在目标函数中的系数为 正 。
11．将线性规划模型化成标准形式时，“≤”的约束条件要在不等式左_端加入 松弛 _ 变量。
12．线性规划模型包括 决策变量 、目标函数 、约束条件 三个要素。
13．线性规划问题可分为目标函数求 最大 _ 值和 最小 _值两类。
14．线性规划问题的标准形式中，约束条件取 等 _ 式，目标函数求 最大 _值，而所有决策变量必须 非负 。
15．线性规划问题的基本可行解与基本解的关系是 基本可行解一定是基本解，反之不然16．在用图解法求解线性规划问题时，如果取得最值的等值线与可行域的一段边界重合，则 _ 最优解不唯一 。
17．求解线性规划问题可能的结果有 唯一最优解，无穷多最优解，无界解，无可行解 。
18.如果某个约束条件是“ ”情形，若化为标准形式，需要引入一个 剩余 _ 变量。
19.如果某个变量X j 为自由变量，则应引进两个非负变量X j ′ , X j 〞, 同时令X j ＝ X j ′ - X j 〞 j 。
运筹学试卷A及参考答案
运筹学试卷A及参考答案北京理工大学《运筹学》期终试卷(A卷)姓名成绩注意：① 答案一律写在答题纸上，写在其他地方无效。
② 考试过程中，不得拆开试卷。
③ 考试完毕后，试卷一律交回。
一、多项选择题(每小题2分，共12分)1、线性规划模型有特点（）。
A、所有函数都是线性函数；B、目标求最大；C、有等式或不等式约束；D、变量非负。
2、下面命题正确的是（）。
A、线性规划的最优解是基本可行解；B、基本可行解一定是基本解；C、线性规划一定有可行解；D、线性规划的最优值至多有一个。
3、一个线性规划问题（P）与它的对偶问题（D）有关系（）。
A、（P）有可行解则（D）有最优解；B、（P）、（D）均有可行解则都有最优解；C、（P）可行（D）无解，则（P）无有限最优解；D、（P）（D）互为对偶。
4、运输问题的基本可行解有特点（）。
A、有m＋n－1个基变量；B、有m+n个位势；C、产销平衡；D、不含闭回路。
5、关于动态规划问题的下列命题中（）是错误的。
A、动态规划分阶段顺序不同，则结果不同；B、状态对决策有影响；C、在求解最短路径问题时，标号法与逆序法求解的思路是相同的；D、动态规划的求解过程都可以用列表形式实现。
6、顾客泊松到达与相继到达的间隔时间服从负指数分布（）。
A、是相同概念的不同说法；B、是完全不相同的概念；C、它们的均值互为倒数；D、它们的均值是相同的。
二、回答下列各题（每小题8分，共16分）1、考虑线性规划问题Min f(x) = -x1 + 5 x2S.t. 2x1–3x2 ≥3 （P）5x1 ＋ 2x2＝4x1 ≥ 0写出（P）的标准形式；2、某企业生产3种产品甲、乙、丙，产品所需的主要原料有A、B两种，原料A每单位分别可生产产品甲、乙、丙底座12、18、16个；产品甲、乙、丙每个需要原料B分别为13kg、8kg、10kg，设备生产用时分别为10.5、12.5、8台时，每个产品的利润分别为1450元、1650元、1300元。
运筹学期中测试参考答案汇总
1线性规划问题,设为问题的最优解。
若目标函数中用代替后，问题的最优解变为，证明：证明：因为为问题的最优解，同时为问题的可行解。
所以有：（1）同理可得：（2）由不等式（1），（2）可知：2、已知线性规划：要求：（1）用单纯形法求解该线性规划问题的最优解和最优值；（2）写出线性规划的对偶问题；（3）根据对偶问题的性质求解对偶问题的最优解和最优值；解：（1）化标准型：根据标准型列单纯形表jB 1 2 3 4 53 14 25 1Z34 31 1Z 9 33 2/5 1/5 /52 /5 /5 3/51 8/5 /5 /5 Z 12 1所以，此线性规划有无穷多最优解最优解之一（18/5，3/5，32/5，0，0）最优值 Zmax=12（2）线性规划的对偶问题为：（3）由原问题的最优单纯形表可知：对偶问题的最优解为：（0，1，0）最优值为：Wmin=123 下表给出了各产地和各销地的产量和销量，以及各产地至各销地的单位运价，试用表上作业法求最优解：销地产地B1B2B3B4产量A122213A 218546A376686销量4344解：利用Vogel法求解第一个运输方案：32221311 0825446131 7362686004344 54333214利用对偶变量法求解检验数：21212113-54 1038546-17663860 43447665所有非基变量的检验数全部大于零，所以此运输方案是最优的运输方案。
最优值为：3*2+1*7+3*6+2*6+2*5+4*4=694 某钻井队要从以下10个可供选择的井位中确定5个钻井探油，使总的钻井费用最小。
若10个井位的代号为，相应的钻井费用为，并且井位选择上要满足下列限制条件：①选择和就不能选择钻探；反过来也一样；②选择了或就不能选，反过来也一样；③在中最多只能选两个；试建立这个问题的整数规划模型。
（不求解）解：设用xi表示第i个井位是否钻井探油，即由题意可知数学模型如下：5 友谊农场有3万亩（每亩等于666.66平方米）农田，欲种植玉米、大豆和小麦三种农作物。
数学：运筹学试题及答案
数学：运筹学试题及答案1、判断题求最小值问题的目标函数值是各分支函数值的下界。
正确答案：对2、填空题动态规划大体上可以分为（）、（）、（）、（）四大类。
正确答案：离散确定型；离散随机型；连续确定型；连续随机（江南博哥）型3、多选系统模型按照抽象模型形式可以分为（）A.数学模型B.图象模型C.模糊性模型D.逻辑模型E.仿真模型正确答案：A, B, D, E4、单选线性规划一般模型中，自由变量可以代换为两个非负变量的（）A.和B.差C.积D.商正确答案：B5、填空题运筹学的目的在于针所研究的系统求得一个合理应用人才，物力和财力的最佳方案。
发挥和提高系统的（），最终达到系统的（）。
正确答案：效能及效益；最优目标6、填空题采用人工变量法时，若基变量中出现了（）的人工变量，表示在原问题有解。
正确答案：非零7、填空题满足（）的基本解称为基本可行解。
正确答案：非负条件8、填空题在箭线式网络图中从始点出发，由各个关键活动连续相接，直到终点的费时最长的线路称为（）。
正确答案：关键线路9、单选在求解运输问题的过程中可运用到下列哪些方法（）。
A.西北角法B.位势法C.闭回路法D.以上都是正确答案：D10、问答题请简要回答一般系统模型的三个特征。
正确答案：①它是现实世界一部分的抽象和模仿；②它由那些与分析的问题有关的要素所构成；③它表明了系统有关要素间的逻辑关系或定量关系。
11、名词解释初始基本可行解正确答案：多个基本可行解中一个，一般情况下在求最大时取最小的基本可行解，求最小时取最大的基本可行解。
12、名词解释不确定条件下的决策正确答案：指在需要决策的问题中，只估测到可能出现的状态，但状态发生的概率，由于缺乏资源和经验而全部未知。
它属于不确定情况下的决策.13、名词解释时间优化正确答案：时间优化是在人力材料设备资金等资源基本上有保证的条件下寻求最短的工程周期14、填空题企业在采购时，供应方根据批发量的大小定出不同的优惠价格，这种价格上的优惠称为（）正确答案：数量折扣15、填空题常用的两种时差是工作总时差和工作（）正确答案：自由时差16、多选根据对偶理论，在求解线性规划的原问题时，可以得到以下结论（）A.对偶问题的解B.市场上的稀缺情况C.影子价格D.资源的购销决策E.资源的市场价格正确答案：A, C, D17、问答题运用单纯形法求解线性规划问题的步骤是什么？正确答案：（1）确定初始基可行解（2）检验初始基可行解是否最优（3）无解检验（4）进行基变换（5）进行旋转运算，之后回到步骤2，循环直到完成整个问题的求解18、单选设一个线性规划问题（P）的对偶问题为（D），则关于它们之间的关系的陈述不正确的是（）。
运筹学习题(期中考试试题)
紧前工 工序时 序 间/d
— a a b,c b,c c c d,e g h,i 3 4 5 7 7 8 4 2 3 2
7.(2004研)某厂每年使用某种配件,经 ABC分类法分析该配件属于A类物资,年需 要量为12500件,消耗均匀发生.该配件的 单价为每件50元,年存贮费用是平均存贮额 的20%,每次订货是费用为400元,每次订 货后货物即可随时送到,不允许发生缺货. (1)求每次的订货数量; (2) 该厂为减少占用资金,希望降低存贮量, 决定宁可使总费用超过最低费用的20%作为 存贮策略,试决定该配件的存贮策略.
�
4. 某公司有资金400万元,向A,B,C三个 项目追加投资,三个项目可以有不同的投 资额度,相应的效益之如下表所示,问如 何分配资金,才使总效益值最大? (用动 态规划方法进行求解)
投资额 效益值 项目 A B C 0 1 2 3 4
47 49 1 88
该配件的单价为每件50元年存贮费用是平均存贮额的20每次订货是费用为400元每次订货后货物即可随时送到不允许发生缺货货后货物即可随时送到不允许发生缺货
1. 某厂在计划期内要安排A,B两种产品的生 产,已知生产单位产品所需的设备台时及甲, 乙两种原材料的消耗,以及资源的限制和每 种产品的单位利润,如下表所示.
76 78 88
5. 某石油公司拥有一个管道网络,使用这个 网络可以把石油从采地运送到一些销售点, 这个网络的一部分如下图所示.由于管道 的直径的变化,它的各段管道的(vi, vj) 的容量cij(单位:万加仑/小时)也是不一 样的.如果使用这个网络系统从采地v1向 销地v7运送石油,问每小时能运送多少加 仑石油?(用图论方法求解)
a) 问工厂分别生产多少A产品和 B产品才能使工厂获利最多? b) 原料甲的影子价格是多少?如 果工厂可以在市场上购得该原 料,单价为60,那么该工厂是 B 资源限制 c) 否应该购进该原料? 1 300台时 d) 若工厂想保持A产品的生产, 1 400千克 则A产品的单位利润不能低于 1 250千克 多少? e) 求保持当前最优基不变时,原 100 料乙的容许变动范围.
管理运筹学期中测试答案
一、下表为求解某线性规划问题的最终单纯形表，已知该LP 问题的目标函数为极大化类型，表中为x 4、x 5为松弛变量，原问题的约束全部为“≤”形式。
C B x B b c 1 c 2 c 3 0 0 x 1 x 2 x 3 x 4 x 5 c 3 x 3 5/2 0 1/2 1 1/2 0 c 1 x 15/2 1 -1/2 0 -1/6 1/3 σn-4-4-2（１）写出原线性规划问题； （２）写出原问题的对偶问题；（３）直接由表写出对偶问题的最优解。
（1）【解一】511222(1)25511111126322632010012105(|)10100404204042A b z z ⨯⎛⎫⎛⎫ ⎪ ⎪=--−−−→-- ⎪ ⎪⎪ ⎪------⎝⎭⎝⎭ 16(2)(1)'101113333(3)(1)'4012105100080220z +⨯+⨯⎛⎫ ⎪−−−−→- ⎪ ⎪-+⎝⎭(2)'3(3)'(2)'6012105311011062100040z ⨯+⨯⎛⎫ ⎪−−−−→- ⎪ ⎪-+⎝⎭因此，原问题为：()12323123max 621025..31001,2,3jz x x x x x s t x x x x j =-+⎧+≤⎪-+≤⎨⎪≥=⎩【解二】由最优表可知12111630B -⎛⎫= ⎪-⎝⎭，则2013B ⎛⎫= ⎪⎝⎭。
由此： 51122251112632012001210510133110110⎛⎫⎛⎫⎛⎫→ ⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭。
求目标函数系数c 1、c 2、c 3，在最终单纯形表中，考虑变量x 5的检验数的计算应有：11302c -=-，得c 1=6，考虑变量x 4的检验数的计算应有：11312604c c -+=-，得c 3=10，在此基础上，考虑变量x2的检验数计算应有：11231224c c c -+=-，得c 2=-2。
《运筹学》课程考试试卷试题(含答案)
《运筹学》课程考试试卷试题(含答案)一、选择题（每题5分，共25分）1. 运筹学的核心思想是（）A. 最优化B. 系统分析C. 预测D. 决策答案：A2. 在线性规划中，约束条件可以用（）表示。
A. 等式B. 不等式C. 方程组D. 矩阵答案：B3. 以下哪个不是运筹学的基本模型？（）A. 线性规划B. 整数规划C. 非线性规划D. 随机规划答案：D4. 在目标规划中，以下哪个术语描述的是决策变量的偏离程度？（）A. 目标函数B. 约束条件C. 偏差变量D. 权重系数答案：C5. 在动态规划中，以下哪个概念描述的是在决策过程中，某一阶段的最优决策对后续阶段的影响？（）A. 最优子结构B. 无后效性C. 最优性原理D. 阶段性答案：B二、填空题（每题5分，共25分）1. 运筹学是一门研究在复杂系统中的______、______和______的科学。
答案：决策、优化、实施2. 在线性规划中，若目标函数为最大化，则其标准形式为______。
答案：max z = c^T x3. 在非线性规划中，若目标函数和约束条件均为凸函数，则该规划问题为______。
答案：凸规划4. 在目标规划中，若决策变量x_i的权重系数为w_i，则目标函数可以表示为______。
答案：min Σ(w_i d_i^+ + w_i d_i^-)5. 在动态规划中，若状态变量为s_n，决策变量为u_n，则状态转移方程可以表示为______。
答案：s_{n+1} = f(s_n, u_n)三、判断题（每题5分，共25分）1. 线性规划问题的最优解一定在可行域的顶点处取得。
（）答案：正确2. 在整数规划中，若决策变量为整数，则目标函数和约束条件也必须为整数。
（）答案：错误3. 目标规划中的偏差变量可以是负数。
（）答案：正确4. 在动态规划中，最优策略具有最优子结构。
（）答案：正确5. 在非线性规划中，若目标函数为凸函数，则约束条件也必须为凸函数。
运筹学考试试卷及答案
运筹学考试试卷及答案一、选择题（每题2分，共20分）1. 线性规划问题的标准形式是：A. 所有变量都非负B. 目标函数是最大化C. 所有约束条件都是等式D. 所有约束条件都是不等式答案：A2. 单纯形法中，如果某个变量的检验数为负数，那么：A. 该变量可以增大B. 该变量可以减小C. 该变量保持不变D. 该变量不能进入基答案：A3. 在运输问题中，如果某种资源的供应量大于需求量，那么应该：A. 增加供应量B. 减少需求量C. 增加需求量D. 减少供应量答案：C4. 动态规划的基本原理是：A. 递归B. 迭代C. 回溯D. 分解答案：D5. 决策树中，每个节点代表：A. 一个决策B. 一个状态C. 一个结果D. 一个概率答案：A6. 排队论中，M/M/1队列的特点是：A. 到达时间服从泊松分布，服务时间服从指数分布，且只有一个服务台B. 到达时间服从指数分布，服务时间服从泊松分布，且只有一个服务台C. 到达时间服从泊松分布，服务时间服从指数分布，且有两个服务台D. 到达时间服从指数分布，服务时间服从泊松分布，且有两个服务台答案：A7. 网络流问题中，最大流最小割定理说明：A. 最大流等于最小割B. 最大流小于最小割C. 最大流大于最小割D. 最大流与最小割无关答案：A8. 整数规划问题中，分支定界法的基本思想是：A. 将问题分解为多个子问题B. 将问题转化为线性规划问题C. 将问题转化为非线性规划问题D. 将问题转化为动态规划问题答案：A9. 在多目标决策中，如果目标之间存在冲突，通常采用的方法是：A. 目标排序B. 目标加权C. 目标合并D. 目标替换答案：B10. 敏感性分析的目的是：A. 确定最优解的稳定性B. 确定最优解的唯一性C. 确定最优解的可行性D. 确定最优解的最优性答案：A二、填空题（每题2分，共20分）1. 线性规划问题的可行域是由所有_________约束条件构成的集合。
答案：可行2. 在单纯形法中，如果目标函数的系数都是正数，则该问题为_________问题。
128505-管理运筹学-运筹学期中考试题14-15-2答案
1、某网络图如下（1）用标号法求出1点至各点的最短路。
（2）建立从1点到6点的数学规划模型（不用求解）求出该项工程的最低成本日程。
3、某产品每月用量为4件，装配费用为50元，存贮费每月每件为8元，求产品每次最佳生产量及最小费用。
若生产速度为每月可生产10件，求每次生产量及最小费用。
4、某商店代销一种产品，每件产品的购进价格为800元，存储费每件40元，缺货费每件试确定该商店的最佳订货数量。
结论：1点出发至各点最短路线及最短路线长为(2) 设⎩⎨⎧=的最短路不经过该弧到从的最短路经过该弧到从610611ij x1,01000015235382min 564656543525465424352313252423121312565446352524231312==+=-++=-+=-+=---=+++++++++=ij x x x x x x x x x x x x x x x x x x x x x x x x x x x x z2、由题绘制网络图如下所示：由该图可得关争路线为：1->2->4->7->8；对应的关键工序为：B->G->H 。
工程工期为15天时，直接费用为15300元，间接费用为7500元，总费用为15300+7500=22800元； 通过缩短关键路线中G 的工序1天后，总费用为：22800+300-500=22600，此时为最优方案。
3、（1）由题意，该问题属于“不允许缺货，生产时间很短”模型，已知350C =，4R=，18C=，由E.O.Q 模型计算Q 0，得07Q ==≈件，最小费用为056.6C ==≈（2）该问题属于“不允许缺货，生产需要一定时间”模型，已知350C =，4R =，18C =，10P =，则可得09Q ==≈，最小费用为043.8C ==≈。
4、本题中12800,40,1015K C C ===，故有21210158000.2038401015C K C C --==++又3040()0.2,()0.4r r P r P r ≤≤==∑∑，应订购40件。
西南交大运筹学BI期中考试答案
运筹BI 期中考试答案1.把以下线性规划问题化为标准形式：解：令)0,0(''2'22''2'2≥≥=-x x x x x ，引入松弛变量x 4≥0，剩余变量x 5≥0,得max z= x 1 +3x’2 -3x”2 +4x 3s.t. 3x 1 +2x’2 -2x”2 +x 4 ＝13x'2 -x”2 +3x 3-x 5 ＝172x 1 +x’2 -x”2 +x 3 ＝13x 1, x'2, x"2, x 3x 4,x 5 ≥02、解：可行域如下图中阴影部分所示：将可行域各顶点坐标代入目标函数可知，最优解为（x 1，x 2）=（2，8），MaxZ=2+3*8=26. 3、单纯形法求解解：引入松弛变量x3，x4和x5，得到线性规划标准形：max z= x 1 -2x 2 +x 3s.t. x 1 +x 2 +x 3 +x 4 =12 2x 1 +x 2 -x 3 +x 5 = 6 -x 1 +3x 2+x 6= 9x 1, x 2, x 3x 4x 5x 6 ≥ 0构造初始单纯形表：Max(Cj-Zj)=1≥0,未取得最优解，选择x做换入变量，根据最小比值法则θ=min{12/1}=12,3做换出变量，在（1，4）处进行基变换得：选择x4因为所有检验数Cj-Zj≤0，所以取得最优解：（x,x2,x3,x4,x5,x6）=(0,0,12,0,18,9),maxZ=12*1=12.1(注意：本题也可以在初始单纯形表中选择x1作为换入变量，得到另一组最优解（（x,x2,x3,x4,x5,x6）=(6,0,6,0,0,15),maxZ=6+6=12.)15、M法或两阶段法求解解：引入松弛变量x4,x5，人工变量x6,得到标准型：Max z= x1+3x2+4x3s.t. 3x1+2x2+x4=13x2+3x3+x5=172x1+x2+x3+x6=13x1, x2, x3x4x5x6≥01）用大M法求解，构造目标函数为：Max z= x1+3x2+4x3-Mx6初始单纯形表如下Max(Cj-Zj)=1+2M≥0,未取得最优解，选择x做换入变量，根据最小比值法则θ=min{13/3，113/2}=13/3,故选择x4做换出变量，在（1，1）处进行基变换得：Max(Cj-Zj)=4+M≥0,未取得最优解，选择x做换入变量，根据最小比值法则θ=min{17/3，313/3}=13/3,故选择x6做换出变量，在（3，3）处进行基变换得：Max(Cj-Zj)=11/3≥0,未取得最优解，选择x做换入变量，根据最小比值法则θ2=min{(13/3)/(2/3)},4/2}=2,故选择x5做换出变量，在（2，2）处进行基变换得：Cj-Zj≤0，所以取得最优解（x1,x2,x3,x4,x5,x6）=(3，2，5，0，0，0),maxZ=3*1+3*2+4*5=29. 2）用两阶段法求解，构造第一阶段目标函数为：Max z= -x6Max(Cj-Zj)=2≥0,未取得最优解，选择x做换入变量，根据最小比值法则θ=min{13/3，113/2}=13/3,故选择x4做换出变量，在（1，1）处进行基变换得：Max(Cj-Zj )=1≥0,未取得最优解，选择x 3做换入变量，根据最小比值法则θ=min{17/3，13/3}=13/3,故选择x 6做换出变量，在（3，3）处进行基变换得：所有Cj-Zj ≤0，所以取得最优解，（x1,x 2,x 3,x 4,x 5,x 6）=(13/3，0，13/3，0，4，0),人工变量X 6=0，故问题有可行解，进入第二阶段。
运筹学期中试题参考答案
运筹学期中试题参考答案（2010-2011 第一学期）试题一：单项选择题（从下列各题四个备选答案中选出一个正确答案，答案选错或未选者，该题不得分。
每小题2分，共16分）1 •线性规划具有唯一最优解，是指（ B ）。
A .最优单纯形表中存在有常数项为零B.最优单纯形表中非基变量的检验数全部不等于零C •最优单纯形表中存在非基变量的检验数为零D .可行解集有界2•设线性规划的约束条件为x1x2x3= 32 x1 2 x2x4二4x1，…，x4兰0下可行列解中，非基可行解为（ D ）。
A. （0,2,1,0）TB. （0, 0,3,4）TC . （2,0,1, 0）T D. （1, 1, 1, 0）T3. 设线性规划原问题为（P）,其对偶问题为（D）,则下列说法错误的是（D ）。
A . （P）、（D）均有可行解则都有最优解；B .若（P ）有m个变量，则（D）就有m个约束条件；C .若（P）的约束均为等式，则（D）的所有变量均无非负限制；D .若（P）的约束均为不等式，则（D）的约束也均为不等式。
4、maxZ 二CX,AX < b, X - 0 及minW 二Yb,YA_C,Y - 0 是互为对偶的两个线性规划问题，则对于其任意可行解X和Y，存在关系（ D ）。
5•有6个产地4个销地的平衡运输问题模型具有特征（ B ）。
A .有10个变量24个约束B .有24个变量10个约束C .有24个变量9约束D.有9个基变量10个非基变量6. 互为对偶的两个线性规划问题存在关系（D ）。
A .原问题无可行解，对偶问题也无可行解B .对偶问题有可行解，原问题也有可行解C .原问题有最优解，对偶问题可能没有最优解D .原问题有无界解，对偶问题无可行解7. 下列说法正确的是（D ）oA. 线性规划问题的基解对应可行域的顶点。
B、若X i, X2分别是某一线性规划问题的可行解，贝V X=収! +冰2也是该线性规划问题的可行解，其中心?2为正的实数。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
大连大学2010/2011学年第一学期期中考试卷
考试科目： 运 筹 学
(考试时间90分钟)（共4
页）
题号 一
二
总得分 1 2 1 2 3 4 得分
给定下述线性规划问题：
12max 2z x x =-
121212
4333,0x x x x x x -+≤⎧⎪
-≤⎨⎪≥⎩ 画出其可行域并找出其最优解。
解:可行域:
最优解为(3,0), 3z *
=
二、模型转换（10分）
写出下列线性规划问题的对偶问题 2
3
11min ij ij i j z c x ===∑∑
11121314121222324
2112111222213233142440ij x x x x a x x x x a x x b x x b x x b x x b x +++=⎧⎪+++=⎪⎪+=⎪+=⎨⎪+=⎪+=⎪
⎪≥⎩
一切 姓 名 学 号 学 院
专 业
班 级
密
封
线
适用专业 工程管理 适用年级
08 考试形式 闭
卷
送卷单位
任课教师
总印数
教研室主任
教学院长
解：112211223344max w a u a u b v b v b v b v =+++++
111112121313142121222223232412123400,,,,,u v c u v c u v c u v u v c u v c u v c u v u u v v v v +≤⎧
⎪+≤⎪⎪+≤⎪
+≤⎪
⎪
+≤⎨⎪+≤⎪
+≤⎪
⎪+≤⎪⎪⎩无符号限制
三、计算题（每小题20分，共80分）
1. 用单纯形法求解下列线性规划问题(列出计算过程)。
12min 35z x x =--
12
12128
2123436,0
x x x x x x -≥-⎧⎪≤⎪⎨
+≤⎪⎪≤⎩ 解：标准化：1
234513241
251
23453500082123436,,,,0MaxW x x x x x x x x x x x x x x x x x ''=--+++'-+=⎧
⎪'-+=⎪⎨
''--+=⎪⎪''≥⎩(标准化可分两段，第一步把决策变量变量，第二步标准化)
最优解
2. 用单纯形法中两阶段法求解下述线性规划问题(列出计算过程)。
(注意步骤，区分人工变量与松驰变量)
12min 4z x x =+
12123
12433436240,1,2,3,4
i x x x x x x x x x i +=⎧⎪+-=⎪⎨++=⎪⎪≥=⎩
解：1)标准化；
'12max 4z x x =--
1212312433
(1)
436(2)
240,1,2,3,4
i x x x x x x x x x i +=⎧⎪+-=⎪⎨
++=⎪⎪≥=⎩
２）在上约束方程组(1)、（2）中加入人工变量，列出第一阶段线性规划问题
将正文中的问题化成标准型：
56min w x x =+
1251236
12433436240,1,2,3,4,5,6
i x x x x x x x x x x x i ++=⎧⎪+-+=⎪⎨
++=⎪⎪≥=⎩ 3)
4)因为第一阶段目标函数值为0，做去掉人工变量，写出第二阶段目标函数为
1234max 400z x x x x =--++，继续用单纯形法求解
故有唯一最优解(,,1,0,0,0),55
5
X Z *
*
==
3. 用对偶单纯形法求解下述线性规划问题(列出计算过程)。
(此问题不是加人工变量，而是根据对偶理论，在保持对偶问题为可行解的基础上，通过迭代，使原问题也达到可行解，即得到了目标函数的最优解。
)
123min 41218z x x x =++
1323123
33225,,0x x x x x x x +≥⎧⎪
+≥⎨⎪≥⎩
解：先将问题改写为：
12345max 4121800w x x x x x =---++
134235332250,1,2,3,4,5i
x x x x x x x i +-=⎧⎪
+-=⎨⎪≥=⎩ 约束条件两端乘“-1”得：
12345max 4121800w x x x x x =---++
134235332250,1,2,3,4,5i
x x x x x x x i --+=-⎧⎪
--+=-⎨⎪≥=⎩
4. 已知某运输问题的产销数量表与单位运价表如表4-1，用表上作业法求最优解(列出计算过程)。
解：1.|
（注：括弧中的数位检验数，下同）
2.
闭回路法调整：
所有检验数都大于0，所以此时为最优解。
最终方案（最优调拨方案）为：
113
x=，
146
x=，
225
x=，
240
x=
（或
120
x=），
323
x=，
334
x=，83
z=。