化学反应工程-24-第八章-流化床反应器
流化床反应器

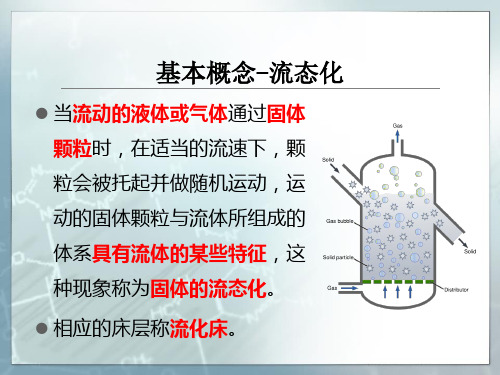
流化床反应器fluidized bed reactor(FBR) :一种利用气体或液体通过颗粒状固体层而使固体颗粒处于悬浮运动状态,并进行气固相反应过程或液固相反应过程的反应器。
在用于气固系统时,又称沸腾床反应器。
流态化过程:当流体向上流过颗粒床层时,其运动状态是变化的。
流速较低时,颗粒静止不动,流体只在颗粒之间的缝隙中通过。
当流速增加到某一速度之后,颗粒不再由分布板所支持,而全部由流体的摩擦力所承托。
此时,对于单个颗粒来讲,它不再依靠与其他邻近颗粒的接触而维持它的空间位置,相反地,在失去了以前的机械支承后,每个颗粒可在床层中自由运动;就整个床层而言,具有了许多类似流体的性质。
这种状态就被称为流态化。
颗粒床层从静止状态转变为流态化时的最低速度,称为临界流化速度。
流化床的性质:(1)在任一高度的静压近似于在此高度以上单位床截面内固体颗粒的重量;(2)无论床层如何倾斜,床表面总是保持水平,床层的形状也保持容器的形状;(3)床内固体颗粒可以像流体一样从底部或侧面的孔口中排出;(4)密度高于床层表观密度的物体在床内会下沉,密度小的物体会浮在床面上;(5)床内颗粒混合良好,因此,当加热床层时,整个床层的温度基本均匀。
一般的液固流态化,颗粒均匀地分散于床层中,称之为“散式”流态化;一般的气固流态化,气体并不均匀地流过颗粒床层,一部分气体形成气泡经床层短路逸出,颗粒则被分成群体作湍流运动,床层中的空隙率随位置和时间的不同而变化,因此这种流态化称为“聚式”流态化。
与固定床反应器相比,流化床反应器的优点是:①可以实现固体物料的连续输入和输出;②流体和颗粒的运动使床层具有良好的传热性能,床层内部温度均匀,而且易于控制,特别适用于强放热反应。
但另一方面,由于返混严重,可对反应器的效率和反应的选择性带来一定影响。
再加上气固流化床中气泡的存在使得气固接触变差,导致气体反应得不完全。
因此,通常不宜用于要求单程转化率很高的反应。
流化床反应器概述

流化床简介按照床层的外形分类可分为圆筒形和圆锥形流化床。
圆筒形流化床反应器结构简单,制造容易,设备容积利用率高。
圆锥形流化床反应器的结构比较复杂,制造比较困难,设备的利用率较低,但因其截面自下而上逐渐扩大,故也具有很多优点: 1、适用于催化剂粒度分布较宽的体系由于床层底部速度大,较大颗粒也能流化,防止了分布板上的阻塞现象,上部速度低,减少了气流对细粒的带出,提高了小颗粒催化剂的利用率,也减轻了气固分离设备的负荷。
这对于在低速下操作的工艺过程可获得较好的流化质量。
2、由于底部速度大,增强了分布板的作用床层底部的速度大,孔隙率也增加,使反应不致过分集中在底部,并且加强了底部的传热过程,故可减少底部过热和烧结现象。
3、适用于气体体积增大的反应过程气泡在床层的上升过程中,随着静压的减少,体积相应增大。
采用锥形床,选择一定的锥角,可适应这种气体体积增大的要求,使流化更趋平稳。
按照床层中是否设置有内部构件分类可分为自由床和限制床。
床层中设置内部构件的称为限制床,未设置内部构件的称为自由床。
设置内部构件的目的在于增进气固接触,减少气体返混,改善气体停留时间分布,提高床层的稳定性,从而使高床层和高流速操作成为可能。
许多流化床反应器都采用挡网、挡板等作为内部构件。
对于反应速度快、延长接触时间不至于产生严重副反应或对于产品要求不严的催化反应过程,则可采用自由床,如石油炼制工业的催化裂化反应器便是典型的一例。
按照反应器内层数的多少分类可分为单层和多层流化床。
对气固相催化反应主要采用单层流化床。
多层式流化床中,气流由下往上通过各段床层,流态化的固体颗粒则沿溢流管从上往下依次流过各层分布板,如用于石灰石焙烧的多层式流化床的结构。
按是否催化反应分类分为气固相流化床催化反应器和气固相流化床非催化反应器两种。
以一定的流动速度使固体催化剂颗粒呈悬浮湍动,并在催化剂作用下进行化学反应的设备是气固相流化床催化反应器,它是气固相催化反应常用的一种反应器。
流化床反应器ppt课件
均密度。
颗粒带出速度 u :
t 流化床中流体速度的上限,流体对粒子的曳
力与粒子的重力相等,粒子将被气流带走。
对于球形颗粒等速沉降时,可得出下式:
4 d p ( p f ) g
ut
f D
3
1
2
式中
D
过程原理
过程原理
过程原理
典型装置
壳体
气体分布装置
换热器
内部构件
催化剂的加入与卸
出装置
气固分离装置
流化床反应器的相关参数
流化过程床层压降变化
临界流化速度 u mf(起始流化速度,也称最低流化速度):颗
粒层由固定床转化为流化床时流体的表现速度。
小颗粒
大颗粒
经验公式
umf
d ( p f ) g ( R 20 )
▪ 有气-固相流化床催化反应器和气-固相流化床
非催化反应器两种
▪ 以一定的流动速度使固体催化剂颗粒呈悬浮湍
动,并在催化剂作用下进行化学反应的设备称
为气-固相流化床催化反应器(常简称为流化
床),它是气-固相催化反应常用的一种反应器
▪ 而在气-固相流化床非催化反应器中,是原料气
直接与悬浮湍动的固体原料发生化学反应。
e
1650 f
u
2
mf
2
p
d p ( p f ) g
( Re 1000 )
24.5 f
umf 0.00923
d
1.82
p
( p f )
0.88
f
0.06
流化床反应器讲解课件

umf
0.00923
d
( 1.82
p
p
0.88 f
f
0.06 f
)0.94
该式适用于临界雷诺数Remf <5的情况
当Remf>5时,所求得的umf应加以校正
20
图10-11临界流化速度的修正系数
21
2.带出速度
• 当气速略大于颗粒的自由沉降速度时,颗粒沉降不下来而被 流体带出。开始把颗粒带出的速度称为带出速度。
对于球形颗粒,当Re<0.4时,
ut
d
2 p
(
p
f
1.835 f
)
对于Ret>0.4的情况,要进行校正 .
校正的方法:先由上式求出ut的近似值
u
' t
,再求出
Re t
=
d put' t t
,由Ret查图10-12得校正系数FD.
实际带出速度为
ut
=
FD
•
u
' t
22
对于非球形颗粒,因它比同体积的球形颗粒具有更大的表面积, 故求出的ut应再乘以校正系数C 。
.
p p f Lf (1 f )( p - f )g
18
10.2.4流化速度
• 1.临界流化速度
19
对于小颗粒:
umf
d
2 p
(
p
f
)g
16501
上式适用于临界雷诺数Remf<20的情况
对于粗颗粒,当Remf >1000时
umf
[ d p ( p f )g ]1/2 24.5 f
临界流化速度还常用经验式李伐公式计算
10.1流化床反应器的特点及结构
流化床反应器简介
流在内层,气固得以分离
旋风分离器
塞阀
图1-4 塞阀的剖视图
翼阀
翼阀的作用:就是避免由于这
一压差的存在而使催化剂由料
腿倒窜。正常的情况下,翼阀 的翼板和阀座处于良好密阀的 状态。当料腿内的催化剂量蓄 积到料腿内的静压超过旋风器 的压降,以及翼阀上方床层静 压及找开翼阀所需压力这三者 之和时,翼阀及时自行打开, 料腿内的催化剂流入床层。若 料腿内的静压低于上述三者压
主要内件
• 分布器
• 换热器
• 旋风分离器 • 塞阀 • 翼阀
分布器
图1-3-1平板型分布板
图1-3-2 拱型分布板
分布器的作用
• 气体分布器是流化床反应器的一个重要的构件,
气体分布器位于流化床底部 • 支撑全部催化剂颗粒,其作用是将反应气体均 匀地送入流化床 • 保证良好的起始流化条件和稳定操作状态,其 引发流化,维持床层颗粒连续运动和均匀分布 气体的作用。
气-固流化床反应器结构
气体 料锁
旋风分离器
加料口
换热介质 ………..体分布板 预分布器
循环管 换热介质 固体粒子
气体
3
主体设备
耐火层
壳 体
保温层
钢壳
壳体 主要是保证流化过程局限在一定范围内 进行,对于存在有强烈放热或吸热过程, 保证热量不散失或少散失。
流化床反应器简介
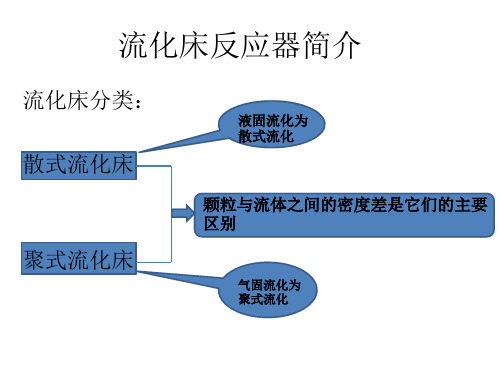
流化床分类:
液固流化为 散式流化
散式流化床
颗粒与流体之间的密度差是它们的主要 区别
聚式流化床
气固流化为 聚式流化
散式流化床
以气泡形式夹带少量颗粒穿过床 层向上运动的不连续的气泡称为 气泡相
图1-1 流化床的模型
聚式流化床
颗粒浓度与空隙率分布 较为均匀且接近初始流 态化状态的连续相,称 为乳化相。
流化床反应器

流化床反应器1. 简介流化床反应器是一种广泛应用于化工领域的反应设备,其特点是颗粒固体在气体流动的作用下呈现流化状态。
流化床反应器具有高传热、高传质、均匀的温度和浓度分布等优点,因此在催化反应、气固反应、气液反应等方面具有重要应用价值。
2. 工作原理流化床反应器由反应器本体、气体分布器、颗粒固体循环器等组成。
在反应器中,气体经过气体分布器均匀地从底部进入反应器,使颗粒固体床呈现流化状态。
底部进入的气体将颗粒固体床推动向上运动,使其呈现明显的液化状态。
在流化床反应器中,颗粒固体的运动状态可以分为床层状态、混合带和床板状态三个区域。
•床层状态:床层状态是指颗粒固体床的顶层,颗粒固体处于相对松散的状态,在底部进气的作用下,床层呈现液化状态,颗粒固体浮在气体流中。
•混合带:混合带是床层状态和床板状态之间的过渡带,颗粒固体在这个区域内的运动状态介于床层状态和床板状态之间。
•床板状态:床板状态是指颗粒固体床的底部,床板上的颗粒固体比较密集,呈现固体状态,床板的作用是支撑颗粒固体床的运动并反应底部进入的气体。
3. 应用领域3.1 催化反应流化床反应器在催化反应方面有着广泛的应用。
其优点是具有较大的接触面积和较高的传质速率,可以提高催化反应的反应速率和转化率。
此外,流化床反应器还具有温度均匀和活性物质的均匀分布等特点,从而有助于提高催化反应的选择性和稳定性。
常见的催化反应包括催化裂化、催化重整、催化加氢等。
3.2 气固反应流化床反应器在气固反应方面也有着重要的应用。
气固反应是指气体与固体之间发生的化学反应。
流化床反应器由于其颗粒固体床的特点,使气体与固体之间的接触充分,从而实现高效的气固反应。
常见的气固反应包括氧化反应、还原反应、氯化反应等。
3.3 气液反应流化床反应器在气液反应方面也有广泛的应用。
气液反应是指气体与液体之间发生的化学反应。
流化床反应器可以通过调节气体和液体的进料速度和浓度,实现气液相的均匀分布和快速混合。
流化床反应器 ppt课件

(即表观气速)超过临界流化速度Umf时,还会经历一个 散式流态化阶段,然后进入鼓泡流化床。此时流化床的 Umb可按Geldart提出的计算式计算,即下式:
umb
4.125
104 0.9 g来自0.1 gumf
(s g )gdp
②反应物以气泡形式通过床层,减少了气-固相之间的接触机 会,降低了反应转化率;
③由于固体催化剂在流动过程中的剧烈撞击和摩擦,使催化 剂加速粉化,加上床层顶部气泡的爆裂和高速运动、大量 细粒催化剂的带出,造成明显的催化剂流失;
④床层内的复杂流体力学、传递现象,使过程处于非定常条 件下,难以揭示其统一的规律,也难以脱离经验放大、经 验操作。
当:0.4
Rep
500时 CDS
10 /
R1/ 2 ep
当:500 Rep 2105时 CD 0.43
这样,可得到ut计算式:
PPT课件
24
当Rep
0.4时 ut
gd
2 p
(s
f
18
)
当0.4
Rep
500时 ut
2d
p
(s 15 f
当气速达到某一定值时,流体对粒子的曳力 与粒子重力相等,则粒子会被带走。这一带出速 度等于粒子的自由沉降速度。
PPT课件
23
对球形粒子作力平衡:
6
d
3 p
s
g
6
d
3 p
f
g
CDS
4
流化床反应器PPT课件

3.1 流化床内的构件
在流化床内设置若干层水平挡板、挡网或 垂直管束,便构成了内部构件。其作用是抑制 气泡成长并且粉碎大气泡,改善气体在床层中 的停留时间分布,减少气体返混合和强化两相 间的结构。
常见的内部构件可分为三类: 横向(水平)构件
纵向(垂直)构件
横向+纵向构件
3.1流化床内的构件
LOREM IPSUM DOLOR
2.1 工业合成甲基氯硅烷的研究 直接合成法反应:
对于综合性生产车间来说,直接法是必不可少的,但还需 辅以其他方法,方能满足生产需要和降低生产成本的要求。
2.2 直接法合成有机硅单体的原理
2.2 直接法合成有机硅单体的原理
反应过程中还可能发生热分解、歧化以及氯硅烷水 解(原料带进的水分)等副反应,致使反应产物变得更 为复杂,甲基氯硅烷产物组分可多达41个。
目前,大多数商用计算流体力学软件如 FLUENT软件都采用有限元法。
4.1 数值计算中的参数影响
在实际计算中,影响的参数因素可以分为以下三方面: (一) 网格的影响 (二) 边界条件的影响
(三) 时间步长的确定
网格是数值计算中求解控制方程的基本单元, 网格的形状及划分数量将直接影响模拟结果的准 确度。它可以分为两大类:结构化网格和非结构 化网格。
目录
02 工艺流程的介绍 05
1.1有机硅在国内外的进展程度
(1)有机硅生产的特点
有机硅单体及中间体生产集中于发达国家,并且生产规模不断扩 大。 有机硅单体生产的原理并不复杂,但是生产工艺复杂、流程长、 技术含量高,长期以来,只有美国、日本、法国、德国等少数发达 国家有这一生产技术,并在行业内形成技术垄断,所以世界上从事 有机硅单体工业生产的厂家并不多。
化学反应工程-25-第八章-流化床反应器ppt课件

二、气泡的速度和大小 1、气泡的速度计算 单个气泡的平均上升速度可取:
u 0 . 711 gd br b
2 ① u u u 0 . 711 gd b 0 mf b 1
1 2
在实际床层中,气泡成群上升,其上升速度有不同的计算公式:
cm gd ② u b s
⑴气泡云与气泡的体积比 C 3 3 3 3 R R C b u 2 u 3 u V R b r f f C 4 C 1 1 C 3 V R u u u u 3 b b r f b r f b R b 4 ⑵气泡晕与气泡的体积比 V V C w Vb 显然: C w
⑶气泡所占床层的体积分率
b
一般认为:大于u0的气体均形成气泡,总的气体流量等于气泡及乳 相中气体流量之和。
u u u 1 0 b b mf b b
L L u u f mf 0 mf 则: b L u u 1 f b mf
四、气泡中的粒子含量 定义: b
有研究者认为:当 u br u t 时,粒子就被气泡带上,并可能从其底部
进入气泡,而使气泡破裂。故当 ubr ut 时为稳定气泡,反之则不稳定。
最大气泡直径应在 u br u t 之时,计算如下:
u 1 t d bmax .711 0 g
但实验表明,气泡的破裂常是由于粒子从气泡顶部侵入所致,故本式 的立论值得商榷。 另一计算式子为:d 0 . 652 A u b max tu 0
u mf u 当 u 时,uf为乳相中的真实气速,气泡内外由于 br f mf
气体环流而形成的气泡云变得明显起来,其相对厚度对圆柱形床,可按 下式计算: 3
流化床反应器工作原理

流化床反应器工作原理
流化床反应器的工作原理主要是利用气体或液体通过颗粒状固体层,使固体颗粒处于悬浮运动状态,并进行气固相反应过程或液固相反应过程。
在气体流化床反应器中,气体从反应器底部进入,通过固体催化剂床层。
气体的流速被控制在一定范围内,使得固体颗粒被气体均匀分散并悬浮于气体中,形成类似于沸腾液体的状态,即流化状态。
在这种状态下,固体颗粒层具有类似于液体的特性,如保持一定水平界面并具有静压力和浮力,以及具有流动性等。
在流化床反应器中,气固相之间的接触面积增大,传质和传热效率提高,从而有利于反应的进行。
此外,由于固体颗粒处于悬浮状态,反应器内的温度分布较为均匀,避免了局部过热或反应不均匀的问题。
流化床反应器可广泛应用于石油、化工、冶金、环保等领域,如石油催化裂化、煤的气化、生物质气化、废气处理等。
根据具体应用需求,流化床反应器可分为固定流化床和循环流化床等不同类型。
流化床反应器工作原理

流化床反应器工作原理
流化床反应器是一种常用的化工设备,它的工作原理是通过向床层中加入一定速度的气体(通常是气流)以使颗粒床呈现流化状态。
在流化床底部通入气体,气体通过床层上升时,颗粒床内部的排列结构呈现出流化状态,颗粒之间的间隙可容纳气体通过,并且颗粒悬浮在气体中。
在这种状态下,颗粒之间与气体之间的传质、传热和反应等过程变得更加充分和高效。
流化床反应器的工作原理可以归结为两个关键方面:气体流化和颗粒床与气体的相互作用。
首先,气体的流化是通过向床层中提供足够的气体速度来实现的。
当气体速度达到一定的阈值时,床层中的颗粒会随之悬浮并形成流态床。
在流化床中,气体流动给予颗粒床悬浮状态,使颗粒间的接触面积和混合程度增加,从而提高了传质和传热的效率。
此外,气流的涡流结构也有利于增强反应物与催化剂之间的接触。
其次,颗粒床与气体之间的相互作用也是流化床反应器工作原理的重要环节。
床层中的颗粒被气体携带并悬浮在气流中,使其与气体之间产生了较大的相对速度。
这种高速相对运动导致气体与颗粒之间的碰撞和撞击,从而促使颗粒间的混合和碰撞传递动量。
反应物通过与颗粒的接触和扩散,在颗粒上发生反应。
这种颗粒床和气体的相互作用促使了反应过程的快速进行,并提高了反应的效率。
总的来说,流化床反应器通过气体的流化和颗粒床与气体的相
互作用,实现了反应物的充分混合和传质传热,提高了反应的速率和效率。
该反应器具有反应均匀性好、传质传热效率高、可实现高反应速率等优点,在化工生产和研究中得到广泛应用。
流化床反应器简介 PPT

分布器的作用
换热装置
• 是反应体系的温度在适宜条件下进 行,使反应稳定进行。如对于放热 反应必须及时撤走热量,而对于吸 热反应必须及时加入热量。
大家学习辛苦了,还是要坚持
继续保持安静
• 1、套管和单管式换热器 • 2、管束式换热器 • 3、蛇管式换热器
旋风分离器
旋风分离器
塞阀
图1-4 塞阀的剖视图
流化床反应器简介
散式流化床Leabharlann 以气泡形式夹带少量颗粒穿过床
层向上运动的不连续的气泡称为 气泡相
图1-1 流化床的模型
聚式流化床
颗粒浓度与空隙率分布 较为均匀且接近初始流 态化状态的连续相,称 为乳化相。
气-固流化床反应器结构
气体 料锁
加料口 换热介质
循环管 换热介质 固体粒子
……….. ………. ..
气体
旋风分离器 壳体
内部构件 换热器 卸料口 气体分布板 预分布器
主体设备
壳 体 壳体 主要是保证流化过程局限在一定范围内 进行,对于存在有强烈放热或吸热过程, 保证热量不散失或少散失。
主要内件
• 分布器 • 换热器 • 旋风分离器 • 塞阀 • 翼阀
分布器
图1-3-1平板型分布板
图1-3-2 拱型分布板
《流化床反应器》课件

04
流化床反应器的优缺点
优点
高转化率
高选择性
流化床反应器能够实现高转化率,使得反 应更加彻底,提高了生产效率和产品质量 。
通过优化反应条件,流化床反应器能够实 现高选择性,从而降低副产物的生成,进 一步提高了产品的纯度和质量。
操作简便
适应性强
流化床反应器的结构简单,操作方便,易 于维护和维修,降低了生产成本。
流化床反应器可用于生产塑料,如 聚乙烯、聚丙烯和聚氯乙烯等,通 过聚合反应将单体转化为高分子聚 合物。
在能源领域的应用
燃烧发电
燃料电池
流化床反应器可用于燃烧煤炭、生物 质和垃圾等燃料,产生高温高压蒸汽 驱动发电机发电。
流化床反应器可用于燃料电池发电, 通过氢气和氧气的化学反应产生电能 。
核能利用
流化床反应器可用于核燃料循环,包 括核燃料溶解、分离、纯化和再处理 等过程,实现核能的可持续利用。
在氢能生产领域,流化床反应 器可用于水蒸气重整和光催化 产氢,为可再生能源的储存和 运输提供床反应器的发展趋势
高效能化 随着技术的不断进步,流化床反 应器的性能将得到进一步提升, 实现更高的转化率和产物收率。
多功能化 未来的流化床反应器将具备更加 丰富的功能,能够适应多种反应 类型和生产需求,提高生产效率 和灵活性。
THANKS
感谢观看
循环流化床反应器
总结词
一种高效、环保的流化床反应器类型。
详细描述
循环流化床反应器是一种高效、环保的流化床反应器,其特点是固体颗粒在反应器内循环流动。这种 反应器的优点在于能够实现高效能、高转化率和低能耗,同时减少废气和废水的排放。循环流化床反 应器在煤燃烧、废弃物处理等领域有广泛应用。
化学反应工程第八章流化床反应器课件

一部分在自由空域内的颗粒在重力作用下返回密相床, 而另一部分较细小的颗粒就被气流带走,只有通过旋风 分离器的作用才能被捕集下来,经过料腿而返回密相床 内。
(3) 节涌流化床
对于高径比较大的流化床,直径较小, 当表观气速大到一定程度时,会由于气 泡直径长大到接近床层直径而产生气栓 (slug)。气栓像活塞一样向上升,而气 栓上面颗粒层中的颗粒纷纷下落,气栓 达到床层表面时即破裂。床层压降出现
A类颗粒称为细颗粒,一般粒度较小(30 ~ 100μm)并且颗
粒密度较小(ρp<1400 kg/m3)。 ➢ A类颗粒形成鼓泡床后,密相中空隙率明显大于临界流
化空隙率εmf ; ➢ 密相中气、固返混较严重,气泡相与密相之间气体交换
速度较高; ➢ 随着颗粒平均粒度降低,气泡尺寸随之减小; ➢ 催化裂化催化剂是典型的A类颗粒。
➢ 对于较小和较轻的A类颗粒,当表观气速ug刚超过临界 流化速度的一段操作范围内,多余的气体仍进入颗粒群 使之均匀膨胀而形成散式流态化,但进一步提高表观气 速将生成气泡而形成聚式流态化,这种情况下产生气泡 的相应表观气速称为起始鼓泡速度或最小鼓泡速度umb。
2. 聚式流态化与散式流态化
决定散式或聚式流态化的主要因素是固体与流体之 间的密度差,其次是颗粒尺寸。 当用水流化密度很大的铅颗粒,液-固流化床中也有大液 泡形成聚式流化行为。 当用1.5~2.0MPa压力下密度增大的空气流化260μm的砂 子,出现了散式流态化现象。 处于散式流态化的液-固流化床为均匀的理想流态化状态。
我国于1956年开始将流态化技术应用于工业装置,南京化学 工业公司自立更生建立了硫铁矿流化床焙烧装置,取代多层 硫铁矿机械焙烧炉,并迅速广泛推广,促进了硫酸工业发展。
流化床反应器化学反应过程与设备课程PPT课件

气体分布装置:
包括气体预分布器和气体分布板。其作用是使气体均匀分布,以形 成良好的初始流化条件,同时支承固体颗粒。以下为常见气体分布板 形式:
凹型筛孔板
单个直孔泡帽
气体分布装置:
泡帽侧缝分布板
泡帽侧孔分布板
条形侧缝分布板
直孔泡帽分布板
直孔筛板
锥型侧孔分布板
锥型侧缝分布板 锥型侧缝分布板
包括档网、档板和气填充体物等预。 分布器
聚式流化床。
作用:回收上升气流中不仅带的细粒和粉尘,并避免带出的粉尘影响产品的纯度。
对于g-s系统,一般在气速超过Umf后,将会出现气泡,气速越高,气泡造成的扰动也越剧烈,使床层波动频繁,这种形态的流化床称
聚式流化床。
帽式分布器
作用:对进入气体起预分布作用、卸催化剂。
同心圆锥壳式分布器
流态化——固体粒子象流体一样进行流动的现象。
•
umf——临界流化速度,是指刚刚能够使固体颗粒流化起来的气
体空床流速度,也称最小流化速度。
•
ut——带出速度,当气体速度超过这一数值时,固体颗粒就不能
沉降下来,而被气流带走,此带出速度也称最大流化速度。
散式流化和聚式流化
➢ 散式流化
db/dp<1 db——气泡直径
dp——颗粒直径
对于l-s系统,流体与粒子的密度相差不大,故umf一般很小,流速进 一步提高时,床层膨胀均匀且波动很小,粒子在床内的分布也比较均
➢ 消除方法:床内设内部构件;降低u
压降:
p (1 mf )hmf (s f )g (1 f )hf (s f )
当dp/D<1/20,L0/D<2时,床层压降计算式较准确。 由式可知:床层处于流化状态时,压降与流化速度无关。
流化床反应器

流化床基本结构
结构分为: 浓相段、稀相段、扩大
段、锥底。
内部构件: 气体分布板、换热装置、
气固分离装置、挡板档 网、气体预分布器等。
流化床反应器的特点
1.床层温度均匀,避免局部过热。 2.颗粒处于运动状态,表面更新,强化传质。 3.颗粒小,催化剂有效系数高。 4.流化状态,便于操作。 5.传热系数大,换热面积小。 6.生产强度大。 7.返混严重,一次转化率低。 8.颗粒磨损,要求催化剂强度大。 9.对设备磨损严重。
流化数
u k 操
u 临
流化床的压力降
颗粒悬浮静止时受力 向下:重力 向上:浮力、流体阻力
平衡时 重力=浮力+流体阻力
公式推导:式(3-6) 说明:床层压力降与流速无关
超过带出速度时,空隙率增大、压力降减 小。
膨胀比和空隙率
膨胀比
VL
R f f
பைடு நூலகம்
VL
0
mf
空隙率
Δtm——平均传热温度差,K
(三)流化床内换热器的结构型式
列管式换热器:单管式和套管式 管束式换热器:直列和横列 鼠笼式换热器 蛇管式换热器
列管式换热器:单管式
列管式换热器:套管式
立式管束式
横排管束式换热器
鼠笼式换热器
蛇管式换热器
三、流化床反应器的计算
(一)流化床直径的计算 (二)流化床高度的确定
确定方法 :半经验公式
带出速度U带
操作速度大于带出速度时,催化剂颗粒将 被带出流化床反应器
确定方法 注意 原则上:临界流化速度<操作速度<带出速度 实际上:往往偏离这个范围。有些工业反应
化学反应工程-24-第八章-流化床反应器

⑵曳力系数 对光滑圆球,影响曳力的诸因素为:
FD = f (d P ,u, ρ , µ )
应用因次分析可以得出: FD = φ d P uρ µ A ⋅ 1 ρu 2 P 2 令: Re P =
d P uρ
, ζ = φ (Re P ) µ
整个流化床反应器由浓相区和稀相区组成。如下图所示: 整个流化床反应器由浓相区和稀相区组成。如下图所示:
3、两种流态化的判别 、 可用四个准数的乘积来表征流化形态:
ρ P − ρ Lmf Frmf ⋅ Re mf ⋅ ⋅ ρ De < 100 ,为散式流化;
ρ P − ρ Lmf Frmf ⋅ Re mf ⋅ > 100 ,为聚式流化。 ⋅ ρ De 2 u mf d P u mf ρ 式中: Frmf = ,为弗鲁特准数;Re mf = ,雷诺准数; dP g µ
P
3 u mf ρ d P ρ (ρ P − ρ )g = ⋯⋯ (1) 2 µ µ
对于小颗粒,当 Re P < 20 时:
u mf
3 (ϕ S d P )2 ρ P − ρ ε mf = ⋅ ⋅ g
150
µ
1 − ε mf
⋯⋯ (2)
对于大颗粒,当 Re P > 1000 时:
⑵沟流 若床层直径大,由于颗粒堆积不匀或气体初始分布不良,可 能在床层内局部地方形成沟流,此时大量气体经过沟流区域上 升,其余部分则未被流化仍处于固定床状态。
8.1.2 流化床内的两相运动 一、流化床的主要特性 1、液体样特性 、
固体颗粒的流出具有实际意义,它使流化床在操作中能够实现固体 固体颗粒的流出 的连续加料和卸料。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2 ρumf ∆P = Lmf λ ' d S
1 − ε mf ε 3 mf
1.75 d P u mf ρ 150(1 − ε mf + 3 2 3 ϕ S ε mf µ ϕ S ε mf
2
) d
u
2 mf
ϕS dP ρP − ρ 3 = ⋅ ⋅ gε mf ⋯⋯ (3) ρ 1.75
ε mf :可从相关图形读出(见陈甘棠主编《化学反应工程》,第一版
P257页图7-2-2); 若该值不知道,则可近似地取: 1 − ε mf 1 , 2 3 ≅ 11 ≅ 14 3
ϕ S ε mf
ϕ S ε mf
u
2 mf
d P (ρ P − ρ ) = g ⋯⋯ (3') 24.5 ρ
Re P > 1000 时:
2、带出速度ut 、带出速度 ⑴两种曳力——表面和形体曳力 两种曳力 表面和形体曳力 当流体以速度u绕过一静止颗粒,流体作用于颗粒表面上任 何一点的力可分解为与表面相切及垂直的两个分力,即剪应 力τW和压强P。
在颗粒表面上任取一微元面积dA,作用于其上的剪力为τWdA、压力 为pdA,设所取微元面积与流动方向成夹角α,则剪力在流动方向上 的分力为τWdAsinα。 则表面曳力: 表面曳力:
∫τ
A
W
sin αdA
同样压力pdA在流动方向上的分力为pdAcosα,将此力 在整个颗粒表面积分可得:
∫ P cosαdA = ∫ Γ cosαdA − ∫
⑵沟流 若床层直径大,由于颗粒堆积不匀或气体初始分布不良,可 能在床层内局部地方形成沟流,此时大量气体经过沟流区域上 升,其余部分则未被流化仍处于固定床状态。
8.1.2 流化床内的两相运动 一、流化床的主要特性 1、液体样特性 、
固体颗粒的流出具有实际意义,它使流化床在操作中能够实现固体 固体颗粒的流出 的连续加料和卸料。
24
0.05 < Re P <
ϕS
0.670 0.806 0.846 0.946 1.000 当
ReP 1 28 27 27 27.5 26.5 10 6 5 4.5 4.5 4.1 100 2.2 1.3 1.2 1.1 1.07 400 2.0 1.0 0.9 0.8 0.6 1000 2.0 1.1 1.0 0.8 0.46
当 500 < Re P < 2 × 10 5 时:u t = 1.74
等速阶段,速度对时间的导数为零,则对球形颗粒:
(ρ P − ρ )gd P
ρ
。
应当注意的是:对于小颗粒,沉降的加速阶段很短,可以忽略,因此 ut称为颗粒的沉降速度或终端速度 沉降速度或终端速度。 沉降速度或终端速度 另一在广泛范围内 Re P < 2 × 10 5 都颇准确且使用也很方便的式子是:
P
3 u mf ρ d P ρ (ρ P − ρ )g = ⋯⋯ (1) 2 µ µ
对于小颗粒,当 Re P < 20 时:
u mf
3 (ϕ S d P )2 ρ P − ρ ε mf = ⋅ ⋅ g
150
µ
1 − ε mf
⋯⋯ (2)
对于大颗粒,当 Re P > 1000 时:
2、固体的混合 、
由于固体颗粒处于悬浮状态并不停地运动,从而造成床内颗 粒的混合。流化床内固体颗粒能够达到宏观上均匀混合。 如果流化床内进行一个放热反应,由于固体颗粒的强烈混合, 很易获得温度的均匀,这是流化床的主要优点。
3、恒定的压降 、 当床层一旦流化,全部颗粒处于悬浮状态,对整个床层作受力分析并 应用动量守恒定律: Fi = ma,由于a = 0 ,故床层受力达到平衡。 ∑ 受力分析如下图所示:
u mf 为初始流化速度;dP 为颗粒平均粒径;
ρ、ρ P 分别为流体和颗粒密度;
Lmf 为初始流化时浓相区高度;
De 为流体扩散系数;
µ
为流体黏度。
4、流态化的不正常现象 、 由于气流的不均匀分布可能导致以下两种现象: ⑴腾涌或节涌
气泡在上升过程中会合并增大,如果床层直径较小而浓相区的高度较 高,则气泡可能大到与床层直径相等的程度。此时气泡将床层分节, 每节颗粒如活塞般的向上移动,部分颗粒在气泡四周或在整个截面均 匀洒落,这种现象称为腾涌或节涌。
2、聚式流化床 、 ①一般发生于气固系统; ②当u0>umf时,床内就出现一些空穴,气体取道空穴至床层顶 部逸出; ③空穴的移动与合并,酷似气泡的运动,又被称为鼓泡流化床。
⑴气泡相和乳化相 聚式流化床内存在两个相,气泡相、乳化相。 气泡相、乳化相 气泡相 乳化相内的状态接近于起始流化状态,其中的空穴率接近于εmf。 气泡相内气体以超过umf速度流过床层。 ⑵浓相区和稀相区 流化床中,颗粒在气流作用下悬浮于床层中,所形成的流固混合物 称为浓相段 浓相段。 浓相段 浓相段特征:上升的气泡在界面上破裂,气泡及乳化相内的固 浓相段特征 体颗粒被抛向浓相区上方空间,该空间由于实际气速较小,固体 颗粒将在重力作用下返回浓相段。 稀相区: 稀相区:颗粒离开浓相区有一定的向上运动速度,故在上方空 间将上升一定距离后才能下降,该段空间称为稀相段或分离段。
2 × 10 3 < Re P < 2 × 10 5 时:ζ = 5.31 − 1.88ϕ S
⑶颗粒在静止流体中的自由沉降 沉降的加速阶段: 沉降的加速阶段: 颗粒在沉降过程时所受的力包括: 场力F ①场力
重场力: Fg = mg ;离心力场: FC
= mrω 2
r:旋转半径;ω:颗粒旋转角速度。 浮力F ②浮力Fb
A A
A
ρgzdA
上式等号右边第一项称为形体曳力,第二项即颗粒所受浮力。 当颗粒与流体无相对运动时,则不存在表面和形体曳力, 当颗粒与流体无相对运动时,则不存在表面和形体曳力,但仍 有浮力存在。 有浮力存在。
总曳力:为表面曳力和形体曳力之和。 总曳力:为表面曳力和形体曳力之和。 只有对几何形状简单的少数情况可以获得曳力的理论计算式,一 只有对几何形状简单的少数情况可以获得曳力的理论计算式, 般流动情况下对球形颗粒及其它形状的颗粒,曳力的数值尚需通 般流动情况下对球形颗粒及其它形状的颗粒, 过实验来解决。 过实验来解决。
流化床有明显的上界面:
3、颗粒输送阶段 、
当 u 0 > u t 时,为颗粒输送阶段。 ε 第二阶段的流化床称为狭义流化床,广义流化床则包括气力输送阶段。
二、实际的流化现象 1、散式流化床 、 ①一般发生于液固系统; ②在流化阶段,床层膨胀,颗粒均布于流体之中并作随机运动, 颗粒充分混合; ③上界面比较清晰; ④较接近理想流化床。
u0
ε
< u t 时,床层为固定床阶段。
ε为固定床的空隙率,大小不变。
2、流化床阶段 、
当
u0
ε
= u t 时,为流化床阶段,
ε随u0的变化而变化,u0越大,ε也越大,但床层实际流速总 等于颗粒的沉降速度ut。 起始(最小)流化速度umf:是指刚刚能够使粒子流化起来的 气体空塔流速;ε 记为εmf。 和ut一样,也是表征流体在床层中运动特征的一个参数。
沉降的等速阶段: 沉降的等速阶段:
4(ρ P − ρ )gd P ut = 3ρζ 2 (ρ P − ρ )gd P 当Re P < 0.4 时: u t = ; 18µ 1 2 2 4 (ρ P − ρ ) g 3 u dP; 当 0.4 < Re P < 500 时, t = ρµ 225
F 重场力: b =
③曳力FD 曳力F
m
ρP
ρg ;离心力场:Fb =
m
ρP
ρrω 2
1 2 FD = ζAP ⋅ ρu 2
u:颗粒相对于流体的运动速度。 以下仅讨论重力场,根据牛顿第二定律: g − Fb − FD = m F 对球形颗粒可得:
du dt
du ρ P − ρ 3ζ g − = ρu 2 dt ρ P 4d P ρ P
床层流化质量优劣判断: 床层流化质量优劣判断 若床内出现腾涌,压降将有大幅度的起伏波动; 若床内发生沟流,压降较正常值为低。
二、流化床的操作范围——内径的确定 流化床的操作范围 内径的确定 1、起始流化速度umf 、起始流化速度 umf确定的两种方法: ⑴通过测定床层压降变化的方法来确定 如上图1所示,实线的拐弯点即umf。 ⑵公式计算 mg ρ P − ρ , m = ALmf 1 − ε mf ρ P ∆P = ρ A P
则前面三式分别为:
d P u mf ρ
µ
d ρ (ρ P − ρ )g 2 = 33.7 + 0.0408 ⋅ µ2
3 P
1
2
− 33.7 ⋯⋯ (1')
对于小颗粒,当 ρ ) = g ⋯⋯ (2') 1650µ
对于大颗粒,当
P1 A = P2 A + W表观 ,W表观
m mg − = ρg ,即:(重量-浮力),故: ρP
mg ρ P − ρ P1 − P2 = ∆P = ρ A P
式中:A:床层截面积;L:床层高度;m:床层颗粒总质量;ρP、 ρ:分别为颗粒和流体的密度;ΔP:床层压降。 由上式可知:压降等于单位截面床层内固体的表观重量,与气速 压降等于单位截面床层内固体的表观重量, 无关,始终保持定值。作图如下: 无关,始终保持定值。
(
)
故: ∆P = Lmf 1 − ε mf (ρ P − ρ )g ⋯ (a )
(
)
根据固定床压降式:
⋯ (b ) d P ρu mf d S ρu mf 150 Re , P = , ϕS dP = dS λ'= + 1.75 ,Re m = µ µ (1 − ε mf ) Re m
