编译原理第七章
合集下载
编译原理_第7章
29
§7.3 赋值语句的翻译
3.例题:写出下列代码段中表达式的翻译制导过 程及其所产生的四元式 begin Integer:B、C、D、X;
X:=-B*(C+D);
end
符号表 <B> B <C> C <D> D <X> X Int Int Int Int (1) (2) (3) (4) 四元式 Op - + * := arg1 <B> <C> T1 T3 arg2 <D> T2 - result T1 T2 T3 X
语义处理分两步:
1.静态语义分析,即验证语法结构合法的程序是否真正有意义。
2.若静态语义正确,语义处理则要执行真正的翻译。 即要么生成程序的一种中间表示形式(中间代码),
要么生成实际的目标代码。
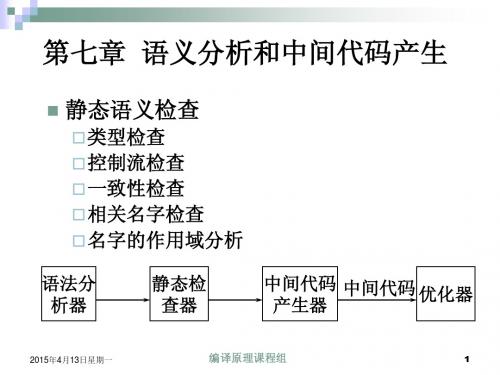
静态语义检查包括:
(1)类型检查; (2)控制流检查; (3)一致性检查; (4)相关名字检查。
2
第七章
8
§7.1 中间语言
例子:如图所示,为a+a*(b-c)+(b-c)*d的DAG
+
+
* a b c
*
d
9
§7.1 中间语言
2.抽象语法树
例子:(1)a:=b*-c+b*-c的图表示法
assign a * b uminus c b + * uminus c DAG
10
assign
a + * b uminus c
数据区中的相对地址offset.
(3)综合属性: T.type-名字的类型; T.width-名字的域宽(即该类型名字所占用 的存储单元个数)
22
§7.2 二、保留作用域信息
编译原理 - 陈火旺版 - 第七章

3
后缀式
后缀式(逆波兰式)
表达式E的后缀形式E’的写法:
• 若E是变量或常量,则E’ = E • 若E=E1 op E2,则E’ =E1’ E2’ op • 若E=(E1),则E’ = E1 表达式变为后缀形式的语义规则
E→E1 op E2 E→(E1) E→i {E.CODE := E1.CODE||E2.CODE||op } {E.CODE := E1.CODE} {E.CODE := i}
推广到表达式外的范围
• 例如 a:=b*c+b*d 后缀形式:abc*bd*+:=
5
图
抽象语法树
内部结点表示运算符,后代表示运算对象
无循环有向图(DAG)
与抽象语法树
• 相同之处:内部结点表示运算符,后代表示运算对象 • 不同之处:考虑到公共子表达式(不只一个父结点),更加紧 凑高效
四元组表示 (1) (-,C, D , T1) (2) (*, B, T1, T2) (3) (+, A, T2 , T3) (4) (↑, F, G , T4) (5) ( /, E, T4, T5) (6) (-, T3, T5 , T6)
13
说明语句的翻译
说明语句
定义局部于该过程的数据对象(以标识符标识) 为数据对象分配空间,在符号表中登记数据对象的名 字,类型,分配的存储地址 有过程嵌套的,表示出嵌套关系
编译方法
中国人民大学信息学院 陈文萍
1
第7章 语义分析和中间代码生成
中间语言 一些语法成分的翻译
说明语句 赋值语句 布尔表达式 控制语句 过程调用
类型检查
2
语义分析概述
编译原理7
编译原理课程组
result T1 T2 T3 T4 T5 a
21
2015年4月13日星期一
三地址语句
三元式
通过计算临时变量值的语句的位置来引用这
个临时变量 三个域:op、arg1和arg2 op arg1 arg2 (0) uminus c (1) * b (0) (2) uminus c (3) * b (2) (4) + (1) (3) (5) assign a (4)
语义规则
S.nptr:=mknode(‘assign’, mkleaf(id,id.place),E.nptr) E.nptr:=mknode(‘+’,E1.nptr,E2.nptr) E.nptr:=mknode(‘*’,E1.nptr,E2.nptr) E.nptr:=mknode(‘uminus’,E1.nptr) E.nptr:=E1.nptr E.nptr:=mkleaf(id,id.place)
2015年4月13日星期一
编译原理课程组
4
逆波兰表示法不用括号。只要知道每个 算符的目数,对于后缀式,不论从哪一 端进行扫描,都能对它进行唯一分解。 后缀式的计算
用一个栈实现。
一般的计算过程是:自左至右扫描后缀式,
每碰到运算量就把它推进栈。每碰到 k 目运 算符就把它作用于栈顶的 k 个项,并用运算 结果代替这k个项。
c 抽象语法树
uminus
c
编译原理课程组
T1:=-c T2:=b*T1 T3:=-c T4:=b*T3 T5:=T2+T4 a:=T5
2015年4月13日星期一
11
抽象语法树对应的代码:
T1:=-c T2:=b*T1 T3:=-c T4:=b*T3 T5:=T2+T4 a:=T5
result T1 T2 T3 T4 T5 a
21
2015年4月13日星期一
三地址语句
三元式
通过计算临时变量值的语句的位置来引用这
个临时变量 三个域:op、arg1和arg2 op arg1 arg2 (0) uminus c (1) * b (0) (2) uminus c (3) * b (2) (4) + (1) (3) (5) assign a (4)
语义规则
S.nptr:=mknode(‘assign’, mkleaf(id,id.place),E.nptr) E.nptr:=mknode(‘+’,E1.nptr,E2.nptr) E.nptr:=mknode(‘*’,E1.nptr,E2.nptr) E.nptr:=mknode(‘uminus’,E1.nptr) E.nptr:=E1.nptr E.nptr:=mkleaf(id,id.place)
2015年4月13日星期一
编译原理课程组
4
逆波兰表示法不用括号。只要知道每个 算符的目数,对于后缀式,不论从哪一 端进行扫描,都能对它进行唯一分解。 后缀式的计算
用一个栈实现。
一般的计算过程是:自左至右扫描后缀式,
每碰到运算量就把它推进栈。每碰到 k 目运 算符就把它作用于栈顶的 k 个项,并用运算 结果代替这k个项。
c 抽象语法树
uminus
c
编译原理课程组
T1:=-c T2:=b*T1 T3:=-c T4:=b*T3 T5:=T2+T4 a:=T5
2015年4月13日星期一
11
抽象语法树对应的代码:
T1:=-c T2:=b*T1 T3:=-c T4:=b*T3 T5:=T2+T4 a:=T5
编译原理第七章

例题
设有文法G(L)
LE,L LE Ea Eb
文法G(L)的LR分析表如下
ACTION表
状态 0 1 2 3 4 5 S3 S4 S5 r3 r4 a S3 b S4 acc r2 r3 r4 2 6 , # E 2
GOTO表
L 1
6
r1
以输入串“a,b,a”为例,给出LR分析 器的分析过程如下表示:
步骤 1 2 3 4 5 0 03 02 025 0254 状态栈 # #a #E #E, #E,b 符号栈 输入符号串 分析动作 a,b,a# S3(移进) ,b,a# r3(规约) ,b,a# S5(移进) b,a# S4(移进) ,a# r4(规约)
6
7 8 9
0252
02525 025253 025252
S4
S6 r2 r2 S8 r3 r3 r3 r2
3
7
r4 r1
r4 r1
r4 r1
以输入串“abbcde”为例,给出LR分析器的分析过程如下表示:
步骤 1 2 3 4 5 6 7 8 9 0 02 024 023 0236 023 0235 02358 02357 状态栈 # #a #ab #aA #aAb #aA #aAc #aAcd #aAcdB 符号栈 输入符号串 分析动作
7.1.2 分析表或分析函数
LR分析表是LR分析器的核心。 分析表由两个子表构成,即动作表(ACTION表)和状 态转换表(GOTO表)。它们都是二维数组形式(数组 名称分别是GOTO和ACTION)。
对于GOTO表。它的一个数组元素GOTO(Sm,Xi)代表一 个状态。表示当状态Sm面临输入符号Xi时转移到的下一个状态 (通常Xi是非终结符)。 对于ACTION表。它的一个数组元素ACTION(Sm, ai)代表一 个动作,表示当状态Sm面临输入符号ai时完成的分析动作(通 常ai是终结符)。动作可以有四种可能,分别是移进、规约、 接受和出错。
编译原理ppt

三地址代码是中间代码的抽象形式,其具体实
现可用记录表示,记录中包含表示运算符和操 作数的域。有以下三种表示方法:
三元式 四元式
间接三元式
四元式
是一个带有四个域的记录结构,格式如下: (算符, 第一运算对象, 第二运算对象, 结果)
如:a=b*c+b*d
(1) (2) (3) (4)
7.3 将下列表达式分别用逆波兰式、DAG图、 三地址语句、及三地址语句的三种具体实现 方法:三元式、间接三元式、四元式表示: A + B * ( C - D ) + E / ( C - D ) ^N 逆波兰 : A B C D - * + E C D – N ^ / + DAG图: +
+ A /
C B A C T4 E T3
D T1 T2 D N T5 T6
T1 ) T2) T3) T4) T5) T6) T7)
A + B * ( C - D ) + E / ( C - D ) ^N
三元式 : (1) ( (2) ( * (3) ( + (4) ( (5) ( ^ (6) ( / (7) ( +
(1)
如:
X:=(A+B)*C ; Y:=D ↑(A+B)
操作码表 (1) (2) (3) (1) (4) (5)
三元式表 (1)( + , A , B ) (2)( * , (1) , C ) (3)( := , X , (2) ) (4)(↑, D , (1) ) (5)(:= , Y , (4) )
例:a+b*(c-d)-e/f**g
(1) ( -, c , d ) (2) ( * , b , (1) ) (3) ( + , a , (2) ) (4) ( ** , f , g ) (5) ( / , e , (4) ) (6) ( -元式表示
编译原理第七章

符号串的前缀是指符号串的任意首部,包括
安徽理工大学
《编译原理》 信息安全系 赵宝
2
空串ε。
定义:对于文法G[S],若有
S
* r
αβ,β∈Vt*
则称α为规范前缀,也称为活前缀。
若α是含句柄的活前缀,并且每个句柄是α 的后缀或本身,则称α是可归规范前缀或可归 前缀(含有句柄的活前缀)。
活前缀不含句柄之右的任何符号。 是规范
由此可见,构造LR分析器的主要工作是构造 分析表
•LR分析表的组成: LR分析表由分析动作(ACTION)表和状态转换 (GOTO)表组成。
1). 分析动作表
安徽理工大学
《编译原理》 信息安全系 赵宝
ቤተ መጻሕፍቲ ባይዱ
10
在分析动作表中,其元素由action(si,aj)来表 示。action(si,aj)表示当前分析栈的状态栈栈顶 元素为si,文法符号栈栈顶元素为aj(当前输入 符号)时,所执行的动作。
特殊符号也可以用“.”,并且要加在产生 式右部的任何地方,表示一个位置。
➢项目集:若干个项目组成的集合称为项目集, 又称为配置集合。
➢后继符号:项目中紧跟在特殊符号“△”后 面的符号称为该项目的后继符号。
安徽理工大学
《编译原理》 信息安全系 赵宝
18
后继符号表示下一时刻读到的符号。有如下两 种情况:
下面我们以输入串 #a,b,a# 为例,具体讲述LR分析过程。
安徽理工大学
《编译原理》 信息安全系 赵宝
15
状态栈 S0 S0S3
S0S2
S0S2S5 S0S2S5S4
S0S2S5S2
S0S2S5S2S5 S0S2S5S2S5S3
S0S2S5S2S5S2
安徽理工大学
《编译原理》 信息安全系 赵宝
2
空串ε。
定义:对于文法G[S],若有
S
* r
αβ,β∈Vt*
则称α为规范前缀,也称为活前缀。
若α是含句柄的活前缀,并且每个句柄是α 的后缀或本身,则称α是可归规范前缀或可归 前缀(含有句柄的活前缀)。
活前缀不含句柄之右的任何符号。 是规范
由此可见,构造LR分析器的主要工作是构造 分析表
•LR分析表的组成: LR分析表由分析动作(ACTION)表和状态转换 (GOTO)表组成。
1). 分析动作表
安徽理工大学
《编译原理》 信息安全系 赵宝
ቤተ መጻሕፍቲ ባይዱ
10
在分析动作表中,其元素由action(si,aj)来表 示。action(si,aj)表示当前分析栈的状态栈栈顶 元素为si,文法符号栈栈顶元素为aj(当前输入 符号)时,所执行的动作。
特殊符号也可以用“.”,并且要加在产生 式右部的任何地方,表示一个位置。
➢项目集:若干个项目组成的集合称为项目集, 又称为配置集合。
➢后继符号:项目中紧跟在特殊符号“△”后 面的符号称为该项目的后继符号。
安徽理工大学
《编译原理》 信息安全系 赵宝
18
后继符号表示下一时刻读到的符号。有如下两 种情况:
下面我们以输入串 #a,b,a# 为例,具体讲述LR分析过程。
安徽理工大学
《编译原理》 信息安全系 赵宝
15
状态栈 S0 S0S3
S0S2
S0S2S5 S0S2S5S4
S0S2S5S2
S0S2S5S2S5 S0S2S5S2S5S3
S0S2S5S2S5S2
编译原理课件第7章

P→MD M→ {offset := 0 }
D→D ; D
D→id : T {enter( , T.type, offset );
offset := offset + T.width}
T→integer {T.type := integer; T.width := 4}
T→real {T.type := real; T.width := 8}
D→id : T {enter( , T.type, offset ); offset := offset + T.width}
P
offset=0
D
D
;
offset=8
D
offset=12
id
:
T
id
:
T
real
enter(x,real,0)
2020/2/3
T.type=real T.width=8
• type row = record
• address: integer;
• lexeme: array[1..15] of char
• end;
• var table : array [1..10] of row;
6.如果T是类型表达式,那么pointer(T)也是类型表 达式,表示“指向类型为T的对象的指针”。
integer T.type=integer
T.width=4
enter(i,integer,8)
20
例 x:real; i:integer 的翻译
P{offset:=0}D {offset:=0}D;D {offset:=0}x:T{enter(x,T.type,offset);
第七章 编译原理

第七章 语义分析和中间代码产生
本章将把上章介绍的属性文法和语法制导翻译的 方法和技术,用于高级语言的语义分析和中间代码产 生中。 紧接词法分析和语法分析之后,编译程序要做的 工作是,静态语义检查和翻译。
●静态语义检查
(1)类型检查
(3) 一致性检查
(2) 控制流检查
(4)相关名字检查
(5)作用域分析
T2:=x+T1
三地址代码可以看成是抽象语法树或DAG图的 一种线性表示。 三地址语句十分类似汇编语言的语句。语句可 以带标号,也可以有各种控制流语句。
本书所使用的三地址语句的种类如下: (1) (2) (3) (4) (5) (6) x :=y op z x := op y x:=y goto L if x relop y goto L param x1
Eid
E.place:=id.place
E.code:=‘’
例如 对 a:=b*-c+b*-c 产生三地址代码
S S
a
:=
E4 *
E9 +
E8
*
.③ E .place = T 2:=b*T1 T 3 1 . E3.code=‘ T13:=-c ’ T :=-c .④ E4.place = T2 4:=b*T3 T
●
例如 写出将表达式翻译成后缀形式的属性文法 SE EE1op E2 E(E1 ) Eid 输入串 (a+b)*c
E.code=ab+ E E.code=a E
{ { { {
print(E.code) } E.code:=E1.code || E2.code || op } E.code:= E1.code } E.code:=id }
本章将把上章介绍的属性文法和语法制导翻译的 方法和技术,用于高级语言的语义分析和中间代码产 生中。 紧接词法分析和语法分析之后,编译程序要做的 工作是,静态语义检查和翻译。
●静态语义检查
(1)类型检查
(3) 一致性检查
(2) 控制流检查
(4)相关名字检查
(5)作用域分析
T2:=x+T1
三地址代码可以看成是抽象语法树或DAG图的 一种线性表示。 三地址语句十分类似汇编语言的语句。语句可 以带标号,也可以有各种控制流语句。
本书所使用的三地址语句的种类如下: (1) (2) (3) (4) (5) (6) x :=y op z x := op y x:=y goto L if x relop y goto L param x1
Eid
E.place:=id.place
E.code:=‘’
例如 对 a:=b*-c+b*-c 产生三地址代码
S S
a
:=
E4 *
E9 +
E8
*
.③ E .place = T 2:=b*T1 T 3 1 . E3.code=‘ T13:=-c ’ T :=-c .④ E4.place = T2 4:=b*T3 T
●
例如 写出将表达式翻译成后缀形式的属性文法 SE EE1op E2 E(E1 ) Eid 输入串 (a+b)*c
E.code=ab+ E E.code=a E
{ { { {
print(E.code) } E.code:=E1.code || E2.code || op } E.code:= E1.code } E.code:=id }
编译原理课后答案——第七章_目标代码生成

第七章 目标代码生成
第七章 目标代码生成
7.1 对下列四元式序列生成目标代码: T=A-B S=C+D
W=E-F
U=W/T V=U*S 其中,V是基本块出口的活跃变量,R0和R1是可用寄存 器。
第七章 目标代码生成 【解答】 简单代码生成算法依次对四元式进行翻译。
我们以四元式T=a+b为例来说明其翻译过程。 汇编语言的加法指令代码形式为 ADD R, X 其中,ADD为加法指令;R为第一操作数,第一操作数必 须为寄存器类型;X为第二操作数,它可以是寄存器类型,也 可以是内存型的变量。ADD R,X指令的含意是:将第一操作数 R与第二操作数相加后,再将累加结果存放到第一操作数所在 的寄存器中。要完整地翻译出四元式T=a+b,则可能需要下面 三条汇编指令:
第七章 目标代码生成 此外,如果必须使用第一条指令,即第一操作数 不在寄存器而是在内存中,且此时所有可用寄存器都 已分配完毕,这时就要根据寄存器中所有变量的待用 信息(也即引用点)来决定淘汰哪一个寄存器留给当前 的四元式使用。寄存器的淘汰策略如下: (1) 如果某寄存器中的变量已无后续引用点且该 变量是非活跃的,则可直接将该寄存器作为空闲寄存 器使用。 (2) 如果所有寄存器中的变量在基本块内仍有引 用点且都是活跃的,则将引用点最远的变量所占用寄 存器中的值存放到内存与该变量对应的单元中,然后 再将此寄存器分配给当前的指令使用。
第七章 目标代码生成 因此,本题所给四元式序列生成的目标代码如下: MOV R0, A SUB R0, C MOV R1, C ADD R1, D /*R1=S*/ /*R0=T*/
MOV S, R1 的值送内存单元S*/
MOV R1, E SUB R1, F SUB R1, R0 MUL R1, S
第七章 目标代码生成
7.1 对下列四元式序列生成目标代码: T=A-B S=C+D
W=E-F
U=W/T V=U*S 其中,V是基本块出口的活跃变量,R0和R1是可用寄存 器。
第七章 目标代码生成 【解答】 简单代码生成算法依次对四元式进行翻译。
我们以四元式T=a+b为例来说明其翻译过程。 汇编语言的加法指令代码形式为 ADD R, X 其中,ADD为加法指令;R为第一操作数,第一操作数必 须为寄存器类型;X为第二操作数,它可以是寄存器类型,也 可以是内存型的变量。ADD R,X指令的含意是:将第一操作数 R与第二操作数相加后,再将累加结果存放到第一操作数所在 的寄存器中。要完整地翻译出四元式T=a+b,则可能需要下面 三条汇编指令:
第七章 目标代码生成 此外,如果必须使用第一条指令,即第一操作数 不在寄存器而是在内存中,且此时所有可用寄存器都 已分配完毕,这时就要根据寄存器中所有变量的待用 信息(也即引用点)来决定淘汰哪一个寄存器留给当前 的四元式使用。寄存器的淘汰策略如下: (1) 如果某寄存器中的变量已无后续引用点且该 变量是非活跃的,则可直接将该寄存器作为空闲寄存 器使用。 (2) 如果所有寄存器中的变量在基本块内仍有引 用点且都是活跃的,则将引用点最远的变量所占用寄 存器中的值存放到内存与该变量对应的单元中,然后 再将此寄存器分配给当前的指令使用。
第七章 目标代码生成 因此,本题所给四元式序列生成的目标代码如下: MOV R0, A SUB R0, C MOV R1, C ADD R1, D /*R1=S*/ /*R0=T*/
MOV S, R1 的值送内存单元S*/
MOV R1, E SUB R1, F SUB R1, R0 MUL R1, S
编译原理-第七章解析资料

中间代码 中间 中间代码 生成器 代码 优化器
静态语义检查和中间代码生成器的位置
2018/10/26
TJNU-COCIE-WJW
5
第七章 语义分析和中间代码产生
中间语言 7.2 说明语句 7.3 赋值语句的翻译 7.4 分情况语句 7.5 回填技术 7.6 类型检查
7.1
2018/10/26 TJNU-COCIE-WJW 6
TJNU-COCIE-WJW 28
2018/10/26
例子:语句a:=b*-c+b*-c 的三元式表示
op arg1 arg2
(0) (1) (2) (3) (4) (5)
uminus * uminus * + Assign
c b c b
(1)
(0) (2) (3) (4)
a
2018/10/26
TJNU-COCIE-WJW
例:x
+ y * z翻译成 t1 := y * z t2 := x + t1
TJNU-COCIE-WJW 16
2018/10/26
1.一般形式(续)
三地址代码是AST或DAG的线性化表示
DAG图对应的三地址代码可能比相应的AST
对应的三地址代码要优化,因为可以复用中 间结果
2018/10/26
29
注意: 有些三地址语句要多个三元式表示 例子: x[i] := y op arg1 arg2 (0) [ ]= x i (1) := (0) y
y := x[i] op arg1 (0) =[ ] x (1) := y arg2 i (0)
2018/10/26
TJNU-COCIE-WJW
编译原理第七章_自下而上的LR(K)分析方法

一、根据形式定义求出活前缀的正规表达式,然 后由此正规表达式构造NFA再确定化为DFA(不 实用,略)
二、求出文法的所有项目,按一定规则构造识别 活前缀的NFA再确定化为DFA(了解)
三、使用闭包函数(CLOSURE)和转向函数 (GOTO(I,X))构造文法G’的LR(0)的项目集规范 族,再由转换函数建立状态之间的连接关系得 到识别活前缀的DFA(掌握)
编译原理 Compilers Principles 第7章9
移进-归约中的问题分析
3) #ab 4) #aA 5) #aAb 6) #aA
bcde# bcde# cde# cde#
归约(A→b) 移进
归约(A→Ab) 移进
分析:已分析过的部分在栈中的前缀不同,而且移 进和归约后栈中的状态会发生变化
S aA cBe
Ab d b
0 S 1*
1 * 句子识别态
2a 3b 4
i
5a 6 A 7 b 8
9 a 10 A 11 c 12 d 13
14 a 15 A 16 c 17 B 18 e 10
构造识别活前缀的有限自动机 例子
句柄识别态
X
0S 2a 5a 9a
14 a
*
1
3b 4 6 A7b 10 A 11 c 15 A 16 c
1) # 2) #a 3) #ab
abbcde# bbcde# bcde#
动作
移进 移进 归约(A→b)
状态栈
0 02 024
ACTION
S2 S4 r2
GOTO
3
对输入串abbcde#的LR分析过程
S
1*
b
4
0 a 2 A 3 b 6
二、求出文法的所有项目,按一定规则构造识别 活前缀的NFA再确定化为DFA(了解)
三、使用闭包函数(CLOSURE)和转向函数 (GOTO(I,X))构造文法G’的LR(0)的项目集规范 族,再由转换函数建立状态之间的连接关系得 到识别活前缀的DFA(掌握)
编译原理 Compilers Principles 第7章9
移进-归约中的问题分析
3) #ab 4) #aA 5) #aAb 6) #aA
bcde# bcde# cde# cde#
归约(A→b) 移进
归约(A→Ab) 移进
分析:已分析过的部分在栈中的前缀不同,而且移 进和归约后栈中的状态会发生变化
S aA cBe
Ab d b
0 S 1*
1 * 句子识别态
2a 3b 4
i
5a 6 A 7 b 8
9 a 10 A 11 c 12 d 13
14 a 15 A 16 c 17 B 18 e 10
构造识别活前缀的有限自动机 例子
句柄识别态
X
0S 2a 5a 9a
14 a
*
1
3b 4 6 A7b 10 A 11 c 15 A 16 c
1) # 2) #a 3) #ab
abbcde# bbcde# bcde#
动作
移进 移进 归约(A→b)
状态栈
0 02 024
ACTION
S2 S4 r2
GOTO
3
对输入串abbcde#的LR分析过程
S
1*
b
4
0 a 2 A 3 b 6
编译原理第7章 语法制导翻译和中间代码生成

语义规则描述的动作:
• 检查静态语义 • 生成中间代码/目标代码
语义处理
语义处理的环境:符号表 • 为语义分析提供类型、作用域等信息。 • 为代码生成提供类型、作用域、存储类别、
存储(相对)位置等信息。
语义处理
PL/0编译程序的语义处理(一)call语句的处理
if sym = callsym
then
源语言程序
词法分析
前
语法分析
端
处理Biblioteka 语义分析语 义 处 理
后 端
代码生成
处
理
汇编代码
语义处理
语义处理的任务: • 静态语义检查
• 静态语义:语法规则的良形式条件 • 静态语义检查:审查静态语义
• 动态语义处理
• 动态语义:程序单元执行的操作 • 动态语义处理:生成(中间/目标)代码
语义处理
语义处理的实现: • 属性文法:描述语义规则。 • 语法制导翻译:在语法分析的同时,执行
类型的基本概念
声明和定义,使用: • 声明:
• 程序通过声明语句把标识符的名称、类型和 作用域等信息传递给编译器。
• 声明语句本身传递名字和类型信息,声明语 句的位置传递作用域信息。
• 定义:
• 变量、类的声明就是定义。 • 函数可以先声明一个原型,在定义中再给出
实现的代码。
类型的基本概念
强类型语言和弱类型语言: • 强类型语言
第七章语法制导翻译和中间代码生成
7.1语义处理概述 7.2属性文法和语法制导翻译 7.3 中间代码生成(一些语句的翻译) 7.4符号表
7.1 语义处理(语义分析和中间代码生成)
在编译中的逻辑阶段
源语言程序
词法分析
• 检查静态语义 • 生成中间代码/目标代码
语义处理
语义处理的环境:符号表 • 为语义分析提供类型、作用域等信息。 • 为代码生成提供类型、作用域、存储类别、
存储(相对)位置等信息。
语义处理
PL/0编译程序的语义处理(一)call语句的处理
if sym = callsym
then
源语言程序
词法分析
前
语法分析
端
处理Biblioteka 语义分析语 义 处 理
后 端
代码生成
处
理
汇编代码
语义处理
语义处理的任务: • 静态语义检查
• 静态语义:语法规则的良形式条件 • 静态语义检查:审查静态语义
• 动态语义处理
• 动态语义:程序单元执行的操作 • 动态语义处理:生成(中间/目标)代码
语义处理
语义处理的实现: • 属性文法:描述语义规则。 • 语法制导翻译:在语法分析的同时,执行
类型的基本概念
声明和定义,使用: • 声明:
• 程序通过声明语句把标识符的名称、类型和 作用域等信息传递给编译器。
• 声明语句本身传递名字和类型信息,声明语 句的位置传递作用域信息。
• 定义:
• 变量、类的声明就是定义。 • 函数可以先声明一个原型,在定义中再给出
实现的代码。
类型的基本概念
强类型语言和弱类型语言: • 强类型语言
第七章语法制导翻译和中间代码生成
7.1语义处理概述 7.2属性文法和语法制导翻译 7.3 中间代码生成(一些语句的翻译) 7.4符号表
7.1 语义处理(语义分析和中间代码生成)
在编译中的逻辑阶段
源语言程序
词法分析
编译原理第七章

7.1.4 控制结构
一个程序设计语言的控制结构是该语言在程序运行期 间用于改变控制流的语言特征集合。
7.2 执行时的内存分配
编译程序需要为源程序中的数据分配执行时的存 储空间,编译程序从操作系统中申请编译程序 计算出的所需的内存,或编译程序生成在运行 时需申请内存的指令。
(1) 确定用来表示某一数据项的内存大小。
目标代码生成
• 输入
– 中间代码
• 三元式 • 四元式
• 输出
– 可执行代码 – 待装配的代码 – 汇编代码
第1章 语言处理程序概述
1.1 语言处理程序的发展过程
• 语言处理程序简介 • 语言处理程序的工作 • 语言处理程序的形式
1.1.1 语言处理程序简介
• 语言处理程序的起源—填补程序设计者的符号 描述与目标机器运行要求之间的差异
一种在程序运行期间均可以对内存实 现分配或解除分配,一旦存储分配解除该 存储空间内的数据便失去意义。叫做动态 存储分配。
7.3 代码优化
目标: 作为一个高级语言的使用者很希望编译 程序所产生的代码能够和直接用机器语言编写 的程序效果一样好。
代码优化是指对原代码进行的变换,从而获得在 时间和空间上效率到:
7.1.1 数据类型
类型的合法性检查是判断数据类型是否与上下文的要求一致 数据类型是对该类型数据(变量或常量)的取值是否合法以 及对该类型数据的运算是否合法的一种说明。
7.1.2 数据结构
一个程序设计语言如允许使用的数组、记录、字符串、 表、栈等形式的数据结构,在编译程序中应为它们提供相 应的翻译。 为了能对数据结构中的元素进行引用,必须完成从逻辑结 构到能够访问这些数据元素的物理结构的映射。应考虑:
1 编译求值 2 合并预算 3 删除死码 4 减少频率 5 强度削弱和变换循环条件 6 减少重写传播
编译原理演示文稿7

例:设有类Pascal程序段 program example(input,output);
type student=record no:integer; name:array[1..10] of char; score:integer end;
weekday=(sun,mon,tue,wed,thu,fri,sat); var st:array[1..50] of student;
name :array[1..20] of char; next:link end; 的无类型结构树或无环 有向图相等即可。检查类型等价也分成静态检查和动态检查。 由编译程序能完成的类型检查叫做静态类型检查;由目标程 序运行时所作的类型检查就称为动态类型检查。一般地,如 果要在生成的目标代码中完成类型检查,则目标代中不但要 保存数据的值,而且还保存该数据的类型,则可完工成相应 的动态类型检查。因算法语言的类型检查多数是静态的类型 检查,在这里仅介绍了静态的类型检查。
7.1.4 控制结构 一种程序设计语言的控制结构是该语言在程序运行期间
用于改变控制流的语言特征集合。它包括有条件控制转移, 条件执行、循环控制、过程序调用、转移和出口。编译程序 在翻译时必须保证源程序不能违法控制结构的语义。如 Pascal中只能从循环体内转向循环体外、C语言中不能从一 个函数转向另一个函数、BASIC中不能在循环体内修改循环 变量的值,而C没有这种限制。 例:错误的控制结构 begin
定义7.1 数据类型是对该类型数据(变量或常量)的取值是 否合法以及对该类型据的运算是否合法的一种说明。
实现和完成数据类型的合法性检查,它包括以下任务:
(1) 检查运算符作用在运算对象上的合法性,这一合法性保 证了该运算能产生正确的运算结果。
编译原理第七章

对例6.1的文法用拓广文法表示成: S′→S[0] S→aAcBe[1] A→b[2] A→Ab[3] B→d[4] 现对句子abbcde的可归前缀列出: S[0] ab[2] aAb[3] aAcd[4] aAcBe[1]
构造识别其活前缀及可归前缀的有限自动机如图7.2。 每一个终态都是句柄识别态,用双圈表示。带"*"号的状态既为句柄识
观察产生式右部的非终结符。 2、应用LR(0)CONTEXT(A→β)=LC(A).β求得包含句柄 的活前缀。 3、由此可构造以文法符号为字母表的识别(包括句柄) 活前缀的不确定有限自动机。 4、应用子集法对上述的不确定有限自动机进行确定化 得到识别可归前缀的确定有限自动机。
结论:对任何一个上下文无关文法只要能构造出识别 可归前缀的有限自动机,就可以构造其相应的分析表。
if ACTION[Si,a]=Sj then begin PUSH j,a (进栈)
ip 前进(指向下一输入符号)
end
else
if ACTION[Si,a]=rj(若第j条产生式 为A→β) then begin
pop |β| 项
对于上面的分析过程我们可以知道:
若当前栈顶状态为Sk push GOTO[Sk,A] 和A(进栈) end
在文法G中每个产生式的右部适当位置添加一个圆点构成项目。
例如,产生式S→aAcBe对应有6个项目:
[0] S→·aAcBe [2] S→aA·cBe [4] S→aAcB·e
7.2.1 可归前缀和子前缀
为了在以后的LR分析中不致引起混淆,现对原文法进行拓广。 若原文法G的开始符号为S,在G中加产生式S′→S后得新的文法G′, 则称G′为原文法G的拓广文法,而S′为拓广后文法G′的开始符号。 对文法进行拓广的目的是为了对某些右部含有开始符号的文法,在 归约过程中能分清是否已归约到文法的最初开始符,还是在文法右 部出现的开始符号,拓广文法的开始符号S′只在左部出现,这样 确保了不会混淆。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014年6月15日12时14分
非终结符号T有两个综合属性 T.type 和T.width,分别表示 名字的类型和名字的域宽 (即该类型名字所占用的存储单 元个数)。 假定整数类型域宽为4;实数域宽为8;一个数组的域宽可 以通过把数组元素数目与一个元素的域宽相乘获得;每个 指针类型的域宽假定为4。 计算说明语句中名字的类型和相对地址的翻译模式如下:
子表达式 (base-((low1*n2)+low2)*w的值是可以在编译时 确定的。
2014年6月15日12时14分
例 1 设A为一个10*20的数组,即n1=10,n2=20。并设w=4。 赋值语句x:=A[y, z] 被翻译成如下三地址语句序列: T1:=y*20 T1:=T1+z T2:=A-84 T3:=4*T1 T4:=T2[T3] x:=T4
2014年6月15日12时14分
7.4 布尔表达式的翻译 在程序设计中,布尔表达式有两个基本作用:一个是用作 计算逻辑值;另一个用作控制流语句之中的条件表达式。 计算布尔表达式的值通常有两种办法。一种办法是,如同 计算算术表达式一样,一步不差地从表达式各部分的值计 算出整个表达式的值。例如,按通常的习惯,用数值1代 表true,用0代表false,那么,布尔式1 or (not 0 and 0) or 0的计算过程是: 1 or (not 0 and 0) or 0 =1 or (1 and 0) or 0 =1 or 0 or 0 =1 or 0 =1
S→id:=E {p:=lookup(); if p≠nil then emit(p’:=’E.place) else error} {E.place:=newtemp; emit(E.place’:=’E1.place’+’E2.place)}
E→E1+E2
2014年6月15日12时14分
2014年6月15日12时14分
另一种计算法是采取某种优化。假定要计算A or B,如果 计算出A 的值为1,那么,B的值就无须计算了。因为不管 B的结果是什么,A or B的值都为1。同时,在计算A and B 时,若发现A为0,则B的值也就无需再计算了。这种计算 法可以用if-then-else来解释or,and和not。也就是 把 A or B 解释成 把 A and B 解释成 把 not A 解释成 if A then true else B if A then B else false if A then false else true
(1)
(2) (3) (4) (5)
2014年6月15日12时14分
*
uminus * + :=
b
c b (1) a
(0)
(2) (3) (4)
(5)间接三元式
为了便于代码优化处理,另设一张指示器(称为间接码表) 它将按运算符的顺序列出有关三元式在三元表中的位置。 换句话说就是,我们用一张间接码表辅以三元式表的办法 来表示中间代码。这种表示法称为间接三元式。 当在代码优化过程中需要调整运算顺序时,只需重新安排 间接码表,无需改动三元式表。事实上,改动三元式表是 很困难的,因为,许多三元式通过指示器紧密相联系。
2014年6月15日12时14分
(2) 三地址代码
三地址代码是由下面一般形式的语句构成的序列:
x:=y op z
其中,x,y,z为名字、常数或编译时产生的临时变量; op代表运算符号加定点运算符、浮点运算符、逻辑运算符 等等。每个语句的右边只能有一个运算符。例如,源语言 表达式 x+y*z 可以被翻译为如下语句序列:
编译原理
主讲教师:雷向东
2014年6月15日12时14分
第七章 语义分析和中间代码产生
紧接词法分析和语法分析之后,编译程序要做的工作就是 进行静态语义检查和翻译。静态语义检查通常包括: (1) 类型检查;如果操作符作用于不相容的操作数,编译 程序必须报告出错信息。 (2) 控制流检查;控制流语句必须使控制转移到合法的地 方。如果不存在包括它的这样的语句,则应报错。 (3) 一致性检查;在很多场合要求对象只能被定义一次。 (4) 相关名字检查。有时,同一名字必须出现两次或多次。 其他如名字的作用域分析等也都是静态语义分析的工作。
2014年6月15日12时14分
虽然源程序可以直接翻译为目标语言代码,但是许多编译 程序却采用了独立于机器的、复杂性介于源语言和机器语 言之间的中间语言。这样的好处是: (1) 于进行与机器无关的代码优化工作;
(2) 便编译程序改变目标机更容易;
(3) 便编译程序的结构在逻辑上更为简单明确。以中间语 言为界面,编译前端和后端的接口更清晰。
2014年6月15日12时14分
上述这两种计算法对于不包含布尔函数调用的式子是没有 什么差别的。但是,假若一个布尔式中含有布尔函数调用, 并且这种函数调用引用起副作用 (指对全局量的赋值) 时, 那么,上述两种计算法未必是等价的。
7.4.1 数值表示法
用1表示真,0表示假来实现布尔表达式的翻译。
E→E1 or E2 E→E1and E2 {E.place:=newtemp; emit(E.place’:=’E1.place’or’E2.place)} {E.place:=newtemp; emit(E.place’:=’E1.place’and’E2.place)}
(1)
7.2 说明语句
在C、PASCAL、FORTRAN D 等语言的语法中,允许在 一个过程中的所有 说明语句作为一个组来处理, 把它们 安排在一个数据区中。 全程变量offset来跟踪一个可用的相对地址的位置; 过程enter (name, type, offset) 用来把名字name填入到符号 表中,并给出此名字的类型为type及在过程数据区中的相 对地址为offset。
2014年6月15日12时14分
例如,赋值语句a:=b*-c+b*-c的四元式为
Op (0) (1) (2) (3) (4) uminus * uminus * + Arg1 c b c b T3 T3 T4 T1 Arg2 Result T1 T2 T3 T4 T5
(5)
:=
T5
a
2014年6月15日12时14分
T1:=y*z T2:=x+T1 其中,T1,T2为编译时产生的临时变量。三地址语句通 常有三种表示方法:四元式、三元式、间接三元式。
2014年6月15日12时14分
(3) 四元式
一个四元式是一个带有四个域的记录结构,这四个域分别 称为op、arg1、arg2及result。域op包含一个代表运算符的 内部码。三地址语句 x;=y op z 可表示为:将y置于arg1域, z置于arg2域,x置于result域,:=为算符。通常,四元式中 的arg1,arg2和result的内容都是一个指针,此指针指向有 关名字的符号表入口。这样,临时变量也要填入符号表中。
2014年6月15日12时14分
产生式
P→D
D→D;D D→id:T T→integer T→real
语义规则
{ offset:=0}
{enter(, T.type, offset); offset:=offset+T.width} { T.type:=integer;
T.width:=4}
(4) 三元式 为了避免把临时变量填入到符号表,我们可以通过计算这 个临时变量值的语句的位置来引用这个临时变量。这样表 示三地址代码的记录只需要三个域:op、arg1和arg2。因 为用了三个域,所以称之为三元式。例如,赋值语句 a:=b*-c+b*-c的三元式为
Op (0) uminus Arg1 c Arg2
2014年6月15日12时14分
例如,语句
X:=(A+B)*C
Y:=D ↑(A+B)
间接三元式为
间接代码
(1) (2) (3)
三元式表
Op (1) (2) (3) + * := arg1 A (1) X arg2 B C (2)
(4)
(5)
2014年6月15日12时14分
(4)
(5)
↑
:=
D
Y
(1)
{E.place:=id.place);
Eቤተ መጻሕፍቲ ባይዱid
2014年6月15日12时14分
例 7.2 将布尔表达式a<b or c<d and e<f 翻译成三地址代码。
100 if a<b goto 103 101 T1:=0 102 goto 104 103 T1:=1 104 if c<d goto 107
2014年6月15日12时14分
对于多维数组也可作类似处理。一个二维数组,可以按 行或按列存放。FORTRAN采用按列存放,PASCAL采用 按行存放。
A[1,1] 第一行 A[1,2] A[1,3] A[2,1] 第二行 A[2,2] A[2,3] A[1,1] A[2,1] A[1,2] A[2,2] A[1,3] A[2,3] 第三列 第二列 第一列
按行存放
2014年6月15日12时14分
按列存放
若二维数组A按行存放,则可用如下公式计算A[i1, i2]的相 对地址: base+((i1-low1)*n2+i1-low2)*w
其中,low1,low2分别为i1、i2的下界;n2是i2可取值的 个数。即若high2为i2的上界,则n2=high2-low2+1。假定i1、 i2是编译时唯一尚未知道的值,重写上述表达式为 ((i1*n2)+i2)*w+(base-((low1*n2)+low2)*w)
E→E1*E2 E→-E1 E→(E1) E→id
{E.place:=newtemp; emit(E.place’:=’E1.place’*’E2.place)} {E.place:=newtemp; emit(E.place’:=’’uminus’E1.place)} {E.place:=E1.place} {p:=lookup(); if p≠nil then E.place:=p else error}
