通信软件设计-第2章 加法器-计数器实例-2011
加法器课程设计---四位二进制同步加法计数器

成绩评定表学生姓名班级学号专业课程设计题目四位二进制同步加法器(缺0000,0001,0100,0101) 评语组长签字:成绩日期 20 年月日课程设计任务书学院专业学生姓名班级学号课程设计题目四位二进制同步加法计数器(缺0000,0001,0100,0101)实践教学要求与任务:1.了解数字系统设计方法。
2.熟悉ISE仿真环境及VHDL下载。
3.熟悉Multisim仿真环境。
4.设计实现四位二进制同步加法计数器(缺0000,0001,0100,0101)工作计划与进度安排:第一周:熟悉Multisim及Xilinx及Xilinx ISE环境,练习数字系统设计方法第二周:(1)在ISE环境中仿真实现四位二进制同步加法计数器(缺0000,0001,0100,0101)。
(2)在Multisim环境中仿真实现四位二进制同步加法计数器(缺0000,0001,0100,0101),并通过虚拟仪器验证其正确性。
指导教师:201 年月日专业负责人:201 年月日学院教学副院长:201 年月日目录一、课程设计目的 (1)二、设计框图 (1)三、实现过程 (1)1、Xilinx ISE10.1实现过程(VHDL) (1)1、1、建立工程 (2)1、2、调试程序 (4)1、3、波形仿真 (5)1、4、引脚锁定与下载 (7)1、5、仿真结果分析 (10)2、Multisim10实现过程(电路设计) (10)2、1、设计原理 (10)2、2、基于Multisim的设计电路 (13)2、3、虚拟观察的波形 (14)2、4、仿真结果分析 (14)四、设计总结 (15)五、参考文献 (15)四位二进制加法计数器一. 课程设计的目的1.了解数字系统设计原理及方法。
2.熟悉Xillinx ISE 仿真环境及VHDL 下载。
3.熟悉Mutisim 仿真环境。
4.设计实现(四位二进制加法计数器(缺0000,0001,0100,0101))。
加法器电路的设计

加法器电路的设计加法器是数字电路中常见的一种逻辑电路,用于实现多个数字信号的加法运算。
它是计算机中基本的运算器件之一,广泛应用于各种计算机及数字电子设备中。
加法器的设计首先要考虑的是输入和输出的位数。
一般情况下,我们需要设计一个n位的加法器,其中n可以是任意正整数。
接下来,我们将详细介绍一个4位加法器的设计过程。
4位加法器的设计可以通过级联多个1位加法器实现。
每个1位加法器有两个输入A和B,以及一个进位输入Cin,两个输出之和S和进位输出Cout。
首先,我们需要实现1位全加器。
1位全加器可以通过两个半加器(Half Adder)和一个或门(OR gate)组合而成。
半加器有两个输入A和B,以及一个进位输入Cin,和两个输出之和S和进位输出Cout。
它的真值表如下所示:```A B Cin S Cout0000001010100101100100110011011010111111```其中,S代表两个输入的和,Cout代表进位输出。
半加器可以用逻辑门来实现。
S可以通过一个异或门(XOR gate)实现,Cout可以通过一个与门(AND gate)实现。
具体实现如下所示:S=A⊕BCout = A ∧ B接下来,我们将两个半加器级联成一个1位全加器。
如下所示:```__________________A---_____B--->,Half , AND ,---->CouCin->, Adder , Gate,________________________,XOR,---->, Gat,_____```在该电路中,两个输入A和B直接连接到两个半加器的对应输入上,进位输入Cin只连接到第一个半加器的进位输入上。
两个半加器的和输出S通过异或门连接在一起,同时使用与门实现进位输出Cout。
有了1位全加器的设计,我们就可以开始组合多个1位全加器来实现4位加法器了。
具体的设计思路是:1.将四个输入A0-A3和B0-B3连接到四个1位全加器的对应输入上。
通信软件设计-第3章 乘法器除法器设计实例-

函数的目的是通过返回一个值来响应输入信 号的值。任务却能支持多种目的,能计算多个 结果值,这些结果值只能通过被调用的任务的 输ቤተ መጻሕፍቲ ባይዱ或总线端口送出.
task 和 function 说明语句 task说明语句
1)任务的定义。 task <任务名>; <端口及数据类型声明语句> <语句1> <语句2> ..... <语句n> endtask
查找表乘法器 lookup_mult module lookup_mult(out,a,b,clk);
output[7:0] out; input[3:0] a,b; input clk; reg[7:0] out; reg[1:0] firsta,firstb; reg[1:0] seconda,secondb; wire[3:0] outa,outb,outc,outd; always @(posedge clk) begin firsta = a[3:2]; seconda = a[1:0]; firstb = b[3:2]; secondb = b[1:0]; end lookup m1(outa,firsta,firstb,clk), m2(outb,firsta,secondb,clk), m3(outc,seconda,firstb,clk), m4(outd,seconda,secondb,clk); always @(posedge clk) begin out = (outa << 4) + (outb << 2) + (outc << 2) + outd; end endmodule
项目2一位加法计算器的设计与制作

根据编码的概念,编码器的输入端子数N和输出端子数n应满足 如下关系:
N
≤
2
n
编码器按编码方式不同,可分为普通编码器和优先编码器。按 输出代码的种类不同,又可分为二进制编码器和二-十进制编码器等。
图2-3 三位二进制普通编码器的逻辑图
1.普通编码器 普通编码器的特点是在任一时刻,只允许输入一个编码信号, 否则输出发生混乱。如图2-3所示的电路是用与非门及非门组成的 三位二进制普通编码器的逻辑图。该电路的输入端子数为7,输出 端子数为3。
[项目实施]
工作任务 名称一位加法Biblioteka 算器的设计与制作元器件选择
仪器设备 1.直流稳电源 2.万用表 3.面包板(或者印制电路板和电烙 铁) 4.集成电路测试装置(配16脚和14脚的集成电路插座) 5.示波 器
序 号
型号规 个 序号 名称 型号规格 个数 格 数 6×6×1 2套, 显示译码 按键S1~ 0mm 1 18 5 74LS48 2 器IC6、 S9 (标注 IC7 个 1~9) LED显示 LG5011A 编码器IC1、 2 74LS147 2 6 2 器IC8、 IC2 H IC9 名称 3 六反相器 IC3、IC4 74LS04 2 7 编码器限 流电阻R 1kΩ 18
74LS147的功能见表2-3所示。 表2-3 74LS147的功能表
3.编码器的应用 74LS148优先编码器的功能扩展。 【例2-1】 用两片74LS148优先编码器扩展成为16线-4线优先 译码器。 解设16线-4线优先编码器的编码输入端为 I15 ~ I 0 ,二进制代码 的输出端为 Y ~ Y 0 。
该编码器任何时刻都不允许有两个或两个以上输入信号同时 请求编码,否则输出将发生混乱。
加法器的实现

19
2.3.3 多功能算术/逻辑运算单元ALU
具有正逻辑和负逻辑两种
2020/3/28
20
2.3.3 多功能算术/逻辑运算单元ALU
算术逻辑运算的实现(74181)
M=L时,对进位信号没有影响,做算术运算 M=H时,进位门被封锁,做逻辑运算
说明:
74181执行正逻辑输入/输出方式的一组算术运算和 逻辑运算和负逻辑输入/输出方式的一组算术运算 和逻辑运算是等效的。
例如:
S3S2S0S1=0000
M
M=1
代入:
X i S3 Ai Bi S2 Ai Bi 0 0 1
Yi Ai S0Bi S1 Bi Ai Fi Yi X i Cn1 Ai 1 Cn1 Ai (设Cn1=0) 所以在S3~S0=0000的时候,输出结果为Ai
2020/3/28
第二章 运算方法和运算器
2.1数据与文字的表示 2.2定点加法、减法运算P45 2.3定点运算器的组成 2.4定点乘法运算 2.5定点除法运算 2.6浮点运算与浮点运算器
2020/3/28
返回 1
2.3 定点运算器的组成
2.3.1 定点运算器的先行进位 2.3.1 逻辑运算 2.3.2 多功能算术/逻辑运算单元ALU
C1 = G1 + P1 C0 = G1 + P1 C0 C2 = G2 + P2 C1 = G2 + P2 G1 + P2 P1 C0 C3 = G3 + P3 C2 = G3 + P3 G2 + P3 P2 G1 + P3 P2 P1 C0
C4 = G4 + P4 G3 + P4 P3 G2 + P4 P3 P2 G1 + P4 P3 P2 P1 C0 C5 = G5 + P5 C4 …… C8 = G8 + P8 G7 + P8 P7 G6 + P8 P7 P6 G5 + P8 P7 P6 P5 C4 C12 = G12+ P12G11 + P12P11G10 + P12P11P10G9 + P12P11P10P9C8 C G P G P P G P P P G P P P P C 16 = 16+ 16 15 + 16 15 14 + 16 15 14 13 + 16 15 14 13 12
加法器及运算

1
1 0
M Ci-1
Ci
⊕ ⊕
Fi
例2. S3S2S1S0 Xi Yi 1 0 0 1 Ai+Bi AiBi
F(M=1) F(M=0)
A B A加 B
1=Ai Bi
M=1:Fi=(Ai + Bi) AiBi 1=Ai Bi
Xi 所以 F=A B Yi
M=0:Fi=(Ai+Bi) AiBi Ci-1=Ai Bi Ci-1 = Ai Bi Ci-1 所以 F = A加B
1
0
∑7 A7 B7
1 0
1
1
0
∑2 A2 B2
1 0
1
0
∑1 A1 B1
1 0
1
C0
(2)影响速度的主要因素 存在着进位信号的传递。
2. 并行加法器的进位链 (1)进位链的基本逻辑关系
Ci = AiBi + (Ai + Bi)Ci-1 = AiBi + (Ai + Bi)Ci-1 或 Ci = AiBi + (Ai + Bi)Ci-1
8
CI
74181
8
C0
第二节 运算器组织 寄存器组 独立结构
小型存储 器结构 单口 双口
独立R、双口RAM用多路选择器作为ALU的 输入逻辑, 单口RAM用锁存器作为ALU的输入逻辑。
2.2.1 带多路选择器的运算器
内部总线(单向) 移位器 R0 Rn
ALU
特点:
多路选择器 多路选择器
R各自独立;
2)结构举例
C2 G2 P2 C1 G1 P1 C0
Gi
Pi
Ai Bi
Ai Bi
第2章 加法器

应用于四个4位先行进位加法器,则有:
Cm1=Gm1+Pm1C0 Cm2=Gm2+Pm2Cm1 = Gm2+ Pm2Gm1 + Pm2 Pm1C0
Cm3=Gm3+Pm3Cm2 = Gm3+ Pm3Gm2 + Pm3Pm2Gm1+ Pm3 Pm2 Pm1C0
Cm4=Gm4+Pm4Cm3 = Gm4+ Pm4Gm3 + Pm4Pm3Gm2+ Pm4Pm3Pm2 Gm1+ Pm4Pm3Pm2P m1C0
cc33cc44cc22cc11gg22pp33gg33pp44gg44gg11pp22pp11先行进位产生电路cc00先行进位线路ff44cc33aa44bb44pp44gg44faff33cc22aa33bb33pp33gg33faff22cc11aa22bb22pp22gg22facc00ff11aa11bb11pp11gg11facc4444位先行进位加法器?理论上讲这种先行进位加法器可以扩充到n位字长但是当加法器位数增加时进位函数ci1会变得越来越复杂n位字长的加法器最高进位位需要一个n1位输入的或门和n1位输入的与门电路实现这给电路的实现带来了困难
• 在行波进位加法器中,进位信号的逻辑表 达式为: Ci= Gi+Pi Ci-1 • C1=G1+P1C0 • C2=G2+P2C1 • C3=G3+P3C2 • ………… • Cn=Gn+PnCn-1 可见,后一级的进位直接依赖前一级,进 位是逐级形成的,最长进位延迟时间为 2.5nty,与n成正比。可见,行波进位加法 器的加法速度比较低。
• 则当实现加法运算时,给出A→FA及B→FA 两个控制命令,则将[A]补和[B]补送到加法 器 FA 的两个输入端, FA 完成 [A] 补+ [B] 补 的加法过程,然后通过FA→A命令将加法运 算结果存入A寄存器。 • 如果实现减法运算,给出 A→FA 及 /B→FA 以及1→C0控制命令,则将[A]补和[-B]补送 到加法器FA的两个输入端,FA完成[A]补+ [-B]补的加法过程,然后通过 FA→A命令将 减法运算结果存入A寄存器。
加法器电路

加法器电路概述:加法器电路是一种基本的数字电路,用于将两个二进制数相加。
它是数字计算机中常用的关键部件之一。
在本文中,我们将探讨加法器电路的原理、分类、设计和应用。
一、原理加法器电路的原理基于基本的二进制加法规则。
在二进制加法中,相加的两个数字(0或1)称为位,而进位(carry)表示相邻位之间的进位情况。
加法器电路的任务是将这两个输入位和进位位相加,并产生正确的输出位和输出进位。
加法器电路的实现有多种方法,包括半加器、全加器和并行加法器。
1. 半加器:半加器是最基本的加法器电路,用于实现单个位的相加。
它有两个输入,即要相加的两个位(A和B),以及一个进位输入(Carry In)。
半加器的输出包括两个部分:和(Sum)和进位(Carry)。
和位表示两个输入位相加的结果,进位位表示进位情况。
半加器电路可以用逻辑门实现,如异或门和与门。
2. 全加器:全加器扩展了半加器的功能,用于实现两个位和一个进位位的相加。
除了输入位(A和B)和进位输入(Carry In),全加器还有一个输出进位(Carry Out)。
当两个输入位和进位位相加时,全加器产生两个输出:和位(Sum)和进位位(Carry Out)。
全加器电路可以通过组合多个半加器电路来实现。
3. 并行加法器:并行加法器是多位加法器的一种形式,用于实现多位的二进制数相加。
它在每一位上使用全加器电路,并将进位位连接在各个全加器之间。
并行加法器通过同时处理多个位来实现快速的二进制加法,因此在计算机中得到广泛应用。
二、分类根据多位加法器的输入和输出方式,加法器电路可以分为串行加法器和并行加法器。
1. 串行加法器:串行加法器按位进行计算,即逐个位地相加和产生进位。
它的输入和输出仅在单个位上进行。
串行加法器的优点是简单且成本低廉,但它的运算速度较慢。
2. 并行加法器:并行加法器可以同时处理多个位的相加和进位。
它的输入和输出可以同时进行,并且每一位之间可以并行操作。
计算机组成原理第2章-二进制加减法器

X←F 选通门
X ← X-Y
F← X
减
F← Y F← 1
X← F
4/12/2021
实现补码加运算的执行过程
X ← X+Y
Fs
00000111
OVR
Z
Fs 加法器
C
完成加运算,需 要把被加数和加 数送ALU的输入
端,运算结果要
F←X
选通门
F←Y 接收到累加器,
二选一
需要给出命令:
X
CP
01001001101
基本的二进制加/减法器
全加器的表达式为:
Si = Ai Bi Ci Ci+1 = AiBi + BiCi + AiCi 一位全加器内部逻辑图
Ci+
Si
C
1
AB C
Ci
Ai
Bi A
B
3
信 息 科 学 与 工 程 学 院3
第二章 运算方法和运算器
数据与文字的表示 定点加减法运算 定点乘法运算 定点除法运算 定点运算器的组成 浮点运算与浮点运算器
4/12/2021
单符号位判断
数值位向符 号位有进位
OV= C0 C1 + C0 C1 判断电路
但符号位无 进位输出或
c0
数值位向符 号位没有进 位但符号位 本身有进位 输出是溢出
x0 y0
x1 y1
FA
z0
c1
FA
z1
OV
4/12/2021
双符号位判断
OV= z0' z0 + z'0 z0 = z0' z0
5
信 息 科 学 与 工 程 学 院5
加法计数器电路设计

加法计数器电路设计需要考虑多个因素,包括输入信号、计数器状态、计数规则等。
以下是一个简单的加法计数器电路设计的步骤:
1. 确定计数器的位数:根据需要计数的最大值和最小值,确定计数器的位数。
例如,如果要计数的范围是0到99,则可以选择一个3位的二进制计数器。
2. 确定计数器的状态:根据确定的位数,确定计数器的所有可能状态。
例如,对于一个3位的二进制计数器,有8个可能的状态:000、001、010、011、100、101、110、111。
3. 确定计数规则:根据计数器的状态和输入信号,确定计数器的计数规则。
例如,对于一个3位的二进制加法计数器,可以采用逢十进一的规则,即当计数器的值达到最大值(111)时,下一个输入信号会使计数器的值回绕到最小值(000)。
4. 设计电路:根据上述步骤,设计加法计数器电路。
可以采用门电路、触发器等电子元件来构成加法计数器。
在设计过程中,需要考虑电路的稳定性和可靠性,以及尽量减小功耗和减小体积等问题。
5. 仿真和测试:使用仿真软件对设计的加法计数器电路进行仿真和测试,以确保其功能正确性和性能可靠性。
总之,加法计数器电路设计需要综合考虑多个因素,并采用合适的电子元件和设计方法来实现。
三位二进制加法计数器(精)

成绩评定表学生姓名班级学号专业自动化课程设计题目数字电子课程设计评语组长签字:成绩日期20 年月日课程设计任务书学院信息科学与工程学院专业自动化学生姓名班级学号课程设计题目 1.三位二进制加法计数器(无效态:001,110)2.序列信号发生器的设计(发生序列100101)3.100进制加法计数器设计实践教学要求与任务:数字电子部分1)采用multisim 仿真软件建立电路模型;2)对电路进行理论分析、计算;3)在multisim环境下分析仿真结果,给出仿真波形图。
工作计划与进度安排:第1天:1. 布置课程设计题目及任务。
2. 查找文献、资料,确立设计方案。
第2-3天:1. 安装multisim软件,熟悉multisim软件仿真环境。
2. 在multisim环境下建立电路模型,学会建立元件库。
第4天:1. 对设计电路进行理论分析、计算。
2. 在multisim环境下仿真电路功能,修改相应参数,分析结果的变化情况。
第5天:1. 课程设计结果验收。
2. 针对课程设计题目进行答辩。
3. 完成课程设计报告。
指导教师:201 年月日专业负责人:201 年月日学院教学副院长:201 年月日目录1 课程设计的目的与作用11.1设计目的及设计思想11.2设计的作用11.3 设计的任务12 所用multisim软件环境介绍13 三位二进制同步加法计数器设计33.1 基本原理33.2 设计过程34序列信号发生器的设计..64.1 基本原理64.2 设计过程66 100进制加法器计数器76.1 基本原理76.2 设计过程75 仿真结果分析85.1 三位二进制同步加法计数器仿真85.2 序列信号发生器(发生序列100101)的仿真116 设计总结和体会147 参考文献141 课程设计的目的与作用1.1设计目的及设计思想根据设计要求设计三位二进制加法计数器和序列信号发生器,加强对数字电子技术的理解,进一步巩固课堂上学到的理论知识。
加法器
Y(A<B)
Y(A=B)
B
B AB
Y(A>B)
(二) 多位数值比较器 可利用 1 位数值比较器构成
比较原理:从最高位开始逐步向低位进行比较。
例 比较 A = A3A2A1A0 和 B = B3B2B1B0 的大小:
若 A3 > B3,则 A > B;若 A3 < B3,则 A < B; 若 A3 = B3,则需比较次高位。 若次高位 A2 > B2,则 A > B;若 A2 < B2,则 A < B; 若 A2 = B2,则再去比较更低位。 依次类推,直至最低位比较结束。
四位数字比较器功能表
A3B3
A2B2 A1B1 A0B0
IA>B
IA<B
IA=B
A3>B3 ×
×
A3<B3 ×
×
A3=B3 A2>B2 ×
A3=B3 A2<B2 ×
A3=B3 A2=B2 A1>B1
A3=B3 A2=B2 A1<B1
A3=B3 A2=B2 A1=B1
A3=B3 A2=B2 A1=B1
YA<B YA>B YA=B
两片CC14585组成8位数值比较器
பைடு நூலகம்
6.7 组合逻辑电路中的竞争冒险
一、竞争冒险现象及其危害
当信号通过导线和门电路时,将产生时间延迟。 因此,同一个门的一组输入信号,由于它们在此前通 过不同数目的门,经过不同长度导线的传输,到达门 输入端的时间会有先有后,这种现象称为竞争。
逻辑门因输入端的竞争而导致输出产生不应有的尖峰 干扰脉冲的现象,称为冒险。
可能导致错误动作
二、竞争冒险的产生原因及消除方法
负尖峰脉冲冒险举例
通信工程设计与监理《多位加法器教案》

多位加法器一、教学目标了解加法器掌握多位加法器、串联进位并行加法器、超前进位二进制并行加法器二、教学重点、难点重点掌握掌握多位加法器、串联进位并行加法器、超前进位二进制并行加法器三、教学过程设计1加法器简介加法器是为了实现加法的。
即是产生数的和的装置。
加数和被加数为输入,和数与进位为输出的装置为半加器。
假设加数、被加数与低位的进位数为输入,而和数与进位为输出那么为全加器。
常用作计算机算术逻辑部件,执行逻辑操作、移位与指令调用。
2.串联进位并行加法器并行加法器按其进位方式的不同,可分为串行进位并行加法器和超前进位并行加法器两种类型。
串行进位并行加法器:由全加器级联构成,高位的进位输出依赖于低位的进位输入。
框图如图1-1所示。
1-13超前进位二进制并行加法器超前进位二进制并行加法器特点:1 根据输入信号同时形成各位向高位的进位。
2 同时产生各位的和。
由全加器的结构可知:ii i i ii i i i i i i i i i ii i i B A C B C B A C B A C B A C B A C C B A S i i +•⊕=+++=⊕⊕=+)(i 1A关键是进位信号Ci i i i i ii i i i i i i i i i i i B A C B A C B A C B A C B A C B A C +⊕=+++=+)(1当 i=1、2、3、4时,根据递推关系,可得到4位并行加法器各位的进位输出函数表达式为:四、课后作业或思考题1、总结超前进位二进制并行加法器。
令 〔进位传递函数〕 〔进位产生函数〕 那么有i i i P B A →⊕i i i G B A →ii i i G C P C +=+1。
第2章 加法器

3.5 定点运算器的组成 1)定点运算器的基本结构 • 不同的计算机其运算器的组成结构是不同的, 但一般都包含以下几部分。 1.算术逻辑运算单元ALU • 在计算机中,通常具体实现算术运算和逻辑 运算的部件称为算术逻辑运算单元 (Arithmetic and Logic Unit),简称ALU, 它是加法器、乘法器和逻辑运算器的集成, 是运算器的核心。ALU通常表示为两个输入 端,一个输出端和多个功能控制信号端的一 个逻辑符号。加法器是ALU的核心,是决定 ALU运算速度的主要因素。
第2 章 加法器
• 计算机要对各种信息进行加工和处理。 • 如对数值数据进行加、减、乘、除的数 值运算,对非数值数据进行与、或、非 的逻辑运算。 • 在计算机中必须有对数据进行处理的部 件,这个部件就是运算器。 • 目前,大多数计算机都将运算器和控制 器集成在一个芯片上,也就是我们常说 的CPU。
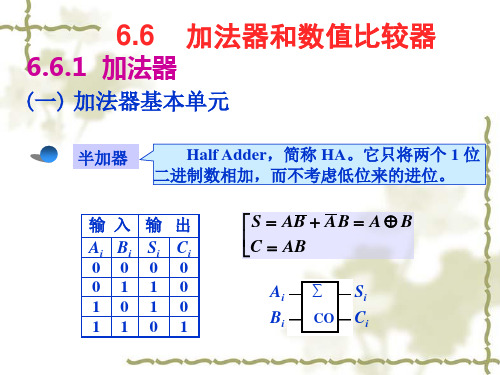
二进制加法器 1.半加器 • 两个一位二进制数相加(不考虑低位的进 位),称为半加。实现半加操作的电路称 为半加器。 • 半加器的真值表、逻辑图和逻辑符号。 2.全加器 • 在实现多位二进制数相加时,不仅考虑本 位,还要考虑低位来的进位,这种考虑低 位的进位加法运算就是全加运算, • 实现全加运算的电路称为全加器。
A8 A7A6A5 B8B7B6B5
A4 A3A2A1B4B3B2B1
16位行波进位加法器
• 在这种结构中,由于组间进位C4、C8、 C12、C16仍然是串行产生的,最高进位 的产生时间为4×(2.5ty)=10ty。 • 采用这种结构,在大大地缩短了进位延迟 时间的同时兼顾了电路设计的复杂性。 • 如果还需要进一步提高速度,可以采用两 级先行进位结构。
• 4)附加的控制线路 运算器要求运算速度快,运算精度高。为 了达到这一目的,通常还在运算器中附加 一些控制线路。 i -i • 如:运算器中的乘2 或乘2 运算和某些逻 辑运算是通过移位操作来实现的。这通常 是在ALU的输出端设置移位线路来实现。 移位包括左移,右移和直送。移位线路也 是一个多路选择器。 • 定点运算器的组成
加法器实例

混合描述
module Full_add(A, B, Cin, Sum, Cout ); input A,B,Cin; output Sum,Cout; reg Sum, Cout, m1,m2,m3; wire s1; xor x1(s1,A,B); //调用门元件 always@ ( A or B or Cin ) //行为描述 begin m1 = A & Cin; m2 = B & Cin ; m3 = A & B; Cout = (m1| m2) | m3; end assign Sum =s1 ^ Cin ; //数据流描述 endmodule
怎样设计复杂的数字系统?
现代的设计方法(续前):
- 选用合适的基本逻辑元件库和宏库 - 租用或购买必要的IP核; - 选用合适的综合器; - 进行综合得到门级电路结构; - 布局布线,得到时延文件; - 后仿真; - 定型, FPGA编码或ASIC投片
第4章 Verilog HDL硬件描述语言
什么是Verilog HDL? Verilog HDL(Hardware Discription Language) 是一种硬件描述语言,用于 从行为级、RTL级、门级到开关级的多种 抽象设计层次的数字系统建模。
第4章 Verilog HDL硬件描述语言概述
Verilog设计方法简介 Verilog建模概述 Verilog的基本语法 结构建模 数据流建模 行为建模 混合建模 Verilog设计的层次
当前数字电路设计层次
1. 算法级设计:利用高级语言如C语言及其他一些系统分析 工具(如MATLAB)对设计从系统的算法级方式进行描述。 算法级不需要包含时序信息。 2. RTL级(寄存器传输)设计:用数据流在寄存器间传输的 模式来对设计进行描述。 3. 门级:用逻辑级的与、或、非门等门级之间的连接对设 计进行描述。 4. 开关级:用晶体管和寄存器及他们之间的连线关系来对 设计进行描述。 算法级是高级的建模,一般对特大型设计或有较复杂的 算法时使用,特别是通讯方面的一些系统,通过算法级的建 模来保证设计的系统性能。在算法级通过后,再把算法级用 RTL级进行描述。门级一般对小型设计可适合。开关级一般 是在版图级进行。
02-16.1 加法器工作原理-课件
依次代入 展开:
第i位的和为:
(CO )i Gi Pi Gi 1 Pi Pi 1Gi 2 K
Pi Pi 1 K P G1
0
PP
(CIi )
i i
1
(KCOP1C) i10
S i Ai Bi (CI )i
《数字电子技术基础》
第十六讲 若干常用中规模组合逻辑电路-加法器
★ 超前进位加法器示例
█ 4位串行进位全加器的Verilog-HDL设计
//4位串行进位全加器设计 full_add1 f0
(a[0],b[0],cin,sum[0],cin1);
module add4_1
full_add1 f1
(sum,cout,a,b,cin); (a[1],b[1],cin1,sum[1],cin2);
目前,常用加法器分类如下:
1位加法器 加
法
器
多位加法器
半加器 全加器 串行进位加法器 超前进位加法器
《数字电子技术基础》
第十六讲 若干常用中规模组合逻辑电路-加法器
█ 1位全加器
◆ 半加器(Half-adder)
若不考虑有来自低位的进位将两个1位二进制数相加, 称为半加。实现半加运算的电路叫做半加器。
output cout; output[3:0] sum; input[3:0] a,b; input cin;
full_add1 f2 (a[2],b[2],cin2,sum[2],cin3); full_add1 f3 (a[3],b[3],cin3,sum[3],cout);
endmodule
下图示出了4位 超前进位加法 器74LS283的电 路图:
图2 74LS283的逻辑电路图
第2章(5)组合逻辑电路1(加法器)

Ci -1
Ai Bi 1 0
Si 的卡诺图
Si m1 m2 m4 m7
2.5 加法器
2.5.1 半加器和全加器 2.5.2 加法器 2.5.3 加法器的应用 退出
2.5.1 1位半加器和1位全加器
1、半加器
能对两个1位二进制数进行相加而求得和及进位的逻辑 电路称为半加器。
半加器真值表 Ai Bi 0 1 0 1 Si 0 1 1 0 Ci 0 0 0 1
本位 的和 向高 位的 进位
V DD B3 C3 S3 S2 S1 S0 C0-1 16 15 14 13 12 11 10 9 4008 1 2 3 4 5 6 7 8 A3 B2 A2 B1 A1 B0 A0 VSS CMOS 加法器 4008 引脚图
图2.42 2片74283组成的8位二进制数加法电路图
2 . 用 74LS283 实 现 余 3 码 到 8421BCD码的转换 对同一个十进制数符,余3码
Ci m3 m5 Ai Bi Ai BiCi 1 Ai BiCi 1 Ai Bi ( Ai Bi Ai Bi )Ci 1 Ai B ( Ai Bi )Ci 1 Ai Bi
Ai Bi Ci-1 =1 =1 & & & (a) 逻辑图 Ci Ai Bi Ci-1 ∑
CO ∑ CI CI CI
CO ∑ CI CI CI
A3
B3
A2
B2
A1
B1
A0
§2~2:加法器

一、 半加器 例题 分析如图 所示电路的逻辑功能。
解: (1) 由逻辑图写出逻辑式 (2) 由逻辑式列出真值表
(3) 分析逻辑功能
S 为 A 和 B 相加之和的最低位, C 是 A 和 B 相加后向高一位的进位。 这一组合逻辑电路完成了两个 1 位二 进制数相加。
位的结构形式。
4 位二进制加法器
只考虑加数与被加数, 不考虑低位进位, 这样 的加法运算称为半加, 相应地, 这一逻辑电路称为 半加器。
半加器的逻辑符号如图 所示 (其中的下标 i 表示某数的
二、 全加器
通常计算中除了完成两个 1 位二进制数的相加外, 还要考虑低位的进位, 这种加法称为全加运算。 实现全 加运算的组合逻辑电路称为全加器。
全加器的真值表
其中 A i 、 B i 表示被加数和加数, C i - l 表示 相邻低位的进位数, S i 、 C i 表示第 i 位全加的和及向 相邻高位的进位数。
使用与非门和异或门构成全加器, 可将 S i 、 C i 表达式进行变换:
全加器的逻辑图和符号
三、 多位二进制加法器 多位二进制数相加时, 通常采用并行相加、串行进
第2章(2)加法器

(mod 2)
(2)x﹥0,y﹤0,则x+y>0或x+y<0。
相加的两数一个为正,一个为负,因此相加结果有正、负两种
可能。根据补码定义,
∵ [x]补=x,
[y]补=2+y
∴ [x]补+[y]补=x+2+y=2+(x+y) 当x+y>0时,2 + (x+y) > 2,进位2必丢失,又因(x+
y)>0,
[例14] x=+0.1100, y=+0.1000,求x+y。
[解:]
[x]补=00.1100, [y]补=00.1000
[x]补 +[y]补
00.1100 00.1000 01.0100
两个符号位出现“01”,表示已溢出,即结果大于+1。
[例15] x=-0.1100, y=-0.1000,求x+y。
[解:]
[x]补=11.0100, [y]补=11.1000
[x]补 +[y]补
11.0100 11.1000 10.1100
两个符号位出现“10”,表示已溢出,即结果小于-1。
由此可以得出如下结论:
1. 当以模4补码运算,运算结果的二符号位相异时,表 示溢出;相同时,表示未溢出。故溢出逻辑表达式为 V=Sf1⊕Sf2,其中Sf1和Sf2分别为最高符号位和第二符 号位。此逻辑表达式可用异或门实现。
而可使模2补码所能表示的数的范围扩大一倍。变形补码定义
为
x
2>x≥0
[x]补=
4+x 0>x≥-2
(2.22)
或用同余式表示为
[x]补=4+x
下式也同样成立:
(mod 4)
[x]补+[y]补=[x+y]补
(mod 4)
变形补码即为双符号位法。 为了得到两数变形补码之和等于两数之和的变形补码, 同样必须:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.1
•
1位半加器adder设计实例
半加器定义:即是产生数的和的装置。加数和被加 数为输入,和数与进位为输出的装置为半加器。
•
全加器定义:若加数、被加数与低位的进位数为输
full_add仿真波形
2.3同步4bit全加法器的设计实例
2.3同步4bit全加法器的设计ial和always说明语句在仿真的一开 始即开始执行。initial语句只执行一次。 相反,always语句则是不断地重复执行,
直到仿真过程结束。
2.3.1 always 语句
全加器的verilog代码
• • • • • • • • • • • • • • module full_add (a,b,cin,sum,cout); input a,b,cin; output sum,cout; reg sum,cout; reg m1,m2,m3; always @(a or b or cin) begin sum = (a ^ b) ^ cin;//^按位逻辑异或 m1 = a & b; m2 = b & cin; m3 = a & cin; cout = (m1|m2)|m3; end endmodule
2.1 模块的结构
2.1.1 模块的端口定义
模块的端口声明了模块的输入输出口。其格式如 下: module 模块名(口1,口2,口3,口4, ………); 模块的内容包括I/O说明、内部信号声明、功能 定义。 • I/O说明的格式 输入口:input[信号位宽-1:0] 端口名1; input[信号位宽-1:0] 端口名2; … input[信号位宽-1:0] 端口名 i; //(共有i个输入口)
• always语句在仿真过程中是不断重复执行的。 其声明格式如下: always <时序控制> <语句> always语句由于其不断重复执行的特性,只有 和一定的时序控制结合在一起才有用。如果一个 always语句没有时序控制,则这个always语句将 会发成一个仿真死锁。
always areg = ~areg; 这个always语句将会生成一个0延迟的无限循环跳变
2.2.3 Testbench仿真波形
• • • • • • • • • • • • • • # # # # # # # # # # # # # # 0 0 + 0 + 0 ={0,0} 5 0 + 0 + 1 ={0,1} 10 0 + 1 + 0 ={0,1} 15 0 + 1 + 1 ={1,0} 20 1 + 0 + 0 ={0,1} 25 1 + 0 + 1 ={1,0} 30 1 + 1 + 0 ={1,0} 35 1 + 1 + 1 ={1,1} 40 0 + 0 + 0 ={0,0} 45 0 + 0 + 1 ={0,1} 50 0 + 1 + 0 ={0,1} 55 0 + 1 + 1 ={1,0} 60 1 + 0 + 0 ={0,1} 65 1 + 0 + 1 ={1,0}
2.1.1 模块的结构
Verilog 模块的结构由在module和 endmodule 关键词之间的四个主要部分组 成:
- 端口定义: - I/O说明 : module block1(a, b, c, d ); input a, b, c ; output d ; - 内部信号声明: wire x; - 功能定义: assign d = a | x ; assign x = ( b & ~c ); endmodule
Adder4的testbench设计
• `timescale 1ns/10ps `include "adder4.v" • module adder4_testbench; • reg [3:0] ina,inb; • reg cin; • reg clk=0; • wire [3:0] sum; • wire cout;
Full_add Testbench代码
• • • • • • • • • • • • • • `timescale 1ns/10ps `include "full_add.v" module full_add_testbench; reg a,b,cin; wire sum,cout; integer i,j,k; full_add full_adder_te( .sum ( sum ), .cout ( cout), .a ( a ), .b ( b ), .cin ( cin) );
adder4 testbench的设 计
• initial • begin • cin=0; • repeat(2) • #200 • cin ={$random}%16; • end adder4 adder4_te( • .clk (clk ), • .sum ( sum ), • .cout ( cout), • .ina ( ina ), • .inb ( inb ), • .cin ( cin ) • ); • initial • begin • $monitor($time,,,"%b + %b + %b ={%b,%b}",ina,inb,cin,cout,sum); • #400 $finish; • end • endmodule
Adder4的I/O口说明
Adder4的I/O口说明
• • • • • • module adder4(cout,sum,ina,inb,cin,clk); output[3:0] sum; output cout; input[3:0] ina,inb; input cin,clk; reg[3:0] tempa,tempb,sum; //tempa,tempb 中间变量说明 • reg cout; • reg tempc; //tempc中间变量说明
initial //a向量 begin a=0; for(i=1;i<16;i=i+1) #20 a=~a; //a周期为40ns end initial //b向量 begin b=0; for(j=1;j<16;j=j+1) #10 b=~b; // b周期为20ns end Initia // cin向量 begin cin=0; for(k=1;k<16;k=k+1) #5 cin=~cin; // cin周期为10ns end initial begin $monitor($time,,,"%d + %d + %d ={%b,%d}",a,b,cin,cout,sum); #80 $finish; end endmodule
系统任务 $random
这个系统函数提供了一个产生随机数的手段。当函数被 调用时返回一个32bit的随机数。它是一个带符号的整形数。 $ramdom % b ,其中 b>0. 它给出了一个范围在(-b+1):(b-1)中的随机数。 reg[23:0] rand; rand = $random % 60; reg[23:0] rand; rand = {$random} % 60; 给出了一个范围在-59到59 之间的随机数 通过位并接操作产生一个值 在0到59之间的数
2.1.2 adder Testbench的编写
• • • • • • • • • • • • • • • • • initial //initial 语句同时立即执行,不需要时间 begin a=0;b=0; for(i=1;i<16;i=i+1) #20 a=i; end initial begin for(j=1;j<16;j=j+1) #10 b=j; end initial begin $monitor($time,,,"%d + %d ={%b,%d}",a,b,cout,sum); #160 $finish; end endmodule
2.1.2 adder Testbench 设计
• 什么是 Testbench
如何编写Testbench
2.1.2 adder Testbench的编写
• • • • • • • • • • • • `timescale 1ns/10ps //定义时间精度 `include “adder.v” //引用模块 module adder_testbench; //定义测试模块 reg a,b; //初始化模块中寄存器定义 wire sum,cout; // 定义线网 integer i,j; adder adder_te( .sum ( sum ), .cout ( cout), .a ( a ), .b ( b ) );
过程,这时会发生仿真死锁。
2.3.1 always 语句
如果加上时序控制,则这个always语句 将变为一条非常有用的描述语句。
always # half_period areg = ~areg; 这个例子生成了一个周期 为:period(=2*half_period) 的无限延续的信号波形,常用这种方法来描 述时钟信号,作为激励信号来测试所设计 的电路。
入,而和数与进位为输出则为全加器。
1位半加法器的设计
• 数字系统通过0与1来实现复杂的系统工程,最简单的逻辑运算就是两 个1位进行加法的操作。
封装后的1bit半加法器
代码
• • • • • • • module adder(cout,sum,a,b); //模块名 output cout; // 输出端口声明 output sum; //输出端口声明 input a,b; //输入端口声明 wire cout,sum ; // wire变量声明 assign {cout,sum}=a+b; // a+b相加 endmodule // 模块结束语句
