matlabhandout
MATLAB神经网络工具箱的详细使用步奏
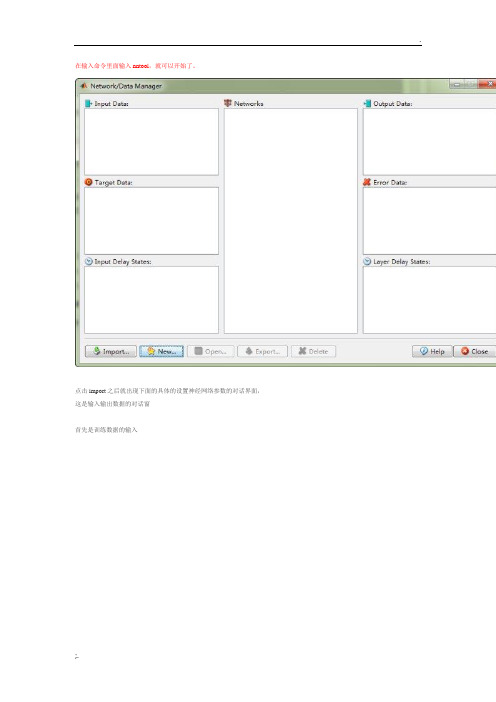
在输入命令里面输入nntool,就可以开始了。
点击import之后就出现下面的具体的设置神经网络参数的对话界面,这是输入输出数据的对话窗
首先是训练数据的输入
然后点击new,创建一个新的神经网络network1,并设置其输入输出数据,包括名称,神经网络的类型以及隐含层的层数和节点数,还有隐含层及输出层的训练函数等
点击view,可以看到这是神经网络的可视化直观表达
创建好了一个network之后,点击open,可以看到一个神经网络训练,优化等的对话框,选择了输入输出数据后,点击train,神经网络开始训练,如右下方的图,可以显示动态结果
下面三个图形则是点击performance,training state以及regression而出现的
下面就是simulate,输入的数据是用来检验这个网络的数据,output改一个名字,这样就把输出数据和误差都存放起来了
在主界面上点击export就能将得到的out结果输入到matlab中并查看
下图就是输出的两个outputs结果。
Matlab_tutorial_4V2

MAA307 MATHEMATICS FOR SPORTS TECHNOLOGYTUTORIAL 4 : ALGEBRA AND THE SYMBOLIC MATH TOOLBOXThe syllabus for this part of the course is contained in Workbooks 1 (all sections), and Workbook sections 2.5 and 3.1, 3.2 and 3.4. There are many exercises in the workbooks and you should ensure that you can do these by hand. Answers can be found in the workbooks.Matlab Handout 2 contains information regarding useful functions within the symbolic math toolbox. This toolbox is used for calculations involving algebra, as opposed to number. Do a selection of the Workbook exercises in Matlab. In particular, make sure that you can change the subject of a formula in Matlab and evaluate formulae for particular values of the variable (see end of Workbook1). If you need assistance with Matlab commands, use the help menu.Extra ExercisesQ1. A shot putter releases a shot from 2.1 m above the ground. The magnitude of the initial velocity of the shot, 0v , is 13.5 m/s and the initial anglethe shot makes with the horizontal is 33︒. If air resistance is ignored, the position (,)x y of the shot at time t is given by equations for projectile motion, namely200001,2x y x x v t y y v t gt =+=+-where 00(,)x y is the initial position of the shot, 0x v and 0y v are the components of the initial velocity in the x and y directions, respectively, and g is the acceleration due to gravity (9.81 m/s 2).Find the time the shot is in the air and the horizontal distance that the shot travels.Answers 1.74 secs, 19.75 mQ2. A golf ball is hit from a tee which is 0.03 m above the ground and which is placed 2 m behind the marked tee-off position. The initial speed of the ball is 0v and the initial angle that the ball makes with the horizontal is θ.If air resistance, lift and drag are ignored, the position (,)x y of the golf ball at time t is given by equations for projectile motion, namely200001,2x y x x v t y y v t gt =+=+- where 00(,)x y is the initial position of the shot, 0x v and 0y v are the components of the initial velocity in the x and y directions, respectively, and g is the acceleration due to gravity (9.81 m/s 2). Note y is the height of the ball above the ground and x the horizontal distance from the marked tee-off position.(a) Show that y can be written as a function of x by the equation2220(2)0.03(2)tan 2cos x y x g v θθ+=++-(b) The ball is now hit in the direction of a clump of trees 10 m high and 50 m in front of the marked tee-off position. Will the ball clear the trees if the initial speed is 60 m/s and initial angle is 12︒?(c) What is the minimum initial velocity required to ensure that the ball clears the trees (assuming all other variables are unchanged)?Answers No, 113.14 m/sQ3. Solve the quadratic equations(a) 3x 2 + 5x +3 = 0 (Ans. x = j 61165±-)(b) 2x 2 + x + 2 = 0 (Ans. x = j 41541±-)。
matlab命令大全

matlab命令大全A aabs 绝对值、模、字符的ASCII码值acos 反余弦acosh 反双曲余弦acot 反余切acoth 反双曲余切acsc 反余割acsch 反双曲余割align 启动图形对象几何位置排列工具all 所有元素非零为真angle 相角ans 表达式计算结果的缺省变量名any 所有元素非全零为真area 面域图argnames 函数M文件宗量名asec 反正割asech 反双曲正割asin 反正弦asinh 反双曲正弦assignin 向变量赋值atan 反正切atan2 四象限反正切atanh 反双曲正切autumn 红黄调秋色图阵axes 创建轴对象的低层指令axis 控制轴刻度和风格的高层指令B bbar 二维直方图bar3 三维直方图bar3h 三维水平直方图barh 二维水平直方图base2dec X进制转换为十进制bin2dec 二进制转换为十进制blanks 创建空格串bone 蓝色调黑白色图阵box 框状坐标轴break while 或for 环中断指令brighten 亮度控制C ccapture (3版以前)捕获当前图形cart2pol 直角坐标变为极或柱坐标cart2sph 直角坐标变为球坐标cat 串接成高维数组caxis 色标尺刻度cd 指定当前目录cdedit 启动用户菜单、控件回调函数设计工具cdf2rdf 复数特征值对角阵转为实数块对角阵ceil 向正无穷取整cell 创建元胞数组cell2struct 元胞数组转换为构架数组celldisp 显示元胞数组内容cellplot 元胞数组内部结构图示char 把数值、符号、内联类转换为字符对象chi2cdf 分布累计概率函数chi2inv 分布逆累计概率函数chi2pdf 分布概率密度函数chi2rnd 分布随机数发生器chol Cholesky分解clabel 等位线标识cla 清除当前轴class 获知对象类别或创建对象clc 清除指令窗clear 清除内存变量和函数clf 清除图对象clock 时钟colorcube 三浓淡多彩交叉色图矩阵colordef 设置色彩缺省值colormap 色图colspace 列空间的基close 关闭指定窗口colperm 列排序置换向量comet 彗星状轨迹图comet3 三维彗星轨迹图compass 射线图compose 求复合函数cond (逆)条件数condeig 计算特征值、特征向量同时给出条件数condest 范 -1条件数估计conj 复数共轭contour 等位线contourf 填色等位线contour3 三维等位线contourslice 四维切片等位线图conv 多项式乘、卷积cool 青紫调冷色图copper 古铜调色图cos 余弦cosh 双曲余弦cot 余切coth 双曲余切cplxpair 复数共轭成对排列csc 余割csch 双曲余割cumsum 元素累计和cumtrapz 累计梯形积分cylinder 创建圆柱D ddblquad 二重数值积分deal 分配宗量deblank 删去串尾部的空格符dec2base 十进制转换为X进制dec2bin 十进制转换为二进制dec2hex 十进制转换为十六进制deconv 多项式除、解卷delaunay Delaunay 三角剖分del2 离散Laplacian差分demo Matlab演示det 行列式diag 矩阵对角元素提取、创建对角阵diary Matlab指令窗文本内容记录diff 数值差分、符号微分digits 符号计算中设置符号数值的精度dir 目录列表disp 显示数组display 显示对象内容的重载函数dlinmod 离散系统的线性化模型dmperm 矩阵Dulmage-Mendelsohn 分解dos 执行DOS 指令并返回结果double 把其他类型对象转换为双精度数值drawnow 更新事件队列强迫Matlab刷新屏幕dsolve 符号计算解微分方程E eecho M文件被执行指令的显示edit 启动M文件编辑器eig 求特征值和特征向量eigs 求指定的几个特征值end 控制流FOR等结构体的结尾元素下标eps 浮点相对精度error 显示出错信息并中断执行errortrap 错误发生后程序是否继续执行的控制erf 误差函数erfc 误差补函数erfcx 刻度误差补函数erfinv 逆误差函数errorbar 带误差限的曲线图etreeplot 画消去树eval 串演算指令evalin 跨空间串演算指令exist 检查变量或函数是否已定义exit 退出Matlab环境exp 指数函数expand 符号计算中的展开操作expint 指数积分函数expm 常用矩阵指数函数expm1 Pade法求矩阵指数expm2 Taylor法求矩阵指数expm3 特征值分解法求矩阵指数eye 单位阵ezcontour 画等位线的简捷指令ezcontourf 画填色等位线的简捷指令ezgraph3 画表面图的通用简捷指令ezmesh 画网线图的简捷指令ezmeshc 画带等位线的网线图的简捷指令ezplot 画二维曲线的简捷指令ezplot3 画三维曲线的简捷指令ezpolar 画极坐标图的简捷指令ezsurf 画表面图的简捷指令ezsurfc 画带等位线的表面图的简捷指令F ffactor 符号计算的因式分解feather 羽毛图feedback 反馈连接feval 执行由串指定的函数fft 离散Fourier变换fft2 二维离散Fourier变换fftn 高维离散Fourier变换fftshift 直流分量对中的谱fieldnames 构架域名figure 创建图形窗fill3 三维多边形填色图find 寻找非零元素下标findobj 寻找具有指定属性的对象图柄findstr 寻找短串的起始字符下标findsym 机器确定内存中的符号变量finverse 符号计算中求反函数fix 向零取整flag 红白蓝黑交错色图阵fliplr 矩阵的左右翻转flipud 矩阵的上下翻转flipdim 矩阵沿指定维翻转floor 向负无穷取整flops 浮点运算次数flow Matlab提供的演示数据fmin 求单变量非线性函数极小值点(旧版)fminbnd 求单变量非线性函数极小值点fmins 单纯形法求多变量函数极小值点(旧版)fminunc 拟牛顿法求多变量函数极小值点fminsearch 单纯形法求多变量函数极小值点fnder 对样条函数求导fnint 利用样条函数求积分fnval 计算样条函数区间内任意一点的值fnplt 绘制样条函数图形fopen 打开外部文件for 构成for环用format 设置输出格式fourier Fourier 变换fplot 返函绘图指令fprintf 设置显示格式fread 从文件读二进制数据fsolve 求多元函数的零点full 把稀疏矩阵转换为非稀疏阵funm 计算一般矩阵函数funtool 函数计算器图形用户界面fzero 求单变量非线性函数的零点G ggamma 函数gammainc 不完全函数gammaln 函数的对数gca 获得当前轴句柄gcbo 获得正执行"回调"的对象句柄gcf 获得当前图对象句柄gco 获得当前对象句柄geomean 几何平均值get 获知对象属性getfield 获知构架数组的域getframe 获取影片的帧画面ginput 从图形窗获取数据global 定义全局变量gplot 依图论法则画图gradient 近似梯度gray 黑白灰度grid 画分格线griddata 规则化数据和曲面拟合gtext 由鼠标放置注释文字guide 启动图形用户界面交互设计工具H hharmmean 调和平均值help 在线帮助helpwin 交互式在线帮助helpdesk 打开超文本形式用户指南hex2dec 十六进制转换为十进制hex2num 十六进制转换为浮点数hidden 透视和消隐开关hilb Hilbert矩阵hist 频数计算或频数直方图histc 端点定位频数直方图histfit 带正态拟合的频数直方图hold 当前图上重画的切换开关horner 分解成嵌套形式hot 黑红黄白色图hsv 饱和色图I iif-else-elseif 条件分支结构ifft 离散Fourier反变换ifft2 二维离散Fourier反变换ifftn 高维离散Fourier反变换ifftshift 直流分量对中的谱的反操作ifourier Fourier反变换i, j 缺省的"虚单元"变量ilaplace Laplace反变换imag 复数虚部image 显示图象imagesc 显示亮度图象imfinfo 获取图形文件信息imread 从文件读取图象imwrite 把imwrite 把图象写成文件ind2sub 单下标转变为多下标inf 无穷大info MathWorks公司网点地址inline 构造内联函数对象inmem 列出内存中的函数名input 提示用户输入inputname 输入宗量名int 符号积分int2str 把整数数组转换为串数组interp1 一维插值interp2 二维插值interp3 三维插值interpn N维插值interpft 利用FFT插值intro Matlab自带的入门引导inv 求矩阵逆invhilb Hilbert矩阵的准确逆ipermute 广义反转置isa 检测是否给定类的对象ischar 若是字符串则为真isequal 若两数组相同则为真isempty 若是空阵则为真isfinite 若全部元素都有限则为真isfield 若是构架域则为真isglobal 若是全局变量则为真ishandle 若是图形句柄则为真ishold 若当前图形处于保留状态则为真isieee 若计算机执行IEEE规则则为真isinf 若是无穷数据则为真isletter 若是英文字母则为真islogical 若是逻辑数组则为真ismember 检查是否属于指定集isnan 若是非数则为真isnumeric 若是数值数组则为真isobject 若是对象则为真isprime 若是质数则为真isreal 若是实数则为真isspace 若是空格则为真issparse 若是稀疏矩阵则为真isstruct 若是构架则为真isstudent 若是Matlab学生版则为真iztrans 符号计算Z反变换J j , K kjacobian 符号计算中求Jacobian 矩阵jet 蓝头红尾饱和色jordan 符号计算中获得 Jordan标准型keyboard 键盘获得控制权kron Kronecker乘法规则产生的数组L llaplace Laplace变换lasterr 显示最新出错信息lastwarn 显示最新警告信息leastsq 解非线性最小二乘问题(旧版)legend 图形图例lighting 照明模式line 创建线对象lines 采用plot 画线色linmod 获连续系统的线性化模型linmod2 获连续系统的线性化精良模型linspace 线性等分向量ln 矩阵自然对数load 从MAT文件读取变量log 自然对数log10 常用对数log2 底为2的对数loglog 双对数刻度图形logm 矩阵对数logspace 对数分度向量lookfor 按关键字搜索M文件lower 转换为小写字母lsqnonlin 解非线性最小二乘问题lu LU分解M mmad 平均绝对值偏差magic 魔方阵maple &nb, sp; 运作 Maple格式指令mat2str 把数值数组转换成输入形态串数组material 材料反射模式max 找向量中最大元素mbuild 产生EXE文件编译环境的预设置指令mcc 创建MEX或EXE文件的编译指令mean 求向量元素的平均值median 求中位数menuedit 启动设计用户菜单的交互式编辑工具mesh 网线图meshz 垂帘网线图meshgrid 产生"格点"矩阵methods 获知对指定类定义的所有方法函数mex 产生MEX文件编译环境的预设置指令mfunlis 能被mfun计算的MAPLE经典函数列表mhelp 引出 Maple的在线帮助min 找向量中最小元素mkdir 创建目录mkpp 逐段多项式数据的明晰化mod 模运算more 指令窗中内容的分页显示movie 放映影片动画moviein 影片帧画面的内存预置mtaylor 符号计算多变量Taylor级数展开N nndims 求数组维数NaN 非数(预定义)变量nargchk 输入宗量数验证nargin 函数输入宗量数nargout 函数输出宗量数ndgrid 产生高维格点矩阵newplot 准备新的缺省图、轴nextpow2 取最接近的较大2次幂nnz 矩阵的非零元素总数nonzeros 矩阵的非零元素norm 矩阵或向量范数normcdf 正态分布累计概率密度函数normest 估计矩阵2范数norminv 正态分布逆累计概率密度函数normpdf 正态分布概率密度函数normrnd 正态随机数发生器notebook 启动Matlab和Word的集成环境null 零空间num2str 把非整数数组转换为串numden 获取最小公分母和相应的分子表达式nzmax 指定存放非零元素所需内存O oode1 非Stiff 微分方程变步长解算器ode15s Stiff 微分方程变步长解算器ode23t 适度Stiff 微分方程解算器ode23tb Stiff 微分方程解算器ode45 非Stiff 微分方程变步长解算器odefile ODE 文件模板odeget 获知ODE 选项设置参数odephas2 ODE 输出函数的二维相平面图odephas3 ODE 输出函数的三维相空间图odeplot ODE 输出函数的时间轨迹图odeprint 在Matlab指令窗显示结果odeset 创建或改写 ODE选项构架参数值ones 全1数组optimset 创建或改写优化泛函指令的选项参数值orient 设定图形的排放方式orth 值空间正交化P ppack 收集Matlab内存碎块扩大内存pagedlg 调出图形排版对话框patch 创建块对象path 设置Matlab搜索路径的指令pathtool 搜索路径管理器pause 暂停pcode 创建预解译P码文件pcolor 伪彩图peaks Matlab提供的典型三维曲面permute 广义转置pi (预定义变量)圆周率pie 二维饼图pie3 三维饼图pink 粉红色图矩阵pinv 伪逆plot 平面线图plot3 三维线图plotmatrix 矩阵的散点图plotyy 双纵坐标图poissinv 泊松分布逆累计概率分布函数poissrnd 泊松分布随机数发生器pol2cart 极或柱坐标变为直角坐标polar 极坐标图poly 矩阵的特征多项式、根集对应的多项式poly2str 以习惯方式显示多项式poly2sym 双精度多项式系数转变为向量符号多项式polyder 多项式导数polyfit 数据的多项式拟合polyval 计算多项式的值polyvalm 计算矩阵多项式pow2 2的幂ppval 计算分段多项式pretty 以习惯方式显示符号表达式print 打印图形或SIMULINK模型printsys 以习惯方式显示有理分式prism 光谱色图矩阵procread 向MAPLE输送计算程序profile 函数文件性能评估器propedit 图形对象属性编辑器pwd 显示当前工作目录Q qquad 低阶法计算数值积分quad8 高阶法计算数值积分(QUADL)quit 推出Matlab 环境quiver 二维方向箭头图quiver3 三维方向箭头图R rrand 产生均匀分布随机数randn 产生正态分布随机数randperm 随机置换向量range 样本极差rank 矩阵的秩rats 有理输出rcond 矩阵倒条件数估计real 复数的实部reallog 在实数域内计算自然对数realpow 在实数域内计算乘方realsqrt 在实数域内计算平方根realmax 最大正浮点数realmin 最小正浮点数rectangle 画"长方框"rem 求余数repmat 铺放模块数组reshape 改变数组维数、大小residue 部分分式展开return 返回ribbon 把二维曲线画成三维彩带图rmfield 删去构架的域roots 求多项式的根rose 数扇形图rot90 矩阵旋转90度rotate 指定的原点和方向旋转rotate3d 启动三维图形视角的交互设置功能round 向最近整数圆整rref 简化矩阵为梯形形式rsf2csf 实数块对角阵转为复数特征值对角阵rsums Riemann和S ssave 把内存变量保存为文件scatter 散点图scatter3 三维散点图sec 正割sech 双曲正割semilogx X轴对数刻度坐标图semilogy Y轴对数刻度坐标图series 串联连接set 设置图形对象属性setfield 设置构架数组的域setstr 将ASCII码转换为字符的旧版指令sign 根据符号取值函数signum 符号计算中的符号取值函数sim 运行SIMULINK模型simget 获取SIMULINK模型设置的仿真参数simple 寻找最短形式的符号解simplify 符号计算中进行简化操作simset 对SIMULINK模型的仿真参数进行设置simulink 启动SIMULINK模块库浏览器sin 正弦sinh 双曲正弦size 矩阵的大小slice 立体切片图solve 求代数方程的符号解spalloc 为非零元素配置内存sparse 创建稀疏矩阵spconvert 把外部数据转换为稀疏矩阵spdiags 稀疏对角阵spfun 求非零元素的函数值sph2cart 球坐标变为直角坐标sphere 产生球面spinmap 色图彩色的周期变化spline 样条插值spones 用1置换非零元素sprandsym 稀疏随机对称阵sprank 结构秩spring 紫黄调春色图sprintf 把格式数据写成串spy 画稀疏结构图sqrt 平方根sqrtm 方根矩阵squeeze 删去大小为1的"孤维"sscanf 按指定格式读串stairs 阶梯图std 标准差stem 二维杆图step 阶跃响应指令str2double 串转换为双精度值str2mat 创建多行串数组str2num 串转换为数strcat 接成长串strcmp 串比较strjust 串对齐strmatch 搜索指定串strncmp 串中前若干字符比较strrep 串替换strtok 寻找第一间隔符前的内容struct 创建构架数组struct2cell 把构架转换为元胞数组strvcat 创建多行串数组sub2ind 多下标转换为单下标subexpr 通过子表达式重写符号对象subplot 创建子图subs 符号计算中的符号变量置换subspace 两子空间夹角sum 元素和summer 绿黄调夏色图superiorto 设定优先级surf 三维着色表面图surface 创建面对象surfc 带等位线的表面图surfl 带光照的三维表面图surfnorm 空间表面的法线svd 奇异值分解svds 求指定的若干奇异值switch-case-otherwise 多分支结构sym2poly 符号多项式转变为双精度多项式系数向量symmmd 对称最小度排序symrcm 反向Cuthill-McKee排序syms 创建多个符号对象T ttan 正切tanh 双曲正切taylortool 进行Taylor逼近分析的交互界面text 文字注释tf 创建传递函数对象tic 启动计时器title 图名toc 关闭计时器trapz 梯形法数值积分treelayout 展开树、林treeplot 画树图tril 下三角阵trim 求系统平衡点trimesh 不规则格点网线图trisurf 不规则格点表面图 triu 上三角阵 try-catch 控制流中的Try-catch结构 type 显示M文件U uuicontextmenu 创建现场菜单uicontrol 创建用户控件uimenu 创建用户菜单unmkpp 逐段多项式数据的反明晰化unwrap 自然态相角upper 转换为大写字母V vvar 方差varargin 变长度输入宗量varargout 变长度输出宗量vectorize 使串表达式或内联函数适于数组运算ver 版本信息的获取view 三维图形的视角控制voronoi Voronoi多边形vpa 任意精度(符号类)数值W wwarning 显示警告信息what 列出当前目录上的文件whatsnew 显示Matlab中 Readme文件的内容which 确定函数、文件的位置while 控制流中的While环结构white 全白色图矩阵whitebg 指定轴的背景色who 列出内存中的变量名whos 列出内存中变量的详细信息winter 蓝绿调冬色图workspace 启动内存浏览器。
Matlab在掌纹识别系统设计中的应用指南

Matlab在掌纹识别系统设计中的应用指南1. 引言掌纹识别是一种现代生物特征识别技术,通过对手掌中的纹理和形状进行分析和比对,实现识别和辨认个体身份。
与其他生物特征相比,掌纹具有独特性高、随着年龄变化程度小等优点,因此在安全认证、刑侦破案等领域有着广泛的应用。
Matlab作为一种强大的科学计算软件,在掌纹识别系统的设计中有着重要的作用。
本文将介绍Matlab在掌纹识别系统设计中的应用指南,以帮助研究人员和工程师更好地利用Matlab的功能和工具进行掌纹识别系统的设计和开发。
2. 图像处理与特征提取掌纹识别系统的核心任务是对手掌图像进行处理和特征提取,以提取出具有识别性的特征信息。
在Matlab中,图像处理工具箱提供了丰富的函数和算法用于图像处理和分析。
可以使用imread函数读取和加载图像,imresize函数进行图像大小调整,imcrop函数进行图像裁剪等。
在特征提取方面,Matlab提供了一系列的特征检测和描述子算法,比如SIFT (尺度不变特征转换)、SURF(加速稳健特征)、HOG(方向梯度直方图)等。
可以通过调用相关函数实现对图像的特征提取,进而用于掌纹识别系统的模式匹配和识别。
3. 图像分类与模式匹配掌纹识别系统需要对提取到的特征进行分类和匹配,以实现对个体身份的识别。
Matlab提供了多种图像分类和模式匹配的算法和函数,比如k近邻算法、支持向量机(SVM)、神经网络等。
可以根据具体需求选择合适的算法,并通过调用相关函数进行模型训练和预测。
此外,Matlab还提供了模型评估和性能分析的工具,比如混淆矩阵、ROC曲线等,可以帮助进行模型性能评估和选择合适的阈值。
这对于掌纹识别系统的优化和改进具有重要意义。
4. 数据预处理与增强在掌纹图像的处理过程中,数据预处理和增强对于提高识别系统的性能至关重要。
Matlab提供了一系列的图像增强和预处理函数,比如灰度化、直方图均衡化、滤波器等。
可以根据实际需要对掌纹图像进行增强和预处理,以提高图像质量和识别效果。
MATLAB显示输出数据的三种方式

MATLAB显⽰输出数据的三种⽅式MATLAB 显⽰输出数据的三种⽅式,转载 https:///qq_35318838/article/details/787804121.改变数据格式当数据重复再命令⾏窗⼝时,整数以整形形式显⽰,其他值将以默认格式显⽰。
的默认格式是精确到⼩数点后4位。
如果⼀个数太⼤或太⼩,那么将会以科学记数法的形式显⽰。
⽐如:>> x=100.11x =100.1100>> y=1001.1y =1.0011e+03>> z=0.00010011z =1.0011e-041234567891011121314151617改变默认输出格式要⽤到format命令,可根据下表改变数据的输出格式format 命令结果例⼦format short保留⼩数点后4位(默认格式)12.3456format long保留⼩数点后14位12.345678901234500format short e带有5位有效数字科学记数法 1.2346e+100format short g总共有5个数字,可以⽤科学记数法,也可不⽤12.346format long e带有15位有效数字科学记数法 1.234567*********e+001format long g总共有15个数字,可以⽤科学记数法,也可不⽤12.3456789012346format bank格式12.35format hex⽤16进制标识4028b0fcd32f6f3bformat rat两个⼩整数的⽐2233/100format compact隐藏多于的换⾏符format loose使⽤多余的换⾏符format +只显⽰这个数的正负+其中美元格式是指按美元精确到的格式记数,隐藏/使⽤多余的换⾏符这个我也试出来有什么卵⽤。
2.disp函数另⼀种显⽰数据的⽅法是⽤disp函数。
disp需要⼀个数组参数,它将值显⽰在命令⾏窗⼝。
Matlab命令大全

cplxpa ir 复数共轭成对排列cs c 余割csch双曲余割cum sum 元素累计和cumt rapz累计梯形积分cy linde r 创建圆柱D d dblq uad 二重数值积分dea l 分配宗量de blank删去串尾部的空格符dec2base十进制转换为X进制dec2bin十进制转换为二进制dec2hex 十进制转换为十六进制deco nv 多项式除、解卷del aunay Dela unay三角剖分del2离散La placi an差分demo Matl ab演示det行列式diag矩阵对角元素提取、创建对角阵diar y Mat lab指令窗文本内容记录d iff 数值差分、符号微分digit s 符号计算中设置符号数值的精度di r 目录列表di sp 显示数组d ispla y 显示对象内容的重载函数dlinm od 离散系统的线性化模型dmper m 矩阵D ulmag e-Men delso hn 分解dos执行DO S 指令并返回结果doub le 把其他类型对象转换为双精度数值drawn ow 更新事件队列强迫Matl ab刷新屏幕ds olve符号计算解微分方程Eee cho M文件被执行指令的显示edi t 启动M文件编辑器eig求特征值和特征向量eig s 求指定的几个特征值en d 控制流FOR等结构体的结尾元素下标eps浮点相对精度er ror 显示出错信息并中断执行err ortra p 错误发生后程序是否继续执行的控制erf 误差函数erfc误差补函数erf cx 刻度误差补函数erf inv 逆误差函数erro rbar带误差限的曲线图etree plot画消去树eval串演算指令ev alin跨空间串演算指令exist检查变量或函数是否已定义exit退出Mat lab环境exp指数函数exp and 符号计算中的展开操作expi nt 指数积分函数expm常用矩阵指数函数expm1 Pad e法求矩阵指数e xpm2Taylo r法求矩阵指数e xpm3特征值分解法求矩阵指数ey e 单位阵ezc ontou r 画等位线的简捷指令ez conto urf 画填色等位线的简捷指令ezg raph3画表面图的通用简捷指令e zmesh画网线图的简捷指令ezm eshc画带等位线的网线图的简捷指令ezpl ot 画二维曲线的简捷指令ezplo t3 画三维曲线的简捷指令ezpol ar 画极坐标图的简捷指令ezsur f 画表面图的简捷指令ez surfc画带等位线的表面图的简捷指令F f fact or 符号计算的因式分解f eathe r 羽毛图fee dback反馈连接fev al 执行由串指定的函数f ft 离散Fouri er变换fft2二维离散Fouri er变换fftn高维离散Fouri er变换ffts hift直流分量对中的谱field names构架域名fig ure 创建图形窗fill3 三维多边形填色图fin d 寻找非零元素下标fin dobj寻找具有指定属性的对象图柄finds tr 寻找短串的起始字符下标find sym 机器确定内存中的符号变量fi nvers e 符号计算中求反函数fi x 向零取整fl ag 红白蓝黑交错色图阵f liplr矩阵的左右翻转flipu d 矩阵的上下翻转flip dim 矩阵沿指定维翻转f loor向负无穷取整fl ops 浮点运算次数flo w Mat lab提供的演示数据fmi n 求单变量非线性函数极小值点(旧版)fmin bnd 求单变量非线性函数极小值点f mins单纯形法求多变量函数极小值点(旧版)fminu nc 拟牛顿法求多变量函数极小值点f minse arch单纯形法求多变量函数极小值点fnde r 对样条函数求导fnin t 利用样条函数求积分fn val 计算样条函数区间内任意一点的值fnpl t 绘制样条函数图形fop en 打开外部文件for构成for环用f ormat设置输出格式f ourie r Fou rier变换f plot返函绘图指令fp rintf设置显示格式f read从文件读二进制数据fsol ve 求多元函数的零点fu ll 把稀疏矩阵转换为非稀疏阵fun m 计算一般矩阵函数fun tool函数计算器图形用户界面fz ero 求单变量非线性函数的零点G g gamm a 函数gamm ainc不完全函数ga mmaln函数的对数gc a 获得当前轴句柄gcbo获得正执行"回调"的对象句柄gcf获得当前图对象句柄gco获得当前对象句柄geom ean 几何平均值get获知对象属性ge tfiel d 获知构架数组的域get frame获取影片的帧画面ginp ut 从图形窗获取数据gl obal定义全局变量gp lot 依图论法则画图gr adien t 近似梯度gr ay 黑白灰度g rid 画分格线gridd ata 规则化数据和曲面拟合gtex t 由鼠标放置注释文字gu ide 启动图形用户界面交互设计工具H hha rmmea n 调和平均值h elp 在线帮助helpw in 交互式在线帮助hel pdesk打开超文本形式用户指南h ex2de c 十六进制转换为十进制h ex2nu m 十六进制转换为浮点数h idden透视和消隐开关hilbHilbe rt矩阵hist频数计算或频数直方图hi stc 端点定位频数直方图histf it 带正态拟合的频数直方图hold当前图上重画的切换开关h orner分解成嵌套形式hot 黑红黄白色图hsv饱和色图I iif-el se-el seif条件分支结构if ft 离散Fouri er反变换iff t2 二维离散Fou rier反变换i fftn高维离散F ourie r反变换ifft shift直流分量对中的谱的反操作ifour ier F ourie r反变换i, j缺省的"虚单元"变量il aplac e Lap lace反变换i mag 复数虚部image显示图象ima gesc显示亮度图象im finfo获取图形文件信息imre ad 从文件读取图象imw rite把im write把图象写成文件ind2s ub 单下标转变为多下标i nf 无穷大in fo Ma thWor ks公司网点地址inlin e 构造内联函数对象inm em 列出内存中的函数名i nput提示用户输入in putna me 输入宗量名int 符号积分int2s tr 把整数数组转换为串数组inte rp1 一维插值inter p2 二维插值i nterp3 三维插值in terpn N维插值int erpft利用FF T插值intro Matl ab自带的入门引导inv求矩阵逆invh ilb H ilber t矩阵的准确逆i permu te 广义反转置isa 检测是否给定类的对象isch ar 若是字符串则为真is equal若两数组相同则为真ise mpty若是空阵则为真i sfini te 若全部元素都有限则为真isfi eld 若是构架域则为真i sglob al 若是全局变量则为真i shand le 若是图形句柄则为真i shold若当前图形处于保留状态则为真isi eee 若计算机执行IEEE规则则为真isin f 若是无穷数据则为真is lette r 若是英文字母则为真is logic al 若是逻辑数组则为真i smemb er 检查是否属于指定集i snan若是非数则为真i snume ric 若是数值数组则为真isobj ect 若是对象则为真is prime若是质数则为真isrea l 若是实数则为真issp ace 若是空格则为真is spars e 若是稀疏矩阵则为真is struc t 若是构架则为真isst udent若是Ma tlab学生版则为真izt rans符号计算Z反变换J j , Kkj acobi an 符号计算中求Jacob ian 矩阵je t 蓝头红尾饱和色jord an 符号计算中获得 Jord an标准型key board键盘获得控制权kronKrone cker乘法规则产生的数组L lla place Lapl ace变换las terr显示最新出错信息lastw arn 显示最新警告信息l easts q 解非线性最小二乘问题(旧版)le gend图形图例ligh ting照明模式line创建线对象li nes 采用plot画线色linm od 获连续系统的线性化模型linm od2 获连续系统的线性化精良模型l inspa ce 线性等分向量ln 矩阵自然对数loa d 从MA T文件读取变量l og 自然对数l og10常用对数log2底为2的对数l oglog双对数刻度图形logm矩阵对数logs pace对数分度向量lo okfor按关键字搜索M文件low er 转换为小写字母lsq nonli n 解非线性最小二乘问题l u LU分解M m mad平均绝对值偏差m agic魔方阵maple &nb, sp;运作 Ma ple格式指令m at2st r 把数值数组转换成输入形态串数组m ateri al 材料反射模式max找向量中最大元素mbuil d 产生E XE文件编译环境的预设置指令mcc创建MEX或EXE文件的编译指令me an 求向量元素的平均值m edian求中位数men uedit启动设计用户菜单的交互式编辑工具m esh 网线图m eshz垂帘网线图mes hgrid产生"格点"矩阵meth ods 获知对指定类定义的所有方法函数mex产生MEX文件编译环境的预设置指令m funli s 能被m fun计算的MAPL E经典函数列表m help引出 Ma ple的在线帮助min 找向量中最小元素m kdir创建目录mkpp逐段多项式数据的明晰化m od 模运算mo re 指令窗中内容的分页显示movi e 放映影片动画movie in 影片帧画面的内存预置mtayl or 符号计算多变量Taylo r级数展开N nndims求数组维数Na N 非数(预定义)变量na rgchk输入宗量数验证nargi n 函数输入宗量数narg out 函数输出宗量数nd grid产生高维格点矩阵newpl ot 准备新的缺省图、轴n extpo w2 取最接近的较大2次幂nnz 矩阵的非零元素总数nonze ros 矩阵的非零元素no rm 矩阵或向量范数nor mcdf正态分布累计概率密度函数n ormes t 估计矩阵2范数norm inv 正态分布逆累计概率密度函数n ormpd f 正态分布概率密度函数n ormrn d 正态随机数发生器not ebook启动Ma tlab和Word的集成环境null零空间num2str 把非整数数组转换为串numd en 获取最小公分母和相应的分子表达式nzma x 指定存放非零元素所需内存Ooo de1 非Stiff微分方程变步长解算器od e15sStiff微分方程变步长解算器od e23t适度Sti ff 微分方程解算器ode23tbStiff微分方程解算器ode45非Sti ff 微分方程变步长解算器odefi le OD E 文件模板od eget获知ODE选项设置参数o depha s2 OD E 输出函数的二维相平面图odeph as3 O DE 输出函数的三维相空间图odep lot O DE 输出函数的时间轨迹图odepr int 在Matla b指令窗显示结果odese t 创建或改写 OD E选项构架参数值ones全1数组opti mset创建或改写优化泛函指令的选项参数值o rient设定图形的排放方式ort h 值空间正交化P ppa ck 收集Matla b内存碎块扩大内存page dlg 调出图形排版对话框patch创建块对象pa th 设置Matla b搜索路径的指令patht ool 搜索路径管理器pa use 暂停pc ode 创建预解译P码文件pcolo r 伪彩图pea ks Ma tlab提供的典型三维曲面permu te 广义转置p i (预定义变量)圆周率p ie 二维饼图p ie3 三维饼图pink粉红色图矩阵pi nv 伪逆plo t 平面线图pl ot3 三维线图plotm atrix矩阵的散点图p lotyy双纵坐标图po issin v 泊松分布逆累计概率分布函数poi ssrnd泊松分布随机数发生器po l2car t 极或柱坐标变为直角坐标polar极坐标图pol y 矩阵的特征多项式、根集对应的多项式poly2str以习惯方式显示多项式pol y2sym双精度多项式系数转变为向量符号多项式poly der 多项式导数poly fit 数据的多项式拟合p olyva l 计算多项式的值poly valm计算矩阵多项式p ow2 2的幂p pval计算分段多项式p retty以习惯方式显示符号表达式print打印图形或SIMU LINK模型pr intsy s 以习惯方式显示有理分式prism光谱色图矩阵p rocre ad 向M APLE输送计算程序pro file函数文件性能评估器prop edit图形对象属性编辑器pwd显示当前工作目录Q qqu ad 低阶法计算数值积分q uad8高阶法计算数值积分(QUADL) qu it 推出Matla b 环境quiv er 二维方向箭头图qui ver3三维方向箭头图R rran d 产生均匀分布随机数ra ndn 产生正态分布随机数randp erm 随机置换向量ran ge 样本极差r ank 矩阵的秩rats有理输出rcon d 矩阵倒条件数估计rea l 复数的实部r eallo g 在实数域内计算自然对数realp ow 在实数域内计算乘方r ealsq rt 在实数域内计算平方根realm ax 最大正浮点数real min 最小正浮点数rec tangl e 画"长方框" rem 求余数r epmat铺放模块数组r eshap e 改变数组维数、大小re sidue部分分式展开r eturn返回ribbo n 把二维曲线画成三维彩带图rmfi eld 删去构架的域roo ts 求多项式的根rose数扇形图rot90 矩阵旋转90度rot ate 指定的原点和方向旋转rota te3d启动三维图形视角的交互设置功能rou nd 向最近整数圆整rre f 简化矩阵为梯形形式rs f2csf实数块对角阵转为复数特征值对角阵r sumsRiema nn和S ssav e 把内存变量保存为文件s catte r 散点图sca tter3三维散点图se c 正割sech双曲正割sem ilogx X轴对数刻度坐标图sem ilogy Y轴对数刻度坐标图ser ies 串联连接set 设置图形对象属性s etfie ld 设置构架数组的域se tstr将ASCI I码转换为字符的旧版指令s ign 根据符号取值函数s ignum符号计算中的符号取值函数sim 运行SIMU LINK模型si mget获取SIM ULINK模型设置的仿真参数simp le 寻找最短形式的符号解simpl ify 符号计算中进行简化操作sim set 对SIMUL INK模型的仿真参数进行设置simu link启动SIM ULINK模块库浏览器si n 正弦sinh双曲正弦siz e 矩阵的大小s lice立体切片图sol ve 求代数方程的符号解s pallo c 为非零元素配置内存sp arse创建稀疏矩阵sp conve rt 把外部数据转换为稀疏矩阵spd iags稀疏对角阵spf un 求非零元素的函数值s ph2ca rt 球坐标变为直角坐标s phere产生球面spi nmap色图彩色的周期变化spli ne 样条插值s pones用1置换非零元素spra ndsym稀疏随机对称阵spran k 结构秩spr ing 紫黄调春色图spr intf把格式数据写成串spy 画稀疏结构图sqr t 平方根sqr tm 方根矩阵s queez e 删去大小为1的"孤维" sscan f 按指定格式读串stai rs 阶梯图st d 标准差ste m 二维杆图st ep 阶跃响应指令str2doubl e 串转换为双精度值str2mat创建多行串数组s tr2nu m 串转换为数s trcat接成长串str cmp 串比较s trjus t 串对齐str match搜索指定串st rncmp串中前若干字符比较str rep 串替换s trtok寻找第一间隔符前的内容s truct创建构架数组s truct2cell把构架转换为元胞数组st rvcat创建多行串数组sub2i nd 多下标转换为单下标s ubexp r 通过子表达式重写符号对象subp lot 创建子图subs符号计算中的符号变量置换s ubspa ce 两子空间夹角sum元素和summe r 绿黄调夏色图super iorto设定优先级su rf 三维着色表面图sur face创建面对象sur fc 带等位线的表面图su rfl 带光照的三维表面图surfn orm 空间表面的法线sv d 奇异值分解s vds 求指定的若干奇异值switc h-cas e-oth erwis e 多分支结构s ym2po ly 符号多项式转变为双精度多项式系数向量sy mmmd对称最小度排序s ymrcm反向Cu thill-McKe e排序syms创建多个符号对象T tta n 正切tanh双曲正切tay lorto ol 进行Taylo r逼近分析的交互界面tex t 文字注释tf创建传递函数对象tic启动计时器tit le 图名toc关闭计时器tr apz 梯形法数值积分tr eelay out 展开树、林tree plot画树图tril下三角阵trim求系统平衡点t rimes h 不规则格点网线图tri surf不规则格点表面图t riu 上三角阵t ry-ca tch 控制流中的T ry-ca tch结构 type显示M文件Uuui conte xtmen u 创建现场菜单uicon trol创建用户控件ui menu创建用户菜单un mkpp逐段多项式数据的反明晰化u nwrap自然态相角up per 转换为大写字母V v var方差v ararg in 变长度输入宗量var argou t 变长度输出宗量vect orize使串表达式或内联函数适于数组运算v er 版本信息的获取vie w 三维图形的视角控制vo ronoi Voro noi多边形vp a 任意精度(符号类)数值W wwa rning显示警告信息w hat 列出当前目录上的文件what snew显示Mat lab中Readm e文件的内容wh ich 确定函数、文件的位置whil e 控制流中的Whi le环结构whi te 全白色图矩阵whit ebg 指定轴的背景色wh o 列出内存中的变量名wh os 列出内存中变量的详细信息win ter 蓝绿调冬色图wor kspac e 启动内存浏览器Xx , Y y ,Z z xlab el X轴名xo r 或非逻辑ye sinpu t 智能输入指令ylabe l Y轴名zer os 全零数组z label Z轴名zoom图形的变焦放大和缩小zt rans符号计算Z变换。
MATLAB 程式设计入门篇握把式图形与GUI设计

MATLAB 程式設計入門篇:握把式圖形與 GUI 設計
MATLAB 7.x 性質編輯器
MATLAB 7.x >>peaks; >>propedit; % 畫出 peaks 3D 圖 % 開啟性質編輯器
MATLAB 程式設計入門篇:握把式圖形與 GUI 設計
MATLAB 7.x
MATLAB 7.x
MATLAB 程式設計入門篇:握把式圖形與 GUI 設計
uicontrol範例1
MATLAB 程式設計入門篇:握把式圖形與 GUI 設計
UI(User Interface)控制物件
Uicontrol產生UI(User Interface)控制物件 按鈕(Push Button) 滑動棒(Sliding Bar) 圓形按鈕(Radio Button) 框架(Frame) 核計方塊(Check Box) 文字欄位(Edit Box) 列表式選單(List Menu) 下拉式選單(Popup Menu)
set範例:
set範例: t = 0:0.1:4*pi; y = exp(-t/5).*sin(t); h = plot(t, y); % h 為曲線的握把 set(h,'Linewidth',3); % 將曲線寬度改為 3 set(h,'Marker','o');%將曲線的線標改成小圓圈 set(h,'MarkerSize',20);% 將線標的大小改成 20
MATLAB 程式設計入門篇:握把式圖形與 GUI 設計
uicontrol範例2
uicontrol範例2: uicontrol('style','check','position',[200 220 80 30]); uicontrol('style','edit','position',[200 270 80 30]); uicontrol('style','list','position',[200 320 80 30],'string', '1|2|3|4'); uicontrol('style','popup','position',[200 370 80 30],'string','one|two|three');
Matlab_Handout_1

MATLAB – HANDOUT 11. Introduction to MATLABTo start MATLAB, select Start > All Programs > Matlab R2010a.After starting MATLAB, the MATLAB desktop opens.(To end your MATLAB session, select Exit MATLAB from the File menu in the desktop, or type quit in the Command Window.)Select Help > Product helpManipulating MatricesIn this section you will work through some of the online tutorial on manipulating matrices.First practice switching between the Matlab desktop and the Help window – use the icons on the taskbar to do this.Online tutorialOpen the Help window. In the Documentation set, click on the link Getting Started and then on the link Matrices and Arrays. Work through the following pages in the online tutorial:Matrices and Arrays>Matrices and Magic Squares∙Entering Matrices∙sum, transpose, and diag∙Subscripts∙The Colon OperatorExpressions∙VariablesScript (M) -filesThe online tutorial advises you to use the command window to type in your commands. However, it is best to get into the habit of using M-files. You can save these to your U-drive and will then have a record of your work. To do this open the Matlab desktop and chooseFile > New > ScriptA new window will open, called Untitled1.Select File > Save As and then name the file, eg Ex1. Note you must avoid spaces in filenames and should start a filename with a letter, not a number. Save the file on your U:drive.To run the file select Debug > Save file and Run from the M-editor or press F5 key or alternatively, type the name of the file at the prompt in the command window. Sharing Script (M) -filesIf you are sharing a computer, it is a good idea if you both have a copy of the M-files you have created. One way to do this is for the person who is logged onto the machine to email the files to the other user at the end of the session.ExercisesYou are now ready to try exercises 1 – 10 on Tutorial Sheet 1.。
第2章 MATLAB基本操作

6. 逻辑操作符 功能: 功能:逻辑操作运算。 格式: 格式:A&B A|B ~A 注意逻辑操作有相应的M文件 文件: 注意逻辑操作有相应的 文件:A&B等效 等效 ),A|B等效于 等效于or(A,B), 于and(A,B), ( , ), 等效于 , , ~A等效为 等效为not(A)。 等效为 。
2.关系操作符 关系操作符 关系运算符包括: 关系运算符包括:< 、< = 、〉、> = 、= = 、 ~= 3.测试用的逻辑函数 测试用的逻辑函数 1)all函数测定矩阵中是否全为非零元素 2)any函数测试出矩阵中是否有非零值 3) find函数可找出矩阵中的非零元素及其下 标 4) exist函数在装入数据之前对数据文件作 检测
利用取整和求余函数,可得到整数或精确到小数点后的第 几位。例如: x1=10-round(20*rand(2,5)) %产生[-10 10]之间的随机数(取整) x1 = -4 4 -1 -4 7 -7 -2 0
2 −7
x2=10-round(2000*rand(2,5))/100 %产生[−10 10]之间的随机 数(精确到0.01) x2 = -8.0000 -2.9000 -3.2000 -6.4300 -6.3600 3.1600 4.2100 -0.6800 3.1800 -4.5400
5.函数 函数 内部函数、工具箱函数、自定义函数。 1)函数的嵌套 x=sqrt(log(z)) 函数的嵌套 2)多输入函数 theta=atan2(y,x) 多输入函数 3)多输出函数 [v,d] = eig(a) 多输出函数 [y,I] = max(x) 6.表达式 表达式 a=(1+sqrt(10))/2 b=abs(3+5i) c=sin(exp(-2.3))
MATLAB基本操作命令

复数z1的输入方式是直接按照书面习惯完成的, 在这种书写格式中10i是一个完整的虚数部分, 因此在10和i之间不允许有任何空格。这种书写 格式符合大家的习惯,但仅限于使用在复数标量 中,不能使用在复数矩阵中。 Z2将虚数部分用*号相连。这种方式适用于复 数矩阵。 如果可以使用第一种书写格式,尽量使用第一 种,因为这种格式比复数z2的输入方式运算速度 要快。
MATLAB
wilkinson
2.2 矩阵和数组的基本运算
2.2.1矩阵和数组的四则运算 1.矩阵算术运算 矩阵算术运算的书写格式与普通的算术 相同,包括加、减、乘、除,也可用括号 来规定运算的优先次序。但它的乘法定义 与普通数(标量)不同。相应地,作为乘 法逆运算的除法也不同,由左除(\)和右 除(/)两种符号。
M圆括号“()”中的数字 (也称为下标)来注明,一维矩阵(也称数组 或向量)中的元素用一个下标表示,二维矩阵 可有两个下标数,以逗号分开。 三维和更高维的矩阵,可有三个或更多下 标。用户可以单独给元素赋值,如: x(2)=1.7321,a(2,3)=6等。如果赋值元素的下标 超出了原来矩阵的大小,矩阵的行列会自动扩 展。如:
MATLAB
矩阵的乘法 现在来看矩阵的乘法,X*Y’,这个式子可读 成X左乘Y’。现在让X右乘Y’,于是有 Y’*X, X左乘和右乘Y’所得的结果是完全不同的。 只有单位矩阵例外,单位矩阵乘以任何矩阵 A(其阶数为nA×mA)时,不管是左乘还是 右乘,积仍等于该矩阵。即 eye(nA)*A=A A* eye(mA) =A
MATLAB
两矩阵的相加(减)就是其对应元素的相加 (减),因此,要求相加的两矩阵的阶数必须 相同。检查矩阵阶数的MATLAB语句是size, 例如:键入 [n,m]=size(fb2) 得 n= 6 m = 5 (6行5列)
MATLAB常用命令及函数大全(字母顺序)

matlab 命令与函数清单花了些时间把MATLAB的命令以及函数按照字母顺序列了一个清单,供大家参考。
. 17A aabs 绝对值、模、字符的ASCII码值acos 反余弦acosh 反双曲余弦acot 反余切acoth 反双曲余切acsc 反余割acsch 反双曲余割align 启动图形对象几何位置排列工具all 所有元素非零为真angle 相角ans 表达式计算结果的缺省变量名any 所有元素非全零为真area 面域图argnames 函数M文件宗量名asec 反正割asech 反双曲正割asin 反正弦asinh 反双曲正弦assignin 向变量赋值atan 反正切atan2 四象限反正切atanh 反双曲正切autumn 红黄调秋色图阵axes 创建轴对象的低层指令axis 控制轴刻度和风格的高层指令B bbar 二维直方图bar3 三维直方图bar3h 三维水平直方图barh 二维水平直方图base2dec X进制转换为十进制bin2dec 二进制转换为十进制blanks 创建空格串bone 蓝色调黑白色图阵box 框状坐标轴break while 或for 环中断指令brighten 亮度控制C ccapture (3版以前)捕获当前图形cart2pol 直角坐标变为极或柱坐标cart2sph 直角坐标变为球坐标cat 串接成高维数组caxis 色标尺刻度cd 指定当前目录cdedit 启动用户菜单、控件回调函数设计工具 cdf2rdf 复数特征值对角阵转为实数块对角阵 ceil 向正无穷取整cell 创建元胞数组cell2struct 元胞数组转换为构架数组celldisp 显示元胞数组内容cellplot 元胞数组内部结构图示char 把数值、符号、内联类转换为字符对象chi2cdf 分布累计概率函数chi2inv 分布逆累计概率函数chi2pdf 分布概率密度函数chi2rnd 分布随机数发生器chol Cholesky分解clabel 等位线标识cla 清除当前轴class 获知对象类别或创建对象clc 清除指令窗clear 清除内存变量和函数clf 清除图对象clock 时钟colorcube 三浓淡多彩交叉色图矩阵colordef 设置色彩缺省值colormap 色图colspace 列空间的基close 关闭指定窗口colperm 列排序置换向量comet 彗星状轨迹图comet3 三维彗星轨迹图compass 射线图compose 求复合函数cond (逆)条件数condeig 计算特征值、特征向量同时给出条件数 condest 范 -1条件数估计conj 复数共轭contour 等位线contourf 填色等位线contour3 三维等位线contourslice 四维切片等位线图conv 多项式乘、卷积cool 青紫调冷色图copper 古铜调色图cos 余弦cosh 双曲余弦cot 余切coth 双曲余切cplxpair 复数共轭成对排列csc 余割csch 双曲余割cumsum 元素累计和cumtrapz 累计梯形积分cylinder 创建圆柱D ddblquad 二重数值积分deal 分配宗量deblank 删去串尾部的空格符dec2base 十进制转换为X进制dec2bin 十进制转换为二进制dec2hex 十进制转换为十六进制deconv 多项式除、解卷delaunay Delaunay 三角剖分del2 离散Laplacian差分demo Matlab演示det 行列式diag 矩阵对角元素提取、创建对角阵diary Matlab指令窗文本内容记录diff 数值差分、符号微分digits 符号计算中设置符号数值的精度dir 目录列表disp 显示数组display 显示对象内容的重载函数dlinmod 离散系统的线性化模型dmperm 矩阵Dulmage-Mendelsohn 分解dos 执行DOS 指令并返回结果double 把其他类型对象转换为双精度数值 drawnow 更新事件队列强迫Matlab刷新屏幕 dsolve 符号计算解微分方程E eecho M文件被执行指令的显示edit 启动M文件编辑器eig 求特征值和特征向量eigs 求指定的几个特征值end 控制流FOR等结构体的结尾元素下标eps 浮点相对精度error 显示出错信息并中断执行errortrap 错误发生后程序是否继续执行的控制 erf 误差函数erfc 误差补函数erfcx 刻度误差补函数erfinv 逆误差函数errorbar 带误差限的曲线图etreeplot 画消去树eval 串演算指令evalin 跨空间串演算指令exist 检查变量或函数是否已定义exit 退出Matlab环境exp 指数函数expand 符号计算中的展开操作expint 指数积分函数expm 常用矩阵指数函数expm1 Pade法求矩阵指数expm2 Taylor法求矩阵指数expm3 特征值分解法求矩阵指数eye 单位阵ezcontour 画等位线的简捷指令ezcontourf 画填色等位线的简捷指令ezgraph3 画表面图的通用简捷指令ezmesh 画网线图的简捷指令ezmeshc 画带等位线的网线图的简捷指令ezplot 画二维曲线的简捷指令ezplot3 画三维曲线的简捷指令ezpolar 画极坐标图的简捷指令ezsurf 画表面图的简捷指令ezsurfc 画带等位线的表面图的简捷指令F ffactor 符号计算的因式分解feather 羽毛图feedback 反馈连接feval 执行由串指定的函数fft 离散Fourier变换fft2 二维离散Fourier变换fftn 高维离散Fourier变换fftshift 直流分量对中的谱fieldnames 构架域名figure 创建图形窗fill3 三维多边形填色图find 寻找非零元素下标findobj 寻找具有指定属性的对象图柄findstr 寻找短串的起始字符下标findsym 机器确定内存中的符号变量finverse 符号计算中求反函数fix 向零取整flag 红白蓝黑交错色图阵fliplr 矩阵的左右翻转flipud 矩阵的上下翻转flipdim 矩阵沿指定维翻转floor 向负无穷取整flops 浮点运算次数flow Matlab提供的演示数据fmin 求单变量非线性函数极小值点(旧版)fminbnd 求单变量非线性函数极小值点fmins 单纯形法求多变量函数极小值点(旧版)fminunc 拟牛顿法求多变量函数极小值点fminsearch 单纯形法求多变量函数极小值点fnder 对样条函数求导fnint 利用样条函数求积分fnval 计算样条函数区间内任意一点的值fnplt 绘制样条函数图形fopen 打开外部文件for 构成for环用format 设置输出格式fourier Fourier 变换fplot 返函绘图指令fprintf 设置显示格式fread 从文件读二进制数据fsolve 求多元函数的零点full 把稀疏矩阵转换为非稀疏阵funm 计算一般矩阵函数funtool 函数计算器图形用户界面fzero 求单变量非线性函数的零点类别:学习工作 | 添加到搜藏 | 浏览(809) 最近读者:登录后,您就出现在这里。
matlab常用函数与常用指令大全[整理版]
![matlab常用函数与常用指令大全[整理版]](https://img.taocdn.com/s3/m/ff905ddadb38376baf1ffc4ffe4733687f21fc56.png)
matlab常用函数与常用指令大全matlab, 函数, 指令, 大全matlab常用函数与常用指令大全matlab常用函数- -1、特殊变量与常数ans 计算结果的变量名computer 确定运行的计算机eps 浮点相对精度Inf 无穷大I 虚数单位inputname 输入参数名NaN 非数nargin 输入参数个数nargout 输出参数的数目pi 圆周率nargoutchk 有效的输出参数数目realmax 最大正浮点数realmin 最小正浮点数varargin 实际输入的参量varargout 实际返回的参量操作符与特殊字符+ 加- 减* 矩阵乘法.* 数组乘(对应元素相乘)^ 矩阵幂 .^ 数组幂(各个元素求幂)\ 左除或反斜杠/ 右除或斜面杠./ 数组除(对应元素除)kron Kronecker张量积: 冒号() 圆括[] 方括 . 小数点.. 父目录 ... 继续, 逗号(分割多条命令); 分号(禁止结果显示)% 注释! 感叹号' 转置或引用= 赋值== 相等<> 不等于& 逻辑与| 逻辑或~ 逻辑非xor 逻辑异或2、基本数学函数abs 绝对值和复数模长acos,acodh 反余弦,反双曲余弦acot,acoth 反余切,反双曲余切acsc,acsch 反余割,反双曲余割angle 相角asec,asech 反正割,反双曲正割secant 正切asin,asinh 反正弦,反双曲正弦atan,atanh 反正切,双曲正切tangent 正切atan2 四象限反正切ceil 向着无穷大舍入complex 建立一个复数conj 复数配对cos,cosh 余弦,双曲余弦csc,csch 余切,双曲余切cot,coth 余切,双曲余切exp 指数fix 朝0方向取整floor 朝负无穷取整*** 最大公因数imag 复数值的虚部lcm 最小公倍数log 自然对数log2 以2为底的对数log10 常用对数mod 有符号的求余nchoosek 二项式系数和全部组合数real 复数的实部rem 相除后求余round 取整为最近的整数sec,sech 正割,双曲正割sign 符号数sin,sinh 正弦,双曲正弦sqrt 平方根tan,tanh 正切,双曲正切3、基本矩阵和矩阵操作blkding 从输入参量建立块对角矩阵eye 单位矩阵linespace 产生线性间隔的向量logspace 产生对数间隔的向量numel 元素个数ones 产生全为1的数组rand 均匀颁随机数和数组randn 正态分布随机数和数组zeros 建立一个全0矩阵colon) 等间隔向量cat 连接数组diag 对角矩阵和矩阵对角线fliplr 从左自右翻转矩阵flipud 从上到下翻转矩阵repmat 复制一个数组reshape 改造矩阵roy90 矩阵翻转90度tril 矩阵的下三角triu 矩阵的上三角dot 向量点集cross 向量叉集ismember 检测一个集合的元素intersect 向量的交集setxor 向量异或集setdiff 向是的差集union 向量的并集数值分析和傅立叶变换cumprod 累积cumsum 累加cumtrapz 累计梯形法计算数值微分factor 质因子inpolygon 删除多边形区域内的点max 最大值mean 数组的均值mediam 中值min 最小值perms 所有可能的转换polyarea 多边形区域primes 生成质数列表prod 数组元素的乘积rectint 矩形交集区域sort 按升序排列矩阵元素sortrows 按升序排列行std 标准偏差sum 求和trapz 梯形数值积分var 方差del2 离散拉普拉斯diff 差值和微分估计gradient 数值梯度cov 协方差矩阵corrcoef 相关系数conv2 二维卷积conv 卷积和多项式乘法filter IIR或FIR滤波器deconv 反卷积和多项式除法filter2 二维数字滤波器cplxpair 将复数值分类为共轭对fft 一维的快速傅立叶变换fft2 二维快速傅立叶变换fftshift 将FFT的DC分量移到频谱中心ifft 一维快速反傅立叶变换ifft2 二维傅立叶反变换ifftn 多维快速傅立叶变换ifftshift 反FFT偏移nextpow2 最靠近的2的幂次unwrap 校正相位角多项式与插值conv 卷积和多项式乘法roots 多项式的根poly 具有设定根的多项式polyder 多项式微分polyeig 多项式的特征根polyfit 多项式拟合polyint 解析多项式积分polyval 多项式求值polyvalm 矩阵变量多项式求值residue 部分分式展开interp1 一维插值interp2 二维插值interp3 三维插值interpft 使用FFT的一维插值interpn 多维插值meshgrid 为3维点生成x和y的网格ndgrid 生成多维函数和插值的数组pchip 分段3次Hermite插值多项式ppval 分段多项式的值spline 3次样条数据插值绘图函数bar 竖直条图barh 水平条图hist 直方图histc 直方图计数hold 保持当前图形loglog x,y对数坐标图pie 饼状图plot 绘二维图polar 极坐标图semilogy y轴对数坐标图semilogx x轴对数坐标subplot 绘制子图bar3 数值3D竖条图bar3h 水平3D条形图comet3 3D慧星图cylinder 圆柱体fill3 填充的3D多边形plot3 3维空间绘图quiver3 3D震动(速度)图slice 体积薄片图sphere 球stem3 绘制离散表面数据wate***ll 绘制瀑布trisurf 三角表面clabel 增加轮廓标签到等高线图中datetick 数据格式标记grid 加网格线gtext 用鼠标将文本放在2D图中legend 图注plotyy 左右边都绘Y轴title 标题xlabel X轴标签ylabel Y轴标签zlabel Z轴标签contour 等高线图contourc 等高线计算contourf 填充的等高线图hidden 网格线消影meshc 连接网格/等高线mesh 具有参考轴的3D网格peaks 具有两个变量的采样函数surf 3D阴影表面图su***ce 建立表面低层对象surfc 海浪和等高线的结合surfl 具有光照的3D阴影表面trimesh 三角网格图1 常用指令(General Purpose Commands) 1.1 通用信息查询(General information) demo 演示程序help 在线帮助指令helpbrowser 超文本文档帮助信息helpdesk 超文本文档帮助信息helpwin 打开在线帮助窗info MA TLAB 和MathWorks 公司的信息subscribe MA TLAB 用户注册ver MA TLAB 和TOOLBOX 的版本信息version MA TLAB 版本whatsnew 显示版本新特征1.2 工作空间管理(Managing the workspace)clear 从内存中清除变量和函数exit 关闭MA TLABload 从磁盘中调入数据变量pack 合并工作内存中的碎块quit 退出MA TLABsave 把内存变量存入磁盘who 列出工作内存中的变量名whos 列出工作内存中的变量细节workspace 工作内存浏览器1.3 管理指令和函数(Managing commands and functions) edit 矩阵编辑器edit 打开M 文件inmem 查看内存中的P 码文件mex 创建MEX 文件open 打开文件pcode 生成P 码文件type 显示文件内容what 列出当前目录上的M、MA T、MEX 文件which 确定指定函数和文件的位置1.4 搜索路径的管理(Managing the seach patli) addpath 添加搜索路径rmpath 从搜索路径中删除目录path 控制MA TLAB 的搜索路径pathtool 修改搜索路径1.5 指令窗控制(Controlling the command window) beep 产生beep 声echo 显示命令文件指令的切换开关diary 储存MA TLAB 指令窗操作内容format 设置数据输出格式more 命令窗口分页输出的控制开关1.6 操作系统指令(Operating system commands) cd 改变当前工作目录computer 计算机类型copyfile 文件拷贝delete 删除文件dir 列出的文件dos 执行dos 指令并返还结果getenv 给出环境值ispc MA TLAB 为PC(Windows)版本则为真isunix MA TLAB 为Unix 版本则为真mkdir 创建目录pwd 改变当前工作目录unix 执行unix 指令并返还结果vms 执行vms dcl 指令并返还结果web 打开web 浏览器! 执行外部应用程序2 运算符和特殊算符(Operators and special characters)2.1 算术运算符(Arithmetic operators)+ 加- 减* 矩阵乘.* 数组乘^ 矩阵乘方.^ 数组乘方\ 反斜杠或左除/ 斜杠或右除./或.\ 数组除张量积[注]本表第三栏括号中的字符供在线救助时help 指令引述用2.2 关系运算符(Relational operators)= = 等号~= 不等号< 小于> 大于<= 小于或等于>= 大于或等于2.3 逻辑操作(Logical operators) & 逻辑与| 逻辑或~ 逻辑非xor 异或any 有非零元则为真all 所有元素均非零则为真2.4 特殊算符(Special characters) :冒号( ) 圆括号[ ] 方括号{ } 花括号@ 创建函数句柄. 小数点. 构架域的关节点.. 父目录续行号, 逗号; 分号% 注释号! 调用操作系统命令= 赋值符号ˊ引号ˊ复数转置号.ˊ转置号[,] 水平串接[;] 垂直串接( ),{ },. 下标赋值( ),{ },. 下标标识subsindex 下标标识3 编程语言结构(Programming language constructs) 3.1 控制语句(Control flow)break 终止最内循环case 同switch 一起使用catch 同try 一起使用continue 将控制转交给外层的for 或while 循环else 同if 一起使用elseif 同if 一起使用end 结束for,while,if 语句for 按规定次数重复执行语句if 条件执行语句otherwise 可同switch 一起使用return 返回switch 多个条件分支try try-cathch 结构while 不确定次数重复执行语句3.2 计算运行(Evaluation and execution)assignin 跨空间赋值builtin 执行内建的函数eval 字符串宏指令evalc 执行MA TLAB 字符串evalin 跨空间计算串表达式的值feval 函数宏指令run 执行脚本文件3.3 脚本文件、函数及变量(Scripts,function,and variables) exist 检查变量或函数是否被定义function 函数文件头global 定义全局变量isglobal 若是全局变量则为真iskeyword 若是关键字则为真mfilename 正在执行的M 文件的名字persistent 定义永久变量script MA TLAB 命令文件3.4 宗量处理(Augument handling) inputname 实际调用变量名nargchk 输入变量个数检查nargin 函数输入宗量的个数nargout 函数输出宗量的个数nargoutchk 输出变量个数检查varagin 输入宗量varagout 输出宗量3.5 信息显示(Message display)disp 显示矩阵和文字内容display 显示矩阵和文字内容的重载函数error 显示错误信息fprintf 把格式化数据写到文件或屏幕lasterr 最后一个错误信息lastwarn 最后一个警告信息sprintf 按格式把数字转换为串warning 显示警告信息3.6 交互式输入(Interactive input)input 提示键盘输入keyboard 激活键盘做为命令文件pause 暂停uicontrol 创建用户界面控制uimenu 创建用户界面菜单4 基本矩阵函数和操作(Elementary matrices and matrix manipulation)4.1 基本矩阵(Elementary matrices)eye 单位阵linspace 线性等分向量logspace 对数等分向量meshgrid 用于三维曲面的分格线坐标ones 全1 矩阵rand 均匀分布随机阵randn 正态分布随机阵repmat 铺放模块数组zeros 全零矩阵: 矩阵的援引和重排4.2 矩阵基本信息(Basic array information)disp 显示矩阵和文字内容isempty 若是空矩阵则为真isequal 若对应元素相等则为1islogical 尤其是逻辑数则为真isnumeric 若是数值则为真length 确定向量的长度logical 将数值转化为逻辑值ndims 数组A 的维数size 确定矩阵的维数4.3 矩阵操作(Matrix manipulateion)blkdiag 块对角阵串接diag 创建对角阵,抽取对角向量end 数组的长度,即最大下标find 找出非零元素1 的下标fliplr 矩阵的左右翻转flipud 矩阵的上下翻转flipdim 交换对称位置上的元素ind2sub 据单下标换算出全下标reshape 矩阵变维rot90 矩阵逆时针90°旋转sub2idn 据全下标换算出单下标tril 抽取下三角阵triu 抽取上三角阵4.4 特殊变量和常数(Special variables and constants) ans 最新表达式的运算结果eps 浮点相对误差i,j 虚数单位inf 或Inf 无穷大isfinite 若是有限数则为真isinf 若是无穷大则为真isnan 若为非数则为真NaN 或nan 非数pi 3.1415926535897?.realmax 最大浮点数realmin 最小正浮点数why 一般问题的简明答案4.5 特殊矩阵(Specialized matrices) compan 伴随矩阵gallery 一些小测试矩阵hadamard Hadamard 矩阵hankel Hankel 矩阵hilb Hilbert 矩阵invhilb 逆Hilbert 矩阵magic 魔方阵pascal Pascal 矩阵rosser 典型对称特征值实验问题toeplitz T oeplitz 矩阵vander V andermonde 矩阵wilkinson Wilkinson’s 对称特征值实验矩阵5 基本数学函数(Elementary math functions)5.1 三角函数(T rigonometric) acos 反余弦acosh 反双曲余弦acot 反余切acoth 反双曲余切acsc 反余割acsch 反双曲余割asec 反正割asech 反双曲正割asin 反正弦asinh 反双曲正弦atan 反正切atanh 反双曲正切atan2 四象限反正切cos 余弦cosh 双曲余弦cot 余切coth 双曲余切csc 余割csch 双曲余割sec 正割sech 双曲正割sin 正弦sinh 双曲正弦tan 正切tanh 双曲正切5.2 指数函数(Exponential)exp 指数log 自然对数log10 常用对数log2 以2 为底的对数nestpow2 最近邻的2 的幂pow2 2 的幂sqrt 平方根5.3 复数函数(Complex)abs 绝对值angle 相角complex 将实部和虚部构成复数conj 复数共轭cplxpair 复数阵成共轭对形式排列imag 复数虚部isreal 若是实数矩阵则为真real 复数实部unwrap 相位角360°线调整5.4 圆整和求余函数(Rounding and remainder)ceil 朝正无穷大方向取整fix 朝零方向取整floor 朝负无穷大方向取整mod 模数求余rem 求余数round 四舍五入取整sign 符号函数6 特殊函数(Specialized math functions)cart2pol 直角坐标变为柱(或极)坐标cart2sph 直角坐标变为球坐标cross 向量叉积dot 向量内积isprime 若是质数则为真pol2cart 柱(或极)坐标变为直角坐标sph2cart 球坐标变为直角坐标7 矩阵函数和数值线性代数(Matrix functions-numerical linear algebra) 7.1 矩阵分析(Matrix analysis)det 行列式的值norm 矩阵或向量范数normest 估计2 范数null 零空间orth 值空间rank 秩rref 转换为行阶梯形trace 迹subspace 子空间的角度7.2 线性方程(Linear equations)chol Cholesky 分解cholinc 不完全Cholesky 分解cond 矩阵条件数condest 估计1-范数条件数inv 矩阵的逆lu LU 分解luinc 不完全LU 分解lscov 已知协方差的最小二乘积nnls 非负二乘解pinv 伪逆qr QR 分解rcond LINPACK 逆条件数\、/ 解线性方程7.3 特性值与奇异值(Eigenvalues and singular values) condeig 矩阵各特征值的条件数eig 矩阵特征值和特征向量eigs 多个特征值gsvd 归一化奇异值分解hess Hessenberg 矩阵poly 特征多项式polyeig 多项式特征值问题qz 广义特征值schur Schur 分解svd 奇异值分解svds 多个奇异值7.4 矩阵函数(Matrix functions)expm 矩阵指数expm1 矩阵指数的Pade 逼近expm2 用泰勒级数求矩阵指数expm3 通过特征值和特征向量求矩阵指数funm 计算一般矩阵函数logm 矩阵对数sqrtm 矩阵平方根7.5 因式分解(Factorization utility)cdf2rdf 复数对角型转换到实块对角型balance 改善特征值精度的平衡刻度rsf2csf 实块对角型转换到复数对角型8 数据分析和傅里叶变换(Date analysis and Fourier transforms)8.1 基本运算(Basic operations) cumprod 元素累计积cumsum 元素累计和cumtrapz 累计积分hist 统计频数直方图histc 直方图统计max 最大值mean 平均值median 中值min 最小值prod 元素积sort 由小到大排序sortrows 由小到大按行排序std 标准差sum 元素和trapz 梯形数值积分var 求方差8.2 有限差分(Finite differentces) del2 五点离散Laplaciandiff 差分和近似微分gradient 梯度8.3 相关(Correlation)corrcoef 相关系数cov 协方差矩阵subspace 子空间之间的角度8.4 滤波和卷积(Filtering and convoluteion) conv 卷积和多项式相乘conv2 二维卷积convn N 维卷积detrend 去除线性分量deconv 解卷和多项式相除filter 一维数字滤波器fliter2 二维数字滤波器8.5 傅里叶变换(Fourier transforms)fft 快速离散傅里叶变换fft2 二维离散傅里叶变换fftn N 维离散傅里叶变换fftshift 重排fft 和fft2 的输出ifft 离散傅里叶反变换ifft2 二维离散傅城叶反变换ifftn N 维离散傅里叶反变换ifftshift 反fftshift9 音频支持(Audio support)9.1 音频硬件驱动(Audio hardware drivers)sound 播放向量soundsc 自动标刻并播放waveplay 利用系统音频输出设配播放waverecor 利用系统音频输入设配录音9.2 音频文件输入输出(Audio file import and export) auread 读取音频文件(.au)auwrite 创建音频文件(.au)wavread 读取音频文件(.wav)wavwrite 创建音频文件(.wav)9.3 工具(Utilities)lin2mu 将线性信号转换为μ 一律编码的信号mu2lin 将μ 一律编码信号转换为线性信号10 插补多项式函数(Interpolation and polynomials) 10.1 数据插补(Data Interpolation)griddata 分格点数据griddata3 三维分格点数据griddatan 多维分格点数据interpft 利用FFT 方法一维插补interp1 一维插补interp1q 快速一维插补interp2 二维插补interp3 三维插补intern N 维插补pchip hermite 插补10.2 样条插补(Spline Interpolation)ppval 计算分段多项式spline 三次样条插补10.3 多项式(Polynomials)conv 多项式相乘deconv 多项式相除poly 由根创建多项式polyder 多项式微分polyfit 多项式拟合polyint 积分多项式分析polyval 求多项式的值polyvalm 求矩阵多项式的值residue 求部分分式表达roots 求多项式的根1#caidaoyiba11 数值泛函函数和ODE 解算器(Function functions and ODE solvers) 11.1 优化和寻根(Optimization and root finding)fminbnd 非线性函数在某区间中极小值fminsearch 单纯形法求多元函数极值点指令fzero 单变量函数的零点11.2 优化选项处理(Optimization Option handling)optimget 从OPTIONS 构架中取得优化参数optimset 创建或修改OPTIONS 构架11.3 数值积分(Numerical intergration)dblquad 二重(闭型)数值积分指令quad 低阶法数值积分quadl 高阶法数值积分11.4 绘图(Plotting)ezcontour 画等位线ezcontourf 画填色等位线ezmesh 绘制网格图ezmeshc 绘制含等高线的网格图ezplot 绘制曲线ezplot3 绘制3 维曲线ezpolar 采用极坐标绘图ezsurf 画曲面图ezsurfc 画带等位线的曲面图fplot 画函数曲线图11.5 内联函数对象(Inline function object) argnames 给出函数的输入宗量char 创建字符传输组或者将其他类型变量转化为字符串数组formula 函数公式inline 创建内联函数11.6 差微分函数解算器(Differential equation solvers) ode113 变阶法解方程ode15s 变阶法解刚性方程ode23 低阶法解微分方程ode23s 低阶法解刚性微分方程ode23t 解适度刚性微分方程odet23tb 低阶法解刚性微分方程ode45 高阶法解微分方程12 二维图形函数(Two dimensional graphs)12.1 基本平面图形(Elementary X-Y graphs) loglog 双对数刻度曲线plot 直角坐标下线性刻度曲线plotyy 双纵坐标图polar 极坐标曲线图semilogx X 轴半对数刻度曲线semilogy Y 轴半对数刻度曲线12.2 轴控制(Axis control)axes 创建轴axis 轴的刻度和表现box 坐标形式在封闭式和开启词式之间切换grid 画坐标网格线hold 图形的保持subplot 创建子图zoom 二维图形的变焦放大12.3 图形注释(Graph annotation)gtext 用鼠标在图上标注文字legend 图例说明plotedit 图形编辑工具text 在图上标注文字texlabel 将字符串转换为T ex 格式title 图形标题xlabel X 轴名标注ylabel Y 轴名标注12.4 硬拷贝(Hardcopy and printing)orient 设置走纸方向print 打印图形或把图存入文件printopt 打印机设置13 三维图形函数(Three dimensional graphs) 13.1 基本三维图形(Elementary 3-D plots) fill3 三维曲面多边形填色mesh 三维网线图plot3 三维直角坐标曲线图surf 三维表面图13.2 色彩控制(Color control)alpha 透明色控制brighten 控制色彩的明暗caxis (伪)颜色轴刻度colordef 用色风格colormap 设置色图graymon 设置缺省图形窗口为单色显示屏hidden 消隐shading 图形渲染模式whitebg 设置图形窗口为白底13.3 光照模式(Lighting)diffuse 漫反射表面系数light 灯光控制lighting 设置照明模式material 使用预定义反射模式specular 漫反射surfnorm 表面图的法线surfl 带光照的三维表面图13.4 色图(Color maps)autumn 红、黄浓淡色bone 蓝色调灰度图colorcube 三浓淡多彩交错色cool 青和品红浓淡色图copper 线性变化纯铜色调图flag 红-白-蓝黑交错色图gray 线性灰度hot 黑-红-黄-白交错色图hsv 饱和色彩图jet 变异HSV 色图lines 采用plot 绘线色pink 淡粉红色图prism 光谱色图spring 青、黄浓淡色summer 绿、黄浓淡色vga 16 色white 全白色winter 蓝、绿浓淡色13.5 轴的控制(Axis control)axes 创建轴axis 轴的刻度和表现box 坐标形式在封闭式和开启式之间切换daspect 轴的DataAspectRatio 属性grid 画坐标网格线hold 图形的保持pbaspect 画坐标框的PlotBoxAspectRatio 属性subplot 创建子图xlim X 轴范围ylim Y 轴范围zlim Z 轴范围zoom 二维图形的变焦放大13.6 视角控制(V iewpoint control)rotate3d 旋动三维图形view 设定3-D 图形观测点viewmtx 观测点转换矩阵13.7 图形注释(Graph annotation)colorbar 显示色条gtext 用鼠标在图上标注文字plotedit 图形编辑工具text 在图上标注文字title 图形标题xlabel X 轴名标注ylabel Y 轴名标注zlabel Z 轴名标注13.8 硬拷贝(Hardcopy and printing)orient 设置走纸方向print 打印图形或把图存入文件printopt 打印机设置verml 将图形保存为VRML2.0 文件14 特殊图形(Specialized graphs)14.1 特殊平面图形(Specialized 2-D graphs) area 面域图bar 直方图barh 水平直方图comet 彗星状轨迹图compass 从原点出发的复数向量图errorbar 误差棒棒图ezplot 画二维曲线ezpolar 画极坐标曲线feather 从X 轴出发的复数向量图fill 多边填色图fplot 函数曲线图hist 统计频数直方图pareto Pareto 图pie 饼形统计图plotmatrix 散点图阵列scatter 散点图stairs 阶梯形曲线图stem 火柴杆图14.2 等高线及二维半图形(Contour and 2-1/2D graphs) clabel 给等高线加标注contour 等高线图contourf 等高线图contour3 三维等高线ezcontour 画等位线ezcontourf 画填色等位线pcolor 用颜色反映数据的伪色图voronoi V oronoi 图14.3 特殊三维图形(Specialized 3-D graphs)bar3 三维直方图bar3h 三维水平直方图comet3 三维彗星动态轨迹线图ezgraph3 通用指令ezmesh 画网线图ezmeshc 画等位线的网线图ezplot3 画三维曲线ezsurf 画曲面图ezsurfc 画带等位线的曲面图meshc 带等高线的三维网线图meshz 带零基准面的三维网线图pie3 三维饼图ribbon 以三维形式绘制二维曲线scatter3 三维散点图stem3 三维离散杆图surfc 带等高线的三维表面图trimesh 三角剖分网线图trisurf 三角剖分曲面图waterfall 瀑布水线图14.4 内剖及向量视图(V olume and vector visualization) coneplot 锥体图contourslice 切片等位线图quiver 矢量场图quiver3 三维方向箭头图slice 切片图14.5 图像显示及文件处理(Image display and file I/O) brighten 控制色彩的明暗colorbar 色彩条状图colormap 设置色图contrast 提高图像对比度的灰色图gray 线性灰度image 显示图像imagesc 显示亮度图像imfinfo 获取图像文件的特征数据imread 从文件读取图像的数据阵(和伴随色图))imwrite 把强度图像或真彩图像写入文件14.6 影片和动画(Movies and animation)capture 当前图的屏捕捉frame2im 将影片动画转换为编址图像getframe 获得影片动画图像的帧im2frame 将编址图像转换为影片动画movie 播放影片动画moviein 影片动画内存初始化rotate 旋转指令14.7 颜色相关函数(Color related function)spinmap 颜色周期性变化操纵14.8 三维模型函数(Solid modeling)cylinder 圆柱面patch 创建块sphere 球面Surf2patch 将曲面数据转换为块数据15 句柄图形(Handle Graphics)15.1 图形窗的产生和控制(Figure window creation and control) clf 清除当前图close 关闭图形figure 打开或创建图形窗口gcf 获得当前图的柄openfig 打开图形refresh 刷新图形shg 显示图形窗15.2 轴的产生和控制(Axis creation and control) axes 在任意位置创建轴axis 轴的控制box 坐标形式在封闭式和开启式之间切换caxis 控制色轴的刻度cla 清除当前轴gca 获得当前轴的柄hold 图形的保持ishold 若图形处保持状态则为真subplot 创建子图15.3 句柄图形对象(Handle Graphics objects) axex 在任意位置创建轴figure 创建图形窗口image 创建图像light 创建光line 创建线patch 创建块rectangle 创建方surface 创建面text 创建图形中文本uicontextmenu 创建现场菜单对象uicontrol 用户使用界面控制uimenu 用户使用菜单控制15.4 句柄图形处理(Handle Graphics operations) copyobj 拷贝图形对象及其子对象delete 删除对象及文件drawnow 屏幕刷新findobj 用规定的特性找寻对象gcbf “正执行回调操作”的图形的柄gcbo “正执行回调操作”的控件图柄指令gco 获得当前对象的柄get 获得对象特性getappdat 获得应用程序定义数据isappdata 检验是否应用程序定义数据reset 重设对象特性rmappdata 删除应用程序定义数据set 建立对象特性setappdata 建立应用程序定义数据15.5 工具函数(Utilities)closereq 关闭图形窗请求函数ishandle 若是图柄代号侧为真newplot 下一个新图16 图形用户界面工具(Graphical user interface tools) align 对齐用户控件和轴cbedit 编辑回调函数ginput 从鼠标得到图形点坐标guide 设计GUImenu 创建菜单menuedit 菜单编辑propedit 属性编辑uicontrol 创建用户界面控制uimenu 创建用户界面菜单2#caidaoyiba17 字符串(Character string)17.1 通用字符串函数(General)blanks 空格符号cellstr 通过字符串数组构建字符串的元胞数组char 创建字符传输组或者将其他类型变量转化为字符串数组deblank 删除最后的空格double 把字符串变成ASCII 码值eval 执行串形式的MATLAB 表达式17.2 字符串查询(String tests)iscellstr 若是字符串组成的元胞数组则为真ischar 若是字符串则为真isletter 串中是字母则为真isspace 串中是空格则为真isstr 若是字符串则为真17.3 字符串操作(String operations)base2dec X-进制串转换为十进制整数bin2dec 二进制串转换为十进制整数dec2base 十进制整数转换为X 进制串dec2bin 十进制整数转换为二进制串dec2hex 十进制整数转换为16 进制串findstr 在一个串中寻找一个子串hex2dec 16-进制串转换为十进制整数hex2num 16-进制串转换为浮点数int2str 将整数转换为字符串lower 把字符串变成小写mat2str 将数组转换为字符串num2str 把数值转换为字符串strcat 把多个串连接成长串strcmp 比较字符串strcmpi 比较字符串(忽略大小写)strings MA TLAB 中的字符串strjust 字符串的对齐方式strmatch 逐行搜索串strnomp 比较字符串的前N 个字符strncmpi 比较字符串的前N 个字符(忽略大小写)strrep 用另一个串代替一个串中的子串strtok 删除串中的指定子串strvcat 创建字符串数组str2mat 将字符串转换为含有空格的数组str2num 将字符串转换为数值upper 把字符串变成大写18 文件输入/输出(File input/output)clc 清除指令窗口disp 显示矩阵和文字内容fprintf 把格式化数据写到文件或屏幕home 光标返回行首input 提示键盘输入load 从磁盘中调入数据变量pause 暂停sprintf 写格式数据到串sscanf 在格式控制下读串19 时间和日期(T ime and dates)clock 时钟cputme MA TLAB 战用CPU 时间date 日期etime 用CLOCK 计算的时间now 当前时钟和日期pause 暂停tic 秒表启动toc 秒表终止和显示20 数据类型(Data types and structures)20.1 数据类型(Data types)cell 创建元胞变量char 创建字符传输组或者将其他类型变量转化为字符串数组double 转化为16 位相对精度的浮点数值对象function handle 函数句柄inline 创建内联函数JavaArray 构建Java 数组JavaMethod 调用某个Java 方法JavaObject 调用Java 对象的构造函数single 转变为单精度数值sparse 创建稀疏矩阵struct 创建构架变量uint8(unit16、unit32) 转换为8(16、32)位无符号整型数int8(nit16、nit32) 转换为8(16、32)位符号整型数20.2 多维数组函数(Multi-dimensional array functions) cat 把若干数组串接成高维数组ndims 数组A 的维数ndgrid 为N-D 函数和插补创建数组ipermute 广义反转置permute 广义非共轭转置shiftdim 维数转换squeeze 使数组降维20.3 元胞数组函数(Cell array functions)cell 创建元胞变量celldisp 显示元胞数组内容cellfun 元胞数组函数cellplot 图示元胞数组的内容cell2struct 把元胞数组转换为构架数组deal 把输入分配给输出is cell 若是元胞则为真num2 cell 把数值数组转换为元胞数组struct2 cell 把构架数组转换为元胞数组20.4 构架函数(Structure functions)fieldnames 获取构架的域名getfield 获取域的内容isfield 若为给定构架的域名则为真isstruct 若是构架则为真rmfield 删除构架的域setfield 指定构架域的内容struct 创建构架变量20.5 函数句柄函数(Function handle functions)@ 创建函数句柄functions 列举函数句柄对应的函数func2str 将函数句柄数组转换为字符串str2func 将字符串转换为函数句柄20.6 面向对象编程(Object oriented programming functions) dlass 查明变量的类型isa 若是指定的数据类型则为真inferiorto 级别较低isjava 若是java 对象则为真isobject 若是对象则为真methods 显示类的方法名substruct 创建构架总量superiorto 级别较高21 示例(E xamples and demonstrations)demo 演示程序flow 无限大水体中水下射流速度数据intro 幻灯演示指令peaks 产生peaks 图形数据22 符号工具包(Symbolic Math T oolbox) 22.1 微积分(Calculus)diff 求导数limit 求极限int 计算积分jacobian Jacobian 矩阵symsum 符号序列的求和trylor T rylor 级数22.2 线性代数(Linear Algebra)det 行列式的值diag 创建对角阵,抽取对角向量eig 矩阵特征值和特征向量expm 矩阵指数inv 矩阵的逆jordan Jordan 分解null 零空间poly 特征多项式rank 秩rref 转换为行阶梯形svd 奇异值分解。
Matlab命令大全

matlab命令,应该很全了!来源:李家叶的日志matlab命令一、常用对象操作:除了一般windows窗口的常用功能键外。
1、!dir 可以查看当前工作目录的文件。
!dir& 可以在dos状态下查看。
2、who 可以查看当前工作空间变量名,whos 可以查看变量名细节。
3、功能键:功能键快捷键说明方向上键 Ctrl+P 返回前一行输入方向下键 Ctrl+N 返回下一行输入方向左键 Ctrl+B 光标向后移一个字符方向右键 Ctrl+F 光标向前移一个字符Ctrl+方向右键 Ctrl+R 光标向右移一个字符Ctrl+方向左键 Ctrl+L 光标向左移一个字符home Ctrl+A 光标移到行首End Ctrl+E 光标移到行尾Esc Ctrl+U 清除一行Del Ctrl+D 清除光标所在的字符Backspace Ctrl+H 删除光标前一个字符Ctrl+K 删除到行尾Ctrl+C 中断正在执行的命令4、clc可以命令窗口显示的内容,但并不清除工作空间。
二、函数及运算1、运算符:+:加,-:减, *:乘, /:除,\:左除 ^:幂,‘:复数的共轭转置,():制定运算顺序。
2、常用函数表:sin( ) 正弦(变量为弧度)Cot( ) 余切(变量为弧度)sind( ) 正弦(变量为度数)Cotd( ) 余切(变量为度数)asin( ) 反正弦(返回弧度)acot( ) 反余切(返回弧度)Asind( ) 反正弦(返回度数)acotd( ) 反余切(返回度数)cos( ) 余弦(变量为弧度)exp( ) 指数cosd( ) 余弦(变量为度数)log( ) 对数acos( ) 余正弦(返回弧度)log10( ) 以10为底对数acosd( ) 余正弦(返回度数)sqrt( ) 开方tan( ) 正切(变量为弧度)realsqrt( ) 返回非负根tand( ) 正切(变量为度数)abs( ) 取绝对值atan( ) 反正切(返回弧度)angle( ) 返回复数的相位角atand( ) 反正切(返回度数)mod(x,y) 返回x/y的余数sum( ) 向量元素求和3、其余函数可以用help elfun和help specfun命令获得。
Matlab常用工具箱及常用函数

Matlab常用工具箱MATLAB包括拥有数百个内部函数的主包和三十几种工具包.工具包又可以分为功能性工具包和学科工具包.功能工具包用来扩充MATLAB的符号计算,可视化建模仿真,文字处理及实时控制等功能.学科工具包是专业性比较强的工具包,控制工具包,信号处理工具包,通信工具包等都属于此类.开放性使MATLAB广受用户欢迎.除内部函数外,所有MATLAB主包文件和各种工具包都是可读可修改的文件,用户通过对源程序的修改或加入自己编写程序构造新的专用工具包.Matlab Main Toolbox——matlab主工具箱Control System Toolbox——控制系统工具箱Communication Toolbox——通讯工具箱Financial Toolbox——财政金融工具箱System Identification Toolbox——系统辨识工具箱Fuzzy Logic Toolbox——模糊逻辑工具箱Higher-Order Spectral Analysis Toolbox——高阶谱分析工具箱Image Processing Toolbox——图象处理工具箱LMI Control Toolbox——线性矩阵不等式工具箱Model predictive Control Toolbox——模型预测控制工具箱μ-Analysis and Synthesis Toolbox——μ分析工具箱Neural Network Toolbox——神经网络工具箱Optimization Toolbox——优化工具箱Partial Differential Toolbox——偏微分方程工具箱Robust Control Toolbox——鲁棒控制工具箱Signal Processing Toolbox——信号处理工具箱Spline Toolbox——样条工具箱Statistics Toolbox——统计工具箱Symbolic Math Toolbox——符号数学工具箱Simulink Toolbox——动态仿真工具箱Wavele Toolbox——小波工具箱常用函数Matlab内部常数[3]eps:浮点相对精度exp:自然对数的底数ei 或 j:基本虚数单位inf 或 Inf:无限大, 例如1/0nan或NaN:非数值(Not a number),例如0/0pi:圆周率 p(= 3.1415926...)realmax:系统所能表示的最大数值realmin:系统所能表示的最小数值nargin: 函数的输入引数个数nargout: 函数的输出引数个数lasterr:存放最新的错误信息lastwarn:存放最新的警告信息MATLAB常用基本数学函数abs(x):纯量的绝对值或向量的长度angle(z):复数z的相角(Phase angle)sqrt(x):开平方real(z):复数z的实部imag(z):复数z的虚部conj(z):复数z的共轭复数round(x):四舍五入至最近整数fix(x):无论正负,舍去小数至最近整数floor(x):地板函数,即舍去正小数至最近整数ceil(x):天花板函数,即加入正小数至最近整数rat(x):将实数x化为分数表示rats(x):将实数x化为多项分数展开sign(x):符号函数 (Signum function).当x0时,sign(x)=1.rem(x,y):求x除以y的馀数gcd(x,y):整数x和y的最大公因数lcm(x,y):整数x和y的最小公倍数exp(x) :自然指数pow2(x):2的指数log(x):以e为底的对数,即自然对数或log2(x):以2为底的对数log10(x):以10为底的对数MATLAB常用三角函数sin(x):正弦函数cos(x):余弦函数tan(x):正切函数asin(x):反正弦函数acos(x):反余弦函数atan(x):反正切函数atan2(x,y):四象限的反正切函数sinh(x):双曲正弦函数cosh(x):双曲余弦函数tanh(x):双曲正切函数asinh(x):反双曲正弦函数acosh(x):反双曲余弦函数atanh(x):反双曲正切函数适用于向量的常用函数有min(x): 向量x的元素的最小值max(x): 向量x的元素的最大值mean(x): 向量x的元素的平均值median(x): 向量x的元素的中位数std(x): 向量x的元素的标准差diff(x): 向量x的相邻元素的差sort(x): 对向量x的元素进行排序(Sorting)length(x): 向量x的元素个数norm(x): 向量x的欧氏(Euclidean)长度sum(x): 向量x的元素总和prod(x): 向量x的元素总乘积cumsum(x): 向量x的累计元素总和cumprod(x): 向量x的累计元素总乘积dot(x, y): 向量x和y的内积cross(x, y): 向量x和y的外积MATLAB基本绘图函数plot: x轴和y轴均为线性刻度(Linear scale)loglog: x轴和y轴均为对数刻度(Logarithmic scale)semilogx: x轴为对数刻度,y轴为线性刻度semilogy: x轴为线性刻度,y轴为对数刻度matlab插值和样条plot绘图函数的参数字元颜色字元图线型态y 黄色 . 点k 黑色 o 圆w 白色 x xb 蓝色 + +g 绿色 * *r 红色 - 实线c 亮青色 : 点线m 锰紫色 -. 点虚线-- 虚线注解xlabel('Input Value'); % x轴注解ylabel('Function Value'); % y轴注解title('Two Trigonometric Functions'); % 图形标题legend('y = sin(x)','y = cos(x)'); % 图形注解grid on; % 显示格线二维绘图函数bar 长条图errorbar 图形加上误差范围fplot 较精确的函数图形polar 极座标图hist 累计图rose 极座标累计图stairs 阶梯图stem 针状图fill 实心图feather 羽毛图compass 罗盘图quiver 向量场图[4]Welcome To Download !!!欢迎您的下载,资料仅供参考!。
Matlab_Handout_3

MATLAB – HANDOUT 3PLOTTING USING MATLABThis handout will give useful information to enable you to plot the functions arising in tutorial sheets 6 and 7 and also to plot the functions you will encounter in your projects.Start by opening the help files within Matlab and finding the page copied below.Click on the link Graphics and Read the first two pages entitled ‘Creating a Plot’ and ‘Multiple Data Sets in One Graph’.Important Note about plotting functions.When specifying a range of values of x, say x =[0: 0.1: 10] a matrix is created to store the values. If you define a function R(x) = (x2+1)/ (x-3) you need to use term-by-term multiplication in Matlab:R(x) = (x.^2 + 1)./(x-3)Interactive Plot EditingTo format a graph to provide readability, for example by setting the scale of axes, including tick marks on the axes, and using colour and line style to distinguish the plots in the graph you can use interactive plot editing (see screenshot overleaf). You can also use command line editing (ie writing commands in your m-file). It is probably easier to start with interactive plot editing, but be aware that you may need to use a combination of interactive editing and command line editing to achieve the effect you desire.To learn about interacti ve plot editing, read the pages in HELP entitled ‘Editing Plots‘, Plot Editing Mode’.Saving a FigureTo save a figure using a graphics format, such as JPEG, select Export from the File menu. You can then open the file in paint, or a similar application and then copy and paste into a Word document.Using the zoom facility to find maxima, minima and roots.When in interactive plot editing mode, the zoom facility can be used to zoom into a local maximum or minimum value of a function or a root, to find it to any given accuracy. It is helpful to have a grid on the figure when using the zoom facility. TablesOne way to obtain a table of values is to form a new matrix with the columns of the table as entries. If, for example, you wish a table with time, t, in one column and pulse-rate, P, in another (see tutorial sheet 7), then form a new matrix A as follows:t = [0:0.1:1800]P = 2*tA = [ t’, P’]To insert the table into a word document, first copy and paste the table from the command window into Excel. If the data is all in one column, then select the data and choose Data from the menus and then select Text to columns. Follow the wizard to get the data into separate columns. Then insert headings, etc. and copy and paste into Word.。
matlab命令

matlab命令Matlab命令汇总作者:佚名教程来源:网络 28一、常用对象操作:除了一般windows窗口的常用功能键外。
1、!dir 可以查看当前工作目录的文件。
!dir& 可以在dos状态下查看。
2、who 可以查看当前工作空间变量名,whos 可以查看变量名细节。
3、功能键:功能键快捷键说明方向上键 Ctrl+P 返回前一行输入方向下键 Ctrl+N 返回下一行输入方向左键 Ctrl+B 光标向后移一个字符方向右键 Ctrl+F 光标向前移一个字符Ctrl+方向右键 Ctrl+R 光标向右移一个字符Ctrl+方向左键 Ctrl+L 光标向左移一个字符home Ctrl+A 光标移到行首End Ctrl+E 光标移到行尾Esc Ctrl+U 清除一行Del Ctrl+D 清除光标所在的字符Backspace Ctrl+H 删除光标前一个字符 Ctrl+K 删除到行尾Ctrl+C 中断正在执行的命令4、clc可以命令窗口显示的内容,但并不清除工作空间。
二、函数及运算1、运算符:+:加,-:减, *:乘, /:除, \:左除 ^:幂,‘:复数的共轭转置,():制定运算顺序。
2、常用函数表:sin( ) 正弦(变量为弧度)Cot( ) 余切(变量为弧度)sind( ) 正弦(变量为度数)Cotd( ) 余切(变量为度数)asin( ) 反正弦(返回弧度)acot( ) 反余切(返回弧度)Asind( ) 反正弦(返回度数)acotd( ) 反余切(返回度数)cos( ) 余弦(变量为弧度)exp( ) 指数cosd( ) 余弦(变量为度数)log( ) 对数acos( ) 余正弦(返回弧度)log10( ) 以10为底对数acosd( ) 余正弦(返回度数)sqrt( ) 开方tan( ) 正切(变量为弧度)realsqrt( ) 返回非负根tand( ) 正切(变量为度数)abs( ) 取绝对值atan( ) 反正切(返回弧度)angle( ) 返回复数的相位角atand( ) 反正切(返回度数)mod(x,y) 返回x/y的余数sum( ) 向量元素求和3、其余函数可以用help elfun和help specfun命令获得。
MATLAB命令大全

MATLAB命令大全分类:VC MatlabA aabs 绝对值、模、字符的ASCII码值acos 反余弦acosh 反双曲余弦acot 反余切acoth 反双曲余切acsc 反余割acsch 反双曲余割align 启动图形对象几何位置排列工具all 所有元素非零为真angle 相角ans 表达式计算结果的缺省变量名any 所有元素非全零为真area 面域图argnames 函数M文件宗量名asec 反正割asech 反双曲正割asin 反正弦asinh 反双曲正弦assignin 向变量赋值atan 反正切atan2 四象限反正切atanh 反双曲正切autumn 红黄调秋色图阵axes 创建轴对象的低层指令axis 控制轴刻度和风格的高层指令B bbar 二维直方图bar3 三维直方图bar3h 三维水平直方图barh 二维水平直方图base2dec X进制转换为十进制bin2dec 二进制转换为十进制blanks 创建空格串bone 蓝色调黑白色图阵box 框状坐标轴break while 或for 环中断指令brighten 亮度控制C ccapture (3版以前)捕获当前图形cart2pol 直角坐标变为极或柱坐标cart2sph 直角坐标变为球坐标cat 串接成高维数组caxis 色标尺刻度cd 指定当前目录cdedit 启动用户菜单、控件回调函数设计工具cdf2rdf 复数特征值对角阵转为实数块对角阵ceil 向正无穷取整cell 创建元胞数组cell2struct 元胞数组转换为构架数组celldisp 显示元胞数组内容cellplot 元胞数组内部结构图示char 把数值、符号、内联类转换为字符对象chi2cdf 分布累计概率函数chi2inv 分布逆累计概率函数chi2pdf 分布概率密度函数chi2rnd 分布随机数发生器chol Cholesky分解clabel 等位线标识cla 清除当前轴class 获知对象类别或创建对象clc 清除指令窗clear 清除内存变量和函数clf 清除图对象clock 时钟colorcube 三浓淡多彩交叉色图矩阵colordef 设置色彩缺省值colormap 色图colspace 列空间的基close 关闭指定窗口colperm 列排序置换向量comet 彗星状轨迹图comet3 三维彗星轨迹图compass 射线图compose 求复合函数cond (逆)条件数condeig 计算特征值、特征向量同时给出条件数condest 范 -1条件数估计conj 复数共轭contour 等位线contourf 填色等位线contour3 三维等位线contourslice 四维切片等位线图conv 多项式乘、卷积cool 青紫调冷色图copper 古铜调色图cos 余弦cosh 双曲余弦cot 余切coth 双曲余切cplxpair 复数共轭成对排列csc 余割csch 双曲余割cumsum 元素累计和cumtrapz 累计梯形积分cylinder 创建圆柱D ddblquad 二重数值积分deal 分配宗量deblank 删去串尾部的空格符dec2base 十进制转换为X进制dec2bin 十进制转换为二进制dec2hex 十进制转换为十六进制deconv 多项式除、解卷delaunay Delaunay 三角剖分del2 离散Laplacian差分demo Matlab演示det 行列式diag 矩阵对角元素提取、创建对角阵diary Matlab指令窗文本内容记录diff 数值差分、符号微分digits 符号计算中设置符号数值的精度dir 目录列表disp 显示数组display 显示对象内容的重载函数dlinmod 离散系统的线性化模型dmperm 矩阵Dulmage-Mendelsohn 分解dos 执行DOS 指令并返回结果double 把其他类型对象转换为双精度数值drawnow 更新事件队列强迫Matlab刷新屏幕dsolve 符号计算解微分方程E eecho M文件被执行指令的显示edit 启动M文件编辑器eig 求特征值和特征向量eigs 求指定的几个特征值end 控制流FOR等结构体的结尾元素下标eps 浮点相对精度error 显示出错信息并中断执行errortrap 错误发生后程序是否继续执行的控制erf 误差函数erfc 误差补函数erfcx 刻度误差补函数erfinv 逆误差函数errorbar 带误差限的曲线图etreeplot 画消去树eval 串演算指令evalin 跨空间串演算指令exist 检查变量或函数是否已定义exit 退出Matlab环境exp 指数函数expand 符号计算中的展开操作expint 指数积分函数expm 常用矩阵指数函数expm1 Pade法求矩阵指数expm2 Taylor法求矩阵指数expm3 特征值分解法求矩阵指数eye 单位阵ezcontour 画等位线的简捷指令ezcontourf 画填色等位线的简捷指令ezgraph3 画表面图的通用简捷指令ezmesh 画网线图的简捷指令ezmeshc 画带等位线的网线图的简捷指令ezplot 画二维曲线的简捷指令ezplot3 画三维曲线的简捷指令ezpolar 画极坐标图的简捷指令ezsurf 画表面图的简捷指令ezsurfc 画带等位线的表面图的简捷指令F ffactor 符号计算的因式分解feather 羽毛图feedback 反馈连接feval 执行由串指定的函数fft 离散Fourier变换fft2 二维离散Fourier变换fftn 高维离散Fourier变换fftshift 直流分量对中的谱fieldnames 构架域名figure 创建图形窗fill3 三维多边形填色图find 寻找非零元素下标findobj 寻找具有指定属性的对象图柄findstr 寻找短串的起始字符下标findsym 机器确定内存中的符号变量finverse 符号计算中求反函数fix 向零取整flag 红白蓝黑交错色图阵fliplr 矩阵的左右翻转flipud 矩阵的上下翻转flipdim 矩阵沿指定维翻转floor 向负无穷取整flops 浮点运算次数flow Matlab提供的演示数据fmin 求单变量非线性函数极小值点(旧版)fminbnd 求单变量非线性函数极小值点fmins 单纯形法求多变量函数极小值点(旧版)fminunc 拟牛顿法求多变量函数极小值点fminsearch 单纯形法求多变量函数极小值点fnder 对样条函数求导fnint 利用样条函数求积分fnval 计算样条函数区间内任意一点的值fnplt 绘制样条函数图形fopen 打开外部文件for 构成for环用format 设置输出格式fourier Fourier 变换fplot 返函绘图指令fprintf 设置显示格式fread 从文件读二进制数据fsolve 求多元函数的零点full 把稀疏矩阵转换为非稀疏阵funm 计算一般矩阵函数funtool 函数计算器图形用户界面fzero 求单变量非线性函数的零点G ggamma 函数gammainc 不完全函数gammaln 函数的对数gca 获得当前轴句柄gcbo 获得正执行"回调"的对象句柄gcf 获得当前图对象句柄gco 获得当前对象句柄geomean 几何平均值get 获知对象属性getfield 获知构架数组的域getframe 获取影片的帧画面ginput 从图形窗获取数据global 定义全局变量gplot 依图论法则画图gradient 近似梯度gray 黑白灰度grid 画分格线griddata 规则化数据和曲面拟合gtext 由鼠标放置注释文字guide 启动图形用户界面交互设计工具H hharmmean 调和平均值help 在线帮助helpwin 交互式在线帮助helpdesk 打开超文本形式用户指南hex2dec 十六进制转换为十进制hex2num 十六进制转换为浮点数hidden 透视和消隐开关hilb Hilbert矩阵hist 频数计算或频数直方图histc 端点定位频数直方图histfit 带正态拟合的频数直方图hold 当前图上重画的切换开关horner 分解成嵌套形式hot 黑红黄白色图hsv 饱和色图I iif-else-elseif 条件分支结构ifft 离散Fourier反变换ifft2 二维离散Fourier反变换ifftn 高维离散Fourier反变换ifftshift 直流分量对中的谱的反操作ifourier Fourier反变换i, j 缺省的"虚单元"变量ilaplace Laplace反变换imag 复数虚部image 显示图象imagesc 显示亮度图象imfinfo 获取图形文件信息imread 从文件读取图象imwrite 把imwrite 把图象写成文件ind2sub 单下标转变为多下标inf 无穷大info MathWorks公司网点地址inline 构造内联函数对象inmem 列出内存中的函数名input 提示用户输入inputname 输入宗量名int 符号积分int2str 把整数数组转换为串数组interp1 一维插值interp2 二维插值interp3 三维插值interpn N维插值interpft 利用FFT插值intro Matlab自带的入门引导inv 求矩阵逆invhilb Hilbert矩阵的准确逆ipermute 广义反转置isa 检测是否给定类的对象ischar 若是字符串则为真isequal 若两数组相同则为真isempty 若是空阵则为真isfinite 若全部元素都有限则为真isfield 若是构架域则为真isglobal 若是全局变量则为真ishandle 若是图形句柄则为真ishold 若当前图形处于保留状态则为真isieee 若计算机执行IEEE规则则为真isinf 若是无穷数据则为真isletter 若是英文字母则为真islogical 若是逻辑数组则为真ismember 检查是否属于指定集isnan 若是非数则为真isnumeric 若是数值数组则为真isobject 若是对象则为真isprime 若是质数则为真isreal 若是实数则为真isspace 若是空格则为真issparse 若是稀疏矩阵则为真isstruct 若是构架则为真isstudent 若是Matlab学生版则为真iztrans 符号计算Z反变换J j , K kjacobian 符号计算中求Jacobian 矩阵jet 蓝头红尾饱和色jordan 符号计算中获得 Jordan标准型keyboard 键盘获得控制权kron Kronecker乘法规则产生的数组L llaplace Laplace变换lasterr 显示最新出错信息lastwarn 显示最新警告信息leastsq 解非线性最小二乘问题(旧版)legend 图形图例lighting 照明模式line 创建线对象lines 采用plot 画线色linmod 获连续系统的线性化模型linmod2 获连续系统的线性化精良模型linspace 线性等分向量ln 矩阵自然对数load 从MAT文件读取变量log 自然对数log10 常用对数log2 底为2的对数loglog 双对数刻度图形logm 矩阵对数logspace 对数分度向量lookfor 按关键字搜索M文件lower 转换为小写字母lsqnonlin 解非线性最小二乘问题lu LU分解M mmad 平均绝对值偏差magic 魔方阵maple &nb, sp; 运作 Maple格式指令mat2str 把数值数组转换成输入形态串数组material 材料反射模式max 找向量中最大元素mbuild 产生EXE文件编译环境的预设置指令mcc 创建MEX或EXE文件的编译指令mean 求向量元素的平均值median 求中位数menuedit 启动设计用户菜单的交互式编辑工具mesh 网线图meshz 垂帘网线图meshgrid 产生"格点"矩阵methods 获知对指定类定义的所有方法函数mex 产生MEX文件编译环境的预设置指令mfunlis 能被mfun计算的MAPLE经典函数列表mhelp 引出 Maple的在线帮助min 找向量中最小元素mkdir 创建目录mkpp 逐段多项式数据的明晰化mod 模运算more 指令窗中内容的分页显示movie 放映影片动画moviein 影片帧画面的内存预置mtaylor 符号计算多变量Taylor级数展开N nndims 求数组维数NaN 非数(预定义)变量nargchk 输入宗量数验证nargin 函数输入宗量数nargout 函数输出宗量数ndgrid 产生高维格点矩阵newplot 准备新的缺省图、轴nextpow2 取最接近的较大2次幂nnz 矩阵的非零元素总数nonzeros 矩阵的非零元素norm 矩阵或向量范数normcdf 正态分布累计概率密度函数normest 估计矩阵2范数norminv 正态分布逆累计概率密度函数normpdf 正态分布概率密度函数normrnd 正态随机数发生器notebook 启动Matlab和Word的集成环境null 零空间num2str 把非整数数组转换为串numden 获取最小公分母和相应的分子表达式nzmax 指定存放非零元素所需内存O oode1 非Stiff 微分方程变步长解算器ode15s Stiff 微分方程变步长解算器ode23t 适度Stiff 微分方程解算器ode23tb Stiff 微分方程解算器ode45 非Stiff 微分方程变步长解算器odefile ODE 文件模板odeget 获知ODE 选项设置参数odephas2 ODE 输出函数的二维相平面图odephas3 ODE 输出函数的三维相空间图odeplot ODE 输出函数的时间轨迹图odeprint 在Matlab指令窗显示结果odeset 创建或改写 ODE选项构架参数值ones 全1数组optimset 创建或改写优化泛函指令的选项参数值orient 设定图形的排放方式orth 值空间正交化P ppack 收集Matlab内存碎块扩大内存pagedlg 调出图形排版对话框patch 创建块对象path 设置Matlab搜索路径的指令pathtool 搜索路径管理器pause 暂停pcode 创建预解译P码文件pcolor 伪彩图peaks Matlab提供的典型三维曲面permute 广义转置pi (预定义变量)圆周率pie 二维饼图pie3 三维饼图pink 粉红色图矩阵pinv 伪逆plot 平面线图plot3 三维线图plotmatrix 矩阵的散点图plotyy 双纵坐标图poissinv 泊松分布逆累计概率分布函数poissrnd 泊松分布随机数发生器pol2cart 极或柱坐标变为直角坐标polar 极坐标图poly 矩阵的特征多项式、根集对应的多项式poly2str 以习惯方式显示多项式poly2sym 双精度多项式系数转变为向量符号多项式polyder 多项式导数polyfit 数据的多项式拟合polyval 计算多项式的值polyvalm 计算矩阵多项式pow2 2的幂ppval 计算分段多项式pretty 以习惯方式显示符号表达式print 打印图形或SIMULINK模型printsys 以习惯方式显示有理分式prism 光谱色图矩阵procread 向MAPLE输送计算程序profile 函数文件性能评估器propedit 图形对象属性编辑器pwd 显示当前工作目录Q qquad 低阶法计算数值积分quad8 高阶法计算数值积分(QUADL)quit 推出Matlab 环境quiver 二维方向箭头图quiver3 三维方向箭头图R rrand 产生均匀分布随机数randn 产生正态分布随机数randperm 随机置换向量range 样本极差rank 矩阵的秩rats 有理输出rcond 矩阵倒条件数估计real 复数的实部reallog 在实数域内计算自然对数realpow 在实数域内计算乘方realsqrt 在实数域内计算平方根realmax 最大正浮点数realmin 最小正浮点数rectangle 画"长方框"rem 求余数repmat 铺放模块数组reshape 改变数组维数、大小residue 部分分式展开return 返回ribbon 把二维曲线画成三维彩带图rmfield 删去构架的域roots 求多项式的根rose 数扇形图rot90 矩阵旋转90度rotate 指定的原点和方向旋转rotate3d 启动三维图形视角的交互设置功能round 向最近整数圆整rref 简化矩阵为梯形形式rsf2csf 实数块对角阵转为复数特征值对角阵rsums Riemann和S ssave 把内存变量保存为文件scatter 散点图scatter3 三维散点图sec 正割sech 双曲正割semilogx X轴对数刻度坐标图semilogy Y轴对数刻度坐标图series 串联连接set 设置图形对象属性setfield 设置构架数组的域setstr 将ASCII码转换为字符的旧版指令sign 根据符号取值函数signum 符号计算中的符号取值函数sim 运行SIMULINK模型simget 获取SIMULINK模型设置的仿真参数simple 寻找最短形式的符号解simplify 符号计算中进行简化操作simset 对SIMULINK模型的仿真参数进行设置simulink 启动SIMULINK模块库浏览器sin 正弦sinh 双曲正弦size 矩阵的大小slice 立体切片图solve 求代数方程的符号解spalloc 为非零元素配置内存sparse 创建稀疏矩阵spconvert 把外部数据转换为稀疏矩阵spdiags 稀疏对角阵spfun 求非零元素的函数值sph2cart 球坐标变为直角坐标sphere 产生球面spinmap 色图彩色的周期变化spline 样条插值spones 用1置换非零元素sprandsym 稀疏随机对称阵sprank 结构秩spring 紫黄调春色图sprintf 把格式数据写成串spy 画稀疏结构图sqrt 平方根sqrtm 方根矩阵squeeze 删去大小为1的"孤维"sscanf 按指定格式读串stairs 阶梯图std 标准差stem 二维杆图step 阶跃响应指令str2double 串转换为双精度值str2mat 创建多行串数组str2num 串转换为数strcat 接成长串strcmp 串比较strjust 串对齐strmatch 搜索指定串strncmp 串中前若干字符比较strrep 串替换strtok 寻找第一间隔符前的内容struct 创建构架数组struct2cell 把构架转换为元胞数组strvcat 创建多行串数组sub2ind 多下标转换为单下标subexpr 通过子表达式重写符号对象subplot 创建子图subs 符号计算中的符号变量置换subspace 两子空间夹角sum 元素和summer 绿黄调夏色图superiorto 设定优先级surf 三维着色表面图surface 创建面对象surfc 带等位线的表面图surfl 带光照的三维表面图surfnorm 空间表面的法线svd 奇异值分解svds 求指定的若干奇异值switch-case-otherwise 多分支结构sym2poly 符号多项式转变为双精度多项式系数向量symmmd 对称最小度排序symrcm 反向Cuthill-McKee排序syms 创建多个符号对象T ttan 正切tanh 双曲正切taylortool 进行Taylor逼近分析的交互界面text 文字注释tf 创建传递函数对象tic 启动计时器title 图名toc 关闭计时器trapz 梯形法数值积分treelayout 展开树、林treeplot 画树图tril 下三角阵trim 求系统平衡点trimesh 不规则格点网线图trisurf 不规则格点表面图 triu 上三角阵 try-catch 控制流中的Try-catch结构 typ e 显示M文件U uuicontextmenu 创建现场菜单uicontrol 创建用户控件uimenu 创建用户菜单unmkpp 逐段多项式数据的反明晰化unwrap 自然态相角upper 转换为大写字母V vvar 方差varargin 变长度输入宗量varargout 变长度输出宗量vectorize 使串表达式或内联函数适于数组运算ver 版本信息的获取view 三维图形的视角控制voronoi Voronoi多边形vpa 任意精度(符号类)数值W wwarning 显示警告信息what 列出当前目录上的文件whatsnew 显示Matlab中 Readme文件的内容which 确定函数、文件的位置while 控制流中的While环结构white 全白色图矩阵whitebg 指定轴的背景色who 列出内存中的变量名whos 列出内存中变量的详细信息winter 蓝绿调冬色图workspace 启动内存浏览器X x , Y y , Z zxlabel X轴名xor 或非逻辑yesinput 智能输入指令ylabel Y轴名zeros 全零数组zlabel Z轴名zoom 图形的变焦放大和缩小ztrans 符号计算Z变换相关信息。
MATLAB如何使用-教程-初步入门大全资料

运算 数学表达式
加 a+b
减
a-b
乘 a×b
除 a÷ b
幂 a^b
MATLAB运算符
+ *
/(右除)或\(左除)
^
MATLAB表达式
a+b a-b a*b a/b或b\a a^b
示例
1+2 5-3 2*3
6/2或2\6 2^3
指出:右除相当于通常的除法。
22
七、MATLAB的变量与函数
1、变量 变量就是在程序的运行过程中,其数值可以变化的量
MATLAB是交互式的语言,输入命令即给出运算结 果。而命令窗口则是MATLAB的主要交互窗口,用 于输入和编辑命令行等信息,显示结果(图形除 外)。
当命令窗口中出现提示符“>>”时,表示MATLAB已 经准备好,可以输入命令、变量或运行函数。提示 符总是位于行首。
在每个指令行输入后要按回车键,才能使指令被 MATLAB执行。
28
矩阵的创建(续)
1、直接输入法-在命令窗口按规则输入方式创建矩阵
例1.在命令窗口创建简单的数值矩阵。
>>A=[1 3 2;3 1 0;2 1 5] 回车后在命令窗口显示如下结果
A=
132
310
215 例2.在命令窗口创建带运算表达式的矩阵,不显示结果。
>>y=[sin(pi/3),cos(pi/6);log(20),exp(2)]; 输入“y”回车,在命令窗口显示出来。
(3)在MATLAB安装目录\MATLAB6p5中双击 MATLAB快捷方式。
(4)在MATLAB安装目录\MATLAB6p5\bin\win32 中双击MATLAB.exe图标。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Matrices and Vectors
Construction: The simplest way to construct a matrix in MATLAB is to enumerate its elements row by row within square brackets, the rows separated by semi-colons, the elements of each row separated by spaces. These elements can be real/complex numbers or other vectors and matrices, as long as the dimensions match up. For example,
Getting started
MATLAB can be started by clicking on the program icon on a Windows/Mac machine, or issuing the command matlab at a shell prompt in a *nix/X-windows environment. The command window can be used to interactively issue commands and evaluate expressions.
The basic mathematical operators (+, -, *, /, ^) can be used directly at the command prompt to perform calculations, as can various elementary mathematical functions. help elfun gives a list of the elementary mathematical functions. Remember that angles are specified in radians to functions like sin() and cos(). Examples of usage:
>> 8 + 3i + 5 ans =
13.0000 + 3.0000i
>> sqrt(-4)
>> sinh(1)
ans =
ans =
0 + 1.4142i
1.1752
Note: “>>” denotes the command prompt, and the lines below show the output corresponding to the command executed at the command prompt. A semi-colon at the end of a command suppresses the output.
The extensive help files are essential for obtaining information about the various commands and functions available. Typing help at the command prompt generates a list of the various function categories and toolboxes with a brief description of each. Typing help topic generates help on the specified topic, which is generally a MATLAB command or toolbox name. This can be used to get the syntax for different commands. A more user-friendly graphical help system is also available via the help menu.
Addressing elements: The element in the ith row and jth column of a matrix A is A(i,j). The subscripts i and j cannot be negative or zero. In the case of a vector x, the ith element of the vector is addressed as x(i).
x = starting value : increment : maximum value
A default increment of 1 is used if the increment is omitted. If the vector has to have a specific last element, we use the linspace command:
x = linspace(first_element,last_element,number_of_elements)
Column vectors are constructed as matrices with several rows of one element each:
>> y = [1;2;3]
There are other built-in functions to generate specific types of matrices: • eye(m,n) generates an m x n matrix with ones on the main diagonal ank Control Design
An Introduction to MATLAB and the Control Systems toolbox
Aravind Parchuri, Darren Hon and Albert Honein
MATLAB is essentially a programming interface that can be used for a variety of scientific calculations, programming and graphical visualization. Its basic data element is an array, and its computations are optimized for this data type, which makes it ideal for problems with matrix and vector formulations. MATLAB is also extendible by means of add-on script packages called toolboxes, which provide application-specific functions for use with MATLAB. For this course, we will mostly be using MATLAB’s basic matrix/vector operations and graphing capabilities in conjunction with the control system toolbox.
>> A = [1 2 3;7 8 9]; >> A(2,1) ans =
7
>> x = [4 5 6]; x(2) ans =
5
Matrix operations: Matrix addition, subtraction and multiplication are implemented using the traditional operators +, - and *. The inverse of a square matrix A is given by inv(A). There are two matrix division operators, \ and /. If A is a non-singular matrix, then A\B and B/A correspond to the left and right multiplication of B by inv(A).
Array operations: It is also possible to work with the matrix as an array, ie, to perform uniform element-wise operations. The array operators (+, -, .*, ./, .^) are used for this purpose. For example, if A and B are of the same dimensions, the expression A.*B would multiply each element of A with the corresponding element of B to produce a matrix of the same dimension as A and B.
