完整word版BP神经网络试验报告
BP神经网络理论与实验结果

神经网络简介:神经网络是大脑的一个组成部分。
James 在1890年的《心理学》一书中这样描述神经网络的基本原理:大脑皮层每一点的活力是由其它点势能释放的综合效能产生的,这些势能与如下因素有关:(1)相关点的兴奋次数;(2)兴奋的强度;(3)与其不相连的其它点所接受的能量。
他的这一原理一直沿用至今。
到目前为止,神经网络的研究主要分为两个派别:一派主要包括生物学家、物理学家和心理学家等,他们研究的主要目的是给出大脑活动的描述和精细模型;另一派主要包括工程技术人员等,他们关心的是怎样利用神经网络的基本原理,来构造解决实际问题的算法,使得这些算法具有有效的计算能力,我们称之为神经网络的工程应用研究,或称为人工神经网络(artificial neural network, ANN ),简称为神经网络。
人工神经网络可以分为前向型和反馈型两类:前向型神经网络的特点是信息传递由后层神经元向前层神经元传递,同一层内的神经元之间没有信息交流;反馈型神经网络中的神经元之间不但相互作用,而且自身也有信息内耗。
BP 神经网络是一种多层前向神经网络,名字源于网络权值的调整规则采用的是后向传播学习算法(也称为反推学习规则),即BP 学习算法(back-propagation, BP )。
BP 学习算法是Rumelhart 等在1986年提出的。
至此以后,BP 神经网络得到了广泛的实际应用,据统计,80%~90%的神经网络模型都采用了BP 网络或者它的变形。
BP 神经网络理论BP 神经网络是一种单向传播的多层前向型网络,其结构如图所示。
由图可见,BP 网络是一种具有三层或三层以上的神经网络,包括输入层、中间层(隐层)和输出层。
上下层之间实现全连接,而每层神经元之间无连接。
当一对学习样本提供给网络后,神经元的激活值从输入层经各中间层向输出层传播,在输出层的各神经元获得网络的输入响应。
接下来,按照减少目标输出与误差的方向,从输出层经过各中间层逐步修正各连接权值,最后回到输入层,这种算法称为“误差逆传播算法”,即BP 算法,随着这种误差逆的传播修正不断进行,网络对输入模式响应的正确率也不断上升。
完整word版,bp神经网络算法
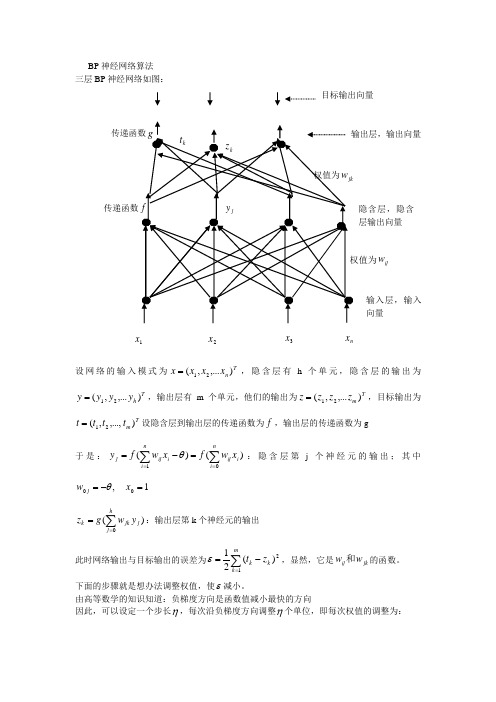
BP 神经网络算法 三层BP 神经网络如图:设网络的输入模式为Tn x x x x ),...,(21=,隐含层有h 个单元,隐含层的输出为T h y y y y ),...,(21=,输出层有m 个单元,他们的输出为T m z z z z ),...,(21=,目标输出为T m t t t t ),...,,(21=设隐含层到输出层的传递函数为f ,输出层的传递函数为g于是:)()(1∑∑===-=ni i ij ni iij j x w f xw f y θ:隐含层第j 个神经元的输出;其中1,00=-=x w j θ)(0∑==hj j jk k y w g z :输出层第k 个神经元的输出此时网络输出与目标输出的误差为∑=-=m k k k z t 12)(21ε,显然,它是jk ij w w 和的函数。
下面的步骤就是想办法调整权值,使ε减小。
由高等数学的知识知道:负梯度方向是函数值减小最快的方向因此,可以设定一个步长η,每次沿负梯度方向调整η个单位,即每次权值的调整为:1x 3x 2x n x隐含层,隐含层输出向量ij w传递函数输入层,输入向量目标输出向量pqpq w w ∂∂-=∆εη,η在神经网络中称为学习速率 可以证明:按这个方法调整,误差会逐渐减小。
BP 神经网络(反向传播)的调整顺序为: 1)先调整隐含层到输出层的权值 设k v 为输出层第k 个神经元的输入∑==hj j jkk y wv 0j k k k jkk k k k m k k k jk m k k k jk y v g z t w v v z z z t w z t w )(')()(21)(211212--=∂∂∂∂∂-=∂-=∂∂∑∑==ε -------复合函数偏导公式若取x e x f x g -+==11)()(,则)1()111(11)1()('2k k v v v v k z z ee e e u g kk k k -=+-+=+=---- 于是隐含层到输出层的权值调整迭代公式为:j k k jk jk y z z t w t w )1()()1(-+=+η2)从输入层到隐含层的权值调整迭代公式为:其中j u 为隐含层第j 个神经元的输入:∑==ni iij j xw u 0注意:隐含层第j 个神经元与输出层的各个神经元都有连接,即jy ∂∂ε涉及所有的权值ij w ,因此∑∑==--=∂∂∂∂∂-∂=∂∂m k jk k k k j k k k m k k k k j w u f z t y u u z z z t y 002)(')()(ε于是:因此从输入层到隐含层的权值调整迭代为公式为:i j ij ij x t w t w ηδ+=+)()1(ijj j j j m k k k ij m k k k ij w u u y y z t w z t w ∂∂∂∂∂-=∂-=∂∂∑∑==1212)(21)(21εi j i j m k jk k k k ij mk k k ij x x u f w u f z t w z t w δε-=--=∂-=∂∂∆==∑∑)('})('){()(21012例:下表给出了某地区公路运力的历史统计数据,请建立相应的预测模型,并对给出的2010和73.3900 3.9635 0.98802011 75.5500 4.0975 1.0268function main()clc % 清屏clear all; %清除内存以便加快运算速度close all; %关闭当前所有figure图像SamNum=20; %输入样本数量为20TestSamNum=20; %测试样本数量也是20ForcastSamNum=2; %预测样本数量为2HiddenUnitNum=8; %中间层隐节点数量取8,比工具箱程序多了1个InDim=3; %网络输入维度为3OutDim=2; %网络输出维度为2%原始数据%人数(单位:万人)sqrs=[20.55 22.44 25.37 27.13 29.45 30.10 30.96 34.06 36.42 38.09 39.13 39.99 ...41.93 44.59 47.30 52.89 55.73 56.76 59.17 60.63];%机动车数(单位:万辆)sqjdcs=[0.6 0.75 0.85 0.9 1.05 1.35 1.45 1.6 1.7 1.85 2.15 2.2 2.25 2.35 2.5 2.6...2.7 2.85 2.953.1];%公路面积(单位:万平方公里)sqglmj=[0.09 0.11 0.11 0.14 0.20 0.23 0.23 0.32 0.32 0.34 0.36 0.36 0.38 0.49 ...0.56 0.59 0.59 0.67 0.69 0.79];%公路客运量(单位:万人)glkyl=[5126 6217 7730 9145 10460 11387 12353 15750 18304 19836 21024 19490 20433 ...22598 25107 33442 36836 40548 42927 43462];%公路货运量(单位:万吨)glhyl=[1237 1379 1385 1399 1663 1714 1834 4322 8132 8936 11099 11203 10524 11115 ...13320 16762 18673 20724 20803 21804];p=[sqrs;sqjdcs;sqglmj]; %输入数据矩阵t=[glkyl;glhyl]; %目标数据矩阵[SamIn,minp,maxp,tn,mint,maxt]=premnmx(p,t); %原始样本对(输入和输出)初始化rand('state',sum(100*clock)) %依据系统时钟种子产生随机数rand是产生0到1的均匀分布,randn是产生均值为0,方差为1的正态分布rand(n)或randn(n)产生n*n阶矩阵,rand(m,n)或randn(n)产生m*n的随机数矩阵NoiseVar=0.01; %噪声强度为0.01(添加噪声的目的是为了防止网络过度拟合)Noise=NoiseVar*randn(2,SamNum); %生成噪声SamOut=tn + Noise; %将噪声添加到输出样本上TestSamIn=SamIn; %这里取输入样本与测试样本相同因为样本容量偏少TestSamOut=SamOut; %也取输出样本与测试样本相同MaxEpochs=50000; %最多训练次数为50000lr=0.035; %学习速率为0.035E0=0.65*10^(-3); %目标误差为0.65*10^(-3)W1=0.5*rand(HiddenUnitNum,InDim)-0.1; %初始化输入层与隐含层之间的权值B1=0.5*rand(HiddenUnitNum,1)-0.1; %初始化输入层与隐含层之间的阈值W2=0.5*rand(OutDim,HiddenUnitNum)-0.1; %初始化输出层与隐含层之间的权值B2=0.5*rand(OutDim,1)-0.1; %初始化输出层与隐含层之间的阈值ErrHistory=[]; %给中间变量预先占据内存for i=1:MaxEpochsHiddenOut=logsig(W1*SamIn+repmat(B1,1,SamNum)); % 隐含层网络输出NetworkOut=W2*HiddenOut+repmat(B2,1,SamNum); % 输出层网络输出Error=SamOut-NetworkOut; % 实际输出与网络输出之差SSE=sumsqr(Error) %能量函数(误差平方和)ErrHistory=[ErrHistory SSE];if SSE<E0,break, end %如果达到误差要求则跳出学习循环% 以下六行是BP网络最核心的程序% 他们是权值(阈值)依据能量函数负梯度下降原理所作的每一步动态调整量Delta2=Error;Delta1=W2'*Delta2.*HiddenOut.*(1-HiddenOut);dW2=Delta2*HiddenOut';dB2=Delta2*ones(SamNum,1);dW1=Delta1*SamIn';dB1=Delta1*ones(SamNum,1);%对输出层与隐含层之间的权值和阈值进行修正W2=W2+lr*dW2;B2=B2+lr*dB2;%对输入层与隐含层之间的权值和阈值进行修正W1=W1+lr*dW1;B1=B1+lr*dB1;endHiddenOut=logsig(W1*SamIn+repmat(B1,1,TestSamNum)); % 隐含层输出最终结果NetworkOut=W2*HiddenOut+repmat(B2,1,TestSamNum); % 输出层输出最终结果a=postmnmx(NetworkOut,mint,maxt); % 还原网络输出层的结果x=1990:2009; % 时间轴刻度newk=a(1,:); % 网络输出客运量newh=a(2,:); % 网络输出货运量figure ;subplot(2,1,1);plot(x,newk,'r-o',x,glkyl,'b--+') %绘值公路客运量对比图;legend('网络输出客运量','实际客运量');xlabel('年份');ylabel('客运量/万人');subplot(2,1,2);plot(x,newh,'r-o',x,glhyl,'b--+') %绘制公路货运量对比图;legend('网络输出货运量','实际货运量');xlabel('年份');ylabel('货运量/万吨');% 利用训练好的网络进行预测% 当用训练好的网络对新数据pnew进行预测时,也应作相应的处理pnew=[73.39 75.553.96354.09750.9880 1.0268]; %2010年和2011年的相关数据;pnewn=tramnmx(pnew,minp,maxp); %利用原始输入数据的归一化参数对新数据进行归一化;HiddenOut=logsig(W1*pnewn+repmat(B1,1,ForcastSamNum)); % 隐含层输出预测结果anewn=W2*HiddenOut+repmat(B2,1,ForcastSamNum); % 输出层输出预测结果%把网络预测得到的数据还原为原始的数量级;anew=postmnmx(anewn,mint,maxt)。
BP神经网络实验报告

作业8编程题实验报告(一)实验内容:实现多层前馈神经网络的反向传播学习算法。
使用3.2节上机生成的数据集对神经网络进行训练和测试,观察层数增加和隐层数增加是否会造成过拟合。
(二)实验原理:1)前向传播:以单隐层神经网络为例(三层神经网络),则对于第k 个输出节点,输出结果为:在实验中采用的激励函数为logistic sigmoid function 。
考虑每一层节点中的偏差项,所以,在上式中:)()(00,1l l j b w x ==在实验中,就相应的需要注意矢量形式表达式中,矢量大小的调整。
2)BP 算法:a) 根据问题,合理选择输入节点,输出节点数,确定隐层数以及各隐层节点数;b) 给每层加权系数,随机赋值;c) 由给定的各层加权系数,应用前向传播算法,计算得到每层节点输出值,并计算对于所有训练样本的均方误差;d) 更新每层加权系数:其中,⎪⎩⎪⎨⎧⋅⋅⋅-=∑+j i ji l i l i i i l i a h w a h d y 其它层,最后一层)('(),(')()1()()(δδe) 重复c),d )迭代过程,直至迭代步数大于预设值,或者每次迭代误差变化值小于预设值时,迭代结束,得到神经网络的各层加权系数。
(三)实验数据及程序:1)实验数据处理:a) 训练样本输入节点数据:在实验中,所用数据中自变量x 的取值,为0—1的25个随机值,为了后续实验结果的分析,将其从小到大排序,并加上偏差项,神经网络的输出节点最终训练结果,即为训练得到的回归结果;b) 训练样本标签值:在实验中,采用的激励函数为logistic sigmoid function ,其值域为[0,1],所以,在神经网络训练前,需要对训练样本标签值进行归一化处理;c) 神经网络输出节点值:对训练样本标签值进行了归一化处理,相应的,对于输出节点,需要反归一化处理。
2)实验程序:实现函数:[Theta]=BP(input_layer_size,hidden_layer_size,hidden_layer_num,num_labels,Niter,leta,X,Y)输入参数:input_layer_size:输入节点数;hidden_layer_size:隐层节点数(对于单隐层,输入值为一数值,对于多隐层,为一矢量);hidden_layer_num:隐层数;num_labels:输出节点数;Niter:为预设的迭代步数;leta:学习速率,即更新步长;X,Y:分别为训练样本输入特征值以及标签值。
实验报告 BP神经网络(2150230509)资料

深圳大学实验报告实验课程名称:神经网络与进化算法实验项目名称:BP神经网络对蝴蝶花进行分类学院:计算机与软件专业:软件工程报告人:文成学号:2150230509 同组人:无指导教师:朱安民实验时间:2016年4月1日至2016年4月7日实验报告提交时间:2016年4月7日教务处制初步熟悉BP神经网络,并设计一个BP神经网络对蝴蝶花进行分类二、实验内容设计一个BP神经网络对蝴蝶花进行分类,要求提交试验报告,内容包括:1.问题说明描。
2.数据述。
3.网络设计,包括输入层、隐含层、输出层节点个数的设计。
4.算法步骤。
5.编程,注意原始数据的通用化,数据输入的随机性。
6.网络训练,注意训练数据与验证数据分开。
7.网络验证7.结果分析,修改隐含层节点个数,修改学习率,分别对结果的影响。
8.体会,例如对下列问题的理解:1)BP学习算法的基本思想?2)BP网络设计中结点个数如何确定?3)为什么要对数据进行通用标准化,即转为[-1,1]?4)为什么要对训练数据的输入顺序进行随机化处理?5)为什么训练数据与测试数据要分开?注意:如果用MatLab编程序,将下列数据存放到一个文本文件(例如data.dat),编写程序存放到一个m文件中(例如你的学号.m),数据文件和程序文件放在同一文件夹下。
运行MatLab后,指定上述文件夹为工作区域,在命令行运行m文件。
前期工作:首先将实验数据分为两组,一组用于训练,一组用于测试。
分别保存在trainData.txt和testData.txt中(115组训练数据和35组测试数据)。
如图所示:各列数据代表的意义如下:序号种类叶长叶宽花长花宽(单位:cm)1 1 49 30 14 22 2 66 29 46 13…150 3 65 33 60 25(本实验设计一个BP网络,先用75%的数据对网络进行训练,然后用25%的数据进行检测。
)网络设计:输入层用4个节点,分别对应文件中的3/4/5/6列,隐层用3个节点。
人工智能实验报告-BP神经网络算法的简单实现[参照]
![人工智能实验报告-BP神经网络算法的简单实现[参照]](https://img.taocdn.com/s3/m/23d1cd32cdbff121dd36a32d7375a417866fc1dc.png)
人工神经网络是一种模仿人脑结构及其功能的信息处理系统,能提高人们对信息处理的智能化水平。
它是一门新兴的边缘和交叉学科,它在理论、模型、算法等方面比起以前有了较大的发展,但至今无根本性的突破,还有很多空白点需要努力探索和研究。
1人工神经网络研究背景神经网络的研究包括神经网络基本理论、网络学习算法、网络模型以及网络应用等方面。
其中比较热门的一个课题就是神经网络学习算法的研究。
近年来己研究出许多与神经网络模型相对应的神经网络学习算法,这些算法大致可以分为三类:有监督学习、无监督学习和增强学习。
在理论上和实际应用中都比较成熟的算法有以下三种:(1) 误差反向传播算法(Back Propagation,简称BP 算法);(2) 模拟退火算法;(3) 竞争学习算法。
目前为止,在训练多层前向神经网络的算法中,BP 算法是最有影响的算法之一。
但这种算法存在不少缺点,诸如收敛速度比较慢,或者只求得了局部极小点等等。
因此,近年来,国外许多专家对网络算法进行深入研究,提出了许多改进的方法。
主要有:(1) 增加动量法:在网络权值的调整公式中增加一动量项,该动量项对某一时刻的调整起阻尼作用。
它可以在误差曲面出现骤然起伏时,减小振荡的趋势,提高网络训练速度;(2) 自适应调节学习率:在训练中自适应地改变学习率,使其该大时增大,该小时减小。
使用动态学习率,从而加快算法的收敛速度;(3) 引入陡度因子:为了提高BP 算法的收敛速度,在权值调整进入误差曲面的平坦区时,引入陡度因子,设法压缩神经元的净输入,使权值调整脱离平坦区。
此外,很多国内的学者也做了不少有关网络算法改进方面的研究,并把改进的算法运用到实际中,取得了一定的成果:(1) 王晓敏等提出了一种基于改进的差分进化算法,利用差分进化算法的全局寻优能力,能够快速地得到BP 神经网络的权值,提高算法的速度;(2) 董国君等提出了一种基于随机退火机制的竞争层神经网络学习算法,该算法将竞争层神经网络的串行迭代模式改为随机优化模式,通过采用退火技术避免网络收敛到能量函数的局部极小点,从而得到全局最优值;(3) 赵青提出一种分层遗传算法与BP 算法相结合的前馈神经网络学习算法。
(完整word版)基于BP神经网络的自整定PID控制仿真

基于BP神经网络的自整定PID控制仿真一、实验目的1.熟悉神经网络的特征、结构及学习算法。
2.通过实验掌握神经网络自整定PID的工作原理。
3.了解神经网络的结构对控制效果的影响。
4. 掌握用Matlab实现神经网络控制系统仿真的方法。
二、实验设备及条件1.计算机系统2.Matlab仿真软件三、实验原理在工业控制中,PID控制是工业控制中最常用的方法。
这是因为PID控制器结构简单,实现简单,控制效果良好,已得到广泛应用。
但是,PID具有一定的局限性:被控制对象参数随时间变化时,控制器的参数难以自动调整以适应外界环境的变化。
为了使控制器具有较好的自适应性,实现控制器参数的自动调整,可以采用神经网络控制的方法。
利用神经网络的自学习这一特性,并结合传统的PID控制理论,构造神经网络PID控制器,实现控制器参数的自动调整。
基于BP神经网络的PID控制器结构如图4所示。
控制器由两部分组成:一是常规PID控制器,用以直接对对象进行闭环控制,且3个参数在线整定;二是神经网络NN,根据系统的运行状态,学习调整权系数,从而调整PID参数,达到某种性能指标的最优化。
图4中神经网络采用结构为4-5-3型的BP网络。
BP网络是一种单向传播的多层前向网络。
输入节点对应系统的运行状态量,如系统的偏差与偏差变化率,必要时要进行归一化处理。
输入变量的个数取决于被控系统的复杂程度,输出节点对应的是PID的3个可调参数。
由于输出不能为负,所以输出层活化函数取2()(1)()(1)1(1)a k y k y k u k y k -=+-+-非负的Sigmoid 函数,隐含层取正负对称的Sigmoid 函数。
本系统选取的BP 网络结构如图5所示。
网络的学习过程由正向和反向传播两部分组成。
如果输出层不能得到期望输出,那么转入反向传播过程,通过修改各层神经元的权值,使得误差信号最小。
输出层节点分别对应3个可调参数K p 、K i 、K d 。
BP神经网络实验报告

BP神经网络实验报告一、引言BP神经网络是一种常见的人工神经网络模型,其基本原理是通过将输入数据通过多层神经元进行加权计算并经过非线性激活函数的作用,输出结果达到预测或分类的目标。
本实验旨在探究BP神经网络的基本原理和应用,以及对其进行实验验证。
二、实验方法1.数据集准备本次实验选取了一个包含1000个样本的分类数据集,每个样本有12个特征。
将数据集进行标准化处理,以提高神经网络的收敛速度和精度。
2.神经网络的搭建3.参数的初始化对神经网络的权重和偏置进行初始化,常用的初始化方法有随机初始化和Xavier初始化。
本实验采用Xavier初始化方法。
4.前向传播将标准化后的数据输入到神经网络中,在神经网络的每一层进行加权计算和激活函数的作用,传递给下一层进行计算。
5.反向传播根据预测结果与实际结果的差异,通过计算损失函数对神经网络的权重和偏置进行调整。
使用梯度下降算法对参数进行优化,减小损失函数的值。
6.模型评估与验证将训练好的模型应用于测试集,计算准确率、精确率、召回率和F1-score等指标进行模型评估。
三、实验结果与分析将数据集按照7:3的比例划分为训练集和测试集,分别进行模型训练和验证。
经过10次训练迭代后,模型在测试集上的准确率稳定在90%以上,证明了BP神经网络在本实验中的有效性和鲁棒性。
通过调整隐藏层结点个数和迭代次数进行模型性能优化实验,可以发现隐藏层结点个数对模型性能的影响较大。
随着隐藏层结点个数的增加,模型在训练集上的拟合效果逐渐提升,但过多的结点数会导致模型的复杂度过高,容易出现过拟合现象。
因此,选择合适的隐藏层结点个数是模型性能优化的关键。
此外,迭代次数对模型性能也有影响。
随着迭代次数的增加,模型在训练集上的拟合效果逐渐提高,但过多的迭代次数也会导致模型过度拟合。
因此,需要选择合适的迭代次数,使模型在训练集上有好的拟合效果的同时,避免过度拟合。
四、实验总结本实验通过搭建BP神经网络模型,对分类数据集进行预测和分类。
神经网络的BP算法实验报告

计算智能基础实验报告实验名称:BP神经网络算法实验班级名称:341521班专业:探测制导与控制技术姓名:***学号:********一、 实验目的1)编程实现BP 神经网络算法;2)探究BP 算法中学习因子算法收敛趋势、收敛速度之间的关系;3)修改训练后BP 神经网络部分连接权值,分析连接权值修改前和修改后对相同测试样本测试结果,理解神经网络分布存储等特点。
二、 实验要求按照下面的要求操作,然后分析不同操作后网络输出结果。
1)可修改学习因子2)可任意指定隐单元层数3)可任意指定输入层、隐含层、输出层的单元数4)可指定最大允许误差ε5)可输入学习样本(增加样本)6)可存储训练后的网络各神经元之间的连接权值矩阵;7)修改训练后的BP 神经网络部分连接权值,分析连接权值修改前和修改后对相同测试样本测试结果 。
三、 实验原理1BP 神经网络算法的基本思想误差逆传播(back propagation, BP)算法是一种计算单个权值变化引起网络性能变化的较为简单的方法。
由于BP 算法过程包含从输出节点开始,反向地向第一隐含层(即最接近输入层的隐含层)传播由总误差引起的权值修正,所以称为“反向传播”。
BP 神经网络是有教师指导训练方式的多层前馈网络,其基本思想是:从网络输入节点输入的样本信号向前传播,经隐含层节点和输出层节点处的非线性函数作用后,从输出节点获得输出。
若在输出节点得不到样本的期望输出,则建立样本的网络输出与其期望输出的误差信号,并将此误差信号沿原连接路径逆向传播,去逐层修改网络的权值和节点处阈值,这种信号正向传播与误差信号逆向传播修改权值和阈值的过程反复进行,直训练样本集的网络输出误差满足一定精度要求为止。
2 BP 神经网络算法步骤和流程BP 神经网络步骤和流程如下:1) 初始化,给各连接权{},{}ij jt W V 及阈值{},{}j t θγ赋予(-1,1)间的随机值;2) 随机选取一学习模式对1212(,),(,,)k k k k k k k n k n A a a a Y y y y ==提供给网络;3) 计算隐含层各单元的输入、输出;1n j ij i j i s w a θ==⋅-∑,()1,2,,j j b f s j p ==4) 计算输出层各单元的输入、输出;1t t jt j t j l V b γ==⋅-∑,()1,2,,t t c f l t q ==5) 计算输出层各单元的一般化误差;()(1)1,2,,k k t t tt t t d y c c c t q =-⋅-=6) 计算中间层各单元的一般化误差;1[](1)1,2,,q kk jt jt j j t e d V b b j p ==⋅⋅-=∑7) 修正中间层至输出层连接权值和输出层各单元阈值;(1)()k jt jt t j V iter V iter d b α+=+⋅⋅(1)()k t t t iter iter d γγα+=+⋅8) 修正输入层至中间层连接权值和中间层各单元阈值;(1)()kk ij ij j i W iter W iter e a β+=+⋅⋅(1)()kj j j iter iter e θθβ+=+⋅9) 随机选取下一个学习模式对提供给网络,返回步骤3),直至全部m 个模式训练完毕;10) 重新从m 个学习模式对中随机选取一个模式对,返回步骤3),直至网络全局误差函数E 小于预先设定的一个极小值,即网络收敛;或者,当训练次数大于预先设定值,强制网络停止学习(网络可能无法收敛)。
智能传感器实验--BP神经网络

BP神经网络实验2010年12月目录1自主学习模块 (2)1.1书面回答预习问题 (2)1.1.1训练神经网络网络之前,需要进行的三个步骤的准备工作是什么? (2)1.1.2神经网络(例如BP 训练仪)训练的中止条件是什么? (2)1.1.3如何根据检验结果判断训练好的网络可用来实测? (2)1.2远程测控实验室网上学习与练习 (2)1.2.1经典常规传感器的交叉敏感与传感器的稳定性 (2)1.2.2多传感器数据融合改善传感器稳定性的基本原理 (3)1.2.3数据融合算法简介 (4)1.2.4 BP神经网络 (6)2自主训练模块 (12)2.1实验目的 (12)2.2实验内容 (12)2.2.1基本训练部分一 (12)2.2.2基本训练部分二 (14)2.2.3用BP 网络训练仪消除压力传感器对工作电流的交叉敏感,提高压力测量精度 (19)2.2.4 组建智能压力传感器系统 (22)3自主应用模块 (23)3.1实验目的 (23)3.2实验内容 (23)3.3实验步骤 (23)3.3.1 消除压力传感器对温度的交叉敏感 (24)3.3.2消除压力传感器对电流的交叉敏感 (26)4.自主提高模块 (27)4.1 神经网络结构的移植与实测 (27)4.2思考问题 (28)1自主学习模块1.1书面回答预习问题1.1.1训练神经网络网络之前,需要进行的三个步骤的准备工作是什么?训练神经网络网络之前,需要进行的三个步骤的准备工作是:准备训练样本、根据实际情况设置神经网络各层节点数及测量误差目标值与迭代次数(反向传播次数)、输入样本训练及检验。
1.1.2神经网络(例如BP 训练仪)训练的中止条件是什么?将网络输出结果与期望输出样本比较,计算其偏差。
若偏差小于给定的目标值,则训练结束;反之,则要调整网络结构参数,进行新的网络训练,直至偏差小于目标值。
如设置网络训练终止条件:如训练代数为1000,均方差指标为1*10-61.1.3如何根据检验结果判断训练好的网络可用来实测?将检验输入样本输入训练好的网络,并计算网络输出结果与期望输出样本的偏差。
实验报告 BP神经网络(2150230509)资料

深圳大学实验报告实验课程名称:神经网络与进化算法实验项目名称:BP神经网络对蝴蝶花进行分类学院:计算机与软件专业:软件工程报告人:文成学号:2150230509 同组人:无指导教师:朱安民实验时间:2016年4月1日至2016年4月7日实验报告提交时间:2016年4月7日教务处制初步熟悉BP神经网络,并设计一个BP神经网络对蝴蝶花进行分类二、实验内容设计一个BP神经网络对蝴蝶花进行分类,要求提交试验报告,内容包括:1.问题说明描。
2.数据述。
3.网络设计,包括输入层、隐含层、输出层节点个数的设计。
4.算法步骤。
5.编程,注意原始数据的通用化,数据输入的随机性。
6.网络训练,注意训练数据与验证数据分开。
7.网络验证7.结果分析,修改隐含层节点个数,修改学习率,分别对结果的影响。
8.体会,例如对下列问题的理解:1)BP学习算法的基本思想?2)BP网络设计中结点个数如何确定?3)为什么要对数据进行通用标准化,即转为[-1,1]?4)为什么要对训练数据的输入顺序进行随机化处理?5)为什么训练数据与测试数据要分开?注意:如果用MatLab编程序,将下列数据存放到一个文本文件(例如data.dat),编写程序存放到一个m文件中(例如你的学号.m),数据文件和程序文件放在同一文件夹下。
运行MatLab后,指定上述文件夹为工作区域,在命令行运行m文件。
前期工作:首先将实验数据分为两组,一组用于训练,一组用于测试。
分别保存在trainData.txt和testData.txt中(115组训练数据和35组测试数据)。
如图所示:各列数据代表的意义如下:序号种类叶长叶宽花长花宽(单位:cm)1 1 49 30 14 22 2 66 29 46 13…150 3 65 33 60 25(本实验设计一个BP网络,先用75%的数据对网络进行训练,然后用25%的数据进行检测。
)网络设计:输入层用4个节点,分别对应文件中的3/4/5/6列,隐层用3个节点。
BP人工神经网络试验报告一

BP⼈⼯神经⽹络试验报告⼀学号:北京⼯商⼤学⼈⼯神经⽹络实验报告实验⼀基于BP算法的XX及Matlab实现院(系)专业学⽣姓名成绩指导教师2011年10⽉⼀、实验⽬的:1、熟悉MATLAB 中神经⽹络⼯具箱的使⽤⽅法;2、了解BP 神经⽹络各种优化算法的原理;3、掌握BP 神经⽹络各种优化算法的特点;4、掌握使⽤BP 神经⽹络各种优化算法解决实际问题的⽅法。
⼆、实验内容:1 案例背景1.1 BP 神经⽹络概述BP 神经⽹络是⼀种多层前馈神经⽹络,该⽹络的主要特点是信号前向传递,误差反向传播。
在前向传递中,输⼊信号从输⼊层经隐含层逐层处理,直⾄输出层。
每⼀层的神经元状态只影响下⼀层神经元状态。
如果输出层得不到期望输出,则转⼊反向传播,根据预测误差调整⽹络权值和阈值,从⽽使BP 神经⽹络预测输出不断逼近期望输出。
BP 神经⽹络的拓扑结构如图1.1所⽰。
图1.1 BP 神经⽹络拓扑结构图图1.1中1x ,2x , ……n x 是BP 神经⽹络的输⼊值1y ,2y , ……n y 是BP 神经的预测值,ij ω和jk ω为BP 神经⽹络权值。
从图1.1可以看出,BP 神经⽹络可以看成⼀个⾮线性函数,⽹络输⼊值和预测值分别为该函数的⾃变量和因变量。
当输⼊节点数为n ,输出节点数为m 时,BP 神经⽹络就表达了从n 个⾃变量到m 个因变量的函数映射关系。
BP 神经⽹络预测前⾸先要训练⽹络,通过训练使⽹络具有联想记忆和预测能⼒。
BP 神经⽹络的训练过程包括以下⼏个步骤。
步骤1:⽹络初始化。
根据系统输⼊输出序列()y x ,确定⽹络输⼊层节点数n 、隐含层节点数l ,输出层节点数m ,初始化输⼊层、隐含层和输出层神经元之间的连接权值ij ω和式中, l 为隐含层节点数; f 为隐含层激励函数,该函数有多种表达形式,本章所选函数为:步骤3:输出层输出计算。
根据隐含层输出H ,连接权值jk ω和阈值b ,计算BP 神经⽹络预测输出O 。
昆明理工大学智能控制(BP神经网络)实验

昆明理工大学信息工程与自动化学院学生实验报告( 2014—2015学年 第二学期 )课程名称:智能控制导论 开课实验室:信自楼442机房 2015年5月30日通过上机实习,熟悉MATLAB 的基本操作命令和神经网络工具箱的使用,掌握MATLAB 编程或神经网络编辑器等方法,进行BP 神经网络设计的基本方法和步骤,为以后利用计算机进行神经网络控制系统分析与设计打下良好的基础。
二、实验内容试设计BP 神经网络来实现正弦函数的逼近。
输入矢量 X= -2: 0.05: 2; 相对应的目标矢量)cos()2sin(X X Y ⋅+⋅=ππ三、实验要求1. 设计一个BP 神经网络来实现对正弦函数关系的逼近; 2. 正确的选择确定BP 神经网络的相关参数; 3. 完成BP 网络函数逼近程序的仿真与调试; 4. 仿真结果分析。
四、实验原理BP 网络是一种多层前馈神经网络,由输入层、隐层和输出层组成。
一个典型的三层BP 网络的拓扑结构,层与层之间采用全互连方式,同一层之间不存在相互连接,隐层可以有一层或多层。
层与层之间有两种信号在流通:一种是工作信号,它是施加输入信号后向前传播直到在输出端产生实际输出的信号,是输入和权值的函数。
另一种是误差信号,网络实际输出与期望输出间的差值即为误差,它由输出端开始逐层向后传播。
BP网络的学习过程程由前向计算过程和误差反向传播过程组成。
在前向计算过程中,输入量从输入层经隐层逐层计算,并传向输出层,每层神经元的状态只影响下一层神经元的状态。
如输出层不能得到期望的输出,则转入误差反向传播过程,误差信号沿原来的连接通路返回,逐次调整网络各层的权值和阈值,直至到达输入层,再重复向计算。
这两个过程一次反复进行,不断调整各层的权值和阈值,使得网络误差最小或达到人们所期望的要求时,学习过程结束。
五、实验过程利用两层BP网络完成函数逼近,隐含层激活函数为S型函数,输出层的激活函数为线性函数。
程序为:clear all;clc;NNTWARN OFF;X=-2:0.05:2;T=sin(2*pi*X)+cos(pi*X);plot(X,T,'+b');pause得到原始曲线截图:建立BP网络,并初始化权值和阈值程序为:[R,N]=size(X);[S2,N]=size(T);S1=20; %隐含层神经元个数[w11,b11,w12,b12]=initff(X,S1,'tansig',S2,'purelin');[y1,y21]=simuff(X,w11,b11,'tansig',w12,b12,'purelin');得到训练前BP网络的函数逼近效果截图:利用不含噪声的理想输入数据训练网络程序为:disp_freq=5;max_epoch=10000; % 训练次数err_goal=0.05; % 训练误差lr=0.01; %学习速率tp=[disp_freq max_epoch err_goal lr];[w21,b21,w22,b22,te,tr]=trainbpx(w11,b11,'tansig',w12,b12,'purelin',X,T,t p);BP网络训练过程参数显示截图为显示训练后网络的函数逼近效果程序为[y1,y22]=simuff(X,w21,b21,'tansig',w22,b22,'purelin'); plot(X,y21,'--g',X,y22,'or')disp('网络训练步数为:')tepause训练后BP网络的函数逼近效果截图为达到要求所用的网络训练步数截图:由于我预设的训练误差为0.05,相对来说比较大,而且预设10000步达到训练目的,但只用了1348步就已经完成了,所以我做了大胆的设想,将训练误差改为0.01,以期望能达到更高的要求。
BP神经网络算法实验报告

计算各层的输入和输出
es
计算输出层误差 E(q)
E(q)<ε
修正权值和阈值
结
束
图 2-2 BP 算法程序流程图
3、实验结果
任课教师: 何勇强
日期: 2010 年 12 月 24 日
中国地质大学(北京) 课程名称:数据仓库与数据挖掘 班号:131081 学号:13108117 姓名:韩垚 成绩:
任课教师: 何勇强
(2-7)
wki
输出层阈值调整公式:
(2-8)
ak
任课教师: 何勇强
E E netk E ok netk ak netk ak ok netk ak
(2-9)
日期: 2010 年 12 月 24 日
中国地质大学(北京) 课程名称:数据仓库与数据挖掘 隐含层权值调整公式: 班号:131081 学号:13108117 姓名:韩垚 成绩:
Ep
系统对 P 个训练样本的总误差准则函数为:
1 L (Tk ok ) 2 2 k 1
(2-5)
E
1 P L (Tkp okp )2 2 p 1 k 1
(2-6)
根据误差梯度下降法依次修正输出层权值的修正量 Δwki,输出层阈值的修正量 Δak,隐含层权 值的修正量 Δwij,隐含层阈值的修正量
日期: 2010 年 12 月 24 日
隐含层第 i 个节点的输出 yi:
M
yi (neti ) ( wij x j i )
j 1
(2-2)
输出层第 k 个节点的输入 netk:
q q M j 1
netk wki yi ak wki ( wij x j i ) ak
bP神经网络控制

doublew_hide_input[numHiddenLayer][numInputLayer]; //隐含结点权值
doublew_output_hide[numOutputLayer][numHiddenLayer]; //输出结点权值
}
//输入层与隐层之间的权值
for(i=0;i<numHiddenLayer;i++)
{
for(intj=0;j<numInputLayer;j++)
{
w_hide_input[i][j]=(2.0*(double)rand()/RAND_MAX)-1;
}
}
//输出层与隐层之间的权值
for(i=0;i<numOutputLayer;i++)
Y[i][0]=sin(X[i][0]);
X[iபைடு நூலகம்[0]=preminmax2(0,2*pi,X[i][0]);//输入[0,2π]归一化到[-1,1]
Y[i][0]=preminmax(-1,1,Y[i][0]);//输出[-1,1]归一化到[0,1]
return 0;
}
void initial()
智能控制实验报告
-BP神经网络
一.实验内容
设计BP网络,映射函数为:
1.y=sin(x) x (0,2 )
2.y=x1^2+x2^2+x1*x2 x1,x2 (0,1)
给出训练后的权值矩阵,并考察训练拟合的效果。
二.实验原理
1.BP网络原理
BP网络模型处理信息的基本原理是:输入信号Xi通过中间节点(隐层点)作用于输出节点,经过非线形变换,产生输出信号Yk,网络训练的每个样本包括输入向量X和期望输出量t,网络输出值Y与期望输出值t之间的偏差,通过调整输入节点与隐层节点的联接强度取值Wij和隐层节点与输出节点之间的联接强度Tjk以及阈值,使误差沿梯度方向下降,经过反复学习训练,确定与最小误差相对应的网络参数(权值和阈值),训练即告停止。此时经过训练的神经网络即能对类似样本的输入信息,自行处理输出误差最小的经过非线形转换的信息。
BP实验报告

BP 实验报告学生姓名 程战战专业/班级 计算机91学 号 09055006所在学院 电信学院指导教师 鲍军鹏提交日期 2012/6/151 实验目的用java语言实现BP网络,解决一个简单的曲线拟合(预测)问题。
要求训练数据不少于400个点,测试数据不少于100个点。
在神经网络训练过程中要记录下误差,最后画出整个学习过程中的网络误差变化曲线。
2 实验原理基本思想是:样本集:S={(X1,Y1),(X2,Y2),…,(X s,Y s)}逐一地根据样本集中的样本(X k,Y k)计算出实际输出O k及其误差E1,然后对各层神经元的权值W(1),W(2),…,W(L)各做一次调整,重复这个循环,直到∑E p<ε(所有样本的误差之和)。
用输出层的误差调整输出层权矩阵,并用此误差估计输出层的直接前导层的误差,再用输出层前导层误差估计更前一层的误差。
如此获得所有其它各层的误差估计,并用这些估计实现对权矩阵的修改。
形成将输出端表现出的误差沿着与输入信号相反的方向逐级向输入端传递的过程。
基本过程是:样本:(输入向量,理想输出向量)1、权初始化:“小随机数”与饱和状态;“不同”的权值保证网络可以学。
2、向前传播阶段:(1)从样本集中取一个样本(X p,Y p),将X p输入网络;(2)计算相应的实际输出O p:O p=F L(…(F2(F1(X p W(1))W(2))…)W(L))3、向后传播阶段——误差传播阶段:(1)计算实际输出O p与相应的理想输出Y p的差。
(2)按极小化误差的方式调整权矩阵。
(3)累计网络关于整个样本集的误差。
4、如果网络误差足够小,则停止训练。
否则重复第2、3步。
算法伪码:样本:(输入向量,理想输出向量)1、权初始化:“小随机数”与饱和状态;“不同”的权值保证网络可以学。
2、向前传播阶段:(1)从样本集中取一个样本(X p,Y p),将X p输入网络;(2)计算相应的实际输出O p:O p=F L(…(F2(F1(X p W(1))W(2))…)W(L))3、向后传播阶段——误差传播阶段:(1)计算实际输出O p与相应的理想输出Y p的差。
神经网络实验报告

实验报告课程名称BP神经网络实验实验名称一级倒立摆实验实验仪器matlab、一级倒立摆实验台系别自动化专业班级/学号学生姓名实验日期2014年4月8日成绩指导老师一级倒立摆实验实验目的:(1)熟悉Matlab/Simulink的使用.(2)掌握BP神经网络的基本原理和基本的设计步骤.(3)了解BP神经网络在实际中的应用.(4)针对简单的实际系统, 能够建立BP神经网络控制模型. 实验原理:1.前馈型人工神经网络前馈型人工神经网络是整个神经网络体系中最常见的一种,其结构模型如图2所示。
网络结构包含输入层、隐层(可能是多层)和输出层,它的连接方式是同层之间不相连接,相邻层之间单元为全连接型。
这种网络没有反馈存在,实际运行是单向的,学习方式是一种监督式学习。
前馈型神经网络具有很强的非线性映射能力,寻找其映射是靠学习实践的,只要学习数据足够完备,就能够描述任意未知的复杂系统。
因此前馈神经网络为非线性系统的建模和控制提供了有力的工具。
图1 前馈型神经网络结构2.BP算法原理BP(Back Propagation)神经网络是一种利用误差反向传播训练算法的前馈型网络,BP学习算法实质是求取网络总误差函数的最小值问题[2]。
这种算法采用非线性规划中的最速下降方法,按误差函数的负梯度方向修改权系数,它是梯度下降法在多层前馈网络中的应用。
具体学习算法包括两大过程,其一是输入信号的正向传播过程,其二是输出误差信号的反向传播过程。
1.正向传播输入的样本从输入层经过隐层单元一层一层进行处理,通过所有的隐层之后,则传向输出层;在逐层处理的过程中,每一层神经元的状态只对下一层神经元的状态产生影响。
在输出层把现行输出和期望输出进行比较,如果现行输出不等于期望输出,则进入反向传播过程。
2.反向传播反向传播时,把误差信号按原来正向传播的通路反向传回,并对每个隐层的各个神经元的权系数进行修改,以望误差信号趋向最小。
网络各层的权值改变量,则由传播到该层的误差大小来决定。
(完整word版)BP神经网络实验报告

BP 神经网络实验报告一、实验目的1、熟悉MATLAB中神经网络工具箱的使用方法;2、经过在MATLAB下面编程实现BP网络逼近标准正弦函数,来加深对BP网络的认识和认识,理解信号的正向流传和误差的反向传达过程。
二、实验原理由于传统的感知器和线性神经网络有自己无法战胜的弊端,它们都不能够解决线性不能分问题,因此在实质应用过程中碰到了限制。
而BP 网络却拥有优异的繁泛化能力、容错能力以及非线性照射能力。
因此成为应用最为广泛的一种神经网络。
BP 算法的根本思想是把学习过程分为两个阶段:第一阶段是信号的正向流传过程;输入信息经过输入层、隐层逐层办理并计算每个单元的实质输出值;第二阶段是误差的反向传达过程;假设在输入层未能获取希望的输出值,那么逐层递归的计算实质输出和希望输出的差值〔即误差〕,以便依照此差值调治权值。
这种过程不断迭代,最后使得信号误差到达赞同或规定的范围之内。
基于 BP 算法的多层前馈型网络模型的拓扑结构如上图所示。
BP 算法的数学描述:三层BP 前馈网络的数学模型如上图所示。
三层前馈网中,输入向量为: X ( x1 , x2 ,..., x i ,..., x n )T;隐层输入向量为:Y( y1 , y2 ,..., y j ,...y m ) T;输出层输出向量为: O (o1 , o2 ,..., o k ,...o l )T;希望输出向量为:d(d1 ,d 2 ,...d k ,...d l )T。
输入层到隐层之间的权值矩阵用 V 表示,V(v1 , v2 ,...v j ,...v m ) Y,其中列向量v j为隐层第 j 个神经元对应的权向量;隐层到输出层之间的权值矩阵用W 表示,W( w1 , w2 ,...w k ,...w l ) ,其中列向量 w k为输出层第k个神经元对应的权向量。
下面解析各层信号之间的数学关系。
对于输出层,有y j f (net j ), j1,2,..., mnet j v ij x i , j1,2,..., m对于隐层,有O k f (net k ), k1,2,...,lm net k wjkyi, k1,2,...,lj0以上两式中,转移函数 f(x) 均为单极性Sigmoid 函数:1f ( x)x1 ef(x) 拥有连续、可导的特点,且有 f ' (x) f ( x)[1 f ( x)]以上共同构成了三层前馈网了的数学模型。
BP神经网络 报告

作业二、BP神经网络的拟合能力一、实验目的学会使用BP神经网络拟合各种函数曲线,学会分析隐层神经元个数、步长训练精度的影响。
二、实验要求设x=0:0.01:3y=3*sin(x)+2*cos(x.^2)+0.3*rand(1,length(x))针对前述函数,建立一个单输入单输出的3层BP网络,并撰写报告,激励函数等可自行选择:要求:神经网络输出与函数输出的误差应小于某小值;报告内容包括:1.输入输出样本集的选取(x取值范围应该覆盖0度到360度,样本数目应该大于50)2.网络隐层节点数目、激励函数形式、所用学习算法;(若有不同选择,说明选择的过程与理由)3.学习步长、学习结束控制参数等参数设置4.学习过程中误差的变化曲线图5.学习前(选择初始权值时)神经网络的输出曲线与实际函数的曲线对比图6.学习后神经网络的输出曲线与实际函数的曲线对比图7.学习次数8.结论9.提供MATLAB源程序三、问题的提出由于所给函数x取值范围是[0 3],而题目要求输入输出样本集x取值范围应该覆盖0度到360度。
所以x在[3 2*pi]内,应观察已训练好的神经网络是否满足目标函数,以此检验训练完的网络。
四、建立网络与参数设置4.1 首先分析几个常用的激励函数(1)logsig对数S型(sigmoid)传递函数,它可以将神经元的输入范围是(-∞,+∞)映射到(0,1)的区间上,它是可微函数,其表达式为:y=1/1+e-x。
(2)tansig双曲正切S型(sigmoid)传递函数,它可以将神经元的输入范围(-∞,+∞)映射到(-1,+1)的区间上,它是可微函数。
对logsig传递函数而言,输出范围是(0,1),对tansig传递函数而言,输出范围是(-1,1)。
如果是purelin型神经元,则整个网络的输出可以是任意值。
对三层BP网络而言,如果最后一层是sigmoid型神经元,那么整个网络的输出就限制在一个较小的范围内。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
BP神经网络实验报告
一、实验目的
1、熟悉MATLAB中神经网络工具箱的使用方法;
通过在MATLAB下面编程实现BP网络逼近标准正弦函数,来加深对BP网络的了2、解和认识,理解信号的正向传播和误差的反向传递过程。
二、实验原理
由于传统的感知器和线性神经网络有自身无法克服的缺陷,它们都不能解决线性不可分问题,因此在实际应用过程中受到了限制。
而BP网络却拥有良好的繁泛化能力、容错能力以及非线性映射能力。
因此成为应用最为广泛的一种神经网络。
BP算法的基本思想是把学习过程分为两个阶段:第一阶段是信号的正向传播过程;输入信息通过输入层、隐层逐层处理并计算每个单元的实际输出值;第二阶段是误差的反向传递过程;若在输入层未能得到期望的输出值,则逐层递归的计算实际输出和期望输出的差值(即误差),以便根据此差值调节权值。
这种过程不断迭代,最后使得信号误差达到允许或规定的范围之内。
基于BP算法的多层前馈型网络模型的拓扑结构如上图所示。
BP算法的数学描述:三层BP前馈网络的数学模型如上图所示。
三层前馈网中,输入向
TT;输出层输出向量;隐层输入向量为:量为:)y,...y?(y,y,...,Y)x,...,x?(x,x,...,X ni21mj21TT。
输入层到隐层之间的为:;期望输出向量为:)d,...d(d,,...,o,oo,...o)d,...d?O?(l1212lkkY,个神经元对应的权向量;为隐层第j其中列向量权值矩阵用V表
示,),...vvvV?(,v,...v jmj12隐层到输出层之间的权值矩阵用W表示,,其中列向量为输出层第),...ww,w,...wW?(w lk12k k个神经元对应的权向量。
下面分析各层信号之间的数学关系。
对于输出层,有
y?f(net),j?1,2,...,m jj?m2,...,j?1net?,vx,ijij对于隐层,有
O?f(net),k?1,2,...,l kk m?l,...,1,?2wy,k?net ikjk0?j1以上两式中,转移函数f(x)均为单极性Sigmoid函数:f(x)?x?e1?f(x)具有连续、可导的特点,且有)]x?f(f(x)[1?f'(x)以上共同构成了三层前馈网了的数学模型。
当网络输出和期望输出不相等时,存在输出误差E如下:
?22)odo)??(E?(d?kk22j?0将以上误差定义式展开至隐层,有
m11
???2 )](y)]?w[d?fE?f[d?(net jkjkjk220??1k?1jk进一步展开至输入层,有
2lml11
?????2 ]}xfw()v[)]}[E?d{?ffw(net?d{?f ijkjkijkjk220i0?0?k1j?i??k1由上式可以看2llnnm11
出,网络输入误差是两层权值W和V的函数,因此调整权值可以改变误差E。
显然,调整权值的原则是使误差不断的减小,因此应使权值的调整量与误差的负梯度成
正比,即:
?E?,j?0,1,2,...m;k?1?w??,2,...,l jk?w jk E??m,...,1,??v?22,...,n;j?,i?0,1,ij v?ij?表示比例系数,在训练中反映了学习速率。
式中负号表示梯度下降,常数),1?(0容易看出,BP学习算法中,各层权值调整公式形式上都是一样的,均有3个因素决定,即:学习速率、本层误差信号和本层输入信号X/Y。
其中输出层误差信号同网络的期望输出与实际输出之差有关,直接反映了输出误差,而各隐层的误差信号与前面各层的误差信号都有关,是从输出层开始逐层反传过来的。
三、程序
clc
clear all
k=1;
n=10;
P=[-1:0.05:1];
T=sin(k*pi*P);
plot(P,T,'-');
title('要逼近的非线性函数');
xlabel('输入向量');
ylabel('非线性函数目标输出向量');
net=newff(minmax(P),[n,1],{'tansig','purelin'},'trainlm');
y1=sim(net,P);
net.trainParam.epochs=50;
net.trainParam.goal=0.01;
net=train(net,P,T);
y2=sim(net,P);
figure;
plot(P,T,'-',P,y1,'--',P,y2,'*');
title('训练前后的网络仿真结果对比');
xlabel('输入向量');
ylabel('输出向量');
legend('目标函数输出向量','未训练BP网络输出','已训练BP网络输出');
仿真结果如下图:
逼近效果不理想,网络输出与目标函数差距很大,由仿真结果图可以看出,未经训练的BP网络的训练迭代次数仅约BPBP网络训练之后的输出可以较精确的逼近目标函数,并且而对次,网络的输出目标误差就达到了精度要求,收敛速度很快。
函数逼近效果、网络训练的1.2网络训练函数网络隐含层单元神经元的数目
以及BPBP收敛速度与原始非线性函数的频率、有关。
四、实验结论网络的信号和误差传递的原理以及隐BPBP通过编程实现使用网络对函数进行逼近,对层、输出层权值调整的规则有了充分的理解和认识。
网络是一个强大的工具,它是应用最为广泛的网络。
用于文字识别、模式分类、文字BP 到声音的转换、图像压缩、决策支持等。
但是,通过实验看出,它还是存在一定的不足。
由于本实验中采用的学习率是固定不变的,从而使得在函数逼近的时候在有些地方出现了偏离,如果能自适应的调整学习率,使网络在学习初期具有较大的学习率,以快速逼近函数,当已经逼近理想输出时再使用较小的学习率,来更加精准的去逼近函数,这样会得到更好的逼近效果和更小的错误率。
网络还具有收敛速度慢、容易陷入局部极小值的问题。
这些问题通过对标准另外,BP 算法的改进能得到一定程度的解决。
BP。
