人教版六年级上册第四章比的知识点及习题
最新人教版六年级上册数学第四章《比》精品教学课件及课后练习讲解(55页)

谁能说一说比
判断题∶
的基本性质?
1、比的基本性质与商不变的性质是一致的。
2、比的前项乘以5,后项除以
1 5
( √) ,比值发生了
改变。
(Х)
3、两个正方形的边长比是2∶5,它们的面积问题。
解答按比分配的应用题时可以把比的前项和后 项的和作为总份数,根据总分数先求出每份数, 再用每份数×对应的份数=对应的数量。 也可以把比转化为分数(分母为比的前项和后 项的和,分子为对应量所占的比),再用总量× 对应的几分之几=对应的数量。
在除法里,被除数 与除数同时扩大 或缩小相同的倍 数,商大小不变。
分数的分子和分母 同时乘或者除以一 个相同的数(0除 外),分数的大小 不变。这叫做分数 的基本性质。
课堂小结
这节课你们都学会了哪些知识?
两个数量之间的关系可以用两个数的比来表示。
在两个数的比中,“:”是比号,比号前面的数叫做比的前项, 比号后面的数叫做比的后项,比的前项除以后项所得的商叫做 比值。 比的前项,后项和比值分别相当于除法算式中的:被除数,除 数和商;分别相当于分数中的:分子、分母和分数值。比的后 项不能是0。
联系
比 前项 比号 后项 比值
除法 被除数 ÷ 除数 商
分数 分子
分母 分数值
除数和分母都不能是0,所 以比的后项也不能是0。
课堂练习
做一做
小敏和小亮在文具店买同样的练习本。小敏买了6本,共花了1.8元。小亮
买了8本,共花了2.4元。小敏和小亮买的练习本数之比是( 6 ):( 8 ),
比值是( 3 );花的钱数是之比是(1.8 ):( 2.4),比值是( 3 )。
=15:30
=(15÷15):(30 ÷15 ) =1:2
六年级上册第四单元《比》基础知识点汇总、参考重点题型与解题思路总结

第四单元《比》基础知识点与解题思路一、比的意义1、比:两个数相除又叫做两个数的比。
2、比的结构:在两个数的比中,比号前面的数叫比的前项,比号后面的数叫比的后项。
比的前项除以后项所得的商,叫做比值。
比值通常用分数表示,也可以用小数或整数表示最简比:比的前项和后项只有公因数1,这样的比称为最简整数比。
3、比可以表示两个同类数量之间的倍数关系:比如一个长方形长和宽的比是15:10;也可以表示两个不同类数量之间的相除关系,得到一个新的量:比如路程÷时间=速度。
4、求比值:前项除以后项所得的商叫做比值,所以用比的前项除以后项即可求得比值(单位不统一时需要先统一单位再计算)。
比值是一个具体的数,通常用分数表示,也可以用小数或整数表示。
比值是否带单位:同类数量的比仅表示数量之间的倍数关系,其比值不带单位;不同类数量的比,其比值是一个新的数量,通常带一个复合单位(如速度)。
5、比与比值的关系:二者在写法上可能相同(都可以用分数表示),但比表示两个数量之间的相除关系;比值则是一个具体的数字。
6、比、除法与分数之间的联系:a:b=a÷b=b a(b≠0)区别:(1)意义不同:比表示两个数量之间的相除关系;除法是一种运算;分数是一个数;(2)表示方法不同:除法是一种运算,只能用算式表示;比和分数都可以用分数的形式表示,但是分数并不一定表示两个数量的比。
(3)、结果不同:除法的计算结果是一个商,这个商可以是整数、小数或分数;比只有当要求比值的时候,才需要用除法计算,比值可以用整数、小数或分数表示;而分数就是一个数,不需要计算。
7、为什么比的后项不能为0:在除法中,除数不能为0;在分数中,分母不能为0;而比的后项就相当于除法中的除数、分数中的分母,所以比的后项也不能为0。
8、求比中的未知项:在除法中,被除数÷除数=商,这3个数量只要知道其中任意2个量,就能求出另一个量,除数=被除数÷商;被除数=商×除数。
六年级上册第四单元《比》基础知识点汇总、参考重点题型与解题思路总结

第四单元《比》基础知识点与解题思路一、比的意义1、比:两个数相除又叫做两个数的比。
2、比的结构:在两个数的比中,比号前面的数叫比的前项,比号后面的数叫比的后项。
比的前项除以后项所得的商,叫做比值。
比值通常用分数表示,也可以用小数或整数表示最简比:比的前项和后项只有公因数1,这样的比称为最简整数比。
3、比可以表示两个同类数量之间的倍数关系:比如一个长方形长和宽的比是15:10;也可以表示两个不同类数量之间的相除关系,得到一个新的量:比如路程÷时间=速度。
4、求比值:前项除以后项所得的商叫做比值,所以用比的前项除以后项即可求得比值(单位不统一时需要先统一单位再计算)。
比值是一个具体的数,通常用分数表示,也可以用小数或整数表示。
比值是否带单位:同类数量的比仅表示数量之间的倍数关系,其比值不带单位;不同类数量的比,其比值是一个新的数量,通常带一个复合单位(如速度)。
5、比与比值的关系:二者在写法上可能相同(都可以用分数表示),但比表示两个数量之间的相除关系;比值则是一个具体的数字。
6、比、除法与分数之间的联系:a:b=a÷b=b a(b≠0)区别:(1)意义不同:比表示两个数量之间的相除关系;除法是一种运算;分数是一个数;(2)表示方法不同:除法是一种运算,只能用算式表示;比和分数都可以用分数的形式表示,但是分数并不一定表示两个数量的比。
(3)、结果不同:除法的计算结果是一个商,这个商可以是整数、小数或分数;比只有当要求比值的时候,才需要用除法计算,比值可以用整数、小数或分数表示;而分数就是一个数,不需要计算。
7、为什么比的后项不能为0:在除法中,除数不能为0;在分数中,分母不能为0;而比的后项就相当于除法中的除数、分数中的分母,所以比的后项也不能为0。
8、求比中的未知项:在除法中,被除数÷除数=商,这3个数量只要知道其中任意2个量,就能求出另一个量,除数=被除数÷商;被除数=商×除数。
第四单元 比(讲义) 小学数学六年级上册专项训练(人教版,含答案)

第四单元比(讲义)小学数学六年级上册专项训练(知识梳理+典例精讲+专项训练)1.比的意义和各个部分的名称。
(1)比:两个数相除也叫两个数的比;(2)比式中,比号(∶)前面的数叫前项,比号后面的项叫做后项,比号相当于除号,比的前项除以后项的商叫做比值。
(3)比的读法、写法:a比b记作a:b,读作a比b。
2.比和除法、分数的联系与区别。
3.比的基本性质。
比的前项和后项同时乘或者除以相同的数(0 除外),比值不变。
4.化简比的意义。
把两个数的比化成最简单的整数比(比的前项和后项是互质数的比),叫作化简比,也叫作比的化简。
5.化简比的方法。
(1)整数比的化简方法。
比的前项和后项同时除以它们的最大公因数。
(2)分数比的化简方法。
比的前项和后项同时乘它们分母的最小公倍数,先转化成整数比,再进行化简。
(3)小数比的化简方法通常把比的前、后项的小数点同时向右移动相同的位数,先转化成整数比,再进行化简。
6.按比分配问题的解题方法。
方法一:先求出总份数,再求出各部分量占总量的几分之几,最后求出各部分量。
方法二:先求出每份是多少,再用每份量乘各部分量所占的份数,求出各部分量。
【典例一】用涂阴影的方式设计一个长与宽的比是3∶2的长方形。
【分析】两数相除又叫两个数的比,长方形的长是3格,宽是2格即可。
【详解】涂法不唯一【点睛】关键是理解比的意义。
【典例二】下表是石家庄市A、B、C三个县城的男、女婴出生人数比。
哪个县城男、女婴出生人数比的比值最高?【分析】用比的前项除以后项即可求出比值,由此解答即可。
【详解】A.28:25=28÷25=1.12;B.121:100=121÷100=1.21;C.59:50=59÷50=1.18;1.21>1.18>1.12;答:B县城男、女婴出生人数比的比值最高。
【点睛】熟练掌握求比值的方法是解答本题的关键。
【典例三】小李和小王读同一本书,小李1小时读了这本书的13,小王1小时读了这本书的25,小王比小李1小时多读了10页。
人教版小学六年级上册数学精品讲义第4讲 比(思维导图+知识梳理+例题精讲+易错专练)(含答案)

第4讲比(思维导图+知识梳理+例题精讲+易错专练)一、思维导图二、知识点梳理知识点一:比的意义和各个部分的名称1、比:两个数相除也叫两个数的比;2、比式中,比号(∶)前面的数叫前项,比号后面的项叫做后项,比号相当于除号,比的前项除以后项的商叫做比值。
3、比的读法、写法:a比b记作a:b,读作a比b。
4、比表示的是两个数的关系,可以用分数表示,写成分数的形式,读作几比几。
例:12∶20= =12÷20= =0.6 12∶20读作:12比20知识点二:比的基本性质和化简比1、比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),比值不变,这叫做比的基本性质。
2、化简比化简之后结果还是一个比,不是一个数。
(1)用比的前项和后项同时除以它们的最大公因数。
(2)两个分数的比,用前项后项同时乘分母的最小公倍数,再按化简整数比的方法来化简。
也可以求出比值再写成比的形式。
(3)两个小数的比,可以先把小数比化成整数比,再按整数比的化简方法化简。
知识点三:比的应用按比例分配问题的解决方法:1、已知单位“1”的量用乘法。
2、未知单位“1”的量用除法。
3、分数应用题基本数量关系(把分数看成比)(1)甲是乙的几分之几?甲=乙×几分之几乙=甲÷几分之几几分之几=甲÷乙(2)甲比乙多(少)几分之几?4、画线段图:(1)找出单位“1”的量,先画出单位“1”,标出已知和未知。
(2)分析数量关系。
(3)找等量关系。
(4)列方程。
两个量的关系画两条线段图,部分和整体的关系画一条线段图。
三、例题精讲考点一:比的意义、比各部分的名称【典型一】一根绳子,用去,用去的和剩下的比是3:2,剩下的是总长度的。
【分析】把一根绳子总长度看作5份,用去,也就是用去5×=3份。
据此可求出用去的和剩下的比,再用除法求出剩下的是总长度的几分之几。
【解答】解:5×=3(份)5﹣3=2(份)用去的和剩下的比是3:2。
第四单元《比》(单元复习课件)六年级数学上册 人教版

最简单整数比
Text重he难re 易错点剖析 6.化简小数比。
比的基本性质
3.2∶0.16 =(3.2×100)∶(0.16×100) =(320÷16)∶(16÷16) =20∶1
比的前项、后项同时 扩大相同的倍数。
整数比
最简单整数比
Text重he难re 易错点剖析
按比分配问题
1.份数法
六(1)班分成两组打扫卫生,室外组有30人,室内组有20人,
),
TeTxet重xth重eh难ree难re 易易错错点点剖剖析析
比的意义
2.比的各部分名称
在两个数的比中,比号前面的数叫做比的前项,比号后面的数 叫做比的后项。比的前项除以后项所得的商,叫做比值。例如:
15 : 10 = 15 10 = 3 2 比值通常用分数表示,能
……
…… …… ……
除尽时也可以用小数表示,
40×
3 3+2
=24(个)
40×
2 3+2
=16(个)
答:室外组分到24个清扫工具,室内组分到16个清扫工具。
方法:把比转化为分数,先求出各部分的数量占总数量的几分之几,再
求出各部分的数量。
总数量×
各部分的份数 总份数
=各部分的数量
Text he深re 化练习
3. 用84 cm长的铁丝围成一个长方形,这个长方形的长与宽
前比 后 项号 项
比 能整除时就用整数表示。 值
15 : 10也可以写成1105 ,读作“15比10” 注意:两个数的比表示两个数相除,要注意比的前项和后项的书写
顺序,不要颠倒。
Text重he难re 易错点剖析 5.化简0÷8) =4∶5
比的前项、后项同时除 以它们的最大公因数。
人教版数学六年级上册 第4单元 比 知识梳理与强化(含答案)
第4单元 比 知识梳理与强化比的意义 一、细心填写。
1.长方形长3分米,宽12厘米,长与宽的比是( ),比值是( )。
2.小李5小时加工60个零件,加工个数与时间的比是( ),比值是( )。
3.一本书读了55页,45页没有读,已读与总数的比是( ),比值是( )。
4.甲数是乙数的38,甲数与乙数的比是( ),甲数与两数和的比是( ),乙数与两数差的比是( )。
5.从甲地到乙地共120千米,王叔叔行驶汽车开完全程要3小时,车辆所行路程与所用时间的比是( ),比值是( )。
二、求比值。
14∶0.5 0.5∶1.25233∶3110.375∶250.21∶6.348∶36三、化简比。
0.125∶58 360∶4500.3∶0.1518∶231.2cm ∶50cm320kg ∶45g0.6时∶20分23m 2∶6dm 2四、解决问题。
1.一辆汽车从甲地到乙地,每小时行80千米,用了34小时,返回时只用了58小时。
返回时每小时行多少千米?2.商店售出2筐橙子,每筐24千克。
售出的橙子占水果总质量的611,售出的香蕉质量占水果总质量的14。
售出香蕉多少千克?比的基本性质 五、细心填写。
1.16∶20=32∶( )=( )÷10=4( )=1.6∶( )=( )∶0.2。
2.甲数是乙数的3倍,乙数与甲数的比是( ),比值是( )。
3.601班男生与女生人数的比是2∶3,女生占全班的( ),男生占全班的( )。
4.在100克水中加入10克盐,盐和盐水的比是( )。
5.甲数是乙数的23,乙数与甲数的比是( ),甲数与乙数的比是( )。
6.甲数比乙数多14,甲数与乙数的比是( ),比值是( )。
7.已知a ∶b =2∶3,如果a =24,那么b =( );如果b =24,那么a =( )。
六、判断。
1.45可以读作“4比5”。
( ) 2.比的前项和后项同时乘一个相同的数,比值不变。
( ) 3.比的基本性质与商不变的性质是一致的。
人教版六年级数学上册第4单元《比》知识归纳总结

一、 比的意义
1、两个数相除又叫做两个数的比。
比和除法、分数的联系
比
比的前项
比号(:)
除法
被除数Biblioteka 除号分数分子
分数线
比的后项 除数 分母
比值 商
分数值
“:”是比号,读作 “比”。比号前面的数叫做比的前项,比号后面的数叫做比的
后项。比的后项不能是零。例如 21:7 其中 21 是前项, 7 是后项。
8 5 3 15
运算
4、 求几个数的连比的方法 ,如:甲∶乙 =5∶6,乙∶丙 =4∶3,因为 [6,4]=12,
所以 5∶ 6=10∶ 12, 4∶ 3=12∶ 9,
得到甲∶乙∶丙 =10∶12∶9。
5、 2 : 3 4 (
)(
( ) 24
三、求比值和化简比的比较
) 15
10
36
2( )
1.目的不同。求比值就是求比的前项除以后项所得的商,而化简比是把两个数 的比化成最简单的整数比 ,
2、比的前项除以后项所得的商,叫做比值。比值通常用分数表示,也可以用小
数表示,有时也可能是整数。
二、比的基本性质
1、比的前项和后项同时乘或除以相同的数( 0 除外 ),比值不变,这叫做分数的
基本性质。
2、比的前项和后项是互质数的比,叫做最简单的整数比 。
把两个数的比化简成最简单的整数比叫做化简比,也叫做比的化简 。(化简后比
的前项和后项没有公因数,化简后要检查)
3、分数比的化简方法 :比的前项和后项同时乘它们分母的最小公倍数,变成整
数比,再进行化简: 例如 : 1 : 2 =( 1 ×18):( 2 ×18) =3:4
六年级数学上册第四单元《比》知识点总结
六年级上册第四单元比知识点总结及重点一、比的意义1、两个数相除又叫做两个数的比。
比和除法、分数的联系比比的前项比号(:)比的后项比值除法被除数除号除数商分数分子分数线分母分数值“:”是比号,读作“比”。
比号前面的数叫做比的前项,比号后面的数叫做比的后项。
比的后项不能是零。
例如21:7其中21是前项,7是后项。
2、比的前项除以后项所得的商,叫做比值。
比值通常用分数表示,也可以用小数表示,有时也可能是整数。
二、比的基本性质1、比的前项和后项同时乘或除以相同的数(0除外),比值不变,这叫做分数的基本性质。
2、比的前项和后项是互质数的比,叫做最简单的整数比。
把两个数的比化简成最简单的整数比叫做化简比,也叫做比的化简。
(化简后比的前项和后项没有公因数,化简后要检查)3、分数比的化简方法:比的前项和后项同时乘它们分母的最小公倍数,变成整数比,再进行化简:例如:61:92=(61×18):(92×18)=3:4也可以用:4:34329619261==⨯=÷15:8158385183:2.0==⨯=可以转为除法的运算4、求几个数的连比的方法,如:甲∶乙=5∶6,乙∶丙=4∶3,因为[6,4]=12,所以5∶6=10∶12,4∶3=12∶9,得到甲∶乙∶丙=10∶12∶9。
判断题常考三、求比值和化简比的比较1.目的不同。
求比值就是求比的前项除以后项所得的商,而化简比是把两个数的比化成最简单的整数比,2.结果不同。
求比值的结果是一个数,这个数可以是整数,也可以是小数或分数。
而化简比最后的结果仍然是一个比,要写成比的形式3.读法不同。
如6:4求比值是6:4=6÷4=46=23读作二分之三还可写作(结果是一个数)。
化简比是6:4=6÷4=46=23读作三比二还可写作3:2(结果是一个比)四、比的应用1、比的第一种应用:已知两个或几个数量的和,这两个或几个数量的比,求这两个或这几个数量是多少?例如:六年级有60人,男女生的人数比是5:7,男女生各有多少人?题目解析:60人就是男女生人数的和。
人教版六年级上册数学第四单元比的知识点总结

第四单元比知识点归纳与总结一、比的意义1、两个数相除又叫做两个数的比。
“:”是比号,读作“比”。
比号前面的数叫做比的前项,比号后面的数叫做比的后项。
比的后项不能是零。
例如21:7 其中21是前项,7是后项。
2、比的前项除以后项所得的商,叫做比值。
比值通常用分数表示,也可以用小数表示,有时也可能是整数。
【求几个数的连比方法】求几个数的连比的方法,如:甲∶乙=5∶6,乙∶丙=4∶3,因为[6,4]=12,所以5∶6=10∶12,4∶3=12∶9,得到甲∶乙∶丙=10∶12∶9。
3、比与分数、除法之间的关系。
比同除法比较:比的前项相当于被除数,后项相当于除数,比值相当于商。
比同分数相比较:比的前项相当于分子,后项相当于分母,比值相当于分数值。
二、比的基本性质1、比的前项和后项同时乘或除以相同的数(0除外),比值不变,这叫做分数的基本性质。
2、比的前项和后项是互质数的比,叫做最简单的整数比。
把两个数的比化简成最简单的整数比叫做化简比,也叫做比的化简。
3、整数比的化简方法:把比的前项和后项同时除以它们的最大公因数。
例如:180:120=(180÷60):(120÷60)=3:24、分数比的化简方法:比的前项和后项同时乘它们分母的最小公倍数,变成整数比,再进行化简:例如::=(×18):(×18)=3:45、小数比的化简方法:把比的前项和后项的小数点同时向右移动相同的位数,变成整数比,再化简。
例如:0.75:0.2=(0.75×100):(0.2×100)=75:20=15:4 6、一个比中,既有小数,又有分数,可以把小数化成分数,按照化简分数比的方法进行化简;也可以把分数化成小数,按照化简小数比的方法进行化简。
例如:0.5:=:=5:6 0.5:=0.5:0.4=5:4三、求比值和化简比的比较1.目的不同。
求比值就是求比的前项除以后项所得的商;而化简比是把两个数的比化成最简单的整数比,也就是化简后的比要符合两个条件,一是比的前、后项都应是整数;二是前、后项的两个数要互质。
人教版数学六年级上册《比》练习题含答案

第四单元 比【例1】甲、乙、丙三位同学分别调制了一杯蜂蜜水。
甲调制时用了40毫升的蜂蜜,200毫升水;乙调制时用了5小杯蜂蜜,20小杯水;丙调制时用的水是蜂蜜的7倍。
( )调制的蜂蜜水最甜。
A.甲B.乙C.丙D.无法判断 解析:本题考查的知识点是利用比的意义解决实际问题。
甲调制的蜂蜜水中,蜂蜜与水的比是40:200=1:5=51;乙调制的蜂蜜水中,蜂蜜与水的比是5:20=1:4=41;丙调制的蜂蜜水中,蜂蜜与水的比是1:7=71。
41>51>71,所以,乙调制的蜂蜜水最甜。
解答:B【例2】已知甲:乙=3:4,乙:丙=3:2,那么甲、乙、丙三个数的大小关系是( )。
A.甲>乙>丙B.丙>乙>甲C.乙>甲>丙D.甲=乙=丙解析:本题考查的知识点是比的基本性质解答连比问题。
解答时,需将两个不同的比中共有的量转化为同一个数。
甲:乙=3:4=9:12;乙:丙=3:2=12:8,则甲:乙:丙=9:12:8,所以,乙>甲>丙,选C 。
解答:C【例3】成年人的足长与身高的比大约是1:7。
某小区发生了一起盗窃事件,在犯罪现场留下了一个长26厘米的足印。
经过周密侦察,锁定了四名犯罪嫌疑人,下表是这四名犯罪嫌疑人的身高记录。
请你根据以上信息计算说明:这四人中,谁的嫌疑最大?解析:本题考查的知识点是利用比的知识解决实际问题。
解答时,先根据“成年人的足长与身高的比大约是1:7”,可以看作成年人的身高是足长的7倍来推算出犯罪嫌疑人的身高。
该题具备探索性和趣味性,同时运用了估算的知识。
解答:26×7=182(cm ),四人中王某的身高最接近182cm 。
答:王某的嫌疑最大。
【例4】骆驼体重250千克,能搬运质量为300千克的货物;蚂蚁体重0.05克,能搬运质量为2克的虫子.写出它们各自搬运的质量与体重的比,并求出比值.相对于自身体重,你觉得谁的力气大?为什么?解析:本题考查的知识点是比和求比值的方法,解答时需要明确的是:比值越大,力气就越大。
人教版六年级上册数学第四单元《比》的知识点总结+相关练习!

第四单元比知识点归纳与总结一、 比的意义1、两个数相除又叫做两个数的比.“:”是比号;读作“比”.比号前面的数叫做比的前项;比号后面的数叫做比的后项.比的后项不能是零.例如21:7 其中21是前项;7是后项.2、比的前项除以后项所得的商;叫做比值.比值通常用分数表示;也可以用小数表示;有时也可能是整数. =5∶6;乙∶丙3;因为[6;4]=12;所以5∶ 6=10∶ 12; 4∶3=12∶9;得到甲∶乙∶丙=10∶12∶9.3、比与分数、除法之间的关系.比同除法比较:比的前项相当于被除数;后项相当于除数;比值相当于商. 比同分数相比较:比的前项相当于分子;后项相当于分母;比值相当于分数值.二、比的基本性质1、比的前项和后项同时乘或除以相同的数(0除外);比值不变;这叫做分数的基本性质.2、比的前项和后项是互质数的比;叫做最简单的整数比.把两个数的比化简成最简单的整数比叫做化简比;也叫做比的化简.3、整数比的化简方法:把比的前项和后项同时除以它们的最大公因数.例如:180:120=(180÷60):(120÷60)=3:24、分数比的化简方法:比的前项和后项同时乘它们分母的最小公倍数;变成整数比;再进行化简:例如:61:92=(61×18):(92×18)=3:4 5、小数比的化简方法:把比的前项和后项的小数点同时向右移动相同的位数;变成整数比;再化简.例如:0.75:0.2=(0.75×100):(0.2×100)=75:20=15:46、一个比中;既有小数;又有分数;可以把小数化成分数;按照化简分数比的方法进行化简;也可以把分数化成小数;按照化简小数比的方法进行化简.例如:0.5:53=21:53=5:6 0.5:52=0.5:0.4=5:4 三、求比值和化简比的比较1.目的不同.求比值就是求比的前项除以后项所得的商;而化简比是把两个数的比化成最简单的整数比;也就是化简后的比要符合两个条件;一是比的前、后项都应是整数;二是前、后项的两个数要互质.2.结果不同.求比值的结果是一个数;这个数可以是整数;也可以是小数或分数.而化简比最后的结果仍然是一个比;要写成比的形式;不能得整数或小数.比有两种书写形式如6比4;可写作6:4也写作46读作6比4.3.读法不同.如6:4求比值是6:4=6÷4=46=23读作二分之三还可写作1.5(结果是一个数).化简比是6:4=6÷4=46=23读作三比二还可写作3:2(结果是一个比)四、比的应用 1、比的第一种应用:已知两个或几个数量的和;这两个或几个数量的比;求这两个或这几个数量是多少?例如:六年级有60人;男女生的人数比是5:7;男女生各有多少人? 题目解析:60人就是男女生人数的和.解题思路:第一步求每份:60÷(5+7)=5人第二步求男女生:男生:5×5=25人 女生:5×7=35人.2、比的第二种应用:已知一个数量是多少;两个或几个数的比;求另外几个数量是多少?例如:六年级有男生25人;男女生的比是5:7;求女生有多少人?全班共有多少人?题目解析:“男生25人”就是其中的一个数量.解题思路:第一步求每份:25÷5=5人第二步求女生: 女生:5×7=35人. 全班:25+35=60人3、比的第三种应用:已知两个数量的差;两个或几个数的比;求这两个或这几个数量是多少?例如:六年级的男生比女生多20人(或女生比男生少20人);男女生的比是7:5;男女生各有多少人?全班共有多少人?4.比练习一【知识要点】比的意义;比的各部分名称.【课内检测】1、两个数( )又叫做两个数的( ).2、 如果A ∶B=C ;那么A 是比的( );B 是比的( );C 是比的( ).3、4÷5=( )∶( )=()()4、从A 地到B 地共180千米;客车要行2小时;货车要行3小时.客车所行的路程与所用时间的比是( );比值是( );客车所用的时间与货车所用的时间比是( );比值是( );货车与客车的速度比是( );比值是( );客车与货车所行的路程比是( );比值是( ).5、判断. ①53可以读作五分之三;也可以读作三比五. ( ) ②配制一种盐水;在200克水中放了20克盐;盐和盐水的比是1∶10. ( ) ③比值是0.8的比只有一个. ( ) ④甲数与乙数的比是3∶4;则乙数是甲数的34倍. ( )【课外训练】1、甲数除以乙数的商是1 .4;乙数与甲数的比是( ).2、正方形的周长与边长的比是( );比值是( ).3、长方形的长比宽多51;长方形的长与宽的比是( ).4、一杯糖水;糖占糖水的101;糖与水的比是( ).5、女生人数与全班人数的比是4∶9;男生人数与女生人数的比是( ).练习二【知识要点】比的基本性质;化简比.【课内检测】1、判断:比的前项和后项同时乘一个相同的数;比值不变.( )2、8∶5=24∶( ) 42∶18=( )∶33、化简下面各比.21∶35 65∶ 94 0.8∶0.324、一辆汽车3小时行驶135千米;汽车所行的路程和时间的比是( );化成最简整数比是( ).5、一根绳子全长 2.4米;用去0.6米.用去的绳子和全长的比是( ),化简比是( ).【课外训练】1、化简下面各比.35140 0.4∶32 0.3吨∶150千克 0.6∶322、判断:最简单的整数比,就是比的前项和后项都是质数的比.( )3、5∶12的前项增加15,要使比值不变,后项应增加( ).4、甲、乙两人每天加工零件个数的比是3∶4,两人合作15天后, 甲、乙两人各自加工零件的个数比是( ).练习三【知识要点】比的意义和基本性质的练习.【课内检测】1、简下面各比;并求出比值.2、六(2)班有男生20人、女生28人.①男生人数是女生人数的)() (; ②女生人数是男生人数的) () (; ③男生人数与女生人数的比是( );比值是( ).④女生人数与全班人数的比是( );比值是( ).3、读完同一本书;小华要4天;小明要6天.小华和小明读完这本书所用的时间比是( );比值是( ).4、一杯糖水;糖占糖水的401;糖与水的比为( ).★★5、甲数与乙数的比是4∶5;乙数与丙数的比是3∶4;甲数∶丙数=( )∶( ).★★6、从六(1)班调全班人数的101到六(2)班,则两班人数相等,原来六(1)班与六(2)班的人数比是( ).★★7、 右图中长方形的面积与阴影部分的面积比是( ).练习四【知识要点】按比例分配应用题.(已知两个量的比与和;求这两个量.)【课内检测】1、公鸡与母鸡的只数比是2∶9;也就是公鸡占总只数的) () (;母鸡占总只数的) () (;公鸡的只数是母鸡的) () (;母鸡的只数是公鸡的)() (. 2、一批货物按2∶3∶4分配给甲、乙、丙三个队去运;甲队运这批货物的) () (;丙队比乙队多运这批货物的)() (.3、公园里柳树和杨树的棵数比是5∶3;柳树和杨树共40棵;柳树和杨树各有多少棵?4、把300个苹果按4∶5∶6分给幼儿园的小、中、大三个班.小班、中班、大班各分得多少个苹果?【课外训练】1、一种药水是把药粉和水按照1∶100配制而成;要配制这种药水5050千克;需要药粉多少千克?★2、水果店运来梨和苹果共50筐;其中梨的筐数是苹果的32;运来梨和苹果各多少筐?★★★3、用24厘米的铁丝围成一个直角三角形;这个三角形三条边长度的比是3∶4∶5;这个直角三角形斜边上的高是多少厘米?练习五【知识要点】按比例分配应用题.(已知两个量的比与其中的一个量;求另一个量.)【课内检测】1、把一根长8米的绳子按3∶2截成甲、乙两段;甲、乙两段各长多少米?2、把一根绳子按3∶2截成甲、乙两段;已知甲段长4.8米, 乙段长多少米?3、把一根绳子按3∶2截成甲、乙两段;已知乙段长4.8米, 这根绳子原来长多少米?4、把一根绳子按3∶2截成甲、乙两段;已知乙段比甲段短1.6米, 甲、乙两段各长多少米?【课外训练】1、商店运来一批洗衣机,卖出24台,卖出的台数与剩下的台数的比是3∶5,这批洗衣机一共有多少台?★2、雏鹰假日小队的同学分3组采集蓖麻籽;第一小组、第二小组、第三小组的工作效率之比是12∶11∶7;第一小组采集蓖麻籽36千克;第二、第三小组各采集蓖麻籽多少千克?★3、已知甲数的52等于乙数的258;甲数是80;则乙数是多少?练习六【知识要点】按比例分配应用题的练习.【课内检测】1、小伟和小英给希望工程捐款的钱数比是7∶8;两人共捐款75元.小伟和小英各捐款多少元?★2、两地相距480千米;甲、乙两辆汽车同时从两地相向开出;4小时后相遇;已知甲、乙两车速度的比是5∶3.甲、乙两车每小时各行多少千米?★3、用36米长的篱笆围成一个长方形菜地;要求长与宽的比是5∶4;这块菜地的面积是多少平方米?★4、已知A 、B 、C 三个数的比是2∶3∶5;这三个数的平均数是90;这三个数分别是多少 ?★★5、把54本图书分给三个组;A 组的21和B 组的31以及C 组的41相等;A 、B 、C 三个组各分得图书多少本?★★6、水果店运进梨和苹果的筐数比是3∶2;当只卖出15筐梨后;苹果的筐数占梨的54.现在的梨和苹果各有多少筐?。
人教版六年级数学上册四单元比的知识点和习题练习

比的基本概念和化简一、比的基本概念1、比的意义:两个数的比表示两个数相除(旧:两个数相除又叫做两个数的比)两个同类量的比表示这两个量之间的倍数关系,两个有联系的不同类量的比表示一个新的量。
2、比的符号和读、写法37是分数形式的比,是比的另一种书写形式。
3、比的各部分名称(1)比的前项:在两个数的比中,比号前面的数; (2)比的后项:在两个数的比中,比号后面的数; (3)比值:比的前项除以后项所得的商。
4、求比值的计算方法:比的前项除以比的后项;比值可用分数、小数或整数表示。
5、比和比值的联系与区别都可以用分数形式表示:53既可表示3:5,又可表示3:5的比值;比表示两个数的一种关系;比值是一个数;比只能写成b a :或ba的形式,比值可以是分数、小数、整数。
6、比与分数、除法的关系 (1)联系 a:b=a ÷b=ba(b ≠0) 除法 被除数 ÷ 除数 商 分数 分子 — 分母 分数值 比 前项 : 后项 比值(2)区别①意义不同:比表示两个量的一种关系;除法是一种运算;分数则是一个数②表示方法不同:除法算式不能用分数表示;比可以用分数表示;但分数不一定表示两个量的比 ③结果表达不同:除法的结果为商;比的结果为比值;分数本身就是一个数值 7、求比中未知项的方法比的前项=比的后项×比值 比的后项=比的前项÷比值二、比的基本性质(与“商不变”性质类同)1、比的基本性质比的前项和后项同时乘或除以相同的数(0除外),比值不变。
同样适用于连比 2、化简比的意义(1)最简整数比:比的前项和后项是互质数的比 (2)化简比: 把两个数的比化成最简单的整数比3、整数比的化简方法:把比的前项和后项同时除以它们的最大公因数4、分数比的化简方法(1)比的前项和后项同时乘它们的分母的最小公倍数,变整数比,再化简 (2)先求比值,再把结果写成比的形式5、小数比的化简方法:先把前项和后项的小数点同时向右移动相同的位数,变成整数比,再化简6、求连比甲数和乙数的比是3:4,乙数和丙数的比是5:6,求甲、乙、丙的连比关键是找中间量(“桥梁”),显然为乙。
最新人教版六年级上册第四章比的知识点及习题

人教版六年级上册第四章比的知识点及习题第六讲 比以及应用基础知识(一)1、求比值的方法:用比的前项除以比的后项.2、区分比和比值比:表示两个数的倍数关系,可以写成比的形式,也可以用分数表示. 比值:相当于商,是一个数,是一个结果,可以是整数,分数,也可以是小数.3、根据分数与除法的关系,两个数的比也可以写成分数形式.例如3:2也可以写成32 ,仍读作“3:2”.4、(二)、比的基本性质1、根据比、除法、分数的关系:商不变的性质:被除数和除数同时乘或除以相同的数(0除外),商不变.分数的基本性质:分数的分子和分母同时乘或除以相同的数时(0除外),分数值不变. 比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),比值不变. 2、最简整数比:比的前项和后项都是整数,并且是互质数,这样的比就是最简整数比. 3、根据比的基本性质,可以把比化成最简单的整数比.一、填一填1、( ):30=30÷( )=53=) (24=( )(小数)2、一辆汽车51小时行驶20千米.这辆汽车行驶的路程与所用时间的比是( ):( ),比值是( ),这个比值表示的意义是( )3、2:41的比值是( ),把这个比化成最简单的整数比是( ).4、明明和亮亮邮票的比是2∶5,亮亮有105张邮票,明明有( )张邮票.5、从甲地到乙地,小李用了4时,小张用了3时.小李和小张所用的时间的比是( ):( ),他们的速度比是( ):( ).6、甲数除以乙数的商是32,那么甲数与乙数的最简整数比是( ):( ).7、体育课上老师拿出40根跳绳,按3:2分给男、女生,男生分得这些跳绳的)() (,女生分得( )根.8.甲、乙两数的比是2:7,且它们的平均数是4.5,那么乙数是( ).9、某班女生比男生多,则男生人数与女生人数比是( ):( );女生人数与全班人数的比是( ):( ).10、甲、乙两篮各盛有35个鸡蛋.如果从甲篮取出5个鸡蛋放入乙篮,那么乙篮与甲篮的鸡蛋个数的比是( ):( ).11、下图中,大圆的半径等于小圆的直径,大圆的周长与小圆周长的比是( ).大圆的面积与小圆面积的比是( ).第11题 第12题12、如上图,阴影部分的面积和平行四边形ABCD 面积的比是( ).阴影部分的面积是 5 平方厘米,那么平行四边形的面积是( ). 二、选一选1、比的前项和后项( ).A.都不能为0B.都可以为0C.前项可以为0D.后项可以为0 2、学校买来380本图书,按一定的比分配给三个班,它们的比可能是( ). A.2:3:5 B.2:3:4 C.1:2:33、一个三角形三个角的比是1:2:3,那么这个三角形是( ).A.直角三角形B.锐角三角形C.钝角三角形4、甲数是乙数的31,甲数和乙数的比是( ).A.1:3B.3:1C. 315、下面各比中,比值是0.5的是( ).A.5:2.5B. 31:61C.0.7:1.46、如右图,由三个等边三角形组成的梯形. 三角形与梯形周长的比是( ). A. 1:3 B.3:5 C.3:77、60平方米的教室与4平方厘米的邮票.它们的面积比是( ).A.15:1B.1500:1C.150000:18、一根小棒锯成3段需要30秒,那么锯成6段需要( )秒.A.60B.75C.90 三、判断题:1、喜乐足球队以3∶0大胜厚木队,说明在特殊情况下,比的后项可以是0.( )2、1米的54等于4米的51.( )3、两个分数相除,商一定大于被除数.( )4、如果A 是B 的53,那么B 是A 的35倍.( ) 5、4÷(20+54)=4÷20+4÷54=51+5=551( ) 6、一个比的前项乘41,后项除以4,它的比值不变.( )四、算一算 1.化简比.(8分)12 : 16 43 : 811 4.5 : 2.7 1.4﹕344.2:7/4 120:72 1/7:1/49 1:1/32.求比值:(8分)36分:1小时 308立方厘米:2立方分米183 : 85 43千米: 500 米应用问题1.按比例分配:把一个数量按照一定的比来进行分配.这种方法通常叫做按比例分配. 2. 路程一定,速度比和时间比成反比.(如:路程相同,速度比是4:5,时间比则为5:4) 工作总量一定,工作效率和工作时间成反比.(如:工作总量相同,工作时间比是3:2,工作效率比则是2:3) 和比的应用题有关的概念1、求每份数的方法和÷份数和=每份数 相差数÷相差份数=每份数 部分数÷对应份数=每份数 2、图形求比的常见公式长方体:(长+宽+高)的和=棱长和÷4 长方形: (长+宽)的和=周长÷2 3、相遇问题速度和 = 路程÷相遇时间五、解决问题1、甲乙两地相距360千米,客车和货车同时从两地出发,相对而行,它们的速度比是5:4.相遇时两车各行驶了多少千米?2、甲、乙两数的平均数是56,甲与乙的比是4:3,甲、乙各是多少?3、甲乙两个工程队共修路360米,甲乙两队所修的长度比是5 :4,甲队比乙队多修了多少米?4、有两堆货物.甲堆比乙堆多18吨.甲堆与乙堆重量的比是9:5,两堆货物各有多少吨?5、学校新购买了一批桌椅.一套桌椅的价钱是90元,其中椅子的价钱和桌子的价钱的比是7:11,桌子和椅子的价钱分别是多少元?6、配制一种消毒药,药液和水的比是1:50,要配制这种消毒药300千克,需要药液和水各多少千克?7、配制一种消毒药,药液和水的比是1:50,现有药液300千克,需要加水多少千克?8、配制一种消毒药,药液和水的比是1:50,现有水300千克,需要加药液多少千克?9、甲乙两地相距450千米,客车和货车同时从两地出发,相对而行,3小时后相遇,它们的速度比是2:3.客车和货车速度各是多少千米?10、一个长方形周长是96cm,长与宽的比是5:7.长方形面积是多少?11. 用120厘米的铁丝做一个长方体的框架.长、宽、高的比是3:2:1.这个长方体的长、宽、高分别是多少?体积是多少?。
第四单元 比(思维导图 知识梳理 真题演练)六年级数学上册(人教版)

第四单元比一、比的意义。
1、比的意义:两个数相除又叫做两个数的比。
2、比的各部分名称。
(1)比号:“:”叫做比号,读作“比”。
(2)比的前项和后项:在两个数的比中,比号前面的数叫做比的前项,比号后面的数叫做比的后项。
(3)比值:比的前项除以后项所得的商,叫做比值。
3、比与分数,除法的关系。
(1)联系:比的前项相当于分数的分子、除法中的被除数;比号相当于分数的分数线、除法中的除号;比的后项相当于分数的分母、除法中的除数;比值相当于分数的分数值、除法中的商。
(2)区别:比表示两个量的倍数关系,分数是一个数,除法是一种运算。
二、比的基本性质。
1、比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),比值不变。
2、化简比:把两个数的比化成最简单的整数比。
(1)整数比的化简方法:比的前项和后项同时除以它们的最大公因数。
(2)分数比的化简方法:比的前项和后项同时乘它们分母的最小公倍数,先转化成整数比,再进行化简;也可以利用求比值的方法化简。
(3)小数比的化简方法:先用恰当的方法转化成整数比,再进行化简。
三、比的应用。
按比例分配问题的解题方法:(1)先求出总份数,再求出各部分量占总量的几分之几,最后求出各部分量。
(2)先求出每份是多少,再用每份数乘各部分量所占的份数,最后求出各部分量。
一、选择题1.(2023秋·江西赣州·六年级统考期末)一条路,已行路程与全部路程之比是3∶7,则已行路程与剩下路程之比是()。
A.3∶7 B.7∶3 C.3∶4 D.4∶32.(2023秋·河南郑州·六年级统考期末)某儿童医院上个月新生男婴儿48名,男、女婴儿人数之比是4∶5。
上月新生女婴儿有()名。
A.108 B.60 C.123.(2023秋·河北保定·六年级校考期末)甲、乙两人从学校走到广场,甲要8分钟,乙要10分钟,甲、乙两人速度的比是()。
A.4∶5 B.5∶4 C.10∶8 D.8∶104.(2022春·浙江绍兴·六年级统考期末)某次数学竞赛中,女生和男生人数的比是3∶4,全体学生的平均成绩是82分,男生的平均成绩是80.5分,女生的平均成绩是()分。
人教版六年级上册第4章《比的应用—按比分配》知识点+同步练习
比的应用—按比分配
电子课本
▼▼▼▼
知识点
按比分配的解题方法:
方法一:把比看作份数之比。
先求每份是多少,再求几份是多少。
解题步骤:①求出总份数;
②求出一份是多少;
③求出各部分的数量。
方法二:把比转化成分率。
利用分数乘法解答。
解题步骤:①求出总份数;
②求出各部分占总量的几分之几;
③求出各部分的数量。
参考答案
同步练习
2.按要求解答。
在学校组织的科技创新大赛上,五、六年级共上交“小发明”作品72件。
五、六年级上交“小发明”作品数量的比是3∶5。
五、六年级上交“小发明”作品各多少件?
方法一:将“小发明”作品总数量平均分成(8)份,先求出1份的数量,再求出几份的数量。
72÷(3+5)=9(件)
五年级:3×9=27(件)
六年级:5×9=45(件)
8.实验小学140名学生分组开展社会实践活动,第一组和第二组人数的比是2∶3,第二组与第三组人数的比是4∶5,这三个组各有学生多少人?
图文解读
▼▼▼▼
部编版六年级上册知识点+图文解读目录语文
第
数学。
人教新课标六年级上册数学第四单元 比(含答案) (共21张PPT)

基础练
1. 填空。 (1)如果故事书和文艺书的数量比是2∶7,那么故事书占
两种书总数的( ),文艺书占两种书总数的( )。
(2)三鲜馅水饺是用1份虾仁、3份韭菜和2份鸡蛋混制而
成的。虾仁、韭菜和鸡蛋的比是( 1 )∶( 3 )∶( 2 ),虾 仁占所有馅料的( ),韭菜占所有馅料的( ),鸡蛋 占所有馅料的( )。
答:还剩300 m没有修。
(2)一块长方形地,周长是120 m,长与宽的比是3∶2, 这块地的面积是多少?
第4单元
2
比
比的基本性质
知识要点要记牢: 1. 比的前项和后项同时乘或除以相同的数(0除外),比 值不变,这叫做比的基本性质。 2. 化简比的一般步骤: (1)观察比的特点。 (2)将分数比、小数比转化为整数比。 (3)把不是最简单的整数比化成最简单的整数比。
基础练
1. 填空。
(1)比的前项和后项同时( 乘或除以相同的数 (0除外) ), 比值不变。 (2)3∶8的前项扩大4倍,要使比值不变,后项应该 ( 扩大4倍 )。
基础练
1. 填空。
(1)两个数相除又叫做两个数的( 比 )。 (2)8∶9读作(八比九 ),这个比还可以写成( )。
(3)在5∶4中,比的前项是( 5 ),比的后项是( 4 ), 比值是( )。 =( 2 )∶( 3 )。
(4)5÷3=( 5 )∶( 3 );
巩固练
2. 判一判,对的画“√”,错的画“×”。 (1)在除法中,除数不能为0;在比中,比的后项也 不能为0。( √ ) (2)比的前项相当于除法算式中的被除数或分数中的 分母。( × ) (3)比值只能用分数表示。( × ) (4)4∶7可以写成 ,读作七分之四。(×)
巩固练
2023-2024年小学数学六年级上册期末考点复习 第四单元《比》(人教版含解析)
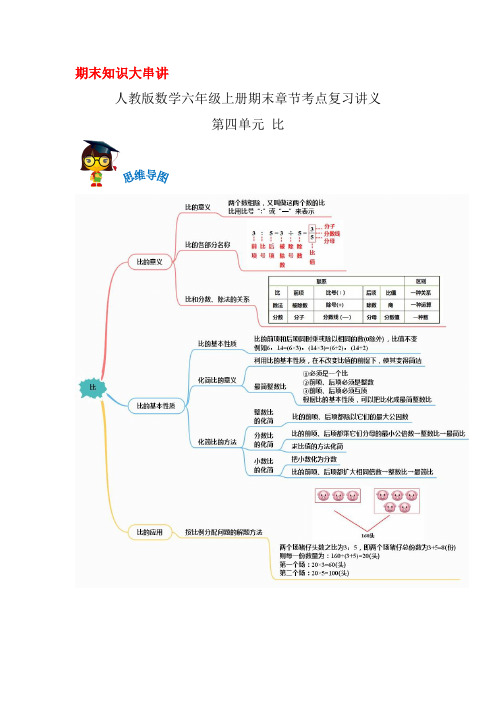
期末知识大串讲人教版数学六年级上册期末章节考点复习讲义第四单元比知识点01:比的意义、各个部分的名称1. 两个数量之间的关系可以用两个数的比来表示。
2. 在两个数的比中,“:”是比号,比号前面的数叫做比的前项,比号后面的数叫做比的后项,比的前项除以后项所得的商叫做比值。
3. 比的前项,后项和比值分别相当于除法算式中的:被除数,除数和商;分别相当于分数中的:分子、分母和分数值。
比的后项不能是0。
知识点02:比的基本性质和化简比1.比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),比值不变,这叫做比的基本性质。
2.化简比的方法:(1)化简整数比时,前、后项同时除以最大公因数。
(2)化简分数比时,前、后项同时乘它们分母的最小公倍数,转化成整数比,再化简。
(3)化简小数比:先把前、后项的小数点同时向右移动相同的位数,转化成整数比,再化简。
知识点03:按比分配按比分配的解题方法:方法一:把比看作份数之比。
先求每份是多少,再求几份是多少。
解题步骤:①求出总份数;②求出一份是多少;③求出各部分的数量。
方法二:把比转化成分率。
利用分数乘法解答。
解题步骤:①求出总份数;②求出各部分占总量的几分之几;③求出各部分的数量。
考点01:比的意义1.(2022秋•湖滨区期中)下面四幅图中的比可以用3:2表示的是()A.B.C.D.解:A.1.5dm:12cm=15cm:12cm=15:12=5:4,所以本选项不符合;B.1.6米:1.2米=1.6:1.2=4:3,所以本选项不符合;C.6:4=3:2,所以本选项符合;D.20:60=1:3,所以本选项不符合。
故选:C。
2.(2022秋•增城区期中)六(1)班有学生45人,其中男、女人数比是()A.4:3 B.8:7 C.5:6 D.6:5解:A、3+4=7,7不是45的约数,此选项错误;B、7+8=15,15是45的约数,此选项正确;C、5+6=11,11不是45的约数,此选项错误;D、6+5=11,11不是45的约数,此选项错误。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
六年级上册数学 专业讲义
第六讲 比以及应用
基础知识
(一)
1、求比值的方法:用比的前项除以比的后项。
2、区分比和比值
比:表示两个数的倍数关系,可以写成比的形式,也可以用分数表示。
比值:相当于商,是一个数,是一个结果,可以是整数,分数,也可以是小数。
3、根据分数与除法的关系,两个数的比也可以写成分数形式。
例如3:2也可以写成32
,仍读作“3:2”。
4、 比和除法、分数的联系:
(二)、比的基本性质
1、根据比、除法、分数的关系:
商不变的性质:被除数和除数同时乘或除以相同的数(0除外),商不变。
分数的基本性质:分数的分子和分母同时乘或除以相同的数时(0除外),分数值不变。
比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),比值不变。
2、最简整数比:比的前项和后项都是整数,并且是互质数,这样的比就是最简整数比。
3、根据比的基本性质,可以把比化成最简单的整数比。
一、填一填
1、( ):30=30÷( )=53=) (24 =( )(小数)
2、一辆汽车5
1小时行驶20千米。
这辆汽车行驶的路程与所用时间的比是( ):( ),比值是( ),这个比值表示的意义是( )
3、2:4
1的比值是( ),把这个比化成最简单的整数比是( )。
4、明明和亮亮邮票的比是2∶5,亮亮有105张邮票,明明有( )张邮票。
5、从甲地到乙地,小李用了4时,小张用了3时。
小李和小张所用的时间的比是( ):( ),他们的速度比是( ):( )。
6、甲数除以乙数的商是3
2,那么甲数与乙数的最简整数比是( ):( )。
7、体育课上老师拿出40根跳绳,按3:2分给男、女生,男生分得这些跳绳的
) () (,女生分得( )根。
8.甲、乙两数的比是2:7,且它们的平均数是4.5,那么乙数是( )。
9、某班女生比男生多,则男生人数与女生人数比是( ):( );女生人数与全班人数的比是( ):( )。
10、甲、乙两篮各盛有35个鸡蛋。
如果从甲篮取出5个鸡蛋放入乙篮,那么乙篮与甲篮的鸡蛋个数的比是( ):( )。
11、下图中,大圆的半径等于小圆的直径,大圆的周长与小圆周长的比是( )。
大圆的面积与小圆面积的比是( )。
第11题 第12题
12、如上图,阴影部分的面积和平行四边形ABCD 面积的比是( )。
阴影部分的面积是5 平方厘米,那么平行四边形的面积是( )。
二、选一选
1、比的前项和后项( )。
A.都不能为0
B.都可以为0
C.前项可以为0
D.后项可以为0
2、学校买来380本图书,按一定的比分配给三个班,它们的比可能是( )。
A.2:3:5
B.2:3:4
C.1:2:3
3、一个三角形三个角的比是1:2:3,那么这个三角形是( )。
A.直角三角形
B.锐角三角形
C.钝角三角形
4、甲数是乙数的31,甲数和乙数的比是( )。
A.1:3 B.3:1 C. 31
5、下面各比中,比值是0.5的是( )。
A.5:2.5
B. 31:61
6、如右图,由三个等边三角形组成的梯形。
三角形与梯形周长的比是( )。
A. 1:3
B.3:5
C.3:7
7、60平方米的教室与4平方厘米的邮票。
它们的面积比是( )。
A.15:1
B.1500:1
C.150000:1
8、一根小棒锯成3段需要30秒,那么锯成6段需要( )秒.
A.60
B.75
C.90
三、判断题:
1、喜乐足球队以3∶0大胜厚木队,说明在特殊情况下,比的后项可以是0。
(
)
2、1米的54
等于4米的51。
( )
3、两个分数相除,商一定大于被除数。
( )
4、如果A 是B 的53
,那么B 是A 的35
倍。
( )
5、4÷(20+54)=4÷20+4÷54=5
1+5=551( ) 6、一个比的前项乘4
1,后项除以4,它的比值不变。
( ) 四、算一算
1.化简比。
(8分) 12 : 16 43 : 8
11 4.5 : 2.7 1.4﹕34 4.2:7/4 120:72 1/7:1/49 1:1/3
2.求比值:(8分)
36分:1小时 308立方厘米:2立方分米 183 : 85 4
3千米: 500 米 应用问题
1.按比例分配:把一个数量按照一定的比来进行分配。
这种方法通常叫做按比例分配。
2. 路程一定,速度比和时间比成反比。
(如:路程相同,速度比是4:5,时间比则为5:4)
工作总量一定,工作效率和工作时间成反比。
(如:工作总量相同,工作时间比是3:2,工作效率比则是2:3)
和比的应用题有关的概念
1、求每份数的方法
和÷份数和=每份数 相差数÷相差份数=每份数 部分数÷对应份数=每份数
2、图形求比的常见公式
长方体:(长+宽+高)的和=棱长和÷4 长方形: (长+宽)的和=周长÷2
3、相遇问题
速度和 = 路程÷相遇时间
五、解决问题
1、甲乙两地相距360千米,客车和货车同时从两地出发,相对而行,它们的速度比是5:4。
相遇时两车各行驶了多少千米?
2、甲、乙两数的平均数是56,甲与乙的比是4:3,甲、乙各是多少?
3、甲乙两个工程队共修路360米,甲乙两队所修的长度比是5 :4,甲队比乙队多修了多少米?
4、有两堆货物。
甲堆比乙堆多18吨。
甲堆与乙堆重量的比是9:5,两堆货物各有多少吨?
5、学校新购买了一批桌椅。
一套桌椅的价钱是90元,其中椅子的价钱和桌子的价钱的比是7:11,桌子和椅子的价钱分别是多少元?
6、配制一种消毒药,药液和水的比是1:50,要配制这种消毒药300千克,需要药液和水各多少千克?
7、配制一种消毒药,药液和水的比是1:50,现有药液300千克,需要加水多少千克?
8、配制一种消毒药,药液和水的比是1:50,现有水300千克,需要加药液多少千克?
9、甲乙两地相距450千米,客车和货车同时从两地出发,相对而行,3小时后相遇,它们的速度比是2:3。
客车和货车速度各是多少千米?
10、一个长方形周长是96cm,长与宽的比是5:7。
长方形面积是多少?
11. 用120厘米的铁丝做一个长方体的框架。
长、宽、高的比是3:2:1。
这个长方体的长、宽、高分别是多少?体积是多少?。
