测量数据平差处理表
测量误差与数据处理(3)

(3)根据改正数方程,可求得改正数为:
V P1ATK
0.5 1.0
1 1
4.8
1 2.4 2.4
0.5 1
4.8
(4)由此得高差的平差值为:
hˆ hV
即:
1.004 4.8
0.9992
1.504
2.4
103
1.5064
2.512 4.8
2.5072
h 1 0 .99 m , h 9 2 1 2 .50 m , h 6 3 2 4 .50 m 7
示例的解算
解:(1)此例n = 3,t = 2,故r = 1,列出 如下平差值条件方程:
H A h ˆ 1 h ˆ 2 h ˆ 3 H B 0
以代入上式,可得条件方程为:
v 1 v 2 v 3 ( H A h 1 h 2 h 3 H B ) 0
将已知高程和观测高差代入计算闭合差( 单位mm),然后用矩阵表示如下:
1. 根据平差的具体问题,确定条件方程的个 数,列出条件方程式,条件方程的个数等于 多余观测数r;
条件方程
➢平差值条件方程:
a1 Lˆ1
a 2 Lˆ 2
a n Lˆ n
a0
0
b1 Lˆ1
b 2 Lˆ 2
b n Lˆ n
b0
0
r1 Lˆ1
r2 Lˆ 2
rn Lˆ n
r0
0
➢改正数条件方程:
0 0 p
n
1
p1
0 1 0
p2
0 0 1
pn
基于闭合差条件的条件平差
❖条件平差原理 ➢ 由于高程控制网中存在r个多余观测,就会产生r 条件方程。
➢高程控制网平差归结为以r个条件方程为基础,根 据最小二乘法求出一组高差改正数。
水准平差计算步骤

水准平差计算步骤水准平差是一种测量方法,用于测量和确定不同点之间的高度差。
水准平差的步骤可以分为以下几个阶段:前方测量、后方处理、闭合检查、精度分析和结果调整。
第一阶段:前方测量1.确定测量线路和测量点:在测量区域内选择一条线路,并在此线路上选择起始点和终点作为测量点。
2.设置基准点:根据需要确定一个基准点,用于参考测量结果。
通常选择已知高程的点作为基准点。
3.进行观测:使用水准仪在起始点和终点之间进行测量。
观测时,需要记录下各点的观测高程和其他相关参数,如气温、大气压、仪器的仰角和方位角等。
4.进行中间高程点的观测:在起始点和终点之间选择若干个中间点,使用水准仪进行观测。
第二阶段:后方处理1.数据处理:对测量得到的数据进行处理,包括计算测点的高程差、观测误差等。
2.误差分析:通过统计学方法对数据进行误差分析,以确定各个观测点的可靠性和测量结果的精度。
3.编制水准平差表:将观测得到的高程数据整理成水准平差表,列出各点的观测高程、观测值的改正数和平差后的高程。
第三阶段:闭合检查1.进行闭合检查:通过计算起始点和终点的高程差,确定测量线路的闭合差。
闭合差越小,说明测量的准确性越高。
2.判断闭合差的合格与否:根据地理和测量精度要求,判断测量的闭合差是否符合要求。
如果闭合差超出了规定的误差范围,则需要对数据进行修正。
第四阶段:精度分析1.进行精度分析:根据测量数据和观测结果的误差范围,对测量线路的观测结果进行精度分析,评估测量的准确性。
第五阶段:结果调整1.进行结果调整:根据精度分析的结果,对测量结果进行调整,以满足测量的要求。
调整的方法可以采用最小二乘法或最小二乘平差法等。
2.重新校正观测数据:在进行结果调整后,需要对所有观测数据进行重新校正,以确保所有数据是正确和一致的。
总结:水准平差计算的步骤包括前方测量、后方处理、闭合检查、精度分析和结果调整。
每个步骤都有其特定的目的和方法,以确保测量结果的准确性和可靠性。
《测量平差》课程标准

《测量平差》课程标准一、课程简介《测量平差》是一门重要的测量学课程,旨在培养学生掌握测量平差的基本理论、方法和技能,为后续课程和实际工作奠定基础。
本课程涉及测量误差理论、最小二乘法原理、平差软件应用等方面,是一门理论与实践相结合的课程。
二、教学目标1. 掌握测量平差的基本概念、原理和方法;2. 能够运用最小二乘法原理进行测量数据平差处理;3. 学会使用平差软件进行数据处理;4. 培养学生解决实际问题的能力和创新思维。
三、教学内容与要求1. 基础知识:掌握测量误差的基本概念、性质和分类,了解测量误差的来源和影响;2. 平差基本原理:掌握最小二乘法原理,了解平差方法的选择和适用条件;3. 平差方法与应用:掌握各种测量平差方法的原理和应用,如普通平差、加权平差、随机模型平差等;4. 平差软件应用:学会使用平差软件进行数据处理,包括数据导入、参数设置、结果输出等;5. 实践环节:通过实验和实习,培养学生解决实际问题的能力和团队协作精神。
四、教学方法与手段1. 理论教学:采用多媒体教学,结合案例分析、课堂讨论等形式,激发学生的学习兴趣和积极性;2. 实验教学:安排实验课程,让学生动手操作平差软件,加深对理论知识的理解;3. 课外学习:鼓励学生自主学习,通过阅读文献、参加学术讲座等方式拓宽知识面;4. 考核方式:采用平时成绩、实验成绩和期末考试相结合的考核方式,注重对学生实际应用能力和创新思维的考核。
五、教材与参考书1. 教材:《测量平差原理与方法》;2. 参考书:《测量误差理论》。
六、课程评估1. 平时成绩:包括出勤率、作业完成情况、课堂表现等,占比30%;2. 实验成绩:包括实验报告、实验操作等,占比30%;3. 期末考试:采用闭卷考试形式,占比40%。
七、课程总结与展望通过本课程的学习,学生应该掌握了测量平差的基本理论、方法和技能,具备了解决实际问题的能力和创新思维。
为了进一步提高本课程的教学质量,可以采取以下措施:1. 加强实践教学,增加实习和实地测量的机会,让学生更好地将理论知识与实践相结合;2. 引入先进的教学手段和方法,如在线课程、虚拟仿真等,提高学生的学习效果;3. 鼓励学生参加学术活动和科研项目,拓宽学生的知识面和视野,培养学生的创新能力和团队协作精神。
房屋产权调查及测绘成果检查常用办法分析

市场调研与统计分析2随着当前城镇化的快速推进,房地产行业得到飞速发展,住房建设与居民的住房需求强劲,人们对房产面积尤其是公摊面积的疑问比较突出,本文主要结合房产面积测绘成果的生产、质量状况,依据国家现行有关房屋产权面积的测算、共有共用面积的分摊、功能区域的划定等文件和规范,对房产面积测算工作中的成果质量进行二次检查,从而确保房屋产权面积测算成果准确可靠。
房产面积测算成果的质量检查元素包括: 房产面积测量精度;测量方法、测量记录的正确性;房产面积技术依据的正确性、房屋边长测量数据处理、非实测数据采用的正确性、合理性、共有共用面积分摊、计算的正确性、房产面积测算基本要件收集的完整性、有效性等。
通常按照同一工程设计要求、同一房产项目、同一测量时间段等一致性条件分组成检验批次,从而确定检查的样本量,抽取的房产面积测量成果样本应具有代表性,检验批次中房屋主要为住宅楼时则应抽取住宅楼作为检验样本;检验批次中房屋主要为商住楼时则应抽取商住楼作为检验样本;检验批次中房屋主要为综合楼时则应抽取综合楼作为检验样本。
主要样本资料为房产面积测量报告,包含测量草图、测量记录表、测量数据平差处理表、面积计算表、计算说明及附件资料等。
1.房产面积测绘检验1.1数据精度检测作业检测过程中应先整体、后局部,先外后内,测点两端选取房屋的相同高度参考点,分层分户实地测量,每条检测边长测量两次以上,两次检测数据较差的符合以下要求:1.1.1使用测距仪两次检测读数之差绝对值不大于0.005m。
检测边长数据平差处理后用于计算房产面积。
1.1.2利用全站仪绘制房产分幅图的所采集的房屋各角点数据于测距仪数据的较差不大于0.025m。
在遇到房屋结构呈圆形、椭圆形、扇形、弓形、梯形、三角形、菱形等不规则形状时,必须利用全站仪测量房屋实体所采集的数据。
检测数据平差处理:a分层逐户绘制房屋权属界线;b对边长观测数据进行平差处理;c房屋外围长度数据与室内分段丈量数据较差在限差内时,以房屋外廓数据为准,分段丈量的数据按比例配赋得到边长平差值;d房产面积计算。
水准测量平差计算

水准测量平差计算
水准测量平差计算是水准测量中的一项重要工作,主要是对测量数据进行分析处理,消除误差和残差,以求得较为准确的高程结果。
具体步骤如下:
1. 建立观测方程
在水准测量中,设定起点高程为0,然后逐站向前观测,求出每个站点的高程。
建立每个站点高程的观测方程,包括自由高差和永久高差的影响。
2. 矩阵方程式
将所有观测方程进行矩阵变换,消除自由高差,得到纯高差矩阵方程组。
3. 固定高程点的影响
将所有观测方程加上固定高程点的影响,消除永久高差,得到纯高差矩阵方程组。
4. 最小二乘方法
利用最小二乘方法解出平差后的高差平差值,分别确定每个站点的高程。
5. 残差分析
对于每个观测方程都会有一个残差,其代表了实际测量值与计算值之间的差异。
进行残差分析,可发现数据中的误差规律和存在的误差来源,为后续的测量和处理提供参考和改进。
6. 高程精度分析
通过对整个水准测量的误差分析和精度分析,得出测量结果的可靠性和精度,为后续的工作提供指导和帮助。
如何进行正确的测绘数据处理

如何进行正确的测绘数据处理测绘数据处理是现代测绘工作中不可或缺的一环,它涉及到测量数据的收集、整理、分析和解释。
正确的测绘数据处理能够保证测绘结果的可靠性和准确性,对于城市规划、地理信息系统以及自然资源管理等领域具有重要意义。
本文将从数据收集、数据预处理、数据分析和数据解释等几个方面讨论如何进行正确的测绘数据处理。
一、数据收集数据收集是测绘数据处理的第一步,它包括现场测量、卫星遥感和地理信息系统等多种方法。
在进行数据收集时,要保证测量仪器的选择合理,使用标定过的仪器,并进行现场验证。
此外,还需要注意数据的采样密度和采样点的选择,尽量保证数据的全面性和代表性。
同时,要严格遵守测量规范,确保数据的质量和可靠性。
二、数据预处理数据预处理是为了减少测量误差和噪声,使数据更加准确和可靠。
在进行数据预处理时,首先要对原始数据进行检查和筛选,排除异常点和错误数据。
其次,对数据进行平差处理,以消除随机误差和系统误差。
平差处理可以采用最小二乘法或者其他合适的方法。
同时,还应对数据进行重复测量和相互校验,以提高数据的准确性和可靠性。
三、数据分析数据分析是对测绘数据进行统计和解释的过程,它可以帮助我们了解地理现象和空间分布规律。
在进行数据分析时,可以采用统计学和地理信息系统的方法。
统计学方法包括均值分析、标准差分析、相关分析等,用来描述和揭示数据之间的联系和规律。
地理信息系统方法则可以用来进行数据的空间分析和空间关系的探索,比如地图叠加分析、空间插值分析等。
通过数据分析,可以得出结论和推断,为后续的决策提供依据。
四、数据解释数据解释是对分析结果的描述和解释,目的是让非专业人士也能够理解和利用测绘数据。
在进行数据解释时,需要注意表达方式的简洁清晰,避免使用专业术语和复杂的公式。
可以借助图表、图像和动画等多媒体手段,直观地展示数据的结果和发现。
此外,还可以进行数据可视化,如热力图、散点图和流量图等,以便更好地传达数据的意义和信息。
测量平差的基本原理和计算方法

测量平差的基本原理和计算方法测量平差是测量学中一个重要的概念,它用于消除测量误差,提高测量精度。
本文将介绍测量平差的基本原理和计算方法。
一、测量平差的基本原理测量平差的基本原理是通过对测量数据进行处理,消除不可避免的误差,得到更为准确的结果。
在实际的测量过程中,由于各种因素的影响,测量结果往往不是完全准确的。
而通过平差可以将这些误差分布在测量要素上,使得整个测量结果更为合理。
平差的基本原理包括以下几个方面:1. 观测误差的性质:观测误差是服从一定的概率分布的,一般满足正态分布或其近似分布。
2. 绘图、观测和计算误差的连接性:测量平差将绘图误差、观测误差和计算误差联系在一起,通过适当的方法进行计算处理。
3. 误差的耦合性:测量过程中的各个要素之间存在着一定的关系,其误差也会相互影响。
通过平差可以将这些误差合理地分配和补偿。
二、测量平差的计算方法测量平差的计算方法有很多种,下面将介绍几种常见的方法。
1. 最小二乘法:最小二乘法是一种常用的测量平差方法,其基本思想是将误差的平方和最小化。
通过对误差进行建模和优化,可以得到一组最优解。
2. 最大似然估计法:最大似然估计法是一种基于统计原理的测量平差方法。
它根据观测数据的概率分布,选择出最具可能性的结果。
通过最大化似然函数,可以得到一组最优解。
3. 权值平差法:权值平差法是一种根据观测精度的大小,给予不同权值的平差方法。
通过给观测数据引入权值,可以使得精度高的数据在计算过程中起到更大的作用,从而提高整体的测量精度。
4. 卡尔曼滤波法:卡尔曼滤波法是一种基于状态估计的测量平差方法。
它通过建立状态模型和测量模型,利用观测数据进行误差修正,从而得到更加准确的结果。
三、测量平差的应用测量平差在实际应用中有着广泛的应用。
以下通过几个领域的案例来说明。
1. 地理测量:在地理测量中,测量平差常用于大地测量和地图制图。
通过平差可以消除地球曲率、大地水准面等因素的影响,得到更加准确的测量结果,提高地图的精度和真实度。
测绘数据处理-自由网平差

4
d就是网中必要的起算数据个数。且有:
二、秩亏自由网平差思路 为了求得未知参数的唯一确定解,除了遵循最小二乘准则外 ,还必须增加新的约束条件,从而达到求得唯一解的目的 。由于约束条件不同,秩亏自由网平差可分为如下几种情 况: (1)、经典自由网平差。它是在假设网中有d个必要起算数据 的条件下,求定未知参数的最佳估计。这种方法早就已为 人们所熟知。不难理解,该法的平差结果(未知参数X的 解及其协因数阵 )将随着假设的d个必要起算数据的不同 而不同,即随着已知点位置的改变而改变。
第七行划去,剩下的6三行u列的阵即为三维测边网平差时的附
加阵。 很明显,上述的附加阵G均未标准化,即只是满足了BG=0, 但尚未满足的条件。
2019/2/15
17
阵标准化
1、用原始阵 2、设 和 阵,求出相应的阵 ; 相应 中第i行主对角元素为gii,把原始阵
的第i行数据均乘以
即可得到标准化阵的相应数据;
2019/2/15
2
在最小二乘准则下,得其法方程为 (1-7-3) 其中N= PB,W= 。此时,系数阵N为满秩方阵,即 (1-7-4) 当平差网没有起算数据时,网中所有的点均为待定点。设未知 参数的个数为u,误差方程为 (1-7-5) 组成的法方程为
2019/2/15
det(N)
,N为非奇异阵,有唯一解,其解为
2019/2/15
26
点号
P1 P2 P3 P4
/m
2019/2/15
27
(1)计算网的重心点坐标
(2)计算以加权重心点坐标为坐标原点的各待定点的坐标值
点号
P1 P2 P3
/km
P4
2019/2/15
水准测量平差

·85·
1—7—1 1957 年中国东南部精密水准平差图(安徽省部分)
·86·
〔长(委)办 二、三 、四等 水准 平 差〕 长(委)办在完成宜昌以下沿江两岸,精密水准测量后进行 7 个水准路线环平差(简称
7 环平差),起算点为镇江 Y .R .C .BM 308’,属吴淞高程系。 中 国东 南 部精 密水 准 平差 后,长(委)办 又在 长 江流 域增 测 新线 ,省境 内 新布 设两 条 二
第二轮全国二等水准网平差,以 1986 年平差的一等水准成果为起算 数据,以一 等水 准路线环为单位,安徽省内及周边地区有 66、33、34、35、38 环参加平差。此项工作由国家 测绘局西安数据处理中心承担,至 1989 年还未结束。
·87·
〔安 徽省 水利 厅 勘测 设计 院 三、四 等水 准 平差〕 1959 年,安徽省水利厅勘测设计院对 前淮委、前水 利厅、长办、总 参测绘 局及本单 位 在省内所测的三、四等水准资料整理分析后,以国家二等水准路线环为单 位,用逐次 趋近 法进行整体平差。全省有 13 个二等环,由北向南依次编号,平差结果载于 1959 年 10 月编 印的《安徽省三、四等水准成果表》中,系 1956 年黄海高程。为了比较和应用方便,表内大 部分 点同 时载 有 1956 年 黄海 高程 和初 算高 程,表内 载有 安徽 省内 三、四等 水 准点 6367 个。 1978 年,该院会同阜阳、宿县地区水利局,整理了 1976 年前,各测量单位在淮北地区 布设的各级水准点,共 3421 个(包括接测水准的三角点),1978 年 6 月,以县为单位,编制 出版《淮 北地 区水 准 成果 表》。表 中绘 有 以县 为单 位 的水 准路 线 图,部 分点 载 有废 黄河 系 统 的高程值。其新、旧高程系统(1956 年黄海高程值减去废黄河高程值)的差值,在+0.100 ~+0.153 米之间,中数为+0.130 米。
测量平差中的常见计算方法及应用

测量平差中的常见计算方法及应用测量平差是地理信息系统中一个重要的环节,它通过收集地理数据并进行处理,来获取地表特征的准确位置和高程信息。
在测量平差的过程中,常用的计算方法和应用显得尤为重要。
本文将讨论测量平差中的常见计算方法及其应用。
一、误差分析与数据处理1.1 误差的来源与分类测量中的误差来源有很多,包括仪器误差、观测误差、人为误差等。
根据其性质和产生原因,可以将误差分为系统误差和随机误差。
系统误差是由于测量仪器或观测方法的固有问题而产生的,对结果产生一定的偏差;随机误差是无法消除的、不可预测的误差,其大小和方向无规律可寻。
1.2 误差传递和传播误差传递是指在测量平差过程中,由于各种误差的存在和相互作用,误差会在计算过程中传递和传播,最终影响到结果的精度。
为了准确评估测量结果的精度,需要对误差进行传递和传播的分析。
1.3 数据处理方法在测量平差中,常用的数据处理方法包括最小二乘法和加权最小二乘法。
最小二乘法是一种基于最小化残差平方和的原理,通过调整参数值来使得观测值与估计值之间的差距最小化。
加权最小二乘法则是在最小二乘法的基础上引入权重因子,使得对于不同的观测值给予不同的重要性。
二、平差计算方法2.1 高程平差高程平差是测量平差中的一个重要部分,其目的是确定地表特征的精确高程。
在高程平差中,常用的计算方法有水准网平差和高程差平差。
水准网平差是利用水准仪在测定不同地点的高程值后,通过测量点之间的高程差来确定各个点的高程。
高程差平差则是通过观测两个点之间的高程差来计算该两点的高程。
2.2 水平平差水平平差是通过测量点之间的方位角和水平角来确定点的坐标位置。
常见的水平平差方法有导线平差和多边形平差。
导线平差是通过在地表上拉设一定长度的导线并进行测量,根据导线引起的方位和水平角观测值,来确定测量点的坐标。
多边形平差则是根据多个导线或边界线的方位角和水平角来计算各个点的坐标。
三、平差的应用3.1 地图制图在地图制图中,平差技术可以用来确定地物的精确位置和形状。
DNA03电子水准仪线路测量步骤及平差表

使用徕卡DNA03电子水准仪线路测量步骤及平差表1、将仪器架设完毕,整平,开机,按程序键“PROG”进入程序,选择“3 线路测量”然后回车,进入线路测量页面;2、进入线路测量后选择第一项“作业”,按回车键进入,按左右方向键可以选择已有的作业,或者将光标移动至下方“增加”处,按回车添加一个作业,输入作业名回车;3.、返回线路测量后进入第二项“线路”,输入线路名称,第二行处选择测量方法(aBFFB:二等水准要求,可根据实际要求选取相应测量方法),第三行输入起始点点号,第四行为高程,输入完成后按回车确定(线路名称不能与已有线路名相同);4、返回线路测量后选择第三项“设置限差”5、按回车进入限差数据输入界面。
翻译如下:[输入限差]1/2累计视距差 3.00 m最大视距50.00 m 最大标尺读数 2.5000 m 最小标尺读数0.5000 m 最大测站高差之差0.0003 m翻译如下:[输入限差]2/2前、后视同一标尺两次读数的最大差值0.00020 m单站前后视视距差最大值 1.00 m最短视距0.00 m以上限差根据测量水准要求,自行设置6、选择第四项“开始”,进入线路测量,首先确认设置信息,没问题后按回车键进入测量。
7、此时进入测量页面,修改“PtID:A1”为控制点,此处以E033为例同时修改“H:0.0000m”为E033的控制高程。
注意⇑指向“BFFB FBBF”中的B,代表后视。
8、测量过程中若遇到超限情况时可选择“重测”,进行本站的重新测量。
9、线路测量完成后,数据是储存在仪器中的,此时可以用数据线导出数据,本文介绍将数据导入IC卡,通过读卡器读取数据到水准处理软件上。
按“DATA”健进入数据管理器查看数据修改、创建、查看和删除作业数据、测量成果、已知点数据和编码表。
初始内存删除全部存储器、单个作业或单个存储区(已知点、测量成果)内存信息作业信息和存贮状况信息。
数据输出把测量数据、某项作业的已知点数据通过接口从内存输出到PC 卡。
基于Excel的条件平差解算

在测量平差计算中 , 涉及非常多的矩阵的运 算 ,计算工作量大且容易出错 , 为此 , 测绘工作者 (软件编制人员 ) 利用不同编程语言编制了各式各 样的测量平差计算软件 。这些软件一般都是整装 式“ 傻瓜化 ” 的操作 — — — 输入起始数据 ,输出计算结 果 ,具有效率高 、 结果准确的特点 ,其缺点在于计算 原理 、 计算公式 、 计算步骤 、 计算方法隐含 (汪祖民 , 2001 ) 。探讨利用电子表格 Excel 2003 强大的数据 计算及处理功能 , 解算测量平差的方法 , 该方法具 有计算步骤 、 计算方法实时 、 可视化 , 且与计算原 理、 计算公式紧密结合的解题式特点 , 尤其适合测 量初学者在解决测量实践中平差计算问题的同时 , 又掌握测量平差基本原理 。
W
T
- 1 0
ห้องสมุดไป่ตู้
0
- 1
0
- 1
0 0
- 1
0 0 1
0 0
0 0 0 0
0 0 0
的单元格中显示计算结果 。 ( 5 )计算待定点高程的最或是值 HP i — — — 先后 选定单元格 AB10 →AB17, 在公式编辑栏中分别输 入各待定点高程最或是值的计算公式 ,如选定单元 格 AB10,在公式栏输入公式 fx “ = S6 - Y8 ” , 回车 即 HP1 = 10. 207 7 m。计算结果为 :
W = AL + A
( 2) ( 3) ( 4) ( 5) ( 6)
改正数方程
V = P A K
-1 T
法方程
N K +W = 0 N = AP A
-1 T
平差值
L = L +V
^
1. 2 精度评定公式
测量数据以及平差结果
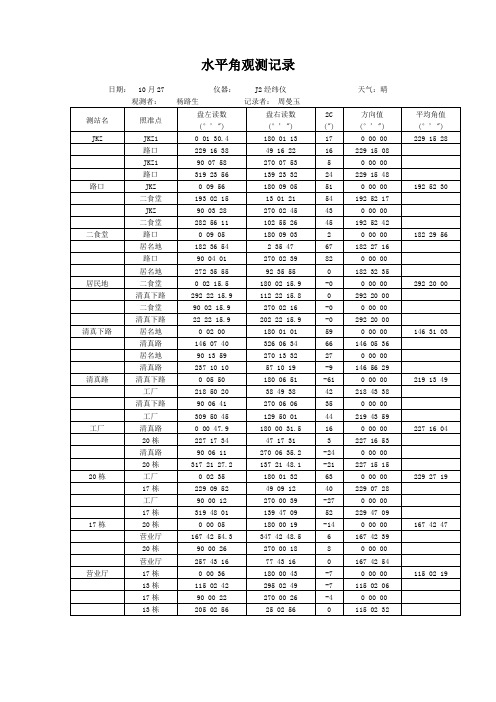
日期: 10月27 仪器: J2经纬仪天气:晴观测者:杨路生记录者:周曼玉测站名照准点盘左读数(°' ")盘右读数(°' ")2C(")方向值(°' ")平均角值(°' ")JKZ JKZ1 0 01 30.4 180 01 13 17 0 00 00 229 15 28 路口229 16 38 49 16 22 16 229 15 08JKZ1 90 07 58 270 07 53 5 0 00 00路口319 23 56 139 23 32 24 229 15 48路口JKZ 0 09 56 180 09 05 51 0 00 00 192 52 30 二食堂193 02 15 13 01 21 54 192 52 17JKZ 90 03 28 270 02 45 43 0 00 00二食堂282 56 11 102 55 26 45 192 52 42二食堂路口0 09 05 180 09 03 2 0 00 00 182 29 56 居名地182 36 54 2 35 47 67 182 27 16路口90 04 01 270 02 39 82 0 00 00居名地272 35 55 92 35 55 0 182 32 35居民地二食堂0 02 15.5 180 02 15.9 -0 0 00 00 292 20 00 清真下路292 22 15.9 112 22 15.8 0 292 20 00二食堂90 02 15.9 270 02 16 -0 0 00 00清真下路22 22 15.9 202 22 15.9 -0 292 20 00清真下路居名地0 02 00 180 01 01 59 0 00 00 146 31 03 清真路146 07 40 326 06 34 66 146 05 36居名地90 13 59 270 13 32 27 0 00 00清真路237 10 10 57 10 19 -9 146 56 29清真路清真下路0 05 50 180 06 51 -61 0 00 00 219 13 49 工厂218 50 20 38 49 38 42 218 43 38清真下路90 06 41 270 06 06 35 0 00 00工厂309 50 45 129 50 01 44 219 43 59工厂清真路0 00 47.9 180 00 31.5 16 0 00 00 227 16 04 20栋227 17 34 47 17 31 3 227 16 53清真路90 06 11 270 06 35.2 -24 0 00 0020栋317 21 27.2 137 21 48.1 -21 227 15 1520栋工厂0 02 35 180 01 32 63 0 00 00 229 27 19 17栋229 09 52 49 09 12 40 229 07 28工厂90 00 12 270 00 39 -27 0 00 0017栋319 48 01 139 47 09 52 229 47 0917栋20栋0 00 05 180 00 19 -14 0 00 00 167 42 47 营业厅167 42 54.3 347 42 48.5 6 167 42 3920栋90 00 26 270 00 18 8 0 00 00营业厅257 43 16 77 43 16 0 167 42 54营业厅17栋0 00 36 180 00 43 -7 0 00 00 115 02 19 13栋115 02 42 295 02 49 -7 115 02 0617栋90 00 22 270 00 26 -4 0 00 0013栋205 02 56 25 02 56 0 115 02 32工程名称:仪器:天气:观测者:记录者:日期:测站名照准点盘左读数(°' ")盘右读数(°' ")2C(")方向值(°' ")平均角值(°' ")13栋营业厅0 00 01 180 00 05 -4 0 00 00 247 33 03 JKZ 247 33 02 67 33 10 -8 247 33 03营业厅90 00 08 270 00 02 6 0 00 00JKZ 337 33 05 157 33 13 -8 247 33 04JKZ2 13栋0 00 16 180 00 23 -7 0 00 00 183 37 27 JKZ1 183 37 42 3 37 52.5 -10 183 37 2813栋90 00 29.5 270 00 32 -3 0 00 00JKZ1 273 37 58.5 93 37 56.5 2 183 37 27JKZ1 JKZ2 0 00 26 180 00 32.5 -7 0 00 00 253 22 14 JKZ 253 22 52 73 22 50 2 253 22 22JKZ2 90 00 28 270 00 32 -4 0 00 00JKZ 343 22 49 163 22 22 27 253 22 05水准观测记录工程名称:仪器:水准仪天气:晴观测者:田野记录者:薛丽 10月27测站编号后视点名前视点名后尺下丝后尺上丝后视距前尺下丝前尺上丝前视距视距差d∑d(m)测段长方向及尺号水准尺读数K + 黑- 红( mm )高差中数黑面( mm )红面( mm )1 1 1505 0959 0.3 后1610 6297 +02 1711 1162 0.3 前1060 5850 -320.6 20.3 40.9 后-前+550 +447 +3 +54852 2 1953 0780 0.2 后2036 6821 +23 2117 0942 0.5 前0862 5550 -116.4 16.2 32.6 后-前+1174 +1271 +3 +117253 3 2068 1236 -0.2 后2144 6832 -14 2221 1391 0.3 前1313 6100 +015.3 15.5 30.8 后-前+831 +732 -1 +83154 4 2125 0100 1.0 后2392 7078 +15 2460 0425 1.3 前0260 4950 -333.5 32.5 66.0 后-前+2132 +2128 +4 +213005 5 2500 0219 -0.3 后2659 7348 -26 2818 0540 1.0 前0378 5167 -231.8 32.1 63.9 后-前+2281 +2181 +0 +228106 6 1701 0507 0.6 后1826 6615 -27 1950 0750 1.6 前0627 5315 -124.9 24.3 49.2 后-前+1199 +1300 -1 +119957 7 1061 1044 0.3 后1205 5896 -48 1345 1325 1.9 前1184 5876 -528.4 28.1 56.5 后-前+21 +20 +1 +2058 8 0372 1237 -0.2 后0512 5299 +09 0652 1519 1.7 前1378 6157 +828.0 28.2 56.2 后-前-866 -858 -8 -86209 9 2285 0655 0.5 后2565 7243 +910 2835 1200 2.2 前0925 5715 -355.0 54.5 109.5 后-前+1640 +1528 +12 +1634010 10 1063 1063 0.9 后1292 5979 +011 1510 1501 3.1 前1290 5978 -144.7 43.8 88.5 后-前 +2 +1 +1 +1511 11 0930 1320 -0.4 后1140 5819 +812 1359 1753 2.7 前1538 6325 +042.9 43.3 86.2 后-前-398 -506 +8 -402012 12 1580 0032 0.5 后1787 6573 +113 1993 0440 3.2 前0238 4925 +041.3 40.8 82.1 后-前+1549 +1648 +1 +1548513 13 1233 2472 0.4 后1400 6086 +114 1565 2800 3.6 前2635 7427 -533.2 32.8 66.0 后-前-1235 -1341 +6 -12380水准观测记录工程名称:仪器:水准仪天气:晴观测者:田野记录者:薛丽 10月27测站编号后视点名前视点名后尺下丝后尺上丝后视距前尺下丝前尺上丝前视距视距差d∑d(m)测段长方向及尺号水准尺读数K + 黑- 红( mm )高差中数黑面( mm )红面( mm )14 14 0122 1471 0.1 后0255 5040 +215 0386 1734 3.7 前1601 6290 -226.4 26.3 52.7 后-前-1346 -1250 +4 -1348015 15 0787 2158 0.3 后1097 5780 +416 1400 2768 4.0 前2460 7250 -361.3 61.0 122.3 后-前-1363 -1470 +7 -1366516 16 0245 1899 0.3 后0457 5240 +417 0669 2320 4.3 前2110 6798 -142.4 42.1 84.5 后-前-1653 -1558 +5 -1655517 17 1369 1360 -0.5 后1501 6287 +118 1639 1635 3.8 前1499 6191 -527.0 27.5 54.5 后-前 +2 +96 +6 -1018 18 0058 2378 0.0 后0328 5006 +919 0598 2918 3.8 前2648 7326 +954.0 54.0 108.0 后-前-2320 -2320 +0 -2320019 19 0380 1960 -0.5 后0538 5224 +120 0695 2280 3.3 前2123 6908 +231.5 32.0 63.5 后-前-1585 -1684 -1 -1584520 20 0475 1075 0.0 后0737 5525 -121 1000 1600 3.3 前1340 6022 +552.5 52.5 105.0 后-前-603 -497 -6 -600021 21 1188 1060 0.0 后1375 6060 +222 1561 1433 3.3 前1250 6036 +137.3 37.3 74.6 后-前+125 +24 +1 +1245后前后-前后前后-前后前后-前后前后-前后前后-前导线图导线严密平差成果表控制测量实习心得体会10测绘二班测量第二小组成员:薛丽,周曼玉,刘锟铭,杨路生,江晶晶熊敏,杨书佳,徐煌达,田野通过一天的控制测量实习,巩固和加深了我们从课堂上所学的理论知识,对控制测量有了更深的认识。
水准测量平差计算表(有公式)
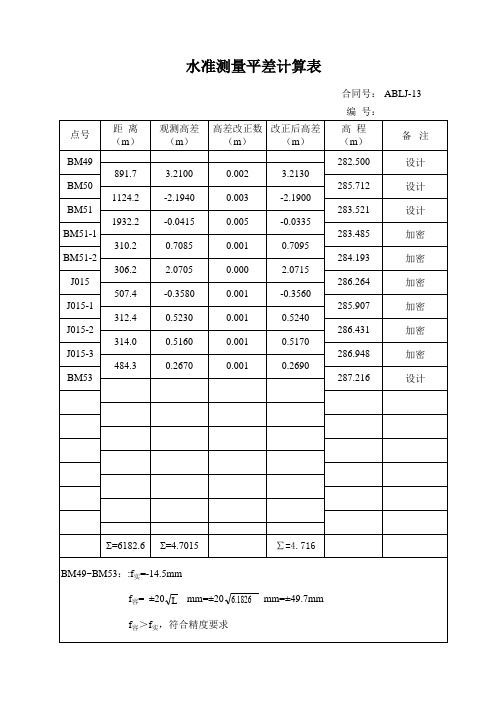
工程测量实训数据表

174°23′10″
174°22′56″
4
174°22′57″
右
6
180°00′01″
174°23′10″
4
354°23′11″
5
左
6
90°00′04″
174°23′00″
174°22′47″
4
264°23′04″
右
6
270°00′13″
174°22′34″
4
84°22′47″
4
-0.286
-2
-0.187
+2.6
+3.9
5
5—6
1243
1460
后视K1
1127
5913
+1
1009
1195
前视K2
1329
6015
+1
23.4
26.5
高差
-0.202
-0.102
0
-0.202
-3.1
+0.8
6
6—7
1261
1479
后视K2
1140
5829
-2
1021
1231
前视K1
1355
6141
0
91°07′12″
32601.403
56131.166
6
330°44′54″
48.88
42.65
0
42.65
-23.89
0
-23.89
7
177°25′21″
0
177°25′21″
32644.053
56107.276
7
333°19′33″
39.56
35.35
测量平差方法及误差分析技巧

测量平差方法及误差分析技巧引言:测量平差在各个领域中都起到了至关重要的作用,无论是土地测量、工程测量还是地理测量都离不开精确的测量平差。
本文将介绍测量平差的基本原理、方法以及误差分析技巧,以帮助读者更好地理解和应用这些知识。
一、测量平差的基本原理1.1 测量平差的定义测量平差是指在测量中,通过对测量数据进行处理和分析,用数学方法将观测值修正为比较可靠的数值,并确定其精度和可靠度的过程。
1.2 测量平差的基本原理测量平差的基本原理是以观测数据为基础,通过适当的计算和修正方法,使测量结果达到满足一定精度要求的条件。
二、测量平差的方法2.1 误差的分类误差是指由于种种原因导致观测值与真值之间的差异。
根据产生误差的原因,可将误差分为系统误差和随机误差两类。
2.2 测量平差的方法2.2.1 最小二乘法最小二乘法是一种常用的测量平差方法,其基本原理是通过构建误差方程,使误差的平方和最小化,从而得到最优的修正数值。
2.2.2 加权最小二乘法加权最小二乘法是在最小二乘法的基础上,引入权重因子,对观测值进行加权处理,以更好地反映各个观测值的可靠性。
2.2.3 置信椭圆法置信椭圆法是一种通过误差椭圆的几何性质,结合观测弥散矩阵,进行测量平差的方法。
通过确定椭圆的长轴、短轴和倾斜角度,可对误差进行合理的修正和分析。
三、误差分析技巧3.1 误差的传递规律误差在测量过程中具有传递性,即观测结果的误差会随着计算过程的推进而逐渐增大。
因此,在进行误差分析时,需要考虑不同环节中误差的传递规律,以准确评估测量结果的可靠性。
3.2 概略误差与精确误差概略误差是指由于设备精度、人为操作等因素导致的测量误差,通过一些常见的公式和方法可以进行较为粗略的估计。
精确误差是在概略误差的基础上,通过更加精细的计算和分析得到的误差值,更贴近实际测量结果的误差。
3.3 误差理论和误差估计误差理论是关于误差发生的规律的理论体系,包括误差分类、误差分布等。
