圆的练习题(阴影部分的面积周长20题)
《圆的周长、面积》练习题加答案(完整版)

《圆的周长、面积》练习题一.选择题(共10题,共20分)1.把一个圆的半径按n:1的比放大,放大后与放大前圆的面积比是()。
A.n:1B.2n:1C.:1 D.:22.圆的面积与它半径成()比例。
A.正B.反C.不成3.强强要在方格纸上画一个圆,要求点(1,4)、(3,2)、(3,6)恰好在圆周上(如图),这个圆的圆心应该在()上。
A.(3,5)B.(4,4)C.(3,4)D.(5,4)4.圆的周长是它的半径的()倍。
A.πB.2πC.3.14D.6.285.画圆时,圆的周长为15.7cm,那么圆规两脚间的距离为()。
A.2.5cmB.5cmC.15.7cm6.一个圆的直径与一个正方形的边长相等,比较它们的面积()。
A.相等B.圆面积大C.正方形面积大D.不能确定7.如图。
以大圆的半径为直径画一小圆。
大圆的周长是小圆周长的()倍。
A.2B.4C.68.一个直径为2厘米的半圆面,它的周长是()厘米。
A.6.28B.3.14C.4.14D.5.149.在同圆或等圆中,扇形的大小和()有关。
A.直径B.半径C.圆心角10.一个圆的半径扩大2倍,那么面积和周长()。
A.面积和周长扩大2倍B.面积扩大4倍,周长扩大2倍 C.周长扩大4倍,面积扩大2倍二.判断题(共10题,共20分)1.如果圆的半径扩大2倍,那么它的周长扩大6倍,它的面积扩大9倍。
()2.把一张圆形纸片从不同方向折叠,折痕都经过圆心。
()3.任何一个圆的周长都是它直径长度的π倍。
()4.圆周率π=3.14。
()5.有两个面积相等的圆,他们的周长也一定相等。
()6.通过圆心的线段是半径。
()7.在一个圆内,剪去一个扇形后,剩下的部分仍是扇形。
()8.半圆的面积是圆面积的一半,半圆的周长也是圆周长的一半。
()9.量角器是把半圆分成180份制成的。
()10.周长相等的长方形正方形和圆,正方形的面积最大。
()三.填空题(共10题,共17分)1.把一个圆平均分成若干(偶数)等份,剪开后可以拼成一个近似的(),这个长方形的长相当于圆的(),宽相当于圆的()。
六年级上册数学常考易错应用题《求圆的阴影部分面积》专项训练

六年级上册数学常考易错应用题《求圆的阴影部分面积》专项训练班级:姓名:亲爱的同学,在做练习的时候一定要认真审题,完成题目后,记得养成认真检查的好习惯。
祝你轻松完成本次练习!【记录卡】亲爱的同学,在完成本专项练习后,你收获了什么?掌握了哪些新本领呢?在这里记录一下你的收获吧!年月日1.计算下面图形的阴影部分面积。
(1)2.求阴影部分的面积(单位:厘米)3.求阴影部分的周长和面积。
(1)(2)4.一个圆环,内圆半径是6厘米,外圆半径是10厘米。
这个圆环的面积是多少平方厘米?5.求下图阴影的面积。
(单位:分米)6.按要求计算。
计算下面图形的周长。
①②7.求阴影部分的面积或周长(π取3.14)。
(1)求阴影部分的面积。
(2)求阴影部分的周长。
8.如图中圆的半径为4分米,求图中阴影部分的面积。
9.求下列图中阴影部分的面积(单位:cm)(1)(2)(3)10.求下面图形中阴影部分的面积。
(1)11.求下列阴影部分的面积。
(1)(2)12.如图,一个长方形中有两个一样的扇形(空白部分),计算下图中阴影部分的周长和面积。
13.求下列各图中阴影部分的面积。
(单位:cm)(1)(2)14.求阴影部分的面积。
(1)(2)15.求阴影部分的面积。
16.求下面各圆的面积(1)(2)17.求下图中阴影部分的面积(单位:cm) (1)(2)18.求下面各图形中阴影部分的面积。
(单位:cm)(1)(2)19.请在如图中画一个最大的圆,并求出这个圆的面积是多少?20.求下面图形中阴影部分的周长和面积。
(1)(2)21.下面是一个圆平均分成若干份后拼成的一个近似于长方形的图形,求该圆的面积。
(单位:cm)22.如图,半圆的面积是25.12平方厘米,求阴影区域的面积。
23.已知梯形的上底为10厘米,下底为4厘米,求阴影部分的面积。
24.求阴影部分的面积。
25.已知下图中的圆的半径是2cm,求阴影部分的面积。
26.求下面各图中阴影部分的面积(1)(2)27.求阴影部分的面积。
小学六年级数学求阴影面积与周长专项练习试题

小学六年级数学求阴影面积与周长专项练习试题以下是小学六年级数学求阴影面积与周长专项练的题目:1.求阴影部分的面积(单位:厘米)。
2.已知正方形面积为7平方厘米,求阴影部分的面积(单位:厘米)。
3.求图中阴影部分的面积(单位:厘米)。
4.求阴影部分的面积(单位:厘米)。
5.求阴影部分的面积(单位:厘米)。
6.已知小圆半径为2厘米,大圆半径是小圆的3倍,问空白部分甲比乙的面积多多少厘米。
7.求阴影部分的面积(单位:厘米)。
8.求阴影部分的面积(单位:厘米)。
9.求阴影部分的面积(单位:厘米)。
10.求阴影部分的面积(单位:厘米)。
11.求阴影部分的面积(单位:厘米)。
12.求阴影部分的面积(单位:厘米)。
13.求阴影部分的面积(单位:厘米)。
14.求阴影部分的面积(单位:厘米)。
15.已知直角三角形面积为12平方厘米,求阴影部分的面积。
16.求阴影部分的面积(单位:厘米)。
17.图中圆的半径为5厘米,求阴影部分的面积(单位:厘米)。
18.在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的周长。
19.正方形边长为2厘米,求阴影部分的面积。
20.正方形ABCD的面积为36平方厘米,求阴影部分的面积。
21.四个圆的半径都是1厘米,求阴影部分的面积。
22.正方形边长为8厘米,求阴影部分的面积。
23.图中的4个圆的圆心是正方形的4个顶点,它们的公共点是该正方形的中心,如果每个圆的半径都是1厘米,那么阴影部分的面积是多少?24.有8个半径为1厘米的小圆,用它们的圆周的一部分连成一个花瓣图形,图中的黑点是这些圆的圆心。
如果圆周π率取3.1416,那么花瓣图形的面积是多少平方厘米?25.四个扇形的半径相等,求阴影部分的面积(单位:厘米)。
26.等腰直角三角形ABC和四分之一圆DEB,AB=5厘米,BE=2厘米,求图中阴影部分的面积。
27.正方形ABCD的对角线AC=2厘米,扇形ACB是以AC为直径的半圆,扇形DAC是以D为圆心,AD为半径的圆的一部分,求阴影部分的面积。
小学六年级圆_阴影部分面积(含答案)

求阴影部分面积例1、求阴影部分得面积、(单位:厘米)ﻫ解:这就是最基本得方法:圆面积减去等腰直角三角形得面积,×-2×1=1.14(平方厘米)ﻫ例2、正方形面积就是7平方厘米,求阴影部分得面积。
(单位:厘米)解:这也就是一种最基本得方法用正方形得面积减去圆得面积。
设圆得半径为r,因为正方形得面积为7平方厘米,所以=7,ﻫ所以阴影部分得面积为:7-=7—×7=1、505平方厘米例3、求图中阴影部分得面积、(单位:厘米)解:最基本得方法之一。
用四个圆组成一个圆,用正方形得面积减去圆得面积,所以阴影部分得面积:2×2-π=0.86平方厘米。
ﻫﻫ例4、求阴影部分得面积。
(单位:厘米)ﻫ解:同上,正方形面积减去圆面积,16-π()=16—4πﻫ=3。
44平方厘米ﻫ例5。
求阴影部分得面积。
(单位:厘米)ﻫ解:这就是一个用最常用得方法解最常见得题,为方便起见,ﻫ我们把阴影部分得每一个小部分称为“叶形",就是用两个圆减去一个正方形,ﻫπ()×2-16=8π-16=9.12平方厘米ﻫ另外:此题还可以瞧成就是1题中阴影部分得8倍。
例6、如图:已知小圆半径为2厘米,大圆半径就是小圆得3倍,问:空白部分甲比乙得面积多多少厘米?ﻫ解:两个空白部分面积之差就就是两圆面积之差(全加上阴影部分)ﻫπ-π()=100。
48平方厘米ﻫ(注:这与两个圆就是否相交、交得情况如何无关)例7、求阴影部分得面积。
(单位:厘米)解:正方形面积可用(对角线长×对角线长÷2,求)ﻫ正方形面积为:5×5÷2=12。
5所以阴影面积为:π÷4-12.5=7。
125平方厘米(注:以上几个题都可以直接用图形得差来求,无需割、补、增、减变形) 例8。
求阴影部分得面积。
(单位:厘米)解:右面正方形上部阴影部分得面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3、14平方厘米例9、求阴影部分得面积。
小学数学六年级圆的阴影面积与周长100道经典题型

小学数学六年级圆的阴影面积与周长100道经典题型六年级圆的阴影面积与周长100道经典题型1.求阴影部分的面积。
(单位:厘米)2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)3.求图中阴影部分的面积。
(单位:厘米)4.求阴影部分的面积。
(单位:厘米)5.求阴影部分的面积。
(单位:厘米)6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?7.求阴影部分的面积。
(单位:厘米)8.求阴影部分的面积。
(单位:厘米)9.求阴影部分的面积。
(单位:厘米)10.求阴影部分的面积。
(单位:厘米)11.求阴影部分的面积。
(单位:厘米)12.求阴影部分的面积。
(单位:厘米)13.求阴影部分的面积。
(单位:厘米)14.求阴影部分的面积。
(单位:厘米)15.已知直角三角形面积是12平方厘米,求阴影部分的面积。
16.求阴影部分的面积。
(单位:厘米)17.图中圆的半径为5厘米,求阴影部分的面积。
(单位:厘米)18.求阴影部分的面积。
(单位:厘米)19.正方形边长为2厘米,求阴影部分的面积。
20.如图,正方形ABCD的面积是36平方厘米,求阴影部分的面积。
21.如图,正方形边长为8厘米,求阴影部分的面积。
22.求阴影部分的面积。
23.求阴影部分的周长与面积。
24.求阴影部分的周长与面积。
25.求阴影部分的周长与面积。
26.求阴影部分的周长与面积。
27.求阴影部分的周长与面积。
28.求阴影部分的周长与面积。
29.求阴影部分的面积。
30.求阴影部分的面积。
31.正方形面积是7平方厘米,求阴影部分的面积和周长。
(单位:厘米)32.求图中阴影部分的面积和周长。
(单位:厘米)33.求图中阴影部分的面积和周长。
(单位:厘米)34.求图中阴影部分的面积和周长。
(单位:厘米)35.求图中阴影部分的面积和周长。
(单位:厘米)36.求图中阴影部分的面积和周长。
(单位:厘米)37.求图中阴影部分的面积和周长。
小学六年级数学求阴影面积与周长专项练习
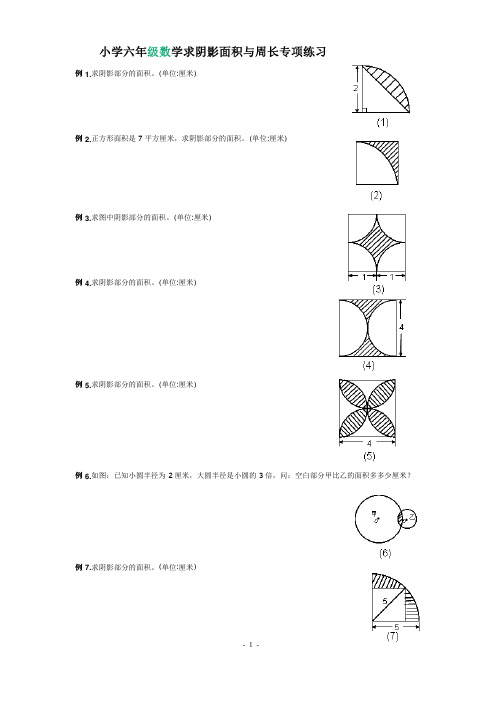
- 1 - 小学六年级数学求阴影面积与周长专项练习例1.求阴影部分的面积。
(单位:厘米) 例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米) 例3.求图中阴影部分的面积。
(单位:厘米) 例4.求阴影部分的面积。
(单位:厘米) 例5.求阴影部分的面积。
(单位:厘米) 例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?例7.求阴影部分的面积。
(单位:厘米) - 2 - 例9.求阴影部分的面积。
(单位:厘米) 例10.求阴影部分的面积。
(单位:厘米) 例11.求阴影部分的面积。
(单位:厘米) 例12.求阴影部分的面积。
(单位:厘米) 例13.求阴影部分的面积。
(单位:厘米) - 3 - 例15.已知直角三角形面积是12平方厘米,求阴影部分的面积。
\ 例16.求阴影部分的面积。
(单位:厘米) 例17.图中圆的半径为5厘米,求阴影部分的面积。
(单位:厘米) 例18.如图,在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的求阴影部分的周长周长。
例19.正方形边长为2厘米,求阴影部分的面积。
- 4 - 20.如图,正方形ABCD 的面积是36平方厘米,求平方厘米,求阴影阴影部分的面积。
例21.图中四个圆的半径都是1厘米,求阴影部分的面积。
厘米,求阴影部分的面积。
例22. 如图,正方形边长为8厘米,求阴影部分的面积。
厘米,求阴影部分的面积。
例23.图中的4个圆的圆心是正方形的4个顶点,,它们的公共点是该正方形的中心,如果每个圆的半径都是1厘米,那么阴影部分的面积是多少?例24.如图,有8个半径为1厘米的小圆,用他们的圆周的一部分连成一个花瓣图形,图中的黑点是这些圆的圆心。
如果圆周π率取3.1416,那么花瓣图形的的面积是多少平方厘米?CBD=,问:阴影部分甲比乙面积小多少?例30.如图,三角形ABC 是直角三角形,阴影部分甲比阴影部分乙面积大28平方厘米,AB=40厘米。
7.25《圆阴影部分的面积专题练习30题》六年级上册数学

六年级上册阴影部分的面积(30道题)1.求阴影部分的面积。
(单位:厘米)2、求阴影部分的面积。
3、如图,平行四边形的高是6厘米,面积是54平方厘米,求阴影三角形的面积。
4、下图是一个半圆形,已知AB=10厘米,阴影部分的面积为24.25平方厘米,求图形中三角形的高。
5、如图,一个长方形长是10cm,宽是4cm,以A点和C点为圆心各画一个扇形,求画中阴影部分的面积是多少平方厘米?6、如图,正方形的面积是10平方厘米,求圆的面积。
7、如图,梯形的面积是60平方厘米,求阴影部分的面积。
8、如图,已知半圆的面积是31.4平方厘米,求长方形的面积。
9、求下图中阴影部分的面积和周长。
(单位:厘米)10、如图,求阴影部分①比阴影部分②的面积少多少?(单位:厘米)11、求阴影部分的面积。
12、求下图阴影部分的面积。
13、求图中阴影部分的面积。
(单位:厘米)14、求阴影部分的面积。
(单位:厘米)15、求下图阴影部分的面积。
(单位:厘米)16、求阴影部分的面积。
(单位:分米)17.如图,直角三角形ABC三条边分别是3cm,4cm,5cm,分别以三边为直径画半圆,求阴影部分的面积。
18.如图,长方形的周长是24cm,求阴影部分的面积。
19.求阴影部分的面积。
(单位:分米)20、求下图中阴影部分的面积和周长。
21、求下图中阴影部分的周长。
(单位:厘米)22、下图中的等边三角形的边长是10厘米,求阴影部分的周长与面积。
23、求下图中阴影部分的面积。
24、求下图中阴影部分的面积。
25、求下图中阴影部分的面积。
26、求图中阴影部分的面积。
27.图中阴影部分的面积是40平方厘米。
求环形的面积。
28、下图中,等腰直角三角形的面积是10平方厘米。
阴影部分的面积是多少平方厘米?29、求下图中阴影部分的面积。
30、求阴影部分的面积。
(单位:厘米)六年级阴影部分的面积(答案解析)1.求阴影部分的面积。
(单位:厘米)解:割补后如右图,易知,阴影部分面积为一个梯形。
阴影部分求面积及周长(含答案)

目标:通过专题复习,加强学生对于图形而积计算的灵活运用。
并加深对而积和周长概念的理解和区分。
而 积求解大致分为以下几类:重难点:观察图形的特点,根拯图形特点选择合适的方法求解图形的而积。
能灵活运用所学过的基本的平而 图形的面积求阴影部分的面积匚Iδl与求阴影部分面积专题练习(20)例21 •图中I 川个闘的半径都是1厘米.求阴影部分的倆积。
例22・如图.正方形边长为8厘米,求阴影部分的面积。
(22)例23・图中的4个圆的圆心是正方形的4个顶点… 它们的公 例24•如图•有8个半径为1厘米的小恻•用他们的圆周的一部分 共点是该正方形的中心,如果每个圆的半径都是1厘米,那 连成一个花瓣图形,图中的黑点是这些圆的圆心。
如果圆周TT 率例15.e 知直角三角形面枳是12平方厘米.求阴影部分的面 例16 •求阴影部分的周长与而枳。
(单 位:厘米)例17•图中圆的半径为5凰米,求阴影部分的面积。
(虹位:厘米) 例18•如图,在边长为6厘米的等边三角形中挖去三个同样的扇形, 求阴影部分的周长。
(17)(18)例19.正方形边长为2厘米,求阴影部分的Ifti 积。
例20•如图•正方形ABCD 的面积是36平方厘米,求阴影部分的而积。
(19)(21)例25•如图•四个扇形的半径相等,求阴影部分的面枳。
仲位: 厘米)例26•如图•等腰直角三角形ABC和四分之一圆DEB. AB=5厘米■ BE=2MX.求图中阴影部分的面积。
例27.如图,正方形ABCD的对角线AC=2厘米,扇形ACB 是以AC为直径的半圆•扇形DAC是以D为圆心∙AD为半径的圆的一部分.求阴影部分的而积。
(27)例29•图中直角三角形ABC的直角三角形的直角边AB=4厘米,BC=6厘米,扇形BCD所在恻是以B为恻心,半径为BC 例30•如图•三角形ABC是直角三角形•阴影部分甲比阴影部分乙面枳大28 T方厘米∙AB=40厘米。
求BC的长度。
么阴影部分的而枳是女少?(23)取 3.1416,方厘米?(26)(29)例28•求阴影部分的面积。
圆 阴影部分面积(含答案)
北京坤宏远泰教育科技有限公司
例 1.求阴影部分的面积。(单位:厘米)
例 2.正方形面积是 7 平方厘米,求阴影部分的面积。 (单位:厘米)
解:这是最基本的方法: 圆 面积减去等腰直角三角形的面积,
× -2×1=1.14(平方厘 米)
解:这也是一种最基本的方法用正方
形的面积减去 圆的面积。 设圆的半径为 r,因为正方形的 面积为 7 平方厘米,所以 =7,
例 17.图中圆的半径为 5 厘米,求阴影部分的面积。 例 18.如图,在边长为 6 厘米的等边三角形中挖去
(单位:厘米)
三个同样的扇形,求阴影部分的周长。
解:上面的阴影部分 以 AB 为轴翻转后, 整个阴影部分成为梯 形减去直角三角形, 或两个小直角三角形 AED、BCD 面积和。 所以阴影部分面积为:5×5÷2+5×10÷2=37.5 平方厘米
解: 连对角线后将"叶形"剪开移 到右上面的空白部分,凑成正方 形的一半. 所以阴影部分面积为: 8×8÷2=32 平方厘米
例 14.求阴影部分的面积。(单位:厘米)
解:梯形面积减去 圆 面积,
(4+10)×4π =28-4π=15.44
平方厘米 .
例 15.已知直角三角形面积是 12 平方厘米,求阴影 例 16.求阴影部分的面积。(单位:厘米) 部分的面积。
解: 甲、乙两个部分同补 上空白部分的三角形后合 成一个扇形 BCD,一个 成为三角形 ABC, 此两部分差即为:π
例 30.如图,三角形 ABC 是直角三角形,阴影部分 甲比阴影部分乙面积大 28 平方厘米,AB=40 厘米。 求 BC 的长度。 解:两部分同补上空白部分后为直角三角形 ABC, 一个为半圆,设 BC 长为 X,则
奥数圆形周长阴影面积试题及解析

奥数圆形周长阴影面积试题及解析Company Document number:WTUT-WT88Y-W8BBGB-BWYTT-19998奥数圆形周长阴影面积试题及解析1、如图,正方形边长为1,正方形的4个顶点和4条边分别为4个圆的圆心和半径,求阴影部分面积.(π取3.14)2、如图中三个圆的半径都是5cm ,三个圆两两相交于圆心.求阴影部分的面积和.(圆周率取3.14)3、如图,ABCD 是正方形,且1FA AD DE ===,求阴影部分的面积.(取π3=)4、如图,边长为3的两个正方形BDKE 、正方形DCFK 并排放置,以BC 为边向内侧作等边三角形,分别以B 、C 为圆心,BK 、CK 为半径画弧.求阴影部分面积.(π 3.14=)5、如图,边长为12厘米的正五边形,分别以正五边形的5个顶点为圆心,12厘米为半径作圆弧,请问:中间阴影部分的周长是多少(π 3.14=)6、下图中每一个小正方形的面积是1平方厘米,那么格线部分的面积是多少平方厘米7、如图,已知扇形BAC 的面积是半圆ADB 面积的34倍,则角CAB 的度数是________. 8、在4×7的方格纸板上面有如阴影所示的”6”字,阴影边缘是线段或圆弧.问阴影面积占纸板面积的几分之几9、先做一个边长为2cm的等边三角形,再以三个顶点为圆心,2cm为半径作弧,形成曲边三角形(如左图).再准备两个这样的图形,把一个固定住(右图中的阴影),另一个围绕着它滚动,如右图那样,从顶点相接的状态下开始滚动.请问此图形滚动时经过的面积是多少平方厘米(π 3.14=) 10、求下图中阴影部分的面积:11、右上图中每个小圆的半径是1厘米,阴影部分的面积是_______平方厘米.(π=)12、如右图,矩形ABCD中,AB=6厘米,BC=4厘米,扇形ABE半径AE=6厘米,扇形CBF的半CB=4厘米,求阴影部分的面积13、如下图,等腰直角三角形ABC的腰为10厘米;以A为圆心,EF为圆弧,组成扇形AEF;阴影部分甲与乙的面积相等。
六年级数学圆的周长和面积练习题

六年级数学圆的周长和面积练习题
1.直径是 12厘米的圆,周长是( ) cm,面积是( ) cm
2.一个圆的半径扩大2倍,它的周长扩大( )倍,面积扩大( )倍。
3.小圆的半径是6厘米,大圆的直径是18 厘米,小圆和大圆的圆长比是( ),面积比是( ).
4.小圆的直径是 4厘米,大圆的直径是6厘米,大圆的周长是小圆周长的( )倍,大圆的面积是( )倍.
5.求下面各图阴影部分的面积。
(单位:厘米)
4.有大、小两个圆,小圆的周长是12.56m,大圆的直径是小圆直径的2倍,大圆的面积是多少?
5.阳光社区修建一个圆形水池,周长是25.12m,在水池的周围修了一条宽1m 的环形小路。
小路的面积是多少?
6.一个环形的外圆直径是10厘米,内圆直径是6厘米,它的面积是多少平方厘米?
7.下图涂色部分是个环形,它的内圆直径是10厘米,外圆直径是 15厘米,它的面积是多少?
8.一片小树林,周围有一条环形小路,外圆直径 20米,内圆半径9米。
环形小路的面积是多少平方米?
9.在一个直径为10m的圆形水池周围有一条1m宽的环形小路,小路的面积是多少平方米?
10. 一个花坛,直径5m,在它的周围有一条宽1m的环形小路,小路的面积是多少平方米?。
奥数训练——圆的周长和面积附答案

奥数训练——圆的周长和面积附答案一.填空题(共11小题)1.边长是10厘米的正方形和直径是10厘米的半圆组成如图所示,其中P点是半圆的中点,点Q是正方形一边的中点,则阴影部分的面积为_________ 平方厘米.(取π=3.14)第1题第2题第3题第4题2.如图是一个边长为4厘米的正方形,则阴影部分的面积是_________ 平方厘米.3.如图,ABCD是边长为10厘米的正方形,且AB是半圆的直径,则阴影部分的面积是______ 平方厘米.(π取3.14)4.如图是半径为6厘米的半圆,让这个半圆绕A点按顺时针方向旋转30°,此时B点移动到B′点,则阴影部分的面积是_________ 平方厘米.第5题第6题第7题第8题5.如图,ABCD是正方形,边长是a厘米,BE=厘米,其中,圆弧BD的圆心是C点.那么,图中阴影部分的面积等于________ 平方厘米(取π=3).6.两个半径为2厘米的圆如右图摆放,其中四边形OABC是正方形,图中阴影部分的面积是___ 平方厘米.7.如右图,正方形DEOF在四分之一圆中,如果圆的半径为1厘米,那么,阴影部分的面积是_________ 平方厘米.(π取3.14.)8.如图,ABC是等腰直角三角形,D是半圆周的中点,BC是半圆的直径.已知AB=BC=10厘米,那么阴影部分的面积是_________ 平方厘米.(π的值取3.14)9.如图,其中AB=10厘米,C点是半圆的中点.那么,阴影部分的面积是_________ 平方厘米.(π取3.14)10.如图,以直角三角形的直角边长20厘米为直径画一个半圆,阴影部分①的面积比②的面积小16平方厘米.BC= _________ .第9题第10题第11题11.如图,阴影部分的面积是_________ 平方厘米.二.解答题(共7小题)12.如图是一个圆心为O,半径是10厘米的圆.以C为圆心,CA为半径画一圆弧,求阴影部分的面积.13.求下列各图中阴影部分的周长.(1)图1中,两个小半圆的半径均为3厘米.(2)图2中,四边形为平行四边形圆弧形对的圆心角为60°,半径为6厘米.(3)图3中,正方形内有一个以正方形的边长为半径的圆弧和两个以正方形边长为直径的圆弧,已知正方形边长为4厘米.(4)图4中,在半径为4厘米的圆内有两个半径为4厘米的圆弧.14.下面是由一个平行四边形和一个半圆形组成的图形,已知半圆的半径是10厘米,计算图中阴影部分的面积.15.如图,有一只狗被缚在一建筑物的墙角上,这个建筑物是边长都等于6米的等边三角形,绳长是8米.求绳被狗拉紧时,狗运动后所围成的总面积.16.左图正方形边长为2厘米.以顶点A为圆心边长 AB为半径作圆弧,再分别以AB、AC为直径作半圆弧.求阴影部分面积.17.如图三角形ABC是直角三角形,阴影部分①的面积比阴影部分②的面积小14.88平方厘米,直径AB长8厘米,BC长多少厘米?18.如图所示,正方形ABCD,等腰三角形ADE,及半圆CAE,若AB=2厘米,则阴影部分的面积是多少平方厘米?参考答案与试题解析一.填空题(共11小题)1.解答:解:正方形和半圆的面积之和:10×10+3.14×(10÷2)2÷2,=100+39.25=139.25(平方厘米),三角形PAB的面积是:10×15÷2=75(平方厘米),三角形PBQ的面积是5×5÷2=12.5(平方厘米),则阴影部分的面积是:139.25﹣75﹣12.5=51.75(平方厘米);答:阴影部分的面积是51.75平方厘米.故答案为:51.75.点评:此题考查了三角形、正方形和圆的面积公式的综合应用;连接BP,找出这两个白色三角形的高,求出空白部分的面积是解决本题的关键.2.解答:解:如图,4×4×+3.14×()2÷2=4×4×+3.14×22÷2=4+6.28=10.28(平方厘米),答:阴影部分的面积是10.28平方厘米;故答案为:10.28.3.解答:解:连接BE,如图:半圆面积:3.14×(10÷2)2÷2=39.25(平方厘米),三角形ABE面积:102÷2÷2=25(平方厘米),月牙面积:(39.25﹣25)÷2=7.125(平方厘米),阴影面积:25﹣7.125=17.875(平方厘米).故答案为:17.875.4.解答:解:S阴影=S扇形ABB'+S半圆ADB'﹣S半圆ADB',又S半圆ACB=S半圆ADB',所以S阴影=S扇形ABB'.扇形部分应该半径为6×2=12(厘米),即:==37.68(平方厘米).故答案为:37.68.5.解答:解:×3a2+a×﹣(a+)a=a2+a2﹣a2=0.45a2(平方厘米).答:图中阴影部分的面积等于 0.45a2平方厘米.故答案为:0.45a2.6.解答:解:阴影部分的面积是:×3.14×22﹣×2××2,=3.14﹣2=1.14(平方厘米),答:阴影部分的面积是1.14平方厘米.故答案为:1.14.7.解答:解:如图,正方形的面积=对角线×对角线×=1×1×=(平方厘米)四分之一圆的面积=×πr2 =×3.14×12=0.785(平方厘米)阴影部分的面积=0.785﹣=0.285(平方厘米)故填0.285.8.解答:解:因为S△AFD=×10×(10÷2)=25(平方厘米),SAFDB=梯形ABEF的面积+半圆BDE的面积,梯形ABEF的面积=(10÷2+10)×(10÷2)÷2=(平方厘米),半圆BDE的面积=πr2=.阴影部分的面积=AFDB的面积﹣三角形AFD的面积,=(+π)﹣25,=32.125(平方厘米).答:阴影部分的面积是32.125平方厘米.故答案为:32.125.9.解答:解: 3.14×102﹣10×÷2,=×3.14×100﹣10×5÷2,=39.25﹣25,=14.25(平方厘米);答:阴影部分的面积是14.25(平方厘米).故答案为:14.25.10.解答:解:BC的长度为x厘米,×20×x﹣3.14×÷2=16 10x﹣3.14×100÷2=16,10x﹣314÷2=16, 10x﹣157=16, 10x=173, x=17.3;答:BC的长度是17.3厘米.故答案为:17.3厘米.11.解答:解:×3.14×22﹣2×2÷2,=3.14﹣2,=1.14(平方厘米);答:阴影部分的面积是1.14平方厘米.故答案为:1.14.二.解答题(共7小题)12.解答:解:三角形ABC的面积为:所以AC2÷2=AB×OC÷2=10×2×10÷2=100(平方厘米),由上面计算可得:AC2=100×2=200,所以阴影部分的面积是:3.14×10×10÷2﹣(×3.14×200﹣100)=157﹣(157﹣100),=157﹣57,=100(平方厘米),答:阴影部分的面积是100平方厘米.13.解答:解:(1)大半圆的圆弧长:2×3.14×(3+3)÷2=18.84(厘米);小半圆的圆弧长:2×3.14×3÷2=9.42(厘米);阴影部分周长:18.84+9.42×2=37.68(厘米).(2)圆弧长:2×3.14×6×=6.28(厘米);平行四边形周长:6×4=24(厘米);阴影部分周长:6.28+24=30.28(厘米).(3)一个以正方形的边长为半径的圆弧长:2×3.14×4×=6.28(厘米);两个以正方形边长为直径的圆弧长:3.14×4=12.56(厘米);阴影部分周长:6.28+12.56=18.84(厘米).(4)阴影部分周长:2×3.14×4=25.12(厘米).14.解答:解:如图,把半圆内的阴影部分从左边割下补到左边,阴影部分即成为一个底为半圆半径的2倍,高是半圆半径的三角形,×10×2×10=100(平方厘米);答:图中阴影部分的面积是100平方厘米15.解答:解:根据图可知:大扇形的圆心角为:360﹣60=300(度),小扇形的圆心角为:180﹣60=120(度),故总面积为:(平方米),答:狗运动后所围成的总面积为175.84平方米.点评:此题考查如何求扇形的面积,还要注意圆心角度数的求法.16.左图正方形边长为2厘米.以顶点A为圆心边长 AB为半径作圆弧,再分别以AB、AC为直径作半圆弧.求阴影部分面积.考点:组合图形的面积.专题:压轴题;平面图形的认识与计算.分析:如图所示,作出辅助线,则4个小弓形的面积相等,将①、②经过旋转、平移到③、④的位置,则阴影部分的面积=以正方形的边长为半径的乙的面积﹣三角形ABC的面积,代入数据即可求解.解答:解:3.14×22×﹣2×2÷2,=3.14﹣2,=1.14(平方厘米);答:阴影部分的面积是1.14平方厘米.点评:此题主要考查了正方形的性质以及旋转的性质,难度适中,关键是将所求的阴影部分的面积转化为与圆和正方形的面积有关的图形的面积.17.如图三角形ABC是直角三角形,阴影部分①的面积比阴影部分②的面积小14.88平方厘米,直径AB长8厘米,BC长多少厘米?考点:组合图形的面积.专题:平面图形的认识与计算.分析:从图中可以看出阴影部分①加上空白部分的面积是半圆的面积,阴影部分②加上空白部分的面积是三角形ABC的面积.又已知①的面积比②的面积小14.88平方厘米,故半圆面积比三角形ABC的面积小14.88平方厘米.求出半圆面积,再加上14.88即为三角形的面积,再根据三角形的面积公式解答即可.解答:解:半圆面积为3.14×(8÷2)2÷2=25.12(平方厘米),三角形ABC的面积为:25.12+14.88=40(平方厘米).BC的长为:40×2÷8=10(厘米).答:BC长10厘米.点评:此题考查了学生三角形以及圆的面积公式及其应用,同时考查了学生观察图形的能力.18.如图所示,正方形ABCD,等腰三角形ADE,及半圆CAE,若AB=2厘米,则阴影部分的面积是多少平方厘米?考点:组合图形的面积.专题:平面图形的认识与计算.分析:把原图ADE以及圆弧AE移补到ADC以及圆弧AC,那么阴影部分的面积就是正方形的面积的一半,然后再进一步解答.解答:解:正方形的面积:2×2=4(平方厘米);阴影部分的面积:4÷2=2(平方厘米).答:阴影部分的面积是2平方厘米.点评:分析图形,根据图形特点进行割补,寻求问题突破点.Welcome To Download欢迎您的下载,资料仅供参考!。
六年级圆的面积20题专项练习

六年级圆的面积20题专项练习学校:___________姓名:___________班级:___________考号:___________一、计算题1.如图,圆的周长是25.12厘米,圆的面积正好和长方形的面积相等,这个长方形的长是多少厘米?2.列式求如图阴影部分的面积。
3.求下面图形的周长。
(单位:厘米)4.求阴影面积。
5.如图,求它的周长和面积。
6.求阴影部分的周长和面积。
7.求下图中阴影部分的面积。
(π取3.14,单位:cm)8.求下图阴影部分的面积。
(单位:厘米)9.求下图阴影部分的面积。
( 取3.14)(单位:厘米)10.如图所示,已知圆的周长是18.84厘米,0为圆心,平行四边形ABCD的面积为42平方厘米,线段DE∶EC=1∶3。
求阴影部分的面积。
(π取3.14)11.计算下图阴影部分的面积。
12.看图计算阴影部分面积(单位:cm)(π取3.14)13.求阴影部分的面积(单位,厘米)14.计算下图阴影部分的面积。
15.求下图阴影部分的面积和周长。
(单位:米)16.如图,求阴影部分的面积。
(单位:厘米)17.一个长方形和一个半圆组成如图所示的图形,长方形长6厘米,宽4厘米,求这个图形的周长和面积。
18.已知直角三角形面积是12平方厘米,求阴影部分的面积。
19.三角形ABC 是等腰直角三角形,以BC 为直径,BC 中点O 为圆心画半圆,D 为半圆周的中点,连结AD ,已知10AB BC ==厘米,求阴影部分的面积。
20.求下图涂色部分的面积。
(单位:m )本卷由系统自动生成,请仔细校对后使用,答案仅供参考。
答案第1页,总1页 参考答案1.12.56厘米2.13.74平方厘米3.15.42厘米4.7.725.37.68厘米;56.52平方厘米6.周长:30.84cm ;面积:36cm ²7.2.28cm 28.6.88平方厘米9.1.14平方厘米10.634平方厘米 11.6.88平方分米12.7.72平方厘米13.13.5平方厘米14.2.28cm 215.面积343平方米;周长101.4米16.13.12平方厘米17.周长22.28厘米;面积17.72平方厘米 18.5.13平方厘米19.57.125平方厘米20.343m 2。
六年级上学期数学 圆的面积 应用题针对性训练20题 后面带详细答案
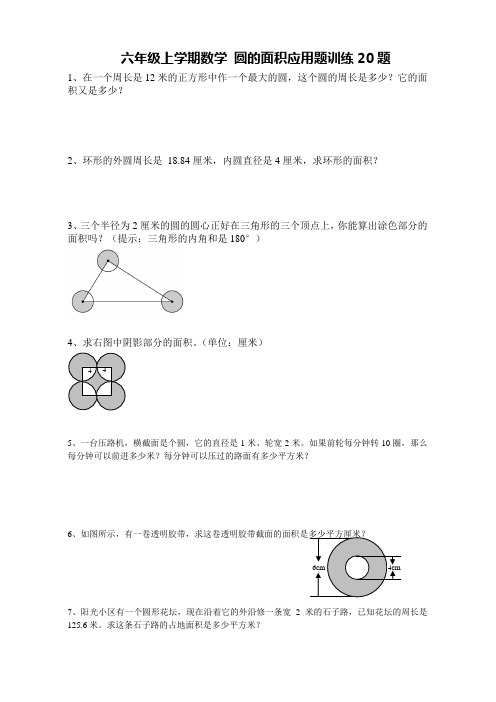
六年级上学期数学 圆的面积应用题训练20题1、在一个周长是12米的正方形中作一个最大的圆,这个圆的周长是多少?它的面积又是多少?2、环形的外圆周长是 18.84厘米,内圆直径是4厘米,求环形的面积?3、三个半径为2厘米的圆的圆心正好在三角形的三个顶点上,你能算出涂色部分的面积吗?(提示:三角形的内角和是180°)4、求右图中阴影部分的面积。
(单位:厘米)5、一台压路机,横截面是个圆,它的直径是1米、轮宽2米。
如果前轮每分钟转10圈,那么每分钟可以前进多少米?每分钟可以压过的路面有多少平方米?6、如图所示,有一卷透明胶带,求这卷透明胶带截面的面积是多少平方厘米?7、阳光小区有一个圆形花坛,现在沿着它的外沿修一条宽2米的石子路,已知花坛的周长是125.6米。
求这条石子路的占地面积是多少平方米?4 44cm 6cm8.图中甲区域比乙区域的面积大57平方厘米,且半圆的半径是10厘米.其中直角三角形竖直的直角边的长度是多少?(л取3.14)9.如图所示,直角三角形ABC的面积是45,分别以B、C为圆心,3为半径画圆。
已知图中阴影部分的面积是35.58。
请问:角A是多少度?(л取3.14)10、如图,正方形的边长是10厘米,阴影部分的面积是多少?(π取3.14)11、正方形的面积是12平方厘米,求下图中阴影部分的面积。
12、如图所示,在直角三角形ABC中,有三个小扇形半径均为4厘米,BC =16求阴影部分的面积多少厘米?13. 已知正方形的面积是30cm²,圆的面积是多少?14、下图中,正方形的面积是50cm2,求涂色部分的面积。
15、一个半圆形的花坛,它的面积是56.52平方米,求这个花坛的周长是多少?16、五个圆环摆放方式如图,每个外圆的半径都是8厘米,内圆的半径都是6厘米,两圆每个相交处的面积大约是4平方厘米,这五个圆环所占的面积是多少平方厘米?17、一个圆和一个正方形的周长都是28.26厘米,它们的面积谁大?大多少?18、一块边长是12厘米的正方形草地,其中一条对角线的两个端点各有棵树,树上各拴着一头牛,绳长都是12米,两头牛都能吃到的草的面积是多少平方米?19、把一只羊拴在一块长8 m,宽6 m的长方形草地上,拴羊的绳长2 m,那么这只羊吃到草的最大面积是多少平方米?如果要使羊吃草的面积最小,应该将羊拴在这个长方形草地的什么位置?20、已知三个圆的半径都是6厘米,O1 O2 O3分别为圆心,求阴影部分的面积。
