第4章 习题及参考解答
第4章习题与解答

第4章数据库和数据仓库4.1本章知识框架与学习要求数据库技术是数据管理的最新技术,是计算机科学的重要分支。
它已经成为先进信息技术的重要组成部分,是现代计算机信息系统和计算机应用系统的基础和核心。
数据库已经成为人们存储数据、管理信息、共享资源的最先进最常用的技术。
认识和掌握有关的数据库技术对学好本课程具有重要作用。
本章主要介绍了数据库技术的相关概念包括数据的组织层次、数据模型、信息模型、关系规范化等,以及数据库的设计方法,数据库仓库和数据挖掘的概念。
4.1.1 知识框架与学习要求一、数据的描述与组织(掌握)(一)三个世界1.现实世界2.信息世界3.计算机世界(二)数据组织的层次1.数据项(字段)2.记录3.数据文件4.数据库二、数据库管理技术(一)数据管理的发展(了解)1.简单应用阶段2.文件系统阶段3.数据库系统阶段(二)数据库管理系统(掌握)1.数据库系统(DBS)2.数据库管理系统(DBMS)(1)数据库的定义功能(2)数据库的操作功能(3)数据库的保护功能(4)数据库的维护功能(5)数据的存储管理三、数据模型(掌握)(一)信息模型(概念模型)1.信息模型的要素2.两个实体集之间联系的分类3.实体联系模型(E-R模型)(二)数据模型1.数据模型的三要素2.数据模型与信息模型的关系3.三种主要的数据模型(1)层次模型(Hierarchical Model)(2)网状模型(Network Model)(3)关系模型(Relational Model)(三)概念模型向关系模型的转换(四)关系的规范化1.第一范式(1NF)2.第二范式(2NF)3.第三范式(3NF)五、数据库设计(掌握)(一)数据库设计方法简述(二)数据库设计步骤六、数据仓库和数据挖掘(了解)(一)数据仓库1.数据仓库的概念2.数据仓库和数据库的区别3.数据仓库的特性4.数据仓库的基本结构5.数据仓库工具的组成(二)数据挖掘1.数据挖掘的概念2.数据仓库与数据挖掘的关系4.1.2 学习重点本章重点掌握以下几方面的内容:1.三个世界即现实世界、信息世界、计算机世界的特点及区别与联系;2.人工管理阶段、文件系统阶段及数据库系统阶段应用程序与数据关系的区别;3.数据库管理系统功能4.信息(概念)模型的要素、E-R模型的绘制方法;5.数据模型的三要素、数据模型与信息模型的关系、关系模型;6.概念模型向关系模型的转换;7.数据库设计方法和步骤4.2 教材习题与解答4.2.1 习题一、名词解释1.数据库2.记录3.DBMS4.DBS5.概念模式6.数据模型7.概念模型8.键或码9.数据操作10.1NF 11. 2NF 12.3NF 13.关系14.关系模式15.数据仓库16.数据挖掘二、简答题1. 数据库系统组织数据的特点是什么?2. 数据库系统与文件系统的区别是什么?3. 数据管理经历了哪几个阶段?各个阶段的特点是什么?4. 数据模型的三要素是什么?5. 数据库管理系统的主要功能是什么?6. 信息模型的要素有哪些?7. 试述概念模式在数据库中的重要地位。
第4章 习题及参考解答

(2)用跳转表实现。
MOV BL,NUMB
MOV CHARS[BX],'$'
MOV DX,OFFSET CHARS
MOV AH,9
INT21H
MOV AH,4CH
INT21H
CODEENDS
ENDSTART
13.某软件共可接收10个键盘命令(分别为A,B,C,…,J),完成这10个命令的程序分别为过程P0,P1,…,P9。编一程序从键盘接收命令,并转到相应的过程去执行。要求用两种方法:
(5)MOV[BX],1000错。两操作数类型不匹配,[BX]只定义了一字节单元,而1000是16位数据。
11.8086汇编语言程序中段的类型有几种?各段如何定义?段定义语句中,定位类型、组合类型、类别各起什么作用?各有什么含义?
解8086汇编语言中,段的类型有三种,即代码段、堆栈段、数据段(附加数据段可归属于数据段)。各段可用段定义语句(SEGMENT与ENDS)和段名赋给段寄存器语句(ASSUME)来定义。段定义语句中,定位类型表示此段的起始边界要求,可允许4种段的起始边界,即PAGE、PARA、WORD或BYTE。它们分别表示段的起始值为以页、节、字、字节为边界,若此项省略,则默认值为PARA。组合类型用来告诉连接程序本段与其他段的关系,分别为NONE、PUBLIC、COMMON、AT表达式、STACK或MEMORY。每一种的含义请参看主教材。类别是连接程序(LINK)需要的。它可以是任何合法的名称,必须用单引号括起来,连接程序只使同类别的段发生关联。典型类别如‘CODE’、'STACK'。
DATASEGMENT
ORG 100H
BUF1DB 00H,01H.02H,…,0FEH,0FFH;共256个数据
概率论第4章习题参考解答

概率论第4章习题参考解答 1. 若每次射击中靶的概率为0.7, 求射击10炮, 命中3炮的概率, 至少命中3炮的概率, 最可能命中几炮. 解: 设ξ为射击10炮命中的炮数, 则ξ~B (10,0.7), 命中3炮的概率为 =⨯⨯==733103.07.0}3{C P ξ0.0090至少命中3炮的概率, 为1减去命中不到3炮的概率, 为=⨯⨯-=<-=≥∑=-2010103.07.01}3{1}3{i i i i C P P ξξ0.9984因np +p =10×0.7+0.7=7.7不是整数, 因此最可能命中[7.7]=7炮. 2. 在一定条件下生产某种产品的废品率为0.01, 求生产10件产品中废品数不超过2个的概率. 解: 设ξ为10件产品中的废品数, 则ξ~B (10,0.01), 则废品数不超过2个的概率为=⨯⨯=≤∑=-20101099.001.0}2{i i i iC P ξ0.99993. 某车间有20部同型号机床, 每部机床开动的概率为0.8, 若假定各机床是否开动彼此独立, 每部机床开动时所消耗的电能为15个单位, 求这个车间消耗电能不少于270个单位的概率. 解: 设每时刻机床开动的数目为ξ, 则ξ~B (20,0.8), 假设这个车间消耗的电能为η个单位, 则η=15ξ, 因此2061.02.08.0}18{}15270{}27015{}270{20182020=⨯⨯==≥=≥=≥=≥∑=-i i i iC P P P P ξξξη4. 从一批废品率为0.1的产品中, 重复抽取20个进行检查, 求这20个产品中废品率不大于0.15的概率. 解: 设这20个产品中的废品数为ξ, 则ξ~B (20,0.1), 假设这20个产品中的废品率为η, 则η=ξ/20. 因此∑=-⨯⨯=≤=≤=≤320209.01.0}3{}15.020{}15.0{i i i iC P P P ξξη=0.8675. 生产某种产品的废品率为0.1, 抽取20件产品, 初步检查已发现有2件废品, 问这20件中, 废品不少于3件的概率. 解: 设ξ为这20件产品中的废品数, 则ξ~B (20,0.1), 又通过检查已经知道ξ定不少于2件的条件, 则要求的是条件概率}2{}23{}2|3{≥≥⋂≥=≥≥ξξξξξP P P因事件}3{}2{≥⊃≥ξξ, 因此2}23{≥=≥⋂≥ξξξ因此5312.06083.02852.019.01.0209.019.01.01}{1}2{1}{}2{1}{}2{}{}{}{}2{}3{}2|3{192018222010202202202202203=-=⨯⨯--⨯⨯-==-=-===-===-=====≥≥=≥≥∑∑∑∑∑∑======C i P P i P P i P P i P i P i P P P P i i i i i i ξξξξξξξξξξξξξ6. 抛掷4颗骰子, ξ为出现1点的骰子数目, 求ξ的概率分布, 分布函数, 以及出现1点的骰子数目的最可能值. 解: 因掷一次骰子出现一点的概率为1/6, 则ξ~B (4,1/6), 因此有⎪⎪⎩⎪⎪⎨⎧≥<≤⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛<==⎪⎭⎫ ⎝⎛⨯⨯==∑≤--4140656100)(),4,3,2,1,0(6561}{4444x x C x x F k C k P x k kk k kk kξ或者算出具体的值如下所示: ξ 0 1 2 3 4 P0.48230.38580.11570.01540.0008⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≥<≤<≤<≤<≤<=41439992.0329838.0218681.0104823.000)(x x x x x x x F从分布表可以看出最可能值为0, 或者np +p =(4/6)+1/6=5/6小于1且不为整数, 因此最可能值为[5/6]=0. 7. 事件A 在每次试验中出现的概率为0.3, 进行19次独立试验, 求(1)出现次数的平均值和标准差; (2)最可能出现的次数. 解: 设19次试验中事件A 出现次数为ξ, 则ξ~B (19,0.3), 因此 (1)ξ的数学期望为E ξ=np =19×0.3=5.7 方差为Dξ=np (1-p )=19×0.3×0.7=3.99标准差为997.199.3===ξσξD(2)因np +p =5.7+0.3=6为整数, 因此最可能值为5和6. 8. 已知随机变量ξ服从二项分布, E ξ=12, D ξ=8, 求p 和n . 解: 由E ξ=np =12 (1) 和D ξ=np (1-p )=8 (2) 由(1)得n =12/p , 代入到(2)得 12(1-p )=8, 解出p =(12-8)/12=1/3=0.3333 代回到(1)式得n =12/p =12×3=36 9. 某柜台上有4个售货员, 并预备了两个台秤, 若每个售货员在一小时内平均有15分钟时间使用台秤, 求一天10小时内, 平均有多少时间台秤不够用. 解: 每个时刻构成一n =4的贝努里试验, 且p =15/60=0.25, 因此, 设ξ为每个时刻要用秤的售货员数, 则ξ~B (4, 0.25), 当ξ>2时, 台秤不够用. 因此每时刻台秤不够用的概率为=+⨯⨯=>433425.075.025.0)2(C P ξ0.0508因此10个小时内平均有0.0508×10=0.508个小时台秤不够用. 10. 已知试验的成功率为p , 进行4重贝努里试验, 计算在没有全部失败的情况下, 试验成功不止一次的概率. 解: 设ξ为4次试验中的成功数, 则ξ~B (4,p ), 事件"没有全部失败"即事件{ξ>0}, 而事件"试验成功不止一次"即事件{ξ>1}, 因此要求的是条件概率P {ξ>1|ξ>0}, 又因事件{ξ>1}被事件{ξ>0}包含, 因此这两个事件的交仍然是{ξ>1}, 因此434141}0{1}1{}0{1}0{}1{}0|1{q pq q P P P P P P ---===-=-=-=>>=>>ξξξξξξξ其中q =1-p 11. ξ服从参数为2,p 的二项分布, 已知P (ξ≥1)=5/9, 那么成功率为p 的4重贝努里试验中至少有一次成功的概率是多少?解: 因ξ~B (2,p ), 则必有9/5)1(1)0(1)1(2=--==-=≥p P P ξξ, 解得3/13/213/219/49/51)1(2=-==-=-=-p p p 则假设η为成功率为1/3的4重贝努里试验的成功次数, η~B (4,1/3), 则802.081161321)1(1)0(1)1(44=-=⎪⎭⎫⎝⎛-=--==-=≥p P P ηη12. 一批产品20个中有5个废品, 任意抽取4个, 求废品数不多于2个的概率解: 设ξ为抽取4个中的废品数, 则ξ服从超几何分布, 且有==≤∑=-204204155}2{i i i C C C P ξ0.968 13. 如果产品是大批的, 从中抽取的数目不大时, 则废品数的分布可以近似用二项分布公式计算. 试将下例用两个公式计算, 并比较其结果. 产品的废品率为0.1, 从1000个产品中任意抽取3个, 求废品数为1的概率. 解: 设任抽3个中的废品数为ξ, 则ξ服从超几何分布, 废品数为0.1×1000=100 ===3100029001100}1{C C C P ξ0.2435 而如果用二项分布近似计算, n =3, p =0.1, ξ~B (3,0.1)=⨯⨯≈=2139.01.0}1{C P ξ0.2430近似误差为0.0005, 是非常准确的.14. 从一副朴克牌(52张)中发出5张, 求其中黑桃张数的概率分布. 解: 设ξ为发出的5张中黑桃的张数, 则ξ服从超几何分布, 则)5,4,3,2,1,0(}{5525135213===--i C C C i P i i ξ则按上式计算出概率分布如下表所示: ξ 0 1 2 3 4 5 P0.22150.41140.27430.08150.01070.000515. 从大批发芽率为0.8的种子中, 任取10粒, 求发芽粒数不小于8粒的概率. 解: 设ξ为10粒种子中发芽的粒数, 则ξ服从超几何分布, 但可以用二项分布近似, 其中p =0.8, n =10, 则∑=-⨯⨯=≥10810102.08.0}8{i i i iC P ξ=0.677816. 一批产品的废品率为0.001, 用普哇松分布公式求800件产品中废品为2件的概率, 以及不超过2件的概率. 解: 设ξ为800件产品中的废品数, 则ξ服从超几何分布, 可以用二项分布近似, 则ξ~B (800, 0.001), 而因为试验次数很大废品率则很小, 可以用普阿松分布近似, 参数为 λ=np =800×0.001=0.89526.0!8.0}2{1438.028.0}2{28.08.02=≈≤=≈=∑=--i i e i P e P ξξ 17. 某种产品表面上的疵点数服从普哇松分布, 平均一件上有0.8个疵点, 若规定疵点数不超过1个为一等品, 价值10元, 疵点数大于1不多于4为二等品, 价值8元, 4个以上为废品, 求产品为废品的概率以及产品的平均价值. 解: 设ξ为产品表面上的疵点数, 则ξ服从普哇松分布, λ=0.8, 设η为产品的价值, 是ξ的函数. 则产品为废品的概率为0014.0!8.01}4{1}4{408.0=-=≤-=>∑=-i i e i P P ξξ==≤==∑=-18.0!8.0}1{}10{i i e i P P ξη0.8088==≤<==∑=-428.0!8.0}41{}8{i i e i P P ξη0.1898则产品的平均价值为 Eη = 10×P {η=10}+8×P {η=8}=10×0.8088+8×0.1898=9.6064(元) 18. 一个合订本共100页, 平均每页上有两个印刷错误, 假定每页上印刷错误的数目服从普哇松分布, 计算该合订本中各页的印刷错误都不超过4个的概率. 解: 设ξ为每页上的印刷错误数目, 则ξ服从普哇松分布, λ=2, 则1页印刷错误都不超过4个的概率为 ==≤∑=-402!2}4{i i e i P ξ0.9473而100页上的印刷错误都不超过4个的概率为[]=≤100}4{ξP 0.00445419. 某型号电子管的“寿命”ξ服从指数分布, 如果它的平均寿命E ξ=1000小时, 写出ξ的概率密度, 并计算P (1000<ξ≤1200). 解: 因Eξ=1000=1/λ, 其概率密度为⎪⎩⎪⎨⎧≤>=-0010001)(1000x x ex xϕ0667.0)12001000(2.111000120010001000=-=-=≤<----e e ee P ξ20. ξ~N (0,1), Φ0(x )是它的分布函数, φ0(x )是它的概率密度, Φ0(0), φ0(0), P (ξ=0)各是什么值? 解: 因有 20221)(x ex -=πϕ, ⎰∞--=Φxt dt ex 20221)(π, 因此φ0(x )为偶函数, 由对称性可知Φ0(0)=0.5, 并有πϕ21)0(0=,因ξ为连续型随机变量, 取任何值的概率都为0, 即P (ξ=0)=0.21. 求出19题中的电子管在使用500小时没坏的条件下, 还可以继续使用100小时而不坏的概率?解: 要求的概率为P (ξ>600|ξ>500), 因此905.0}500{}600{}500|600{1.010005001000600===>>=>>---e e eP P P ξξξξ22. 若ξ服从具有n 个自由度的χ2-分布, 证明ξ的概率密度为⎪⎪⎩⎪⎪⎨⎧<≥⎪⎭⎫ ⎝⎛Γ=---022)(21212x x e n x x x nn ϕ称此分为为具有n 个自由度的χ-分布 证: 设ξη=, 则因ξ的概率密度函数为⎪⎪⎩⎪⎪⎨⎧≤>⎪⎭⎫ ⎝⎛Γ=--0221)(2122x x e x n x xn nξϕη的分布函数为)0()()()()()(22>=≤=≤=≤=x x F x P x P x P x F ξηξξη对两边求导得)0(22222)(2)(2121222222>⎪⎭⎫ ⎝⎛Γ=⎪⎭⎫ ⎝⎛Γ==-----x en x en x xx x x x n n x n n ξηϕϕ23. ξ~N (0,1), 求P {ξ≥0}, P {|ξ|<3}, P {0<ξ≤5}, P {ξ>3}, P {-1<ξ<3} 解: 根据ξ的对称性质及查表得: P {ξ≥0}=1-Φ0(0)=0.5 P {|ξ|<3}=2Φ0(3)-1=2×0.99865-1=0.9973 P {0<ξ≤5}=Φ0(5)-0.5=0.5P {ξ>3}=1-Φ0(3)=1-0.99865=0.00135P {-1<ξ<3}=Φ0(3)-Φ0(-1)=Φ0(3)+Φ0(1)-1=0.99865+0.8413-1=0.83995 24. ξ~N (μ,σ2), 为什么说事件"|ξ-μ|<2σ"在一次试验中几乎必然出现?解: 因为)1,0(~N σμξ- 19545.0197725.021)2(2}2{}2|{|0≈=-⨯=-Φ=<-=<-σμξσμξP P因此在一次试验中几乎必然出现.25. ξ~N (10,22), 求P (10<ξ<13), P (ξ>13), P (|ξ-10|<2). 解: 因为)1,0(~210N -ξ6826.018413.021)1(2}1210{}2|10{|0.0668193319.01)5.1(1}5.1210{}13{43319.05.093319.0)0()5.1(}5.12100{}1310{0000=-⨯=-Φ=<-=<-=-=Φ-=>-=>=-=Φ-Φ=<-<=<<ξξξξξξP P P P P P26. 若上题中已知P {|ξ-10|<c }=0.95, P {ξ<d }=0.0668, 分别求c 和d .解: 因为)1,0(~210N -ξ, 则有95.01)2(2}2210{}|10{|0=-Φ=<-=<-cc P c P ξξ 解得975.0295.01)2(0=+=Φc, 查表得,96.12=c得c =3.92 再由5.00668.0)210(}210210{}{0<=-Φ=-<-=<d d P d P ξξ知,0210<-d 因此0668.0)210(1)210(00=-Φ-=-Φdd 即9332.00668.01)210(0=-=-Φd, 查表得5.1210=-d, 解得7310=-=d 27. 若ξ~N (μ,σ2), 对于P {μ-kσ<ξ<μ+kσ}=0.90, 或0.95, 或0.99, 分别查表找出相应的k值.解: 先求P {μ-kσ<ξ<μ+kσ}=0.90对应的k 值. 因)1,0(~N σμξ-, 因此 90.01)(2}{}{0=-Φ=<-=+<<-k k P k k P σμξσμξσμ 即95.0290.01)(0=+=Φk , 查表得k =1.64 同理, 由975.0295.01)(0=+=Φk , 查表得k =1.96 由995.0299.01)(0=+=Φk , 查表得k =2.57 28. 某批产品长度按N (50, 0.252)分布, 求产品长度在49.5cm 和50.5cm 之间的概率, 长度小于49.2cm 的概率.解: 设ξ为产品长度, 则ξ~N (50, 0.252), 且有)1,0(~25.050N -ξ, 则9545.0197725.021)2(2}225.050{}225.0502{}5.505.49{0=-⨯=-Φ=<-=<-<-=<<ξξξP P P0006871.09993129.01)2.3(1)2.3(}25.0502.4925.050{}2.49{00=-=Φ-=-Φ=-<-=<ξξP P29. ξi ~N (0,1)(i =1,2,3), 并且ξ1,ξ2,ξ3相互独立, ∑==3131i i ξξ,∑=-=312)(i i ξξη, 求),cov(,),,cov(1ηξηξξE解: 此题要用到, 两个独立的服从正态分布的随机变量相加后得到的随机变量仍然服从正态分布. 因此, 因为3131,031=⎪⎭⎫ ⎝⎛==∑=i i D D E ξξξ, 则)31,0(~N ξ313131)()cov(2131111==⎪⎭⎫ ⎝⎛==∑=ξξξξξξξE E E i i32313121)cov(2)2()(22222=+⨯-=+-=+-=-ξξξξξξξξξξE E E E i i i i i因此2323)()(312312=⨯=-=⎪⎭⎫ ⎝⎛-=∑∑==i i i i E E E ξξξξη ξξ-i 也服从正态分布, 且有03131)]([),cov(2=-=-=-=-ξξξξξξξξξE E E i i i即ξ与ξξ-i 不相关, 而因为它们服从正态分布, 因此也就是ξ与ξξ-i 相互独立,则ξ与2)(ξξ-i 也相互独立, 则ξ与η中的加和中的每一项相互独立, 当然也与η相互独立, 因此有0),cov(=ηξ, 因为相互独立的随机变量一定不相关.30. (ξ,η)有联合概率密度22)(21,2122ηξζπ+=+-y x e , 求ζ的概率密度.解: 由联合概率密度看出, ξ与η相互独立服从标准正态分布, 则有 ξ2与η2也相互独立且服从自由度为1的χ2-分布, 即ξ2~χ2(1), η2~χ2(1), 因此ζ=ξ2+η2~χ2(2), 即它的概率密度为⎪⎩⎪⎨⎧<>=-00212x x exζϕ即ζ服从λ=1/2的指数分布.。
仪器分析第四章课后习题答案24页PPT

敏化电极是指气敏电极、酶电极、细菌电极及生物电极等。 这类电极的结构特点是在原电极上覆盖一层膜或物质,使得 电极的选择性提高。典型电极为氨电极。
以氨电极为例,气敏电极是基于界面化学反应的敏化电极, 事实上是一种化学电池,由一对离子选择性电极和参比电极 组成。试液中欲测组分的气体扩散进透气膜,进入电池内部, 从而引起电池内部某种离子活度的变化。而电池电动势的变 化可以反映试液中欲测离子浓度的变化。
14.以0.03318mol.l-1的硝酸镧溶液电位滴定100.0mL氟化物溶 液,滴定反应为:
L3a 3F La3 F
滴定时用氟离子离子选择性电极为指示电极,饱和甘汞电极 为参比电极,得到下列数据:
加入La(NO)3 的体积/mL
电动势/V
加入La(NO)3 的体积/mL
电动势/V
0.00 29.00 30.00 30.30 30.60 30.90
00) 01)1
故:Cx = 2.73 × 10-3 mol.L-1
13.下面是用0.1000mol.L-1NaOH 溶液电位滴定50.00mL某一元 弱酸的数据:
V/mL pH V/mL pH V/mL pH
0.00
2.90 14.00 6.60 17.00
11.30
1.00
4.00 15.00 7.04 18.00
Dp H/DV
12
10
8
6
4
2
0
11
12
13
14
15
16
17
V/m L
(c) 从(b)表数据可以计算如下的二阶微商,可以看出终 点应该介于15.60-15.70之间.
人工智能教程习题及答案第4章习题参考解答

第四章不确定性推理习题参考解答4.1 练习题4.1什么是不确定性推理?有哪几类不确定性推理方法?不确定性推理中需要解决的基本问题有哪些?4.2什么是可信度?由可信度因子CF(H,E)的定义说明它的含义。
4.3什么是信任增长度?什么是不信任增长度?根据定义说明它们的含义。
4.4当有多条证据支持一个结论时,什么情况下使用合成法求取结论的可信度?什么情况下使用更新法求取结论可信度?试说明这两种方法实际是一致的。
4.5设有如下一组推理规则:r1:IF E1THEN E2(0.6)r2:IF E2AND E3THEN E4 (0.8)r3:IF E4THEN H (0.7)r4:IF E5THEN H (0.9)且已知CF(E1)=0.5,CF(E3)=0.6,CF(E5)=0.4,结论H的初始可信度一无所知。
求CF(H)=?4.6已知:规则可信度为r1:IF E1THEN H1(0.7)r2:IF E2THEN H1(0.6)r3:IF E3THEN H1(0.4)r4:IF (H1 AND E4) THEN H2(0.2)证据可信度为CF(E1)=CF(E2)=CF(E3)=CF(E4)=CF(E5)=0.5H1的初始可信度一无所知,H2的初始可信度CF0(H2)=0.3计算结论H2的可信度CF(H2)。
4.7设有三个独立的结论H1,H2,H3及两个独立的证据E1与E2,它们的先验概率和条件概率分别为P(H1)=0.4,P(H2)=0.3,P(H3)=0.3P(E1/H1)=0.5,P(E1/H2)=0.6,P(E1/H3)=0.3P(E2/H1)=0.7,P(E2/H2)=0.9,P(E2/H3)=0.1利用基本Bayes方法分别求出:(1)当只有证据E1出现时,P(H1/E1),P(H2/E1),P(H3/E1)的值各为多少?这说明了什么?(2)当E1和E2同时出现时,P(H1/E1E2),P(H2/E1E2),P(H3/E1E2)的值各是多少?这说明了什么?4.8在主观Bayes方法中,请说明LS与LN的意义。
第4章习题参考解答

p3()
{
P(s);
…
}
参考解答:
因p1和p2进程是p3进程开始执行的先决条件,即当p1和p2进程均执行完毕时,p3才能执行,则p3需有两个信号量,分别表示p1进程执行完毕的信号量s1,以及p2进程执行完毕的信号量s2。则同步算法描述如下:
main()
{
int s1=0,s2=0;
cobegin
p1();
p4();
coend
}
p1()
{
p1 execute;
V(s12);
V(s13);
V(s14);
}
p2()
{
P(s12);
p2 execute;
}
p3()
{
P(s13);
p3 execute;
}
p4()
{
P(s14);
p4 execute;
}
4-15
解:
main()
{
int sa=1,sb=0;// sa表示缓冲区S是否为空,sb表示是否为满。
(3)设a、b两并发进程,它们共享一临界资源。其执行临界区的算法框图如下图,
进程A和进程B为互斥进程,则需一个互斥信号量s,初值为1,表示临界资源初始情况下无进程使用。
main()
{
int s=1;
cobegin
pa();
pb();
coend
}
pa()
{
P(s);
进入csa…
V(s);
}
pb()
{
P(s);
进入csb…
V(s);
}
4-21
答:线程有时也称为轻量级进程,它是比进程更小的活动单位,它是进程中的一个执行路径。一个进程可以有多个执行路径即线程。
大学精品课件:哈工大_结构力学(王焕定第二版)第四章习题参考答案解密版

4-2(b) 答:本题三次超静定,但在横向荷载下轴力为零,因此可如下求解:
FP
X1 FP
X2
A l/2
B l/2
A B
基本体系
FP A
B FPl/4 MP 图
1
1
A X1 =1
B
M 1图
FPl/8
FPl/8
A
X2 =1 B
M 2图
A M图
B FPl/4
在上述荷载及单位弯矩图下,可图乘求系数、建立力法方程并求解,最后叠加出最终
F
G
3 C
3 3D
E 3
X1 =1
A
B
48 120
M 1图
F
G
72
E
CD
72
120 48
A
B
M (kN ⋅ m)
4-4 (c)本题求解过程如下面图形所示
A
MB
D
C l
基本体系
X1 l
M
M
M
M
图
P
l
M 1图
X1 =1
0.75M 0.25M
M图
δ11 X1 + ∆1P = 0
∑ ∫ δ11 =
2
M1 dx =
A
M图
本体也可取变 B 结点为铰以一对力矩为未知力求解,工作量和上述解法相同。
4-3 (b) 本题也一次超静定,基本体系、荷载与单位弯矩图如下所示
10 kN/m
10 kN/m
B
C
20 kN
B
C
20 kN
X1
3m 3m
A 6m
A
基本体系
180 B
180
土力学习题集及详细解答

《土力学》第四章习题集及详细解答第4章土中应力一填空题1. 土中应力按成因可分为 ____________________ 和。
2. 土中应力按土骨架和土中孔隙的分担作用可分为和3.地下水位下降则原水位出处的有效自重应力__________________________ 。
4.计算土的自重应力应从____________________________________ 算起。
5.计算土的自重应力时,地下水位以下的重度应取。
二选择题1.建筑物基础作用于地基表面的压力,称为(A )。
(A)基底压力;(B)基底附加压力;(C)基底净反力;(D)附加应力2.在隔水层中计算土的自重应力仃。
时,存在如下关系(B )。
(A)%=静水压力(B)5=总应力,且静水压力为零(C)旦=总应力,但静水压力大于零(D)%=总应力一静水压力,且静水压力大于零3.当各土层中仅存在潜水而不存在毛细水和承压水时,在潜水位以下的土中自重应力为(C )。
(A)静水压力(B)总应力(C)有效应力,但不等于总应力(D)有效应力,但等于总应力4.地下水位长时间下降,会使(A )。
(A)地基中原水位以下的自重应力增加(B)地基中原水位以上的自重应力增加(C)地基土的抗剪强度减小(D) 土中孔隙水压力增大5.通过土粒承受和传递的应力称为(A )。
(A)有效应力;(B)总应力;(C)附加应力;(D)孔隙水压力6.某场地表层为4m厚的粉质黏土,天然重度尸=18kN/m3,其下为饱和重度产sat=19 kN/m3 的很厚的黏土层,地下水位在地表下4m处,经计算地表以下2m处土的竖向自重应力为(B )。
(A)72kPa ;(B)36kPa ;(C)16kPa ;(D)38kPa7.同上题,地表以下5m处土的竖向自重应力为(A )。
(A)91kPa ;(B)81kPa ;(C)72kPa ;(D)41kPa8.某柱作用于基础顶面的荷载为800kN,从室外地面算起的基础深度为1.5m,室内地面比室外地面高0.3m,基础底面积为4m2,地基土的重度为17kN/m3,则基底压力为(C )。
第4章INTEL80X86系列微处理器习题参考答案

第4章 Intel80X86系列微处理器习题解答 4.1 8086/8088内部寄存器有哪些?哪些属于通用寄存器?哪些用于存放段地址?标志寄存器的含义是什么?答:8086/8088内部有14个16位的寄存器。
位的寄存器。
88个通用寄存器AX AX、、BX BX、、CX CX、、DX DX、、SP SP、、BP BP、、SI SI、、DI DI。
4个16位的段寄存器CS CS、、DS DS、、SS SS、、ES ES,用于存放段地址。
标志寄存器,用于存放段地址。
标志寄存器FLAGS 用于存放指令执行结果的特征和CPU 工作方式,其内容通常称为处理器状态字PSW PSW。
4.2 对于8086/8088CPU ,确定以下运算的结果与标志位。
(1)5439H+456AH(2)2345H+5219H (3)54E3H-27A0H (4)3881H+3597H (5)5432H-6543H (6)9876H+1234H略。
4.3 8086/8088为什么要对存储器采用分段管理?一个段最多包含多少存储单元?答:8086/8088内部与地址有关的寄存器都是16位的,只能处理16位地址,对内存的直接寻址范围最大只能达64KB 64KB。
为了实现对。
为了实现对1MB 单元的寻址,单元的寻址,8086/80888086/8088系统采用了存储器分段技术。
一个段最多包含64K 个存储单元。
个存储单元。
4.4 8086/8088CPU 内部共有多少个段?分别称为什么段?段地址存放在哪些寄存器中?答:8086/8088 CPU 内部共有4个段。
分别称为代码段、数据段、堆栈段和附加段。
段地址存放在4个16位的段寄存器,位的段寄存器,CS CS 代码段寄存器、代码段寄存器、DS DS 数据段寄存器、数据段寄存器、SS SS 堆栈段寄存器、堆栈段寄存器、ES ES 附加段寄存器中。
附加段寄存器中。
4.5 简述物理地址、逻辑地址、段基地址和偏移量的含义及其相互关系。
无机分析化学第4章 习题答案

第四章配位化合物习题参考解答1. 试举例说明复盐与配合物,配位剂与螯合剂的区别。
解复盐(如KCl·MgCl2·6H2O)在晶体或在溶液中均无配离子,在溶液中各种离子均以自由离子存在;配合物K2[HgI4]在晶体与溶液中均存在[HgI4]2-配离子,在溶液中主要以[HgI4]2-存在,独立的自由Hg2+很少。
配位剂有单基配位剂与多基配位剂:单基配位剂只有一个配位原子,如NH3(配位原子是N);多基配位剂(如乙二胺H2N-CH2-CH2-NH2)含有两个或两个以上配位原子,这种多基配位体能和中心原子M形成环状结构的化合物,故称螯合剂。
2. 哪些元素的原子或离子可以作为配合物的形成体?哪些分子和离子常作为配位体?它们形成配合物时需具备什么条件?解配合物的中心原子一般为带正电的阳离子,也有电中性的原子甚至还有极少数的阴离子,以过渡金属离子最为常见,少数高氧化态的非金属元素原子也能作中心离子,如Si(Ⅳ)、P(Ⅴ)等。
配位体可以是阴离子,如X-、OH-、SCN-、CN-、C2O4-等;也可以是中性分子,如H2O、CO、乙二胺、醚等。
它们形成配合物时需具备的条件是中心离子(或原子)的价层上有空轨道,配体有可提供孤对电子的配位原子。
3. 指出下列配合物中心离子的氧化数、配位数、配体数及配离子电荷。
[CoCl2(NH3)(H2O)(en)]Cl Na3[AlF6] K4[Fe(CN)6] Na2[CaY] [PtCl4(NH3)2]数。
K2[PtCl6] [Ag(NH3)2]Cl [Cu(NH3)4]SO4 K2Na[Co(ONO)6] Ni(CO)4[Co(NH2)(NO2)(NH3)(H2O)(en)]Cl K2[ZnY] K3[Fe(CN)6]二硫代硫酸合银(I)酸钠四硫氰酸根⋅二氨合铬(III)酸铵;四氯合铂(II)酸六氨合铂(II) 二氯⋅一草酸根⋅一乙二胺合铁(III)离子硫酸一氯⋅一氨⋅二乙二胺合铬(III)解Na3[Ag(S2O3)2] NH4[Cr(SCN)4(NH3)2] [Pt(NH3)6][PtCl4][FeCl2(C2O4)(en)]-[CrCl(NH3)(en)2]SO46. 下列配离子具有平面正方形或者八面体构型,试判断哪种配离子中的CO32-为螯合剂?[Co(CO3)(NH3)5]+[Co(CO3)(NH3)4]+[Pt(CO3)(en)] [Pt(CO3)(NH3)(en)]解[Co(CO3)(NH3)4]+、[Pt(CO3)(en)]中CO32-为螯合剂。
(新)曹广福版实变函数与泛函分析第四章答案

第四章习题参考解答1.设)(x f 是E 上的可积函数,如果对于E 上的任意可测子集A ,有0)(=⎰dx x f A ,试证:)(x f ,].[.E e a证明:因为}1)(|{}0)(|{1k x f x E x f x E k ≥=≠∞= ,而N k ∈∀,}1)(|{kx f x E ≥}1)(|{}1)(|{kx f x E k x f x E -≤≥= .由已知,=+=-≤≥≥⎰⎰⎰kx f x E kx f x E kx f x E dx x f dx x f dx x f 1)(|{1)(|{1|)(|{)()()(000=+.又因为0}1)(|{11)(0}1)(|{}1)(|{≥≥=≥=≥≥⎰⎰kx f x mE k dx k dx x f kx f x E kx f x E , 0}1)(|{1)1()(0}1)(|{}1)(|{≤-≤-=-≤=≥≥⎰⎰k x f x mE k dx k dx x f kx f x E kx f x E所以,0}1)(|{}1)(|{=-≤=≥k x f x mE k x f x mE .故,0}1)(|{}1)(|{}1|)(|{=-≤+≥=≥kx f x mE k x f x mE k x f x mE ,从而00}1|)(|{}1|)(|{[}0)(|{111==≥≤≥=≠∑∑∞=∞=∞=k k k k x f x mE k x f x E m x f x mE .即,0)(=x f ,].[.E e a .2.设f ,g 都是E 上的非负可测函数,并且对任意常数a ,都有})(|{})(|{a x g x mE a x f x mE ≥=≥,试证:)()(x g x f =,从而,=⎰dx x f E )(dx x g E⎰)(.证明:我们证f ,g 是同一个简单函数序列∞=1){m m ψ的极限函数.N m ∈∀及12,,1,0-=m m k ,令}21)(2|{,mm k m k x f k x E E +≤≤=,并且 })(|{2,m x f x E E m m m ≥=.则k m E ,是互不相交的可测集,并且k m m k E E m ,21== ,定义简单函数∑==mk m m k E m m x kx 20)(2)(,χψ. 下面证明:)()(lim x f x m m =∞→ψ,E x ∈.E x ∈∀0,若+∞=)(0x f ,则N m ∈∀,m m m E x 2,0∈,所以)()(0∞→∞→=m m x m ψ,即)()(lim 00x f x m n =∞→ψ;若+∞<)(0x f ,则可取正整数)(00x f m >,0m m ≥∀时,}21)(2|{})(0|{1210m m m k k x f k x E m x f x E x m +<≤=<≤∈-= .故,存在)120(-≤≤mm k k , }21)(2|{0m m k x f k x E x +<≤∈.即,m m k x f k 21)(20+<≤,m m k E m m k x k x mk m 2)(2)(20,==∑=χψ.所以,0212212)()()(|)()(|00000→=-+<-=-=-mm m m m m k k k x f x x f x x f ψψ,从而, )()(lim 00x f x m n =∞→ψ.同理,N m ∈∀,定义简单函数列∑==mkm m k E m m x kx 20)(2)(*,χψ,其中:}21)(2|{*,mm k m k x g k x E E +<≤=,12,,1,0-=mm k .})(|{*,m x g x E E k m ≥=.同上一样可证明:)()(lim 0x g x m n =∞→ψ,E x ∈.因为R a '∈∀,有})(|{})(|{a x g x mE a x f x mE ≥=≥.故R a '∈∀,})(|{b x f a x mE <≤})(|{b x g a x mE <≤=.从而,)120(-≤≤∀mm k k ,有k m m m m m k m mE k x g k x mE k x f k x mE mE ,*,}21)(2|{}21)(2|{=+<≤=+<≤=m m m m m m mE m x g x mE m x f x mE mE 2,*2,})(|{})(|{=≥=≥=.即,N m ∈∀,=)(x m ψ)(x m ϕ.因此)()(lim )(lim )(x g x x x f m m m m ===∞→∞→ϕψ.3.若⎪⎩⎪⎨⎧=为有理数,当为无理数,当x x x x x f 31)(,计算⎰1,0[)(dx x f .解:设x x E |]1,0[{0∈=为有理数},01]1,0[E E -=,则+=⎰⎰1)()(]1,0[E dx x f dx x f⎰]1,0[)(dx x f ⎰⎰⎰+==111E EE dx xdx xdx x=+==⎰⎰⎰1111E E E dx xdx xdx x2]2[11101]1,0[====⎰⎰x dx xdx x.4.设21,,E E 是]1,0[中n 个可测集,若]1,0[内每一点至少属于n 个集中的q个集,证明:21,,E E 中至少有一个测度不小于nq.证明:令∑==ni E x x f i1)()(χ,其中iEχ为i E 上的特征函数]1,0[∈∀x ,有q x x f ni E i≥=∑=1)()(χ,所以q qdx dx x f =≥⎰⎰]1,0]1,0[)(.∑∑⎰∑∑⎰⎰⎰========≤ni ni i E ni E ni E mE dx x dx x dx x f q i i 11111,0]1,0[]1,0[)()()(χχ.如果每个n qmE i <,则∑∑===⋅=>n i n i i q n q n n q mE 11.这与∑=≤ni i mE q 1矛盾.从而,)1(n i i ≤≤∃使得nqmE i ≥. 5.设f ,g 都是E 上的可积函数,试证明:22g f+也是E 上可积函数.证明:(1)先证:设)(x f 与)(x F 都是E 上的可测函数且)()(0x F x f ≤≤ ].[.E e a ,若)(x F 在E 可积,则)(x f 在E 可积.事实上,N m l ∈∀,,因为)()(0x F x f ≤≤ ].[.E e a ,故l l x F x f )}({)}({0≤≤,即+∞<≤≤≤⎰⎰⎰EE llE ldx x f dx x F dx x F dx x f mm)()}({)}({)}({,其中:m mS E E=,}||||{∞<=x x S m .从而∞=⎰1})}({{l l E dx x F m是单调递增有上界⎰Edx x F )(的数列,故:⎰⎰⎰≤=∞→EE ll E dx x F dx x f dx x f mm)()}({lim )(.又因为⎰∞=mE m dx x f 1})({单调递增有上界,所以⎰∞→mE l dx x f )(lim存在,并且⎰⎰⎰+∞<≤=∞→EE ll Edx x F dx x f dx x f m)()}({lim )(,即⎰∞→∞→mE ll m dx x f )}({lim lim+∞<≤⎰dx x f E)(.所以)(x f 在E 可积.(2)再证:22g f+在E 上可积.事实上,因为f ,g 在E 上可积,所以||f 与||g 在E 上可积,从而||f +||g 在E 上可积. 又因为||||22g f g f+≤+,由(1)。
机械制造技术基础(第)第四章课后习题答案

《机械制造技术基础》部分习题参考解答第四章机械加工质量及其控制4-1什么是主轴回转精度?为什么外圆磨床头夹中的顶尖不随工件一起回转,而车床主轴箱中的顶尖则是随工件一起回转的?解:主轴回转精度——主轴实际回转轴线与理想回转轴线的差值表示主轴回转精度,它分为主轴径向圆跳动、轴向圆跳动和角度摆动。
车床主轴顶尖随工件回转是因为车床加工精度比磨床要求低,随工件回转可减小摩擦力;外圆磨床头夹中的顶尖不随工件一起回转是因为磨床加工精度要求高,顶尖不转可消除主轴回转产生的误差。
4-2 在镗床上镗孔时(刀具作旋转主运动,工件作进给运动),试分析加工表面产生椭圆形误差的原因。
答:在镗床上镗孔时,由于切削力F的作用方向随主轴的回转而回转,在F作用下,主轴总是以支承轴颈某一部位与轴承内表面接触,轴承内表面圆度误差将反映为主轴径向圆跳动,轴承内表面若为椭圆则镗削的工件表面就会产生椭圆误差。
4-3为什么卧式车床床身导轨在水平面内的直线度要求高于垂直面内的直线度要求?答:导轨在水平面方向是误差敏感方向,导轨垂直面是误差不敏感方向,故水平面内的直线度要求高于垂直面内的直线度要求。
4-4某车床导轨在水平面内的直线度误差为0.015/1000mm,在垂直面内的直线度误差为0.025/1000mm,欲在此车床上车削直径为φ60mm、长度为150mm的工件,试计算被加工工件由导轨几何误差引起的圆柱度误差。
解:根据p152关于机床导轨误差的分析,可知在机床导轨水平面是误差敏感方向,导轨垂直面是误差不敏感方向。
水平面内:0.0151500.002251000R y∆=∆=⨯=mm;垂直面内:227()0.025150/60 2.341021000zRR-∆⎛⎫∆==⨯=⨯⎪⎝⎭mm,非常小可忽略不计。
所以,该工件由导轨几何误差引起的圆柱度误差0.00225R∆=mm。
4-5 在车床上精车一批直径为φ60mm、长为1200mm的长轴外圆。
已知:工件材料为45钢;切削用量为:v c=120m/min,a p=0.4mm, f =0.2mm/r; 刀具材料为YT15。
概率论与数理统计第四章习题参考答案

=
⎡ E⎢
1
⎢⎣ n −1
n i =1
(Xi
−
⎤ X )2 ⎥
⎥⎦
=
1 n −1
⎡ E⎢
⎢⎣
n i =1
X
2 i
−
nX
2⎤ ⎥ ⎥⎦
=
1 n −1
⎡n ⎢ ⎢⎣ i=1
E
(
X
2 i
)
−
nE( X
2⎤ )⎥ ⎥⎦
∑[ ] [ ] =
1 n −1
⎧ ⎨ ⎩
n i =1
D(X i ) + E 2 (X i )
X −µ 3/2
<
⎫ 1.96⎬
=
0.95
⎭
故,正态总体均值 µ 的 95%的置信区间为 (X − 2.94, X + 2.94)
代入样本值得正态总体均值 µ 的 95%的置信区间为(-2.565,3.315)。
(2)当σ 未知时,由 T = X − µ ~ t(n − 1) 即T = X − µ ~ t(3) ,所以
n
−a n
=0 =0
无解。由此不能求得
a,
b
的极大似然估计量。
⎩ ∂b
b−a
解:X
的概率密度为
f
(x)
=
⎪⎧ ⎨b
1 −
a
,
a
≤
x
≤
b
,
⎪⎩ 0, 其它
似然函数为 L(a, b) = 1 , θ1 ≤ xi ≤ θ 2 ,i = 1,2,L, n , (b − a)n
对于给定的样本值 (x1 , x2 ,L, xn )
−
n
D(
计量经济学(庞浩主编)第四章练习题参考解答
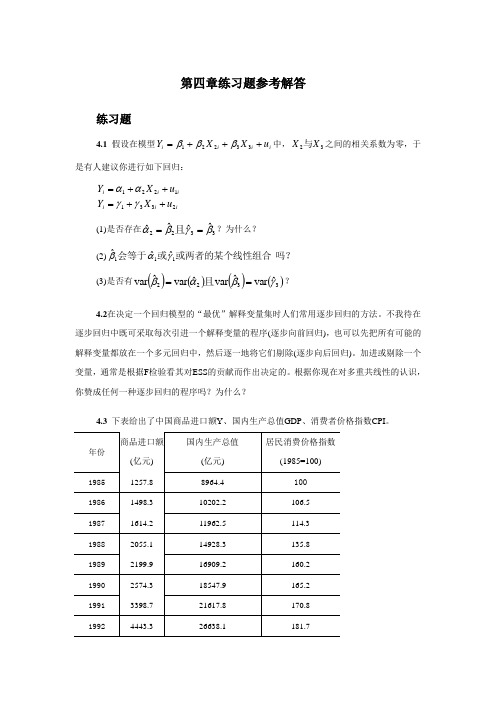
第四章练习题参考解答练习题4.1 假设在模型i i i i u X X Y +++=33221βββ中,32X X 与之间的相关系数为零,于是有人建议你进行如下回归:ii i i i i u X Y u X Y 23311221++=++=γγαα(1)是否存在3322ˆˆˆˆβγβα==且?为什么? (2)吗?或两者的某个线性组合或会等于111ˆˆˆγαβ (3)是否有()()()()3322ˆvar ˆvar ˆvar ˆvar γβαβ==且? 4.2在决定一个回归模型的“最优”解释变量集时人们常用逐步回归的方法。
不我待在逐步回归中既可采取每次引进一个解释变量的程序(逐步向前回归),也可以先把所有可能的解释变量都放在一个多元回归中,然后逐一地将它们剔除(逐步向后回归)。
加进或剔除一个变量,通常是根据F 检验看其对ESS 的贡献而作出决定的。
根据你现在对多重共线性的认识,你赞成任何一种逐步回归的程序吗?为什么?4.3 下表给出了中国商品进口额Y 、国内生产总值GDP 、消费者价格指数CPI 。
2资料来源:《中国统计年鉴》,中国统计出版社2000年、2004年。
请考虑下列模型:i t t t u CPI GDP Y ++=ln ln ln 321βββ+ (1)利用表中数据估计此模型的参数。
(2)你认为数据中有多重共线性吗? (3)进行以下回归:it t i t t i t t v CPI C C GDP v CPI B B Y v GDP A A Y 321221121ln ln ln ln ln ln ++=+=+=++根据这些回归你能对数据中多重共线性的性质说些什么?(4)假设数据有多重共线性,但32ˆˆββ和在5%水平上个别地显著,并且总的F 检验也是显著的。
对这样的情形,我们是否应考虑共线性的问题?4.4 自己找一个经济问题来建立多元线性回归模型,怎样选择变量和构造解释变量数据矩阵X 才可能避免多重共线性的出现?4.5 克莱因与戈德伯格曾用1921-1950年(1942-1944年战争期间略去)美国国内消费Y 和工资收入X1、非工资—非农业收入X2、农业收入X3的时间序列资料,利用OLSE 估计得出了下列回归方程:337.107 95.0 (1.09) (0.66) (0.17) (8.92) 3121.02452.01059.1133.8ˆ2==+++=F R X X X Y(括号中的数据为相应参数估计量的标准误)。
计算机体系结构第四章练习题参考解答

计算机体系结构第四章练习题参考解答第四章4.52 浮点数系统使⽤的阶码基值r e =2,阶值位数q=2,尾数基值r m =10,尾数位数p ′=1,即按照使⽤的⼆进制位数来说,等价于p=4。
计算在⾮负阶、正尾数、规格化情况下的最⼩尾数值、最⼤尾数值、最⼤阶值、可表⽰的最⼩值和最⼤值及可表⽰数的个数。
解: 最⼩尾数值:r m -1 = 10-1 = 0.1最⼤尾数值:1- r m -p ′ =1-10-1 = 0.9 最⼤阶值:2q -1=3可表⽰数的最⼩值:1×r m -1 = 10-1 = 0.1 可表⽰数的最⼤值:r m 2q-1×(1- r m -p ′)=103(1-10-1)= 900可表⽰数的个数:2q ×r m p ′(r m -1)/r m = 22×101(10-1)/10 = 364.53 ⼀台机器要求浮点数的字长的精度不低于10-7.2,表数的范围正数不⼩于1038,且正负对称。
尾数⽤原码、纯⼩数表⽰,阶码⽤移码、整数表⽰。
设计这种浮点数的格式。
解依题意,取表数范围N =1038,表数精度δ=10-7.2。
由式(4-4)得:37log(log10log 21)log 2q +> = 6.99,上取整,得到阶码字长q=7。
由式(4-5)得:16log1053.2log 2p -->=,上取整,得到尾数字长p=24。
从⽽加上⼀个尾数符号位和⼀个阶码符号位,浮点数的总字长为:p+q+2=24+7+2=33。
实际浮点数总字长应为8的倍数,故取浮点数总字长为40位。
多出的7位可以加到尾数字长p 中⽤于提⾼浮点数的表数精度,也可以加到阶码字长q 中来扩⼤浮点数的表数范围。
暂且让p 增加6位,q 增加1位,即p=30,q=8。
如图4-8所⽰是设计出来的浮点数格式。
图4-8 例4.2浮点数的设计格式4.58 ⽤于⽂字处理的某专⽤机,每个⽂字符⽤4位⼗进制数字(0~9)编码表⽰,空格⽤︼表⽰。
信息论与编码理论-第4章无失真信源编码-习题解答-20071202
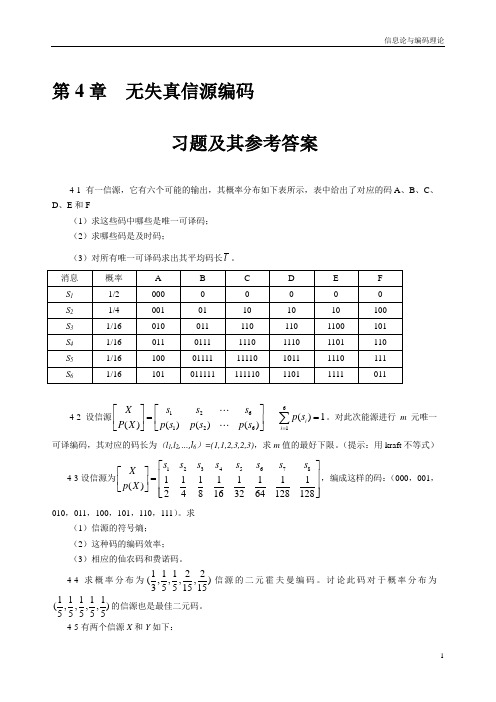
第4章无失真信源编码习题及其参考答案4-1 有一信源,它有六个可能的输出,其概率分布如下表所示,表中给出了对应的码A、B、C、D、E和F(1)求这些码中哪些是唯一可译码;(2)求哪些码是及时码;(3)对所有唯一可译码求出其平均码长l。
4-2 设信源61261126()1()()()()iis s sXp sp s p s p sP X=⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦∑。
对此次能源进行m元唯一可译编码,其对应的码长为(l1,l2,…,l6)=(1,1,2,3,2,3),求m值的最好下限。
(提示:用kraft不等式)4-3设信源为1234567811111111()248163264128128s s s s s s s sXp X⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦,编成这样的码:(000,001,010,011,100,101,110,111)。
求(1)信源的符号熵;(2)这种码的编码效率;(3)相应的仙农码和费诺码。
4-4求概率分布为11122(,,,,)3551515信源的二元霍夫曼编码。
讨论此码对于概率分布为11111(,,,,)55555的信源也是最佳二元码。
4-5有两个信源X和Y如下:121234567()0.200.190.180.170.150.100.01X s s s s s s s p X ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦123456789()0.490.140.140.070.070.040.020.020.01Y s s s s s s s s s p Y ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦(1)用二元霍夫曼编码、仙农编码以及费诺编码对信源X 和Y 进行编码,并计算其平均码长和编码效率;(2)从X ,Y 两种不同信源来比较三种编码方法的优缺点。
4-6设二元霍夫曼码为(00,01,10,11)和(0,10,110,111),求出可以编得这样 霍夫曼码的信源的所有概率分布。
4-7设信源为12345678()0.40.20.10.10.050.050.050.05X s s s s s s s s p X ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦,求其三元霍夫曼编码。
第4章集成运算放大器习题解答

第4章集成运算放⼤器习题解答第四章习题参考答案4-1 什么叫“虚短”和“虚断”?答虚短:由于理想集成运放的开环电压放⼤倍数⽆穷⼤,使得两输⼊端之间的电压近似相等,即-+≈u u 。
虚断:由于理想集成运放的开环输⼊电阻⽆穷⼤,流⼊理想集成运放的两个输⼊端的电流近似等于零,即0≈=-+i i 。
4-2 理想运放⼯作在线性区和⾮线性区时各有什么特点?分析⽅法有何不同?答理想运放⼯作在线性区,通常输出与输⼊之间引⼊深度负反馈,输⼊电压与输出电压成线性关系,且这种线性关系只取决于外部电路的连接,⽽与运放本⾝的参数没有直接关系。
此时,利⽤运放“虚短”和“虚断”的特点分析电路。
理想运放⼯作在⾮线性去(饱和区),放⼤器通常处于开环状态,两个输⼊端之间只要有很⼩的差值电压,输出电压就接近正、负电压饱和值,此时,运放仍具有“虚断”的特点。
4-3 要使运算放⼤器⼯作在线性区,为什么通常要引⼊负反馈?答由于理想运放开环电压放⼤倍数∞=uo A ,只有引⼊深度负反馈,才能使闭环电压放⼤倍数FA 1u =,保证输出电压与输⼊电压成线性关系,即运放⼯作在线性区。
4-4 已知F007运算放⼤器的开环放⼤倍数dB A uo 100=,差模输⼊电阻Ω=M r id 2,最⼤输出电压V U sat o 12)(±=。
为了保证⼯作在线性区,试求:(1)+u 和-u 的最⼤允许值;(2)输⼊端电流的最⼤允许值。
解(1)由运放的传输特性5o uo 1012===++u u u A 则V 102.1101245--+?===u u(2)输⼊端电流的最⼤允许值为A 106102102.11164id --+?=??==r u I 4-5 图4-29所⽰电路,设集成运放为理想元件。
试计算电路的输出电压o u 和平衡电阻R 的值。
解由图根据“虚地”特点可得0==+-u u图中各电流为601.01--=u i 305.02---=u i 180o f u u i -=- 由“虚断”得f 21i i i =+以上⼏式联⽴,可得V 7.2o =u平衡电阻为Ω==k R 18180//60//30图4-29 题4-5图4-6 图4-30所⽰是⼀个电压放⼤倍数连续可调的电路,试问电压放⼤倍数uf A 的可调范围是多少?图4-30 题4-6图解设滑线变阻器P R 被分为x R 和x P R R -上下两部分。
第4章 字符串 习题参考答案

第4章串习题参考答案一、基础知识题4.1 简述下列每对术语的区别:空串和空格串;串常量与串变量;主串和子串;串变量的名字和串变量的值;静态分配的顺序串与动态分配的顺序串。
【解答】不含任何字符的串称为空串,其长度为0。
仅含有空格字符的串称为空格串,其长度为串中空格字符的个数。
空格符可用来分割一般的字符,便于人们识别和阅读,但计算串长时应包括这些空格符。
空串在串处理中可作为任意串的子串。
用引号(数据结构教学中通常用单引号,而C语言中用双引号)括起来的字符序列称为串常量,串值可以变化的量称为串变量。
串中任意个连续的字符组成的子序列被称为该串的子串。
包含子串的串又被称为该子串的主串。
子串在主串中第一次出现的第一个字符的位置称子串在主串中的位置。
串变量的与其它变量一样,要用名字引用其值,串变量的名字也是标识符,串变量的值可以修改。
串的存储也有静态存储和动态存储两种。
静态存储指用一维数组,通常一个字符占用一个字节,需要静态定义串的长度,具有顺序存储结构的优缺点。
若需要在程序执行过程中,动态地改变串的长度,则可以利用标准函数malloc()和free()动态地分配或释放存储单元,提高存储资源的利用率。
在C语言中,动态分配和回收的存储单元都来自于一个被称之为“堆”的自由存储区,故该方法可称为堆分配存储。
类型定义如下所示:typedef struct{ char *str;int length;}HString;4.2设有串S=’good’,T=’I︼am︼a︼student’,R=’!’,求:(1)StringConcat(T,R) (2)SubString(T,8,7)(3)StringLength(T) (4)Index(T,’a’)(5)StringInsert(T,8,S)(6)Replace(T,SubString(T,8,7),’teacher’)【解答】(1) StringConcat(T,R)=’I︼am︼a︼student!’(2) SubString(T,8,7)=’student’(3) StringLength(T)=14(4) Index(T,’a’)=3(5) StringInsert(T,8,S)=’I︼am︼a︼goodstudent’(6) Replace(T,SubString(T,8,7),’teacher’)= ’I︼am︼a︼teacher’4.3若串S1=‘ABCDEFG’,S2=‘9898’,S3=‘###’,S4=‘012345’,执行concat(replace(S1,substr(S1,length(S2),length(S3)),S3),substr(S4,index(S2,‘8’),length(S2))) 操作的结果是什么?【解答】concat(replace(S1,substr(S1,length(S2),length(S3)),S3),substr(S4,index(S2,‘8’),length(S2))) = concat(replace(S1,substr(S1,4,3),S3),substr(S4,2,4))= concat(replace(S1,’DEF’,S3),’1234’)= concat(‘ABC###G ’,’1234’)= ‘ABC###G1234’4.4 设S 为一个长度为n 的字符串,其中的字符各不相同,则S 中的互异的非平凡子串(非空且不同于S 本身)的个数是多少?【解答】长度为n 的字符串中互异的非平凡子串(非空且不同于S 本身)的个数计算如下: 长度为1的子串有n 个,长度为2的子串有n-1个,长度为3的子串有n-2个,……,长度为n-1的子串有2个,长度为n 的子串有1个(按题意要求这个子串就是S 本身,不能计算在总数内)。
《电工与电子技术基础》第4章半导体器件习题解答

第4章半导体器件习题解答习题4.1计算题4.1图所示电路的电位U Y 。
(1)U A =U B =0时。
(2)U A =E ,U B =0时。
(3)U A =U B =E 时。
解:此题所考查的是电位的概念以及二极管应用的有关知识。
假设图中二极管为理想二极管,可以看出A 、B 两点电位的相对高低影响了D A 和D B 两个二极管的导通与关断。
当A 、B 两点的电位同时为0时,D A 和D B 两个二极管的阳极和阴极(U Y )两端电位同时为0,因此均不能导通;当U A =E ,U B =0时,D A 的阳极电位为E ,阴极电位为0(接地),根据二极管的导通条件,D A 此时承受正压而导通,一旦D A 导通,则U Y >0,从而使D B 承受反压(U B =0)而截止;当U A =U B =E 时,即D A 和D B 的阳极电位为大小相同的高电位,所以两管同时导通,两个1k Ω的电阻为并联关系。
本题解答如下:(1)由于U A =U B =0,D A 和D B 均处于截止状态,所以U Y =0;(2)由U A =E ,U B =0可知,D A 导通,D B 截止,所以U Y =Ω+Ω⋅Ωk k E k 919=109E ;(3)由于U A =U B =E ,D A 和D B 同时导通,因此U Y =Ω+Ω×⋅Ω×k k E k 19292=1918E 。
4.2在题4.2图所示电路中,设VD 为理想二极管,已知输入电压u I 的波形。
试画出输出电压u O 的波形图。
题4.1图题4.2图解:此题的考查点为二极管的伏安特性以及电路的基本知识。
首先从(b)图可以看出,当二极管D 导通时,电阻为零,所以u o =u i ;当D 截止时,电第4章半导体器件习题解答阻为无穷大,相当于断路,因此u o =5V,即是说,只要判断出D导通与否,就可以判断出输出电压的波形。
要判断D 是否导通,可以以接地为参考点(电位零点),判断出D 两端电位的高低,从而得知是否导通。
线性代数习题答案4

a2 + b2 3 (a2 + b2 3)(a2 − b2 3) a22 − 3b22
a22 − 3b22
3,
a1 ± a2 , b1
± b2;
a1a2
+ 3b1b2 , a1b2
+ a2b1;
a1a2 a22
− 3b1b2 − 3b22
,
(a2b1 − a1b2 a22 − 3b22
)
都是有理数,故 K2 是数域.
x + y = (x1 + y1, x2 + y2 , x3 + y3 )T , 2(x1 + y1) + 3(x2 + y2 ) − (x3 + y3 ) = 0 ⇒ x + y ∈W4 , kx = (kx1, kx2 , kx3)T , 2(kx1) + 3(kx2 ) − (kx3) = 0 ⇒ kx ∈W4 故W4 对 R3 中的加法与数乘运算封闭, 它是 R3 的子空间. (5) W5 = {x ∈ R3 | 2x1 + 3x2 − x3 = 1}; 【解】W5 不是 R3 的子空间. 显然W5 中不含有零向量, 故W5 不是 R3 的子空间. (6) W6 = {x ∈ R3 | x1 − x22 = 0}.
=
a1a2 a22
+ b1b2 + b22
+
(a2b1 a22
− a1b2 ) + b22
i,
a1
± a2 , b1
± b2;
a1a2
− b1b2 , a1b2
+ a2b1;
a1a2 + b1b2 a22 + b22
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第4章习题及参考解答第4章习题及参考解答1.试编一程序,把地址偏移量为100H单元开始的256个单元分别写入00H,01H,02H,03H,…,FFH 数据。
解源程序如下DATA SEGMENTORG 100HBUF1 DB 256 DUP(?)COUNT EQU$-BUF1DATA ENDSSTK SEGMENT STACKDB 100 DUP(?)STK ENDSCODE SEGMENTASSUME CS:CODE,DS:DATASTART:M OV AX,DATAMOV DS,AXMOV SI,OFFSET BUF1 ;戓LEA SI,BUF1MOV CX,COUNTXOR AL,AL ;或MOV AL,00HNEXT:MOV [SI],ALINC ALINC SILOOP NEXTMOV AH,4CHINT 21 HCODE ENDSEND START2.统计上题写入的数据块中0元素、正元素、负元素的个数,并分别把统计结果送入上述数据块之后的三个单元中。
解DATA SEGMENTO RG 100HBUF1 DB 00H,01H.02H,…,0FEH,0FFH ;共256个数据COUNT EOU$-BUF1DB 3 DUP(?)DATA E NDSSTK SEGMENT STACKDB 100 DUP(?)STK ENDSCODE SEGMENTA SSUME CS:CODE,DS:DATASTART: MOV AX,DATAMOV DS,AXMOV S1,OFFSET BUF1MOC CX,COUNTXOR BX,BX ;BL与BH分别存放正、负元素的个数XOR DH,DH ;DH寄存器存放0元素个数NEXT2: MOV AL,[SI]CMP AL,0JZ ZER0 ;若ZF=1,则为0,转至ZERO,DH+1JS NEGAT ;若SF=0则为负数,BH+1INC BL ;既不是0又不是负,则为正数,BL+1JMP NEXT3ZERO: INC DH ;0的个数加1 J MP NEXT3NEGAT:INC BH ;负数个数加1 NEXT3: INC SI ;修改地址指针SI L OOP NEXT2 ;未完,继续循环M OV [SI],DH ;存入0元素个数统计结果I NC SIM OV [SI],BX ;存入正、负数个数统计结果M OV AH,4CHI NT 21HCODE ENDSE ND START4.把地址偏移量为STRG1单元开始的128个单元的内容传送到地址偏移量为STRG2开始的单元中。
解DATA SEGMENTSTRGl DB XXH,XXH,XXH,….XXH;1 28个数据COUNT EOU$-STRGlSTRG2 DB 128 DUP(?)DATA ENDSCODE SEGMENTASSUME CS:CODE,DS:DATASTART:MOV AX,DATAMOV DS,AXMOV SI,OFFSET STRG1MOV DI,OFFSET STRG2MOV CX,COUNTCLDREP MOVSBMOV AH,4CHINT 21 HCODE ENDSEND START5.寄存器SI做地址指针,自SI所指的内存单元开始连续存放三个无符号数(以字为单位),编一程序求它们的和,并将结果存放在这三个数之后的单元中。
解DATA SEGMENTBUF DW XXH,YYH,ZZHSUM DW ?,?DATA ENDSCODE SEGMENTASSUME CS:CODE,DS:DATASTART:MOV AX,DATAMOV DS,AXMOV SI,OFFSET BUFMOV DI,OFFSET SUMMOV AX,[SI]ADD AX,[SI+2]MOV [DI],AXMOV AX,0ADDC AX,0MOV [DI+2],AXMOV AX,[DI]ADDC AX,[SI+4]MOV [DI],AXMOV AX,0ADDC AX,[DI+2]MOV [DI+2],AXMOV AH,4CHINT 21HCODE ENDSEND START6.读下面程序段,问:在什么情况下本段程序的执行结果是AH=0?START:IN AL,5FHMOV AH,0JZ BRCHMOV AH,0JMP STOPBRCH:MOV AH,0FFHSTOP:INT 20H解当标志寄存器的ZF=0时,执行结果AH=0。
(JZ之前的两条指令对零标志没有影响)7.下面语句在存储器中分别为变量分配多少字节? 0NE DW 10TW0 DW 4 DUP(?),5THREE DB 2 DUP(?,8 DUP(0))COUNT EQU 10FOUR DD COUNT DUP(?)FIVE DB‘HOW ARE YOU?’解ONE DW 10 ;为ONE分配2个字节TWO DW 4 DUP(?),5 ;为TWO分配10个字节THREE DB 2 DUP(?,8 DUP(0)) ;为THREE 分配18个字节COUNT EQU 10 ;不给COUNT分配存储单元FOUR DD COUNT DUP(?) ;为FOUR分配40个字节FIVE DB ‘HOW ARE YOU?’;为FIVE分配12个字节8.数据定义语句如下所示:FIRST DB 90H,5FH,6EH,69HSECOND DB 5 DUP(?)THIRD DB 5 DUP(?)FORTH DB DUP(?)自FIRST单元开始存放的是一个四字节的十六进制数(低位字节在前),要求:(1)编一段程序将这个数左移两位后存放到自SECOND开始的单元(注意保留移出部分);(2)编一段程序将这个数右移两位后存放到自THIRD开始的单元(注意保留移出部分);(3)编一段程序将这个数求补后存放到自FORTH开始的单元。
解DATA SEGMENTFIRST DB 90H,5FH,6EH,69HSECOND D B 5 DUP (?)THIRD DB 5 DUP (?)FORTH DB DUP (?)DATA ENDSCODE SEGMENTASSUME CS:CODE,DS:DATA START:M OV AX,DATAMOV DS,AXCALL SUBP1CALL SUBP2CALL SUBP3MOV AH,4CHINT 21HSUBP1 PROCMOV SI,OFFSET FIRSTMOV DI,OFFSET SECONDXOR BL,BLMOV CL,2MOV AX,[SI]MOV DX,[SI+2]LOP1:SHL AX,1RCL DX,1RCL BL,1DEC CLJNZ LOP1MOV [DI],AXMOV [DI+2],DXMOV [DI+4],BLRETSUBP1 ENDPSUBP2 PROCMOV SI,OFFSET FIRSTMOV DI,OFFSET THIRDXOR BL,BLMOV CL,2MOV AX,[SI]MOV DX,[SI+2]LOP2:SHR DX,1RCR AX,1RCR BL,1DEC CLJNZ LOP2MOV [DI],BLMOV [DI+1],AXMOV [DI+3],DXRETSUBP2 ENDPSUBP3 PROCMOV SI,OFFSET FIRSTMOV DI,OFFSET FORTHMOV AX,[SI]MOV DX,[SI+2]NOT AXNOT DXADD AX,1ADC DX,0MOV [DI],AXMOV [DI+2],DXRETSUBP3 ENDPCODE ENDSEND START9.指令语句AND AX,OPD1 AND OPD2中,OPD1和OPD2是两个已赋值的变量,问两个AND操作分别在什么时间进行?有什么区别?解前面的AND是指令,在程序运行时执行,后面的AND是运算符,在汇编的时候由汇编程序计算,表达式计算结果出现在执行程序中。
二者的区别在于,前者是指令,程序运行时执行,后者是运算符,汇编时计算。
10.如下指令或程序是否有错,若有错,请指出错在哪里?(1)KI EOU 1024┇MOV K1,AX(2) MOV DS,100MOV [1000],[2000](3)IMP DB ?┇MOV IMP,AX(4)A1 DB ?A2 DB 10┇CMP A1,A2(5)将1000送入X1单元,用如下程序:X1 DB ?┇MOV BX,X1MOV [BX],1000解(1)MOV K1,AX错。
因为K1为立即数,它不能作为目的操作数。
(2)这两条指令都是错的。
第一条立即数不能直接送给段寄存器;第二条两个操作数不能同时为内存操作数。
(3)MOV IMP,AX错。
两操作数类型不匹配,IMP 是一字节内存单元,而AX寄存器中为16位数据。
(4)CMP A1,A2错。
两个操作数A1与A2不能同时为内存操作数。
(5)MOV [BX],1000错。
两操作数类型不匹配,[BX]只定义了一字节单元,而1000是16位数据。
11.8086汇编语言程序中段的类型有几种?各段如何定义?段定义语句中,定位类型、组合类型、类别各起什么作用?各有什么含义?解8086汇编语言中,段的类型有三种,即代码段、堆栈段、数据段(附加数据段可归属于数据段)。
各段可用段定义语句(SEGMENT与ENDS)和段名赋给段寄存器语句(ASSUME)来定义。
段定义语句中,定位类型表示此段的起始边界要求,可允许4种段的起始边界,即PAGE、PARA、WORD或BYTE。
它们分别表示段的起始值为以页、节、字、字节为边界,若此项省略,则默认值为PARA。
组合类型用来告诉连接程序本段与其他段的关系,分别为NONE、PUBLIC、COMMON、AT表达式、STACK或MEMORY。
每一种的含义请参看主教材。
类别是连接程序(LINK)需要的。
它可以是任何合法的名称,必须用单引号括起来,连接程序只使同类别的段发生关联。
典型类别如‘CODE’、'STACK'。
12.使用DOS功能调用0AH从键盘输入40个字符的字符串并将其送入一输入缓冲区。
在按下Enter键后,显示这些字符。
解NAME KBDINPUTCODE SEGMENTASSUME CS:CODE,DS:CODEORG 100HSTART:JMP BEGINBUF DB41NUMB DB ?CHARS DB 41 DUP(?)MSG1DB'Type anything,followed by enter.',0DH,0AH,'$'MSG2 DB 0DH,0AH,'Contents of the KBD input buf:',0DH,0AH,'$'BEGIN:MOV AX,CSMOV DS,AXMOV DX,OFFSET MSG1MOV AH,9INT 21HMOV DX,OFFSET BUFMOV AH,0AHINT 21 HMOV DX,OFFSET MSG2MOV AH,9INT 21HXOR BX,BXMOV BL,NUMBMOV CHARS[BX],'$'MOV DX,OFFSET CHARSMOV AH,9INT 21HMOV AH,4CHINT 21HCODE ENDSEND START说明本题把数据区放在代码段中,没有单独定义数据段。
