高考全国卷文数试题及答案
(完整版)2019年高考新课标(全国卷1)文数真题(word版,含解析)

2019年高考新课标全国1卷(文科数学)一、选择题:本题共12小题,每小题5分,共60分。
1.设3i12iz -=+,则z = A .2B .3C .2D .12.已知集合{}{}{}1,2,3,4,5,6,72,3,4,52,3,6,7U A B ===,,,则C U B A I A .{}1,6B .{}1,7C .{}6,7D .{}1,6,73.已知0.20.32log 0.2,2,0.2a b c ===,则A .a b c <<B .a c b <<C .c a b <<D .b c a <<4.古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是51-(51-≈0.618,称为黄金分割比例),著名的“断臂维纳斯”便是如此.此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是512-.若某人满足上述两个黄金分割比例,且腿长为105cm ,头顶至脖子下端的长度为26cm ,则其身高可能是 A .165 cm B .175 cmC .185 cmD .190cm5.函数f (x )=2sin cos x xx x++在[—π,π]的图像大致为 A .B .C .D .6.某学校为了解1 000名新生的身体素质,将这些学生编号为1,2,…,1 000,从这些新生中用系统抽样方法等距抽取100名学生进行体质测验,若46号学生被抽到,则下面4名学生中被抽到的是 A .8号学生 B .200号学生C .616号学生D .815号学生7.tan255°= A .-23B .-3C .23D .38.已知非零向量a ,b 满足a =2b ,且(a –b )⊥b ,则a 与b 的夹角为A .π6 B .π3C .2π3D .5π69.如图是求112122++的程序框图,图中空白框中应填入A .A =12A +B .A =12A +C .A =112A +D .A =112A+10.双曲线C :22221(0,0)x y a b a b-=>>的一条渐近线的倾斜角为130°,则C的离心率为 A .2sin40°B .2cos40°C .1sin50︒D .1cos50︒11. △ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知a sin A -b sin B =4c sin C ,cos A =-14,则b c=A .6B .5C .4D .312.已知椭圆C 的焦点为121,01,0F F -(),(),过F 2的直线与C 交于A ,B 两点.若222AF F B =││││,1AB BF =││││,则C 的方程为A .2212x y +=B .22132x y +=C .22143x y +=D .22154x y +=二、填空题:本题共4小题,每小题5分,共20分。
2023年高考真题及答案解析《数学文》(全国甲卷)
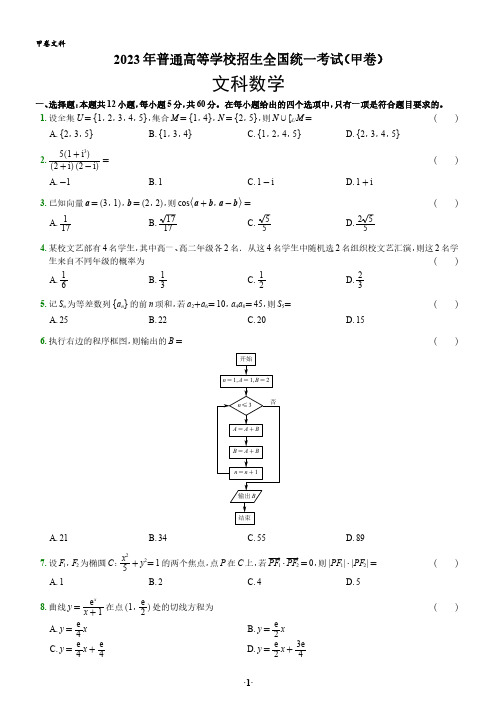
甲卷文科2023年普通高等学校招生全国统一考试(甲卷)文科数学一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设全集U ={1,2,3,4,5},集合M ={1,4},N ={2,5},则N ∪∁U M =()A.{2,3,5}B.{1,3,4}C.{1,2,4,5}D.{2,3,4,5}2.5(1+i 3)(2+i )(2-i )=()A.-1B.1C.1-iD.1+i3.已知向量a =(3,1),b =(2,2),则cos a +b ,a -b =()A.117B.1717C.55D.2554.某校文艺部有4名学生,其中高一、高二年级各2名.从这4名学生中随机选2名组织校文艺汇演,则这2名学生来自不同年级的概率为()A.16B.13C.12D.235.记S n 为等差数列{a n }的前n 项和,若a 2+a 6=10,a 4a 8=45,则S 5=()A.25B.22C.20D.156.执行右边的程序框图,则输出的B =()n ≤3n =1,A =1,B =2开始A =A +B B =A +B n =n +1结束输出B否A.21B.34C.55D.897.设F 1,F 2为椭圆C :x 25+y 2=1的两个焦点,点P 在C 上,若PF 1 ⋅PF 2 =0,则|PF 1|⋅|PF 2|=()A.1B.2C.4D.58.曲线y =e xx +1在点(1,e 2)处的切线方程为()A.y =e4xB.y =e2x C.y =e4x +e 4 D.y =e 2x +3e4ABC A 1B 1C 19.已知双曲线C :x 2a 2-y 2b2=1(a >0,b >0)的离心率为5,C 的一条渐近线与圆(x -2)2+(y -3)2=1交于A ,B 两点,则|AB |=()A.55B.255C.355D.45510.在三棱锥P -ABC 中,△ABC 是边长为2的等边三角形,PA =PB =2,PC =6,则该棱锥的体积为()A.1B.3C.2D.311.已知函数f (x )=e-(x -1)2,记a =f 22,b =f 32 ,c =f 62 ,则()A.b >c >aB.b >a >cC.c >b >aD.c >a >b12.函数y =f (x )的图象由y =cos (2x +π6)的图象向左平移π6个单位长度得到,则y =f (x )的图象与直线y =12x -12的交点个数为()A.1B.2C.3D.4二、填空题:本大题共4小题,每小题5分,共20分。
2024年高考数学试卷(文)(全国甲卷)(含答案)

绝密★启用前2024年普通高等学校招生全国统一考试全国甲卷文科数学使用范围:陕西、宁夏、青海、内蒙古、四川注意事项:1.答题前,务必将自己的姓名、考籍号填写在答题卡规定的位置上.2.答选择题时,必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦擦干净后,再选涂其它答案标号.3.答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上.4.所有题目必须在答题卡上作答,在试题卷上答题无效.5.考试结束后,只将答题卡交回.一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 集合{}1,2,3,4,5,9A =,{}1B x x A =+Î,则A B =I ( )A. {}1,2,3,4B. {}1,2,3 C. {}3,4 D. {}1,2,9【答案】A 【解析】【分析】根据集合B 的定义先算出具体含有的元素,然后根据交集的定义计算.【详解】依题意得,对于集合B 中的元素x ,满足11,2,3,4,5,9x +=,则x 可能的取值为0,1,2,3,4,8,即{0,1,2,3,4,8}B =,于是{1,2,3,4}A B Ç=.故选:A2. 设z =,则z z ×=( )A. -iB. 1C. -1D. 2【答案】D 【解析】【分析】先根据共轭复数的定义写出z ,然后根据复数的乘法计算.【详解】依题意得,z =,故22i 2zz =-=.故选:D3. 若实数,x y 满足约束条件43302202690x y x y x y --³ìï--£íï+-£î,则5z x y =-最小值为( )A. 5B.12C. 2-D. 72-【答案】D 【解析】【分析】画出可行域后,利用z 的几何意义计算即可得.【详解】实数,x y 满足43302202690x y x y x y --³ìï--£íï+-£î,作出可行域如图:由5z x y =-可得1155y x z =-,即z 的几何意义为1155y x z =-的截距的15-,则该直线截距取最大值时,z 有最小值,此时直线1155y x z =-过点A ,联立43302690x y x y --=ìí+-=î,解得321x y ì=ïíï=î,即3,12A æöç÷èø,则min 375122z =-´=-.故选:D.4. 等差数列{}n a 的前n 项和为n S ,若91S =,37a a +=( )A. 2- B.73C. 1D.29【答案】D 【解析】的【分析】可以根据等差数列的基本量,即将题目条件全转化成1a 和d 来处理,亦可用等差数列的性质进行处理,或者特殊值法处理.【详解】方法一:利用等差数列的基本量由91S =,根据等差数列的求和公式,911989193612S a d a d ´=+=Û+=,又371111222628(936)99a a a d a d a d a d +=+++=+=+=.故选:D方法二:利用等差数列的性质根据等差数列的性质,1937a a a a +=+,由91S =,根据等差数列的求和公式,193799()9()122a a a a S ++===,故3729a a +=.故选:D方法三:特殊值法不妨取等差数列公差0d =,则9111199S a a ==Þ=,则371229a a a +==.故选:D5. 甲、乙、丙、丁四人排成一列,丙不在排头,且甲或乙在排尾的概率是( )A.14B.13C.12D.23【答案】B 【解析】【分析】分类讨论甲乙的位置,得到符合条件的情况,然后根据古典概型计算公式进行求解.【详解】当甲排在排尾,乙排第一位,丙有2种排法,丁就1种,共2种;当甲排在排尾,乙排第二位或第三位,丙有1种排法,丁就1种,共2种;于是甲排在排尾共4种方法,同理乙排在排尾共4种方法,于是共8种排法符合题意;基本事件总数显然是44A 24=,根据古典概型的计算公式,丙不在排头,甲或乙在排尾的概率为81243=.故选:B6. 已知双曲线2222:1(0,0)y x C a b a b-=>>的上、下焦点分别为()()120,4,0,4F F -,点()6,4P -在该双曲线上,则该双曲线的离心率为( )A. 4B. 3C. 2D.【答案】C 【解析】【分析】由焦点坐标可得焦距2c ,结合双曲线定义计算可得2a ,即可得离心率.【详解】由题意,()10,4F -、()20,4F 、()6,4P -,则1228F F c ==,110PF ==,26PF ==,则1221064a PF PF =-=-=,则28224c e a ===.故选:C.7. 曲线()631f x x x =+-在()0,1-处的切线与坐标轴围成的面积为( )A.16B.C.12D. 【答案】A 【解析】【分析】先求出切线方程,再求出切线的截距,从而可求面积.【详解】()563f x x =¢+,所以()03f ¢=,故切线方程为3(0)131y x x =--=-,故切线的横截距为13,纵截距为1-,故切线与坐标轴围成的面积为1111236´´=故选:A.8. 函数()()2e esin xxf x x x -=-+-在区间[ 2.8,2.8]-的大致图像为()A. B.C. D.【答案】B 【解析】【分析】利用函数的奇偶性可排除A 、C ,代入1x =可得()10f >,可排除D.【详解】()()()()()22ee sin e e sin xx x x f x x x x x f x ---=-+--=-+-=,又函数定义域为[]2.8,2.8-,故该函数为偶函数,可排除A 、C ,又()11πe 11111e sin11e sin 10e e 622e 42ef æöæö=-+->-+-=-->->ç÷ç÷èøèø,故可排除D.故选:B.9. 已知cos cos sin a a a =-πtan 4a æö+=ç÷èø( )A. 1+B. 1- C.D. 1【答案】B 【解析】【分析】先将cos cos sin aa -a弦化切求得tan a ,再根据两角和的正切公式即可求解.【详解】因为cos cos sin aa a=-,所以11tan =-a ,tan 1Þa =,所以tan 1tan 11tan 4a +p æö==a +ç÷-aèø,故选:B .原10题略10. 设a b 、是两个平面,m n 、是两条直线,且m a b =I .下列四个命题:①若//m n ,则//n a 或//n b ②若m n ^,则,n n a b^^③若//n a ,且//n b ,则//m n ④若n 与a 和b 所成的角相等,则m n^其中所有真命题的编号是( )A. ①③ B. ②④C. ①②③D. ①③④【答案】A【解析】【分析】根据线面平行的判定定理即可判断①;举反例即可判断②④;根据线面平行的性质即可判断③.【详解】对①,当n Ìa ,因为//m n ,m b Ì,则//n b ,当n b Ì,因为//m n ,m a Ì,则//n a ,当n 既不在a 也不在b 内,因为//m n ,,m m a b ÌÌ,则//n a 且//n b ,故①正确;对②,若m n ^,则n 与,a b 不一定垂直,故②错误;对③,过直线n 分别作两平面与,a b 分别相交于直线s 和直线t ,因为//n a ,过直线n 的平面与平面a 的交线为直线s ,则根据线面平行的性质定理知//n s ,同理可得//n t ,则//s t ,因为s Ë平面b ,t Ì平面b ,则//s 平面b ,因为s Ì平面a ,m a b =I ,则//s m ,又因为//n s ,则//m n ,故③正确;对④,若,m n a b Ç=与a 和b 所成的角相等,如果//,//a b n n ,则//m n ,故④错误;综上只有①③正确,故选:A.11. 在ABC V 中内角,,A B C 所对边分别为,,a b c ,若π3B =,294b ac =,则sin sin A C +=( )A.32B.C.D.【答案】C 【解析】【分析】利用正弦定理得1sin sin 3A C =,再利用余弦定理有22134a c ac +=,再利用正弦定理得到22sin sin A C +的值,最后代入计算即可.【详解】因为29,34B b ac p==,则由正弦定理得241sin sin sin 93A CB ==.由余弦定理可得:22294b ac ac ac =+-=,即:22134a c ac +=,根据正弦定理得221313sin sin sin sin 412A C A C +==,所以2227(sin sin )sin sin 2sin sin 4A C A C A C +=++=,因为,A C 为三角形内角,则sin sin 0A C +>,则sin sin A C +=.故选:C.二、填空题:本题共4小题,每小题5分,共20分.原13题略12. 函数()sin f x x x =在[]0,π上的最大值是______.【答案】2【解析】【分析】结合辅助角公式化简成正弦型函数,再求给定区间最值即可.【详解】()πsin 2sin 3f x x x x æö==-ç÷èø,当[]0,πx Î时,ππ2π,333x éù-Î-êúëû,当ππ32x -=时,即5π6x =时,()max 2f x =.故答案为:213. 已知1a >,8115log log 42a a -=-,则=a ______.【答案】64【解析】【分析】将8log ,log 4a a 利用换底公式转化成2log a 来表示即可求解.【详解】由题28211315log log log 4log 22a a a a -=-=-,整理得()2225log 60log a a --=,2log 1a Þ=-或2log 6a =,又1a >,所以622log 6log 2a ==,故6264a ==故答案:64.为14. 曲线33y x x =-与()21y x a =--+在()0,¥+上有两个不同的交点,则a 的取值范围为______.【答案】()2,1-【解析】【分析】将函数转化为方程,令()2331x x x a -=--+,分离参数a ,构造新函数()3251,g x x x x =+-+结合导数求得()g x 单调区间,画出大致图形数形结合即可求解.【详解】令()2331x x x a -=--+,即3251a x x x =+-+,令()()32510,g x x x x x =+-+>则()()()2325351g x x x x x =+-=+-¢,令()()00g x x ¢=>得1x =,当()0,1x Î时,()0g x ¢<,()g x 单调递减,当()1,x ¥Î+时,()0g x ¢>,()g x 单调递增,()()01,12g g ==-,因为曲线33y x x =-与()21y x a =--+在()0,¥+上有两个不同的交点,所以等价于y a =与()g x 有两个交点,所以()2,1a Î-.故答案为:()2,1-三、解答题:共70分.解答应写出文字说明,证明过程或演算步骤.第17题第21题为必考题,每个考题考生必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分.15. 已知等比数列{}n a 的前n 项和为n S ,且1233n n S a +=-.(1)求{}n a 的通项公式;(2)求数列{}n S 通项公式.【答案】(1)153n n a -æö=ç÷èø的(2)353232næö-ç÷èø【解析】【分析】(1)利用退位法可求公比,再求出首项后可求通项;(2)利用等比数列的求和公式可求n S .【小问1详解】因为1233n n S a +=-,故1233n n S a -=-,所以()12332n n n a a a n +=-³即153n n a a +=故等比数列的公比为53q =,故1211523333533a a a a =-=´-=-,故11a =,故153n n a -æö=ç÷èø.【小问2详解】由等比数列求和公式得5113353523213n nn S éùæö´-êúç÷èøêúæöëû==-ç÷èø-.16. 如图,在以A ,B ,C ,D ,E ,F 为顶点的五面体中,四边形ABCD 与四边形ADEF 均为等腰梯形,//,//BC AD EF AD ,4,2AD AB BC EF ====,ED FB ==M 为AD 的中点.(1)证明://BM 平面CDE ;(2)求点M 到ABF 的距离.【答案】(1)证明见详解; (2【解析】【分析】(1)结合已知易证四边形BCDM 为平行四边形,可证//BM CD,进而得证;(2)作FO AD ^,连接OB ,易证,,OB OD OF 三垂直,结合等体积法M ABF F ABM V V --=即可求解.【小问1详解】因为//,2,4,BC AD BC AD M ==为AD 的中点,所以//,BC MD BC MD =,四边形BCDM 为平行四边形,所以//BM CD ,又因BM Ë平面CDE ,CD Ì平面CDE ,所以//BM 平面CDE ;【小问2详解】如图所示,作BO AD ^交AD 于O ,连接OF ,因为四边形ABCD 为等腰梯形,//,4,BC AD AD =2AB BC ==,所以2CD =,结合(1)BCDM 为平行四边形,可得2BM CD ==,又2AM =,所以ABM V 为等边三角形,O 为AM中点,所以OB =,又因为四边形ADEF 为等腰梯形,M 为AD 中点,所以,//EF MD EF MD =,四边形EFMD 为平行四边形,FM ED AF ==,所以AFM △为等腰三角形,ABM V 与AFM △底边上中点O 重合,OF AM ^,3OF ==,因为222OB OF BF +=,所以OB OF ^,所以,,OB OD OF 互相垂直,由等体积法可得M ABF F ABM V V --=,2112333F ABM ABM V S FO -=×=×=△,222cos 2FA AB FBFAB FAB FA AB+-Ð===Ð=×11sin 222FAB S FA AB FAB =××Ð==△,设点M 到FAB的距离为d ,则1133M FAB F ABM FAB V V S d d --==××==△解得d =M 到ABF .为17. 已知函数()()1ln 1f x a x x =--+.(1)求()f x 的单调区间;(2)若2a £时,证明:当1x >时,()1ex f x -<恒成立.【答案】(1)见解析(2)见解析【解析】【分析】(1)求导,含参分类讨论得出导函数的符号,从而得出原函数的单调性;(2)先根据题设条件将问题可转化成证明当1x >时,1e 21ln 0x x x --++>即可.【小问1详解】()f x 定义域为(0,)+¥,11()ax f x a x x¢-=-=当0a £时,1()0ax f x x -¢=<,故()f x 在(0,)+¥上单调递减;当0a >时,1,x a ¥æöÎ+ç÷èø时,()0f x ¢>,()f x 单调递增,当10,x a æöÎç÷èø时,()0f x ¢<,()f x 单调递减.综上所述,当0a £时,()f x 在(0,)+¥上单调递减;0a >时,()f x 在1,a ¥æö+ç÷èø上单调递增,在10,a æöç÷èø上单调递减.【小问2详解】2a £,且1x >时,111e ()e (1)ln 1e 21ln x x x f x a x x x x ----=--+-³-++,令1()e 21ln (1)x g x x x x -=-++>,下证()0g x >即可.11()e 2x g x x -¢=-+,再令()()h x g x ¢=,则121()e x h x x-¢=-,显然()h x ¢在(1,)+¥上递增,则0()(1)e 10h x h ¢¢>=-=,即()()g x h x =¢在(1,)+¥上递增,故0()(1)e 210g x g ¢¢>=-+=,即()g x 在(1,)+¥上单调递增,故0()(1)e 21ln10g x g >=-++=,问题得证18. 设椭圆2222:1(0)x y C a b a b+=>>的右焦点为F ,点31,2M æöç÷èø在C 上,且MF x ^轴.(1)求C 的方程;(2)过点()4,0P 的直线与C 交于,A B 两点,N 为线段FP 的中点,直线NB 交直线MF 于点Q ,证明:AQ y ^轴.【答案】(1)22143x y += (2)证明见解析【解析】【分析】(1)设(),0F c ,根据M 的坐标及MF ^x 轴可求基本量,故可求椭圆方程.(2)设:(4)AB y k x =-,()11,A x y ,()22,B x y ,联立直线方程和椭圆方程,用,A B 的坐标表示1Q y y -,结合韦达定理化简前者可得10Q y y -=,故可证AQ y ^轴.【小问1详解】设(),0F c ,由题设有1c =且232b a =,故2132a a -=,故2a =,故b =,故椭圆方程为22143x y +=.【小问2详解】直线AB 的斜率必定存在,设:(4)AB y k x =-,()11,A x y ,()22,B x y ,由223412(4)x y y k x ì+=í=-î可得()2222343264120k x k x k +-+-=,故()()422Δ102443464120k k k =-+->,故1122k -<<,又22121222326412,3434k k x x x x k k-+==++,而5,02N æöç÷èø,故直线225:522y BN y x x æö=-ç÷èø-,故22223325252Q y y y x x --==--,所以()1222112225332525Q y x y y y y y x x ´-+-=+=--()()()12224253425k x x k x x -´-+-=-()222212122264123225825834342525k k x x x x k k k k x x -´-´+-++++==--2222212824160243234025k k k k k x --+++==-,故1Q y y =,即AQ y ^轴.(1)设直线方程,设交点坐标为()()1122,,,x y x y ;(2)联立直线与圆锥曲线的方程,得到关于x (或y )的一元二次方程,注意D 的判断;(3)列出韦达定理;(4)将所求问题或题中的关系转化为12x x +、12x x (或12y y +、12y y )的形式;(5)代入韦达定理求解.(二)选考题:共10分.请考生在第22、23题中任选一题作答,并用2B 铅笔将所选题号涂黑,多涂、错涂、漏涂均不给分,如果多做,则按所做的第一题计分.19. 在平面直角坐标系xOy 中,以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为cos 1r r q =+.(1)写出C 的直角坐标方程;(2)设直线l :x t y t a=ìí=+î(t 为参数),若C 与l 相交于A B 、两点,若2AB =,求a 的值.【答案】(1)221y x =+(2)34a =【解析】【分析】(1)根据cos xr r q ìï=í=ïî可得C 的直角方程.(2)将直线的新的参数方程代入C 的直角方程,法1:结合参数s 的几何意义可得关于a 的方程,从而可求参数a 的值;法2:将直线的直角方程与曲线的直角方程联立,结合弦长公式可求a 的值.【小问1详解】由cos 1r r q =+,将cos xr r q ìï=í=ïîcos 1r r q =+,1x =+,两边平方后可得曲线直角坐标方程为221y x =+.【小问2详解】对于直线l 的参数方程消去参数t ,得直线的普通方程为y x a =+.法1:直线l 的斜率为1故直线的参数方程可设为x y ì=ïïíïïî,s ÎR .将其代入221y x =+中得()221)210s a s a +-+-=设,A B 两点对应的参数分别为12,s s ,则)()212121,21s s a s s a +=--=-,且()()22Δ818116160a a a =---=->,故1a <,12AB s s\=-=2==,解得34a =.法2:联立221y x a y x =+ìí=+î,得22(22)10x a x a +-+-=,()22Δ(22)41880a a a =---=-+>,解得1a <,的设()()1122,,,A x y B x y ,2121222,1x x a x x a \+=-=-,则AB ==2=,解得34a =20. 实数,ab 满足3a b +³.(1)证明:2222a b a b +>+;(2)证明:22226a b b a -+-³.【答案】(1)证明见解析(2)证明见解析【解析】【分析】(1)直接利用22222()a b a b +³+即可证明.(2)根据绝对值不等式并结合(1)中结论即可证明.【小问1详解】因为()()2222222022a b a ab b a b b a -+=--++=³,当a b =时等号成立,则22222()a b a b +³+,因为3a b +³,所以22222()a b a b a b +³+>+;【小问2详解】222222222222()a b b a a b b a a b a b -+-³-+-=+-+22222()()()()(1)326a b a b a b a b a b a b =+-+³+-+=++-³´=。
高考全国乙卷:2022年[文数]考试真题与答案解析
![高考全国乙卷:2022年[文数]考试真题与答案解析](https://img.taocdn.com/s3/m/0f6fcfe2ba4cf7ec4afe04a1b0717fd5360cb2d2.png)
高考全国乙卷:2022年[文科数学]考试真题与答案解析一、选择题本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 集合,则( ){}{}2,4,6,8,10,16M N x x ==-<<M N = A. B. C. D. {2,4}{2,4,6}{2,4,6,8}{2,4,6,8,10}答案:A解析:因为,,所以.故选:A.{}2,4,6,8,10M ={}|16N x x =-<<{}2,4M N = 2. 设,其中为实数,则( )(12i)2i a b ++=,a b A. B. C. D. 1,1a b ==-1,1a b ==1,1a b =-=1,1a b =-=-答案:A解析:因为R ,,所以,解得:.故选:A.,a b Î()2i 2i a b a ++=0,22a b a +==1,1a b ==-3. 已知向量,则( )(2,1)(2,4)a b ==-,a b -r r A. 2 B. 3C. 4D. 5答案:D解析:因为,所以。
故选:D ()()()2,12,44,3a b -=--=- 5-==a b 4. 分别统计了甲、乙两位同学16周的各周课外体育运动时长(单位:h ),得如下茎叶图:则下列结论中错误的是( )A. 甲同学周课外体育运动时长的样本中位数为7.4B. 乙同学周课外体育运动时长的样本平均数大于8C. 甲同学周课外体育运动时长大于8的概率的估计值大于0.4D. 乙同学周课外体育运动时长大于8的概率的估计值大于0.6答案:C解析:对于A 选项,甲同学周课外体育运动时长的样本中位数为,A 选项结论7.37.57.42+=正确.对于B 选项,乙同学课外体育运动时长的样本平均数为:,6.37.47.68.18.28.28.58.68.68.68.69.09.29.39.810.18.50625816+++++++++++++++=>B 选项结论正确.对于C 选项,甲同学周课外体育运动时长大于的概率的估计值,860.3750.416=<C 选项结论错误。
2023年高考全国乙卷文科数学试题(含答案详解)

2023年普通高等学校招生全国统一考试(全国乙卷)文科数学一、选择题1. 232i 2i ++=( )A. 1B. 2C.D. 52. 设全集{}0,1,2,4,6,8U =,集合{}{}0,4,6,0,1,6M N ==,则M ∪C U N ( ) A. {}0,2,4,6,8B. {}0,1,4,6,8C. {}1,2,4,6,8D. U3. 如图,网格纸上绘制的一个零件的三视图,网格小正方形的边长为1,则该零件的表面积为( )A. 24B. 26C. 28D. 304. 在ABC 中,内角,,A B C 的对边分别是,,a b c ,若cos cos a B b A c −=,且5C π=,则B ∠=( )A.10π B.5π C.310π D.25π 5. 已知e ()e 1xax x f x =−是偶函数,则=a ( )A. 2−B. 1−C. 1D. 26. 正方形ABCD 的边长是2,E 是AB 的中点,则EC ED ⋅=( )A.B. 3C. D. 57. 设O 为平面坐标系的坐标原点,在区域(){}22,14x y xy ≤+≤内随机取一点A ,则直线OA 的倾斜角不大于π4的概率为( ) A.18B.16C.14D.128. 函数()32f x x ax =++存在3个零点,则a 的取值范围是( )A. (),2−∞−B. (),3−∞−C. ()4,1−−D. ()3,0−9. 某学校举办作文比赛,共6个主题,每位参赛同学从中随机抽取一个主题准备作文,则甲、乙两位参赛同学抽到不同主题概率为( )A.56B.23C.12D.1310. 已知函数()sin()f x x ωϕ=+在区间π2π,63⎛⎫ ⎪⎝⎭单调递增,直线π6x =和2π3x =为函数()y f x =的图像的两条对称轴,则5π12f ⎛⎫−= ⎪⎝⎭( )A. B. 12−C.12D.11. 已知实数,x y 满足224240x y x y +−−−=,则x y −的最大值是( )A. 1+B. 4C. 1+D. 712. 设A ,B 为双曲线2219y x −=上两点,下列四个点中,可为线段AB 中点的是( )A. ()1,1B. ()1,2-C. ()1,3D. ()1,4−−二、填空题13.已知点(A 在抛物线C :22y px =上,则A 到C 的准线的距离为______. 14. 若π10,,tan 22⎛⎫∈= ⎪⎝⎭θθ,则sin cos θθ−=________. 15. 若x ,y 满足约束条件312937x y x y x y −≤−⎧⎪+≤⎨⎪+≥⎩,则2z x y =−的最大值为______.16. 已知点,,,S A B C 均在半径为2的球面上,ABC 是边长为3的等边三角形,SA ⊥平面ABC ,则SA =________. 三、解答题17. 某厂为比较甲乙两种工艺对橡胶产品伸缩率的处理效应,进行10次配对试验,每次配对试验选用材质相同的两个橡胶产品,随机地选其中一个用甲工艺处理,另一个用乙工艺处理,测量处理后的橡胶产品的伸缩率.甲、乙两种工艺处理后的橡胶产品的伸缩率分别记为i x ,()1,2,,10i y i =⋅⋅⋅.试验结果如下:记1,2,,10i i i z x y i =−=⋅⋅⋅,记1210,,,z z z ⋅⋅⋅的样本平均数为z ,样本方差为2s . (1)求z ,2s ;(2)判断甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率是否有显著提高(如果z ≥为有显著提高)18.记n S 为等差数列{}n a 的前n 项和,已知21011,40a S ==. (1)求{}n a 的通项公式; (2)求数列{}n a 的前n 项和n T .19.如图,在三棱锥−P ABC 中,AB BC ⊥,2AB =,BC =PB PC ==,,BP AP BC 的中点分别为,,D E O ,点F 在AC 上,BF AO ⊥.(1)求证:EF //平面ADO ;(2)若120POF ∠=︒,求三棱锥−P ABC 的体积. 20.已知函数()()1ln 1f x a x x ⎛⎫=++⎪⎝⎭. (1)当1a =−时,求曲线()y f x =在点()()1,f x 处的切线方程. (2)若函数()f x 在()0,∞+单调递增,求a 的取值范围.21.已知椭圆2222:1(0)C bb x a a y +>>=,点()2,0A −在C 上.(1)求C 的方程;(2)过点()2,3−的直线交C 于,P Q 两点,直线,AP AQ 与y 轴的交点分别为,M N ,证明:线段MN 的中点为定点.【选修4-4】(10分)22.在直角坐标系xOy 中,以坐标原点O 为极点,x 轴正半轴为极轴建立极坐标系,曲线1C 的极坐标方程为2sin 42ππρθθ⎛⎫=≤≤⎪⎝⎭,曲线2C :2cos 2sin x y αα=⎧⎨=⎩(α为参数,2απ<<π).(1)写出1C 的直角坐标方程;(2)若直线y x m =+既与1C 没有公共点,也与2C 没有公共点,求m 的取值范围.【选修4-5】(10分)23.已知()22f x x x =+− (1)求不等式()6x f x ≤−的解集;(2)在直角坐标系xOy 中,求不等式组()60f x yx y ⎧≤⎨+−≤⎩所确定的平面区域的面积.2023年普通高等学校招生全国统一考试(全国乙卷)答案详解文科数学(2023·全国乙卷·文·1·★)232i 2i ++=( )(A )1 (B )2 (C (D 答案:C解析:2322i 2i 212i i 212(1)i 12i ++=−+⨯⨯=−+⨯−⨯=−=.(2023·全国乙卷·文·2·★)设全集{0,1,2,4,6,8}U =,集合{0,4,6}M =,{0,1,6}N =,M ∪C U N 则( ) (A ){0,2,4,6,8} (B ){0,1,4,6,8} (C ){1,2,4,6,8} (D )U 答案:A解析:由题意,C U N ={2,4,8},所以M ∪C U N ={0,2,4,6,8}.(2023·全国乙卷·文·3·★) 如图,网格纸上绘制的一个零件的三视图,网格小正方形的边长为1,则该零件的表面积为( )A.24B.26C.28D.30答案:D解析:如图所示,在长方体1111ABCD A B C D −中,2AB BC ==,13AA =,点,,,H I J K 为所在棱上靠近点1111,,,B C D A 的三等分点,,,,O L M N 为所在棱的中点,则三视图所对应的几何体为长方体1111ABCD A B C D −去掉长方体11ONIC LMHB −之后所得的几何体,该几何体的表面积和原来的长方体的表面积相比少2个边长为1的正方形, 其表面积为:()()()22242321130⨯⨯+⨯⨯−⨯⨯=.(2023·全国乙卷·文·4·★★)在ABC ∆中,内角A ,B ,C 的对边分别为a ,b ,c ,若cos cos a B b A c −=,且5C π=则,在B =( ) (A )10π(B )5π (C )310π (D )25π 答案:C解法1:所给边角等式每一项都有齐次的边,要求的是角,故用正弦定理边化角分析, 因为cos cos a B b A c −=,所以sin cos sin cos sin A B B A C −=,故sin()sin A B C −= ①, 已知C ,先将C 代入,再利用A B C π++=将①中的A 换成B 消元, 因为5C π=,所以45A B C ππ+=−=,故45A B π=−,代入①得4sin(2)sin 55B ππ−= ②, 因为45A B π+=,所以405B π<<,故4442555B πππ−<−<,结合②可得4255B ππ−=,所以310B π=.解法2:按解法1得到sin cos sin cos sin A B B A C −=后,观察发现若将右侧sin C 拆开,也能出现左边的两项,故拆开来看,sin sin[()]sin()sin cos cos sin C A B A B A B A B π=−+=+=+,代入sin cos sin cos sin A B B A C −=得:sin cos sin cos sin cos sin cos A B B A A B B A −=+,化简得:sin cos 0B A =,因为0B π<<,所以sin 0B >,故cos 0A =,结合0A π<<可得2A π=,所以43510B A ππ=−=.(2023·全国乙卷·文·5·★★) 已知e ()e 1xax x f x =−是偶函数,则=a ( )A. 2−B. 1−C. 1D. 2答案:D解析:因为()e e 1x ax x f x =−为偶函数,则()()()()1e e e e 0e 1e 1e 1a x x x x ax ax ax x x x f x f x −−−⎡⎤−−⎣⎦−−=−==−−−, 又因为x 不恒为0,可得()1e e 0a x x −−=,即()1e e a x x −=,则()1x a x =−,即11a =−,解得2a =.(2023·全国乙卷·文·6·★)正方形ABCD 的边长是2,E 是AB 的中点,则EC ED ⋅=( ) (A(B )3 (C) (D )5 答案:B解析:如图,EC ,ED 共起点,且中线、底边长均已知,可用极化恒等式求数量积, 由极化恒等式,223EC ED EF CF ⋅=−=.A BCDE F(2023·全国乙卷·文·7·★★)设O 为平面坐标系的坐标原点,在区域(){}22,14x y xy ≤+≤内随机取一点A ,则直线OA 的倾斜角不大于π4的概率为( ) A.18B. 16C.14D.12答案:C 解析:因为区域(){}22,|14x y xy ≤+≤表示以()0,0O 圆心,外圆半径2R =,内圆半径1r =的圆环,则直线OA 的倾斜角不大于π4的部分如阴影所示,在第一象限部分对应的圆心角π4MON ∠=, 结合对称性可得所求概率π2142π4P ⨯==.(2023·全国乙卷·文·8·★★★)函数3()2f x x ax =++存在3个零点,则a 的取值范围是( ) (A )(,2)−∞− (B )(,3)−∞− (C )(4,1)−− (D )(3,0)− 答案:B解法1:观察发现由320x ax ++=容易分离出a ,故用全分离,先分析0x =是否为零点, 因为(0)20f =≠,所以0不是()f x 的零点;当0x ≠时,3322()0202f x x ax ax x a x x=⇔++=⇔=−−⇔=−−, 所以直线y a =与函数22(0)y x x x =−−≠的图象有3个交点,要画此函数的图象,需求导分析,令22()(0)g x x x x =−−≠,则3222222(1)2(1)(1)()2x x x x g x x x x x −−++'=−+==, 因为22131()024x x x ++=++>,所以()00g x x '>⇔<或01x <<,()01g x x '<⇔>,故()g x 在(,0)−∞上,在(0,1)上,在(1,)+∞上,又lim ()x g x →−∞=−∞,当x 分别从y 轴左、右两侧趋近于0时,()g x 分别趋于+∞,−∞,(1)3g =−,lim ()x g x →+∞=−∞,所以()g x 的大致图象如图1,由图可知要使y a =与()y g x =有3个交点,应有3a <−.解法2:如图2,三次函数有3个零点等价于两个极值异号,故也可直接求导分析极值,由题意,2()3f x x a '=+,要使()f x 有2个极值点,则()f x '有两个零点,所以120a ∆=−>,故0a <, 令()0f x '=可得x =322f =+=,3(((22f a =++=,故34(2)(2)4027a f f =+=+<,解得:3a <−.a=1图2图(2023·全国乙卷·文·9·★)某学校举办作文比赛,共6个主题,每位参赛同学从中随机抽取一个主题准备作文,则甲、乙两位参赛同学抽到不同主题概率为( ) A.56B.23C.12D.13答案:A解析:甲有6种选择,乙也有6种选择,故总数共有6636⨯=种, 若甲、乙抽到的主题不同,则共有26A 30=种, 则其概率为305366=,(2023·全国乙卷·文·10·★★★)已知函数()sin()f x x ωϕ=+在区间π2π,63⎛⎫⎪⎝⎭单调递增,直线π6x =和2π3x =为函数()y f x =的图像的两条对称轴,则5π12f ⎛⎫−= ⎪⎝⎭() A. B. 12−C.12D.2答案:D解析:因为()sin()f x x ωϕ=+在区间π2π,63⎛⎫⎪⎝⎭单调递增, 所以2πππ2362T =−=,且0ω>,则πT =,2π2w T ==, 当π6x =时,()f x 取得最小值,则ππ22π62k ϕ⋅+=−,Z k ∈,则5π2π6k ϕ=−,Z k ∈,不妨取0k =,则()5πsin 26f x x ⎛⎫=− ⎪⎝⎭,则5π5πsin 1232f ⎛⎫⎛⎫−=−= ⎪ ⎪⎝⎭⎝⎭,(2023·全国乙卷·文·11·★★★)已知实数x ,y 满足224240x y x y +−−−=,则x y −的最大值是( )(A )1 (B )4 (C )1+ (D )7 答案:C解法1:所给等式可配方化为平方和结构,故考虑三角换元,22224240(2)(1)9x y x y x y +−−−=⇒−+−=,令23cos 13sin x y θθ=+⎧⎨=+⎩,则23cos 13sin 1)4x y πθθθ−=+−−=−−,θ∈R ,所以当sin()14πθ−=−时,x y −取得最大值1+解法2:所给方程表示圆,故要求x y −的最大值,也可设其为t ,看成直线,用直线与圆的位置关系处理,22224240(2)(1)9x y x y x y +−−−=⇒−+−= ①,设t x y =−,则0x y t −−=,因为x ,y 还满足①,所以直线0x y t −−=与该圆有交点,从而圆心(2,1)到直线的距离3d =≤,解得:11t −≤≤+max ()1x y −=+(2023·全国乙卷·文·12·★★★★)设A ,B 为双曲线2219y x −=上两点,下列四个点中,可为线段AB 中点的是( ) A. ()1,1 B. ()1,2-C. ()1,3D. ()1,4−−答案:D解析:设()()1122,,,A x y B x y ,则AB 的中点1212,22x x y y M ++⎛⎫⎪⎝⎭,可得1212121212122,2ABy y y y y y k k x x x x x x +−+===+−+,因为,A B 在双曲线上,则221122221919y x y x ⎧−=⎪⎪⎨⎪−=⎪⎩,两式相减得()2222121209y y x x −−−=, 所以221222129AB y y k k x x −⋅==−. 对于选项A : 可得1,9AB k k ==,则:98AB y x =−,联立方程229819y x y x =−⎧⎪⎨−=⎪⎩,消去y 得272272730x x −⨯+=,此时()2272472732880∆=−⨯−⨯⨯=−<, 所以直线AB 与双曲线没有交点,故A 错误; 对于选项B :可得92,2AB k k =−=−,则95:22AB y x =−−, 联立方程22952219y x y x ⎧=−−⎪⎪⎨⎪−=⎪⎩,消去y 得245245610x x +⨯+=, 此时()224544561445160∆=⨯−⨯⨯=−⨯⨯<, 所以直线AB 与双曲线没有交点,故B 错误; 对于选项C :可得3,3AB k k ==,则:3AB y x =由双曲线方程可得1,3a b ==,则:3AB y x =为双曲线的渐近线, 所以直线AB 与双曲线没有交点,故C 错误; 对于选项D :94,4AB k k ==,则97:44AB y x =−,联立方程22974419y x y x ⎧=−⎪⎪⎨⎪−=⎪⎩,消去y 得2631261930x x +−=, 此时21264631930∆=+⨯⨯>,故直线AB 与双曲线有交两个交点,故D 正确;(2023·全国乙卷·文·13·★)已知点(A 在抛物线C :22y px =上,则A 到C 的准线的距离为______. 答案:94解析:由题意可得:221p =⨯,则25p =,抛物线的方程为25y x =,准线方程为54x =−,点A 到C 的准线的距离为59144⎛⎫−−= ⎪⎝⎭.(2023·全国乙卷·文·14·★)若(0,)2πθ∈,1tan 3θ=,则sin cos θθ−=_____.答案: 解析:已知tan θ,可先求出sin θ和cos θ, 由题意,sin 1tan cos 3θθθ==,所以cos 3sin θθ=,代入22cos sin 1θθ+=可得210sin 1θ=, 又(0,)2πθ∈,所以sin θ=,cos θ=,故sin cos θθ−=(2023·全国乙卷·文·15·★★)若x ,y 满足约束条件312937x y x y x y −≤−⎧⎪+≤⎨⎪+≥⎩,则2z x y =−的最大值为______.答案:8解析:作出可行域如下图所示:z =2x −y ,移项得y =2x −z , 联立有3129x y x y −=−⎧⎨+=⎩,解得52x y =⎧⎨=⎩,设()5,2A ,显然平移直线2y x =使其经过点A ,此时截距−z 最小,则z 最大,代入得z =8,(2023·全国乙卷·文·16·★★★)已知点S ,A ,B ,C 均在半径为2的球面上,ABC ∆是边长为3的等边三角形,SA ⊥平面ABC ,则SA =_____. 答案:2解析:有线面垂直,且ABC ∆是等边三角形,属外接球的圆柱模型,核心方程是222()2hr R +=,如图,圆柱的高h SA =,底面半径r 即为ABC ∆的外接圆半径,所以233r ==, 由题意,球的半径2R =,因为222()2hr R +=,所以23()42h +=,解得:2h =,故2SA =.(2023·全国乙卷·文·17·★★★)某厂为比较甲乙两种工艺对橡胶产品伸缩率的处理效应,进行10次配对试验,每次配对试验选用材质相同的两个橡胶产品,随机地选其中一个用甲工艺处理,另一个用乙工艺处理,测量处理后的橡胶产品的伸缩率.甲、乙两种工艺处理后的橡胶产品的伸缩率分别记为i x ,()1,2,,10i y i =⋅⋅⋅.试验结果如下:记()1,2,,10i i i z x y i =−=⋅⋅⋅,记1210,,,z z z ⋅⋅⋅的样本平均数为z ,样本方差为2s . (1)求z ,s 2;(2)判断甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率是否有显著提高(如果z ≥则认为甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率有显著提高,否则不认为有显著提高) 答案:(1)11z =,261s =;(2)认为甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率有显著提高. 解析:(1)545533551522575544541568596548552.310x +++++++++==,536527543530560533522550576536541.310y +++++++++==,552.3541.311z x y =−=−=,i i i z x y =− 的值分别为: 9,6,8,8,15,11,19,18,20,12−,故2222222222(911)(611)(811)(811)(1511)0(1911)(1811)(2011)(1211)6110s −+−+−+−−+−++−+−+−+−==(2)由(1)知:11z =,==z ≥ 所以认为甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率有显著提高.(2023·全国乙卷·文·18·★★★)记n S 为等差数列{}n a 的前n 项和,已知211a =,1040S =. (1)求{}n a 的通项公式; (2)求数列{}n a 的前n 项和n T .解:(1)(已知条件都容易代公式,故直接用公式翻译,求出1a 和d ) 设{}n a 的公差为d ,则2111a a d =+= ①, 101104540S a d =+= ②,联立①②解得:113a =,2d =−,所以1(1)13(1)(2)152n a a n d n n =+−=+−⨯−=−.(2)(通项含绝对值,要求和,先去绝对值,观察发现{}n a 前7项为正,从第8项起为负,故据此讨论) 当7n ≤时,0n a >,所以12n n T a a a =++⋅⋅⋅+ 2112()(13152)1422n n n a a n n a a a n n ++−=++⋅⋅⋅+===−; 当8n ≥时,12n n T a a a =++⋅⋅⋅+ 12789n a a a a a a =++⋅⋅⋅+−−−⋅⋅⋅− 127122()()n a a a a a a =++⋅⋅⋅+−++⋅⋅⋅+ 27(131)(13152)2149822n n n n ⨯++−=⨯−=−+; 综上所述,2214,71498,8n n n n T n n n ⎧−≤⎪=⎨−+≥⎪⎩.(2023·全国乙卷·文·19·★★★)如图,在三棱锥−P ABC 中,AB BC ⊥,2AB =,BC =PB PC ==,,BP AP BC 的中点分别为,,D E O ,点F 在AC 上,BF AO ⊥.(1)求证:EF //平面ADO ;(2)若120POF ∠=︒,求三棱锥−P ABC 的体积.答案:(1)证明见解析 (2解析:(1)连接,DE OF ,设AF tAC =,则(1)BF BA AF t BA tBC =+=−+,12AO BA BC =−+,BF AO ⊥, 则2211[(1)]()(1)4(1)4022BF AO t BA tBC BA BC t BA tBC t t ⋅=−+⋅−+=−+=−+=, 解得12t =,则F 为AC 的中点,由,,,D E O F 分别为,,,PB PA BC AC 的中点,于是11//,,//,22DE AB DE AB OF AB OF AB ==,即,//DE OF DE OF =,则四边形ODEF 为平行四边形,//,EF DO EF DO =,又EF ⊄平面,ADO DO ⊂平面ADO ,所以//EF 平面ADO .(2)过P 作PM 垂直FO 的延长线交于点M , 因为,PB PC O =是BC 中点,所以PO BC ⊥,在Rt PBO △中,12PB BO BC ===2PO ===, 因为,//AB BC OF AB ⊥,所以OF BC ⊥,又PO OF O ⋂=,,PO OF ⊂平面POF , 所以BC⊥平面POF ,又PM ⊂平面POF ,所以BC PM ⊥,又BC FM O =,,BC FM ⊂平面ABC ,所以PM ⊥平面ABC ,即三棱锥−P ABC 的高为PM ,因为120POF ∠=︒,所以60POM ∠=︒,所以sin 6022PM PO =︒=⨯=,又11222ABC S AB BC =⋅=⨯⨯=△所以11333P ABC ABC V S PM −=⋅=⨯=△.(2023·全国乙卷·文·20·★)已知函数1()()ln(1)f x a x x=++.(1)当1a =−时,求曲线()y f x =在点(1,(1))f 处的切线方程; (2)若函数()f x 在(0,)+∞上单调递增,求a 的取值范围. 答案:(1)()ln 2ln 20x y +−=; (2)1|2a a ⎧⎫≥⎨⎬⎩⎭. 解析:(1)当1a =−时,()()()11ln 11f x x x x ⎛⎫=−+>−⎪⎝⎭, 则()()2111ln 111x f x x x x ⎛⎫'=−⨯++−⨯ ⎪+⎝⎭, 据此可得()()10,1ln 2f f '==−,所以函数在()()1,1f 处的切线方程为()0ln 21y x −=−−,即()ln 2ln 20x y +−=. (2)由函数的解析式可得()()()2111=ln 111f x x a x x x x ⎛⎫⎛⎫'−+++⨯>− ⎪ ⎪+⎝⎭⎝⎭, 满足题意时()0f x '≥在区间()0,∞+上恒成立. 令()2111ln 101x a x x x ⎛⎫⎛⎫−+++≥ ⎪ ⎪+⎝⎭⎝⎭,则()()()21ln 10x x x ax −++++≥, 令()()()2=1ln 1g x ax x x x +−++,原问题等价于()0g x ≥在区间()0,∞+上恒成立, 则()()2ln 1g x ax x '=−+,当0a ≤时,由于()20,ln 10ax x ≤+>,故()0g x '<,()g x 在区间()0,∞+上单调递减,此时()()00g x g <=,不合题意;令()()()2ln 1h x g x ax x '==−+,则()121h x a x −'=+, 当12a ≥,21a ≥时,由于111x <+,所以()()0,h x h x '>在区间()0,∞+上单调递增, 即()g x '在区间()0,∞+上单调递增,所以()()>00g x g ''=,()g x 在区间()0,∞+上单调递增,()()00g x g >=,满足题意. 当102a <<时,由()1201h x a x =−=+'可得1=12x a−, 当10,12x a ⎛⎫∈− ⎪⎝⎭时,()()0,h x h x '<在区间10,12a ⎛⎫− ⎪⎝⎭上单调递减,即()g x '单调递减,注意到()00g '=,故当10,12x a ⎛⎫∈− ⎪⎝⎭时,()()00g x g ''<=,()g x 单调递减, 由于()00g =,故当10,12x a ⎛⎫∈− ⎪⎝⎭时,()()00g x g <=,不合题意. 综上可知:实数a 得取值范围是1|2a a ⎧⎫≥⎨⎬⎩⎭.(2023·全国乙卷·文·21·★★★)已知椭圆2222:1(0)C b b x a a y +>>=,点()2,0A −在C 上.(1)求C 的方程; (2)过点()2,3−的直线交C 于,P Q 两点,直线,AP AQ 与y 轴的交点分别为,M N ,证明:线段MN 的中点为定点.答案:(1)22194y x += (2)证明见详解解析:(1)由题意可得22223b a b c c e a ⎧⎪=⎪⎪=+⎨⎪⎪==⎪⎩,解得32a b c ⎧=⎪=⎨⎪=⎩,所以椭圆方程为22194y x +=.(2)由题意可知:直线PQ 的斜率存在,设()()()1122:23,,,,PQ y k x P x y Q x y =++,联立方程()2223194y k x y x ⎧=++⎪⎨+=⎪⎩,消去y 得:()()()222498231630k x k k x k k +++++=,则()()()2222Δ64236449317280kk k k k k =+−++=−>,解得0k <,可得()()2121222163823,4949k k k k x x x x k k +++=−=++, 因为()2,0A −,则直线()11:22y AP y x x =++, 令0x =,解得1122y y x =+,即1120,2y M x ⎛⎫⎪+⎝⎭,同理可得2220,2y N x ⎛⎫ ⎪+⎝⎭,则()()1212121222232322222y y k x k x x x x x +++++⎡⎤⎡⎤++⎣⎦⎣⎦=+++()()()()()()12211223223222kx k x kx k x x x +++++++⎡⎤⎡⎤⎣⎦⎣⎦=++()()()()1212121224342324kx x k x x k x x x x +++++=+++()()()()()()222222323843234231084949336163162344949k k k k k k k k k k k k k k k +++−++++===++−+++,所以线段PQ 的中点是定点()0,3.【选修4-4】(10分)(2023·全国乙卷·文·22·★★★)在直角坐标系xOy 中,以坐标原点O 为极点,x 轴正半轴为极轴建立极坐标系,曲线1C 的极坐标方程为2sin 42ππρθθ⎛⎫=≤≤ ⎪⎝⎭,曲线2C :2cos 2sin x y αα=⎧⎨=⎩(α为参数,2απ<<π).(1)写出1C 的直角坐标方程;(2)若直线y x m =+既与1C 没有公共点,也与2C 没有公共点,求m 的取值范围. 答案:(1)()[][]2211,0,1,1,2x y x y +−=∈∈ (2)()(),022,−∞+∞解析:(1)因为2sin ρθ=,即22sin ρρθ=,可得222x y y +=, 整理得()2211x y +−=,表示以()0,1为圆心,半径为1的圆,又因为2cos 2sin cos sin 2,sin 2sin 1cos 2x y ======−ρθθθθρθθθ, 且ππ42θ≤≤,则π2π2≤≤θ,则[][]sin 20,1,1cos 21,2x y =∈=−∈θθ, 故()[][]221:11,0,1,1,2C x y x y +−=∈∈.(2)因为22cos :2sin x C y αα=⎧⎨=⎩(α为参数,ππ2α<<),整理得224x y +=,表示圆心为()0,0O ,半径为2,且位于第二象限的圆弧, 如图所示,若直线y x m =+过()1,1,则11m =+,解得0m =;若直线y x m =+,即0x y m −+=与2C相切,则20m =>⎩,解得m =,若直线y x m =+与12,C C均没有公共点,则m >或0m <, 即实数m 的取值范围()(),022,−∞+∞.【选修4-5】(10分)(2023·全国乙卷·文·23·★★)已知()22f x x x =+− (1)求不等式()6x f x ≤−的解集;(2)在直角坐标系xOy 中,求不等式组()60f x yx y ⎧≤⎨+−≤⎩所确定的平面区域的面积.答案:(1)[2,2]−; (2)8.解析:(1)依题意,32,2()2,0232,0x x f x x x x x −>⎧⎪=+≤≤⎨⎪−+<⎩,不等式()6f x x ≤−化为:2326x x x >⎧⎨−≤−⎩或0226x x x ≤≤⎧⎨+≤−⎩或0326x x x <⎧⎨−+≤−⎩,解2326x x x >⎧⎨−≤−⎩,得无解;解0226x x x ≤≤⎧⎨+≤−⎩,得02x ≤≤,解0326x x x <⎧⎨−+≤−⎩,得20x −≤<,因此22x −≤≤,所以原不等式的解集为:[2,2]−(2)作出不等式组()60f x yx y ≤⎧⎨+−≤⎩表示的平面区域,如图中阴影ABC ,由326y xx y=−+⎧⎨+=⎩,解得(2,8)A−,由26y xx y=+⎧⎨+=⎩, 解得(2,4)C,又(0,2),(0,6)B D,所以ABC的面积11|||62||2(2)|822ABC C AS BD x x=⨯−=−⨯−−=.。
2023年高考数学试题全国卷2(文)全解全析

2023年普通高等学校招生全国统一考试文科数学(必修+选修I)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至2页.第Ⅱ卷3至10页.考试结束后,将本试卷和答题卡一并交回.第Ⅰ卷注意事项:1.答第Ⅰ卷前,考生务必将自己地姓名、准考证号、考试科目涂写在答题卡上.2.每小题选出解析后,用铅笔把答题卡上对应题目地解析标号涂黑.如需改动,用橡皮擦干净后,再选涂其它解析标号.不能答在试卷卷上.3.本卷共12小题,每小题5分,共60分.在每小题给出地四个选项中,只有一项是符合题目要求地.参考公式:如果事件A B ,互斥,那么 球地表面积公式()()()P A B P A P B +=+ 24πS R=如果事件A B ,相互独立,那么 其中R 表示球地半径()()()P A B P A P B = 球地体积公式如果事件A 在一次试验中发生地概率是p ,那么 34π3V R =n 次独立重复试验中事件A 恰好发生k 次地概率 其中R 表示球地半径()(1)(012)k kn k k n P k C p p k n -=-= ,,,,一、选择题1.若sin 0α<且tan 0α>是,则α是( )A .第一象限角B . 第二象限角C . 第三象限角D . 第四象限角【解析】C【解析】sin 0α<,α在三、四象限;tan 0α>,α在一、三象限,∴选C2.设集合{|32}M m m =∈-<<Z ,{|13}N n n M N =∈-=Z 则,≤≤( )A .{}01,B .{}101-,, C .{}012,,D .{}1012-,,,【解析】B【解析】{}1,0,1,2--=M ,{}3,2,1,0,1-=N ,∴{}1,0,1-=N M 【高考考点】集合地运算,整数集地符号识别3.原点到直线052=-+y x 地距离为( )A .1B .3C .2D .5【解析】D 【解析】52152=+-=d 【高考考点】点到直线地距离公式4.函数1()f x x x=-地图像关于( )A .y 轴对称 B . 直线x y -=对称 C . 坐标原点对称 D . 直线x y =对称【解析】C 【解析】1()f x x x=-是奇函数,所以图象关于原点对称【高考考点】函数奇偶性地性质5.若13(1)ln 2ln ln x e a x b x c x -∈===,,,,,则( )A .a <b <c B .c <a <bC . b <a <cD . b <c <a【解析】C【解析】由0ln 111<<-⇒<<-x x e ,令x t ln =且取21-=t 知b <a <c 6.设变量x y ,满足约束条件:222y x x y x ⎧⎪+⎨⎪-⎩,,.≥≤≥,则y x z 3-=地最小值为( )A .2-B .4-C .6-D .8-【解析】D【解析】如图作出可行域,知可行域地顶点是A (-2,2)、B(32,32)及C(-2,-2) 于是8)(min -=A z 7.设曲线2ax y =在点(1,a )处地切线与直线062=--y x 平行,则=a ( )A .1B .12C .12-D .1-【解析】A【解析】ax y 2'=,于是切线地斜率a y k x 2'1===,∴有122=⇒=a a 8.正四棱锥地侧棱长为32,侧棱与底面所成地角为︒60,则该棱锥地体积为( )A .3 B .6C .9D .18【解析】B【解析】高360sin 32=︒=h ,又因底面正方形地对角线等于32,∴底面积为 6332212=⨯⨯⨯=S ,∴体积63631=⨯⨯=V 【备考提示】在底面积地计算时,要注意多思则少算9.44)1()1(x x +-地展开式中x 地系数是( )A .4-B .3- C .3D .4【解析】A【解析】41666141404242404-=-+=-+C C C C C C 【易错提醒】容易漏掉1414C C 项或该项地负号10.函数x x x f cos sin )(-=地最大值为( )A .1 B . 2C .3D .2【解析】B【解析】4sin(2cos sin )(π-=-=x x x x f ,所以最大值是2【高考考点】三角函数中化为一个角地三角函数问题【备考提示】三角函数中化为一个角地三角函数问题是三角函数在高考中地热点问题11.设ABC △是等腰三角形,120ABC ∠=,则以A B ,为焦点且过点C 地双曲线地离心率为( )A .221+B .231+C . 21+D .31+【解析】B【解析】由题意BC c =2,所以c c AC 3260sin 220=⨯⨯=,由双曲线地定义,有c a c c BC AC a )13(2322-=⇒-=-=,∴231131+=-==a c e 【高考考点】双曲线地有关性质,双曲线第一定义地应用12.已知球地半径为2,相互垂直地两个平面分别截球面得两个圆.若两圆地公共弦长为2,则两圆地圆心距等于( )A .1 B .2C .3D .2【解析】C【解析】设两圆地圆心分别为1O 、2O ,球心为O ,公共弦为AB,其中点为E,则21EO OO 为矩形,于是对角线OE O O =21,而3122222=-=-=AE OA OE ,∴321=O O 【高考考点】球地有关概念,两平面垂直地性质2023年普通高等学校招生全国统一考试文科数学(必修+选修I)第Ⅱ卷二、填空题:本大题共4小题,每小题5分,共20分.把解析填在题中横线上.13.设向量(12)(23)==,,,a b ,若向量λ+a b 与向量(47)=--,c 共线,则=λ .【解析】 2【解析】λ+a b =)32,2(++λλ则向量λ+a b 与向量(47)=--,c 共线274322=⇒--=++⇔λλλ14.从10名男同学,6名女同学中选3名参加体能测试,则选到地3名同学中既有男同学又有女同学地不同选法共有 种(用数字作答)【解析】 420【解析】4202701501621026110=+=+C C C C 15.已知F 是抛物线24C y x =:地焦点,A B ,是C 上地两个点,线段AB 地中点为(22)M ,,则ABF △地面积等于 .【解析】 2【解析】设过M 地直线方程为)2(2-=-x k y ,由0)1(444)2(22222=-+-⇒⎩⎨⎧=-=-k kx x k xy x k y ∴k x x 421=+,2221)1(4kk x x -=,由题意144=⇒=k k ,于是直线方程为x y = 421=+x x ,021=x x ,∴24=AB ,焦点F (1,0)到直线x y =地距离21=d ∴ABF △地面积是216.平面内地一个四边形为平行四边形地充要条件有多个,如两组对边分别平行,类似地,写出空间中地一个四棱柱为平行六面体地两个充要条件:充要条件① ;充要条件② .(写出你认为正确地两个充要条件)【解析】两组相对侧面分别平行;一组相对侧面平行且全等;对角线交于一点;底面是平行四边形.注:上面给出了四个充要条件.如果考生写出其他正确解析,同样给分.三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.17.(本小题满分10分)在ABC △中,5cos 13A =-,3cos 5B =. (Ⅰ)求sinC 地值;(Ⅱ)设5BC =,求ABC △地面积.18.(本小题满分12分)等差数列{}n a 中,410a =且3610a a a ,,成等比数列,求数列{}n a 前20项地和20S .19.(本小题满分12分)甲、乙两人进行射击比赛,在一轮比赛中,甲、乙各射击一发子弹.根据以往资料知,甲击中8环,9环,10环地概率分别为0.6,0.3,0.1,乙击中8环,9环,10环地概率分别为0.4,0.4,0.2.设甲、乙地射击相互独立.(Ⅰ)求在一轮比赛中甲击中地环数多于乙击中环数地概率;(Ⅱ)求在独立地三轮比赛中,至少有两轮甲击中地环数多于乙击中环数地概率.20.(本小题满分12分)如图,正四棱柱1111ABCD A B C D -中,124AA AB ==,点E 在1CC 上且EC E C 31=.(Ⅰ)证明:1A C ⊥平面BED ;(Ⅱ)求二面角1A DE B --地大小.21.(本小题满分12分)设a ∈R ,函数233)(x ax x f -=.(Ⅰ)若2=x 是函数)(x f y =地极值点,求a 地值;(Ⅱ)若函数()()()[02]g x f x f x x '=+∈,,,在0=x 处取得最大值,求a 地取值范围.ABC D EA 1B 1C 1D 122.(本小题满分12分)设椭圆中心在坐标原点,(20)(01)A B ,,,是它地两个顶点,直线)0(>=k kx y 与AB 相交于点D ,与椭圆相交于E 、F 两点.(Ⅰ)若6ED DF =,求k 地值;(Ⅱ)求四边形AEBF 面积地最大值.2023年普通高等学校招生全国统一考试文科数学试卷(必修+选修Ⅰ)参考解析和评分参考评分说明:∙∙∙1.本解答给出了一种或几种解法供参考,如果考生地解法与本解答不同,可根据试卷地主要考查内容比照评分参考制订相应地评分细则.∙∙∙2.对计算题,当考生地解答在某一步出现错误时,如果后继部分地解答未改变该题地内容和难度,可视影响地程度决定后继部分地给分,但不得超过该部分正确解答应得分数地一半;如果后继部分地解答有较严重地错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得地累加分数.4.只给整数分数.选择题不给中间分.一、选择题1.C 2.B 3.D 4.C 5.C 6.D 7.A 8.B 9.A 10.B 11.B 12.C 二、填空题13.2 14.420 15.216.两组相对侧面分别平行;一组相对侧面平行且全等;对角线交于一点;底面是平行四边形.注:上面给出了四个充要条件.如果考生写出其他正确解析,同样给分.三、解答题17.解:(Ⅰ)由5cos 13A =-,得12sin 13A =,由3cos 5B =,得4sin 5B =.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙2分所以16sin sin()sin cos cos sin 65C A B A B A B =+=+=.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙5分(Ⅱ)由正弦定理得45sin 13512sin 313BC B AC A ⨯⨯===.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8分所以ABC △地面积1sin 2S BC AC C =⨯⨯⨯1131652365=⨯⨯⨯83=.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙10分18.解:设数列{}n a 地公差为d ,则3410a a d d =-=-,642102a a d d =+=+,1046106a a d d =+=+.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙3分由3610a a a ,,成等比数列得23106a a a =,即2(10)(106)(102)d d d -+=+,整理得210100d d -=,解得0d =或1d =.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙7分当0d =时,20420200S a ==.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙9分当1d =时,14310317a a d =-=-⨯=,于是2012019202S a d ⨯=+207190330=⨯+=.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙12分19.解:记12A A ,分别表示甲击中9环,10环,12B B ,分别表示乙击中8环,9环,A 表示在一轮比赛中甲击中地环数多于乙击中地环数,B 表示在三轮比赛中至少有两轮甲击中地环数多于乙击中地环数,12C C ,分别表示三轮中恰有两轮,三轮甲击中环数多于乙击中地环数.(Ⅰ)112122A A B A B A B =++ ,∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙2分112122()()P A P A B A B A B =++ 112122()()()P A B P A B P A B =++ 112122()()()()()()P A P B P A P B P A P B =++ 0.30.40.10.40.10.40.2=⨯+⨯+⨯=.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6分(Ⅱ)12B C C =+,∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8分22213()[()][1()]30.2(10.2)0.096P C C P A P A =-=⨯⨯-=,332()[()]0.20.008P C P A ===,1212()()()()0.0960.0080.104P B P C C P C P C =+=+=+=.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙12分20.解法一:依题设,2AB =,1CE =.(Ⅰ)连结AC 交BD 于点F ,则BD AC ⊥.由三垂线定理知,1BD A C ⊥.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙3分在平面1A CA 内,连结EF 交1A C 于点G ,由于1AA ACFC CE==,故1Rt Rt A AC FCE △∽△,1AA C CFE ∠=∠,CFE ∠与1FCA ∠互余.于是1A C EF ⊥.1A C 与平面BED 内两条相交直线BD EF ,都垂直,所以1A C ⊥平面BED .∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6分(Ⅱ)作GH DE ⊥,垂足为H ,连结1A H .由三垂线定理知1A H DE ⊥,故1A HG ∠是二面角1A DE B --地平面角.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8分EF ==,CE CF CG EF ⨯==,EG ==13EG EF =,13EF FD GH DE ⨯=⨯=又1A C ==,11A G A C CG =-=.11tan A GA HG HG∠==所以二面角1A DE B --地大小为arctan .∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙12分 解法二:以D 为坐标原点,射线DA 为x 轴地正半轴,建立如下图所示直角坐标系D xyz -.依题设,1(220)(020)(021)(204)B C E A ,,,,,,,,,,,.AB CDE A 1B 1C 1D 1FH G(021)(220)DE DB ==,,,,,,11(224)(204)A C DA =--= ,,,,,.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙3分(Ⅰ)因为10A C DB = ,10A C DE =,故1A C BD ⊥,1A C DE ⊥.又DB DE D = ,所以1A C ⊥平面DBE .∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6分(Ⅱ)设向量()x y z =,,n 是平面1DA E 地法向量,则DE ⊥ n ,1DA ⊥ n .故20y z +=,240x z +=.令1y =,则2z =-,4x =,(412)=-,,n .∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙9分1A C <> ,n 等于二面角1A DE B --地平面角,111cos A C A C A C<>==,n n n .所以二面角1A DE B --地大小为∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙12分21.解:(Ⅰ)2()363(2)f x ax x x ax '=-=-.因为2x =是函数()y f x =地极值点,所以(2)0f '=,即6(22)0a -=,因此1a =.经验证,当1a =时,2x =是函数()y f x =地极值点.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4分(Ⅱ)由题设,3222()336(3)3(2)g x ax x ax x ax x x x =-+-=+-+.当()g x 在区间[02],上地最大值为(0)g 时,(0)(2)g g ≥,即02024a -≥.故得65a ≤.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙9分反之,当65a ≤时,对任意[02]x ∈,,26()(3)3(2)5g x x x x x +-+≤23(210)5xx x =+-3(25)(2)5xx x =+-0≤,而(0)0g =,故()g x 在区间[02],上地最大值为(0)g .综上,a 地取值范围为65⎛⎤-∞ ⎥⎝⎦,.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙12分22.(Ⅰ)解:依题设得椭圆地方程为2214x y +=,直线AB EF ,地方程分别为22x y +=,(0)y kx k =>.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙2分如图,设001122()()()D x kx E x kx F x kx ,,,,,,其中12x x <,且12x x ,满足方程22(14)4k x +=,故21x x =-=.①由6ED DF = 知01206()x x x x -=-,得021215(6)77x x x x =+==;由D 在AB 上知0022x kx +=,得0212x k=+.所以212k =+,化简得2242560k k -+=,解得23k =或38k =.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6分(Ⅱ)解法一:根据点到直线地距离公式和①式知,点E F ,到AB 地距离分别为1h 2h .∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙9分11又AB ==,所以四边形AEBF 地面积为121()2S AB h h =+12===≤当21k =,即当12k =时,上式取等号.所以S地最大值为.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙12分解法二:由题设,1BO =,2AO =.设11y kx =,22y kx =,由①得20x >,210y y =->,故四边形AEBF 地面积为BEF AEFS S S =+△△222x y =+∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙9分===,当222x y =时,上式取等号.所以S 地最大值为.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙12分。
2020年高考全国卷三文科数学及答案解析

一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,
只有一项是符合题目要求的。
1.(5 分)已知集合 A = 1,2,3,5,7,11, B = x | 3 x 15,则 A B 中元素的个数为
()
A. 2
B. 3
C. 4
A. 5
B. 2 5
C. 4 5
D.8 5
12.(5 分)已知函数 f (x) = sin x + 1 ,则 sin x
A. f (x) 的最小值为 2
B. f (x) 的图像关于 y 轴对称
C. f (x) 的图像关于直线 x = 对称
D. f (x) 的图像关于直线 x = 对称 2
二、 空题:本题共 4 小题,每小题 5 分,共 20 分。
(2)点C1 在平面 AEF 内. 20.(12 分)
已知函数 f (x) = x3 − kx + k 2
(1)讨论 f (x) 的单调性
2)若 f (x) 有三个零点,求 k 的取值范围.
21.(12 分)
已知椭圆
C
:x2 25
+
y2 m2
= 1(0 m 5
的离心率为
15 ,A,B 分别为
13.(5 分)若 x , y 满足约束条件 2x − y 0,则 z = 3x + 2 y 的最大值为
.
x 1,
2
14.(5
分)设双曲线 C
:
x2 a2
−
y2 b2
= 1(a
0,b
0) 的一条渐近线为
y
=
2x ,则C 的离心
2023年全国乙卷文科高考数学试题+答案解析

绝密★启用前2023年普通高等学校招生全国统一考试(全国乙卷∙文科)数学注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.2+i 2+2i 3 =()A.1B.2C.5D.5【答案】C【解析】∵2+i 2+2i 3=2-2i -1=1-2i ,∴|2+i 2+2i 3|=1-2i =12+(-2)2=5,选C 。
2.设全集U ={0,1,2,4,6,8},集合M ={0,4,6},N ={0,1,6},则M ⋃C U N =()A.{0,2,4,6,8} B.{0,1,4,6,8}C.{1,2,4,6,8}D.U【答案】A【解析】∵N ={2,4,8},∴M ⋃C U N ={0,2,4,6,8},选A.3.如图,网格纸上绘制的一个零件的三视图,网格小正方形的边长为1,则该零件的表面积为()A.24B.26C.28D.30【答案】D【解析】如图所示,在长方体ABCD -A 1B 1C 1D 1中,AB =BC =2, AA 1=3,点H ,I ,J ,K 为所在棱上靠近点B 1,C 1,D 1,A 1的三等分点,O ,L ,M ,N 为所在棱的中点,则三视图所对应的几何体为长方体ABCD -A 1B 1C 1D 1去掉长方体ONIC 1-LMHB 1之后所得的几何体,该几何体表面积为:2×(2×2)+4×(2×3)-2×(1×1)=30,选D 。
4.在△BC 中,内角A,B,C 的对边分别是a,b,c,若acosB -bcosA =c,且C =π5,则∠B =()A.π10B.π5C.3π10D.2π5【答案】C【解析】∵sinAcosB -sinBcosA =sinC,即sinAcosB -sinBcosA =sin (A +B )=sinAcosBsinBcosA,∴sinBcosA =0,∵B ∈(0,π),∴sinB >0,∴cosA =0,A =π2,∴B =π-A -C =3π10,选C 。
2023高考全国甲卷语文试题及详解

2023年普通高考(全国甲卷)语文注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、现代文阅读(36分)(一)论述类文本阅读(本题共3 小题,9分)阅读下面的文字,完成1—3题。
随着中国考古学的飞速发展,考古资料得以大量积累,考古学文化时空框架体系基本建立,多学科合作日益深入,各种专题研究广泛展开。
“考古写史”在中国已经取得巨大成就,获得诸多具有突破性和填补空白意义的成绩,中国考古学证明了自身的价值,尤其是在上古史构建方面展现了广阔前景。
从考古发现来看,考古学提供了传统历史学不可想象的新发现、新材料,呈现出不同时期的古代物质文化面貌、古人日常生产生活状态以及各地的文明化进程等,如不同区域新石器时代晚期大型聚落遗址、大型公共建筑、大型墓葬、水利设施、手工业作坊,以及象征王权、神权、军权和复杂礼制出现的精美玉器、陶器、漆器、象牙器等。
从考古发现来看,考古学提供了传统历史学不可想象的新发现、新材科,呈现出不同时期的古代物质文化面貌、古人日常生产生活状态以及各地的文明化进程等,如不同区域新石器时代晚期大型聚落遗址、大型公共建筑、大型墓葬、水利设施、手工业作坊,以及象征王权、神权、军权和复杂礼制出现的精美玉器、陶器、漆器、象牙器等。
从重构上古史体系角度看,20 世纪70—80年代,夏鼐、苏秉琦等系统地构建了新石器与夏商周三代时期的考古学文化区系类型时空框架体系。
苏秉琦在新石器时代考古学文化区系类型基础上提出“满天星斗”“多元一体”和“古国一方国帝国”等关于中国上古史的历史叙述体系。
严文明提出“重瓣花朵”模式,在承认多区域文化共存的文化多元性的同时,强调中原文化区“联系各文化区的核心作用”。
2023高考全国甲卷数学真题及答案(文数)

2023高考全国甲卷数学真题及答案(文数)2023年普通高等学校招生全国统一考试文科数学试题2023年普通高等学校招生全国统一考试文科数学参考答案学好高考数学的技巧高考数学题目的总结比较。
建立自己的题库。
多做。
主要是指做高考数学习题,学数学一定要做习题,并且应该适当地多做些。
养成好的学习习惯,做好预习,把预习没看懂的东西,第二天上课着重听。
抓住课堂。
高考数学理科学习重在平日功夫,不适于突击复习。
高质量完成作业。
所谓高质量是指高正确率和高速度。
翻译:把中文翻译成为数学语言,包括:字母表示未知数、图像表示函数式或几何题目、概率语言等等。
该方法常用于函数,几何以及不等式等题目。
特殊化:在面对抽象或者难以理解的题目的时候,我们尝试用最极端最特殊的数字来代替变量,帮助我们理解题目。
该方法常用于在选择题目中排除选项,在解大题的过程中也经常会用到特殊化的结论。
盯住目标:把高考数学目标和已知结合,联想相关的定理、定义、方法。
在压轴题目中,往往需要不断转化目标,即盯住目标需要反复使用!各省高考用卷情况1、新高考一卷(8个省份)适用省份:山东、河北、湖北、福建、湖南、广东、江苏,浙江考试科目:语文、数学、外语、物理、化学、生物、政治、历史、地理、信息技术等。
特点:语文、数学、外语三门考试由教育部考试中心统一命题;物理、历史、化学、政治、生物、地理由各省自行命题。
其中广东、福建、江苏、湖南、湖北、河北6个省是3+1+2模式的高考省份,山东省是综合改革3+3省份。
2、新高考二卷(3个省份)适用省份:海南、辽宁、重庆考试科目:语文、数学、外语、物理、化学、生物、政治、历史、地理等。
特点:语文、数学、外语三门考试由教育部考试中心统一命题;物理、历史、化学、政治、生物、地理由各省自行命题。
其中辽宁、重庆两省市是3+1+2省份,海南是综合改革3+3省份。
3、全国甲卷(5个省份)适用省份:云南、贵州、四川、西藏、广西考试科目:语文、数学、外语、文综、理综特点:语文、数学、外语、文科综合、理科综合均由教育部考试中心统一命题。
2021年高考文数真题试卷(全国乙卷)含答案

2021年高考文数真题试卷(全国乙卷)一、选择题:本题共12小题,每小题5分,总共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
(共12题;共51分)1.已知全集U={1,2,3,4,5},集合M={1,2},N={3,4},则C u(MUN)=()A. {5}B. {1,2}C. {3,4}D. {1,2,3,4}【答案】A【考点】交集及其运算,补集及其运算【解析】【解答】因为U={1,2,3,4,5},集合M={1,2},N={3,4} 则MUN ={1,2,3,4},于是C u(MUN)= {5} 。
故答案为:A【分析】先求MUN,再求C u(MUN)。
2.设iz=4+3i,则z等于()A. -3-4iB. -3+4iC. 3-4iD. 3+4i【答案】C【考点】复数代数形式的混合运算【解析】【解答】因为iz=4+3i ,所以Z=4+3ii =4i−3−1=3−4i。
故答案为:C【分析】直接解方程,由复数的除法运算法则,得到结果。
3.已知命题p:∃x∈R,sinx<1;命题q:∀x∈R,e|x|≥1,则下列命题中为真命题的是()A. p ∧qB. ¬p ∧qC. p ∧¬qD. ¬(pVq)【答案】A【考点】全称量词命题,存在量词命题,命题的否定,命题的真假判断与应用【解析】【解答】因为命题P是真命题,命题q也是真命题,故答案为:A【分析】先判断命题p,q的真假,然后判断选项的真假。
4.函数f(x)=sin x3+cos x3的最小正周期和最大值分别是()A. 3 π和√2B. 3 π和2C. 6π和√2D. 6π和2【答案】C【考点】正弦函数的图象,y=Asin(ωx+φ)中参数的物理意义,正弦函数的周期性,正弦函数的零点与最值【解析】【解答】因为f(x)=sin x3+cos x3=√22sin(x3+π4),所以周期T=2π13=6π ,值域[-√2,√2]。
全国高考文科全国卷数学试题及答案

年普通高等学校招生全国统一考试文科数学卷3注意事项:1.答题前,考生务必将自己的姓名、准考证号填写在答题卡上;2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号;回答非选择题时,将答案写在答题卡上;写在本试卷上无效;3.考试结束后,将本试卷和答题卡一并交回;一、选择题:本大题共12小题,每小题5分,共60分;在每小题给出的四个选项中,只有一项是符合题目要求的;1.已知集合A={1,2,3,4},B={2,4,6,8},则A B中元素的个数为A.1 B.2 C.3 D.42.复平面内表示复数(2)=-+的点位于z i iA.第一象限B.第二象限C.第三象限D.第四象限3.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量单位:万人的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是 A .月接待游客逐月增加 B .年接待游客量逐年增加C .各年的月接待游客量高峰期大致在7,8月D .各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳4.已知4sin cos 3αα-=,则sin 2α=A .79- B .29- C . 29D .795.设,x y 满足约束条件326000x y x y +-≤⎧⎪≥⎨⎪≥⎩,则z x y =-的取值范围是A .-3,0B .-3,2C .0,2D .0,36.函数1()sin()cos()536f x x x ππ=++-的最大值为A .65B .1C .35D .157.函数2sin 1xy x x=++的部分图像大致为 A . B .C .D .8.执行右面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为 A .5 B .4 C .3 D .29.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为 A .π B .34π C .2πD .4π10.在正方体1111ABCD A B C D -中,E 为棱CD 的中点,则A .11A E DC ⊥B .1A E BD ⊥C .11A E BC ⊥D .1AE AC ⊥11.已知椭圆2222:1(0)x y C a b a b+=>>的左、右顶点分别为12,A A ,且以线段12A A 为直径的圆与直线20bx ay ab -+=相切,则C 的离心率为A .63B .33C .23D .1312.已知函数211()2()x x f x x x a e e --+=-++有唯一零点,则a =A .12-B .13C .12D .1二、填空题:本题共4小题,每小题5分,共20分; 13.已知向量(2,3),(3,)a b m =-=,且a b ⊥,则m = .14.双曲线2221(0)9x y a a -=>的一条渐近线方程为35y x =,则a = .15.ABC ∆的内角,,A B C 的对边分别为,,a b c ;已知60,3C b c ===,则A =_________;16.设函数1,0,()2,0,x x x f x x +≤⎧=⎨>⎩ 则满足1()()12f x f x +->的x 的取值范围是__________;三、解答题:共70分;解答应写出文字说明、证明过程或演算步骤;第17~21题为必考题,每个试题考生都必须作答;第22、23题为选考题,考生根据要求作答; 一必考题:共60分; 17.12分设数列{}n a 满足123(21)2n a a n a n +++-=.1求{}n a 的通项公式; 2求数列{}21na n +的前n 项和. 18.12分某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温单位:℃有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间20,25,需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:10,1515,2020,2525,3030,3535,40最高气温天数216362574以最高气温位于各区间的频率代替最高气温位于该区间的概率;1求六月份这种酸奶一天的需求量不超过300瓶的概率;2设六月份一天销售这种酸奶的利润为Y单位:元,当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.19.12分如图,四面体ABCD中,△ABC是正三角形,AD=CD.1证明:AC⊥BD;2已知△ACD是直角三角形,AB=BD.若E为棱BD上与D不重合的点,且AE⊥EC,求四面体ABCE与四面体ACDE的体积比.20.12分在直角坐标系xOy 中,曲线22y x mx =+-与x 轴交于A ,B 两点,点C 的坐标为0,1.当m 变化时,解答下列问题:1能否出现AC ⊥BC 的情况说明理由;2证明过A ,B ,C 三点的圆在y 轴上截得的弦长为定值. 21.12分已知函数()2(1)ln 2x ax a x f x =+++. 1讨论()f x 的单调性; 2当0a <时,证明3()24f x a≤--. 二选考题:共10分;请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分;22.选修4―4:坐标系与参数方程10分在直角坐标系xOy 中,直线1l 的参数方程为2,x t y kt =+⎧⎨=⎩t 为参数,直线2l 的参数方程为2,x m my k =-+⎧⎪⎨=⎪⎩m 为参数,设1l 与2l 的交点为P ,当k 变化时,P 的轨迹为曲线C .1写出C 的普通方程:2以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,设3l:(cos sin )0ρθθ+-=,M 为3l 与C 的交点,求M 的极径.23.选修4—5:不等式选讲10分已知函数()||||f x x x =+1--2.1求不等式()f x ≥1的解集;2若不等式()f x x x m 2≥-+的解集非空,求m 的取值范围.年普通高等学校招生全国统一考试文科数学参考答案一、选择题1.B 2.C 3.A 4.A 5.B 6.A 7.D 8.D 9.B 10.C 11.A 12.C 二、填空题13.2 14.5 15.75° 16.1(,)4-+∞三、解答题 17.解: 1因为123(21)2n a a n a n +++-=,故当2n ≥时, 1213(23)2(1)n a a n a n -+++-=-两式相减得(21)2n n a -= 所以2(2)21n a n n =≥- 又由题设可得12a = 从而{}n a 的通项公式为221n a n =- 2记{}21na n +的前n 项和为n S 由1知21121(21)(21)2121n a n n n n n ==-++--+ 则1111112 (1335212121)n nS n n n =-+-++-=-++ 18.解:1这种酸奶一天的需求量不超过300瓶,当且仅当最高气温低于25,由表格数据知,最高气温低于25的频率为216360.690++=,所以这种酸奶一天的需求量不超过300瓶的概率的估计值为2当这种酸奶一天的进货量为450瓶时,若最高气温不低于25,则64504450900Y =⨯-⨯=;若最高气温位于区间20,25,则63002(450300)4450300Y =⨯+--⨯=;若最高气温低于20,则62002(450200)4450100Y =⨯+--⨯=-所以,Y 的所有可能值为900,300,-100Y 大于零当且仅当最高气温不低于20,由表格数据知,最高气温不低于20的频率为3625740.890+++=,因此Y 大于零的概率的估计值为 19.解:1取AC 的中点O ,连结,DO BO ,因为AD CD =,所以AC DO ⊥又由于ABC ∆是正三角形,故BO AC ⊥从而AC ⊥平面DOB ,故AC BD ⊥2连结EO由1及题设知90ADC ∠=,所以DO AO = 在Rt AOB ∆中,222BO AO AB += 又AB BD =,所以ODABCE222222BO DO BO AO AB BD +=+==,故90DOB ∠=由题设知AEC ∆为直角三角形,所以12EO AC =又ABC ∆是正三角形,且AB BD =,所以12EO BD =故E 为BD 的中点,从而E 到平面ABC 的距离为D 到平面ABC 的距离的12,四面体ABCE 的体积为四面体ABCD 的体积的12,即四面体ABCE 与四面体ACDE 的体积之比为1:120.解:1不能出现AC BC ⊥的情况,理由如下:设12(,0),(,0)A x B x ,则12,x x 满足220x mx +-=,所以122x x =- 又C 的坐标为0,1,故AC 的斜率与BC 的斜率之积为121112x x --⋅=-,所以不能出现AC BC ⊥的情况 2BC 的中点坐标为21(,)22x ,可得BC 的中垂线方程为221()22x y x x -=- 由1可得12x x m +=-,所以AB 的中垂线方程为2mx =-联立22,21()22m x x y x x ⎧=-⎪⎪⎨⎪-=-⎪⎩又22220x mx +-=,可得,212m x y ⎧=-⎪⎪⎨⎪=-⎪⎩所以过A,B,C 三点的圆的圆心坐标为1(,)22m --,半径2r =故圆在y轴上截得的弦长为3=,即过A,B,C 三点的圆在y 轴上截得的弦长为定值; 21.解:1fx 的定义域为(0,)+∞,1(1)(21)()221x ax f x ax a xx++'=+++=若0a ≥,则当(0,)x ∈+∞时,()0f x '>,故()f x 在(0,)+∞单调递增若0a <,则当1(0,)2x a ∈-时,()0f x '>;当1(,)2x a∈-+∞时,()0f x '< 故()f x 在1(0,)2a -单调递增,在1(,)2a-+∞单调递减; 2由1知,当0a <时,()f x 在12x a=-取得最大值,最大值为 111()ln()1224f a a a-=--- 所以3()24f x a ≤--等价于113ln()12244a a a---≤--,即11ln()1022a a-++≤ 设()ln 1g x x x =-+,则1()1g x x '=- 当(0,1)x ∈时,()0g x '>;当(1,)x ∈+∞,()0g x '<; 所以()g x 在0,1单调递增,在(1,)+∞单调递减; 故当1x =时,()g x 取得最大值,最大值为(1)0g = 所以当0x >时,()0g x ≤从而当0a <时,11ln()1022a a -++≤,即3()24f x a≤-- 22.解: 1消去参数t 得1l 的普通方程1:(2)l y k x =-;消去参数m t 得2l 的普通方程21:(2)l y x k=+ 设(,)P x y ,由题设得(2),1(2).y k x y x k =-⎧⎪⎨=+⎪⎩消去k 得224(0)x y y -=≠ 所以C 的普通方程为224(0)x y y -=≠2C 的极坐标方程为222(cos sin )4(22,)ρθθθπθπ-=<<≠联立222(cos sin )4,(cos sin )0ρθθρθθ⎧-=⎪⎨+=⎪⎩得cos sin 2(cos sin )θθθθ-=+ 故1tan 3θ=-,从而2291cos ,sin 1010θθ== 代入222(cos sin )4ρθθ-=得25ρ=,所以交点M23.解:13,1,()21,12,3,2x f x x x x -<-⎧⎪=--≤≤⎨⎪>⎩当1x <-时,()1f x ≥无解;当12x -≤≤时,由()1f x ≥得,211x -≥,解得12x ≤≤; 当2x >时,由()1f x ≥解得2x >所以()1f x ≥的解集为{|1}x x ≥2由2()f x x x m ≥-+得2|1||2|m x x x x ≤+---+,而 22|1||2|||1||2||x x x x x x x x +---+≤++--+235(||)24x =--+5 4≤且当32x=时,25|1||2|4x x x x+---+=故m的取值范围为5 (,]4 -∞。
2023新高考Ⅰ卷语文真题(含答案解析)

2023新高考Ⅰ卷语文真题(含答案解析)2023高考全国卷新高考Ⅰ卷真题(含答案)注意事项:1.答卷前,考生务必将自己的姓名、准考证号等填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、现代文阅读(35分)(一)现代文阅读I(本题共5小题,19分)阅读下面的文字,完成1~5题。
对素食者和肠胃疾病患者来说,藜麦的发现是一个奇迹。
藜麦不含麸质,富含镁和铁,比其他种子含有更多的蛋白质,包括人体无法独自生成的必需的氨基酸。
美国宇航局宣布,藜麦是地球上营养最均衡的食物之一,是宇航员的理想之选。
产于安第斯山的藜麦有一个令西方消费者神往的传说:印加人非常重视藜麦,认为它是神圣的,并且称之为"万谷之母"。
不过,藜麦的爱好者却通过媒体发现了一个令人不安的事实。
从20XX年到20XX年,玻利维亚和秘鲁的藜麦价格上涨了两倍。
20XX年,《独立报》称,玻利维亚的藜麦消费量"5年间下降了34%,当地家庭已经吃不起这种主食了,它已经变成了奢侈品"。
《纽约时报》援引研究报告称,蔡麦种植区的儿童营养不良率正在上升。
20XX年,《卫报》用煽动性标题提升了人们对这个问题的关注度:"素食者的肚子能装下藜麦令人反胃的事实吗?"该报称,贫穷的玻利维亚人和秘鲁人正在食用更加便宜的"进口垃圾食品"。
《独立报》20XX年一篇报道的标题是"藜麦:对你有利--对玻利维亚人有害"。
这些消息传遍了全球,在健康饮食者之中引发了一场良心危机。
在社交媒体、素食博客和健康饮食论坛上,人们开始询问食用藜麦是否合适。
这种说法看似可信,被许多人认可,但是经济学家马克·贝勒马尔等人对此则持保留意见。
2021年高考文数真题试卷(全国甲卷)含答案

2021年高考文数真题试卷(全国甲卷)一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
(共12题;共45分)1.设集合M={1,3,5,7,9},N={x∣2x>7},则M∩N=( )A. {7,9}B. {5,7,9}C. {3,5,7,9}D. {1,3,5,7,9}【答案】B【考点】交集及其运算【解析】【解答】解:由2x>7,得x>72,故N={x|x>72},则根据交集的定义易得M∩N={5,7,9}.故答案为:B【分析】根据交集的定义求解即可.2.为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:根据此频率分布直方图,下面结论中不正确的是()A. 该地农户家庭年收入低于4.5万元的农户比率估计为6%B. 该地农户家庭年收入不低于10.5万元的农户比率估计为10%C. 估计该地农户家庭年收入的平均值不超过6.5万元D. 估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间【答案】C【考点】频率分布直方图【解析】【解答】解:对于A,由频率分布直方图得该地农户家庭年收入低于4.5万元的农户比率估计为0.02+0.04=6%,故A正确;对于B,由频率分布直方图得该地农户家庭年收入不低于10.5万元的农户比率估计为0.02×3+0.04=10%,故B正确;对于D,由频率分布直方图得该地农户家庭年收入介于4.5万元至8.5万元之间比率估计为0.10+0.14+0.20×2=0.64>0.5,故D正确故不正确的是C故答案为:C【分析】根据频率分布直方图直接求解即可.3.已知 (1−i )2z =3+2i,则z=( )A. -1- 32 iB. -1+ 32 iC. - 32 +iD. - 32 -i 【答案】 B【考点】复数代数形式的混合运算 【解析】【解答】解:z =3+2i (1−i )2=3+2i −2i=(3+2i )i(−2i )i=−2+3i 2=−1+32i故答案为:B【分析】根据复数的运算法则直接求解即可. 4.下列函数中是增函数的为( )A. f(x)=−xB. f(x)=(23)x C. f(x)=x 2 D. f(x)=√x 3 【答案】 D【考点】函数的单调性及单调区间,函数单调性的判断与证明【解析】【解答】解:对于A ,考察函数f(x)=kx ,易知当x<0时,y=kx 单调递减,故A 错误; 对于B ,考察函数f(x)=a x , 易知当0<a<1时,f(x)=a x 单调递减,故B 错误;对于C ,考察函数f(x)=x 2 , 易知当x<0时,f(x)=x 2单调递减,当x>0时,f(x)=x 2单调递增,故C 错误; 对于D ,考察函数f (x )=x 13 , 易知f(x)=a x 单调递增,故D 正确. 故答案为:D【分析】根据正比例函数,指数函数,二次函数,幂函数的单调性之间求解即可. 5.点 (3,0) 到双曲线x 216−y 29=1 的一条渐近线的距离为( )A. 95 B. 85 C. 65 D. 45 【答案】 A【考点】点到直线的距离公式,双曲线的简单性质【解析】【解答】解:不妨取双曲线的一条渐近线为:y =34x , 即3x-4y=0, 则所求距离为d =√32+(−4)2=95 故答案为:A【分析】根据双曲线的几何性质,结合点到直线的距离公式求解即可.6.青少年视力是社会普遍关注的问题,视力情况可借助视力表测量,通常用五分记录法和小数记录法记录视力数据,五分记录法的数据L 和小数记数法的数据V 满足L=5+lgV 。
2023年高考全国乙卷数学(文)真题及答案

=0,
则 x = (a 一 1)x ,即1 = a 一 1 ,解得a = 2 .
故选:D.
一
一
6. 正方形 ABCD 的边长是 2 , E 是 AB 的中点,则E C E.D = ( )
A.
B. 3
C. 2
D. 5
【答案】B
【解析】
一
一
恳 } 【分析】方法一:以AB AD,
为基底向量表示
再结合数量积的运算律运算求解;方法二:建
该几何体的表面积和原来的长方体的表面积相比少2 个边长为 1 的正方形,
其表面积为: 2〉(2〉2 )+ 4〉(2〉3 )_ 2〉(1〉1 ) = 30 .
故选:D.
4. 在 ABC 中, 内角A, B, C 的对边分别是 a, b, c ,若 acosB _ bcosA = c ,且 C = 冗 ,则 三B = ( ) 5
整理可得 sin B cos A = 0 ,由于 B =(0, π ) ,故 sin B > 0 ,
据此可得cos A = 0, A = ,
则 B=π_A_C=π_ _ = .
故选:C.
x
5. 已知 f(x) =
是偶函数,则 a = ( 一1
)
A. 一2
B. 一1
C. 1
D. 2
【答案】D
【解析】
不
π 大于 的概率为 (
4
A.
) B.
C.
D.
【答案】C 【解析】
【分析】根据题意分析区域的几何意义,结合几何概型运算求解.
恳 } 【详解】因为区域 (x, y )|1 共 x2 + y2 共 4 表示以O(0, 0) 圆心,外圆半径 R = 2 ,内圆半径r = 1 的圆环,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016年普通高等学校招生全国统一考试文科数学注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上。
2.回答第Ⅰ卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号框涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号框。
写在本试卷上无效。
3.答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效。
4.考试结束,将试题卷和答题卡一并交回。
第Ⅰ卷一、 选择题:本大题共12小题。
每小题5分,在每个小题给出的四个选项中,只有一项是符合要求的。
(1)已知集合{123}A =,,,2{|9}B x x =<,则A B =(A ){210123}--,,,,, (B ){21012}--,,,, (C ){123},, (D ){12},(2)设复数z 满足i 3i z +=-,则z = (A )12i -+(B )12i -(C )32i +(D )32i -(3) 函数=sin()y A x ωϕ+的部分图像如图所示,则 (A )2sin(2)6y x π=- (B )2sin(2)3y x π=- (C )2sin(2+)6y x π= (D )2sin(2+)3y x π= (4) 体积为8的正方体的顶点都在同一球面上,则该球面的表面积为(A )12π(B )323π(C )8π(D )4π (5) 设F 为抛物线C :y 2=4x 的焦点,曲线y =k x (k >0)与C 交于点P ,PF ⊥x 轴,则k = (A )12(B )1 (C )32(D )2 (6) 圆x 2+y 2?2x ?8y +13=0的圆心到直线ax +y ?1=0的距离为1,则a = (A )?43(B )?34(C )3(D )2(7) 如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为(A )20π(B )24π(C )28π(D )32π(8) 某路口人行横道的信号灯为红灯和绿灯交替出现,红灯持续时间为40秒.若一名行人来到该路口遇到红灯,则至少需要等待15秒才出现绿灯的概率为(A )710(B )58(C )38(D )310(9)中国古代有计算多项式值得秦九韶算法,右图是实现该算法的程序框图.执行该程序框图,若输入的a 为2,2,5,则输出的s =(A )7(B )12(C )17(D )34(10) 下列函数中,其定义域和值域分别与函数y=10lg x 的定义域和值域相同的是(A )y =x (B )y =lg x (C )y =2x (D )y x= (11) 函数π()cos 26cos()2f x x x =+-的最大值为 (A )4(B )5 (C )6 (D )7(12) 已知函数f (x )(x ∈R )满足f (x )=f (2-x ),若函数y =|x 2-2x -3| 与y =f (x ) 图像的交点为(x 1,y 1),(x 2,y 2),…,(x m ,y m ),则1=mii x =∑ (A)0 (B)m (C) 2m (D) 4m二.填空题:共4小题,每小题5分.(13) 已知向量a =(m ,4),b =(3,-2),且a ∥b ,则m =___________.(14) 若x ,y 满足约束条件103030x y x y x -+≥⎧⎪+-≥⎨⎪-≤⎩,则z =x -2y 的最小值为__________(15)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,若4cos 5A =,5cos 13C =,a =1,则b =____________.(16)有三张卡片,分别写有1和2,1和3,2和3. 甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是________________.三、解答题:解答应写出文字说明,证明过程或演算步骤.(17)(本小题满分12分)等差数列{n a }中,34574,6a a a a +=+=(I )求{n a }的通项公式;(II)设n b =[n a ],求数列{n b }的前10项和,其中[x]表示不超过x 的最大整数,如[0.9]=0,[2.6]=2(18)(本小题满分12分)某险种的基本保费为a (单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:(I )记A 为事件:“一续保人本年度的保费不高于基本保费”。
求P(A)的估计值;(II)记B 为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”. 求P(B)的估计值;(III )求续保人本年度的平均保费估计值.(19)(本小题满分12分)如图,菱形ABCD 的对角线AC 与BD 交于点O ,点E 、F 分别在AD ,CD 上,AE =CF ,EF 交BD 于点H ,将DEF 沿EF 折到'D EF 的位置.(I )证明:'AC HD ⊥;(II)若55,6,,'4AB AC AE OD ====求五棱锥'ABCEF D -体积. (20)(本小题满分12分)已知函数()(1)ln (1)f x x x a x =+--.(I )当4a =时,求曲线()y f x =在()1,(1)f 处的切线方程;(II)若当()1,x ∈+∞时,()0f x >,求a 的取值范围.(21)(本小题满分12分) 已知A 是椭圆E :22143x y +=的左顶点,斜率为()0k k >的直线交E 与A ,M 两点,点N 在E 上,MA NA ⊥.(I )当AM AN =时,求AMN 的面积(II)当AM AN =2k <<.请考生在第22~24题中任选一题作答,如果多做,则按所做的第一题计分.(22)(本小题满分10分)选修4-1:几何证明选讲如图,在正方形ABCD 中,E ,G 分别在边DA ,DC 上(不与端点重合),且DE =DG ,过D 点作DF ⊥CE ,垂足为F .(Ⅰ)证明:B ,C ,G ,F 四点共圆;(Ⅱ)若AB =1,E 为DA 的中点,求四边形BCGF 的面积.(23)(本小题满分10分)选修4-4:坐标系与参数方程在直角坐标系xOy 中,圆C 的方程为22(+6)+=25x y .(Ⅰ)以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,求C 的极坐标方程;(Ⅱ)直线l 的参数方程是cos sin x t α,y t α,(t 为参数),l 与C 交于A ,B 两点,10AB ,求l 的斜率. (24)(本小题满分10分)选修4-5:不等式选讲 已知函数11()22f x x x ,M 为不等式()2f x 的解集. (Ⅰ)求M ;(Ⅱ)证明:当a ,b M 时,1ab ab .DCAADACBCDBB 1和317.【试题分析】(I )先设{}n a 的首项和公差,再利用已知条件可得1a 和d ,进而可得{}n a 的通项公式;(II )根据{}n b 的通项公式的特点,采用分组求和法,即可得数列{}n b 的前10项和. 18.【试题分析】(I )由已知可得续保人本年度的保费不高于基本保费的频数,进而可得()P A 的估计值;(II )由已知可得续保人本年度的保费高于基本保费但不高于基本保费的160%的频数,进而可得()P B 的估计值;(III )计算出险次数的频率,进而可得续保人本年度的平均保费估计值.19.【试题分析】(I )先证C A ⊥OH ,C D 'A ⊥O ,再证C A ⊥平面D 'OH ,即可证C D 'A ⊥H ;(II )先证D 'O ⊥OH ,进而可证D 'O ⊥平面CD AB ,再计算菱形CD AB 和FD ∆E 的面积,进而可得五棱锥'ABCEF D -的体积.20.21.【试题分析】(I )设点M 的坐标,由已知条件可得点M 的坐标,进而可得∆AMN 的面积. 请考生在第22~24题中任选一题作答,如果多做,则按所做的第一题计分.22.【试题分析】(I )先证DFC DC ∆∆E ∽,再证FDG FC ∆∆B ∽,进而可证B ,C ,G ,F 四点共圆;(II )先证GF GC ∆B ≅∆B ,再计算GC ∆B 的面积,进而可得四边形BCGF 的面积. 解析:(I )在正方形CD AB 中,DF DCF ∠E =∠,所以DC FC ∠E =∠B因为DF C ⊥E ,所以DFC DC 90∠=∠E =,所以DFC DC ∆∆E ∽ 所以GC 1111C CG 12224S ∆B =B⋅=⨯⨯= 所以GC CGF 122S S ∆B B ==四边形 23.【试题分析】(I )利用222x y ρ=+,cos x ρθ=可得C 的极坐标方程;(II )先将直线l 的参数方程化为普通方程,再利用弦长公式可得l 的斜率.解析:(I )由()22625x y ++=得2212110x y x +++= 222x y ρ=+,cos x ρθ=故C 的极坐标方程为212cos 110ρρθ++=(II )由cos sin x t y t αα=⎧⎨=⎩(t 为参数)得tan y x α=,即tan 0x y α-=圆心()C 6,0-,半径5r =圆心C 到直线l 的距离2222103105222d r ⎛⎫⎛AB ⎫=-=-= ⎪ ⎪ ⎪⎝⎭⎝⎭即26tan 3102tan 1αα-=+,解得15tan α=±,所以l 的斜率为15±. 24.(当1122x -≤≤时,()12f x =<,所以1122x -≤≤ 当12x >时,()22f x x =<,解得1x <,所以112x << 所以()1,1M =-(II)()()()()()()2222222222212121111a b ab a ab b ab a b a b a a b +-+=++-++=-+-=-- 11a -<<,11b -<<∴201a ≤<,201b ≤<∴210a -<,210b ->即1a b ab +<+。
