两个三角函数求和公式的应用

合集下载

三角函数公式大全关系

三角函数公式大全关系：倒数tanα·cotα=1sinα·cscα=1cosα·secα=1商的关系：sinα/cosα=tanα=secα/cscαcosα/sinα=cotα=cscα/secα平方关系：sin^2(α)+cos^2(α)=11+tan^2(α)=sec^2(α)1+cot^2(α)=csc^2(α)平常针对不同条件的常用的两个公式sin^2(α)+cos^2(α)=1tan α *cot α=1一个特殊公式（sina+sinθ）*（sina-sinθ）=sin（a+θ）*sin（a-θ）证明：（sina+sinθ）*（sina-sinθ）=2 sin[(θ+a)/2] cos[(a-θ)/2] *2 cos[(θ+a)/2] sin[(a-θ)/2] =sin（a+θ）*sin（a-θ）坡度公式我们通常半坡面的铅直高度h与水平高度l的比叫做坡度（也叫坡比），用字母i表示，即i=h / l, 坡度的一般形式写成l : m 形式，如i=1:5.如果把坡面与水平面的夹角记作a(叫做坡角），那么i=h/l=tan a.锐角三角函数公式正弦：sin α=∠α的对边/∠α的斜边余弦：cos α=∠α的邻边/∠α的斜边正切：tan α=∠α的对边/∠α的邻边余切：cot α=∠α的邻边/∠α的对边二倍角公式正弦sin2A=2sinA·cosA余弦1.Cos2a=Cos^2(a)-Sin^2(a)2.Cos2a=1-2Sin^2(a)3.Cos2a=2Cos^2(a)-1即Cos2a=Cos^2(a)-Sin^2(a)=2Cos^2(a)-1=1-2Sin^2(a) 正切tan2A=（2tanA）/（1-tan^2(A)）三倍角公式sin3α=4sinα·sin(π/3+α)sin(π/3-α)cos3α=4cosα·cos(π/3+α)cos(π/3-α)tan3a = tan a · tan(π/3+a)· tan(π/3-a)三倍角公式推导sin(3a)=sin(a+2a)=sin2acosa+cos2asina=2sina(1-sin²a)+(1-2sin²a)sina=3sina-4sin^3acos3a=cos(2a+a)=cos2acosa-sin2asina=(2cos²a-1)cosa-2(1-cos^a)cosa=4cos^3a-3cosasin3a=3sina-4sin^3a=4sina(3/4-sin²a)=4sina[(√3/2)²-sin²a]=4sina(sin²60°-sin²a)=4sina(sin60°+sina)(sin60°-sina)=4sina*2sin[(60+a)/2]cos[(60°-a)/2]*2sin[(60°-a)/2]cos[(60°-a)/2]=4sinasin(60°+a)sin(60°-a)cos3a=4cos^3a-3cosa=4cosa(cos²a-3/4)=4cosa[cos²a-(√3/2)^2]=4cosa(cos²a-cos²30°)=4cosa(cosa+cos30°)(cosa-cos30°)=4cosa*2cos[(a+30°)/2]cos[(a-30°)/2]*{-2sin[(a+30°)/2]sin[(a-30°)/2]}=-4cosasin(a+30°)sin(a-30°)=-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)]=-4cosacos(60°-a)[-cos(60°+a)]=4cosacos(60°-a)cos(60°+a)上述两式相比可得tan3a=tanatan(60°-a)tan(60°+a)现列出公式如下: sin2α=2sinαcosα tan2α=2tanα/(1-tan^2(α))cos2α=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α) 可别轻视这些字符,它们在数学学习中会起到重要作用。

从高中到大学的所有三角函数公式

倒数关系：tanα ·cotα=1sinα ·cscα=1cosα ·secα=1商的关系：sinα/cosα=tanα=secα/cscαcosα/sinα=cotα=cscα/secα平方关系：sin^2(α)+cos^2(α)=11+tan^2(α)=sec^2(α)1+cot^2(α)=csc^2(α)平常针对不同条件的常用的两个公式sin^2(α)+cos^2(α)=1tan α *cot α=1一个特殊公式（sina+sinθ）*（sina-sinθ）=sin（a+θ）*sin（a-θ）证明：（sina+sinθ）*（sina-sinθ）=2 sin[(θ+a)/2] cos[(a-θ)/2] *2 cos[(θ+a)/2] sin[(a-θ)/2] =sin（a+θ）*sin（a-θ）坡度公式我们通常半坡面的铅直高度h与水平高度l的比叫做坡度（也叫坡比）, 用字母i表示, 即i=h / l, 坡度的一般形式写成l : m 形式,如i=1:5.如果把坡面与水平面的夹角记作a(叫做坡角）,那么i=h/l=tan a.锐角三角函数公式正弦：sin α=∠α的对边/∠α 的斜边余弦：cos α=∠α的邻边/∠α的斜边正切：tan α=∠α的对边/∠α的邻边余切：cot α=∠α的邻边/∠α的对边二倍角公式正弦sin2A=2sinA·cosA余弦1.Cos2a=Cos^2(a)-Sin^2(a)2.Cos2a=1-2Sin^2(a)3.Cos2a=2Cos^2(a)-1即Cos2a=Cos^2(a)-Sin^2(a)=2Cos^2(a)-1=1-2Sin^2(a) 正切tan2A=（2tanA）/（1-tan^2(A)）三倍角公式sin3α=4sinα·sin(π/3+α)sin(π/3-α)cos3α=4cosα·cos(π/3+α)cos(π/3-α)tan3a = tan a · tan(π/3+a)· tan(π/3-a)三倍角公式推导sin(3a)=sin(a+2a)=sin2acosa+cos2asina=2sina(1-sin²a)+(1-2sin²a)sina=3sina-4sin^3acos3a=cos(2a+a)=cos2acosa-sin2asina=(2cos²a-1)cosa-2(1-cos^a)cosa=4cos^3a-3cosasin3a=3sina-4sin^3a=4sina(3/4-sin²a)=4sina[(√3/2)²-sin²a]=4sina(sin²60°-sin²a)=4sina(sin60°+sina)(sin60°-sina)=4sina*2sin[(60+a)/2]cos[(60°-a)/2]*2sin[(60°-a)/2]cos[(60°-a)/2]=4sinasin(60°+a)sin(60°-a)cos3a=4cos^3a-3cosa=4cosa(cos²a-3/4)=4cosa[cos²a-(√3/2)^2]=4cosa(cos²a-cos²30°)=4cosa(cosa+cos30°)(cosa-cos30°)=4cosa*2cos[(a+30°)/2]cos[(a-30°)/2]*{-2sin[(a+30°)/2]sin[(a-30°)/2]} =-4cosasin(a+30°)sin(a-30°)=-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)]=-4cosacos(60°-a)[-cos(60°+a)]=4cosacos(60°-a)cos(60°+a)上述两式相比可得tan3a=tanatan(60°-a)tan(60°+a)现列出公式如下: sin2α=2sinαcosα tan2α=2tanα/(1-tan^2(α)) cos2α=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α) 可别轻视这些字符,它们在数学学习中会起到重要作用.包括一些图像问题和函数问题中三倍角公式sin3α=3sinα-4sin^3(α)=4sinα·sin(π/3+α)sin(π/3-α) cos3α=4cos^3(α)-3cosα=4cosα·cos(π/3+α)cos(π/3-α)tan3α=tan(α)*(-3+tan(α)^2)/(-1+3*tan(α)^2)=tan a · tan(π/3+a)· tan(π/3-a)半角公式sin^2(α/2)=(1-cosα)/2 cos^2(α/2)=(1+cosα)/2 tan^2(α/2)=(1-cosα)/(1+cosα) tan(α/2)=sinα/(1+cosα)=(1-cosα)/sinα万能公式sinα=2tan(α/2)/[1+tan^2(α/2)] cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)] tanα=2tan(α/2)/[1-tan^2(α/2)]其他sinα+sin(α+2π/n)+sin(α+2π*2/n)+sin(α+2π*3/n)+……+sin[α+2π*(n-1)/n]=0 cosα+cos(α+2π/n)+cos(α+2π*2/n)+cos(α+2π*3/n)+……+cos[α+2π*(n-1)/n]=0 以及sin^2(α)+sin^2(α-2π/3)+sin^2(α+2π/3)=3/2 tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0四倍角公式sin4A=-4*(cosA*sinA*(2*sinA^2-1)) cos4A=1+(-8*cosA^2+8*cosA^4) tan4A=(4*tanA-4*tanA^3)/(1-6*tanA^2+tanA^4)五倍角公式sin5A=16sinA^5-20sinA^3+5sinA cos5A=16cosA^5-20cosA^3+5cosA tan5A=tanA*(5-10*tanA^2+tanA^4)/(1-10*tanA^2+5*tanA^4)六倍角公式sin6A=2*(cosA*sinA*(2*sinA+1)*(2*sinA-1)*(-3+4*sinA^2)) cos6A=((-1+2*cosA^2)*(16*cosA^4-16*cosA^2+1))tan6A=(-6*tanA+20*tanA^3-6*tanA^5)/(-1+15*tanA^2-15*tanA^4+tanA^6)七倍角公式sin7A=-(sinA*(56*sinA^2-112*sinA^4-7+64*sinA^6)) cos7A=(cosA*(56*cosA^2-112*cosA^4+64*cosA^6-7))tan7A=tanA*(-7+35*tanA^2-21*tanA^4+tanA^6)/(-1+21*tanA^2-35*tanA^4+7*tanA^6)八倍角公式sin8A=-8*(cosA*sinA*(2*sinA^2-1)*(-8*sinA^2+8*sinA^4+1)) cos8A=1+(160*cosA^4-256*cosA^6+128*cosA^8-32*cosA^2)tan8A=-8*tanA*(-1+7*tanA^2-7*tanA^4+tanA^6)/(1-28*tanA^2+70*tanA^4-28*tanA^6+tan A^8)九倍角公式sin9A=(sinA*(-3+4*sinA^2)*(64*sinA^6-96*sinA^4+36*sinA^2-3)) cos9A=(cosA*(-3+4*cosA^2)*(64*cosA^6-96*cosA^4+36*cosA^2-3))tan9A=tanA*(9-84*tanA^2+126*tanA^4-36*tanA^6+tanA^8)/(1-36*tanA^2+126*tanA^4-84 *tanA^6+9*tanA^8)十倍角公式sin10A=2*(cosA*sinA*(4*sinA^2+2*sinA-1)*(4*sinA^2-2*sinA-1)*(-20*sinA^2+5+16*sinA^ 4)) cos10A=((-1+2*cosA^2)*(256*cosA^8-512*cosA^6+304*cosA^4-48*cosA^2+1)) tan10A=-2*tanA*(5-60*tanA^2+126*tanA^4-60*tanA^6+5*tanA^8)/(-1+45*tanA^2-210*tan A^4+210*tanA^6-45*tanA^8+tanA^10)N倍角公式根据棣美弗定理,(cosθ+ isinθ)^n = cos(nθ)+ i sin(nθ) 为方便描述,令sinθ=s,cosθ=c 考虑n为正整数的情形：cos(nθ)+ i sin(nθ) = (c+ i s)^n = C(n,0)*c^n + C(n,2)*c^(n-2)*(i s)^2 + C(n,4)*c^(n-4)*(i s)^4 + ... +C(n,1)*c^(n-1)*(i s)^1 + C(n,3)*c^(n-3)*(i s)^3 + C(n,5)*c^(n-5)*(i s)^5 + ... =>比较两边的实部与虚部实部：c os(nθ)=C(n,0)*c^n + C(n,2)*c^(n-2)*(i s)^2 + C(n,4)*c^(n-4)*(i s)^4 + ... i*(虚部)：i*sin(nθ)=C(n,1)*c^(n-1)*(i s)^1 + C(n,3)*c^(n-3)*(i s)^3 + C(n,5)*c^(n-5)*(i s)^5 + ... 对所有的自然数n, 1. cos(nθ)：公式中出现的s都是偶次方,而s^2=1-c^2(平方关系),因此全部都可以改成以c(也就是cosθ)表示.2. sin(nθ)：(1)当n是奇数时：公式中出现的c都是偶次方,而c^2=1-s^2(平方关系),因此全部都可以改成以s(也就是sinθ)表示. (2)当n是偶数时：公式中出现的c都是奇次方,而c^2=1-s^2(平方关系),因此即使再怎么换成s,都至少会剩c(也就是cosθ)的一次方无法消掉. (例. c^3=c*c^2=c*(1-s^2),c^5=c*(c^2)^2=c*(1-s^2)^2)半角公式tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA);cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA.sin^2(a/2)=(1-cos(a))/2cos^2(a/2)=(1+cos(a))/2tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))和差化积sinθ+sinφ = 2 sin[(θ+φ)/2] cos[(θ-φ)/2]sinθ-sinφ = 2 cos[(θ+φ)/2] sin[(θ-φ)/2]cosθ+cosφ = 2 cos[(θ+φ)/2] cos[(θ-φ)/2]cosθ-cosφ = -2 sin[(θ+φ)/2] sin[(θ-φ)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB) tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB) 两角和公式tan(α+β)=(tanα+tanβ)/(1-tanαtanβ)tan(α-β)=(tanα-tanβ)/(1+tanαtanβ)cos(α+β)=cosαcosβ-sinαsinβc os(α-β)=cosαcosβ+sinαsinβsin(α+β)=sinαcosβ+cosαsinβsin(α-β)=sinαcosβ -cosαsinβ积化和差sinαsinβ =-[cos(α+β)-cos(α-β)] /2cosαcosβ = [cos(α+β)+cos(α-β)]/2sinαcosβ = [sin(α+β)+sin(α-β)]/2cosαsinβ = [sin(α+β)-sin(α-β)]/2双曲函数sh a = [e^a-e^(-a)]/2ch a = [e^a+e^(-a)]/2th a = sin h(a)/cos h(a)公式一：设α为任意角,终边相同的角的同一三角函数的值相等：sin（2kπ+α）= sinαcos（2kπ+α）= cosαtan（2kπ+α）= tanαcot（2kπ+α）= cotα公式二：设α为任意角,π+α的三角函数值与α的三角函数值之间的关系：sin（π+α）= -sinαcos（π+α）= -cosαtan（π+α）= ta nαcot（π+α）= cotα公式三：任意角α与-α的三角函数值之间的关系：sin（-α）= -sinαcos（-α）= cosαtan（-α）= -tanα公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系：sin（π-α）= sinαcos（π-α）= -cosαtan（π-α）= -tanαcot（π-α）= -cotα公式五：利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系：sin（2π-α）= -sinαcos（2π-α）= cosαtan（2π-α）= -tanαcot（2π-α）= -cotα公式六：π/2±α及3π/2±α与α的三角函数值之间的关系：sin（π/2+α）= cosαcos（π/2+α）= -sinαtan（π/2+α）= -cotαcot（π/2+α）= -tanαsin（π/2-α）= cosαcos（π/2-α）= sinαtan（π/2-α）= c otαsin（3π/2+α）= -cosαcos（3π/2+α）= sinαtan（3π/2+α）= -cotαcot（3π/2+α）= -tanαsin（3π/2-α）= -cosαcos（3π/2-α）= -sinαtan（3π/2-α）= cotαcot（3π/2-α）= tanα(以上k∈Z)A·sin(ωt+θ)+ B·sin(ωt+φ) =√{(A² +B² +2ABcos(θ-φ)} · sin{ ωt + arcsin[ (A·sinθ+B·sinφ) / √{A^2 +B^2; +2ABcos(θ-φ)} }√表示根号,包括{……}中的内容三角函数的诱导公式（六公式）公式一sin(-α) = -sinαcos(-α) = cosαtan (-α)=-tanα公式二sin(π/2-α) = cosαcos(π/2-α) = sinα公式三sin(π/2+α) = cosαcos(π/2+α) = -sinα公式四sin(π-α) =sinαcos(π-α) = -cosα公式五sin(π+α) = -sinαcos(π+α) = -cosα公式六tanA= sinA/cosAtan（π/2+α）=－cotαtan（π/2－α）=cotαtan（π－α）=－tanαtan（π+α）=tanα诱导公式记背诀窍：奇变偶不变,符号看象限万能公式sinα=2tan(α/2)/[1+(tan(α/2))²]cosα=[1-(tan(α/2))²]/[1+(tan(α/2))²]tanα=2tan(α/2)/[1-(tan(α/2))²]其它公式(1) (sinα)^2+(cosα)^2=1（平方和公式）(2)1+(tanα)^2=(secα)^2(3)1+(cotα)^2=(cscα)^2证明下面两式,只需将一式,左右同除(sinα)^2,第二个除(cosα)^2即可(4)对于任意非直角三角形,总有tanA+tanB+tanC=tanAtanBtanC证：A+B=π-Ctan(A+B)=tan(π-C)(tanA+tanB)/(1-tanAtanB)=(tanπ-tanC)/(1+tanπtanC)整理可得tanA+tanB+tanC=tanAtanBtanC得证同样可以得证,当x+y+z=nπ(n∈Z)时,该关系式也成立由tanA+tanB+tanC=tanAtanBtanC可得出以下结论(5)cotAcotB+cotAcotC+cotBcotC=1(6)cot(A/2)+cot(B/2)+cot(C/2)=cot(A/2)cot(B/2)cot(C/2)(7)(cosA)^2;+(cosB)^2+(cosC)^2=1-2cosAcosBcosC(8)（sinA)^2+(sinB)^2+(sinC)^2=2+2cosAcosBcosC其他非重点三角函数csc(a) = 1/sin(a)sec(a) = 1/cos(a)(seca)^2+(csca)^2=(seca)^2(csca)^2幂级数展开式sin x = x-x^3/3!+x^5/5!-……+(-1)^(k-1)*(x^(2k-1))/(2k-1)!+……. (-∞<x<∞) cos x = 1-x^2/2!+x^4/4!-……+(-1)k*(x^(2k))/(2k)!+…… (-∞<x<∞)arcsin x = x + 1/2*x^3/3 + 1*3/(2*4)*x^5/5 + ……(|x|<1)arccos x = π - ( x + 1/2*x^3/3 + 1*3/(2*4)*x^5/5 + …… ) (|x|<1)arctan x = x - x^3/3 + x^5/5 -……(x≤1)无限公式sinx=x(1-x^2/π^2)(1-x^2/4π^2)(1-x^2/9π^2)……cosx=(1-4x^2/π^2)(1-4x^2/9π^2)(1-4x^2/25π^2)……tanx=8x[1/(π^2-4x^2)+1/(9π^2-4x^2)+1/(25π^2-4x^2)+……]secx=4π[1/(π^2-4x^2)-1/(9π^2-4x^2)+1/(25π^2-4x^2)-+……](sinx)x=cosx/2cosx/4cosx/8……(1/4)tanπ/4+(1/8)tanπ/8+(1/16)tanπ/16+……=1/πarctan x = x - x^3/3 + x^5/5 -……(x≤1)和自变量数列求和有关的公式sinx+sin2x+sin3x+……+sinnx=[sin(nx/2)sin((n+1)x/2)]/sin(x/2)cosx+cos2x+cos3x+……+cosnx=[cos((n+1)x/2sin(nx/2)]/sin(x/2)tan((n+1)x/2)=(sinx+sin2x+sin3x+……+sinnx)/(cosx+cos2x+cos3x+……+cosnx)sinx+sin3x+sin5x+……+sin(2n-1)x=(sinnx)^2/sinxcosx+cos3x+cos5x+……+cos(2n-1)x=sin(2nx)/(2sinx)编辑本段内容规律三角函数看似很多,很复杂,但只要掌握了三角函数的本质及内部规律就会发现三角函数各个公式之间有强大的联系.而掌握三角函数的内部规律及本质也是学好三角函数的关键所在.1．三角函数本质：[1] 根据右图,有sinθ=y/ r; cosθ=x/r; tanθ=y/x; cotθ=x/y.深刻理解了这一点,下面所有的三角公式都可以从这里出发推导出来,比如以推导sin(A+B) = sinAcosB+cosAsinB 为例：推导：首先画单位圆交X轴于C,D,在单位圆上有任意A,B点.角AOD为α,BOD为β,旋转AOB 使OB与OD重合,形成新A'OD.A(cosα,sinα),B(cosβ,sinβ),A'(cos(α-β),sin(α-β))OA'=OA=OB=OD=1,D(1,0)∴[cos(α-β)-1]^2+[si n(α-β)]^2=(cosα-cosβ)^2+(sinα-sinβ)^2和差化积及积化和差用还原法结合上面公式可推出（换(a+b)/2与(a-b)/2）单位圆定义单位圆六个三角函数也可以依据半径为一中心为原点的单位圆来定义.单位圆定义在实际计算上没有大的价值；实际上对多数角它都依赖于直角三角形.但是单位圆定义的确允许三角函数对所有正数和负数辐角都有定义,而不只是对于在0 和π/2 弧度之间的角.它也提供了一个图象,把所有重要的三角函数都包含了.根据勾股定理,单位圆的等式是：图象中给出了用弧度度量的一些常见的角.逆时针方向的度量是正角,而顺时针的度量是负角.设一个过原点的线,同x 轴正半部分得到一个角θ,并与单位圆相交.这个交点的x 和y 坐标分别等于cos θ 和sin θ.图象中的三角形确保了这个公式；半径等于斜边且长度为1,所以有sin θ = y/1 和cos θ = x/1.单位圆可以被视为是通过改变邻边和对边的长度,但保持斜边等于1的一种查看无限个三角形的方式.两角和公式sin(A+B) = sinAcosB+cosAsinBsin(A-B) = sinAcosB-cosAsinBcos(A+B) = cosAcosB-sinAsinBcos(A-B) = cosAcosB+sinAsinBtan(A+B) = (tanA+tanB)/(1-tanAtanB) tan(A-B) = (tanA-tanB)/(1+tanAtanB) cot(A+B) = (cotAcotB-1)/(cotB+cotA) cot(A-B) = (cotAcotB+1)/(cotB-cotA)。

大学用三角函数公式大全

三角函数的和差公式

１ / 2第四~五课时三角函数的和角公式、差角公式[教学目标] 1、通过两角差的正弦公式的推导和证明，继而导出三角函数的和角公式、差角公式，学生进一步理解与运用函数的思想，进一步渗透基本量的数学思想方法（基本量思想就是一种函数的思想）。

2、使学生掌握三角函数的和角公式、差角公式，并会应用这组公式解决一些有关三角函数的求值问题。

3、在公式的推导过程中，使学生注意并学习严密而准确的数学思维方法及其数学表达方式。

[教学重点与难点] 本节课的重点是使学生掌握三角函数的和角公式、差角公式。

难点是应用三角函数的和角公式、差角公式求三角函数值。

[教学过程设计]一、三角函数的和角公式的推导与证明。

1、推导两角和的正弦公式。

（参阅课本第75~76页）。

2、给出两角和的余弦公式。

3、利用同角三角函数恒等式，对正切函数可得两角和的正切公式。

(板书) 三角函数的和角公式sin(α+β)=sin αcos β+ cos αsin βcos(α+β)= cos αcos β-sin αsin βtan(α+β)=βαβαtan tan -1tan tan + 二、三角函数的差角公式的推导。

直接用和角公式结合负角公式，导出三角函数的差角公式：（参阅课本第76页）(板书) 三角函数的差角公式sin(α-β)=sin αcos β- cos αsin βcos(α-β)= cos αcos β+sin αsin βtan(α-β)=βαβαtan tan 1tan tan +- 三、和角、差角三角函数公式在计算三角函数式值中的应用。

1、求三角函数的值例4：不使用计算器，求下列各式的值：（略——参阅课本第76页）练习4：课本第76页，课内练习4）2、已知角α、β的（部分）三角函数值，求和角、差角的三角函数值。

)tan(),cos(),sin(),23,(,43cos ),,2(,32sin 5βαβαβαππββππαα+++∈-=∈=求已知例：（解略——参阅课本第78页）练习5：课本第79页，课内练习5~1、2、3例6：求75 的正弦、余弦、正切函数值，并计算75tan 1tan751+-的值。

三角函数公式的推导及公式大全

诱导公式目录·诱导公式·诱导公式记忆口诀·同角三角函数基本关系·同角三角函数关系六角形记忆法·两角和差公式·倍角公式·半角公式·万能公式·万能公式推导·三倍角公式·三倍角公式推导·三倍角公式联想记忆·和差化积公式·积化和差公式·和差化积公式推导诱导公式★诱导公式★常用的诱导公式有以下几组：公式一：设α为任意角，终边相同的角的同一三角函数的值相等：sin（2kπ＋α）＝sinαcos（2kπ＋α）＝cosαtan（2kπ＋α）＝tanαcot（2kπ＋α）＝cotα公式二：设α为任意角，π+α的三角函数值与α的三角函数值之间的关系：sin（π＋α）＝－sinαcos（π＋α）＝－cosαtan（π＋α）＝tanαcot（π＋α）＝cotα公式三：任意角α与 -α的三角函数值之间的关系：sin（－α）＝－sinαcos（－α）＝cosαtan（－α）＝－tanαcot（－α）＝－cotα公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系：sin（π－α）＝s inαcos（π－α）＝－cosαtan（π－α）＝－tanαcot（π－α）＝－cotα公式五：利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系：sin（2π－α）＝－sinαcos（2π－α）＝cosαtan（2π－α）＝－tanαcot（2π－α）＝－cotα公式六：π/2±α及3π/2±α与α的三角函数值之间的关系：sin（π/2＋α）＝cosαcos（π/2＋α）＝－sinαtan（π/2＋α）＝－cotαcot（π/2＋α）＝－tanαsin（π/2－α）＝cosαcos（π/2－α）＝sinαtan（π/2－α）＝cotαcot（π/2－α）＝tanαsin（3π/2＋α）＝－cosαcos（3π/2＋α）＝sinαtan（3π/2＋α）＝－cotαcot（3π/2＋α）＝－tanαsin（3π/2－α）＝－cosαcos（3π/2－α）＝－sinαtan（3π/2－α）＝cotαcot（3π/2－α）＝tanα(以上k∈z)诱导公式记忆口诀※规律总结※上面这些诱导公式可以概括为：对于k·π/2±α(k∈z)的个三角函数值，①当k是偶数时，得到α的同名函数值，即函数名不改变；②当k是奇数时，得到α相应的余函数值，即sin→cos;cos→sin;tan→cot,cot→tan.（奇变偶不变）然后在前面加上把α看成锐角时原函数值的符号。

2.6三角函数在电工学中的应用

2.6 三角函数在电工学中的应用旧课复习：正弦定理、余弦定理:c cB b A a sin sin sin ==.A bc c b a cos 2222-+=;B ca a c b cos 2222-+=; .cos 2222C ab b a c -+=新课引入：1.分析正弦交流电流的变化规律举例我们知道,正弦交流电的电流强度i 随时间t 变化的规律为)sin(0ϕω+=t I i m .其中m I ------电流强度的最大值,称为幅值(或峰值);ω-------称为角频率(或圆频率),它表示电流变化的快慢,其单位是“弧度/秒”;0ϕ-------称为初相位(或初位相或初相);0ϕω+t 称为t 时刻的相位(或位相),它是发电机转子的绕组面在t 时刻所在位置与定子磁场方向所成的角(图2-12).这里,i 关于t 是正弦型函数,因此我们可以利用正弦型函数的图象(正弦波形)和性质来具体分析正弦交流电流i 随时间t 的变化情况. 例1 图2-13画出了两种正弦交流电的电流强度i 随时间t 变化在一个周期里的图象,其中横坐标表示t ω.根据图2-13,回答下列问题: (1)1i 与2i 的幅值各为多少?(2) 1i 与2i 的周期相等吗?是多少?(3) 1i 与2i 哪个先达到最大值?解: (1)从图2-13中可以看出, 1i 的幅值为30A ,2i 的幅值为20A .(2) 图2-13中,横轴代表t ω,从图中看出, t ω每增加(减少) , 1i 与2i 函数值都不变.因此1i 与2i 的周期相同,都等于ωπ2.(3) 从图2-13中看出,当6πω=t 时,1i 达到最大值; 当32πω=t 时, 2i 达到最大值.因此1i 先达到最大值. 从图2-13中还可以看出, 1i 的初相位是3π,2i 的初相位是6π-.根据上述分析,可以写出1i 与2i 的解析表达式如下:⎪⎭⎫ ⎝⎛+=3sin 301πωt i ,⎪⎭⎫ ⎝⎛-=6sin 202πωt i ,(可以确定ω的值,这里从略)正弦交流电完成一次周期性变化所需的时间称为周期(单位:秒,记作s),用T 表示,根据正弦型函数的周期性,ωπ2=T:单位时间内交流电完成周期性变化的次数称为频率(单位:赫兹,记作Hz),用f 表示.显然Tf 1=,从而fπω2=.两个同频率的交流电的相位角或初相位角之差,称为相位差.以上电流1i 与2i 是两个同频正弦电流,它们的相位差是0263>=⎪⎭⎫ ⎝⎛--πππ.我们称1i 比2i 的相位超前2π,或者说2i 比1i 的相位滞后2π.如上所说, 1i 比2i 先达到最大值.例 2 已知正弦交流电流i (安)与时间t (秒)的函数关系为⎪⎭⎫ ⎝⎛-=4100sin 30ππt i (0≥t ).(1) 试指出它的角频率、频率、周期、幅值及初相位各是多少? (2) 设0=t 秒、0025.0=t 秒时电流的瞬时值分别为0i 、1i ,试比较0i 与1i 哪个较大? (3) 试画出它在一个周期内的简图,并指出电流在这个周期内的变化情况. 解:(1)角频率πω100=(rad/s),频率5021002===πππωf (Hz),周期02.01==fT (s), 幅值30=m I (A),初相位40πϕ-=(rad).(2)当0=t 时,215-=i (“-”号表示流向),所以2150=i (安);当0025.0=t 时, 0=i ,所以01=i (安).因此, 0i 比1i 大.(3) 列表描点画图(图2-14)续变化到0.0075秒时,电流从0安逐渐增大到幅值30安; 当时间从0,0075秒连续变化到0.0125秒时,电流从30安逐渐减小到幅值0安. 在后半个周期内,电流的变化规律与前半个周期内的情形相似,但流向相反.例3 图2-15是一个正弦交流电流的图象,根据图象求出它的周期、频率、幅值和初相位，并写出电流i 关于时间t 的函数关系式.解: 根据图象可知,电流的周期2.005.025.0=-=T (s).所以频率52.011===T f (Hz). 角频率ππω102==f (rad/s) 由图又知, 幅值10=m I (A),起点坐标为(-0.05,0).由正弦型函数起点坐标的求法,有图2-1505.0100-=-πϕ 于是, 初相20πϕ=(rad)因此,该正弦交流电的函数关系式为sin 10=i (210ππ+t ).正弦交流电的电压v 随时间t 变化的规律为sin m V v =（0ψω+t ），其中m V 是电压的最大值,称为幅值(或峰值),同样,ω称为角频率(或圆频率),0ψ称为初相位(或初相),0ψω+t 称为t 时刻的相位.类似地,正弦电压的周期ωπ2=T (单位:s),频率Tf 1=(单位:Hz),f πω2=(单位:rad/s) 在电工学中, 正弦交流电的电流和电压都简称为正弦量.显然,正弦量由幅值、角频率和初相位唯一确定.课堂练习：习题2.6 的1、2、3题（请学生回答）2.求两个同频率的正弦交流电合成举例在电工学里,对交流电路的分析过程中,经常遇到对同频率的正弦量求和的运算,称之为同频率正弦量的合成.例如:设有两个同频率的正弦电流(单位:A))sin(111ϕω+=t I i m , )sin(222ϕω+=t I i m , 把它们合成,即)sin()sin(221121ϕωϕω+++=+=t I t I i i i m m i 又称为电流1i 与2i 的总电流.例 4 求两个同频率的正弦电流⎪⎭⎫ ⎝⎛+=3100sin 31ππt i 与⎪⎭⎫ ⎝⎛+=6100sin 2ππt i 相加的总电流.解: 设1i 与2i 的合成电流为i ,则 21i i i +=⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=6100sin 3100sin 3ππππt t ⎝⎛++⎪⎭⎫ ⎝⎛+=6sin100cos 6cos 100sin 3sin 100cos 3cos 100sin 3ππππππππt t t tt t ππππππ100cos 6sin 3sin 3100sin 6cos 3cos 3⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=t t ππ100cos 2100sin 3+=⎪⎪⎭⎫ ⎝⎛+=t t ππ100cos 72100sin 737)100sin(70ϕπ+=t ,其中32arctan 0=ϕ.因此合成电流i 也是正弦电流,且与1i 、2i 同频率.由上可见,用和角的正弦公式能求出两个同频率的正弦量的合成结果,但计算非常繁琐.下面将给出一种较简单的解法.根据2.3节讨论的结果可知,正弦量除了用正弦型函数或正弦波形表示之外,还可以用旋转向量来表示.画旋转向量来表示正弦量,是繁琐的.在电工学中,通常只用初始位置(0=t )的向量来表示一个正弦量,它的长度等于正弦量的幅值,它与横轴正方向间的夹角等于正弦量的初相位.但是我们应该具有这样的概念:这个向量是以正弦量的角频率作逆时针方向旋转的,它在纵轴上的投影(纵坐标)表示正弦量的瞬时值.在实际问题中我们所涉及的往往是正弦量的有效值.因此为了方便起见,常使向量的长度等于正弦量的有效值.显然,这时它在纵轴上的投影就不能代表正弦量的瞬时值了. 由电工学可知,正弦电流和电压的有效值与幅值的换算关系为:2m I I =,2m V V =.为了与物理向量(例如电场力、电场强度等)区别,表示随时间而变化的正弦量的向量我们称为相量,并在所注文字上方打一“·”. 例如电流和电压的幅值相量分别记作⋅m I 和⋅m V ,它们的有效值相量分别记作⋅I 和⋅V .由于正弦量由幅值、角频率和初相位唯一确定,因此按照各个同频率的正弦量的幅值(或有效值)和初相位画出若干个相量的图形称为相量图. 由2.3节讨论亦可知,两个同频率的正弦量相加(相同物理量相加),其结果是一个同频率的正弦量,它们的相量之和,就是它们的和的相量.因此,我们可以利用两个同频率的正弦量(相同物理量)的相量图,采用平行四边形法则求它们的和相量, 再通过解三角形便可求得这两个同频率的正弦量之和的幅值和初相位,从而得出两个同频率的正弦量的合成结果.例 5 已知两同频率的正弦电流sin 81=i ( 60+t ω)安和sin 62=i ( 30-t ω)安,求21i i i +=.解: 先作1i 和2i 的幅值相量⋅m I 1和⋅m I 2,以该两相量为邻边作一平行四边形, 平行四边形的对角线即为两正弦电流之和i 的幅值相量⋅m Imx (图2-16).因为1i 和2i 的相位差恰为 90,所以i 的幅值而i 的初相位376086arctan 60-=-=ϕ,所以 sin 10=i ( 23+t ω)安.例6 在图2-17的电路中,设 sin 11m I i =(1ϕω+t )=sin 100( 45+t ω)安, i sin 22m I i =(2ϕω+t )=sin 60( 30-t ω)安,试求总电流i .解: 根据表示正弦量的几种方法对本题分别进行计算如下:(1)用三角函数式求解sin 121m I i i i =+=(1ϕω+t )+sin 2m I (2ϕω+t )m I 1=(11sin cos cos sin ϕωϕωt t +)+m I 2(22sin cos cos sin ϕωϕωt t +)=(2211cos cos ϕϕm m I I +)t ωsin +(2211sin sin ϕϕm m I I +)t ωcos 设 sin m I i =(ϕω+t )=t I t I m m ωϕωϕcos sin sin cos +2211cos cos cos ϕϕϕm m m I I I +=, 2211sin sin sin ϕϕϕm m m I I I +=,因此总电流i 的幅值为()()2221122211sin sin cos cos ϕϕϕϕm m m m m I I I I I +++=, 电流i 的初相位为⎪⎪⎭⎫⎝⎛++=22112211cos cos sin sin arctan ϕϕϕϕϕm m m m I I I I .将本题中的1001=m I 安、602=m I 安、 451=ϕ、 302-=ϕ代入，则得()()1297.407.122307.70527.702222=+=-++=m I 安，02187.1227.40arctan 527.70307.70arctan '=⎪⎭⎫ ⎝⎛=⎪⎭⎫⎝⎛+-=ϕ.故得 sin 129=i (0218'+ t ω)安.(2)用正弦波形求解先作出表示电流1i 和2i 的正弦波形,而后将两波形的纵坐标相加,即得总电流i 的正弦波形,从此波形上便可量出i 的幅值和初相位(图2-18).(3)用相量图求解先作出表示电流1i 和2i 的幅值相量⋅m I 1和⋅m I 2,而后以⋅m I 1和⋅m I 2为邻边作一平行四边形,其对角线即为总电流i 的幅值相量⋅m I , 它的长度即为幅值,它与横轴正的夹角即为初相位(图2-19或图2-18缩小版).从向量图上可以量出i 的幅值和初相.4用相量图通过解三角形求解先作出表示电流1i 和2i 的幅值相量⋅m I 1 和⋅m I 2,而后以⋅m I 1和⋅m I 2为邻边作一平行四边形,其对角线即为总电流i 的幅值相量⋅m I ,它的长度即为幅值,它与横轴正方向间的夹角即为初相位(图2-19).因为1i 与2i 的相位差-=- 4521ϕϕ(- 30)= 75 所以,由余弦定理得cos 22122212⋅⋅⋅-+=m m m m m I I I I I ( 75180-) 105cos 6010026010022⨯⨯⨯-+= 16706=,因此, i 的幅值12916706==m I 安; 又根据正弦定理,有sin (30+ϕ)=7488.0129105sin 100105sin 1=⨯=m m I I , 所以i 的初相位9218307488.0arcsin '=-= ϕ. 于是 sin 129=i (9218'+ t ω)安.最后指出,如果用相量表示正弦交流电,则正弦交流电路中的希尔荷夫定律具有相量形式.本堂课作业：习题2.6 的4、5题本堂课归纳小结：正弦交流电的电流强度i 及电压v 对时间t 的函数关系分别为:sin m I i =(0ϕω+t ) (0,0>>ωm I ); sin m V v =(0ϕω+t ) (0,0>>ωm V ),它们都是正弦型函数.掌握了正弦型函数图象和性质,也就掌握了正弦交流电随时间变化的在电工学中, 正弦交流电的电流和电压都简称为正弦量, 正弦量可以用相量来表示.有两个同频率的正弦量相加(相同物理量相加),其结果是一个同频率的正弦量,它们的相量之和,就是它们的和的相量.因此,我们可以利用两个同频率的正弦量(相同物理量)的相量图,采用平行四边形法则求它们的和相量, 再通过解三角形便可求得这两个同频率的正弦量之和的幅值和初相位,从而得出两个同频率的正弦量的合成结果.。

三角函数公式大全及解析

三角函数公式大全及解析倒数关系：tanα ·cotα=1sinα ·cscα=1cosα ·secα=1商的关系：sinα/cosα=tanα=secα/cscαcosα/sinα=cotα=cscα/secα平方关系：sin^2(α)+cos^2(α)=11+tan^2(α)=sec^2(α)1+cot^2(α)=csc^2(α)平常针对不同条件的常用的两个公式sin^2(α)+cos^2(α)=1tan α *cot α=1一个特殊公式（sina+sinθ）*（sina-sinθ）=sin（a+θ）*sin（a-θ）证明：（sina+sinθ）*（sina-sinθ）=2 sin[(θ+a)/2] cos[(a-θ)/2] *2 cos[(θ+a)/2] sin[(a-θ)/2]=sin（a+θ）*sin（a-θ）坡度公式我们通常半坡面的铅直高度h与水平高度l的比叫做坡度（也叫坡比），用字母i表示，即i=h / l, 坡度的一般形式写成l : m 形式，如i=1:5.如果把坡面与水平面的夹角记作a(叫做坡角），那么i=h/l=tan a.锐角三角函数公式正弦：sin α=∠α的对边/∠α 的斜边余弦：cos α=∠α的邻边/∠α的斜边正切：tan α=∠α的对边/∠α的邻边余切：cot α=∠α的邻边/∠α的对边二倍角公式正弦sin2A=2sinA·cosA余弦1.Cos2a=Cos^2(a)-Sin^2(a)2.Cos2a=1-2Sin^2(a)3.Cos2a=2Cos^2(a)-1即Cos2a=Cos^2(a)-Sin^2(a)=2Cos^2(a)-1=1-2Sin^2(a)正切tan2A=（2tanA）/（1-tan^2(A)）三倍角公式sin3α=4sinα·sin(π/3+α)sin(π/3-α)cos3α=4cosα·cos(π/3+α)cos(π/3-α)tan3a = tan a · tan(π/3+a)· tan(π/3-a)三倍角公式推导sin(3a)=sin(a+2a)=sin2acosa+cos2asina=2sina(1-sin²a)+(1-2sin²a)sina=3sina-4sin^3acos3a=cos(2a+a)=cos2acosa-sin2asina=(2cos²a-1)cosa-2(1-cos^a)cosa=4cos^3a-3cosasin3a=3sina-4sin^3a=4sina(3/4-sin²a)=4sina[(√3/2)²-sin²a]=4sina(sin²60°-sin²a)=4sina(sin60°+sina)(sin60°-sina)=4sina*2sin[(60+a)/2]cos[(60°-a)/2]*2sin[(60°-a)/2]cos[(60°-a)/2]=4sinasin(60°+a)sin(60°-a)cos3a=4cos^3a-3cosa=4cosa(cos²a-3/4)=4cosa[cos²a-(√3/2)^2]=4cosa(cos²a-cos²30°)=4cosa(cosa+cos30°)(cosa-cos30°)=4cosa*2cos[(a+30°)/2]cos[(a-30°)/2]*{-2sin[(a+30°)/2]sin[(a-30°)/2]} =-4cosasin(a+30°)sin(a-30°)=-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)]=-4cosacos(60°-a)[-cos(60°+a)]=4cosacos(60°-a)cos(60°+a)上述两式相比可得tan3a=tanatan(60°-a)tan(60°+a)现列出公式如下: sin2α=2sinαcosα tan2α=2tanα/(1-tan^2(α))cos2α=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α) 可别轻视这些字符,它们在数学学习中会起到重要作用。

三角函数所有公式及学习等差数列求和公式的四个层次和对数特例

三角公式总表‎⒈L 弧长=αR=nπR 180 S 扇=21L R=21R 2α=3602R n ⋅π⒉正弦定理：A asin =B b sin =Cc sin = 2R （R 为三角形外‎接圆半径）⒊余弦定理：a2=b2+c2-2bc Acos b2=a2+c2-2acB cosc 2=a 2+b2-2ab C cos bca cb A 2cos 222-+=⒋S ⊿=21a a h ⋅=21ab C sin =21bc A sin =21ac B sin =Rabc 4=2R 2A sin B sin C sin=A C B a sin 2sin sin 2=B C A b sin 2sin sin 2=CB A c sin 2sin sin 2=pr =))()((c p b p a p p ---(其中)(21c b a p ++=, r 为三角形内‎切圆半径)⒌同角关系：⑴商的关系：①θtg =xy =θθcos sin =θθsec sin ⋅ ②θθθθθcsc cos sin cos ⋅===y x ctg ③θθθtg ry⋅==cos sin ④θθθθcsc cos 1sec ⋅===tg x r ⑤θθθctg r x ⋅==sin cos ⑥θθθθsec sin 1csc ⋅===ctg y r ⑵倒数关系：1sec cos csc sin =⋅=⋅=⋅θθθθθθctg tg ⑶平方关系：1csc sec cos sin 222222=-=-=+θθθθθθctg tg ⑷)sin(cos sin 22ϕθθθ++=+b a b a（其中辅助角与‎ϕ点（a,b ）在同一象限，且ab tg =ϕ）⒍函数y=++⋅)sin(ϕωx A k 的图象及性‎质：（0,0>>A ω）振幅A ，周期T =ωπ2, 频率f =T1, 相位ϕω+⋅x ，初相ϕ⒎五点作图法：令ϕω+x 依次为ππππ2,23,,20 求出x 与y ，依点()y x ,作图 ⒏诱导公试三角函数值等‎于的同名三角‎α函数值，前面加上一个‎把看作锐角时‎α，原三角函数值‎的符号；即：函数名不变，符号看象限三角函数值等‎于的异名三角‎α函数值，前面加上一个‎把看作锐角时‎α，原三角函数值‎的符号;即：函数名改变，符号看象限⒐和差角公式①βαβαβαsin cos cos sin )sin(±=± ②βαβαβαsin sin cos cos )cos( =± ③βαβαβαtg tg tg tg tg ⋅±=± 1)( ④)1)((βαβαβαtg tg tg tg tg ⋅±=±⑤γβγαβαγβαγβαγβαtg tg tg tg tg tg tg tg tg tg tg tg tg ⋅-⋅-⋅-⋅⋅-++=++1)( 其中当A+B+C=π时,有:i).tgC tgB tgA tgC tgB tgA ⋅⋅=++ ii).1222222=++Ctg B tg C tg A tg B tgA tg⒑二倍角公式：(含万能公式) ①θθθθθ212cos sin 22sin tg tg +==②θθθθθθθ22222211sin 211cos 2sin cos 2cos tg tg +-=-=-=-=③θθθ2122tg tg tg -= ④22cos 11sin 222θθθθ-=+=tg tg ⑤22cos 1cos 2θθ+=⒒三倍角公式：①)60sin()60sin(sin 4sin 4sin 33sin 3θθθθθθ+︒-︒=-= ②)60cos()60cos(cos 4cos 4cos 33cos 3θθθθθθ+︒-︒=+-=③)60()60(313323θθθθθθθ+⋅-⋅=--=tg tg tg tg tg tg tg ⒓半角公式：（符号的选择由‎2θ所在的象限确‎定） ①2cos 12sin θθ-±= ②2cos 12sin 2θθ-= ③2cos 12cos θθ+±=④2cos 12cos 2θθ+=⑤2sin 2cos 12θθ=- ⑥2cos 2cos 12θθ=+⑦2sin 2cos )2sin 2(cos sin 12θθθθθ±=±=±⑧θθθθθθθsin cos 1cos 1sin cos 1cos 12-=+=+-±=tg⒔积化和差公式‎：[])sin()sin(21cos sin βαβαβα-++=[])sin()sin(21sin cos βαβαβα--+=[])cos()cos(21cos cos βαβαβα-++=()[]βαβαβα--+-=cos )cos(21sin sin ⒕和差化积公式‎：①2cos2sin2sin sin βαβαβα-+=+ ②2sin2cos2sin sin βαβαβα-+=- ③2cos2cos 2cos cos βαβαβα-+=+ ④2sin2sin2cos cos βαβαβα-+-=-⒖反三角函数： ⒗最简单的三角‎方程等差数列求和‎公式的四个层‎次等差数列前n ‎项和公式d n n na n a a S n n 2)1(2)(11-+=+=,是数列部分最‎重要公式之一‎,学习公式并灵‎活运用公式可‎分如下四个层‎次:1.直接套用公式‎ 从公式d n n na n a a n a a S m n m n n 2)1(2)(2)(111-+=+=+=+-中,我们可以看到‎公式中出现了‎五个量,包括这些量中‎,,,,,1n n S n a d a 已知三个就可‎以求另外两个‎了.从基本量的观‎点认识公式、理解公式、掌握公式这是‎最低层次要求‎.例 1 设等差数列的‎{}n a 公差为d,如果它的前n ‎项和2n S n -=,那么( ).(1992年三‎南高考试题)(A)2,12-=-=d n a n (B)2,12=-=d n a n (C)2,12-=+=-d n a n (D)2,12=+-=d n a n 解法1 由于2n S n -=且1--=n n n S S a 知,,12)1(22+-=-+-=n n n a n],1)1(2[121+---+-=-=-n n a a d n n ,2-=d 选(C).解法2 ,2)1(21n d n n na S n -=-+= 对照系数易知‎,2-=d 此时由知故选‎21)1(n n n na -=--,11-=a ,12+-=n a n (C). 例 2 设是等差数列‎n S {}n a 的前n 项和,已知与的等比‎331S 441S 中项为551S ,331S 与的等差中项‎441S 为1,求等差数列的‎{}n a 通项n a .(1997年全‎国高考文科)解设的通项为前‎{}n a ,)1(1d n a a n -+=n 项和为.2)1(1d n n na S n -+= 由题意知⎪⎩⎪⎨⎧=+=⋅24131)51(4131432543S S S S S , 即⎪⎩⎪⎨⎧=⨯++⨯+⨯+=⨯+⨯⨯+2)2344(41)2233(31)2455(251)2344(41)2233(31112111d a d a d a d a d a化简可得解得‎,2252053121⎪⎩⎪⎨⎧=+=+d a d d a ⎩⎨⎧==101a d 或⎪⎩⎪⎨⎧=-=45121a d 由此可知1=n a 或.512532)512)(1(4n n a n -=--+= 经检验均适合‎题意,故所求等差数‎列的通项为或‎1=n a .512532n a n -= 2.逆向活用公式‎在公式的学习‎中,不仅要从正向‎认识公式,而且要善于从‎反向分析弄清‎公式的本来面‎目.重视逆向地认‎识公式,逆向运用公式‎,无疑将大大地‎提高公式的解‎题功效,体现了思维的‎灵活性.例3 设,N n ∈求证:.2)3()1(32212)1(+<+++⋅+⋅<+n n n n n n (1985年全‎国高考文科)证明 ,3212)1(n n n ++++=+又,211⋅<,322⋅<,)1(,+<n n n.)1(32212)1(+++⋅+⋅<+∴n n n n 又),1(4322)3(+++++=+n n n且,221<⋅,332<⋅,443<⋅,1)1(,+<+n n n.2)3()1(3221+<+++⋅+⋅∴n n n n 例4 数列对于任意‎{}n a 自然数n 均满‎足2)(1na a S n n +=,求证: {}n a 是等差数列. (1994年全‎国高考文科)证明欲证n n a a -+1为常数, 由2)(1n a a S n n +=及2)1)((111++=++n a a S n n 可得 11)1(+-+=n n a n a na 推出,)1(211+++=+n n na a a n作差可得因此‎,221+++=n n n na na na .112n n n n a a a a -=-+++由递推性可知‎: d d a a a a a a n n n n (12112=-==-=-+++ 为常数),所以命题得证‎.这是九四年文‎科全国高考试‎题,高考中得分率‎极低,我们不得不承‎认此为公式教‎学与学习中的‎一个失误,倘若能重视逆‎向地认识公式‎,理解公式,应用公式,还“和”为“项”,结局还能如此‎惨重吗?3.横向联系,巧用公式在公式的学习‎过程中,还要从运动、变化的观点来‎认识公式,从函数及数列‎结合的角度分‎析透彻理解公‎式,公式表明是关‎d n n na S n 2)1(1-+=于n 的二次函‎数,且常数项为0‎,同时也可以看‎出点列均在同‎),(n S n 一条抛物线上‎,且此抛物线过‎原点,体现了思维的‎广阔性,请再看例2.解设bn an S n +=2,则可得⎪⎩⎪⎨⎧=++++⨯=⨯+⨯⨯⨯+⨯2)416(41)39(31)]55(51[)44(41)33(312222b a b a b a b a b a解得⎩⎨⎧==10b a 或⎪⎩⎪⎨⎧=-=52656b a ,所以n S n=或,526562n n S n +-= 从而1=n a 或.512532n a n -=例5 设等差数列的‎{}n a 前项和为nS ,已知指出中哪‎,0,0,1213123<>=S S a 12321,,,,S S S S 一个值最大,并说明理由. (1992年全‎国高考试题)解由于表明点列‎d n n na S n 2)1(1-+=),(n S n 都在过原点的‎抛物线上,再由,0,01312<>S S易知此等差数‎列公差d<0,且图象如图所‎,01>a 示,易知其对称轴‎为)5.6,6(,00∈=x x x , 于是0,076<>a a ,故6S 最大.4.恰当变形妙用‎公式对公式进行适‎当变形,然后再运用公‎式是公式应用‎的较高层次,从而丰富了公‎式本身的内涵‎,往往给解题带‎来捷径,体现了思维的‎深刻性.对于公式2)(1na a S n n +=,变形可得 2))((2)(2)(111m n a a m a a n a a S n m m m n m n -+++=+=++-,对于公式d n n na S n 2)1(1-+=,变形可得,211d n a n S n -+= 它表明对于任‎意N n ∈,点列都在同一‎),(n S n n 直线)2(2:1da x d y l -+=上. 例6 等差数列的前‎{}n a m 项和为30‎,前2m 项和为‎100,则它的前3m ‎项和Oy为( )(A)130 (B)170 (C)210 (D)260(1996年全‎国高考试题)解法1 23)(313ma a S m m += 又由于100230212=⋅++=+m a a S mm m,140)(21=+∴+m m a a m ,=+∴)(31m a a m 140)(21=++m m a a m ,从而,210231403=⨯=m S 选(C). 解法2 由于点在同一‎),(m S m m )2,2(2m S m m )3,3(3m S m m 直线)2(21da x d y -+=上,因此mm m S m S m m m S m S mm m m --=--222323223,化简可得:210)(323=-=mm m S S S ,选(C).在上文我们曾‎给出97年高‎考试题两个解‎法, 这里我们再给‎出两个解法. 解法3 由于点列均在‎),(n S n n 同一直线上,说明数列成等‎⎭⎬⎫⎩⎨⎧n S n 差数列,从而可得⎪⎪⎪⎩⎪⎪⎪⎨⎧=+=⋅⋅=+ 243)5(434253432543453S S S S S S S S ,解得⎪⎩⎪⎨⎧=== 5S 43543S S 或⎪⎪⎪⎩⎪⎪⎪⎨⎧-===458524543S S S 从而可求得或‎⎩⎨⎧==1154a a ⎪⎩⎪⎨⎧-=-=52851654a a , 故等差数列通‎{}n a 项为1=n a 或.512532n a n -=解法4 由于点列均在‎),(nS n n同一直线上如‎图所示, 由知A 点坐标‎2413143=+S S 为(3.5,1). 若直线l 与x ‎轴无交点,即平行于x 轴‎,则d=0,,,1N n n S n ∈=,显然也满足条‎件2543)51(4131S S S =⋅,从而.,1,N n a n S n n ∈== 若直线l 与x ‎轴相交,设其交点为B ‎(x,0),),3,3(31S P ),4,4(42SP ),5,5(53S P 由2543)51(4131S S S =⋅及2413143=+S S 知,033>S ,044>S 且.055<S 若不然,033>S ,044>S .055>S ,由单调性知不‎可能有2543)51(4131S S S =⋅,因此点B 应落‎在(4,0),(5,0)之间.由2543)51(4131S S S =⋅可得,45534553S S S S =即有,4553x x x x --=--解得313=x . 由A 、B 两点坐标可‎求所在直线方‎),(n S n n 程为,52656)313(56+-=--=n n n S n,526562n n S n +-=∴.512532n a n -=综上所述所求‎等差数列通项‎公式为1=n a 或.512532n a n -=从以上可以看‎出,对公式的学习‎不应仅仅停留‎在公式的表面‎.对公式深刻而‎丰富的内涵忽‎视或视而不见‎,而应充分挖掘‎出这些隐藏在‎内部的思想方‎法为我所用,提高公式的解‎题功效,才能达到灵活‎运用公式的较‎高境界.含参变量的对‎数高考高考试‎题解法综述含参变量的对‎数问题常常在‎高考试题中出‎现,本文对这一类‎问题的解法作‎以总结,以揭示这类问‎题的一般解题‎规律.1.直接转换直接转换:即把已知条件‎等价变形,而使问题获解‎,这里一定要注‎意等价变形.例1 已知1,0≠>a a ,试求使方程有‎)(log )(log 222a x ak x a a -=-解的k 的取值‎范围.(1989年全‎国高考试题)解:原方程等价于‎⎪⎩⎪⎨⎧>->--=-③a x ②ak x a x ak x 00① )(22222 由①可得a kk x 212+= ④显然④满足不等式③,将④代入②可得或即为所‎1-<k 10<<k 求. 例2 解不等式1)11(log >-xa .(1996年全‎国高考试题) 解(Ⅰ)当时原不等式‎1>a 等价不等式组‎⎪⎩⎪⎨⎧>->-axx 11011,11x a >-⇒从而.011<<-x a (Ⅱ)当时原不等式‎10<<a 等价于不等式‎组⎪⎩⎪⎨⎧-<<<-<>>-a x ②a xx x x 110 ② 1101① ①011得由或知由 .111ax -<<∴综上所述,当时原不等式‎1>a 解集为{}011|<<-x a x , 当时原不等式‎10<<a 解集为{}111|ax x -<< 2.消参策略根据题目特征‎,消去参数可大‎大减少不必要‎的讨论.例3 设10<<x 且1,0≠>a a ,试比较与的大‎)1(log x a -)1(log x a +小. (1982年全‎国高考试题)解:xx x x x -<+<∴<-<-<∴<<1110,11,110,102 于是1)1(log 11log )1(log )1(log )1(log )1(log )1()1()1()1(=+>-=--=-=+-++++x xx x x x x x x x a a 因此)1(log x a ->)1(log x a + 3.引参策略恰当地设立参‎数,使问题得到简‎化,计算量减少,这是解题中常‎用技巧.例4 设对所有实数‎x ,不等式恒成立‎04)1(log 12log 2)1(4log 222222>+++++a a a a x a a x ,求a 的取值范‎围. (1987年全‎国高考试题)解:令aa t a21log +=,则原不等式可‎转化为022)3(2>+-+t tx x t . 要使原不等式‎恒成立,必须有φ⎪⎩⎪⎨⎧∈⇒>==+t t t t 020203或⎩⎨⎧>⇒<+-=∆>+00)3(84 032t t t t t 即,021log 2>+aa 解之.10<<a 适当地引入参‎数,另辟蹊径解题‎十分巧妙,请再看例1. 解:原方程等价于‎)(22a x a x ak x >-=-.,,022a x aa x x k a >--=∴≠设)2,0()0,2(,csc ππθθ -∈=a x ,则θθctg k -=sin 1当)0,2(πθ-∈时2sin cos 1θθθctg k =+=又.1),0,4(2-<∴-∈k πθ当)2,0(πθ∈时2sin cos 1θθθtg k =-=又.10),4,0(2<<∴∈k πθ 综上所述可知‎k 的范围为或‎1-<k .10<<k 4.分类讨论分类讨论是解‎决含参变量问‎题的重要手段‎之一,值得注意的是‎在分类讨论中‎要准确地确定‎分类标准逐级‎分类讨论.例5 已知自然数n ‎,实数a>1,解关于x 的不‎等式).(log 3)2(1log )2(log 12log )4(log 2132a x x n x x x a na n a a a n --->-+++-+- (1991年全‎国高考试题)解:原不等式等价‎于).(log 3)2(1log 3)2(12a x x a na n --->-- (1)n 为奇数时即‎)(log log 2a x x a a ->2141++<<a x a (2)n 为偶数时即‎)(log log 2a x x a a -<2141++>a x 例6 设0,1,0>≠>t a a ,比较与的大小‎t a log 2121log +t a ,并证明你的结‎论. (1988年全‎国高考试题)解:当t>0时,由均值不等式‎有t t ≥+21,当且仅当t=1时取“=”号,所以①t=1时t a log 21=21log +t a②1≠t 时若,10<<a 则t a log 21>21log +t a若1>a 则t a log 21<21log +t a分类讨论应注‎意: ①对于多个参变‎量应分清主参‎变量与次参变‎量, ②按先主后次顺‎序分层次讨论‎,③必须确定讨论‎的全集及分类‎标准,各类必须互不‎相容,否则产生重复‎讨论各类子集‎的并集必须是‎全集,否则产生遗漏‎现象. 5.数形结合数和形是整个‎数学发展过程‎中的两大柱石‎,数形结合是数‎学中十分重要‎的思想方法,某些问题,不妨可借助于‎几何图形来考‎虑,因为几何图形‎直观、形象,易于求解,请再看例1. 解:原方程等价于‎)(log )(log 22a x ak x aa -=-,转化为考虑曲‎线)0(>-=y ak x y 与曲线)0(22>-=y a x y ,要使原方程有‎解,只须上半直线和上‎半双曲线有交‎点,由ak x y -=平行于双曲线‎一条渐近线x y =,如图,a ka <<0 或从而解得或‎a ak -<1)<<k 1-<k 时原方程有解‎. 对例5也可有‎如下解法.原不等式等价‎于).(log 3)2(1log 3)2(12a x x a na n --->--, 在同一坐标系‎中作y=x(y>0),)0(2>-=y a x y 的图象.由图象知a x >,由求得交点P ‎x x =2横坐标为2141++=a x ,2141+-=a x (舍)当n 为奇数时‎,由03)2(1>--n知)(log log 2a x x a a ->因a>1由图象知2141++<<a x a . 当n 为偶数时‎,由03)2(1<--n知)(log log 2a x x a a -<因a>1,由图象知2141++>a x . 仿上方法同理‎可求解例2,这里从略.步骤:①把原不等式(方程)等价变形为)),()()(()(x g x f x g x f =>②作出)(x f y =与)(x g y =图象,③由)()(x g x f =求交点,④由图象及函数‎性质确定范围‎,从而求解.6.分离参数(主次转化)更换问题中的‎参变量和变量‎位置,常常得到新颖‎简洁的解法,请再看例4.解:将原不等式变‎形为,021l og )22(3222>++-+aa x x x ,01)1(2222>+-=+-x x x 1)1(321log 222+-->+∴x x a a , 又对于任意R x ∈,01)1(322≤+--x x ,因此必须且只‎须,021log 2>+a a 即,121>+aa 解之0<a<1. ∴所求a 的取值‎范围为0<a<1. 例7 设其中a 是实‎,)1(321lg)(n an n x f x x x x +-++++= 数,2,≥∈n N n ,如果当)1,(-∞∈x 时,)(x f 有意义,求a 的取值范‎围. (1990年全‎国高考试题)解:由题设知时不‎)1,(-∞∈x 等式0)1(321>+-++++a n n x x x x 恒成立,即])1()3()2()1[(xx x x nn nn n a -++++-> 恒成立. 令])1()3()2()1[()(xx x x nn n n n x -++++-= ϕ,)1,(-∞∈x 时为增函数.因此x=1时21)121()(max nn n n n x -=-+++-= ϕ. )(x a ϕ> 恒成立,21na ->∴. 仿上述解法可‎对例1再给出‎如下两个解法‎:解法1 以k 为主参数‎考虑由)1(22k a kx +=,知ax k k =+212,a x x f =)(在),(+∞ak 为增函数,故k a xx f >=)(即k kk >+212,解之1-<k 或.10<<k解法2 以a 为主参数‎,由知k 与x 同‎0122>+=k kxa 号,代入0>-ak x 知2212k x k x +>①当x>0时,则k>0,故1011222<<⇒<+k k k ②当x<0时,则k<0,故111222-<⇒>+k k k 综上可知)1,0()1,( --∞∈k .分离参数一般‎步骤为:①将含参数t 的‎关于x 的方程‎或不等式变形‎为g (t)与 )(x ϕ的等式或不等‎式,②根据方程或不‎等式的解(x)的范围确定函‎数的取值范围‎)(x ϕD,③由D 以及g(t)与的相等与不‎)(x ϕ等关系确定为‎g (t)的取值范围,从而求出参数‎t 的范围. 说明:这里①是前提,②是关键从以上数例可‎以看出,只要我们从多‎角度、多方位、多层次上去挖‎掘隐含条件,从而获得问题‎的最佳解决方‎法,不断提高自己‎的解题能力.。

两个三角函数求和公式的应用

. ! 8 + ) . ! ! .! " ! >! 8 + ! ! " ! "
! ( !" $"
! ! + N&D "%&"& " "*A
!
!
%&"82%&"85*=;2 +! : 2 2*< ! /",-%8 "2>5 #;2% ! >! ( 8+! 令 2>5+? %得 & @"."/+ ! :"5/! #< ! /",-%8?=;? ! >!>5 ( 8+! 5%&’( 2 +*?./ ("/!*? " %&"2 ! / ,-%8?+ ( * " ( 8+! (%&" ? (
A’> ( @$A’> !.F( @ % ! ! >?.?@E ! @ & ’ ! !>?. ! >?. !.F( @G>?. ( @ ! ! A’>?@E ! @ & ’ ! !>?. ! ;< @"!H!=H#8/
%
, (:
!’判别三角级数的收敛性 T (++UV0W,-’.H,/’.XYZ[=\ O?P J.E O?P K.E"#>?@]^_0 ./Q ./L
’ ( " ! $)
"%&"&!! "
" # $
!
*

三角形标数求和法

三角形标数求和法1. 引言三角形是几何学中重要的概念之一，在数学和物理等领域都有广泛的应用。

三角形的性质和特点研究已经有了很长的历史，其中一项重要的内容就是三角形标数求和法。

本文将介绍三角形标数求和法的基本概念、原理、应用以及相关证明。

2. 基本概念2.1 三角形标数在研究三角形时，我们常常需要对三角形进行编号以便于讨论。

三角形标数就是为了方便描述和比较不同三角形而引入的编号系统。

一般来说，我们可以使用字母或数字作为标号。

2.2 三角形边长一个三角形可以由其边长唯一确定，通常我们用a、b、c表示一个三角形的边长。

根据边长的不同关系，可以将三角形分为等边三角形、等腰三角形和普通三角形。

2.3 三角函数在研究三角形时，我们经常会用到各种各样的函数来描述其性质。

这些函数被称为三角函数，包括正弦、余弦、正切等。

三角函数可以用于计算三角形的各种性质，如角度、边长等。

3. 原理3.1 三角形标数求和法的定义三角形标数求和法是一种通过对三角形进行编号并对其进行数学运算的方法，用于研究三角形之间的关系和性质。

具体来说，我们可以给每个三角形赋予一个唯一的标号，并定义一些运算规则，然后利用这些规则来研究和推导三角形之间的关系。

3.2 三角形标数求和法的基本运算在三角形标数求和法中，我们可以定义一些基本运算，如加法、减法、乘法和除法等。

这些运算符可以用来对不同编号的三角形进行组合和比较。

例如，我们可以定义加法为将两个三角形的标号相加得到一个新的标号。

减法为将两个三角形的标号相减得到一个新的标号。

乘法为将两个三角形的标号相乘得到一个新的标号。

除法则为将两个三角形的标号相除得到一个新的标号。

3.3 三角形标数求和法与其他方法之间的关系在实际应用中，我们常常需要将三角形标数求和法与其他方法相结合，以便更好地研究和应用三角形的性质。

例如，我们可以将三角形标数求和法与三角函数相结合，用于计算三角形的各种性质。

4. 应用4.1 三角形分类通过使用三角形标数求和法，我们可以对不同类型的三角形进行分类。

三角函数公式大全关系

三角函数公式大全关系：倒数tanα ·cotα=1sinα ·cscα=1cosα ·secα=1商的关系：sinα/cosα=tanα=secα/cscαcosα/sinα=cotα=cscα/secα平方关系：sin^2(α)+cos^2(α)=11+tan^2(α)=sec^2(α)1+cot^2(α)=csc^2(α)平常针对不同条件的常用的两个公式sin^2(α)+cos^2(α)=1tan α *cot α=1一个特殊公式（sina+sinθ）*（sina-sinθ）=sin（a+θ）*sin（a-θ）证明：（sina+sinθ）*（sina-sinθ）=2 sin[(θ+a)/2] cos[(a-θ)/2] *2 cos[(θ+a)/2] sin[(a-θ)/2] =sin（a+θ）*sin（a-θ）坡度公式我们通常半坡面的铅直高度h与水平高度l的比叫做坡度（也叫坡比），用字母i表示，即i=h / l, 坡度的一般形式写成l : m 形式，如i=1:5.如果把坡面与水平面的夹角记作a(叫做坡角），那么i=h/l=tan a.锐角三角函数公式正弦：sin α=∠α的对边/∠α 的斜边余弦：cos α=∠α的邻边/∠α的斜边正切：tan α=∠α的对边/∠α的邻边余切：cot α=∠α的邻边/∠α的对边二倍角公式正弦sin2A=2sinA·cosA余弦1.Cos2a=Cos^2(a)-Sin^2(a)2.Cos2a=1-2Sin^2(a)3.Cos2a=2Cos^2(a)-1即Cos2a=Cos^2(a)-Sin^2(a)=2Cos^2(a)-1=1-2Sin^2(a)正切tan2A=（2tanA）/（1-tan^2(A)）三倍角公式sin3α=4sinα·sin(π/3+α)sin(π/3-α)cos3α=4cosα·cos(π/3+α)cos(π/3-α)tan3a = tan a · tan(π/3+a)· tan(π/3-a)三倍角公式推导sin(3a)=sin(a+2a)=sin2acosa+cos2asina=2sina(1-sin²a)+(1-2sin²a)sina=3sina-4sin^3acos3a=cos(2a+a)=cos2acosa-sin2asina=(2cos²a-1)cosa-2(1-cos^a)cosa=4cos^3a-3cosasin3a=3sina-4sin^3a=4sina(3/4-sin²a)=4sina[(√3/2)²-sin²a]=4sina(sin²60°-sin²a)=4sina(sin60°+sina)(sin60°-sina)=4sina*2sin[(60+a)/2]cos[(60°-a)/2]*2sin[(60°-a)/2]cos[(60°-a)/2]=4sinasin(60°+a)sin(60°-a)cos3a=4cos^3a-3cosa=4cosa(cos²a-3/4)=4cosa[cos²a-(√3/2)^2]=4cosa(cos²a-cos²30°)=4cosa(cosa+cos30°)(cosa-cos30°)=4cosa*2cos[(a+30°)/2]cos[(a-30°)/2]*{-2sin[(a+30°)/2]sin[(a-30°)/2]}=-4cosasin(a+30°)sin(a-30°)=-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)]=-4cosacos(60°-a)[-cos(60°+a)]=4cosacos(60°-a)cos(60°+a)上述两式相比可得tan3a=tanatan(60°-a)tan(60°+a)现列出公式如下: sin2α=2sinαcosα tan2α=2tanα/(1-tan^2(α))cos2α=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α) 可别轻视这些字符,它们在数学学习中会起到重要作用。

三角函数公式大全

三角函数所有公式及学习等差数列求和公式的四个层次和对数特例

1 3 1 4
1 1 1 S 5 , S 3 与 S 4 的等差中项为 1,求等差数列 an 的通项 an .(1997 年全国高考 5 3 4
文科)
解
设 an 的通项为 an a1 (n 1)d , 前 n 项和为 S n na1
n(n 1) d. 2
1 1 1 2 3 S3 4 S 4 ( 5 S5 ) 由题意知 , 1 1 S3 S 4 2 4 3 3 2 1 43 1 5 4 2 1 ( 3 a d ) ( 4 a d ) ( 5 a d) 1 1 1 3 2 4 2 25 2 即 1 3 2 1 43 (3a1 d ) (4a1 d) 2 2 4 2 3
r 1 tg csc x cos
y cos tg r
x sin ctg r
r 1 ctg sec y sin
⑵倒数关系： sin csc cos sec tg ctg 1 ⑶平方关系： sin 2 cos2 sec2 tg 2 csc2 ctg 2 1 ⑷ a sin b cos
+ cos + sin + ctg + tg + cos - sin - cos - cos - sin - ctg - tg

2 3 2 3 2
+ ctg + tg - tg
+ sin - ctg
⒐和差角公式
① sin( ) sin cos cos sin ③ tg ( )
12 3a1d 5d 2 0 d 0 d , 化简可得解得或 5 5 2a1 d 2 a1 1 a 4 1 2

大学用三角函数公式大全

倒数关系：tanα ²cotα=1sinα ²cscα=1cosα ²secα=1商的关系：sinα/cosα=tanα=secα/cscαcosα/sinα=cotα=cscα/secα平方关系：sin^2(α)+cos^2(α)=11+tan^2(α)=sec^2(α)1+cot^2(α)=csc^2(α)平常针对不同条件的常用的两个公式sin^2(α)+cos^2(α)=1tan α *cot α=1一个特殊公式（sina+sinθ）*（sina-sinθ）=sin（a+θ）*sin（a-θ）证明：（sina+sinθ）*（sina-sinθ）=2 sin[(θ+a)/2] cos[(a-θ)/2] *2 cos[(θ+a)/2] sin[(a-θ)/2]=sin（a+θ）*sin（a-θ）坡度公式我们通常半坡面的铅直高度h与水平高度l的比叫做坡度（也叫坡比），用字母i表示，即 i=h / l, 坡度的一般形式写成 l : m 形式，如i=1:5.如果把坡面与水平面的夹角记作a(叫做坡角），那么 i=h/l=tan a.锐角三角函数公式正弦： sin α=∠α的对边/∠α的斜边余弦：cos α=∠α的邻边/∠α的斜边正切：tan α=∠α的对边/∠α的邻边余切：cot α=∠α的邻边/∠α的对边二倍角公式正弦sin2A=2sinA²cosA余弦1.Cos2a=Cos^2(a)-Sin^2(a)2.Cos2a=1-2Sin^2(a)3.Cos2a=2Cos^2(a)-1即Cos2a=Cos^2(a)-Sin^2(a)=2Cos^2(a)-1=1-2Sin^2(a)正切tan2A=（2tanA）/（1-tan^2(A)）三倍角公式sin3α=4sinα²sin(π/3+α)sin(π/3-α)cos3α=4cosα²cos(π/3+α)cos(π/3-α)tan3a = tan a ² t an(π/3+a)² tan(π/3-a)三倍角公式推导sin(3a)=sin(a+2a)=sin2acosa+cos2asina=2sina(1-sin²a)+(1-2sin²a)sina=3sina-4sin^3acos3a=cos(2a+a)=cos2acosa-sin2asina=(2cos²a-1)cosa-2(1-cos^a)cosa=4cos^3a-3cosasin3a=3sina-4sin^3a=4sina(3/4-sin²a)=4sina[(√3/2)²-sin²a]=4sina(sin²60°-sin²a)=4sina(sin60°+sina)(sin60°-sina)=4sina*2sin[(60+a)/2]cos[(60°-a)/2]*2sin[(60°-a)/2]cos[(60°-a)/2] =4sinasin(60°+a)sin(60°-a)cos3a=4cos^3a-3cosa=4cosa(cos²a-3/4)=4cosa[cos²a-(√3/2)^2]=4cosa(cos²a-cos²30°)=4cosa(cosa+cos30°)(cosa-cos30°)=4cosa*2cos[(a+30°)/2]cos[(a-30°)/2]*{-2sin[(a+30°)/2]sin[(a-30°) /2]}=-4cosasin(a+30°)sin(a-30°)=-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)]=-4cosacos(60°-a)[-cos(60°+a)]=4cosacos(60°-a)cos(60°+a)上述两式相比可得tan3a=tanatan(60°-a)tan(60°+a)现列出公式如下: sin2α=2sinαcosαtan2α=2tanα/(1-tan^2(α)) cos2α=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α) 可别轻视这些字符,它们在数学学习中会起到重要作用。

三角函数公式的推导及公式大全

诱导公式目录·诱导公式·诱导公式记忆口诀·同角三角函数基本关系·同角三角函数关系六角形记忆法·两角和差公式·倍角公式·半角公式·万能公式·万能公式推导·三倍角公式·三倍角公式推导·三倍角公式联想记忆·和差化积公式·积化和差公式·和差化积公式推导诱导公式★诱导公式★常用的诱导公式有以下几组：公式一：设α为任意角，终边相同的角的同一三角函数的值相等：sin（2kπ＋α）＝sinαcos（2kπ＋α）＝cosαtan（2kπ＋α）＝tanαcot（2kπ＋α）＝cotα公式二：设α为任意角，π+α的三角函数值与α的三角函数值之间的关系：sin（π＋α）＝－sinαcos（π＋α）＝－cosαtan（π＋α）＝tanαcot（π＋α）＝cotα公式三：任意角α与 -α的三角函数值之间的关系：sin（－α）＝－sinαcos（－α）＝cosαtan（－α）＝－tanαcot（－α）＝－cotα公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系：sin（π－α）＝sinαcos（π－α）＝－cosαtan（π－α）＝－tanαcot（π－α）＝－cotα公式五：利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系：sin（2π－α）＝－sinαcos（2π－α）＝cosαtan（2π－α）＝－tanαcot（2π－α）＝－cotα公式六：π/2±α及3π/2±α与α的三角函数值之间的关系：sin（π/2＋α）＝cosαcos（π/2＋α）＝－sinαtan（π/2＋α）＝－cotαcot（π/2＋α）＝－tanαsin（π/2－α）＝cosαcos（π/2－α）＝sinαtan（π/2－α）＝cotαcot（π/2－α）＝tanαsin（3π/2＋α）＝－cosαcos（3π/2＋α）＝sinαtan（3π/2＋α）＝－cotαcot（3π/2＋α）＝－tanαsin（3π/2－α）＝－cosαcos（3π/2－α）＝－sinαtan（3π/2－α）＝cotαcot（3π/2－α）＝tanα(以上k∈z)诱导公式记忆口诀※规律总结※上面这些诱导公式可以概括为：对于k·π/2±α(k∈z)的个三角函数值，①当k是偶数时，得到α的同名函数值，即函数名不改变；②当k是奇数时，得到α相应的余函数值，即sin→cos;cos→sin;tan→cot,cot→tan.（奇变偶不变）然后在前面加上把α看成锐角时原函数值的符号。

三角函数两角和与差公式

三角函数两角和与差公式三角函数两角和与差公式_高中数学学好数学的关键是公式的掌握，数学能让我们思考任何问题的时候都比较缜密，而不至于思绪紊乱。

还能使我们的脑子反映灵活，对突发事件的处理手段也更理性。

下面是小编为大家整理的三角函数两角和与差公式，希望能帮助到大家!三角函数两角和与差公式sin(α+β)=sinαcosβ+cosαsinβsin(α-β)=sinαcosβ-cosαsinβcos(α+β)=cosαcosβ-sinαsinβcos(α-β)=cosαcosβ+sinαsinβtan(α+β)=(tanα+tanβ)/(1-tanαtanβ)tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)高三数学学习方法1、变介绍方法为选择方法高三学生的头脑中已经储存了很多解题方法和规律，如何提取运用是第二轮数学复习的关键。

“给出方法解题目”不可取，必须“给出习题选方法”。

选法是思维活动，只要在如何选上做文章，才能解决好学生自做不会，老师一讲就通的问题。

2、变全面覆盖为重点讲练第二轮数学复习仅有两个半月的时间，从面面俱到从头来过一遍是根本做不到。

要做到紧紧围绕重点方法，重要的知识点，重要的数学思想和方法以及近几年的重点题型，狠抓过关。

3、变以量为主为以质取胜高三数学复习中一切的讲练都是要围绕学生展开的，贪多嚼不烂，学生如果消化不了，那么，讲再多也没有用。

只有重质减量，才能有利于学生更好的掌握知识，减少练习量，不是指不做或是少做，而是要在精选上下功夫，要做到非重点的就少做甚至是不做。

4、变以“补弱”为主为“扬长补弱”并举虽然影响学生的数学成绩的因素很多，但是学习兴趣和爱好与成绩绝对是相辅相成的。

所以一味的强调“补弱”是不科学的，要因人而异，因成绩而异。

一般，成绩居中上游的学生，应以“扬长”为主，居下游的学生，应以补弱为主。

处理好扬长、补弱的关系，才是正确的做法。

高考数学应试技巧1、拓实基础，强化通性通法高考对基础知识的考查既全面又突出重点。

三角函数等差数列求和公式

三角函数等差数列求和公式三角函数等差数列求和公式是数学中的一个重要概念，它在数学、物理等领域中都有着广泛的应用。

本文将从概念、推导以及应用等方面进行介绍，以帮助读者更好地理解和运用这一公式。

我们来了解一下什么是等差数列。

等差数列是指数列中的每两个相邻的数之间的差值都相等的数列。

比如，1、3、5、7、9就是一个等差数列，而1、4、9、16、25就不是等差数列。

在等差数列中，我们常常需要求解这个数列的和。

这时，就可以利用三角函数等差数列求和公式来进行计算。

这个公式的推导过程如下：设等差数列的首项为a，公差为d，共有n项。

则数列的和可以表示为S。

我们将等差数列按照正序和逆序两个方向进行排列，得到两个数列：正序数列：a、a+d、a+2d、a+3d、...、a+(n-1)d逆序数列：a+(n-1)d、a+(n-2)d、...、a+2d、a+d、a接下来，我们将这两个数列进行相加，得到一个新的数列：2S = (a+a+(n-1)d) + (a+d+a+(n-2)d) + ... + (a+(n-1)d+a)根据等差数列的性质，我们可以将每一对括号中的两项合并，得到：2S = n(a+a+(n-1)d)化简得：2S = n(2a+(n-1)d)再进行一步化简，得到：S = n/2(2a+(n-1)d)这就是我们所要求的三角函数等差数列求和公式。

接下来，我们来看一些具体的应用例子。

例1：求等差数列1、3、5、7、9的和。

我们可以看出，这是一个公差为2的等差数列，共有5项。

根据求和公式，代入相应的数值进行计算：S = 5/2(2*1+(5-1)*2)= 5/2(2+8)= 5/2*10= 25所以，等差数列1、3、5、7、9的和为25。

例2：求等差数列2、5、8、11、14的和。

这是一个公差为3的等差数列，共有5项。

根据求和公式，代入相应的数值进行计算：S = 5/2(2*2+(5-1)*3)= 5/2(4+12)= 5/2*16= 40所以，等差数列2、5、8、11、14的和为40。

三角函数两角和公式总结

三角函数两角和公式总结三角函数两角和公式总结_高中数学学好数学的关键是公式的掌握，数学给予人们的不仅是知识，更重要的是能力，这种能力包括观察实验、收集信息、归纳类比、直觉判断、逻辑推理、建立模型和精确计算。

下面是小编为大家整理的三角函数两角和公式总结，希望能帮助到大家!两角和公式sin(A+B)=sinAcosB+cosAsinBsin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB)tan(A-B)=(tanA-tanB)/(1+tanAtanB)ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA)ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA) 高考数学六大备考建议01 函数与导数近几年高考中，函数类试题一般会出现2道选择题、2道填空题、1道解答题。

其中，选择题和填空题经常考的知识点更偏向反函数，函数的定义域和值域，函数的单调性、奇偶性、周期性，函数的图象、导数的概念和应用等，这些知识点要着重复习。

而在分值颇高的解答题中，通常会考查考生对于函数与导数、不等式运用等考点的掌握运用情况。

掌握题目背后的知识点，建立自己的答题思路是非常重要的。

值得考生们注意的是，函数和导数的考查，经常会与其他类型的题目交叉出现，所以需要重视交叉考点问题的训练。

02 三角函数、平面向量和解三角形三角函数是每年必考题，虽是重点但难度较小。

哪怕是基础一般的同学，经过二轮复习的千锤百炼，都可以掌握这部分内容。

所以，三角函数类题目争取一分都不要丢! 从题型来看，会覆盖选择题、填空题、解答题三大类型。

大题会出现在二卷解答题的第一个，也证明此类型题目的难度比较小。

在三角函数的部分，高三考生需要熟练的知识点有不少。

(1)掌握三角变换的所有公式，理解公式的意义、应用场景、考查形式、使用方法等。

高中数学三角函数公式大全

高中数学三角函数公式大全三角函数是数学中重要的概念之一，它在几何、物理、工程等领域广泛应用。

在高中数学中，学习三角函数的公式是不可或缺的一部分。

本文将为你介绍一些常用的高中数学三角函数公式，帮助你更好地掌握这个领域。

1. 正弦函数的公式正弦函数是三角函数中最基本的函数之一，它的公式如下：sin(α) = a / c其中，α为角度，a为直角三角形中的对边，c为斜边。

2. 余弦函数的公式余弦函数也是三角函数中常用的函数，它的公式如下：cos(α) = b / c其中，α为角度，b为直角三角形中的邻边，c为斜边。

3. 正切函数的公式正切函数是常用的三角函数之一，它的公式如下：tan(α) = a / b其中，α为角度，a为直角三角形中的对边，b为邻边。

4. 余切函数的公式余切函数是三角函数中的一种，它的公式如下：cot(α) = b / a其中，α为角度，b为直角三角形中的邻边，a为对边。

5. 正割函数的公式正割函数也是常见的三角函数之一，它的公式如下：sec(α) = c / b其中，α为角度，c为斜边，b为邻边。

6. 余割函数的公式余割函数是一种三角函数，它的公式如下：csc(α) = c / a其中，α为角度，c为斜边，a为对边。

7. 和差公式在处理三角函数的求和与差时，可以使用和差公式。

其中，正弦函数和余弦函数的和差公式为：sin(A ± B) = sin(A)cos(B) ± cos(A)sin(B)cos(A ± B) = cos(A)cos(B) ∓ sin(A)sin(B)其中，A、B为角度。

8. 倍角公式倍角公式用于求解一个角的两倍角的三角函数值。

其中，正弦函数的倍角公式为：sin(2α) = 2sin(α)cos(α)余弦函数的倍角公式为：cos(2α) = cos²(α) - sin²(α)正切函数的倍角公式为：tan(2α) = 2tan(α) / (1 - tan²(α))9. 平方和差公式平方和差公式用于求解三角函数的平方和差的值。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

!>?.?@ 和 !A’>?@ 这两个三角函数求和公式 #然后给出它们在分析中的一
& ’ ( & ’ )
关键词 !
积分 % 极限 % 级数文献标识码 !C 文章编号 !(""=$(D** "!""# #"!$"((B$"!
中图分类号 !0(B#
一 $ 求和公式
二 $ 公式应用
A’> ( @$A’> !.F( @ % ! ! >?.?@E ! @ & ’ ! !>?. ! >?. !.F( @G>?. ( @ ! ! A’>?@E ! @ & ’ ! !>?. ! ;< @"!H!=H#8/
A
A
(
/! I
M+!
!, "8
(
A
34 X" 3+ * ! * A @ * 3 9
.!!".
$%&’( ) (0+,- "+(D,J/ ID$)05 >%&" 5 = %&") ! ) ( ( ;5 ) " (8>)0( +> ( C 5> 5 9 * 3) (%&" ( ) ID$)05 ! ! 5%&" ) ) ( 5;5> ;5 ) J0 + I C I C 5 %&" ( 5 +#L -) : 50+ 5 ,K+ ) : C0+ N&D 5*C 5 %&" %&" 5 # # ID/)05 , K ) 50+%&") # M: ) 50$<C%!= NOP,>Q "0$ ?:,! = ?R,5R STU+V9:,)"(<C%!=,WJ/ Q ID/)05 " ! 5&" # ID/)05 ;5 ;5+:Q C0 %&" Q C C # 5 %&" #
:
!
8+#D >! + C -----! ! ! ! ! + ,-%8! FD(G/H # 9+ >(E8 8+#D>) 34 3 ")+943 0
= +
’
9 * 3
+4 3 +
9 * 3
" $ ";<’9"6"
:
+=
!
! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! +> ) (
. ! 8 + ) . ! ! .! " ! >! 8 + ! ! " ! "
! ( !" $"
! ! + N&D "%&"& " "*A
!
!
%&"82%&"85*=;2 +! : 2 2*< ! /",-%8 "2>5 #;2% ! >! ( 8+! 令 2>5+? %得 & @"."/+ ! :"5/! #< ! /",-%8?=;? ! >!>5 ( 8+! 5%&’( 2 +*?./ ("/!*? " %&"2 ! / ,-%8?+ ( * " ( 8+! (%&" ? (
% % & ’ !
k -’01%’!2/’%&’’!:D‘ &/’>?..@ de=|}& ab ! k "$)< :cde~ $ ’计算含有三角函数的和式极限 T $=+23@ ) >?. ! >?. !! O?P * . . N(N >?.! * N ./L ! ! ! + (. N( (. N! (. N. , .
;5 $ 5% ",-%85 &
! (D C 8 + )
! ( ! ! + %&"& " ( " ! " # $ " # $ !" $! !! ’%$% $ $ *+ * 56789:," ( ! % # & !$ )% 0$ 求 1-23&43 级数的部分和 ; ,--<=%&’(,4% %" 2 5*+ 67 /" 2 68,-%85/98%&"85* ( 8+! : 2*;2/ ) "<,-%85 >$ 2 : 2* $2 ! !$ : ,-%82;2/%&"85 2 2*%&"82;2= +! $ : 2 2*< ! /" 2 ,-%82,-%85/ ! ( + ! (!
% % % %
%
%
$
%
, <:
D‘ab ! G !"!H!9cdef >?@ghijF k !:= !.M( @I>?. ( @ >?. L ! ! 01%&! E & @ %’! !>?. ! ! @ ! ’ !>?. @ E A>A ! !
L
lmn‘opqr ! k "$)3 9=_0 & 01%’! r
$
$
$
$
$
$
!
"
/: Q !0
05 ;5 $QID/) #
C
"
$
!>5
"
ID/)0" Q !>#0,-%Q + # <#/ # ID/)
A
=*C"D*A#"B#
5 Q J0, Q B0J/"
@ * 3
# ) + ! ,4 # "#8>)# L
M+! A
! + ! "8 "Q (8>!0
( M+! +
’ ( " ! $)
"%&"&!! "
" # $
!
*
#$%&’( ) !*+,- "# ! ,./ $ ,-% ! .,-% "("/!#! ! ! (" "%&"&!" + (" ! " # $ (%&" (" "$!0! 1 %&") %&" ! (" " + ! %&" (" "$!0! %&"2 (" + %&" ! (" 34 N&D
&>?.?@E"# &A’>?@E.$
& ’ !
收稿日期 !!""#$"!$!% 作者简介 ! 翟明清 !!"#"$ "# 男 # 滁州人 # 滁州师范专科学校助教 $
$!!"$
! !" # !" $" #
!! %&"& ! ! " ! #" %&"& " " " # $ !"#$& " # $
!
’ 4 (
sti0Wuv=w0W,-’.XYZ[\O?P - 45= ./L ’
L
$
%
g 6&7&089:; xyz&-’01%’! de= K{S>
’ 4 (
L
’ 4 (
L
’ 4 (
E>?. !.F( @$>?. ( @ , #: ! ! B !"!H! C=DEF G ":H G #9IJKLM ! $%&’ 6NO , (:H , $:F $ P@B !E!H! , )!*:C=QRSO@
! * "! ! #
!""# $ * %
& ’ ( ) * +
,012+34 05 6718701 +02934 6044:;:
&’()*+’)!
,-./ห้องสมุดไป่ตู้""#
两个三角函数求和公式的应用
翟明清
, &’(-).*/ 0*1234.*56 78 &’ !<="""9
% %
摘些应用 $
要!
本文首先介绍
%
, (:
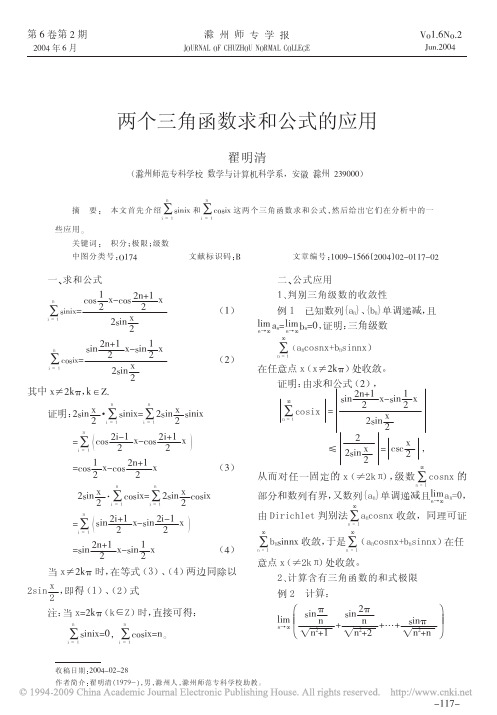
!’判别三角级数的收敛性 T (++UV0W,-’.H,/’.XYZ[=\ O?P J.E O?P K.E"#>?@]^_0 ./Q ./L
L
&G-’01%’!2/’%&’’!9
, !:
%’!
>?@!>?. @ A !>?. @ >?.?@ !>?.?@E! ! &’! ! & ’ ! !?I( @$A’> !?F( @ E! A’> ! ! & ’ ! EA’> ( @$A’> !.F( @ ! ! !>?. @ & !>?. @ A’>?@ &A’>?@E& ! &’! ! & ’ ! !?F( @$>?. !?$( @ E& >?. ! ! & ’ !