最新小升初面积计算真题专项
小升初真题复习-面积表面积体积(专项突破)-小升初数学计算问题重难点特训真题专项汇编(通用版)
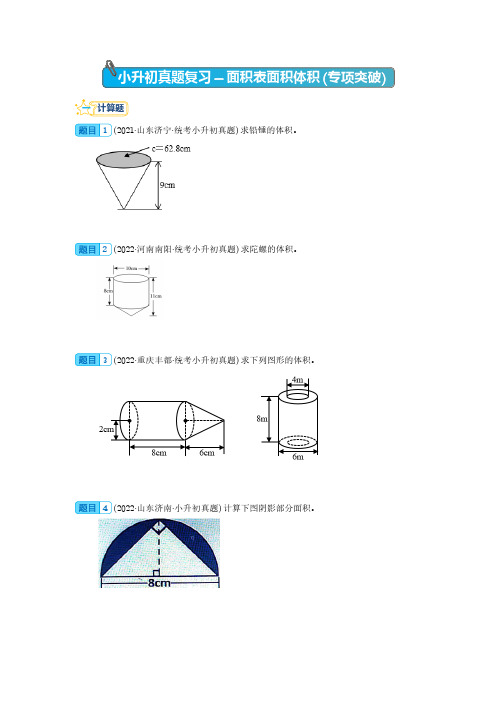
小升初真题复习-面积表面积体积(专项突破)一计算题1(2021·山东济宁·统考小升初真题)求铅锤的体积。
2(2022·河南南阳·统考小升初真题)求陀螺的体积。
3(2022·重庆丰都·统考小升初真题)求下列图形的体积。
4(2022·山东济南·小升初真题)计算下图阴影部分面积。
5(2021·河南驻马店·统考小升初真题)一个零件的形状如下图所示,求这个零件的体积。
6(2021·山东济宁·统考小升初真题)求下面图形的体积。
(单位:dm)7(2021·甘肃陇南·统考小升初真题)计算阴影部分面积。
(单位:厘米)8(2021·浙江宁波·统考小升初真题)求下图中阴影部分的面积。
9(2022·福建漳州·统考小升初真题)求阴影部分的周长和面积(单位:dm)。
10(2022·浙江温州·统考小升初真题)下图中四边形ABCD是一个长方形,长8厘米,宽4厘米,求阴影部分的面积。
11(2022·广东深圳·统考小升初真题)下图中阴影部分面积之和是多少平方厘米?12(2022·云南曲靖·统考小升初真题)求阴影部分的面积。
(单位:厘米)13(2022·安徽阜阳·统考小升初真题)下图中空白四边形是正方形,求图中阴影部分的面积。
(提示:你能把两个阴影三角形合成一个三角形吗?)14(2022·广东汕头·统考小升初真题)求出如图中三角形绕直角边旋转一周后形成图形的体积。
15(2022·湖南永州·统考小升初真题)下图是一个半圆,已知AB=10cm,阴影部分的面积是24.25cm2,求图中三角形的高。
16(2021·陕西渭南·统考小升初真题)计算下面组合图形的体积。
小升初分班考重点专题:圆的周长与面积(专项训练)-2023-2024学年数学六年级下册人教版

小升初分班考重点专题:圆的周长与面积-2023-2024学年数学六年级下册人教版一、单选题1.圆形花坛的半径是2米,绕花坛走一周,长度是()。
A.25.12米B.12.56米C.12.56平方米D.25.12平方米2.一个半圆形的半径是r,周长是()A.兀r B.2兀r÷2C.兀r+r D.(兀+2)r3.如果小圆的直径等于大圆的半径,那么小圆的面积是大圆的()A.B.C.2倍D.4倍4.一张圆形的纸,要想找到它的圆心,至少要对折()次。
A.1B.2C.4D.85.下面四句话中,表述正确的有()句①一件衣服提价10%后,再降价10%,价格还和原来相等。
②圆的面积和半径成正比例。
③如果两个质数的和是质数,那么它们的积一定是偶数。
④比的前项乘2,比的后项除以2,比值扩大到原来的4倍。
A.1B.2C.3D.46.松山湖举办了“折叠自行车竞赛”,一辆折叠自行车的车轮半径是2.5dm,通过其中一段1570m长的赛道,车轮要转()周。
A.10B.100C.1000D.20007.毛毛和豆豆在玩“猫捉老鼠”的游戏(如右图)。
毛毛从圆心O向点A跑,豆豆从点B沿弧线也向点A跑。
豆豆的速度至少是毛毛的()倍,才能在A处追上毛毛。
A.2B.3C.πD.π8.下图中,两个大正方形的大小相同,则下列说法()是正确的。
A.甲图阴影部分比较大B.乙图阴影部分比较大C.两图阴影部分一样大D.缺少条件,无法确定二、判断题9.当长方形、正方形、圆的周长相等时,圆的面积最大。
()10.在同一个圆内,长度是直径的一半的线段叫做半径。
()11.圆的周长是它的直径的3.14倍。
()12.大小两个圆的半径都增加1m,那么它们的周长各增加6.28m。
()13.大圆里剪去一个小圆,剩下的就是圆环。
()三、填空题14.一个圆的周长是25.12dm,它的面积是。
15.如图,正方形的面积与圆面积的比是。
16.量得一个树桩的直径是32cm,这个树桩的横截面的面积是。
小升初圆与组合图形面积专题(含解析)

小学数学圆与组合图形面积专题1.如图所示,大正方形与小正方形的面积之差为50平方厘米,阴影部分的面积是( )平方厘米.A .33.5πB .37.5πC .40πD .47.5π2.如图中,三角形ABC 是等腰直角三角形,图中阴影部分和空白部分的面积相比较,( )A .阴影部分的面积大B .空白部分的面积大C .面积一样大D .无法判断 3.计算如图阴影部分面积,正确的列式是( )A .266 3.14() 3.142⨯-⨯ B .22166 3.14() 3.1422⨯⨯-⨯ C .2216[6 3.14() 3.14]22⨯⨯-⨯ D .1(62 3.146 3.14)2⨯⨯⨯-⨯ 4.下面是两张同样大小的正方形纸,分别剪出不同规格的圆片,剩下的面积( )A .第一张纸剩下的面积大B .第二张纸剩下的面积大C .两张纸剩下的面积一样大5.如图,长方形ABCD 的面积是26m ,圆的面积是 2m6.如图两个圆的半径都是4厘米,涂色部分的面积之和是 平方厘米.7.长方形里有两个圆(如图),阴影部分的面积是27cm ,那么一个圆的面积是 平方厘米.8.如图,这个图形的周长是 厘米.9.如图阴影部分的面积是25cm ,环形的面积是 2cm .三.计算题(共7小题)10.如图中正方形的边长为4cm ,求阴影部分的面积.11.求如图阴影部分的面积.(单位:厘米)12.计算如图图形中阴影部分的面积.13.求如图阴影部分的面积.14.求图中阴影部分面积.15.如图中,已知圆的周长是25.12厘米,圆的面积与长方形的面积相等,图中阴影部分的面积是多少平方厘米?cm16.求阴影部分的面积.(单位:)17.求如图阴影部分的面积和周长.面积:.周长:.18.如图,三角形ABC是等腰直角三角形,8C∠=︒,求:==,45AB AC cm(1)弧AD的长度;(2)图中阴影部分的面积.19.如图,三角形ABC是等腰直角三角形,D是圆周的中点,BC是半圆的直径,已知==厘米,求阴影部分的面积.AB BC1020.如图,ABCD是一个长方形草坪,长20米,宽14米,中间有一条宽2米的曲折小路,求小路的面积.21.如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为多少平方厘米?22.如图所示的多边形是由一个三角形和三个长方形组成的.已知三个长方形的面积分别是12平方厘米、4平方厘米和6平方厘米.三角形面积是多少平方厘米?23.公园里有一块长方形的草坪,为方便游客,在草坪中间开辟了两条小路(如图).现在m草坪的面积是多少?(单位:)24.如图,已知大圆半径为6cm,四个小圆的面积相等.阴影部分面积是多少平方厘米?(分合割补法)25.一个容积为550mL的水瓶,里面装了一些水,正放时,水面高20cm,倒放时,空气高7.5cm.求水有多少升?26.如图是直角三角形中有一个内接正方形,求图中阴影部分的面积.单位:厘米.提示:分拆图形时常用“分割、填补、组合、旋转”等方法.27.如图四边形ABCD中,角DAB和角DCB都是直角,边CD和边BC的长度相等,从点C 到边AB的垂线CE长为10厘米,求四边形ABCD的面积.28.图形计算(1)求下图阴影部分的周长和面积.(单位:厘米)(2)三条边长分别是6厘米、8厘米、10厘米的直角三角形.将它的最短边对折到斜边相重合,(如图)图中阴影部分面积是 平方厘米.29.如图,1S 的面积比2S 的面积大多少?30.图中正方形的边长是10厘米,三角形甲的面积比三角形乙的面积少20平方厘米,求线段AB 的长.。
不规则或组合平面图形阴影部分面积计算-2024年小升初数学复习热点题型专项训练(通用版)(含解析)
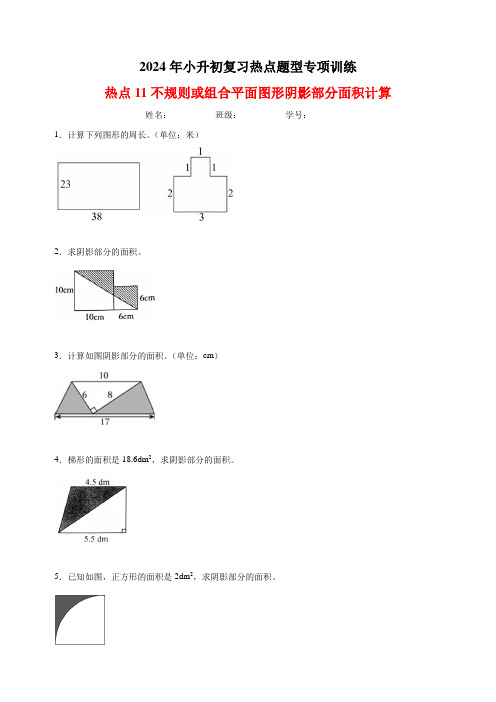
2024年小升初复习热点题型专项训练热点11不规则或组合平面图形阴影部分面积计算姓名:_________ 班级:_________ 学号:_________1.计算下列图形的周长。
(单位:米)2.求阴影部分的面积。
3.计算如图阴影部分的面积。
(单位:cm)4.梯形的面积是18.6dm2,求阴影部分的面积。
5.已知如图,正方形的面积是2dm2,求阴影部分的面积。
6.求阴影部分的周长。
7.求下列组合图形的面积。
(单位:cm)8.计算如图中阴影部分的面积。
9.计算下边阴影图形的周长。
10.求组合图形的面积。
(单位:米)11.求组合图形的面积。
(单位:cm)12.求图中阴影部分的面积(单位:厘米)13.如图中阴影部分的面积是多少?14.求如图阴影部分的周长和面积。
15.求阴影部分的面积(单位:厘米)。
16.求下面图形中阴影部分的面积。
17.求图中涂色部分的面积。
(单位:厘米)18.如图中,大圆的半径等于小圆的直径。
请计算阴影部分的周长。
19.计算如图阴影部分的面积。
20.求图形中阴影部分的面积。
(单位:分米)21.求下面图形阴影部分的周长和面积。
22.求下图中阴影部分的周长和面积。
23.求图中阴影部分的面积。
(单位:厘米)( 取3.14)24.求阴影部分的面积。
(单位:厘米)25.求下面图中阴影部分的面积(单位:厘米)。
26.计算如图所示图形阴影部分的面积。
(单位:厘米;圆周率取3.14)27.求下面图形中阴影部分的周长和面积。
28.计算如图所示图形阴影部分的面积。
(单位:厘米;圆周率取3.14)29.求出下图中阴影部分的面积。
(单位:米)30.求出前两个图形的面积和第三个图形中涂色部分的面积。
参考答案1.122米;12米【分析】(1)长方形的周长=(长+宽)×2,代入数据即可解答;(2)把这个图形上方的小线段分别向上、向左及向右平移,则这个图形的周长就是边长为3米的正方形的周长,据此利用正方形的周长公式即可解答。
小升初面积计算真题专项

面积计算部分典型题总结1.填空(每小题2分,共4分)1.如右图,AB 平行于CD ,图中甲和图形乙的一组对边分别平行,它们的面积相比较,乙 甲。
(填“>”“=”或“<”)2. 把长、宽分别为9厘米、6厘米的长方形划分为如图的4个三角形,其中的面积关系有4321s s s s +==,则3s = 平分厘米。
2.操作、应用(10分)1. 如图,等腰直角三角形的一腰的长是8厘米,以它的两腰为直径分别画了两个半圆,那么阴影部分的面积共有多少平方厘米?(π取3.14)3.求图形面积(6分)1. 如图,已知边长为8的正方形ABCD ,E 为AD 的中点,P 为CE 的中点,求△BDP 的面积。
4.求阴影部分的面积(共12分)(1)右图是由两个平行的四边形组成的,求阴影部分面积。
(6分)(2)求阴影部分的面积(6分)甲 乙5.计算(共29分)1.右图中阴影部分占长方形的() ()。
(2分)2. 右图是圆柱沿一平面切掉一块后剩余部分,请计算它的体积。
(5分)6.我有办法(每小题4分,共8分)1.用四个一样的长方形拼成下图,一个长方形面积是864平方米,长比宽多12米,求长方形的长和宽。
2.求下面阴影部分的面积。
7.计算1.右图平行四边形的高是6厘米,它的面积是()平方厘米(3分)A.35B.42C.30D.362.一个长5厘米,宽2.4厘米的长方形,沿对角线对折后,得到如右图所示的几何图形,阴影部分的周长是厘米(3分)3.在右图中,平行四边形的面积是20平方厘米,图中甲、乙、丙三个三角形的面积比是 (3分)4.综合应用(每小题5分,共10分)(1)阅读理解:“数学小知识”“勾股定理”是指一个直角三角形中,两条直角边的平方和等于斜边的平方。
例如:两条直角边的长分别为3、4,则222543=+,即斜边的长为5。
已知图中两条直角边的长度,求图中以斜边为直角所作圆的面积。
(2)如右图,已知长方形ABCD 的面积是88平方厘米,E 和F 分别是长和宽的中点。
小升初数学求阴影部分面积专项训练

小升初数学复习题『求阴影部分面积——专项训练』1.求图形中阴影部分的面积.(单位:分米)解:4×4﹣3.14×22=3.44(平方分米)答:阴影部分的面积是3.44平方分米。
2.计算下面图形的面积。
解:(16-9)×(10-4.5)÷2+16×4.5=91.25(平方米)答:图形的面积是91.25平方米.3.计算如图阴影部分的面积,已知d=6厘米。
解:6×(6÷2)-3.14×(6÷2)2÷2=3.87(平方厘米)答:阴影部分的面积是3.87平方厘米小升初数学复习题『求阴影部分面积——专项训练』4.计算下面两个图形阴影的面积。
(单位:厘米)(1)(2)(1)解:5×5-3×3=16(平方厘米)(2)解:8×8-(8-6)×(8-2)=52(平方厘米)5.如图所示,正方形的面积是9平方厘米,圆的面积是多少?解:3.14×9=28.26(平方厘米)答:这个圆的面积是28.26平方厘米。
6.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:1/4圆面积减去等腰直角三角形的面积,π/4×2²-2×1=1.14(平方厘米)答:阴影部分的面积是1.14平方厘米。
小升初数学复习题『求阴影部分面积——专项训练』7.如图的平行四边形中,空白部分的面积是20平方厘米,求阴影部分的面积?解:20×2÷5=8(厘米)(3+5)×8﹣20=44(平方厘米)答:阴影部分的面积是44平方厘米。
8.如图,甲、乙两图形都是正方形,它们的边长分别是5厘米和6厘米,求阴影部分的面积?解:5×5+6×6-5×5÷2-(5+6)×6÷2-(6-5)×6÷2=12.5(平方厘米)答:阴影部分的面积是12.5平方厘米。
小升初数学求阴影部分的面积计算题

小升初数学复习题『求阴影部分的面积——计算题』1.解:(4+6)×4÷2÷2﹣3.14×(42)²÷2=3.72(平方厘米)答:阴影部分的面积是3.72平方厘米。
2.解:扇形的半径是10÷2=5(厘米)10×10﹣3.14×5×5=21.5(平方厘米)答:阴影部分的面积为21.5平方厘米。
3.解:10÷2=5(厘米)长方形的面积=长×宽=10×5=50(平方厘米)半圆的面积=πr²÷2=3.14×5²÷2=39.25(平方厘米)阴影部分的面积=50﹣39.25=10.75(平方厘米)答:阴影部分的面积是10.75。
小升初数学复习题『求阴影部分的面积——计算题』4.解:8×4﹣3.14×42÷2=6.88(平方厘米)答:阴影部分的面积是6.88平方厘米。
5.解:S=πr²=3.14×(4÷2)²=12.56(平方厘米)阴影部分的面积=2个圆的面积=2×12.56=25.12(平方厘米)答:阴影部分的面积是25.12平方厘米。
6.解:圆的半径:15×20÷2×2÷25=12(厘米)阴影部分的面积:14×3.14×122=0.785×144答:阴影部分的面积是113.04平方厘米。
小升初数学复习题『求阴影部分的面积——计算题』7.解:周长:3.14×(10+3)=40.82(厘米)面积:12×3.14×[(10+3)÷2]²﹣12×3.14×(10÷2)²﹣12×3.14×(3÷2)²=23.55(平方厘米)答:阴影部分的周长是40.82厘米,面积是23.55平方厘米。
30道小升初数学几何问题(附答案)
图1
图2
【解析】我们可以让静止的瓷砖动起来,把对角线上的黑瓷砖,通过平移这种动态的
处理,移到两条边上(如图 2).在这一转化过程中瓷砖的位置发生了变化,但数量没
有变,此时白色瓷砖组成一个正方形.大正方形的边长上能放 (1011) 2 51(块),白
色 瓷 砖 组 成 的 正 方 形 的 边 长 上 能 放 : 511 50 ( 块 ) , 所 以 白 色 瓷 砖 共 用 了 :
60 的扇形面积 60 π 32 3 π 4.5(cm2 ) .
360
2
2.【割补法求面积】求下列各图中阴影部分的面积(图中长度单位为 cm ,圆周率按 3 计 算):
3
⑴
4
⑵
1
2
1
⑶
1
⑷
【解析】⑴ 4.5 ⑵ 4 ⑶1 ⑷ 2
3.【差不变】三角形 ABC 是直角三角形,阴影 I 的面积比阴影 II 的面积小 25cm2 , AB 8cm ,求 BC 的长度.
5
【解析】根据题意可知,挖去的 6 个边长 1 厘米的正方体相互之间是独立的,所以挖 去之后,原正方体的表面积相当于增加了六个小正方体的侧面积,所以现在它的表面 积为: 4 4 6 11 4 6 120 平方厘米. 16.【共高模型】如图,把四边形 ABCD 的各边都延长 2 倍,得到一个新四边形 EFGH 如果 ABCD 的面积是 5 平方厘米,则 EFGH 的面积是多少平方厘米?
【解析】该图形的上、左、前三个方向的表面分别由 9、7、7 块正方形组成.
该图形的表面积等于 (9 7 7) 2 46 个小正方形的面积,所以该图形表面积 为 46 平方厘米.
21.【取特殊点】长方形 ABCD 的面积为 36, E 、 F 、 G 为各边中点, H 为 AD 边上任 意一点,问阴影部分面积是多少?
小升初数学《阴影部分面积》专项试题及答案
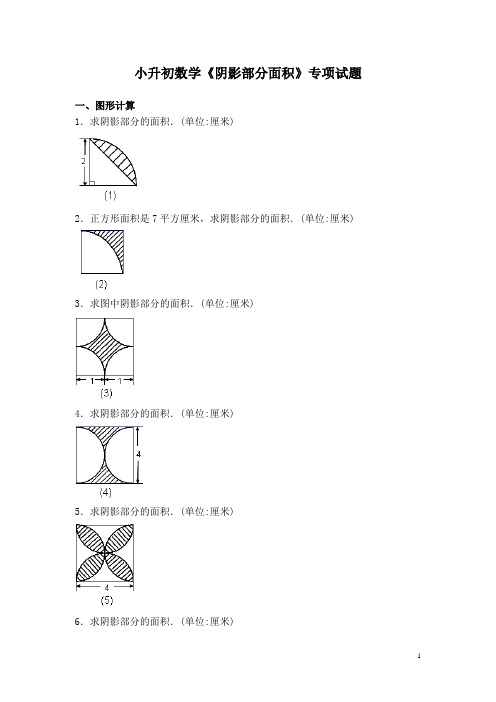
小升初数学《阴影部分面积》专项试题一、图形计算1.求阴影部分的面积.(单位:厘米)2.正方形面积是7平方厘米,求阴影部分的面积.(单位:厘米)3.求图中阴影部分的面积.(单位:厘米)4.求阴影部分的面积.(单位:厘米)5.求阴影部分的面积.(单位:厘米)6.求阴影部分的面积.(单位:厘米)7.求阴影部分的面积.(单位:厘米)8.求阴影部分的面积.(单位:厘米)9.求阴影部分的面积.(单位:厘米)10.求阴影部分的面积.(单位:厘米)11.求阴影部分的面积.(单位:厘米)12.求阴影部分的面积.(单位:厘米)13.求阴影部分的面积.(单位:厘米)14.已知直角三角形面积是12平方厘米,求阴影部分的面积.15.求阴影部分的面积.(单位:厘米)16.图中圆的半径为5厘米,求阴影部分的面积.(单位:厘米)17.如图,在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的周长.18.正方形边长为2厘米,求阴影部分的面积.19.如图,正方形ABCD的面积是36平方厘米,求阴影部分的面积.20.图中四个圆的半径都是1厘米,求阴影部分的面积.21.如图,正方形边长为8厘米,求阴影部分的面积.22.求阴影部分的面积.(单位:厘米)23.如下图,大正方形的边长为6厘米,小正方形的边长为4厘米.求阴影部分的面积.24.求阴影部分的面积.(单位:厘米)25.求阴影部分的面积.(单位:厘米)26.下图中,大小正方形的边长分别是9厘米和5厘米,求阴影部分的面积.27..下图中,大小正方形的边长分别是12厘米和10厘米.求阴影部分面积.28.求下图中阴影部分图形的面积及周长.29.已知下图阴影部分三角形的面积是5平方米,求圆的面积.30.已知下图中,圆的直径是2厘米,求阴影部分的面积.31.求下图中阴影部分图形的面积及周长.32.求下图中阴影部分的面积.(单位:厘米)33.求下图中阴影部分的面积.34.求下图中阴影部分的面积.35.求下图中阴影部分的面积.36.求下图中阴影部分的面积.二、解答题37.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?38.图中的4个圆的圆心是正方形的4个顶点,,它们的公共点是该正方形的中心,如果每个圆的半径都是1厘米,那么阴影部分的面积是多少?39.如图,有8个半径为1厘米的小圆,用他们的圆周的一部分连成一个花瓣图形,图中的黑点是这些圆的圆心。
小升初数学总复习计算图形面积分类练习题解析

五、巧用比例
1、一个大长方形被两条平行于它的两条边的线分成 a、b、c、d四个长方形。已知a的面积是10平方厘米,
b的面积是14平方厘米,c的面积是35平方厘米。求d的 面积。
【分析与解答】:长方形a、b等高;长方形c、d 等高
a:b=d:c
【分析与解答】: 阴影部分的面积就是梯形 ABGD的面积。
(3+8)×4÷2=22平方厘米
2、下图是正方形与平行四边形组成的图形, 求阴影部分的面积。(单位:分米)
【分析与解答】阴影部分的面积就是左下梯 形的面积。
(2+6)×6÷2=24平方分米
二、面积的转化 1、如下左图的长方形是一块草坪,中间有两
【分析与解答】阴影部分的面积等 于大长方形的面积减去两个小长方形的面积。 15×10-15×1-(10-1)×1=126平方米
三、图形分割 1、已知大正方形ABCD的边长是12厘米,小正 方形GCEF的边长是8厘米,求阴影部分面积。
【分析与解答】:阴影部分经过分割后是三个 小三角形的面积之和。
3.14×42÷4 =12.56平方厘米
八、综合练习 1、如图,大正方形和小正方形的边长分别是6厘米
和5厘米。求阴影部分的面积。
【分析与解答】:
阴影部分=大三角形-长方形-小三角形 (6+5)×6÷2=33平方厘米 5×(6-5)÷2=2.5平方厘米 5×5÷2=12.5平方厘米 33-2.5-12.5=18平方厘米
9、一个长方形被分成六个长方形,其中四个长方 形的面积如图所示,求A和B的面积。
【分析与解答】:用比例解决。
(1)20:40=15:A
A=60
(2)20:40=B:36
六年级下册数学试题-小升初专项训练 与面积相关的量 人教版(含答案)

小学数学试卷一、单选题1.()最接近1平方厘米.A. 数学书课本面B. 课桌面C. 大拇指指甲面2.学校篮球场占地面积约是6000()A. 平方米B. 米C. 平方千米3.用地毯铺满一间房的地面,地毯的大小就是这间房地面的()A. 周长B. 面积C. 面积单位4.周长相等,面积最大的是()A. 长方形B. 正方形C. 三角形D. 圆5.把面积为15dm2的长方形框拉成一个平行四边形后,面积()15dm2.A. 小于B. 大于C. 等于D. 不能确定6.8平方分米+4平方厘米=()A. 84平方分米B. 804平方厘米7.进率是100的两个面积单位是()A. 公顷和m2B. m2和dm2C. m2和km2二、判断题8.边长是1千米的正方形土地,面积是1平方千米.9.小明的房间面积是15米。
()10.用三根一样长的铁丝分别围成一个长方形、正方形和圆,圆的面积最大.11.1平方厘米和我们大拇指指甲的面积差不多.12.一块玻璃长25分米,宽8分米。
每平方米要8元钱,买这块玻璃需要1600元。
三、填空题13.边长是1________的正方形,面积是1平方分米,和平方分米相邻的两个面积单位是________和________。
每相邻两个面积单位间的进率是________。
14.0.973平方米=________平方分米,2300平方厘米=________平方米15.在下面横线上填上适当的数。
①300厘米=________分米=________米②30000平方厘米=________平方分米=________平方米。
③250平方厘米=________平方分米________平方厘米。
④105平方分米=________平方米________平方分米=________平方厘米。
⑤22分米=________米________分米=________厘米。
16.7.02吨=________千克25分=________小时2000平方米=________公顷17.(1)3.4平方分米=________平方厘米(2)60厘米=________米18.3000平方米=________公顷0.61平方千米=________公顷2.3时=________时________分3.2吨=________千克.19.一个正方形的周长是2000米,这个正方形的面积是________公顷。
小升初面积试题及答案

小升初面积试题及答案一、选择题1. 下列哪个图形的面积不是长方形的面积公式计算的?A. 正方形B. 圆形C. 长方形D. 三角形答案:B2. 一个长方形的长是12厘米,宽是8厘米,那么它的面积是多少平方厘米?A. 96B. 100C. 80D. 120答案:A3. 如果一个正方形的边长是10厘米,那么它的面积是多少平方厘米?A. 50B. 100C. 200D. 400答案:B4. 一个三角形的底是8厘米,高是6厘米,它的面积是多少平方厘米?A. 24B. 30C. 36D. 40答案:C5. 圆形的半径是3厘米,那么它的面积是多少平方厘米?(π取3.14)A. 28.26B. 15.7C. 9.42D. 7.07答案:C二、填空题6. 长方形的面积公式是:______,其中长为a,宽为b。
答案:S = a * b7. 正方形的面积公式是:______,其中边长为a。
答案:S = a * a 或 S = a²8. 三角形的面积公式是:______,其中底为b,高为h。
答案:S = (b * h) / 29. 圆形的面积公式是:______,其中半径为r。
答案:S = π * r²10. 如果一个长方形的面积是60平方厘米,长是15厘米,那么它的宽是______厘米。
答案:4三、解答题11. 小明家的地板是一个长方形,长为5米,宽为3米。
请问小明家的地板面积是多少平方米?解:根据长方形面积公式 S = a * b,将长a=5米,宽b=3米代入公式,得到 S = 5 * 3 = 15平方米。
答:小明家的地板面积是15平方米。
12. 小华用一根长20厘米的铁丝围成一个正方形,请问这个正方形的面积是多少平方厘米?解:正方形四条边长相等,所以每条边长为 20厘米 / 4 = 5厘米。
根据正方形面积公式 S = a²,将边长a=5厘米代入公式,得到S = 5² = 25平方厘米。
小升初面积试题及答案

小升初面积试题及答案1. 计算下列图形的面积:- 长方形:长为6米,宽为4米。
- 正方形:边长为5米。
- 圆形:半径为3米。
2. 一个梯形的上底是10厘米,下底是15厘米,高是8厘米,求梯形的面积。
3. 一个平行四边形的底边长为12厘米,高为7厘米,求平行四边形的面积。
4. 一个三角形的底边长为9厘米,高为6厘米,求三角形的面积。
5. 一个扇形的半径为8厘米,圆心角为60度,求扇形的面积。
答案1.- 长方形面积 = 长× 宽 = 6米× 4米 = 24平方米。
- 正方形面积 = 边长× 边长 = 5米× 5米 = 25平方米。
- 圆形面积= π × 半径² = 3.14 × 3米² = 28.26平方米。
2. 梯形面积 = (上底 + 下底) × 高÷ 2 = (10厘米 + 15厘米) × 8厘米÷ 2 = 25厘米× 8厘米 = 200平方厘米。
3. 平行四边形面积 = 底边长× 高 = 12厘米× 7厘米 = 84平方厘米。
4. 三角形面积 = 底边长× 高÷ 2 = 9厘米× 6厘米÷ 2 = 27平方厘米。
5. 扇形面积 = (圆心角÷ 360°) × π × 半径² = (60° ÷ 360°) × 3.14 × 8厘米² = 3.14 × 8厘米² × (1/6) = 13.04平方厘米。
小升初图形面积40题

小升初图形面积40题一、计算下列图形的面积1、一个正方形边长是4米,面积是()平方米。
2、一个长方形长是6厘米,宽是4厘米,面积是()平方厘米。
3、一个三角形底是8分米,高是5分米,面积是()平方分米。
4、一个梯形上底是3厘米,下底是5厘米,高是4厘米,面积是()平方厘米。
5、一个平行四边形底是10分米,高是4分米,面积是()平方分米。
二、求下列图形的面积6、有一个平行四边形,它的一组邻边分别长5厘米和8厘米,这个平行四边形的面积是多少平方厘米?61、有一个三角形,它的底长是10厘米,高是6厘米,这个三角形的面积是多少平方厘米?611、有一个梯形,它的上底长是3厘米,下底长是5厘米,高是4厘米,这个梯形的面积是多少平方厘米?6111、有一个正方形,它的边长是6厘米,这个正方形的面积是多少平方厘米?三、比较图形的面积大小10、下面的两个图形,哪一个的面积更大一些?101、下面的两个图形,哪一个的面积更大一些?1011、下面的两个图形,哪一个的面积更大一些?下面的两个图形,哪一个的面积更大一些?下面的两个图形,哪一个的面积更大一些?下面的两个图形,哪一个的面积更大一些?小升初组合图形的面积典型试题在数学的学习中,组合图形的面积是一个重要的概念,尤其在小升初阶段,这一概念的重要性更加凸显。
它不仅涉及到基础几何知识,还考察了学生的逻辑思维和问题解决能力。
本文将通过一些典型的试题,探讨如何解决这类问题。
一、理解基本概念我们需要理解什么是组合图形。
组合图形是由两个或两个以上的基本图形组合而成的图形。
例如,一个房子可以由一个矩形和一个三角形组成,一个汽车可以由一个圆形和一个矩形组成。
二、掌握基本方法在计算组合图形的面积时,我们通常使用以下两种方法:1、分解法:将组合图形分解成几个基本图形,然后分别计算每个基本图形的面积,最后将它们相加得到组合图形的总面积。
2、直接计算法:如果组合图形无法分解成基本图形,或者分解起来比较复杂,我们可以直接计算整个组合图形的面积。
小升初数学阴影部分面积“拓展型”专项练习

小升初数学典型奥数题『阴影部分面积“拓展型”专项练习』1.求图中阴影部分的面积。
(单位:cm)8×(8÷2)=8×4=32(cm2)阴影部分的面积是32cm2。
8×8÷2 =64÷2=32(cm2)2.求出阴影部分的面积和周长。
阴影部分的面积:3×3=9(cm2)阴影部分的周长:2×3.14×3÷2+3×2=15.42(cm)答:阴影部分的面积是9cm2,阴影部分的周长是15.42cm。
3.大圆半径5厘米,小圆半径3厘米,求两圆中阴影部分的面积差。
3.14×52-3.14×32=3.14×(52-32)=50.24(平方厘米)答:两圆中阴影部分的面积差是50.24平方厘米。
小升初数学典型奥数题『阴影部分面积“拓展型”专项练习』4.图中圆的周长是25.12厘米,空白部分是一个正方形,阴影部分的面积是多少平方厘米?25.12÷3.14÷2 =8÷2=4(厘米)3.14×42-4×4÷2×4 =3.14×16-16÷2×4 =50.24-8×4=50.24-32=18.24(平方厘米)答:阴影部分的面积是18.24平方厘米。
5.求阴影部分的面积。
2×2-14×3.14×22=4-14×4×3.14=4-3.14=0.86(平方厘米)4×2÷2-0.86 =4-0.86=3.14(平方厘米)答:阴影部分的面积是3.14平方厘米。
小升初数学典型奥数题『阴影部分面积“拓展型”专项练习』6.计算如图中阴影部分的面积。
6×6+4×4-(6-4+6)×6÷2-3.14×42×1/4 =36+16-8×6÷2-50.24×1/4=36+16-8×6÷2-12.56=36+16-48÷2-12.56=36+16-24-12.56=52-24-12.56=28-12.56=15.44(cm2)答:阴影部分的面积是15.44cm2。
小升初必考面积试题及答案

小升初必考面积试题及答案一、选择题1. 下列哪个图形的面积是最大的?A. 边长为5厘米的正方形B. 长为6厘米,宽为4厘米的长方形C. 半径为3厘米的圆答案:C2. 一个长方形的长是10厘米,宽是5厘米,它的面积是多少平方厘米?A. 50B. 60C. 70答案:A3. 如果一个正方形的面积是64平方厘米,那么它的边长是多少厘米?A. 8B. 16C. 32答案:A二、填空题4. 一个长方形的长是12厘米,宽是长的一半,那么这个长方形的面积是________平方厘米。
(答案:72)5. 一个圆的直径是14厘米,那么它的半径是________厘米,面积是________平方厘米。
(答案:7;153.94)三、计算题6. 一个梯形的上底是8厘米,下底是14厘米,高是6厘米,求这个梯形的面积。
解:梯形面积 = (上底 + 下底)× 高÷ 2= (8 + 14) × 6 ÷ 2= 22 × 6 ÷ 2= 132 ÷ 2= 66(平方厘米)答案:66平方厘米7. 一个三角形的底是10厘米,高是6厘米,求这个三角形的面积。
解:三角形面积 = 底× 高÷ 2= 10 × 6 ÷ 2= 60 ÷ 2= 30(平方厘米)答案:30平方厘米四、应用题8. 小明家有一个长方形的菜园,长是20米,宽是15米。
如果每平方米的菜地可以种植5棵蔬菜,那么这个菜园一共可以种植多少棵蔬菜?解:首先计算菜园的面积,然后乘以每平方米可以种植的蔬菜数量。
菜园面积 = 长× 宽= 20米× 15米= 300平方米可以种植的蔬菜总数 = 菜园面积× 每平方米的蔬菜数量= 300平方米× 5棵/平方米= 1500棵答案:这个菜园一共可以种植1500棵蔬菜。
9. 一个圆形花坛的周长是31.4米,求这个花坛的面积。
2023年小升初经典图形面积计算汇总

图形面积计算汇总1、如图,由大、小两个正方形组成的图形中,小正方形的边长是6厘米,求图中阴影部分的面积是多少平方厘米?2、正方形的边长分别是10厘米、6厘米,求阴影部分的面积。
3、两条对角线把梯形ABCD分割成四个三角形。
已知两个三角形的面积(如图所示),求梯形ABCD的面积是多少?(单位:平方厘米)4、如下图,图中BO=2DO,阴影部分的面积是4平方厘米,求梯形ABCD的面积是多少平方厘米?5、四边形ABCD中,M为AB的中点,N为CD的中点,假如四边形ABCD的面积是80平方厘米,求阴影部分BNDM的面积是多少?6、在右图中,三角形EDF的面积比三角形ABE的面积大75平方厘米,已知正方形ABCD的边长为15厘米,DF的长是多少厘米?7、如右图,四边形ABCD和四边形CEFG都是正方形,EF长20厘米。
求图中阴影部分的面积。
8、如图,长方形面积为35平方厘米,左边直角三角形的面积为5平方厘米,右上角直角三角形面积为7平方厘米,那么中间三角形(阴影部分)面积是多少平方厘米。
9、在正方形ABCD中,AB长4厘米,△BCF比△DEF的面积多2平方厘米,求DE的长。
10、图中是两个完全相同的直角三角形叠在一起,求阴影面积。
(单位:分米)11、如右图,ABCD是长8厘米、宽6厘米的长方形,AF的长是4厘米,求阴影部分△AEF的面积。
12、求图中阴影部分的面积。
13、ABCD是直角梯形,AB=20厘米,求梯形的面积?14、如图长方形ABCD的边AD=8cm,AB=6cm,E为AD中点,对角线AC、BD相交于O点。
BE、CE分别交两对角线于F、G点,△ABF的面积为8cm2,求阴影部分EFOG的面积。
15、已知长方形的长是10厘米,宽是8厘米,四边形EFGH 的面积是3平方厘米,求阴影部分的面积?16、如左下图所示,三角形ABC 的面积是10厘米2,将CA ,AB ,BC 分别延长1倍,2倍,3倍到F ,D ,E ,两两连结D ,E ,F ,得到一个新的三角形DEF 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
面积计算部分典型题总结
1.填空(每小题2分,共4分)
1.如右图,AB 平行于CD ,图中甲和图形乙的一组对边分别平行,它们的面积相比较,乙 甲。
(填“>”“=”或“<”)
2. 把长、宽分别为9厘米、6厘米的长方形划分为如图的4个三角形,其中的面积关系有4321s s s s +==,则3s = 平分厘米。
2.操作、应用(10分)
1. 如图,等腰直角三角形的一腰的长是8厘米,以它的两腰为直径分别画了两个半圆,那么阴影部分的面积共有多少平方厘米?(π取3.14)
3.求图形面积(6分)
1. 如图,已知边长为8的正方形ABCD ,E 为AD 的中点,P 为CE 的中点,求△BDP 的面积。
4.求阴影部分的面积(共12分)
(1)右图是由两个平行的四边形组成的,求阴影部分面积。
(6分)
(2)求阴影部分的面积(6分)
甲 乙
5.计算(共29分)
1. 右图中阴影部分占长方形的()()。
(2分) 2. 右图是圆柱沿一平面切掉一块后剩余部分,请计算它的体积。
(5分)
6.我有办法(每小题4分,共8分) 1.用四个一样的长方形拼成下图,一个长方形面积是864平方米,长比宽多12米,求长方形的长和宽。
2.求下面阴影部分的面积。
7.计算
1.右图平行四边形的高是6厘米,它的面积是( )平方厘米(3分)
A.35
B.42
C.30
D.36
2.一个长5厘米,宽2.4厘米的长方形,沿对角线对折后,得到如右图所示的几何图形,阴影部分
的周长是 厘米(3分)
3.在右图中,平行四边形的面积是20平方厘米,图中甲、乙、丙三个三角形的面积比是 (3分)
4.综合应用(每小题5分,共10分)
(1)阅读理解:“数学小知识”
“勾股定理”是指一个直角三角形中,两条直角边的平方和等于斜边的平方。
例如:两条直角边的长分别为3、4,则2
22543=+,即斜边的长为5。
已知图中两条直角边的长度,求图中以斜边为直角所作圆的面积。
(2)如右图,已知长方形ABCD 的面积是88平方厘米,E 和F 分别是长和宽的中点。
①画出长方形ABCD 的所有对称轴。
②求出阴影部分的面积。
8.解答题(每小题5分,共10分)
1.下图中三个圆的半径都是2厘米,求阴影部分的面积共是多少厘米?(π去3.14)
2.如右图,甲三角形比乙三角形的面积大6平方厘米,求DE 的长。
1.已知如图,O 为边长为1的正方形ABCD 的对角线BD 中点,
那么直角三角形OPQ 与正方形重叠部分(阴影)面积为 。
(3分)
2.梯形ABCD 的面积是20,E 点在BC 上,三角形ADE 的面积是三角形ABE 面积的2倍,BE 长为2,EC 长为5,则三角形DEC 面积为( )(2分) A.1118 B. 1119 C. 1219 D. 12
18
10.
1.图中梯形ABCD 的高为6厘米,下底AB=10厘米,则阴影面积为 平方厘米(6分)
2.如图,半圆直角AB=4厘米,以A 为中心把半圆沿逆时针方向旋转45°,B 点移至C ,求阴影面积。
(8分)
1.如图,有一只狗被缚在一建筑物的墙角上,这个建筑物是边长都等于6米的等边三角形,绳长是8米,求绳被狗拉紧时,狗运动后所围成的总面积为 (结果保留π)(3分)
2.下图是一块长方形铁皮(每个方格的边长表示1分米),剪下图中的涂色部分可以围成一个圆柱,
这个圆柱的体积是多少?(结果保留π)(5分)
11.
1.如图阴影面积为 (3分)
12.
1.如图,在正方形ABCD 中,阴影部分的面积是三角形BEF 面积的2倍,阴影部分的面积是8.则此
正方形ABCD 的面积是多少?(5分)
13.
1.如图,大小两个长方形的重合部分的面积是1S ,去除重合部分,两个长方形中的剩余部分的面积
分别是2S 和3S 。
求2S 比3S 大多少平方厘米。
(5分)
14.
1.如图,已知大圆半径小于小圆直径,4个小圆面积相同,大圆周长为12厘米,那么阴影部分的
周长为 厘米。
(3分)
1. 如图,已知大圆半径小于小圆直径,4个小圆面积相同,每个小圆的面积是7平方厘米,阴影部
分的面积和为平方厘米。
(3分)
16.
1.某块大标语牌上面画如下图所示的三种标点符号:句号、逗号、问号。
已知大圆半径为R,小圆半
径为r,且R=2r,现在分别给这些标点符号涂上油漆,若均匀用料,则标点符号的油漆用的最多。
(3分)
2.如图所示,在三角形ABC中,DC=3BD,DE=EA,若三角形ABC的面积是1,则阴影部分的面积
是多少?(10分)
17.
1.如下图,一块长方形的布料ABCD,被剪成面积相等的甲、乙、丙、丁四块,其中甲块布料的长与宽的比为a:b=3:2,那么丁块布料的长与宽的比是(3分)
18.
1.如图,已知正方形ABCD和三角形ABE有一部分重叠,阴影部分的三角形乙比三角形甲面积大7平方厘米,则x= 厘米。
(3分)
1.如图,OA、OB分别是小半圆的直径,且OA=OB=6厘米,∠BOA为直角,阴影部分的面积是多少平方厘米?。
