控制工程试卷(合工大)
合肥工业大学2018年硕士研究生初试专业课笔试试题

合肥工业大学2018年硕士研究生初试专业课笔试试题考试科目名称:电路适用专业:电机与电器、电力系统及其自动化、高电压与绝缘技术、电力电子与电力传动、电工理论与新技术、电气工程(专业学位)。
(考生请注意:答案请写在报考点统一发放的答题纸上,写在试卷上的一律无效) 一、判断(2x10=20分)你认为正确的,请在答题纸上作出如下表格,并在对应的题号下面画“√”,若认为说法不正确则在相应题号下画“×”。
1.1 基尔霍夫定律的适用范围是集总电路。
1.2 多个独立电压源共同作用于一个线性电路时,某一个电阻元件所消耗的功率,可以等于各个独立电压源单独作用该电阻所消耗的功率代数和。
多个独立电流源共同作用于一个线性电路,某一电阻元件所消耗的功率,则不等于各个独立电流源单独作用时该电阻所消耗的功率代数和。
1.3 理想运算放大器的同相输入端和反相输入端之间电压为零,同相输入端和反相输入端流入放大器内部的电流也为零,电路分析中称之为“虚短”和“虚断”。
1.4 换路定则在任何情况下都适用。
1.5 含有互感器的两个线圈串联,其等效电感总大于两个线圈不含互感串联的等效电感。
1.6 若电阻元件伏安特性曲线对称于坐标原点,则电阻元件具有单向性。
接入电路需考虑元件的方向性。
1.7 某非线性元件的电压和电流采用关联参考方向,其伏安特性位于u i -平面的第一象限。
其静态电阻和动态电阻都是正值。
1.8 正弦交流的频率越高,则电容元件在电路中的阻抗就越大。
1.9 压控型非线性电阻的伏安特性为保证其为单值函数,应写成()i g u =。
1.10用两表法测量三相电路的总功率时,也适用于不对称的三线制三相电路。
二、基本计算(每题9分,共99分)2.1电路和参数如图1所示,试求电流源和受控源的吸收功率。
2.2 试用戴维宁定理求图2所示电路中的电流i 。
2.3 图3所示电路中,电阻R 可调节,试求R 为何值时可获得最大功率,并求此最大功率。
合肥工业大学硕士研究生初试自动控制原理试题及答案

六.(20分)略
七.(18分)
(9分)
(9分)
语文课本中的文章都是精选的比较优秀的文章,还有不少名家名篇。如果有选择循序渐进地让学生背诵一些优秀篇目、精彩段落,对提高学生的水平会大有裨益。现在,不少语文教师在分析课文时,把文章解体的支离破碎,总在文章的技巧方面下功夫。结果教师费劲,学生头疼。分析完之后,学生收效甚微,没过几天便忘的一干二净。造成这种事倍功半的尴尬局面的关键就是对文章读的不熟。常言道“书读百遍,其义自见”,如果有目的、有计划地引导学生反复阅读课文,或细读、默读、跳读,或听读、范读、轮读、分角色朗读,学生便可以在读中自然领悟文章的思想内容和写作技巧,可以在读中自然加强语感,增强语言的感受力。久而久之,这种思想内容、写作技巧和语感就会自然渗透到学生的语言意识之中,就会在写作中自觉不自觉地加以运用、创造和发展。
八.(15分)
与当今“教师”一称最接近的“老师”概念,最早也要追溯至宋元时期。金代元好问《示侄孙伯安》诗云:“伯安入小学,颖悟非凡貌,属句有夙性,说字惊老师。”于是看,宋元时期小学教师被称为“老师”有案可稽。清代称主考官也为“老师”,而一般学堂里的先生则称为“教师”或“教习”。可见,“教师”一说是比较晚的事了。如今体会,“教师”的含义比之“老师”一说,具有资历和学识程度上较低一些的差别。辛亥革命后,教师与其他官员一样依法令任命,故又称“教师”为“教员”。
合肥工业大学2019年硕士研究生初试专业课笔试试题参考答案和评分标准系统仿真、系统预测或预报。
2.保持不变
3.(3)2 (4)1 (5)10
4.(6) (7)
5.左
6.(9)减小 (10)增加
7.
8.幅频高频衰减特性
9.
10.
最新合工大《单片机与接口技术》试卷A及标准答案

合工大《单片机与接口技术》试卷A评分标准和标准答案一、【20分】简答题(每小题2分)1、微处理器如何定义?微处理器是一个独立的IC芯片,内含算术运算和逻辑运算部件(ALU),不含存储器、I/O接口等,只能接受机器语言。
2、单片机如何定义?在一块IC芯片上集成了微处理器(μP)、存储器(RAM、ROM)、I/O 接口、定时/计数器、中断系统、系统时钟,以及系统总线等的微型计算机。
3、什么叫微机接口?采用硬件与软件相结合的方法,研究CPU如何与外设进行最佳匹配,从而在CPU与外设之间实现高效、可靠的信息交换。
通俗地说,所谓“接口”就是CPU与外设的连接电路,是CPU与外设交换信息的中转站。
4、51单片机串行发送和串行接收各用什么指令?串行发送:MOV SBUF, #XXH;串行接收:MOV A, SBUF。
5、晶振频率、振荡周期、机器周期三者之间是什么关系?晶振频率即外接晶体振荡器的标称频率,也叫振荡频率,它与振荡周期互为倒数关系;一个机器周期包含12个振荡周期。
6、MOVX指令用在哪些场合?(1)CPU与外部RAM之间交换数据;(2)CPU与外部I/O之间交换数据。
7、用哪条指令可将P1口高四位同时取反,低四位不变?XRL P1,#1111 0000B8、三总线包括哪三种?地址总线、数据总线、控制总线。
9、USB接口全称叫什么?通用串行总线。
10、T0、T1计数时,对外部输入的脉冲信号有什么要求?(1)计数脉冲最高频率不超过系统振荡频率的1/24;(2)计数脉冲下降沿有效,高、低电平持续时间均要大于1个机器周期。
二、【14分】分析题1、CPU为AT89S52,已知(PSW)= 0000 1000 B,分析以下各组指令的运行结果(每小题2分):(1)MOV R0,#90H ; (R0)<== 90H,即(08H)= 90HMOV @R0,#90H ;((R0))<==90H,即RAM(90H)=90H(2)MOV R0,#90H ; (R0)<== 90H,即(08H)= 90HMOV @R0,90H ;((R0))<==(90H),即RAM(90H)=SFR(90H)2、已知程序执行前:(A)=04H,(SP)=42H,(41H)=7CH,(42H)=7DH。
合肥工业大学试卷参考答案B卷

=
1 2π
π −π
X
2
(e
jω
)dω
所以
∫ ∫ ∫ 1
2π
π −π
X1 (e
jω
)X 2 (e
jω
)dω
=
{21π
π −π
X1 (e
jω
)dω}{21π
π −π
X
2 (e
jω
)dω}
第4页共4页
x(n) =
x(t) t =nTs
=
x(nTs ) =
x⎜⎜⎝⎛
n fs
⎟⎟⎠⎞
=
3
cos⎜⎜⎝⎛
2π
⎜⎛ ⎝
1 5
⎟⎞n ⎠
⎟⎟⎠⎞
+
5
sin⎜⎜⎝⎛
2π
⎜⎛ ⎝
3 5
⎟⎞n ⎠
⎟⎟⎠⎞
+
10
cos⎜⎜⎝⎛
2π
⎜⎛ ⎝
6 5
⎟⎞n ⎠
⎟⎟⎠⎞
=
3
cos⎜⎜⎝⎛
2π
⎜⎛ ⎝
1 5
⎟⎞n ⎠
⎟⎟⎠⎞
−
2π
⎜⎛ ⎝
1 5
⎟⎞n ⎠
⎟⎟⎠⎞
−
5 sin ⎜⎜⎝⎛
2π
⎜⎛ ⎝
2 5
⎟⎞n ⎠
⎟⎟⎠⎞
2. 设 x(n)的傅里叶变换为 X(ejω),试利用 X(ejω)表示下列序列的傅里叶变换:
(1) x1(n) = x(1 − n) + x(−1 − n) (2) x(n) = 1 [x(n) + x∗ (−n)]
一. 计算题(共 60 分,12 分/题) 1. 设模拟信号 x(t)=3cos2000πt +5sin6000πt +10cos12000πt,求: (1) 该信号的最小采样频率; (2) 若采样频率 fs=5000Hz,其采样后的输出信号; 解:(1)在模拟信号中含有的频率成分是
合工大自动控制理论历年内部试题01

第一章自动控制的一般概念1-1自动控制的基本原理与方式自动控制技术及其应用在现代科学技术的许多领域中,自动控制技术起着越来越重要的作用。
所谓自动控制,是指在没有人直接参与的情况下,利用外加的设备或装置(称控制装置或控制器),使机器、设备或生产过程(统称控制对象)的某个工作状态或参数(即被控量)自动地按照预定的规律运行。
在国民经济各部门中,由于广泛应用了自动控制技术,改善了劳动条件,提高了生产品质和劳动生产率。
近几十年来,随着电子计算机技术的发展和应用,在宇宙航行、导弹制导以及核动力等高新技术领域中,自动控制技术更具有特别重要的作用。
不仅如此,自动控制技术的应用范围现已扩展到生物、医学、环境、经济管理和其他许多社会生活中,自动控制已成为现代社会生活中不可缺少的重要组成部分。
自动控制理论自动控制理论是研究自动控制共同规律的技术科学。
它的发展初期,是以反馈理论为基础的自动调节原理,并主要用于工业控制。
第二次世界大战期间,为了设计和制造飞机及船用自动驾驶仪、火炮定位系统、雷达跟踪系统以及其他基于反馈原理的军用装备,进一步促进并完善了自动控制理论的发展。
到战后,以形成完整的自动控制理论体系,这就是以传递函数为基础的经典控制理论,它主要研究单输入-单输出、线性定常系统的分析和设计。
60年代初期,随着现代应用数学新成果的推出和电子计算机技术的应用,为适应宇航技术的发展,自动控制理论跨入了一个新阶段——现代控制理论。
它主要研究具有高性能、高精度的多变量变参数系统的最优控制问题,采用的方法是以状态为基础的时域法。
目前,自动控制理论还在继续发展,并且已跨越学科界限,正向已控制论、信息论、仿生学为基础的智能控制理论发展。
自动控制的任务任何技术设备、机器和生产过程都必须按要求运行。
例如,要想发电机正常供电,其输出电压必须保持恒定,尽量不受负荷变化的干扰;要想数控机床加工出高精度的零件,其刀架的进给量必须准确地按照程序指令的设定值变化;要想热处理炉提供合格的产品,其炉温必须严格地按规定操纵,等等。
(完整word版)合工大电子信息工程单片机试卷

1.什么是单片机,其特色与主要应用是什么。
答:①中央处理器CPU ,随机存取存储器(数据)RAM ,只读存储器(程序)ROM ,并行接口PIO ,串行接口SIO ,定时器/计数器CTC ,模数转换A/D ,数模转换D/A 等集成在一块芯片中(即:组成微型计算机的各功能部件),构成一个完整的微型计算机。
②特色:集成度高;系统结构简单;可靠性高:军用品,工业品和商用品;处理功能强,速度快;容易产品化。
应用:智能化仪器,通信技术,工业控制,家用电器。
2.MCS —51系列单片机内部存储器可以分为几个不同的区域,各有什么特色。
答:①分为:工作寄存器区,位寻址区,数据缓冲区,特殊功能寄存器区(SFR )。
②工作寄存器区被均匀分成4组,每组包含8个工作寄存器;位寻址区既可以作为一般数据单元使用,也可以按位对每个单元进行操作;数据缓冲区,用户以字节形式使用,开辟有堆栈区;特殊功能寄存器区,为专用寄存器提供。
3.MCS —51系列单片机内部工作寄存器以什么形式形成?分成几个区?如何切换工作寄存器区?答:以RAM 的形式形成;内部工作寄存器均匀地分为0~3,4个区;用PSW 的3D 位和4D 位的编码来切换工作寄存器区。
4.MCS —51系列单片机的地址总线和数据总线形成各有多少条?程序存储器和数据存储器寻址能力是多少节?地址范围是多少?答:16条地址总线,8条数据总线;64K 字节;地址范围:0000H —0FFFFH 。
5.MCS —51系列单片机提供了几个中断源几个中断优先级?每个中断源的入口地址是什么?答:5个中断源;2个中断优先级。
入口地址:外部中断0INT :0003H ,外部中断1INT :0013H ,定时器0CTC :000BH ,定时器1CTC :001BH ,串行口中断SIO :0023H 。
6.什么是时钟周期,机器周期,和指令周期?当晶振周期的频率为12MHz 时,一条双周期指令的执行时间是多少?答:1个机器周期=6个状态周期(时钟周期)=12个振荡周期;1个指令周期=1~4个机器周期。
合工大自动控制理论历年内部试题06

第六章 线性系统的校正通常,控制系统由控制器和受控对象组成,如图6-1所示。
为了满足给定的各项性能指标,可以调整控制器的参数(如放大器增益等)。
如通过调整控制器的参数仍无法满足系统的性能指标要求,就必须在系统中加入一些机构和装置,使整个系统的特性发生变化,从而满足给定的各项性能指标。
6-1 引言所谓校正,就是在系统中加入一些机构和装置,使整个系统的特性发生变化,从而满足给定的各项性能指标。
一:性能指标性能指标通常由使用单位或被控对象的设计制造单位提出,不同的控制系统对性能指标的要求应有不同的侧重。
例如,调速系统对平稳性和稳态精度要求较高,而随动系统则侧重于快速性要求。
性能指标的提出,应符合实际系统的需要与可能。
一般地说,性能指标不应当比完成给定任务所需要的指标更高。
在控制系统的设计中,采用的设计方法一般依据性能指标的形式而定。
如果性能指标以单位阶跃响应的峰值时间、调节时间、超调量、阻尼比、稳态误差等时域特征量给出时,一般采用根轨迹法校正。
如果性能指标以系统的相角裕度、幅值裕度、谐振峰值、闭环带宽、静态误差系数等频域特征量给出时,一般采用频率法校正。
目前,工程技术界多习惯采用频率法,故通常通过近似公式进行两种指标的互换。
1:二阶系统频域指标与时域指标的关系谐振峰值谐振频率带宽频率截止频率相角裕度 超调量调节时间)707.0(1212≤-=ζζζr M )707.0(212≤-=ζζωωn r 42244221ζζζωω+-+-=n b 24241ζζωω--=n c 24241ζζζγ--=arctg %100%21/⨯=--ζπζσe γωζωtg t t s c ns 75.3==2:高阶系统频域指标与时域指标的关系谐振峰值超调量调节时间二:校正的作用在系统设计的初步阶段,总是先选择一些元部件(如执行元件、测量元件、放大元件)构成系统的基本组成部分,它往往不能满足系统的各项性能指标要求。
为此,须引入校正装置,使最后的系统满足要求。
控制工程试卷(合工大)

控制工程试卷(合工大)一、 填空 (8、9、10小题每空2分,其它每空1分,共20分)1.控制系统的基本要求为___稳定性__、 快速性 和 准确性 。
2.系统的相对稳定性可以用___幅值裕量____及____相位裕量___来定量表征。
3.系统稳定与否,只与_系统本身的结构和参数_有关,与__输入__无关。
4.所谓传递函数就是在__零初始__条件下,__系统输出函数与输入函数_拉氏变换之比。
5.系统稳定的充要条件为_系统特征方程的根全部具有负实部(或闭环极点都位于S 平面左半平面);6.二阶系统性能指标中, 超调量p M 只与_阻尼比ξ_有关,因此p M 的大小直接反映了系统的 _ 相对稳定性(或相对平稳性) 性。
7、某最小相位系统的相频特性为101()()90()tg tg T ϕωτωω--=--,开环增益为K ,则该系统的开环传递函数为(1)(1)K S S TS τ++。
8、已知系统的开环NYQUIST 图如下图所示, 则图中相应闭环系统不稳定的是 B 。
系统① 系统② 系统③A 、系统① B 、系统② C 、系统③ D 、都不稳定9、某单位反馈系统的开环传递函数为)2()(2n nk s s s G ξωω+=,则闭环系统的幅频特性 )(ωA 为22222()(2)n n n ωωξωω-+, 相频特性 )(ωϕ为 222arctann n ξωωωω--。
二、计算与分析(共 80 分)1、分析图1所示电路,写出以()r u t 为输入,()c u t 为输出的微分方程及传递函数。
(10分)解:将图1变换成图1-b ,显然有: ()()f I s I s =,即 120()()1(//)C r fU s U s R R R CS-=+化简得传递函数:11212()()()()f f C B rR R CS R U s G S U s R R CS R R+==-++ 进行拉氏反变换即可得以()r u t 为输入,()C u t 为输出的微分方程:12121()()()()()C r C f f r du t du t R R CR R u t R R C R u t dt dt++=--2、已知系统结构如图2所示,试求传递函数C(S)/R(S) 及E(S)/R(S)。
合工大自控考研真题试卷

合工大自控考研真题试卷合肥工业大学(简称合工大)的自动控制原理(自控)考研真题试卷通常包含以下几个部分:选择题、填空题、简答题、计算题和论述题。
以下是一份模拟的自控考研真题试卷内容。
合肥工业大学自动控制原理考研真题试卷一、选择题(每题2分,共20分)1. 状态空间表示法中,状态变量的选取是______。
A. 任意的B. 唯一的C. 固定的D. 非线性的2. 在控制系统中,开环传递函数与闭环传递函数的关系是______。
...(此处省略其他选择题)二、填空题(每空1分,共10分)1. 根据奈奎斯特判据,系统稳定性的判断可以通过分析________的频率特性曲线。
2. 控制系统的稳态误差与输入信号的形式有关,对于单位阶跃响应,其稳态误差为________。
...(此处省略其他填空题)三、简答题(每题10分,共20分)1. 简述PID控制器的基本原理及其各参数的作用。
2. 解释什么是系统的超调量和调节时间,并说明它们对系统性能的影响。
四、计算题(每题15分,共30分)1. 给定一个二阶系统的开环传递函数G(s) = K / (s^2 + 2ζωn*s + ωn^2),其中K=1,ζ=0.5,ωn=1,求该系统的单位阶跃响应,并画出其阶跃响应曲线。
2. 对于一个具有纯积分环节的控制系统,其开环传递函数为G(s) =1/s,试求出该系统的稳态误差。
五、论述题(每题15分,共30分)1. 论述现代控制理论中的最优控制方法与传统PID控制方法的异同。
2. 分析在实际工程中,如何根据系统性能要求选择合适的控制器类型。
六、附加题(10分)1. 假设你正在设计一个温度控制系统,试述你将如何考虑并应用控制理论来优化系统性能。
试卷结束语考生请注意,本试卷仅供学习和练习使用,实际考试内容和形式可能有所不同。
请根据合肥工业大学的官方指南和教材进行复习。
请注意,以上内容为模拟试卷示例,实际的合工大自控考研真题试卷内容会有所不同,考生应以官方发布的考试大纲和历年真题为准进行复习。
合肥工业大学机械控制工程B卷
函授站名: 专业年级 层次 学号 学生姓名 成绩
一、简单题(5×6=30分)
1. 机械控制工程的研究对象及任务是什么?
2. 举例说明日常生活中有开环和闭环控制的控制系统的工作原理。
3. 传递函数的定义
4. 用框图表示系统有哪些优点?
5. 控制系统的时域和频域性能指标?
6. 按照校正装置在系统中的接法不同,可以把校正分为哪几类?
二、 计算题(14×5=70分)
1. 下图为简化了的直流发电机组图。
转子恒速转动,R 为电阻,L 为电感,输人是励磁
电压i u ,输出电压O u ,求此系统的传递函数。
2. 系统框图如下图所示,求以N (s )为输入,当Xi (s )=0时,分别以Xo (s )、Y (s )、
B (s )、E (s )为输出的闭环传递函数。
3. 系统框图示于下,当输入信号时,求系统的稳态误差。
4. 系统的负载变化往往是系统的主要干扰,已知系统结构图如下所示,分析N (s ) 对系统稳态误差的影响。
函授站名:专业年级层次学号学生姓名成绩
5.设某非最小相位系统的开环传递函数为试判断该控制
系统的稳定性。
函授站名:专业年级层次学号学生姓名成绩装
订
线
函授站名:专业年级层次学号学生姓名成绩
考生注意:答题内容勿超过装订线左侧装线订。
合工大企业管理试题库

题目内容管理学的研究方法包括()。
管理学是研究管理活动的基本规律和一般方法及其应用的学科,下面哪项不是管理学的自身特点()。
组织是对完成特定使命的人们的系统性安排,关于组织特征的描叙,正确的选项为()。
高层管理者计划工作重点是()。
管理者的首要职能是()管理的二重属性是指()下列有关企业含义正确的表述是( )尽管人们对企业管理的具体职能说法不一,但认识比较一致的三个职能是()()的最大成就是创立了古典经济学理论体系,按照他的思想,劳动分工是人们追求最大经济利益的结果。
()提出以人为中心的管理思想,他的改革实验验证,重视人的作用和尊重人的地位,可以使工厂获得更多的利润。
被誉为科学管理之父的管理学家是()在泰罗的单工序动作研究的基础上,()围绕多工序作业劳动生产率的提高,创造了用于汽车生产的世界上第一条流水生产线。
被后人称为“组织管理之父”的行政组织理论的代表人物是()。
亨利·法约尔把管理看做一组普遍的职能,即()法约尔认为,经营包括六项职能,以下属于经营的六项职能的是()法约尔认为,经营包括六项职能中,最重要的职能是()韦伯在《社会和经济组织的理论》中提出“理想的行政组织体系”,以下哪项不属于“理想的行政组织体系”()亚伯拉罕·马斯洛提出的需要层次理论中,五种需要从低到高排列依次为()非正式组织通过提供()可对正式组织目标的实现起到积极的促进作用管理人员通过一系列基本管理职能来实现组织目标,不属于管理职能范畴的是()“霍桑实验”直接为()做论证。
“经济人”假设又称为“唯利人”假设,其代表人物是()。
下列哪一种人性假设关心员工的高层次需要和个人发展,这是人本理论的一大进步()。
“胡萝卜加大棒”的管理政策是根据()进行管理的方式20世纪50年代,美国心理学家()根据在匹兹堡地区的调查结果提出了“双因素理论”。
美国麻省理工学院心理学教授()1960年在其著作《企业中人的方面》提出了X理论和Y理论所谓目标管理,就是一种程序或者过程,它使组织中的上级和下级一起协商,根据组织的使命和一定时期内组织的总目标,由此决定上、下级的责任和分目标,并把这些目标作为组织经营、评估和奖励每个单位和个人的贡献标准。
合工大自动控制理论 试题

线性系统的时域分析法动态数学模型,是对控制系统进行理论研究的前提。
在确定系统的数学模型后,便可以用几种不同的方法去分析控制系统的动态性能和稳态性能。
在经典控制理论中,常用时域分析法、根轨迹法或频域分析法来分析线性控制系统的性能。
显然,不同的方法有不同的特点和适用范围,但是比较而言,时域分析法是一种直接在时间域中对系统进行分析的方法,具有直观、准确的优点,并且可以提供时间响应的全部信息。
时域分析法是根据系统的微分方程(或传递函数),用拉普拉斯变换直接解出动态方程,并依据过程曲线及表达式分析系统的性能。
3-1线性系统时间响应的性能指标 一:典型初始状态规定系统的初始状态为零状态,即:0)0()0()0(====--- c cc 。
表明在输入加于系统之前,被控量及其各阶导数相对于平衡工作点的增量为零,系统处于相对平衡状态。
二:典型输入信号典型输入信号是众多而复杂的实际输入的近似和抽象,它的选择不仅应使数学运算简单,而且还应便于实验验证。
所谓典型输入信号,是指根据系统常遇到的输入信号形式,在数学描述上加以理想化的一些基本输入函数。
常用的典型输入信号有以下几种:1:单位阶跃函数⎩⎨⎧≤>=0001)(1t t t st L 1)](1[=2:单位斜坡函数⎩⎨⎧≤>=⋅000)(1t t t t t 21)](1[st t L =⋅3:单位加速度函数⎪⎩⎪⎨⎧≤>=⋅00021)(12122t t t t t 321)](121[st t L =⋅ 4:单位脉冲函数⎰∞+∞-=⎩⎨⎧≠=∞=1)(000)(dt t t t t δδ1)]([=t L δ5:正弦函数⎩⎨⎧≤>=⋅000sin )(1sin t t t A t t A ωω 22)](1sin [ωωω+=⋅s t t A L三:典型时间响应初始状态为零的系统,在典型输入信号作用下的输出,称为典型时间响应。
典型时间响应由动态过程和稳态过程两部分组成。
2007年合肥工业大学工业工程专业817生产计划与控制考研试题

合肥工业大学2007年攻读硕士学位研究生入学考试试题考试科目名称:生产计划与控制适用专业:工业工程一、判断题(15分)1.产品流程矩阵表明了流程选择与产品数量种类关系。
√2.按对象原则布置的生产系统具有生产柔性。
×3.MRP处理的是独立需求。
×4.列车时刻表属于作业计划。
√5.甘特图揭示了作业活动之间的顺序关系。
√6.订货生产不会出现存货生产现象。
×7.虚作业的主要作用是表明前后作用之间的逻辑关系。
√8.非增值作业是为维持增值作业所需要的活动。
√9.有什么样的原材料就制造什么样的产品,是输入决定了输出。
×10.加工装配式生产是离散性生产。
√IL基于时间竞争就是不计成本、不顾质量和品种,最快地将产品和服务提交给顾客。
×12.并行工程的主要目标是改善产品的质量。
×13.准时性是组织生产过程的基本要求。
√14.我们通常所说的“某企业年产电冰箱多少台”,是按假定产品来计量的。
√15.产品的包装物不是相关需求。
×二、填空题(15分)1.生产系统(制造业而言)是由段△、转换、产出组成,其中转换子系统是生产系统的核心。
2.对制造业而言,企业的三项基本职能是萱销、生产和购物。
3.新产品开发构思两种动力模式分别是技术推动型和需求拉动型。
4.工艺设计的内容有产品图纸的工艺分析和审查、拟定工作方案、编订工艺规程、工艺装备的设计和制造。
5.生产系统的定位是指比晶逡让类型、H过程类型、和狂圈钮类型的组合。
6.开环的MRP系统由主生产计划(MB)子系统、物料清单维护(BOM)子系统、库存管理(IM)系统及物料需求计划编制子系统构成07.大量流水生产的主要期量标准有苴也、流水线工作指示图表、在制品定额。
8.累计编号法是编制嵋生产车间作业计划的常用方法。
9.生产调度常用的工具是工>、加工路线单、调度板。
10.存货生产是按预测市场需求来组织生产:订货生产是按空来组织生产的。
合肥工业大学控制工程 复试回忆版

控制工程复试回忆版
模电80分
1、共射极放大电路。
课本例题求电压增益、输入电阻、输出电阻第五版康华生例4.4.1
p137
2、运算放大电路仪用放大电路加积分电路。
个人觉得这个题目比较棘手。
3、反馈放大电路判断反馈类型。
对输入输出电阻的影响以及深度负反馈下的电压增益
数电部分:
1、74ls138 和151数据选择器
2、同步时序电路图。
写驱动方程、状态方程,输出方程。
画状态转换图、说明电路功能,能否自启动
3、161计数器。
十二进制。
用置零法。
微机原理:70分
总体感觉比较简单
一、判断题:都是8086的基本知识,包括数制。
20分
二、简答题:关于堆栈、寻址看过一遍书之后基本都能回答。
三、程序体:1 NEG AX
NEG DX
SBB DX ,0
问程序运行后AX DX 的值程序的功能大概是这样。
6分
2 考的是test 80H ,jnz 的功能
3、写一段简单的程序:检测一个端口某位的状态(0、1),是1就输出。
大概是这样子。
类似8255的程序
四:8255,A口接七个开光,B口接LED 。
画图,cp3什么条件下发出中断请求。
基本上就是这样。
难度不是很大。
好好复习,九十分还是比较轻松的。
合肥工业大学 自动化考研真题
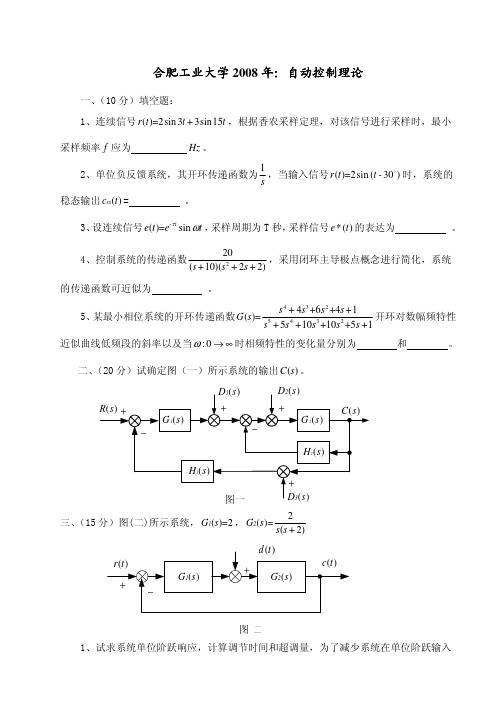
1 s +1 +
4 s ( s + 2)
c(t )
四、 (16 分)设单位负反馈系统的开环传递函数 G ( s )=
K * (1-s ) s (as +2)
1)a = 1 时,绘制 K * : 0 → ∞ 变化时的闭环根轨迹,求系统产生重根和纯虚根的 K * 值。
2) K * =1 时,绘制 a : 0 → ∞ 变化时的闭环根轨迹。
Gc ( s )=
0.05s + 1 ,试画出校正前、后开环系统对数幅频特性曲线渐近线,计算校正前、后 0.002 s + 1 系统的稳定裕量。
七、 (16 分)已知系统结构如图所示,K>0,T=1 秒。 1)求系统的开环脉冲传递函数和闭环脉冲传递函数; 2)求系统稳定时 K 的取值范围。
r (t )
-1
1
0 1
m(t )
-1
−
1 s2
c (t )
1 0 1 ɺ= 九、 (20 分)设系统动态方程为: x x + u 0 0 1 1)求系统的传递函数 G ( s ) ; 2)欲利用状态反馈使 G ( s ) =
y = [ 2 −1] x
1 ,求反馈矩阵 K,并画出系统的动态结构图。 s +1 3)设观测器的极点为-10,设计全维状态观测器,写出观测器的动态方程。 ɺ = A(t ) x 的状态转移矩阵,求证 十、 (8 分)已知 φ (t ,τ ) 是 x d φ (t ,τ ) = −φ (t ,τ ) A(τ ) 。 dτ
m(t )
−
1 s2
c (t )
1+ s
.
7、已经系统的微分方程为: y+ 3 y+ 2 y = 2 u + u ,求传递函数;并求其能控标准形、 能观标准形、对角形动态方程。
合肥工业大学机械复试控制工程题目
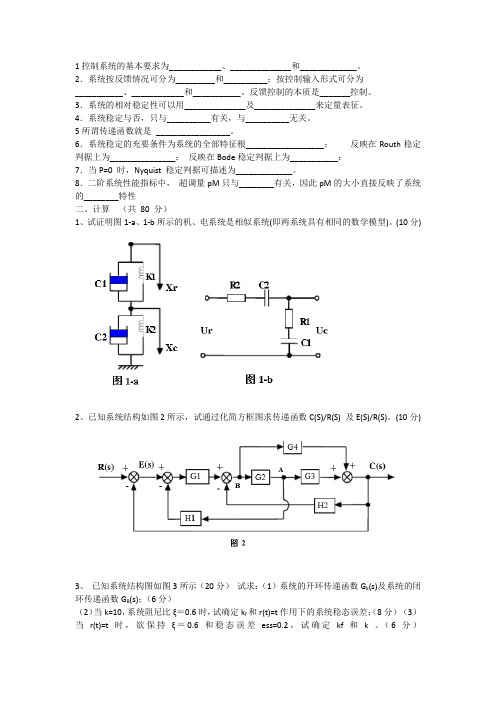
1控制系统的基本要求为____________、______________和_____________。
2.系统按反馈情况可分为_________和__________;按控制输入形式可分为___________、____________和___________。
反馈控制的本质是_______控制。
3.系统的相对稳定性可以用______________及______________来定量表征。
4.系统稳定与否,只与__________有关,与__________无关。
5所谓传递函数就是_________________。
6.系统稳定的充要条件为系统的全部特征根__________________;反映在Routh稳定判据上为_______________;反映在Bode稳定判据上为___________;7.当P=0 时,Nyquist 稳定判据可描述为_____________。
8.二阶系统性能指标中,超调量pM只与________有关,因此pM的大小直接反映了系统的________特性二、计算(共80 分)1、试证明图1-a、1-b所示的机、电系统是相似系统(即两系统具有相同的数学模型)。
(10分)2、已知系统结构如图2所示,试通过化简方框图求传递函数C(S)/R(S) 及E(S)/R(S)。
(10分)3、已知系统结构图如图3所示(20分)试求:(1)系统的开环传递函数G k(s)及系统的闭环传递函数G B(s);(6分)(2)当k=10,系统阻尼比ξ=0.6时,试确定k f和r(t)=t作用下的系统稳态误差;(8分)(3)当r(t)=t时,欲保持ξ=0.6和稳态误差ess=0.2,试确定kf 和k 。
(6分)4、由质量、弹簧、阻尼组成的机械系统如图4所示,已知m=1kg,k为弹簧刚度,c为阻尼系数。
若外力 f (t)=2sin2tN, 由实验得到系统稳态响应为sin(2)2。
试确定k和c。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、 填空 (8、9、10小题每空2分,其它每空1分,共20分)1.控制系统的基本要求为___稳定性__、 快速性 和 准确性 。
2.系统的相对稳定性可以用___幅值裕量____及____相位裕量___来定量表征。
3. 系统稳定与否,只与_系统本身的结构和参数_有关,与__输入__无关。
4.所谓传递函数就是在__零初始__条件下,__系统输出函数与输入函数_拉氏变换之比。
5.系统稳定的充要条件为_系统特征方程的根全部具有负实部(或闭环极点都位于S 平面左半平面); 6.二阶系统性能指标中, 超调量p M 只与_阻尼比ξ_有关,因此p M 的大小直接反映了系统的 _ 相对稳定性(或相对平稳性) 性。
7、某最小相位系统的相频特性为11()()90()tg tg T ϕωτωω--=--,开环增益为K ,则该系统的开环传递函数为(1)(1)K S S TS τ++。
8、已知系统的开环NYQUIST 图如下图所示, 则图中相应闭环系统不稳定的是 B 。
系统① 系统② 系统③A 、 系统①B 、系统②C 、系统③D 、都不稳定9、某单位反馈系统的开环传递函数为)2()(2n nk s s s G ξωω+=,则闭环系统的幅频特性 )(ωA 为2, 相频特性 )(ωϕ为222arctann n ξωωωω--。
二、计算与分析(共 80 分)1、分析图1所示电路,写出以()r u t 为输入,()c u t 为输出的微分方程及传递函数。
(10分)解:将图1变换成图1-b ,显然有:()()f I s I s=, 即120()()1(//)C r fU s U s R R R CS-=+化简得传递函数:11212()()()()f f C B r R R CS R U s G S U s R R CS R R +==-++ 进行拉氏反变换即可得以()r u t 为输入,()C u t 为输出的微分方程:12121()()()()()C r C f f r du t du t R R CR R u t R R C R u t dt dt++=--2、已知系统结构如图2所示,试求传递函数C(S)/R(S) 及E(S)/R(S)。
(12分) (提示:化简到只剩一个反馈回路再求E(S)/R(S) )解:化简图2(A 右移到`再化简图2-a ,得:计算与分析题图2计算与分析题图1 图1-b)(s 图 2-a继续化简得:根据图2-d 可得:2221()1(2)1()311(2)C s RCS RCS RCS R s R C S RCS RCS RCS +==+++++222()1(2)1()311(2)E s RCS RCS RCS R s R C S RCS RCS RCS +==+++++用其它方法及梅逊公式也可。
3、已知某二阶系统的单位阶跃响应曲线如下图3所示,求此二阶系统的传递函数。
(6分)解: 由图可知得因为稳态值为2,所以4、 已知系统结构图如图4所示, 试求:(共18分) (1)系统的开环传递函数()k G s 及偏差传递函数()()E s R s ;(6分); (2)当k=10,系统阻尼比ξ=0.6时,试确定k f 和()r t t =作用下的系统稳态误差;(6分) (3)当()r t t =时,欲保持ξ=0.6和 稳态误差e ss =0.2,试确定k f 和k 。
(6分)(1)由结构图直接可得:212(2)()11(2)1(1)(2)2f K f f f k k k S S G S k S k S k S S S S S k ++=⨯==+++⨯+++ 22(2)()11()1()(2)1(2)f K f f S S k E s kR s G s S k S kS k S++===+++++++(2)222222(2)()(2)21(2)f n B f n nf kS k S kG S k S k S k S S S k Sωξωω++===++++++++计算与分析题图4 计算与分析题图3图 2-b图 2-c图 2-d2.182100%9%20.8p p M et ξπ-⋅-⎧=⨯==⎪⎪⎨⎪==⎪⎩0.614.96nξω=⎧⎨=⎩222224.6()22 6.0524.6n n n G s k S S S S ωξωω=⋅=⋅++++对比二阶系统的传递函数标准形式有:22222n f n fkk k ωξω⎧=⎪⇒=⎨=+⎪⎩ 代入 10,0.6k ξ==后得: 1.795f k = 又由终值定理知系统稳态误差:2(2)lim ()lim ()lim ()(2)f ss t s s f S S k e e t S E S S R S S k S k→∞→→++==⋅=⋅⋅+++22(2)212 1.795lim 0.379(2)10f f s f S S k k S S S k S k k →++++=⋅⋅===+++ 也可以根据开环传递函数的型次为I 型及输入信号类型为单位斜坡t 可知ss e =212 1.7950.379102f f k k k k ++====+ (3)参考前面两解答过程有:222f fss k k e k ⎧=⎪⎨+=⎪⎩代入 0.6,0.2ss e ξ== 计算得: 365.2fk k =⎧⎨=⎩5、设某控制系统方框图如图5所示。
(12)(1) 试确定使系统稳定的K 值范围。
(8分)(2) 若使系统特征方程的根均位于S=-1垂线左侧,试确定K 值范围。
(4分)解:(1)系统闭环传递函数为:324040(0.11)(0.252)(10)(8)()4018804011(0.11)(0.252)(10)(8)B K Kk S S S S S S G S K K S S S k S S S S S S ++++===+++++++++ 闭环系统特征方程:D(S)=321880400S S S k +++=列劳斯表:3S 1 802S1840k1S 18804018k⨯-0S40k要使系统稳定,则第一列元素全为正值,即 144040018400kk -⎧>⎪⎨⎪>⎩ 解得使系统稳定的p k 值范围: 036k <<(2)在闭环系统特征方程中,令 1S Z =-, 则有:3232D(Z)=(1)18(1)80(1)400154740630Z Z Z k Z Z Z k -+-+-+=⇒+++-=列劳斯表: 3Z 1 47 2Z154063k -1Z 1547(4063)15k ⨯--0Z4063k -令第一列值全为正: 7684001.57519.240630k k k ->⎧⇒<<⎨->⎩6、 最小相位系统的开环对数幅频特性曲线()L ω如图6所示:(22分)(提示:先用符号代替进行化简,最后代入具体值进行计算)(1) 分析并写出该系统的开环传递函数)(s G k ;(6分)(2) 作开环传递函数的Nyquist 图,并在Nyquist 图上表示出相位裕度及幅值裕度; (6分) (3) 计算系统的相位裕度γ及幅值裕度()g K dB ;。
(8)计算与分析题图5(4) 若系统稳定裕度不足,试分析提高系统稳定裕度的方法与措施?(2分)解:(1)从开环对数幅频特性曲线()L ω可知,系统由一个比例环节、一个积分环节、两个惯性环节组成。
开环传递函数形式 12()(1)(1)K KG s s T s T s =++由图可知:1ω=处的纵坐标为40dB, 则(1)20lg 40L K ==, 得100K = 由图可知:1210T T ωω=和=100 所以 1212110.10.01T T T T ωω== ==故系统的开环传递函数为 ()()101.011.0100)(++=S S s s G K(2)开环频率特性 ()()()()12100()110.110.011K K G j j j T j T j j j ωωωωωωω==++++幅频特性()A ω==相频特性:12()90arctan arctan 90arctan0.1arctan0.01T T ϕωωωωω=---=---实频特性:虚频特性:实频低频渐近线令()0v ω= 可得 g ω=,代入()u ω,可得1110()0.9111 1.111g u ω=-=-≈-⨯ 0,ω→ (),A ω=∞ 0()90ϕω=- ,ω→∞ ()0,A ω= 0()270ϕω=-作出的开环Nyquist 图如右图所示。
标出的稳定裕量(相位裕量r 及幅值裕量gK )如 Nyquist 图中所示。
(3) 计算相位裕量r :由开环对数幅频特性曲线()L ω可得:204010cc lgωω=⇒=9001001900180()arctan .arctan .=-arctan .c c c οϕωωω=---︒=-︒相位裕量 1801801800()c r οοϕω=+=︒-︒=由于对数幅频特性图中画的曲线是渐近线,所以c ω的计算存在一定的误差,实际的剪切频率比计算的c ω要小,实际相位裕量比0ο大。
计算幅值裕量g K (dB):令 οοοωωωω9001.0arctan 1.0arctan 18001.0arctan 1.0arctan 90=+⇒-=---g g g g 1010001.0101.01.0arctan 2=⇒+∞=-+⇒g ggg ωωωω 故幅值裕量()20lg ()g g K dB A ω=--===-20lg0.83(dB)计算与分析题图62212m 2222221210.1100()I [()](1)(1)(10.01)(10.0001)k TT v G j K T T ωωωωωωωωω--==⋅=++++0lim ()11u ωω→=-1222222212()11()[()](1)(1)(10.01)(10.0001)e k K T T u R G j T T ωωωωωω+-==-=++++(或求出() 1.1g g A K ω===⇒=0.91)(4)适当降低开环增益K ,可使剪切频率c ω减小,相位穿越频率g ω不变, 从而可以提高相位裕量r 与幅值裕量g K (dB),总体上提高了稳定裕度。
