全等三角形常见的几何模型精编版

合集下载

全等三角形的10个模型(一)2024

全等三角形的10个模型（一）引言概述：全等三角形是指两个或多个三角形的对应边和对应角完全相等的情况。

全等三角形在几何学中有广泛的应用，不仅在证明和推导定理时起到重要的作用，还在实际问题的解决中提供了有力的工具。

本文将介绍十个关于全等三角形的模型。

这些模型旨在帮助读者更好地理解和运用全等三角形的性质和应用。

正文：1. 模型一：完全相等的三边- 全等三角形的基本条件就是三边相等。

- 通过边的对应关系确定两个三角形是否全等。

- 证明时可利用边长相等的性质进行推导。

2. 模型二：完全相等的两边和夹角- 如果已知两个三角形的两边和夹角都相等，则这两个三角形全等。

- 通过边角边（SAS）或角边角（ASA）的条件可以判定两个三角形相等。

3. 模型三：完全相等的两角和夹边- 如果已知两个三角形的两角和夹边都相等，则这两个三角形全等。

- 边角边（SAS）或角边角（ASA）的条件可以判定两个三角形相等。

4. 模型四：等腰三角形和全等条件- 等腰三角形是指两边相等或两角相等的三角形。

- 如果两个三角形中有一个是等腰三角形，且两个等腰三角形的两边或两角都相等，则这两个三角形全等。

5. 模型五：直角三角形和全等条件- 直角三角形是指其中一个角为90度的三角形。

- 如果两个三角形中有一个是直角三角形，且两个直角三角形的两边或两个锐角均相等，则这两个三角形全等。

总结：通过十个模型的介绍，我们可以看到全等三角形是几何学中一个重要而广泛应用的概念。

理解全等三角形的性质和应用对于解决几何问题具有重要意义。

在实际问题中，我们常常可以利用全等三角形的模型来推导和证明定理，从而得出更深入的结论。

全等三角形八大模型归纳

全等三角形八大模型归纳全等三角形是初中数学中重要的概念之一，它是指两个三角形的对应边相等且对应角相等。

全等三角形具有许多性质和特点，可以归纳为八大模型，分别是SSS、SAS、ASA、AAS、HL、LLL、LLA、LAL。

下面将分别介绍这八种模型的特点和应用。

第一种模型是SSS，即三边全等。

当两个三角形的三条边分别相等时，这两个三角形就是全等的。

这种模型在实际生活中的应用非常广泛，比如在建筑、工程设计中，需要测量房屋的各个边长是否相等，以确保建筑物的稳定性和均衡性。

第二种模型是SAS，即两边夹角边全等。

当两个三角形的两边和夹角分别相等时，这两个三角形就是全等的。

这种模型常常用于证明两个三角形全等的情况，可以通过辅助线的引入来简化证明过程。

第三种模型是ASA，即两角边角全等。

当两个三角形的两个角和夹边分别相等时，这两个三角形就是全等的。

这种模型在解题过程中也经常用到，特别是在证明题中，可以根据已知条件找到相等的角和边，从而得出结论。

第四种模型是AAS，即两角边角全等。

当两个三角形的两个角和一边分别相等时，这两个三角形也是全等的。

这种情况在证明过程中比较常见，可以通过找到两个角和一边相等来得出结论。

第五种模型是HL，即斜边和直角边全等。

当两个直角三角形的斜边和一个直角边分别相等时，这两个三角形就是全等的。

这种情况在解决直角三角形的问题时经常用到，可以利用勾股定理和全等三角形的性质来求解。

第六种模型是LLL，即三边全等。

这种模型和SSS模型类似，只不过LLL模型更加具体，强调了三个边全部相等的情况。

在实际问题中，可以通过测量三角形的三边长度来判断两个三角形是否全等。

第七种模型是LLA，即两边和一个角全等。

当两个三角形的两个边和一个非夹角的角相等时，这两个三角形是全等的。

这种情况在解题过程中也会经常遇到，可以通过找到两个边和一个非夹角的角相等来证明两个三角形全等。

第八种模型是LAL，即一边和两个角全等。

当两个三角形的一条边和两个角分别相等时，这两个三角形也是全等的。

完整全等三角形的相关模型总结推荐文档

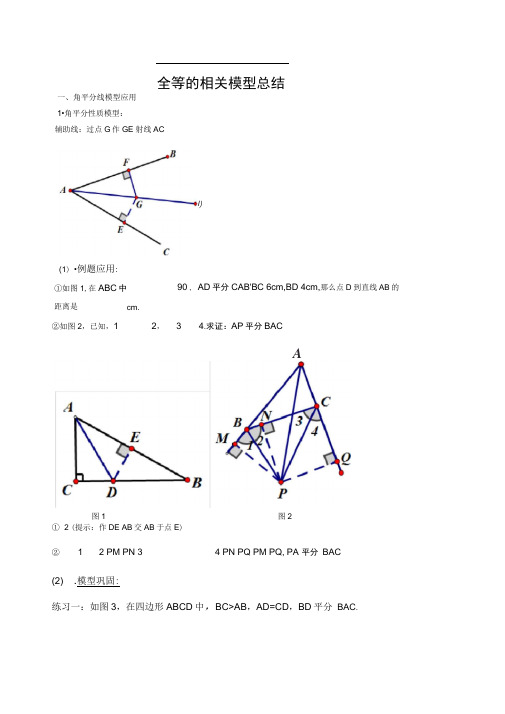
全等的相关模型总结一、角平分线模型应用 1•角平分性质模型：②如图2，已知，1 2， 3 4.求证：AP 平分BACA① 2 (提示：作DE AB 交AB 于点E )②1 2 PM PN 3 4 PN PQ PM PQ, PA 平分 BAC(2) .模型巩固:练习一：如图3，在四边形ABCD 中，BC>AB ，AD=CD ，BD 平分 BAC .①如图1,在ABC 中距离是90°, AD 平分CAB'BC 6cm,BD 4cm,那么点D 到直线AB 的cm.I)(1) •例题应用: 辅助线：过点G 作GE 射线AC图1图2•求证： A C 180练习二：已知如图4,四边形ABCD中，B D 1800,BC CD•求证：AC平分BAD.练习三：如图5 Rt ABC中，ACB 90 , CD AB,垂足为D , AF平分CAB,交CD于点E 交CB于点F.(1)求证：CE=CF.(2)将图5中的△ ADE沿AB向右平移到ADE的位置，使点E落在BC边上，其他条件不变，如图6所示，是猜想：BE于CF又怎样的数量关系？请证明你的结论图5 图6练习四：如图7，/ A 90，AD // BC，P是AB的中点，PD平分/ ADC求证：CP 平分/ DCB图7练习五：如图 8, AB> AC / A 的平分线与 BC 的垂直平分线相交于 D,自D 作DE L AB, DF 丄AC,垂足分别为E , F .求证：BE=CF图8练习六：如图9所示，在△ ABC 中，BC 边的垂直平分线 DF 交厶BAC 的外角平分线 AD 于点D , F 为垂足，DE 丄AB 于E ,并且 AB>AC 。

求证：BE — AC=AE 。

练习七：如图10, D 、E 、F 分别是△ ABC 的三边上的点， CE=BF ，且△ DCE 的面积与厶 DBF 的面积相等，求证：AD 平分/ BAC 。

全等三角形常见模型整理

全等三角形几何模型归纳总结《全等三角形几何模型归纳总结——那些年我们一起追的“全等”》嘿，各位小伙伴们！今天咱来唠唠全等三角形几何模型这档子事。

这可是咱在几何世界里摸爬滚打的一大法宝呀！全等三角形就像是一对双胞胎，长得一模一样，各种特征都完全相符。

咱和它们打交道的过程，那真是有苦有乐啊！就比如说那“手拉手”模型吧，就像是两个好兄弟手牵手一起走。

看到这种模型，咱就得赶紧瞪大眼睛，找到那关键的对应边和对应角，一旦弄清楚了，那解决问题就跟玩似的。

有时候我都感觉自己像是个小侦探，在各种图形里寻找线索呢！还有那个“一线三等角”模型，嘿，这可神奇了！一条线上面整出来三个等角，就像变魔术一样。

刚开始遇到的时候，还真有点摸不着头脑，心里直犯嘀咕：“这是啥玩意呀？”不过随着咱经验的积累，慢慢地也能看穿它的小把戏啦。

有时候碰到那些复杂的图形，感觉就像是掉进了一个大迷宫，找不着北。

但咱可不能气馁，得静下心来仔细分析分析，说不定就能找到那隐藏的全等三角形。

一旦找到了，就像是找到了迷宫的出口，那叫一个痛快！不过，也有犯迷糊的时候。

明明感觉能找到全等三角形，可就是差那么一点点，死活对不上。

这时候就恨不得给自己脑袋上敲两下，让自己清醒清醒。

但咱不能怕失败呀，失败是成功的妈妈嘛，多总结总结经验，下次咱就能一眼看穿啦。

在这个过程中，咱也得学会和小伙伴们一起探讨。

有时候自己一个人苦思冥想半天，还不如小伙伴的一句话点拨呢。

这样大家一起研究，一起进步，多有意思呀！全等三角形几何模型就是咱几何世界里的宝藏，等着咱去挖掘。

虽然有时候会遇到困难，但每次突破难关的时候，那种成就感真是无与伦比。

所以呀，大家可别小瞧了这些模型，好好研究它们，咱就能在几何的海洋里畅游啦！让我们一起加油，把全等三角形几何模型玩得团团转！哈哈！。

数学复习：全等三角形相关模型

数学复习：全等三角形相关模型一、角平分线模型（1）角平分线+两边垂线→全等三角形：角平分线的性质定理：角平分线上的点到角的两边距离相等；已知：AD平分∠BAC，CD⊥AC，垂足为C，过点D作DB⊥AB，垂足为B；辅助线：过点D作DB⊥AB，垂足为B；结论：①△ACD≌△ABD；②CD=DB（角分线垂两边，对称全等必呈现）（2）角平分线+垂线模型等腰三角形必呈现：遇到垂直于角平分线的线段，则延长该线段与角的另一边相交，构成等腰三角形；已知：OP平分∠AOB，MP⊥OP，垂足为P，延长MP交OB于点N；结论：①△OPM≌△OPN；②△OMN为等腰三角形；③P是MN的中点（三线合一）；（3）在角的两边上截取相等的线段，构造全等三角形：已知：OC是∠AOB的角平分线，D为OC上一点；辅助线：在OA上取一点E，在OB取一点F，使得OE=OF，并连接DE，结论：△OED≌△OFD；（4）作平行线①以角分线上一点作角的另一边的平行线，则△OAB 等腰三角形；②过一边上的点作角平分线的平行线与另一边的反向延长线相交，则△ODH 等腰三角形；已知：OP 平分∠MON ，AB ∥ON ，已知：OC 平分∠AOD ，DH ∥OC ，结论：△OAB 等腰三角形结论：△ODH 等腰三角形角平分线+两边垂线→全等三角形辅助线：过点G 作GE ⊥射线AC已知：AD 是∠BAC 的角平分线，CD ⊥AC ，DB ⊥AB ，求证：CD=DB证明：∵AD 是∠BAC 的角平分线，∴∠1=∠2，∵CD ⊥AC ，DB ⊥AB ，∴∠ACD=∠ABD=90°，在△ACD 和△ABD 中，∴△ACD ≌△ABD （AAS ）∴CD=BD⎪⎩⎪⎨⎧AD =AD 90=ABD ∠=ACD ∠2∠=1∠例1：已知：∠1=∠2，∠3=∠4，求证：AP平分∠BAC．例2：如图，AB＞AC，∠A的平分线与BC的垂直平分线相交于D，过D作DE⊥AB、DF⊥AC，垂足分别为E、F．求证：BE=CF．例4：如图，在△ABC中，M为BC的中点，DM⊥BC，DM与∠BAC的角平分线交于点D，DE⊥AB，DF⊥AC，E、F为垂足，求证：BE=CF．角平分线+垂线模型等腰三角形必呈现例1：如图，在Rt△ABC中，AB=AC，∠BAC=90°，∠1=∠2，CE⊥BE交BA的延长于F．求证：BD=2CE例2、如图，在△ABC中，∠BAC的角平分线AD交BC于点D，且AB=AD，作CM⊥AD 交AD的延长线于M.求证：2AM=（AB+AC）例3：如图，已知△ABC中，CF平分∠ACB，且AF⊥CF，∠AFE+∠CAF=180°，求证：EF∥BC.截取构造全等：例1：如图，AB>AC ，∠1=∠2，求证：AB －AC>BD －CD 。

初中数学三角形全等经常使用几何模型及构造方式大全初二

初二数学三角形全等经常使用几何模型及构造方式大全把握它轻松弄定全等题！全等是初中数学中超级重要的内容，一样会在压轴题中进行考察，而把握几何模型能够为考试节省很多时刻，这次整理了经常使用的各大模型，必然要认真把握~全等变换类型：（一）平移全等：平行等线段（平行四边形）（二）对称全等模型：角平分线或垂直或半角1：角平分线模型；2：对称半角模型；（三）旋转全等模型：相邻等线段绕公共极点旋转1. 旋转半角模型2. 自旋转模型3. 共旋转模型4. 中点旋转如图，在△ABC的边上取两点D、E，且BD=CE，求证：AB+AC>AD+AE分析：将△ACE平移使EC与BD重合。

B\D，上方交点，左右两个三角形，两边和大于第三边！1：角平分线模型：说明：以角平分线为轴在角两边进行截长补短或作边的垂线，形成对称全等。

两边进行边或角的等量代换，产生联系。

垂直也能够做为轴进行对称全等。

2：对称半角模型说明：上图依次是45°、30°、45+ 22.5°、对称（翻折）15°+30°直角三角形对称（翻折）30+60+90直角三角形对称（翻折）翻折成正方形或等腰直角三角形、等边三角形、对称全等。

1. 半角：有一个角含1/2角及相邻线段2. 自旋转：有一对相邻等线段，需要构造旋转全等3. 共旋转：有两对相邻等线段，直接寻觅旋转全等（共极点）4. 中点旋转：倍长中点相关线段转换成旋转全等问题（专题七）一、旋转半角模型说明：旋转半角的特点是相邻等线段所成角含一个二分之一角，通过旋转将另外两个和为二分之一的角拼接在一路，成对称全等。

二、自旋转模型构造方式：遇60度旋60度，造等边三角形遇90度旋90度，造等腰直角遇等腰旋极点，造旋转全等遇中点旋180度，造中心对称3、共旋转模型说明：旋转中所成的全等三角形，第三边所成的角是一个常常考察的内容。

通过“8”字模型能够证明。

（接上------共旋转模型）模型变形说明：模型变形要紧是两个正多边形或等腰三角形的夹角的转变，另外是等腰直角三角形与正方形混用。

专题02 全等三角形中的六种模型梳理

专题02 全等三角形中的六种模型梳理一、概述全等三角形是初中数学中一个重要且常见的概念，对于几何学的学习具有重要的意义。

在全等三角形的学习中，有六种基本模型，它们是解决全等三角形问题的重要工具。

本文将对全等三角形中的六种模型进行深入探讨和梳理，帮助读者更加全面地理解和掌握这一知识点。

二、模型一：SSS全等模型在全等三角形中，如果两个三角形的三条边分别相等，则可以确定它们是全等三角形，这就是SSS全等模型。

如果已知两个三角形的三边分别相等，那么这两个三角形一定是全等的。

模型二：SAS全等模型SAS全等模型是指如果两个三角形的一条边和夹角以及另一边的长度分别相等，则可以确定它们是全等三角形。

如果已知两个三角形的一个角和两边分别相等，那么可以确定这两个三角形是全等的。

模型三：ASA全等模型在全等三角形中，如果两个三角形的一个角和两个角边相等，则可以确定它们是全等三角形，这就是ASA全等模型。

如果已知两个三角形的一个角和两个角边分别相等，那么可以确认这两个三角形是全等的。

模型四：HL全等模型HL全等模型是指如果两个直角三角形的斜边和一个直角边的长度分别相等，则可以确定它们是全等三角形。

如果已知两个直角三角形的斜边和一个直角边的长度分别相等，那么可以确定这两个三角形是全等的。

模型五：LL全等模型LL全等模型是指如果两个三角形的两个角和一个边分别相等，则可以确定它们是全等三角形。

如果已知两个三角形的两个角和一个边分别相等，那么可以确定这两个三角形是全等的。

模型六：对顶全等模型对顶全等模型是指如果两个三角形的两个对顶角和一个边分别相等，则可以确定它们是全等三角形。

如果已知两个三角形的两个对顶角和一个边分别相等，那么可以确定这两个三角形是全等的。

三、总结与回顾通过上述对全等三角形中六种模型的梳理，我们可以发现几何学中的相似和全等的概念是非常重要的。

在实际问题中，我们可以通过判断形状的相似或全等，推断出一些未知的信息，帮助我们解决问题。

全等三角形经典模型总结

全等三角形相关模型总结一、角平分线模型(一）角平分线的性质模型辅助线：过点G作GE⊥射线ACA、例题1、如图，在△ABC中，∠C=90°，AD平分∠CAB，BC=6cm，BD=4cm，那么点D到直线AB的距离是cm.2、如图，已知，∠1＝∠2，∠3＝∠4，求证：AP平分∠BAC.B、模型巩固1、如图，在四边形ABCD中，BC＞AB，AD＝CD，BD平分∠ABC，求证：∠A＋∠C＝180°.（二）角平分线＋垂线，等腰三角形必呈现A、例题辅助线：延长ED交射线OB于F 辅助线：过点E作EF∥射线OB 例1、如图，在△ABC中，∠ABC＝3∠C，AD是∠BAC的平分线，BE⊥AD于F .求证：1()2BE AC AB=-.例2、如图，在△ABC中，∠BAC的角平分线AD交BC于点D，且AB＝AD，作CM⊥AD交AD的延长线于M. 求证：1()2AM AB AC=+.（三）角分线，分两边，对称全等要记全两个图形飞辅助线都是在射线ON上取点B，使OB＝OA，从而使△OAC≌△OBC .A、例题1、如图，在△ABC中，∠BAC=60°，∠C=40°，AP平分∠BAC交BC于P，BQ平分∠ABC交AC于Q，求证：AB＋BP＝BQ＋AQ .2、如图，在△ABC中，AD是∠BAC的外角平分线，P是AD上异于点A的任意一点，试比较PB＋PC与AB＋AC的大小，并说明理由.B、模型巩固1、在△ABC中，AB＞AC，AD是∠BAC的平分线，P是线段AD上任意一点（不与A重合）.求证：AB－AC＞PB－PC .2、如图，△ABC中，AB＝AC，∠A＝100°，∠B的平分线交AC于D，求证：AD＋BD＝BC .3、如图，△ABC中，BC＝AC，∠C＝90°，∠A的平分线交BC于D，求证：AC＋CD＝AB .二、等腰直角三角形模型（一）旋转中心为直角顶点，在斜边上任取一点的旋转全等：操作过程：（1）将△ABD逆时针旋转90°，得△ACM ≌△ABD，从而推出△ADM为等腰直角三角形.（2）辅助线作法：过点C作MC⊥BC，使CM＝BD，连结AM.（二）旋转中心为斜边中点，动点在两直角边上滚动的旋转全等：操作过程：连结AD.（1）使BF＝AE（或AF＝CE），导出△BDF ≌△ADE.（2）使∠EDF＋∠BAC＝180°，导出△BDF ≌△ADE.A、例题1、如图，在等腰直角△ABC中，∠BAC＝90°，点M、N在斜边BC上滑动，且∠MAN＝45°，试探究BM、MN、CN之间的数量关系.2、两个全等的含有30°，60°角的直角三角板ADE和ABC，按如图所示放置，E、A、C 三点在一条直线上，连接BD，取BD的中点M，连接ME、MC.试判断△EMC的形状，并证明你的结论.B、模型巩固1、已知，如图所示，Rt△ABC中，AB＝AC，∠BAC＝90°，O为BC中点，若M、N分别在线段AC、AB上移动，且在移动中保持AN＝CM.（1）试判断△OMN的形状，并证明你的结论.（2）当M、N分别在线段AC、AB上移动时，四边形AMON的面积如何变化？2、在正方形ABCD中，BE＝3，EF＝5，DF＝4，求∠BAE＋∠DCF为多少度.（三）构造等腰直角三角形（1）利用以上（一）和（二）都可以构造等腰直角三角形（略）；（2）利用平移、对称和弦图也可以构造等腰直角三角形.（四）将等腰直角三角形补全为正方形，如下图：A、例题应用1、如图，在等腰直角△ABC中，AC＝BC，∠ACB＝90°，P为三角形ABC内部一点，满足PB＝PC，AP＝AC，求证：∠BCP＝15°.三、三垂直模型（弦图模型）A、例题已知：如图所示，在△ABC中，AB＝AC，∠BAC＝90°，D为AC中点，AF⊥BD于点E，交BC于F，连接DF .求证：∠ADB＝∠CDF .变式1、已知：如图所示，在△ABC中，AB＝AC，AM＝CN，AF⊥BM于E，交BC于F，连接NF .求证：（1）∠AMB＝∠CNF；（2）BM＝AF＋FN .变式2、在变式1的基础上，其他条件不变，只是将BM和FN分别延长交于点P，求证：（1）PM＝PN；（2）PB＝PF＋AF .四、手拉手模型1、△ABE和△ACF均为等边三角形结论：（1）△ABF≌△AEC .（2）∠BOE＝∠BAE＝60°.（3）OA平分∠EOF .（四点共圆证）拓展：△ABC和△CDE均为等边三角形结论：（1）AD＝BE；（2）∠ACB＝∠AOB；（3）△PCQ为等边三角形；（4）PQ∥AE；（5）AP＝BQ；（6）CO平分∠AOE；（四点共圆证）（7）OA＝OB＋OC；（8）OE＝OC＋OD .（（7），（8）需构造等边三角形证明）例、如图①，点M为锐角三角形ABC内任意一点，连接AM、BM、CM．以AB为一边向外作等边三角形△ABE，将BM绕点B逆时针旋转60°得到BN，连接EN．（1）求证：△AMB≌△ENB；（2）若AM+BM+CM的值最小，则称点M为△ABC的费尔马点．若点M为△ABC的费尔马点，试求此时∠AMB、∠BMC、∠CMA的度数；（3）小翔受以上启发，得到一个作锐角三角形费尔马点的简便方法：如图②，分别以△ABC 的AB、AC为一边向外作等边△ABE和等边△ACF，连接CE、BF，设交点为M，则点M 即为△ABC的费尔马点．试说明这种作法的依据．2、△ABD和△ACE均为等腰直角三角形结论：（1）BE＝CD；（2）BE⊥CD .3、四边形ABEF 和四边形ACHD 均为正方形结论：（1）BD ＝CF ；（2）BD ⊥CF .变式1、四边形ABEF 和四边形ACHD 均为正方形，AS ⊥BC 交FD 于T ，求证：（1）T 为FD 中点；（2）ABC ADF S S V V .变式2、四边形ABEF和四边形ACHD均为正方形，T为FD中点，TA交BC于S，求证：AS⊥BC .4、如图，以△ABC的边AB、AC为边构造正多边形时，总有：360 12180n︒∠=∠=︒-五、半角模型条件：1,+=1802αββθβ=︒且，两边相等 . 思路：1、旋转辅助线：①延长CD 到E ，使ED=BM ，连AE 或延长CB 到F ，使FB=DN ，连AF②将△ADN 绕点A 顺时针旋转90°得△ABF ，注意：旋转需证F 、B 、M 三点共线结论：（1）MN ＝BM ＋DN ；（2）=2CMN C AB V ；（3）AM 、AN 分别平分∠BMN 、∠MND .2、翻折（对称）辅助线：①作AP⊥MN交MN于点P②将△ADN、△ABM分别沿AN、AM翻折，但一定要证明M、P、N三点共线 .A、例题例1、在正方形ABCD中，若M、N分别在边BC、CD上移动，且满足MN＝BM＋DN，求证：（1）∠MAN＝45°；（2）=2CMN C AB V ；（3）AM 、AN 分别平分∠BMN 和∠DNM .变式：在正方形ABCD 中，已知∠MAN ＝45°，若M 、N 分别在边CB 、DC 的延长线上移动，AH ⊥MN ，垂足为H ，（1）试探究线段MN 、BM 、DN 之间的数量关系；（2）求证：AB ＝AH例2、在四边形ABCD中，∠B＋∠D＝180°，AB＝AD，若E、F分别为边BC、CD上的点，且满足EF＝BE＋DF，求证：12EAF BAD ∠=∠.变式：在四边形ABCD中，∠B＝90°，∠D＝90°，AB＝AD，若E、F分别为边BC、CD上的点，且12EAF BAD∠=∠，求证：EF＝BE＋DF .。

(完整)全等三角形的相关模型总结,推荐文档.docx

全等的相关模型总结一、角平分线模型应用1.角平分性质模型：辅助线：过点G 作 GE射线AC（1） .例题应用：①如图 1，在ABC中，C900， AD 平分 CAB , BC 6cm, BD 4cm,那么点 D 到直线 AB 的距离是cm.②如图 2，已知，1 2 ，34 .求证： AP平分 BAC .图 1图2① 2（提示：作 DE AB 交 AB 于点 E ）②12 ， PM PN ，3 4 ， PN PQ ， PM PQ, PA平分 BAC .(2).模型巩固：练习一：如图3，在四边形 ABCD 中， BC>AB ， AD=CD ，BD 平分BAC ..求证：A C180图3练习二：已知如图4，四边形 ABCD 中，B D 1800 , BC CD.求证： AC 平分BAD .图 4练习三：如图5，Rt ABC 中， ACB900， CD AB, 垂足为 D ， AF 平分CAB ,交 CD 于点 E ，交 CB 于点 F.(1)求证： CE=CF.(2)将图 5 中的△ ADE 沿 AB 向右平移到A' D ' E '的位置，使点 E'落在BC边上，其他条件不变，如图 6 所示，是猜想：BE'于 CF 又怎样的数量关系？请证明你的结论.图 5图6练习四：如图7，∠ A90 ， AD ∥ BC ， P 是 AB的中点， PD平分∠ ADC．求证： CP平分∠ DCB．A D214E3PB C图 7练习五：如图8，AB＞ AC，∠ A 的平分线与 BC的垂直平分线相交于D，自 D 作 DE⊥ AB，DF⊥ AC，垂足分别为 E， F．求证： BE=CF．图 8练习六：如图9 所示，在△ ABC 中， BC 边的垂直平分线DF 交△ BAC 的外角平分线AD 于点 D， F 为垂足， DE ⊥AB 于 E，并且 AB>AC 。

求证： BE－ AC=AE 。

专题13 全等三角形重难点模型(五大模型)(解析版)

专题13全等三角形重难点模型（五大模型）模型一：一线三等角型模型二：手拉手模型模型三：半角模型模型四：对角互补模型模型五：平行+线段中点构造全等模型【典例分析】【模型一：一线三等角型】如图一，∠D=∠BCA=∠E=90°，BC=AC。

结论：Rt△BDC≌Rt△CEA模型二一线三等角全等模型如图二，∠D=∠BCA=∠E，BC=AC。

结论：△BEC≌△CDA图一图二应用：①通过证明全等实现边角关系的转化，便于解决对应的几何问题；②与函数综合应用中有利于点的坐标的求解。

【典例1】如图，平面直角坐标系中有点A（﹣1，0）和y轴上一动点B（0，a），其中a＞0，以B点为直角顶点在第二象限内作等腰直角△ABC，设点C的坐标为（c，d）．（1）当a＝2时，则C点的坐标为；（2）动点B在运动的过程中，试判断c+d的值是否发生变化？若不变，请求出其值；若发生变化，请说明理由．【解答】解：（1）如图1中，过点C作CE⊥y轴于E，则∠CEB＝∠AOB．∵△ABC是等腰直角三角形，∴BC＝BA，∠ABC＝90°，∴∠BCE+∠CBE＝90°＝∠BAO+∠CBE，∴∠BCE＝∠ABO，在△BCE和△BAO中，，∴△CBE≌△BAO（AAS），∵A（﹣1，0），B（0，2），∴AO＝BE＝1，OB＝CE＝2，∴OE＝1+2＝3，∴C（﹣2，3），故答案为：（﹣2，3）；（2）动点A在运动的过程中，c+d的值不变．理由：过点C作CE⊥y轴于E，则∠CEA＝∠AOB，∵△ABC是等腰直角三角形，∴BC＝BA，∠ABC＝90°，∴∠BCE+∠CBE＝90°＝∠ABO+∠CBE，∴∠BCE＝∠ABO，在△BCE和△BAO中，，∴△CBE≌△BAO（AAS），∵B（﹣1，0），A（0，a），∴BO＝AE＝1，AO＝CE＝a，∴OE＝1+a，∴C（﹣a，1+a），又∵点C的坐标为（c，d），∴c+d＝﹣a+1+a＝1，即c+d的值不变．【变式1】点A的坐标为（4，0），点B为y轴负半轴上的一个动点，分别以OB、AB为直角边在第三象限和第四象限作等腰Rt△OBC和等腰Rt△ABD．（1）如图一，若点B坐标为（0，﹣3），连接AC、OD．①求证：AC＝OD；②求D点坐标．（2）如图二，连接CD，与y轴交于点E，试求BE长度．【解答】（1）①证明：∵△OBC和△ABD是等腰直角三角形，∴OB＝CB，BD＝AB，∠ABD＝∠OBC＝90°，∴∠ABD+ABO＝∠OBC+∠A∠O，∴∠OBD＝∠CBA，∴△OBD≌△CBA（SAS），∴AC＝OD；②如图一、∵A（4，0），B（0，﹣3），∴OA＝4，OB＝3，过点D作DF⊥y轴于F，∴∠BOA＝∠DFB＝90°，∴∠ABO+∠OAB＝90°，∵∠ABD＝90°，∴∠ABO+∠FBD＝90°，∴∠OAB＝∠FBD，∵AB＝BD，∴△AOB≌△BFD（AAS），∴DF＝OB＝3，BF＝OA＝4，∴OF＝OB+BF＝7，∴D（3，﹣7）；（2）如图二、过点D作DF⊥y轴于F，则∠DFB＝90°＝∠CBF，同（1）②的方法得，△AOB≌△BFD（AAS），∴DF＝OB，BF＝OA＝4，∵OB＝BC，∴BC＝DF，∵∠DEF＝∠CEB，∴△DEF≌△CEB（AAS），∴BE＝EF，∴BF＝BE+EF＝2BE＝4，∴BE＝2．【典例2】（1）猜想：如图1，已知：在△ABC中，∠BAC＝90°，AB＝AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E．试猜想DE、BD、CE有怎样的数量关系，请直接写出；（2）探究：如果三个角不是直角，那结论是否会成立呢？如图2，将（1）中的条件改为：在△ABC中，AB＝AC，D，A、E三点都在直线m上，并且有∠BDA＝∠AEC＝∠BAC＝α（其中α为任意锐角或钝角）如果成立，请你给出证明；若不成立，请说明理由；（3）解决问题：如图3，F是角平分线上的一点，且△ABF和△ACF均为等边三角形，D、E分别是直线m上A点左右两侧的动点，D、E、A互不重合，在运动过程中线段DE的长度始终为n，连接BD、CE，若∠BDA＝∠AEC＝∠BAC，试判断△DEF的形状，并说明理由．【解答】解：（1）DE＝BD+CE，理由如下：∵∠BAC＝90°，∴∠BAD+∠CAE＝90°，∵BD⊥m，CE⊥m，∴∠ADB＝∠CEA＝90°，∴∠BAD+∠ABD＝90°，∴∠ABD＝∠CAE，在△ADB和△CEA中，，∴△ADB≌△CEA（AAS），∴BD＝AE，AD＝CE，∴DE＝AD+AE＝BD+CE；（2）结论DE＝BD+CE成立，理由如下：∵∠BAD+∠CAE＝180°﹣∠BAC，∠BAD+∠ABD＝180°﹣∠ADB，∠ADB＝∠BAC，∴∠ABD＝∠CAE，在△BAD和△ACE中，，∴△BAD≌△ACE（AAS），∴BD＝AE，AD＝CE，∴DE＝DA+AE＝BD+CE；（3）△DFE为等边三角形，理由如下：由（2）得，△BAD≌△ACE，∴BD＝AE，∠ABD＝∠CAE，∴∠ABD+∠FBA＝∠CAE+FAC，即∠FBD＝∠FAE，在△FBD和△FAE中，，∴△FBD≌△FAE（SAS），∴FD＝FE，∠BFD＝∠AFE，∴∠DFE＝∠DFA+∠AFE＝∠DFA+∠BFD＝60°，∴△DFE为等边三角形．【变式2】已知，在△ABC中，AB＝AC，D，A，E三点都在直线m上，且DE ＝9cm，∠BDA＝∠AEC＝∠BAC（1）如图①，若AB⊥AC，则BD与AE的数量关系为，CE与AD 的数量关系为；（2）如图②，判断并说明线段BD，CE与DE的数量关系；（3）如图③，若只保持∠BDA＝∠AEC，BD＝EF＝7cm，点A在线段DE上以2cm/s的速度由点D向点E运动，同时，点C在线段EF上以xcm/s的速度由点E向点F运动，它们运动的时间为t（s）．是否存在x，使得△ABD与△EAC全等？若存在，求出相应的t的值；若不存在，请说明理由．【解答】解：（1）∵∠BDA＝∠AEC＝∠BAC，∴∠BAD+∠CAE＝∠BAD+∠ABD，∴∠CAE＝∠ABD，∵∠BDA＝∠AEC，BA＝CA，∴△ABD≌△CAE（AAS），∴BD＝AE，CE＝AD，故答案为：BD＝AE，CE＝AD；（2）DE＝BD+CE，由（1）同理可得△ABD≌△CAE（AAS），∴BD＝AE，CE＝AD，∴DE＝BD+CE；（3）存在，当△DAB≌△ECA时，∴AD＝CE＝2cm，BD＝AE＝7cm，∴t＝1，此时x＝2；当△DAB≌△EAC时，∴AD＝AE＝4.5cm，DB＝EC＝7cm，∴t＝，x＝7÷＝，综上：t＝1，x＝2或t＝，x＝．【模型二：手拉手模型】应用：①利用手拉手模型证明三角形全等，便于解决对应的几何问题；②作辅助线构造手拉手模型，难度比较大。

全等三角形常见的几何模型正规版

全等三角形常见的几何模型(可以直接使用，可编辑优秀版资料，欢迎下载）1、绕点型（手拉手模型）（1）自旋转：⎪⎪⎩⎪⎪⎨⎧，造中心对称遇中点旋全等遇等腰旋顶角，造旋转，造等腰直角旋遇，造等边三角形旋遇自旋转构造方法0000018090906060（2）共旋转（典型的手拉手模型）例1、在直线ABC 的同一侧作两个等边三角形△ABD 和△BCE ，连接AE 与CD ，证明：（1） △ABE ≌△DBC （2） AE=DC （3） AE 与DC 的夹角为60。

（4） △AGB ≌△DFB （5） △EGB ≌△CFB（6） BH 平分∠AHC（7） GF ∥AC变式练习1、如果两个等边三角形△ABD 和△BCE ，连接HFG EDEBAE与CD，证明：（1）△ABE≌△DBC（2）AE=DC（3）AE与DC的夹角为60。

（4）AE与DC的交点设为H,BH平分∠AHC变式练习2、如果两个等边三角形△ABD和△BCE，连接Array AE与CD，证明：(1)△ABE≌△DBC(2)AE=DC(3)AE与DC的夹角为60。

（4）AE与DC的交点设为H,BH平分∠AHC（1）如图1，点C是线段AB上一点，分别以AC，BC为边在AB的同侧作等边△ACM和△CBN，连接AN，BM．分别取BM，AN的中点E，F，连接C E，CF，EF．观察并猜想△CEF的形状，并说明理由．（2）若将（1）中的“以AC，BC为边作等边△ACM和△CBN”改为“以AC，BC为腰在AB的同侧作等腰△ACM和△CBN，”如图2，其他条件不变，那么（1）中的结论还成立吗？若成立，加以证明；若不成立，请说明理由．例4、例题讲解：1. 已知△ABC为等边三角形，点D为直线BC上的一动点（点D不与B,C重合），以AD为边作菱形ADEF(按A,D,E,F逆时针排列），使∠DAF=60°,连接CF.(1) 如图1，当点D在边BC上时，求证：① BD=CF ‚②AC=CF+CD.(2)如图2，当点D在边BC的延长线上且其他条件不变时，结论AC=CF+CD 是否成立？若不成立，请写出AC、CF、CD之间存在的数量关系，并说明理由；(3)如图3，当点D在边BC的延长线上且其他条件不变时，补全图形，并直接写出AC、CF、CD之间存在的数量关系。

(完整版)全等三角形经典模型总结

全等三角形相关模型总结一、角平分线模型(一）角平分线的性质模型辅助线：过点G作GE⊥射线ACA、例题1、如图，在△ABC中，∠C=90°，AD平分∠CAB，BC=6cm，BD=4cm，那么点D到直线AB 的距离是cm.2、如图，已知，∠1＝∠2，∠3＝∠4，求证：AP平分∠BAC.B、模型巩固1、如图，在四边形ABCD中，BC＞AB，AD＝CD，BD平分∠ABC，求证：∠A＋∠C＝180°.（二）角平分线＋垂线，等腰三角形必呈现A、例题辅助线：延长ED交射线OB于F 辅助线：过点E作EF∥射线OB 例1、如图，在△ABC中，∠ABC＝3∠C，AD是∠BAC的平分线，BE⊥AD于F .求证：1()2BE AC AB=-.例2、如图，在△ABC中，∠BAC的角平分线AD交BC于点D，且AB＝AD，作CM⊥AD交AD的延长线于M. 求证：1()2AM AB AC=+.（三）角分线，分两边，对称全等要记全两个图形飞辅助线都是在射线ON上取点B，使OB＝OA，从而使△OAC≌△OBC .A、例题1、如图，在△ABC中，∠BAC=60°，∠C=40°，AP平分∠BAC交BC于P，BQ平分∠ABC 交AC于Q，求证：AB＋BP＝BQ＋AQ .2、如图，在△ABC中，AD是∠BAC的外角平分线，P是AD上异于点A的任意一点，试比较PB＋PC与AB＋AC的大小，并说明理由.B、模型巩固1、在△ABC中，AB＞AC，AD是∠BAC的平分线，P是线段AD上任意一点（不与A重合）.求证：AB－AC＞PB－PC .2、如图，△ABC中，AB＝AC，∠A＝100°，∠B的平分线交AC于D，求证：AD＋BD＝BC .3、如图，△ABC中，BC＝AC，∠C＝90°，∠A的平分线交BC于D，求证：AC＋CD＝AB .二、等腰直角三角形模型（一）旋转中心为直角顶点，在斜边上任取一点的旋转全等：操作过程：（1）将△ABD逆时针旋转90°，得△ACM ≌△ABD，从而推出△ADM为等腰直角三角形.（2）辅助线作法：过点C作MC⊥BC，使CM＝BD，连结AM.（二）旋转中心为斜边中点，动点在两直角边上滚动的旋转全等：操作过程：连结AD.（1）使BF＝AE（或AF＝CE），导出△BDF ≌△ADE.（2）使∠EDF＋∠BAC＝180°，导出△BDF ≌△ADE.A、例题1、如图，在等腰直角△ABC中，∠BAC＝90°，点M、N在斜边BC上滑动，且∠MAN＝45°，试探究BM、MN、CN之间的数量关系.2、两个全等的含有30°，60°角的直角三角板ADE和ABC，按如图所示放置，E、A、C三点在一条直线上，连接BD，取BD的中点M，连接ME、MC.试判断△EMC的形状，并证明你的结论.B、模型巩固1、已知，如图所示，Rt△ABC中，AB＝AC，∠BAC＝90°，O为BC中点，若M、N分别在线段AC、AB上移动，且在移动中保持AN＝CM.（1）试判断△OMN的形状，并证明你的结论.（2）当M、N分别在线段AC、AB上移动时，四边形AMON的面积如何变化？2、在正方形ABCD中，BE＝3，EF＝5，DF＝4，求∠BAE＋∠DCF为多少度.（三）构造等腰直角三角形（1）利用以上（一）和（二）都可以构造等腰直角三角形（略）；（2）利用平移、对称和弦图也可以构造等腰直角三角形.（四）将等腰直角三角形补全为正方形，如下图：A、例题应用1、如图，在等腰直角△ABC中，AC＝BC，∠ACB＝90°，P为三角形ABC内部一点，满足PB＝PC，AP＝AC，求证：∠BCP＝15°.三、三垂直模型（弦图模型）A、例题已知：如图所示，在△ABC中，AB＝AC，∠BAC＝90°，D为AC中点，AF⊥BD于点E，交BC于F，连接DF .求证：∠ADB＝∠CDF .变式1、已知：如图所示，在△ABC中，AB＝AC，AM＝CN，AF⊥BM于E，交BC于F，连接NF .求证：（1）∠AMB＝∠CNF；（2）BM＝AF＋FN .变式2、在变式1的基础上，其他条件不变，只是将BM和FN分别延长交于点P，求证：（1）PM＝PN；（2）PB＝PF＋AF .四、手拉手模型1、△ABE和△ACF均为等边三角形结论：（1）△ABF≌△AEC .（2）∠BOE＝∠BAE＝60°.（3）OA平分∠EOF .（四点共圆证）拓展：△ABC和△CDE均为等边三角形结论：（1）AD＝BE；（2）∠ACB＝∠AOB；（3）△PCQ为等边三角形；（4）PQ∥AE；（5）AP＝BQ；（6）CO平分∠AOE；（四点共圆证）（7）OA＝OB＋OC；（8）OE＝OC＋OD .（（7），（8）需构造等边三角形证明）例、如图①，点M为锐角三角形ABC内任意一点，连接AM、BM、CM．以AB为一边向外作等边三角形△ABE，将BM绕点B逆时针旋转60°得到BN，连接EN．（1）求证：△AMB≌△ENB；（2）若AM+BM+CM的值最小，则称点M为△ABC的费尔马点．若点M为△ABC的费尔马点，试求此时∠AMB、∠BMC、∠CMA的度数；（3）小翔受以上启发，得到一个作锐角三角形费尔马点的简便方法：如图②，分别以△ABC 的AB、AC为一边向外作等边△ABE和等边△ACF，连接CE、BF，设交点为M，则点M 即为△ABC的费尔马点．试说明这种作法的依据．2、△ABD 和△ACE 均为等腰直角三角形结论：（1）BE ＝CD ；（2）BE ⊥CD .3、四边形ABEF 和四边形ACHD 均为正方形结论：（1）BD ＝CF ；（2）BD ⊥CF .变式1、四边形ABEF 和四边形ACHD 均为正方形，AS ⊥BC 交FD 于T ，求证：（1）T 为FD 中点；（2）ABC ADF SS .变式2、四边形ABEF和四边形ACHD均为正方形，T为FD中点，TA交BC于S，求证：AS⊥BC .4、如图，以△ABC的边AB、AC为边构造正多边形时，总有：360 12180n︒∠=∠=︒-五、半角模型条件：1,+=1802αββθβ=︒且，两边相等.思路：1、旋转辅助线：①延长CD到E，使ED=BM，连AE或延长CB到F，使FB=DN，连AF②将△ADN绕点A顺时针旋转90°得△ABF，注意：旋转需证F、B、M三点共线结论：（1）MN＝BM＋DN；（2）=2CMNC AB；（3）AM、AN分别平分∠BMN、∠MND .2、翻折（对称）辅助线：①作AP⊥MN交MN于点P②将△ADN、△ABM分别沿AN、AM翻折，但一定要证明M、P、N三点共线 .A、例题例1、在正方形ABCD中，若M、N分别在边BC、CD上移动，且满足MN＝BM＋DN，求证：（1）∠MAN＝45°；C AB；（2）=2CMN（3）AM、AN分别平分∠BMN和∠DNM .变式：在正方形ABCD中，已知∠MAN＝45°，若M、N分别在边CB、DC的延长线上移动，AH⊥MN，垂足为H，（1）试探究线段MN、BM、DN之间的数量关系；（2）求证：AB＝AH例2、在四边形ABCD中，∠B＋∠D＝180°，AB＝AD，若E、F分别为边BC、CD上的点，且满足EF＝BE＋DF，求证：12EAF BAD ∠=∠.变式：在四边形ABCD中，∠B＝90°，∠D＝90°，AB＝AD，若E、F分别为边BC、CD上的点，且12EAF BAD∠=∠，求证：EF＝BE＋DF .。

模型03 全等三角形中的常见五种基本模型(解析版)

模型介绍全等三角形的模型种类多，其中有关中点的模型与垂直模型在前面的专题已经很详细的讲解，这里就不在重复。

模型一、截长补短模型①截长：在较长的线段上截取另外两条较短的线段。

如图所示，在BF上截取BM=DF，易证△BMC≌△DFC（SAS），则MC=FC=FG，∠BCM=∠DCF，可得△MCF为等腰直角三角形，又可证∠CFE=45°，∠CFG=90°∠CFG=∠MCF，FG∥CM，可得四边形CGFM为平行四边形，则CG=MF，于是BF=BM+MF=DF+CG②补短：选取两条较短线段中的一条进行延长，使得较短的两条线段共线并寻求解题突破。

如图所示，延长GC至N，使CN=DF，易证△CDF≌△BCN（SAS）可得CF=FG=BN，∠DFC=∠BNC=135°又知∠FGC=45°，可证BN∥FG，于是四边形BFGN为平行四边形，得BF=NG所以BF=NG=NC+CG=DF+CG模型二、平移全等模型模型三、对称全等模型模型四、旋转全等模型模型五、手拉手全等模型例题精讲模型一、截长补短模型【例1】.如图，AD⊥BC，AB+BD＝DC，∠B＝54°，则∠C＝27°解：在DC上截取DE＝BD，连接AE∵AD⊥BC，DE＝BD∴AD是BE的垂直平分线∴AB＝AE∴∠B＝∠AEB＝54°∵AB+BD＝DC，DE+EC＝DC∴AB＝EC∴AE＝EC∴∠C＝∠EAC∵∠C+∠EAC＝∠AEB＝54°∴∠C＝∠EAC＝∠AEB＝27°故答案为：27°变式训练【变式1-1】．如图，点P是△ABC三个内角的角平分线的交点，连接AP、BP、CP，∠ACB ＝60°，且CA+AP＝BC，则∠CAB的度数为（）A．60°B．70°C．80°D．90°解：如图，在BC上截取CE＝AC，连接PE∵∠ACB＝60°∴∠CAB+∠ABC＝120°∵点P是△ABC三个内角的角平分线的交点∴∠CAP＝∠BAP＝∠CAB，∠ABP＝∠CBP＝∠ABC，∠ACP＝∠BCP ∴∠ABP+∠BAP＝60°∵CA＝CE，∠ACP＝∠BCP，CP＝CP∴△ACP≌△ECP（SAS）∴AP＝PE，∠CAP＝∠CEP∵CA+AP＝BC，且CB＝CE+BE∴AP＝BE∴BE＝PE∴∠EPB＝∠EBP∴∠PEC＝∠EBP+∠EPB＝2∠PBE＝∠CAP∴∠PAB＝2∠PBA，且∠ABP+∠BAP＝60°∴∠PAB＝40°∴∠CAB＝80°故选：C【变式1-2】．如图，在四边形ABCD中，BC＞BA，AD＝CD，BD平分∠ABC，求证：∠A+∠C＝180°证明：在线段BC上截取BE＝BA，连接DE，如图所示∵BD平分∠ABC∴∠ABD＝∠EBD在△ABD和△EBD中，，∴△ABD≌△EBD（SAS），∴AD＝ED，∠A＝∠BED∵AD＝CD∴ED＝CD，∴∠DEC＝∠C∵∠BED+∠DEC＝180°，∴∠A+∠C＝180°【变式1-3】．如图，△ABC为等腰直角三角形，AB＝AC，∠BAC＝90°，点D在线段AB 上，连接CD，∠ADC＝60°，AD＝2，过C作CE⊥CD，且CE＝CD，连接DE，交BC 于F。

一网打尽全等三角形模型-十个模型(解析版)

一网打尽全等三角形模型(10个模型)目录模型梳理题型一倍长中线模型题型二一线三等角模型题型三半角模型2022·山东日照真题题型四手拉手模型2022·张家界真题2022·贵阳中考题型五对角互补+邻边相等模型题型六平行线夹中点模型题型七截长补短模型题型八绝配角模型2023·深圳宝安区二模2023·深圳中学联考二模题型九婆罗摩笈模型2022武汉·中考真题2020·宿迁中考真题题型十脚蹬脚模型(海盗埋宝藏)模型梳理模型1倍长中线模型(一)基本模型已知：在△ABC中，AD是BC边上的中线，延长AD到点E，使ED=AD，连接BE．结论1：△ACD≌△EBD．已知：在△ABC中，点D是BC边的中点，点E是AB边上一点，连接ED，延长ED到点F，使DF=DE，连接CF．结论2：△BDE≌△CDF．(二)结论推导结论1：△ACD≌△EBD．证明：∵AD是BC边上的中线，∴CD=BD．∵∠ADC=∠EDB，AD=ED，∴△ACD≌△EBD．结论2：△BDE≌△CDF．证明：∵点D是BC边的中点，∴BD=CD．∵∠BDE=∠CDF，DE=DF，∴△BDE≌△CDF．(三)解题技巧遇到中点或中线，则考虑使用“倍长中线模型”，即延长中线，使所延长部分与中线相等，然后连接相应的顶点，构造出全等三角形．模型2一线三等角模型(一)基本模型已知：点P在线段AB上，∠1=∠2=∠3，AP=BD(或AC=BP或CP=PD)．结论1：△CAP≌△PBD．已知：点P在AB的延长线上，∠1=∠2=∠3，AP=BD(或AC=BP或CP=PD)．结论2：△APC≌△BDP．(二)结论推导结论1：△CAP≌△PBD．证明：∵∠1+∠C+∠APC=180°，∠2+∠BPD+∠APC=180°，∠1=∠2，∴∠C=∠BPD．∵∠1=∠3，AP=BD(或AC=BP或CP=PD)，∴△CAP≌△PBD．结论2：△APC≌△BDP．证明：∵∠1=∠C+∠APC，∠2=∠BPD+∠D，∠3=∠BPD+∠APC，∠1=∠2=∠3，∴∠C=∠BPD，∠APC=∠D．∵AP=BD(或AC=BP或CP=PD)，∴△APC≌△BDP．(三)解题技巧在一条线段上出现三个相等的角，且有一组边相等时，则考虑使用一线三等角全等模型．找准三个等角，再根据平角性质、三角形内角和进行等角代换，判定三角形全等，然后利用全等三角形的性质解题．一线三等角模型常以等腰三角形、等边三角形、四边形(正方形或矩形)为背景，在几何综合题中考查．模型3半角模型(一)基本模型等边三角形含半角已知：△ABC是等边三角形，D为△ABC外一点，∠BDC=120°，BD=CD，点E，F分别在AB，AC上，∠EDF=60°．结论1：EF=BE+CF，∠DEB=∠DEF，∠DFC=∠DFE．正方形含半角已知：四边形ABCD是正方形，点E，F分别在BC，CD上，∠EAF=45°．结论2：EF=BE+DF，∠AEB=∠AEF，∠AFD=∠AFE．等腰直角三角形含半角已知：△ABC是等腰直角三角形，∠BAC=90°，点D，E在BC上，∠DAE=45°．结论3：DE2=BD2+CE2．(二)结论推导结论1：EF=BE+CF，∠DEB=∠DEF，∠DFC=∠DFE．证明：延长AC到点G，使CG=BE，连接DG．∵△ABC是等边三角形，∴∠ABC=∠ACB=60°．∵∠BDC=120°，BD=CD，∴∠DBC=∠DCB=30°，∴∠DBE=∠DCF=90°，∴∠DBE=∠DCG=90°，∴△BDE≌△CDG，∴DE=DG，∠DEB=∠G，∠BDE=∠CDG．∵∠EDF=60°，∴∠BDE+∠CDF=60°，∴∠CDG+∠CDF=60°，即∠GDF=60°．∵DF=DF，∴△DEF≌△DGF，∴EF=FG，∠DEF=∠G，∠DFC=∠DFE．∴∠DEB=∠DEF．∵FG=CG+CF，∴EF=BE+CF．结论2：EF=BE+DF，∠AEB=∠AEF，∠AFD=∠AFE．证明：延长CB到点G，使BG=DF，连接AG．∵正方形ABCD，∴∠ABG=∠D=90°，AB=AD，∴△ABG≌△ADF，∴AG=AF，∠G=∠AFD，∠BAG=∠DAF．∵∠EAF=45°，∴∠BAE+∠DAF=45°，∴∠BAE+∠BAG=45°，即∠EAG=45°．∵AE=AE，∴△AEF≌△AEG，∴EF=EG，∠AEB=∠AEF，∠AFE=∠G．∴∠AFD=∠AFE．∵EG=BE+BG，∴EF=BE+DF．结论3：DE2=BD2+CE2．证明：将△ABD绕点A逆时针旋转90°到△ACF，连接EF．∵△ABC是等腰直角三角形，∠BAC=90°，∴∠B=∠ACB=45°，∴∠ACF=∠B=45°，∴∠ECF=90°，∴EF2=CF2+CE2=BD2+CE2，∵∠DAE=45°，∴∠BAD+∠CAE=45°，∴∠CAF+∠CAE=45°，即∠FAE=45°．∵AE=AE，∴△AEF≌△AED，∴EF=DE，∴DE2=BD2+CE2．(三)解题技巧对于半角模型，一般情况下都需要做辅助线(延长或旋转)，构造全等，通过等量代换得到相关的结论．模型4手拉手模型(一)基本模型已知：在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE，连接BD，CE相交于O，连接OA．结论1：△ABD≌△ACE，BD=CE，结论2：∠BOC=∠BAC，结论3：OA平分∠BOE．(二)结论推导结论1：△ABD≌△ACE，BD=CE．证明：∵∠BAC=∠DAE，∴∠BAD=∠CAE．∵AB=AC，AD=AE，∴△ABD≌△ACE，∴BD=CE．结论2：∠BOC=∠BAC．证明：设OB与AC相交于点F．∵△ABD≌△ACE，∴∠ABD=∠ACE．∵∠AFB=∠OFC，∴∠BOC=∠BAC．结论3：OA平分∠BOE．证明：过点A分别做BD，CE的垂线，垂足为G，H．∵△ABD≌△ACE，∴S△ABD=S△ACE，∴12BD⋅AG=12CE⋅AH．∵BD=CE，∴AG=AH，∴OA平分∠BOE．(三)解题技巧如果题目中出现两个等腰三角形，可以考虑连接对应的顶点，用旋转全等模型；如果只出现一个等腰三角形，可以用旋转的方法构造旋转全等．模型5对角互补+邻边相等模型模型解读：通过做垂线或者利用旋转构造全等三角形解决问题。

模型构建专题：全等三角形中的常见七种解题模型全攻略(解析版)

模型构建专题：全等三角形中的常见七种解题模型【考点导航】目录【典型例题】【模型一平移型模型】【模型二轴对称型模型】【模型三四边形中构造全等三角形解题】【模型四一线三等角模型】【模型五三垂直模型】【模型六旋转型模型】【模型七倍长中线模型】【典型例题】【模型一平移型模型】1(2023秋·江苏淮安·八年级淮安市浦东实验中学校考开学考试)如图，点E，C在线段BF上，AB∥DE，AB=DE，BE=CF．(1)求证：△ABC≌△DEF；(2)若∠B=40°，∠D=70°，求∠ACF的度数．【答案】(1)见解析(2)110°【分析】(1)首先根据，AB∥DE可得∠B=∠DEF，再根据BE=CF，可得出BC=EF，即可判定△ABC≌△DEF；(2)首先根据(1)中两三角形全等，可得∠A=∠D=70°，在△ABC中根据外角的性质即可求出∠ACF．【详解】(1)证明：∵AB∥DE，∴∠B=∠DEF∵BE=CF，∴BE+EC=CF+EC，即BC=EF，∴在△ABC和△DEF中，AB=DE∠B=∠DEFBC=EF，∴△ABC≌△DEF．(2)∵△ABC≌△DEF，∠B=40°，∠D=70°，∴∠A=∠D=70°，∵∠ACF是△ABC的外角，∴∠ACF=∠A+∠B=110°．【点睛】此题主要考查平行线的性质，三角形全等的判定和性质，熟练运用性质定理，即可解题．【变式训练】1(2023秋·浙江·八年级专题练习)如图，在△ACD和△CBE中，点A、B、C在一条直线上，∠D=∠E，AD⎳EC，AD=EC．求证：△ACD≌△CBE．【答案】见解析【分析】根据平行线的性质得出∠A=∠ECB，再根据全等三角形的判定定理ASA证明△ACD≌△CBE．【详解】∵AD⎳EC，∴∠A=∠ECB，在△ACD和△CBE中，∠A=∠ECB AD=EC∠D=∠E，∴△ACD≌△CBE(ASA)．【点睛】本题考查了全等三角形的判定定理和平行线的性质，能熟记全等三角形的判定定理是解此题的关键．2(2023秋·浙江·八年级专题练习)如图，已知△ABC≌△DEF，点B，E，C，F在同一条直线上．(1)若∠BED=140°，∠D=75°，求∠ACB的度数；(2)若BE=2，EC=3，求BF的长．【答案】(1)65°(2)7【分析】(1)由三角形外角性质，得∠F=∠BED-∠D=65°，由三角形全等知∠ACB=∠F=65°；(2)由条件可推出BC=BE+EC=5，由三角形全等知BC=EF=5，故BF=BE+EF=7．【详解】(1)解：∵∠BED=140°，∠D=75°，∴∠F=∠BED-∠D=65°．∵△ABC≌△DEF，∴∠ACB=∠F=65°；(2)解：∵BE=2，EC=3，∴BC=BE+EC=5∵△ABC≌△DEF，∴BC=EF=5，∴BF=BE+EF=2+5=7．故答案为：7．【点睛】本题考查三角形外角的性质，全等三角形的性质，由全等三角形得出角之间，线段之间的相等关系是解题的关键．3(2023春·山西太原·八年级统考期中)综合与实践--探索图形平移中的数学问题问题情境：如图1，已知△ABC是等边三角形，AB=6，点D是AC边的中点，以AD为边，在△ABC外部作等边三角形ADE．操作探究：将△ADE从图1的位置开始，沿射线AC方向平移，点A，D，E的对应点分别为点A ，D ，E ．(1)如图2，善思小组的同学画出了BA =BD 时的情形，求此时△ADE平移的距离；(2)如图3，点F是BC的中点，在△ADE平移过程中，连接E F 交射线AC于点O，敏学小组的同学发现OE =OF始终成立！请你证明这一结论；拓展延伸：(3)请从A，B两题中任选一题作答，我选择题.A.在△ADE平移的过程中，直接写出以F，A ，D 为顶点的三角形成为直角三角形时，△ADE平移的距离．B．在△ADE平移的过程中，直接写出以F，D ，E 为顶点的三角形成为直角三角形时，△ADE平移的距离．【答案】(1)32；(2)见解析；拓展延伸：A：32或92；B：6或12【分析】(1)连接BD，由△ABC是等边三角形，AB=6，点D是AC边的中点，得AD=3=CD，BD⊥AC，根据平移可得A D =AD=3，即可得A D=DD =12A D =32，故△ADE平移的距离DD为32；(2)证明△A OE ≌△COF AAS，即可得OE =OF；(3)选A：分两种情况：当∠A D F=90°时，可得DD =CD-CD =32，故△ADE平移的距离是3 2；当∠FA D =90°时，可得AA =AC -A C =92，从而△ADE 平移的距离是92；选B ：分两种情况：当A 与C 重合时，可得∠FD E =∠A D F +∠A D E =90°，即以F ，D ，E 为顶点的三角形成为直角三角形，此时DD =6，即△ADE 平移的距离是6；当∠D E F =90°时，可得DD =CD +CO +A O +A D =12，故△ADE 平移的距离是12．【详解】(1)解：连接BD ，如图：∵△ABC 是等边三角形，AB =6，点D 是AC 边的中点，∴AD =3=CD ，BD ⊥AC ，∵将△ADE 从图1的位置开始，沿射线AC 方向平移，点A ，D ，E 的对应点分别为点A ，D ，E ，∴A D =AD =3，∵A B =BD ，BD ⊥AC ，∴A D =DD =12A D =32，△ADE 平移的距离DD 为32；(2)证明：如图：∵△ADE 是等边三角形，AD =3，∴∠DAE =60°，AE =3，∵将△ADE 从图1的位置开始，沿射线AC 方向平移，点A ，D ，E 的对应点分别为点A ，D ，E ，∴∠D A E =∠DAE =60°，A E =3，∵△ABC 是等边三角形，AB =6，点F 是BC 边的中点，∴∠ACB =60°，CF =12BC =3，∴∠D A E =∠ACB =60°，A E =CF =3，∵∠A OE =∠COF ，∴△A OE ≌△COF AAS ，∴OE =OF ；(3)解：选择A (或B )题：选A ：当∠A D F =90°时，如图：∴∠CD F =90°，∵∠C =60°，∴∠D FC =30°，∴CD =12CF =32，∴DD =CD -CD =3-32=32；∴△ADE 平移的距离是32；当∠FA D =90°时，如图：同理可得A C =32，∴AA =AC -A C =6-32=92；△ADE 平移的距离是92；综上所述，以F ，A ，D 为顶点的三角形成为直角三角形时，△ADE 平移的距离是32或92；选B ：当A 与C 重合时，如图：∵△A D E 是等边三角形，∴∠E A D =∠A D E =∠E =60°，∵A F =A D =3，∴∠A FD =∠A D F =30°，∴∠FD E =∠A D F +∠A D E =90°，即以F ，D ，E 为顶点的三角形成为直角三角形，此时DD =CD +A D =3+3=6，△ADE 平移的距离是6；当∠D E F =90°时，如图：∵∠A E D =60°=∠E A D ，∴∠A E O =∠D E F -∠A E D =30°，∴∠A OE =∠D A E -∠A E O =30°，∴∠A E O =∠A OE ，∴A O =A E =3，由2 知△A OE ≌△COF ，∴CO =A O =3，∴DD =CD +CO +A O +A D =3+3+3+3=12，△ADE 平移的距离是12；综上所述，以F ，D ，E 为顶点的三角形成为直角三角形时，△ADE 平移的距离是6或12．【点睛】本题考查几何变换综合应用，涉及等边三角形的性质及应用，全等三角形的判定与性质，平移变换等知识，解题的关键是分类讨论思想的应用．【模型二轴对称型模型】1(2023秋·内蒙古呼伦贝尔·八年级校考期中)如图，AB =AD ，BC =DC ，求证：∠B =∠D．【答案】见解析【分析】根据SSS 证明△ABC ≌△ADC ，得出∠B =∠D 即可．【详解】证明：∵在△ABC 和△ADC 中AB =ADAC =AC BC =DC，∴△ABC ≌△ADC SSS ，∴∠B =∠D ．【点睛】本题主要考查了三角形全等的判定和性质，解题的关键是熟练掌握三角形全等的判定方法，证明△ABC ≌△ADC ．【变式训练】1(2023春·四川成都·七年级成都嘉祥外国语学校校考期中)如图，在中，，是的中点，，且，求证：．【答案】见解析【分析】由等腰三角形的性质得，，再证，得，即可得出结论．【详解】解：证明：连接，，是的中点，，，，，，即，在与中，，，，，即．【点睛】本题考查了全等三角形的判定与性质以及等腰三角形的性质等知识，熟练掌握等腰三角形的性质，证明三角形全等是解题的关键．2(2023秋·河南南阳·八年级统考期末)如图，点E、F是线段上的两个点，与交于点M．已知，，．(1)求证：；(2)若．求证：是等边三角形．【答案】(1)证明见解析(2)证明见解析【分析】(1)证明即可．(2)根据得到，根据有一个角是的等腰三角形是等边三角形证明．【详解】(1)证明：∵，∴，∴，∵，∴，∴．(2)∵，∴，∴，∵，∴是等边三角形．【点睛】本题考查了三角形全等的判断和性质，等边三角形的判定，熟练掌握三角形全等的判断和性质，等边三角形的判定是解题的关键．3(2023春·湖南益阳·八年级校考期中)两组邻边分别相等的四边形我们称它为筝形．如图，在筝形中，，，、相交于点，求证：(1)；(2)．【答案】(1)见解析；(2)见解析．【分析】(1)分别利用证即可；(2)由得，利用等腰三角形的性质即可得．【详解】(1)证明：在和中，，∴()．(2)证明：由(1)得，∴，∵，【点睛】此题考查全等三角形的判定与性质以及等腰三角形的性质，解题关键在于掌握全等三角形的判定定理．【模型三四边形中构造全等三角形解题】1(2023春·江苏淮安·七年级校考阶段练习)已知：如图，AC =BC ，AD =BD ，E 、F 分别是AC 和BC 的中点．求证：DE =DF．【答案】证明见解析．【分析】由三边对应相等的两个三角形是全等三角形可证△ADC ≌△BDC ，再根据全等三角形的性质可由两边对应相等以及它们的夹角相等的两个三角形全等可证△CDE ≌△CDF ，即可得出结论．【详解】证明：连接CD在△ADC 与△BDC 中，AC =BCCD =CDAD =BD∴△ADC ≌△BDC SSS ，∴∠ACD =∠BCD ，∵AC =BC ，且E 、F 分别是AC 和BC 的中点，∴CE =12AC ,CF =12BC ，即CE =CF ，在△CDE 与△CDF 中，CE =CF∠ECD =∠FCD CD =CD，∴△CDE ≌△CDF SAS∴DE =DF ．【点睛】本题考查了全等三角形的性质与判定，灵活根据条件选择恰当的判定方法，证明两个三角形全等是解题的关键．【变式训练】1(2023春·广西玉林·八年级统考期末)如图，在四边形中，，，我们把这种两组邻边分别相等的四边形叫做筝形．根据学习平行四边形性质的经验，小文对筝形的性质进行了探究．(1)小文通过观察、实验、猜想、证明得到筝形角的性质是“筝形有一组对角相等”．请你帮他将证明过程补充完整．已知：如图，在筝形中，，．求证：．证明：(2)小文连接筝形的两条对角线，探究得到筝形对角线的性质是．(写出一条即可)【答案】(1)，见解析(2)(或垂直平分线段)【分析】(1)，连接，证明，即可得结论；(2)根据全等三角形的性质即可得筝形的两条对角线互相垂直．【详解】(1)解：证明：连接，在和中，，，；(2)证明：如图，连接，交于点，由(1)知，，在与中，，，，，，两条对角线互相垂直．【点睛】本题考查了三角形全等的判定与性质，熟记三角形全等的判定方法是解题的关键．2如图，在四边形ABCD中，CB⊥AB于点B，CD⊥AD于点D，点E，F分别在AB，AD上，AE =AF，CE=CF．(1)若AE=8，CD=6，求四边形AECF的面积；(2)猜想∠DAB，∠ECF，∠DFC三者之间的数量关系，并证明你的猜想．【答案】(1)48(2)∠DAB+∠ECF=2∠DFC，证明见解析【解析】【分析】(1)连接AC，证明△ACE≌△ACF，则S△ACE=S△ACF，根据三角形面积公式求得S△ACF与S△ACE，根据S四=S△ACF+S△ACE求解即可；边形AECF(2)由△ACE≌△ACF可得∠FCA=∠ECA，∠FAC=∠EAC，∠AFC=∠AEC，根据垂直关系，以及三角形的外角性质可得∠DFC +∠BEC =∠FCA +∠FAC +∠ECA +∠EAC =∠DAB +∠ECF ．可得∠DAB +∠ECF =2∠DFC(1)解：连接AC ，如图，在△ACE 和△ACF 中AE =AFCE =CFAC =AC∴△ACE ≌△ACF (SSS )．∴S △ACE =S △ACF ，∠FAC =∠EAC ．∵CB ⊥AB ，CD ⊥AD ，∴CD =CB =6．∴S △ACF =S △ACE =12AE ·CB =12×8×6=24．∴S 四边形AECF =S △ACF +S △ACE =24+24=48．(2)∠DAB +∠ECF =2∠DFC证明：∵△ACE ≌△ACF ，∴∠FCA =∠ECA ，∠FAC =∠EAC ，∠AFC =∠AEC ．∵∠DFC 与∠AFC 互补，∠BEC 与∠AEC 互补，∴∠DFC =∠BEC ．∵∠DFC =∠FCA +∠FAC ，∠BEC =∠ECA +∠EAC ，∴∠DFC +∠BEC =∠FCA +∠FAC +∠ECA +∠EAC=∠DAB +∠ECF ．∴∠DAB +∠ECF =2∠DFC【点睛】本题考查了三角形全等的性质与判定，三角形的外角的性质，掌握三角形全等的性质与判定是解题的关键．3在四边形ABDC 中，AC =AB ，DC =DB ，∠CAB =60°，∠CDB =120°，E 是AC 上一点，F 是AB 延长线上一点，且CE =BF ．(1)试说明：DE =DF ：(2)在图中，若G 在AB 上且∠EDG =60°，试猜想CE ，EG ，BG 之间的数量关系并证明所归纳结论．(3)若题中条件“∠CAB =60°，∠CDB =120°改为∠CAB =α，∠CDB =180°-α，G 在AB 上，∠EDG 满足什么条件时，(2)中结论仍然成立？【答案】(1)见解析；(2)CE +BG =EG，理由见解析；(3)当∠EDG =90°-12α时，(2)中结论仍然成立．【解析】【分析】(1)首先判断出∠C =∠DBF ，然后根据全等三角形判定的方法，判断出ΔCDE ≅ΔBDF ，即可判断出DE =DF ．(2)猜想CE 、EG 、BG 之间的数量关系为：CE +BG =EG ．首先根据全等三角形判定的方法，判断出ΔABD ≅ΔACD ，即可判断出∠BDA =∠CDA =60°；然后根据∠EDG =60°，可得∠CDE =∠ADG ，∠ADE =∠BDG ，再根据∠CDE =∠BDF ，判断出∠EDG =∠FDG ，据此推得ΔDEG ≅ΔDFG ，所以EG =FG ，最后根据CE =BF ，判断出CE +BG =EG 即可．(3)根据(2)的证明过程，要使CE +BG =EG 仍然成立，则∠EDG =∠BDA =∠CDA =12∠CDB ，即∠EDG =12(180°-α)=90°-12α，据此解答即可．(1)证明：∵∠CAB +∠C +∠CDB +∠ABD =360°，∠CAB =60°，∠CDB =120°，∴∠C +∠ABD =360°-60°-120°=180°，又∵∠DBF +∠ABD =180°，∴∠C=∠DBF ，在ΔCDE 和ΔBDF 中，CD =BD∠C =∠DBFCE =BF∴ΔCDE ≅ΔBDF (SAS )，∴DE =DF ．(2)解：如图，连接AD ，猜想CE 、EG 、BG 之间的数量关系为：CE +BG =EG ．证明：在ΔABD 和ΔACD 中，AB =ACBD =CD AD =AD，∴ΔABD ≅ΔACD (SSS )，∴∠BDA =∠CDA =12∠CDB =12×120°=60°，又∵∠EDG =60°，∴∠CDE =∠ADG ，∠ADE =∠BDG ，由(1)，可得ΔCDE ≅ΔBDF ，∴∠CDE =∠BDF ，∴∠BDG +∠BDF =60°，即∠FDG =60°，∴∠EDG =∠FDG ，在ΔDEG 和ΔDFG 中，DE =DF∠EDG =∠FDGDG =DG∴ΔDEG ≅ΔDFG (SAS )，∴EG =FG ，又∵CE =BF ，FG =BF +BG ，∴CE +BG =EG ；(3)解：要使CE +BG =EG 仍然成立，则∠EDG =∠BDA =∠CDA =12∠CDB ，即∠EDG =12(180°-α)=90°-12α，∴当∠EDG =90°-12α时，CE +BG =EG 仍然成立．【点睛】本题综合考查了全等三角形的性质和判定，此题是一道综合性比较强的题目，有一定的难度，能根据题意推出规律是解此题的关键．【模型四一线三等角模型】1(2023春·广西南宁·七年级南宁市天桃实验学校校考期末)(1)问题发现：如图1，射线AE 在∠MAN 的内部，点B 、C 分别在∠MAN 的边AM 、AN 上，且AB =AC ，若∠BAC =∠BFE =∠CDE =90°，求证：△ABF ≌△CAD ；(2)类比探究：如图2，AB =AC ，且∠BAC =∠BFE =∠CDE ．(1)中的结论是否仍然成立，请说明理由；(3)拓展延伸：如图3，在△ABC 中，AB =AC ，AB >BC ．点E 在BC 边上，CE =2BE ，点D 、F 在线段AE 上，∠BAC =∠BFE =∠CDE ．若△ABC 的面积为15，DE =2AD ，求△BEF 与△CDE 的面积之比．【答案】(1)证明见详解；(2)成立，证明见详解；(3)1:4【分析】(1)根据∠BAC =∠BFE =∠CDE =90°即可得到∠BAF +∠CAF =90°，∠DCA +∠CAF =90°，从而得到∠BAF =∠DCA ，即可得到证明；(2)根据∠BAC =∠BFE =∠CDE 得到∠BAF +∠CAF =∠DCA +∠CAF ，即可得到∠BAF =∠DCA ，即可得到证明；(3)根据△ABC 的面积为15，CE =2BE ，即可得到S △ABE =5，S △AEC =10，结合DE =2AD 可得S △ADC =103，S △EDC =203，根据AB =AC ，∠BAC =∠BFE =∠CDE 得到△ABF ≌△CAD ，即可得到S △BEF ，即可得到答案；【详解】(1)证明：∵∠BAC =∠BFE =∠CDE =90°，∴∠BFA =∠CDA =90°，∠BAF +∠CAF =90°，∠DCA +∠CAF =90°，∴∠BAF =∠DCA ，在△ABF 与△CAD 中，∵∠BFA =∠CDA∠BAF =∠DCA AB =AC，∴△ABF ≌△CAD (AAS )；(2)解：成立，理由如下，∵∠BAC =∠BFE =∠CDE ，∴∠BAF +∠CAF =∠DCA +∠CAF ，∠BFA =∠CDA ，∴∠BAF =∠DCA ，在△ABF 与△CAD 中，∵∠BFA =∠CDA∠BAF =∠DCA AB =AC，∴△ABF ≌△CAD (AAS )；(3)解：∵△ABC 的面积为15，CE =2BE ，∴S △ABE =5，S △AEC =10，∵DE =2AD ，∴S △ADC =103，S △EDC =203，∵∠BAC =∠BFE =∠CDE ，∴∠BAF +∠CAF =∠DCA +∠CAF ，∠BFA =∠CDA ，∴∠BAF =∠DCA ，在△ABF 与△CAD 中，∵∠BFA =∠CDA∠BAF =∠DCA AB =AC，∴△ABF ≌△CAD (AAS )∴S △BEF =5-103=53，∴S △BEF :S △CDE =53:203=1:4；【点睛】本题考查三角形全等的判定与性质及同高不同底三角形的面积，解题的关键是根据内外角关系得到三角形全等的条件．【变式训练】1已知CD 是经过∠BCA 顶点C 的一条直线，CA =CB ．E 、F 分别是直线CD 上两点，且∠BEC =∠CFA =∠α．(1)若直线CD 经过∠BCA 的内部，且E 、F 在射线CD 上，请解决下面问题：①如图1，若∠BCA =90°，∠α=90°，求证：BE =CF ；②如图2，若∠α+∠BCA =180°，探索三条线段EF ，BE ，AF 的数量关系，并证明你的结论；(2)如图3，若直线CD 经过∠BCA 的外部，∠α=∠BCA ，题(1)②中的结论是否仍然成立？若成立，请给予证明；若不成立，请你写出正确的结论再给予证明．【答案】(1)①见解析；②EF =BE -AF ，见解析(2)不成立，EF =BE +AF ，见解析【分析】(1)①利用垂直及互余的关系得到∠ACF =∠CBE ，证明△BCE ≌△CAF 即可；②利用三等角模型及互补证明∠ACF =∠CBE ，得到△BCE ≌△CAF 即可；(2)利用互补的性质得到∠EBC =∠ACF ，证明△BCE ≌△CAF 即可．【详解】(1)①证明：∵EE ⊥CD ，AF ⊥CD ，∠ACB =90°，∴∠BEC =∠AFC =90°，∴∠BCE +∠ACF =90°，∠CBE +∠BCE =90°，∴∠ACF =∠CBE ，在△BCE 和△CAF 中，∠EBC =∠FCA∠BEC =∠CFA BC =CA，∴△BCE ≌△CAF AAS ，∴BE =CF ；②解：EF =BE -AF ．证明：∵∠BEC =∠CFA =∠α，∠α+∠ACB =180°，∴∠CBE =180°-∠BCE -∠α，∠ACF =∠ACB -∠BCE =180°-∠α-∠BCE ，∴∠ACF =∠CBE ，在△BCE 和△CAF 中，∠EBC =∠FCA∠BEC =∠CFA BC =CA，∴△BCE ≌△CAF AAS ，∴BE =CF ，CE =AF ，∴EF =CF -CE =BE -AF ；(2)解：EF =BE +AF ．理由：∵∠BEC =∠CFA =∠α，∠α=∠BCA ，又∵∠EBC =∠BCE =∠BEC =180°，∠BCE +∠ACF +∠ACB =180°，∴∠EBC +∠BCE =∠BCE +∠ACF ，∴∠EBC =∠ACF ，在△BCE 和△CAF 中，∠EBC =∠FCA∠BEC =∠CFA BC =CA，∴△BCE ≌△CAF AAS ，∴AF =CE ，BE =CF ，∵EF =CE +CF ，∴EF =BE +AF ．【点睛】本题主要考查三角形全等的判定及性质，能够熟练运用三等角模型快速证明三角形全等是解题关键．2(2023春·上海·七年级专题练习)在直线m 上依次取互不重合的三个点D ,A ,E ，在直线m 上方有AB =AC ，且满足∠BDA =∠AEC =∠BAC =α．(1)如图1，当α=90°时，猜想线段DE ,BD ,CE 之间的数量关系是；(2)如图2，当0<α<180°时，问题(1)中结论是否仍然成立？如成立，请你给出证明；若不成立，请说明理由；(3)应用：如图3，在△ABC 中，∠BAC 是钝角，AB =AC ，∠BAD <∠CAE ,∠BDA =∠AEC =∠BAC ，直线m 与CB 的延长线交于点F ，若BC =3FB ，△ABC 的面积是12，求△FBD 与△ACE 的面积之和．【答案】(1)DE =BD +CE(2)DE =BD +CE 仍然成立，理由见解析(3)△FBD 与△ACE 的面积之和为4【分析】(1)由∠BDA =∠BAC =∠AEC =90°得到∠BAD +∠EAC =∠BAD +∠DBA =90°，进而得到∠DBA =∠EAC ，然后结合AB =AC 得证△DBA ≌△EAC ，最后得到DE =BD +CE ；(2)由∠BDA =∠BAC =∠AEC =α得到∠BAD +∠EAC =∠BAD +∠DBA =180°-α，进而得到∠DBA =∠EAC ，然后结合AB =AC 得证△DBA ≌△EAC ，最后得到DE =BD +CE ；(3)由∠BAD >∠CAE ，∠BDA =∠AEC =∠BAC ，得出∠CAE =∠ABD ，由AAS 证得△ADB ≌△CAE ，得出S △ABD =S △CEA ，再由不同底等高的两个三角形的面积之比等于底的比，得出S △ABF 即可得出结果．【详解】(1)解：DE =BD +CE ，理由如下，∵∠BDA =∠BAC =∠AEC =90°，∴∠BAD +∠EAC =∠BAD +∠DBA =90°，∴∠DBA =∠EAC ，∵AB =AC ，∴△DBA ≌△EAC (AAS )，∴AD =CE ，BD =AE ，∴DE =AD +AE =BD +CE ，故答案为：DE =BD +CE ．(2)DE =BD +CE 仍然成立，理由如下，∵∠BDA =∠BAC =∠AEC =α，∴∠BAD +∠EAC =∠BAD +∠DBA =180°-α，∴∠DBA =∠EAC ，∵AB =AC ，∴△DBA ≌△EAC (AAS )，∴BD =AE ，AD =CE ，∴DE =AD +AE =BD +CE ；(3)解：∵∠BAD <∠CAE ，∠BDA =∠AEC =∠BAC ，∴∠CAE =∠ABD ，在△ABD 和△CAE 中，∠ABD =∠CAE∠BDA =∠CEA AB =AC，∴△ABD ≌△CAE (AAS )，∴S △ABD =S △CAE ，设△ABC 的底边BC 上的高为h ，则△ABF 的底边BF 上的高为h ，∴S △ABC =12BC •h =12，S △ABF =12BF •h ，∵BC =3BF ，∴S △ABF =4，∵S △ABF =S △BDF +S △ABD =S △FBD +S △ACE =4，∴△FBD 与△ACE 的面积之和为4．【点睛】本题考查了全等三角形的判定与性质、直角三角形的性质，三角形的面积，解题的关键是熟练掌握全等三角形的判定与性质．【模型五三垂直模型】1(2023春·辽宁本溪·七年级统考期末)已知∠ACB =90°，AC =BC ，AD ⊥NM ，BE ⊥NM ，垂足分别为点D ，E．(1)如图①，求证：AD =BE +DE(2)如图②，(1)中的结论还成立吗？如果不成立，请写出线段AD ，BE ，DE 之间的数量关系，并说明理由．【答案】(1)见解析(2)(1)中的结论不成立．结论：DE =AD +BE ，理由见解析【分析】(1)证明△ADC ≌△CEB AAS ，推出CD =BE ，AD =CE ，再利用线段间的代换即得结论；(2)证明△ADC ≌△CEB AAS ，推出CD =BE ，AD =CE ，利用线段间的代换即可得到结论，进而作出判断．【详解】(1)证明：∵AD ⊥NM ，BE ⊥NM ，∴∠ADC =∠CEB =90°，∴∠CAD +∠ACD =90°∵∠ACB =90°，∴∠BCE +∠ACD =90°，∴∠CAD =∠BCE ，在△ADC 和△CEB 中∠ADC =∠CEB∠CAD =∠BCEAC =BC∴△ADC ≌△CEB AAS ，∴CD =BE ，AD =CE ，∴CE =CD +DE =BE +DE ，∴AD =BE +DE ；(2)(1)中的结论不成立．结论：DE =AD +BE ；理由如下：∵AD ⊥NM ，BE ⊥NM ，∴∠ADC =∠CEB =90°∵∠ACB =90°，∴∠BCE +∠ACD =90°，∴∠CAD =∠BCE在△ADC 和△CEB 中∠ADC =∠CEB∠CAD =∠BCE AC =BC，∴△ADC ≌△CEB AAS ，∴CD =BE ，AD =CE，∵DE=CD+CE，∴DE=AD+BE．【点睛】本题考查了全等三角形的判定和性质，属于常考题型，证明三角形全等是解题的关键．【变式训练】1(2023春·甘肃酒泉·八年级校联考期末)在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E.(1)当直线MN绕点C旋转到图1的位置时，求证：①△ADC≌△CEB；②DE=AD+BE；(2)当直线MN绕点C旋转到图2的位置时，求证：DE=AD-BE；【答案】(1)①见解析，②见解析(2)见解析【分析】(1)①由已知推出∠ADC=∠BEC=90°，∠DAC+∠ACD=90°推出∠DAC=∠BCE，根据角角边即可推出．②由①得到AD=CE,CD=BE，即可求出答案．(2)与(1)类似证出△ADC≌△CEB，得到AD=CE,CD=BE代入已知即可知道答案．【详解】(1)①证明：∵AD⊥DE，BE⊥DE，∴∠ADC=∠BEC=90°，∵∠ACB=90°，∴∠ACD+∠BCE=90°，∠DAC+∠ACD=90°，∴∠DAC=∠BCE，在△ADC和△CEB中，∠CDA=∠BEC ∠DAC=∠ECB AC=BC，∴△ADC≌△CEB AAS．②证明：由(1)知：△ADC≌△CEB，∴AD=CE，CD=BE，∵DC+CE=DE，∴AD+BE=DE．(2)证明：∵BE⊥EC，AD⊥CE，∴∠ADC=∠BEC=90°，∴∠EBC+∠ECB=90°，∵∠ACB=90°，∴∠ECB+∠ACE=90°，∴∠ACD=∠EBC，AC=BC∴△ADC≌△CEB AAS，∴AD=CE，CD=BE，∴DE=EC-CD=AD-BE．【点睛】本题考查了全等三角形的性质和判定，等根据已知条件证出符合全等的条件是解题的关键．2如图，已知：在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，AD⊥MN，BE⊥MN．(1)当直线MN绕点C旋转到图(1)的位置时，求证：△ADC≅△CEB；(2)当直线MN绕点C旋转到图(2)的位置时，求证：DE=AD-BE；(3)当直线MN绕点C旋转到图(3)的位置时，试问DE、AD、BE具有怎样的等量关系？请直接写出这个等量关系：．【答案】(1)见解析；(2)见解析；(3)DE=BE-AD【分析】(1)由已知推出∠ADC=∠BEC=90°，因为∠ACD+∠BCE=90°，∠DAC+∠ACD=90°，推出∠DAC=∠BCE，根据AAS即可得到答案；(2)结论：DE=AD-BE．与(1)证法类似可证出∠ACD=∠EBC，能推出△ADC≌△CEB，得到AD= CE，CD=BE，即可得到答案．(3)结论：DE=BE-AD．证明方法类似．【详解】解：(1)证明：如图1，∵AD⊥DE，BE⊥DE，∴∠ADC=∠BEC=90°，∵∠ACB=90°，∴∠ACD+∠BCE=90°，∠DAC+∠ACD=90°，∴∠DAC=∠BCE，在△ADC和△CEB中，∠CDA=∠BEC∠DAC=∠ECBAC=BC，∴△ADC≌△CEB(AAS)；(2)如图2，∵BE⊥EC，AD⊥CE，∴∠ADC=∠BEC=90°，∴∠EBC+∠ECB=90°，∵∠ACB=90°，∴∠ECB+∠ACE=90°，∴∠ACD=∠EBC，AC =BC∴△ADC ≌△CEB (AAS )，∴AD =CE ，CD =BE ，∴DE =EC -CD =AD -BE ．(3)DE =BE -AD ；如图3，∵∠ACB =90°，∴∠ACD +∠BCE =90°∵AD ⊥MN ，BE ⊥MN ，∴∠ADC =∠CEB =90°，∴∠ACD +∠DAC =90°，∴∠DAC =∠ECB ，在△ACD 和△CBE 中，∠ADC =∠CEB∠DAC =∠ECB AC =BC，∴△ACD ≌△CBE (AAS )，∴AD =CE ，CD =BE ，∴DE =CD -CE =BE -AD ．【点睛】本题主要考查了余角的性质，全等三角形的性质和判定等知识点，能根据已知证明△ACD ≌△CBE 是解此题的关键，题型较好，综合性比较强．【模型六旋转型模型】1在Rt △ABC 中，∠ACB =90°，CA =CB ，点D 是直线AB 上的一点，连接CD ，将线段CD 绕点C 逆时针旋转90°，得到线段CE ，连接EB ．(1)操作发现如图1，当点D 在线段AB 上时，请你直接写出AB 与BE 的位置关系为；线段BD 、AB 、EB 的数量关系为；(2)猜想论证当点D 在直线AB 上运动时，如图2，是点D 在射线AB 上，如图3，是点D 在射线BA 上，请你写出这两种情况下，线段BD 、AB 、EB 的数量关系，并对图2的结论进行证明；(3)拓展延伸若AB =5，BD =7，请你直接写出△ADE 的面积．【答案】(1)AB⊥BE，AB=BD+BE；(2)图2中BE=AB+BD，图3中，BD=AB+BE，证明见解析；(3)72或2【分析】(1)首先通过SAS证明△ACD≌△BCE，然后利用全等三角形的性质和等量代换即可得出答案；(2)仿照(1)中证明△ACD≌△BCE，然后利用全等三角形的性质即可得出结论；•AD•EB即可求解．(3)首先求出BE的长度，然后利用S△AED=12【详解】解：(1)如图1中，∵∠ACB=∠DCE=90°，∴∠ACD=∠BCE，∵CA=CB，CD=CE，∴△ACD≌△BCE(SAS)，∴AD=BE，∠CBE=∠A，∵CA=CB，∠ACB=90°，∴∠A=∠CBA=45°，∴∠CBE=∠A=45°，∴ABE=90°，∴AB⊥BE，∵AB=AD+BD，AD=BE，∴AB=BD+BE，故答案为AB⊥BE，AB=BD+BE．(2)①如图2中，结论：BE=AB+BD．理由：∵∠ACB=∠DCE=90°，∴∠ACD=∠BCE，∵CA=CB，CD=CE，∴△ACD≌△BCE(SAS)，∴AD=BE，∵AD=AB+BD，AD=BE，∴BE=AB+BD．②如图3中，结论：BD=AB+BE．理由：∵∠ACB =∠DCE =90°，∴∠ACD =∠BCE ，∵CA =CB ，CD =CE ，∴△ACD ≌△BCE (SAS )∴AD =BE ，∵BD =AB +AD ，AD =BE ，∴BD =AB +BE ．(3)如图2中，∵AB =5，BD =7，∴BE =AD =5+7=12，∵BE ⊥AD ，∴S △AED =12•AD •EB =12×12×12=72．如图3中，∵AB =5，BD =7，∴BE =AD =BD -AB =7-5=2，∵BE ⊥AD ，∴S △AED =12•AD •EB =12×2×2=2．【点睛】本题主要考查全等三角形，掌握全等三角形的判定及性质并分情况讨论是关键．【变式训练】2(2023秋·湖南长沙·八年级长沙市湘郡培粹实验中学校考开学考试)【问题初探】△ABC 和△DBE 是两个都含有45°角的大小不同的直角三角板(1)当两个三角板如图(1)所示的位置摆放时，D 、B ，C 在同一直线上，连接AD 、CE ，请证明：AD =CE【类比探究】(2)当三角板ABC 保持不动时，将三角板DBE 绕点B 顺时针旋转到如图(2)所示的位置，判断AD 与CE 的数量关系和位置关系，并说明理由．【拓展延伸】如图(3)，在四边形ABCD 中，∠BAD =90°,AB =AD ,BC =34CD ，连接AC ，BD ，∠ACD =45°，A 到直线CD 的距离为7，请求出△BCD 的面积．【答案】(1)见解析；(2)AD =CE ，AD ⊥CE ；(3)24【分析】(1)由等腰直角三角形的性质判断出△DBA ≅△EBC 即可得出结论；(2)先证明△DBA ≅△EBC 得到AD =CE ，∠ADB =∠CEB ，再延长AD 与CE 交于点O ，证明∠ODE +∠OED =90°即可得到AD ⊥CE ；(3)过A 作AC ⊥AM 交CD 延长线于M ，可证得△ABC ≅△ADM ，可得BC =DM ，再由CM =14求出BC 和CD 的长即可．【详解】(1)∵△ABC 和△DBE 是两个都含有45°角的大小不同的直角三角板，∴∠DBE=∠ABC=90°，AB=BC，BD=BE，∴△DBA≅△EBC SAS，∴AD=CE；(2)AD=CE，AD⊥CE，理由如下：∵∠DBE=∠ABC=90°，∴∠DBA=∠BCE=90°-∠DBC，∵AB=BC，BD=BE，∴△DBA≅△EBC SAS，∴AD=CE，∠ADB=∠CEB，延长AD与CE交于点O，∵∠BDE+∠BED=90°，∴∠BDE+∠BEC+∠CED=90°，∴∠BDE+∠ADB+∠CED=90°，∴∠ODE+∠OED=90°，∴∠O=90°，∴AD⊥CE；(3)过A作AC⊥AM交CD延长线于M，过A作AN⊥CD交CD于N，∵∠ACD=45°，∴∠ACD=∠M=45°，∴AC=AM，∵∠BAD=90°,AB=AD∴∠BAC=∠DAM=90°-∠DAC，∴△ABC≅△ADM SAS，∴BC=DM，∠ACB=∠M=45°，∴∠ACD=∠ACB+∠ACD=90°，∵A到直线CD的距离为7，∴AN=7，∵AC=AM，∴CM=2AN=14，∵BC=34CD，CM=BC+DM=BC+CD，∴BC=6，CD=8，∴S△BCD=12BC⋅CD=12×6×8=24．【点睛】此题是几何变换综合题，主要考查了等腰直角三角形的性质，全等三角形的判定和性质，垂直的判断方法，解本题的关键是判断出△DBA≅△EBC SAS，是一道难度不大的中考常考题．3(2023·全国·九年级专题练习)阅读以下材料，并按要求完成相应的任务：从正方形的一个顶点引出夹角为45°的两条射线，并连接它们与该顶点的两对边的交点构成的基本平面几何模型称为半角模型．半角模型可证出多个几何结论，例如：如图1，在正方形ABCD中，以A为顶点的∠EAF=45°，AE、AF与BC、CD边分别交于E、F两点．易证得EF=BE+FD．大致证明思路：如图2，将△ADF绕点A顺时针旋转90°，得到△ABH，由∠HBE=180°可得H、B、E三点共线，∠HAE=∠EAF=45°，进而可证明△AEH≌△AEF，故EF=BE+DF．任务：如图3，在四边形ABCD中，AB=AD，∠B=∠D=90°，∠BAD=120°，以A为顶点的∠EAF=60°，AE、AF与BC、CD边分别交于E、F两点．请参照阅读材料中的解题方法，你认为结论EF=BE+ DF是否依然成立，若成立，请写出证明过程；若不成立，请说明理由．【答案】成立，见解析【分析】根据旋转的性质得到△ABM≌△ADF，∠ABM=∠D=90°，∠MAB=∠FAD，AM=AF，MB =DF，推出M、B、E三点共线，根据全等三角形的性质即可得到结论．【详解】解：成立．证明：将△ADF绕点A顺时针旋转120°得到△ABM，∴△ABM≌△ADF，∠ABM=∠D=90°，∠MAB=∠FAD，AM=AF，MB=DF，∴∠MBE=∠ABM+∠ABE=180°，∴M、B、E三点共线，∴∠MAE=∠MAB+∠BAE=∠FAD+∠BAE=∠BAD-∠EAF=60°，∴∠MAE=∠FAE，∵AE=AE，AM=AF，∴△MAE≌△FAE(SAS)，∴ME=EF，∴EF=ME=MB+BE=DF+BE．【点睛】本题考查了旋转的性质，全等三角形的判定和性质，正确地作出辅助线是解题的关键．4(2023·山西大同·校联考模拟预测)综合与实践课上，李老师让同学们以“等腰直角三角形的旋转”为主题开展数学活动．数学兴趣小组将两块大小不同的等腰直角三角形AOB和等腰直角三角形COD按图1的方式摆放，∠AOB=∠COD=90°，随后保持△AOB不动，将△COD绕点O按逆时针方向旋转α0°<α<90°，连接BC,AD，延长BC交AD于点M．该数学兴趣小组进行如下探究，请你帮忙解答：,【初步探究】(1)如图1，直接写出线段BC和AD的关系：．(2)如图2，当CD∥BO时，则α=．【深入探究】(3)如图3，当0°<α<90°时，连接OM，兴趣小组认为不仅(1)中的结论仍然成立，而且在△COD旋转过程中,∠CMO的度数不发生变化，请给出推理过程并求出∠CMO的度数．【拓展延伸】(4)如图3，试探究线段AM,BM,OM，之间是否存在某种特定的数量关系，若存在，直接写出数量关系式；若不存在，请说明理由．【答案】(1)BC=AD,BC⊥AD；(2)45°；(3)见解析，45°；(4)存在，BM=AM+2OM【分析】(1)由条件根据三角形全等判定定理SAS得△BOC≌△AOD，可证；(2)利用平行的性质．两线平行，内错角相等，结合条件易得α=45°；(3)类比上面思路，通过构建三角形全等△BON≌△AOM推出ON=OM，进而易得∠COM=45°，(4)根据(3)的结论，推导出△NOM是等腰直角三角形，然后根据等腰直角三角形的性质，化简即可得到答案．【详解】(1)由题意得，AO=BO，OC=OD，∠AOB=∠COD=90°，∴△BOC≌△AOD SAS，∴BC=AD，∠CBO=∠DAO，在Rt△AOD中，∠DOA+∠ADO=90°，∴∠CBO+∠ADO=90°，∴∠BMD=90°，即BC⊥AD，故答案为：BC=AD,BC⊥AD.(2)∵∠OCD=∠ODC=45°，CD∥BO，∴∠COB=∠OCD=45°，又∠AOB=90°，∴∠AOC=∠AOB-∠BOC=45°,即α=45°，故答案为：45°.(3)如图，过O点作NO⊥OM，交MB于N点，由(1)易知△BOC≌△AOD SAS，∴∠CBO=∠DAO，∵∠BON+∠NOA=∠NOA+∠AOM，∴∠BON=∠AOM，又AO=BO，易得△BON≌△AOM ASA，∴ON=OM，又∵NO⊥OM，∴∠BMO=45°，即∠CMO=45°；(4)存在，BM=AM+2OM，理由如下：由(3)可知，△BON≌△AOM(ASA)，∴BN=AM，∵△NOM是等腰直角三角形，OM=ON∴MN=ON2+OM2=2OM，∴BM=BN+MN=AM+2OM．【点睛】本题考查了旋转的性质、三角形全等的判定和性质，等腰直角三角形的性质，解题的关键是作出相应的辅助线以及确定全等三角形．【模型七倍长中线模型】1(2023春·全国·七年级专题练习)[阅读理解]课外兴趣小组活动时，老师提出了如下问题：如图1，在ΔABC中，若AB=8，AC=6，求BC边上的中线AD的取值范围．小明在组内经过合作交流，得到了如下的解决方法：如图2，延长AD到点E，使DE=AD，连结BE，请根据小明的方法思考：(1)由已知和作图能得到△ADC≌△EDB，其理由是什么？(2)AD的取值范围是什么？[感悟]解题时，条件中出现“中点”“中线”等字样，可以考虑延长中线构造全等三角形，把分散的已知条件和结论转化到一个三角形中．[问题解决](3)如图3，AD是ΔABC的中线，BE交AC于点F，且AE=EF，试说明AC=BF．【答案】(1)见解析(2)1<AD<7(3)见解析【分析】(1)根据AD=DE，∠ADC=∠BDE，BD=DC推出ΔADC和ΔEDB全等即可；(2)根据全等得出BE=AC=6，AE=2AD，由三角形三边关系定理得出8-6<2AD<8+6，求出即。