数学表达式解析汇报(前缀、中缀、后缀)
前缀、中缀、后缀表达式

前缀、中缀、后缀表达式在计算机科学中,表达式是由操作符和操作数组成的数学式子。
为了方便计算机进行计算,表达式可以以不同的形式表示,包括前缀、中缀和后缀表达式。
一、前缀表达式前缀表达式,也称为波兰表达式,是将操作符写在操作数之前的一种表达式形式。
例如,加法操作符写在两个操作数之前,减法操作符写在两个操作数之前,以此类推。
前缀表达式的一个特点是,操作符和操作数之间没有括号,而是通过空格或其他分隔符进行分隔。
这种形式的表达式可以直接被计算机解析和计算。
例如,表达式"+ 2 3"可以被解析为2加3,得到结果5。
同样地,表达式"- 5 3"可以被解析为5减去3,得到结果2。
二、中缀表达式中缀表达式是我们平时最常见的表达式形式,操作符位于两个操作数之间。
例如,"2 + 3"就是一个中缀表达式。
中缀表达式的一个特点是使用了括号来表示优先级,以及操作符的结合性。
例如,"(2 + 3) * 4"表示先计算括号内的加法,再将结果乘以4。
中缀表达式的解析和计算相对复杂,需要考虑操作符的优先级和结合性,以及括号的使用。
为了方便计算机进行计算,通常需要将中缀表达式转换为其他形式。
三、后缀表达式后缀表达式,也称为逆波兰表达式,是将操作符写在操作数之后的一种表达式形式。
例如,"2 3 +"就是一个后缀表达式。
后缀表达式的一个特点是,操作符和操作数之间也没有括号,而是通过空格或其他分隔符进行分隔。
这种形式的表达式同样可以直接被计算机解析和计算。
后缀表达式的解析和计算相对简单,不需要考虑操作符的优先级和结合性,也不需要使用括号。
计算机可以通过从左到右依次处理操作数和操作符,最终得到结果。
例如,表达式"2 3 +"可以被解析为2加3,得到结果5。
同样地,表达式"5 3 -"可以被解析为5减去3,得到结果2。
前缀、中缀、后缀表达式

本文将让您从头至尾认识 W3Eval 功能性的要点;您将看到一些用于表达式求值的代码。
不过,我们还是先看看表达式求值的经典算法,这样您就会明白 W3Eval 方法的差异究竟有多少。
表达式求值的经典算法编写代码对算术表达式求值的经典方法由 Donald Knuth 描述于 1962 年(请参阅参考资料)。
Knuth 将此概括为三个步骤:∙对中缀表达式进行语法分析∙中缀表达式到后缀表达式的转换∙对后缀表达式求值注意到我们谈到的这个经典算法有些简化:算术表达式只包含操作数、二元操作符和一种括号。
此外,对于每个操作数和操作符,只用单个字符表示,使语法分析直观。
表达式表示法算术表达式中最常见的表示法形式有中缀、前缀和后缀表示法。
中缀表示法是书写表达式的常见方式,而前缀和后缀表示法主要用于计算机科学领域。
中缀表示法中缀表示法是算术表达式的常规表示法。
称它为中缀表示法是因为每个操作符都位于其操作数的中间,这种表示法只适用于操作符恰好对应两个操作数的时候(在操作符是二元操作符如加、减、乘、除以及取模的情况下)。
对以中缀表示法书写的表达式进行语法分析时,需要用括号和优先规则排除多义性。
前缀表示法前缀表示法中,操作符写在操作数的前面。
这种表示法经常用于计算机科学,特别是编译器设计方面。
为纪念其发明家— Jan Lukasiewicz(请参阅参考资料),这种表示法也称波兰表示法。
后缀表示法在后缀表示法中,操作符位于操作数后面。
后缀表示法也称逆波兰表示法(reverse Polish notation,RPN),因其使表达式求值变得轻松,所以被普遍使用。
前缀和后缀表示法有三项公共特征:∙操作数的顺序与等价的中缀表达式中操作数的顺序一致∙不需要括号∙操作符的优先级不相关中缀表达式到后缀表达式的转换要把表达式从中缀表达式的形式转换成用后缀表示法表示的等价表达式,必须了解操作符的优先级和结合性。
优先级或者说操作符的强度决定求值顺序;优先级高的操作符比优先级低的操作符先求值。
前缀 中缀 后缀表达式 题目

前缀中缀后缀表达式题目摘要:一、前缀表达式的概念与作用1.前缀表达式的定义2.前缀表达式的特点3.前缀表达式在编程中的应用二、中缀表达式的概念与作用1.中缀表达式的定义2.中缀表达式的特点3.中缀表达式在编程中的应用三、后缀表达式的概念与作用1.后缀表达式的定义2.后缀表达式的特点3.后缀表达式在编程中的应用四、题目:比较前缀、中缀、后缀表达式的优缺点1.前缀表达式的优缺点2.中缀表达式的优缺点3.后缀表达式的优缺点正文:一、前缀表达式的概念与作用前缀表达式是一种计算表达式的方式,它将运算符写在表达式的最前面,然后是运算对象。
前缀表达式的优点是便于实现计算的逆序,即从右到左进行计算。
在编程中,前缀表达式常用于实现计算器、文本编辑器等程序。
二、中缀表达式的概念与作用中缀表达式是一种将运算符写在表达式的中间,然后是运算对象的表达式形式。
中缀表达式的优点是便于实现程序的递归,因为在递归过程中,可以很容易地知道当前运算符的优先级。
在编程中,中缀表达式常用于实现编译器、解释器等程序。
三、后缀表达式的概念与作用后缀表达式是一种将运算符写在表达式的最后面,然后是运算对象的表达式形式。
后缀表达式的优点是便于实现计算的顺序,即从左到右进行计算。
在编程中,后缀表达式常用于实现数据结构、算法等课程的相关练习。
四、比较前缀、中缀、后缀表达式的优缺点1.前缀表达式的优点:便于实现计算的逆序,常用于计算器等程序;缺点:不利于实现程序的递归。
2.中缀表达式的优点:便于实现程序的递归,常用于编译器等程序;缺点:不利于实现计算的顺序。
3.后缀表达式的优点:便于实现计算的顺序,常用于数据结构等程序;缺点:不利于实现程序的递归。
综上所述,前缀、中缀、后缀表达式各有优缺点,适用于不同的编程场景。
什么是前缀表达式
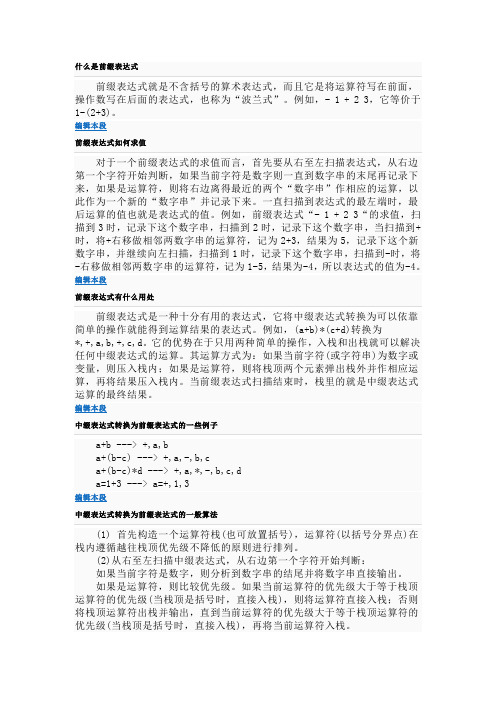
前缀表达式就是不含括号的算术表达式,而且它是将运算符写在前面,操作数写在后面的表达式,也称为“波兰式”。
例如,- 1 + 2 3,它等价于1-(2+3)。
编辑本段前缀表达式如何求值对于一个前缀表达式的求值而言,首先要从右至左扫描表达式,从右边第一个字符开始判断,如果当前字符是数字则一直到数字串的末尾再记录下来,如果是运算符,则将右边离得最近的两个“数字串”作相应的运算,以此作为一个新的“数字串”并记录下来。
一直扫描到表达式的最左端时,最后运算的值也就是表达式的值。
例如,前缀表达式“- 1 + 2 3“的求值,扫描到3时,记录下这个数字串,扫描到2时,记录下这个数字串,当扫描到+时,将+右移做相邻两数字串的运算符,记为2+3,结果为5,记录下这个新数字串,并继续向左扫描,扫描到1时,记录下这个数字串,扫描到-时,将-右移做相邻两数字串的运算符,记为1-5,结果为-4,所以表达式的值为-4。
编辑本段前缀表达式有什么用处前缀表达式是一种十分有用的表达式,它将中缀表达式转换为可以依靠简单的操作就能得到运算结果的表达式。
例如,(a+b)*(c+d)转换为*,+,a,b,+,c,d。
它的优势在于只用两种简单的操作,入栈和出栈就可以解决任何中缀表达式的运算。
其运算方式为:如果当前字符(或字符串)为数字或变量,则压入栈内;如果是运算符,则将栈顶两个元素弹出栈外并作相应运算,再将结果压入栈内。
当前缀表达式扫描结束时,栈里的就是中缀表达式运算的最终结果。
编辑本段中缀表达式转换为前缀表达式的一些例子a+b ---> +,a,ba+(b-c) ---> +,a,-,b,ca+(b-c)*d ---> +,a,*,-,b,c,da=1+3 ---> a=+,1,3编辑本段中缀表达式转换为前缀表达式的一般算法(1) 首先构造一个运算符栈(也可放置括号),运算符(以括号分界点)在栈内遵循越往栈顶优先级不降低的原则进行排列。
前缀表达式计算方法

前缀表达式计算方法前缀表达式,也称为波兰表达式,是一种数学表达式的表示方法。
与我们常见的中缀表达式(运算符位于操作数之间)和后缀表达式(运算符位于操作数之后)不同,前缀表达式将运算符置于操作数之前。
本文将介绍前缀表达式的计算方法及其应用。
一、前缀表达式的基本概念前缀表达式是一种无歧义的数学表达式表示方法,它可以通过简单的规则进行计算。
在前缀表达式中,运算符位于操作数之前,每个运算符都与其相应的操作数紧密相连,形成一个完整的表达式。
例如,加法运算符(+)位于操作数2和3之前的前缀表达式为"+ 2 3"。
二、前缀表达式的计算方法前缀表达式的计算方法相对简单,可以通过以下步骤进行:1. 从右至左扫描前缀表达式,遇到操作数则入栈。
2. 遇到运算符,则从栈中弹出两个操作数进行运算,并将结果入栈。
3. 重复步骤2,直到扫描完整个前缀表达式。
4. 栈中最后剩下的元素即为计算结果。
例如,对于前缀表达式"+ * 2 3 4"的计算过程如下:1. 从右至左扫描前缀表达式,首先遇到的是操作数4,将其入栈。
2. 继续扫描,遇到操作数3,将其入栈。
3. 再次扫描,遇到操作数2,将其入栈。
4. 继续扫描,遇到乘法运算符(*),从栈中弹出操作数2和3,计算结果6,并将其入栈。
5. 最后扫描到加法运算符(+),从栈中弹出操作数6和4,计算结果10,并将其入栈。
6. 完成扫描后,栈中剩下的元素10即为计算结果。
三、前缀表达式的应用前缀表达式在计算机科学和数学领域有着广泛的应用。
其中,其主要应用之一是在编译器和解释器中进行数学表达式的计算。
通过将中缀表达式转换为前缀表达式,可以简化计算过程,提高计算效率。
前缀表达式还可以用于构建抽象语法树(Abstract Syntax Tree,AST)。
AST是一种用于表示程序语言结构的树状数据结构,通过前缀表达式可以方便地构建出相应的AST,进而进行语法分析和程序优化。
前缀中缀后缀表达式转换 题目

前缀中缀后缀表达式转换题目摘要:1.前缀表达式转换成中缀表达式的方法2.中缀表达式转换成后缀表达式的方法3.常见的前缀、中缀和后缀表达式示例4.实践操作:转换实例正文:一、前缀表达式转换成中缀表达式的方法前缀表达式是指由运算符和操作数组成的一种表达式,其中运算符放在操作数之前。
将前缀表达式转换为中缀表达式,主要是将运算符插入到相应的操作数之间。
以下是一个简单的转换方法:1.遍历前缀表达式,遇到运算符,将其插入到操作数之间。
2.若遇到左括号,将其与当前操作数一起放入一个队列。
3.遇到右括号,从队列中弹出两个操作数,进行运算,并将结果放入队列。
4.直到队列为空,依次弹出队列中的操作数,进行运算,得到中缀表达式。
二、中缀表达式转换成后缀表达式的方法中缀表达式是指由运算符和操作数组成的一种表达式,其中运算符放在操作数之间。
将中缀表达式转换为后缀表达式,主要是根据运算符的优先级和结合性进行排序。
以下是一个简单的转换方法:1.遍历中缀表达式,遇到操作数,将其放入一个栈。
2.遇到运算符,根据其优先级和结合性,从栈中弹出相应的操作数进行运算,并将结果放入栈。
3.直到栈为空,依次弹出栈中的操作数,得到后缀表达式。
三、常见的前缀、中缀和后缀表达式示例前缀表达式:+(a*b)中缀表达式:a*b+后缀表达式:ab*+四、实践操作:转换实例1.转换前缀表达式:+(a*(b+c))中缀表达式:a*(b+c)+后缀表达式:abc*+2.转换前缀表达式:-a*(b-c)中缀表达式:-a*(b-c)后缀表达式:-abc*+通过以上内容,我们可以掌握前缀表达式、中缀表达式和后缀表达式的转换方法。
前序表达式中序表达式后序表达式

前序表达式中序表达式后序表达式前序表达式 , 中序表达式 , 后序表达式中序表达式中序表达式即我们⽇常使⽤的表达式,从左往右阅读,结构清晰,但是需要括号改变优先级,对计算机不友好eg:(1+4)*3+10/5,2*3/(2-1)+3*(4-1)前序表达式(波兰表⽰法Polish notation,或波兰记法)前序表达式的特点是操作符置于操作数前⾯,如果操作符的元数(+是⼆元操作符,故元数是2),则语法上不需要括号仍然能被⽆歧义的解释,不需要⼝号改变优先级。
eg:中序表达式: (1+4)*3+10/5前序表达式: + * + 1 4 3 / 10 5前序表达式的计算:eg:+ * + 1 4 3 / 10 5step1: 10 / 5 => 2new expression: + * + 1 4 3 2step2: 1 + 4 => 5new expression: + * 5 3 2step3: 5 * 3 => 15new expression: + 15 2step4: 15 + 2 => 17前序表达式的求值:⾸先要从右⾄左扫描表达式,从右边第⼀个字符开始判断,如果当前字符是数字则继续扫描,如果当前字符是运算符,将运算符右边最近的两个数字做运算,结果作为新的字符记录下来。
⼀直扫描到表达式的最左端时,最后运算的值也就是表达式的值。
后序表达式(逆波兰表⽰法(Reverse Polish notation,RPN,或逆波兰记法)后序表达式所有的操作符置于操作数后⾯,因此也被称为后缀表⽰法。
逆波兰表⽰法不需要括号标识操作符的优先级。
eg:中序表达式: (1+4)*3+10/5后序表达式: 1 4 + 3 * 10 5 / +后序表达式的计算:eg:1 4 + 3 * 10 5 / +step1: 1 + 4 => 5new expression: 5 3 * 10 5 / +step2: 5 * 3 => 15new expression: 15 10 5 / +step3: 10 / 5 => 2new expression: 15 2 +step4: 15 + 2 => 17后序表达式的求值:后序表达式的求值和前序表达式⼗分相似,后序表达式是从左⾄右扫描表达式,从左边第⼀个字符开始判断,如果的那个字符是数字继续扫描,如果是运算符,将运算符左边最近的两个数字做运算,结果作为新的字符记录下来。
前缀表达式

前缀表达式目录前缀表达式就是不含括号的算术表达式,而且它是将运算符写在前面,操作数写在后面的表达式,也称为“波兰式”。
例如,- 1 + 2 3,它等价于1-(2+3)。
对于一个前缀表达式的求值而言,首先要从右至左扫描表达式,从右边第一个字符开始判断,如果当前字符是数字则一直到数字串的末尾再记录下来,如果是运算符,则将右边离得最近的两个“数字串”作相应的运算,以此作为一个新的“数字串”并记录下来。
一直扫描到表达式的最左端时,最后运算的值也就是表达式的值。
例如,前缀表达式“- 1 + 2 3“的求值,扫描到3时,记录下这个数字串,扫描到2时,记录下这个数字串,当扫描到+时,将+右移做相邻两数字串的运算符,记为2+3,结果为5,记录下这个新数字串,并继续向左扫描,扫描到1时,记录下这个数字串,扫描到-时,将-右移做相邻两数字串的运算符,记为1-5,结果为-4,所以表达式的值为-4。
前缀表达式是一种十分有用的表达式,它将中缀表达式转换为可以依靠简单的操作就能得到运算结果的表达式。
例如,(a+b)*(c+d)转换为*,+,a,b,+,c,d。
它的优势在于只用两种简单的操作,入栈和出栈就可以解决任何中缀表达式的运算。
其运算方式为:如果当前字符(或字符串)为数字或变量,则压入栈内;如果是运算符,则将栈顶两个元素弹出栈外并作相应运算,再将结果压入栈内。
当前缀表达式扫描结束时,栈里的就是中缀表达式运算的最终结果。
a+b ---> +,a,ba+(b-c) ---> +,a,-,b,ca+(b-c)*d ---> +,a,*,-,b,c,da=1+3 ---> a=+,1,3(1) 首先构造一个运算符栈(也可放置括号),运算符(以括号分界点)在栈内遵循越往栈顶优先级不降低的原则进行排列。
(2)从右至左扫描中缀表达式,从右边第一个字符开始判断:如果当前字符是数字,则分析到数字串的结尾并将数字串直接输出。
C#算术表达式求值(后缀法),看这一篇就够了

C#算术表达式求值(后缀法),看这⼀篇就够了⼀、种类介绍算术表达式有三种:前缀表达式、中缀表达式和后缀表达式。
⼀般⽤的是中缀,⽐如1+1,前后缀就是把操作符移到前⾯和后⾯,下⾯简单介绍⼀下这三种表达式。
1、前缀表⽰法前缀表⽰法⼜叫波兰表⽰法,他的操作符置于操作数的前⾯(例:+ 1 2),是波兰数学家扬·武卡谢维奇1920年代引⼊的,⽤于简化命题逻辑。
因为我们⼀般认为操作符是在操作数中间的,所以在⽇常⽣活中⽤的不多,但在计算机科学领域占有⼀席之地。
⼀般的表⽰法对计算机来说处理很⿇烦,每个符号都要考虑优先级,还有括号这种会打乱优先级的存在,将使计算机花费⼤量的资源进⾏解析。
⽽前缀表⽰法没有优先级的概念,他是按顺序处理的。
举个例⼦:9-2*3这个式⼦,计算机需要先分析优先级,先乘后减,找到2*3,再进⾏减操作;化成前缀表⽰法就是:- 9 * 2 3,计算机可以依次读取,操作符作⽤于后⼀个操作数,遇到减就是让9减去后⾯的数,⽽跟着9的是乘,也就是说让9减去乘的结果,这对计算机来说很简单,按顺序来就⾏了。
2、中缀表⽰法这也就是我们⼀般的表⽰法,他的操作符置于操作数的中间(例:1 + 2),前⾯也说过这种⽅法不容易被计算机解析,但他符合⼈们的普遍⽤法,许多编程语⾔也就⽤这种⽅法了。
在中缀表⽰法中括号是必须有的,要不然运算顺序会乱掉。
3、后缀表⽰法后缀表⽰法⼜叫逆波兰表⽰法,他的操作符置于操作数的后⾯(例:1 2 +),他和前缀表⽰法都对计算机⽐较友好,但他很容易⽤堆栈解析,所以在计算机中⽤的很多。
他的解释过程⼀般是:操作数⼊栈;遇到操作符时,操作数出栈,求值,将结果⼊栈;当⼀遍后,栈顶就是表达式的值。
因此逆波兰表达式的求值使⽤堆栈结构很容易实现,且能很快求值。
注意:逆波兰记法并不是简单的波兰表达式的反转。
因为对于不满⾜交换律的操作符,它的操作数写法仍然是常规顺序,如,波兰记法/ 6 3的逆波兰记法是6 3 /⽽不是3 6 /;数字的数位写法也是常规顺序。
C语言实现中缀、后缀、前缀表达式_相互转化并求值

1.问题描述(1)表达式求值问题表达式是数据运算的基本形式。
人们的书写习惯是中缀式,如:11+22*(7-4)/3。
中缀式的计算按运算符的优先级及括号优先的原则,相同级别从左到右进行计算。
表达式还有后缀式(如:22 7 4 - * 3 / 11 +)和前缀式(如:+ 11 / * 22 – 7 4 3)。
后缀表达式和前缀表达式中没有括号,给计算带来方便。
如后缀式计算时按运算符出现的先后进行计算。
本设计的主要任务是进行表达式形式的转换及不同形式的表达式计算。
2.数据结构设计(1)表达式求值问题由于表达式中有字符与数字两种类型,故定义结点一个标志域data,标志结点存储的为字符data=2还是数字data=1,再寻找结点中对应的存储位置,读取数字域data1,字符域data2。
而在前缀表达式时,存在表达式逆序,因表达式类型不统一,用栈逆序极不方便,选择构建双向链表,存储表达式。
typedef struct Node //定义存储中缀表达式的结点类型{int data;int data1;char data2;struct Node *next;}Lnode;typedef struct Node2 //定义存储前缀表达式的结点类型{int data;int data1;char data2;struct Node2 *next;struct Node2 *prior;}Lnode2;3.运行、测试与分析(1)表达式求值问题(1)按提示输入中缀表达式,如图1.1所示。
如输入中缀表达式不正确,提示输入有误,如图1.2,1.3所示。
图1.1图1.2图1.3(2)选择表达式转换并求值方式。
按“1”选择中缀表达式求值,如图1.4所示。
图1.4(3)按“2”选择中缀表达式转变为后缀表达式并求值,如图1.5所示。
图1.5(4)按“3”选择中缀表达式转变为前缀表达式并求值,如图1.6所示。
图1.6附录:源代码(1)表达式求值问题#include<stdio.h>#include<stdlib.h>#define MAXNUM 100typedef struct Node //定义存储中缀表达式的结点类型{int data;int data1;char data2;struct Node *next;}Lnode;typedef struct Node2 //定义存储前缀表达式的结点类型{int data;int data1;char data2;struct Node2 *next;struct Node2 *prior;}Lnode2;typedef int selemtype1; //定义运算数栈的结点typedef struct //定义运算数栈的类型{selemtype1 *base;selemtype1 *top;}sqstack1;void InitStack1(sqstack1 &s) //新建一个空运算数栈{s.base=(selemtype1 *)malloc(MAXNUM*sizeof(selemtype1)); s.top=s.base;if(!s.base) printf("出错:申请空间失败!\n");}void Push1(sqstack1 &s,selemtype1 &e) //运算数栈,入栈:插入元素e为新的栈顶元素{ if(s.top-s.base>=MAXNUM)printf("出错:表达式过长!1\n");*s.top++ =e;}void GetTop1(sqstack1 s,selemtype1 &e) //运算数栈,用e返回栈顶元素{e=*(s.top-1);}void Popopnd1(sqstack1 &s,selemtype1 &e) //运算数栈,退栈:删除栈顶元素,并用e返回其值{e=*--s.top;}int stackempy1(sqstack1 s) //运算数栈,若为空栈返回1,否则返回0{if(s.top==s.base) return 1;else return 0;}typedef char selemtype2; //定义运算符栈的结点类型typedef struct //定义运算符栈类型{selemtype2 *base;selemtype2 *top;}sqstack2;void InitStack2(sqstack2 &s) //新建一个空运算符栈{s.base=(selemtype2 *)malloc(MAXNUM*sizeof(selemtype2));s.top=s.base;if(!s.base) printf("出错:申请空间失败!\n");}void Push2(sqstack2 &s,selemtype2 &e) //运算符栈,入栈:插入元素e为新的栈顶元素{ if(s.top-s.base>=MAXNUM)printf("出错:表达式过长!2\n");*s.top++ =e;}void GetTop2(sqstack2 s,selemtype2 &e) //运算符栈,用e返回栈顶元素{e=*(s.top-1);}void Popopnd2(sqstack2 &s,selemtype2 &e) //运算符栈,退栈:删除栈顶元素,并用e返回其值{e=*--s.top;}int stackempy2(sqstack2 s) //运算符栈,若为空栈返回1,否则返回0{if(s.top==s.base) return 1;else return 0;}void priority(char c,int &i) //确定运算符优先级{if (c=='*'||c=='/'||c=='%') i=2 ;else if (c=='+'||c=='-') i=1 ;else i=0;}int compare(char a,char b) //比较栈顶元素运算符与外部运算符优先级大小,外部优先级大则返回1,反之返回0{int in,out;priority(a,in);priority(b,out);if(out>in) return 1;else return 0;}void Operat(sqstack1 &OPND,sqstack2 &OPTR){int num1,num2,num;char c;Popopnd1(OPND,num2);Popopnd1(OPND,num1);Popopnd2(OPTR,c);switch(c){case '+':num=num1+num2;break;case '-':num=num1-num2;break;case '*':num=num1*num2;break;case '/':num=num1/num2;break;case '%':num=num1%num2;break;}Push1(OPND,num);}void Operatqianzhui(sqstack1 &OPND,sqstack2 &OPTR){int num1,num2,num;char c;Popopnd1(OPND,num1);Popopnd1(OPND,num2);Popopnd2(OPTR,c);switch(c){case '+':num=num1+num2;break;case '-':num=num1-num2;break;case '*':num=num1*num2;break;case '/':num=num1/num2;break;case '%':num=num1%num2;break;}Push1(OPND,num);}void houzhuiqiuzhi(Lnode *p,int &e) //后缀表达式求值{sqstack1 OPND; //运算数栈sqstack2 OPTR; //运算符栈int n;char c;p=p->next;InitStack1(OPND);InitStack2(OPTR);while(p){switch(p->data){case 1:n=p->data1;Push1(OPND,n);break;case 2:c=p->data2;Push2(OPTR,c);Operat(OPND,OPTR);break;default:printf("结点有误");break;}p=p->next;}Popopnd1(OPND,n);e=n;}void zhongzhui(Lnode *p) //中缀表达式求值{sqstack1 OPND; //运算数栈sqstack2 OPTR; //运算符栈int n;char c,c2;Lnode *first;first=p;p=p->next;InitStack1(OPND);InitStack2(OPTR);while(!stackempy2(OPTR)||p){while(p){switch(p->data){case 1:n=p->data1;Push1(OPND,n);break;case 2:c=p->data2;if(stackempy2(OPTR)) Push2(OPTR,c);else { switch(c){case '(': Push2(OPTR,c);break;case ')': GetTop2(OPTR,c2);while(c2!='('){Operat(OPND,OPTR);GetTop2(OPTR,c2);}Popopnd2(OPTR,c2);break;default: GetTop2(OPTR,c2);if(compare(c2,c)) Push2(OPTR,c); else { Operat(OPND,OPTR);Push2(OPTR,c);}break;}}break;default: printf("结点有误");break;}p=p->next;}while(!stackempy2(OPTR))Operat(OPND,OPTR);}Popopnd1(OPND,n);p=first->next;while(p){if(p->data==1) printf("%d ",p->data1);if(p->data==2) printf("%c",p->data2);p=p->next;}printf("=%d ",n);}void houzhui(Lnode *p) //中缀表达式转化为后缀表达式{sqstack2 OPTR; //运算符栈Lnode *r,*q,*head;int n;char c,c2;InitStack2(OPTR);p=p->next;q=(Lnode*)malloc(sizeof(struct Node));head=q;while(p){ switch(p->data){case 1:n=p->data1;r=(Lnode*)malloc(sizeof(struct Node));q->next=r;q=q->next;q->data=1;q->data1=n;break;case 2:c=p->data2;if(stackempy2(OPTR)) Push2(OPTR,c);else { switch(c){ case '(': Push2(OPTR,c);break;case ')': Popopnd2(OPTR,c2);while(c2!='('){ r=(Lnode*)malloc(sizeof(struct Node));q->next=r;q=q->next;q->data=2;q->data2=c2;Popopnd2(OPTR,c2);}break;default: GetTop2(OPTR,c2);while(!compare(c2,c)){ Popopnd2(OPTR,c2);r=(Lnode*)malloc(sizeof(struct Node));q->next=r;q=q->next;q->data=2;q->data2=c2;GetTop2(OPTR,c2);}Push2(OPTR,c);break;}}break;default: printf("结点有误");break;}p=p->next;}while(!stackempy2(OPTR)){ Popopnd2(OPTR,c2);r=(Lnode*)malloc(sizeof(struct Node));q->next=r;q=q->next;q->data=2;q->data2=c2;}q->next=NULL;q=head->next;while(q){if(q->data==1) printf("%d ",q->data1);if(q->data==2) printf("%c",q->data2);q=q->next;}houzhuiqiuzhi(head,n);printf("=%d ",n);}void qianzhuiqiuzhi(Lnode2 *p,int &e) //前缀表达式求值{sqstack1 OPND; //运算数栈sqstack2 OPTR; //运算符栈int n;char c;Lnode2 *head;head=p;p=p->next;InitStack1(OPND);InitStack2(OPTR);while(p!=head){switch(p->data){case 1:n=p->data1;Push1(OPND,n);break;case 2:c=p->data2;Push2(OPTR,c);Operatqianzhui(OPND,OPTR); break;default:printf("结点有误");break;}p=p->next;}Popopnd1(OPND,n);e=n;}void qianzhui(Lnode *p) //中缀表达式转化为前缀表达式{sqstack2 OPTR; //运算符栈InitStack2(OPTR);int n;char c,c2;Lnode *first;Lnode2 *q,*head,*r,*head2,*s;first=p;p=p->next;q=(Lnode2*)malloc(sizeof(struct Node2)); //建立存中缀表达式的双向循环链表head=q;while(p){r=(Lnode2*)malloc(sizeof(struct Node2));q->next=r;r->prior=q;q=q->next;q->data=p->data;q->data1=p->data1;q->data2=p->data2;p=p->next;}q->next=head;head->prior=q;s=(Lnode2*)malloc(sizeof(struct Node2)); //建立存前缀表达式的双向循环链表head2=s;while(q!=head){switch(q->data){case 1:n=q->data1;r=(Lnode2*)malloc(sizeof(struct Node2));s->next=r;r->prior=s;s=s->next;s->data=1;s->data1=n;break;case 2:c=q->data2;if(stackempy2(OPTR)) Push2(OPTR,c);else{ GetTop2(OPTR,c2);if(c2==')') Push2(OPTR,c);else{ switch(c){ case ')':Push2(OPTR,c);break;case '(': Popopnd2(OPTR,c2);while(c2!=')'){ r=(Lnode2*)malloc(sizeof(struct Node2));s->next=r;r->prior=s;s=s->next;s->data=2;s->data2=c2;Popopnd2(OPTR,c2);}break;default: GetTop2(OPTR,c2);while(!compare(c2,c)){ Popopnd2(OPTR,c2);r=(Lnode2*)malloc(sizeof(struct Node2));s->next=r;r->prior=s;s=s->next;s->data=2;s->data2=c2;GetTop2(OPTR,c2);}Push2(OPTR,c);break;}}}break;default:printf("结点有误");break;}q=q->prior;}while(!stackempy2(OPTR)){ Popopnd2(OPTR,c2);r=(Lnode2*)malloc(sizeof(struct Node2));s->next=r;r->prior=s;s=s->next;s->data=2;s->data2=c2;}s->next=head2;head2->prior=s;while(s!=head2){if(s->data==1) printf("%d ",s->data1); if(s->data==2) printf("%c",s->data2); s=s->prior;}qianzhuiqiuzhi(head2,n);printf("=%d ",n);}int main(){ char n[10];char c;int i,j,k,a,b,z,y,e;Lnode *p,*q,*first;i=0;e=1;a=0;b=1;z=0;y=0;p=(Lnode*)malloc(sizeof(struct Node));first=p;printf("请输入中缀表达式");do{ c = getchar();if('0'<=c&&c<='9'){ n[i]=c;i++;}else{ switch (c){ case '+':case '-':case '*':case '/':case '%':case '(':case ')':case '\n':{ if(n[0]>'0'&&n[0]<='9'){ q=(Lnode*)malloc(sizeof(struct Node)); p->next=q;p=p->next;for(k=0;k<i;k++){ for(j=0;j<=i-k-2;j++)e=e*10;a=a+(n[k]-'0')*e;e=1;n[k]='0';}p->data=1;p->data1=a;i=0;a=0;}if(c!='\n'){ if(p->data==2){ if(p->data2!=')'&&c!='(')b=0;}q=(Lnode*)malloc(sizeof(struct Node));p->next=q;p=p->next;p->data=2;p->data2=c;if(c=='(') z++;if(c==')') y++;}}default:if(c!='+'&&c!='-'&&c!='*'&&c!='/'&&c!='%'&&c!='\n'&&c!='('&&c!=')') b=0;}}}while (c != '\n');if(z!=y) b=0;p->next=NULL;if(b==0)printf("输入中缀表达式有误");else{printf("输入1中缀表达式求值,输入2后缀表达式求值,输入3前缀表达式求值");scanf("%d",&b);if(b==1) zhongzhui(first);if(b==2) houzhui(first);if(b==3) qianzhui(first);}return 1;}。
C语言实现中缀、后缀、前缀表达式 相互转化并求值

C语言实现中缀、后缀、前缀表达式相互转化并求值1.问题描述(1)表达式求值问题表达式是数据运算的基本形式。
人们的书写习惯是中缀式,如:11+22*(7-4)/3。
中缀式的计算按运算符的优先级及括号优先的原则,相同级别从左到右进行计算。
表达式还有后缀式(如:22 7 4 - * 3 / 11 +)和前缀式(如:+ 11 / * 22 –7 4 3)。
后缀表达式和前缀表达式中没有括号,给计算带来方便。
如后缀式计算时按运算符出现的先后进行计算。
本设计的主要任务是进行表达式形式的转换及不同形式的表达式计算。
2.数据结构设计(1)表达式求值问题由于表达式中有字符与数字两种类型,故定义结点一个标志域data,标志结点存储的为字符data=2还是数字data=1,再寻找结点中对应的存储位置,读取数字域data1,字符域data2。
而在前缀表达式时,存在表达式逆序,因表达式类型不统一,用栈逆序极不方便,选择构建双向链表,存储表达式。
typedef struct Node //定义存储中缀表达式的结点类型{int data;int data1;char data2;struct Node *next;}Lnode;typedef struct Node2 //定义存储前缀表达式的结点类型{int data;int data1;char data2;struct Node2 *next;struct Node2 *prior;}Lnode2;3.运行、测试与分析(1)表达式求值问题(1)按提示输入中缀表达式,如图1.1所示。
如输入中缀表达式不正确,提示输入有误,如图1.2,1.3所示。
图1.1图1.2图1.3(2)选择表达式转换并求值方式。
按“1”选择中缀表达式求值,如图1.4所示。
图1.4(3)按“2”选择中缀表达式转变为后缀表达式并求值,如图1.5所示。
图1.5(4)按“3”选择中缀表达式转变为前缀表达式并求值,如图1.6所示。
什么是前缀表达式

前缀表达式就是不含括号的算术表达式,而且它是将运算符写在前面,操作数写在后面的表达式,也称为“波兰式”。
例如,- 1 + 2 3,它等价于1-(2+3)。
编辑本段前缀表达式如何求值对于一个前缀表达式的求值而言,首先要从右至左扫描表达式,从右边第一个字符开始判断,如果当前字符是数字则一直到数字串的末尾再记录下来,如果是运算符,则将右边离得最近的两个“数字串”作相应的运算,以此作为一个新的“数字串”并记录下来。
一直扫描到表达式的最左端时,最后运算的值也就是表达式的值。
例如,前缀表达式“- 1 + 2 3“的求值,扫描到3时,记录下这个数字串,扫描到2时,记录下这个数字串,当扫描到+时,将+右移做相邻两数字串的运算符,记为2+3,结果为5,记录下这个新数字串,并继续向左扫描,扫描到1时,记录下这个数字串,扫描到-时,将-右移做相邻两数字串的运算符,记为1-5,结果为-4,所以表达式的值为-4。
编辑本段前缀表达式有什么用处前缀表达式是一种十分有用的表达式,它将中缀表达式转换为可以依靠简单的操作就能得到运算结果的表达式。
例如,(a+b)*(c+d)转换为*,+,a,b,+,c,d。
它的优势在于只用两种简单的操作,入栈和出栈就可以解决任何中缀表达式的运算。
其运算方式为:如果当前字符(或字符串)为数字或变量,则压入栈内;如果是运算符,则将栈顶两个元素弹出栈外并作相应运算,再将结果压入栈内。
当前缀表达式扫描结束时,栈里的就是中缀表达式运算的最终结果。
编辑本段中缀表达式转换为前缀表达式的一些例子a+b ---> +,a,ba+(b-c) ---> +,a,-,b,ca+(b-c)*d ---> +,a,*,-,b,c,da=1+3 ---> a=+,1,3编辑本段中缀表达式转换为前缀表达式的一般算法(1) 首先构造一个运算符栈(也可放置括号),运算符(以括号分界点)在栈内遵循越往栈顶优先级不降低的原则进行排列。
中缀、前缀、后缀表达式的运算

中缀、前缀、后缀表达式的运算 中缀表达式,就是在表达式中,操作符在操作数的中间,⽐如 (1+2)*3,+和*在1, 2, 3的中间。
前缀表达式,就是操作符在操作数的前⾯,⽐如 +12,+在1, 2的前⾯。
后缀表达式,就是操作符在操作数的后⾯,⽐如 12+,+在1, 2的后⾯。
为什么会有这么多表达式呢?它们⽬的不同。
中缀表达式,便于我们书写,也符合我们的阅读习惯,在计算机程序中,都是写中缀表达式,但它却不利于计算机进⾏算术计算,因为涉及到优先级和括号。
前缀表达式和后缀表达式中没有括号,并且运算符的优先级也通过它们在表达式中的顺序体现出来了,有利于计算机进⾏算术运算。
前缀表达式也叫波兰表达式,因为它是由⼀个波兰⼈发明的,相应的,后缀表达式也称为逆波兰表达式。
举个例⼦来说明⼀下三者的运算过程,假设计算(3+4)*5-6 使⽤中缀表达式进⾏计算 1,创建两个栈,⼀个是数字栈,⽤来存放操作数,⼀个是字符栈,⽤来存放操作符。
2,算术表达式是⼀个字符串,从左到右循环遍历表达式,依次取出每⼀个字符。
当取出的字符是操作数时,⼊数字栈。
当取出的字符是操作符时,这时还要看操作符的优先级和字符栈是否为空 如果字符栈为空,直接把取出的字符放⼊到字符栈中。
如果字符栈不为空,则要⽐较字符的优先级 如果取出的字符的优先级⼤于等于字符栈中栈顶的字符的优先级,直接把取出的字符放⼊到字符栈中。
如果取出的字符的优先级⽐字符栈中栈顶的字符的优先级低,则要循环进⾏如下操作,直到取出的字符的优先级⼤于等于字符栈中栈顶字符的优先级或者栈为空,此时,把取出的字符放⼊到字 符栈中。
如下操作就是: 1,从字符栈中弹出操作符 2,从数字栈中弹出两个操作数。
3,操作数结合操作符进⾏计算,要注意操作数顺序,后⾯pop出的数在求值的表达式中是前⾯的操作数,尤其是在做减法的时候 4,计算出的值放⼊到数字栈。
为什么要⽐较操作符的优先级呢?因为要确定操作数属于哪个操作符,相邻两个操作符之间的数字是共享的。
算术表达式的前缀表达式,中缀表达式和后缀表达式

算术表达式的前缀表达式,中缀表达式和后缀表达式这里所谓的前缀,中缀,后缀是根据操作符的位置来定的,如果操作符在操作数前面,则称为前缀表达式,例如“- + 1 × + 2 3 4 5”;如果操作符在操作数之间,则称为中缀表达式,例如“1+((2+3)×4)-5”;如果操作符在操作数后面,则称为后缀表达式,例如“1 2 3 + 4 × + 5 -”。
虽然中缀表达式符合人类的日常思维习惯,但是计算机在存储中缀表达式时,需要使用树这种数据结构,如果表达式过于复杂,那么树的高度会变得很高,大大增加了时间复杂度和空间复杂度。
如果转换成线性结构,那么效率将变得高很多,所以需要将中缀表达式先转换成前缀或者后缀表达式,然后依靠栈这种线性数据结构来进行计算。
前缀表达式又叫波兰表达式,后缀表达式又叫逆波兰表达式。
前缀表达式基本没有在商业计算机中使用过,所以现实中用的更多的是后缀表达式。
如何将中缀表达式转化成后缀表达式呢?利用两个栈S1,S2:其中S1存放操作符,S2存放操作数从左往右遍历中缀表达式,如果遇到数字,则放入S2中,如果遇到操作符,则放入S1中。
在放操作符的时候有一定的规则,如果栈为空或栈顶元素为(,则直接压栈。
如果是(,也直接压栈;如果栈顶元素为普通操作符,则比较优先级,如果待压栈的操作符比栈顶操作符优先级高,则直接压栈,否则将S1中的栈顶元素出栈,并压入S2中,再接着比较S1栈顶元素的优先级。
如果遇到),则依次弹出S1栈顶的运算符,并压入S2,直到遇到左括号为止,此时将这一对括号丢弃。
最后将S1中剩余的运算符依次弹出并压入S2,逆序输出S2(从栈底到栈顶)便得到了后缀表达式。
(注意:等号的优先级最低,因为要到最后才进行赋值操作)得到后缀表达式之后,计算就变得方便多了,遇到数字就压栈,遇到操作符的时候,pop出栈顶的两个元素,进行计算后将结果又压入栈中,这样一直下去,直到得到最终结果。
解析算术表达式

解析算术表达式[1]后缀式(逆波兰式)六212011293Leave a Comment Written by Blueve后缀(postfix, 也成逆波兰 reverse Polish)表达式在我们的生活中并不常见,在我们日常中见到的,通常都是中缀(infix)式,例如:3.14 + 15 * (9.2 – 6.5)这是便于人类理解的表达式,之所以便于人类理解,是因为人从小便接受识别此类表达式的教育,而且这种记号方式将运算符和数字明确的分开,不会产生数字堆叠在一起的混乱情况。
但是对于计算机而言,这样的表达式并不好理解,计算机是一种线性读入信息,线性输出信息的工具,人类所通识的中缀式,对于这种规规矩矩按照顺序计算的工具而言,是不容易理解的。
你可能一眼就看出来要先算小括号里的表达式,然后算乘法,最后算加法。
而计算机直接读入的话,可能会先算3.14 + 15,这自然是荒谬的,而后缀法就为计算机计算表达式提供了一种非常有效的解决方案。
这篇文章主要的内容是介绍如何将中缀表达式转换为后缀表达式。
说了这么半天,后缀表达式又是什么样子呢?它又有什么样的优势呢?我们现在来看一组对比:中缀式后缀式a +b a b +a +b *c a b c * +(a + b) * c a b + c *后缀表达式为什么会有优势呢?因为计算机线性读入的特征,我们以第二个表达式为例,以:用后缀式,在计算机的计算过程就是:1. a2. a b3. a b c4. a b c *5. a (b * c) 计算出b * c的值记作x6. a x +7.(a + x) 计算出a + x 的值就是这样一个符合线性读入过程的运算,这样就合理的解决了运算之间优先关系的处理。
那么如何将一个中缀式装换为后缀式呢?其实算法很简单,运用之前我介绍过的“栈”就可以轻易达到这个目的,我们使用两个栈,一个是表达式栈,用来存储转换成后缀表达式的结果,一个是运算符栈,用来暂存表达式中的运算符,这个栈满足条件“从栈顶到栈底,运算符的优先级依次下降”,我们以表达式a + b * (c + d) 作为例子,来模拟一下转换的过程:1.读入数字a,存入表达式栈,紧接着读入运算符+,存入运算符栈2.读入数字b,存入表达式栈,紧接着读入运算符*,由于*比+运算优先级高,所以也可以存入运算符栈3.读入左括号(,(具有最高优先级,所以也存入运算符栈,后面的数字c存入表达式栈4.读入运算符+,存入运算符栈,然后读入数字d,存入表达式栈5.读入右括号),开始弹出运算符栈中的运算符到表达式栈,直到遇到左括号为止6.表达式已经读完了,将运算符栈中的运算符全部弹出到表达式栈,至此后缀表达式已经转换完成!总结下来,基本步骤很明确,就是以下几个步骤:(1)读入,如果是数字,就置入表达式栈,然后重复(1)。
后缀算术表达式求值

实验名称:后缀算术表达式求值背景描述:表达式求值是程序设计语言编译中的一个最基本的问题。
因为任何程序设计语言都必须具有表达式求值的功能,同时表达式的计算应用也相当广泛,比如电力调度系统中的计算遥测、车站票务系统中的票价类型计算公式等。
通常,我们所说的表达式是由运算符、操作数、界限符所组成。
而算术表达式中最常见的表示法形式有中缀、前缀和后缀表示法。
中缀表示法是书写表达式的常见方式,而前缀和后缀表示法主要用于计算机科学领域。
一、表达式表示法1、中缀表达式---将运算符放在两操作数的中间。
在运算中存在运算符的优先权与结合性的问题。
例如运算:a*b+(c-d/e)*f 时,编译器即自左向右逐一检查,当检查到第一个运算符"*"时还无法知道是否执行;待检查到第二个运算符" + "时,因为知道"*"的优先级别高于" + "时,才知道执行"a*b";当继续检查到" ( "时,可知道先执行括号以内部分等。
2、前缀表达式---将运算符放在两操作数的前面。
这种表示法经常用于计算机科学,特别是编译器设计方面。
为纪念其发明家-Jan Lukasiewicz,这种表示法也称波兰表示法。
3、后缀表达式---将运算符放在两操作数的后面。
后缀表达式也称逆波兰表达式,因其使表达式求值变得轻松,所以被普遍使用。
前缀和后缀表示法有三项公共特征:(1)操作数的顺序与等价的中缀表达式中操作数的顺序一致;(2)不需要括号;(3)操作符的优先级不相关。
问题描述:读入一个后缀表达式表达式,利用堆栈来计算该表达式的值,同时要效验后缀表达式是否正确。
输入输出格式:第一种方式:输入:在字符界面上输入一个后缀表达式,其中两相邻操作数之间利用空格隔开。
以"#"表示结束。
输出:如果该后缀表达式正确,那么在字符界面上输出其结果,计算结果小数点后面保留两位有效数字,如果不正确,请在字符界面上输出表达式错误提示。
中缀及后缀算术表达式在运算中的应用研究

Computer Knowledge and Technology 电脑知识与技术第5卷第32期(2009年11月)软件设计开发本栏目责任编辑:谢媛媛中缀及后缀算术表达式在运算中的应用研究郭萌萌,许永昌(山东英才学院,山东济南250104)摘要:表达式求值是程序设计语言编译中的一个最基本问题。
与人们习惯的中缀表示的表达式相比,后缀表达式不存在括号,没有优先级的差别,表达式中各个运算是按照运算符出现的顺序进行的。
因此非常适合串行工作的计算机处理方式。
该文首先对这两种表达式表示方法进行了分析比较,然后通过具体分析实现这两种表达式求值的算法来论证表达式后缀表示优于中缀表示。
最后简要谈一下中缀表达式到后缀表达式的转换。
关键词:中缀表达式;后缀表达式;算符优先;堆栈中图分类号:TP31文献标识码:A 文章编号:1009-3044(2009)32-8921-03A Study of Index and Suffix Arithmetic Expression in the Operation Applied ResearchGUO Meng-meng,XU Yong-chang(Shandong Yingcai College,Jinan 250104,China)Abstract:The expression evaluation is the most basic question in programming language pared with infix expression with which people are familiar,suffix expression does not have the parenthesis,nor does it have the priority difference;each operation is carried out according to the order in which the operator appears.Therefore it is suitable for the serial work of the computer processing mode.This article first analyses and compares these two kinds of expression,then attempts to prove that suffix expression is superior to infix expression through the concrete analysis of the realization of evaluation algorithm of these two kinds of expression.Finally it discusses briefly the trans -formation of infix expression into the suffix expression.Key words:infix expression;suffix expression;priority operator;stack表达式求值是程序设计语言编译中的一个最基本问题。
数学表达式解析汇报(前缀、中缀、后缀)

前缀、中缀、后缀表达式它们都是对表达式的记法,因此也被称为前缀记法、中缀记法和后缀记法。
它们之间的区别在于运算符相对与操作数的位置不同:前缀表达式的运算符位于与其相关的操作数之前;中缀和后缀同理。
举例:(3 + 4) × 5 - 6 就是中缀表达式- × + 3 4 5 6 前缀表达式3 4 + 5 × 6 - 后缀表达式中缀表达式(中缀记法)中缀表达式是一种通用的算术或逻辑公式表示方法,操作符以中缀形式处于操作数的中间。
中缀表达式是人们常用的算术表示方法。
虽然人的大脑很容易理解与分析中缀表达式,但对计算机来说中缀表达式却是很复杂的,因此计算表达式的值时,通常需要先将中缀表达式转换为前缀或后缀表达式,然后再进行求值。
对计算机来说,计算前缀或后缀表达式的值非常简单。
前缀表达式(前缀记法、波兰式)前缀表达式的运算符位于操作数之前。
前缀表达式的计算机求值:从右至左扫描表达式,遇到数字时,将数字压入堆栈,遇到运算符时,弹出栈顶的两个数,用运算符对它们做相应的计算(栈顶元素 op 次顶元素),并将结果入栈;重复上述过程直到表达式最左端,最后运算得出的值即为表达式的结果。
例如前缀表达式“- × + 3 4 5 6”:(1) 从右至左扫描,将6、5、4、3压入堆栈;(2) 遇到+运算符,因此弹出3和4(3为栈顶元素,4为次顶元素,注意与后缀表达式做比较),计算出3+4的值,得7,再将7入栈;(3) 接下来是×运算符,因此弹出7和5,计算出7×5=35,将35入栈;(4) 最后是-运算符,计算出35-6的值,即29,由此得出最终结果。
可以看出,用计算机计算前缀表达式的值是很容易的。
将中缀表达式转换为前缀表达式:遵循以下步骤:(1) 初始化两个栈:运算符栈S1和储存中间结果的栈S2;(2) 从右至左扫描中缀表达式;(3) 遇到操作数时,将其压入S2;(4) 遇到运算符时,比较其与S1栈顶运算符的优先级:(4-1) 如果S1为空,或栈顶运算符为右括号“)”,则直接将此运算符入栈;(4-2) 否则,若优先级比栈顶运算符的较高或相等,也将运算符压入S1;(4-3) 否则,将S1栈顶的运算符弹出并压入到S2中,再次转到(4-1)与S1中新的栈顶运算符相比较;(5) 遇到括号时:(5-1) 如果是右括号“)”,则直接压入S1;(5-2) 如果是左括号“(”,则依次弹出S1栈顶的运算符,并压入S2,直到遇到右括号为止,此时将这一对括号丢弃;(6) 重复步骤(2)至(5),直到表达式的最左边;(7) 将S1中剩余的运算符依次弹出并压入S2;(8) 依次弹出S2中的元素并输出,结果即为中缀表达式对应的前缀表达式。
前缀中缀后缀表达式转换 题目

前缀中缀后缀表达式转换题目摘要:1.表达式的基本概念2.前缀、中缀和后缀表达式的定义3.表达式转换的方法和应用4.总结正文:一、表达式的基本概念在计算机科学中,表达式是指用运算符连接操作数的式子。
表达式可以是数字、字符、变量或者函数调用等。
根据运算符的优先级和结合性,表达式可以按照特定的顺序进行计算,得到一个结果。
二、前缀、中缀和后缀表达式的定义1.前缀表达式:前缀表达式是一种特殊的表达式,它的每个操作都只有一个前驱。
也就是说,我们可以从左到右依次计算每个操作的值,而不需要考虑运算符的优先级。
例如,表达式"a+b"就是一个前缀表达式。
2.中缀表达式:中缀表达式是包含了运算符优先级的表达式。
它的每个操作都可以有零个或多个前驱和后继。
例如,表达式"a*b+c"就是一个中缀表达式。
3.后缀表达式:后缀表达式是一种特殊的中缀表达式,它的每个操作符都有一个后驱,但没有前驱。
后缀表达式的计算顺序是按照运算符的顺序进行的,这样可以避免运算符优先级的问题。
例如,表达式"ab+c"就是一个后缀表达式。
三、表达式转换的方法和应用表达式转换是一种将一种类型的表达式转换为另一种类型的表达式的操作。
常见的表达式转换有前缀表达式转换为中缀表达式,中缀表达式转换为后缀表达式等。
1.前缀表达式转换为中缀表达式:可以通过递归地将前缀表达式的每个操作转换为中缀表达式来实现。
例如,对于前缀表达式"a+b",我们可以转换为中缀表达式"a,+,b"。
2.中缀表达式转换为后缀表达式:可以通过将中缀表达式的每个操作转换为后缀表达式,并将运算符转换为后缀表达式的操作符来实现。
例如,对于中缀表达式"a*b+c",我们可以转换为后缀表达式"ab,+,c"。
表达式转换在编译原理、计算理论等领域有广泛的应用。
例如,在编译器中,将源代码转换为目标代码的过程中,就需要进行表达式的转换和优化。
c#数学表示法(后缀表示法)详解

c#数学表⽰法(后缀表⽰法)详解在笔试中有这么⼀道题⽬,写出⼀个表达式的后缀表⽰形式,当时就迷茫了,什么是后缀表达式,还真没听过。
后来查了下原来是⼀种⽐较特殊的数学表达式,因为在⽇常⽣活中⽤的不多,不太了解。
有三种表达式:前缀表达式、中缀表达式和后缀表达式。
⼀般⽤的是中缀,⽐如1+1,前后缀就是把操作符移到前⾯和后⾯,下⾯我就来介绍⼀下这三种表达式。
1.前缀表⽰法前缀表⽰法⼜叫波兰表⽰法,他的操作符置于操作数的前⾯(例:+ 1 2),是波兰数学家扬·武卡谢维奇1920年代引⼊的,⽤于简化命题逻辑。
因为我们⼀般认为操作符是在操作数中间的,所以在⽇常⽣活中⽤的不多,但在计算机科学领域占有⼀席之地。
⼀般的表⽰法对计算机来说处理很⿇烦,每个符号都要考虑优先级,还有括号这种会打乱优先级的存在,将使计算机花费⼤量的资源进⾏解析。
⽽前缀表⽰法没有优先级的概念,他是按顺序处理的。
举个例⼦:9-2*3这个式⼦,计算机需要先分析优先级,先乘后减,找到2*3,再进⾏减操作;化成前缀表⽰法就是:- 9 * 2 3,计算机可以依次读取,操作符作⽤于后⼀个操作数,遇到减就是让9减去后⾯的数,⽽跟着9的是乘,也就是说让9减去乘的结果,这对计算机来说很简单,按顺序来就⾏了。
再看⼀个复杂点的前缀表达式:复制代码代码如下:- * / 15 - 7 + 1 1 3 + 2 + 1 1- * / 15 - 7 2 3 + 2 + 1 1- * / 15 5 3 + 2 + 1 1- * 3 3 + 2 + 1 1- 9 + 2 + 1 1- 9 + 2 2- 9 45这是⼀个前缀表达式的计算过程,可以看出每次只需计算第⼀个满⾜操作符后跟两个操作数的式⼦,直到最后就是结果了。
2.中缀表⽰法这也就是我们⼀般的表⽰法,他的操作符置于操作数的中间(例:1 + 2),前⾯也说过这种⽅法不容易被计算机解析,但他符合⼈们的普遍⽤法,许多编程语⾔也就⽤这种⽅法了。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
前缀、中缀、后缀表达式它们都是对表达式的记法,因此也被称为前缀记法、中缀记法和后缀记法。
它们之间的区别在于运算符相对与操作数的位置不同:前缀表达式的运算符位于与其相关的操作数之前;中缀和后缀同理。
举例:(3 + 4) × 5 - 6 就是中缀表达式- × + 3 4 5 6 前缀表达式3 4 + 5 × 6 - 后缀表达式中缀表达式(中缀记法)中缀表达式是一种通用的算术或逻辑公式表示方法,操作符以中缀形式处于操作数的中间。
中缀表达式是人们常用的算术表示方法。
虽然人的大脑很容易理解与分析中缀表达式,但对计算机来说中缀表达式却是很复杂的,因此计算表达式的值时,通常需要先将中缀表达式转换为前缀或后缀表达式,然后再进行求值。
对计算机来说,计算前缀或后缀表达式的值非常简单。
前缀表达式(前缀记法、波兰式)前缀表达式的运算符位于操作数之前。
前缀表达式的计算机求值:从右至左扫描表达式,遇到数字时,将数字压入堆栈,遇到运算符时,弹出栈顶的两个数,用运算符对它们做相应的计算(栈顶元素 op 次顶元素),并将结果入栈;重复上述过程直到表达式最左端,最后运算得出的值即为表达式的结果。
例如前缀表达式“- × + 3 4 5 6”:(1) 从右至左扫描,将6、5、4、3压入堆栈;(2) 遇到+运算符,因此弹出3和4(3为栈顶元素,4为次顶元素,注意与后缀表达式做比较),计算出3+4的值,得7,再将7入栈;(3) 接下来是×运算符,因此弹出7和5,计算出7×5=35,将35入栈;(4) 最后是-运算符,计算出35-6的值,即29,由此得出最终结果。
可以看出,用计算机计算前缀表达式的值是很容易的。
将中缀表达式转换为前缀表达式:遵循以下步骤:(1) 初始化两个栈:运算符栈S1和储存中间结果的栈S2;(2) 从右至左扫描中缀表达式;(3) 遇到操作数时,将其压入S2;(4) 遇到运算符时,比较其与S1栈顶运算符的优先级:(4-1) 如果S1为空,或栈顶运算符为右括号“)”,则直接将此运算符入栈;(4-2) 否则,若优先级比栈顶运算符的较高或相等,也将运算符压入S1;(4-3) 否则,将S1栈顶的运算符弹出并压入到S2中,再次转到(4-1)与S1中新的栈顶运算符相比较;(5) 遇到括号时:(5-1) 如果是右括号“)”,则直接压入S1;(5-2) 如果是左括号“(”,则依次弹出S1栈顶的运算符,并压入S2,直到遇到右括号为止,此时将这一对括号丢弃;(6) 重复步骤(2)至(5),直到表达式的最左边;(7) 将S1中剩余的运算符依次弹出并压入S2;(8) 依次弹出S2中的元素并输出,结果即为中缀表达式对应的前缀表达式。
例如,将中缀表达式“1+((2+3)×4)-5”转换为前缀表达式的过程如下:因此结果为“- + 1 × + 2 3 4 5”。
后缀表达式(后缀记法、逆波兰式)后缀表达式与前缀表达式类似,只是运算符位于操作数之后。
后缀表达式的计算机求值:与前缀表达式类似,只是顺序是从左至右:从左至右扫描表达式,遇到数字时,将数字压入堆栈,遇到运算符时,弹出栈顶的两个数,用运算符对它们做相应的计算(次顶元素 op 栈顶元素),并将结果入栈;重复上述过程直到表达式最右端,最后运算得出的值即为表达式的结果。
例如后缀表达式“3 4 + 5 × 6 -”:(1) 从左至右扫描,将3和4压入堆栈;(2) 遇到+运算符,因此弹出4和3(4为栈顶元素,3为次顶元素,注意与前缀表达式做比较),计算出3+4的值,得7,再将7入栈;(3) 将5入栈;(4) 接下来是×运算符,因此弹出5和7,计算出7×5=35,将35入栈;(5) 将6入栈;(6) 最后是-运算符,计算出35-6的值,即29,由此得出最终结果。
将中缀表达式转换为后缀表达式:与转换为前缀表达式相似,遵循以下步骤:(1) 初始化两个栈:运算符栈S1和储存中间结果的栈S2;(2) 从左至右扫描中缀表达式;(3) 遇到操作数时,将其压入S2;(4) 遇到运算符时,比较其与S1栈顶运算符的优先级:(4-1) 如果S1为空,或栈顶运算符为左括号“(”,则直接将此运算符入栈;(4-2) 否则,若优先级比栈顶运算符的高,也将运算符压入S1(注意转换为前缀表达式时是优先级较高或相同,而这里则不包括相同的情况);(4-3) 否则,将S1栈顶的运算符弹出并压入到S2中,再次转到(4-1)与S1中新的栈顶运算符相比较;(5) 遇到括号时:(5-1) 如果是左括号“(”,则直接压入S1;(5-2) 如果是右括号“)”,则依次弹出S1栈顶的运算符,并压入S2,直到遇到左括号为止,此时将这一对括号丢弃;(6) 重复步骤(2)至(5),直到表达式的最右边;(7) 将S1中剩余的运算符依次弹出并压入S2;(8) 依次弹出S2中的元素并输出,结果的逆序即为中缀表达式对应的后缀表达式(转换为前缀表达式时不用逆序)。
因此结果为“1 2 3 + 4 × + 5 -”(注意需要逆序输出)。
编写Java程序将一个中缀表达式转换为前缀表达式和后缀表达式,并计算表达式的值。
其中的toPolishNotation()方法将中缀表达式转换为前缀表达式(波兰式)、toReversePolishNotation()方法则用于将中缀表达式转换为后缀表达式(逆波兰式):注:(1) 程序很长且注释比较少,但如果将上面的理论容弄懂之后再将程序编译并运行起来,还是比较容易理解的。
有耐心的话可以研究一下。
(2) 此程序是笔者为了说明上述概念而编写,仅做了简单的测试,不保证其中没有Bug,因此不要将其用于除研究之外的其他场合。
[java]view plain copy1.package qmk.simple_test;2.import java.util.Scanner;3.import java.util.Stack;4./**5.* Example of converting an infix-expression to6.* Polish Notation (PN) or Reverse Polish Notation (RPN).7.* Written in 2011-8-258.* author QiaoMingkui9.*/10.public class Calculator {11.public static final String USAGE = "== usage ==\n"12.+ "input the expressions, and then the program "13.+ "will calculate them and show the result.\n"14.+ "input 'bye' to exit.\n";15./**16.* param args17.*/18.public static void main(String[] args) {19.System.out.println(USAGE);20.Scanner scanner = new Scanner(System.in);21.String input = "";22.final String CLOSE_MARK = "bye";23.System.out.println("input an expression:");24.input = scanner.nextLine();25.while(input.length() != 026.&& !CLOSE_MARK.equals((input))) {27.System.out.print("Polish Notation(PN):");28.try{29.toPolishNotation(input);30.} catch(NumberFormatException e){31.System.out.println("\ninput error, not a number.");32.} catch(IllegalArgumentExceptione) {33.System.out.println("\ninput error:"+ e.getMessage());34.} catch(Exception e) {35.System.out.println("\ninput error, invalid expression.");36.}37.System.out.print("Reverse Polish Notation (RPN):");38.try{39.toReversePolishNotation(input);40.} catch(NumberFormatException e){41.System.out.println("\ninput error, not a number.");42.} catch(IllegalArgumentExceptione) {43.System.out.println("\ninput error:"+ e.getMessage());44.} catch(Exception e) {45.System.out.println("\ninput error, invalid expression.");46.}47.System.out.println("input a new expression:");48.input = scanner.nextLine();49.}50.System.out.println("program exits");51.}52./**53.* parse the expression , and calculate it.54.* param input55.* throws IllegalArgumentException56.* throws NumberFormatException57.*/58.private static void toPolishNotation(String input)59.throws IllegalArgumentException, NumberFormatException {60.int len = input.length();61.char c, tempChar;62.Stack<Character> s1 = new Stack<Character>();63.Stack<Double> s2 = new Stack<Double>();64.Stack<Object> expression = new Stack<Object>();65.double number;66.int lastIndex = -1;67.for(int i=len-1; i>=0; --i) {68. c = input.charAt(i);69.if(Character.isDigit(c)) {stIndex = readDoubleReverse(input, i);71.number = Double.parseDouble(input.substring(lastIndex, i+1));72.s2.push(number);73.i = lastIndex;74.if((int) number ==number)75.expression.push((int) number);76.else77.expression.push(number);78.} else if(isOperator(c)) {79.while(!s1.isEmpty()80.&& s1.peek() != ')'81.&& priorityCompare(c, s1.peek()) < 0) {82.expression.push(s1.peek());83.s2.push(calc(s2.pop(), s2.pop(), s1.pop()));84.}85.s1.push(c);86.} else if(c == ')') {87.s1.push(c);88.} else if(c == '(') {89.while((tempChar=s1.pop()) != ')') {90.expression.push(tempChar);91.s2.push(calc(s2.pop(), s2.pop(), tempChar));92.if(s1.isEmpty()) {93.throw new IllegalArgumentException(94."bracket dosen't match, missing right bracket ')'.");95.}96.}97.} else if(c == ' ') {98.// ignore99.} else{100.throw new IllegalArgu mentException(101."wrong character '"+ c + "'");102.}103.}104.while(!s1.isEmpty()) {105.tempChar = s1.pop();106.expression.push(tempChar);107.s2.push(calc(s2.pop(), s2.pop(), tempChar));108.}109.while(!expression.isEmpty()) {110.System.out.print(expression.pop() + " ");111.}112.double result = s2.pop();113.if(!s2.isEmpty())114.throw new IllegalArgumentExceptio n("input is a wrong expression.");115.System.out.println();116.if((int) result == result)117.System.out.println("the result is "+ (int) result);118.else119.System.out.println("the result is "+ result);120.}121./**122.* parse the expression, and calculate it.123.* param input124.* throws IllegalArgumentException125.* throws NumberFormatException126.*/127.private static void toReversePolishNotation(String inp ut)128.throws IllegalArgumentException, NumberFormatException {129.int len = input.length();130.char c, tempChar;131.Stack<Character> s1 = new Stack<Character>( );132.Stack<Double> s2 = new Stack<Double>(); 133.double number;134.int lastIndex = -1;135.for(int i=0; i<len; ++i) {136. c = input.charAt(i);137.if(Character.isDigit(c) || c = = '.') {stIndex = readDoubl e(input, i);139.number = Double.parse Double(input.substring(i, lastIndex));140.s2.push(number);141.i = lastIndex - 1;142.if((int) number == number)143.System.out.print((int) number + " ");144.else145.System.out.print(number + " ");146.} else if(isOperator(c)) { 147.while(!s1.isEmpty()148.&& s1.peek() != '('149.&& priorityCompare(c, s1.peek()) <= 0) {150.System.out.print(s1.peek() + " ");151.double num1 = s2.pop();152.double num2 = s2.pop();153.s2.push(cal c(num2, num1, s1.pop()));154.}155.s1.push(c);156.} else if(c == '(') {157.s1.push(c);158.} else if(c == ')') {159.while((tempChar=s1.po p()) != '(') {160.System.out.print(tempChar + " ");161.double num1 = s2.pop();162.double num2 = s2.pop();163.s2.push(cal c(num2, num1, tempChar));164.if(s1.isE mpty()) {165.throw new IllegalArgumentException(166."bracket dosen't match, missing left bracket '('.");167.}168.}169.} else if(c == ' ') { 170.// ignore171.} else{172.throw new IllegalArgu mentException(173."wrong character '"+ c + "'");174.}175.}176.while(!s1.isEmpty()) {177.tempChar = s1.pop();178.System.out.print(tempChar + " ") ;179.double num1 = s2.pop();180.double num2 = s2.pop();181.s2.push(calc(num2, num1, tempChar ));182.}183.double result = s2.pop();184.if(!s2.isEmpty())185.throw new IllegalArgumentExceptio n("input is a wrong expression.");186.System.out.println();187.if((int) result == result)188.System.out.println("the result is "+ (int) result);189.else190.System.out.println("the result is "+ result);191.}192./**193.* calculate the two number with the operation. 194.* param num1195.* param num2196.* param op197.* return198.* throws IllegalArgumentException199.*/200.private static double calc(double num1, double num2, char op)201.throws IllegalArgumentException {202.switch(op) {203.case'+':204.return num1 + num2;205.case'-':206.return num1 - num2;207.case'*':208.return num1 * num2;209.case'/':210.if(num2 == 0) throw new Ille galArgumentException("divisor can't be 0.");211.return num1 / num2;212.default:213.return0; // will never catch up here214.}215.}216./**217.* compare the two operations' priority.218.* param c219.* param peek220.* return221.*/222.private static int priorityCompare(char op1, char op2) {223.switch(op1) {224.case'+': case'-':225.return(op2 == '*'|| op2 == '/'? -1: 0);226.case'*': case'/':227.return(op2 == '+'|| op2 == '-'? 1: 0);228.}229.return1;230.}231./**232.* read the next number (reverse)233.* param input234.* param start235.* return236.* throws IllegalArgumentException237.*/238.private static int readDoubleReverse(String input, in t start)239.throws IllegalArgumentException {240.int dotIndex = -1;241.char c;242.for(int i=start; i>=0; --i) {243. c = input.charAt(i);244.if(c == '.') {245.if(dotIndex != -1)246.throw new IllegalArgumentException(247."there have more than 1 dots in the number.");248.else249.dotIndex = i;250.} else if(!Character.isDigit(c) ) {251.return i + 1; 252.} else if(i == 0) {253.return0;254.}255.}256.throw new IllegalArgumentException("not a n umber.");257.}258.259./**260.* read the next number261.* param input262.* param start263.* return264.* throws IllegalArgumentException265.*/266.private static int readDouble(String input, int star t)267.throws IllegalArgumentException {268.int len = input.length();269.int dotIndex = -1;270.char c;271.for(int i=start; i<len; ++i) {272. c = input.charAt(i);273.if(c == '.') {274.if(dotIndex != -1)275.throw new IllegalArgumentException(276."there have more than 1 dots in the number.");277.else if(i == len - 1)278.throw new IllegalArgumentException(279."not a nu mber, dot can't be the last part of a number.");280.else281.dotIndex = i;282.} else if(!Character.isDigit(c) ) {283.if(dotIndex == -1 || i - dotIndex > 1)284.return i;285.else286.throw new IllegalArgumentException(287."not a nu mber, dot can't be the last part of a number.");288.} else if(i == len - 1) {289.return len;290.}291.}292.293.throw new IllegalArgumentException("not a n umber.");294.}295./**296.* return true if the character is an operator. 297.* param c298.* return299.*/300.private static boolean isOperator(char c) {301.return(c=='+'|| c=='-'|| c=='*'|| c= ='/');302.}303.}下面是程序运行结果(绿色为用户输入):== usage ==input the expressions, and then the program will calculate them and show the result. input 'bye' to exit.input an expression:3.8+5.3Polish Notation (PN):+ 3.8 5.3the result is 9.1Reverse Polish Notation (RPN):3.8 5.3 +the result is 9.1input a new expression:5*(9.1+3.2)/(1-5+4.88)Polish Notation (PN):/ * 5 + 9.1 3.2 + - 1 5 4.88the result is 69.364Reverse Polish Notation (RPN):5 9.1 3.2 + * 1 5 - 4.88 + /the result is 69.364input a new expression:1+((2+3)*4)-5Polish Notation (PN):- + 1 * + 2 3 4 5the result is 16Reverse Polish Notation (RPN):1 2 3 + 4 * + 5 -the result is 16input a new expression:byeprogram exits。
