极点配置与状态反馈
状态反馈极点配置基本理论与方法

状态反馈极点配置基本理论与方法IMB standardization office【IMB 5AB- IMBK 08- IMB 2C】第2章 状态反馈极点配置设计基本理论引言大多数的控制系统的基本结构是由被控对象和反馈控制器构成的闭环系统。
反馈的基本类型包括状态反馈和输出反馈。
其中状态反馈能够提供更加丰富的状态信息。
状态反馈是将系统的每一个状态变量乘相应的反馈系数,然后反馈到输入端与参考输入相加形成的控制规律,作为被控系统的控制输入。
图是一个多输入多输出线性时不变系统状态反馈的基本结构:图 多输入-多输出系统的状态反馈结构图其中受控系统的状态空间表达式为:x Ax Buy Cx=+=由图可知,加入状态反馈后,受控系统的输入为:u Fx v =+其中v 为参考输入,F 为状态反馈增益阵,因此可以得到状态反馈闭环系统的状态空间表达式:()x A BF x Bv y Cx=++=闭环系统的传递函数矩阵:()()1s W s C sI A BF B -=-+⎡⎤⎣⎦由此可见,引入状态反馈后,通过F 的选择,可以改变闭环系统的特征值,是系统获得所要求的性能。
极点配置方法的选择对于一个线性时不变系统进行状态反馈极点配置,一般有四种方法: (1) 传统方法—将系统转化为一个或多个单输入单输出系统。
(2) 直接法—使用稳定的酉矩阵,将这种系统转化为标准型。
(3)矩阵方程法—对矩阵F ,直接解方程AX X BG -Λ=FX G =(4)特征向量法—先找到特征向量x j (等式中矩阵X 的列向量),然后利用等式求解F 。
方法(1)一般难以应用或者数值不稳定。
方法(3)需要解方程,并且对于系统矩阵A 的特征值不能再分配。
最有效并且数值稳定的方法是方法(2)和方法(4)。
其中方法(4)通过使用一系列的迭代算法找到最优解,所以比较复杂。
对于方法(2),当系统的输入多于一个信号输入时,不能确定系统的鲁棒性。
本文结合以上方法提出了一种新的设计方法:首先通过酉变换将状态方程化为一种控制规范形,然后利用最小二乘法解方程的得到最佳的状态反馈矩阵。
极点配置法设计状态反馈控制器——自动控制原理理论篇

设计算法--适用于用能控标准形表示的SI系统的算法
a0 f1 0 a1 f 2 1
an1 f n n1
f1 0 a0 f2 1 a1
fn n1 an1
举例
例8-21 设系统的状态空间描述为
x(t)
0 6
1 0 5x(t) 1u(t)
y(t) 2 1x(t)
试求:(1)求状态反馈矩阵F使闭环系统有期望 极点s1,2=-3±2j; (2)绘制带有状态反馈控制器的状态变量图
举例----求解过程
解: 0
B 1
0 1 0 1 AB 6 51 5
rankS
rankB
AB
0 1
1 5
2
系统能控。
举例----求解过程
期望闭环系统特征多项式为:
(s s1)(s s2 ) (s 3 2 j)(s 3 2 j) s2 6s 13
设: F f1 f2
s sI A BF
6 f1
SI系统,所以设 F f1 f2 fn
| sI A BF |
0 1
0 0
s 0
0
s
s
0
a0
0 a1
1
0
1
0
f1
f
2
f
n
an1 1
极点配置法设计状态反馈控制器
——《自动控制原理-理论篇》第8.8节
7.4 状态反馈和极点配置

可配置条件_极点配置定理
考虑线性定常系统
x Ax Bu
假设控制输入u的幅值是无约束的。如果选取控制规律为
u r Kx
式中K为线性状态反馈矩阵。
定理 (极点配置定理) 线性定常系统可通过线性状态反馈任意地 配置其全部极点的充要条件是,此被控系统状态完全可控。
该定理对多变量系统也成立。
证明 (对单输入单输出系统) 1、充分性 2、必要性
kn 1 ]
由于 u r Kx r KPx ,此时该系统的状态方程为 x ( Ac Bc K ) x Bcr
相应的特征方程为 sI Ac BcK 0
因为非奇异线性变换不改变系统的特征值,当利用 u=r-Kx作为控制输 入时,相应的特征方程与上式相同,均有如下结果。
s
1
0
0
s
0
sI Ac BcK
◆确定将系统状态方程变换为可控标准形的变换矩阵P。若给定的状态方程已是 可控标准形,则P = I。此时无需再写出系统的可控标准形状态方程。非奇异线 性变换矩阵P=QW。
◆利用给定的期望闭环极点,可写出期望的特征多项式为
(s 1() s 2 ) (s n ) sn an1sn1 a1s a0
从而确定出a1* , a2 *,… an *的值。
◆最后得到状态反馈增益矩阵K为
K [ a0 a0 a1 a1
a n1
an1
]
P 1
10
极点配置 例1
【例】 考虑如下线性定常系统
0
1
0
0
x Ax Bu A 0
0
1 , B 0
1 5 6
1
利用状态反馈控制,希望该系统的闭环极点为s = -2±j4和s = -10。试确定状
线性系统的状态反馈及极点配置

现代控制理论实验(一)线性系统的状态反馈及极点配置——09级自动化本科一.实验目的1.了解和掌握状态反馈及极点配置的原理。
2.了解和掌握利用矩阵法及传递函数法计算状态反馈及极点配置的原理与方法。
3.掌握在被控系统中如何进行状态反馈及极点配置,构建一个性能满足指标要求的新系统的方法。
二.实验原理及说明一个控制系统的性能是否满足要求,要通过解的特征来评价,也就是说,当传递函数是有理函数时,它的全部信息几乎都集中表现为它的极点、零点及传递函数。
因此若被控系统完全能控,则可以通过状态反馈任意配置极点,使被控系统达到期望的时域性能指标。
若有被控系统如图3-3-61所示,它是一个Ⅰ型二阶闭环系统。
图3-3-61 被控系统如图3-3-61所示的被控系统的传递函数为:12021S 11)1(1)(a S a S b T TS T TS S T S i i i ++=++=++=φ (3-3-51) 采用零极点表达式为:))(()(210λλφ--=S S b S (3-3-52)进行状态反馈后,如图3-3-62所示,图中“输入增益阵”L 是用来满足静态要求。
图3-3-62 状态反馈后被控系统设状态反馈后零极点表达式为:))(()(21**--=λλφS S b S (3-3-53)1.矩阵法计算状态反馈及极点配置1)被控系统被控系统状态系统变量图见图3-3-63。
图3-3-63 被控系统状态系统变量状态反馈后的被控系统状态系统变量图见图3-3-64。
图3-3-64 状态反馈后的被控系统状态系统变量图图3-3-61的被控系统的状态方程和输出方程为:状态方程:⎪⎪⎪⎩⎪⎪⎪⎨⎧=+-=+-=••1i 1i 2211X Y u T 1X T 1X X T 1X T 1X (3-3-54)⎪⎩⎪⎨⎧=+==•∑CxY u Ax X B C B A 0),,(式中[]01,T 10B 0T 1T 1T 1A ,i i 21=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=⎥⎦⎤⎢⎣⎡=C x x x , 被控系统的特征多项式和传递函数分别为:12010a a b S b )(+++=S S S φB A)C(SI 1--=)(A -SI det a a )(f 0120=++=S S S 可通过如下变换(设P 为能控标准型变换矩阵): —x P X =将∑0C B A ),,(化为能控标准型 ),,(————C B A ∑,即: ⎪⎩⎪⎨⎧=+=•——————x C Y u x A B X 式中 ⎥⎦⎤⎢⎣⎡-==-101a -a 10AP P A — , ⎥⎦⎤⎢⎣⎡==-10B P B 1— , []10b b CP C ==— 2)被控系统针对能控标准型),,(————C B A ∑引入状态反馈:⎥⎦⎤⎢⎣⎡=-=—————式中10k k k xk u ν (3-3-55)可求得对—x 的闭环系统),,—————C B k B A (-∑的状态空间表达式: 仍为能控标准型,即: ⎪⎩⎪⎨⎧=+-=•————————)(x C Y u x B k B A X 式中 ⎥⎦⎤⎢⎣⎡+-+-=-)()(—————1100k a k a 10k B A则闭环系统),,(——————C B k B A -∑的特征多项式和传递函数分别为: )()(—————00112k k a k a k)B (A SI det )(f ++++=⎥⎦⎤⎢⎣⎡--=S S S )k a (k a b S b B )k B A (SI C )(00112011k ———————)(+++++=⎥⎦⎤⎢⎣⎡--=-S S S φ3)被控系统如图3-3-61所示:其中:05.01==T T i则其被控系统的状态方程和输出方程为:[]XY uX X 0110012020=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--=期望性能指标为:超调量M P ≤20%;峰值时间t P ≤0.5秒。
6.2-6.3 反馈控制与极点配置-系统镇定

n 1
状态反馈极点配置定理(6/6)
如果由期望的闭环极点所确定的特征多项式为 f*(s) sn a1*sn-1 … an*
那么,只需令fK(s) f*(s),即取
a1 kn a1*, , an k1 an* 则可将状态反馈闭环系统K(ABK, B, C)的极点配置在特 征多项式f*(s)所规定的极点上 即证明了充分性 同时, 我们还可得到相应的状态反馈阵为 K=[k1 k2 … kn] 其中
能通过反馈控制而达到渐近稳定的系统是可镇定的
镇定只要求闭环极点位于复平面的左半开平面之内
镇定问题的重要性主要体现在3个方面: 首先, 稳定性往往是控制系统能够正常工作的必要条 件, 是对控制系统的最基本的要求; 其次, 许多实际的控制系统是以渐近稳定作为最终设 计目标;
系统镇定(2/2)
SISO系统状态反馈极点配置方法(5/10)
3. 求反馈律: 因此开环特征多项式
f(s) s22s5,
而由期望的闭环极点1j2所确定的期望闭环特征多项式 f*(s) s22s5,
则得状态反馈阵K为
~ 1 * K K Tc 2 [ a 2 - a 2 [ 5 - ( -5 ) - 7 / 3 a 1 - a 1 ]T c 2
对能控规范II形 馈阵如下
( A, B) 进行极点配置,
求得相应的状态反
*
~ * K an an
an 1 an 1
*
a1 a1
因此, 原系统的相应状态反馈阵K为
~ 1 K KTc 2
SISO系统状态反馈极点配置方法(3/10)
下面通过两个例子来说明计算状态反馈阵K的方法 例6-2 设线性定常系统的状态方程为
线性系统状态反馈与极点配置

实验报告课程名称:现代控制理论实验名称:线性系统状态反馈与极点配置、实验目的1. 学习并掌握利用MATLAB编程平台进行控制系统设计与仿真的方法。
2. 通过仿真实验,研究并总结线性定常系统状态反馈对系统控制性能影响的规律。
3. 通过仿真实验,研究并总结状态反馈对状态不完全能控系统控制性能影响的规律。
二、实验内容(一)实验任务:1. 自行选择一个状态完全能控型SISO 系统模型及参数,并设定系统控制性能指标,根据性能指标要求计算期望的极点并进行极点配置,设计MatLab实验程序(或SimuLink模拟图)及实验步骤,仿真研究状态反馈矩阵对系统控制性能的影响;2. 自行选择一个状态不完全能控型SISO 系统模型及参数,并设定系统控制性能指标,根据性能指标要求进行极点配置,设计MatLab实验程序(或SimuLink模拟图)及实验步骤,仿真研究状态反馈矩阵对系统控制性能的影响;根据实验结果,总结各自的规律。
三、实验设计1. 实验条件1. 利用本学期所学的现代控制理论的知识为基础。
2. 笔记本电脑,matlab四、实验过程1. 设计状态完全能控型SISO 系统模型及参数:a)首先判断系统的能控性= ,是Rack([B AB]) = 2,因此此系统为可控的系统。
可以进行任意极点配置。
则期望极点配置二重根1b ) 再求状态反馈阵 :c ) 根据给定的极点,得到期望特征多项式:d )比较和 各对应项系数,可解得:e )即状态反馈控制器:u=-K*x状态反馈闭环系统空间表达式 x=A-B*K*xA1 = A -B*K = [0 1 ; 1 -2]2. 设计状态不完全能控型 SISO 系统模型及参数:a )首先判断系统的能控性, Rank ([B AB]) = 1,因此系统是不完全能控的,b )再求状态反馈阵c )将期望极点配置二重根 1,则:d )比较 和 各对应项系数,可解得:任意值e )即状态反馈控制器:u=-K*x 状态反馈闭环系统空间表达式 x=A-B*K*xA1 = A -B*K = [01; 1 1]五、实验结果(曲线、数据等)1 •状态完全能控型SISO 系统模型:a )配置极点前的波形: A=[0 1; 0 1]不能进行任意极点配 设)b)配置极点后的波形: A1 = A -B*K = [01; 1-2]3. 状态不完全能控型SISO 系统模型a )配置极点前的波形:A=[1 01]■* l-lgu-'E 1 fit E占Jl 血血JWEfllulk 氐*lap ffilndort 也 b□X Fi1J j dk %鵲 、七禺v 插-<2 D £ ■ dM IP 2*S4«|> R :吐parish13ID ・■-霊■・4卜2-1J ftTO2D3) 4D 也Ihrme liucondy.)*a)配置极点后的波形:六、实验结果分析与讨论1•状态完全能控型SISO系统模型通过配置极点后动态性能变好,但是稳态误差不能消除。
状态反馈与极点配置报告

自动控制原理(课程设计)一、题目用MATLAB创建用户界面,并完成以下功能:(1)由用户输入被控系统的状态空间模型、闭环系统希望的一组极点;(2)显示未综合系统的单位阶跃响应曲线;(3)显示采用一般设计方法得到的状态反馈矩阵参数;(4)显示闭环反馈系统的单位阶跃响应曲线;(5)将该子系统嵌入到寒假作业中程序中。
分别对固定阶次和任意阶次的被控系统进行设计。
分别给出设计实例。
二、运行结果界面:如图由用户输入被控系统的状态空间模型、闭环系统希望的一组极点例如,输入010001034A⎡⎤⎢⎥=⎢⎥⎢⎥--⎣⎦,1B⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,[]2000C=,0D=,闭环系统希望的一组极点:22j-+、22j--、5-如图所示:被控系统的单位阶跃响应曲线闭环系统的单位阶跃响应曲线状态反馈矩阵显示三、讨论该闭环控制系统的状态反馈与极点配置设计系统可用于任意阶次的控制系统。
在此之前,我还做了一个固定阶次的控制系统状态反馈与极点配置的Matlab 控制台程序(见附录二)。
该系统的利用状态反馈进行极点任意配置所采用的方法为一般方法,其步骤如下:①判断受控系统是否完全能控;②由给定的闭环极点要求确定希望的闭环特征多项式的n个系数~i a;③确定原受控系统的特征多项式系数ia;④确定系统状态反馈矩阵~~~~[,,,]12nff fF=的诸元素~~11ii if a a-=--;⑤确定原受控系统化为能控标准形的变换阵的逆1P-,⑥确定受控系统完成闭环极点配置任务的状态反馈阵~1F F P-=。
四、参考文献[1]黄家英.《自动控制原理》.高等教育出版社,2010.5[2]唐向红,郑雪峰.《MATLAB及在电子信息类》.电子工业出版社,2009.6[3]吴大正,高西全.《MATLAB新编教程》.机械工业出版社,2008.4五、附录function varargout = tufeiqiang(varargin)%TUFEIQIANG M-file for tufeiqiang.fig% TUFEIQIANG, by itself, creates a new TUFEIQIANG or raises the existing% singleton*.%% H = TUFEIQIANG returns the handle to a new TUFEIQIANG or the handle to% the existing singleton*.%% TUFEIQIANG('Property','Value',...) creates a new TUFEIQIANG usingthe% given property value pairs. Unrecognized properties are passed via % varargin to tufeiqiang_OpeningFcn. This calling syntax produces a% warning when there is an existing singleton*.%% TUFEIQIANG('CALLBACK') and TUFEIQIANG('CALLBACK',hObject,...) call the% local function named CALLBACK in TUFEIQIANG.M with the given input % arguments.%% *See GUI Options on GUIDE's Tools menu. Choose "GUI allows only one% instance to run (singleton)".%% See also: GUIDE, GUIDATA, GUIHANDLES% Edit the above text to modify the response to help tufeiqiang% Last Modified by GUIDE v2.5 20-May-2015 23:49:56% Begin initialization code - DO NOT EDITgui_Singleton = 1;gui_State = struct('gui_Name', mfilename, ...'gui_Singleton', gui_Singleton, ...'gui_OpeningFcn', @tufeiqiang_OpeningFcn, ...'gui_OutputFcn', @tufeiqiang_OutputFcn, ...'gui_LayoutFcn', [], ...'gui_Callback', []);if nargin && ischar(varargin{1})gui_State.gui_Callback = str2func(varargin{1});endif nargout[varargout{1:nargout}] = gui_mainfcn(gui_State, varargin{:});elsegui_mainfcn(gui_State, varargin{:});end% End initialization code - DO NOT EDIT% --- Executes just before tufeiqiang is made visible.function tufeiqiang_OpeningFcn(hObject, eventdata, handles, varargin) % This function has no output args, see OutputFcn.% hObject handle to figure% eventdata reserved - to be defined in a future version of MATLAB% handles structure with handles and user data (see GUIDATA)% varargin unrecognized PropertyName/PropertyValue pairs from the% command line (see VARARGIN)% Choose default command line output for tufeiqianghandles.output = hObject;% Update handles structureguidata(hObject, handles);% UIWAIT makes tufeiqiang wait for user response (see UIRESUME)% uiwait(handles.figure1);% --- Outputs from this function are returned to the command line. function varargout = tufeiqiang_OutputFcn(hObject, eventdata, handles) % varargout cell array for returning output args (see VARARGOUT);% hObject handle to figure% eventdata reserved - to be defined in a future version of MATLAB% handles structure with handles and user data (see GUIDATA)% Get default command line output from handles structurevarargout{1} = handles.output;function WZH_Callback(hObject, eventdata, handles)% hObject handle to WZH (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB% handles structure with handles and user data (see GUIDATA)A=get(handles.edit1,'String');A=char(A);A=str2num(A);B=get(handles.edit2,'String');B=char(B);B=str2num(B);C=get(handles.edit3,'String');C=char(C);C=str2num(C);D=get(handles.edit4,'String');D=char(D);D=str2num(D);sys = ss(A,B,C,D);axes(handles.axes1);set(handles.axes1,'unit','normalized');step(sys);%title('••×••••••••••••×•••ì•••ú••')set(findobj(gca,'Type','line','Color',[0 0 1]),...'Color','red',...'LineWidth',2)% --- Executes on button press in BFK.function BFK_Callback(hObject, eventdata, handles)% hObject handle to BFK (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)A=get(handles.edit1,'String');A=char(A);A=str2num(A);B=get(handles.edit2,'String');B=char(B);B=str2num(B);C=get(handles.edit3,'String');C=char(C);C=str2num(C);D=get(handles.edit4,'String');D=char(D);D=str2num(D);P=get(handles.edit5,'String');P=char(P);P=str2num(P);K = acker(A,B,P);at = A-B*K;bt = B;ct = C;dt = D;%[num,den]=zp2tf(z,p,k);%[num1,den1]=cloop(num,den);axes(handles.axes1);set(handles.axes1,'unit','normalized');%step(cloop(num,den));%rlocus(A,B,K,0)%step(num1,den1);sys = ss(at,bt,ct,dt);step(sys);title('±••··••••••••••••×•••ì•••ú••')set(findobj(gca,'Type','line','Color',[0 3 3]),...'Color','yellow',...'LineWidth',2)function FKC_Callback(hObject, eventdata, handles)% hObject handle to FKC (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)A=get(handles.edit1,'String');A=char(A);A=str2num(A);B=get(handles.edit2,'String');B=char(B);B=str2num(B);Z=get(handles.edit5,'String');Z=char(Z);Z=str2num(Z);Zif rank(ctrb(A,B)) == rank(A)N = acker(A,B,Z);Nstr=num2str(N)H = findobj('tag','edit6');set(H,'string',str);elsemsgbox('•••••••••••••••••••••••• ');endfunction pushbutton6_Callback(hObject, eventdata, handles)% hObject handle to pushbutton6 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)A=get(handles.edit1,'String');AA=char(A);AA=str2num(A);AB=get(handles.edit2,'String');BB=char(B);BB=str2num(B);BM = ctrb(A,B);if rank(M) == rank(A)msgbox('•••••ê••••••••••••••••••');%[num,den]=zp2tf(z,p,k);%[num1,den1]=cloop(num,den);%step(cloop(num,den));%rlocus(A,B,K,0)%step(num1,den1);elsemsgbox('•••••••••••••••••••••••• '); end。
自动控制原理学生实验:线性系统的状态反馈及极点配置
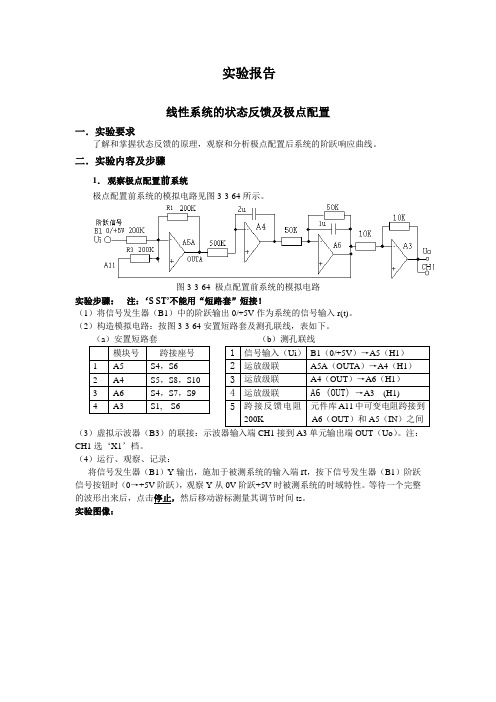
实验报告线性系统的状态反馈及极点配置一.实验要求了解和掌握状态反馈的原理,观察和分析极点配置后系统的阶跃响应曲线。
二.实验内容及步骤1.观察极点配置前系统极点配置前系统的模拟电路见图3-3-64所示。
图3-3-64 极点配置前系统的模拟电路实验步骤:注:‘S ST’不能用“短路套”短接!(1)将信号发生器(B1)中的阶跃输出0/+5V作为系统的信号输入r(t)。
(2)构造模拟电路:按图3-3-64安置短路套及测孔联线,表如下。
(3)虚拟示波器(B3)的联接:示波器输入端CH1接到A3单元输出端OUT(Uo)。
注:CH1选‘X1’档。
(4)运行、观察、记录:将信号发生器(B1)Y输出,施加于被测系统的输入端rt,按下信号发生器(B1)阶跃信号按钮时(0→+5V阶跃),观察Y从0V阶跃+5V时被测系统的时域特性。
等待一个完整的波形出来后,点击停止,然后移动游标测量其调节时间ts。
实验图像:由图得ts=3.880s 2.观察极点配置后系统 极点的计算:受控系统如图所示,若受控系统完全可控,则通过状态反馈可以任意配置极点。
受控系统设期望性能指标为:超调量M P ≤5%;峰值时间t P ≤0.5秒。
由1095.01t 707.0%5eM n n 2n p 1/p 2=≥⇒≤-==⇒≤=--ωωζωπζζζπ取因此,根据性能指标确定系统希望极点为:⎪⎩⎪⎨⎧--=+-=07.707.707.707.7*2*1j j λλ受控系统的状态方程和输出方程为:⎪⎩⎪⎨⎧=+=-----⋅-xC y b x A x μ式中][01,10,020120,21=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡=----C b A x x x系统的传递函数为:202020a S a S βS β)(2012010++=+++=S S S G受控制系统的可控规范形为:[][]020T C C b T b a a T A T A X T X X C Y U b X A X K K i o K K KK k K K K ===⎥⎦⎤⎢⎣⎡==⎥⎦⎤-⎢⎣⎡-=⎥⎦⎤-⎢⎣⎡-===⎩⎨⎧=+=---10111,1020120010T ββ为变换阵),(式中当引入状态反馈阵K K =[K 0K 1]后,闭环系统()K K K K K C b K b A ,,-的传递函数为:()()()01201120120)20(20)(K S K S K a S K a S S S G o ++++=+++++=ββ而希望的闭环系统特征多项为:1001.14))(()(2*2*1**12*++=--=++=S S S S a S a S S f oλλ 令G K (S)的分母等于F #(S),则得到K K 为:[][]9.58010-==K K K k最后确定原受控系统的状态反馈阵K :由于 1-=T K K k求得和===---111,T C b T b T A T A K k K求得 ⎥⎥⎦⎤⎢⎢⎣⎡-=-1102011T所以状态反馈阵为: [][]9.59.91102019.580-=⎥⎥⎦⎤⎢⎢⎣⎡--=K极点配置系统如图所示:极点配置后系统根据极点配置后系统设计的模拟电路见下图所示。
状态反馈与闭环极点配置

16
§3.2-2 单输入系统的极点配置 确定反馈增益阵 K 为
1 ⎤ ⎡0 0 ˆ −1 = [ −4 66 14] ⎢0 1 −12 ⎥ K = KT ⎢ ⎥ ⎢ ⎣1 −18 144 ⎥ ⎦ = [14 −186 1220]
− 1 ± j.
则 A + BK 的特征值为 −2,
17
§3.2-3 多输入系统的极点配置 分两种情形进行讨论。 (1) A 为循环矩阵 A 为循环矩阵,则必有向量 引理3.1 若 ( A, B ) 能控, α ∈ \ p×1 , 使得 ( A, Bα ) 单输入能控。 证明:因为 A 为循环矩阵,故 A 的互异特征根各自对应 一个若当块,设 λ1 , λ 2 , " λσ 为 A 的互异特征值,对( A, B ) 进行非奇异线性变换,令
的系数。
使得
9
§3.2-2 单输入系统的极点配置 令 则由
ˆ = KT = [k K 0
k1 " kn −1 ]
(3.2.7)
ˆ ˆ = T −1 AT + T −1bKT = T −1 ( A + bK )T ˆ + bK A ˆK ˆ +b ˆ 与 A + bK 有相同的特征值。 知 A
由(3.2.5), (3.2.7)得
24
§3.2-3 多输入系统的极点配置 证明:必要性:即定理3.4。 充分性:用反证法。设 ( A, B ) 不完全能控,则对其进行 能控性分解
⎡ A11 A12 ⎤ ⎡ B1 ⎤ −1 −1 ˆ ˆ A = T AT = ⎢ , B = T B = ⎢ ⎥ (3.2.18) ⎥ ⎣0⎦ ⎣ 0 A22 ⎦ ( A11 , B1 ) 为完全能控。则对任一状态反馈矩阵 K , 令 ˆ = KT = [ K K ], 则有 K
现代控制理论基础_周军_第五章状态反馈与状态观测器
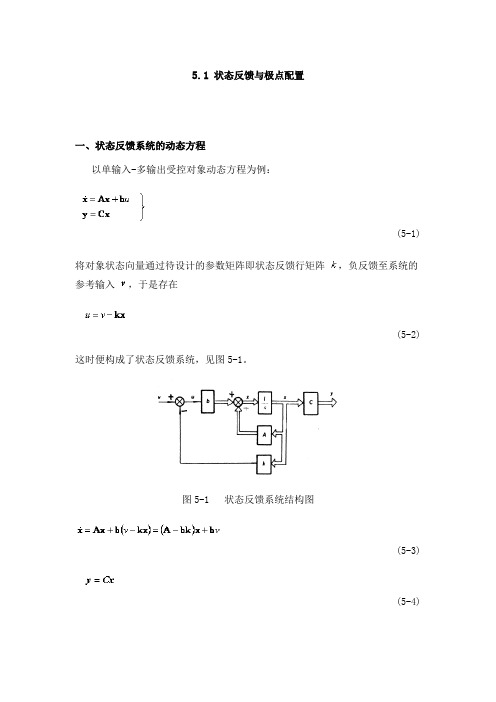
5.1状态反馈与极点配置一、状态反馈系统的动态方程以单输入-多输出受控对象动态方程为例:(5-1)将对象状态向量通过待设计的参数矩阵即状态反馈行矩阵,负反馈至系统的参考输入,于是存在(5-2)这时便构成了状态反馈系统,见图5-1。
图5-1 状态反馈系统结构图(5-3)(5-4)式中v为纯量,为维向量,为维矩阵,为维向量,为维行矩阵,为维向量,为维矩阵。
为闭环状态阵,为闭环特征多项式。
二、用状态反馈使闭环极点配置在任意位置上的充要条件是:受控对象能控证明若式(5-1)所示对象可控,定可通过变换化为能控标准形,有若在变换后的状态空间内引维状态反馈矩阵:(5-5)其中分别为由状态变量引出的反馈系数,则变换后的状态反馈系统动态方程为:(5-6)(5-7)式中(5-8)该式与仍为能控标准形,故引入状态反馈后,系统能控性不变。
特征方程为:(5-9)显见,任意选择阵的个元素,可使特征方程的个系数满足规定要求,能保证特征值(即闭环极点)任意配置。
将逆变换代入式(5-6),可求出原状态空间内的状态反馈系统状态方程:(5-10)与式(5-3)相比,式(5-10)所示对象应引入状态反馈阵为:(5-11)需指出,当受控对象可控时,若不具有能控标准形形式,并不必象如上证明那样去化为能控标准形,只要直接计算状态反馈系统闭环特征多项式,这时,其系数为的函数,与给定极点的特征多项式系数相比较,便可确定。
能控的多输入-多输出系统,经如上类似分析可知,实现闭环极点任意配置的状态反馈阵K为维。
若受控对象不稳定,只要有能控性,完全可由状态反馈配置极点使系统稳定。
状态变量受控情况下,引入状态反馈表示增加一条反馈通路,它能改变反馈所包围环节的传递特性,即通过改变局部回路的极点来改变闭环极点配置。
不能控状态变量与控制量无关,即使引入状态反馈,对闭环极点位置也不会产生任何影响,这是因为传递函数只与系统能控、能观测部分有关的缘故。
若不能控状态变量是稳定的状态变量,那么系统还是能稳定的,否则,系统不稳定。
7.4 状态反馈和极点配置

这是具有线性状态反馈的闭环系统的特征方程,它一定与期望特征方程相等。 通过使s的同次幂系数相等,可得
7
极点配置定理_充分性
a0 k0 a0
a1 k1 a1
an 1 kn 1 an 1 求解上述方程组,得到 ki
的值,则
K KP 1 [k 0 k1
[ a0 a0 a1 a1
0 1 an1 0
0 0 1 Bc P B 0 1
6
极点配置定理_充分性
设 K KP [k 0 k1 kn 1 ] 由于 u r Kx r KPx ,此时该系统的状态方程为 x ( Ac Bc K ) x Bc r
从而确定出a1* , a2 *,… an *的值。 ◆最后得到状态反馈增益矩阵K为 K [ a0 a0 a1 a1
1 an 1 an 1 ] P
10
极点配置 例1
【例】 考虑如下线性定常系统
1 0 0 0 , B 0 A 0 0 1 Ax Bu x 5 6 1 1 利用状态反馈控制,希望该系统的闭环极点为s = -2±j4和s = -10。试确定状 态反馈增益矩阵K。
0 0 1 Ac P AP 0 a0
x Ac x Bcu
1 0 0 a1
0 1 0 a2
上式为可控标准形。选取一组期望的特征值为 1 , 2 , , n ,则 期望的特征方程为
( s 1 )( s 2 )
* n 1 * * ( s n ) s n an s ... a s a 1 1 0 0
an1 1 0 0 1 0 0 0
线性系统的状态反馈及极点配置

线性系统的状态反馈及极点配置1.前言随着现代控制理论的不断发展和成熟,线性系统的状态反馈控制在控制理论中得到了广泛的应用,并成为了控制领域中重要的一种控制方法。
状态反馈控制能够将系统的状态进行反馈,并利用反馈得到的信息对系统进行控制,从而达到使系统达到预期控制目标的目的。
本文将从状态反馈控制的原理和实现方法两方面介绍线性系统的状态反馈及极点配置。
2.状态反馈控制的原理状态反馈控制是建立在现代控制理论的基础上的一种高级控制方法。
状态反馈控制的基本思想是在系统中引入反馈环节,设计一个反馈控制器,将系统的状态量反馈给控制器,控制器再根据反馈信号输出控制量,以期望控制系统按照预期的运动轨迹运行。
因此,状态反馈控制要实现以下两个步骤:- 系统状态量的测量:首先要在系统中安装测量传感器,实时地测量系统状态量,使得状态量可以被反馈到控制器中。
- 反馈控制器的设计:设计一个反馈控制器,将系统的状态量反馈给控制器,控制器再根据反馈信号输出控制量,实现对系统的精确控制。
因此,状态反馈控制的基本原理就是将系统状态量反馈到控制器中,以期望控制系统按照预期的运动轨迹运行。
2.2 状态空间模型与状态反馈控制状态空间模型是状态反馈控制的基础。
状态空间模型是一种方便描述线性系统动态行为和控制器的模型。
对于线性时不变系统,我们可以用如下的状态变量描述:x(t) = [x1(t),x2(t),...,xn(t)]T其中,x(t) 是系统在时刻 t 的状态量,n 是状态量的数量,x1(t),x2(t),...,xn(t) 分别是系统的每个状态量。
状态空间模型可以用一组线性常微分方程描述:dx/dt = Ax + Bu其中,A 是系统的状态方程矩阵,B 是输入矩阵,C 是输出矩阵,D 是直接耦合矩阵。
系统的状态反馈控制可以表示为:u(t) = -Kx(t)其中,K 是状态反馈矩阵。
将状态反馈控制引入到状态空间模型中,可以得到控制器的状态空间模型为:y = Cx上述控制器的状态空间模型就是一个闭环系统,通过反馈控制器将系统状态返回到系统,形成了一个反馈环。
状态反馈极点配置方法的研究

实验报告课程线性系统理论基础实验日期2016 年月日专业班级姓名学号同组人实验名称状态反馈极点配制方法的研究评分批阅教师签字一、实验目的1.掌握状态反馈系统的极点配置;2.研究不同配置对系统动态特性的影响。
二、实验内容原系统如图3—2所示。
图中,X1和X2是可以测量的状态变量.图3-2 系统结构图试设计状态反馈矩阵,使系统加入状态反馈后其动态性能指标满足给定的要求:(1) 已知:K=10,T=1秒,要求加入状态反馈后系统的动态性能指标为:σ%≤20%,ts≤1秒.(12) 已知:K=1,T=0。
05秒,要求加入状态反馈后系统的动态性能指标为:σ%≤5%,ts≤0.5秒。
状态反馈后的系统,如图3-3所示:图3—3 状态反馈后系统结构图分别观测状态反馈前后两个系统的阶跃响应曲线,并检验系统的动态性能指标是否满足设计要求。
三、实验环境 MATLAB R2015B四、实验原理(或程序框图)及步骤 (1)实验原理一个受控系统只要其状态是完全能控的,则闭环系统的极点可以任意配置。
极点配置有两种方法:①采用变换矩阵T ,将状态方程转换成可控标准型,然后将期望的特征方程和加入状态反馈增益矩阵K 后的特征方程比较,令对应项的系数相等,从而决定状态反馈增益矩阵K;②基于Carlay-Hamilton 理论,它指出矩阵状态矩阵A 满足自身的特征方程,改变矩阵特征多项式)(A 的值,可以推出增益矩阵K ,这种方法推出增益矩阵K 的方程式叫Ackermann 公式。
五、程序源代码(1)num=[10];den=[1 1 10];[A,B,C,D]=tf2ss(num,den);p=eig(A)'P=[-3+sqrt(—142)/2;-3—sqrt(—142)/2;] K=place(A,B,P)p=eig(A—B*K)'sysnew=ss(A-B*K,B,C,D)step(sysnew/dcgain(sysnew))title('极点配置后系统阶跃响应’)num=[10];den=[1 1 10];[A,B,C,D]=tf2ss(num,den);step(A,B,C,D)title('极点配置前系统的阶跃响应’)(2)num=[1];den=[1 1 0.5];[A,B,C,D]=tf2ss(num,den);p=eig(A)’P=[—6+sqrt(-36);-6-sqrt(—36);]K=place(A,B,P)p=eig(A-B*K)'sysnew=ss(A—B*K,B,C,D)step(sysnew/dcgain(sysnew))title('极点配置后系统的阶跃响应’)num=[1];den=[1 1 0。
(第11讲)极点配置与状态反馈

Ao P 1 AP, bo P 1b, co cP
第一能观标准型 四川理工自动化教研室
tgq77@
Review
SISO系统第二能控、能观标准型
第二能控标准型 1 0 0 0 0 0 0 0 0 1 0 0 Ac 0 0 0 1 0 , b c 0, cc b0 b1 b2 b3 b4 0 0 0 0 1 0 a0 a1 a2 a3 a4 1 1 n 1 1 cAn 1
•在外扰下无静差跟踪。如使状态和控制的 二次型积分函数最小,即最优控制。
J (x, u) xT Qx uT Ru dt
0
四川理工自动化教研室
tgq77@
SISO系统的极点配置:问题表述
已知系统方程
x Ax bv y cx
* * 1 , * ,, * 和n个期望闭环极点值 2 n
A
y
四川理工自动化教研室
tgq77@
Review
0 1 Ac 0 0 0
SISO系统第一能控、能观标准型
T Qc b Ab An 1b
第一能控标准型
Ao
0 0 0 a0 1 Ac T 1 AT , b c T 1b, c c cT 0 0 0 0 a1 1 0 0 a2 , b c 0, c c 1 2 3 4 5 0 1 0 a3 0 0 0 0 1 a4 T T T T P 1 Qo c cA cAn1 A ,b c ,c b
u
B
x
A
H
线性系统状态反馈与极点配置

实验报告课程名称:现代控制理论实验名称:线性系统状态反馈与极点配置一、实验目的1. 学习并掌握利用MATLAB编程平台进行控制系统设计与仿真的方法。
2. 通过仿真实验,研究并总结线性定常系统状态反馈对系统控制性能影响的规律。
3. 通过仿真实验,研究并总结状态反馈对状态不完全能控系统控制性能影响的规律。
二、实验内容(一)实验任务:1. 自行选择一个状态完全能控型SISO系统模型及参数,并设定系统控制性能指标,根据性能指标要求计算期望的极点并进行极点配置,设计MatLab实验程序(或SimuLink模拟图)及实验步骤,仿真研究状态反馈矩阵对系统控制性能的影响;2. 自行选择一个状态不完全能控型SISO系统模型及参数,并设定系统控制性能指标,根据性能指标要求进行极点配置,设计MatLab实验程序(或SimuLink模拟图)及实验步骤,仿真研究状态反馈矩阵对系统控制性能的影响;根据实验结果,总结各自的规律。
三、实验设计1.实验条件1.利用本学期所学的现代控制理论的知识为基础。
2.笔记本电脑,matlab四、实验过程1.设计状态完全能控型SISO系统模型及参数:X=(0101)X+(01)Xy=(11)Xa)首先判断系统的能控性[X XX] = [0111],是Rack([B AB]) = 2,因此此系统为可控的系统。
可以进行任意极点配置。
则期望极点配置二重根1。
b)再求状态反馈阵K=(X0 ,X1):X(x)=det[λI−(A+bK)]=X2−X1X−X0c)根据给定的极点,得到期望特征多项式:X∗(X)=(X−1)(X−1)d)比较X(x)和X∗(X)各对应项系数,可解得:X0=−1X1=2K=(−12)e)即状态反馈控制器:u=-K*x状态反馈闭环系统空间表达式x=A-B*K*xA1 = A – B*K = [0 1;1 -2]2.设计状态不完全能控型SISO系统模型及参数:X=(1001)X+(1)Xy=(11)Xa)首先判断系统的能控性[X XX] = [1100], Rank([B AB]) = 1,因此系统是不完全能控的,不能进行任意极点配置。
线性系统状态反馈区域极点配置算法研究

线性系统状态反馈区域极点配置算法研究摘要20世纪50年代后期,控制理论由经典控制理论向现代控制理论转变,现代控制理论是在引入状态和状态空间概念的基础上发展起来的。
与经典控制理论一样,现代控制系统中仍然主要采用反馈控制结构,但不同的是,经典控制理论中主要采用输出反馈,而现代控制系统中主要采用内部状态反馈。
状态反馈可以为系统控制提供更多的信息反馈,从而实现更优的控制。
闭环系统极点的分布情况决定于系统的稳定性和动态品质,因此,可以根据对系统动态品质的要求,规定闭环系统的极点所应具备的分布情况,把极点的配置作为系统的动态品质指标。
这种把极点配置在某位置的过程称为极点配置。
在空间状态法中,一般采用反馈系统状态变量或输出变量的方法,来实现系统的极点配置。
本论文对线性系统的状态反馈区域极点配置的算法进行了研究,分别以具有 稳定裕度和具有圆域极点约束的状态反馈控制器设计为例,利用线性矩阵不等式LMI处理方法,编写系统的MATLAB仿真程序。
最后以同样的方法对不确定系统状态反馈区域极点配置进行了研究,结果证明了设计方法的正确性和有效性。
关键词:线性系统;状态反馈;极点配置;线性矩阵不等式;不确定系统Algorithmic Research for Regional PoleAssignment of Linear System Via StateFeedback ControllersABSTRACTIn the late 1950s, control theory later by classical control theory to modern control theory shift, modern control theory is introducing state and state space concept developed on the basis of. As with classical control theory, modern control system still mainly uses the feedback control structure, but different is, classical control theory mainly uses the output feedback, and modern control system mainly uses the internal state feedback. State feedback control for system provide more information feedback, so as to achieve better control.The distribution of closed-loop system poles depends on system stability and dynamic quality, therefore, can according to the system dynamic quality request, provisions that poles of close-loop system should have the distribution of the pole, configuration of the system dynamic quality indicators. The position of the poles in the process called poles. In space, the general state method in the feedback system state variables or output variable method to achieve system poles. This thesis studied the algorithm of linear system state feedback regional poles, and respectively by the state feedback controller design of stability margin of and has round domain constraints as examples, by using the linear matrix inequality LMI treatment methods, writing MATLAB simulation program of system. Finally in the same way the uncertain system state feedback regional poles are studied, and the result shows the design method is correct and effective.Key words:Linear system;State feedback;Pole placement;LMI;Uncertain system目录摘要............................................................................................................................................ΙABSTRACT...........................................................................................................................П1 绪论 (1)1.1课题背景及意义 (1)1.2 极点配置简介 (1)1.3 本论文研究的主要工作 (2)2理论基础及数学准备 (3)2.1 区域极点配置问题 (3)2.2 状态反馈 (4)2.3 线性矩阵不等式LMI (6)2.3.1 线性矩阵不等式LMI基本变换引理 (7)2.3.2 LMI工具箱介绍 (8)2.4 本章小结 (10)3线性定常系统状态反馈区域极点配置算法研究 (11)3.1 精确极点配置 (11)3.1.1 问题描述 (11)3.1.2 算法步骤 (12)3.1.3 仿真分析 (12)3.2具有稳定裕度的区域极点配置 (15)3.2.1 问题描述 (16)3.2.2具有稳定裕度的状态反馈控制器设计 (16)3.2.3程序清单 (17)3.2.4仿真结果 (18)3.3具有圆域极点约束的状态反馈控制器设计 (21)3.3.1 问题描述 (21)3.3.2具有圆域极点约束的状态反馈控制器设计 (21)3.3.3 程序清单 (22)3.3.4仿真结果 (23)3.4 本章小结 (26)4 线性不确定系统状态反馈区域极点配置算法研究 (27)4.1 不确定性 (27)4.2线性不确定系统区域极点配置 (27)4.2.1 问题描述 (27)4.2.2 不确定系统区域极点约束的状态反馈控制器设计 (28)4.2.3 仿真分析 (30)4.3 本章小结 (32)结论 (33)致谢 (34)参考文献 (35)1 绪 论1.1 课题背景及意义在20世纪50年代蓬勃兴起的航天技术的推动下,1960年前后开始了从经典控制理论到现代控制理论的过渡,其中一个重要标志就是卡尔曼系统地将状态空间概念引入到控制理论中来。
状态反馈极点配置基本理论与方法

第2章 状态反馈极点配置设计基本理论2.1引言大多数的控制系统的基本结构是由被控对象和反馈控制器构成的闭环系统。
反馈的基本类型包括状态反馈和输出反馈。
其中状态反馈能够提供更加丰富的状态信息。
状态反馈是将系统的每一个状态变量乘相应的反馈系数,然后反馈到输入端与参考输入相加形成的控制规律,作为被控系统的控制输入。
图2.1是一个多输入多输出线性时不变系统状态反馈的基本结构:图2.1 多输入-多输出系统的状态反馈结构图其中受控系统的状态空间表达式为:x Ax Buy Cx=+= (2.1)由图2.1可知,加入状态反馈后,受控系统的输入为:u Fx v =+ (2.2)其中v 为参考输入,F 为状态反馈增益阵,因此可以得到状态反馈闭环系统的状态空间表达式:()x A BF x Bv y Cx=++= (2.3)闭环系统的传递函数矩阵:()()1s W s C sI A BF B -=-+⎡⎤⎣⎦ (2.4)由此可见,引入状态反馈后,通过F 的选择,可以改变闭环系统的特征值,是系统获得所要求的性能。
2.2极点配置方法的选择对于一个线性时不变系统进行状态反馈极点配置,一般有四种方法: (1) 传统方法—将系统转化为一个或多个单输入单输出系统。
(2) 直接法—使用稳定的酉矩阵,将这种系统转化为标准型。
(3) 矩阵方程法—对矩阵F ,直接解方程AX X BG -Λ= (2.5a) FX G = (2.5b)(4) 特征向量法—先找到特征向量x j (等式(2.5)中矩阵X 的列向量),然后利用等式(2.5b)求解F 。
方法(1)一般难以应用或者数值不稳定。
方法(3)需要解(2.5a)方程,并且对于系统矩阵A 的特征值不能再分配。
最有效并且数值稳定的方法是方法(2)和方法(4)。
其中方法(4)通过使用一系列的迭代算法找到最优解,所以比较复杂。
对于方法(2),当系统的输入多于一个信号输入时,不能确定系统的鲁棒性。
状态反馈与闭环极点配置极点配置条件

状态观测器的闭环极点可任意配置的充要条件为
系统状态完全可观测
30
例: 设系统的状态空间表达式为 1 1 0 1 状态方程同前 1 1 0 x 0 u x 面极点配置例 0 1 3 0
4
状态反馈系统的状态方 程为 ( A BK ) x Br x yCx
状态反馈系统的传递函 数为 G ( s ) C ( sI A BK ) 1 B
综合的手段:改变 K 阵的参数 综合的目的:改变系统矩阵,从而改变系统的特性 注:状态反馈通常只用系数阵即可满足要求, 一般不需要采用动态环节
自动控制原理
控制系统分析与设计的
状态空间方法2 ——综合与设计
(第八章)
1
状态空间法综合的基本概念
综合问题的三大要素:
受控系统、性能指标、反馈控制律
综合与设计的主要特点:
以采用状态反馈为主 具有较系统的综合理论 基于非优化型指标的极点配置方法 基于优化类性能指标的目标函数极值法
2
主要内容
通过状态反馈,将系统的闭环极点配置为
1 2 3 1
15
解: 状态反馈系统的特征多项式为
f ( s ) det[ sI A BK ] s 3 ( k 1 3 )s 2 ( k 2 2 k 1 2 )s ( k 3 3 k 2 3 k 1 6 )
r
-
u
B
x
∫
A
x
C
y
H
6
3.
状态反馈与输出反馈比较
反馈功能: 状态反馈——完全反馈 输出反馈——不完全反馈
反馈作用: 两种反馈均可改变系统的特征方程和特征值; 输出反馈可视为状态反馈的一种特例。
实验二 状态反馈与极点配置

实验二 状态反馈与极点配置一、实验目的a) 掌握状态反馈极点配置的设计方法。
b) 掌握运用模拟运算放大电路实现状态反馈。
c) 验证极点配置理论。
二、实验仪器a) TDN —AC/ACS 型自动控制系统实验箱一台b) 示波器c) 万用表三、实验原理和电路为了更好地达到系统所要求的各种性能指针,需要通过设计系统控制器,改善原有系统的性能。
由于系统的性能与其极点分布位置有密切关系,因而极点配置是系统设计的关键。
极点配置就是利用状态反馈或输出反馈使闭环系统的极点位于所希望的极点位置。
在系统综合设计中,状态反馈和输出反馈是两种常用的反馈形式,而在现代控制理论中系统的物理特性是采用系统内部状态变量来描述的,利用内部状态变量乘以系数(向量)与系统参考输入综合构成的反馈系统,具有更优的控制效果。
1、单输入单输出状态反馈的极点配置受控系统如图2-1,图2-1受控系统其中状态变量1()1/G S S =,2()1/(0.051)G S S =+,状态变量1x 、2x ,对系统进行极点配置,达到系统期望的性能指针:输出超调量5%P M ≤;峰值时间0.5p t s ≤;系统频宽10b ω≤;跟踪误差0p e =(对于阶跃输入)。
i. 确定受控系统的状态空间模型211()()x u x G S =-,122()x x G S =,1y x =,系统的状态方程为:.11.2220200101x x u x x ⎡⎤-⎡⎤⎡⎤⎡⎤⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦⎢⎥⎣⎦;[]1210x y x ⎡⎤=⎢⎥⎣⎦ ii.确定期望的极点21P M e ζ-=;21p n t ωζ=-;22412244b ωωζζζ=-+-+可解得0.707ζ≥,选0.707ζ=;9n ω≥由10b ω≤选10n ω=。
这样期望极点为:*17.077.07j λ=-+*27.077.07j λ=--iii. 确定状态反馈矩阵K原系统特征多项式:12110det()...2020n s n sI A s a s a s a s s ---=++++=++期望的闭环系统特征多项式:**212det()()()14.1100sI A BK s s s s λλ--=--=++ 计算K :K =[10020-,14.120-]=[80,-5.9]计算变换矩阵p :1111111[...]...1n n n a p A b Ab b a a ----⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦1/20011p ⎡⎤=⎢⎥-⎣⎦[][]1/20080 5.99.9 5.911K K p ⎡⎤==-=-⎢⎥-⎣⎦iv. 确定输入放大系数L闭环传递函数为2()20/(14.1100)G s s s =++系统要求跟踪阶跃信号误差为0则000lim(1())lim (1/()/)1/5p t s e y t s s G s s L →→==-=-=- 得L=52、极点配置的系统结构图图2-2极点配置后的系统将原系统的反馈线路与状态x1反馈线路合并后图2-3极点配置后的系统一、实验内容及步骤1、根据图2-4接线图2-4极点配置后系统的模拟电路M、峰值时间2、输入阶跃信号,用示波器观察并记录系统输出的波形,测量超调量Pt。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
输出反馈对能控性、能观性的影响
定理:输出至状态微分处的反馈不改变系统 的能观性,但可能改变系统的能控性。
u
B
x x C y
A
x (A HC)x Bv
y Cx
H
示例:Y (s) U (s)
b1s b0 s2 a1s a0
A
0 1
a0 a1
,
b
b1 b2
,
c
0
1
A
hc
0 1
无直接传输系统的状态反馈
原系统
x Ax Bu
y Cx
引入状态反馈 新系统
u v Kx
x (A BK)x Bv
y Cx
v uB
x x C y
A
K
状态反馈增益矩阵K的维数?系统的特征多项式和传 递函数?
输出反馈至参考微分处
新系统
x (A HC)x Bu y Cx
传递函数 C(sI A HC)1B
Ao P1AP, bo P1b, co cP
0 1 0 0 0 0
0
0
1
0
0
1
Ao
0 0
0 0
0 0
1 0
0 1
,
bo
2 3
,
co
1
0
0
0
0
a0 a1 a2 a3 a4 4
第一能观标准型
Review
SISO系统第二能控、能观标准型1
第二能控标准型
0 1 0 0 0
0 0 0 0 a0
b1
1
0
0
0
a1
b2
Ao
0 0
1 0
0 1
0 0
a2 a3
,
b
o
bb43
,
co
0
1 n1 1 cAn1
P1
1
n1 1
cA c
Ao P1AP,bo P1b,co cP
0 0 0 1
0 0 0 1 a4
b5
第二能观标准型
Review
状态变换不改变系统能控/能观性
x
Ax Bu y Cx
状态变换
x Px
x P1x
x P1APx P1Bu
y CPx
D
u
B x P1
x
s 1 I
x Px C
y
P1
x
AP
D
u
B
x
P1 x s1I x P
x
C
y
A
基于状态空间模型的设计与综合
包括如下主要内容:
状态反馈与输出反馈 闭环系统的能控性和能观性 SISO系统的极点配置 全维观测器及其设计
k1
0 a0
k0
Y (s) V (s)
s2
(a1
b1s b0 k1)s
(a0
k0 )
1
a1
k1
例题:状态反馈的影响
给定系统
0 1 0
x
1
0 x 1 u
y
0
1 x
引入状态反馈 u v kx,k k0 k1
问题:引入状态反馈,对闭环能控性、能 观性有何影响?
思路:计算引入状态反馈前后系统的能控、能观阵
教学要求与重点内容
教学要求: 熟练掌握状态反馈与输出反馈、极点配置 熟练掌握状态观测器的设计方法 掌握分离原理、全维观测器设计方法
重点内容 状态反馈与输出反馈的基本结构、性质和有关定理 SISO系统的极点配置 全维观测器的设计
Agenda 状态反馈与输出反馈 闭环系统的能控性和能观性 SISO系统的极点配置
Agenda 状态反馈与输出反馈 闭环系统的能控性和能观性 SISO系统的极点配置
线性反馈系统的时间域综合
综合问题的提法
•问题:受控系统。限于考虑严格真连续时 间线性时不变系统
•一目些标特:征性量能x或指y运A标x动C。xB过综v程合的后某系种统期应望该形满式足。的 •手段:控制输入。用反馈控制形式,包括 状态反馈和输出反馈。即:
定理:状态反馈不改变系统的能控性,但
可能改变系统的能观性。(我们不证明)
v uB
x x C y
x (A BK)x Bv
A
y Cx
K
示例:Y (s) U (s)
b1s b0 s2 a1s a0
A
0 a0
1 a1
,
b
10,
c
b0
b1
0 A bk a0
1 a1
10k0
a0 a1
h0
h1
0
1
0 1
a0 h0
a1
h1
Y (s) V (s)
s2
(a1
b1s b0 h1)s (a0
h0 )
输出反馈对能控性、能观性的影响
定理:输出至参考输入的反馈不改变系统的 能控性和能观性。
vu
B
x x C y
x (A BFC)x Bv
A
y Cx
F
有谁来示意或说明,为什么输出至参考输入 的反馈不改变系统的能控性和能观性?
现代控制理论
(第11讲 2009年4月26日) 状态反馈与输出反馈 闭环系统能控性和能观性 SISO系统的极点配置 自动化教研室 谭功全
Review
状态空间模型的结构图和状态图
D
u
x B
s1I x
C
y
x Ax Bu
A
y Cx Du
D
u
B x s1I x C
y
A
Review
SISO系统第一能控、能观标准型
0
0
1
0
0
0 0
T An1b
Ab
b
n1
1
1
n1 1
Ac T 1AT, bc T 1b, cc cT
Ac
0 0
0 0
0 0
1 0
0 1
,
bc
0, 0
cc
b0
b1
b2
b3
b4
a0 a1 a2 a3 a4
1
Ao AcT , bo cTc , co bTc
uB
x x C y
A H
输出反馈至参考输入处
新系统
x (A BFC)x Bv y Cx
传递函数 C(sI A BFC)1B
vu B
x x C y
A F
状态反馈与输出反馈的比较
反馈属性:状态反馈是完全信息反馈,输 出反馈往往是不完全信息反馈。
反馈功能:(基于时间域性能指标进行综 合)状态反馈优于输出反馈,输出反馈一 定能由状态反馈实现,即令FC=K即可。
反馈途径:输出反馈是物理可构成的,状 态反馈在物理上不能构成。即,输出反馈 实现起来比较方便。
扩展等价:不能测量或不便测量的状态, 需要利用状态观测器进行重构,才能进行 状态反馈;提高输出反馈的能力是进行输
Agenda
状态反馈与输出反馈
闭环系统的能控性和能观性
SISO系统的极点配置
状态反馈对能控性、能观性的影响
u v Kx,或u v Fy
性能指标的类型
第一能控标准型
0 0 0 0 a0
1
1
0
0
0
a1
0
T Qc b Ab An1b
Ac T 1AT,bc T 1b,cc cT
Ac
0 0
10 01Biblioteka 0 0a2 a3,
b
c
0, 0
cc
1
2
3
4
5
0 0 0 1 a4
0
Ao AcT , bo cTc , co bTc
P1 Qo c cA cAn1 T
