金融计量学实验报告
金融计量实训报告

金融计量实训报告一、实训背景随着金融市场的不断发展,金融计量分析在金融领域的应用越来越广泛。
金融计量分析是运用数学、统计学和计算机技术对金融市场进行定量分析和预测的一种方法。
为了提高我们的金融计量分析能力,我们进行了金融计量实训。
二、实训目的1. 熟悉金融计量分析的基本概念和方法;2. 掌握金融计量分析软件的使用;3. 提高金融计量分析在实际问题中的应用能力;4. 培养团队合作精神。
三、实训内容1. 金融计量分析基本概念和方法(1)金融时间序列分析:介绍了时间序列的平稳性、自相关性、季节性等概念,以及单位根检验、自回归模型、移动平均模型等方法。
(2)金融回归分析:介绍了线性回归、多元线性回归、非线性回归等模型,以及变量选择、模型诊断和模型修正等方法。
(3)金融风险管理:介绍了风险度量、风险控制、风险对冲等概念,以及VaR模型、压力测试等方法。
2. 金融计量分析软件的使用(1)EViews:介绍了EViews的基本操作、数据导入、模型估计、结果分析等功能。
(2)R语言:介绍了R语言的基本语法、数据操作、统计函数、绘图功能等。
3. 金融计量分析在实际问题中的应用(1)股票市场预测:选取某只股票的历史数据,运用时间序列分析方法对其未来走势进行预测。
(2)债券收益率分析:选取某只债券的历史数据,运用回归分析方法分析其收益率与影响因素之间的关系。
(3)金融风险管理:运用VaR模型对某金融机构的资产组合进行风险度量,并制定相应的风险控制措施。
四、实训过程1. 实训前期:学习金融计量分析的基本概念和方法,了解EViews和R语言的基本操作。
2. 实训中期:运用所学知识对实际金融问题进行分析,如股票市场预测、债券收益率分析等。
3. 实训后期:对实训过程进行总结,撰写实训报告。
五、实训成果1. 熟悉了金融计量分析的基本概念和方法,掌握了EViews和R语言的使用。
2. 提高了金融计量分析在实际问题中的应用能力,培养了团队合作精神。
计量经济实验报告多元(3篇)

第1篇一、实验目的本次实验旨在通过多元线性回归模型,分析多个自变量与因变量之间的关系,掌握多元线性回归模型的基本原理、建模方法、参数估计以及模型检验等技能,提高运用计量经济学方法解决实际问题的能力。
二、实验背景随着经济的发展和社会的进步,影响一个变量的因素越来越多。
在经济学、管理学等领域,多元线性回归模型被广泛应用于分析多个变量之间的关系。
本实验以某地区居民消费支出为例,探讨影响居民消费支出的因素。
三、实验数据本实验数据来源于某地区统计局,包括以下变量:1. 消费支出(Y):表示居民年消费支出,单位为元;2. 家庭收入(X1):表示居民家庭年收入,单位为元;3. 房产价值(X2):表示居民家庭房产价值,单位为万元;4. 教育水平(X3):表示居民受教育程度,分为小学、初中、高中、大专及以上四个等级;5. 通货膨胀率(X4):表示居民消费价格指数,单位为百分比。
四、实验步骤1. 数据预处理:对数据进行清洗、缺失值处理和异常值处理,确保数据质量。
2. 模型设定:根据理论知识和实际情况,建立多元线性回归模型:Y = β0 + β1X1 + β2X2 + β3X3 + β4X4 + ε其中,Y为因变量,X1、X2、X3、X4为自变量,β0为截距项,β1、β2、β3、β4为回归系数,ε为误差项。
3. 模型估计:利用统计软件(如SPSS、R等)对模型进行参数估计,得到回归系数的估计值。
4. 模型检验:对估计得到的模型进行检验,包括以下内容:(1)拟合优度检验:通过计算R²、F统计量等指标,判断模型的整体拟合效果;(2)t检验:对回归系数进行显著性检验,判断各变量对因变量的影响是否显著;(3)方差膨胀因子(VIF)检验:检验模型是否存在多重共线性问题。
5. 结果分析:根据模型检验结果,分析各变量对因变量的影响程度和显著性,得出结论。
五、实验结果与分析1. 拟合优度检验:根据计算结果,R²为0.812,F统计量为30.456,P值为0.000,说明模型整体拟合效果较好。
金融计量实验总结范文

随着我国金融市场的不断发展,金融计量方法在金融领域的研究和应用日益广泛。
为了更好地理解和掌握金融计量方法,我参加了本次金融计量实验课程。
通过近一段时间的学习和实践,我对金融计量方法有了更深入的认识,以下是我对本次实验的总结。
一、实验目的本次实验旨在通过实际操作,让学生掌握金融计量方法的基本原理和应用,提高学生运用计量经济学方法解决实际问题的能力。
二、实验内容本次实验主要内容包括:1. 金融时间序列数据的处理:通过对金融时间序列数据的收集、整理和分析,了解金融市场的动态变化,为后续的计量模型建立提供数据基础。
2. 市场异常现象的检验:运用计量经济学方法,对金融市场中的异常现象进行检验,如过度波动、长期反转等。
3. 股票收益率的预测:通过建立计量模型,预测股票收益率,为投资者提供决策依据。
4. 风险度量:运用计量经济学方法,对金融市场中的风险进行度量,为金融机构提供风险管理参考。
三、实验过程1. 数据收集与处理:首先,我们收集了相关金融数据,包括股票收益率、市场指数、宏观经济指标等。
然后,对数据进行清洗和整理,确保数据的准确性和完整性。
2. 模型建立与检验:根据实验要求,我们建立了相应的计量模型,并对模型进行拟合和检验。
在模型建立过程中,我们充分考虑了模型的设定、变量选择和参数估计等问题。
3. 实验结果分析:通过对实验结果的观察和分析,我们发现了一些有意义的结论。
例如,某些股票收益率与市场指数之间存在显著的相关性,某些宏观经济指标对股票收益率有显著影响等。
四、实验收获1. 深入理解金融计量方法:通过本次实验,我对金融计量方法的基本原理和应用有了更深入的认识,为今后从事金融领域研究奠定了基础。
2. 提高数据分析能力:在实验过程中,我们学会了如何运用计量经济学方法进行数据分析,提高了自己的数据分析能力。
3. 培养严谨的科学态度:在实验过程中,我们严格按照科学方法进行操作,培养了严谨的科学态度。
4. 增强团队合作意识:本次实验需要团队成员之间的密切配合,通过实验,我们增强了团队合作意识。
计量经济学期末报告

精品文库计量经济学实验报告我国居民储蓄余额的影响因素的计量分析XX学院XX专业小组成员:〔姓名及学号〕我国居民储蓄余额的影响因素的计量分析一.研究的目的要求1.研究的背景居民储蓄额作为一个国家经济增长中来源最稳定、数额最大的影响因素,它的上下对一国的经济开展、投资和居民生活等方面都有不同程度的影响。
目前我国国内居民储蓄意愿强劲、储蓄额居高不下,形成了储蓄的超常增长,主要呈现以下特点:〔 1〕储蓄率世界之冠;〔 2〕储蓄增长速度高于经济和居民收入增长速度;〔 3〕城乡之间差异大;〔 4〕不同收入阶层分布不均匀;〔5〕不同地区分布极不平均。
我国储蓄的超常增长一方面能为银行提供了充足的信贷资金,保证金融机构的稳健运行,还能为国家提供了物质根底;此外,面对世界的日益开展,高储蓄额还能帮助我国进一步改革。
但是,在另一方面我还国存在金融机构对资本的运用效益不高、居民投资渠不多、投资效益不稳定等问题。
这些问题导致我国现在储蓄存款过剩、消费缺乏和资本形成缺乏同时并存的局面。
2021 年 6 月余额宝正式上线,在此后的一年中该产品的客户数量和管理资产出现爆炸式的增长。
截止 2021 年 3 月余额宝资金规模已经到达 5413 亿元,截止 2021 年 4 月,居民人民币存款减少1.23 万亿元。
余额宝作为一条“鲶鱼〞和随后出现的众多“宝宝〞们一起加速了中国利率市场化的进程,对未来我国储蓄额有着重大影响。
为了分析我国居民储蓄存款如今的开展状况、更好地把握我国储蓄余额未来的走向,所以对我国储蓄余额的及其影响因素的研究是十分必要的。
2.影响因素的分析为了研究影响中国储蓄余额上下的主要原因,分析居民储蓄余额增长规律,预测中国储蓄余额的增长趋势,需要建立计量经济模型。
通过参考相关文献并结合我国经济开展的实际情况提出了以下几个变量。
〔1〕收入水平。
根据经济理论可以认为,收入水平是影响储蓄的最主要因素。
〔2〕利率水平。
利率作为消费的时机本钱也会对储蓄产生影响。
金融学计量实训报告范文

一、实训背景随着金融市场的日益复杂化和金融工具的不断创新,金融学计量分析在金融决策、风险管理、投资组合优化等方面发挥着越来越重要的作用。
为了提高金融专业学生的实际操作能力和对金融计量分析的理解,我校组织开展了金融学计量实训。
本次实训旨在使学生掌握金融计量分析的基本方法,提高学生运用统计软件进行数据分析的能力,为今后从事金融工作打下坚实的基础。
二、实训目的1. 使学生掌握金融学计量分析的基本理论和方法;2. 培养学生运用统计软件进行金融数据分析的能力;3. 提高学生运用计量分析解决实际问题的能力;4. 增强学生的团队协作精神和沟通能力。
三、实训内容1. 实训一:金融时间序列分析(1)了解金融时间序列的基本概念和性质;(2)学习时间序列数据的平稳性检验、自相关函数和偏自相关函数分析;(3)掌握ARIMA模型、GARCH模型等常用模型的应用;(4)运用Eviews软件进行时间序列数据的分析。
2. 实训二:金融回归分析(1)了解金融回归分析的基本概念和假设;(2)学习线性回归、多元线性回归、非线性回归等常用回归模型;(3)掌握金融变量之间的相关关系,进行回归分析;(4)运用Stata软件进行金融回归分析。
3. 实训三:金融风险管理(1)了解金融风险的基本概念和类型;(2)学习VaR、CVaR等风险度量方法;(3)掌握金融风险管理的常用模型和工具;(4)运用Excel和R软件进行风险管理分析。
四、实训步骤1. 实训一:金融时间序列分析(1)学生分组,每组选择一个金融时间序列数据;(2)运用Eviews软件进行时间序列数据的平稳性检验、自相关函数和偏自相关函数分析;(3)根据分析结果,选择合适的模型进行拟合;(4)对模型进行诊断,评估模型拟合效果;(5)撰写实训报告。
2. 实训二:金融回归分析(1)学生分组,每组选择一个金融变量,寻找相关变量;(2)运用Stata软件进行金融回归分析;(3)对回归结果进行解读,分析变量之间的关系;(4)撰写实训报告。
金融计量学个人实训报告

一、实训背景随着金融市场的日益复杂化和金融工具的不断创新,金融计量学在金融领域的重要性日益凸显。
金融计量学是运用数学和统计学的方法对金融市场进行分析、预测和决策的学科。
为了更好地理解金融计量学在金融领域的应用,提高自己的金融分析能力,我参加了本次金融计量学个人实训。
二、实训目的1. 掌握金融计量学的基本理论和方法;2. 学习运用金融计量学工具进行金融市场分析和预测;3. 提高自己的金融数据分析能力;4. 培养自己的实证研究能力。
三、实训内容1. 金融计量学基本理论(1)金融时间序列分析:学习了时间序列的基本概念、平稳性检验、自回归模型、移动平均模型等。
(2)多元统计分析:学习了主成分分析、因子分析、聚类分析等。
(3)回归分析:学习了线性回归、多元回归、非线性回归等。
2. 金融计量学软件应用(1)EViews:学习了EViews软件的基本操作,包括数据导入、模型估计、结果分析等。
(2)R语言:学习了R语言的基本语法,包括数据操作、图形绘制、统计分析等。
3. 实证研究(1)选取合适的金融市场数据,如股票市场、债券市场、外汇市场等。
(2)运用金融计量学方法对金融市场进行分析和预测。
(3)撰写实证研究报告。
四、实训过程1. 学习金融计量学基本理论首先,我通过阅读教材、参加讲座等方式,系统地学习了金融计量学的基本理论。
在理论学习的阶段,我重点掌握了时间序列分析、多元统计分析、回归分析等基本方法。
2. 金融计量学软件应用在掌握了金融计量学基本理论后,我开始学习EViews和R语言这两种软件。
通过自学和查阅相关资料,我掌握了EViews和R语言的基本操作,并能够运用这些软件进行金融市场分析和预测。
3. 实证研究为了提高自己的实证研究能力,我选取了我国股票市场数据作为研究对象。
首先,我收集了上证综指、深证成指、中小板指等数据,然后运用EViews软件对数据进行平稳性检验、自回归模型估计等。
接着,我运用R语言进行多元回归分析,以预测股票市场的未来走势。
金融计量经济学实验报告

影响股票价格因素一、实验目的:影响我国股票价格波动的宏观因素分析二、实验软件:Eviews6.0三、实验步骤1、选择数据:(1)将上证综指作为股票价格指数的因变量Y,之所以选择上证综指是因为深圳证券市场股票价格指数与上海证券市场价格指数存在很强的相关性,同时上证综指具有广泛的代表性。
(2)影响股票价格指数的因素众多,从影响上市公司股票价格整体水平的角度出发,选择了10个影响股票价格指数的经济变量:1.工业增加值X1;2. 社会消费品零售总额X2;3.城镇固定资产投资增长率X3;4.外贸进出口总额X4;5 居民消费物价指数X5.;6.商品零售价格指数X6;7.企业商品价格指数X7;8.成交量X8;9.汇率X9;10.货币供应量M1X10。
由于股票市场环境状况对股价也有着十分重要的影响,因此,我们选择成交量X7反映股票市场的状况。
(3)选取2000年1月至2004年3月的相应10个月度数据。
2、模型建立tttttttttttteXaXaXaXaXaXaXaXaXaXaaY+++++++++++=1010998877665544332211lnlnlnlnln相对变量(增长率、价格指数变量以及汇率),以原变量形式进入模型;而对于其他绝对数额变量,为了消除异方差,以对数形式进入模型3、进行回归估计(1)建立workfile,选择时间区域(2)建立object X1\X2\X3\X4\X5\X6\X7\X8\X9和Y,并输入数据(3)由于模型中存在对数形式,需要对将其变为对数形式(4)对解释变量和被解释变量进行回归,得到如下回归结果:得到的结果为:lnY=925304.2-0.207559x1-803.1408lnx2+0.0085370x3+129.4639lnx4-101.2330x5+107.4131x6+85.08400x7+41.50782lnx8-110189.2x9-1342.723lnx102R =0.798804 2R =0.748505 F=15.88110对数据进行分析:在10%的显著性水平下,查表得=-)(2/k n t a 1.684. ,故X1、X3、lnX4、lnX8系数估计值的t 值不显著,表明很可能存在多重共线性。
金融计量经济学实验报告

【实验一】利用古典线性回归模型对经济数据进行研究分析1.案例分析:我国预算外资金分项目支出(2002-2012)研究分析新中国成立之初实行高度集中的统收统支体制。
进入第一个五年计划时期后,为了调动地方的积极性,开始把原来预算内的一部分收入,放到预算外管理,国家财政资金开始分为预算内和预算外两部分,这才形成预算外资金这个特殊范畴。
十年动乱时期,预算外资金迅速膨胀,1976年已相当于预算内收入的35.5%。
1979年我国进入全面体制改革的新时期,对地方预算扩大了自主权,对企业放权让利,所以预算外资金的增长超过任何一个时期,已经成为经济运行的一个重要特点和问题,按当时口径统计的预算外资金的增长变化有以下四个特点:(1)预算外资金增长过快,1992年比1978年增长11倍,相当于预算内收入的97.7%,名副其实地成为国家的“第二预算”。
(2)预算外资金历年增长速度均超过同年的GDP和预算内收入的增长速度,造成资金的严重分散。
(3)由于管理不严,财经纪律松弛,化预算内为预算外、化生产资金为消费基金、化公为私等现象有所滋长和蔓延。
因此,预算外资金迅速增长,已成为预算内收入占GDP的比重偏低的重要原因,也是当时固定资产投资膨胀和消费基金膨胀的重要原因。
预算外资金是财政资金体系的重要补充,在经济发展过程中起着重要作用。
特别在2002年之后,预算外资金作为预算内资金的重要补充,在满足政府履行其职能需要、减轻财政负担方面发挥了积极作用。
2.研究目的:预算外资金是财政资金体系的重要补充,在经济发展过程中起着重要作用。
因此,如何加强预算外资金管理,减轻财政压力,维护财经纪律,从而有效地发挥预算外资金作用,具有十分重要的现实意义。
3.使用古典线性回归模型的原因:古典线性回归模型中“回归”一词是描述和估计一个给定变量与一个或更多的其他变量之间的关系,具体地说是“回归”试图解释一个变量如何随着其他一个或更多变量的变化而变化。
金融计量学实验报告

金融计量学实验报告
金融计量学是一门将统计学、计量经济学和金融学相结合的学科,其主要研究金融市场中的各种现象和规律,并提供数据分析和预测的方法。
在本次实验中,我们将应用金融计量学的相关方法,对股票市场的投资组合进行分析和优化。
我们需要收集股票市场的历史数据,包括各股票的收盘价和交易量等信息。
使用Excel软件进行数据处理和分析,计算各股票的收益率和波动率,并对不同股票的相关系数进行计算。
然后,我们需要根据所得数据,构建股票市场的投资组合。
根据投资组合理论,我们可以通过优化投资组合的权重,以实现最优的风险收益平衡。
在本次实验中,我们采用了马科维茨投资组合模型,利用Excel软件进行计算和优化。
通过调整权重,我们可以得到不同风险收益水平的投资组合,以满足不同投资者的需求。
我们需要对所得结果进行验证和评估。
使用Excel软件进行模拟和回测,对不同投资组合的历史表现进行分析和比较。
同时,我们还需要考虑一些风险因素,如市场风险和特定风险等,以保证投资组合的稳健性和可持续性。
通过本次实验,我们可以发现金融计量学在股票市场投资中的重要性和应用价值。
通过数据分析和优化,我们可以构建出最优的投资
组合,以实现最大化的收益和最小化的风险。
同时,我们也需要注意市场的变化和风险因素的影响,以保证投资组合的长期稳健。
金融计量学实训报告结论

随着金融市场的日益复杂和金融产品的不断创新,金融计量学作为一门研究金融现象和金融市场规律的重要学科,在我国金融领域发挥着越来越重要的作用。
为了使金融专业学生更好地掌握金融计量学知识,提高实际操作能力,我们开展了为期一个月的金融计量学实训。
现将实训情况及结论总结如下:一、实训背景金融计量学是一门应用数学、统计学和经济学知识,研究金融现象和金融市场规律的科学。
随着我国金融市场的快速发展,金融计量学在金融领域中的应用越来越广泛。
为了提高金融专业学生的实际操作能力,我们组织开展了金融计量学实训。
二、实训目的1. 使学生掌握金融计量学的基本理论和方法;2. 提高学生运用金融计量学分析金融问题的能力;3. 培养学生实际操作金融计量软件的能力;4. 激发学生对金融计量学的兴趣,为今后从事金融工作奠定基础。
三、实训内容1. 金融计量学基本理论:介绍金融计量学的发展历程、基本概念、主要方法和应用领域;2. 统计学知识:讲解统计学的基本概念、概率分布、假设检验等;3. 金融计量软件操作:教授EViews、R、Python等金融计量软件的使用方法;4. 实际案例分析:选取典型案例,指导学生运用金融计量学方法进行分析;5. 实践项目:要求学生独立完成一个金融计量学项目,如股票收益率预测、利率期限结构分析等。
四、实训过程1. 讲解阶段:教师讲解金融计量学基本理论、统计学知识和金融计量软件操作方法;2. 案例分析阶段:教师选取典型案例,指导学生运用金融计量学方法进行分析;3. 实践项目阶段:学生独立完成金融计量学项目,教师进行指导;4. 总结阶段:学生总结实训过程中的收获和不足,教师进行点评。
五、实训结论1. 学生对金融计量学的基本理论和方法有了更深入的了解,为今后从事金融工作奠定了基础;2. 学生掌握了金融计量软件的使用方法,提高了实际操作能力;3. 学生运用金融计量学方法分析金融问题的能力得到了提高;4. 学生在实训过程中培养了团队协作精神,提高了沟通能力;5. 学生对金融计量学的兴趣得到了激发,为今后进一步学习提供了动力。
金融计量学实验报告

金融计量学实验报告金融计量学实验报告引言:金融计量学是一门应用数学的学科,主要研究经济与金融领域中的数据分析与建模。
它既有严格的数学基础,又能够对实际问题进行解答,因此在金融领域中有着重要的地位。
本实验报告主要探讨金融计量学中的一些知识点,并以实验来帮助理解。
第一部分:数据的分布在金融计量学中,数据分布是一项非常重要的内容,即使在其他学科也同样重要。
数据分布可以帮助我们预测未来的情况,并提供给我们知道变量之间的关系的手段。
然而,在分析数据分布时,我们需要遵循一些基本规则。
首先,我们需要了解中心极限定理。
它告诉我们,大量的独立随机变量的平均值将会近似于正态分布。
这是由于正态曲线在大多数情况下都是连续的,可以被用来模仿许多方面的实际数据。
另外,我们还需要了解离散度。
离散度由方差和标准差来测量。
方差用来说明数据的分布程度,而标准差则是方差的平方根。
第二部分:利率和股票价格利率和股票价格是金融领域中的两个关键指标。
在计量金融领域,我们会研究这些指标,并尝试确定它们之间的关系。
在实验中,我们可以使用统计工具来分析利率和股票价格之间的关系。
具体来说,我们可以使用描述性统计学来测量这些指标。
我们还可以使用回归分析来确定它们之间的影响关系。
此外,我们还可以进行某些变量的概率分析,例如假设我们想预测股票价格在特定时间点上的情况。
使用概率分析,我们可以了解不同方案的可能性和风险。
第三部分:时间序列分析时间序列分析是金融计量学中的另一个重要领域。
这种分析包括对大量数据的收集、整理、分析和呈现。
时间序列分析可以帮助我们预测未来,这是因为我们可以分析过去的数据来发现趋势。
例如,如果我们发现某一股票在过去几年中保持稳定增长,我们可以预测未来也会继续增长。
在时间序列分析中,我们可以使用许多不同的统计工具,例如滑动平均值和指数平滑。
这些工具可以帮助我们提取趋势和周期组成的各个部分。
结论:金融计量学实验的结果表明,我们可以使用数学工具帮助我们分析数据、预测未来和决策投资。
金融计量经济实验报告

一、实验背景随着金融市场的日益复杂和金融产品的多样化,金融计量经济学在金融领域的研究和应用越来越广泛。
本实验旨在通过Eviews软件,对金融数据进行计量经济学分析,验证金融模型的假设,并分析模型的预测能力。
二、实验目的1. 掌握Eviews软件的基本操作和功能。
2. 学习并应用计量经济学的基本原理和方法。
3. 对金融数据进行实证分析,验证金融模型的假设。
4. 评估模型的预测能力。
三、实验内容1. 数据来源与处理本实验所使用的数据来源于中国金融市场数据库,包括上证指数、深证成指、银行间同业拆借利率、人民币对美元汇率等金融指标。
数据时间跨度为2010年1月至2020年12月,共96个月。
2. 实验步骤(1)导入数据:打开Eviews软件,选择“文件”菜单中的“打开”命令,导入实验数据。
(2)数据预处理:对数据进行查看和清洗,包括去除缺失值、异常值等。
(3)建立模型:根据研究目的,选择合适的金融模型,如自回归模型(AR)、移动平均模型(MA)、自回归移动平均模型(ARMA)等。
(4)模型估计:使用Eviews软件对模型进行估计,得到模型参数。
(5)模型检验:对模型进行残差分析、自相关检验、平稳性检验等,以验证模型的假设。
(6)模型预测:使用估计出的模型进行预测,分析模型的预测能力。
四、实验结果与分析1. 模型选择根据研究目的,本实验选择ARMA模型进行金融数据的分析。
ARMA模型是一种结合自回归(AR)和移动平均(MA)两种模型的混合模型,可以描述金融数据的自相关性。
2. 模型估计使用Eviews软件对ARMA模型进行估计,得到模型参数如下:AR(1)系数:0.9MA(1)系数:-0.2常数项:1003. 模型检验(1)残差分析:对残差进行查看,发现残差基本呈随机分布,没有明显的规律性。
(2)自相关检验:使用Ljung-Box检验对残差进行自相关检验,结果显示在5%的显著性水平下,残差不存在自相关性。
金融计量学实验报告

金融计量学实验报告金融计量学实验报告引言:金融计量学是一门研究金融市场和经济现象的学科,通过运用统计学和计量经济学的方法,对金融市场的行为和变化进行量化分析。
本实验报告旨在通过实证研究的方式,探讨金融计量学在预测金融市场变动和风险管理方面的应用。
一、数据收集与处理为了进行金融计量学实验,我们首先需要收集相关的金融市场数据。
在这个实验中,我们选择了股票市场作为研究对象,并收集了一段时间内的股票价格和成交量数据。
在数据处理方面,我们对原始数据进行了去除异常值、填补缺失值等预处理操作,以确保数据的准确性和可靠性。
二、相关性分析在金融计量学中,相关性分析是一种常用的方法,用于研究不同变量之间的关系。
我们选取了股票价格和成交量作为两个变量,利用相关系数计算它们之间的相关性。
结果显示,股票价格和成交量之间存在一定的正相关关系,即成交量的增加会对股票价格产生积极影响。
这一发现对于投资者来说具有重要的意义,可以帮助他们更好地把握市场走势。
三、时间序列分析时间序列分析是金融计量学中的另一种重要方法,用于研究时间上的变化趋势和周期性变动。
我们选取了股票价格作为研究对象,利用时间序列分析方法,对其进行了拟合和预测。
通过对历史数据的拟合,我们可以得到一个数学模型,用于预测未来的股票价格。
这一模型可以帮助投资者制定更为科学的投资策略,降低投资风险。
四、风险管理金融市场的波动性和风险是投资者非常关注的问题。
在金融计量学中,风险管理是一个重要的研究领域。
我们选取了股票市场的波动性作为研究对象,通过计算历史波动率和预测波动率,帮助投资者评估市场风险。
同时,我们还利用VaR(Value at Risk)模型,对投资组合的风险进行评估和管理。
这些方法的应用,可以帮助投资者更好地控制风险,提高投资收益。
结论:金融计量学作为一门重要的学科,对于金融市场的分析和预测具有重要的意义。
通过本次实验,我们了解到金融计量学在预测金融市场变动和风险管理方面的应用。
金融计量实验报告总结

金融计量实验报告总结引言本实验使用金融计量模型来分析金融市场中的相关变量之间的关系。
通过利用计量经济学的方法,我们可以揭示出金融市场中的规律和趋势,帮助投资者做出更准确的决策。
本实验主要围绕着股市指数与利率之间的关系展开,通过运用多元线性回归模型和单位根检验等方法对所选取的数据进行分析,得出了一些有意义的结论。
数据选取与处理我们选择了过去十年来的上证指数和中国人民银行公布的一年期存款利率作为研究对象。
为了进行计量分析,我们从相关数据源中获取了这两个变量的每日数据。
为了使数据更合理,我们对它们进行了对数化处理。
通过对数化处理,我们可以更好地展示变量之间的变化趋势,并且简化模型的回归系数的解释。
实证分析单位根检验在进行多元线性回归分析之前,首先需要进行单位根检验,以确定变量是否为平稳的。
我们使用了ADF (Augmented Dickey-Fuller) 检验来进行单位根检验。
通过对两个变量进行ADF检验,我们得出了以下结论:上证指数的差分序列和一年期存款利率的差分序列都为平稳序列,不存在单位根。
这意味着我们可以直接对差分序列进行回归分析,而不需要担心存在伪回归的问题。
多元线性回归接下来,我们使用多元线性回归模型来研究上证指数与一年期存款利率之间的关系。
通过最小二乘法,我们得到了如下的回归方程:上证指数= β0 + β1 * 一年期存款利率+ ε通过对回归结果进行统计显著性检验,我们得出了以下结论:一年期存款利率对上证指数有显著的影响。
具体地说,一年期存款利率的增加会导致上证指数的下降。
这与我们的预期相符,即利率上升会减少资金流入股市,从而影响股市的表现。
结论通过金融计量实验分析,我们得出了一年期存款利率对上证指数有显著的影响的结论。
这一结论对于投资者来说是有实际意义的,可以帮助他们在投资决策中考虑到利率的因素。
同时,我们也发现了一年期存款利率的增加会导致上证指数的下降,这为投资者提供了对冲市场风险的一种思路。
大学金融计量学实验-报告 (2)

20XX年复习资料大学复习资料专业:班级:科目老师:日期:《金融计量学》实验报告二开课实验室: 20XX20XXXX 年姓名张荣芳成绩年级专业20XXXX级金融学学号20XXXX220XXXX695实验名称简单外推模型应用指导教师曲春青一、实验目的与要求1. 准确掌握简单外推模型的各种形式和方法原理。
2. 熟练掌握运用Eviews软件建立简单外推模型。
3. 学会利用多种方法对多个模型进行比较分析。
4. 熟练掌握运用简单外推模型对样本序列进行外推预测。
5. 在老师的指导下独立完成实验,得到正确的结果,并完成实验报告。
二、实验原理阐述(经济原理,实验所用理论、模型、公式)1.企业存款作为金融机构一项重要的负债业务,一直以来受到各金融机构的普遍重视。
企业存款余额不仅能够反映企业的财务状况、经营能力、发展态势,更能够为金融机构制定发展规划提供重要的参考依据。
影响金融机构企业存款的因素有:外部因素(1)经济水平:人均GDP较高,存款较多;GDP的增长率较高,存款的增长较快;外贸、投资顺差。
(2)货币政策:存款利率、存款准备金率、公开市场、货币掉期。
(3)金融法规:如利率管制、金融分业、存款实名制等。
(4)税收政策:利息税。
(5)股票、房地产市场:股票、房地产市场上升,存款减少。
(6)汇率、通货膨胀率:本币升值、通货膨胀率下降,存款增加。
(7)消费倾向:消费增加,储蓄减少。
如私家车。
内部因素(1)银行声誉:资产规模,政府背景。
(2)服务水平:服务网点、电话银行、网上银行、银行卡,客户经理制。
(3)银行形象:CI策略,广告宣传。
(4)存款品种:定活两便、通知存款。
(5)存款利率:通过理财产品实现差异化,高息或变相高息揽存屡禁不止。
(6)贷款便利:以贷吸存,存贷结合。
(7)咨询服务:如项目评估、融资策划、理财咨询。
(8)营销能力:业务关系、人脉关系、血缘关系,营销手段。
(9)激励机制:吸存的考核和奖励。
2.使用简单外推模型的理由简单外推模型虽然不像结构模型那样具有较高的预测精度,但由于其方法简单、便于操作,在许多情况下也得到广泛的应用,比如:需要在很短时间对大规模的时间序列进行预测,时间和资源上不允许使用正规的模型技术;当有理由认为一个特定的时间序列有一个简单的趋势,也不必使用较复杂的模型。
金融计量学实验报告
实验报告哈尔滨工程大学教务处制目录第1章股票估值 (3)1.1实验目的 (3)1.2实验方法和手段 (3)1.3实验内容 (3)1.4实验数据来源 (4)1.5实验步骤及结果分析 (4)1.6.实验结论 (5)第2章资产流动性 (6)2.1实验目的 (6)2.2实验方法和手段 (6)2.3实验内容 (6)2.4实验数据来源 (6)2.5实验步骤及结果分析 (6)2.6实验结论 (7)第3章投资组合分析 (8)3.1实验目的 (8)3.2实验方法和手段 (8)3.3实验内容 (8)3.4实验数据来源 (9)3.5实验步骤及结果分析 (9)3.6实验结论 (10)第1章股票估值1.1实验目的学习股票估值原理,经典的金融理论认为,金融市场上的资产价格由其未来产生的现金流量所决定,这种由未来产生的现金流量所决定的资产价格被称为资产的内在价值。
如果我们能够精确地预测股票的未来现金流,并且能够找到一个合适的市场贴现率,那么股票的内在价值就是股票的未来现金流在一定市场贴现率下的贴现值。
通过对同仁堂股票的分析进行实践应用,分析其股票内在价值,学会如何进行股票估值。
1.2实验方法和手段利用固定红利模型理论方法,通过Excel数据分析进行股票估值。
1.3实验内容对上证股票中同仁堂(600085.SH)股利发放情况进行分析,通过固定红利增长模型,计算其股票内在价值。
1.4实验数据来源实验数据:同仁堂(600085.SH )从2016年4月29日到2017年4月28日日收盘价,及同期上证综合指数。
及同仁堂从2005年到2016年每股税后盈余和每期股利。
来源:Wind 资讯 新浪财经1.5实验步骤及结果分析1.5.1利用CAPM 模型算出股票回报率k将同仁堂(600085.SH )从2016年4月29日到2017年4月28日日收盘价,及同期上证综指数据导入Excel ,算出相应日收益率,对两者收益率利用slope 函数,算出β=1.084200339。
金融计量学实验报告
0.130372
Schwarz criterion
-3.326599
Log likelihood
120.6795
Hannan-Quinn criter.
-3.365324
F-statistic
167.3207
Durbin-Watson stat
1.003630
Prob(F-statistic)
Included observations: 70
Variable
Coefficient
Std. Error
t-Statistic
Prob.
C
-0.069029
0.013489
-5.117299
0.0000
X
0.696416
0.047786
14.57360
0.0000
R-squared
0.757481
表2.5
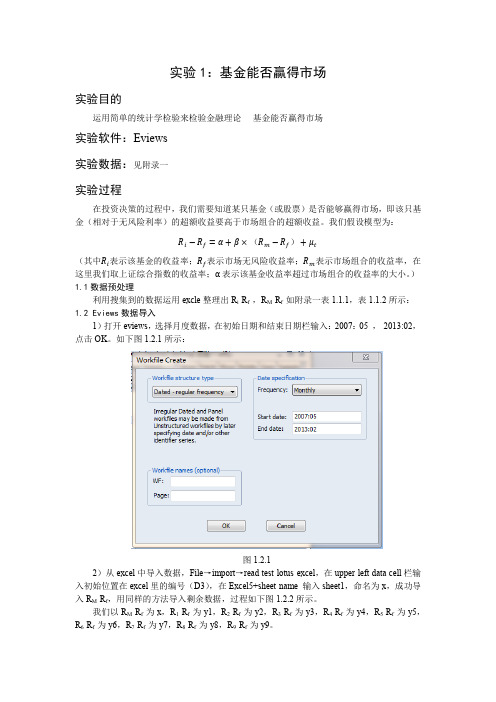
从上表中我们不难发现作为詹森指数的常数项C的t比率非常显著,且方程的R2达到了0.757481,拟合结果比较满意,F统计量明显通过检验,方程总体的显著性也比较满意。以上种种均表明方程的回归结果比较不错。
截距项为-0.069029,说明基金的整体表现不如市场预期。也即光大量化没有打败市场。
2.6对于上投内需的分析
0.0000
R-squared
0.731259
Mean dependent var
-0.248914
Adjusted R-squared
0.727307
S.D. dependent var
0.068864
S.E. of regression
0.035961
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验1:基金能否赢得市场实验目的运用简单的统计学检验来检验金融理论----基金能否赢得市场实验软件:Eviews实验数据:见附录一实验过程在投资决策的过程中,我们需要知道某只基金(或股票)是否能够赢得市场,即该只基金(相对于无风险利率)的超额收益要高于市场组合的超额收益。
我们假设模型为:R i−R f=α+β×(R m−R f)+μt(其中R i表示该基金的收益率;R f表示市场无风险收益率;R m表示市场组合的收益率,在这里我们取上证综合指数的收益率;α 表示该基金收益率超过市场组合的收益率的大小。
)1.1数据预处理利用搜集到的数据运用excle整理出R i-R f ,R M-R f 如附录一表1.1.1,表1.1.2所示:1.2 Eviews数据导入1)打开eviews,选择月度数据,在初始日期和结束日期栏输入:2007:05 ,2013:02,点击OK。
如下图1.2.1所示:图1.2.12)从excel中导入数据,File→import→read test-lotus-excel,在upper-left data cell栏输入初始位置在excel里的编号(D3),在Excel5+sheet name 输入sheet1,命名为x,成功导入R M-R f,用同样的方法导入剩余数据,过程如下图1.2.2所示。
我们以R M-R f 为x,R1-R f 为y1,R2-R f 为y2,R3-R f 为y3,R4-R f 为y4,R5-R f 为y5,R6-R f 为y6,R7-R f 为y7,R8-R f 为y8,R9-R f 为y9。
图1.2.2 导入x1.3拟合回归模型输入ls y1 c x 做出第一只基金的CAPM模型的回归方程,如下图1.3所示图1.3其他的回归模型操作步骤与之类似,在此不再赘述。
实验结果一、单个结果分析2.1对于博时价值的分析在上面实验步骤的1.3中我们用Eviews得到了第一只基金的回归分析的表格如下表2.1所示:Dependent Variable: Y1Method: Least SquaresDate: 05/05/13 Time: 16:19Sample: 2007M05 2013M02Included observations: 70Variable Coefficient Std. Error t-Statistic Prob.C -0.125066 0.010068 -12.42173 0.0000X 0.485169 0.035667 13.60264 0.0000R-squared 0.731259 Mean dependent var -0.248914Adjusted R-squared 0.727307 S.D. dependent var 0.068864S.E. of regression 0.035961 Akaike info criterion -3.784617Sum squared resid 0.087936 Schwarz criterion -3.720374Log likelihood 134.4616 Hannan-Quinn criter. -3.759099F-statistic 185.0317 Durbin-Watson stat 1.129516Prob(F-statistic) 0.000000表2.1从上表中我们不难发现作为詹森指数的常数项C的t比率非常显著,且方程的R2 达到了0.731259,拟合结果比较满意,F统计量明显通过检验,方程总体的显著性也比较满意。
以上种种均表明方程的回归结果比较不错。
截距项为-0.125066,说明基金的整体表现不如市场预期。
也即博时价值没有打败市场。
2.2对于嘉实沪深的分析在上面实验步骤的1.3中我们用Eviews得到了嘉实沪深基金的回归分析的表格如下表2.2所示:Dependent Variable: Y2Method: Least SquaresDate: 05/05/13 Time: 16:39Sample: 2007M05 2013M02Included observations: 70Variable Coefficient Std. Error t-Statistic Prob.C -0.067134 0.014373 -4.670885 0.0000X 0.701310 0.050916 13.77384 0.0000R-squared 0.736146 Mean dependent var -0.246157Adjusted R-squared 0.732266 S.D. dependent var 0.099212S.E. of regression 0.051335 Akaike info criterion -3.072724Sum squared resid 0.179201 Schwarz criterion -3.008482Log likelihood 109.5454 Hannan-Quinn criter. -3.047206F-statistic 189.7186 Durbin-Watson stat 1.660885Prob(F-statistic) 0.000000表2.2从上表中我们不难发现作为詹森指数的常数项C的t比率非常显著,且方程的R2 达到了0.73146,拟合结果比较满意,F统计量明显通过检验,方程总体的显著性也比较满意。
以上种种均表明方程的回归结果比较不错。
截距项为-0.067134,说明基金的整体表现不如市场预期。
也即嘉实沪深没有打败市场。
2.3对于金鹰成份的分析在上面实验步骤的1.3中我们用Eviews得到了金鹰成份基金的回归分析的表格如下表2.3所示:Dependent Variable: Y3Method: Least SquaresDate: 05/05/13 Time: 16:42Sample: 2007M05 2013M02Included observations: 70Variable Coefficient Std. Error t-Statistic Prob.C -0.114734 0.011175 -10.26702 0.0000X 0.526502 0.039588 13.29959 0.0000R-squared 0.722312 Mean dependent var -0.249134Adjusted R-squared 0.718228 S.D. dependent var 0.075192S.E. of regression 0.039914 Akaike info criterion -3.576037Sum squared resid 0.108331 Schwarz criterion -3.511795Log likelihood 127.1613 Hannan-Quinn criter. -3.550519F-statistic 176.8790 Durbin-Watson stat 1.542766Prob(F-statistic) 0.000000表2.3从上表中我们不难发现作为詹森指数的常数项C的t比率非常显著,且方程的R2 达到了0.722312,拟合结果比较满意,F统计量明显通过检验,方程总体的显著性也比较满意。
以上种种均表明方程的回归结果比较不错。
截距项为-0.114734,说明基金的整体表现不如市场预期。
也即金鹰成份没有打败市场。
2.4对于广发聚丰的分析在上面步骤1.3中我们用Eviews得到了广发聚丰基金的回归分析的表格如下表2.4所示:Dependent Variable: Y4Method: Least SquaresDate: 05/05/13 Time: 16:48Sample: 2007M05 2013M02Included observations: 70Variable Coefficient Std. Error t-Statistic Prob.C -0.103263 0.012259 -8.423304 0.0000X 0.561761 0.043429 12.93525 0.0000R-squared 0.711033 Mean dependent var -0.246664Adjusted R-squared 0.706783 S.D. dependent var 0.080862S.E. of regression 0.043786 Akaike info criterion -3.390842Sum squared resid 0.130372 Schwarz criterion -3.326599Log likelihood 120.6795 Hannan-Quinn criter. -3.365324F-statistic 167.3207 Durbin-Watson stat 1.003630Prob(F-statistic) 0.000000表2.4从上表中我们不难发现作为詹森指数的常数项C的t比率非常显著,且方程的R2 达到了0.711033,拟合结果比较满意,F统计量明显通过检验,方程总体的显著性也比较满意。
以上种种均表明方程的回归结果比较不错。
截距项为-0.103263,说明基金的整体表现不如市场预期。
也即广发聚丰没有打败市场。
2.5对于光大量化的分析在上面实验步骤的1.3中我们用Eviews得到了光大量化基金的回归分析的表格如下表2.5所示:Dependent Variable: Y5Method: Least SquaresDate: 05/05/13 Time: 16:52Sample: 2007M05 2013M02Included observations: 70Variable Coefficient Std. Error t-Statistic Prob.C -0.069029 0.013489 -5.117299 0.0000X 0.696416 0.047786 14.57360 0.0000R-squared 0.757481 Mean dependent var -0.246802Adjusted R-squared 0.753914 S.D. dependent var 0.097122S.E. of regression 0.048179 Akaike info criterion -3.199611Sum squared resid 0.157846 Schwarz criterion -3.135368Log likelihood 113.9864 Hannan-Quinn criter. -3.174093F-statistic 212.3898 Durbin-Watson stat 1.262447Prob(F-statistic) 0.000000表2.5从上表中我们不难发现作为詹森指数的常数项C的t比率非常显著,且方程的R2 达到了0.757481,拟合结果比较满意,F统计量明显通过检验,方程总体的显著性也比较满意。
