2017最新线性代数期末考试题及答案
线性代数期末考试题及答案

线性代数期末考试题及答案一、选择题1. 下列哪个不是线性代数的基本概念?A. 矩阵B. 向量C. 函数D. 行列式答案:C. 函数2. 矩阵A的转置记作A^T,则(A^T)^T等于A. AB. -AC. A^TD. 2A答案:A. A3. 对于矩阵A和B,满足AB = BA,则称A和B是A. 相似矩阵B. 对角矩阵C. 线性无关D. 对易矩阵答案:D. 对易矩阵4. 行列式的性质中,不能成立的是A. 行列式交换行B. 行列式某一行加上另一行不变C. 行列式等于数乘其中某一行对应的代数余子式的和D. 行列式的某一行的系数乘以另一行不变答案:D. 行列式的某一行的系数乘以另一行不变5. 给定矩阵A = [3, -1; 4, 2],则A的秩为A. 0B. 1C. 2D. 3答案:C. 2二、填空题1. 给定矩阵A = [2, 1; -3, 5],则A的行列式为______答案:132. 设矩阵A的逆矩阵为A^-1,若AA^-1 = I,其中I是单位矩阵,则A的逆矩阵为______答案:I3. 若矩阵的秩为r,且矩阵的阶数为n,若r < n,则该矩阵为______矩阵答案:奇异三、简答题1. 解释什么是线性相关性和线性无关性?答案:若存在不全为零的数k1, k2,...,kn,使得方程组中的向量k1v1 + k2v2 + ... + knvn = 0成立,则称向量组{v1, v2, ..., vn}线性相关;若该方程仅在k1 = k2 = ... = kn = 0时成立,则称向量组{v1, v2, ..., vn}线性无关。
2. 如何判断一个矩阵是对称矩阵?答案:若矩阵A的转置等于自身,即A^T = A,则称矩阵A是对称矩阵。
四、计算题1. 给定矩阵A = [1, 2; 3, 4],求A的逆矩阵。
答案:A的逆矩阵为1/(-2)[4, -2; -3, 1]2. 求向量v = [1, 2, 3]的模长。
《 线性代数》2016-2017-2-A卷答案

2016~2017学年第二学期《 线性代数A 》课程期末考试卷A 卷考核方式: 闭卷 考试日期:20 年 月 适用专业、班级:一. 填空题 (每小题3分,共15分)1. 排列()()12321n n n --的逆序数为(2)(1)2n n -- 2. 向量组()()()123,0,,,,0,0,,TTTa cbc a b ααα===线性相关,则a,b,c 应 满足 abc=03. ,A B 为三阶方阵,1,3,2A B ==则12T B A -= 484. 若齐次线性方程组1232312320250320x x x x x x x kx ++=⎧⎪+=⎨⎪--+=⎩有非零解,则k=___7___5. 设4阶矩阵A 与B 相似,矩阵A 的特征值为11111,,,,B E 2345--=则__24__二. 选择题(每小题3分,共15分).1. 若11121321222331323312a a a D a a a a a a ==,则11131112121232122313331322 22 22 2a a a a D a a a a a a a a -=-=-( C ) (A ) 4 (B ) 4- (C )2 (D )2-.2. 设,A B 均为n 阶对称矩阵,AB 仍为对称矩阵的充要条件是( D ) (A )A 可逆. (B )B 可逆 (C )AB 0≠ (D )AB BA =3. A 为m 行n 列矩阵,A 的n 个列向量线性无关,则r(A)( D )(A )>m (B )<n (C )=m (D )=n 4. 向量组12,,,s ααα线性无关,且可由向量组12,,,t βββ线性表示则必有(A )t s ≤ (B )t s ≥ (C )t s < (D )t s > ( B )5.2λ=是非奇异矩阵A 的特征值,则1213A -⎛⎫⎪⎝⎭有一个特征值为( B )(A )43 (B )34 (C )12 (D )14三. 计算下列行列式的值(每小题6分,共12分)1.1 3 5 73 5 7 1 5 7 1 3 7 1 3 5解:1 3 5 71 3 5 7 1253 5 7 1 0 -4 -8 -20128134 5 7 1 3 0 -8 -24 -3258117 1 3 50 -20 -32 -44==-12512801120480214=--=--2.1 3 3 3 3 32 33 33 3 3 3 3 3 3 3 1 33 3 33 nn n- 解:1 3 3 3 32 0 0 0 03 2 33 3 0 -1 0 0 03 3 3 3 3 3 3 3 3 3 3 3 3 1 30 0 0 3 3 33 nn n-=- 4 00 0 00 3nn n --2 0 0 0 0 0 -1 0 0 036(3)!0 0 0 4 00 0 0 0 3n n n -==--- 四给定向量组()()()()12341, 1, 0, 4,2, 1, 5, 6,1, 2, 5, 2,1,1, 2, 0,αααα=-===--()53,0, 7, 14α= 求它的一个极大无关组,其余向量用此极大无关组线性表示。
线性代数期末考试题及答案

《线性代数》期末考试题及答案一、单项选择题(每小题3分,共24分).1.设行列式1112132122233132331a a a a a a a a a =,则111112132121222331313233234234234a a a a a a a a a a a a --=-( ). A. 6; B. -6; C. 8; D. -8.2.设B A ,都是n 阶矩阵,且0=AB , 则下列一定成立的是( ).A. 0A =或0B =;B. 0A =且0B =;C. 0=A 或0=B ;D. 0=A 且0=B .3.设A ,B 均为n 阶可逆矩阵,则下列各式中不正确...的是( ). A. ()T T T A B A B +=+; B . 111()A B A B ---+=+; C. 111()AB B A ---= ; D. ()T T T AB B A =.4.设12,αα是非齐次线性方程组Ax b =的解,是β对应的齐次方程组0Ax =的解,则Ax b =必有一个解是( ).A .21α+α;B .21α-α;C . 21α+α+β ;D .121122βαα++.5.齐次线性方程组123234 020x x x x x x ++=⎧⎨--=⎩的基础解系所含解向量的个数为( ).A. 1;B. 2;C. 3;D. 4. 6.向量组12,,αα…,s α(2)s ≥线性无关的充分必要条件是( ).A. 12,,αα…,s α都不是零向量;B. 12,,αα…,s α任意两个向量的分量不成比例;C. 12,,αα…,s α每一个向量均不可由其余向量线性表示;D. 12,,αα…,s α至少有一个向量不可由其余向量线性表示. 7.若( ),则A 相似于B .A. A B = ; B . 秩(A )=秩(B );C. A 与B 有相同的特征多项式;D. n 阶矩阵A 与B 有相同的特征值,且n 个特征值各不相同. 8.正定二次型1234(,,,)f x x x x 的矩阵为A ,则( )必成立.A. A 的所有顺序主子式为非负数;B. A 的所有顺序主子式大于零;C. A 的所有特征值为非负数;D. A 的所有特征值互不相同.二、填空题(每小题3分,共18分)1.设3阶矩阵100220333A ⎛⎫ ⎪= ⎪ ⎪⎝⎭,*A 为A 的伴随矩阵,则*A A =_____________.2.1111n⎛⎫⎪⎝⎭=__________________(n 为正整数). 3.设a b A c d ⎛⎫= ⎪⎝⎭,且det()0A ad bc =-≠,则1A -=________________.4.已知4阶方阵A 的秩为2,则秩(*A )=_________________.5.已知向量组123(1,3,1),(0,1,1),(1,4,)a a a k ===线性相关,则k =____________.6.3阶方阵A 的特征值分别为1,-2,3,则1A -的特征值为_________.三、计算题(10分,共44分)1.(7分)计算行列式01231000100001x x a a a a ---2.(7分)设矩阵121348412363A a -⎛⎫ ⎪=- ⎪ ⎪-⎝⎭,问a 为何值时,(1) 秩(A )=1; (2) 秩(A )=2.3.(15分)给定向量组12103a -⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭=,21324a ⎛⎫⎪- ⎪ ⎪ ⎪ ⎪⎝⎭=,33021a ⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭=,40149a ⎛⎫ ⎪- ⎪ ⎪ ⎪ ⎪⎝⎭=,试判断4a 是否为123,,a a a 的线性组合;若是,则求出组合系数4.(15分)λ取何实值时,线性方程组12233414x x x x x x x x λλλλλλλλ-=⎧⎪-=⎪⎨-=⎪⎪-+=⎩有唯一解、无穷多解、无解?在有无穷多解的情况求通解。
中国农业大学2016-2017(春)《线性代数》期末考试试题解析

2016~2017学年春季学期《线性代数》课程考试试题解析一、填空题(本题满分15分,共有5道小题,每道小题3分,请将合适的答案填在每题的空中)1.设A 为3阶方阵,A 的第3列的元素分别为1,-3,2,其对应的余子式为3,1,2,则||A =10..解析:313233||(1)13+(1)3)1+(1)2210(-A +++=-⨯⨯-⨯⨯-⨯⨯=注释本题知识点:行列式按行按列展开答案:102.设矩阵1223135()4()2()αααααα-+-=+,其中1=(3,-1,0,1)Tα,2=(3,-3,6,3)Tα则3=α(1,0-1,0)T,解析:由1223135()4()2()αααααα-+-=+得到12336ααα-=所以31211=3-=(9-303)(3-36,3)(10-10)66(),,,,,,,,T T T ααα⎡⎤-=⎣⎦注释本题知识点:向量的运算答案:0(1,0,-1,)T3.设四元非齐次线性方程组Ax b =的系数矩阵的秩为3,已知123,,ηηη是它的三个解向量,且12-2=(2,1,1,1)T ηη,3=(0,2,1,1)T η,则齐次方程组的通解为(2,3,2,2),T k k R∈.解析:因为四元非齐次线性方程组系数矩阵的秩为3,所以其对应的齐次线性方程组的基础解系中只包含一个解量,而123-2+=(2,3,2,2)Tηηη为齐次线性方程组0Ax =的解,则齐次方程组的通解为(2,3,2,2)()Tk k R ∈注释本题知识点:(1)齐次线性方程组的基础解系所包含的向量个数n r-(2)齐次线性方程组的通解1122+++(,1,2,)n r n r i k k k k R i n r ξξξ--∈=-L L 答案:(2,3,2,2)()T k k R ∈4.设矩阵123(,,)A ααα=有三个不同的特征值,且312=+ααα,则矩阵的秩()R A =2.解析:由312=+ααα知向量123,,ααα线性相关,而三个特征值不同,所以12,αα线性无关,故()2R A =注释本题知识点:矩阵的秩等于矩阵中行向量组或者列向量组的最大无关组的秩,即最大无关组所包含的向量的个数。
2017线性代数试题及答案

(试卷一)一、 填空题(本题总计20分,每小题2分)1. 排列7623451的逆序数是 15_______。
2. 若122211211=a aa a ,则=16030322211211a aa a 33. 已知n 阶矩阵A 、B 和C 满足E ABC =,其中E 为n 阶单位矩阵,则CAB =-1。
4. 若A 为n m ⨯矩阵,则非齐次线性方程组AX b =有唯一解的充分要条件是 R(A)=R(A,b)=n_5.设A 为86⨯的矩阵,已知它的秩为4,则以A 为系数矩阵的齐次线性方程组的解空间维数为__2___________。
6. 设A 为三阶可逆阵,⎪⎪⎪⎭⎫ ⎝⎛=-1230120011A,则=*A7.若A 为n m ⨯矩阵,则齐次线性方程组0Ax =有非零解的充分必要条件是R (A ) < n 8.已知五阶行列式1234532011111112140354321=D ,则=++++4544434241A A A A A 09. 向量α=(2,1,0,2)T-的模(范数)______________。
10.若()Tk 11=α与()T121-=β正交,则=k 1 1-2k+1=0二、选择题(本题总计10分,每小题2分) 1. 向量组rααα,,,21 线性相关且秩为s ,则(D)A.s r = B.s r ≤ C.r s ≤ D.r s <2. 若A 为三阶 方阵,且043,02,02=-=+=+E A E A E A ,则=A (A )A.8 B.8-C.34 D.34- 3.设向量组A 能由向量组B 线性表示,则( D )A.)()(A R B R ≤ B.)()(A R B R < C.)()(A R B R = D.)()(A R B R ≥4. 设n 阶矩阵A 的行列式等于D ,则()*kA 等于_____。
C)(A *kA )(B *A k n)(C *-A k n 1)(D *A5. 设n 阶矩阵A ,B 和C ,则下列说法正确的是B _____。
中国农业大学2017-2018.doc(秋)《线性代数》期末考试试题解析

2017~2018学年秋季学期《线性代数》课程考试试题解析一、填空题(本题满分15分,共有5道小题,每道小题3分,请将合适的答案填在每题的空中)1.设100220345A ⎛⎫⎪= ⎪ ⎪⎝⎭,*A 为A 的伴随矩阵,则1*1|()|4A A --=.解析:由于2211110,|10,,10A A A A A A A *-**=====则31*116(6)|()|441010A A A A A --**---=-==注释本题知识点:(1)1;n A A -*=(2);AA A A A E **==(3).n A A λλ=答案:3(6)10-2.设矩阵101112,011A ⎛⎫⎪= ⎪ ⎪⎝⎭321,,ααα为线性无关的三维列向量组,则向量组123,,A A A ααα的秩为.解析:矩阵101112011A ⎛⎫⎪= ⎪⎪⎝⎭的秩为2,321,,ααα为线性无关的三维列向量组,因此,矩阵123(,,)ααα可逆,而123123(,,)(,,)A A A A αααααα=,则123,,A A A ααα的秩为2.注释本题知识点:(1)矩阵的秩的定义;(2)矩阵秩的性质:若=A PBQ ,其中,P Q 为可逆的矩阵,则=()()R A R B (3)向量组的秩与矩阵秩的关系:向量组321,,ααα的秩等于矩阵123(,,)ααα的秩.答案:2.3.设100020001A -⎛⎫⎪= ⎪⎪⎝⎭,要使A kE +为正定矩阵,k 应满足.解析:100020001A -⎛⎫⎪= ⎪⎪⎝⎭特征值为1,2,1λ=-,则A kE +的特征值为1,2,1k k k λ=-+++,若A kE +为正定矩阵,则10,20,10k k k -+>+>+>,故1k >.注释本题知识点:(1)A 为正定矩阵的充要条件是A 的所有特征值大于零;答案:1k >4.设A 是三阶实对称矩阵,A 的秩()1,R A =若25A A O -=,则A 的非零特征值是.解析:由25A A O -=知矩阵A 的特征值为0λ=或5λ=,由A 的秩()1,R A =知A 的非零特征值是5.注释本题知识点:(1)特征值的定义;(2)正定矩阵的性质.答案:55.在四元非齐次线性方程组Ax b =中,A 的秩R (A )=3,且123,,ααα为它的三个解向量,已知()()1232,0,5,1,1,0,0,2,T Tααα=-+=则方程组Ax b =的通解可以写成.解析:由于A 的秩R (A )=3,则在四元齐次线性方程组0Ax =的基础解系中含有一个非零的解向量.又123,,ααα为Ax b =的三解向量,且()()1232,0,5,1,1,0,0,2,TTααα=-+=则231()2(1,0,0,2)2(2,0,5,1)(3,0,10,4),T T T ααα+-=--=--是齐次线性方程组0Ax =的一个基础解系,则非齐次线性方程组Ax b =的通解为-⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪+∈ ⎪ ⎪- ⎪ ⎪-⎝⎭⎝⎭2300,51014k k R .注释本题知识点:(1)线性方程组通解的结构答案:-⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪+∈ ⎪ ⎪- ⎪ ⎪-⎝⎭⎝⎭2300,51014k k R 二、选择题(本题满分15分,共有5道小题,每道小题3分.在每小题给出的四个选项中,只有一项是符合题目要求的,把所选项前的字母填在题后的括号内)1.设矩阵123456789A ⎛⎫ ⎪= ⎪ ⎪⎝⎭,001010100P ⎛⎫ ⎪= ⎪ ⎪⎝⎭,100001010Q ⎛⎫⎪= ⎪ ⎪⎝⎭,则PAQ 为()(A)123456789⎛⎫ ⎪ ⎪ ⎪⎝⎭.(B)132465798⎛⎫⎪ ⎪ ⎪⎝⎭.(C)798465132⎛⎫⎪ ⎪⎪⎝⎭.(D)321987.654⎛⎫⎪ ⎪ ⎪⎝⎭解析:001123100789100798010456001456001465100789010123010132PAQ ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎪⎪⎪ ⎪⎪ ⎪=== ⎪⎪⎪ ⎪⎪ ⎪⎪⎪⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭注释本题知识点:(1)初等矩阵在矩阵行列变换中的作用答案:C2.下列矩阵中,不能相似于对角阵的是()(A)001010.100⎛⎫⎪ ⎪ ⎪⎝⎭(B)111022.003⎛⎫⎪⎪ ⎪⎝⎭(C)121242.121-⎛⎫⎪- ⎪ ⎪-⎝⎭(D)211020.403-⎛⎫⎪⎪ ⎪-⎝⎭解析:(A)中矩阵⎛⎫⎪ ⎪ ⎪⎝⎭001010100是实对称矩阵,能与对角阵相似;(B)中矩阵⎛⎫⎪ ⎪⎪⎝⎭111022003有三个不同的特征值1,2,3λ=,则能对角化;(C)中矩阵-⎛⎫⎪- ⎪⎪-⎝⎭121242121特征值为0,0,3λ=,0λ=为二重特征值,但对应两个线性无关的特征向量,因此能对角化.(D)中矩阵-⎛⎫⎪ ⎪⎪-⎝⎭211020403特征值2λ=为二重特征值,但对应一个线性无关的特征向量,因此不能能对角化.注释:本题知识点:(1)n 阶方阵对角化的充分必要条件是:存在n 个线性无关的特征向量;(2)实对称矩阵一定能对角化.答案:D3.设)(ij a A =是三阶方阵,满足*T A A =,其中*A 为A 的伴随矩阵,A 为A 的行列式,则||A =()(A)0.(B)0或1.(C)-1.(D)1.解析:由*T A A =得,T A A A *==,由于2A A *=,得(1)0A A -=,故0A =或1.注释本题知识点:(1)行列式性质TA A =;(2)行列式性质1n A A-*=.答案:B4.设123,,ξξξ是方程组0Ax =的基础解系,则下列向量组中也是方程组0Ax =的基础解系的是()(A)122331,,ξξξξξξ+++.(B)122331,,ξξξξξξ+-+.(C)122331,,ξξξξξξ---.(D)1231312,,2ξξξξξξξ+-++.解析:(A)中122331123101(,,)(,,)110011ξξξξξξξξξ⎛⎫ ⎪+++= ⎪ ⎪⎝⎭,而矩阵101110011⎛⎫⎪⎪ ⎪⎝⎭可逆,则122331,,ξξξξξξ+++线性无关,为方程组0Ax =的基础解系;(B)中122331123101(,,)(,,)110011ξξξξξξξξξ⎛⎫ ⎪+-+= ⎪ ⎪-⎝⎭,而矩阵101110011⎛⎫ ⎪⎪ ⎪-⎝⎭不可逆,则122331,,ξξξξξξ+++线性相关,不为方程组0Ax =的基础解系;(C)中122331123101(,,)(,,)110011ξξξξξξξξξ-⎛⎫ ⎪---=- ⎪ ⎪-⎝⎭,而矩阵101110011-⎛⎫ ⎪- ⎪⎪-⎝⎭不可逆,则122331,,ξξξξξξ---线性相关,不为方程组0Ax =的基础解系;(D)中1231312123112(,,2)(,,)101110ξξξξξξξξξξ⎛⎫ ⎪+-++= ⎪ ⎪-⎝⎭,而矩阵112101110⎛⎫⎪⎪⎪-⎝⎭不可逆,则1231312,,2ξξξξξξξ+-++线性相关,不为方程组0Ax =的基础解系;注释本题知识点:(1)线性方程组基础解系的定义;(2)向量组的秩与矩阵秩的关系;(3)矩阵秩的性质.答案:A5.设n 维列向量组1,,()m m n αα< 线性无关,则n 维列向量组1,,m ββ 线性无关的充分必要条件为()(A)向量组1,,m αα 可由向量组1,,m ββ 线性表示.(B)向量组1,,m ββ 可由向量组1,,m αα 线性表示.(C)向量组1,,m αα 与向量组1,,m ββ 等价.(D)矩阵1(,,)m A αα= 的秩()R A 等于矩阵1(,,)m B ββ= 的秩()R B .解析:(A)中令12(1,0,0,0),(0,1,0,0)T T αα==;12(0,0,1,0),(0,0,0,1)T T ββ==,则(A)、(B)、(C)都不成立.在(D)中若矩阵1(,,)m A αα= 的秩()R A 等于矩阵1(,,)m B ββ= 的秩()R B ,则1,,m ββ 线性无关;反之1,,m ββ 线性无关,则矩阵1(,,)m A αα= 的秩()R A 等于矩阵1(,,)m B ββ= 的秩()R B .注释本题知识点:(1)向量组的线性表示;(2)向量组的等价;(3)向量组秩的定义及性质.答案:D三、(本题满分14分)计算下列各题1.计算四阶行列式0052002112341326D =--.解析:()()00521234002113263254112340052132621D --===--=--2.设n 阶行列式=det()n ij D a ,其中||(1,)ij a i j i j n =-≤≤,求n D .解析:122301231111111012211111310131111132104111111234012340r r n r r n n n D n n n n n n n n n -----------==-------------213112100001200012200(1)(1)2.1222012324251c c n n c c n n n n n n +--+------==-----------注释本题知识点:(1)行列式性质;(2)行列式的计算方法.四、(本题满分16分)1.设三阶方阵A,B 满足16,A BA A BA -=+且131415A ⎛⎫ ⎪⎪⎪= ⎪ ⎪ ⎪ ⎪⎝⎭,求B .解析:显然A 可逆,用1A -右乘方程两边,得--=+⇒-=116()6A B E B A E B E ,从而--=-116()B A E .--⎛⎫⎛⎫ ⎪ ⎪=-= ⎪ ⎪⎪ ⎪⎝⎭⎝⎭11324,354A A E --⎛⎫⎪⎪⎪-= ⎪⎪⎪ ⎪⎝⎭11121()314A E .从而--⎛⎫ ⎪ ⎪=-= ⎪ ⎪⎪⎝⎭1136()232B A E 2.已知三阶方阵A 的三个特征值分别为1231,0,1,λλλ===-对应的特征向量依次为123(1,2,2),(2,2,1),(2,1,2),T T T p p p ==-=--求矩阵A .解析:由已知,A 可以对角化.令123122(,,)221212P p p p -⎛⎫⎪==-- ⎪⎪⎝⎭,则1101P AP -⎛⎫ ⎪= ⎪ ⎪-⎝⎭,从而1101A P P -⎛⎫⎪= ⎪ ⎪-⎝⎭.112212219212P -⎛⎫ ⎪=- ⎪ ⎪--⎝⎭,10210123220A -⎛⎫ ⎪= ⎪ ⎪⎝⎭.注释本题知识点:(1)矩阵的运算;(2)特征值特征向量的定义与矩阵对角化的定义.五、(本题满分12分)设有向量组12341111101121,,,,,2324335185a a a a a b a β⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪- ⎪ ⎪ ⎪ ⎪ ⎪===== ⎪ ⎪ ⎪ ⎪ ⎪++ ⎪ ⎪ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭问,a b 为何值时,1.β不能由1234,,,a a a a 线性表示.2.β能由1234,,,a a a a 线性表示,且表示式唯一.3.β能由1234,,,a a a a 线性表示,且表示式不唯一,并写出一般表示式.解析:设=++121233x a x a x a β,设1234(,,,)A a a a a =,对增广矩阵(,)A β实行初等行变换()11111111110112101121,2324300103518500010A r a b a b a a β⎛⎫⎛⎫⎪ ⎪--⎪⎪= ⎪ ⎪+++ ⎪⎪++⎝⎭⎝⎭,由此可见(1)当1,0a b =-≠时,方程组无解,即β不能由1234,,,a a a a 线性表示;(2)当1a ≠-时,β能由1234,,,a a a a 线性表示,且表示式唯一;(3)当1,0a b =-=,方程组有无穷多解,并且112212123142202112112010001x k k x k k k k x k x k -+-⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪+-- ⎪⎪ ⎪ ⎪ ⎪=++= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭即=-+++-++∈121122132412(2)(12),(,).k k a k k a k a k a k k R β.注释本题知识点:(1)向量的线性表示与线性方程组的关系;(2)线性方程组的求解过程与方法.六、(本题满分10分)设A 是n 阶方阵,,,123ααα是n 维列向量,且10α≠,11A αα=,212A ααα=+,323A ααα=+,证明:向量组,,123ααα线性无关.解析:设有三个数123,,k k k 使得1122330k k k ααα++=(1),(1)式两边同时左乘A,可得1122330k A k A k A ααα++=,即11212323()()0k k k ααααα++++=,整理得12123233()()0k k k k k ααα++++=.(2)(2)减(1)得21320k k αα+=,(3)(3)式两边左乘A,得2131320k k k ααα++=(4)(4)减(3)得310k α=,因为10α≠,可得30k =,代入(3)式,可得20k =,从而10k =,即123,,ααα线性无关.注释本题知识点:(1)向量组的线性无关性的定义;(2)证明向量组的线性相关性的方法.七、(本题满分12分)设二次型22212312313(,,)222(0)T f x x x x Ax ax x x bx x b ==+-+>中二次型的矩阵A 的特征值之和为1,特征值之积为-12.1.求,a b 的值.2.用正交变换将二次型f 化为标准形,并写出所用的正交变换及标准形.解析:(1)二次型f 的矩阵为002002a b A b ⎛⎫⎪= ⎪⎪-⎝⎭,设A 的特征值为123,,λλλ,由已知条件知123221a λλλ++=+-=,21230020421202a ba b b λλλ==--=--,得1,2a b ==(2)由矩阵A 的特征多项式2102||020(2)(3)202E A λλλλλλ---=-=-+-+,得到A 的特征值为1232,2,3λλλ===-,对于特征值122λλ==,解齐次线性方程组(2)0E A x -=,得基础解系12(2,0,1),(0,1,0)T T ξξ==,对于33λ=-,解齐次线性方程组(3)0E A x --=,得基础解系3(1,0,2),T ξ=-由于123,,ξξξ已经是正交向量组,故只需将其单位化123,(0,1,0),T T T ηηη===-令010Q ⎫⎪⎪= ⎪ ⎪,则Q 为正交矩阵,在正交变换x Qy =下,二次型的标准行为222123223f y y y =+-.注释本题知识点:(1)矩阵特征值、特征向量的定义与性质;(2)二次型化标准形的方法.八、(本题满分6分)设α为n 维单位列向量,E 为n 阶单位矩阵,求n 阶矩阵T A E αα=-的全部特征值并证明其不可逆.解析:因为-=T E A αα为对称矩阵,由=()1T R αα,知-=()1R E A ,则-=()1R A E .所以A-E 的特征值有一个是非零的,其余n -1个都是0.设矩阵A 的所有特征值为12,,n λλλ ,则A-E 的特征值为121,1,,1n λλλ--- .因此,121,1,,1n λλλ--- 中有n -1个都是0,即12,,n λλλ 有n -1个都是1,由121,1,,1n λλλ--- 中有一个非零知,12,,n λλλ 中有一个不等于1.又因为0T A E ααααα=-=,所以0是A 的特征值.所以矩阵A 的所有特征值为1,1, ,1,0.因为0是A 的特征值,所以A 不可逆.注释本题知识点:(1)矩阵秩的有关结论:()1,0T R ααα=≠;(2)矩阵特征值、特征向量的定义与性质.。
线性代数期末试题及答案

线性代数期末试题及答案一、选择题(每题5分,共20分)1. 设矩阵A为3阶方阵,且|A|=2,则|2A|等于:A. 4B. 8C. 16D. 32答案:C2. 若向量α=(1, 2, 3),β=(2, 1, 0),则α·β等于:A. 4B. 5C. 6D. 7答案:B3. 设A为n阶方阵,且A^2=I,则A的行列式|A|等于:A. 1B. -1C. 0D. 2答案:A4. 若矩阵A的秩为2,则矩阵A的行向量线性相关还是线性无关?A. 线性相关B. 线性无关C. 线性独立D. 不能确定答案:A二、填空题(每题5分,共20分)1. 设矩阵B为2阶方阵,且B^2=0,则称矩阵B为______。
答案:幂零矩阵2. 若矩阵A和B可交换,即AB=BA,则称矩阵A和B为______。
答案:可交换矩阵3. 设向量α=(1, 2),β=(3, 4),则向量α和β的夹角的余弦值为______。
答案:3/54. 设矩阵A为3阶方阵,且A的特征值为1, 2, 3,则矩阵A的迹为______。
答案:6三、简答题(每题10分,共30分)1. 简述矩阵的转置矩阵的定义。
答案:矩阵A的转置矩阵记为A^T,其元素满足A^T_{ij}=A_{ji},即A^T的第i行第j列的元素是A的第j行第i列的元素。
2. 什么是线性方程组的齐次解?答案:线性方程组的齐次解是指当方程组的常数项全为零时,方程组的解,通常表示为零向量。
3. 说明矩阵的相似对角化的条件。
答案:矩阵A相似对角化的条件是矩阵A有n个线性无关的特征向量,其中n是矩阵A的阶数。
四、计算题(每题15分,共30分)1. 已知矩阵A=\[\begin{matrix} 1 & 2 \\ 3 & 4 \end{matrix}\],求矩阵A的行列式。
答案:|A| = 1*4 - 2*3 = -22. 设线性方程组为:\[\begin{matrix} x + 2y - z = 1 \\ 3x - y + 2z = 2 \\ x + y + z = 3 \end{matrix}\]求方程组的解。
中国农业大学2017-2018年(春) 《线性代数》期末考试试题解析

2017~2018学年(春)学期《线性代数》课程考试试题解析一、填空题(本题满分15分,共有5道小题,每道小题3分,请将合适的答案填在每题的空中)1.已知321,,ααα为3维列向量,且三阶行列式,3,,321=ααα则三阶行列式.18,26,2131321=++++ααααααα解析:12313123131231123312312123 |++, 62,|=|, 62,|=|, 6,||, 2,|=|, 6,|=6|, ,|=18.αααααααααααααααααααααααααα+++++++注释本题知识点:此题主要考察行列式的如下性质:111111111(1) |, ,,,,,|=|, ,,,k ,,|;(2) |, ,,,|=|, ,,,|+|, ,,,|;(3) |, ,,,|=k|, ,,,|;(4) |, ,,,,,|=-|, ,,,,,|.i j n i i j n i j n i n j n i n i n i j n j i n k ααααααααααααααααααααααααααααααααα++ 2.设向量组()()()TTTa 1,,1,1,5,3,1,1,3,2,0,1321-===ααα线性相关,则.1=a 解析:若向量组123,,ααα线性相关,则齐次线性方程组1122330x x x ααα++=有非零解.因此,123(,,) 3.R ααα<123111011(,,)001000r a ααα⎛⎫ ⎪- ⎪ ⎪- ⎪⎝⎭ ,当1a =时,123(,,)2 3.R ααα=<注释:本题知识点:此题主要考察向量组的线性相关性的概念及齐次线性方程组存在非0解的条件.通常需借助线性方程组的理论来研究向量组的线性相关性,当齐次线性方程组系数矩阵的秩比未知量个数小时,齐次线性方程组有非0解,系数矩阵所对应的列向量组线性相关.3.若二次型()31212322213214456,,x x x x tx x x x x x f +-++=为正定二次型,那么t 的取值范围是1310>t .解析:二次型123(,,)f x x x 的矩阵为62225020t -⎛⎫ ⎪- ⎪ ⎪⎝⎭.若为正定二次型,则其矩阵为正定矩阵.故62225020t -⎛⎫⎪- ⎪ ⎪⎝⎭的各阶顺序主子式均大于0.由6222552620025t t--=->得1013t >.注释本题知识点:矩阵为正定矩阵当且仅当其各阶顺序主子式均为正.4.设123,,ηηη是4元非齐次线性方程组=Ax b 的3个解向量,矩阵A 的秩为3,若T T )0,1,1,0(32,)4,3,2,1(321-=-=ηηη,则方程组=Ax b 的通解为ℜ∈+k k T )4,2,3,1(1η.解析:若()3R A =,则4元齐次方程0Ax =的基础解系中只有一个线性无关的向量.由于123,,ηηη是b Ax =的解,123(23)0A ηηη+-=,故bAx =通解为1231(23)(1,32,23,44)T k k k k k ηηηη+-+=++++.注释本题知识点:此题主要考察非齐次线性方程组的结构,Ax b =通解为R ()1n A i ii x k ηη-*==+∑,其中,η*为Ax b=的特解,R(A)1n i ii k η-=∑为齐次方程Ax =的通解.5.设2阶矩阵A 有两个不同的特征值,21,αα是A 的线性无关的特征向量,且满足21212()+=+A αααα,则A 相似于对角阵.10011001⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫⎝⎛-或解析:由21212()()0,0-+=+≠E A αααα知1是2A 的特征值.设12,λλ是A 两个不同的特征值,则2212,λλ均是2A 的特征值.假设2212λλ≠,则+αβ不可能是特征向量.故2212==1λλ,12,λλ为1,-1.A 相似于diag(1,-1).设21,αα对应的特征值为12,λλ,由21212()A αααα+=+得221122(1)(1)0.-+-=λαλα又12,αα线性无关,则221210,10.-=-=λλ由于12,λλ不同,则A 相似于对角阵.10011001⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛-或注释本题知识点:(1)若λ为A 的特征值,则多项式()f λ为()f A 的特征值;(2)不同的特征值对应的特征值向量线性无关,不同特征值的特征向量相加不是特征向量;(3)同一特征值对应的特征值向量构成一个特征子空间;(4)若A 有n 个不同的特征值12,,,n λλλ ,则A 相似于12diag(,,,).n λλλ 二、选择题(本题满分15分,共有5道小题,每道小题3分.在每小题给出的四个选项中,只有一项是符合题目要求的,把所选项前的字母填在题后的括号内)1.三阶行列式,0798031042=+-+--x x x 则x 的可能取值为【C】()()()().7,1,1D .2,7,1C .2,1,1B .2,7,1A -----解析:把行列式按最后一列进行展开得(x+7)(x+2)(x-1)=0,故x=-7,-2,1.注释:此题主要考察行列式的计算,如果行列式的某一行或某一列含有较多的0,我们通常把行列式按改行或该列展开进行计算.2.设A 为3阶方阵,交换A 的第1行与第2行得到矩阵B ,再把B 的第3列的2倍加到第1列得单位矩阵,记,1000010101⎪⎪⎪⎭⎫ ⎝⎛=P ,1020100012⎪⎪⎪⎭⎫ ⎝⎛=P 则=A 【D 】()()()().D .C .B .A 121111121221----P P P P P P P P 解析:利用初等矩阵的性质得12P AP E =,故1112.A P P --=注释本题知识点:对一个矩阵做初等行变换相当于左乘一个相应的初等矩阵,做初等列变换相当于右乘一个相应的初等矩阵.3.若二次型32232132122),,(x x ax x x x x f ++=经正交变换Py x =可化成标准形232221y by y -+,则【B 】()()()().2,0D .2,1C .2,0B .2,1A -==-======b a b a b a b a 解析:二次型的矩阵为20000101A a ⎛⎫⎪= ⎪⎪⎝⎭,经正交变换后其标准型的矩阵为(1,,1)B diag b =-,则A相似于B.由,||||trA trB A B ==得2, 2.a b b +==故0, 2.a b ==注释本题知识点:此题主要考察相似矩阵的性质,若A 相似于B ,则,||||.trA trB A B ==4.线性方程组b Ax =的系数矩阵A 是43⨯的矩阵,且A 的行向量组线性无关,则下列命题错误的是【C】()0A =x A T 只有零解.()0B =Ax A T 必有无穷多解.()C 对任意b x A b T=,总有唯一解.()D 对任意b Ax b =,总有无穷多解.解析:由A 的行向量组线性无关知T ()()=3R A R A =,因TA 为43⨯矩阵,对于(A)()()3TR A R A ==,故0=x A T 只有零解;对于(B)因T AA 为44⨯矩阵,()()34T A A R A ==<,故0=Ax A T 必有无穷多解;对于(C)T A 为43⨯矩阵,当()3(,)4TT R A R A b =<=时,b x A T=无解;对于(D)对任意的b ,()(,)34R A R A b ==<,b Ax =总有无穷多解.注释本题知识点:(1)对于n 元齐次线性方程组0Ax =,当()R A n =时,有唯一解;当()R A n <时,有无穷多解.(2)对于n元非齐次线性方程组Ax b=,当()(,)R A R A b <时,无解;当()(,)R A R A b n ==时,有唯一解;当()(,)R A R A b n =<时,有无穷多解.(3)对任意的矩阵A ,()()T R A R A A =.5.设P 为三阶非零矩阵,⎪⎪⎪⎭⎫⎝⎛=96342321t Q ,且满足O PQ =,则关于矩阵P 的秩,下列说法正确的是【C 】(A)6=t 时,P 的秩必为1.(B)6=t 时,P 的秩必为2.(C)6≠t 时,P 的秩必为1.(D)6≠t 时,P 的秩必为2.解析:由P 为3阶非零矩阵,PQO =知()1,()()3R P R P R Q ≥+≤.当6t =时,()1,1()2R Q R P =≤≤;当6t ≠时,()2,() 1.R Q R P ==注释本题知识点:若A 为m n ⨯矩阵,B 为n s ⨯矩阵,则()()()R A R B n R AB +≤+.三、(本题满分14分)计算下列各题解析:1.计算1n +阶行列式∑=----=+++ni ii i nn r a b r r a b r r a b r nn n a c b a c a c a c a a b b b c a ca c a nnnn n n 10221102122110000000000000122211111解:.1021⎪⎪⎭⎫⎝⎛-=∑=ni i i i n a c b a a a a 2.设行列式,1253422266254233335554321--求.353433M M M ++353433353433A A A M M M +-=++解:1253422266111003335554321---=.01253400066111000005554321343223=-=--r r r r 注释本题知识点:计算行列式时通常需利用行列式的性质化上、下三角行列式进行计算或是把行列式按某一行、某一列进行展开.若()i j n n A a ⨯⨯=,则1||nij ijj A a A ==∑.改变行列式的某一行时并不会影响该行的代数余子式,故计算1nijijj b A =∑时,只需用12,,,i i in b bb 去替换||A 的第i 行即可.四、(本题满分12分)设,321011330⎪⎪⎪⎭⎫ ⎝⎛-=A 且,2B A AB +=求.B 解析:()AB E A B A AB =-⇒+=22因为,021210113322≠=---=-E A 所以E A 2-可逆且(),2/12/12/12/32/12/12/32/32/121⎪⎪⎪⎭⎫⎝⎛---=--E A 故().0113213303210113302/12/12/12/32/12/12/32/32/121⎪⎪⎪⎭⎫⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛---=-=-A E A B 注释本题知识点:若A 可逆,对分块矩阵(,)A E 做初等行变换化为1(,)E A -,即可得到A 的逆.五、(本题满分12分)讨论当q p ,满足什么条件时,线性方程组⎪⎪⎩⎪⎪⎨⎧=+++=-++-=+--=+--.143,105,1263,0324321432143214321x px x x q x x x x x x x x x x x x 无解?有惟一解?有无穷多解?在有无穷多解时,求出通解.解析:设该线性方程组的增广矩阵为B ,,7312020021212102127001~1413110511263103211⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛----⎪⎪⎪⎪⎪⎭⎫ ⎝⎛------=q q p p q B r 当22≠=q p 且时,()(),43=<=B R A R 该线性方程组无解;当2≠p 时,()(),4==B R A R 该线性方程组有惟一解;当22==q p 且时,()(),43<==B R A R 该线性方程组有无穷多解.此时,,0000071100073021000001~⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛r B 得与原线性方程组同解的方程组为,,71732,04321⎪⎪⎪⎩⎪⎪⎪⎨⎧==+=x x x x 为自由未知数取3x ,令k x =3,得该线性方程组的通解为:.,71073001204321取任意常数其中k k x x x x ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛注释本题知识点:讨论线性方程组解的存在情况时,通常要先对方程组的增广矩阵做初等行变换化行最简型矩阵,然后利用系数矩阵及增广矩阵的秩与未知量个数的关系进行判断,参看二(4)的注释.六、(本题满分12分)已知二次型()323121232232184234,,x x x x x ax x x x x x f +-+-=的一个特征值为1,1.求a 的值;2.求正交变换将此二次型化成标准形,并写出标准形.解析:1.该二次型的矩阵为.3424420⎪⎪⎪⎭⎫ ⎝⎛---=a a A 因该二次型的一个特征值为1,所以有().202444243212=⇒=-=----=-a a a a E A 2.该二次型的矩阵为.342442220⎪⎪⎪⎭⎫ ⎝⎛---=A ()()(),66134244222+---=------=-λλλλλλλE A A 的特征值为.6,6,1321-===λλλ当11=λ时,()0=-x E A 的基础解系为:,1021⎪⎪⎪⎭⎫⎝⎛-=ξ单位化;5/105/21⎪⎪⎪⎪⎭⎫ ⎝⎛-=p 当62=λ时,()06=-x E A 的基础解系为:,2512⎪⎪⎪⎭⎫ ⎝⎛=ξ单位化得;30/230/530/12⎪⎪⎪⎪⎭⎫⎝⎛=p 当63-=λ时,()06=+x E A 的基础解系为:,2113⎪⎪⎪⎭⎫ ⎝⎛-=ξ单位化得;6/26/16/13⎪⎪⎪⎪⎭⎫ ⎝⎛-=p -令,6/230/25/16/130/506/130/15/2⎪⎪⎪⎪⎭⎫⎝⎛--=P 则P 为正交矩阵,正交变换Py x =,将此二次型化为标准形.66232221y y y f -+=注释本题知识点:(1)实对称矩的特征值均为实数且不同的特征值对应的特征向量是正交的;(2)实对称矩阵可正交相似于对角矩阵,其特征向量可构成一组标准正交基.七、(本题满分8分)设γβα,,均为n 维向量,且向量组γαβγαβ---,2,3线性无关,证明:向量组γβα,,线性无关.解析:证法一设()1,0321=++γβαk k k 令,,2,3321γαβγαβ-=-=-=a a a 则解得()()(),351,2251,6351321321321a a a a a a a a a ++==++=++=γβα代入()1式得()()(),026332332123211321=++++++++a k k k a k k k a k k k 由于γαβγαβ-=-=-=321,2,3a a a 线性无关,所以有⎪⎩⎪⎨⎧=++=++=++,026,033,02321321321k k k k k k k k k 解得,0321===k k k 故向量组γβα,,线性无关.证法二向量组γαβγαβ---,2,3与向量组γβα,,的关系可合写为()()⎪⎪⎪⎭⎫ ⎝⎛---=---120013101,,,2,3γβαγαβγαβ记作.AK B =,0512013101≠=---=K()().A RB R =∴而向量组γαβγαβ---,2,3线性无关,所以().3=B R 从而().3=A R 故向量组γβα,,线性无关.注释本题知识点:向量组12,,,n ααα 线性无关,当且仅当10niii k α==∑时,120n k k k ==== .此题也可用向量组秩的性质证明,因向量组γαβγαβ---,2,3线性无关,且可用γβα,,线性表示,故3(3,2,)(,,)3R R βαγβαγαβγ=---≤≤,则(,,)3R αβγ=,向量组,,αβγ线性无关.八(本题满分12分)设A 为n 阶实方阵,且满足O E A A =+-232,1.求A 的特征值;2.证明()()n E A R E A R =-+-2;3.问A 是否可以和对角阵相似?请说明理由.解析:1.设λ为A 的特征值,A 对应于特征值λ的特征向量为x ,即,0,≠=x x Ax λ又由于A 满足O E A A =+-232,所以有()(),0,0232322≠=+-=+-x x x E A A λλ从而.210232==⇒=+-λλλλ或故A 的特征值只可能为.21或2.一方面,()()O E A E A E A A =--=+-2232()(),2n E A R E A R ≤-+-∴另一方面,()()()()()(),222n E R A E E A R A E R E A R E A R E A R ==-+-≥-+-=-+-综上所述,有()().2n E A R E A R =-+-3.(1)当A 的特征值都是2时,E A -可逆,由O E A A =+-232得,E A 2=则A 可以和对角阵相似;----10分(2)当A 的特征值都是1时,E A 2-可逆,由O E A A =+-232得E A =,则A可以和对角阵相似;(3)当21和均为A 的特征值时,E A -不可逆且E A 2-不可逆,()0=-x E A 的基础解系所含向量个数为()E A R n l --=1,()02=-x E A 的基础解系所含向量个数为()E A R n l 22--=,由2知()()n E A R E A R =-+-2,从而有,221n n n l l =-=+故n 阶方阵A 有n 个线性无关的特征向量,从而A 可以和对角阵相似.注释本题知识点:(1)若λ为A 的特征值,则多项式()f λ为()f A 的特征值;(2)若,A B 为n 阶方阵,则()()()R A R B n R AB +≤+,()()()R A B R A R B +≤+.(3)若n 阶方阵有n 个线性无关的特征向量,则其可相似于对角矩阵.。
大学《线性代数》2016-2017第二学期期末卷答案

大学2016—2017学年第二学期末卷课程名称: 线性代数 考试时间: 100 分钟 考试方式:闭卷一、填空题(每小题3分,共18分)1.设向量α=(-1,2,-2,4),则其单位向量的是ß= b =(-0.2,0.4,-0.4,0.8) 2. 如果n 元齐次线性方程组0=Ax 有基础解系并且基础解系含有)(n s s <个解向量,那么矩阵的秩为()=A R s n -3.设矩阵A =⎪⎪⎭⎫ ⎝⎛-4321,则矩阵A 的伴随矩阵A *= ⎪⎪⎭⎫ ⎝⎛-13244. 设 123,,λλλ为方阵270056004A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦的三个特征值,则123λλλ= 405. 若向量组1a =(1,4,3),2a =(-2,-3,1), 3a =(2,t,-1)线性相关,则t = 36. 已知矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=113421201A 满足⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=421113201BA ,写出初等矩阵B=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=010100001B二、单项选择题(每小题3分,共18分)7. 设行列式111213212223313233a a a a a a a a a =2,则111213313233213122322333333a a a a a a a a a a a a ------=( D ) (A).-6 (B).-3 (C).3 (D).68. 设A 为m n ⨯矩阵,且非齐次线性方程组AX b =有唯一解,则必有( C )(A) m n = (B)()R A m = (C) ()R A n = (D)()R A n <姓名: 学号: 教学班级: 教学小班序号:9. 设1234,,,αααα都是3维向量,则必有( B ) (A) 1234,,,αααα线性无关(B) 1234,,,αααα线性相关(C) 1α可由234,,ααα线性表示 (D) 1α不可由234,,ααα线性表示10. 设A 为n 阶方阵,则0=A 的充要条件是(B ).(A).两行(列)元素对应成比例; (B).必有一行为其余行的线性组合; (C).A 中有一行元素全为零; (D).任一行为其余行的线性组合. 11. 设A 、B 均为n 阶矩阵,下列各式恒成立的是( B ).(A). 111---=B A AB )( (B). (AB)T =B T A T (C). (A+B)2=A 2+2AB+B 2 D. (A+B)(A-B)=A 2-B 212. 若方程组 02020kx z x ky z kx y z +=⎧⎪++=⎨⎪-+=⎩有非零解,则k =( D )(A). -2 (B). -1 (C). 0 (D). 2三、计算题(每小题5分,共10分)13.求行列式21021001201002。
17 线性代数复习测试卷参考答案

8
3
0
1 19
1 19
3 19
1
2
3
故X 5
9
0
9 19
10 19
11 19
4
5
6
2 15
0
13 19
25 19
18 19
7
8
9
3. 求向量组1 (2,1,4,3),2 (1,1,6,6),3 (1,2,2,9),4 (1,1,2,7),
5 (2,4,4,9) 的一个极大无关组,并把其余向量用该极大无关组线性表示出来。
是它的一个极大无关组,且
3 5
1 2 41 32
34
。
2 2 0 4. 已知矩阵 A 2 1 2 ,求一个正交矩阵 P,使 PT AP Λ 为对角阵。
0 2 0
第2页共3页
2 2 0
解:由 A E 2 1 2 2 1 4
0 2
知 A 的特征值为 1 2,2 1,3 4
0
0
0
1 3
r2
1 3
0 1 0 0
1 6 0 22
21
66
r4
22r2
0 0
1 0
1 0 00
3
0
1 0 1 0 4
1 0 1 0 4
r1r2
3
r2r3
0
1
1
0
3
0 1 1 0 3
0 0 0 1 3
0 0 0 0 0
0 0 0 0 0
从而1,2 ,4
7 9
1 2
4 。
7
4 6 1 2
2 解: D 3
5 4
5 7 9 6
线性代数期末考试试题及答案

线性代数期末考试试题及答案一、选择题(每题2分,共20分)1. 向量空间的基是该空间的一组向量,满足以下哪两个条件?A. 线性无关B. 可以表示空间中的任何向量C. 可以线性组合出空间中的任何向量D. 以上都是2. 矩阵的秩是指:A. 矩阵中非零行的最大数目B. 矩阵中非零列的最大数目C. 矩阵的行向量组的秩D. 矩阵的列向量组的秩3. 线性变换的核是指:A. 变换后为零的向量集合B. 变换后为单位向量的向量集合C. 变换后保持不变的向量集合D. 变换后向量长度为1的向量集合4. 特征值和特征向量是线性变换中的基本概念,特征向量满足以下条件:A. 变换后保持不变B. 变换后与原向量成比例C. 变换后与原向量垂直D. 变换后与原向量正交5. 对于矩阵A,下列哪个矩阵是A的逆矩阵?B. A的伴随矩阵C. A的行列式D. 与A相乘结果为单位矩阵的矩阵6. 行列式的性质不包括:A. 行列式与矩阵的转置相等B. 行列式与矩阵的伴随矩阵无关C. 行列式与矩阵的行(列)交换有关D. 行列式与矩阵的行(列)乘以常数有关7. 线性方程组有唯一解的条件是:A. 方程组的系数矩阵是可逆的B. 方程组的系数矩阵是方阵C. 方程组的系数矩阵的秩等于增广矩阵的秩D. 方程组的系数矩阵的秩等于未知数的个数8. 矩阵的迹是指:A. 矩阵的对角线元素之和B. 矩阵的行向量长度之和C. 矩阵的列向量长度之和D. 矩阵的行列式9. 线性无关的向量组可以作为向量空间的基,其必要条件是:A. 向量组中的向量数量等于向量空间的维数B. 向量组中的向量数量大于向量空间的维数C. 向量组中的向量数量小于向量空间的维数D. 向量组中的向量数量可以任意10. 对于矩阵A,下列哪个矩阵是A的共轭转置?A. A的转置矩阵C. A的伴随矩阵D. A的复共轭矩阵的转置答案:1. D 2. D 3. A 4. B 5. D 6. B 7. D 8. A 9. A 10. D二、填空题(每空2分,共20分)1. 设向量空间V的基为{v1, v2, ..., vn},则向量v可以表示为______ 。
2017级线代试卷B答案

1 2 2 3 1 0 0 1
= 1时, B 0
1
1
1
0
1
1
1
0 0 0 0
0 0 0 0
R A R B 2 3,方程组有无穷多解;
此时,
x1 x2
=1 x3
, 1
令
x3 c,得通解
0 1
X
c
11
01
其中 c为任意常数. 12
2
江南大学考试卷专用纸
本题 得分
(B) 存在可逆阵 P , 使得P T A P B;
(C) 存在可逆阵 P , Q , 使得 P A Q B ; (D) A B .
(4) 设 A , B 为 n 阶相似方阵,则下列结论错误的是
[D]
(A) R A R B ;
(B) A , B 的特征值相同 ; (C) A 与 B 同时可逆或不可逆;
江南大学考试卷专用纸
2017 级《线性代数 II》期末考试卷(B)答案
使用专业、班级
学号
姓名
题号
一
二
三
四
五
六
七
得分
l
总分
本题 得分
一、填空题(每小题 4 分, 共 24 分)
2 0 0
(1 )
设矩阵
A
0
3
4
,则
A 1 =
0 4 5
1 2
0
0
0 0
5 4
4
3
.
(2) 设向量 = 1 , 1 , 0 T , 2 , 3 , 1 ,矩阵 A , 则 A100
又由1 , 2 , 3 线性相关 可知 3 能由1 , 2 线性表示 若 1 , 2 , 3 4 线性相关,则 3 4 能由 1 , 2 线性表示 故 4 能由 1 , 2 线性表示 即1 , 2 , 4 线性相关 与1 , 2 , 4 线性无关矛盾. 因此 1 , 2 , 3 4 线性无关.
线性代数期末考试试题及答案

线性代数期末考试试题及答案一、选择题(每题5分,共25分)1.下列哪一个不是线性空间?A. 实数集RB. 矩阵的集合M(n,R)C. 正实数集R+D. 空集答案:C2.下列关于线性变换的叙述,正确的是()A. 线性变换保持向量的长度不变B. 线性变换保持向量的方向不变C. 线性变换保持向量的数量积不变D. 线性变换保持向量的线性组合关系不变答案:D3.若向量组α1,α2,α3线性无关,则向量组()A. 2α1,3α2,4α3 线性相关B. 2α1+3α2,4α3 线性无关C. α1+α2,α2+α3,α3+α1 线性无关D. α1,α1+α2,α1+α2+α3 线性相关答案:C4.设A是3阶矩阵,且|A|=5,则|2A|=()A. 10B. 25C. 50D. 125答案:D5.下列关于线性方程组的叙述,正确的是()A. 如果系数矩阵的秩小于未知数的个数,则方程组一定有解B. 如果系数矩阵的秩等于未知数的个数,则方程组一定有唯一解C. 如果系数矩阵的秩等于增广矩阵的秩,则方程组一定有解D. 如果系数矩阵的秩小于增广矩阵的秩,则方程组一定无解答案:C二、填空题(每题5分,共25分)6.若向量组α1,α2,α3线性无关,则其极大线性无关组所含向量的个数为______。
答案:37.设A是3阶矩阵,且|A|=4,则|A的逆矩阵|=______。
答案:1/48.若线性方程组Ax=b有解,则系数矩阵A的秩r(A)与增广矩阵B的秩r(B)满足关系______。
答案:r(A)=r(B)9.设A是n阶对称矩阵,则A的转置矩阵A^T______。
答案:等于A10.线性空间V的维数等于______。
答案:V中极大线性无关组所含向量的个数三、计算题(每题10分,共30分)11.已知向量组α1=(1,2,3),α2=(4,5,6),α3=(7,8,9),判断向量组是否线性相关,并说明理由。
答案:线性相关。
因为α3=α1+α2,所以向量组线性相关。
中国农业大学2016-2017(秋)《线性代数》期末考试试题解析

2016~2017学年秋季学期《线性代数》课程考试试题解析一、填空题(本题满分15分,共有5道小题,每道小题3分,请将合适的答案填在每题的空中)1.设,A B 均为四阶方阵,且1,2,A B ==-*A 是A 的伴随矩阵,则*B A B =.解析:由于31,1,2,A A A B *====-所以4**4(2)1(2)32.B A B B A B ==-⋅⋅-=-注释本题知识点:1(1);n A A -*=(2);n A A λλ=(3).AB A B =答案:32.-2.设矩阵A 满足2230,A A E ++=则1()A E --=.解析:由2230,A A E ++=得2236,A A E E +-=-即3()(3)6,(),6A EA E A E E A E E +-+=--=-所以11()(3).6A E A E --=-+注释本题知识点:1.AA E -=答案:11()(3).6A E A E --=-+3.已知向量组123,,ααα线性无关,若向量组112223313,,k k k βααβααβαα=+=+=+线性相关,则参数k =.解析:由题设可得12312310(,,)(,,)10,01k k k βββααα⎛⎫ ⎪= ⎪ ⎪⎝⎭因为123,,ααα线性无关,123,,βββ线性相关.所以10100,01kk k =解得 1.k =-注释本题知识点:(1)向量组的线性相关性与向量组的秩.(2)向量组123,,βββ线性相关的充分必要条件是齐次线性方程组123(,,)0x βββ=有非零解.答案: 1.k =-4.已知向量组1231111,1,3,262ααα⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪==-= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭则向量组的秩为.解析:123111111111(,,)113~022~022*********ααα⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=--- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭,所以向量组的值秩为2.注释本题知识点:(1)矩阵的秩等于它的列向量组的秩,也等于它的行向量组的秩.(2)矩阵的初等变换不改变矩阵的秩.答案:2.5.设三阶实对称矩阵A 的两个非零特征值对应的特征向量分别为T T 12(1,1,1),=(0,-1,1),αα=且秩()2,R A =则齐次方程组0Ax =的通解为.解析:因为三阶实对称矩阵的秩()2,R A =所以该矩阵有特征值零,设零特征值对应的特征向量为,α由于不同特征值对应的特征向量正交所以T 1T 2=0,ααα⎛⎫ ⎪ ⎪⎝⎭即1110,011α⎛⎫=⎪-⎝⎭解得一个非零解T (2,1,1)α=-,因此有0A α=,又因为()2,R A =所以齐次方程组0Ax =的通解为T (2,1,1),().x k k R =-∈注释本题知识点:(1)齐次线性方程组的通解.(2)方阵的特征值和特征向量的定义.(3)不同的特征值对应的特征向量正交.答案:T (2,1,1),().x k k R =-∈二、选择题(本题满分15分,共有5道小题,每道小题3分.在每小题给出的四个选项中,只有一项是符合题目要求的,把所选项前的字母填在题后的括号内)1.已知三阶行列式11131221232231333232326,32a a a a a a a a a --=-则111213212223313233a a a a a a a a a =【】.(A)2;(B)6;(C)-1;(D)1解析:由11131221232231333232326,32a a a a a a a a a --=-根据行列式的性质可得11131221232231333266,a a a a a a a a a -=即1112132122233132331.a a a a a a a a a =注释本题知识点:行列式的性质答案:1.2.设A 是m n ⨯矩阵,0Ax =是非齐次线性方程组Ax b =对应的齐次线性方程组,则下列结论正确的是【】.(A)若0Ax =仅有零解,则Ax b =有唯一解;(B)若0Ax =有非零解,则Ax b =有无穷多解;(C)若Ax b =有无穷多解,则0Ax =仅有零解;(D)若Ax b =有无穷多解,则0Ax =有非零解.解析:0Ax =仅有零解,可得(),R A n =但不能得出()(,),R A R A b =所以Ax b =不一定有解.0Ax =有非零解,可得(),R A n <但不能得出()(,),R A R A b =所以Ax b =不一定有解.Ax b =有无穷多解,可得()(,),R A R A b n =<所以0Ax =有非零解.注释本题知识点:线性方程组的解的个数非齐次线性方程组,Ax b A =为m n ⨯矩阵,有解的充分必要条件是()(,).R A R A b =(1)当()(,)R A R A b n ==时,有唯一解.(2)当()(,)R A R A b n =<时,有无穷多解.n 元线性方程组Ax b =无解的充分必要条件是()(,).R A R A b <n 元齐次线性方程组0Ax =总有解.有非零解的充分必要条件是().R A n <答案:D.3.设A 是34⨯阶矩阵,A 的行向量组线性无关,则【】.(A)A 中必有两列元素对应成比例;(B)A 中必有一个列向量是其余列向量的线性组合;(C)A 的列向量组线性无关;(D)A 中必有一列元素全为零;解析:由于矩阵A 的行向量组线性无关,所以() 3.R A =设1234,,,ββββ为A 的列向量组,则有1234(,,,)3,R ββββ=因此1234,,,ββββ线性相关,且有三个列向量线性无关故矩阵A 中必有一个列向量是其余列向量的线性组合.注释本题知识点:(1)矩阵的秩等于它的列向量组的秩,也等于它的行向量组的秩(2)向量组线性相关和线性无关答案:D4.已知齐次方程组(2)0A E x -=的基础解系有一个向量,则行列式22A A E --=【】(A)2;(B)0;(C)1;(D) 3.解析:由题设知矩阵2A E -为方阵,且(2)0A E x -=的基础解系有一个向量所以20A E -=故22(2)()20.A A E A E A E A E A E --=-+=-+=注释本题知识点:(1)齐次线性方程组有非零解的充分必要条件是系数矩阵的秩小于变元的个数.(2).AB A B =答案:B 5.当t 满足【】时,二次型222123123121323(,,)22222f x x x x x x tx x x x x x =--+++-是负定的.(A)(t ∈(B)t ∈(C)(0);t ∈(D)空集.解析:二次型矩阵为1121,112tA t -⎛⎫ ⎪=-- ⎪ ⎪⎝⎭根据负定二次型判定可得2222112233111510,202,21250,22112t t t t tt t t--∆=-<∆==->⇒<∆=--=-+<⇒>-所以不存在t 使得二次型为负定的.注释本题知识点:负定二次型的判定n 元实二次型T f x Ax =负定的充分必要条件是下列条件之一成立:(1)f 的负惯性性指数为n ;(2)A 的特征值全为负数;(3)A 合同于E -;(4)A 的各阶顺序主子式负正相间,即奇数阶顺序主子式为负数,偶数阶顺序主子式为负数.答案:D三、(本题满分14分)计算下列行列式的值:1.111235.4925D =解析:111235(53)(52)(32) 6.4925D ==---=注释本题知识点:利用范德蒙行列式求解1222212111112111().nn ni j j i nn n n nx x x D x x x x x x x x ≤<≤---==-∏答案:6.2.计算行列式30402222075120500D =-的第四行元素的余子式之和.解析:行列式D 的第四行元素的余子式之和为32304034022227(1)22228.0701111111D +==-⋅-=------注释本题知识点:(1)余子式和代数余子式的定义;(2)行列式等于它的任一行(列)的各元素与其对应的代数余子式乘积之和.答案:-28四、(本题满分12分)已知矩阵方程*111(2)2A XA AX E --=+,其中011101,110A ⎛⎫⎪= ⎪ ⎪⎝⎭*A 是矩阵A 的伴随矩阵,求.X 解析:因为0111012,110A ==所以矩阵A 可逆.方程两端左乘*2,A 右乘,A 可得(2)4,X E A E -=所以112244(2)212.9221X E A ---⎛⎫⎪=-=-- ⎪ ⎪--⎝⎭注释本题知识点:(1)n 阶方阵可逆的充分必要条件是0;A ≠(2)**;AA A A A E ==.(3)11;AAA A E --==(4)逆矩阵的求法.答案:1224212.9221X --⎛⎫⎪=-- ⎪ ⎪--⎝⎭五、(本题满分12分)设向量组T T T T 1234:(1,2,3,1,2),(2,1,2,2,3),(3,1,5,3,1),(5,0,7,5,4),A a a a a =--=--=---=--(1)求向量组A 的秩;(2)求向量组A 的一个最大线性无关组;(3)把其它向量用最大线性无关组表示.解析:1235123512351011211005510011201123257~0448~0000~000012350000000000002314077140000⎛⎫⎛⎫⎛⎫⎛⎫⎪⎪ ⎪ ⎪-- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪---⎪⎪ ⎪ ⎪---- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪------⎝⎭⎝⎭⎝⎭⎝⎭(1)向量组A 的秩为2;(2)向量组A 的一个最大线性无关组为12,;a a (3)312412,2.a a a a a a =+=+注释本题知识点:(1)矩阵的秩等于它的列向量组的秩,也等于它的行向量组的秩(2)初等行变换不改变矩阵的秩(3)向量组的最大无关组与向量组的秩答案:(1)向量组A 的秩为2;(2)向量组A 的一个最大线性无关组为12,;a a (3)312412,2.a a a a a a =+=+六、(本题满分12分)已知非齐次线性方程组为1234123412341234422,52113,36312,231,x x x qx x x x x x x x x p x x x x +++=⎧⎪+++=⎪⎨+++=⎪⎪+++=-⎩试求当参数,p q 为何值时,方程组无解,方程组有唯一解,方程组有无穷多解.解析:4212121311213152111352111308448(,)~~363123631200033121314212063126q A b p p p q q --⎛⎫⎛⎫⎛⎫⎪⎪ ⎪---⎪ ⎪ ⎪= ⎪ ⎪ ⎪+ ⎪⎪ ⎪----⎝⎭⎝⎭⎝⎭10021121311213101121210844802112~~~000330003300033(3)(9)06312600900003p p p p q q q ⎛⎫--⎛⎫⎛⎫⎪- ⎪ ⎪⎪---- ⎪ ⎪ ⎪+ ⎪ ⎪++⎪+- ⎪ ⎪⎪---- ⎪⎝⎭⎝⎭⎝⎭(1)当3,p ≠-且9q ≠时,方程组无解;(2)当3,p =-或9q =时,方程组有无穷解;(3)方程组不存在唯一解.注释本题知识点:线性方程组的解的个数非齐次线性方程组,Ax b A =为m n ⨯矩阵,有解的充分必要条件是()(,).R A R A b =(1)当()(,)R A R A b n ==时,有唯一解.(2)当()(,)R A R A b n =<时,有无穷多解.n 元线性方程组Ax b =无解的充分必要条件是()(,).R A R A b <答案:(1)当3,p ≠-且9q ≠时,方程组无解;(2)当3,p =-或9q =时,方程组有无穷解;(3)方程组不存在唯一解.七、(本题满分12分)求正交变换,x py =将二次型222123123121323(,,)222222f x x x x x x x x x x x x =++---化为标准形,并写出其标准形.解析:二次型矩阵为211121,112A --⎛⎫ ⎪=--⎪ ⎪--⎝⎭2123(3),0,3,A E λλλλλλ-=--===当10λ=时,解0,Ax =得T 1(1,1,1)ξ=,当23=3λλ=,时,解(3)0,A E x -=得T T 23(1,1,0)(1,0,1)ξξ=-=-,,正交化T22232111,,,1.222ηξηξξ⎛⎫==-=-- ⎪⎝⎭单位化T T123,0,.p p p ⎛⎛⎫===- ⎪ ⎝⎭⎝正交矩阵,P⎛⎫--⎪⎪=-⎪⎪⎭正交变换,x py=标准形为222333.f y y=+注释本题知识点:正交变换化二次型为标准型答案:222333.f y y=+八、(本题满分8分)设A和B均为n阶方阵,且22,2,A B E B B=+=证明:A可逆.解析:由22,B B=得2288,B B E E--=-即4(2),8B EB E E-+=-故2B E+可逆而2,A B E=+所以A可逆.注释本题知识点:若n阶方阵A和B满足AB E=,则A可逆,且1.A B-=。
工大2017级线性代数期末试卷(B)参考答案及解析

2017级线性代数期末试卷(B)解答与参考评分标准一、单项选择题(每小题3分,共15分)1.当()k C ≠时,方程组02020kx z x ky z kx y z +=⎧⎪++=⎨⎪-+=⎩只有零解。
A. 0;B. -1 ;C. 2 ;D. -22.设,A B 均为n 阶方阵,且()0A B E -=, 则 ( B ) A. 0A =或 B E =;B. 0A =或 0B E -=;C. 0A =或 1B =;D. A BA =.3.以初等矩阵100001010⎛⎫ ⎪ ⎪ ⎪⎝⎭左乘矩阵001100010A ⎛⎫ ⎪= ⎪ ⎪⎝⎭相当于对矩阵A (A )的初等变换.A. 23r r ↔,B. 23c c ↔,C. 13r r ↔, B. 13c c ↔,4.设向量组的秩为r ,则( D )A. 该向量组所含向量的个数必大于r 。
B. 该向量组中任何r 个向量必线性无关,任何1r +个向量必线性相关。
C. 该向量组中有r 个向量线性无关,有1r +个向量线性相关。
D. 该向量组中有r 个向量线性无关,任何1r +个向量必线性相关。
5.设A 为n 阶方阵,则“0是A 的一个特征值“是“A 为奇异矩阵“的( D )A. 充分非必要条件;B. 必要非充分条件;C. 既非充分也非必要条件;D. 充分必要条件。
二、填空题(每小题3分,共15分)6. 设()2201x x e f x =,则()'0f = 27. 设A,B 均为n 阶方阵,2,3A B ==-,则*12A B-=2123n --。
8.设A 是43⨯矩阵,且()2R A =,而102020103B ⎛⎫ ⎪= ⎪ ⎪-⎝⎭,则()R AB = 2 。
9. 设()()()1231,1,1,,0,,1,3,2a b ααα===,若1,23,ααα线性相关,则,a b 满足关系式2a b =。
10.设n 阶方阵A 有n 个特征值0,1,2,L ,1n -,且方阵B 与A 相似,则B E +=!n 。
线性代数期末考试题及答案

线性代数期末考试题及答案一、选择题(每题4分,共20分)1. 设矩阵A为3阶方阵,且|A|=2,则矩阵A的逆矩阵的行列式为:A. 1/2B. 1/4C. 2D. 4答案:B2. 向量α=(1,2,3)和向量β=(4,5,6),则向量α和向量β的点积为:A. 32B. 22C. 14D. 0答案:A3. 设A为3×3矩阵,且A的秩为2,则A的行向量线性相关,下列说法正确的是:A. 正确B. 错误答案:A4. 若A为n阶方阵,且A^2=0,则A的秩为:A. nB. n-1C. 0D. 不确定答案:C5. 设A为3阶方阵,且A的特征值为1,2,3,则矩阵A的迹为:A. 6B. 1C. 2D. 3答案:A二、填空题(每题5分,共30分)1. 设矩阵A=\[\begin{bmatrix}1 & 2 \\ 3 & 4\end{bmatrix}\],则矩阵A的转置为\[\begin{bmatrix}1 & 3 \\ 2 & 4\end{bmatrix}\]。
答案:\[\begin{bmatrix}1 & 3 \\ 2 & 4\end{bmatrix}\]2. 设向量α=(2,3),向量β=(4,6),则向量α和向量β共线,其比例系数为2。
答案:23. 若矩阵A=\[\begin{bmatrix}1 & 1 \\ 2 & 2\end{bmatrix}\],则矩阵A的行列式为2。
答案:24. 设矩阵B=\[\begin{bmatrix}0 & 1 \\ -1 & 0\end{bmatrix}\],则矩阵B的逆矩阵为\[\begin{bmatrix}0 & -1 \\ 1 &0\end{bmatrix}\]。
答案:\[\begin{bmatrix}0 & -1 \\ 1 & 0\end{bmatrix}\]5. 设矩阵C=\[\begin{bmatrix}1 & 0 \\ 0 & 2\end{bmatrix}\],则矩阵C的特征值为1和2。
大学《线性代数》2016-2017第二学期期末A卷及答案
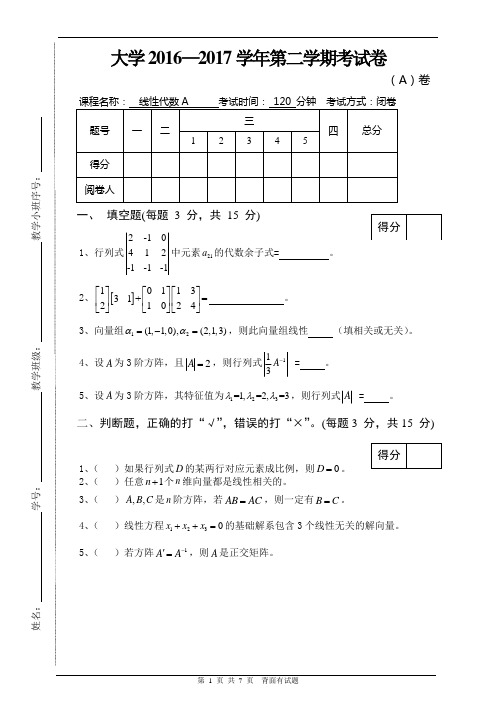
第 1 页 共 7 页 背面有试题大学2016—2017学年第二学期考试卷(A )卷一、 填空题(每题 3 分,共 15 分)1、行列式2-10412-1-1-1中元素21a 的代数余子式= 。
2、[]1011331+=21024⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦。
3、向量组12(1,1,0),(2,1,3)αα=-=,则此向量组线性 (填相关或无关)。
4、设A 为3阶方阵,且2A =,则行列式113A - = 。
5、设A 为3阶方阵,其特征值为123=1,=2,=3λλλ,则行列式A = 。
二、判断题,正确的打“√”,错误的打“×”。
(每题3 分,共15 分)1、( )如果行列式D 的某两行对应元素成比例,则0D =。
2、( )任意1n +个n 维向量都是线性相关的。
3、( ),,A B C 是n 阶方阵,若AB AC =,则一定有B C =。
4、( )线性方程1230x x x ++=的基础解系包含3个线性无关的解向量。
5、( )若方阵1A A -'=,则A 是正交矩阵。
第 2 页 共 7 页 背面有试题2装O订O线O三、计算题(每题12 分,共60分)1、(12)计算行列式1150211112210133D =。
2、(12)求向量组1234(1,4,1,0),(2,5,-1,-3),(1,0,-3,-4),(0,2,-6,3)αααα====的秩和一个最大线性无关组。
3、(12)求矩阵111120212A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦的逆矩阵。
4、(12)求齐次线性方程组的通解。
123412341234123450,230,380,3970.x x x x x x x x x x x x x x x x -+-=⎧⎪+-+=⎪⎨-++=⎪⎪+-+=⎩5、(12)求矩阵1232A ⎡⎤=⎢⎥⎣⎦的特征值和特征向量。
四、证明题(10分)设向量123,,ααα线性无关,请证明1223312,,3αααααα+++也线性无关。
线性代数期末试卷及详细答案

(A )A=E
(B ) A 相似于 E ( C) A2 E
( D) A 合同于 E
8、若 1, 2, 3 , 4 是线性方程组 AX O 的基础解系,则 1 + 2 + 3 + 4 是 AX O 的
(A )解向量
( B)基础解系
( C )通解;
( D) A 的行向量;
9、 1 , 2 都是 n 阶矩阵 A 的特征值, 1 2 ,且 X 1 和 X 2 分别是对应于 1 和 2 的特征
准型,并求出正交变换。 四、证明题( 7 分)
设 A 为 m× n 矩阵, B 为 n 阶矩阵,已知 R(A) n
证明:若 AB=O ,则 B=O
《线性代数》期末考试题 A 题参考答案与评分标准
填空题
1、 -10;
2、 81;
3、
4,
6,
12;
1
4、
A
3E ;
2
5、 5;
二、单项选择题 ( 每小题 2 分,共 20 分)
填空题 (将正确答案填在题中横线上。每小题 2 分,共 10 分)
345
1、设 D1 = 3 1
5 , D2= 5
2
2
1 0
0 ,则 D = D1 O
0
O
= _____________。
D2
2、四阶方阵
A、B ,已知
1 A=
,且 B= 2A -1
16
1
2A ,则 B =_____________ 。
1b1
002
求 a,b 6、齐次线性方程组
2 x1 x2 3x3 0 x1 3x2 4 x3 0
x1 2 x2 ax 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、 24;
11
2、;
3、 -2 ;
01
4、0;
5、无关
三、计算行列式( 12 分) 1、原式 =4 ;
………… 10 分
四、( 10 分)
解
:
3 40
2
A
4
30
0 04
……… 4 分
4 80 4A 8 4 0
008
fA
0 12 0 12 0 0 0 0 11
……………… 8 分
0 33 12 3 1 10
课程考核试题卷 ( A 卷)
试卷编号
( 2016 至 2017 学年 第 __2_学期 )
课程名称 :
线性代数 A
考试时间: 110 分钟
课程代码:
7100059
试卷总分 : 100 分
考试形式: 闭卷
学生自带普通计算器 : 否
:
姓名名:
题号 一 二 三 四 五 六 七 八 九 十 十一 十二 总分
正交,则
k
_.
年级专业级专业:
1
11
2、
=
01
.
年
3、设 3 阶矩阵 A 的行列式 | A |=8 ,已知 A 有 2 个特征值 - 1 和 4,则另一特征值为 .
4、如果 X 1 , X 2 都是方程 A n n X O 的解,且 X 1 X 2 ,则 An n
;
5、设向量组
1
T
(1, 0 , 0 ) , 2
5、设矩阵 A 的秩为 r ,则 A 中(
)
A. 所有 r - 1 阶子式都不为 0 B. 所有 r - 1 阶子式全为 0
装
C. 至少有一个 r 阶子式不等于 0 D. 所有 r 阶子式都不为 0
装
得分
二、填空题(每小题 3 分,共 15 分)
:
1、已知向量
T
(1,3,2, 4)
与
(k,
1,
T
3,2k )
00
所以 1 , 2 , 4 为一组极大无关组
50 10 01 00
……… 3 分
6分 8分
3
51
2
八、( 8 分)
……… 10 分
解: 解:(1)、由于 A 与 B 相似,则 tr ( A ) tr ( B ) 。因为 tr ( A ) 5 , tr ( B ) 3 x ,
则x 2。
……… 4 分
B. A 的 列 向 量 组 线 性 无 关 D. A 的 列 向 量 组 线 性 相 关
4、若 x1 是方程 A X B 的解, x 2 是方程 A X O 的解,则()是方程 A X B 的解( c R )
教
A. x1 cx 2 B. cx 1 cx 2 C.
cx 1 cx 2 D.
cx 1 x2
。
取P
a1 , 2 , 3
C 时 A=0 C. A 0 时 B=C D. |A| 0 时 B=C
订 3、设 A 是 s n 矩 阵 ,则 齐 次 线 性 方 程 组 A x 0 有 非 零 解 的 充 分 必 要 条 件 是 ( )
: 教学班号学班号:
A. A 的 行 向 量 组 线 性 无 关 C. A 的 行 向 量 组 线 性 相 关
五、(10 分)求齐次线性方程组
通解 .
2 x1 3 x2 x3 5 x4 0 3x1 x2 2 x3 4 x4 0 的一个基础解系及其 x1 2 x 2 3 x3 x 4 0
得分 六、(12 分)判定二次型 f 该二次型的秩。
2
x1
2
x2
2
x3
4 x1x2
4 x1 x3
4 x2 x3 的正定性,并求
第 3 页 共 4页
得分
1
2
3
七、(10 分)求向量组: 1
2
,2
1
5
,3
2
5
,4
7
1
1
4
个极大线性无关组,并将其余向量通过该极大线性无关组表示出来 .
1 6
的秩及一
17 9
得分
110
八、(12 分)已知矩阵 A 1 1 0 与 B
003
( 1)求 x ;
( 2)求可逆矩阵
P ,使得
1
P AP
B。
………… 10 分
五、( 12 分) 解:齐次线性方程组的系数矩阵
A 为:
2 x1 3 x2 x3 5 x4 0 3 x1 x2 2 x3 4 x4 0 x1 2 x 2 3 x3 x 4 0
2 31 5
1 23 1
10 1 1
A
3 1 2 4~ 0 7
7 7~0 1 1 1
…4 分
1 23 1
0 77 7
00 0 0
一般解为:
x1 x3 x4 x2 x3 x4
x3 x3 x4 x4
( x3 为自由未知量)
…………………… 6 分
第 5 页 共 4页
故齐次线性方程组的通解为
六、( 12 分) 解:二次型对应的矩阵为
1
1
1
1
X =k 1
+k 2
1
0
0
1
( k1k 2 为 常 数 )0 , 相似 00x
1
得分
九、(6 分)设 3 阶矩阵 A 的特征值为 2(二重),-4 ,求
1 A
。
2
一、单项选择题(每小题 3 分,共 15 分) 评分标准: 选对得 3 分,不选或选错得 0 分
第 4 页 共 4页
1、D ;2、 D; 3、 D; 4、 A; 5、 C
二、填空题(每小题 3 分,共 15 分): 评分标准: 填对得 3 分,不填或填错得 0 分
( 2 )、 因 为 B 的 特 征 值 为 1
0, 2
3, 3
2 ,所以
A 的特征值为
。 1 0 , 2 3 , 3 2
第 6 页 共 4页
当1
0 时,它对应的特征向量为
a1
T
(1, 1, 0)
当对于 2
3 时,它对应的特征向量为
a2
T
( 0,0,1)
当3
2 时,它对应的特征向量为
a3
T
(1,1, 0 )
T
( 1,3,0 ) , 3
(1, 2,
T
1)
线性
(填相关或无关)
第 1页 共 7页
得分
3 1 12
51 3 4
三、(10 分)计算行列式
.
201 1
1 53 3
得分
1 20
四、(10 分)已知 f ( x) x2 4 x 1 , A 2 1 0 ,求 f ( A) 。
002
第 2 页 共 4页
得分
姓
得分
线
线 评卷 教师
得分 一、单项选择题(每小题 3 分,共 15 分)
: 学号号:
学
1、 A 和 B 均为 n 阶矩阵,且 ( A
2
B)
2
A 2 AB
B 2 ,则必有(
)
A A E; B B E; C A B. D
AB BA 。
2、设 A 是方阵,如有矩阵关系式 AB=AC,则必有(
)
订
A. A =0 B. B
12 2
A2
1
2
……… 4 分
2
21
1
1 0; ……… 2 分
12 21
30
……… 2 分
12 2
2
12
13
2
21
所以矩阵的秩为 3,即二次型的秩为 3
0 ……… 2 分
2分
七、( 10 分) 解:向量组对应的矩阵为
( 1 2 3 4)
12 25 12
31
10
56
01
~
7 17
00
1 1 49
所以矩阵的秩为 3
