实验一图像的傅立叶变换
图像傅里叶变换详解

图像傅里叶变换冈萨雷斯版<图像处理>里面的解释非常形象:一个恰当的比喻是将傅里叶变换比作一个玻璃棱镜。
棱镜是可以将光分解为不同颜色的物理仪器,每个成分的颜色由波长(或频率)来决定。
傅里叶变换可以看作是数学上的棱镜,将函数基于频率分解为不同的成分。
当我们考虑光时,讨论它的光谱或频率谱。
同样, 傅立叶变换使我们能通过频率成分来分析一个函数。
Fourier theory讲的就是:任何信号(如图像信号)都可以表示成一系列正弦信号的叠加,在图像领域就是将图像brightness variation 作为正弦变量。
比如下图的正弦模式可在单傅里叶中由三个分量编码:频率f、幅值A、相位γ这三个value可以描述正弦图像中的所有信息。
1.frequencyfrequency在空间域上可由亮度调节,例如左图的frequency比右图的frequency 低……2.幅值magnitude(amplitude)sin函数的幅值用于描述对比度,或者说是图像中最明和最暗的峰值之间的差。
(一个负幅值表示一个对比逆转,即明暗交换。
)3.相位表示相对于原始波形,这个波形的偏移量(左or右)。
=================================================================一个傅里叶变换编码是一系列正弦曲线的编码,他们的频率从0开始(即没有调整,相位为0,平均亮度处),到尼奎斯特频率(即数字图像中可被编码的最高频率,它和像素大小、resolution有关)。
傅里叶变换同时将图像中所有频率进行编码:一个只包含一个频率f1的信号在频谱上横坐标f为f1的点处绘制一个单峰值,峰值高度等于对应的振幅amplitude,或者正弦曲线信号的高度。
如下图所示。
DC term直流信号对应于频率为0的点,表示整幅图像的平均亮度,如果直流信号DC=0就表示整幅图像平均亮度的像素点个数=0,可推出灰度图中,正弦曲线在正负值之间交替变化,但是由于灰度图中没有负值,所以所有的真实图像都有一个正的DC term,如上图所示。
图像的傅里叶变换

在MATLAB中提供了fft函数用于实现一维快速傅里 叶变换。其调用格式为: (1)Y=fft(X):返回向量X的离散傅里叶变换。如果X 为矩阵,fft函数返回矩阵每列的傅里叶变换。 (2)Y=fft2(X):返回二维离散傅里叶变换,结果Y和 X的大小相同。 (3)Y=fftn(X):返回X的多维离散傅里叶变换,结果 Y和X的大小相同。 (4)Y=fftshift(X):把fft函数、fft2函数和fftn函数输 出结果的零频率部分移到数组的中间。
傅里叶变换的MATLAB函数
例二:对一幅图像实施二维DFT,显示并观察其频 谱。对单缝进行快速傅里叶变换,以三种方式显 示频谱。即:直接显示(坐标原点在左上角); 把坐标原点平移至中心后显示;以对数方式显示。 >>f=zeros(512,512); >>f(246:266,230:276)=1; >>subplot(221);imshow(f,[]); >>xlabel(‘单狭缝图像’); >>F=fft2(f); >>S=abs(F);
傅里叶变换的MATLAB函数
>>F=fftshift(abs(fft2(f))); >>subplot(224);imshow(F,[-1,5],’notruesize’); >>xlabel(‘(d)图像旋转45度的傅里叶变换频 谱’);
பைடு நூலகம்
傅里叶变换的MATLAB函数
>>f=zeros(1000,1000); >>f(350:649,475:524)=1; >>subplot(221); >>imshow(f,’notruesize’);% ‘notruesize’图片去适应 窗口,窗口大小不动,自动调节图片大小。所以 显示出来的图片跟实际尺寸可能不一致。 ‘truesize’ 就是按图片实际大小显示图片,窗口 会自动调节大小去适应图片尺寸。这个是默认情 况,跟省略这个参数一样。 >>xlabel(‘(a)原始图像’); >>subplot(222);F=fftshift(abs(fft2(f)));
图像的二维傅里叶变换

图像傅立叶变换(二维傅立叶变换fourier, 二维DFT, 2d-fft)的原理和物理意义图像傅立叶变换图像的傅立叶变换,原始图像由N行N列构成,N必须是基2的,把这个N*N个包含图像的点称为实部,另外还需要N*N个点称为虚部,因为FFT是基于复数的,如下图所示:计算图像傅立叶变换的过程很简单:首先对每一行做一维FFT,然后对每一列做一维FFT。
具体来说,先对第0行的N个点做FFT(实部有值,虚部为0),将FFT输出的实部放回原来第0行的实部,FFT输出的虚部放回第0行的虚部,这样计算完全部行之后,图像的实部和虚部包含的是中间数据,然后用相同的办法进行列方向上的FFT变换,这样N*N的图像经过FFT得到一个N*N的频谱。
下面展示了一副图像的二维FFT变换:频域中可以包含负值,图像中灰色表示0,黑色表示负值,白色表示正值。
可以看到4个角上的黑色更黑,白色更白,表示其幅度更大,其实4个角上的系数表示的是图像的低频组成部分,而中心则是图像的高频组成部分。
除此以外,FFT的系数显得杂乱无章,基本看不出什么。
将上述直角坐标转换为极坐标的形式,稍微比较容易理解一点,幅度中4个角上白色的区域表示幅度较大,而相位中高频和低频基本看不出什么区别来。
上述以一种不同的方法展示了图像频谱,它将低频部分平移到了频谱的中心。
这个其实很好理解,因为经2D-FFT的信号是离散图像,其2D-FFT的输出就是周期信号,也就是将前面一张图周期性平铺,取了一张以低频为中心的图。
将原点放在中心有很多好处,比如更加直观更符合周期性的原理,但在这节中还是以未平移之前的图来解释。
行N/2和列N/2将频域分成四块。
对实部和幅度来说,右上角和左下角成镜像关系,左上角和右下角也是镜像关系;对虚部和相位来说,也是类似的,只是符号要取反,这种对称性和1维傅立叶变换是类似的,你可以往前看看。
为简单起见,先考虑4*4的像素,右边是其灰度值,对这些灰度值进行2维fft变换。
图像的傅里叶变换、反变换地实现

课程大作业实验报告图像傅里叶变幻、反变换的实现课程名称:数字图像处理组长:王文雄学号:200730590323 年级专业班级:07通信3班成员一:庞柱坚学号:200730590318 年级专业班级:07通信3班成员二:王弥光学号:200730590322年级专业班级:07通信3班成员三:学号:年级专业班级:07通信3班指导教师邓继忠报告提交日期2010年6月1日项目答辩日期2010年6月1日目录1. 项目要求 (4)2. 项目开发环境 (4)3. 系统分析 (4)3.1. 系统的主要功能分析 (4)3.2. 系统的关键问题及解决方法(或思路) (7)4. 系统设计 (11)4.1. 程序流程图及说明 (11)4.2. 程序主要模块(或功能)介绍 (12)4.2.1. 一维FFT 和IFFT (12)4.2.2. 二维图像FFT 和IFFT: (14)5. 实验结果与分析 (15)5.1. 实验结果 (15)5.2. 项目的创新之处 (16)5.3. 存在问题及改进设想 (17)6. 心得体会 (17)6.1. 系统开发的体会 (17)6.2. 对本门课程的改进意见或建议 (18)7. 附件一 (19)1.项目要求1.基本要求:自修教材相关内容(P52-74)或其它参考资料,在CVI下编程对尺寸为2N(N 为正整数)的图像进行FFT(快速傅里叶变换)和(快速傅里叶反变换)。
(不能利用CVI下的函数)2.题目拓展:编程实现任意大小图像的二维傅立叶的变换与反变换。
2.项目开发环境项目开发环境主要分为软件环境和硬件环境软件:Lab Windows/CVI和IMAQ_Vision for LabWindows/CVI。
Lab Windows/CVI 是美国National Instrument(简称NI)公司开发的基于C语言的虚拟仪器开发平台,适用于自动测试、自动控制、测试仪器通信、测试硬件控制、信号分析及图像处理等软件的开发。
图像处理1--傅里叶变换(FourierTransform)

图像处理1--傅⾥叶变换(FourierTransform)楼下⼀个男⼈病得要死,那间壁的⼀家唱着留声机;对⾯是弄孩⼦。
楼上有两⼈狂笑;还有打牌声。
河中的船上有⼥⼈哭着她死去的母亲。
⼈类的悲欢并不相通,我只觉得他们吵闹。
OpenCV是⼀个基于BSD许可(开源)发⾏的跨平台计算机视觉库,可以运⾏在Linux、Windows、Android和Mac OS操作系统上。
它轻量级⽽且⾼效——由⼀系列 C 函数和少量 C++ 类,同时提供了Python、Ruby、MATLAB等语⾔的接⼝,实现了和计算机视觉⽅⾯的很多通⽤算法。
OpenCV⽤C++语⾔编写,它的主要接⼝也是C++语⾔,但是依然保留了⼤量的C语⾔。
该库也有⼤量的Python、Java andMATLAB/OCTAVE(版本2.5)的接⼝。
这些语⾔的API接⼝函数可以通过在线获得。
如今也提供对于C#、Ch、Ruby,GO的⽀持。
所有新的开发和算法都是⽤C++接⼝。
⼀个使⽤CUDA的GPU接⼝也于2010年9⽉开始实现。
图像的空间域滤波:空间域滤波,空间域滤波就是⽤各种模板直接与图像进⾏卷积运算,实现对图像的处理,这种⽅法直接对图像空间操作,操作简单,所以也是空间域滤波。
频域滤波说到底最终可能是和空间域滤波实现相同的功能,⽐如实现图像的轮廓提取,在空间域滤波中我们使⽤⼀个拉普拉斯模板就可以提取,⽽在频域内,我们使⽤⼀个⾼通滤波模板(因为轮廓在频域内属于⾼频信号),可以实现轮廓的提取,后⾯也会把拉普拉斯模板频域化,会发现拉普拉斯其实在频域来讲就是⼀个⾼通滤波器。
既然是频域滤波就涉及到把图像⾸先变到频域内,那么把图像变到频域内的⽅法就是傅⾥叶变换。
关于傅⾥叶变换,感觉真是个伟⼤的发明,尤其是其在信号领域的应⽤。
⾼通滤波器,⼜称低截⽌滤波器、低阻滤波器,允许⾼于某⼀截频的频率通过,⽽⼤⼤衰减较低频率的⼀种滤波器。
它去掉了信号中不必要的低频成分或者说去掉了低频⼲扰。
图像处理中的傅里叶变换

FFT是DFT的一种高效实现,它广 泛应用于信号处理、图像处理等 领域。
频域和时域的关系
频域
频域是描述信号频率特性的区域,通过傅里叶变换可以将 时域信号转换为频域信号。在频域中,信号的频率成分可 以被分析和处理。
时域
时域是描述信号时间变化的区域,即信号随时间的变化情 况。在时域中,信号的幅度和时间信息可以被分析和处理。
其中n和k都是整数。
计算公式
X(k) = ∑_{n=0}^{N-1} x(n) * W_N^k * n,其中W_N=exp(-
2πi/N)是N次单位根。
性质
DFT是可逆的,即可以通过DFT 的反变换将频域信号转换回时域
信号。
快速傅里叶变换(FFT)
定义
快速傅里叶变换(FFT)是一种高 效计算DFT的算法,它可以将DFT 的计算复杂度从O(N^2)降低到 O(NlogN)。
通过傅里叶变换,我们可以方便地实现图像的滤波操作,去除噪声或突出某些特 征。同时,傅里叶变换还可以用于图像压缩,通过去除高频成分来减小图像数据 量。此外,傅里叶变换还可以用于图像增强和图像识别,提高图像质量和识别准 确率。
PART 02
傅里叶变换的基本原理
离散傅里叶变换(DFT)
定义
离散傅里叶变换(DFT)是一种 将时域信号转换为频域信号的方 法。它将一个有限长度的离散信 号x(n)转换为一个复数序列X(k),
傅里叶变换的物理意义是将图像中的每个像素点的灰度值表 示为一系列正弦波和余弦波的叠加。这些正弦波和余弦波的 频率和幅度可以通过傅里叶变换得到。
通过傅里叶变换,我们可以将图像中的边缘、纹理等高频成 分和背景、平滑区域等低频成分分离出来,从而更好地理解 和处理图像。
图像傅里叶变换

空间域进行
A
18
傅里叶变换定义
一维连续傅里叶变换及反变换
✓ 单变量连续函数f(x)的傅里叶变换F(u)定义为
其中,j
F(u) f(x)ej2uxdx
1
✓ 给定F(u),通过傅里叶反变换可以得到f(x)
f(x) F(u)ej2uxdu
A
19
傅里叶变换定义
A
20
A
21
A
22
A
23
A
A
46
一幅二维图像的傅里叶频谱 中心化的傅里叶频谱
傅里叶变换
6. 分离性
F u,v
1 M 1 j2ux/M e
1 N1
f x, y e j2vy/ N
M
x 0
N y 0
1 M
M 1 j2ux/M
x 0e
F x,v
F(x,v)是沿着f(x,y)的一行所进行的傅里叶变 换。当x=0,1,…,M-1,沿着f(x,y)的所有行计 算傅里叶变换。
Fu,v Fu,v
傅里叶变换的频率谱是对称的
Fu,v Fu,v
A
34
A
35
傅里叶变换
A
36
傅里叶变换
A
37
傅里叶变换
二维傅里叶变换的性质
1. 平移性质 2. 分配律
3. 尺度变换(缩放)
4. 旋转性
5. 周期性和共轭对称性
6. 平均值
7. 可分性
8. 卷积
A
38Βιβλιοθήκη 9. 相关性傅里叶变换
✓ 相角或相位谱为
Iu,v
u,varctanRu,v
A
31
傅里叶变换
二维DFT的极坐标表示
数字图像处理--图像的傅里叶变换
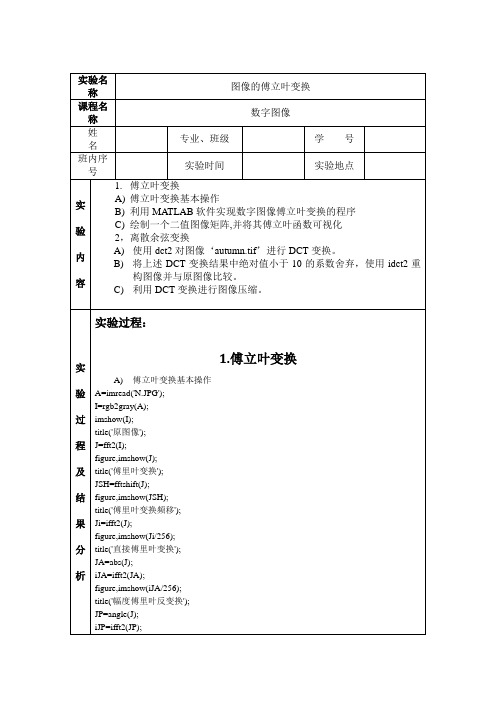
figure,imshow(abs(iJP)*100);title('相应的傅里叶反变换');B)利用MATLAB软件实现数字图像傅立叶变换的程序B=imread('M.JPG');I=rgb2gray(B);imshow(I);fftI=fft2(I);sfftI=fftshift(fftI);RR=real(sfftI);II=imag(sfftI);A=sqrt(RR.^2+II.^2);A=(A-min(min(A)))/(max(max(A))-min(min(A)))*225;figure;imshow(A);C)绘制一个二值图像矩阵,并将其傅立叶函数可视化f=zeros(30,30);f(5:24:13:17)=1;imshow(f,'notruesize')F=fft2(f);F2=log(abs(F));figure,imshow(F2,[-1 5],'notruesize');colormap(jet);F=fft2(f,256,256);figure,imshow(log(abs(F)),[-1 5],'notruesize');colormap(jet);F2=fftshift(F);figure,imshow(log(abs(F2)),[-1 5],'notruesize');colormap(jet);1.离散余弦变换A)使用dct2对图像‘N.jpg’进行DCT变换。
RGB=imread('N.jpg');imshow(RGB)I=rgb2gray(RGB);figure,imshow(I)J=dct2(I);figure,imshow(log(abs(J)),[]),colormap(jet(64));colorbar;B)将上述DCT变换结果中绝对值小于10的系数舍弃,使用idct2重构图像并与原图像比较。
基于Python实现图像的傅里叶变换

基于Python实现图像的傅⾥叶变换⽬录前⾔(1)基本概念(2)读取图像信息1. 傅⾥叶变换(1)基本概念(2)numpy实现(3)OpevCV实现2. 傅⾥叶逆变换(1)基本概念(2)代码实现前⾔⾸先是本⽂总体代码,改⼀下图像的读取路径就可以运⾏了,但我还是建议⼤家先看后⾯的步骤⼀⾏⾏敲代码,这样效果更好:"""Author:XiaoMadate:2021/11/7"""import cv2import matplotlib.pyplot as pltimport numpy as np#读取图像信息from numpy.fft import ifftshiftimg0 = cv2.imread("E:\From Zhihu\For the desk\cvthirteen2.jpg")img1 = cv2.resize(img0, dsize = None, fx = 0.5, fy = 0.5)img2 = cv2.cvtColor(img1, cv2.COLOR_BGR2GRAY) #转化为灰度图h, w = img1.shape[:2]print(h, w)dWindow("W0")cv2.imshow("W0", img2)cv2.waitKey(delay = 0)#将图像转化到频域内并绘制频谱图##numpy实现plt.rcParams['font.family'] = 'SimHei' #将全局中⽂字体改为⿊体f = np.fft.fft2(img2)fshift = np.fft.fftshift(f) #将0频率分量移动到图像的中⼼magnitude_spectrum0 = 20*np.log(np.abs(fshift))#傅⾥叶逆变换#Numpy实现ifshift = np.fft.ifftshift(fshift)# 将复数转为浮点数进⾏傅⾥叶频谱图显⽰ifimg = np.log(np.abs(ifshift))if_img = np.fft.ifft2(ifshift)origin_img = np.abs(if_img)imggroup = [img2, magnitude_spectrum0, ifimg, origin_img]titles0 = ['原始图像', '经过移动后的频谱图', '逆变换得到的频谱图', '逆变换得到的原图']for i in range(4):plt.subplot(2, 2, i + 1)plt.xticks([]) #除去刻度线plt.yticks([])plt.title(titles0[i])plt.imshow(imggroup[i], cmap = 'gray')plt.show()##OpenCV实现dft = cv2.dft(np.float32(img2), flags = cv2.DFT_COMPLEX_OUTPUT)dft_shift = np.fft.fftshift(dft)magnitude_spectrum1 = 20*np.log(cv2.magnitude(dft_shift[:, :, 0], dft_shift[:, :, 1]))plt.subplot(121), plt.imshow(img2, cmap = 'gray')plt.title('原图'), plt.xticks([]), plt.yticks([])plt.subplot(122), plt.imshow(magnitude_spectrum1, cmap = 'gray')plt.title('频谱图'), plt.xticks([]), plt.yticks([])plt.show()(1)基本概念⼀般我们观察信号是直接在时域内(声⾳信号)或者空间内(图像)对其进⾏分析,这样虽然符合常理,但信号中的⼀些有⽤的条件就不会被我们考虑进去,从⽽达不到分析的效果,所以我们要将信号转化到其他的⼀些变换域中进⾏分析。
图像处理之傅里叶变换matlab实现

图像处理之傅里叶变换matlab实现傅里叶变换是一种将时域信号转换为频域信号的数学工具。
在图像处理中,傅里叶变换可以用于图像的频域分析和滤波,以及图像的压缩和增强等应用。
Matlab是一种功能强大的数值计算和图形化工具,它提供了丰富的函数和工具箱,可以方便地进行傅里叶变换的实现。
在Matlab中,可以使用fft2函数对图像进行二维傅里叶变换。
该函数的基本语法如下:Y = fft2(X)其中,X是输入的图像矩阵,Y是输出的频域图像矩阵。
Y的大小与X 相同,表示了图像在频域中的分布情况。
为了更好地理解傅里叶变换的过程,我们可以使用一幅灰度图像作为示例进行实现。
首先,我们需要读取图像并将其转换为灰度图像。
可以使用imread函数读取图像,并使用rgb2gray函数将图像转换为灰度图像:img = imread('image.jpg');gray_img = rgb2gray(img);接下来,我们可以对灰度图像进行傅里叶变换。
首先,我们需要将图像矩阵进行归一化操作,以避免频谱的幅度过大。
可以使用im2double函数将图像矩阵转换为双精度类型:normalized_img = im2double(gray_img);然后,我们可以使用fft2函数对归一化后的图像矩阵进行傅里叶变换:fft_img = fft2(normalized_img);得到的fft_img是一个复数矩阵,包含了图像在频域中的幅度和相位信息。
为了更好地可视化频域图像,可以使用fftshift函数将频域图像的零频率移到中心位置:shifted_fft_img = fftshift(fft_img);最后,我们可以使用abs函数计算频域图像的幅度谱,并使用matshow函数将其显示出来:amplitude_spectrum = abs(shifted_fft_img);imshow(amplitude_spectrum, []);通过以上步骤,我们就可以实现对图像的傅里叶变换,并显示出频域图像的幅度谱。
(精心整理)图像的傅里叶变换 ppt课件

解决办法: 对数化
ppt课件
18
ppt课件
19
ppt课件
20
ppt课件
21
ppt课件
22
ppt课件
23
ppt课件
24
ppt课件
25
ppt课件
幅值
时域分析
ppt课件
频域分析
3
ppt课件
4
一维FT及其反变换
连续函数f(x)的傅立叶变换F(u):
F (u) f (x)e j2uxdx
傅立叶变换F(u)的反变换:
f (x) F (u)e j2uxdu
ppt课件
5
一维DFT及其反变换
离散函数f(x)(其中x,u=0,1,2,…,N-1)的傅立叶变换:
ppt课件
33
Fc=fftshift(F); %把频谱坐标原点由左上角移至屏幕中央 subplot(223) Fd=abs(Fc); imshow(Fd,[]) ratio=max(Fd(:))/min(Fd(:)) %ratio = 2.3306e+007,动态范围太大,显示器无法正常显 示 title('幅度谱(频谱坐标原点在屏幕中央)') S2=log(1+abs(Fc)); subplot(224) imshow(S2,[]) title('以对数方式显示频谱')
c1
f1
x, y
e
j
2
ux M
vy N
太原理工大学matlab课程设计报告图像的傅里叶变换及其应用doc

课程名称: MATLAB 及在电子信息课程中的应用 实验名称: 图像的傅里叶变换及其应用设计四 图像的傅里叶变换及其应用一、设计目的通过该设计,掌握傅里叶变换的定义及含义。
二、设计容及主要的MATLAB 函数1、图像的离散傅里叶变换假设),(n m f 是一个离散空间中的二维函数,那么该函数的二维傅里叶变换定义为其中21ωω和是频域变量,单位是弧度/采样单元。
函数),(21ωωf 为函数),(n m f 的频谱。
二维傅里叶反变换的定义为21212121),(),(ωωωωωωππωππωd d e e f n m f n j m j ⎰⎰-=-==因此,函数),(n m f 可以用无数个不同频率的复指数信号的和表示,在频率),(21ωω处复指数信号的幅度和相位为),(21ωωfMATLAB 提供的快速傅里叶变换函数1〕fft2:用于计算二维快速傅里叶变换,其语法格式为b=fft2(I),返回图像I 的二维傅里叶变换矩阵,输入图像I 和输出图像B 大小一样;b=fft2(I,m,n),通过对图像I 剪切或补零,按用户指定的点数计算二维傅里叶变换,返回矩阵B 的大小为m ⨯n 。
很多MATLAB 图像显示函数无法显示复数图像,为了观察图像傅里叶变换后的结果,应对变换后的结果求模,方法是对变换结果使用abs 函数。
2〕fftn:用于计算n维快速傅里叶变换,其语法格式为b=fftn(I),计算图像的n维傅里叶变换,输出图像B和输入图像I大小一样;b=fftn(I,size),通过对图像I剪切或补零,按size指定的点数计算n维傅里叶变换,返回矩阵B的大小为size。
3)fftshift:用于将变换后的图像频谱中心从矩阵的原点移到矩阵的中心,其语法格式为b=fftshift(I),将变换后的图像频谱中心从矩阵的原点移到矩阵的中心。
2、快速傅里叶变换的应用1〕滤波器频率响应滤波器冲击响应的傅里叶变换就是该滤波器的频率响应MATLAB提供的freqz2函数可以同时计算和显示滤波器的频率响应,其语法格式为freqz2(h),可同时计算和显示滤波器的频率响应。
第四章实验指导(Experimentguidance)实验1图像的傅里叶变换…

第四章实验指导(E x p e r i m e n t g u i d a n c e )实验1 图像的傅里叶变换一(平移性质)1、实验内容对图4.1(a )进行平移,观察原图的傅里叶谱与平移后的傅里叶谱的对应关系。
(a )原图像 (b )沿X 轴平移图像 (c )沿Y 轴平移图像图4.1 实验一所需图像2、实验原理如果()u F 的频率变量v u ,个移动了00,v u 距离,则傅里叶变换对有下面的形式:()()()N vy ux j e v u F y y x x f /20000,,-+−⇔−π (4.33) 因此,傅里叶变换的平移性质表明了函数与一个指数相乘等于将变换后的空域中心(如式(4.33)移到新的位置,从(4.33)还可知,对()y x f ,的平移将不改变频谱的幅值(amplitude )。
3、实验方法及程序 选取一幅图像,进行离散傅里叶变换,再对其分别进行X 轴与Y 轴上的平移,得其离散傅里叶变换,观察三幅结果图。
I=imread('1.bmp'); figure(1)imshow(real(I)); I=I(:,:,3); fftI=fft2(I);sfftI=fftshift(fftI);%求离散傅里叶频谱 %对原始图像进行二维傅里叶变换,并将其坐标原点移到频谱图中央位置 RRfdp1=real(sfftI); IIfdp1=imag(sfftI);a=sqrt(RRfdp1.^2+IIfdp1.^2);a=(a-min(min(a)))/(max(max(a))-min(min(a)))*225; figure(2)imshow(real(a));4、实验结果与分析1)实验结果如图4.1所示.(a )原图像 (b )原图像傅里叶幅度谱(c )沿X 轴平移图像 (d )沿X 轴平移后傅里叶幅度谱(e )沿Y 轴平移图像 (f )沿Y 轴平移后傅里叶幅度谱图4.2 实验一结果图2)结果分析由所得结果可知,原图像(a )分别经过X 轴与Y 轴上的平移后所得到的离散傅里叶变换频谱图(d )、(f )与原图像所得的傅里叶谱(b )基本相同。
图像的傅里叶变换实验报告

计算机科学与技术系实验报告专业名称计算机科学与技术 _____课程名称数字图像处理项目名称Matlab 语言、图像的傅里叶变换班级14 计科2班_________学号23 _____________姓名 _______ 卢爱胜______________同组人员张佳佳、王世兜、张跃文_________实验日期 ________________、实验目的与要求:(简述本次实验要求达到的目的,涉及到的相关知识点,实验的具体要求。
)实验目的:1 了解图像变换的意义和手段;2 熟悉傅立叶变换的基本性质;3 熟练掌握FFT 变换方法及应用;4 通过实验了解二维频谱的分布特点;5通过本实验掌握利用MATLABS程实现数字图像的傅立叶变换。
6 评价人眼对图像幅频特性和相频特性的敏感度。
实验要求:应用傅立叶变换进行图像处理傅里叶变换是线性系统分析的一个有力工具,它能够定量地分析诸如数字化系统、采样点、电子放大器、卷积滤波器、噪音和显示点等的作用。
通过实验培养这项技能,将有助于解决大多数图像处理问题。
对任何想在工作中有效应用数字图像处理技术的人来说,把时间用在学习和掌握博里叶变换上是很有必要的。
二、实验内容(根据本次实验项目的具体任务和要求,完成相关内容,可包括:实验目的、算法原理、实验仪器、设备选型及连线图、算法描述或流程图、源代码、实验运行步骤、关键技术分析、测试数据与实验结果、其他 )1. 傅立叶( Fourier )变换的定义对于二维信号,二维Fourier 变换定义为:F (u, v) f (x,y)e j2 (ux uy)dxdy逆变换:f (x, y) F (u,v)e j2 (ux uy)dudv二维离散傅立叶变换为:clc;clear alll=imread('Fig0707(a)(Original).'); imshow(l); %title(' 原始图像')fftl=fft2(l); sfftl=fftshift(fftl);RR=real(sfftl); ll=imag(sfftl);% % %%% % 读入原图像文件 显示原图像 二维离散傅立叶变换 直流分量移到频谱中心 取傅立叶变换的实部 取傅立叶变换的虚部 计算频谱幅值A=sqrt(RR.A2+ll.A2); A=(A-mi n(mi n( A)))/(max(max(A))-mi n(mi n( A)))*225;%figure; %imshow(A); %title(' 原始图像的频谱')f1=ifft2(A); %设定窗口 显示原图像的频谱 Fourier 系数的幅度进行 Fourier 系数的相位进行 归一化 Fourier 反变换 Fourier 反变换;d N 1N 1 j2 (m 丄 n 上) F(m, n) —f(i,k)e N NN i o k o 逆变换: d N 1N 1 j2 (m 丄 nl)f(i,k) 1F(m, n)e N NN m 0 n 0 图像的傅立叶变换与一维信号的傅立叶变换变换一样,有快速算法,具体参见参考书目,有关傅立叶变换的快速算法的程序不难找到 傅立叶变换的芯片,可以实时实现傅立叶变换。
实验一 图像的傅立叶变换

实验一图像的傅立叶变换一、实验目的1了解图像变换的意义和手段;2熟悉傅里叶变换的孩本性质;3热练掌握FFT酌方法反应用;4通过实验了解二维频谱的分布特点;5通过本实验掌握利用MATLAB编程实现数字图像的傅立叶变换。
二、实验仪器1计算机;2 MATLAB程序;3移动式存储器(软盘、U盘等)。
4记录用的笔、纸。
三、实验原理1应用傅立叶变换进行图像处理傅里叶变换是线性系统分析的一个有力工具,它能够定量地分析诸如数字化系统、采样点、电子放大器、卷积滤波器、噪音和显示点等的作用。
通过实验培养这项技能,将有助于解决大多数图像处理问题。
对任何想在工作中有效应用数字图像处理技术的人来说,把时间用在学习和掌握博里叶变换上是很有必要的。
2傅立叶(Fourier)变换的定义对于二维信号,二维Fourier变换定义为:二维离散傅立叶变换为:图像的傅立叶变换与一维信号的傅立叶变换变换一样,有快速算法,具体参见参考书目,有关傅立叶变换的快速算法的程序不难找到。
实际上,现在有实现傅立叶变换的芯片,可以实时实现傅立叶变换。
3利用MATLAB软件实现数字图像傅立叶变换、DCT变换的程序:四、实验步骤1、打开计算机,安装和启动MATLAB程序;程序组中“work”文件夹中应有待处理的图像文件;2、利用MatLab工具箱中的函数编制FFT频谱显示的函数;3、a).调入、显示图像b)对这图像做FFT、DCT并利用自编的函数显示其频谱;c)讨论不同的图像内容与FFT、DCT频谱之间的对应关系。
4、记录和整理实验报告。
五、实验内容Matlab源程序如下:clcclear allimg=imread('Dolphin.jpg');subplot(2,2,1),imshow(img);title('原图');f=rgb2gray(img);F=fft2(f);subplot(2,2,2),imshow(F);title('傅里叶变换');%二维傅里叶变换FS=fftshift(F);%频率图%频谱S=log(1+abs(FS));subplot(2,2,3);imshow(S,[])title('直接变换频谱图');%二维傅里叶逆变换fr=real(ifft2(ifftshift(FS)));%频域的图反变ret=im2uint8(mat2gray(fr));%取其灰度图subplot(2,2,4),imshow(ret);title('逆傅里叶变换');I=imread('logo.tif');figure(2);imshow(I);DCT=dct2(I);figure(3);imshow(log(abs(DCT)),[ ]);六、实验结果在matlab中运行后,实验结果如图:原图傅里叶变换直接变换频谱图逆傅里叶变换七、思考题1.傅里叶变换有哪些重要的性质?答:线性性质、奇偶虚实性、对称性质、尺度变换性质、时移性质、频移特性。
图像处理技术中的傅里叶变换方法介绍

图像处理技术中的傅里叶变换方法介绍傅里叶变换是一种将信号从时域转换到频域的方法,图像处理中广泛应用的一种数学工具。
傅里叶变换将图像转换为频域信号,使我们能够观察和分析图像中不同频率的成分。
在图像处理领域,傅里叶变换常用于图像的滤波、去噪、增强等任务。
本文将介绍傅里叶变换的原理和在图像处理中的应用。
让我们了解一下傅里叶变换的原理。
傅里叶变换基于傅里叶级数展开的思想,将函数分解成一组正弦和余弦函数的和。
对于一维信号,傅里叶变换可以表示为以下公式:F(u) = ∫ f(x) * e^(-2πiux) dx其中,F(u)表示信号在频域中的复数表示,f(x)表示输入信号在时域中的复数表示,u表示频率,i为虚数单位。
在图像处理中,傅里叶变换可以应用于二维信号,即图像。
图像可以通过对其在两个方向上进行傅里叶变换,得到其在频率域上的表示。
图像的傅里叶变换可以表示为以下公式:F(u,v) = ∬ f(x,y) * e^(-2πi(ux+vy)) dx dy其中,F(u,v)表示图像在频率域中的复数表示,f(x,y)表示输入图像在空域中的灰度值,u和v表示频率,i为虚数单位。
在图像处理中,我们经常使用的是傅里叶变换的逆变换,即将图像从频域转换回空域。
逆傅里叶变换可以表示为以下公式:f(x,y) = ∬ F(u,v) * e^(2πi(ux+vy)) du dv通过逆傅里叶变换,我们可以将对图像进行频域操作后的图像恢复到原始的空域。
在图像处理中,傅里叶变换有着广泛的应用。
其中之一是频域滤波。
通过将图像转换到频域,在频域中对图像进行滤波操作,可以实现一些空域中难以实现的效果。
傅里叶变换后的频域图像中较低频率成分代表图像的平滑部分,较高频率成分代表图像的细节和边缘。
通过选择不同的滤波器,在频域中滤除或增强不同频率的成分,可以实现图像的模糊、锐化、边缘检测等效果。
傅里叶变换还可以用于图像的压缩和去噪。
在图像压缩中,通过对图像进行傅里叶变换,并保留较低频率成分来实现图像的压缩。
(精心整理)图像的傅里叶变换

g(x, y) G( ,) exp[ j2 ( x y)]d d
G( ,)是g(x,y)的频谱,物函数g(x,y)可以看作不同方
向传播的单色平面波分量的线性叠加。G( ,)d d为
权重因子。空间频率 cos , co表s 示了单色平面
波的传播方向。
第14页,共72页。
二维离散傅里叶变换
F (u)
1 4
1 1
j 1
1 1
j
f
(1)Βιβλιοθήκη 1 f (2)1j
1
j
f
(3)
第17页,共72页。
yj
-1
1
x
-j
图像的频谱幅度随频率增大而迅速衰减
许多图像的傅里叶频谱的幅度随着频率的增大而迅速减小,这使得在显 示与观察一副图像的频谱时遇到困难。但以图像的形式显示它们时,其高频项 变得越来越不清楚。
第35页,共72页。
二维离散傅里叶变换的性质
➢ 线性性
f1 f2
x, x,
y y
F1 u, v F2 u, v
c1
f1
x,
y
c2
f2
x,
y
c1F1
u,
v
c2
F2
u,
v
证明:
DFT c1 f1 x, y c2 f2 x, y
M 1 N 1
c1 f1
x, y
c2 f2
第31页,共72页。
主极大的值用Fmax表示,第一个旁瓣的峰值用Fmin表示 R loga (1 KFmax ) loga (1 KFmin )
第32页,共72页。
例题:对一幅图像实施二维DFT,显示并观察其频谱。
解:源程序及运行结果如下:
图像傅里叶变换ppt课件

图像傅里叶变换
57
快速傅里叶变换(FFT)
FFT算法基本思想
FFT算法基于一个叫做逐次加倍的方法。通 过推导将原始傅里叶转换成两个递推公式
Fu
1 M 1
f x e j2ux /M
u 0,1,2,...,M 1
M x0
Fu 1 Feven u Fodd u W2uk 2
Fu K 1 Feven u Fodd u W2uk 2
原点的傅里叶变换即等于图像的平均灰度
级
图像傅里叶变换
50
傅里叶变换
8. 卷积理论
大小为M×N的两个函数f(x,y)和h(x,y)的离散 卷积
fx, yhx, y 1 M1N1 fm,nhxm, yn MN m0 n0
卷积定理
fx,yhx,yFu,vHu,v
fx,yhx,yFu,vHu,v
图像傅里叶变换
全周期的傅里叶频谱
图像傅里叶变换
46
一幅二维图像的傅里叶频谱 中心化的傅里叶频谱
傅里叶变换
6. 分离性
F u,v
1 1 M 1 j2ux/M
N1
e
f x, y e j2vy/ N
M
x 0
N y 0
1 M 1 j2ux/M
x 0e
F x,v
M
F(x,v)是沿着f(x,y)的一行所进行的傅里叶变 换。当x=0,1,…,M-1,沿着f(x,y)的所有行计
➢ f(x,y)是原始图像
➢ h(x,y)作为感兴趣的物体或区域(模板)
➢中相如应果点匹的配位,置两上个达函到数最的大相关值会在h找到f
图像傅里叶变换
54
相关性匹配举例
图像f(x,y)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验一图像的傅立叶变换
一、实验目的
1了解图像变换的意义和手段;
2熟悉傅里叶变换的孩本性质;
3热练掌握FFT酌方法反应用;
4通过实验了解二维频谱的分布特点;
5通过本实验掌握利用MATLAB编程实现数字图像的傅立叶变换。
二、实验仪器
1计算机;
2 MATLAB程序;
3移动式存储器(软盘、U盘等)。
4记录用的笔、纸。
三、实验原理
1应用傅立叶变换进行图像处理
傅里叶变换是线性系统分析的一个有力工具,它能够定量地分析诸如数字化系统、采样点、电子放大器、卷积滤波器、噪音和显示点等的作用。
通过实验培养这项技能,将有助于解决大多数图像处理问题。
对任何想在工作中有效应用数字图像处理技术的人来说,把时间用在学习和掌握博里叶变换上是很有必要的。
2傅立叶(Fourier)变换的定义
对于二维信号,二维Fourier变换定义为:
二维离散傅立叶变换为:
图像的傅立叶变换与一维信号的傅立叶变换变换一样,有快速算法,具体参见参考书目,有关傅立叶变换的快速算法的程序不难找到。
实际上,现在有实现傅立叶变换的芯片,可以实时实现傅立叶变换。
3利用MATLAB软件实现数字图像傅立叶变换、DCT变换的程序:
四、实验步骤
1、打开计算机,安装和启动MATLAB程序;程序组中“work”文件夹中应有待处理的图像文件;
2、利用MatLab工具箱中的函数编制FFT频谱显示的函数;
3、a).调入、显示图像
b)对这图像做FFT、DCT并利用自编的函数显示其频谱;
c)讨论不同的图像内容与FFT、DCT频谱之间的对应关系。
4、记录和整理实验报告。
五、实验内容
Matlab源程序如下:
clc
clear all
img=imread('');
subplot(2,2,1),imshow(img);
title('原图');
f=rgb2gray(img);
F=fft2(f);
subplot(2,2,2),imshow(F);title('傅里叶变换');
%二维傅里叶变换
FS=fftshift(F);%频率图
%频谱
S=log(1+abs(FS));
subplot(2,2,3);imshow(S,[])
title('直接变换频谱图');
%二维傅里叶逆变换
fr=real(ifft2(ifftshift(FS)));%频域的图反变ret=im2uint8(mat2gray(fr));%取其灰度图subplot(2,2,4),imshow(ret);
title('逆傅里叶变换');
I=imread('');
figure(2);
imshow(I);
DCT=dct2(I);
figure(3);
imshow(log(abs(DCT)),[ ]);
六、实验结果
在matlab中运行后,实验结果如图:
原图傅里叶变换
直接变换频谱图逆傅里叶变换
七、思考题
1.傅里叶变换有哪些重要的性质
答:线性性质、奇偶虚实性、对称性质、尺度变换性质、时移性质、频移特性。
2.图像的二维频谱在显示和处理时应注意什么
答:1.进行傅里叶变换的图像应该是灰度图形,原rgb彩色图像无法进行相应变换;
2.注意使用fftshift函数将频谱的零频分量移至频谱的中心。
