流体力学伯努利方程
伯努利流体方程

伯努利流体方程
伯努利方程(Bernoulli's equation)是流体力学基本方程之一,常用于描述静止流体或运动流体在流经不同位置时,压力、速度、高度等物理量的变化关系。
伯努利方程最早由瑞士数学家和物理学家伯努利(Daniel Bernoulli)在1738年提出,被称
为伯努利定理,也称作伯努利方程或伯努利流体方程。
伯努利方程的数学形式为:
P + 1/2ρv^2 + ρgh = constant
其中,P表示流体的压力,ρ表示流体的密度,v表示流体的
速度,g表示重力加速度,h表示流体的高度,constant表示一个常数。
伯努利方程可以表达出一个流体在液体静压力、动能和势能三者之间的平衡状态。
在一个理想的流体中,如果流体穿过一段水管,那么在这段水管的任何位置,液体静压力、动能和势能总和相等。
应用伯努利方程,可以计算液体在不同位置的压力、速度和高度等物理量的变化。
伯努利方程可以应用在气体、液体等不同介质的流体力学问题中,如风力发电机、水压机等。
伯努利方程三种形式公式

伯努利方程三种形式公式
第一种形式的伯努利方程公式是:
P₁ + 1/2ρv₁² + ρgh₁ = P₂ + 1/2ρv₂² + ρgh₂
其中P₁和P₂分别表示两个位置的压力,ρ表示流体的密度,v₁和v₂表示两个位置的流速,g为重力加速度,h₁和h₂表示两个位置的高度。
这个公式描述了流体在两个位置之间能量守恒的关系。
等式左边的第
一项表示压力能,第二项表示动能,第三项表示单位质量的重力势能。
等
式右边的三项表示相应位置的压力能、动能和重力势能。
这个公式适用于
流体在不完全关闭的管道、管道两端处于同一高度的情况。
第二种形式的伯努利方程公式是:
P + 1/2ρv² + ρgh = const
这是一个简化形式的伯努利方程,它将两个位置的参数合并成一个常数。
这个公式的物理意义是,当流体在流动过程中没有受到外界力的作用时,流体的总能量保持不变。
这个公式适用于理想的水平管道、无摩擦的
流动。
第三种形式的伯努利方程公式是:
P + 1/2ρv² = const
这是伯努利方程的最简形式,它忽略了重力势能的影响。
这个公式适
用于理想的非粘性流体在无重力情况下的流动,如气体等。
这三种形式的伯努利方程公式分别适用于不同的流体力学问题。
选择
适用的公式取决于具体的流动条件和需要分析的问题。
无论选择哪种形式,
伯努利方程都提供了一个重要的工具,可以帮助我们研究流体力学中的能量转换和守恒。
流体力学 伯努力方程
测流速原理该点在水面下的深度为d故该处的压强pgdb点在管口之前流速v根据伯努利方程所以在实际应用时上式须修正为其中c为比多管的修正系数由实验来确定
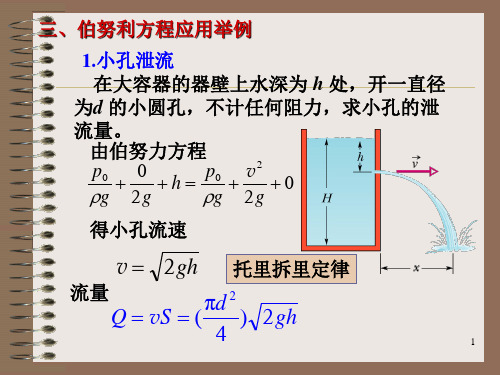
三、伯努利方程应用举例 1.小孔泄流 在大容器的器壁上水深为 h 处,开一直径 为d 的小圆孔,不计任何阻力,求小孔的泄 流量。 由伯努力方程 p0 p0 v 2 0 h 0 g 2 g g 2 g
h1
B
C A
pC p0 gh1
h2
其中p0为大气压
11
(2)当虹吸管下端开启时, h1 下端和A处的压强仍为:
p下 端 p0 , pA p0
B
C A
h2
而vB vc v下端 , v A 0 . 所以 pB p0 g( h2 h1 ) , pC p0 gh2
(2)取1-2-4的一个流线,由伯努利方程
P1 1 2 1 1 v1 P2 v 2 P4 v2 2 4 2 2 2 P4 P0
1 2 2 P1 P0 v 4 v1 P0 100, P1 -P0 100Pa 2 1 2 2 P2 P0 v 4 v 2 P0 , 2 P3 =P0 P2 P0 0 P3 P0 0
Qv v1S1 v2 S2
2( 汞 )g hS1 S 2
2 2
( S1 S 2 )
2 2
6
H
1 1 2 2 p1 v1 p2 v2 2 2
v1S1 v2 S2
v1 主管 细管 v2
p p1 p2 gh
•
Q v1S1 S1S2
例题2 在如图所示的虹吸管装置中,已 知 h1 和 h2 ,试问:(1)当截面均匀的虹吸管 下端被塞住时,A、B和C处的压强各为多大? (2)当虹吸管下端开启时,A、B和C处的压 强又各为多大? 这时水流出虹吸管的速率为 多大?
伯努利方程 单位

伯努利方程单位
伯努利方程是描述流体力学中流速、压力和高度之间关系的基本方程。
它可以用于分析流体在不同位置的动能、压力和势能之间的转换。
在国际单位制(SI)中,伯努利方程的单位如下:
流速:米每秒(m/s)
压力:帕斯卡(Pa)或牛顿每平方米(N/m²)
高度:米(m)
伯努利方程可以表示为:
P + 1/2ρv² + ρgh = constant
其中,P是压力,ρ是流体的密度,v是流速,g是重力加速度,h是高度。
这个方程的左侧是压力、动能和势能的总和,右侧是一个常数,表示在沿流线的任何点上这些量之间的相对关系保持不变。
请注意,伯努利方程的单位可以根据具体情况进行调整,例如使用千帕(kPa)或毫米汞柱(mmHg)等作为压力单位,使用千克每立方米(kg/m³)作为密度单位。
流体力学-伯努利方程

2.流管:流体内部,通过某一个截面的流线围成的管状空间;
流体质点不会任意穿出或进入流管 ;(与实际管道相似) 流体可视为由无数个稳定的流管组成,分析每个流管中流体的运动规律, 是掌握流体整体运动规律的基础;
四.连续性原理
1. 推导过程:
假设: ①.取一个截面积很小的细流管,垂直于流管的同一截面上的 各点流速相同; ②.流体由左向右流动 ; ③.流体具有不可压缩性 ; ④.流体质点不可能穿入或者穿出流管 ; ⑤.在一个较短的时间t内,流进流管的流体质量等于流出流 管的流体质量(质量守恒),即: S11t S 2 2 t
皮托管:由双层圆头玻璃管组 成,内外管分别通过橡皮管与 U 形压强计的两管相连、内管的 开口在 A ,外管的开门 ( 即管壁 上钻的几个小孔)在B。A 正对流 速方向,A、B间忽略高度差;
驻点 :当流体遇到障碍物受阻时, 在障碍物前会有一点,该点流体 静止不动,故称驻点;
v
1 2 p A pB v 2
H
2 pA pB
2 gH
应用实例4.
小孔流速:
敞口的液槽内离开液面h处开一小孔,液体密度为,液面 上方是空气,在液槽侧面小孔处压强为大气压 p0, 求小孔 处的液体流速? 注:由于液槽中液面下降很 慢,可以看成是稳定流动, 把液体作为理想流体;
2 gh
托里拆利定律:忽略粘滞性,任何液体质点从小孔 中流出的速度与它从h高度处自由落下的速度相等;
6.飞机的机翼的翼型使得飞行中前面的空 气掠过机翼向后时,流经机翼上部的空 气要通过的路程大于流经机翼下部的空 气通过的路程,因此上部空气流速大 于下部空气的流速,上部空气对机翼 向下的压力就会小于下部空气对机翼向 上的压力,从而产生升力 ;
伯努利方程实验

伯努利方程实验1. 引言伯努利方程是流体力学中的基本方程之一,描述了沿着流体流线的速度、压力及流体高度之间的关系。
在流体力学领域,伯努利方程常常应用于流体的运动分析和工程设计中。
本文将介绍伯努利方程的基本原理,并通过实验验证伯努利方程在实际情况下的适用性和有效性。
2. 原理伯努利方程描述了在稳态流动条件下,沿着流线的速度、压力和流体高度之间的关系。
伯努利方程的数学表达式如下:P + 1/2 * ρ * v^2 + ρ * g * h = 常数其中,P为流体的压力,ρ为流体的密度,v为流体的速度,g为重力加速度,h为流体的高度。
方程右侧的常数表示一个特定点上的总能量,并保持不变。
根据伯努利方程,当速度增大时,压力会降低;当速度减小时,压力会增加。
这是因为速度增大意味着流体动能的增加,而伯努利方程将动能和势能进行了平衡。
3. 实验目的通过伯努利方程实验,我们的目标是验证伯努利方程在实际情况下的有效性,并观察流体速度、压力和流体高度之间的关系。
4. 实验装置与方法4.1 实验装置本实验所需的主要装置和器材如下:•水槽:用于放置流体,并提供流体高度。
•流体加速装置:用于产生流体速度。
•压力计:用于测量流体压力。
•尺子:用于测量流体高度。
4.2 实验方法1.将水槽中注满水,并确保水槽内部无气泡。
2.调节流体加速装置,使得流体在水槽中保持稳定流动。
3.使用压力计测量不同位置的流体压力,并记录下来。
4.使用尺子测量不同位置的流体高度,并记录下来。
5. 实验结果与讨论根据实验所得的数据,我们可以计算出不同位置的流体速度,并代入伯努利方程进行验证。
下表为实验数据记录表:位置压力 (Pa) 高度(m)A 1000 2B 800 1.5C 600 1D 400 0.5根据伯努利方程,在流体稳态流动过程中,流体的总能量保持不变。
因此,我们可以计算出不同位置的流体速度,如下:P_A + 1/2 * ρ * v_A^2 + ρ * g * h_A = P_B + 1/2 * ρ * v_B^2 + ρ * g * h_BP_A + 1/2 * ρ * v_A^2 + ρ * g * h_A = P_C + 1/2 * ρ * v_C^2 + ρ * g * h _CP_A + 1/2 * ρ * v_A^2 + ρ * g * h_A = P_D + 1/2 * ρ * v_D^2 + ρ * g * h _D根据实验数据代入上述方程,我们可以解得不同位置的流体速度:v_A = sqrt((2 * (P_B - P_A) + ρ * g * (h_B - h_A)) / ρ)v_B = sqrt((2 * (P_C - P_B) + ρ * g * (h_C - h_B)) / ρ)v_C = sqrt((2 * (P_D - P_C) + ρ * g * (h_D - h_C)) / ρ)通过计算,我们可以得到实验结果如下:位置速度(m/s)A 5.35B 3.99C 2.79实验结果表明,在实际情况下,伯努利方程在描述流体运动时具有良好的适用性和有效性。
伯努利方程

• • • •
参考链接:/view/94269.htm?fr=ala0_1
还有一个相近回答:这个方程并非是描述液体的运动,而应该是描述理想气体的绝热定常流动的,比如它 可以近似地描述火箭或者喷气式发动机中的气流(你可以参考第26届全国中学生物理竞赛复赛中的热学 题)。其中的伽马(像r一样的那个希腊字母,我打不出来,用r来替代)是气体的比热容比,即气体的定 压摩尔热容与定体摩尔热容之比,对理想气体来说是个常数。这个公式中,左边v是气体流动的速度,p是 气体的压强,p下面的希腊字母代表气体的密度。右边的p0\pho0是指速度为0的地方气体的压强和密度。 这个公式的推导和流体的伯努利方程思想相同,只是要考虑到此时气体是可压缩的,结合理想气体的状态 方程即可推导出。
• •
编辑本段]p+ρgh+(1/2)*ρv^2=C 式中p、ρ、v分别为流体的压强、密度和速度;h为铅垂高度;g为重力加速度。 上式各项分别表示单位体 积流体的压力能 p、重力势能ρg z和动能(1/2)*ρv ^2,在沿流线运动过程中,总和保持不变,即总能量守恒。 但各流线之间总能量(即上式中的常量值)可能不同。对于气体,可忽略重力,方程简化为p+(1/2)*ρv ^2 =常量(p0),各项分别称为静压 、动压和总压。显然 ,流动中速度增大,压强就减小;速度减小, 压强就 增大;速度降为零,压强就达到最大(理论上应等于总压)。飞机机翼产生举力,就在于下翼面速度低而压强 大,上翼面速度高而压强小 ,因而合力向上。 据此方程,测量流体的总压、静压即可求得速度,成为皮托 管测速的原理。在无旋流动中,也可利用无旋条件积分欧拉方程而得到相同的结果但涵义不同,此时公式 中的常量在全流场不变,表示各流线上流体有相同的总能量,方程适用于全流场任意两点之间。在粘性流 动中,粘性摩擦力消耗机械能而产生热,机械能不守恒,推广使用伯努利方程时,应加进机械能损失项[1]。 图为验证伯努利方程的空气动力实验。 补充:p1+1/2ρv1^2+ρgh1=p2+1/2ρv2^2+ρgh2(1) p+ρgh+(1/2)*ρv^2=常量 (2) 均为伯努利方程 其中ρv^2/2项与流速有关,称为动压强,而p和ρgh称为静 压强。 伯努利方程揭示流体在重力场中流动时的能量守恒。 由伯努利方程可以看出,流速高处压力低, 流速低处压力高。 图II.4-3为一喷油器,已知进口和出口直径D1=8mm,喉部直径D2=7.4mm,进口空气压 力p1=0.5MPa,进口空气温度T1=300K,通过喷油器的空气流量qa=500L/min(ANR),油杯内油的密度 ρ=800kg/m。问油杯内右面比喉部低多少就不能将油吸入管内进行喷油? 解: 由气体状态方程,知进口 空气密度ρ=p1/(RT1)=(0.5+0.1)/(287*300)kg/m=6.97kg/m
伯努利方程知识点总结

伯努利方程知识点总结一、基本概念1. 流体流动在物理学和工程学中,流体流动是一个非常重要的研究领域。
流体包括气体和液体,其流动特性受到各种因素的影响,如流速、流量、压力、密度等。
2. 伯努利方程伯努利方程是描述流体流动的基本方程之一,它是根据能量守恒定律和流体动力学原理推导而来的。
伯努利方程可以用来描述流体在不同位置的流速、静压和动压之间的关系。
它的最基本形式可以表示为:P + 1/2 ρv^2 + ρgh = 常数其中,P代表流体的静压力,ρ代表流体的密度,v代表流体的流速,g代表重力加速度,h代表流体的高度。
这个方程表明了在流体流动的过程中,静压力、动压力和重力势能之间的相互转化关系。
3. 流线与流线管在描述流体流动的过程中,我们经常会使用流线和流线管这两个概念。
流线是指流体在流动过程中所呈现出的路径,它可以用来描述流体的流动轨迹和速度分布。
流线管是指将流线沿着其流动方向构成的管道,它是探索流体流动规律的有力工具。
二、公式推导现在我们来推导伯努利方程的基本形式。
我们假设在一个流线管内部的流体流动,忽略粘性和外部力的影响。
根据流体力学原理和能量守恒定律,我们可以得到以下推导过程:首先,我们考虑流体在不同位置的能量变化。
在流线管的两个不同位置1和2,流体分别具有静压力P1和P2,动压力1/2 ρv1^2和1/2 ρv2^2,重力势能ρgh1和ρgh2。
根据能量守恒定律,我们有:P1 + 1/2 ρv1^2 + ρgh1 = P2 + 1/2 ρv2^2 + ρgh2将上式简化,可得到伯努利方程的基本形式:P1 + 1/2 ρv1^2 + ρgh1 = P2 + 1/2 ρv2^2 + ρgh2这就是伯努利方程的基本公式,它描述了流体在不同位置的静压、动压和重力势能之间的关系。
三、应用领域伯努利方程在许多领域都具有广泛的应用价值,下面我们将对其应用领域进行简要介绍。
1. 空气动力学在航空航天领域,伯努利方程被广泛应用于描述飞机在不同飞行状态下的空气动力学性能。
伯努利方程 流体

伯努利方程 流体
伯努利方程描述了不可压缩流体的流动,即在定常流动过程中,沿着流线流动的液体粒子总能量相同。
液体的总能量由止压能、动能和势能三部分组成。
伯努
利方程可用于分析流体在不同位置的流速、压力和密度之间的关系。
根据伯努利方程,对于不可压缩流体,沿着流线流动的任意的两个点之间的总动能、总势能和总压力是相等的。
由此,伯努利方程的数学表达式为:P1 +
1/2rouV1^2 + rough1 = P2 + 1/2rouV2^2 + rough2,其中P、ρ、V和h分别表示压力、密度、速度和高度,下标1和2分别表示不同位置的压力、密度、速度和高度。
通过伯努利方程,我们可以推导出很多有用的结论。
例如,当两个液体点之间的高度差增加时,压力差就会增加,流速也会增加。
另外,当流速增加时,压力就会降低,这一点在研究飞机和自行车等高速运动问题时也有很大的应用价值。
总之,伯努利方程是流体力学中重要的基础方程之一。
通过伯努利方程,我们可以分析流体的运动规律,深入探究它的性质和行为,为众多领域的技术应用提供了基础理论支撑。
伯努利方程即伯努利原理

伯努利方程即伯努利原理伯努利方程,或称为伯努利原理,是流体力学中的一个基本原理。
它描述了在静止的流体中,沿着流线方向的速度增加时,压力会减小,而在速度减小时,压力会增加的关系。
伯努利方程是流体运动中的重要原理,它解释了一系列现象和技术原理,如飞机飞行、水泵、喷气式发动机和气候解释等。
伯努利方程可以通过能量守恒定律推导得到。
在没有外部力的情况下,流体在流动的过程中,机械能守恒。
机械能守恒原理包括了静能和动能的平衡。
静能即通过压力施加到流体上的能量,而动能则通过流体在流动过程中动能的变化。
根据伯努利方程,对于沿着流线方向的流动,流体的总能量保持不变。
总能量包括了静能和动能两部分。
静能可以表示为流体单位质量的压力与比体积的乘积,即E=p/ρ。
其中,p是压力,ρ是流体的密度。
动能由流体单位质量的速度平方的一半给出,即K=v²/2、将静能和动能结合起来,我们可以得到伯努利方程。
伯努利方程描述了在光滑的管道中,流速增加时,压力会降低;流速减小时,压力会增加。
这一现象可以通过许多实际的例子来解释。
例如,在自来水供应系统中,水流从供水塔顶部到家里的水龙头,因为下降的高度和流速的增加,水龙头的压力会增加,因此水可以自然地从水龙头中流出。
在喷气式发动机中,高速空气流通过喷嘴时,速度增加,从而使喷气式发动机产生推力。
另一个例子是飞机的升力产生原理。
当空气在机翼上方流动时,由于机翼上方流速较快,压力降低,而在机翼下方流速较慢,压力增加,这就产生了向上的升力。
伯努利方程在流体力学中有广泛的应用。
在航空工程中,它解释了飞机飞行的原理和飞行器的气动特性。
在医学中,它可以解释血流动力学和血管疾病。
在水力工程中,它解释了水泵、水轮机和水电站的原理。
此外,伯努利方程还在气象学、海洋学和环境工程等领域的研究中起到了重要的作用。
然而,伯努利方程也有其限制。
首先,它假设是一个定常流动的情况,即流体的速度和压力在时间和空间上都是不变化的。
流体的稳定流动伯努利方程

无热传导
理想流体假设中,流体被 视为无热传导的,即流体 的温度在整个流场中保持 一致。
流体的能量守恒原理
能量守恒
流体的能量守恒原理指出,在封闭系 统中,流体的总能量(包括动能和势 能)在流动过程中保持不变。
动能与势能转换
在流体的流动过程中,动能和势能之 间可以相互转换,但总能量保持不变 。
伯努利方程的推导过程
伯努利方程的重要性
01
描述流体稳定流动的规律
伯努利方程是流体力学中的基本方程,用于描述流体在稳定流动状态下
的压力、速度和密度等物理量的关系。
02 03
解决实际问题
在实际生产和生活中,许多问题都涉及到流体的流动,如管道输送、流 体机械、航空航天等。通过应用伯努利方程,可以解决这些实际问题, 提高生产效率和生活品质。
伯努利方程是流体力学中的基本方程,用于描述流体在稳 定流动状态下的压力、速度和位势之间的关系,是理解和 预测流体运动的关键。
广泛应用领域
伯努利方程在多个领域中都有应用,如航空航天、流体机 械、管道输送、气象学等,对于指导工程设计和优化流体 系统性能具有重要意义。
理论基石
作为流体力学的基础理论之一,伯努利方程为后续深入研 究流体动力学、湍流理论等提供了重要的理论支撑。
详细描述
流体静压强的计算公式为 P = ρgh,其中ρ为流体密度,g为重 力加速度,h为流体高度。该公式适用于计算液体在容器中的静 压强。
流体动压强的计算
总结词
流体动压强是指流体在运动状态下对物体表面产生的压力。
详细描述
流体动压强的计算公式为 P = ρv²/2,其中ρ为流体密度,v为流体速度。该公式适用于计算气体或液体在管道或 容器中的动压强。
伯努利方程及各项物理意义

伯努利方程及各项物理意义P + 1/2 ρv² + ρgh = constant其中,P代表压力,ρ代表流体的密度,v代表流体的速度,g代表重力加速度,h代表高度。
1.压力(P):压力是流体分子对容器壁或物体表面单位面积的作用力。
在伯努利方程中,压力项代表了流体受到的压力影响。
当流体速度增加时,压力会降低,反之亦然。
这是因为在速度增加的情况下,流体分子对容器壁的撞击次数减少,所以压力降低。
这也解释了为什么在狭窄的管道中流速加大时,压力会降低。
2.速度(v):速度是流体分子通过管道截面的速度。
在伯努利方程中,速度项代表了流体运动的动能。
当流体速度增加时,动能也增加。
当流体通过一个较窄的管道截面时,由于截面积减小,流速会增加,从而增加流体的动能。
3.高度(h):高度是参考点(通常是整个流体系统的底部或参照物体)到流体表面的距离。
在伯努利方程中,高度项代表了流体的重力势能。
当流体高度增加时,重力势能也增加。
这就解释了为什么在收缩管道中,当流体速度增加时,流体的高度会下降。
通过伯努利方程,我们可以得出以下几个重要的结论:1.当管道中的速度增加时,压力降低。
这就是为什么喷嘴的尖端以及飞机翼的顶部会产生较低的压力,从而产生升力。
2.在收缩管道中,由于速度增加而导致的压力降低被称为“文丘科效应”。
这解释了为什么在收缩管道中的喷水口附近会形成很强的吸力。
3.在扩张管道中,由于速度减小而导致的压力增加被称为“波利效应”。
这解释了为什么在一些喷嘴的口处会产生强大的喷射力。
4.伯努利方程可以解释一些常见的自然现象,如水下潜水时,潜水者会感到耳朵堵塞,这是因为水压力使耳膜移位。
总的来说,伯努利方程描述了流体力学中压力、速度和高度之间的相互关系。
它帮助我们理解和解释了一系列与流体运动相关的现象,并广泛应用于工程、气象学、航空航天等领域。
同时,伯努利方程也是流体力学研究的基础,为更深入地理解和探索流体行为提供了基本的理论基础。
伯努利方程的应用概述

伯努利方程的应用概述伯努利方程是流体力学中的一个重要方程,它描述了流体在非粘性、定常、不可压缩条件下的运动。
该方程以瑞士科学家伯努利的名字命名,它是由动能项、重力势能项和压力项组成的一个总能量方程。
伯努利方程的应用非常广泛,涉及到众多领域,如航空、水利、土木工程等。
下面我将对伯努利方程的应用进行一概述。
1.流体力学中的伯努利方程应用:伯努利方程可以应用于气体、液体以及浆体等不可压缩流体的运动分析。
在管道、管路中,通过应用伯努利方程可以计算出流体在管道中的流速、压力、位能等重要物理量。
在涡街流量计、毛细管压力计等仪器中,也可以利用伯努利方程进行测量。
2.航空航天中的应用:伯努利方程的应用在航空航天工程中尤为重要。
例如,在飞机机翼和喷气引擎中,通过应用伯努利方程可以解释大气压力差所产生的升力。
同时,伯努利方程也可以用来研究流体在飞行器周围的流动,以及飞行器上部分区域的压力变化。
3.汽车工程中的应用:在汽车运动中,伯努利方程可以帮助我们理解气流对于汽车行驶的影响。
例如,通过应用伯努利方程可以研究汽车的风阻问题,从而优化汽车的车身设计,减少气流阻力,提高汽车的驾驶性能。
4.水利工程中的应用:伯努利方程在水利工程中的应用非常广泛。
例如,在水坝中,通过应用伯努利方程可以计算出水流的速度和压力,帮助我们理解水流的运动规律,并根据需要进行设计和维护。
另外,伯努利方程也可以应用于水力发电厂的设计和运行过程中,对水流能量的转化及损耗进行估算和优化。
5.土木工程中的应用:在土木工程中,伯努利方程可以用来分析液体或气体在管道、水泵以及水塔等结构中的运动。
通过应用伯努利方程,可以计算出管道中的流速和压力,帮助我们设计和维护城市的供水和污水处理系统。
6.海洋工程中的应用:伯努利方程可以应用于海洋工程领域的水流分析和水动力学特性研究。
例如,在海岸工程中,通过应用伯努利方程可以预测海浪的高度和速度,以及对于海岸线的冲击力。
同时,伯努利方程还可以帮助我们理解和控制河道和港口中的水流行为。
伯努利流体力学方程

伯努利流体力学方程
伯努利流体力学方程是描述理想流体在恒定流动状态下,沿着一根流线流动过程中能量守恒的基本物理定律。
它在流体力学中具有广泛的应用,特别是对于液体和气体流动问题。
伯努利流体力学方程可以写成如下形式:
$$P+\frac{1}{2}\rho v^2+\rho gh=C$$
其中:
- P是流体的静压力,即流体在静止状态下所受的压强;
- ρ是流体的密度;
- v是流体的流速,即在流体中某一点上,每单位时间通过该点的流体体积;
- g是重力加速度;
- h是流体在该点上的高度差,相对于某一基准面;
- C是一个常数,即伯努利常数,它在整个流体的过程中保持不变。
伯努利方程从能量的角度来描述了流体在流动中的变化,它表明流体的总能量保持不变,即流体压力、动能和重力势能之和在任意一点上都保持相等,从而可以用于分析流体在不同处的流态变化。
例如,当流体贯穿缩流器或狭窄部分的管道时,流速会增加,而压力会降低,这是因为伯努利方程中流速的平方项会导致压力降低。
类似地,当流体流经扩张部分的管道时,
流速会降低,而压力会升高,这是由于伯努利方程对能量的绝对守恒要求。
流体力学_-伯努利方程

1 S1 4 2 1 3m 2 2 1 S 2 2 1 0.5 2 1.5m 2 2 S2 1 2 0.1m / s S1
§1.3.3 伯努利方程及其应用
伯努利方程是瑞士物理学家伯努利提出来的,是理想流体作稳定流动时的 基本方程,对于确定流体内部各处的压力和流速有很大的实际意义、在水 利、造船、航空等部门有着广泛的应用。
6.飞机的机翼的翼型使得飞行中前面的空 气掠过机翼向后时,流经机翼上部的空 气要通过的路程大于流经机翼下部的空 气通过的路程,因此上部空气流速大 于下部空气的流速,上部空气对机翼 向下的压力就会小于下部空气对机翼向 上的压力,从而产生升力 ;
应用实例1. 水流抽气机、喷雾器 空吸作用:当流体流速增大时 压强减小,产生对周围气体或液 体的吸入作用; 水流抽气机、喷雾器就是根据空吸 作用的原理(速度大、压强小)设 计的。
伯努利个人简介:(Daniel Bernouli,1700~1782)瑞士物理学家、数学家、
医学家。他是伯努利这个数学家族(4代10人)中最杰出的代表,16岁时就 在巴塞尔大学攻读哲学与逻辑,后获得哲学硕士学位,17~20岁又学习医 学,并于1721年获医学硕士学位,成为外科名医并担任过解剖学教授。但 在父兄熏陶下最后仍转到数理科学。伯努利成功的领域很广,除流体动力 学这一主要领域外,还有天文测量、引力、行星的不规则轨道、磁学、海 洋、潮汐等等。
经过微小时间t后,流体a1 a2 移到了b1 b2, 从 整体效果看,相当于将流体 a1 b1 移到了a2 b2, 设a1 b1段流体的质量为m,则:
1 E1= m12 mgh1 2
1 2 E 2= m 2 mgh2 2
机械能的增量: E=E 2-E1
浅谈伯努利方程在流体力学中的应用

伯努利方程是一种常用的描述流体运动的数学方程。
它是由英国物理学家詹姆斯·伯努利发现的,在流体力学中有广泛的应用。
伯努利方程通常用来描述流体的运动规律,它可以用来计算流体的速度、压力和流量。
它的一般形式为:
∂υ/∂t + (υ·∇)υ = -∇P + ν∇²υ
其中,υ表示流体的速度,t表示时间,P表示流体的压力,ν表示流体的粘度。
伯努利方程在流体力学中有着广泛的应用,它可以用来求解流体的静态和动态问题。
例如,它可以用来计算水流的速度、水流对建筑物的冲击力等。
同时,伯努利方程也可以用来描述空气流动的情况,如风的速度、气压和气流的流量等。
因此,它在气象学和航空工程中也有着广泛的应用。
总的来说,伯努利方程是一个重要的工具,在流体力学中有着广泛的应用。
它可以帮助我们理解流体运动的规律,为我们设计和分析各种流体系统提供重要的参考。
流体力学伯努利方程推导过程

流体力学伯努利方程推导过程伯努利方程是描述流体在不同位置速度和压力之间关系的基本方程。
下面是伯努利方程的推导过程:考虑一个流体在沿着一条流线流动的情况。
我们选择两个不同的点A和B,分别代表流线上的两个位置。
在这两个位置上,我们可以考虑以下几个因素:1. 动能:流体具有速度,速度的大小与其动能有关。
动能可以表示为:K = 0.5 * m * v^2,其中m是单位体积的流体质量,v是流体的速度。
2. 势能:流体在重力场中,具有重力势能。
重力势能可以表示为:P = m * g * h,其中g是重力加速度,h是流体相对于某一参考位置的高度。
3. 压力:流体在不同位置上由于受到外部力的作用,会产生压力。
压力可以表示为:P = F / A,其中F是作用在单位面积上的外部力。
根据以上三个因素,我们可以写出点A和点B的能量守恒方程:在点A:K_A + P_A = K_B + P_B根据动能和势能的表达式,我们可以得到:0.5 * m_A * v_A^2 + m_A * g * h_A + P_A = 0.5 * m_B * v_B^2 + m_B * g * h_B + P_B由于流体是连续的,单位质量的流体在不同位置上的性质相同,即m_A = m_B = m。
同时,我们可以使用流体的密度(ρ)和单位体积的质量(ρ = m / V)进行替换,其中V为单位体积。
将以上替换和简化得到伯努利方程的一般形式:P_A + ρ * g * h_A + 0.5 * ρ * v_A^2 = P_B + ρ* g * h_B + 0.5 * ρ * v_B^2这就是伯努利方程的推导过程。
伯努利方程描述了在无黏度、不可压缩、非旋转流体中沿着流线流动时速度、压力和高度之间的关系。
伯努利方程 单位

伯努利方程1. 介绍伯努利方程是流体力学中的一个重要方程,描述了在不可压缩、粘性流体中流动的基本原理。
该方程以瑞士数学家丹尼尔·伯努利(Daniel Bernoulli)的名字命名,他在1738年首次提出了这个方程。
伯努利方程可以用来描述流体在不同位置的速度、压力和高度之间的关系。
它基于质量守恒和能量守恒的原理,是流体力学中最基本的方程之一。
2. 方程表达式伯努利方程的数学表达式如下:P+12ρv2+ρgℎ=常数其中:•P是流体的压力•ρ是流体的密度•v是流体的速度•g是重力加速度•ℎ是流体的高度3. 方程解释伯努利方程可以通过以下三个项来解释:3.1. 压力项压力项代表了流体的压力对流体运动的影响。
在伯努利方程中,压力项用P表示。
当流体的速度增加时,压力会下降,反之亦然。
这是因为流体的速度增加会导致流体分子之间的相互碰撞减少,从而降低了压力。
3.2. 动能项动能项代表了流体的动能对流体运动的影响。
在伯努利方程中,动能项用12ρv2表示,其中ρ是流体的密度,v是流体的速度。
当流体的速度增加时,动能项也会增加。
这意味着流体的速度越大,动能项的贡献越大。
3.3. 重力势能项重力势能项代表了流体的重力势能对流体运动的影响。
在伯努利方程中,重力势能项用ρgℎ表示,其中g是重力加速度,ℎ是流体的高度。
当流体的高度增加时,重力势能项也会增加。
这意味着流体的高度越高,重力势能项的贡献越大。
4. 应用伯努利方程在许多领域都有广泛的应用,包括:4.1. 管道流动伯努利方程可以用来描述管道中的流体流动。
通过应用伯努利方程,可以计算出流体在管道中的速度、压力和高度的变化。
这对于设计和优化管道系统非常重要。
4.2. 飞行原理伯努利方程在飞行原理中起着重要的作用。
它可以解释为什么飞机的翅膀会产生升力。
根据伯努利方程,在飞机翅膀上方的气流速度较大,压力较小,而在翅膀下方的气流速度较小,压力较大。
这种压力差产生了向上的升力,使得飞机能够飞行。
化工原理伯努利方程

化工原理伯努利方程伯努利方程是流体力学中的重要定律,它描述了流体在不同位置的动能、压力和重力势能之间的关系。
化工原理中,伯努利方程被广泛应用于流体力学、管道设计、泵站运行等方面,对于化工工程的设计和运行具有重要意义。
首先,让我们来了解一下伯努利方程的基本原理。
伯努利方程是以瑞士数学家伯努利的名字命名的,它描述了沿着流体流线的动能、压力和重力势能之间的定量关系。
在没有粘性损失和外力做功的情况下,沿着流体流线的总能量保持不变。
伯努利方程的数学表达式为:\[P + \frac{1}{2} \rho v^2 + \rho gh = \text{常数}\]其中,\(P\)为流体的静压力,\(\rho\)为流体密度,\(v\)为流体流速,\(g\)为重力加速度,\(h\)为流体的重力势能。
这个方程表明了流体在不同位置的动能、压力和重力势能之间的平衡关系。
在化工工程中,伯努利方程可以用于分析流体在管道中的流动情况。
例如,在管道的设计中,我们可以利用伯努利方程来计算流体在管道中的流速、压力等参数,从而确定管道的尺寸和泵站的选型。
此外,在泵站的运行中,我们也可以利用伯努利方程来分析流体在管道中的流动情况,从而确定泵站的运行参数,保证流体能够正常输送。
除此之外,伯努利方程还可以用于分析流体在不同高度的能量转换。
例如,在化工生产中,我们经常需要将流体从低处输送到高处,这涉及到流体的重力势能的变化。
利用伯努利方程,我们可以计算出流体在不同高度的压力和流速,从而确定输送过程中所需的能量消耗和泵站的选型。
总之,伯努利方程在化工工程中具有重要的应用价值。
它可以帮助我们分析流体在管道中的流动情况,确定管道的尺寸和泵站的选型;同时,它还可以帮助我们分析流体在不同高度的能量转换,确定输送过程中所需的能量消耗和泵站的选型。
因此,对于化工工程师来说,掌握伯努利方程的原理和应用是非常重要的。
希望本文的介绍能够帮助大家更好地理解伯努利方程在化工原理中的应用。
恒定总流能量方程(伯努利方程)

恒定总流能量方程(伯努利方程)
恒定总流能量方程式也称作恒定总流伯努利方程式,是流体力学领域极其实用的一个公式,其表达
式如下:
式中,h 、h ——流体截面被研究点相对于选定基准面的高度;
p 、p ——流体截面被研究点的压强;
v 、v ——流体截面被研究点的平均流速;
h ——流体在两截面被研究点之间的水头损失。
注意:截面上的被研究点可以为截面上的任意点。
伯努利方程的适用性分析:
(1)方程是在恒定流速前提下推导得到。
从理论上将讲,没有绝对的恒定流;但是,对于多数流动,流速随时间变化缓慢,由此所导致的惯性力较小,方程仍然适用。
(2)方程的推导以不可压缩流体为基础。
当在工程应用中,它仍然适用于压缩性极小的液体流动,也适用于常规的大多数气体流动。
只有当气体压强变化较大、流速很高时,才需要考虑气体的可压缩性。
(3)方程推导所选流体截面处于渐变流段。
渐变流是指各流线接近于平行直线的流动。
这在一般条件下是要遵守的,特别是断面流速非常大时,更应该严格遵守。
伯努利方程的扩展应用:
121212l1-2
(1)对于两截面之间有能量输出(水轮机或汽轮机)或输入(水泵或风机)的场合。
(2)对于两截面之间有分流或合流的场合。
方程的推导是根据两截面间没有分流或合流的情况下推得到的。
但是,对于两截面间存在两分流或合流的情况,方程仍然适用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
管的流体质量(质量守恒),即:
S11t S22t
S11 S22
2. 理想流体的连续性方程(连续性原理、流量方程):
S 恒量
体积流量:表示单位时间内流过任意截面S的流体体积,
是一种理想化的流动方式。
三.流线、流管
1. 流线:为了形象地描述定常流动的流体
而引入的假想的直线或曲线
流线上任意点的切线方向就是流体质点流经该点的速度方向 稳定流动时,流线的形状和分布不随时间变化,且流线与流体质点的运
动轨迹重合; 流线的疏密程度可定性地表示流体流速的大小; 流线不相交;
实际流体在流动时.其内部有相对运动的相邻两部分之间存在类似 两固体相对运动时存在的摩擦阻力(内摩擦力),流体的这种性质称 为粘滞性。
2.流体的可压缩性:
实际流体在外界压力作用下、其体积会发生变化,即具有可压缩 性;
3.理想流体模型:
绝对不可压缩、没有粘滞性的流体叫做理想流体; 一般情况下,密度不发生明显变化的气体或者液体、粘滞性小的
一.基本概念: 1. 流体:
具有流动性的液体和气体;
2. 流体动力学:
研究流体的运动规律以及流体与其他物体 之间相互作用的力学;
二.流体动力学的应用: 生物体液和氧分的输送,动物体内血液的循
环,土壤中水分的运动,农田排灌、昆虫迁 飞;
§1.3.1 理想流体的稳定流动
一.基本概念
1.流体的粘滞性:
1 2
4
21
3m 2
S2
1 2
2
1 0.5
2
1.5m 2
1
S2 S1
2
0.1m
/
s
§1.3.3 伯努利方程及其应用
伯努利方程是瑞士物理学家伯努利提出来的,是理想流体作稳定流动时的 基本方程,对于确定流体内部各处的压力和流速有很大的实际意义、在水 利、造船、航空等部门有着广泛的应用。
伯努利个人简介:(Daniel Bernouli,1700~1782)瑞士物理学家、数学家、 医学家。他是伯努利这个数学家族(4代10人)中最杰出的代表,16岁时就 在巴塞尔大学攻读哲学与逻辑,后获得哲学硕士学位,17~20岁又学习医 学,并于1721年获医学硕士学位,成为外科名医并担任过解剖学教授。但 在父兄熏陶下最后仍转到数理科学。伯努利成功的领域很广,除流体动力 学这一主要领域外,还有天文测量、引力、行星的不规则轨道、磁学、海 洋、潮汐等等。
试求浴室水管内水的流速和压强? (已知水的密度为=103 kg/m3)。
2 16m / s
p2 2.25105 (Pa)
1.3.4. 伯努利方程的应用
•一.水平流管的伯努利方程:
p 1 2 恒量
伯努利方程,是理想流体作稳定流动时的基本方程; 对于实际流体,如果粘滞性很小,如:水、空气、酒精等,可应用伯 努利方程解决实际问题; 对于确定流体内部各处的压力和流速有很大的实际意义、在水利、造 船、航空等部门有着广泛的应用。
补充例题, 水管里的水在压强为p=4×105 Pa的作用下流入房间, 水管的内直径为2.0 cm,管内水的流速为4 m/s。引入 到5 m高处二楼浴室的水管,内直径为1.0 cm,
补充例题
有一条灌溉渠道,横截面是梯形,底宽2m,水面宽 4m,水深1m,这条渠道再通过两条分渠道把水引到 田间,分渠道的横截面也是梯形,底宽1m,水面宽 2m , 水 深 0.5m , 如 果 水 在 两 条 渠 道 内 的 流 速 均 为 0.2m/s,求水在总渠道中的流速?
S11 S22
S1
称为体积流量,简称流量,用QV表示,单位为m3/s.
流体在同一细流管中作稳定流动时,通过任一截面S的体 积流量保持不变。
推广,对于不可压缩的实际流体,任意流管、真实导流管、 流体管道都满足连续性原理。
如果同一截面上流速相同,不可压缩的流体在流管中做稳 定流动时流体的流速与流管的截面积S成反比,即截面大 处流速小,狭窄处流速大。
E1=
1 2
m12
m
gh1
E2=
1 2
m
2 2
m
gh2
机械能的增量: E=E2-E1
功能原理: 系统受到非保守力做功,系统机械能的增量 等于非保守力对系统作的功;
外界对系统作的功?
受力分析=端面压力+侧壁压力
W=p1S11t p2 S22tV=S11t=S22t
1 2
m
2 2
m gh2
1 ( 2
2.流管:流体内部,通过某一个截面的流线围成的管状空间;
流体质点不会任意穿出或进入流管 ;(与实际管道相似) 流体可视为由无数个稳定的流管组成,分析每个流管中流体的运动规律,
是掌握流体整体运动规律的基础;
四.连续性原理
1. 推导过程:
假设: ①.取一个截面积很小的细流管,垂直于流管的同一截面上的
m12
m gh1 )=p1S11t
p2 S22t
1 2
V
2 2
Vgh2
(1 2
V12
Vgh1 )=p1V
p2V
p1
1 2
12
gh1=p2
1 2
22
gh2
二. 对于同一流管的任意截面,伯努利方程:
p 1 2 gh 恒量
2
•含义:对于理想流体作稳定流动,在同一流管中任一处,
每单位体积流体的动能、势能和该处压强之和是一个恒量。
伯努利方程:理想流体在重力场中作稳定流动时,能量守
衡定律在流动液体中的表现形式。
一. 伯努利方程的推导:
稳定流动的理想流体中,忽略流体的粘滞性,任意细流管中的 液体满足能量守恒和功能原理!
设:流体密度,细流管中分析一段流体a1 a2 : a1处:S1,1,h1, p1 a2处:S2,2,h2, p2 经过微小时间t后,流体a1 a2 移到了b1 b2, 从 整体效果看,相当于将流体 a1 b1 移到了a2 b2, 设a1 b1段流体的质量为m,则:
流体均可看成理想流体.
二.流体的运动形式:
1. 一般流动形式:
通常流体看做是由大量流体质点所组成的连续介质。 一般情况流体运动时,由于流体各部分可以有相对运动,各部分质
点的流动速度是空间位置的函数,又是时间t的函数
2. 定常流动:
流体质点经过空间各点的流速虽 然可以不同,但如果空间每一点 的流速不随时间而改变,这样的 流动方式称为定常流动,也称为 稳定流动
