2020-2021湖南省长郡中学高三12月(第四次)月考历史试题(含答案)
湖南师范大学附属中学2024-2025学年高三上学期月考卷(三)历史试卷(附中高三3次)
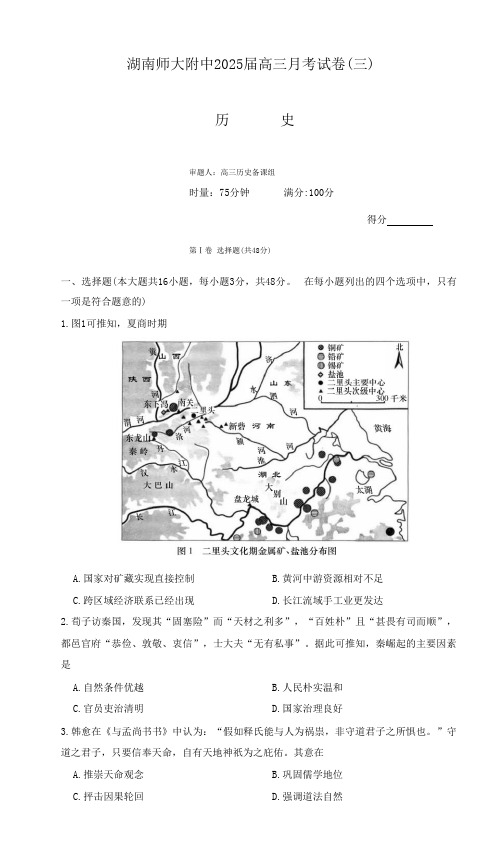
湖南师大附中2025届高三月考试卷(三)历史审题人：高三历史备课组时量：75分钟满分:100分得分第Ⅰ卷选择题(共48分)一、选择题(本大题共16小题，每小题3分，共48分。
在每小题列出的四个选项中，只有一项是符合题意的)1.图1可推知，夏商时期A.国家对矿藏实现直接控制B.黄河中游资源相对不足C.跨区域经济联系已经出现D.长江流域手工业更发达2.荀子访秦国，发现其“固塞险”而“天材之利多”，“百姓朴”且“甚畏有司而顺”，都邑官府“恭俭、敦敬、衷信”，士大夫“无有私事”。
据此可推知，秦崛起的主要因素是A.自然条件优越B.人民朴实温和C.官员吏治清明D.国家治理良好3.韩愈在《与孟尚书书》中认为：“假如释氏能与人为祸祟，非守道君子之所惧也。
”守道之君子，只要信奉天命，自有天地神祇为之庇佑。
其意在A.推崇天命观念B.巩固儒学地位4.辽朝的国号变迁复杂。
建国之初称大契丹，辽太宗时期实行双重国号(燕云汉地称大辽，草原地区称大契丹)；后多次在大辽和契丹中复改国号。
这体现出辽A.疆域版图不断变迁B.政治体制的二元性C.民族交融逐渐加深D.内外政策左右摇摆5.明朝中后期，有史料记载“无籍之徒”日渐猖獗，“投托权豪势要之家，充为家人伴当”，“不务本等生业，三五成群，白昼在街撒泼、殴打平人、抢夺财物”。
这一群体A.加剧了土地兼并的矛盾B.有利于人身依附的放松C.推动了社会阶层的流动D.削弱了政府的行政效力6.1898年，湖广总督张之洞主编《劝学篇》一书，在序言中写道：“学者摇摇，中无所主，邪说暴行，横流天下……吾恐中国之祸，不在四海之外，而在九州之内矣。
”《劝学篇》的指向是A.纠正维新派理论中的偏颇之处B.为康梁变法革新运动造势C.抨击顽固派学者们的保守论调D.为光绪帝看世界提供帮助7.湖南手工业向称发达。
然而20世纪初，时人“欲求一匹真土纱织布，几如披沙拣金”；大批手工业者被抛入城市，正业之农耕变成副业，副业的苦力变成正业。
湖南省长沙市2023-2024学年高三下学期3月质量检测历史试题(原卷版)
7.美国有学者曾撰文指出：“1852年，上海租界内的地皮平均每英亩售价50英镑，到1862年已涨到平均每英亩10000英镑。”清人葛元煦在《沪游杂记》也记载，当时“上海租屋获利最厚，租界内洋商出赁者十有六七”。导致这一现象的直接原因是（）
A.太平天国运动 影响B.洋人恶意开发哄抬地价
A.革命根据地建设成果显著B.苏维埃政权赢得民众认同
C.反围剿斗争取得阶段胜利D.“左”倾错误理论得到纠正
10.20世纪60年代，中法的角色类似：一个是在全球范围向美国霸权挑战的不驯服的盟国；一个是不听从指挥棒直至公开脱离苏联轨道的“大家庭成员”。这说明（）
A.中法具有独立自主的共性B.欧美关系已经走向对峙
3.晚唐诗人李频在《长安感怀》中说“一第知何日，全家待此身”，将诗人的压力表露无遗；王建《送薛蔓应举》中写到“一士登甲科，九族光彩新”，则生动地反映了士人登科的社会现实。据此可知，科举制（）
A.有助于打破社会阶层壁垒B.践行了四民平等思想
C.注重士子文化才能的培养D.缓和了统治阶级矛盾
4.元政府规定除“五岳四渎等载在祀典者，所在官司依例岁时致祭”外，不许在城邑、村坊“聚集人众，祈赛神社”。到元代中期，对城乡“唱词聚众的勾当”等娱乐活动也明令禁止。元政府此举（）
C.剩余产品大量出现D.渔猎活动逐渐消失
2.汉孝惠、高后时，为天下初定，复弛商贾之律。文帝时，晁错提出“入粟拜爵”，这在客观上便利了富商购买爵位。景帝时期，降低了缴纳算赋做官的标准，以免使廉洁之士长期不能做官，但商贾之人可从中谋取厚利。汉初这些政策（）
A.导致抑商政策的废弛B.导致社会风气败坏
C.迟滞了经济复苏进程D.有助于商业的发展
A.冲击了社会人伦道德观B.意在强化地方社会控制
湖南省长沙市长郡中学2024-2025学年高三上学期月考地理试题(一)及答案
大联考长郡中学2025 届高三月考试卷(一)地理得分本试题卷分选择题和非选择题两部分，共8页。
时量 75 分钟，满分100 分.一、选择题(本大题共16小题，每小题3分，共48分。
在每小题给出的四个选项中，只有一项是符合题目要求的)大源村是广州郊区的一个城中村，邻近服装批发市场。
2018年以来，大源村逐步把旧厂房改造为电商产业园，同时成立了大源电子简务协会，并构建了“政—校一企”三方合作平台。
下图为大源利由传统电商向新型电商转型示意图。
据此完成1~3题。
1.2012年前后，影响广州部分电商企业布局变化的主要因素是A.市场B.基础设施C.土地价格 B.政策2.大源村将旧厂房改造为电商产业园，首先影响到当地电商产业发展的A.产业环境B.产业布局C.产业链条 D 产业结构3.大源村电商产业园区吸引个体电商入驻的原因是A.竞争压力小B.销售方式多C.供货渠道广D.产业规模大J古城由都城、离宫和军事卫城构成。
战国时期，都城是古城中心，离宫的东南角城门可供船只通行。
秦汉时期，离宫成为古城中心。
此后，由于环境变迁，J古城衰落。
19世纪起，S市人口集聚，现已发展为地级市。
下图示意长江流域局部地区。
据此完成4~6题。
4. J古城建设之初，都城未建在离宫处，主要是考虑A.减少水患B.便于取水C.方便耕作D.利于防卫b.古城中心的变迁，反映了战国至秦汉期间该地区气候趋向A.湿润B.干旱C.温暖·I).寒冷6.根据J古城和S市的地理位置，可推知战国时期至现代长江干流图示河段A.整体向北移动B.8市附近河道没有明显摆动C. 整体向南移动D. S市附近河道摆动幅度较大大小交路是指列车在线路上的运行距离有长、短路两种方式，在线路的部分区段共线运行。
石家庄地铁1号线于2021年起在规定时间段内执行该运行模式(如下图)：大交路(西王—福泽)10分钟/次，小交路(西王—汶河大道)5分钟/次。
据此完成7~8题。
7.石家庄地铁1号线采用大小交路运行的目的有①提高运输能力②缓解客流压力③提高运行速度④降低能源消耗A.①②B.②③C.①④D.③④8.下列时间段中；最适合以大小交路运行的是A 工作日·6:00-7:30 B.工作日9:00—19:30C.节假日6:00—7:30D.节假日9:00—19:30温度露点差是温度与露点(露点：在气象学中是指在固定气压之下，空气中所含的气态水达到饱和而凝结成液态水所需要降至的温度)的差值，是相对湿度的一种度量，温度露点差越大，湿度越小，当温度露点差接近0℃时，表示空气中的水汽达到近似饱和状态。
专题19 椭圆(客观题)(新高考地区专用)(解析版)
专题19 椭 圆（客观题）一、单选题1．如图，椭圆22221(0)x y a b a b+=>>的右焦点为,,F A B 分别为椭圆的上､下顶点，P 是椭圆上一点，//,||||AP BF AF PB =，记椭圆的离心率为e ，则2e =A ．2BC ．12D 【试题来源】2021年1月浙江省普通高中学业水平考试 【答案】B【解析】()()0,,,0B b F c -，则BF b k c=，所以直线:bAP y x b c =+，与椭圆方程联立()222220a c x a cx ++=，所以点P 的横坐标是2222a c x a c =-+，322b y a c=-+，即2322222,a c b P a c a c ⎛⎫-- ⎪++⎝⎭，222322222222a c b PB a b a a c a c ⎛⎫⎛⎫=⇒+-+= ⎪ ⎪++⎝⎭⎝⎭， 整理为6244264321c a c a c a --+=，两边同时除以6a 得64243210e e e --+=，()()2421410ee e -+-=，210e -≠，所以42410e e +-=，得2e =或2e =（舍）．故选B ． 2．已知椭圆()222210x y a b a b+=>>，点M 在椭圆上，以M 为圆心的圆与x 轴相切与椭圆的焦点，与y 轴相交于P ，Q ，若MPQ 为正三角形，则椭圆的离心率为A ．12B ．13C ．2D ．3【试题来源】浙江省金华市义乌市2020-2021学年高三上学期第一次模拟考试 【答案】D【解析】不妨设()00,M x y 在第一象限，以M 为圆心的圆与x 轴相切于椭圆右焦点，则0x c =，又M 在椭圆上，则20b y a =，∴圆M 的半径2br a =，MPQ 为正三角形，c r ∴==2220ac +=220e +=，解得3e =．故选D ． 【名师点睛】本题考查椭圆离心率的求解问题，求解离心率的关键是能够通过图形中的长度关系构造出关于,a c 的齐次方程，利用齐次方程配凑出离心率e ，解方程求得结果．3．已知椭圆()222210x y a b a b+=>>上一点A 关于原点的对称点为点B ，F 为其右焦点，若AF BF ⊥，设ABF α∠=，且,64ππα⎡⎤∈⎢⎥⎣⎦，则该椭圆的离心率e 的取值范围是A ．,12⎤⎢⎥⎣⎦B ．12⎤⎥⎣⎦C ．,22⎣⎦D ．33⎣⎦【试题来源】河北省衡水中学2021届高三上学期期中（理） 【答案】B【解析】设椭圆()222210x y a b a b+=>>的左焦点为1F ，因为AF BF ⊥，所以四边形为1AF BF 为矩形，所以12AB FF c == 因为ABF α∠=，所以2sin ,2cos ,AF c BF c αα==由椭圆的定义得22sin 2cos a c c αα=+，所以11sin cos 4c e a πααα===+⎛⎫+ ⎪⎝⎭， 因为,64ππα⎡⎤∈⎢⎥⎣⎦，所以5,4122πππα⎡⎤+∈⎢⎥⎣⎦，所以sin 4πα⎤⎛⎫+∈⎥ ⎪⎝⎭⎣⎦，4πα⎛⎫+∈ ⎪⎝⎭⎣，所以1e ⎤∈⎥⎣⎦，故选B. 【名师点睛】椭圆定义的应用主要有两个方面：一是确认平面内与两定点有关的轨迹是否为椭圆；二是当P 在椭圆上时，与椭圆的两焦点F 1，F 2组成的三角形通常称为“焦点三角形”，利用定义可求其周长；利用定义和余弦定理可求|PF 1|·|PF 2|；通过整体代入可求其面积等．4．已知F 是椭圆22221(0)x y a b a b+=>>的一个焦点，若直线y kx =与椭圆相交于A ，B 两点，且120AFB ∠=︒，则椭圆离心率的取值范围是A．⎫⎪⎪⎣⎭B．⎛ ⎝⎦C ．1,12⎡⎫⎪⎢⎣⎭D ．10,2⎛⎤ ⎥⎝⎦【试题来源】湖北省黄冈市部分普通高中2020-2021学年高三上学期12月联考 【答案】C【解析】连接A ，B 与左右焦点F ，F '的连线，由120AFB ∠=︒，由椭圆及直线的对称性可得四边形AFBF '为平行四边形，60FAF '∠=︒，在三角形AFF '中，()22222cos 3FF AF AF AF AF FAF AF AF AF AF ''''=+-⋅∠=+-⋅，所以()222332AF AF AF AF FF AF AF '+⎛⎫''+-=⋅≤ ⎪⎝⎭，即()2214AF AF FF ''+≤即221444a c ⋅≤，可得1 2c e a =≥，所以椭圆的离心率1,12e ⎡⎫∈⎪⎢⎣⎭，故选C ． 【名师点睛】该题考查的是有关椭圆离心率的取值范围的求解问题，解题方法如下： （1）根据题意，结合椭圆的对称性，连接相应点，得到平行四边形； （2）根据平行四边形的性质，得到角的大小；（3）根据余弦定理，列出相应等式，结合椭圆定义以及基本不等式求得结果．5．已知P 是椭圆22221x y a b+=（0a b >>）上一点，过原点的直线交椭圆于A ，B 两点，且34PA PB k k ⋅=-，则椭圆的离心率为 A ．12B ．13C ．14D．2【试题来源】安徽省六安市第一中学2020-2021学年高三上学期第四次月考（文） 【答案】A【解析】由题可设(),P x y ，()11,A x y ，11,B x y ，则2211122111PA PBy y y y y y k k x x x x x x -+-⋅=⋅=-+-，22221x y a b +=，2211221x y a b+=，两式相减可得222211220x x y y a b --+=，即22212221y y b x x a -=--，2234b a ∴-=-，22234a c a -∴=，12c a ∴=，故选A.【名师点睛】（1）该题来自椭圆的一个小结论：若椭圆方程为()222210x y a b a b+=>>，,A B是该椭圆上关于原点对称的两点，P 为椭圆上异于,A B 的任意一点，则PA PB k k ⋅为定值，为22b a-．（2）椭圆的离心率是椭圆最重要的几何性质，求椭圆的离心率(或离心率的取值范围)，常见有两种方法：①求出a ，c ，代入公式ce a=；②只需要根据一个条件得到关于a ，b ，c 的齐次式，结合b 2＝a 2－c 2转化为a ，c 的齐次式，然后等式(不等式)两边分别除以a 或a 2转化为关于e 的方程(不等式)，解方程(不等式)即可得e (e 的取值范围)．6．已知椭圆22:195x y E +=的左、右焦点分别为1F ，2F ，P 为椭圆上一个动点，Q 为圆22:108400M x y x y +--+=上一个动点，则1PF PQ +的最大值为 A ．12 B 1+ C ．11D ．18【试题来源】江苏省苏州市常熟市2020-2021学年高三上学期阶段性抽测二 【答案】A【解析】由题意得12(2,0),(2,0)F F -，根据椭圆的定义可得1226PF PF a +==，所以126PF PF =-，又圆22:108400M x y x y +--+=，变形可得22(5)(4)1x y -+-=，即圆心(5,4)M ，半径1r =，所求1PF PQ +的最大值，即求1PF PM r ++的最大值，126PF PM PF PM +=-+，如图所示：当2,,P F M 共线时，2PM PF -有最大值，且为25F M ==， 所以126PF PM PF PM +=-+的最大值为5611+=，所以1PF PQ +的最大值，即1PF PM r ++的最大值为11+1=12，故选A7．已知A ､B 分别为椭圆C ：2214x y +=的左､右顶点，P 为椭圆C 上一动点，PA ，PB与直线3x =交于M ，N 两点，PMN 与PAB △的外接圆的周长分别为1L ，2L ，则12L L 的最小值为 ABCD ．14【试题来源】湖南省长郡中学、湖南师大附中、长沙市一中联合体2020-2021学年高三上学期12月联考【答案】A【解析】由已知得(2,0)A -、(2,0)B ，设椭圆C 上动点(,)P x y ， 则利用两点连线的斜率公式可知02-=+PA y k x ，02-=-PA y k x ， ()()22222100142222444---∴⋅=⋅====-+-+---PA PBx y y y y k k x x x x x x 设直线PA 方程为()2y k x =+，则直线PB 方程为()124y x k=--，根据对称性设0k >， 令3x =得5M y k =，14N y k =-，即()3,5M k ，13,4-⎛⎫ ⎪⎝⎭k N ，则154MN k k =+ 设PMN 与PAB △的外接圆的半径分别为1r ，2r ， 由正弦定理得1sin 2N P r M M N =∠，22sin ABr APB=∠，又180∠+∠=︒MPN APB ，sin sin ∴∠=∠MPN APB111222152424+∴====≥=k L r r MNk L r r ABππ，当且仅当154=k k ，即=k 等号成立，即12L LA 8．若点M 到两定点()10,1-F ，()20,1F 的距离之和为2，则点M 的轨迹是 A ．椭圆B ．直线C ．线段D ．线段的中垂线．【试题来源】四川省绵阳市绵阳南山中学2020-2021学年高三上学期11月月考（文） 【答案】C【分析】根据M 到12,F F 的距离之和正好等于12F F ，可得M 的轨迹．【解析】()10,1-F ，()20,1F ，122F F ∴=，因为点M 到两定点()10,1-F ，()20,1F 的距离之和为2，M ∴的轨迹是线段12F F ，故选C ．9．已知椭圆C 经过点()()5004A B -，，，，则椭圆C 的标准方程为 A ．22154x y +=B ．2212516x y +=C ．2211625x y +=D ．221259x y +=【试题来源】西藏日喀则市拉孜县中学2021届高三上学期第二次月考（理） 【答案】B【分析】由所给的椭圆上的点为顶点，即可求出椭圆的方程．【解析】因为椭圆C 经过点()()5004A B -，，，，所以5,4a b ==，且焦点在x 轴上， 所以椭圆的方程为2212516x y +=，故选B. 10．关于x ，y 的方程()22211ax a y +-=表示的曲线为椭圆的一个充分不必要条件为A ．12a >B ．1a >C ．12a >且1a ≠D ．12a >或0a < 【试题来源】百师联盟2021届一轮复习（二） 全国卷III 理数试题 【答案】B【分析】根据椭圆的方程可得021021a a a a >⎧⎪->⎨⎪≠-⎩，求出a 的取值，再根据充分条件、必要条件的定义即可求解．【解析】若方程()22211ax a y +-=表示的曲线为椭圆，则有021021a a a a >⎧⎪->⎨⎪≠-⎩，所以12a >且1a ≠，故选项A 和D 非充分条件，选项C 为充要条件，选项B 为充分不必要条件，故选B ．11．已知实数1,,9m 成等比数列，则椭圆221x y m+=的离心率为AB ．2 C或2D．2【试题来源】宁夏石嘴山市2020届高三适应性测试（理） 【答案】A【分析】由1，m ，9构成一个等比数列，得到m=±3．当m=3时，圆锥曲线是椭圆；当m=﹣3时，圆锥曲线是双曲线，(舍）由此即可求出离心率．【解析】因为1，m ，9构成一个等比数列，所以m 2=1×9，则m=±3．当m=3时，圆锥曲线2xm +y 2=13；当m=﹣3时，圆锥曲线2x m +y 2=1是双曲线，故舍去，则离心率为3．故选A ． 12．椭圆()2222101x y m m m+=>+的焦点为1F 、2F ，上顶点为A ，若123F AF π∠=，则m =A ．1 BCD ．2【试题来源】2021年普通高等学校招生全国统一考试模拟演练数学 【答案】C【解析】在椭圆()2222101x y m m m+=>+中，a ，b m =，1c ==，如下图所示：因为椭圆()2222101x y m m m +=>+的上顶点为点A ，焦点为1F 、2F ，所以12AF AF a ==，123F AF π∠=，12F AF ∴△为等边三角形，则112AF F F =22a c ===，因此，m ．故选C ．13．已知椭圆C ：()222210x y a b a b+=>>的左､右焦点分别为1F ､2F ，B 是椭圆C 的上顶点，直线13x c =与直线2BF 交于点A ，若124AF F π∠=，则椭圆C 的离心率为ABC．2D．2【试题来源】江西省吉安市2021届高三大联考数学（理）（3-2）试题 【答案】A【解析】由题设知，()0,B b ，()2,0F c ，所以直线2BF 的方程为1x y c b +=，联立131x c x y c b⎧=⎪⎪⎨⎪+=⎪⎩得，12,33A c b ⎛⎫ ⎪⎝⎭，设直线13x c =与x 轴交于点M ，则143F M c =，23MA b =， 因为124AF F π∠=，所以14233F M MA c b =⇒=，即2b c =， 所以2224a c c -=，即225a c =，所以2155e e =⇒=，故选A. 14．已知ABCDEF 为正六边形，若A 、D 为椭圆W 的焦点，且B 、C 、E 、F 都在椭圆W 上，则椭圆W 的离心率为 A1B1 C．12D．12【试题来源】湖南省株洲市2020-2021学年高三上学期第一次教学质量统一检测 【答案】A【分析】设正六边形ABCDEF 的边长为1，则1c OA ==，由21AF FD a +==可得a ，从而可得椭圆的离心率．【解析】设正六边形ABCDEF 的边长为1，如图由A 、D 为椭圆W 的焦点，则在椭圆中，1c OA ==，由B 、C 、E 、F 都在椭圆W 上，则在直角三角形ADF中，DF ===由椭圆的定义可得21AF FD a +==+a =，所以12c e a ===，故选A.15．椭圆22221(0)y x a b a b +=>>的上、下焦点分别为1F 、2F ，过椭圆上的点M 作向量MN使得12MN F F =，且12 F F N 为正三角形，则该椭圆的离心率为 A．2B．12CD【试题来源】2021届高三湘豫名校联考（2020年11月）（文） 【答案】D【分析】根据12 F F N 为正三角形得到点N 必在x 轴上，即可求出ON ，再根据12MN F F =，即可求出M 点的坐标，代入椭圆方程，根据离心率的公式即可求出离心率．【解析】12F F N 为正三角形，∴点N 必在x 轴上，且1260NF F ∠=︒，1tan60ON OF ∴=︒⋅=，又12MN F F =，),2Mc ∴，又点M在椭圆上，)2222(2)1c ab ∴+=，化简得424810e e -+=，解得2e ==，又01e <<，e ∴=．故选D ． 16．已知曲线Γ：22123x y λλ+=-，则以下判断错误的是A ．0λ<或3λ>时，曲线Γ一定表示双曲线B ．03λ<<时，曲线Γ一定表示椭圆C ．当3λ=-时，曲线Γ表示等轴双曲线D ．曲线Γ不能表示抛物线【试题来源】云南省西南名校联盟2021届高三12月高考适应性月考卷（理） 【答案】B【解析】对Γ：22123x y λλ+=-，当2(3)0λλ-<，即0λ<或3λ>时，曲线Γ表示双曲线，当3λ=-时，Γ：22166y x -=表示等轴双曲线，因为无论λ取何值，曲线方程均只含2x ，2y 项与常数项，因此A ，C ，D 正确；当1λ=时，Γ：222x y +=表示圆，B 错误．选B ．17．已知点P 是椭圆C ：22110064x y +=上一点，M ，N 分别是圆()2261x y -+=和圆()2261x y ++=上的点，那么PM PN +的最小值为A ．15B ．16C ．17D ．18【试题来源】安徽省六安市第一中学2020-2021学年高三上学期第四次月考（理） 【答案】D【解析】如图，椭圆C ：22110064x y +=的108a b ==，，所以6c =，故圆()2261x y -+=和圆()2261x y ++=的圆心为椭圆的两个焦点，则当M ，N 为如图所示位置时，PM PN +最小， 值为12122218PF PF MF MF a +--=-=，故选D ．18．椭圆C ：2221(0)3x y a a +=>的焦点在x 轴上，其离心率为12，则A ．椭圆CB ．椭圆C 的长轴长为4 C ．椭圆C 的焦距为4D ．4a =【试题来源】辽宁省葫芦岛市协作校2020-2021学年高三12月联考 【答案】B【分析】由离心率可求出2a =，结合椭圆的性质可求出椭圆的短轴长，长轴长，焦距．【解析】由椭圆的性质可知，椭圆C 的短轴长为12e ==，则24a =，即2a =，2231c a =-=，所以椭圆C 的长轴长24a =，椭圆C 的焦距22c =，故选B ．19．已知1F ，2F 是椭圆2212516x y +=的左、右焦点，P 是椭圆上任意一点，过1F 引12F PF ∠的外角平分线的垂线，垂足为Q ，则Q 与短轴端点的最近距离为 A ．1 B ．2 C ．4D ．5【试题来源】河南省洛阳市2021届高三上学期第一次统一考试（文） 【答案】A【分析】根据角平分线的性质和椭圆的定义可得OQ 是12F F M △的中位线， ||5OQ a ==，可得Q 点的轨迹是以O 为圆心，以5为半径的圆，由此可得选项．【解析】因为P 是焦点为1F ，2F 的椭圆2212516x y +=上的一点，PQ 为12F PF ∠的外角平分线，1QF PQ ⊥，设1F Q 的延长线交2F P 的延长线于点M ，所以1||||PM PF =，12212210,PF PF a MF PF PF +==∴=+，所以由题意得OQ 是12F F M △的中位线，所以||5OQ a ==，所以Q 点的轨迹是以O 为圆心，以5为半径的圆，所以当点Q 与y 轴重合时， Q 与短轴端点取最近距离54 1.d =-=故选A ．20．已知椭圆()222210x y a b a b+=>>的左、右焦点分别为1F ，2F ，过1F 且与x 轴垂直的直线交椭圆于A ，B 两点，直线2AF 与椭圆的另一个交点为C ，若23ABCBCF S S=，则椭圆的离心率为A BC ．3D ．10【试题来源】云南省昆明市第一中学2021届高三第三次双基检测（理） 【答案】A【解析】设椭圆的左、右焦点分别为()1,0F c -，()2,0F c ，由x c =-，代入椭圆方程得2by a =±，设2,b A c a ⎛⎫- ⎪⎝⎭，(),C x y ，由23ABCBCF SS=，可得222AF F C =，即22,2(,)b c x c y a ⎛⎫-=- ⎪⎝⎭，即222c x c =-，22b y a -=，所以2x c =，22b y a =-，代入椭圆得，2222414c b a a+=，由222b a c =-得2153e =，解得e =，由01e <<，所以e =．故选A ．21．已知抛物线()220y px p =>的准线与椭圆22194x y +=相交的弦长为p =A ．1B ．2C ．3D ．4【试题来源】云南师大附中2020届高三（下）月考（理）（七） 【答案】C【解析】抛物线的准线方程为2px =-，设其与椭圆相交于A ，B两点，AB = 不妨设0A y >，根据对称知A y =32A x =-或32A x =（舍去），3p =，故选C ．22．椭圆()2222:10x y C a b a b+=>>的左、右焦点为1F ，2F ，过2F 垂直于x 轴的直线交C于A ，B 两点，若1AF B △为等边三角形，则椭圆C 的离心率为 A ．12B．2C ．13D．3【试题来源】天津市第一中学2020-2021学年高三上学期第二次月考 【答案】D【分析】利用椭圆方程，求出焦点坐标，通过三角形是等边三角形求解椭圆的离心率即可．【解析】椭圆()2222:10x y C a b a b+=>>的左、右焦点为1F ，2F ，过2F 垂直于x 轴的直线交C 于A ，B 两点，若1AF B △为等边三角形，可得222b c a=，所以：)222ac a c =-，即220e +=， 因为()01e ∈，，解得3e =，故选D ． 23．椭圆C ：22221(0)x y a b a b+=>>的左､右焦点分别为F 1，F 2，点P (x 1，y 1)，Q (-x 1，-y 1)在椭圆C 上，其中x 1>0，y 1>0，若|PQ |=2|OF 2|，11||||QF PF ≥ A．10,2⎛⎤ ⎥⎝⎦B．2]C．12⎛⎤ ⎥⎝⎦D．1]【试题来源】江苏省镇江市丹阳市吕叔湘中学2020-2021学年高三上学期11月教学调研 【答案】C【分析】根据2||2PQ OF =，可得四边形12PF QF 为矩形，设12,PF n PF m ==，根据椭圆的定义以及勾股定理可得()22242c m n n m a c =+-，再分析18m t n m=+的取值范围， 进而求得()222422c a c <≤-，再求离心率的范围即可 【解析】设12,PF n PF m ==，由210,0x y >>，知m n <， 因为()()1111,,,P x y Q x y --，在椭圆C 上，222PQ OP OF ==， 所以，四边形12PFQF 为矩形，12=QFPF；由113QF PF ≥1mn≤<， 由椭圆定义可得2222,4m n a m n c +=+=①；平方相减可得()222mn a c=-②；由①②得()2222242c m n m nmn n m a c +==+-； 令=+m nt n m，令m v n ⎫=∈⎪⎪⎣⎭，所以，1t v v ⎛=+∈ ⎝⎦， 即()2224232c a c <≤-，所以，()222223a c c a c -<≤-，所以，()22211e e e-<≤-，所以，2142e <≤-解得12e <≤，故选C. 24．已知椭圆22221(0)x y a b a b+=>>的左、右焦点分别为1F 、2F ，点A 是椭圆短轴的一个顶点，且123cos 4F AF ∠=，则椭圆的离心率e = A ．12B．2 C ．14D．4【试题来源】江苏省泰州市姜堰中学、南通市如东中学、宿迁市沭阳如东中学2020-2021学年高三上学期联考 【答案】D【分析】依题意，不妨设点A 的坐标为()0b ，，在12F AF 中，由余弦定理得22142a c =，再根据离心率公式计算即可．【解析】设椭圆22221(0)x y a b a b+=>>的焦距为2(0)c c >，则椭圆22221(0)x y a b a b+=>>的左焦点1F 的坐标为()0c -，，右焦点2F 的坐标为()0c ，， 依题意，不妨设点A 的坐标为()0b ，，在12F AF 中，由余弦定理得 22212121212||||2cos F F AF AF AF AF F AF ∠=+-⋅⋅，123cos 4F AF ∠=，22223142242c a a a ∴=-⨯=，22218c e a ∴==，解得4e =．故选D ． 25．已知A ､B 为椭圆的左、右顶点，F 为左焦点，点P 为椭圆上一点，且PF ⊥x 轴，过点A 的直线与线段PF 交于M 点，与y 轴交于E 点，若直线BM 经过OE 中点，则椭圆的离心率为A ．12BC ．13D 【试题来源】黑龙江省哈尔滨市道里区第三中学校2020-2021学年高三上学期期末 【答案】C【分析】根据已知条件求出,,B H M 三点坐标，再由三点共线可得斜率相等，从而得出3a c =可得答案．【解析】由题意可设(,0),(,0),(,0)F c A a B a --，设直线AE 的方程（由题知斜率存在）为()y k x a =+，令x c =-，可得(),()M c k a c --，令0x =，可得(0,)E ka ，设OE 的中点为H ，可得0,2ka H ⎛⎫⎪⎝⎭，由,,B H M 三点共线，可得BH BM k k =，即()2kak a c a c a-=---，即为3a c =，可得13c e a ==，故选C ．26．已知命题p ：22x my =表示焦点在y 轴的正半轴上的抛物线，命题q：22162x y m m +=-+表示椭圆，若命题“p q ∧”为真命题，则实数m 的取值范围是 A ．26m -<< B ．06m <<C ．06m <<且2m ≠D ．26m -<<且2m ≠【试题来源】安徽省皖江名校联盟2021届高三第二次联考（理） 【答案】C【解析】对于命题2:2p x my =表示焦点在y 轴的正半轴上的抛物线，所以0m >，对于命题22:162x yq m m +=-+表示椭圆，所以602062m m m m ->⎧⎪+>⎨⎪-≠+⎩，解得26m -<<且2m ≠， 因为命题“p q ∧”为真命题，所以命题p 和命题q 均为真命题， 所以实数m 的取值范围是06m <<且2m ≠．故选C ．27．已知()11,0F -，21,0F ，M 是第一象限内的点，且满足124MF MF +=，若I 是12MF F △的内心，G 是12MF F △的重心，记12IF F △与1GF M △的面积分别为1S ，2S ，则A ．12S S >B ．12S SC ．12S S <D ．1S 与2S 大小不确定【试题来源】浙江省十校联盟2020-2021学年高三上学期10月联考 【答案】B【分析】作出图示，根据,I G 的特点分别表示出1S ，2S ，即可判断出12,S S 的大小关系．【解析】因为121242MF MF F F +=>=，所以M 的轨迹是椭圆22143x y +=在第一象限内的部分，如图所示：因为I 是12MF F △的内心，设内切圆的半径为r ，所以()12121222MMFMF F F rF F y ++⋅⋅=，所以3M y r =，所以12121223I MF F y F F r y S ⋅⋅===，因为G 是12MF F △的重心，所以:1:2OG GM =， 所以12112221133323M M MOF F OF F F yy S S S ⋅===⋅=，所以12S S ，故选B ． 28．已知1F 、2F 为椭圆和双曲线的公共焦点，P 为其一个公共点，且123F PF π∠=，则椭圆和双曲线的离心率的倒数之和的最大值为A ．BCD ．【试题来源】【新东方】【2020】【高三上】【期中】【HD -LP367】【数学】 【答案】C【解析】设椭圆的长半轴长为1a ，双曲线的实半轴长为2a 12()a a >，半焦距为c ， 椭圆和双曲线的离心率分别为1e 和2e ，11||PF r =，22||PF r =， 由椭圆和双曲线的定义可知，1212r r a +=，1222r r a -=±， 因为123F PF π∠=，由余弦定理得222121242cos3c r r r r π=+-221212r r r r =+-，所以22212121124()343c r r r r a r r =+-=-，且22212122124()4c r r r r a r r =-+=+，所以222212443(44)a c c a -=-，即2221234a a c +=，则2221314e e +=，由柯西不等式得22212121131(1)()(13e e e e ++≥⨯+，所以12113e e +≤=，当且仅当13e =，2e =时，等号成立．故选C 29．如图，设1F 、2F 分别是椭圆的左、右焦点，点P 是以12F F 为直径的圆与椭圆在第一象限内的一个交点，延长2PF 与椭圆交于点Q ，若124PF QF =，则直线2PF 的斜率为A ．2-B ．1-C ．12-D ．1【试题来源】浙江省宁波十校2020-2021学年高三上学期期中联考 【答案】A【解析】如下图，连接11,PF QF ，设()20QF x x =>，则14PF x =，因为122PF PF a +=，122QF QF a +=，所以224PF a x =-，12QF a x =-，在△1PF Q 中，1290F PF ︒∠=，所以22211+=PF PQ QF ，即()()()2224242x a x x a x +-+=-，整理得3a x =， 所以121244tan 22464PF x xPF F PF a x x x∠====--，所以直线2PF 的斜率为()21tan 1802k PF F ︒=-∠=-．故选A ．30．已知P 是椭圆()2222:10x y C a b a b+=>>上的点，1F ，2F 分别是C 的左，右焦点，O是坐标原点，若212OP OF OF +=且1260F PF ∠=︒，则椭圆的离心率为 A ．12BCD 【试题来源】福建省莆田第一中学2021届高三上学期期中考试 【答案】A【解析】如图所示，设M 是2PF 中点，则22OP OF OM +=，1||2||PF OM =， 因为212OP OF OF +=，所以1||||OM OF =，所以112||||2PF F F c ==，因为1260F PF ∠=︒，所以1122||||||2PF F F PF c ===．由椭圆的定义得12||||2PF PF a +=， 所以11222,,22c c c a e a +=∴=∴=．故选A 二、多选题1．已知椭圆()2222:10x y M a b a b+=>>的左、右焦点分别为1F ，2F ，若椭圆M 与坐标轴分别交于A ，B ，C ，D 四点，且从1F ，2F ，A ，B ，C ，D 这六点中，可以找到三点构成一个直角三角形，则椭圆M 的离心率的可能取值为A ．3 B ．2 C ．512- D ．312- 【试题来源】湘鄂部分重点学校2020-2021学年高三上学期11月联考（理） 【答案】BC【分析】结合椭圆的对称性，只需要考虑三种情况，即以D 、C ，2F 作为三角形的三个顶点；以C 、1F 、2F 作为三角形的三个顶点或以C 、A 、2F 作为三角形的三个顶点，分别根据图形列出关于以a 、b 、c 的齐次式，化简求离心率．【解析】①如图，若以D 、C ，2F 作为三角形的三个顶点，则2DC CF ⊥， 由勾股定理可得，()()2222a ba a c ++=+，由222b ac =-，可得220c ac a +-=，即210e e +-=，因为01e <<，解得512e =；②如图，若以C 、1F 、2F 作为三角形的三个顶点， 则12CF CF ⊥，故245OCF ∠=︒，则2c e a ==；③如图，若以C 、A 、2F 作为三角形的三个顶点， 则22CF AF ⊥，245CF O ∠=︒，则22c e a ==；故选BC ．2．已知F 是椭圆2212516x y +=的右焦点，M 为左焦点，P 为椭圆上的动点，且椭圆上至少有21个不同的点()1,2,3,i P i =，1FP ，2FP ，3FP ，…组成公差为d 的等差数列，则A ．FPM 的面积最大时，24tan 7FPM ∠= B ．1FP 的最大值为8 C ．d 的值可以为310D ．椭圆上存在点P ，使2FPM π∠=【试题来源】湖北省十一校考试联盟2020-2021学年高三上学期12月联考 【答案】ABC【解析】由椭圆2212516x y +=，当点P 为短轴顶点时，FPM ∠最大，FPM 的面积最大，此时24tan 7FPM ∠=，此时角为锐角，故A 正确、D 错误； 椭圆上的动点P ，1a c PF a c -≤≤+，即有128PF ≤≤，又椭圆上至少有21个不同的点()1,2,3,i P i =，1FP ，2FP ，3FP ，…组成公差为d 的等差数列，所以1FP 最大值8，B 正确；设1FP ，2FP ，3FP ，…组成的等差数列为{}n a ，公差0d >，则12a ≥，8n a ≤，又11n a a d n -=-，所以663121110d n ≤≤=--，所以3010d <≤，所以d 的最大值是310，故C 正确．故选ABC【名师点睛】由椭圆性质知在椭圆上的点中，与焦点构成的三角形面积、以该点为顶点的角最大时，点在短轴端点上；且2||8FP ≤≤，进而可得d 的范围．3．椭圆2222:1(0)x y C a b a b+=>>，1F ，2F 分别为左、右焦点，1A ，2A 分别为左、右顶点，P 为椭圆上的动点，且12120PF PF PA PA ⋅+⋅≥恒成立，则椭圆C 的离心率可能为A ．12BC D ．2【试题来源】云南省楚雄州2021届高三上学期期中教学质量检测（理） 【答案】AC【解析】设()00,P x y ，1(,0)F c -，2(,0)F c ，则()100,PF c x y =---，()200,PF c x y =--， ()100,PA a x y =---，()200,PA a x y =--．因为22221212022PF PF PA PA x y a c ⋅+⋅=+--2222220222b x b x a c a ⎛⎫=+--- ⎪⎝⎭222222022330c x a c a c a =+-≥-≥恒成立，所以离心率3c e a =≤．故选AC 【名师点睛】此题考查椭圆的几何性质的应用，考查的离心率的求法，解题的关键是由12120PF PF PA PA ⋅+⋅≥转化为坐标的关系，进而可得到,a c 的关系，考查计算能力，属于中档题4．设椭圆22193x y +=的右焦点为F ，直线(0y m m =<<与椭圆交于A ， B 两点，则下述结论正确的是 A ．AF +BF 为定值 B ．△ABF 的周长的取值范围是[6，12]C ．当m =时，△ABF 为直角三角形D ．当m =1时，△ABF【试题来源】海南省2020届高三高考数学五模试题 【答案】AD【解析】设椭圆的左焦点为F '，则AF BF '= 所以=6AF BF AF AF '+=+为定值，A 正确；ABF 的周长为AB AF BF ++，因为AF BF +为定值6，所以AB 的范围是()0,6， 所以ABF 的周长的范围是()6,12，B 错误；将y =(A ，B，因为)F，所以(?60BA BF ⋅=-=-<，所以ABF 不是直角三角形，C 不正确；将1y =与椭圆方程联立，解得()A -，)B ，所以112ABFS=⨯=D 正确．故选AD. 5．已知椭圆22:163x y C +=的左、右两个焦点分别为12,F F ，直线(0)y kx k =≠与C 交于A ，B 两点，AE x ⊥轴，垂足为E ，直线BE 与C 的另一个交点为P ，则下列结论正确的是A ．四边形12AF BF 为平行四边形B ．1290F PF ︒∠<C ．直线BE 的斜率为12k D ．90PAB ︒∠>【试题来源】重庆市第八中学2021届高三上学期高考适应性月考（二） 【答案】ABC 【解析】A 选项：根据对称性，如上图有2112,,OA OB BOF AOF OF OF =∠=∠=，所以21BOF AOF ≅，即12OAF OBF ∠=∠，则12//AF BF ，12AF BF =，所以四边形12AF BF 为平行四边形；A 正确．B 选项：由余弦定理222121212122cos F F PF PF PF PF F PF =+-⋅⋅∠，12F F =，12,PF x PF x ==，由直线(0)y kx k =≠中k 存在故x ≠所以212cos F PF ∠=，令t x <=，则x t =+，所以212226cos 166t F PF t t∠==---，203t ≤<， 120cos 1F PF ≤∠<，即1290F PF ∠<︒；B 正确．C 选项：若(,)A m km ，则(,)B m km --，(m,0)E ，所以直线BE 的斜率为22km km =；C 正确．D 选项：由上可设:()2k PB y x m =-，联立椭圆方程22:163x y C +=，整理得22222(2)2120k x mk x m k +-+-=，若(,)p p P x y ，则2222p mkx m k -=+，即2222p mk x m k =++，322p mk y k =+，所以直线PA 的斜率为32221222mk km k mk k k -+=-+，故AB AP ⊥，即90PAB ∠=︒，故D 错误．故选ABC ． 三、填空题1．点P 是椭圆22:1167x y C +=上的一点，12,F F 是椭圆的两个焦点，且12PF F △的内切圆半径为1．当点P 在第一象限时，它的纵坐标为__________．【试题来源】云南省昆明市第一中学2021届高三第五次复习检测（理） 【答案】73【分析】椭圆的焦点三角形问题，充分利用椭圆的定义，从两个角度表示出12PF F S ，建立关于p y 的关系式求解．【解析】因为128PF PF +=，126F F =，所以()1212121172PF F S PF PF F F =++⨯=；因为12121372PF F p p SF F y y =⋅==，所以73p y =．故答案为73【名师点睛】椭圆上一点与两焦点构成的三角形，称为椭圆的焦点三角形，与焦点三角形有关的计算或证明常利用正弦定理、余弦定理、|PF 1|＋|PF 2|＝2a 等．2．已知椭圆221164x y +=上的一点P 到椭圆一个焦点的距离为6，则点P 到另一个焦点的距离为__________．【试题来源】上海市奉贤区2021届高三上学期一模 【答案】2【解析】利用椭圆定义122PF PF a +=，4a =，可知268PF +=，即22PF =.3．已知F 1，F 2是椭圆C ：22221(0)x y a b a b+=>>的左、右焦点，过左焦点F 1的直线与椭圆C 交于A ，B 两点，且|AF 1|＝3|BF 1|，|AB |＝|BF 2|，则椭圆C 的离心率为__________． 【试题来源】广西北海市北海中学2021届高三12月考试（理）【答案】5【解析】设1BF k =，则13AF k =，24BF k =，由12122BF BF AF AF a +=+=， 得25a k =，22AF k =，在2ABF 中，21cos 4BAF ∠=， 又在12F AF 中，22212(3)(2)(2)1cos 2324k k c F AF k k +-∠==⨯⨯，得2c =故离心率5c e a ==．故答案为54．已知椭圆22221(0)x y a b a b+=>>，点F 为左焦点，点P 为下顶点，平行于FP 的直线l交椭圆于A B ，两点，且A B ，的中点为112M ⎛⎫⎪⎝⎭，，则椭圆的离心率为__________． 【试题来源】吉林省梅河口市第五中学2021届高三上学期第三次月考（文）【答案】2【解析】由题意知(),0F c -，()0,P b -，所以直线FP 的斜率为00()b bc c--=---，设()11,A x y ，()22,B x y ，则2211221x y a b +=①，2222221x y a b+=②，①-②得2222121222x x y y a b --=-，即()()()()1112221222x x y y y y a x x b =-+--+， 因为112M ⎛⎫ ⎪⎝⎭，是A B ，的中点，所以122x x +=，121y y +=，所以()()2112222x y y a b x =---，所以2122122ABy y b k x x a-==--， 因为//AB FE ，所以222b b c a-=-，即22a bc =，所以222b c bc +=，所以b c =，所以22222a b c c =+=，所以c e a ==【名师点睛】本题的关键点是利用点差法设设()11,A x y ，()22,B x y ，则2211221x y a b +=，2222221x y a b+=，两式相减得2222121222x x y y a b --=-，112M ⎛⎫ ⎪⎝⎭，是A B ，的中点，所以 122x x +=，121y y +=，可得2122122ABy y b k x x a-==--，再计算00()FP b b k c c --==---， 利用AB FP k k =结合222a b c =+即可求离心率．5．已知椭圆()222210x y a b a b+=>>的焦距等于其过焦点且与长轴垂直的弦长，则该椭圆的离心率为__________．【试题来源】北京市中国人民大学附属中学2021届高三上学期数学统练5试题【解析】如下图所示，设椭圆()222210x y a b a b+=>>的左、右焦点分别为1F 、2F ，设过椭圆右焦点2F 且垂直于长轴的弦为AB ，则2AB c =，212AF AB c ==，由勾股定理可得1AF ==，由椭圆的定义可得122AF AF a +=2c a +=，所以，该椭圆的离心率为21cea====．6．已知椭圆22221(0)x ya ba b+=>>，左焦点(,0)F c-，右顶点(,0)A a，上顶点(0,)B b，满足0FB AB=，则椭圆的离心率为__________．【试题来源】四川省成都市第七中学2020-2021学年高三期中（文）【解析】由0FB AB=可得，()(),,0c b a b⋅-=，即222ac b a c==-，则210e e+-=，解得e=（舍）7．已知椭圆1C：()222210x ya ba b+=>>和双曲线2C：22221(0,0)x ym nm n-=>>的焦点相同，1F，2F分别为左､右焦点，P是椭圆和双曲线在第一象限的交点，PM x⊥轴，M为垂足，若223OM OF=(O为坐标原点)，则椭圆和双曲线的离心率之积为__________．【试题来源】浙江省台州市六校2020-2021学年高三上学期期中联考【答案】32【分析】设椭圆和双曲线的半焦距为c，根据223OM OF=，得到P的横坐标为23c，设12,PF s PF t==，分别利用椭圆和双曲线的定义求得,s t，然后再利用椭圆和双曲线的第二定义求解．【解析】设椭圆和双曲线的半焦距为c，所以22233OM OF c==，即P的横坐标为23c，设12,PF s PF t==，由椭圆的定义得2s t a+=，由双曲线的定义得2s t m-=，联立解得,s a m t a m=+=-，设椭圆和双曲线的离心率分别为12,e e，由椭圆的第二定义得22223pPF t ca a ax cc c==--，解得123t a e c=-，由双曲线的第二定义得22223p PF t cm m m x c c c==--，解得223t e c m =-，又t a m =-，则223a e c =，1232e e =，所以12232c e e e a ==，故答案为328．已知F 为椭圆22:143x y C +=的左焦点，定点()3,3A --，点P 为椭圆C 上的一个动点，则PA PF +的最大值为__________．【试题来源】湖南省长沙市广益实验中学2020-2021学年高三上学期第一次新高考适应性考试 【答案】9【分析】设椭圆的右焦点为1(1,0)F ，再利用数形结合分析求解． 【解析】设椭圆的右焦点为1(1,0)F ，111=||24||4||49PA PF PA a PF PA PF AF ++-=+-≤+==．【名师点睛】圆锥曲线中的最值问题常用的解题方法有：（1）函数法；（2）数形结合法；（3）导数法；（4）基本不等式法．要根据已知条件，灵活选择方法求解．9．椭圆C ：22221x y a b+=()0a b >>，以原点为圆心，半径为椭圆C 的半焦距的圆恰与椭圆四个项点围成的四边形的四边都相切，则椭圆C 的离心率为__________． 【试题来源】江苏省镇江市2020-2021学年高三上学期期中【分析】由题意画出图形，利用等面积法可得关于a ，b ，c 的等式，结合隐含条件即可求得椭圆的离心率．【解析】如图所示，过点O 作22OM A B ⊥，则290OMA ∠=︒，由题意可得，22221122OB OA A B OM ⋅=⋅，即a b c ⋅=，又由222a b c =+可得，()()2222222a a c a a c c -=+-，整理可得442230a c a c +-=，因为c e a =，所以42310e e -+=，解得2e =，因为01e <<，所以12e =．故答案为12． 10．如图，过原点O 的直线AB 交椭圆C ：22221x y a b+=（a ＞b ＞0）于A ，B 两点，过点A分别作x 轴、AB 的垂线AP ，AQ 分别交椭圆C 于点P ，Q ，连接BQ 交AP 于一点M ，若34AM AP =，则椭圆C 的离心率是__________．【试题来源】重庆市第八中学2021届高三上学期高考适应性月考（三）【分析】设11(,)A x y ，22(,)Q x y ，根据已知条件得B 、P 、M 的坐标，AB AQ ⊥、B ，M ，Q 三点共线，211211y y x x x y -=--以及1212y y x x +=+114y x ，由A ，Q 在椭圆上有2221222212y y b x x a-=--，联立所得方程即可求离心率．【解析】设11(,)A x y ，22(,)Q x y ，则11(,)B x y --，11(,)P x y -，11,2y M x ⎛⎫- ⎪⎝⎭，由AB AQ ⊥，则1212111212111y y y y y xx x x x x y --=-⇒=--- ①， 由B ，M ，Q 三点共线，则BQ BM k k =，即1212y y x x +=+114yx ②．因为2211221x y a b +=，2222221x y a b +=，即22221212220x x y y a b--+=，2221222212y y b x x a -=--③， 将①②代入③得2214b e a =⇒=．11．已知椭圆2222:1(0)x y E a b a b+=>>的左焦点为F ，经过原点O 的直线l 与椭圆E 交于P，Q 两点，若||3||PF QF =，且120PFQ ∠=，则椭圆E 的离心率为__________．【试题来源】四川省眉山市仁寿第二中学2020-2021学年高三上学期第四次诊断（理） 【答案】4【解析】取椭圆的右焦点F '，连接QF '，PF '，由椭圆的对称性，可得四边形PFQF '为平行四边形，则PF QF '=，180********FPF PFQ ∠='=-∠-=，||3||PF QF =3||PF '=，而||||2PF PF a '+=，所以2a PF '=，所以32a PF =， 在PFF '中，2222222914||||58144cos 32332222a a c PF PF FF FPF e a PF PF a +-+-∠===-''''=⨯⨯，解得4e =，故答案为4． 【名师点睛】本题考查求椭圆的离心率，解题关键是找到关于,,a b c 的等量关系．本题中，由椭圆的对称性以及椭圆的定义得到2a PF '=，所以32aPF =，然后在PFF '中，根据余弦定理得到所要求的等量关系．考查了学生的运算求解能力，逻辑推理能力．属于中档题．12．椭圆22221(0)x y a b a b +=>>的左､右焦点分别为12,F F ，椭圆上的点M 满足：1223F MF π∠=且122MF MF →→⋅=-，则b =__________．【试题来源】河北省保定市2021届高三上学期10月摸底考试 【答案】1【分析】先根据数量积运算得124MF MF =，再结合椭圆的定义与余弦定理即可得1b =． 【解析】因为1223F MF π∠=且122MF MF →→⋅=-，所以124MF MF =， 由椭圆的定义得122MF MF a +=，故222121224MF MF MF MF a++= 所以在12F MF △中，由余弦定理得1222212124cos 2MF M F M F c M F F MF =+-∠，代入数据得222144848288a cb ----==，解得1b =．故答案为1． 【名师点睛】解题的关键在于应用定义122MF MF a +=与余弦定理1222212124cos 2MF M F M F c M F F MF =+-∠列方程求解得1b =．13．已知椭圆的方程为222116x y m+=，焦点在x 轴上，m 的取值范围是__________．【试题来源】江西省贵溪市实验中学2021届高三上学期第二次月考数学（三校生）试题。
湖南省长沙市湖南师范大学附属中学2024-2025学年高三上学期月考历史试题+答案
大联考湖南师大附中2025届高三月考试卷（一）历史时量：75分钟满分：100分第I卷选择题（共48分）一、选择题（本大题共16小题，每小题3分，共48分。
在每小题列出的四个选项中，只有一项是符合题意的）1．岭南石峡遗址已发掘64座大小不一的墓葬，出土遗物三千余件。
有出七成套的木作工具石锛和石凿，数百件实战用的石镞、石钺；还有礼器如琮、璧等，玉琮与良渚一带相近。
据此可推断，该遗址A.已出现掌握贵重礼器的祭司阶层B.处于石器时代向国家迈进的阶段C.有直接或间接远距离的商品交换D.农业生产水平得到一定程度发展2．图1、2所示文物均被学界命名为“蜻蜓眼玻璃器”。
据此可知图1古埃及玻璃器（前＋4世纪）图2曾侯乙墓玻璃器（战国）A.社会分工发生了进一步细化B.战国手工制造水平超过古埃及C.玻璃器的生产中心发生转移D.玻璃器是中外文明交流的物证3．《史记·儒林列传》记载，“家人子”（宫侍女）出身的窦太后喜好黄老之学，召辕固生问老子书，辕固生答“家人言耳”太后大怒，命他去刺野猪，幸得景帝帮助才脱困。
这一记载最能印证汉初A.无为而治思想发生动摇B.弃道崇儒思想开始抬头C.社会等级意识仍然强烈D.皇权独尊遭受外戚挑战4．王莽改制，根据周朝办法造大钱，后又相继发行契刀、错刀、宝货等货币，民间仍用五铢钱。
王莽下诏：“敢非井田、挟五铢钱者为惑众，投诸四裔以御魑魅。
”可见当时A.制度变革获得法律保障B.币制由复杂走向简单C.托古改制重视民众基础D.政府的货币信用不足5．《公羊传》记载：“桓何以贵？母贵也。
母贵则子何以贵？子以母贵，母以子贵。
”然而汉武帝却在立幼子为太子后杀其生母，北魏时期道武帝将子贵母死立为定制。
这一转变的目的在于A.提高三纲五常的地位B.促进华夏认同C.推动少数民族封建化D.加强集权统治6．唐太宗审查《氏族志》时，认为山东崔氏“世代衰微，全无冠盖”，不配第一等。
他指示“不须论数世以前，止取今日官爵高下作等级”，新修订的《氏族志》以皇族为首，外戚次之，崔干被降为第三等。
湖南师范大学附属中学2024-2025学年高三上学期月考卷(三)历史答案(附中高三3次)
湖南师大附中2025届高三月考试卷(三)历史参考答案一、选择题(本大题共16小题，每小题3分，共48分)题号12345678910111213141516答案C D B B D A A A B D C A C B C B1. C【解析】题中显示夏商时期早期金属矿、盐池的分布情况，政治中心在黄河中游，金属矿多分布于长江流域。
矿藏分布跨越南北方，这在一定程度上能够表明南北方之间可能因为资源的开发和利用存在着经济方面的联系，C项“跨区域经济联系已经出现”较为合理。
仅从图中所给的矿藏分布情况，无法直接得出“国家对矿藏实现直接控制”的结论，没有相关明确证据支持，A项错误。
从图中可以看到黄河中游有一定的矿藏分布，不能得出资源相对不足的结论，B项错误。
图中只是展示了矿藏的分布，并没有直接体现出手工业发达程度的比较，不能仅依据矿藏分布就得出“长江流域手工业更发达”的结论，D项错误。
2. D【解析】题干中提到秦国“圆塞险”而“天材之利多”，这只是自然条件方面的优势，但不是最主要因素；“百姓朴”且“甚畏有司而顺”说明百姓朴实且顺从管理；都邑官府“恭俭、敦敬、衷信”，士大夫“无有私事”，这些都体现了秦国在国家治理方面，官员清正廉洁、百姓顺从，整个国家治理良好。
A项自然条件优越只是一方面；B项人民朴实温和也只是一个方面；C项官员吏治清明也只是国家治理的一部分。
只有D项国家治理良好能够全面概括题干中所体现的泰国的优势。
3. B【解析】根据材料，韩愈认为：如果佛有灵，能给人带来灾祸，坚守儒道的君子只要信奉天命，就不用惧怕。
根据所学知识可知，韩愈提倡复兴儒学，他用天命观反对佛教的因果轮回，以巩固儒学地位，故B项正确。
A、C两项均为手段而非目的，故排除；材料中的“道”为儒道，而非道家思想，故D项错误。
4. B【解析】辽朝以契丹为国号，体现其对游牧民族传统和文化的重视；以辽为国号，体现其吸收汉文化和制度的意图；实行双重国号是要在保持游牧民族的传统和吸收汉文化中寻求平衡。
湖南省长沙市长郡中学2020-2021学年高三上学期月考(三)数学试题(含解析)
B
ABFP
轴的垂线交抛物线于点，记
P
，则的值为（
）
2
4
8
A.
B.
C.6
D.
二、多项选择题(本题共小题，每小题分，共分)
4520
9.针对当下的“抖音热”，某校团委对“学生性别和喜欢抖音是否有关”作了一次调查，其中被调查的男
4
3
女生人数相同，男生喜欢抖音的人数占男生人数的，女生喜欢抖音的人数占女生人数的，若有
10
当进行到第次时，即停止抽球；记停止抽球时已抽球总次数为X，求X的数学期望.(精确到小数点后1
位)
9
4
9
4
11
k1
k1
k
k
9
10
1.80
2.05
，
参考数据：
，
10
5
10
5
k2
k2
11
9
4
11
9
4
k
k
k
k
9
10
10.79
13.32.
k
k
，
10
5
10
5
k2
k2
一、选择题(本题共小题，每题分，共分)
8540
n
2a12a13
n
a
n
n
n
C,D
19.在如图所示的圆柱OO
中，为圆O的直径，
AB
是AB
的两个三等分点，，，都是圆柱
EAFCGB
1
1
2
OO
1
的母线．
2
的
FO//
（1）求证：
平面ADE；
1
（2）设BC=1，已知直线
湖南省长沙市长郡中学2024届高三下学期一模历史试题(解析版)
A.商业发展推动阿拉伯的社会变革B.麦加地区区国际商业易迅速发展
C.南北阿拉伯人进行了深度的融合D.各部落更大规模联合的发展趋势
13.某学派认为，“宗教必须被当作单纯的迷信抛弃掉，原有的政治形式必须被当作……压迫性的存在消灭掉，人的良善本性必须成为主导性力量”。要实现这一切，他们寻求的最佳途径是（ ）
A.暴力革命B.重塑信仰C.诉诸理性D.实行共和
【答案】C
【解析】
【详解】本题是单类型单项选择题。依据材料主题干的设问词可知本题是正向题。依据材料时间信息可知准确时空是：17-18世纪（世界）。据材料及所学知识可知，这个学派是启蒙运动时期出现的“百科全书派”，他们认为“宗教必须被当作单纯的迷信抛弃掉，原有的政治形式必须被当作……压迫性的存在消灭掉，人的良善本性必须成为主导性力量”而要实现这一切，就要诉诸理性，C项正确；材料并未提及暴力革命，排除A项；材料要抛弃宗教，而不是重塑信仰，排除B项；材料也没有提到实现共和的内容，排除D项。故选C项。
8.这些言论（ ）
A.完全突破了天朝上国的观念B.体现了传统文化和西学结合
C.顺应了近代社会发展的潮流D.揭开了近代学习西方的序幕
【答案】C
【解析】
【详解】本题是单类型单项选择题。据本题主题干的设问词，可知这是推断题。据本题时间信息可知准确时空是：晚清（中国）。根据材料可知，早期维新派人物在西方文化的冲击下看到了西方技术和制度的先进性，主张向西方学习，顺应近代社会发展潮流，C项正确；完全突破说法绝对，不符合史实，排除A项；材料内容未体现传统文化和西学的具体结合，涉及到的是向西方学习，排除B项；洋务运动开启向西方学习的历程，是中国近代化的开端，排除D项。故选C项。
2024-2025学年湖南省长沙市长郡中学大联考高三(上)月考数学试卷(二)(含答案)
2024-2025学年湖南省长沙市长郡中学大联考高三（上）月考数学试卷（二）一、单选题：本题共8小题，每小题5分，共40分。
在每小题给出的选项中，只有一项是符合题目要求的。
1.已知集合A ={x||x|⩽2}，B ={t|1⩽2t ⩽8(t ∈Z)}，则A ∩B =( )A. [−1,3]B. {0,1}C. [0,2]D. {0,1,2}2.已知复数z 满足|z−i|=1，则|z|的取值范围是( )A. [0,1]B. [0,1)C. [0,2)D. [0,2]3.已知p ：f(x)=ln(21−x +a)(−1<x <1)是奇函数，q ：a =−1，则p 是q 成立的( )A. 充要条件 B. 充分不必要条件C. 必要不充分条件D. 既不充分也不必要条件4.若锐角α满足sinα−cosα=55，则sin (2α+π2)=( )A. 45B. −35 C. −35或35D. −45或455.某大学在校学生中，理科生多于文科生，女生多于男生，则下述关于该大学在校学生的结论中，一定成立的是( )A. 理科男生多于文科女生B. 文科女生多于文科男生C. 理科女生多于文科男生D. 理科女生多于理科男生6.如图，某车间生产一种圆台形零件，其下底面的直径为4cm ，上底面的直径为8cm ，高为4cm ，已知点P 是上底面圆周上不与直径AB 端点重合的一点，且AP =BP ，O 为上底面圆的圆心，则OP 与平面ABC 所成的角的正切值为( )A. 2B. 12C.5D.557.在平面直角坐标系xOy 中，已知直线l ：y =kx +12与圆C ：x 2+y 2=1交于A ，B 两点，则△AOB 的面积的最大值为( )A. 1B. 12C.32D.348.设函数f(x)=(x 2+ax +b)lnx ，若f(x)≥0，则a 的最小值为( )A. −2B. −1C. 2D. 1二、多选题：本题共3小题，共18分。
2023届湖南省长沙市长郡中学高三上学期月考(六)历史
长郡中学2023届高三月考试卷（六）历史得分：本试题卷分选择题和非选择题两部分，共8页。
时量75分钟，满分100分。
第Ⅰ卷选择题（共48分）一、选择题（本大题共16小题，每小题3分，共48分。
在每小题列出的四个选项中，只有一项是符合题意的）★1.考古发现，在浙江的反山、瑶山、汇观山等良渚文化遗址墓地，大都建有大型墓台，具有宽大的墓穴，随葬大批制作精美的玉礼器。
在徐步桥、千金角、平邱墩、吴家埠、庙前等良渚文化遗址的墓地中，墓穴狭小，随葬的只是简陋的陶器及小件的装饰用玉饰件。
这些遗存可印证，良渚文化时期A.中原文化得到扩展B.阶级分化较为明显C.神灵崇拜开始兴起D.贵族等级秩序确立年，湖北睡虎地出土的《法律问答》中记录了秦朝的一个判例：如果丈夫偷钱一千，妻子藏匿三百，妻子应该怎样定罪？答：如果妻子知道丈夫偷钱而藏匿，当以偷钱三百论处，如果不知道，就不予追究。
这一判例说明，秦律A.量刑较为宽松B.具有形式主义特征C.借鉴儒家思想D.蕴含一定理性因素3.东晋时期，凉州僧人竺佛念翻译的《长阿含经》中有“父母所为，恭顺不逆”“父母正令，不敢违背”这样的句子。
但查阅《长阿含经》的巴利文原版，发现这些句子是译者自己添加的，这一现象说明A.传统的价值观逐渐变异B.佛教已融入中国文化C.佛教主动适应社会需要D.三教合流的趋势出现4.柳宗元在他的文章里说，天地虽大，但其实本质和草木是一样的，并无主观意识，是不能赏善罚恶的，雷霆霜雪不过是自然现象。
所以施政应该顺应人事，而不应该固执于虚无的天命。
据此可知，柳宗元A.摒弃了儒家旧有的天命观B.继承了孔、孟的人文精神C.回应了道家对儒学的挑战D.发展了中国传统唯物思想5.斡脱是蒙古语合伙人的音译，从成吉思汗开始，蒙古贵族就提供本金，委托中亚商人为斡脱，经营商业，发放高利贷。
元朝建立后，蒙古贵族的斡脱不断发展，官方还成立斡脱总管府管理斡脱事务，斡脱贸易还发展到远洋海外。
据此可知，斡脱贸易A.为早期全球化注入雄厚资金B.适应了元代社会发展的需要C.突破了传统的重农抑商政策D.不利于元代商业的健康发展6.根据明代的档案记录，明朝中后期，地处江南，商业高度繁荣的浙江湖州某县，其官方户口登记人口，在三十年的时间里，减少了二成。
湖南省长沙市雅礼中学2022-2023学年高三上学期12月月考历史试题含答案
雅礼中学2023届高三月考试卷(四)历史本试题卷分选择题和非选择题两部分，共8页。
时量75分钟，满分100分。
第Ⅰ卷选择题(共48分)一、选择题(本题共16小题，每小题3分，共48分。
每小题只有一个选项符合题目要求)1．墨子在《法仪》中提出“法不仁，不可以为法。
故父母、学、君三者，莫可以为治法。
然则奚以为治法而可？”“莫若法天。
天之行广而无私，其施厚而不德，其明久而不衰，故圣王法之。
”墨子的这一主张A．重视个人的道德修养B．旨在维护君主专制秩序C．突出法的客观公正性D．强调天命主宰人们行为2．如表是开皇年间隋朝政府前后两次下诏的情况。
这反映出隋朝A.C．社会矛盾有所缓和D．政策制定较为务实灵活3．有学者指出，两宋都亡于国内的少数民族，但在某种程度上也体现了宋朝政治制度的“成功”，这与唐末以来的战乱摧毁了世家大族密切相关。
这里的“政治制度”是指A．沿用唐朝藩镇以加强地方控制B．多次推行变法加重财政负担C．削弱地方实力以加强中央集权D．实行平民政治提升皇权专制4．黄宗羲说：“故治之以本，使小民吉凶，一循于礼……治之以末，倡优有禁，酒食有禁，除布帛外皆有禁……此古圣王崇本抑末之道。
世儒不察，以工商为末，妄议抑之。
夫工固圣王之所欲来，商又使其愿出于途者，盖皆本也。
”这一思想A．体现了资本主义萌芽时代的要求B．推动了清代前期经济的转型C．打破了重农抑商的传统经济政策D．隐含对君主专制制度的批判5．轮船招商局成立后，承运漕粮成为招商局发展的重要条件。
为抢夺这笔生意，1875年，美国旗昌轮船公司表示，情愿将漕粮运费从招商局的每担6钱左右降至1钱。
《申报》惊呼：“此事惊闻之下，未免太觉其减价。
”因李鸿章和招商局的坚决抵制，旗昌公司才未能如愿。
这反映了洋务派创办的民用企业A．受到中外反动势力双重压迫B．成本太高经营十分艰难C．一定程度上抵制了西方列强的经济侵略D．官督商办是其主要形式6．1941年，晋冀鲁豫边区进行了参议员选举工作，最后选出由共产党员为参议长，2位国民党员为副议长，共计参议员197名的临时参议会，其中共产党员参议员46人。
湖南省炎德●英才大联考长郡中学2024-2025学年高三上学期月考地理试卷(含答案)
A.冷锋B.暖锋C.气旋D.反气旋
12.导致该地一天内150米高度风向发生改变是因为（）
A.冷气团的势力强大B.地表冷热变化
C.气压中心位置变化D.植被性质改变
奥里诺科河发源于圭亚那高原，下游流经奥里诺科平原，每年汛期，下游会有干流倒灌支流的现象。干流下游在涨水和退水期间，均会出现含沙量的峰值，下图为奥里诺科河流域示意图和奥里诺科平原上的甲城气候资料。据此完成下面小题。
（1）说明1996年德国M集团在上海市建立工厂对其企业发展的主要意义。
（2）在2017年部分下游客户转移至东南亚的背景下，M集团仍然在威海市投资建设新厂。指出M集团做出该决定看重的“中国优势”。
（3）说明M集团选择在威海市建立在华第三家工厂的合理性。
18.阅读图文材料，完成下列要求。
土壤温度、积雪、植被覆盖影响冻土的最大冻结深度、冻结时长。受地形因素影响，山区往往发生逆温现象。伊犁河谷逆温现象在海拔800m-1600m之间，非常典型。6月的伊犁河谷，沉浸在薰衣草最大紫色花海中，8月人们就可早早品尝种植在海拔800m-1200m山坡的“糖心”苹果，满山的绿草中，牛羊成群。下图为伊犁河谷地的位置及其年降水量和土壤冻结最大深度随海拔变化情况示意图。
①商业活动活跃②房价基数较大③公共交通密度较大④环境质量更好
A.①②B.①④C.②③D.③④
6.该统计低估了地铁对住宅价格的影响，主要是因为忽略了（ ）
A.地铁站周边噪声及震动的影响B.地铁规划期到建设期的房价涨幅
C.地铁开通后对房地产的长期效应D.地铁对公共设施带动的正面影响
太原市地处山西省中部，地势北高南低。受山地—平原的共同作用，城区实测风表现出明显的山谷风特征，加之当地较明显的热岛环流，对污染物的扩散、输送产生直接影响。如图示意太原市城区地形特征及某月尖草坪（北部城区）和小店（南部城区）2个气象观测站实测风频（单位：次）日变化统计。完成下面小题。
江西省萍乡实验学校暨长郡十八校联考2024-2025学年高三上学期月考四历史试题
大联考萍乡实验学校2025届高三月考试卷（四）暨长郡十八校联考考前演练历史高三历史备课组组稿注意事项：1.答卷前，考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上。
2.回答选择题，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动，用橡皮擦干净后，再选涂其他答案标号。
回答非选择题，将答案写在答题卡上。
试卷上无效。
3.考试结束后，将本试卷和答题卡一并交回。
一、选择题(本大题共16小题，每小题3分，共48分。
在每小题给出的四个选项中，只有一项是符合题目要求的) 1．下图是我国主要古人类遗址分布图，其中的云南元谋人、陕西蓝田人、湖北郧县人等古人类遗址距今约100万年左右。
由此可推知，我国（）A．早期人类主要分布在黄河流域B．人类活动的历史较为久远C．南稻北粟的农业作物格局形成D．先民渔猎和采集活动频繁2．秦朝规定，官员的奏折需由专人传递至中央，并且在书写格式、内容规范等方面有严格要求。
若有紧急军情，则通过特殊渠道快速上奏。
这一制度主要是为了（）A．规范官员行为，防止贪污腐败B．保证信息传达效率和中央集权C．减轻皇帝处理日常政务的负担D．促进不同地区间经济文化交流3．宋代，典卖田宅时须订立合同契，须经官“输钱印契”，此合同契才成为“赤契”。
此后，“贫富无定势，田宅无定主”成为普遍现象。
这反映了宋代（）A．适当放松对社会的控制B．限制了土地买卖的数量C．开始重视交易税的征收D．强化了地方政府的权力4．据《济州臧氏种蜀黍记》载，乾隆年间，“亩得烟叶五百斤，斤得钱十五文。
”至道光年间，“济州种烟草……大约膏腴尽为烟所占，而五谷反皆瘠土。
人之骛利，其忘本一至此乎！”这说明（）A．传统自然经济正在解体B．工商皆本思想逐渐成为潮流C．政府主导外来作物推广D．市场价值影响人们经济活动5．1867年《天津条约》期满，清政府提出修改条约的要求；1902年，英国在清政府法律“皆臻妥善”下与清政府达成“即允放弃治外法权”的协议；次年，中美、中日通商续约也达成了同样的协议。
湖南省长沙市长郡中学2024-2025学年高一上学期期中考试历史试题(含答案)
长郡中学2024-2025学年高一上学期期中考试历史时量：75分钟满分：100分第Ⅰ卷选择题（共48分）一、选择题（本大题共16小题，每小题3分，共48分。
每小题所列的四个选项中，只有一项符合题目要求）1．据现有的考古资料所知，中华民族的祖先分别在多个地区创造了原始文化，这些早期先民的文化区，时间上有先后，规模上有大小，水平上有高低，但是它们各有特点，自成系统，既有个性，又有共性。
这体现了中华文明的起源（）A．以中原地区为主，逐渐向外辐射B．分布广泛，多元一体C．在诸多区域同时出现，各自发展D．不断趋向文明的历史进程2．中国新石器时代的文化遗存星罗棋布，多姿多彩。
以下新石器时代文化遗存属于中原文化区的是（）A．仰韶文化B．良渚文化C．龙山文化D．红山文化3．李时珍曰：“古者以粟为黍、稷、粱、秫之总称。
”世界上最早种植“粟”的是（）A．北京人B．元谋人C．半坡居民D．河姆渡居民4．殷商时期，盘庚提出“罔不惟民之承保”“式敷民德”；西周时期，文王提倡“怀保小民，惠鲜鳏寡”“用咸和万民”。
这说明，商周时期（）A．统治者推行“仁政”B．儒家民本思想受到重视C．宗法观念日益强化D．养济保民思想已经出现5．《史记》记述周幽王“烽火戏诸侯”之事时，基本以《国语·郑语》为其叙事依据，但并未采信《国语》中褒姒是祸害周室、流毒三代的“龙漦妖子”的说法，也未采纳《诗经》中“赫赫宗周，褒姒灭之”“乱匪降自天，生自妇人”的评论，反而认为西周灭亡主要是周幽王的责任。
司马迁的这一看法反映了（）A．汉代儒家以人为本的价值观B．历史认识与现实的有机联系C．开放包容的大一统时代气象D．司马迁对周幽王抱有偏见6．江南原本被中原诸国视为蛮荒的“夷人”聚居之地，但公元前544年，吴国公子季札出使中原诸国，对于中原各国贵族视为“文明”象征的乐舞与诗歌，皆能一一点评，得其精髓；对于各国政治现状，也能作出准确的研判。
这反映了（）A．中华文明多元起源B．江南地区融合中原文化C．中原诸国傲慢无礼D．江南地区开始超越北方7．“乐与君子听之，废君子听治”“与贱人听之，废贱人之从事”表达了某位思想家对听乐曲行为的批评态度。
2024-2025学年湖南省长沙市雅礼中学高三上学期月考(二)历史试题及答案
雅礼中学2025届高三月考试卷（二）历史本试题卷分选择题和非选择题两部分，共8页。
时量75分钟，满分100分。
第Ⅰ卷选择题一、选择题（本题共16小题，每小题3分，共48分。
每小题只有一个选项符合题目要求）1. 陕西神木石峁遗址是龙山文化晚期重要遗址，考古发掘证实了其城址由皇城台、内城和规模宏大的外城等三重城垣构成，并出土了成排房屋建筑基址，高等级贵族墓葬群以及数以万计的玉器、陶器等。
据此可知（）A. 神权在石峁文化中占据主导地位B. 石峁人的手工业技艺十分精湛C. 中原为核心的文明格局已经形成D. 该遗址已具备邦国都邑的特征2. “出奔”在《春秋释例》中解释为“奔者，迫窘而去，逃死四邻，不以礼出也”。
春秋时期，主要诸侯国接受贵族出奔者次数为：鲁国37人次，楚国33人次，晋国38人次，宋国20人次，郑国19人次，齐国36人次，卫国18人次。
这反映出当时（）A. 统治秩序的变动B. 思想文化的碰撞C. 礼乐制度的崩溃D. 新兴阶层的壮大3. 有学者指出：“东汉初期既然在洛阳立高庙，合祭西汉五帝，作为刘氏后裔，将世祖及以后历代皇帝神主纳于高庙中序昭穆、享祭祀，属于合乎情理的举措。
但汉明帝为光武帝单独立世祖庙，随后诸帝又皆立神主于世祖庙，却似乎隐隐含有与西汉帝系截然有别的蕴意，此举被后世视为违礼之举而加以掊击。
”这表明（）A. 宗法观念已被摒弃B. 儒学影响政治伦理C皇权传承缺乏规范 D. 祖先崇拜源远流长.4. 唐开元年间，关中农业的收成非常好。
于是，开元二十五年（737）敕曰：“宜令户部郎中郑防，殿中侍御史郑章，于京畿据时价外，每斗加三两钱，和籴粟三四百万石，所在贮掌。
江淮漕运，固甚烦劳，务在安人，宜令休息。
其江淮间今年所运租停。
”据此可知，唐朝（）A. 漕运贸易退出历史舞台B. 政府对物资流通进行理性干预C. 经济重心南移趋势显现D. 官民交易具有强制和掠夺色彩5. 如表为文献中有关宋代史事的部分记载。
湖南省长沙市长郡中学2023-2024学年高三上学期月考(四)英语
大联考长郡中学2024届高三月考试卷(四)英语注意事项:1 . 答卷前, 考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上。
2 . 回答选择题时, 选出每小题答案后, 用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动, 用橡皮擦干净后, 再选涂其他答案标号。
回答非选择题时, 将答案写在答题卡上, 写在本试卷上无效。
3 . 考试结束后, 将本试卷和答题卡一并交回。
第一部分听力(共两节, 满分30 分)第一节 (共5 小题; 每小题1 . 5 分, 满分7 . 5 分)听下面5 段对话。
每段对话后有一个小题, 从题中所给的 A、B、C 三个选项中选出最佳选项。
听完每段对话后, 你都有10 秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
例: How much is the shirt?A ·19 . 15 .B ·9 . 18 .C ·9 . 15 .答案是C。
1 . who got the toy car at last?A. Lily.B. Frank.C. Eddie.2 . where does the conversation probably take place?A. At an airport.B. In a hotel.C. In a library.3 . why does the woman want to return the trousers?A. They are uncomfortable.B. Their pockets are too big ·C. They are too expensive.4 . How does the man feel about the problem?A. He is angry.B. He is understanding ·C. He is confused.5 . what's the man doing now?A. Having a swim.B. Going shopping ·C. Eating some ice cream .第二节 (共15 小题;每小题1 . 5 分, 满分22 . 5 分)听下面5 段对话或独白。