(完整版)用字母表示数练习题一
五年级数学上册《用字母表示数》练习题(一)

6、甲数是x,比乙数少y,甲乙两数之和是〔〕,两数之差是〔 〕
二、依据运算定律填空。
1、a+18=□+□ a×15=□×□
2、m×2.5×0.4=□×〔□×□〕
3、〔a+b〕×C=□×□+□×□
4、m-a-b=□-〔□+□〕
三、省略乘号写出下面各式。
a×12= b×b=a×b= x×y×7=
5×x= 2×c×c= 7x×5= 2×a×b=
四、判别。〔对的打〝√〞,错的打〝×〞。〕
1、5+x=5x〔 〕 2、x+x=x2〔 〕
3、a×3=3a〔〕4、y2式,在我国有悠久的历史。但随着素质教育的展开,融会贯串被作为一种僵化的、阻碍先生才干开展的教学方式,渐渐为人们所摒弃;而另一方面,教员们又为提高先生的语文素养煞费苦心。其实,只需运用妥当,〝融会贯串〞与提高先生素质并不矛盾。相反,它恰是提高先生语文水平的重要前提和基础。
五年级数学上册《用字母表示数》练习题(一)
用字母表示数〔一〕
一、填空:
1、学校有图书4000本,又买来a本,如今一共有〔 〕本。
2、学校有先生a人,其中男生b人,女生有〔〕人。
3、李徒弟每小时消费x个零件,10小时消费〔〕个。
4、食堂买来大米400千克,每天吃a千克,吃了几天后还剩b千克,已吃了〔 〕天。
7、5×a×b=5ab〔 〕 8、a×7+a=8a〔 〕
其实,任何一门学科都离不开融会贯串,关键是记忆有技巧,〝死记〞之后会〝活用〞。不记住那些基础知识,怎样会向高层次进军?尤其是语文学科涉猎的范围很广,要真正提高先生的写作水平,单靠剖析文章的写作技巧是远远不够的,必需从基础知识抓起,每天挤一点时间让先生〝死记〞名篇佳句、名言警句,以及丰厚的词语、新颖的资料等。这样,就会在有限的时间、空间里给先生的脑海里注入有限的内容。日积月累,集腋成裘,从而收到水滴石穿,绳锯木断的成效。5、2a+3b=5ab〔 〕6、2a+3a=5a〔 〕
用字母表示数(原卷版)

第07讲 用字母表示数1. 能用字母表示以前学过的运算律、计算公式以及一些简单问题中的数量关系和变化规律;2.能解释一些简单代数式的实际背景或几何意义,发展符号感;3.能在做题时注意到书写代数式的注意事项;4.在具体情境中能求出代数式的值,并解释它的实际意义.知识点 代数式1.定义:用运算符号(加、减、乘、除、乘方、开方等)把数或表示数的字母连接而成的式子叫做代数式。
单独的一个数或一个字母也是代数式。
注意:①代数式中除了含有数、字母和运算符号外,还可以有括号;②代数式中不含有“=、>、<、≠”等符号。
等式和不等式都不是代数式,但等号和不等号两边的式子一般都是代数式;③代数式中的字母所表示的数必须要使这个代数式有意义,是实际问题的要符合实际问题的意义。
2.代数式的书写格式:①代数式中出现乘号,通常省略不写,如vt ;②数字与字母相乘时,数字应写在字母前面,如4a ; ③带分数与字母相乘时,应先把带分数化成假分数,如a 312⨯应写作a 37; ④数字与数字相乘,一般仍用“×”号,即“×”号不省略;⑤在代数式中出现除法运算时,一般写成分数的形式,如4÷(a-4)应写作4a 4-;注意:分数线具有“÷”号和括号的双重作用。
⑥在表示和(或)差的代数式后有单位名称的,则必须把代数式括起来,再将单位名称写在式子的后面,如)(22b a 平方米。
考点1:代数式的书写规范 例1.(2022秋•朝阳区期末)下列各式中,符合单项式书写要求的是( )A .a ×b 2B .﹣1abC .D .【变式1-1】(2022秋•射洪市期末)下列代数式中符合书写要求的是( )A .3abB .a ÷bC .(50﹣a )元D .﹣1ab【变式1-2】(2022秋•宛城区期末)下列式子中,符合代数式书写形式的是( )A .2xy 2B .ba 2c •5C .D .﹣a ×b ÷c【变式1-3】(2022秋•江津区期末)下列代数式书写规范的是( )A .B .5÷hC .9+x 千克D .3y考点2:代数式的意义 例2.(2022秋•东平县校级期末)若x 表示某件物品的原价,则式子(1﹣10%)x 表示的意义是( )A .该物品价格上涨10%时上涨的价格B .该物品价格下降10%时下降的价格C .该物品价格上涨10%后的售价D .该物品价格下降10%后的售价【变式2-1】(2022秋•邢台期末)代数式3(y ﹣3)的正确含义是( )A .3乘y 减3B .y 的3倍减去3C .y 与3的差的3倍D .3与y 的积减去3 【变式2-2】(2023•开封一模)如果水位升高3m 记作“+3m ”,那么“﹣3m ”表示的意义是 .【变式2-3】(2022秋•宛城区期中)我们知道,用字母表示的代数式是具有一般意义的,请仔细分析下列赋予4a 实际意义的例子,其中错误的是( )A .若葡萄的价格是4元/千克,则4a 表示买a 千克该种葡萄的金额B .若a 表示一个正方形的边长,则4a 表示这个正方形的周长C .汽车行驶逨度是a 千米/小时,则4a 表示这辆汽车行驶4小时的路程D.若一个两位数的十位数字是4,个位数字a则表示这个两位数是4a考点3:列代数式(数字问题)例3.(2023•古冶区二模)某两位数,十位数字为a,个位数字为b,将其十位上的数与个位上的数交换位置,得到一个新的两位数,新两位数用代数式表示为()A.ba B.a+b C.10a+b D.10b+a【变式3-1】(2022秋•邹平市期末)一个两位数,它的个位数字是x,十位数字是y,那么这个两位数是()A.yx B.x+10y C.10x+y D.x+y【变式3-2】(2022秋•滨城区校级期末)已知a是两位数,b是一位数,把b接在a的后面,就成了一个三位数,这个三位数可以表示为()A.a+b B.100b+a C.100a+b D.10a+b【变式3-3】(2022秋•文登区期末)一个两位数,个位数字是a,十位数字比个位数字小2,这个两位数可表示为()A.11a﹣2 B.11a+2 C.11a+20 D.11a﹣20考点4:列代数式(和倍差问题)例4.(2023•濉溪县模拟)某服装店新上一款运动服,第一天销售了m件,第二天的销售量是第一天的两倍少3件,第三天比第二天多销售5件,则第三天的销售量是()A.(m+2)件B.(2m﹣2)件C.(2m+2)件D.(2m+8)件【变式4-1】(2022秋•凤山县期末)用式子表示:a的3倍与5的和.下列表达式正确的是()A.3a﹣5 B.3(a﹣5)C.3a+5 D.3(a+5)【变式4-2】(2022秋•思明区校级期末)为落实“双减”政策,某校利用课后服务开展了主题为“书香满校园”的读书活动.现需购买甲、乙两种读本共100本供学生阅读,其中甲种读本的价格为10元/本,乙种读本的价格为8元/本,若购买甲种读本x本,则购买乙种读本的费用为()A.8x元B.8(100﹣x)元C.10(100﹣x)元D.(100﹣8x)元【变式4-3】(2022秋•湘潭县期末)为向党的二十大献礼,某校成功举办了“经典诵读”比赛,其中参加比赛的男同学有a人,女同学比男同学的少24人,则参加“经典诵读”比赛的学生一共有()A.人B.人C.人D.人考点5:列代数式(百分率问题)例5.(2023•贵池区一模)某产品的成本价为a元,销售价比成本价增加了14%,现因库存积压,按销售价的八折出售,那么该产品的实际售价为()A.(1+14%)(1+0.8)a元B.0.8(1+14%)a元C.(1+14%)(1﹣0.8)a元D.(1+14%+0.8)a元【变式5-1】(2023•福田区模拟)一件商品售价x元,利润率为a%(a>0),则这种商品每件的成本是()元.A.(1+a%)x B.(1﹣a%)x C.D.【变式5-2】(2022秋•青县期末)某种商品的价格是a元,降价10%后又降价10%,则降价后这种商品的价格是()A.a元B.0.80a元C.0.81a元D.0.96a元【变式5-3】(2023•瓯海区二模)某企业今年1月份产值为a万元,2月份比1月份减少了10%,3月份比2月份增加了15%,则3月份的产值是()A.(a﹣10%)(a+15%)万元B.a(1﹣90%)(1+85%)万元C.a(1﹣10%)(1+15%)万元D.a(1﹣10%+15%)万元考点6:列代数式(几何图形问题)例6.(2022秋•微山县期末)如图1,将一个边长为a的正方形纸片剪去两个矩形,得到一个“S”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为()A.2a﹣2b B.2a﹣4b C.4a﹣8b D.4a﹣9b【变式6-1】(2023•安庆一模)一个矩形的周长为50,若矩形的一边长用字母x表示,则此矩形的面积为()A.x(25﹣x)B.x(50﹣x)C.x(50﹣2x)D.x(25+x)【变式6-2】(2022秋•东港市期末)如图,阴影部分的周长为()A.3.5x+5y B.3.5x+6y C.4x+5y D.4x+6y【变式6-3】(2022秋•防城港期末)如图,一块直径为a+b的圆形钢板,从中挖去直径分别为a和b的两个圆,则剩下的钢板的面积为()A.2abπB.2a2b2πC.D.考点7:代数式-整体法代入求值例7.(2022秋•江北区校级期末)若整式2x2+5x的值为8,那么整式6x2+15x﹣10的值是.【变式7-1】(2022秋•兴化市校级期末)若2x﹣y=﹣3,则2﹣6x+3y的值是.【变式7-2】(2022秋•新乡县校级期末)已知a﹣2b的值是﹣4,则1﹣2a+4b的值等于.【变式7-3】(2022秋•于洪区期末)若2x﹣y=3,则代数式4x﹣2y+4的值是.【变式7-4】(2022秋•鼓楼区校级期末)整式x2﹣3x的值是4,则3x2﹣9x+8的值是.考点8:规律题例8.(2022秋•安庆期末)一只小球落在数轴上的某点P0处,第一次从P0处向右跳1个单位到P1处,第二次从P1向左跳2个单位到P2处,第三次从P2向右跳3个单位到P3处,第四次从P3向左跳4个单位到P4处…,若小球按以上规律跳了(2n+3)次时,它落在数轴上的点P2n+3处所表示的数恰好是n﹣3,则这只小球的初始位置点P0所表示的数是()A.﹣4 B.﹣5 C.n+6 D.n+3【变式8-1】(2022•云岩区模拟)“数学是将科学现象升华到科学本质认识的重要工具”,比如在化学中,乙烯的化学式是C2H4,丙烯的化学式是C3H6…,碳原子和氢原子的数目满足一定数学规律.设碳原子的数目为n(n为正整数,且n≥2),则这类烯的化学式可用式子来表示.【变式8-2】(2023•孟村县二模)如图,学校准备新建一个长度为L的读书长廊,并准备用若干块带有花纹和没有花纹的两种规格大小相同的正方形地面砖搭配在一起,按图中所示的规律拼成图案铺满长廊,已知每个小正方形地面砖的边长均为0.5m.(1)按图示规律,第一图案的长度L1=m;第二个图案的长度L2=m;(2)用代数式表示带有花纹的地面砖块数n与走廊的长度L n(m)之间的关系.1.(2022•长沙)为落实“双减”政策,某校利用课后服务开展了主题为“书香满校园”的读书活动.现需购买甲,乙两种读本共100本供学生阅读,其中甲种读本的单价为10元/本,乙种读本的单价为8元/本,设购买甲种读本x本,则购买乙种读本的费用为()A.8x元B.10(100﹣x)元C.8(100﹣x)元D.(100﹣8x)元2.(2022•杭州)某体育比赛的门票分A票和B票两种,A票每张x元,B票每张y元.已知10张A票的总价与19张B票的总价相差320元,则()A.||=320 B.||=320C.|10x﹣19y|=320 D.|19x﹣10y|=3203.(2021•青海)一个两位数,它的十位数字是x,个位数字是y,那么这个两位数是()A.x+y B.10xy C.10(x+y)D.10x+y4.(2021•温州)某地居民生活用水收费标准:每月用水量不超过17立方米,每立方米a元;超过部分每立方米(a+1.2)元.该地区某用户上月用水量为20立方米,则应缴水费为()A.20a元B.(20a+24)元C.(17a+3.6)元D.(20a+3.6)元5.(2023•萧山区一模)植树节,某校需完成一定的植树任务,其中九年级共种了任务数的一半,八年级种了剩下任务数的,七年级共种了a棵树苗.则该校植树的任务数为()棵.A.6a B.5a C.4a D.3a6.(2022•邵阳)已知x2﹣3x+1=0,则3x2﹣9x+5=.7.(2022•吉林)篮球队要购买10个篮球,每个篮球m元,一共需要元.(用含m的代数式表示)1.(2022秋•长安区校级期末)下列各式中,不是代数式的是()A.﹣3 B.C.5x﹣1=9 D.x2﹣4x2.(2022秋•乐亭县期末)下列代数式,书写不规范的是()A.a3B.3x+1 C.D.1×m3.(2022秋•广平县期末)下列用语言叙述式子:﹣4表示的数量关系,表述不正确的是()A.比x的倒数小4的数B.比x的倒数大4的数C.x的倒数与4的差D.1除以x的商与4的差4.(2022秋•衡南县期末)一个两位数,个位数字为a,十位数字为b,则这个两位数为()A.a+b B.ba C.10b+a D.10a+b5.(2022秋•聊城期末)某中学组织七年级学生秋游,有m名师生租用45座的大客车若干辆,若有2个空座位,那么用含m的代数式表示租用大客车的辆数是()A.B.C.+2 D.﹣26.(2022秋•昆都仑区校级期末)某地居民生活用水收费标准:每月用水量不超过17立方米,每立方米a 元;超过部分每立方米(a+1.2)元.该地区某用户上月用水量为20立方米,则应缴水费为()A.20a元B.(20a+1.2)元C.(17a+3.6)元D.(20a+3.6)元7.(2022秋•泉港区期末)某电子产品进价为a元,商店将价格提高30%作零售价销售,则该商品售价为()A.(a+0.3)元B.1.3a元C.(1+0.3a)元D.1.03a元8.(2022秋•江夏区期末)某校七年级1班有学生a人,其中女生人数比男生人数的少3人,则女生的人数为()A.B.C.D.9.(2023•瓯海区二模)小李家住房的结构如图所示,小李打算把卧室和客厅铺上木地板,请你帮他算一算,他至少需买多少平方米的木地板()A.12ab B.10ab C.8ab D.6ab10.(2022秋•高新区期末)单项式“2a”可以解释为:一个长方形的长是2米,宽是a米,这个长方形的面积是2a平方米,请你对“2a”再赋予一个含义:.11.(2022•阿坝州)若x+2y﹣3=0,则3x+6y的值为.12.(2022秋•沭阳县期中)根据表,回答问题:x…﹣2﹣1012…﹣2x+5…9753a…2x+8…46810b…【初步感知】(1)a=;b=;【归纳规律】(2)表中﹣2x+5的值的变化规律是:x的值每增加1,﹣2x+5的值就减少2.类似地,2x+8的值的变化规律是什么?【问题解决】(3)请直接写出一个含x的代数式,要求x的值每增加1,代数式的值就减小5,且当x=0时,代数式的值为﹣7.13.(2022秋•广阳区校级期末)已知有下列两个代数式:①a2﹣b2;②(a+b)(a﹣b).(1)当a=5,b=3时,代数式①的值是,代数式②的值是.(2)当a=﹣2,b=1时,代数式①的值是;代数式②的值是.(3)观察(1)和(2)中代数式的值,你发现代数式a2﹣b2和(a+b)(a﹣b)的关系为(用式子表示).(4)利用你发现的规律,求20232﹣20222.。
七年级数学上册(字母表示数)练习1 试题

乏公仓州月氏勿市运河学校字母表示数一.填空:1、代数式-322y x 的系数是 2、│x │=2,│y │=3,且xy <0,那么│x-y │= 。
3、a 、b 互为倒数,c 、d 互为相反数,并且m 的绝对值为3,那么ab-m 2-m d c 533 = 。
4、-(a+b)+(a-b)= .5、a-b+c-d=a-d-( )6、如果5x 2y 3+ax 2y 3=13y 3x 2,那么a=7、3a-b-2c=-3( )8、[7x 2-( )+8]-[( )-6x+( )]=3x 2+3x-4 9、在代数式3x 2y-xy 2-31x 2y+5xy 2-4中,3x 2y 与 是同类项 ,-xy 2与 是同类项。
10、7a-3b+2与10+2b-4的差是 。
二.选择1、以下各式正确的选项是( )A.3x 2-3x 2=x 2B.m 2+m 3=m 5C.4x 2-2x 2=2D.5a 4b 3-4b 3a 4=a 4b 32、下面式子中,去括号后得a-b+c 的是( )A.a-(b+c)B.-(a-b)+cC.a-(b-c)D.-(a+b)+c3、如果xy ≠0,31xy 2+axy 2=0,那么a 的值为( ) A.0 B.3 C.-3 D.-31 4、256b 和5m a 2m b 是同类项,那么m 的值为( )。
A.2 B.3 C.6 D.2或35、以下各组中的两个单项式,不是同类项的是( )。
A.-54xy 和3yxB.a 2b 2和-a 2b 2C.3.5a 2b 和21a 2cD.-64和436、化简-{-[-(2a-b)]}的结果是( )。
A.2a-bB.2a+bC.-2a+bD.-2a-b7、以下去括号正确的选项是( )。
A.2a-(3b-c)=2a-3b-cB.4a 2+(2b-3c)-(-a)=4a 2+2b-3c-a C.7a-(0-2b+5c)=7a+2b+5c D.-(5a 2-3ab)-(2a-c)=-5a 2+3ab-2a+c 三.合并同类项(1)(6m 2-4mn-3n 2)-(2m 2-4mn+n 2) (2)-(-2x 2+3x 3-4)+(-7x+5x 2+2x 3) (3)2a-3a+5a-7a (4)x x x 413121-- (5)5a 2b-3ab 2-7a 2b+ab 2 (6)7m-3n+5m+3n(7)-3(2a-b)2+4(2a-b)2-8(2a-b)2 (8)-17(3x+5y)+21(3x+5y)+4(3x+5y)四.求代数式的值 32-(2x-21y)+(y x 23312+),其中 x=32,y=-1 五.计算题(1)7x-{-3x+[-2x-(8x-1)]-4}(2)(3x 2-5y 0)+[-3xy-2(x 2-xy)+y 2] (3)2(a+2b)-3(2a-3b)+5(4a-2b) (4)-21(3x 2-4xy-5y 2)+41(6x 2+8xy-20y 2) 六.:A=4x 2-7x-1,B=-2x 2+3x-4,求:(1)A+B (2)2A-3B。
用字母表示数练习题及答案

用字母表示数练习题及答案精品文档用字母表示数练习题及答案一、判断1. a×4可以写成a4.2.×7就是73. b,2可以写成b.4.xy就是5. b×b就是2b6. 1×a简写成1a7、x2表示2个x相加。
8、18×18的乘号可以省略不写。
二、填空1、m×5简写为2、x×2×y简写为3、×6简写为4、n×1,a?2简写为5、a×a简写为6、乘法的结合律用字母的式子表示乘法的分配律用字母的式子表示长方形的周长公式。
三、用字母式子表示下面的数量关系1、从100里减去a加上b的和。
、x除以5的商加上n。
、320减去12的m 倍。
4、80加上b的和乘5。
5、S的6倍,减去2的差, 、 b与90的和的6倍1 / 10精品文档四、用字母式子表示下面的数1、一本书X元,买10本同样的书应付多少元,2、搭一个正方形要4根小棒,搭n个正方形要多少根小棒,3、仓库里有一批水泥,运走5车,每车n吨,一共运了多少吨水泥,4、装订练习本,每本用纸25页,装订b本共用多少页纸.5、一个工厂制造500辆自行车,总价是a元,单价是多少元。
用字母表示数练习1、甲数比乙数大5,如果乙数是m,那么甲数是,如果甲数是m,那么乙数是2、a、b、c 三个数的平均数是3、当x,15时,2x,2×4的值是4、有两筐同样的梨,第一筐重,千克,第二筐重,千克,第一筐比第二筐少卖,元。
、用式子表示出梨的价钱。
、当,,24,,,27,,,9时,每千克梨价钱是多少元,6、一个正方形周长是m米,这个正方形的边长是7、食堂买来200千克煤,已烧了a天,还剩b千克,平均每天烧了千克.2 / 10精品文档8、果园里有苹果树和梨树共45棵,其中梨树有a棵,苹果树比梨树多棵.9、学校有图书4000本,又买来,本,现在一共有本。
10、学校有学生,人,其中男生,人,女生有人。
人教版数学五年级上册 第五单元《用字母表示数》同步练习(含答案)

《用字母表示数》(同步练习)-五年级上册数学人教版一.填空题(共13小题)1.用含有字母的式子可以表示运算定律、计算公式和数量关系简明方便。
例如:a(b+c)=,s=vt等。
2.贺卡的单价是a元,小明买了n张这样的贺卡,给售货员付了10元,应找回元。
3.一个正方形的边长是a分米,它的周长是分米,它的面积是平方分米。
4.在算式(8a﹣60)÷12中,当a=时,这道算式的结果是0;当a=时,这道算式的结果是1。
5.桶里原有18千克水,又加入5勺,每勺x千克,桶里现在有水千克,当x=3.25时,桶里现在有水千克。
6.已知一个等腰三角形的底角为α°,它的顶角是度,如果α=40时,它的顶角是度。
7.小明有60元,买了a本练习本,每本4元。
4a表示,60﹣4a表示。
8.工厂中,贾师傅每天生产10个零件,李师傅每天生产20个零件,现需要200个零件。
若全由贾师傅生产,a天后可以完成,列出等量关系式为。
9.1千克苹果的价钱是a元,李老师买了6千克这样的苹果,应付元,付出50元,应找回元。
(50>6a)10.小红今年10岁,爸爸比小红大a岁,爸爸今年岁;妈妈比爸爸小b岁,妈妈今年岁。
11.一本童话故事书,小华每天看8页,看了x天后,还剩下15页,这本书一共有页(用含有字母的式子表示)。
12.当x=0.5时,x2=,2x+9=。
13.我国测量温度常用℃(摄氏度)作单位,有时还使用℉(华氏度)作单位。
华氏温度和摄氏温度的换算公式是:华氏温度=摄氏温度×1.8+32。
如果今天的最低气温是1℃,那么华氏温度表示是℉;如果今天的最高气温用华氏温度表示是86℉,那么相当于℃。
二.选择题(共7小题)14.一个正方形花坛的边长是a米,这个花坛的周长可以表示为()米。
A.4a B.a÷4C.a2D.a315.孙爷爷今年a岁,张伯伯今年(a﹣20)岁,过x年后,他们相差()岁.A.20B.x+20C.x﹣2016.鞋的尺码通常用“码”和“厘米”作单位,它们的关系是m=2n﹣10(m表示码数,n 表示厘米数)。
人教版五年级数学上册第五单元第1课时《用字母表示数》练习题(附答案)

人教版五年级数学上册第五单元第1课时《用字母表示数》练习题(附答案)一、填空。
1.用a、b、c分别表示三个数,那么加法结合律可写成(),乘法分配律可写成()。
2.某电脑专卖店卖出35台电脑,销售总额达b元,每台电脑卖了()元。
3.用a表示单价,b表示数量,c表示总价,那么c=(),a=()。
二、选择。
1.a×6省略乘号,可写成()。
A.6a B.a6C.a62.x2表示()。
A.x·x B.x+x C.2x3.b不能为0的式子是()。
A.a+b B.a÷bC.a×b三、用含有字母的式子表示数量关系。
水果店运来苹果a筐,每筐25千克;橘子5筐,每筐b千克。
苹果一共()千克,橘子一共()千克;苹果比橘子多()筐,每筐橘子比苹果少()千克。
四、生活中的数学。
1.自行车速度是a千米/时,从甲地到乙地行4小时。
(1)用式子表示甲、乙两地距离。
含有字母的式子里,字母中间的乘号可以记作“·”,也可以省略不写。
(2)当a=5时,甲、乙两地的距离是多少千米?2.粮店上午卖出9袋大米,每袋x千克,下午又卖出10袋。
(1)粮店一天卖出大米()千克。
(2)当x=30时,这一天共卖出大米多少千克?五、欢欢家到学校的距离是0.6千米,一天欢欢上学从家出发去学校,走了a千米时,发现忘记拿语文书。
于是立即转身回家拿上语文书去学校,欢欢这次从家去学校比平时多走多少千米?口算1.8÷6=2.4×5= 1.25×8= 1.4×0.6=3.3×3=7.2÷4= 6.9-1.9=8÷0.5= 3.7×200=12×0.4=参考答案一、1.(a+b)+c=a+(b+c)(b+c)a=ab+ac 2.b÷35 3.ab c÷b二、1.A 2.A 3.B三、25a5b a-525-b四、1.(1)4a(2)a=5时,4a=4×5=20(千米) 2.(1)19x(2)x=30时,19x=19×30=570(千克)五、答:欢欢这次从家去学校比平时多走2a千米。
用字母表示数的练习题

用字母表示数的练习题用字母表示数的练习题在数学中,我们通常使用数字来表示数量。
然而,在某些情况下,我们也可以使用字母来表示数。
这种方法可以帮助我们更好地理解数学问题,并提供一种抽象的方式来解决复杂的计算。
接下来,我们将通过一些练习题来探索如何用字母表示数。
练习题一:用字母表示一个未知数假设有一个未知数,我们可以用字母x来表示它。
那么,如果x加上5等于10,我们该如何计算x的值呢?我们可以用方程式来表示这个问题:x + 5 = 10。
为了求解x的值,我们需要将5从等式两边减去,得到x = 10 - 5,即x = 5。
所以,x的值为5。
练习题二:用字母表示多个未知数有时候,我们可能需要用多个字母来表示多个未知数。
让我们来看一个例子:假设有两个未知数x和y,它们的和等于10,而它们的差等于2。
我们该如何计算x和y的值呢?我们可以用以下方程组来表示这个问题:x + y = 10x - y = 2为了求解x和y的值,我们可以使用消元法或代入法。
这里我们使用代入法来解决。
首先,我们将第二个方程式中的x替换为10 - y,得到(10 - y) - y = 2。
然后,我们将这个方程式简化为10 - 2y = 2。
接下来,我们将-2y移到等式的另一边,得到10 - 2 = 2y,即8 = 2y。
最后,我们将等式两边除以2,得到y =4。
将y的值代入第一个方程式中,我们可以计算出x的值:x + 4 = 10,即x = 10 - 4,即x = 6。
所以,x的值为6,y的值为4。
练习题三:用字母表示系数和指数在代数中,我们经常使用字母来表示系数和指数。
让我们来看一个例子:假设有一个多项式2x^2 + 3x + 1,我们该如何计算它的值呢?在这个多项式中,2是x^2的系数,3是x的系数,1是常数项。
x^2表示x的指数为2。
为了计算多项式的值,我们可以将x的值代入并进行计算。
假设x = 2,那么我们可以计算出多项式的值:2(2)^2 + 3(2) + 1 = 2(4) + 6 + 1 = 8 + 6+ 1 = 15。
用字母表示数练习题(1)

用字母表示数练习题(1)用字母表示数练习题一、判断1. a×4可以写成a4. ()2.(b+a)×7就是7(b+a)()3. b+2可以写成2 b. ()4. 5xy就是5(x+y)()5. b×b就是2b ()6. 1×a简写成1a ()7、x²表示2个x相加。
()8、18×18的乘号可以省略不写。
()二、填空1、m×5简写为()2、x×2×y简写为()3、(3+a)×6简写为()4、n×1+a÷2简写为()5、a×a简写为()6、乘法的结合律用字母的式子表示()乘法的分配律用字母的式子表示()长方形的周长公式()。
三、用字母式子表示下面的数量关系1、从100里减去a加上b的和。
2、x除以5的商加上n。
3、320减去12的m倍。
4、80加上b的和乘5。
5、S的6倍,减去2的差,6、 b与90的和的6倍四、用字母式子表示下面的数1、一本书X元,买10本同样的书应付多少元?2、搭一个正方形要4根小棒,搭n个正方形要多少根小棒?3、仓库里有一批水泥,运走5车,每车n吨,一共运了多少吨水泥?4、装订练习本,每本用纸25页,装订b本共用多少页纸.5、一个工厂制造500辆自行车,总价是a元,单价是多少元。
解方程方程:含有未知数的等式叫做方程。
方程的解:使方程成立的未知数的值叫做方程的解。
解方程:求方程的解的过程叫做解方程。
解方程的依据:1. 等式性质(①等式两边同时加上或减去同一个数,等式仍然成立;②等式两边同时乘以或除以同一个数,等式仍然成立。
)2. 加减乘除法的变形。
加法:加数1 + 加数2 = 和加数1 =加数2 =减法:被减数–减数= 差被减数=减数=乘法:乘数1 ×乘数2 = 积乘数1 =乘数2 =除法:被除数÷除数= 商被除数=除数=一、解方程:20x-50=50 28+6 x =88 32-22 x =1024-3 x =3 10 x ×(5+1)=60 99 x =100- x36÷ x=18 x÷6=12 56-2 x =204y+2=6 x+32=76 3x+6=1816+8x=40 2x-8=8 4x-3×9=29二、口算:a+2a= 3c+5c= 4m-2m= X+3x=5x-x= 6x-2x= 1.5x-x= 3.6x+1.4x=作业(一)一、填空。
小学五年级数学用字母表示数练习题一(含答案)

小学五年级数学用字母表示数练习题一(含答案)小学五年级数学用字母表示数练题一(含答案)姓名:__________一、填空题。
1.一筐橙子重x千克,28筐重28x千克。
2.a是大于1的自然数,与a相邻的两个自然数是a-1和a+1.3.新中小学共有a名学生,其中男生350名,女生a-350名。
4.XXX运送了a千克苹果,比XXX多运20.5千克。
XXX 运了(a+20.5)千克苹果,两人共运了(2a+20.5)千克。
如果a=130,那么XXX运了(130-20.5)千克苹果。
5.超市苹果x元一斤,XXX买8斤共8x元。
XXX付给售货员50元,应找回(50-8x)元。
如果每斤苹果3.5元,应找回(50-28)元。
6.工地用汽车运土,每辆车运m吨。
一天上午运了a车,下午运了b车。
这一天共运土(a+b)m吨,上午比下午多运土2am吨。
如果a=10,b=8,m=8,那么,一天共运土144吨,上午比下午多运土160吨。
7.一本书有a页,XXX每天看6页,看了XXX表示6天内看的页数,XXX表示还没看的页数。
如果这本书有94页,XXX看了6天。
用上面的式子求出还有58页没看。
8.两辆车从A地同时出发背向而行。
客车开往甲地,每小时行a千米;货车开往乙地,每小时行(a-5)千米,b小时后两车同时分别到达甲、乙两地。
用含字母的式子表示下列数量:货车的速度为(a-5)千米每小时;到达甲地时客车的路程为ab 千米;到达乙地时货车的路程为(a-5)b千米;甲、乙两地相距ab千米;乙地比甲地离A地近ab/2千米。
9.甲数比乙数大a,若甲数是b,乙数是(b-a)。
10.如果用a表示工作效率,t表示工作时间,C表示工作总量,那么a=C/t,t=C/a,c=at。
11.长方形的面积为长×宽,周长为2×(长+宽);正方形的面积为边长的平方,周长为4×边长。
12.汽车走160千米用了a小时,其速度为160/a千米每小时;从甲地到乙地640千米,需要640/(160/a)=4a小时。
小学数学用字母表示数练习题
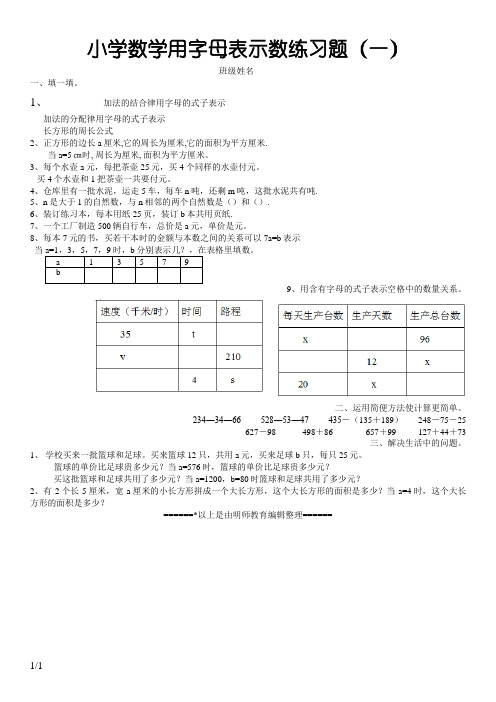
小学数学用字母表示数练习题(一)班级姓名一、填一填。
1、加法的结合律用字母的式子表示加法的分配律用字母的式子表示长方形的周长公式2、正方形的边长a厘米,它的周长为厘米,它的面积为平方厘米.当a=5㎝时, 周长为厘米, 面积为平方厘米。
3、每个水壶a元,每把茶壶25元,买4个同样的水壶付元。
买4个水壶和1把茶壶一共要付元。
4、仓库里有一批水泥,运走5车,每车n吨,还剩m吨,这批水泥共有吨.5、n是大于1的自然数,与n相邻的两个自然数是()和().6、装订练习本,每本用纸25页,装订b本共用页纸.7、一个工厂制造500辆自行车,总价是a元,单价是元。
8、每本7元的书,买若干本时的金额与本数之间的关系可以7a=b表示当a=1,3,5,7,9时,b分别表示几?,在表格里填数。
a13579b9、用含有字母的式子表示空格中的数量关系。
二、运用简便方法使计算更简单。
234―34―66 528―53―47 435-(135+189) 248-75-25627-98 498+86 657+99 127+44+73三、解决生活中的问题。
1、学校买来一批篮球和足球。
买来篮球12只,共用a元,买来足球b只,每只25元。
篮球的单价比足球贵多少元?当a=576时,篮球的单价比足球贵多少元?买这批篮球和足球共用了多少元?当a=1200,b=80时篮球和足球共用了多少元?2、有2个长5厘米,宽a厘米的小长方形拼成一个大长方形,这个大长方形的面积是多少?当a=4时,这个大长方形的面积是多少?======*以上是由明师教育编辑整理======1/1。
5.1用字母表示数(同步练习)-2024-2025学年五年级数学上册人教版

简易方程---用字母表示数例1:用含有字母的式子表示简单的数量关系。
1. 12与a的积减去20.3。
2. 8.8与c的和乘0.2。
3.0.2减去b的差除以5。
4. 比63.3多y的数。
5.a与21的和时67。
6.n的5倍与18 的差等于95例2:化简含有字母的式子。
v×7= m×n-4.6= a×b×c=0.8×b= x×2= 20+a×b=a×x= x×x= b×1=例3:用字母表示复杂的数量关系。
1. 明明家本月的用电量是92千瓦时,交电费f元,那么电价是每千瓦时()元。
2. 鸟的骨骼约是体重的0.05~0.06倍,人的骨骼约是体重的0.18倍。
一个人重a 千克,骨骼约是()kg。
3. 张奶奶买了单价是1.2元/千克的黄瓜3.5千克,付了a元(a>4.2),应找回()元。
4.人的身高早晚可能会相差2 cm,在早上最高,晚上最矮。
一个人早上身高是b cm,晚上身高可能是()cm。
5. 王师傅a天做了6个零件(a>0,b>0),他平均每天做()个零件。
6.苹果每千克a元,梨每千克b元,各买m千克。
(a>b)。
①am 表示( )。
②)bm 表示( )。
④(a-b)m 表示( )。
③(a+b)m 表示( )。
例4:代入求值。
1、某工厂存煤 400 吨,每天用去b吨。
① 3b 表示( )。
当b=5 时,3b=( )。
②400-56 表示( )。
当b=23 时,400-5b=( )。
③ 400÷b 表示()。
当b=50时,400÷b=( )。
2、豪豪看一本180页的故事书,每天看15页,看了y天,还剩多少页没看?当y=6时,还剩多少页没看?3、和谐号列车的平均速度为220千米/时,复兴号列车的平均速度为350千米/时。
(1)行驶x小时,和谐号和复兴号相遇,相遇时一共行驶多少千米?(2)行驶x小时,复兴号和谐号多行驶多少千米?4、爷爷早上做锻炼,爷爷以150米/分的速度往家走,奶奶同时以130米/分的速度从家出发去迎接。
完整版)五年级上册数学用字母表示数练习题

完整版)五年级上册数学用字母表示数练
习题
一、填空
1.骨骼约是0.18a kg。
2.晚上身高可能是bcm-2cm。
3.电费每千瓦时是c/80元。
4.今天卖出48+m个足球,当m=10时,今天卖出58个;当m=12时,今天卖出60个。
5.2分钟骑2v m,t分钟骑tv m。
如果每分钟行260m,时间是30分,路程是7800米。
6.工作5分钟,共打了5x个字。
7.商店里___的总质量是120+10a kg。
当a等于25时,商店一共有370千克苹果。
8.仓库里剩下货物的吨数为96-12b吨。
当b等于5时,仓库里剩下的货物有66吨。
9.动车和普通列车一共行了340x千米。
动车比普通列车多行了100x千米。
10.b+8表示中午的温度。
二、用含有字母的式子表示下面的数量关系。
1.t+3,20-a,2x,b÷12,5a-4.8,x-9.
2.可买20/a本练本。
3.桶里现在水的质量为3+5x kg。
当x=2时,桶里现在水的质量是13kg。
4.每天共投报135份,共投报30x135份。
他们30天的总投报数为3675份。
5.还没看的页数为a-8b页。
如果这本书有94页,___看了7天,还没看的页数为50页。
6.离开重庆有36t km,如果t=10,离开重庆有360km。
到宜昌还有648-36t km,如果t=12时,到宜昌还有216km。
7.摆n个正方形需要4n-4根小棒。
摆21个正方形需要80根小棒。
(完整版)用字母表示数练习题

用字母表示数练习题一一、填空(每空2分)1、长为a,宽为b的长方形周长是。
2、教室里有x人,走了y人,此时教室里有人。
3、三个连续的自然数,中间的一个为n,则第一个为,第三个为。
4、用a、b表示两个数,加法交换率律可表示成()。
5、用字母a表示苹果的单价,b表示数量,c表示总价。
那么c=(),b=()。
6、一个等边三角形,每边长a米。
它的周长()米。
7、一辆汽车t小时行了300千米,平均每小时行()千米。
李师傅每小时加工40个零件,加工了a小时,一共加工了()个。
8、每袋面粉重a千克,每袋大米重b千克,8袋面粉和5袋大米共重()千克。
9、苏宁公司在5月5日这一天,某品牌的手机十分畅销,上午卖出75部,下午卖出100部,已知每部手机a元,这一天一共卖出()元,上午比下午少卖出()元。
10、5x+4x=() 8y-y=() 7x+7x+6x=()7a×a=() 15x+6x=() 5b+4b-9b=()11、学校买来x盒红粉笔,买来白粉笔的盒数是红粉笔的10倍,学校买来()盒粉笔;当x=10时,学校买来()盒粉笔。
二、选择(将正确答案的序号填在括号里)(每题2分)1、a2与()相等。
(1)a×2 (2)a+2 (3)a×a2、2x一定()x2。
(1)大于(2)小于(3)等于(4)不能确定3、丁丁比昕昕小,丁丁今年a岁,昕昕今年b岁,2年后丁丁比昕昕小()岁。
(1)2 (2)b-a (3)a-b (4)b-a+24、当a=5、b=4时,ab+3的值是()。
(1)5+4+3=12 (2)54+3=57 (3)5×4+3=235、甲数是a,比乙数的4倍少b,乙数是()。
(1)a÷4-b(2)(a-b)÷4(3)(a+b)÷4三、用含有字母的式子表示下面各题的数量关系(每题4分)1、在一个三角形中,∠1=a°,∠2=b°,用含有字母的式子表示∠3的度数。
小学数学《用字母表示数》练习题(含答案)

小学数学《用字母表示数》练习题(含答案)【例1】有一辆汽车沿山路行驶,上山平均每小时行10千米,下山时沿原路返回,每小时行15千米。
求这辆汽车上、下山往返一趟的平均速度。
分析与解:通常,要求平均速度需要知道上、下山所行驶的总路程以及上、下山所行驶的总时间。
但这道题中只知道上、下山的速度,怎样求平均速度呢?我们可发挥字母的作用。
设上、下山所行的路程都是S千米,那么上山时间为:下山时间为:由于汽车往返一趟所行驶的总路程是2S,所以,汽车上、下山的平均速度是【例2】一个直角梯形ABCD的中位线EF长15厘米,G是EF上的一点米?注:“梯形中位线”的长等于梯形上底加下底的和的一半。
分析与解:根据梯形“中位线”的特点,我们想到:根据乘法交换律,梯形面积公式不是可以写成下面这种形式吗?S=中位线×高在这道题中,梯形的高是AB。
设AB=a,那么,S=15×a梯形ABCD=15a(平方厘米)根据题目的第二个已知条件,我们可以推算出,三角形ABG的面积是:另一方面,由三角形面积公式,可得也就是说,÷aEG=2×S△ABG=2×3a÷a=6a÷a=6(厘米)拓展训练有一个蓄水池装有9根水管,其中一根为进水管,其余8根为相同的出水管。
进水管以均匀的速度不停地向这个蓄水池注水。
后来有人想打开出水管,使池内的水全部排光(这时池内已注入了一些水)。
如果把8根出水管全部打开,需3小时把池内的水全部排光;如果仅打开5根出水管,需6小时把池内的水全部排出。
问要想在4.5小时内把池内的水全部排光。
需同时打开几根出水管?答案:设同时打x根出水管,可在4.5小时内把池内的水全部排光。
再设池中原有的水为a,每小时放进来的水为b,每根出水管每小时排水为c。
那么8×3c=a+3b ①5×6c=a+6b ②4.5x×c=a+b×4.5 ③把②-①,得b=2c ④把④代入①,得a=18c ⑤把④、⑤都代入③,得4.5xc=18c+2c×4.5也就是:4.5c×x=27c从而x=27c÷(4.5c)x=6【例 3】如图,一个人要从A到B,他可按①号箭头所表示的路线走,也可以按②号箭头所表示的路线走。
完整版)用字母表示数练习题(专项)

完整版)用字母表示数练习题(专项)一、填空题1、今天,是我最快乐的一天!早上我和同学们一起乘车前往游乐园。
车上有男同学b人,女同学c人,一共有(b+c)人。
2、游乐园可真漂亮!门口摆着五颜六色的花,其中红花最多,有50盆,黄花有n盆,红花比黄花多(50-n)盆。
3、游乐园儿童门票每张s元,儿童门票的价钱是成人门票的一半。
买一张成人门票要(2s)元。
4、正方形的边长为a分米,4a表示(正方形的周长),a²表示(正方形的面积)。
5、在校运动会上,四年级同学获得a枚金牌,五年级同学获得18枚金牌。
①两个年级一共获得(a+18)枚牌。
XXX表示(四年级同学比五年级同学少获得的金牌数)。
③a÷18表示(四年级同学获得金牌数是五年级同学获得金牌数的几倍)。
6、说一说,下面的式子表示什么意思?篮球每个68元,足球每个45元。
某个学校买了a个篮球,b个足球.那么①68 a表示(购买篮球的总价)②a-b表示(篮球和足球的数量差)③68a+45b表示(购买篮球和足球的总价)④68a-45b表(购买篮球比购买足球多花费的金额)7、某班有40名学生,其中男生有40-a名,在向“希望工程”捐书活动中,平均每人捐书3本,试分析下面问题。
1)a表示什么?(女生的人数)2)3a表示什么?(女生捐书的总数量)8、学校买来9个足球,每个a元,又买来b个篮球,每个45.6元9a表示(买9个足球的总价)45.6b表示(买b个篮球的总价)45.6b–9a表示(买篮球比买足球多花费的金额)9a + 45.6b表示(买足球和篮球的总价)。
9、用线段把左右两边相等的数连接起来。
比a多3的数:a+3比a少3的数:a-33个a相加的和:3a3个a相乘的积:a³a的3倍:3a10、想一想,填一填。
①b与21的和是(b+21),积是(b×21)②比c少3.2的数是(c-3.2)③每盒装5块月饼,c盒装(5c)块月饼。
(完整版)用字母表示数练习题一

用字母表示数练习题一1、把结果相同的式子连起来。
a2 ﹒2a x﹒x 82 3.1×3.1a+a x2 a﹒a 3.12 8×82、写出每个式子所表示的意义。
每套运动服a元,比每套休闲服贵15元。
6a表示:,6(a-15)表示3、甲、乙两车分别从相距350千米的两地想向开出,甲车每小时行驶a千米,乙车每小时行驶b千米。
(1)当a=45,b=55时,经过几小时两车相遇?(2)当a=60,b=80时,2小时后两车相距多少千米?4、学校买了20个足球,每个b元,用式子表示总价。
当b=15时,共花多少元?5、先写出含有字母的式子,再求出式子的值。
(1)比 x多7.5的数用含有字母的式子表示是()。
当x=12时,这个式子的值是()。
(2)食堂买了40千克大米,60千克面粉,每千克大米x元,每千克面粉y元,买面粉比买大米多付的钱为()。
当x=2.70,y=2.52时,上面的式子的值是()。
(3)甲汽车从A地开往B地,每小时行a千米,5小时后,乙汽车从B地开往A地,每小时行60千米,行了t小时后,甲乙两车还相距x千米,两地之间的距离是()千米。
当a=80,t=4,x=150时,上面的式子的值是()。
6、用简便方法表示下面的式子。
2x×y x×x 3×x×x a×b 1×ca +a+a x+x x×7 s×t x×17、用含有字母的式子表示下面各题中的数量关系。
(1)a的8倍。
()(2)x与y的和的7倍。
(3)x的7倍与y的3倍的和。
()(4)b的3倍与16的差。
()8、判断。
(对的在括号里画“√”,错的在括号里画“×”)(1)32=6 ()(2)x×2.6+y×1=2.6x+y( ) (3)a×7+b=7ab ( ) (4)2.52 =5 ( ) (5) 32=3×2 ( )。
(完整版)五年级英语用字母表示数练习题

(完整版)五年级英语用字母表示数练习题第一部分:单词转数字将下列单词转换为用字母表示的数字。
1. three2. eight3. five4. nine5. two6. seven7. one8. six9. four10. ten1. 三2. 八3. 五4. 九5. 二6. 七7. 一8. 六9. 四10. 十第二部分:用字母表示的数字转单词将下列用字母表示的数字转换为相应的单词。
1. 22. 63. 94. 45. 76. 17. 58. 109. 310. 81. two2. six3. nine4. four5. seven6. one7. five8. ten9. three10. eight第三部分:填入正确的字母表示的数字请根据下列句子的要求填入相应的字母表示的数字。
1. There are _ _ _ days in a week.2. My birthday is on the _ _ _ _ of December.3. I have _ _ _ brothers and _ _ _ sisters.4. I am _ _ _ years old.5. There are _ _ _ months in a year.6. I have _ _ _ pet dog.7. The year has _ _ _ days.8. My phone number starts with _ _ _.9. My address is _ _ _ Main Street.10. The time is _ _ _ o'clock.1. seven2. fifteenth3. three, two4. ten5. twelve6. a7. three hundred sixty-five8. eight9. one hundred10. nine结束语这些练习题可以帮助五年级学生巩固用字母表示数的能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用字母表示数练习题一
1、把结果相同的式子连起来。
a2 ﹒2a x﹒x 82 3.1×3.1
a+a x2 a﹒a 3.12 8×8
2、写出每个式子所表示的意义。
每套运动服a元,比每套休闲服贵15元。
6a表示:,6(a-15)表示
3、甲、乙两车分别从相距350千米的两地想向开出,甲车每小时行驶a千米,乙车每小时行驶b千米。
(1)当a=45,b=55时,经过几小时两车相遇?
(2)当a=60,b=80时,2小时后两车相距多少千米?
4、学校买了20个足球,每个b元,用式子表示总价。
当b=15时,共花多少元?
5、先写出含有字母的式子,再求出式子的值。
(1)比 x多7.5的数用含有字母的式子表示是()。
当x=12时,这个式子的值是()。
(2)食堂买了40千克大米,60千克面粉,每千克大米x元,每千克面粉y元,买面粉比买大米多付的钱为()。
当x=2.70,y=2.52时,上面的式子的值是()。
(3)甲汽车从A地开往B地,每小时行a千米,5小时后,乙汽车从B地开往A地,每小时行60千米,行了t小时后,甲乙两车还相距x千米,两地之间的距离是()千米。
当a=80,t=4,x=150时,上面的式子的值是()。
6、用简便方法表示下面的式子。
2x×y x×x 3×x×x a×b 1×c
a +a+a x+x x×7 s×t x×1
7、用含有字母的式子表示下面各题中的数量关系。
(1)a的8倍。
()(2)x与y的和的7倍。
(3)x的7倍与y的3倍的和。
()
(4)b的3倍与16的差。
()
8、判断。
(对的在括号里画“√”,错的在括号里画“×”)(1)32=6 ()(2)x×2.6+y×1=2.6x+y( ) (3)a×7+b=7ab ( ) (4)2.52 =5 ( ) (5) 32=3×2 ( )。
