MATLAB机器人仿真程序
利用matlab的机器人试验仿真
选择MATLAB2016a版,高版本不能安装。
安装好按照下面的操作做出来,然后截图做成Word文档发给我。
MATLAB2016a版同学们网上下载安装,安装方法网上随便可找到。
机器人工具箱我发给你们。
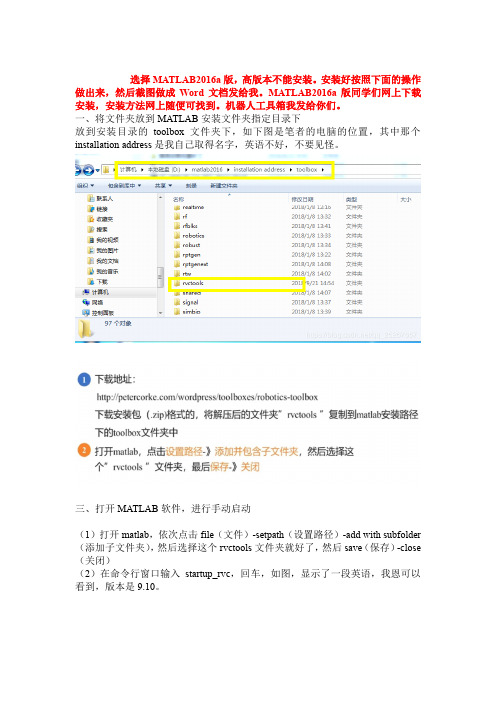
一、将文件夹放到MATLAB安装文件夹指定目录下放到安装目录的toolbox文件夹下,如下图是笔者的电脑的位置,其中那个installation address是我自己取得名字,英语不好,不要见怪。
三、打开MATLAB软件,进行手动启动(1)打开matlab,依次点击file(文件)-setpath(设置路径)-add with subfolder (添加子文件夹),然后选择这个rvctools文件夹就好了,然后save(保存)-close (关闭)(2)在命令行窗口输入startup_rvc,回车,如图,显示了一段英语,我恩可以看到,版本是9.10。
本文主要是给大家一个系统的概念,如何用Matlab实现六轴机器人的建模和实现轨迹规划。
以后将会给大家讲解如何手写正逆解以及轨迹插补的程序。
程序是基于Matlab2016a,工具箱版本为Robotic Toolbox 9.10。
1.D-H建模三个两两相互垂直的XYZ轴构成欧几里得空间,存在六个自由度:沿XYZ 平移的三个自由度,绕XYZ旋转的三个自由度。
在欧几里得空间中任意线性变换都可以通过这六个自由度完成。
Denavit-Hartenberg提出的D-H参数模型能满足机器人学中的最小线性表示约定,用4个参数就能描述坐标变换:绕X轴平移距离a;绕X轴旋转角度alpha;绕Z轴平移距离d;绕Z轴旋转角度theta。
2.标准D-H模型和改进D-H模型对比来看参数并没有改变,标准的D-H 模型是将连杆的坐标系固定在该连杆的输出端(下一关节),也即坐标系i-1与关节i对齐;改进的D-H模型则是将坐标系固定在该连杆的输入端(上一关节),也即坐标系i-1与关节对齐i-1。
MATLAB建模与仿真应用程序_第12章 机器人控制系统的设计与仿真

根据动力学模型及控制律完成控制器 S 函数“chap12_1ctrl.m”、 被控对象 S 函数“chap12_1plant.m”及作图程序“chap12_1plot.m” M文件的编写。
12.1 基于模糊补偿的机器人自适应模糊控制
12.1.4 仿真实例
1. 仿真实例一:针对带有摩擦的情况 9. 运行仿真模型
系统函数模块的参数设置
12.1 基于模糊补偿的机器人自适应模糊控制
12.1.4 仿真实例
1. 仿真实例一:针对带有摩擦的情况 4. 模型参数设置
数据输出模块 的参数设置
仿真时间模块的参数设置
12.1 基于模糊补偿的机器人自适应模糊控制
12.1.4 仿真实例
1. 仿真实例一:针对带有摩擦的情况
5. 仿真参数设置
12.2 工作空间中机器人的神经网络自适应控制
12.2.4 仿真实例
6. 运行仿真模型
末关节节点的位置跟踪
末关节节点的速度跟踪
12.2 工作空间中机器人的神经网络自适应控制
12.2.4 仿真实例
6. 运行仿真模型
末关节节点的位置跟踪
的逼近
第12章 结束
自适应模糊控制器的设计,不需要对被控对象建立精确的数学 模型,它能对模糊系统的参数进行在线调整,设计合适的自适应律 来保证控制系统的稳定性。
12.1 基于模糊补偿的机器人自适应模糊控制
12.1.1 机器人动力学模型建立
机器人系统的动力学模型反映了系统中各个关节位置、速度和加速度 三者之间的数学关系。
普通高等教育系列教材
MATLAB 建模与仿真应用教程
MATLAB建模与仿真应用教程 第12章 机器人控制系统的设计与仿真
在MATLAB中进行机器人编程和仿真

在MATLAB中进行机器人编程和仿真机器人编程和仿真在现代科技领域扮演着至关重要的角色。
随着科技的不断发展,人们对机器人的需求也越来越高。
而MATLAB作为一种强大的编程和仿真工具,为机器人领域提供了许多便捷和高效的解决方案。
在本文中,我们将探讨如何在MATLAB中进行机器人编程和仿真,并介绍一些相关应用和实例。
第一部分:MATLAB中的机器人编程基础机器人编程是指为机器人设定行为和任务,使其能够执行特定的工作。
MATLAB为机器人编程提供了丰富的函数库和工具箱,使得编程过程更加简便和高效。
1. MATLAB中的机器人模型首先,在进行机器人编程和仿真之前,我们需要定义一个机器人模型。
MATLAB中的机器人模型包括机器人的几何结构、运动学特性和动力学参数等信息。
通过使用MATLAB中的Robotic System Toolbox,我们可以方便地创建机器人模型,并对其进行各种操作和分析。
2. 机器人运动学分析机器人的运动学分析是机器人编程的重要一环。
在MATLAB中,我们可以使用Robotic System Toolbox提供的函数和工具进行机器人的运动学分析。
例如,可以使用forwardKinematics函数计算机器人末端执行器的位置和姿态,或者使用inverseKinematics函数计算关节的角度和位置。
3. 机器人路径规划路径规划是机器人编程中的核心问题之一。
在MATLAB中,我们可以利用Path Planning Toolbox提供的算法和函数,实现机器人在给定环境中的路径规划。
通过设置起始点和目标点,以及环境的障碍物信息,可以使用MATLAB中的路径规划算法自动生成机器人的轨迹,使其能够高效地避开障碍物并到达目标位置。
第二部分:机器人编程和仿真的应用案例机器人编程和仿真在许多领域都有广泛的应用。
下面将介绍两个典型的应用案例,以展示MATLAB在机器人领域的强大功能。
1. 机器人控制系统设计机器人控制系统是机器人编程中的关键环节。
MATLAB机器人仿真程序

附录MATLAB 机器人工具箱仿真程序:1)运动学仿真模型程序(Rob1.m)L1=link([pi/2 150 0 0])L2=link([0 570 0 0])L3=link([pi/2 130 0 0])L4=link([-pi/2 0 0 640])L5=link([pi/2 0 0 0])L6=link([0 0 0 95])r=robot({L1 L2 L3 L4 L5 L6})=’MOTOMAN-UP6’ % 模型的名称>>drivebot(r)2)正运动学仿真程序(Rob2.m)L1=link([pi/2 150 0 0])L2=link([0 570 0 0])L3=link([pi/2 130 0 0])L4=link([-pi/2 0 0 640])L5=link([pi/2 0 0 0])L6=link([0 0 0 95])r=robot({L1 L2 L3 L4 L5 L6})=’MOTOMAN-UP6’t=[0:0.01:10];%产生时间向量qA=[0 0 0 0 0 0 ]; %机械手初始关节角度qAB=[-pi/2 -pi/3 0 pi/6 pi/3 pi/2 ];%机械手终止关节角度figure('Name','up6机器人正运动学仿真演示');%给仿真图像命名q=jtraj(qA,qAB,t);%生成关节运动轨迹T=fkine(r,q);%正向运动学仿真函数plot(r,q);%生成机器人的运动figure('Name','up6机器人末端位移图')subplot(3,1,1);plot(t, squeeze(T(1,4,:)));xlabel('Time (s)');ylabel('X (m)');subplot(3,1,2);plot(t, squeeze(T(2,4,:)));xlabel('Time (s)');ylabel('Y (m)');subplot(3,1,3);plot(t, squeeze(T(3,4,:)));xlabel('Time (s)');ylabel('Z (m)');x=squeeze(T(1,4,:));y=squeeze(T(2,4,:));z=squeeze(T(3,4,:));figure('Name','up6机器人末端轨迹图'); plot3(x,y,z);3)机器人各关节转动角度仿真程序:(Rob3.m)L1=link([pi/2 150 0 0 ])L2=link([0 570 0 0])L3=link([pi/2 130 0 0])L4=link([-pi/2 0 0 640])L5=link([pi/2 0 0 0 ])L6=link([0 0 0 95])r=robot({L1 L2 L3 L4 L5 L6})='motoman-up6't=[0:0.01:10];qA=[0 0 0 0 0 0 ];qAB=[ pi/6 pi/6 pi/6 pi/6 pi/6 pi/6]; q=jtraj(qA,qAB,t);Plot(r,q);subplot(6,1,1);plot(t,q(:,1));title('转动关节1');xlabel('时间/s');ylabel('角度/rad');subplot(6,1,2);plot(t,q(:,2));title('转动关节2');xlabel('时间/s');ylabel('角度/rad');subplot(6,1,3);plot(t,q(:,3));title('转动关节3');xlabel('时间/s');ylabel('角度/rad');subplot(6,1,4);plot(t,q(:,4));title('转动关节4');xlabel('时间/s');ylabel('角度/rad' );subplot(6,1,5);plot(t,q(:,5));title('转动关节5');xlabel('时间/s');ylabel('角度/rad');subplot(6,1,6);plot(t,q(:,6));title('转动关节6');xlabel('时间/s');ylabel('角度/rad');4)机器人各关节转动角速度仿真程序:(Rob4.m)t=[0:0.01:10];qA=[0 0 0 0 0 0 ];%机械手初始关节量qAB=[ 1.5709 -0.8902 -0.0481 -0.5178 1.0645 -1.0201]; [q,qd,qdd]=jtraj(qA,qAB,t);Plot(r,q);subplot(6,1,1);plot(t,qd(:,1));title('转动关节1');xlabel('时间/s');ylabel('rad/s');subplot(6,1,2);plot(t,qd(:,2));title('转动关节2');xlabel('时间/s');ylabel('rad/s');subplot(6,1,3);plot(t,qd(:,3));title('转动关节3');xlabel('时间/s');ylabel('rad/s');subplot(6,1,4);plot(t,qd(:,4));title('转动关节4');xlabel('时间/s');ylabel('rad/s' );subplot(6,1,5);plot(t,qd(:,5));title('转动关节5');xlabel('时间/s');ylabel('rad/s');subplot(6,1,6);plot(t,qd(:,6));title('转动关节6');xlabel('时间/s');ylabel('rad/s');5)机器人各关节转动角加速度仿真程序:(Rob5.m)t=[0:0.01:10];%产生时间向量qA=[0 0 0 0 0 0]qAB =[1.5709 -0.8902 -0.0481 -0.5178 1.0645 -1.0201]; [q,qd,qdd]=jtraj(qA,qAB,t);figure('name','up6机器人机械手各关节加速度曲线');subplot(6,1,1);plot(t,qdd(:,1));title('关节1');xlabel('时间 (s)');ylabel('加速度 (rad/s^2)');subplot(6,1,2);plot(t,qdd(:,2));title('关节2');xlabel('时间 (s)');ylabel('加速度 (rad/s^2)');subplot(6,1,3);plot(t,qdd(:,3));title('关节3');xlabel('时间 (s)');ylabel('加速度 (rad/s^2)')subplot(6,1,4);plot(t,qdd(:,4));title('关节4');xlabel('时间 (s)');ylabel('加速度 (rad/s^2)')subplot(6,1,5);plot(t,qdd(:,5));title('关节5');xlabel('时间 (s)');ylabel('加速度 (rad/s^2)')subplot(6,1,6);plot(t,qdd(:,6));title('关节6');xlabel('时间 (s)');ylabel('加速度 (rad/s^2)')如有侵权请联系告知删除,感谢你们的配合!。
基于MATLAB的六自由度工业机器人运动分析和仿真

基于MATLAB的六⾃由度⼯业机器⼈运动分析和仿真基于MATLAB 的六⾃由度⼯业机器⼈运动分析及仿真摘要:以FANUC ARC mate100⼯业机器⼈为研究对象,对其机构和连杆参数进⾏分析,采⽤D-H 法对机器⼈进⾏正运动学和逆运动学分析,建⽴运动学⽅程。
在MATLAB 环境下,运⽤机器⼈⼯具箱进⾏建模仿真,仿真结果证明了所建⽴的运动学正、逆解模型的合理性和正确性。
关键词:FANUC ARC mate100⼯业机器⼈; 运动学; MATLAB 建模仿真 1引⾔⼯业机器⼈技术是在控制⼯程、⼈⼯智能、计算机科学和机构学等多种学科的基础上发展起来的⼀种综合性技术。
经过多年的发展,该项技术已经取得了实质性的进步[1]。
⼯业机器⼈的发展⽔平随着科技的进步和⼯业⾃动化的需求有了很⼤的提⾼,同时⼯业机器⼈技术也得到了进⼀步的完善。
⼯业机器⼈的运动学分析主要是通过⼯业机器⼈各个连杆和机构参数,以确定末端执⾏器的位姿。
⼯业机器⼈的运动学分析包括正运动学分析和逆运动学分析。
随着对焊接件要求的提⾼,弧焊等机器⼈的需求越来越多。
本⽂就以FANUC ARC mate100机器⼈为研究对象,通过分析机构和连杆参数,运⽤D-H 参数法建⽴坐标系,求出连杆之间的位姿矩阵,建⽴⼯业机器⼈运动学⽅程。
并在MATLAB 环境下,利⽤RoboticsToolbox 进⾏建模仿真。
2 FANUC ARC mate100 D-H 坐标系的建⽴mate100是FANUC 公司⽣产的6⾃由度⼯业机器⼈,包括底座、机⾝、臂、⼿腕和末端执⾏器,每个⾃由度对应⼀个旋转关节,如图1所⽰。
图1FANUC ARC mate 100机器⼈三维模型DENAVIT 和HARTENBERG 于1955年提出了⼀种为关节链中的每⼀个杆件建⽴坐标系的矩阵⽅法,即D-H 参数法,在机器⼈运动学分析得到了⼴泛运⽤。
采⽤这种⽅法建⽴坐标系:(1) Z i 轴沿关节i +1的轴线⽅向。
MATLAB机器人仿真程序

MATLAB仿真程序1、摘要:简要介绍仿真程序的目的和应用领域。
2、简介2.1 背景:介绍仿真技术的背景和发展趋势。
2.2 目标:阐述本文档旨在实现的目标和预期成果。
2.3 使用范围:说明本文档适用的MATLAB版本和相关工具。
3、系统需求3.1 软件需求:列出在运行仿真程序时需要的MATLAB版本和相关工具。
3.2 硬件需求:描述在运行仿真程序时所需的最低硬件配置要求。
4、数据准备4.1 输入数据:说明仿真程序所需的输入数据,包括模型、环境参数、运动规划等。
4.2 数据处理:描述对输入数据进行预处理和转换的方法和算法。
5、仿真实现5.1 建模:介绍如何使用MATLAB建立模型。
5.2 运动规划:讲解如何使用运动规划算法的轨迹。
5.3 运动控制:详细说明如何控制的关节运动和末端执行器的运动。
6、结果分析6.1 数据保存:指示如何保存仿真过程和结果的数据。
6.2 数据可视化:说明如何使用MATLAB绘制仿真结果图表。
6.3 结果评估:解析实验结果,验证仿真程序的准确性和可行性。
7、总结和下一步工作简要总结此次仿真程序的实现和结果,提出改进的建议,并探讨下一步工作的方向。
附件:本文档涉及的附件包括:- 模型文件- 仿真环境场景文件- 运动规划算法实现代码- 仿真结果数据文件法律名词及注释:1、版权:著作权法规定的著作物享有的法律保护。
2、许可证:根据许可证要求,特定行为(如使用、复制、修改)被允许或拒绝使用。
3、商标:商标是注册商标办公室注册的标志,用于识别产品或服务来源。
4、法律依据:涉及到法律的相关内容,应根据当地法律依据进行操作。
matlab机器人运动学仿真代码

matlab机器人运动学仿真代码以下是一个简单的MATLAB机器人运动学仿真代码示例,假设机器人是一个二维平面上的两轴机器人,其中关节1和关节2的长度分别为L1和L2:matlab.% 定义关节长度。
L1 = 1;L2 = 1;% 定义关节角度。
theta1 = 0:0.01:2pi; % 关节1角度范围。
theta2 = 0:0.01:2pi; % 关节2角度范围。
% 初始化末端点坐标。
x = zeros(length(theta1), length(theta2));y = zeros(length(theta1), length(theta2));% 计算末端点坐标。
for i = 1:length(theta1)。
for j = 1:length(theta2)。
x(i,j) = L1 cos(theta1(i)) + L2 cos(theta1(i) + theta2(j));y(i,j) = L1 sin(theta1(i)) + L2 sin(theta1(i) + theta2(j));end.end.% 绘制机器人末端点轨迹。
figure;plot(x(:), y(:), 'b.');xlabel('X');ylabel('Y');title('机器人末端点轨迹');这段代码实现了一个简单的两轴机器人的运动学仿真。
首先定义了机器人的关节长度和关节角度范围,然后计算了末端点的坐标,并绘制了机器人末端点的轨迹。
当然,实际的机器人运动学仿真会更加复杂,涉及到不同类型的机器人和运动学模型,但这段代码可以作为一个简单的起点,帮助你开始进行机器人运动学仿真的工作。
MATLAB机器人仿真程序

MATLAB机器人仿真程序哎呀,说起 MATLAB 机器人仿真程序,这可真是个有趣又充满挑战的领域!我还记得有一次,我带着一群学生尝试做一个简单的机器人行走仿真。
那时候,大家都兴奋极了,眼睛里闪着好奇的光。
我们先从最基础的开始,了解 MATLAB 这个工具的各种函数和命令。
就像是给机器人准备好各种“零部件”,让它能顺利动起来。
比如说,我们要设定机器人的初始位置和姿态,这就好像是告诉机器人“嘿,你从这里出发,站好啦!”然后,再通过编程来控制它的运动轨迹。
有的同学想让机器人走直线,有的同学想让它拐个弯,还有的同学想让它走个复杂的曲线。
在这个过程中,可遇到了不少问题呢。
有个同学不小心把坐标设置错了,结果机器人“嗖”地一下跑到了不知道哪里去,大家哄堂大笑。
还有个同学在计算速度和加速度的时候出了差错,机器人的动作变得奇奇怪怪的,像是在跳“抽筋舞”。
不过,大家并没有气馁,而是一起努力找错误,修改代码。
终于,当我们看到那个小小的机器人按照我们设想的轨迹稳稳地行走时,那种成就感简直无法形容。
回到 MATLAB 机器人仿真程序本身,它其实就像是一个神奇的魔法盒子。
通过输入不同的指令和参数,我们可以创造出各种各样的机器人运动场景。
比如说,我们可以模拟机器人在不同地形上的行走,像是平坦的地面、崎岖的山路或者是湿滑的冰面。
这时候,我们就要考虑摩擦力、重力等各种因素对机器人运动的影响。
想象一下,机器人在冰面上小心翼翼地走着,生怕滑倒,是不是很有趣?而且,MATLAB 机器人仿真程序还能帮助我们优化机器人的设计。
比如说,如果我们发现机器人在某个动作上消耗了太多的能量,或者动作不够灵活,我们就可以通过调整程序中的参数来改进。
这就像是给机器人做了一次“整形手术”,让它变得更完美。
另外,我们还可以用它来进行多机器人的协同仿真。
想象一下,一群机器人在一起工作,有的负责搬运东西,有的负责巡逻,它们之间需要相互配合,避免碰撞。
这就需要我们精心设计它们的通信和协调机制,让它们像一支训练有素的团队一样高效工作。
基于Matlab的空间描点机器人建模与仿真报告

课程设计课程名称机器人学题目名称空间描点机器人建模仿真学生学院专业班级学号学生姓名指导教师目录1.课程设计要求 (1)2.空间描点机器人的设计 (2)2.1机器人构型及坐标 (2)2.2D-H参数表 (4)3.正运动学 (5)3.1齐次变换矩阵 (5)3.2 空间描点机器人工作空间 (6)4.几何法求逆解 (7)5.程序流程图 (8)6.总结分析 (9)7.Matlab程序附录 (10)7.1 Mov_6DOF_Rob_Lnya.m (10)7.2 DHfk6Dof_Lnya.m (12)7.3 IK_6DOF_Rob_Lnya.m (13)7.4 Build_6DOFRobot_Lnya.m (14)7.5 Erzhihua.m (14)7.6 draw_Workplace.m (15)7.7 Matrix_DH_Ln.m (16)7.8 Connect3D.m (17)1. 课程设计要求一,按照附件模板填写,要求有封面和目录,除签名处不能有手写。
二,主要内容包括下面几个部分,1,设计一款六自由度机器人,要求2,3,4,5关节中有一个是滑动关节,其余关节应为转动关节。
试构想该机器人的功能,并根据功能设定机器人的介绍参数(杆件长度及关节极限)2,建立机器人的正运动学模型,进行Matlab 运动仿真。
(分析机器人的工作空间,制作机器人各个运动的动画。
)注意事项:1)要求画出机器人的关节坐标系,列出DH 参数表,以及各个关节间的齐次变换矩阵。
2)Matlab仿真应画出工作空间的立体图和剖面图。
采用机器人产品的同学应与实际说明书的工作空间做对比。
自行设计的同学要做简单的分析讨论。
3)直接采用例程里面的三自由度机器人该部分得0 分。
3,实现逆运动学轨迹规划注意事项:1)这里特指机器人末端的轨迹规划,不是关节空间的轨迹规划。
2)要实现控制机器人末端在空间中完成某种轨迹。
(如直线,圆弧,心型,写字等)3)可以采用求解逆运动的方程或者是利用微分运动。
matlab程序--二自由度机器人的Matlab仿真

fo r k = 1: 1: 1000 tim e = k3 ts; H11 = a1 + 23 a33 co s( q (2) ) + 23 a43 sin ( q (2) ) ; H12 = a2 + a33 co s( q (2) ) + a43 sin ( q (2) ) ; H21 = a2 + a33 co s( q (2) ) + a43 sin ( q (2) ) ;
程的数值解 ,如图 1,图 2所示 。
op t = odese t; op t. R e lTo l = 1e - 8; u = 1; m c = 0. 85; m1 =
0. 04; m2 = 0. 14; L1 = 0. 1524; L2 = 0. 4318; g = 9. 81;
[ t, x ] = ode45 ( @ inv_pendulum , [ 0, 0. 5 ] , ze ro s(6, 1) , op t, …
(南京航空航天大学 , 南京 210016)
摘要 : 本文介绍了控制系统中的经典问题 ———倒立摆及其基本原理 , 简要介绍了 M a tlab中倒立摆控制的实现方法 。由于倒立摆的研究具 有重要的工程背景 , 本文结合了二级倒立摆的 ma tlab仿真 , 实现二自 由度机器人 PD 控制的 ma tlab仿真 ,取得了较好的效果 。
下面介绍倒立摆的动力学模型 。
根据动力学理论可得出二级倒立摆的运动方程 :
M (θ)θ¨+ C (θ,θ·)θ· = F (θ)
式中 ,θ = [α,θ1 ,θ2 ]T,且 α为小车位置 ,θ1 ,θ2 分别为下摆杆 、
上摆杆与垂直方向夹角 ,倒立摆系统的各个矩阵为
工业机器人Matlab仿真

工业机器人Matlab仿真工业机器人 Matlab 仿真,这可是个超级有趣的领域!先跟您唠唠工业机器人到底是啥。
您就想象一下,在一个大工厂里,有一群不知疲倦的“大力士”,它们的动作精准又迅速,能把各种复杂的工作完成得漂漂亮亮的。
这些“大力士”就是工业机器人啦。
那 Matlab 又是啥呢?它就像是一个神奇的魔法盒子,能帮我们把那些复杂的工业机器人的动作和行为模拟出来。
比如说,我之前去一家汽车生产厂参观,那里面的工业机器人可真是让我大开眼界。
有个机器人负责给汽车安装车门,它的手臂灵活得就像人的胳膊一样,准确无误地抓起车门,然后稳稳地安装到位。
我就在想啊,这背后肯定有一套厉害的程序在指挥它。
而 Matlab 仿真就是帮助工程师们在电脑上先把机器人的动作设计好,测试没问题了,再让机器人在实际生产中大展身手。
这就好比我们玩游戏前,先在心里演练一遍怎么通关,能大大提高成功率。
在 Matlab 仿真中,我们要给机器人设定各种参数,像它的运动速度、工作范围、抓取力度等等。
这就像是给机器人制定了一套“行为准则”,让它知道什么时候该快,什么时候该慢,什么时候该用力,什么时候该轻柔。
比如说,我们要让一个机器人去搬运一堆零件。
在 Matlab 里,我们就得先告诉它零件的位置、重量,还有搬运的路径。
然后通过一系列的计算和模拟,看看机器人能不能顺利完成任务。
如果中间出了问题,比如机器人碰到了障碍物,或者零件掉落了,我们就可以及时调整参数,重新再来,直到一切都完美无缺。
还有一次,我看到一个工程师在电脑前对着 Matlab 里的机器人模型发愁。
原来,他设计的机器人在搬运重物的时候总是不太稳定。
经过一番仔细的检查,发现是速度设置得太快了。
经过调整后,机器人终于能够稳稳地完成任务,工程师脸上也露出了满意的笑容。
通过 Matlab 仿真,我们不仅可以提前发现问题,还能优化机器人的工作效率,节省大量的时间和成本。
想象一下,如果没有这个仿真过程,直接让机器人在生产线上工作,一旦出了问题,那可就麻烦大了,会造成很大的损失。
matlab反演控制的机械手程序设计与仿真

MATLAB反演控制的机械手程序设计与仿真在MATLAB中设计并仿真一个反演控制(Inverse Kinematics Control)的机械手程序涉及多个步骤。
反演控制是机器人控制中的一个重要概念,它指的是从期望的末端执行器位置(例如机械手的末端)反推出关节的角度或位置。
以下是一个基本的步骤指南,用于在MATLAB中设计和仿真一个机械手的反演控制程序:1. 定义机械手的几何参数和模型首先,你需要定义机械手的几何参数,例如连杆长度、关节角度范围等。
然后,你可以使用MATLAB的Robotics Toolbox或其他相关工具箱来创建机械手的模型。
2. 编写反演运动学算法反演运动学算法是根据末端执行器的期望位置来计算关节角度的。
这个算法通常是基于机械手的几何参数和约束条件来编写的。
3. 设计控制器设计一个控制器来根据反演运动学算法计算出的关节角度来控制机械手的运动。
这可以是一个简单的PD(比例-微分)控制器或其他更复杂的控制策略。
4. 编写仿真程序使用MATLAB的Simulink或其他仿真工具来编写仿真程序。
在仿真程序中,你需要定义机械手的初始状态、输入信号(例如期望的末端执行器轨迹)以及控制算法。
5. 运行仿真并分析结果运行仿真程序,观察机械手的运动轨迹和性能。
你可以使用MATLAB的绘图功能来可视化结果,并分析机械手的运动是否符合期望。
示例代码框架以下是一个简化的示例代码框架,用于说明如何在MATLAB中编写反演控制程序:matlab% 定义机械手的几何参数和模型% ...% 编写反演运动学算法function joint_angles = inverse_kinematics(end_effector_position)% 根据末端执行器的位置计算关节角度% ...end% 设计控制器function control_input = controller(joint_angles, joint_velocities, desired_joint_angles)% 根据当前关节角度和速度以及期望的关节角度计算控制输入% ...end% 编写仿真程序% 定义初始状态、期望轨迹等% ...% 运行仿真循环for t = 1:num_timesteps% 计算期望的末端执行器位置desired_end_effector_position = ...;% 使用反演运动学算法计算期望的关节角度desired_joint_angles = inverse_kinematics(desired_end_effector_position);% 使用控制器计算控制输入control_input = controller(current_joint_angles, current_joint_velocities, desired_joint_angles);% 更新机械手的状态(例如使用Simulink或其他仿真方法)% ...% 保存或可视化结果(例如绘制轨迹)% ...end请注意,这只是一个简化的示例框架,实际的反演控制程序可能涉及更多的细节和复杂性。
SCARA机器人MATLAB仿真实验过程考核3(仿真图+程序)

专业实践I 过程考核表程序:L1 = Link([0 0 32 0 0],'standard');L2 = Link([0 0 25 pi 0],'standard');L3 = Link([0 30 0 0 1],'standard');L3.qlim=[0,30];%行程限制L4 = Link([0 15 0 0 0],'standard');%D-H建模DHS = SerialLink([L1 L2 L3 L4]);%建立机器人连杆DHS.plotopt={'workspace',[-50 50 -50 50 -50 50]}; = 'SCARA';%命名qz=[pi,0,0,0];qr=[3/2*pi,-pi/3,20,pi];step=40;[q,qd,qdd] = jtraj(qz, qr, step);%该函数假定时间从0变到1,共经过M步。
它将轨迹返回到Q中,速度和加速度返回到QD和QDD中,它们都是MxN矩阵,%每个时间步长一行,每个joint一列。
Tc = fkine(DHS,q);%正运动变换矩阵qi = ikine(DHS,Tc,qz,[1 1 1 1 0 0]);%逆运动学求解ikine(机器人,变换矩阵,关节角度,六自由度以下用零隐藏)qq=qi(40,:)T = fkine(DHS,qi);%逆运动变换矩阵[qL,qdL,qddL] = jtraj(qz, qq, step);DHS.plot(q)DHS.plot(qi)figure%绘制位移、速度、加速度曲线%正运动学图像subplot(2,2,1);i=1:4;plot(q(:,i));title('位置');grid on;subplot(2,2,2);i=1:4;plot(qd(:,i));title('速度');grid on;subplot(2,2,3);i=1:4;plot(qdd(:,i));title('加速度');grid on;x = zeros(40,1);y = zeros(40,1);z = zeros(40,1);for j = 1:40x(j) = T(1,4,j);y(j) = T(2,4,j);z(j) = T(3,4,j);endsubplot(2,2,4)plot3(x,y,z,'b')title('运行轨迹')grid onfigure%绘制位移、速度、加速度曲线%逆运动学图像subplot(2,2,1);i=1:4;plot(qL(:,i));title('位置');grid on;subplot(2,2,2);i=1:4;plot(qdL(:,i));title('速度');grid on;subplot(2,2,3);i=1:4;plot(qddL(:,i));title('加速度');grid on;x = zeros(40,1);y = zeros(40,1);z = zeros(40,1);for j = 1:40x(j) = Tc(1,4,j);y(j) = Tc(2,4,j);z(j) = Tc(3,4,j);endsubplot(2,2,4)plot3(x,y,z,'b')title('运行轨迹')grid on。
基于MATLAB的六自由度工业机器人运动分析及仿真

基于MATLAB的六自由度工业机器人运动分析及仿真六自由度工业机器人是一种常见的工业自动化设备,通过对其运动进行分析和仿真,可以对其性能进行评估和优化。
MATLAB是一种强大的数学计算软件,在工程领域广泛应用,可以帮助我们进行机器人的运动分析和仿真。
首先,我们可以使用MATLAB对六自由度机器人进行建模。
六自由度机器人具有六个自由度,分别为三个旋转自由度和三个平移自由度。
我们可以使用MATLAB的机器人工具箱来建立机器人的模型,并定义其关节参数和连接方式。
通过模型可以获得机器人的几何结构、动力学参数和运动学方程。
接下来,我们可以使用MATLAB进行机器人的运动分析。
运动分析是指通过对机器人的运动学和动力学进行计算,从而获得机器人的运动和力学特性。
机器人的运动学分析主要是利用机器人的几何结构来推导出末端执行器的位置和姿态。
可以使用MATLAB的运动学工具函数来计算机器人的正运动学和逆运动学。
机器人的动力学分析主要是研究机器人的运动和力学特性之间的关系。
动力学分析可以帮助我们确定机器人的运动特性和关节力矩。
我们可以使用MATLAB的动力学工具箱来建立机器人的动力学模型,并使用动力学工具函数来计算机器人的动力学性能。
最后,我们可以使用MATLAB进行机器人的仿真。
机器人的仿真是通过对机器人的动力学进行数值计算,来模拟机器人的运动和力学特性。
通过仿真可以验证机器人的设计和控制方案,并进行参数优化。
在MATLAB 中,我们可以使用数值计算函数和绘图函数来进行机器人的仿真和可视化。
总结起来,基于MATLAB的六自由度工业机器人运动分析及仿真可以帮助我们对机器人的运动和力学特性进行研究和优化。
通过建立机器人的模型,进行运动分析和动力学分析,以及进行仿真和可视化,可以帮助我们理解和改进机器人的性能,在工业自动化领域发挥更大的作用。
多机器人编队控制matlab仿真代码

多机器人编队控制matlab仿真代码1.引言1.1 概述在引言部分的概述中,我们将重点介绍多机器人编队控制的基本概念和研究背景。
随着技术的不断发展,机器人在各个领域中得到了广泛的应用,尤其是在无人系统和自主导航领域。
多机器人编队控制是指通过在多个机器人之间建立合作关系和协同工作,实现一定的任务目标。
在这种编队控制中,多个机器人之间需要交换信息、协调动作,并按照一定的规则进行排列或者协同工作。
在过去的几十年中,多机器人编队控制已经成为机器人领域的一个热点研究方向。
它在军事、灾害救援、工业生产等领域中发挥重要的作用。
多机器人编队控制可以提高任务的执行效率,增强系统的鲁棒性和可靠性,并且可以应对一些单个机器人无法完成的大规模任务。
为了实现多机器人编队控制,研究人员提出了各种不同的控制策略和算法。
这些控制策略可以分为集中式和分布式两种方式。
集中式控制是指由一个中心节点来控制整个编队的行为,而分布式控制则是指每个机器人根据本地信息和与邻近机器人的通信,来决定自己的行为。
通过多机器人编队控制,可以实现机器人之间的任务分工和协同工作,提高整个系统的性能和效率。
此外,多机器人编队控制还涉及到一些重要的问题,如编队形成、路径规划、障碍物避障、通信协议等。
本文将从多机器人编队控制的概述开始,介绍其重要性,并对未来的研究方向进行展望。
通过对多机器人编队控制的研究,我们可以进一步推动机器人技术的发展,并为解决各种实际问题提供更加高效和可靠的解决方案。
1.2 文章结构文章结构部分的内容可以这样编写:本文将按照以下结构进行介绍和讨论多机器人编队控制的相关内容:1. 引言:首先概述了多机器人编队控制的概念和背景,以及本文的目的。
2. 正文:分为两个部分进行介绍。
2.1 多机器人编队控制概述:详细解释了什么是多机器人编队控制,包括其定义、目标和应用领域。
同时,介绍了多机器人编队控制的研究现状和发展趋势。
2.2 多机器人编队控制的重要性:着重论述了多机器人编队控制的重要性和优势。
MATLAB机器人仿真程序

MATLAB机器人仿真程序随着机器人技术的不断发展,机器人仿真技术变得越来越重要。
MATLAB是一款强大的数学计算软件,也被广泛应用于机器人仿真领域。
本文将介绍MATLAB在机器人仿真程序中的应用。
一、MATLAB简介MATLAB是MathWorks公司开发的一款商业数学软件,主要用于算法开发、数据可视化、数据分析以及数值计算等。
MATLAB具有丰富的工具箱,包括信号处理、控制系统、神经网络、图像处理等,可以方便地实现各种复杂的计算和分析。
二、MATLAB机器人仿真程序在机器人仿真领域,MATLAB可以通过Robotics System Toolbox实现各种机器人的仿真。
该工具箱包含了机器人运动学、动力学、控制等方面的函数库,可以方便地实现机器人的建模、控制和可视化。
下面是一个简单的MATLAB机器人仿真程序示例:1、建立机器人模型首先需要定义机器人的几何参数、连杆长度、质量等参数,并使用Robotics System Toolbox中的函数建立机器人的运动学模型。
例如,可以使用robotics.RigidBodyTree函数来建立机器人的刚体模型。
2、机器人运动学仿真在建立机器人模型后,可以使用Robotics System Toolbox中的函数进行机器人的运动学仿真。
例如,可以使用robotics.Kinematics函数计算机器人的位姿,并使用robotics.Plot函数将机器人的运动轨迹可视化。
3、机器人动力学仿真除了运动学仿真外,还可以使用Robotics System Toolbox中的函数进行机器人的动力学仿真。
例如,可以使用robotics.Dynamic函数计算机器人在给定速度下的加速度和力矩,并使用robotics.Plot函数将机器人的运动轨迹可视化。
4、机器人控制仿真可以使用Robotics System Toolbox中的函数进行机器人的控制仿真。
例如,可以使用robotics.Controller函数设计机器人的控制器,并使用robotics.Plot函数将机器人的运动轨迹可视化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
附录
MATLAB 机器人工具箱仿真程序:
1)运动学仿真模型程序(Rob1.m)
L1=link([pi/2 150 0 0])
L2=link([0 570 0 0])
L3=link([pi/2 130 0 0])
L4=link([-pi/2 0 0 640])
L5=link([pi/2 0 0 0])
L6=link([0 0 0 95])
r=robot({L1 L2 L3 L4 L5 L6})
=’MOTOMAN-UP6’ % 模型的名称
>>drivebot(r)
2)正运动学仿真程序(Rob2.m)
L1=link([pi/2 150 0 0])
L2=link([0 570 0 0])
L3=link([pi/2 130 0 0])
L4=link([-pi/2 0 0 640])
L5=link([pi/2 0 0 0])
L6=link([0 0 0 95])
r=robot({L1 L2 L3 L4 L5 L6})
=’MOTOMAN-UP6’
t=[0:0.01:10];%产生时间向量
qA=[0 0 0 0 0 0 ]; %机械手初始关节角度
qAB=[-pi/2 -pi/3 0 pi/6 pi/3 pi/2 ];%机械手终止关节角度figure('Name','up6机器人正运动学仿真演示');%给仿真图像命名q=jtraj(qA,qAB,t);%生成关节运动轨迹
T=fkine(r,q);%正向运动学仿真函数
plot(r,q);%生成机器人的运动
figure('Name','up6机器人末端位移图')subplot(3,1,1);
plot(t, squeeze(T(1,4,:)));
xlabel('Time (s)');
ylabel('X (m)');
subplot(3,1,2);
plot(t, squeeze(T(2,4,:)));
xlabel('Time (s)');
ylabel('Y (m)');
subplot(3,1,3);
plot(t, squeeze(T(3,4,:)));
xlabel('Time (s)');
ylabel('Z (m)');
x=squeeze(T(1,4,:));
y=squeeze(T(2,4,:));
z=squeeze(T(3,4,:));
figure('Name','up6机器人末端轨迹图'); plot3(x,y,z);
3)机器人各关节转动角度仿真程序:(Rob3.m)L1=link([pi/2 150 0 0 ])
L2=link([0 570 0 0])
L3=link([pi/2 130 0 0])
L4=link([-pi/2 0 0 640])
L5=link([pi/2 0 0 0 ])
L6=link([0 0 0 95])
r=robot({L1 L2 L3 L4 L5 L6})
='motoman-up6'
t=[0:0.01:10];
qA=[0 0 0 0 0 0 ];
qAB=[ pi/6 pi/6 pi/6 pi/6 pi/6 pi/6]; q=jtraj(qA,qAB,t);
Plot(r,q);
subplot(6,1,1);
plot(t,q(:,1));
title('转动关节1');
xlabel('时间/s');
ylabel('角度/rad');
subplot(6,1,2);
plot(t,q(:,2));
title('转动关节2');
xlabel('时间/s');
ylabel('角度/rad');
subplot(6,1,3);
plot(t,q(:,3));
title('转动关节3');
xlabel('时间/s');
ylabel('角度/rad');
subplot(6,1,4);
plot(t,q(:,4));
title('转动关节4');
xlabel('时间/s');
ylabel('角度/rad' );
subplot(6,1,5);
plot(t,q(:,5));
title('转动关节5');
xlabel('时间/s');
ylabel('角度/rad');
subplot(6,1,6);
plot(t,q(:,6));
title('转动关节6');
xlabel('时间/s');
ylabel('角度/rad');
4)机器人各关节转动角速度仿真程序:(Rob4.m)
t=[0:0.01:10];
qA=[0 0 0 0 0 0 ];%机械手初始关节量
qAB=[ 1.5709 -0.8902 -0.0481 -0.5178 1.0645 -1.0201]; [q,qd,qdd]=jtraj(qA,qAB,t);
Plot(r,q);
subplot(6,1,1);
plot(t,qd(:,1));
title('转动关节1');
xlabel('时间/s');
ylabel('rad/s');
subplot(6,1,2);
plot(t,qd(:,2));
title('转动关节2');
xlabel('时间/s');
ylabel('rad/s');
subplot(6,1,3);
plot(t,qd(:,3));
title('转动关节3');
xlabel('时间/s');
ylabel('rad/s');
subplot(6,1,4);
plot(t,qd(:,4));
title('转动关节4');
xlabel('时间/s');
ylabel('rad/s' );
subplot(6,1,5);
plot(t,qd(:,5));
title('转动关节5');
xlabel('时间/s');
ylabel('rad/s');
subplot(6,1,6);
plot(t,qd(:,6));
title('转动关节6');
xlabel('时间/s');
ylabel('rad/s');
5)机器人各关节转动角加速度仿真程序:(Rob5.m)
t=[0:0.01:10];%产生时间向量
qA=[0 0 0 0 0 0]
qAB =[1.5709 -0.8902 -0.0481 -0.5178 1.0645 -1.0201]; [q,qd,qdd]=jtraj(qA,qAB,t);
figure('name','up6机器人机械手各关节加速度曲线');
subplot(6,1,1);
plot(t,qdd(:,1));
title('关节1');
xlabel('时间 (s)');
ylabel('加速度 (rad/s^2)');
subplot(6,1,2);
plot(t,qdd(:,2));
title('关节2');
xlabel('时间 (s)');
ylabel('加速度 (rad/s^2)');
subplot(6,1,3);
plot(t,qdd(:,3));
title('关节3');
xlabel('时间 (s)');
ylabel('加速度 (rad/s^2)') subplot(6,1,4);
plot(t,qdd(:,4));
title('关节4');
xlabel('时间 (s)');
ylabel('加速度 (rad/s^2)') subplot(6,1,5);
plot(t,qdd(:,5));
title('关节5');
xlabel('时间 (s)');
ylabel('加速度 (rad/s^2)') subplot(6,1,6);
plot(t,qdd(:,6));
title('关节6');
xlabel('时间 (s)');
ylabel('加速度 (rad/s^2)')。
