大学概率论必背公式
大学概率论与数理统计公式全集

大学概率论与数理统计公式全集一、随机事件和概率1、随机事件及其概率2、概率的定义及其计算二、随机变量及其分布1、分布函数性质P(X 乞b) =F(b) P(a :: X 冬b) = F(b) _ F(a)2、离散型随机变量3、连续型随机变量三、多维随机变量及其分布1、离散型二维随机变量边缘分布 P i =P(X =X i )二% P(X = xi ,丫二 yj ) = ' pij pj =P( Y=yj )=' P(X 二 X j , 丫二 yj )=' pij j j离散型二维随机变量条件分布P(X =X j ,Y =yj )pij…= P(X =X j Y =y j ),i=1,2jP(丫 =yj )P j P(X=X j ,Y=y j )p j2、 P i j P ji3、x yf(u,v)dvdu4、连续型二维随机变量边缘分布函数与边缘密度函数 边缘分布函数: F x (x) = [「f(u,v)dvdu 边缘密度函数:f x (x)二.-^o a-bof(u,y)du*^0.■bof (x, v)y ■:: F y (y)f (u,v)dudv f Y (y)二 5、二维随机变量的条件分布fYx (yx)二■■■■■y < fxY (xy)二<x ::: ■::x Y四、随机变量的数字特征1、数学期望离散型随机变量:E(X)=.;「X k P k连续型随机变量:E(X)二=xf(x)dx2、数学期望的性质(1)E(C) =C,C为常数E[E(X)] =E(X) E(CX) =CE(X)(2)E(X _Y) =E(X) _E(Y) E(aX _b) =aE(X) _b E(C^X^ ■ C n X n^C1E(X1^ ■ C n E(X n) ⑶ 若GY相互独立则:E(XY) =E(X)E(Y)(4) [E(XY)]2 <E2(X)E2(Y)3、万差:D(x) =E(X2) —E2(x)4、方差的性质(1) D(C) =0 D[D(X)] =0 D(aX _b) =a2D(X) D(X) :::E(X -C)2⑵ D(X _Y)二D(X) • D(Y) _2Cov(X,Y)若 GY相互独立则:D(X _Y)二D(X) • D(Y)5、协方差:Cov(X,Y)二E(X,Y) _E(X)E(Y)若 GY相互独立则:Cov(X,Y)=06、相关系数:认「(X,Y)〜Cov(X,丫)若GY相互独立则:认=0即GY不相关J D(X)阿石7、协方差和相关系数的性质(1)Cov(X,X) =D(X) Cov(X,Y)二Cov(Y, X)(2)Cov(X1 X2,Y) =Cov(X1,Y) Cov(X2,Y) Cov(aX c, bY • d)二abCov(X,Y)&常见数学分布的期望和方差五、大数定律和中心极限定理1、 切比雪夫不等式若 E(X)-」.,D(X)=:;2,对于任意'.0 有 P{X _E(X) _ }空里^2 或 P{X _E(X) ::: }n n2、 大数定律:若X i …X n 相互独立且「时,—、• X i —D r-7 E(X i )ni 4ni二nn(1)若 X i X n 相互独立,E(X i ) =A i , D(X i ) =52且 O i 2兰M 贝y : -Z X i — 1瓦 E(X i ),(n T ©nyny1n⑵若X i …X n 相互独立同分布,且E(X j )=n 则当n 时:―、X, P> Jn y3、 中心极限定理(1) 独立同分布的中心极限定理:均值为 」,方差为C 20的独立同分布时,当n 充分 大时有:n' X k —n ・iY n = ------------------- 二 N(0,1)U n cr(2) 拉普拉斯定理:随机变量n (n =1,2 )~B( n, p)则对任意G 有:xt 2lim P { :n np兰x} = f -j^e 2dt =Q (x) x -°p(1-p) - : .2 二六、数理统计1、总体和样本n _(5) 样本 k 阶中心距:B k =Mk(X i -X)k ,^2,3'nm(1)样本平均值: n n n2X 」、X i (2)样本方差:S 2匚、(X i -X)2L' (X i 2-nx )n-1y n -1(3)样本标准差:,彳 n ns= 1v(X i-X)2(4)样本 k 阶原点距:A k X i k,k=1,2 … ,n -1^(X 1,X 2 X n )的联合分布为 F(X 1,X 2 X n )F (X k )心(3)近似计算:nP(a 乞、X k Eb) =P(生' X k -n 」■k'.nc<^n 1才一门.」:泸- nc、、..总体X 的分布函数F(X)样本 2、统计量(6)次序统计量:设样本(X1,X2…X n)的观察值凶七和,将为,X?…X.按照由小到大的次,记取值为X(i)的样本分量为X(i),则称X(1宀(2)「乞x(n) 序重新排列,得到X(1)乞X(2) <X(n)为样本(X1,X2…X n)的次序统计量。
概率论的公式大全

概率论的公式大全概率论是数学中的一门重要分支,用于研究随机事件的发生概率和规律性。
下面是概率论中的一些常用公式和定理,供参考:1.基本概率公式:P(A)=n(A)/n(S)其中,P(A)表示事件A发生的概率,n(A)表示事件A发生的情况数,n(S)表示样本空间中所有事件发生的情况数。
2.加法定理:P(A∪B)=P(A)+P(B)-P(A∩B)其中,P(A∪B)表示事件A或事件B发生的概率,P(A∩B)表示事件A和事件B发生的概率。
3.乘法定理:P(A∩B)=P(B,A)×P(A)其中,P(B,A)表示在事件A已经发生的条件下,事件B发生的概率。
4.互斥事件的概率:若事件A和事件B互斥(即不能同时发生),则P(A∪B)=P(A)+P(B) 5.条件概率:P(A,B)=P(A∩B)/P(B)其中,P(A,B)表示在事件B已经发生的条件下,事件A发生的概率。
6.贝叶斯定理:P(A,B)=P(B,A)×P(A)/P(B)其中,P(A,B)表示在事件B已经发生的条件下,事件A发生的概率;P(B,A)表示在事件A已经发生的条件下,事件B发生的概率。
7.全概率公式:P(A)=∑[P(A∩B_i)]其中,事件B_1,B_2,...,B_n互斥且构成样本空间,P(B_i)不为0,P(A∩B_i)表示事件A和事件B_i同时发生的概率。
8.期望值:E(X)=∑[x_i×P(X=x_i)]其中,X为随机变量,x_i为随机变量X的取值,P(X=x_i)为随机变量X取值为x_i的概率。
9.方差:Var(X) = E[(X - E(X))^2]其中,X为随机变量。
10.协方差:Cov(X, Y) = E[(X - E(X)) × (Y - E(Y))]其中,X和Y为两个随机变量。
11.独立事件的概率:若事件A和事件B独立,即P(A∩B)=P(A)×P(B)12.独立随机变量的期望值:E(XY)=E(X)×E(Y)其中,X和Y为独立随机变量。
概率论与数理统计公式大全

概率论与数理统计公式大全概率论和数理统计作为数学的两个重要分支,被广泛应用于各个领域。
无论是在学术研究还是实际应用中,熟悉并掌握相关的公式是非常重要的。
本文将为您提供概率论与数理统计公式的大全,帮助您更好地理解和应用这两门学科。
一、概率论公式1. 概率公式- 概率的定义:P(A) = N(A) / N(S),其中P(A)表示事件A发生的概率,N(A)代表事件A的样本点个数,N(S)表示样本空间中的样本点总数。
- 加法法则:P(A∪B) = P(A) + P(B) - P(A∩B),其中P(A∪B)表示事件A或事件B发生的概率,P(A∩B)表示事件A和事件B同时发生的概率。
- 乘法法则:P(A∩B) = P(A) × P(B|A),其中P(B|A)表示在事件A 发生的条件下,事件B发生的概率。
2. 条件概率公式- 条件概率的定义:P(A|B) = P(A∩B) / P(B),其中P(A|B)表示在事件B发生的条件下,事件A发生的概率。
- 全概率公式:P(A) = ∑[P(Bi) × P(A|Bi)],其中Bi为样本空间的一个划分,P(Bi)表示事件Bi发生的概率,P(A|Bi)表示在事件Bi发生的条件下,事件A发生的概率。
3. 事件独立性公式- 事件A和事件B独立的定义:P(A∩B) = P(A) × P(B),即事件A和事件B同时发生的概率等于事件A发生的概率乘以事件B发生的概率。
- 事件的相互独立:若对于任意的事件A1,A2,...,An,有P(A1∩A2∩...∩An) = P(A1) × P(A2) × ... × P(An),则称事件A1,A2,...,An相互独立。
4. 随机变量- 随机变量的定义:随机变量X是样本空间到实数集的映射。
- 随机变量的分布函数:F(x) = P(X≤x),表示随机变量X小于等于x的概率。
- 随机变量的概率密度函数(连续型随机变量):f(x)是非负函数,且对于任意实数区间[a, b],有P(a≤X≤b) = ∫[a, b]f(x)dx。
《概率论公式大全》Word文档

概率论公式1.随机事件及其概率吸收律:AAB A A A A =⋃=∅⋃Ω=Ω⋃)( AB A A A A A =⋃⋂∅=∅⋂=Ω⋂)( )(AB A B A B A -==-反演律:B A B A =⋃ B A AB ⋃=n i i n i i A A 11=== ni in i i A A 11===2.概率的定义及其计算)(1)(A P A P -=若B A ⊂ )()()(A P B P A B P -=-⇒对任意两个事件A , B , 有 )()()(AB P B P A B P -=-加法公式:对任意两个事件A , B , 有)()()()(AB P B P A P B A P -+=⋃)()()(B P A P B A P +≤⋃)()1()()()()(2111111n n n n k j i k j i n j i j i n i i n i i A A A P A A A P A A P A P A P -≤<<≤≤<≤==-+++-=∑∑∑3.条件概率()=A B P)()(A P AB P乘法公式 ())0)(()()(>=A P A B P A P AB P()())0)(()()(12112112121>=--n n n n A A A P A A A A P A A P A P A A A P全概率公式 ∑==n i i AB P A P 1)()( )()(1i ni i B A P B P ⋅=∑=Bayes 公式)(A B P k )()(A P AB P k = ∑==n i i i k k B A P B P B A P B P 1)()()()(4.随机变量及其分布分布函数计算)()()()()(a F b F a X P b X P b X a P -=≤-≤=≤<5.离散型随机变量(1) 0 – 1 分布1,0,)1()(1=-==-k p p k X P k k(2) 二项分布 ),(p n B若P ( A ) = pn k p p C k X P k n k k n ,,1,0,)1()( =-==-*Possion 定理0lim >=∞→λn n np 有 ,2,1,0!)1(lim ==---∞→k k e p p C kk n n k n kn n λλ(3) Poisson 分布 )(λP,2,1,0,!)(===-k k e k X P kλλ6.连续型随机变量(1) 均匀分布 ),(b a U⎪⎩⎪⎨⎧<<-=其他,0,1)(b x a ab x f ⎪⎪⎩⎪⎪⎨⎧--=1,,0)(a b a x x F(2) 指数分布 )(λE⎪⎩⎪⎨⎧>=-其他,00,)(x e x f x λλ ⎩⎨⎧≥-<=-0,10,0)(x e x x F x λ(3) 正态分布 N (m , s 2 )+∞<<∞-=--x e x f x 222)(21)(σμσπ⎰∞---=x t t e x F d 21)(222)(σμσπ*N (0,1) — 标准正态分布 +∞<<∞-=-x e x x 2221)(πϕ +∞<<∞-=Φ⎰∞--x t e x xt d 21)(22π7.多维随机变量及其分布二维随机变量( X ,Y )的分布函数⎰⎰∞-∞-=xy dvdu v u f y x F ),(),(边缘分布函数与边缘密度函数⎰⎰∞-+∞∞-=xX dvdu v u f x F ),()( ⎰+∞∞-=dv v x f x f X ),()( ⎰⎰∞-+∞∞-=y Y dudv v u f y F ),()(⎰+∞∞-=du y u f y f Y ),()(8.连续型二维随机变量(1) 区域G 上的均匀分布,U ( G ) ⎪⎩⎪⎨⎧∈=其他,0),(,1),(G y x A y x f(2)二维正态分布+∞<<-∞+∞<<∞-⨯-=⎥⎥⎦⎤⎢⎢⎣⎡-+------y x e y x f y y x x ,121),(2222212121212)())((2)()1(21221σμσσμμρσμρρσπσ9.二维随机变量的 条件分布 0)()()(),(>=x f x y f x f y x f X X Y X 0)()()(>=y f y x f y f Y Y X Y ⎰⎰+∞∞-+∞∞-==dy y f y x f dy y x f x f Y Y X X )()(),()( ⎰⎰+∞∞-+∞∞-==dx x f x y f dx y x f y f X X Y Y )()(),()( )(y x f Y X )(),(y f y x f Y = )()()(y f x f x y f Y X X Y =)(x y f X Y )(),(x f y x f X = )()()(x f y f y x f X Y Y X =10.随机变量的数字特征数学期望 ∑+∞==1)(k k k p x X E⎰+∞∞-=dx x xf X E )()(随机变量函数的数学期望X 的 k 阶原点矩)(k X EX 的 k 阶绝对原点矩)|(|k X EX 的 k 阶中心矩)))(((k X E X E -X 的 方差)()))(((2X D X E X E =-X ,Y 的 k + l 阶混合原点矩)(l k Y X EX ,Y 的 k + l 阶混合中心矩()l k Y E Y X E X E ))(())((--X ,Y 的 二阶混合原点矩)(XY EX ,Y 的二阶混合中心矩 X ,Y 的协方差()))())(((Y E Y X E X E --X ,Y 的相关系数XY Y D X D Y E Y X E X E ρ=⎪⎪⎭⎫ ⎝⎛--)()())())(((X 的方差D (X ) =E ((X - E (X ))2))()()(22X E X E X D -=协方差()))())(((),cov(Y E Y X E X E Y X --=)()()(Y E X E XY E -= ())()()(21Y D X D Y X D --±±= 相关系数)()(),cov(Y D X D Y X XY =ρ(注:素材和资料部分来自网络,供参考。
大学概率论公式总结

密度函数具有下面性质: f (x) 0 。
f (x)dx 1
P(X x) P(x X x dx) f (x)dx 。积分元 f (x)dx 在连续型随机变量理论
中所起的作用与 P( X xk) pk 在离散型随机变量理论中所起的作用相类似。
-1-
概率论与数理统计
设随机变量 X 的值只落在[a,b]内,其密度函数 f (x) 在[a,b]
上为常数 1 ,即 ba
当 a≤x1<x2≤b 时,X 落在区间
f
(x)
1
b
0,
a
,
a≤x≤b 其他
( x1, x2 )内的概率为
P( x1
X
x2 )
x2 b
x1 a
-2-
概率论与数理统计
指数分布
ex , x 0 ,
正态分布或高斯(Gauss)分布,记为 X ~ N(, 2) 。
f (x) 具有如下性质:
1° f (x) 的图形是关于 x 对称的;
2° 当 x 时, f () 1 为最大值;
若
X
~
N(, 2) ,则
X
2
的分布函数为
F(x) 1
(t )2
x
e
2 2
dt
2
(x) 是不可求积函数,其函数值,已编制成表可供查用。
D
并称 f(x,y)为 =(X,Y)的分布密度或称为 X 和 Y 的联合分
布密度。分布密度 f(x,y)具有下面两个性质: (1) f(x,y)≥0;
(2)
f (x, y)dxdy 1.
离 散 型 与 P(X x,Y y) P(x X x dx,y Y y dy) f (x,y)dxdy
概率论基本公式

概率论与数理统计基本公式第一部分 概率论基本公式1、A BA B AAB; A BA(B A) 2、对偶率: AB A B ;ABA B .3、概率性率:P ( A B ) P( A) P(AB ), 特别, BA 时有:P( A B) P( A) P(B); P(A) P(B)有限可加: A 1、 A 2 为不相容事件,则 P( A 1A 2 ) P( A 1)P(A 2 )对任意两个事件有:P( AB)P( A) P( B)P( AB)4、古典概型例: n 双鞋总共 2n 只,分为 n 堆,每堆为 2只,事件 A 每堆自成一双鞋的概率 解:分堆法: C 22 n( (2n)!,自成一双为: n !,则 P( A)n!!!22n - 2) 2C2n5、条件概率P(B | A)P( AB), 称为在事件 A 条件下,事件 B 的条件概率, P( B)称为无条件概率。
P( A)乘法公式: P(AB)P(A)P(B | A) P(AB)P(B)P(A | B)全概率公式: P(B)P(A i )P(B | A i )i贝叶斯公式: P(A i | B)P( A i B)P( A i )P(B | A i )P( B) P( A j )P( B | A j )j例:有三个罐子, 1 号装有 2 红1黑共 3个球,2号装有 3红1黑 4个球,3 号装有 2 红 2黑 4 个球,某人随机从其中一罐,再从该罐中任取一个球, ( 1)求取得红球的概率; ( 2)如果取得是红球,那么是从第一个罐中取出的概率为多少?解: 设B i { 球取自 i 号罐 } , i。
{ 取得是红球 } ,由题知、、是一个完备事件(1) 1,2,3 AB 1B 2B 3由全概率公式 P( B)P( A i )P( B | A i ),依题意,有: P( A | B 1 )2;P(A|B 2)3;P(A|B 3) 1 .i342P( B 1)P(B 2 ) P( B 3 )1, P( A) 0.639.3(2)由贝叶斯公式: P(B 1 | A)P( A | B 1)P(B 1)0.348.P( A)6、独立事件( 1) P(AB)=P(A)P(B), 则称 A 、 B 独立。
(完整版)大学概率论与数理统计公式全集

大学概率论与数理统计公式全集一、随机事件和概率1、随机事件及其概率2、概率的定义及其计算二、随机变量及其分布1、分布函数性质FbF(aba<≤=P-X)(b()()bFX()P=≤)2、离散型随机变量3、连续型随机变量三、多维随机变量及其分布1、离散型二维随机变量边缘分布∑∑======⋅jjijjii i py Y x X P x X P p ),()(∑∑======⋅iiijjij j py Y x X P y Y P p ),()(2、离散型二维随机变量条件分布2,1,)(),()(=========⋅i P p y Y P y Y x X P y Y x X P p jij j j i j i j i2,1,)(),()(=========⋅j P p x X P y Y x X P x X y Y P p i ij i j i i j i j3、连续型二维随机变量( X ,Y )的联合分布函数⎰⎰∞-∞-=xydvdu v u f y x F ),(),( 4、连续型二维随机变量边缘分布函数与边缘密度函数边缘分布函数:⎰⎰∞-+∞∞-=xX dvdu v u f x F ),()( 边缘密度函数:⎰+∞∞-=dv v x f x f X ),()( ⎰⎰∞-+∞∞-=y Y dudv v u f y F ),()( ⎰+∞∞-=du y u f y f Y ),()(5、二维随机变量的条件分布+∞<<-∞=y x f y x f x y f X X Y ,)(),()( +∞<<-∞=x y f y x f y x f Y Y X ,)(),()(四、随机变量的数字特征1、数学期望离散型随机变量:∑+∞==1)(k k k p x X E 连续型随机变量:⎰+∞∞-=dx x xf X E )()(2、数学期望的性质(1)为常数C ,)(C C E = )()]([X E X E E = )()(X CE CX E =(2))()()(Y E X E Y X E ±=± b X aE b aX E ±=±)()( )()()(1111n n n n X E C X E C X C X C E +=+ (3)若XY 相互独立则:)()()(Y E X E XY E = (4))()()]([222Y E X E XY E ≤ 3、方差:)()()(22X E X E X D -= 4、方差的性质(1)0)(=C D 0)]([=X D D )()(2X D a b aX D =± 2)()(C X E X D -<(2)),(2)()()(Y X Cov Y D X D Y X D ±+=± 若XY 相互独立则:)()()(Y D X D Y X D +=± 5、协方差:)()(),(),(Y E X E Y X E Y X Cov -= 若XY 相互独立则:0),(=Y X Cov 6、相关系数:)()(),(),(Y D X D Y X Cov Y X XY==ρρ 若XY 相互独立则:0=XYρ即XY 不相关7、协方差和相关系数的性质 (1))(),(X D X X Cov = ),(),(X Y Cov Y X Cov =(2)),(),(),(2121Y X Cov Y X Cov Y X X Cov +=+ ),(),(Y X abCov d bY c aX Cov =++8、常见数学分布的期望和方差五、大数定律和中心极限定理1、切比雪夫不等式若,)(,)(2σμ==X D X E 对于任意0>ξ有2)(})({ξξX D X E X P ≤≥-或2)(1})({ξξX D X E X P -≥<- 2、大数定律:若n X X 1相互独立且∞→n 时,∑∑==−→−ni iDni i X E nX n 11)(11(1)若n X X 1相互独立,2)(,)(i i i i X D X E σμ==且M i ≤2σ则:∑∑==∞→−→−ni iPni i n X E nX n11)(),(11(2)若n X X 1相互独立同分布,且i i X E μ=)(则当∞→n 时:μ−→−∑=Pn i i X n 11 3、中心极限定理(1)独立同分布的中心极限定理:均值为μ,方差为02>σ的独立同分布时,当n 充分大时有:)1,0(~1N n n XY nk kn −→−-=∑=σμ(2)拉普拉斯定理:随机变量),(~)2,1(p n B n n =η则对任意x 有:⎰∞--+∞→Φ==≤--xt n x x dtex p np np P )(21})1({lim 22πη(3)近似计算:)()()()(11σμσμσμσμσμn n a n n b n n b n n Xn n a P b X a P nk knk k -Φ--Φ≈-≤-≤-=≤≤∑∑==1、总体和样本总体X 的分布函数)(x F 样本),(21n X X X 的联合分布为)(),(121k nk n x F x x x F =∏=2、统计量(1)样本平均值:∑==ni i X n X 11(2)样本方差:∑∑==--=--=ni i ni i X n X n X X n S 122122)(11)(11(3)样本标准差:∑=--=ni i X X n S 12)(11(4)样本k 阶原点距: 2,1,11==∑=kXn A ni ki k(5)样本k 阶中心距:∑==-==ni k ik k k X XnM B 13,2,)(1(6)次序统计量:设样本),(21n X X X 的观察值),(21n x x x ,将n x x x 21,按照由小到大的次序重新排列,得到)()2()1(n x x x ≤≤≤ ,记取值为)(i x 的样本分量为)(i X ,则称)()2()1(n X X X ≤≤≤ 为样本),(21n X X X 的次序统计量。
概率论重要公式大全必看
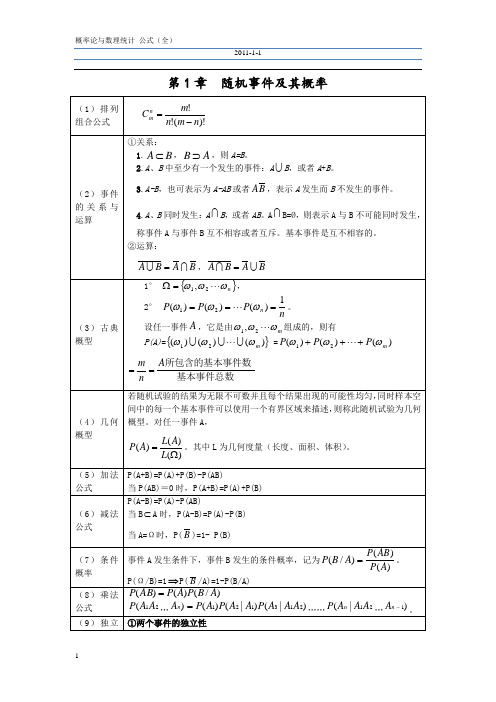
称事件 A 与事件 B 互不相容或者互斥。基本事件是互不相容的。 ②运算:
AB AB,AB AB
(3)古典 概型
1° 1, 2 n ,
2°
P(1 )
P( 2
)
P( n
)
1 n
。
设任一事件 A ,它是由1, 2 m 组成的,则有
F
1 (n2 , n1 )
第四章 随机变量的数字特征
(1) 一维 随机 变量 的数 字特 征
期望 期望就是平均值
函数的期望
离散型
n
E( X ) xk pk k 1
Y=g(X)
n
E(Y ) g(xk ) pk k 1
方差 D(X)=E[X-E(X)]2,
标准差 (X ) D(X ) , D( X ) [xk E( X )]2 pk k
Cii , 2
C
i2
2 i
i
i
若 X1, X2 Xn 相 互 独 立 , 其 分 布 函 数 分 别 为
Fx1 (x),Fx2 (x) Fxn (x) ,则 Z=max,min(X1,X2,…Xn)的分布
函数为:
Fmax(x) Fx1 (x) • Fx2 (x) Fxn (x)
Fmin (x) 1 [1 Fx1 (x)] • [1 Fx2 (x)][1 Fxn (x)]
否是互不影响的。
C Pn(k)
k n
pk qnk
,
k
0,1,2,, n
。
第二章 随机变量及其分布
(1)离散 型随机变 量的分布 律
(2)连续 型随机变 量的分布 密度 (3)分布 函数
概率论及统计学地重要公式和解地题目思路

一、基本概率公式及分布 1、概率常用公式:P(A+B)=P(A)+P(B)-P(AB) ;P(A-B)=P(A)-P(AB) ; 如A 、B 独立,则P(AB)=P(A)P(B) ; P(A )=1-P(A) ; B 发生的前提下A 发生的概率==条件概率 :P(A|B)=P (AB )P (B );或记 : P(AB)=P(A|B)*P(B) ;2、随机变量分布律、分布函数、概率密度 分布律:离散型X 的取值是x k (k=1,2,3...), 事件X=x k 的概率为: P{X=x k }=P k , k=1,2,3...; --- 既 X 的分布律;X 的分布律也可以是上面的表格形式,二者都可以。
分布函数:F(x)=P(X ≤x ), -∞<x <+∞ ; 是概率的累积! P(x1<X<x2)=F(x2)-F(x1) ;离散型rv X; F(x)= P{X ≤x }=∑p k x k <x ;(把X<x 的概率累加) 连续型rvX ;F(x)=∫f (x )dx x −∞, f(x)称密度函数;既分布函数F(X)是密度函数f(x)和X 轴上的(-∞,x)围成的面积! 性质:F(∞)=1; F(−∞)=0;二、常用概率分布:①离散:二项分布:事件发生的概率为p,重复实验n 次,发生k 次的概率(如打靶、投篮等),记为B(n,p) P{X=k}=(n k)p k (1−p )n −k ,k=0,1,2,...n; E(X)=np,D(X)=np(1-p);②离散:泊松分布:X ~Π(λ) P{X=k}=λk e−λk !,k=0,1,2,...; E(X)=λ, D(X)=λ ;③连续型:均匀分布:X 在(a,b)上均匀分布,X ~U(a,b),则:密度函数:f(x)={1b −a,a <x <x0,其它分布函数F(x)=∫f (x )dx x−∞={0, x <x x −ab −a 1,x ≥b,a <x <x④连续型:指数分布,参数为θ,f(x)= {1θe −xθ,0<x0,其它F(x)={1−e −xθ0,x >0 ;⑤连续型:正态分布:X ~N(μ,σ2), most importment! 密度函数 f(x),表达式不用记!一定要记住对称轴x=µ, E(X)=µ,方差D(X)=σ2; 当µ=0,σ2=1时,N(0,1)称标准正态,图形为:分布函数F(x)为密度函数f(x)从(-∞,x)围成的面积。
概率论公式

n
注:如果有 n 个变量服从同一个 0-1 分布, Xi ~ b(1, p) ,则其和 X Xi 服从二项 i
分布 X ~ b(n, p)
11. Poisson 分布
X ~ P() P( X k) k e , k 0,1,...
F
(x)
0, 1,
x x
c c
E(X ) c
Var( X ) 0
9. 二项分布
X ~ b(n, p)
P( X k) Cnk pk (1 p)nk E(X ) np
Var( X ) np(1 p)
10. 二点分布(0-1 分布)
X ~ b(1, p)
P( X x) px (1 p)1x , x 0,1
p(
x)
2
n 2
1 (
n
)
e
x 2
x
n 2
1
,
x
0
2
0, x 0
E(X ) n
Var( X ) 2n
Gamma 分布变为 2 分布:
当 X ~ Ga(,) ,则 2 X ~ Ga(, 1) 2 (2 ) 2
20. 严格单调函数Y g(X )
pY ( y) px[h(x)] | h '(x) |
21. K 阶原点矩和中心矩
k E(X k ) k E( X E( X ))k
中心矩和原点矩关系:
k
k Cik i (i )ki i0
22. 变异系数
Cv
(
X
)
( E(
概率论常用公式

概率论常⽤公式 有些概率公式常常会⼀段时间内要⽤到,但是有经常忘记,这⾥备注⼀下1、乘法法则 p\left ( x,y \right )=p\left ( x|y \right )p\left ( y \right )=p\left ( y|x \right )p\left ( x \right ) 实际上就是条件概率公式的⼀个等价形式2、独⽴性 如果x和y是相互独⽴的,那么有: p\left ( x, y \right ) = p\left ( x\right )p\left ( y\right )3、贝叶斯规则(Bayes' Rule) 贝叶斯规则⼜成为贝叶斯公式,在许多领域都有着⼴泛的应⽤,其公式如下: p\left ( y|x \right )=\frac{p\left ( x|y \right )p\left ( y \right )}{p\left ( x \right )} 分母是标准化常数,⽤于确保左边的后验概率其所有可能的值之和为1。
因此,我们通常可写成: p\left ( y|x \right )=\eta p\left ( x|y \right )p\left ( x \right ) 在给定背景知识e给定的情况下,贝叶斯变成:p\left ( y|x,e \right )=\frac{p\left ( x|y,e \right )p\left ( y|e \right )}{p\left ( x|e \right )}4、边缘化 边缘概率公式如下: p\left ( x \right )= \int_{y}^{ } p\left ( x,y \right )dy 在离散的情况下,积分变成求和: p\left ( x \right )= \sum_{y}^{ } p\left ( x,y \right ) 5、全概率法则 全概率是边缘概率的⼀种变体,能通过乘法法则推导⽽来,即: p\left ( x \right )= \int_{y}^{ } p\left ( x|y \right )p\left ( y \right )dy 且,对于离散情况则为相应概率之和,即: p\left ( x \right )= \sum_{y}^{ } p\left ( x|y \right )p\left ( y \right )dy 对于连续情况,条件概率的全概率公式:p\left ( x|y \right )= \int_{z}^{ } p\left ( x|y,z \right )p\left ( z|y \right )dz 对于离散情况,条件概率的全概率公式:p\left ( x|y \right )= \sum_{z}^{ } p\left ( x|y,z \right )p\left ( z|y \right )dz6、马尔科夫假设 马尔科夫假设是指变量x_{t},只与它直接的前⼀时刻状态x_{t-1}有关,和x_{t^{‘}-1}⽆关,其中t^{'}<t-1,则有 p\left ( x_{t}|x_{1:t-1} \right )= p\left(x_{t}|x_{t-1} \right)latax公式编辑器:,博客园只需要在选项中勾选⼀下“”即可。
概率论与数理统计公式整理(大学考试必备)

设 F (x) 是随机变量 X 的分布函数,若存在非负函数 f (x) ,对任意实数 x ,有
x
F(x) f (x)dx
,
则称 X 为连续型随机变量。 f (x) 称为 X 的概率密度函数或密度函数,简称概
率密度。 密度函数具有下面 4 个性质:
1° f (x) 0 。
f (x)dx 1
2°
则称上式为离散型随机变量 X 的概率分布或分布律。有时也用分布列的形
式给出:
X
| x1, x2,, xk,
P( X xk) p1, p2,, pk, 。
显然分布律应满足下列条件:
(1) pk 0 , k 1,2,,
pk 1
(2) k 1
。
(2)连续 型随机变 量的分布 密度
(3)离散 与连续型 随机变量 的关系
(16)贝叶 斯公式
设事件 B1 , B2 ,„, Bn 及 A 满足
1° B1 , B2 ,„, Bn 两两互不相容, P(Bi) >0, i 1,2,„, n ,
n
A Bi
2°
i1 , P( A) 0 ,
则
P(Bi / A)
P(Bi )P( A / Bi )
n
,i=1,2,„n。
P(Bj )P(A/ Bj )
1
概率论与数理统计 公式
(13)乘法 公式
例如 P(Ω /B)=1 P( B /A)=1-P(B/A) 乘法公式: P(AB) P(A)P(B / A)
更一般地,对事件 A1,A2,„An,若 P(A1A2„An-1)>0,则有
P( A1A2 „ An) P( A1)P( A2 | A1)P( A3 | A1A2) „„ P( An | A1A2 „
概率论与数理统计考前必备公式

概率论与数理统计考前必备公式==================================概率论与数理统计是大学生必修的数学课程之一,也是多个专业领域的基础知识。
这门课程主要研究随机现象以及随机事件的概率,探索统计规律,并应用于实际问题的分析与决策。
在概率论与数理统计的学习过程中,我们会接触到大量的公式,这些公式是我们进行问题求解的基础。
本文档将为大家整理并介绍概率论与数理统计考前必备的公式,帮助大家在考试中更好地把握重点,提高成绩。
1.随机变量与分布1.1随机变量随机变量是一种数值型的随机量,它的取值由随机实验的结果决定。
我们将随机变量分为离散型和连续型两类。
1.离散型随机变量定义:$X$是一个随机变量,如果它的取值有穷多个或者可列无穷多个,那么$X$是离散型随机变量。
2.连续型随机变量定义:$X$是一个随机变量,如果它的取值为一个区间或者多个区间,那么$X$是连续型随机变量。
1.2分布函数分布函数是描述随机变量取值情况的函数,记作$F(x)$,其中$x$为实数。
根据随机变量的类型,分布函数可为离散型随机变量的概率质量函数或连续型随机变量的概率密度函数。
1.离散型随机变量概率质量函数概率质量函数描述离散型随机变量取值的概率分布。
对于离散型随机变量$X$,其概率质量函数定义如下:$$P(X=x_i)=p_i,\q u ad i=1,2,\d ot s$$2.连续型随机变量概率密度函数概率密度函数描述连续型随机变量取值的概率分布。
对于连续型随机变量$X$,其概率密度函数定义如下:$$F(x)=\in t_{-\in f ty}^{x}f(x)d x$$1.3均匀分布均匀分布是最简单的连续型随机变量分布之一,主要用于描述在一个区间内所有点出现的概率相等的情况。
1.均匀分布的概率密度函数均匀分布的概率密度函数定义如下:$$f(x)=\be gi n{cas e s}\f ra c{1}{b-a},&a\le qx\l eq b\\0,&\t ex t{其他}\e n d{ca se s}$$其中$a$为区间下界,$b$为区间上界。
《概率论与数理统计》公式汇总(全)

若随机试验的结果为无限不可数并且每个结果出现的可能性均匀,同时样本空 间中的每一个基本事件可以使用一个有界区域来描述,则称此随机试验为几何 概型。对任一事件 A,
P( A) L( A) 。其中 L 为几何度量(长度、面积、体积)。 L()
(10)加法 公式
(11)减法 公式
P(A+B)=P(A)+P(B)-P(AB) 当 P(AB)=0 时,P(A+B)=P(A)+P(B) P(A-B)=P(A)-P(AB)
如果事件 A 的组成部分也是事件 B 的组成部分,(A 发生必有事件 B 发生):
A B 如果同时有 A B , B A ,则称事件 A 与事件 B 等价,或称 A 等于 B:
A=B。 A、B 中至少有一个发生的事件:A B,或者 A+B。 属于 A 而不属于 B 的部分所构成的事件,称为 A 与 B 的差,记为 A-B,也可
并且同时满足 P(ABC)=P(A)P(B)P(C)
那么 A、B、C 相互独立。
对于 n 个事件类似。
设事件 B1, B2,, Bn 满足 1° B1, B2,, Bn 两两互不相容, P(Bi) 0(i 1,2,, n) ,
n
A Bi
2°
i1 ,
则有
P(A) P(B1)P(A | B1) P(B2)P(A | B2) P(Bn)P(A | Bn) 。
C Pn(k)
k n
pk qnk
,
k
0,1,2,, n
。
第二章 随机变量及其分布
(1)离散 型随机变 量的分布 律
设离散型随机变量 X 的可能取值为 Xk(k=1,2,…)且取各个值的概率,即事
概率论考试必记公式

1.随机事件及其概率吸收律:A AB A A A A =⋃=∅⋃Ω=Ω⋃)( AB A A A AA =⋃⋂∅=∅⋂=Ω⋂)( )(AB A B A B A -==-反演律:B A B A =⋃ B A AB ⋃=n i in i iA A 11=== ni in i iA A 11===2.概率的定义及其计算)(1)(A P A P -= 若B A ⊂ )()()(A P B P A B P -=-⇒对任意两个事件A , B , 有 )()()(AB P B P A B P -=- 加法公式:对任意两个事件A , B , 有)()()()(AB P B P A P B A P -+=⋃ )()()(B P A P B A P +≤⋃)()1()()()()(2111111n n nnk j i kjinj i jini i n i i A A A P A A A P A A P A P A P -≤<<≤≤<≤==-+++-=∑∑∑3.条件概率()=A B P)()(A P AB P 乘法公式())0)(()()(>=A P A B P A P AB P()())0)(()()(12112112121>=--n n n n A A A P A A A A P A A P A P A A A P全概率公式∑==ni i AB P A P 1)()( )()(1i ni i B A P B P ⋅=∑=Bayes 公式)(A B P k )()(A P AB P k =∑==n i i i k k B A P B P B A P B P 1)()()()( 4.随机变量及其分布分布函数计算 )()()()()(a F b F a X P b X P b X a P -=≤-≤=≤<5.离散型随机变量(1) 0 – 1 分布1,0,)1()(1=-==-k p p k X P k k(2) 二项分布 ),(p n B 若P ( A ) = pn k p p C k X P k n kk n ,,1,0,)1()( =-==-*Possion 定理0lim >=∞→λn n np有,2,1,0!)1(l i m ==---∞→k k ep p C kkn n k nkn n λλ(3) Poisson 分布 )(λP,2,1,0,!)(===-k k ek X P kλλ6.连续型随机变量 (1) 均匀分布 ),(b a U⎪⎩⎪⎨⎧<<-=其他,0,1)(b x a ab x f ⎪⎪⎩⎪⎪⎨⎧--=1,,0)(a b a x x F (2) 指数分布 )(λE⎪⎩⎪⎨⎧>=-其他,00,)(x e x f x λλ ⎩⎨⎧≥-<=-0,10,0)(x e x x F xλ(3) 正态分布 N (μ , σ 2 )+∞<<∞-=--x e x f x 222)(21)(σμσπ ⎰∞---=xt t ex F d 21)(22)(σμσπ*N (0,1) — 标准正态分布+∞<<∞-=-x e x x 2221)(πϕ +∞<<∞-=Φ⎰∞--x t ex xt d 21)(22π7.多维随机变量及其分布二维随机变量( X ,Y )的分布函数⎰⎰∞-∞-=xydvdu v u f y x F ),(),(边缘分布函数与边缘密度函数⎰⎰∞-+∞∞-=xX dvdu v u f x F ),()( ⎰+∞∞-=dv v x f x f X ),()(⎰⎰∞-+∞∞-=yY dudv v u f y F ),()( ⎰+∞∞-=du y u f y f Y ),()(8.连续型二维随机变量(1) 区域G 上的均匀分布,U ( G )⎪⎩⎪⎨⎧∈=其他,0),(,1),(Gy x A y x f(2)二维正态分布+∞<<-∞+∞<<∞-⨯-=⎥⎥⎦⎤⎢⎢⎣⎡-+------y x ey x f y y x x ,121),(2222212121212)())((2)()1(21221σμσσμμρσμρρσπσ9.二维随机变量的 条件分布0)()()(),(>=x f x y f x f y x f X X Y X0)()()(>=y f y x f y f Y Y X Y⎰⎰+∞∞-+∞∞-==dy y f y x f dy y x f x f Y Y X X )()(),()(⎰⎰+∞∞-+∞∞-==dx x f x y f dx y x f y f X X Y Y )()(),()()(y x f Y X )(),(y f y x f Y =)()()(y f x f x y f Y X X Y = )(x y f X Y )(),(x f y x f X =)()()(x f y f y x f X Y Y X = 10.随机变量的数字特征数学期望∑+∞==1)(k k k p x X E⎰+∞∞-=dx x xf X E )()(随机变量函数的数学期望 X 的 k 阶原点矩)(k X EX 的 k 阶绝对原点矩)|(|k X EX 的 k 阶中心矩)))(((k X E X E -X 的 方差)()))(((2X D X E X E =-X ,Y 的 k + l 阶混合原点矩)(l k Y X EX ,Y 的 k + l 阶混合中心矩()l k Y E Y X E X E ))(())((--X ,Y 的 二阶混合原点矩)(XY EX ,Y 的二阶混合中心矩 X ,Y 的协方差()))())(((Y E Y X E X E --X ,Y 的相关系数XY Y D X D Y E Y X E X E ρ=⎪⎪⎭⎫⎝⎛--)()())())((( X 的方差D (X ) =E ((X - E (X ))2))()()(22X E X E X D -=协方差()))())(((),cov(Y E Y X E X E Y X --=)()()(Y E X E XY E -=())()()(21Y D X D Y X D --±±= 相关系数)()(),cov(Y D X D Y X XY =ρ。
概率论与数理统计必背公式

概率论与数理统计必背公式在概率论与数理统计中,掌握好一些重要的公式是非常重要的,这些公式可以帮助我们解决问题、推导证明以及计算概率和统计量。
下面将介绍一些必须掌握的概率论与数理统计的重要公式。
一、概率论公式:1.加法定理:如果事件A和B是互不相容的(即A和B不会同时发生),则它们的和事件的概率为P(A∪B)=P(A)+P(B)。
2.条件概率公式:对于两个事件A和B,A在给定B发生的条件下发生的概率定义为P(A,B)=P(A∩B)/P(B)。
3.乘法定理:对于两个事件A和B,其交事件的概率可以通过条件概率公式来计算,即P(A∩B)=P(A,B)*P(B)。
4.全概率公式:如果事件B1,B2,...,Bn是一组互不相容的且其并集为样本空间(即事件B1∪B2∪...∪Bn=S),则对于事件A,它的概率可以通过条件概率公式和全概率公式来计算,即P(A)=P(A,B1)*P(B1)+P(A,B2)*P(B2)+...+P(A,Bn)*P(Bn)。
5.贝叶斯公式:贝叶斯公式是条件概率公式的推广,对于事件A和B,其交事件的概率可以通过贝叶斯公式来计算,即P(A,B)=P(B,A)*P(A)/P(B)。
二、数理统计公式:1.期望:对于一组随机变量X,其期望(也称为均值)定义为E(X)=ΣX*P(X),即随机变量X乘以其概率的和。
2. 方差:对于一组随机变量X,其方差定义为Var(X) = E((X - μ)^2),其中μ为X的期望。
3. 协方差:对于两组随机变量X和Y,其协方差定义为Cov(X,Y) = E((X - μx)(Y - μy)),其中μx和μy分别为X和Y的期望。
4. 标准差:对于一组随机变量X,其标准差定义为σ = √Var(X),即方差的平方根。
5. 协方差矩阵:对于多组随机变量X1,X2,...,Xn,其协方差矩阵定义为Cov(X) = [Cov(Xi,Xj)],其中i和j分别表示第i组和第j组随机变量。
大学概率论必背公式

数学期望、方差、协方差等都是一些特殊的矩。
五、样本及抽样分布
1、常用统计量 (1)样本均值(样本平均数)
(2)样本方差
(3)k 阶样本矩
2、抽样分布 统计量的分布称为抽样分布。 (1) 2—分 布
性质: A. 可加性 若1 ~ 2(n1),2~ 2(n2 ),1, 2 独立,则1 + 2 ~ 2(n1+n2 )。 B. 期望与方差 若 ~ 2(n),则 E()= n,D()=2n。 (2)t—分布 若 ~ N(0, 1), ~ 2(n), 与独立,则
8、相关系数: 若 r.v. X,Y 的方差和协方差均存在, 且 D(X )> 0, D(Y )> 0,则
称为 X 与 Y 的相关系数. X 与 Y 不相关 Cov(X, Y )=0 E(XY )= E(X )E (Y )。
8、矩 (1)k 阶原点矩 E(X k ), k=1, 2, … 而 E(|X|k)称为 X 的 k 阶绝对原点矩; (2)k 阶中心矩 E[XE(X )]k, k=1, 2, … 而 E|X-E(X )|k 称为 X 的 k 阶绝对中心矩;
称 X 服从参数为 p 的几何分布。 (3)二项分布 ( B(n, p) ) 以 X 记 n 重贝努里试验中 A 发生的次数,则其分布率为:
P( X k) C k p k (1 p)nk , (k 0,1, , n) n 称 X 服从参数为(n,p)的二项分布,记为 X~B(n,p)
(4)泊松(Poisson)分布 ( P() ) 若随机变量 X 的所有取值为一切非负整数,且其分布律为:
5. 边缘分布 6. 二维连续型随机变量及其密度函数 联合密度 f (x , y )的性质
7. 边缘密度函数
(完整版)大学概率论与数理统计公式全集

大学概率论与数理统计公式全集一、随机事件和概率1、随机事件及其概率运算律名称交换律结合律分配律德摩根律2、概率的定义及其计算公式名称求逆公式加法公式条件概率公式乘法公式全概率公式贝叶斯公式(逆概率公式)伯努利概型公式两件事件相互独立相应公式P(AB)=P(A)P(B)表达式A+B=B+A(A+B)+C=A+(B+C)=A+B+CA(B±C)=AB±ACA+B=ABAB=BA(AB)C=A(BC)=ABCA+(BC)=(A+B)(A+C)AB=A+B公式表达式P(A)=1-P(A)P(A+B)=P(A)+P(B)-P(AB)P(B A)=P(AB)P(A)P(AB)=P(A)P(B A)nP(AB)=P(B)P(A B)i iP(B)=∑P(A)P(B A)i=1P(AjB)=P(Aj)P(B Aj)∑P(A)P(B A)j ii=1∞k kPn(k)=Cnp(1-p)n-k,k=0,1,Λn;P(B A)=P(B);P(B A)=P(B A);P(B A)+P(B A)=1;P(B A)+P(B A)=1二、随机变量及其分布1、分布函数性质P(X≤b)=F(b)P(a<X≤b)=F(b)-F(a)2、离散型随机变量分布名称0–1分布B(1,p)二项分布B(n,p)泊松分布P(λ)几何分布G(p)超几何分布H(N,M,n)3、连续型随机变量分布名称均匀分布U(a,b)密度函数⎧1⎪b-a,f(x)=⎨⎪0,⎩a<x<b其他分布律P(X=k)=p k(1-p)1-k,k=0,1k kP(X=k)=Cnp(1-p)n-k,k=0,1,Λ,nP(X=k)=e-λλkk!,k=0,1,2,ΛP(X=k)=(1-p)k-1p,P(X=k)=k n-kCMCN-MnCN,k=l,l+1,Λ,min(n,M)k=0,1,2,Λ分布函数0,x<a⎧⎪⎪x-aF(x)=⎨,a≤x<bb-a⎪1,x≥b⎪⎩指数分布E(λ)正态分布N(μ,σ2)标准正态分布N(0,1)f(x)=-λx⎧⎪λe,x>0f(x)=⎨⎪其他⎩0,x<0⎧0,F(x)=⎨-λx1-e,x≥0⎩2πσ⎰2πσ⎰11x12πσe-(x-μ)22σ2-∞<x<+∞F(x)=-∞e-(t-μ)22σ2d tϕ(x)=12πe-x22-∞<x<+∞F(x)=x-∞e-(t-μ)22σ2d t三、多维随机变量及其分布1、离散型二维随机变量边缘分布p i⋅=P(X=xi)=∑P(X=x,Y=y)=∑pi jj jijp⋅j=P(Y=yj)=∑P(X=x,Y=y)=∑pi ji iij2、离散型二维随机变量条件分布p i j =P(X=xiY=yj)=P(X=xi,Y=yj)P(Y=yj)=pijP⋅j,i=1,2Λx yp j i =P(Y=yjX=xi)=P(X=xi,Y=yj)P(X=xi)=pijPi⋅,j=1,2Λ3、连续型二维随机变量(X ,Y)的联合分布函数F(x,y)=⎰-∞⎰-∞f(u,v)dvdu4、连续型二维随机变量边缘分布函数与边缘密度函数边缘分布函数:FX (x)=⎰-∞⎰-∞f(u,v)dvdu边缘密度函数:fX(x)=⎰-∞f(x,v)dvF Y (y)=x+∞+∞⎰⎰y+∞-∞-∞f(u,v)dudv fY(y)=⎰+∞-∞f(u,y)du5、二维随机变量的条件分布fY X (y x)=f(x,y)f(x,y),-∞<y<+∞fX Y(x y)=,-∞<x<+∞fX(x)fY(y)四、随机变量的数字特征1、数学期望离散型随机变量:E(X)=∑xk pk连续型随机变量:E(X)=⎰-∞xf(x)dxk=1+∞+∞2、数学期望的性质(1)E(C)=C,C为常数E[E(X)]=E(X)E(CX)=CE(X)(2)E(X±Y)=E(X)±E(Y)E(aX±b)=aE(X)±b E(C1X1+ΛCnXn)=C1E(X1)+ΛCnE(Xn)(3)若XY相互独立则:E(XY)=E(X)E(Y)(4)[E(XY)]2≤E2(X)E2(Y)3、方差:D(X)=E(X2)-E2(X)4、方差的性质(1)D(C)=0D[D(X)]=0D(aX±b)=a2D(X)D(X)<E(X-C)2(2)D(X±Y)=D(X)+D(Y)±2Cov(X,Y)若XY相互独立则:D(X±Y)=D(X)+D(Y)5、协方差:Cov(X,Y)=E(X,Y)-E(X)E(Y)若XY相互独立则:Cov(X,Y)=06、相关系数:ρXY =ρ(X,Y)=Cov(X,Y)D(X)D(Y)若XY相互独立则:ρXY=0即XY不相关7、协方差和相关系数的性质(1)Cov(X,X)=D(X)Cov(X,Y)=Cov(Y,X)(2)Cov(X1+X2,Y)=Cov(X1,Y)+Cov(X2,Y)Cov(aX+c,bY+d)=abCov(X,Y)8、常见数学分布的期望和方差分布0-1分布B(1,p)二行分布B(n,p)泊松分布P(λ)几何分布G(p)超几何分布H(N,M,n)均匀分布U(a,b)正态分布N(μ,σ2)指数分布E(λ)数学期望p方差p(1-p)np(1-p)npλ1pλ1-ppn2nMNM M N-m(1-)N N N-1 a+b2(b-a)212σ2μ1λ1λ2五、大数定律和中心极限定理1、切比雪夫不等式)D (X )若E (X )=μ,D (X )=σ2,对于任意ξ>0有P {X -E (X )≥ξ}≤D (X 或P {X -E (X )<ξ}≥1-22ξξ2、大数定律:若X1ΛXn相互独立且n →∞时,1n(1)若X 1ΛX n 相互独立,E (X i )=μi ,D (X i )=σi 2∑i =1n1Xi−−→nD n∑E (X )ii =1n且σi 21≤M 则:n ∑i =11Xi−−→nP ∑E (X ),(n →∞)ii =1n1nP −→μ(2)若X1ΛXn相互独立同分布,且E (Xi )=μi则当n →∞时:∑X i−ni =13、中心极限定理(1)独立同分布的中心极限定理:均值为μ,方差为σ2>0的独立同分布时,当n 充分大时有:∑X Y n=k =1nk -n μ~−−→N (0,1)n σ(2)拉普拉斯定理:随机变量ηn(n =1,2Λ)~B (n ,p )则对任意x 有:x →+∞lim P {ηn-npnp (1-p )≤x }=⎰x 12π-∞e-t 22dt=Φ(x )n(3)近似计算:P (a ≤∑Xk≤b )=P (a -n μ≤k =1n∑Xk =1k-n μ≤b -n μn σn σn σ)≈Φ(b -n μn σ)-Φ(a -n μn σ)六、数理统计1、总体和样本总体X 的分布函数F (x )样本(X 1,X 2Λ2、统计量(1)样本平均值:X =1n(3)样本标准差:S =Xn)的联合分布为F (x 1,x2Λx n)=∏F (x k)k =1n∑i =1n1X i(2)样本方差:S =n -12∑1(Xi-X )=n -1i =12nn ∑i =1n (Xi2-nX )21n -1∑1(X i -X ) (4)样本k 阶原点距:Ak=ni =12n ∑Xi =1k i,k =1,2Λ(5)样本k 阶中心距:Bk=M k =1n∑(Xi =1n i-X )k ,k =2,3Λ(6)次序统计量:设样本(X 1,X 2Λ序重新排列,得到x (1)≤x(2)≤Λ为样本(X 1,X 2ΛX n)X n)的观察值(x 1,x 2Λx n),将x 1,x 2Λxn按照由小到大的次≤x(n ),记取值为x (i )的样本分量为X (i ),则称X(1)≤X(2)≤Λ≤X(n )的次序统计量。
概率论常用公式整理

则有
h g ( x, y) f ( x, y)dxdy h( z ) p( z )dz ,
f Z ( z ) p( z ), z
随机变量的数字特征
数学期望: E ( X ) 性质: (1) (2)
xf ( x)dx
E ( Y ) E ( g ( X ) )
(5) 收缩性: E ( X ) E ( X ) (6) 马尔可夫不等式: P( X c)
E( X ) c
(7) 若 E ( X ) 0 ,则 P( X 0) 1 几种常见分布的期望: 1)
X ~ B(n, p) E( X ) np
2) 3)
X ~ N ( , 2 ) E( X )
随机变量的函数分布:已知随机变量 X 的概率密度 f X x ,则随机变量 Y g X 的概率 密度的求法: (1)
' fY y f X h y h y , a y b ,其中 x h y 为y g x 的反函数
(2) (积分转化法)h(x)为任意有界连续函数, 则有 fY ( y) p( y), y
h g ( x) f X ( x)dx h( y) p( y )dy ,
(3) 假设 g(X)是单调递增函数, FY ( y) P( g ( X ) y) P( X h( y)) FX (h( y))
概率论 D 常用公式整理
条件概率
乘法公式: P( AB) P( B) P( A | B)
全概率公式:
概率论基本公式

概率论与数理统计基本公式第一部分 概率论基本公式1、)(;A B A B A AB A B A B A -⋃=⋃-==--例:证明:成立。
得证。
成立,也即成立,也即(不发生,从而发生,则不发生,,知由(证明:(B A B A AB A B B A AB A B B B A B A B A AB A B B A --=-⋃-⋃-==-=-⋃--)).) 2、对偶率:.----⋃=⋂⋂=⋃B A B A B A B A ;3、概率性率:(1))()()(212121A P A P A A P A A +=⋃为不相容事件,则、有限可加:(2))()();()()(),()()(B P A P B P A P B A P A B AB P A P B A P ≥-=-⊂-=-时有:特别,(3))()()()(AB P B P A P B A P -+=⋃对任意两个事件有:)();();();()1(.4.0)(2.0)(5.0)(AB P B A P B A P AB P B P B A P A P ⋃-===--求:,,例:已知:.3.0)(1)(,7.0)()()()(3.0)()()(,5.0)(.,2.0)()()()(,=⋃-=⋃==-+=⋃=-=-∴===+∴=+---B A P B A P AB P AB P B P A P B A P AB P A P B A P A P AB P B P B A P AB P B A B B B A AB 又即是不相容事件,、且解:4、古典概型222n 2!)(n ,22)-n 2)!n 2(22nC n A P C A n n n ==!,则自成一双为:!!(解:分堆法:每堆自成一双鞋的概率只,事件堆,每堆为只,分为双鞋总共例: 5、条件概率称为无条件概率。
的条件概率,条件下,事件称为在事件)(,)()()|(B P B A A P AB P A B P =B)|P(B)P(A P(AB) A)|P(A)P(B P(AB)==乘法公式:)|()()(i i A B P A P B P i∑=全概率公式:)|()()|()()()()|(j j ji i i A B P A P A B P A P B P B A P B A P i ∑==贝叶斯公式:例:有三个罐子,1号装有2红1黑共3个球,2号装有3红1黑4个球,3号装有2红2黑4个球,某人随机从其中一罐,再从该罐中任取一个球,(1)求取得红球的概率;(2)如果取得是红球,那么是从第一个罐中取出的概率为多少?.348.0)()()|()|()2(.639.0)(31)()()(.21)|(;43)|(;32)|()|()()(}{3,2,1i }{)1(111321321i i 321≈=≈∴==========∑A P B P B A P A B P A P B P B P B P B A P B A P B A P A B P A P B P B B B A i B ii 由贝叶斯公式:,,依题意,有:由全概率公式是一个完备事件、、,由题知取得是红球。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
,使对任意实数 x,都有
F ( x)=P( X x)=x f (u)du
则称 X 为连续型随机变量,f (x)为 X 的概率密度函数,简称概率密度或密度函数。 记为 X~ f (x) , (- < x <+)
2. 密度函数的性质
(3)
若
x是
f(x )
f (x)的连续点,
dF(x dx
)
.
(4)
P(a X b)= b f (u)du a
P{X xk } pk ,k 1,2,
数学期望 E(X)是一个常数,而非变量.它是一种以概率为权的加权平均值 (1)X ~(0—1)分布
(2)X~B(n,p)二项分布 (3)X~(或)Poisson 分布
2. 连续型随机变量的数学期望
(1)X~U(a,b)均匀分布 其概率密度函数为:
f(x )
5. 边缘分布 6. 二维连续型随机变量及其密度函数 联合密度 f (x , y )的性质
7. 边缘密度函数
8. 条件密度函数
1)fX|Y (x
y)
f (x, y) 称为Y fY ( y)
y下, X的条件密度函数
2)fY|X ( y
x)
f (x, y) 称为X fX (x)
x下,Y的条件密度函数
8、相关系数: 若 r.v. X,Y 的方差和协方差均存在, 且 D(X )> 0, D(Y )> 0,则
称为 X 与 Y 的相关系数. X 与 Y 不相关 Cov(X, Y )=0 E(XY )= E(X )E (Y )。
8、矩 (1)k 阶原点矩 E(X k ), k=1, 2, … 而 E(|X|k)称为 X 的 k 阶绝对原点矩; (2)k 阶中心矩 E[XE(X )]k, k=1, 2, … 而 E|X-E(X )|k 称为 X 的 k 阶绝对中心矩;
P(ABC)= P(C|AB)P(B|A)P(A)
3. 全概率公式: 设 B1,…, Bn 是 的一个划分,且 P(Bi )>0,
(i=1,…,n),则对任何事件 A,有
n
n
P(A)= P(ABi ) P(Bi )P(A | Bi )
i 1
i 1
注:全概率公式应用范围
随机试验可以看成分两阶段进行,且第一个阶段的试验结果是不确定的,我们需要求的是第
3、正态总体的抽样分布
六、参 数 估 计(重&难)
1、矩估计法 用样本矩作为总体同阶矩的估计,从而解出未知参数的方法称为矩估计法或矩法。
2、极大似然估计法
(1) 解似然方程法 称为未知参数 j 的似然方程。若该方程有解,则其解就是
(2) 直接法 由似然方程解不出 j 的似然估计时,可由定义通过分析直接推求。 解:X 的概率密度为:
或
或 2. 分布律的性质
(2) pk 1. k 1 3. 几个常见的离散型分布 (1)(0-1)分布(两点分布)
(2)几何分布( G(p) ) 一次试验中只考虑某事件 A 出现或不出现,设 P(A)=p, P(A)=1-p。现重复独立地做试验,一
旦 A 发生就立即停止试验。 以 X 表示 A 首次发生所需的试验次数,则其分布率为:
二阶段的结果发生的概率,这时候用全概率公式。
4. 贝叶斯公式: 设 B1,…, Bn 是 的一个划分,且 P(Bi ) > 0,(i=1,…,n),则对任何事件 A,有
P(Bj
| A)
P(Bj )P(A | Bj ) P(A)
P(Bj )P(A | Bj ) ,
n
P(Bi )P(A | Bi )
3、无 偏 性
设ˆ ˆ(X 1, ,X n )为的估计量, 若E(ˆ) 则称ˆ是的无偏估计量.
4、正 态 总 体参数的 区间估计(双侧) ( 1) 单 正态总体 均值的置信区间
iid
~ 设X1, ,X n N( , 2 ),给定 ,由观测值
x1, ,xn求出 的置信区间. A. 已知
B. 未知
t (n)称为自由度为 n 的 t—分布
性质: A. f (t )关于 t =0(纵轴)对称。f ( t )= f (t )。 B. f (t )的极限为 N(0,1)的密度函数,即
(3)F—分布 若1 ~ 2(n1), 2~ 2(n2),1, 2 独立,则 F(n1, n2)称为第一自由度为 n1 ,第二自由度为 n2 的 F—分布。 性质:
数学期望、方差、协方差等都是一些特殊的矩。
五、样本及抽样分布
1、常用统计量 (1)样本均值(样本平均数)
(2)样本方差
(3)k 阶样本矩
2、抽样分布 统计量的分布称为抽样分布。 (1) 2—分 布
性质: A. 可加性 若1 ~ 2(n1),2~ 2(n2 ),1, 2 独立,则1 + 2 ~ 2(n1+n2 )。 B. 期望与方差 若 ~ 2(n),则 E()= n,D()=2n。 (2)t—分布 若 ~ N(0, 1), ~ 2(n), 与独立,则
(2). 指数分布 E( )
则称 X 服从参数为
的指数分布。
F(x )
1 e x
0
,
,
x 0 x 0
(3) 正态分布(高斯(Gauss)分布)
其中 > 0 , 为实数,则称 X 服从参数为( , )的正态分布,
三个特性:
i. 其图形关于直线 x = 对称;
参数 0 , 2 1 的正态分布称为标准正态分布,
称 X 服从参数为 p 的几何分布。 (3)二项分布 ( B(n, p) ) 以 X 记 n 重贝努里试验中 A 发生的次数,则其分布率为:
P( X k) C k p k (1 p)nk , (k 0,1, , n) n 称 X 服从参数为(n,p)的二项分布,记为 X~B(n,p)
(4)泊松(Poisson)分布 ( P() ) 若随机变量 X 的所有取值为一切非负整数,且其分布律为:
(1 p)k 1 p, (k 1,2,...)
(3) 中第 r 次成功发生在第 k 次试验的概率(即可列重贝努里试验中 A 发生 r 次需要 k 次 试验的概率)是
C kr11(1 p)k r p r ,(1 r k)
二、离散性随机变量及其分布
1. r .v . X的分布律 pk P{X xk }, k 1, 2,
(3)几个常用函数的密度函数 a. 和的分布
若 X 与 Y 相互独立,则 Z=X+Y 的密度函数
或
fZ(z) fX(z y )fY(y )dy = fX(x )fY(z x )dx .Leabharlann 称为连续型随机变量的卷积公式。
b. 极大(小)统计量的分布
四、随机变量的数字特征
1、离散型随机变量的数学期望 离散型随机变量 X,其分布律为:
其密度函数表示为
(x )
1
x2
e 2 , x .
2
N(0, 1)的性质:
4. 联合分布函数 设(X , Y )是二维随机变量,(x , y ) R^2, 则称
F(x , y )=P{X x , Y y } 为(X , Y )的分布函数,或 X 与 Y 的联合分布函数。 联合分布函数 F( x, y )具有如下性质: (1)非负规范
则称事件 A 与 B 相互独立。 若 A,B 独立,且 P(A)>0, P(B)>0,则 A,B 一定相容
6.贝努力概型: (1) E n 中成功 k 次的概率(即 n 重贝努里试验中 A 发生 k 次的概率)是
Pn(k )
C
k n
p
k(1
p)n k ,
(0
k
n)
(2) 中首次成功发生在第 k 次试验的概率(即可列重贝努里试验中 A 首次发生在第 k 次 试验的概率)是
(2). 单正态总体方差的置信区间(经管类非重点)
A. 未知
B. 已知
即得 2 和 的置信度为 1的置信区间分别为
七、假 设 检 验(略)
综上有单个正态总体的检验表:
1、 关于均值的假设检验 :
2、 关于均值 2的假设检验 :
i 1
(j 1,..., n)
注:贝叶斯公式应用范围 随机试验可以看成分两阶段进行,且第一个阶段的试验结果是不确定的,但第二个阶段的某 个结果是已知的,我们需要求的是第二阶段的这个结果为第一阶段某一个结果所 引起的概 率,这时候用贝叶斯公式
5. 设 A、B 是两事件, P(B)>0,若 P(A)=P(A|B)
性质:设(X, Y )~ f (x, y), (x, y) R2, fX(x), fY(y)分别为 X 与 Y 的边缘密度,则 X 与 Y 相
互独立等价于 f (x, y) = fX(x) fY(y),对任意(x, y) R2
9.密度函数: 连续型随机变量函数的密度函数 (1)一维变量-分布函数法
(2)多个随机变量函数的密度函数-分布函数法
大学概率论必背公式
1. 加法公式: 对任意两事件 A、B,有 P(A B)=P(A)+P(B)-P(AB)
一、概率
2. 设 A、B 是中的两个事件,且 P(B)> 0,称
P(A | B )
P(AB ) P(B )
为事件 B 发生的条件下事件 A 发生的条件概率。 事件 A、B 的概率乘法公式:
P(AB ) P(A | B )P(B )
b
1
a
,
0,
a x b elsewhere
(2)指数分布 X 服从参数为的指数分布,其概率密度函数为:
(3)正态分布
3、对于 r.v.X 的函数的数学期望
一维: 二维:
4、数学期望的性质
5、方差是衡量随机变量取值与其均值的偏离程度的一个数字特征。 若 E(X)存在,则称 E[XE(X)]2 为 r.v. X 的方差,记为 D(X),或 Var(X). D(X )=E(X 2 ) [E(X )]2. (1)两点分布:
