凸轮理论轮廓曲线设计c语言程序
直动凸轮轮廓线设计源程序模板

}
/*---------------------------------------*/
circle(X0,Y0,ro); /*画基圆*/
circle(X0,Y0,e); /*画偏距园*/
{s[i]=h;
ds[i]=0;
dv[i]=0;}
if(p>A2&&p<=A5) /*等加速回程段*/
{s[i]=h-2*h*(p-A2)*(p-A2)/(A3-A2)/(A3-A2);
ds[i]=-4*h*W*(p-A2)/(A3-A2)/(A3-A2);
#define A5 240
#define X0 500 /*凸轮转轴坐标*/
#define Y0 280
#define pi 3.14159
#define t pi/180 /*度-->弧度*/
main() /*主程序*/
ct=dx/sqrt(dx*dx+dy*dy); /* COS 值*/
xp[i]=x[i]+rr*st; /*外实际廓线坐标*/
yp[i]=y[i]-rr*ct;
da[i]=(atan((ds[i]/(W*t)-e)/(so+s[i])))/(t);
x[i]=X0+(so+s[i])*sin(p*t)+e*cos(p*t); /*理论廓线坐标*/
y[i]=Y0+(so+s[i])
*cos(p*t)-e*sin(p*t);
{ float e,ro,rr,p,so,dx,dy,st,ct; /*变量说明*/
float s[200],ds[200],dv[200],da[200],x[200],y[200],xp[200],yp[200];
凸轮设计 程序

1、建立凸轮轮廓的数学模型。
图为往复式偏心从动件盘形凸轮的机构运动简图,B 为理论轮廓线上的任意一点,在图示的直角坐标系中,B 的坐标,即凸轮理论廓线上的直角坐标参数方程为:X=OE+EF=(S0+S )*Sin (J )+e*Cos (J )Y=BD – FD=(S0+S )*Cos (J ) – e*Sin (J )式中:X ,Y :凸轮理论廓线上的某一点坐标 (mm)e :从动件的偏心距(mm),OCR :凸轮的基圆半径(mm),OAS 0:220E R S -=(mm),CKJ :凸轮的转角 S :S =f(J)从动件运动方程,KBBC =CK 十KB =S 0十S因为工作廓线在法线方向的距离处处相等,且等于滚子半径r ’,故当已知理论廓线上的任意一点B(X,Y)时,只要沿理论廓线在该点的法线的方向取距离为r ’,即得到工作廓线上的相应点B ’(X ’,Y ’).由高等数学可知,理论廓线B 点处的法线n-n 的斜率(与切线斜率互为负倒数)应为 Tan a=-dx/dy=(dx/dJ)/(dx/dJ)/(-dy/dJ)=sina/cosa注: a 为理论廓线B 点处的法线和X 轴的夹角。
根据(1)(2)两式有dx/dJ=(ds/dJ-e)sin(J)+(s0+s)cos(J) (3)dy/dJ=(ds/dJ-e)cos(J)-(s0+s)sin(J) (4)可得Sin a=(dx/dJ)/((dx/dJ)^2+(dy/dJ)^2)^0.5 (5)Cos a=-(dy/dJ)/((dx/dJ)^2+(dy/dJ)^2)^0.5 (6)工作廓线上对应的点B ’(x ’,y ’)坐标为:x ’=x-r ’cos ay ’=y- r ’sin a2、从动件运行规律:五次多项式运行规律推程(升)δ1远休止(停)δ2回程(降)δ3近休止(停)δ4等加速等减速S1=10h(δ/δ1)^3-15h (δ/δ1)^4+6h(δ/δ1)^5); S2=h 等减速等加速S1=h-h(10(δ/δ3)^3-15(δ/δ3)^4+6(δ/δ3)^5)S4=03、绘制凸轮曲线的程序框图(1)升回程运动函数的子程序框图(2)d s/dδ运动函数的子程序框图while(3)绘制凸轮轮廓的主程序框图(4)绘制S-δ曲线的程序框图4.编程%(1)升回程运动函数的子程序%s.mfunction y = s(x) %申明从动件运行规律函数deg=pi/180; %转化为弧度制的参数h=8; %从动件行程if (x<0)|(x>2*pi)error('Input Range error(0~2*pi)'); elseif x<(60*deg)&(x>=0)y=h*(10*(x/(60*deg))^3-15*(x/(60*deg))^4+6*(x/(60*deg))^5); %升程运动规律elseif(x>=60*deg)&(x<70*deg)y=h; %远休运动规律elseif(x>=70*deg)&(x<130*deg)y=h-h*(10*((x-70*deg)/(60*deg))^3-15*((x-70*deg)/(60*deg))^4+6*((x-70*deg)/(60 *deg))^5);%回程运动规律elsey=0; %近休运动规律endendendend%(2)绘制ds/dδ运动函数的子程序%ds.mfunction d=ds(x) %申明ds/dδ运行规律函数h=8; %凸轮2行程deg=pi/180;if (x<0)|(x>2*pi)error('Input Range error(0~2*pi)');elseif x<(60*deg)&(x>=0)d=h/(60*deg)*((30*(x/(60*deg))^2-60*(x/(60*deg))^3+30*(x/(60*deg))^4)); %对S求导elseif(x>=60*deg)&(x<70*deg)d=0; %对S求导elseif(x>=70*deg)&(x<130*deg)d=-h/(60*deg)*((30*((x-70*deg)/(60*deg))^2-60*((x-70*deg)/(60*deg))^3+30*((x-7 0*deg)/(60*deg))^4)); %对S求导elsed=0; %对S求导endendendend%(3)绘制凸轮轮廓的主程序%main.mclear;i=1;r0=55; %基圆半径rr=4; %滚子圆半径e=0; %偏距eta=1; %凸轮顺时钉转向s0=(r0^2-e^2)^0.5;deg=pi/180;st=0.05*deg; %步长a=0;while (a<2*pi)x(i)=(s(a)+s0)*sin(eta*a)-e*cos(eta*a); %定义理论轮廓线的X座标y(i)=(s(a)+s0)*cos(eta*a)+e*sin(eta*a); %定义理论轮廓线的Y座标dx=ds(a)*sin(eta*a)-eta*(s(a)+s0)*cos(eta*a)-e*eta*sin(eta*a);dy=ds(a)*cos(eta*a)+eta*(s(a)+s0)*sin(eta*a)-e*eta*cos(eta*a);sino=dx/(dx^2+dy^2)^0.5;coso=dy/(dx^2+dy^2)^0.5;X(i)=x(i)-rr*coso; %定义实际轮廓线的X座标Y(i)=y(i)+rr*sino; %定义实际轮廓线的Y座标i=i+1;a=a+st;endplot(x,y,X,Y); %绘制理论和实际轮廓线axis('square','equal');grid on主程序运行的结果为凸轮轮廓曲线:%(4)绘制S-δ曲线的程序为:%myline.mh=10;deg=pi/180;t1=linspace(0,60*pi/180); %定义升程角范围y1=h*(10*(t1/(60*deg)).^3-15*(t1/(60*deg)).^4+6*(t1/(60*deg)).^5); %升程运动规律t2=linspace(60*pi/180,70*pi/180); %定义远休角范围y2=h; %远休运动规律t3=linspace(70*pi/180,130*pi/180); %定义回程角范围y3=h-h*(10*((t3-70*deg)/(60*deg)).^3-15*((t3-70*deg)/(60*deg)).^4+6*((t3-70*deg)/(60*deg)). ^5);%回程运动规律t4=linspace(130*pi/180,360*pi/180); %定义近休角范围y4=0; %近休运动规律plot(t1,y1,t2,y2,t3,y3,t4,y4) %绘制S-δ曲线xlabel('t');ylabel('y');grid程序运行的结果为:。
凸轮程序

for(i=0;i<N;i++) { for(j=0;j<2;j++) {shuju[i][j]=lz[i][j];} for(j=2;j<4;j++) {shuju[i][j]=sz[i][j-2];} fprintf(fp,"\n"); for(j=0;j<4;j++) fprintf(fp,"%12.3f\t",shuju[i][j]); } fprintf(fp,"\n"); for(j=0;j<4;j++) fprintf(fp,"%12.3f\t",shuju[0][j]); fprintf(fp,"\n pmin\t a1max\t a2max\t r0\t"); fprintf(fp,"\n %f\t %f\t %f\t ",pmin[0],a1max[0],a2max[0]); fprintf(fp,"\n %9.3f\t %9.3f\t %9.3f\t %9.3f\t",pmin[1],a1max[1]*180/PI,a2max[1]*180/PI,r0 ); fclose(fp); //屏幕输出 printf("\n pmin a1max a2max r0"); printf("\n %f %f %f ",pmin[0],a1max[0],a2max[0]); printf("\n %9.3f %9.3f %9.3f %9.3f",pmin[1],a1max[1]*180/PI,a2max[1]*180/PI,r0); } } //求最大压力角 void max(double a[N],double amax[2]) { int i; amax[0]=0;amax[1]=a[0]; for(i=1;i<N;i++) { if(a[i]>amax[1]) {amax[0]=i;amax[1]=a[i];} } } //求最小曲率半径 void min(double p[N],double pmin[2]) { int i; pmin[0]=0;pmin[1]=p[0]; for(i=1;i<N;i++) {
凸轮轮廓曲线的设计[精]
![凸轮轮廓曲线的设计[精]](https://img.taocdn.com/s3/m/7c1b767efe4733687e21aa33.png)
④作平底直线族的内包络线。
JM 返回
4)偏置直动尖顶推杆盘形凸轮
偏置直动尖顶推杆凸轮机构中,已知凸 轮的基圆半径r0,角速度ω 和推杆的运动规律
e
和偏心距e,设计该凸轮轮廓曲线。
8’ 7’ 5’ 3’ 1’
1 3 5 78
9’ 11’ 12’
13’ 14’
9 11 13 15ωAΒιβλιοθήκη 15’13’ 12’
12 3 4 5 67 8
-V
4’
3’
5’
v
2’
6’
β 1’
7’β '
s
12
34
5
6
7β " 8
2π R
V=ω R R
JM 返回
7)摆动推杆圆柱凸轮机构
φ
已知:圆柱凸轮的半径R,滚子 半径rr从动件的运动规律,设计该凸轮 机构。
φ
A
δ
0 1 2 3 4 5 67890
ω
2πR 2πR
-V
2rr
4’,5’,6’
y O
φA
φ0
δ
a
x
asinδ
acosδ
JM 返回
JM 返回
2)对心直动滚子推杆盘形凸轮
对心直动滚子推杆凸轮机构中,已知凸轮的
基圆半径r0,角速度ω 和推杆的运动规律,设计该
凸轮轮廓曲线。
-ω
8’ 9’
7’
11’
ω
5’ 3’
1’
12’
13’ 14’
1 3 5 7 8 9 11 13 15
设计步骤:
①选比例尺μ l作基圆r0。 ②反向等分各运动角。原则是:陡密缓疏。
一、凸轮轮廓曲线的设计
凹槽凸轮轮廓线的解析设计及C语言实现

解析表 达 式和 计 算程序 的 正确 性 。给 出的 c语 言程序 可方便 地 改造 为数控 机 床控 制程 序 。
关 键 词 : 械 制 造 自动 化 ; 槽 凸 轮 机 构 ; 语 言 ; 析 法 ; 论 凸 轮 廓 线 机 凹 C 解 理
中 图 分 类 号 : H1 2 T 2 文 献标 识码 : A
收 稿 日期 :0 1 2—1 2 1 —0 8 基 金 项 目 : 东 省 自然 科 学 基 金 研 究 项 目( 2 0 A 8 山 Q 06 0 )
作 者 简 介 : 静 ( 9 4 ) 女 , 北 秦 皇 岛人 , 南 工 程 学 院 机 械 工 程 系 副 教 授 , 士 , 究 方 向 为 机 械 设 计 及 制 造 , E —m i zc e j g 0 0 陈 16 一 , 河 河 硕 研 ( al z h ni 2 0 ) n
s
i 鲁 ) √ )( :( +
( 3 )
【 )m S sp 0 i s
1
…
Y =(0 s c。 s + )o ~ei ̄ s J n
其 中 , 、 分别 为 曰点 的为
一 一 、一 /一
第 5期
21 0 1年 5 月
组 合 机 床 与 自 动 化 加 工 技 术
M o l r M a hi o du a c ne To l& A ut m a i a uf c ur ng Te hni ue o tc M n a t i c q
NO. 5 M a y. 2 1 01
。: 鲁 + ) 。 ) (。 √ (
~
( 4 )
() 5
根 据 内 、 凹 槽 廓 线 与 理 论 廓 线 的 关 系 , 凹 槽 外 外
VC 凸轮机构运动仿真编程示例
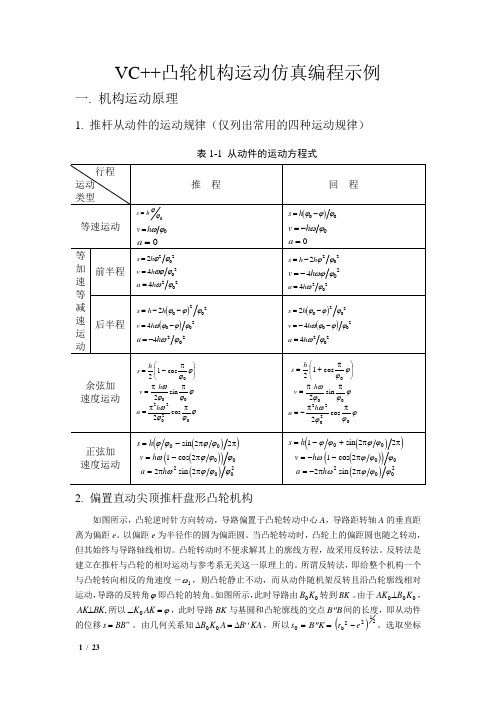
推程运动规律一组单选钮:IDC_TUI_1;IDC_TUI_2;IDC_TUI_3;IDC_TUI_4
回程运动规律一组单选钮:IDC_HUI_1;IDC_HUI_2;IDC_HUI_3;IDC_HUI_4
推程角:IDC_TUI_ANGLE;回程角:IDC_HUI_ANGLE;远停角:IDC_FAR_REST_ANGLE
VC++凸轮机构运动仿真编程示例
一.机构运动原理
1.推杆从动件的运动规律(仅列出常用的四种运动规律)
表1-1从动件的运动方程式
行程
运动
类型
推程
回程
等速运动
等加速等
减速运
动
前半程
后半程
余弦加
速度运动
正弦加
速度运动
2.偏置直动尖顶推杆盘形凸轮机构
如图所示,凸轮逆时针方向转动,导路偏置于凸轮转动中心A,导路距转轴A的垂直距离为偏距e。以偏距e为半径作的圆为偏距圆。当凸轮转动时,凸轮上的偏距圆也随之转动,但其始终与导路轴线相切。凸轮转动时不便求解其上的廓线方程,故采用反转法。反转法是建立在推杆与凸轮的相对运动与参考系无关这一原理上的。所谓反转法,即给整个机构一个与凸轮转向相反的角速度 ,则凸轮静止不动,而从动件随机架反转且沿凸轮廓线相对运动,导路的反转角 即凸轮的转角。如图所示,此时导路由 转到 。由于 , 所以 ,此时导路BK与基圆和凸轮廓线的交点 间的长度,即从动件的位移 。由几何关系知 ,所以 。选取坐标系xAy,B0点为凸轮廓线起始点。当凸轮转过角,由反转法知此时从动件位于BK。则B点的坐标为
机构设计凸轮曲线程序

ClsDim t(7) as doubleDim p(7) as doubleDim f(7) as doubleDim c(7) as doubleDim b(7) as doubleDim jsd(7) as doubleDim yd(7) as doubleDim sd(7) as doubleDim wy(7) as doubleDim pi as doubleDim a1 as doubleDim a2 as doubleDim m as doubleDim i as doubleDim j as doubleDim mc as doubleDim ss as doubleJ=0Dim tt as doubleDim aa as doubleStar:Pi=3.1415926ss=”请选择通用间歇体形曲线的名称:”& chr(10)+chr(13)&”1、修正等速“& chr(10)+chr(13)&”2、修正梯形”& chr(10)+chr(13) &”3、修正正弦”mc=inputbox(ss)if mc=1 thent(0)=0t(1)=1/16t(2)=1/16t(3)=1/4t(4)=3/4t(5)=15/16t(6)=15/16t(7)=1if mc=2 thent(0)=0t(1)=1/8t(2)=3/8t(3)=1/2t(4)=1/2t(5)=5/8t(6)=7/8t(7)=1elseif mc=3 thent(0)=0t(1)=1/8t(2)=1/8t(3)=1/2t(4)=1/2t(5)=7/8t(6)=7/8t(7)=1elsemsgbox(“请输入1-3的数”)goto startend iffor i= 1 to7f(i)=2*(t(i)-f(i-1))/pinext im=(f(1)+f(2)*pi/2+f(3))/(f(5)+f(6)*pi/2+f(7))a1=(f(3)^2+0.5*((t(2)-t(1))^2)-f(1)^2+f(3)*(1-t(3))+(t(2)-t(1))*(1-t(2))+f(1)-m*(f(7)^2+0.5*((t(6) -t(5))^2)- f(5)^2+f(5)*(1-t(4))+(t(6)-t(5))*(1-t(6))))^(-1)a2=m*a1c(1)=f(1)*a1c(2)=-t(1)*a1+c(1)c(3)= t(2)*a1+c(2)c(4)= f(3)*a1+c(3)c(5)=-f(5)*a2+c(4)c(6)=t(5)*a2+c(5)c(7)=- t(6)*a2+c(6)b(1)=0b(2)=-a1*(f(1)^2+0.5*t(1)^2)+t(1)*(c(1)-c(2))+b(1)b(3)= a1*(f(3)^2+0.5*t(2)^2)+t(2)* (c(2)-c(3))+b(2)b(4)=t(3)*(c(3)-c(4))+b(3)b(5)=t(4)*(c(4)-c(5))+b(4)b(6)=a(2)*(f(5)^2+0.5*t(5)^2)+t(5)*(c(5)-c(6))+b(5)b(7)=-a(2)*(f(7)^2+0.5*t(6)^2)+t(6)*(c(6)-c(7))+b(6)for tt=0 to 1 step 0.01for i=1 to 7select case icase 1 and (tt>=t(0) and tt<=t(1))p(i)=(tt-t(i-1))/f(i)+(i-1)*pi/4j=j+1jsd(j)=a1*sin(p(i))yd(j)=a1*cos(p(i))/pisd(j)= -a1*f(1)*cos(p(i))+c(i)wy(j)=-a1*(f(i)^2)*sin(p(i))+c(i)*c(i)*tt+b(i)open “d:\加速度.txt”for append as #1 print #1,jsd(j)closeopen “d:\跃度.txt”for append as #1 print #1,yd(j)closeopen “d:\速度.txt”for append as #1 print #1,sd(j)closeopen “d:\位移.txt”for append as #1 print #1,wy(j)closecase 2 and (tt>t(1)and tt<=t(2))j=j+1jsd(j)=a1yd(j)=0sd(j)=a1*tt+c(2)wy(j)=a1*(tt^2)*0.5+c(2)*tt+b(2)open “d:\加速度.txt”for append as #1 print #1,jsd(j)closeopen “d:\跃度.txt”for append as #1 print #1,yd(j)closeopen “d:\速度.txt”for append as #1 print #1,sd(j)closeopen “d:\位移.txt”for append as #1 print #1,wy(j)closecase 3 and (tt>t(2)and tt<=t(3))p(i)=(tt-t(i-1))/f(i)+(i-1)*pi/4j=j+1jsd(j)=a1*sin(p(i))yd(j)=a1*cos(p(i))/f(i)sd(j)=-a1*f(i)*cos(p(i))+c(i)*ttwy(j)= -a1*(f(i)^2)*sin(p(i))+c(i)*tt+b(i) open “d:\加速度.txt”for append as #1 print #1,jsd(j)closeopen “d:\跃度.txt”for append as #1 print #1,yd(j)closeopen “d:\速度.txt”for append as #1closeopen “d:\位移.txt”for append as #1 print #1,wy(j)closecase 4 and (tt>t(3)and tt<=t(4))j=j+1jsd(j)=0yd(j)=0sd(j)=c(4)wy(j)=c(4)*tt+b(4)open “d:\加速度.txt”for append as #1 print #1,jsd(j)closeopen “d:\跃度.txt”for append as #1 print #1,yd(j)closeopen “d:\速度.txt”for append as #1 print #1,sd(j)closeopen “d:\位移.txt”for append as #1 print #1,wy(j)closecase 5 and (tt>t(4)and tt<=t(5))p(i)=(tt-t(i-1))/f(i)+(i-1)*pi/4j=j+1jsd(j)=a2*sin(p(i))yd(j)=a2*cos(p(i))/f(i)sd(j)=-a2*f(i)*cos(p(i))+c(i)*ttwy(j)= -a2*(f(i)^2)*sin(p(i))+c(i)*tt+b(i) open “d:\加速度.txt”for append as #1 print #1,jsd(j)closeopen “d:\跃度.txt”for append as #1 print #1,yd(j)closeopen “d:\速度.txt”for append as #1 print #1,sd(j)closeopen “d:\位移.txt”for append as #1 print #1,wy(j)closecase 6 and (tt>t(5)and tt<=t(6))j=j+1yd(j)=0sd(j)=-a1*tt+c(6)wy(j)=-a1*(tt^2)*0.5+c(6)*tt+b(6)open “d:\加速度.txt”for append as #1print #1,jsd(j)closeopen “d:\跃度.txt”for append as #1print #1,yd(j)closeopen “d:\速度.txt”for append as #1print #1,sd(j)closeopen “d:\位移.txt”for append as #1print #1,wy(j)closecase 7 and (tt>t(6)and tt<=t(7))p(i)=(tt-t(i-1))/f(i)+(i-1)*pi/4j=j+1jsd(j)=a2*sin(p(i))yd(j)=a2*cos(p(i))/f(i)sd(j)=-a2*f(i)*cos(p(i))+c(i)wy(j)= -a2*(f(i)^2)*sin(p(i))+c(i)*tt+b(i)open “d:\加速度.txt”for append as #1print #1,jsd(j)closeopen “d:\跃度.txt”for append as #1print #1,yd(j)closeopen “d:\速度.txt”for append as #1print #1,sd(j)closeopen “d:\位移.txt”for append as #1print #1,wy(j)closeend selectnext inext iimsgbox (“计算完毕”&chr(10)+chr(13)&”位移数据在d:\位移.txt” &chr(10)+chr(13)& ”速度数据在d:\速度.txt”&chr(10)+chr(13)&”加速度数据在d:\加速度.txt”&chr(10)+chr(13)& ”跃度数据在d:\位移.txt”)msbox(“输出图形“)for i=1 to 1200 step 2form1.currentx=i*5+100print”.”Nextfor i=1 to 101currentx=i*20+1500 currenty=-wy(i)*600+1500 print”.”Nextcurrentx=1500currenty=2500print”位移曲线”for i=1500 to 3000 step 2 form1.currentx=i*5+100 form1.currenty=1500 print”.”Nextfor i=1 to 101currentx=i*20+8500 currenty=-sd(i)*200+1500 print”.”Nextcurrentx=9500currenty=2500print”速度曲线”for i=1 to 1200 step 2 form1.currentx=i*5+100 form1.currenty=5500 print”.”Nextfor i=1 to 1000 step 2 form1.currentx=i*2+5000 form1.currenty=1500 print”.”Nextfor i=1 to 101currentx=i*20+1500 currenty=-jsd(i)*50+5500 print”.”Nextcurrentx=2000currenty=7000print”加速度曲线”for i=1500 to 3000 step 2 form1.currentx=i*5+100print”.”Nextfor i=1 to 1000 step 2form1.currentx=i*2+5000form1.currenty=8500 print”.”Nextfor i=1 to 101 step 0.8 currentx=i*20+8500currenty=-yd(i)*6+5500 print”.”Nextcurrentx=9000currenty=7000print”跃度曲线”printprintselect case mccase 1currentx=6000currenty=12000print “修正等速”;”的四个曲线”case 2currentx=6000currenty=12000print “修正梯形”;”的四个曲线”case 3currentx=6000currenty=12000print “修正正弦”;”的四个曲线”end selectend subprivate sub command2_click() endend subend sub。
牛头刨床凸轮轮廓曲线设计vb程序

Dim pi!, p!, i!, F0!, F01!, F02!, L4c!, L24!, r0!, q!, qm!, q0!, Mm!, F!, F1!, R! '程序中F代表δ;q代表φ;st代表θDim F2!, SF!, CF!, X!, Y!, dpdf!, dxdf!, dydf!, st!, X1!, Rr!, X2!, Y2!Print Spc(2); "凸轮转角"; Spc(2); " 摆杆摆角"; Spc(3); " 理论廓线xy值"; Spc(3); "理论廓线向径"; Spc(3); "内实际廓线xy值";Print Spc(3); "外实际廓线xy值"pi = 3.1415926: p = pi / 180: L4c = 140: L24 = 150: F0 = 60: F01 = 10: F02 = 60: r0 = 55: Rr = 15 qm = 15 * p: F0 = F0 * p: F01 = F01 * p: F02 = F02 * pFor i = 0 To 36 Step 1F = 10 * i * pIf F <= F0 / 2 ThenF1 = F / F0: q = 2 * qm * F1 * F1: dqdf = 4 * qm * F1 / F0ElseIf F > F0 / 2 And F <= F0 ThenF1 = (F0 - F) / F0: q = qm - 2 * qm * F1 * F1: dqdf = 4 * qm * F1 / F0ElseIf F > F0 And F < F0 + F01 Thenq = qm: dqdf = 0ElseIf F >= F0 + F01 And F <= F0 + F01 + F0 / 2 ThenF2 = (F - F0 - F01) / F02: q = qm * (1 - 2 * F2 * F2): dqdf = 4 * q * F2 / F02ElseIf F > F0 + F01 + F0 / 2 And F <= F0 + F01 + F0 ThenF2 = (F02 - F + F0 + F01) / F02: q = 2 * qm * F2 * F2: dqdf = 4 * qm * F2 / F02Elseq = 0: dqdf = 0End Ifq0 = Atn(Sqr(1 - ((L24 ^ 2 + L4c ^ 2 - r0 ^ 2) / 2 / L24 / L4c) ^ 2) / ((L24 ^ 2 + L4c ^ 2 - r0 ^ 2) / 2 / L24 / L4c))SF = Sin(F - q - q0)CF = Cos(F - q - q0)Y = L24 * Sin(F) - L4c * SFX = L24 * Cos(F) - L4c * CFR = Sqr(X ^ 2 + Y ^ 2)dydf = L24 * Cos(F) - L4c * Cos(F - q - q0) * (1 - dqdf)dxdf = -L24 * Sin(F) + L4c * Sin(F - q - q0) * (1 - dqdf)st = Atn(-dxdf / dydf)Select Case dydfCase Is > 0If -dxdf < 0 Thenst = 360 * p + stElsest = stEnd IfCase Elsest = 180 * p + stEnd SelectY1 = Y - Rr * Sin(st)X1 = X - Rr * Cos(st)Y2 = Y + Rr * Sin(st)X2 = X + Rr * Cos(st)Print Spc(2); Format(F / p, "0.00"); Spc(7); Format(q / p, "0.00"); Spc(7); Format(X, "0.00"); Print Spc(2); Format(Y, "0.00"); Spc(7); Format(R, "0.00"); Spc(5); Format(X1, "0.00"); Spc(2); Format(Y1, "0.00");Print Spc(7); Format(X2, "0.00"); Spc(2); Format(Y2, "0.00")Next i。
解析法设计凸轮轮廓曲线

由方程
x y
= =
(s0 (s0
+ +
s) sin d s) cosd
+ ecosd - e sin d
ü ý þ
可得
dx / dd = (ds / dd - e) sin d + (s0 + s) cosd ü
dy / dd
= (ds / dd
- e) cosd
- (s0
+
s)
sin
d
ý þ
sinq = (dx / dd ) / (dx / dd )2 + (dy / dd )2 ïü
ý
cosq = -(dy / dd ) / (dx / dd )2 + (dy / dd )2 ïþ
式中e为代数值: (1)当凸轮逆时针转动,推杆在O点右侧时,正偏置,取“+”号;
推杆在O点左侧时,负偏置,取“”号; (2)当凸轮顺时针转动,推杆在O点左侧时,正偏置,取“+”号;
推杆在O点右侧时,负偏置,取“”号;
2.对心平底推杆盘形凸轮机构
已知:基圆半径r0、s=s(d)、凸轮转动角 速度w。 建立图示坐标系,当凸轮转过d角, 推杆产生位移s,平底与凸轮在B点 相切,P为凸轮与推杆的相对瞬心。
n =n P = OPw
OP =n / w = ds / dd
B点的坐标为:
x y
= =
(r0 (r0
+ +
s) s)
解析法设计凸轮轮廓曲线
1.偏置直动滚子推杆盘形凸轮机构
已知:基圆半径r0、偏心距e、s=s(d)、凸 轮转动角速度w、滚子半径rr。
建立图示坐标系,当凸轮转过d角,推 杆产生位移s,采用反转法,确定滚子 中心在B点的坐标。
凸轮轮廓曲线的设计

2、偏置直动滚子推杆盘形凸轮(图9-19) 已知:增加滚子半径rr,其他条件同上。
设计思路:把滚子中心A看作是尖顶推 杆凸轮机构的尖顶。
作图步骤:
1)按尖顶设计方法定出滚子中心A在推杆 复合运动中依次占据的位置1′、2′、 3′、……,并连成光滑的曲线; 2)以光滑的曲线上的一些点为圆心, 以滚子半径rr为半径作一系列的圆;
对于对心直动推杆盘形凸轮机构可以认为是e0时的偏置凸轮机构其设计方法与上述方法基本相同只需将过基圆上各分点作偏距圆的切线改为作过凸轮回转中心o的径向线即可
§ 9 —3
凸轮轮廓曲线的设计
(Designing Cam Profile动规律和基圆半径后,就可以进行凸轮轮廓曲线 的设计了。
作图步骤: 1)按尖顶设计方法定出点A在推 杆复合运动中依次占据的位 置1′、2′、3′、……; 2)过点1′、2′、3′、……作 一系列代表推杆平底的直线, 得直线族; 3)作此直线族的内包络线β ,即为所求的凸轮廓线。 注意: 1)β 0与β 是非等距曲线,也不是相似曲线。 2)为了保证在所有位置平底都能与轮廓相切,平底左右 两侧的宽度必须大于导路至最远切点的距离Lmax(图 9-20),取整个平底长度 L=2Lmax+(5~7)mm。
2)取作图比例尺μL(mm/mm),由LOA 定O 、 A两点,以O为圆心r0为半径 作基圆、LOA为半径作中心距圆; 3)以A为中心,LAB为半径作弧交基圆于B点(摆杆尖顶的起始位 置);
4)以OA为基准,沿-ω方向依次 取角度δ0、δ01、δ0′、δ02,并将角 δ0、δ0′等分成与ψ线图对应的等 分,与中心距圆相交得点A1、A2、 A3、……(此即代表反转后推杆 回转中心占据的一系列位置); 5)以点A1、A2、A3、……为圆心,以LAB为半径作圆弧,与基圆交 于点B1、B2、B3、……,连A1B1、A2B2、A3B3、……(此即代 表摆动推杆在反转中只转不摆时依次占据的位置);
凸轮理论轮廓曲线设计c语言程序

/************习题4-1凸轮轮廓曲线绘制程序**********/#include<stdio.h>#include<math.h>#define PI 3.1415926void main(){double e=10.0,ro=40.0,rt=10.0,h=20.0,phi1=150.0,phis=30.0,phi_1=120.0,phi_s=60;/*各字母含义:e偏距,基圆半径ro,滚子半径rt,行程h,推程运动角phi1,远休止角phis,回程运动角phi_1,近休止角phi_s*/double s,alp[73],x[73],y[73],x1,y1,xr[73],yr[73];/*分别代表从动件位移,压力角,理论轮廓曲线点的位置x,y,x,y对运动角的微分,实际轮廓曲线的位置x,y*/double ic,ic1,ic2,ic3,ic4,so,s1,cop,sip,phi,gam,bel,del=5.0,q,t; /*定义变量*/int i;gam=phi1+phis;bel=phi1+phis+phi_1;ic=(int)(360.0/del);ic1=(int)(phi1/del);ic2=(int)(gam/del);ic3=(int)((phi1+phis+phi_1/2.0)/del);ic4=(int)(bel/del);so=sqrt(ro*ro-e*e);printf("\n No THETA Theoretical contour curve. Actual contour curve of cam. pressure angle \n");/*在屏幕上输出文件头*/printf(" deg x/mm y/mm X/mm Y/mm rad\n");for(i=0;i<=ic;i++) /*每隔五度建立循环*/{phi=i*del*PI/180.0; /*将角度化为幅度*/cop=cos(phi);sip=sin(phi);if(i<=ic1) /*推程运动判断*/{s=h/2.0*(1.0-cos(180.0*phi/phi1));s1=h*PI*sin(180.0*phi/phi1)/2.0/phi1;x1=-(s+so)*sip+s1*cop-e*cop;y1=(s+so)*cop+s1*sip-e*sip;}else if(i<=ic2) /*远休止角*/{s=h;s1=0;x1=-(s+so)*sip-e*cop;y1=(so+s)*cop-e*sip;}else if(i<=ic3) /*回程等加速运动判断*/{s=h-2.0*h*(phi-gam)*(phi-gam)/phi_1/phi_1;s1=-4.0*h*(phi-gam)/phi_1/phi_1;x1=s1*cop-(s+so)*sip-e*cop;y1=s1*sip+(so+s)*cop-e*sip;}else if(i<=ic4) /*回程等减速运动判断*/{s=2.0*h*(bel-phi)*(bel-phi)/phi_1/phi_1;s1=-4.0*h*(bel-phi)/phi_1/phi_1;x1=s1*cop-(so+s)*sip-e*cop;y1=s1*sip+(so+s)*cop-e*sip;}else /*近休止角*/{s=0;s1=0;x1=-(s+so)*sip-e*cop;y1=so*cop-e*sip;}t=fabs(s1-e);alp[i]=atan2(t,(s+so)); /*计算压力角*/q=rt/sqrt(x1*x1+y1*y1);x[i]=(s+so)*cop-e*sip; /*理论轮廓曲线位置*/y[i]=(s+so)*sip+e*cop;xr[i]=x[i]-q*y1; /*实际轮廓曲线位置*/yr[i]=y[i]+q*x1;phi=i*del;printf("\n%2d%12.3f%12.3f%12.3f%12.3f%12.3f%12.3f",i+1,phi,x[i],y[i],xr[i],yr[i],alp[i]);}}凸轮理论轮廓曲线和实际轮廓曲线计算数据(以教材东南大学机械学科组郑文伟,吴克坚主编《机械原理》(第七版)p521页题4-1为例)No THETA Theoretical contour curve. Actual contour curve of cam. pressure angle deg x/mm y/mm X/mm Y/mm rad1 0.000 38.730 10.000 29.047 7.500 0.2532 5.000 37.765 13.342 28.335 10.016 0.2523 10.000 36.620 16.611 27.509 12.490 0.2504 15.000 35.295 19.810 26.567 14.929 0.2485 20.000 33.786 22.939 25.502 17.339 0.2456 25.000 32.089 25.997 24.304 19.721 0.2427 30.000 30.195 28.980 22.960 22.076 0.2388 35.000 28.094 31.879 21.458 24.398 0.2349 40.000 25.776 34.682 19.782 26.677 0.23010 45.000 23.230 37.372 17.919 28.899 0.22611 50.000 20.449 39.927 15.855 31.044 0.22112 55.000 17.426 42.321 13.581 33.090 0.21613 60.000 14.160 44.525 11.089 35.008 0.21214 65.000 10.652 46.506 8.379 36.768 0.20715 70.000 6.912 48.229 5.452 38.336 0.20316 75.000 2.953 49.658 2.318 39.678 0.19817 80.000 -1.205 50.755 -1.008 40.757 0.19418 85.000 -5.534 51.487 -4.504 41.540 0.19019 90.000 -10.000 51.820 -8.142 41.994 0.18720 95.000 -14.564 51.725 -11.887 42.090 0.18421 100.000 -19.178 51.177 -15.700 41.802 0.18122 105.000 -23.793 50.159 -19.534 41.111 0.17823 110.000 -28.352 48.659 -23.341 40.005 0.17624 115.000 -32.798 46.673 -27.068 38.477 0.17425 120.000 -37.070 44.208 -30.661 36.532 0.17226 125.000 -41.109 41.275 -34.065 34.178 0.17127 130.000 -44.856 37.900 -37.226 31.435 0.17028 135.000 -48.253 34.111 -40.094 28.330 0.16929 140.000 -51.250 29.950 -42.620 24.898 0.16930 145.000 -53.800 25.463 -44.762 21.182 0.16831 150.000 -55.862 20.705 -46.485 17.229 0.16932 155.000 -57.453 15.757 -47.810 13.112 0.16933 160.000 -58.608 10.690 -48.770 8.896 0.16934 165.000 -59.317 5.541 -49.360 4.611 0.16935 170.000 -59.574 0.350 -49.574 0.291 0.16936 175.000 -59.378 -4.843 -49.411 -4.030 0.16937 180.000 -58.730 -10.000 -48.872 -8.321 0.16938 185.000 -57.635 -15.081 -47.960 -12.549 0.16939 190.000 -56.072 -20.041 -46.656 -16.673 0.16940 195.000 -54.109 -24.851 -45.023 -20.675 0.16941 200.000 -51.736 -29.472 -43.049 -24.520 0.16942 205.000 -48.969 -33.868 -40.746 -28.177 0.16943 210.000 -45.829 -38.007 -38.134 -31.620 0.16944 215.000 -42.341 -41.855 -35.232 -34.823 0.16945 220.000 -38.530 -45.385 -32.061 -37.759 0.16946 225.000 -34.427 -48.569 -28.647 -40.409 0.16947 230.000 -30.062 -51.383 -25.015 -42.750 0.16948 235.000 -25.468 -53.806 -21.193 -44.766 0.16949 240.000 -20.680 -55.819 -17.210 -46.441 0.16950 245.000 -7.306 -39.330 -5.481 -29.498 0.25351 250.000 -3.867 -39.862 -2.896 -29.909 0.25252 255.000 -0.379 -40.051 -0.278 -30.052 0.25253 260.000 3.113 -39.934 2.342 -29.964 0.25254 265.000 6.581 -39.513 4.944 -29.648 0.25255 270.000 10.000 -38.792 7.510 -29.107 0.25256 275.000 13.343 -37.775 10.019 -28.343 0.25257 280.000 16.585 -36.470 12.451 -27.365 0.25258 285.000 19.701 -34.888 14.790 -26.177 0.25259 290.000 22.668 -33.041 17.016 -24.791 0.25260 295.000 25.462 -30.942 19.113 -23.216 0.25261 300.000 28.063 -28.607 21.065 -21.463 0.25262 305.000 30.406 -25.990 22.805 -19.492 0.25363 310.000 32.555 -23.241 24.417 -17.431 0.25364 315.000 34.457 -20.315 25.843 -15.236 0.25365 320.000 36.097 -17.235 27.072 -12.926 0.25366 325.000 37.461 -14.023 28.096 -10.517 0.25367 330.000 38.541 -10.705 28.906 -8.028 0.25368 335.000 39.327 -7.305 29.495 -5.479 0.25369 340.000 39.814 -3.849 29.861 -2.887 0.25370 345.000 39.998 -0.365 29.999 -0.274 0.25371 350.000 39.878 3.123 29.908 2.342 0.25372 355.000 39.454 6.586 29.591 4.940 0.25373 360.000 38.730 10.000 29.047 7.500 0.253。
机械原理课程设计 凸轮机构设计 C程序

b=4*h*a1/a0/a0;printf("ds/dδ= %f\n",b);
a3=(b-e)/(s0+s);printf("tanα= %f\n",a3);
}
if(a>45&&a<=90)
for(a;a<=360;a=a+step)
{
a1=a*pi/180;
s0=sqrt(r0*r0-e*e); printf("s0= %f\n",s0);
if(a>=0&&a<=)
{
if(a>=0&&a<=45)
{
a0=90*pi/180;
y=(s0+s)*cos(a1)-e*sin(a1);printf("y= %f\n",y);
b1=(b-e)*sin(a1)+(s0+s)*cos(a1);printf("dx/dδ= %f\n",b1);
b2=(b-e)*cos(a1)-(s0+s)*sin(a1);printf("dy/dδ= %f\n",b2);
fprintf(fp,"δ=%d, s=%7.3f, x=%7.3f, y=%7.3f, x'=%7.3f, y'=%7.3f\n",a,s,x,y,x1,y1);
}
else printf("输出错误\n");
}fclose(fp);
图解法设计凸轮轮廓曲线法设计凸轮轮廓曲线
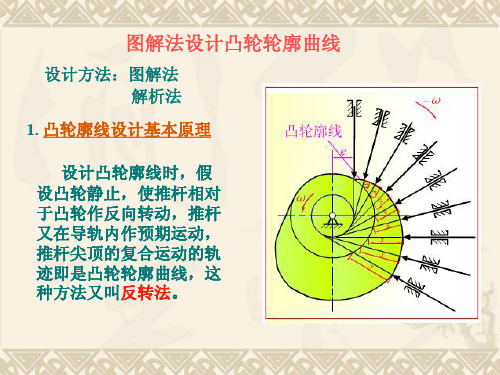
设计方法:图解法 解析法 1. 凸轮廓线设计基本原理 设计凸轮廓线时,假 设凸轮静止,使推杆相对 于凸轮作反向转动,推杆 又在导轨内作预期运动, 推杆尖顶的复合运动的轨 迹即是凸轮轮廓曲线,这 种方法又叫反转法 种方法又叫 反转法。 。
2. 图解法设计凸轮轮廓曲线
1)偏置直动尖顶推杆盘形凸轮机构
5)摆动尖顶推杆盘形凸轮机构 已知:基圆半径r ,凸轮逆时针 0 转动w,推杆的运动规律 j=j(d),LOA、LAB
A B
确定基圆 A点所在圆、AB初始位置 确定基圆、 将A点所在圆瓜分
O
自基圆向外量取等分点角位移 确定推程、远休、回程、近休廓线
3)对心直动滚子推杆盘形凸轮机构
以滚子中心为尖顶,按尖顶推杆设计凸轮廓线 按尖顶推杆设计凸轮廓线, 得到理论廓线。 以理论廓线上的各点为圆心,滚子半径为半径 滚子半径为径, 画一系列滚子圆,这些滚子圆的包络线即为 这些滚子圆的包络线即为实 际廓线。 注意:基圆半径是理论廓线上的最小向径。
4)对心直动平底推杆盘形凸轮机构 以平底中心A为尖顶,按尖顶推杆 设计凸轮廓线,得到理论廓线。 以理论廓线上的各点为平底中心, 画一系列平底,这些平底的包络线 即为实际廓线。
已知:基圆半径r ,凸轮逆时针转动w,推 0 杆的运动规律s=s(d),偏距为e,推杆在 凸轮回转中心右侧。
作偏距圆、基圆、推杆的初始位置 将偏距圆瓜分 将推程运动角等分,作偏距圆的切线 从基圆向外量推杆的位移,得推程廓线
2)对心直动尖顶推杆盘形凸轮机构
对心直动尖顶推杆盘形凸轮机构推杆在反转过 程中始终通过凸轮的回转中心。
凸轮轮廓线绘制程序

凸轮轮廓线绘制程序j=0:1:360;s=rand(1,361);v=rand(1,361);a=rand(1,361);jj=31;w=1;j1=80;j2=20;j3=80;j4=180;j5=360;t=pi/180;for i=1:361if j(i)<=j1 %升程,余弦加速度运动规律,转过的角度是j1。
s(i)=jj*[1-cos(pi*j(i)/j1)]/2;v(i)=36*(pi*jj*w*sin(pi*j(i)/j1)/(2*j1));a(i)=36*pi^2*jj*t*w^2*cos(pi*j(i)/j1)/(2*(j1*t)^2);elseif j(i)<=j1+j2 %远休。
s(i)=31;v(i)=0;a(i)=0;elseif j(i)<=j1+j2+j3 %回程,余弦加速度运动规律,转过的角度是j3。
s(i)=jj-jj*[1-cos(pi*(j(i)-90)/j3)]/2;v(i)=-36*(pi*jj*w*sin(pi*(j(i)-90)/j3)/(2*j3));a(i)=-36*pi^2*jj*t*w^2*cos(pi*(j(i)-90)/j3)/(2*(j3*t)^2);else %推程,余弦加速度运动规律,转过的角度是45。
s(i)=0;v(i)=0;a(i)=0;endend%绘制凸轮理论廓线、实际廓线r0=39;rr=9;l=36;loa=70;jj0=23;X=rand(1,361);Y=rand(1,361);Xa=rand(1,361);Ya=rand(1,361);Xaa=rand(1,361);Yaa=rand(1,361);dr=rand(1,361);A=rand(1,361);B=rand(1,361);for i=1:361%if j(i)<=j1X(i)=-l*sin((j(i)+s(i)+jj0)*t)+loa *sin(j(i)*t);Y(i)=-l*cos((j(i)+s(i)+jj0)*t)+loa*cos(j(i)*t);dx=loa*cos(j(i)*t)-l*(1+v(i)/10)*cos((j(i)+s(i)+jj0)*t);dy=-loa*sin(j(i)*t)+l*(1+v(i)/10)*sin((j(i)+s(i)+jj0)*t);st=dx/sqrt(dy^2+dx^2);ct=-dy/sqrt(dy^2+dx^2);Xa(i)=X(i)+rr*ct;Ya(i)=Y(i)+rr*st;Xaa(i)=X(i)-rr*ct;Yaa(i)=Y(i)-rr*st;%X(i)=l*sin((j(i)-s(i)-jj0)*t)-loa*sin(j(i)*t);%Y(i)=-l*cos((j(i)-s(i)+jj0)*t)+loa*cos(j(i)*t);%dx=-loa*cos(j(i)*t)-l*(-1+v(i)/10)*cos((-j(i)+s(i)+jj0)*t);%dy=-loa*sin(j(i)*t)+l*(-1+v(i)/10)*sin((-j(i)+s(i)+jj0)*t);%st=dx/sqrt(dy^2+dx^2);%ct=-dy/sqrt(dy^2+dx^2);%Xa(i)=X(i)+rr*ct;%Ya(i)=Y(i)+rr*st;%Xaa(i)=X(i)-rr*ct;%Yaa(i)=Y(i)-rr*st;% else%X(i)=l*sin((j(i)-s(i)-jj0)*t)-loa*sin(j(i)*t);%Y(i)=-l*cos((j(i)-s(i)+jj0)*t)+loa*cos(j(i)*t);%dx=-loa*cos(j(i)*t)-l*(-1-v(i)/10)*cos((-j(i)-s(i)-jj0)*t);%dy=-loa*sin(j(i)*t)+l*(-1-v(i)/10)*sin((-j(i)-s(i)-jj0)*t);%st=dx/sqrt(dy^2+dx^2);%ct=-dy/sqrt(dy^2+dx^2);%Xa(i)=X(i)+rr*ct;%Ya(i)=Y(i)+rr*st;%Xaa(i)=X(i)-rr*ct;%Yaa(i)=Y(i)-rr*st;% endjr=0:1:360;Xr=rand(1,361);Yr=rand(1,361);for z=1:361Xr(z)=X(i)+rr*sin(jr(z)*pi/180);Yr(z)=Y(i)+rr*cos(jr(z)*pi/180);A(i,z)=Xr(z);B(i,z)=Yr(z);endendj0=0:1:360;X0=rand(1,361);Y0=rand(1,361);for i=1:361X0(i)=r0*sin(jr(i)*pi/180);Y0(i)=r0*cos(jr(i)*pi/180);endR0=[j' X' Y' Xa' Ya' Xaa' Yaa' ]plot(X0,Y0,'-.k',X,Y,'--k',Xa,Ya,'-.k',Xaa,Yaa,'-k',A(1:8:361,:),B(1:8:361,:),'.k') ;title('凸轮的理论廓线和实际廓线');xlabel('水平坐标');ylabel('竖直坐标');legend('基圆','实际廓线','理论廓线');位移速度加速度曲线程序j=0:3:360;s=rand(1,121);v=rand(1,121);a=rand(1,121);jj=31;w=1;j1=80;j2=20;j3=80;j4=180;j5=360;t=pi/180;for i=1:121if j(i)<=j1 %升程,余弦加速度运动规律,转过的角度是j1。
凸轮设计_C语言编程

一、编程:(注:程序中各个符号的含义)PI:常数错误!未找到引用源。
s0:理论廓线的基圆半径 s:各个角度的推杆位移 i:转角e:偏心距 rr:滚子半径 r0:基圆半径 h:行程ya0:许用压力角 yah:弧度制压力角 yaj:角度制压力角p:曲率半径st:推程段推杆位移 sy:远休段推杆位移 sh:回程段推杆位移 sj:近休段推杆位移dx_di:理论坐标x对转角i的一次导 dy_di:理论坐标y对转角i的一次导d2x:理论坐标x对转角i的二次导 d2y:理论坐标y对转角i的二次导ds_di:推杆位移s对角度i的一次导 d2s:推杆位移s对转角i的二次导xli:理论坐标x yli:理论坐标y x:实际坐标想 y:实际坐标y sink:凸轮廓线法向倾斜角θ正弦 cosk:凸轮廓线法向倾斜角θ余弦子函数1:求x、y的实际坐标子函数2:求转角i处的曲率半径子函数3:求转角i处的压力角#include "stdio.h"#include "math.h"#define PI 3.1415926void zuobiao (float s0, float s,float ds_di,int i, int e,int rr); ;子函数1float qulv (float s0, float s,float ds_di,float d2s,int i, int e,int rr,int r0); ;子函数2float yalijiao (float s,float ds_di,int e,int r0); ;子函数3main(){int e,rr,r0,h,i,ya0=30;float s0,ds_di,d2s,st,sy,sh,sj,yah,yaj,p;scanf("%d%d%d%d",&e,&rr,&r0,&h);printf("e=%d,rr=%d,r0=%d,h=%d\n",e,rr,r0,h);s0=sqrt(r0*r0-e*e);for(i=0;i<=360;i++){if(i<=120) ;推程{for(i=0;i<=120;i++){st=50*(3*i*PI/180-sin(3*i*PI/180))/(2*PI);ds_di=50*(3-3*cos(3*i*PI/180))/(2*PI);d2s=50*9*sin(3*i*PI/180)/(2*PI);yaj=yalijiao(st,ds_di,e,r0); ;调用子函数3,求压力角if(yaj<ya0) ;if~else校核推程段压力角{p=qulv(s0,st,ds_di,d2s,i,e,rr,r0); ;调用子函数2,求曲率半径if(p>=rr) ;if~else校核推程段曲率半径zuobiao(s0,st,ds_di,i,e,rr); ;调用子函数1,求xy坐标elseprintf("chongxinshuru r0,rr\n");}elseprintf("chongxinshuru e,r0\n");printf("%f,",p); ;输出曲率半径printf("%f\n",yaj); ;输出压力角}}else if(i<=150) ;远休{for(i=121;i<=150;i++){sy=50;ds_di=0;d2s=0;yaj=yalijiao(sy,ds_di,e,r0); ;调用子函数3,求压力角p=qulv(s0,sy,ds_di,d2s,i,e,rr,r0); ;调用子函数2,求曲率半径if(p>=rr) ;if~else校核曲率半径zuobiao(s0,sy,ds_di,i,e,rr); ;调用子函数1,求xy坐标elseprintf("chongxinshuru r0,rr\n");printf("%f,",p); ;输出曲率半径printf("%f\n",yaj); ;输出压力角}}else if(i<=210) ;回程{for(i=151;i<=210;i++){sh=50*(1+cos(3*i*PI/180-5*PI/2))/2;ds_di=-50*3*sin(3*i*PI/180-5*PI/2)/2;d2s=-50*9*cos(3*i*PI/180-5*PI/2)/2;yaj=yalijiao(sh,ds_di,e,r0); ;调用子函数3,求压力角p=qulv(s0,sh,ds_di,d2s,i,e,rr,r0); ;调用子函数2,求曲率半径if(p>rr) ;if~else校核曲率半径zuobiao(s0,sh,ds_di,i,e,rr); ;调用子函数1,求xy坐标elseprintf("chongxinshuru r0,rr\n");printf("%f,",p); ;输出曲率半径printf("%f\n",yaj); ;输出压力角}}else ;近休{for(i=211;i<=360;i++){sj=0;ds_di=0;d2s=0;yaj=yalijiao(sj,ds_di,e,r0); ;调用子函数3,求压力角p=qulv(s0,sj,ds_di,d2s,i,e,rr,r0); ;调用子函数2,求曲率半径if(p>rr) ;if~else校核曲率半径zuobiao(s0,sj,ds_di,i,e,rr); ;调用子函数1,求xy坐标elseprintf("chongxinshuru r0,rr\n");printf("%f,",p); ;输出曲率半径printf("%f\n",yaj); ;输出压力角}}}}void zuobiao (float s0, float s,float ds_di,int i, int e,int rr){float dx_di, dy_di,xli,yli,x,y,sink,cosk;xli=(s0+s)*sin(i*PI/180)+e*cos(i*PI/180); ;计算理论x坐标yli=(s0+s)*cos(i*PI/180)-e*sin(i*PI/180); ;计算理论y坐标dx_di=(ds_di-e)*sin(i*PI/180)+(s0+s)*cos(i*PI/180);dy_di=(ds_di-e)*cos(i*PI/180)-(s0+s)*sin(i*PI/180);sink=dx_di/sqrt(dx_di*dx_di+dy_di*dy_di);cosk=-dy_di/sqrt(dx_di*dx_di+dy_di*dy_di);x=xli-rr*cosk; ;计算实际x坐标y=yli-rr*sink; ;计算实际y坐标printf("%d:%f,%f,",i,x,y); ;输出角度、xy实际坐标return;}float qulv (float s0, float s,float ds_di,float d2s,int i, int e,int rr,int r0){float dx_di,d2x,dy_di,d2y,p,q;dx_di=(ds_di-e)*sin(i*PI/180)+(s0+s)*cos(i*PI/180);dy_di=(ds_di-e)*cos(i*PI/180)-(s0+s)*sin(i*PI/180);d2x=(d2s-s0-s)*sin(i*PI/180)+(2*ds_di-e)*cos(i*PI/180);d2y=(d2s-s0-s)*cos(i*PI/180)-(2*ds_di-e)*sin(i*PI/180);q=dx_di*dx_di+dy_di*dy_di;p=sqrt(q*q*q)/fabs(dx_di*d2y-dy_di*d2x); ;计算曲率半径return p;}float yalijiao (float s,float ds_di,int e,int r0){float yaj,yah;yah=fabs(atan(((ds_di)-e)/(sqrt(r0*r0-e*e)+s))); ;计算弧度制压力角yaj=180*yah/PI; ;计算角度制压力角return yaj;}二、运行数据结果:e=20,rr=10,r0=50,h=50(注:每组数据依次是转角i、坐标x、坐标y、曲率半径p、压力角yaj)。
06-凸轮轮廓的设计计算与绘图

06-凸轮轮廓的设计计算与绘图disp ' ******** 偏置移动从动件盘形凸轮设计********'disp '已知条件:'disp ' 凸轮作逆时针方向转动,从动件偏置在凸轮轴心的右边'disp ' 从动件在推程作等加速/等减速运动,在回程作余弦加速度运动' rb = 40;rt = 10;e = 15;h = 50;ft = 100;fs = 60;fh = 90;alp = 35;fprintf (1,' 基圆半径rb = %3.4f mm \n',rb)fprintf (1,' 滚子半径rt = %3.4f mm \n',rt)fprintf (1,' 推杆偏距 e = %3.4f mm \n',e)fprintf (1,' 推程升程h = %3.4f mm \n',h)fprintf (1,' 推程运动角ft = %3.4f 度\n',ft)fprintf (1,' 远休止角fs = %3.4f 度\n',fs)fprintf (1,' 回程运动角fh = %3.4f 度\n',fh)fprintf (1,' 推程许用压力角alp = %3.4f 度\n',alp)hd= pi / 180;du = 180 / pi;se=sqrt( rb^2 - e^2 );d1 = ft + fs;d2 = ft + fs + fh;disp ' 'disp '计算过程和输出结果:'disp ' 1- 计算凸轮理论轮廓的压力角和曲率半径'disp ' 1-1 推程(等加速/等减速运动)'s = zeros(ft);ds = zeros(ft);d2s = zeros(ft);at = zeros(ft);atd = zeros(ft);pt = zeros(ft);for f = 1 : ftif f <= ft / 2s(f)=2 * h * f ^ 2 / ft ^ 2;s = s(f);ds(f)=4 * h * f * hd / (ft * hd) ^ 2;ds = ds(f);d2s(f)=4 * h / (ft * hd) ^ 2;d2s = d2s(f);elses(f)=h - 2 * h * (ft - f) ^ 2 / ft ^ 2;s = s(f);ds(f)=4 * h * (ft - f) * hd / (ft * hd) ^ 2;ds = ds(f);d2s(f)=-4 * h / (ft * hd) ^ 2;d2s = d2s(f);endat(f)= atan(abs(ds - e) / (se + s));atd(f) = at(f) * du;p1=((se + s ) ^ 2 + (ds - e) ^ 2) ^ 1.5;p2= abs((se + s) * (d2s - se - s) - (ds - e) * (2 * ds - e));pt(f)= p1 /p2;p = pt(f);endatm = 0;for f = 1 : ftif atd(f) > atmatm = atd(f);endendfprintf (1,' 最大压力角atm = %3.4f 度\n',atm)for f = 1 : ftif abs(atd(f) - atm) < 0.1ftm = f;breakendendfprintf (1,' 对应的位置角ftm = %3.4f 度\n',ftm)if atm > alpfprintf (1,' * 凸轮推程压力角超过许用值,需要增大基圆!\n') endptn = rb + h;for f = 1 : ftif pt(f) < ptnptn = pt(f);endendfprintf (1,' 轮廓最小曲率半径ptn = %3.4f mm\n',ptn)for f = 1 : ftif abs(pt(f) - ptn) < 0.1ftn = f;breakendendfprintf (1,' 对应的位置角ftn = %3.4f 度\n',ftn)if ptn < rt + 5fprintf (1,' * 凸轮推程轮廓曲率半径小于许用值,需要增大基圆或减小滚子!\n') enddisp ' 1-2 回程(余弦加速度运动)'s = zeros(fh);ds = zeros(fh);d2s = zeros(fh);ah = zeros(fh);ahd = zeros(fh);ph = zeros(fh);for f = d1 : d2k = f - d1;s(f) = .5 * h * (1 + cos(pi * k / fh)); s = s(f);ds(f)=-.5 * pi * h * sin(pi * k / fh) / (fh * hd);ds = ds(f);d2s(f)= -.5 * pi ^2 * h * cos(pi * k / fh)/(fh * hd) ^2;d2s = d2s(f);ah(f)=atan(abs(ds + e) / (se + s));ahd(f) = ah(f) * du;p1=((se + s ) ^ 2 + (ds - e) ^ 2) ^ 1.5;p2= abs((se + s) * (d2s - se - s) - (ds - e) * (2 * ds - e));ph(f)= p1 /p2;p = ph(f);endahm = 0;for f = d1 : d2if ahd(f) > ahm;ahm = ahd(f);endendfprintf (1,' 最大压力角ahm = %3.4f 度\n',ahm)for f = d1 : d2if abs(ahd(f)- ahm) < 0.1fhm = f;breakendendfprintf (1,' 对应的位置角fhm = %3.4f 度\n',fhm)phn = rb + h;for f = d1 : d2if ph(f) < phnphn = ph(f);endendfprintf (1,' 轮廓最小曲率半径phn = %3.4f mm\n',phn)for f = d1 : d2if abs(ph(f) - phn) < 0.1fhn = f;breakendendfprintf (1,' 对应的位置角fhn = %3.4f 度\n',fhn)if phn < rt + 5fprintf (1,' * 凸轮回程轮廓曲率半径小于许用值,需要增大基圆或减小滚子!\n') enddisp ' 2- 计算凸轮理论廓线与实际廓线的直角坐标'n = 360;s = zeros(n);ds = zeros(n);r = zeros(n);rp = zeros(n);x = zeros(n);y = zeros(n);dx = zeros(n);dy = zeros(n);xx = zeros(n);yy = zeros(n);xp = zeros(n);yp = zeros(n);xxp = zeros(n);yyp = zeros(n);for f = 1 : nif f <= ft/2s(f) = 2 * h * f ^ 2 / ft ^ 2; s = s(f);ds(f) = 4 * h * f * hd / (ft * hd) ^ 2; ds = ds(f);elseif f > ft/2 & f <= fts(f) = h - 2 * h * (ft - f) ^ 2 / ft ^ 2; s = s(f);ds(f) = 4 * h * (ft - f) * hd / (ft * hd) ^ 2; ds = ds(f);elseif f > ft & f <= d1s = h;ds = 0;elseif f > d1 & f <= d2k = f - d1;s(f) = .5 * h * (1 + cos(pi * k / fh)); s = s(f);ds(f)= -.5 * pi * h * sin(pi * k / fh) / (fh * hd); ds = ds(f);elseif f > d2 & f <= ns = 0;ds = 0;endxx(f) = (se + s) * sin(f * hd) + e * cos(f * hd); x = xx(f);yy(f) = (se + s) * cos(f * hd) - e * sin(f * hd); y = yy(f);dx(f) = (ds - e) * sin(f * hd) + (se + s) * cos(f * hd); dx = dx(f);dy(f) = (ds - e) * cos(f * hd) - (se + s) * sin(f * hd); dy = dy(f);xp(f) = x + rt * dy / sqrt(dx ^ 2 + dy ^ 2);xxp = xp(f);yp(f) = y - rt * dx / sqrt(dx ^ 2 + dy ^ 2);yyp = yp(f);r(f) = sqrt (x ^2 + y ^2 );rp(f) = sqrt (xxp ^2 + yyp ^2 );enddisp ' 2-1 推程(等加速/等减速运动)'disp ' 凸轮转角理论x 理论y 实际x 实际y' for f = 10 : 10 :ftnu = [f xx(f) yy(f) xp(f) yp(f)];disp(nu)enddisp ' 2-2 回程(余弦加速度运动)'disp ' 凸轮转角理论x 理论y 实际x 实际y' for f = d1 : 10 : d2nu = [f xx(f) yy(f) xp(f) yp(f)];disp(nu)enddisp ' 2-3 凸轮轮廓向径'disp ' 凸轮转角理论r 实际r'for f = 10 : 10 : nnu = [f r(f) rp(f)];disp(nu)enddisp '绘制凸轮的理论轮廓和实际轮廓:'plot(xx,yy,'r-.') % 理论轮廓(红色,点划线)axis ([-(rb+h-10) (rb+h+10) -(rb+h+10) (rb+rt+10)]) % 横轴和纵轴的下限和上限axis equal % 横轴和纵轴的尺度比例相同text(rb+h+3,0,'X') % 标注横轴text(0,rb+rt+3,'Y') % 标注纵轴text(-5,5,'O') % 标注直角坐标系原点title('偏置移动从动件盘形凸轮设计') % 标注图形标题hold on; % 保持图形plot([-(rb+h) (rb+h)],[0 0],'k') % 横轴(黑色)plot([0 0],[-(rb+h) (rb+rt)],'k') % 纵轴(黑色)plot([e e],[0 (rb+rt)],'k--') % 初始偏置位置(黑色,虚线)ct = linspace(0,2*pi); % 画圆的极角变化范围plot(rb*cos(ct),rb*sin(ct),'g') % 基圆(绿色)plot(e*cos(ct),e*sin(ct),'c--') % 偏距圆(蓝绿色,虚线)plot(e + rt*cos(ct),se + rt*sin(ct),'y') % 滚子圆(黄色)plot(xp,yp,'b') % 实际轮廓(蓝色)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
/************习题4-1凸轮轮廓曲线绘制程序**********/#include<stdio.h>#include<math.h>#define PI 3.1415926void main(){double e=10.0,ro=40.0,rt=10.0,h=20.0,phi1=150.0,phis=30.0,phi_1=120.0,phi_s=60;/*各字母含义:e偏距,基圆半径ro,滚子半径rt,行程h,推程运动角phi1,远休止角phis,回程运动角phi_1,近休止角phi_s*/double s,alp[73],x[73],y[73],x1,y1,xr[73],yr[73];/*分别代表从动件位移,压力角,理论轮廓曲线点的位置x,y,x,y对运动角的微分,实际轮廓曲线的位置x,y*/double ic,ic1,ic2,ic3,ic4,so,s1,cop,sip,phi,gam,bel,del=5.0,q,t; /*定义变量*/int i;gam=phi1+phis;bel=phi1+phis+phi_1;ic=(int)(360.0/del);ic1=(int)(phi1/del);ic2=(int)(gam/del);ic3=(int)((phi1+phis+phi_1/2.0)/del);ic4=(int)(bel/del);so=sqrt(ro*ro-e*e);printf("\n No THETA Theoretical contour curve. Actual contour curve of cam. pressure angle \n");/*在屏幕上输出文件头*/printf(" deg x/mm y/mm X/mm Y/mm rad\n");for(i=0;i<=ic;i++) /*每隔五度建立循环*/{phi=i*del*PI/180.0; /*将角度化为幅度*/cop=cos(phi);sip=sin(phi);if(i<=ic1) /*推程运动判断*/{s=h/2.0*(1.0-cos(180.0*phi/phi1));s1=h*PI*sin(180.0*phi/phi1)/2.0/phi1;x1=-(s+so)*sip+s1*cop-e*cop;y1=(s+so)*cop+s1*sip-e*sip;}else if(i<=ic2) /*远休止角*/{s=h;s1=0;x1=-(s+so)*sip-e*cop;y1=(so+s)*cop-e*sip;}else if(i<=ic3) /*回程等加速运动判断*/{s=h-2.0*h*(phi-gam)*(phi-gam)/phi_1/phi_1;s1=-4.0*h*(phi-gam)/phi_1/phi_1;x1=s1*cop-(s+so)*sip-e*cop;y1=s1*sip+(so+s)*cop-e*sip;}else if(i<=ic4) /*回程等减速运动判断*/{s=2.0*h*(bel-phi)*(bel-phi)/phi_1/phi_1;s1=-4.0*h*(bel-phi)/phi_1/phi_1;x1=s1*cop-(so+s)*sip-e*cop;y1=s1*sip+(so+s)*cop-e*sip;}else /*近休止角*/{s=0;s1=0;x1=-(s+so)*sip-e*cop;y1=so*cop-e*sip;}t=fabs(s1-e);alp[i]=atan2(t,(s+so)); /*计算压力角*/q=rt/sqrt(x1*x1+y1*y1);x[i]=(s+so)*cop-e*sip; /*理论轮廓曲线位置*/y[i]=(s+so)*sip+e*cop;xr[i]=x[i]-q*y1; /*实际轮廓曲线位置*/yr[i]=y[i]+q*x1;phi=i*del;printf("\n%2d%12.3f%12.3f%12.3f%12.3f%12.3f%12.3f",i+1,phi,x[i],y[i],xr[i],yr[i],alp[i]);}}凸轮理论轮廓曲线和实际轮廓曲线计算数据(以教材东南大学机械学科组郑文伟,吴克坚主编《机械原理》(第七版)p521页题4-1为例)No THETA Theoretical contour curve. Actual contour curve of cam. pressure angle deg x/mm y/mm X/mm Y/mm rad1 0.000 38.730 10.000 29.047 7.500 0.2532 5.000 37.765 13.342 28.335 10.016 0.2523 10.000 36.620 16.611 27.509 12.490 0.2504 15.000 35.295 19.810 26.567 14.929 0.2485 20.000 33.786 22.939 25.502 17.339 0.2456 25.000 32.089 25.997 24.304 19.721 0.2427 30.000 30.195 28.980 22.960 22.076 0.2388 35.000 28.094 31.879 21.458 24.398 0.2349 40.000 25.776 34.682 19.782 26.677 0.23010 45.000 23.230 37.372 17.919 28.899 0.22611 50.000 20.449 39.927 15.855 31.044 0.22112 55.000 17.426 42.321 13.581 33.090 0.21613 60.000 14.160 44.525 11.089 35.008 0.21214 65.000 10.652 46.506 8.379 36.768 0.20715 70.000 6.912 48.229 5.452 38.336 0.20316 75.000 2.953 49.658 2.318 39.678 0.19817 80.000 -1.205 50.755 -1.008 40.757 0.19418 85.000 -5.534 51.487 -4.504 41.540 0.19019 90.000 -10.000 51.820 -8.142 41.994 0.18720 95.000 -14.564 51.725 -11.887 42.090 0.18421 100.000 -19.178 51.177 -15.700 41.802 0.18122 105.000 -23.793 50.159 -19.534 41.111 0.17823 110.000 -28.352 48.659 -23.341 40.005 0.17624 115.000 -32.798 46.673 -27.068 38.477 0.17425 120.000 -37.070 44.208 -30.661 36.532 0.17226 125.000 -41.109 41.275 -34.065 34.178 0.17127 130.000 -44.856 37.900 -37.226 31.435 0.17028 135.000 -48.253 34.111 -40.094 28.330 0.16929 140.000 -51.250 29.950 -42.620 24.898 0.16930 145.000 -53.800 25.463 -44.762 21.182 0.16831 150.000 -55.862 20.705 -46.485 17.229 0.16932 155.000 -57.453 15.757 -47.810 13.112 0.16933 160.000 -58.608 10.690 -48.770 8.896 0.16934 165.000 -59.317 5.541 -49.360 4.611 0.16935 170.000 -59.574 0.350 -49.574 0.291 0.16936 175.000 -59.378 -4.843 -49.411 -4.030 0.16937 180.000 -58.730 -10.000 -48.872 -8.321 0.16938 185.000 -57.635 -15.081 -47.960 -12.549 0.16939 190.000 -56.072 -20.041 -46.656 -16.673 0.16940 195.000 -54.109 -24.851 -45.023 -20.675 0.16941 200.000 -51.736 -29.472 -43.049 -24.520 0.16942 205.000 -48.969 -33.868 -40.746 -28.177 0.16943 210.000 -45.829 -38.007 -38.134 -31.620 0.16944 215.000 -42.341 -41.855 -35.232 -34.823 0.16945 220.000 -38.530 -45.385 -32.061 -37.759 0.16946 225.000 -34.427 -48.569 -28.647 -40.409 0.16947 230.000 -30.062 -51.383 -25.015 -42.750 0.16948 235.000 -25.468 -53.806 -21.193 -44.766 0.16949 240.000 -20.680 -55.819 -17.210 -46.441 0.16950 245.000 -7.306 -39.330 -5.481 -29.498 0.25351 250.000 -3.867 -39.862 -2.896 -29.909 0.25252 255.000 -0.379 -40.051 -0.278 -30.052 0.25253 260.000 3.113 -39.934 2.342 -29.964 0.25254 265.000 6.581 -39.513 4.944 -29.648 0.25255 270.000 10.000 -38.792 7.510 -29.107 0.25256 275.000 13.343 -37.775 10.019 -28.343 0.25257 280.000 16.585 -36.470 12.451 -27.365 0.25258 285.000 19.701 -34.888 14.790 -26.177 0.25259 290.000 22.668 -33.041 17.016 -24.791 0.25260 295.000 25.462 -30.942 19.113 -23.216 0.25261 300.000 28.063 -28.607 21.065 -21.463 0.25262 305.000 30.406 -25.990 22.805 -19.492 0.25363 310.000 32.555 -23.241 24.417 -17.431 0.25364 315.000 34.457 -20.315 25.843 -15.236 0.25365 320.000 36.097 -17.235 27.072 -12.926 0.25366 325.000 37.461 -14.023 28.096 -10.517 0.25367 330.000 38.541 -10.705 28.906 -8.028 0.25368 335.000 39.327 -7.305 29.495 -5.479 0.25369 340.000 39.814 -3.849 29.861 -2.887 0.25370 345.000 39.998 -0.365 29.999 -0.274 0.25371 350.000 39.878 3.123 29.908 2.342 0.25372 355.000 39.454 6.586 29.591 4.940 0.25373 360.000 38.730 10.000 29.047 7.500 0.253。
