第二章核磁共振氢谱
合集下载
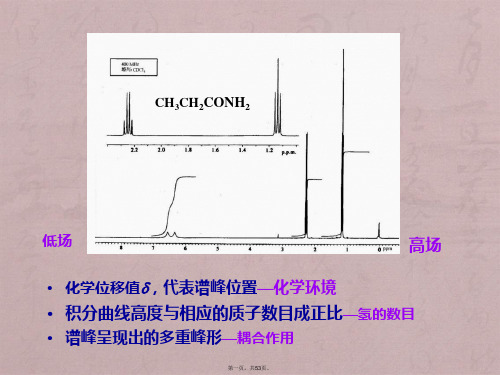
核磁共振氢谱(1H-NMR)
（2）双键
>C=O, >C=C<的屏蔽作用与苯环类似。在其平面的上、下方各有一个锥形屏蔽区（“+”），其它区域为去屏蔽区。
（3）三键
互相垂直的两个π键轨道电子绕σ键产生环电流，在外加磁场作用下产生与三键平行但方向与外加磁场相反的感应磁场。三键的两端位于屏蔽区（“+”），上、下方为去锥形屏蔽区（“-”）δ值比烯氢小。
δ3=5.25-0.35=4.90
δ4=5.25+2.11=7.36
e芳环氢
δHi=7.26+ΣZi
1溶剂影响:
低极性溶剂,CDCL3,CCL4,δoHi =7.26
高极性溶剂, DMSOδoHi =7.41
2.取代基在邻间对位作用不同
f.芳杂环
环上的氢的化学位移与其相对于杂原子的位置有关
g.醛基氢:9-12ppm
(1).自旋-自旋耦合引起谱峰分裂，裂距大小反映了耦合作用的强弱，即核磁矩之间相互作用能的大小，称为耦合常数（coupling constant) J（单位Hz）
有耦合作用的两核,取向相同时能量较高, J<0
取向相反时能量较低, J>0
(2)偶合常数J与分子特定的结构有关，即与两个核在分子中相隔化学键的数目、键的性质、偶合核的二面角有关。
由于吸收峰都集中在狭窄的范围内，故对一些较为复杂的化合物要准确地分析其吸收峰是有困难的。
烯烃
δ= 5．28＋σgem＋σcis＋σtrans
Jgem=0-3Hz
Jcis=8-12Hz
Jtrans=12-18Hz
苯
δHi=7.26+ΣZi
J邻位7-8.5Hz
J间位2-3Hz
J对位0-1Hz
>C=O, >C=C<的屏蔽作用与苯环类似。在其平面的上、下方各有一个锥形屏蔽区（“+”），其它区域为去屏蔽区。
（3）三键
互相垂直的两个π键轨道电子绕σ键产生环电流，在外加磁场作用下产生与三键平行但方向与外加磁场相反的感应磁场。三键的两端位于屏蔽区（“+”），上、下方为去锥形屏蔽区（“-”）δ值比烯氢小。
δ3=5.25-0.35=4.90
δ4=5.25+2.11=7.36
e芳环氢
δHi=7.26+ΣZi
1溶剂影响:
低极性溶剂,CDCL3,CCL4,δoHi =7.26
高极性溶剂, DMSOδoHi =7.41
2.取代基在邻间对位作用不同
f.芳杂环
环上的氢的化学位移与其相对于杂原子的位置有关
g.醛基氢:9-12ppm
(1).自旋-自旋耦合引起谱峰分裂，裂距大小反映了耦合作用的强弱，即核磁矩之间相互作用能的大小，称为耦合常数（coupling constant) J（单位Hz）
有耦合作用的两核,取向相同时能量较高, J<0
取向相反时能量较低, J>0
(2)偶合常数J与分子特定的结构有关，即与两个核在分子中相隔化学键的数目、键的性质、偶合核的二面角有关。
由于吸收峰都集中在狭窄的范围内，故对一些较为复杂的化合物要准确地分析其吸收峰是有困难的。
烯烃
δ= 5．28＋σgem＋σcis＋σtrans
Jgem=0-3Hz
Jcis=8-12Hz
Jtrans=12-18Hz
苯
δHi=7.26+ΣZi
J邻位7-8.5Hz
J间位2-3Hz
J对位0-1Hz
核磁共振谱图解析-一维氢谱第二部分
32
自旋-自旋耦合（spin-spin coupling)
33
自旋-自旋耦合（spin-spin coupling)
34
22
自旋-自旋耦合（spin-spin coupling)
裂分峰的面积比
由n个相同质子裂分成的n+1重峰，各峰的面积比遵循Pascal’s triangel规律。
23
自旋-自旋耦合（spin-spin coupling)
峰的裂分峰形
由n个相同质子裂分成的n+1重峰，各峰的面积比遵循Pascal’s triangel规律。
核磁共振谱图解析 一维氢谱-第二部分
曹焕岩
08-27-2013
1
氢谱溶剂
简单的核磁谱图都是在溶剂里测的，溶剂的质子一定不能有干扰。 所以测核磁的溶剂一般用氘代（Deuterated)试剂。Deutrium = 2H, 经常写为D。 常用的有D2O(重水），(CD3)CO （氘代丙酮）,CD3OD （氘代甲醇），(CD3)2SO （氘 代DMSO，DMSO-D6), CDCl3 (氘代氯仿）。 有的时候，一些不含质子的溶剂也用来测核磁，如CCl4 (四氯化碳），CS2 （二硫化 碳）等。
27
自旋-自旋耦合（spin-spin coupling)
28
自旋-自旋耦合（spin-spin coupling)
29
自旋-自旋耦合（spin-spin coupling)
30
自旋-自旋耦合（spin-spin coupling)
31
自旋-自旋耦合（spin-spin coupling)
24
自旋-自旋耦合（spin-spin coupling)
峰的裂分举例
波谱分析第二章HNMR谱
等 奇数 奇数或偶数 3/2 ,5/2… 1,2,3…
11B,17O，33S，35Cl, 37C1, 79Br,127I等
偶数
奇数
2H，10B,14N等
没有自旋
自旋球体
自旋椭圆体
2.原子核的磁矩 原子核是带正电荷的粒子，具有自旋角动 量的原子核也具有磁矩μ，其方向与P一致， 且二者之间的关系如下：
h P 2
I ( I 1)
(2-1)
试中 h—Planck常数 I—自旋量子数，其值与该核的质量数 和原子序数有关 (见下表)
表2-1各种原子核的自旋量子数
质量数 原子序数 自旋量 子数I 0 实 例
偶数
偶数
12C，16O,32S，28Si，
奇数
奇数或偶数
1/2
1H,13C,15N,19F,29Si 31P
ν
共振=
γB0/2π
参见下面的示意图
核磁能量吸收和跃迁过程
★下面对核磁共振方程进行讨论
（ν
共振=
γB0/2π ）
①对于同一核，如I=1/2的1H核，发生共振时，
ν照射∝B0
例如将1H核放在B0=1.4092T的磁场中，发生 NMR时，射频频率为60MHz 放在B0=4.69T的磁场中，发生NMR时，射频 频率为200MHz
样品 标准 6 10 仪器
讨论：这种表达方式的特点
(2-12)
①如果不用化学位移δ来表示不同化学环境的 核在核磁谱图上的相对位置，则使用不同类型 的核磁共振谱仪时，测定的结果就无法统一。 这是因为Δ∝B0。 例如：用60MHz和100MHz核磁共振谱仪分别 测定1,1,2-三氯丙烷时，其甲基的吸收峰与 TMS(基准物)峰相差分别是134Hz和223Hz。 若用δ表示：60MHz仪 δ=134/60=2.23 100MHz仪 δ=223/100=2.23 因此用δ表示化学位移，就可使不同核磁共振 谱仪测定的数值统一起来！
第二章 核磁共振氢谱2讲解
7 .4 5 0
7 .4 0 0
7 .3 5 0
7 .3 0 0
7 .2 5 0
7 .2 0 0
7 .1 5 0
7 .1 0 0
7 .0 5 0
7 .0 0 0
P-CH3OC6H4CH2Cl 芳氢核磁共振吸收的展开图
S a t A p r 2 2 0 9 :0 8 :0 0 2 0 0 0 : (u n title d ) W 1 : 1 H A x is = p p m S c a le = 3 .7 7 H z / c m
为复杂。对于对位取代，苯环上四个氢将分成 Ha=Ha’和Hb=Hb’两组，而且两组氢会发生偶合
作用，在谱图上表现为两组双重峰。对于邻位和
间位取代，苯环上四个氢完全不同，依据两个取 代基的情况，会分成2－4组各自分裂的峰 。
双硝基不同位置取代苯的核磁共 振谱图
• 对硝基苯谱图只有单峰，表明苯环上四个 氢一致。间硝基苯谱图有三组分裂的峰， 表明苯环上四个氢在两个硝基的作用下分 成三组各自偶合的峰。而邻硝基苯谱图上 有一个分裂的双重峰，表明苯环上四个氢 分成能偶合的两组。顺便一提：由于两个 硝基强大的吸电子和共轭作用，苯环上氢 的化学位移δ值大大增加，已达到8.0ppm以 上。
X
X
Ha
Ha' Ha
Ha'
Hb
Hb' Hb
Hb'
Hc
X'
苯环单 取代
苯环对位双 取代
Ha
Hb
X
Hb'
X'
Ha'
苯环邻位双 取代
X
Hb
Ha
Hc
X'
Hb'
第二章 核磁共振氢谱2
7 .1 5 0
7 .1 0 0
7 .0 5 0
7 .0 0 0
6 .9 5 0
6 .9 0 0
6 .8 5 0
6 .8 0 0
6 .7 5 0
6 .7 0 0
6 .6 5 0
6 .6 0 0
Jo 两主峰间的距离, 8Hz Jm 两侧峰间的距离的1/2， 2Hz.
δAA′,δBB′ˊ近似估计或经验计算。
间和对-硝基苯乙酸的核磁共振氢 谱
• 由于苯环上两个取代基不同，苯环上四 个氢至少被分成两组。对于对硝基苯乙 酸，苯环上四个氢分成对称的两组，因 而谱图上是对称的两组双峰。而间硝基 苯甲酸，苯环上四个氢不再对称，因而 谱图上峰的分裂也是不规则的。另外， 硝基苯甲酸分子中除了苯环氢外，还有 羧基中羟基氢和一个亚甲基氢，3.8ppm 的单峰是亚甲基氢
• 数，因而Eu3＋位移试剂使用比较普遍。 最常见的商品位移试剂是Eu(DPM)3 （Dipivalomethanato Europium），其对 不同类型有机物分子中的特定氢分子位 移的影响有显著差异（表9.2）。 Eu(DPM)3能将胺基和羟基氢的化学位移 增加到100ppm以上，而对其它有机基团 氢的位移分别从3ppm增加到30ppm。对 硝基和卤化物、烯类和酚等酸性有机 物，位移试剂将被分解而不可用。
四旋系统
4个质子间的相互偶合, 常见的有 AX3, A2X2, A2B2, AA′ BB ′ AX3 A2B2, A2X2 一级谱
AA′BB′ˊ二级谱
例如：CH3CHO, CH3CHX-, -OCH2CH2CO- 等 一级谱处理。
A2B2系统
A2B2系统理论上18条峰，常见14条峰，A、B各自为 7条峰，峰形对称。vA = v5，v
核磁共振 氢谱
核磁共振氢谱核磁共振氢谱（Nuclear Magnetic Resoce, NMR）是一种用于测定物质分子结构的重要方法。
它利用了原子核在磁场中的磁矩与外加磁场的相互作用，通过观测原子核吸收或发射电磁波的情况，来确定物质分子的结构。
在核磁共振氢谱中，我们主要关注的是氢原子核（质子）的行为。
这是因为在大多数化合物中，氢原子的数量最多，其行为对整个分子的性质有着重要影响。
此外，由于氢原子核的磁矩比其他原子核大得多，因此它在NMR实验中的信号最强，最容易被检测到。
核磁共振氢谱的基本原理是：当样品处于强磁场中时，如果给予样品一个射频脉冲，那么处于不同化学环境的氢原子核就会吸收不同数量的能量，从而发生能级的跃迁。
当射频脉冲停止后，这些氢原子核会以不同的速率重新放射出能量，产生不同的信号。
通过测量这些信号的强度和时间间隔，我们就可以得到关于样品的信息。
在实际操作中，我们会将样品溶解在一种称为氘代溶剂的液体中，然后放入NMR仪器中进行测量。
氘代溶剂是一种含有重氢（即氘，其原子核也是由一个质子和一个中子组成）的液体，它的优点是不会产生信号干扰。
通过分析核磁共振氢谱，我们可以确定样品中各种不同类型的氢原子的数量，以及它们之间的相对位置关系。
这对于研究物质的分子结构、化学反应过程等都有着重要的意义。
总的来说，核磁共振氢谱是一种非常强大的分析工具，它不仅可以提供关于样品的详细信息，而且操作简便、准确度高。
然而，它也有一些局限性，例如对于含有大量未定域电子的样品，或者对于某些特定的化学环境，NMR信号可能会受到干扰。
因此，在使用NMR进行分析时，我们需要根据具体的样品和目标来选择合适的条件和方法。
《核磁共振氢谱》课件
芳烃的氢谱解析
芳烃的氢谱特征
芳烃的氢谱峰形较复杂，有多个峰，且峰与峰之间的距离较近。
芳烃的氢谱解析要点
根据峰的数量和位置，确定芳烃的类型和碳原子数；根据峰的强度 和形状，确定氢原子的类型和数量。
实例分析
以苯为例，其氢谱有多个峰，分别对应于不同位置上的氢原子。
PART 04
氢谱解析中的常见问题与 解决策略
偶合常数
当两个氢原子之间的距离足够近时， 它们的核磁共振信号会发生偶合，导 致峰分裂成双重峰。偶合常数是衡量 两个氢原子之间距离的指标。
氢谱解析的一般步骤
确定峰的位置和强度
根据核磁共振氢谱中的峰位置和强度，可以推断出分子中氢原子 的类型和数量。
确定氢原子的连接关系
通过分析峰的偶合常数，可以确定氢原子之间的连接关系，从而确 定分子的结构。
峰的简化问题
总结词
峰的简化问题是指某些情况下氢谱峰的数量过多，使得解析变得复杂。
详细描述
在某些情况下，由于分子结构中存在多个等效氢原子，会产生大量的重叠峰。这增加了氢谱解析的难 度。解决策略包括利用分子对称性来简化氢谱，以及利用去偶技术来消除某些峰的干扰，从而使得氢 谱更加简洁明了。
解析中的不确定性问题
多核共振技术
总结词
多核共振技术能够同时研究多个原子核的相 互作用和动态行为，有助于更全面地了解分 子结构和化学反应过程。
详细描述
多核共振技术是一种新兴的技术，它通过同 时研究多个原子核的相互作用和动态行为， 能够提供更全面、更深入的分子结构和化学 反应过程信息。这一技术的应用，将有助于 推动化学、生物学、物理学等领域的发展， 为解决复杂体系的研究提供新的手段。
2023-2026
ONE
第二章核磁共振氢谱
第二章 核磁共振氢谱
核磁共振氢谱主要是通过测定有机物分 子中氢原子的位置来推断有机物的结构 的。从一张有机物的核磁共振氢谱图上， 我们可得到有机物分子中氢原子的种类 （根据化学位移δ值）和氢原子的数量 （根据峰面积）。即核磁共振氢谱图上 有多少个峰，就表明有机分子中有多少 种类的氢，各个峰的面积积分比表示各 种氢原子的数目的比例。
H3C
例 如
O
CH3
H CH(CH3)2
第二章核磁共振氢谱
2.分子内存在着快速运动
R1
R5
R6
R3
R2
R4
常见的分子内存在有链的旋转,环的翻转.由于 分子内的快速运动,一些不能通过对称操作而 交换的基团有可能为化学等价,但也不是两个 相同的基团就一定成为化学等价基团.
第二章核磁共振氢谱
RCH2-CXYZ
第二章核磁共振氢谱
亚甲基与次甲基的δ计算
对于亚甲基可以用Shoolery公式加以计 算
δ=1.25 +Σσ (2-1) 式中σ为取代基的经验屏蔽常数.表中给
出其数值.
第二章核磁共振氢谱
表2.2 Shoolery 公式中的经验屏蔽常数(σ)
取代基
R
C=C-
Ph Cl Br I OH -OR -OPh -OCOR -OCOPh NH2 NR2 NO2 SR -CHO -COR -COOH -COOR CN
第二章核磁共振氢谱
2.谱图分类的原则
1).分子中化学位移相同而且对外偶合常数也相同 (磁等价),用一个大写英文字母表示,如A1,A2,A3…., 下标为核的数目. 2).分子中化学位移不同的核用不同的大写英文字 母表示.如果核之间的化学位移之差Δν与J数值相 当,用AB,ABC,ABCD….表示,如果Δν比J大许多 (Δν/J>6),用AX,AMX,AMPX…表示. 3).化学等价但磁不等价的核用AA’,BB’表示
核磁共振氢谱主要是通过测定有机物分 子中氢原子的位置来推断有机物的结构 的。从一张有机物的核磁共振氢谱图上， 我们可得到有机物分子中氢原子的种类 （根据化学位移δ值）和氢原子的数量 （根据峰面积）。即核磁共振氢谱图上 有多少个峰，就表明有机分子中有多少 种类的氢，各个峰的面积积分比表示各 种氢原子的数目的比例。
H3C
例 如
O
CH3
H CH(CH3)2
第二章核磁共振氢谱
2.分子内存在着快速运动
R1
R5
R6
R3
R2
R4
常见的分子内存在有链的旋转,环的翻转.由于 分子内的快速运动,一些不能通过对称操作而 交换的基团有可能为化学等价,但也不是两个 相同的基团就一定成为化学等价基团.
第二章核磁共振氢谱
RCH2-CXYZ
第二章核磁共振氢谱
亚甲基与次甲基的δ计算
对于亚甲基可以用Shoolery公式加以计 算
δ=1.25 +Σσ (2-1) 式中σ为取代基的经验屏蔽常数.表中给
出其数值.
第二章核磁共振氢谱
表2.2 Shoolery 公式中的经验屏蔽常数(σ)
取代基
R
C=C-
Ph Cl Br I OH -OR -OPh -OCOR -OCOPh NH2 NR2 NO2 SR -CHO -COR -COOH -COOR CN
第二章核磁共振氢谱
2.谱图分类的原则
1).分子中化学位移相同而且对外偶合常数也相同 (磁等价),用一个大写英文字母表示,如A1,A2,A3…., 下标为核的数目. 2).分子中化学位移不同的核用不同的大写英文字 母表示.如果核之间的化学位移之差Δν与J数值相 当,用AB,ABC,ABCD….表示,如果Δν比J大许多 (Δν/J>6),用AX,AMX,AMPX…表示. 3).化学等价但磁不等价的核用AA’,BB’表示
核磁共振——氢谱.pdf
核磁共振——氢谱PB07206298龚智良实验目的1. 掌握制样技术；2. 了解超导傅立叶变换核磁共振谱仪的工作原理，实习上机操作；3. 初步掌握获得1H-NMR谱图的操作程序与技术，做出给定未知物的1H-NMR谱图；4. 掌握解析未知物的1H-NMR谱图的方法；5. 掌握使用几种不同的谱图索引查找标准谱NMR图。
实验原理核磁共振的研究对象为具有磁矩的原子核。
由于原子核是带正电的粒子，故在自旋运动时将产生磁矩，但并非所有同位素的原子核都有自旋运动，只有存在自旋运动的原子核才具有磁矩。
原子核的自旋运动与自旋量子数I相关。
I=0的原子核没有自旋运动，I≠0的原子核有自旋运动。
I=1/2的原子核具有电荷在核表面均匀分布的旋转球体。
这类核不具有电四极矩，核磁共振谱线较窄，最适宜核磁共振检测。
氢原子就是这样的原子。
根据量子力学规则，原子核自旋角动量在z轴上的投影只能取一些不连续的值P z=mℏ式中m为原子核的磁量子数。
从而原子核不同能级之间的能量差为∆E=−γ∆mℏB0由量子力学选择定则，只有∆m=±1的跃迁才是允许的。
所以相邻能级之间发生跃迁所对应的能量差为∆E=γℏB0在静磁场中，具有磁矩的原子核存在着不同的能级。
此时，如果运用一特定频率的电磁波来照射样品，并使该电磁波满足hυ=γℏB0即可产生核磁共振现象。
仪器结构脉冲傅立叶变换核磁共振谱仪主要由五个部分组成。
射频发射头、探头、磁场系统、信号接收系统和信号处理系统与控制系统。
仪器的结构框图如图1所示。
图1：脉冲傅立叶变换核磁共振谱仪结构框图射频发射系统是将一个稳定、已知频率的石英晶体震荡器（即主钟）产生的电磁波，经频率综合器精确地合成出欲观测核、被辐照核和锁定核的三个通道所需要的频率射频源。
探头是整个仪器的心脏，固定在磁极间隙中间。
备有多种探头组件和插件。
这些组件和插件中除了有放置样品管的支架和驱使样品管旋转的系统外，还装有向样品管发射射频场的发射线圈和用于接受共振信号的接受线圈。
核磁共振氢谱解析2
3.05
电负性大的原子越多， 影响越大
Br CH3 2.68
I CH3 2.60
距离越远，影响越小
H3C Br H3CH2C Br CH3(CH2)2 Br
2.68
1.65
1.04
CH3(CH2)3 Br 0.90
• 电负性大的取代基（吸电子基团），可使邻近氢 核的电子云密度减少（去屏蔽效应），导致该质 子的共振信号向低场移动，δ值增大。
蔽作用很强，一般化合物的峰大都出现在TMS峰 的左边，即一般化合物的δ均为正值 • TMS沸点仅27℃，很易于从样品中除去，便于样 品回收 • TMS与样品之间不会发生分子缔合 • 在氢谱、碳谱中都规定δTMS=0
低场 δC 200 去屏蔽 δH 10
高场 屏蔽
CH3CH2OH: δ(CH2) =148Hz/60MHz×106 =247Hz/100MHz×106 =2.47
HH
CCH
HH
CH3 C CH3 H
1:6:15:20:15:6:1
1:1
1H核与两组等价1H核相邻时，裂分峰数：（n+ n´+1) 个；
1H核与几组不等价1H核相邻时，裂分峰数： （n+1)( n´+1)……个；
Hb Ha Hc CCC
C
Hd
(nb+1)(nc+1)(nd+1)=2×2 × 2=8 Ha裂分为8重峰
H3C C
~3.0
~1.8
H 3C N H3C C C
~3.7 H H3C O
H CC
~0.9 H3C C
15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 化学位移 δ(ppm)
核磁共振氢谱 (2)
I 1, 2 H 1 ,14 N 7 , I 3,10 B5
讨论:
(1) I=0 的原子核 16 O； 12 C； 22 S等 ，无自 旋，没有磁矩，不产生共振吸收 (2) I=1 或 I >0的原子核 I=1 ：2H，14N I=3/2： 11B，35Cl，79Br，81Br I=5/2：17O，127I 这类原子核的核电荷分布可看作一个椭圆体，电荷分布 不均匀，共振吸收复杂，研究应用较少； (3)Ｉ＝1/2的原子核
atomic nuclear spin
若原子核存在自旋，产生核磁矩： h I ( I 1) 自旋角动量： p 2 p 核 磁 矩： 1 H 2.79270 13 0.70216 磁旋比 ；自旋量子数（I）不为零的核都具有磁矩
C
质量数（a） 原子序数（Z） 自旋量子（I） 奇数 偶数 偶数
1H，13C，19F，31P
原子核可看作核电荷均匀分布的球体，并象陀螺一样自 旋，有磁矩产生，是核磁共振研究的主要对象，C，H也是有 机化合物的主要组成元素。
18:35:41
z B0
z m=1/2 m=1 m=0 m= -1
z m=2 m=1 m=0 m= -1 m= -2
m=-1/2 I=1 I=1/2
18:35:41
美国化学家Paul C. Lauterbur和英国物理 家Peter Mansfield 因为在核磁共振成像 技术（Magnetic Resonance Imaging, MRI ）领域的奠基性的成就，以及该技术在 医学领域的广泛应用而一同分享了2003 年生理学医学奖。
一、 原子核的自旋
(2)与外磁场相反，能量高，磁量 子数ｍ＝－1/2;
18:35:41
核磁共振氢谱(1H NMR)
➢ 因交换缓慢，常可观察到与邻碳质子的耦合作用（ J~8Hz）。
➢ 巯基质子与氘的交换是足够快的，因而可以用重水交 换而使其信号消除。
➢ 硫醇SH, δ= 1.2~1.6；硫酚SH，δ= 2.8~3.6；可变
第五十页，共53页。
第五十一页，共53页。
当结构中存在多个活泼氢（羧基、氨基、羟基等），若 相互之间交换速率快，只产生一个平均的活泼氢信号， 不发生偶合裂分。若交换慢，则表现为各自的吸收峰。
α-二酮只有稳定的烯醇式出现在NMR谱中。
第四十三页，共53页。
e) 羧酸
➢ 弱极性溶剂中，羧酸通常以稳定的氢键二聚体形式存在， 因此其质子吸收范围较窄（δ= 10.0~13.2)。极性溶剂使 二聚体部分断裂，吸收峰位移。
➢ 羧酸质子与水或醇的质子交换很快而给出一个单峰，吸收 峰的位置与浓度有关。
第二十七页，共53页。
(7)溶剂效应
由于溶质分子受到不同溶剂影响而引起的化学位移变化 称为溶剂效应。例如：
在氘代氯仿溶剂中，2.88；2.97。 逐步加入各向异性溶剂苯，和甲基的化学位移逐渐靠 近，然后交换位置。
第二十八页，共53页。
第二十九页，共53页。
➢ 溶剂效应的产生是由于溶剂的磁各向异性造成或者是由于不
ab
cd
c 、 b 、d效应
第八页，共53页。
(2) 相连碳原子的杂化态影响
电负性：Csp > Csp2 > C sp3 乙烷 0.88； 乙烯 5.23； 乙炔 2.88
第九页，共53页。
(3) 磁的各向异性效应
化合物中非球形对称的电子云(如：π电子系统)因电子的流动而产生诱导磁场， 这个磁场是各向异性的。在不同区域，磁场方向不一致。
➢ 巯基质子与氘的交换是足够快的，因而可以用重水交 换而使其信号消除。
➢ 硫醇SH, δ= 1.2~1.6；硫酚SH，δ= 2.8~3.6；可变
第五十页，共53页。
第五十一页，共53页。
当结构中存在多个活泼氢（羧基、氨基、羟基等），若 相互之间交换速率快，只产生一个平均的活泼氢信号， 不发生偶合裂分。若交换慢，则表现为各自的吸收峰。
α-二酮只有稳定的烯醇式出现在NMR谱中。
第四十三页，共53页。
e) 羧酸
➢ 弱极性溶剂中，羧酸通常以稳定的氢键二聚体形式存在， 因此其质子吸收范围较窄（δ= 10.0~13.2)。极性溶剂使 二聚体部分断裂，吸收峰位移。
➢ 羧酸质子与水或醇的质子交换很快而给出一个单峰，吸收 峰的位置与浓度有关。
第二十七页，共53页。
(7)溶剂效应
由于溶质分子受到不同溶剂影响而引起的化学位移变化 称为溶剂效应。例如：
在氘代氯仿溶剂中，2.88；2.97。 逐步加入各向异性溶剂苯，和甲基的化学位移逐渐靠 近，然后交换位置。
第二十八页，共53页。
第二十九页，共53页。
➢ 溶剂效应的产生是由于溶剂的磁各向异性造成或者是由于不
ab
cd
c 、 b 、d效应
第八页，共53页。
(2) 相连碳原子的杂化态影响
电负性：Csp > Csp2 > C sp3 乙烷 0.88； 乙烯 5.23； 乙炔 2.88
第九页，共53页。
(3) 磁的各向异性效应
化合物中非球形对称的电子云(如：π电子系统)因电子的流动而产生诱导磁场， 这个磁场是各向异性的。在不同区域，磁场方向不一致。
核磁共振氢谱[1] (2) (1)
![核磁共振氢谱[1] (2) (1)](https://img.taocdn.com/s3/m/e52d2a23b4daa58da0114a1f.png)
CH3COOH + H2O 1:1
残留H2O对活泼质子信号的影响：活 泼H信号不固定
影响化学位移的因素
⑦ 溶剂效应：溶剂不同使化学位移改变的效应 溶剂效应的产生是由于溶剂的磁各向异性造成或者是由 于不同溶剂极性不同,与溶质形成氢键的强弱不同引起的.
第二节 核磁共振氢谱
4、有机化合物中质子化学位移规律：
② 磁各向异性
双键
CH3CH3 CH2=CH2 0.96 5.25
A α=1.27，β=0.85
B α=1.23，β=0.72
C α=1.17，β=1.01
② 磁各向异性
单键
影响化学位移的因素
③ 共轭效应(C效应):
当芳环、C=C与-OR，=C=O，-NO2等吸电 、供电基团相连时，d值发生相应的变化 例：
用惰性溶剂稀释时，δ↓ -OH ： 0.5~5 ； -CONH2 ： 5~8 ； -COOH ： 10~13
O R C CH2
O C R' R
OH
O R' R
O
H
O R'
C CH C 11~16 ppm
影响化学位移的因素
⑥活泼质子交换:
酸性 H( 与 O 、 N 、 S 相连的 H) ，存在 H交换反应：
饱和碳原子上的质子的 d 值：叔碳 > 仲碳 > 伯碳
与H相连的碳上有电负性大的原子或吸电子基团（N, O, X, NO2, CO等）， d 值变大。电负性越大，吸电子能力越强 ， d 值越大。 d 值：芳氢 > 烯氢 > 烷氢
有机化合物中各种质子的化学位移值
《核磁共振氢谱》课件
《核磁共振氢谱》课件课程目标：1. 理解核磁共振氢谱的基本原理2. 学会分析核磁共振氢谱图3. 掌握核磁共振氢谱在有机化学中的应用第一部分：核磁共振氢谱的基本原理1. 核磁共振现象核磁共振的定义核磁共振的产生条件核磁共振的物理过程2. 核磁共振氢谱的化学位移化学位移的定义化学位移的影响因素化学位移的计算方法3. 核磁共振氢谱的耦合常数耦合常数的定义耦合常数的影响因素耦合常数的计算方法4. 核磁共振氢谱的积分强度积分强度的定义积分强度的影响因素积分强度的计算方法第二部分：核磁共振氢谱的解析1. 核磁共振氢谱图的解读谱线的数量和位置谱线的形状和积分强度谱线的耦合情况2. 等效氢的判断等效氢的定义等效氢的判断方法等效氢的例外情况3. 核磁共振氢谱的应用实例简单有机化合物的分析复杂有机化合物的分析手性化合物的分析第三部分：核磁共振氢谱的实验操作1. 核磁共振氢谱的样品制备样品的选择和制备方法样品的纯化和干燥样品的装载和测试2. 核磁共振氢谱的仪器操作核磁共振仪的基本结构核磁共振仪的操作步骤核磁共振氢谱的获取和保存3. 核磁共振氢谱的数据处理核磁共振氢谱的数据分析核磁共振氢谱的峰拟合核磁共振氢谱的定量分析第四部分：核磁共振氢谱的实践练习1. 练习题目简单有机化合物的核磁共振氢谱分析复杂有机化合物的核磁共振氢谱分析手性化合物的核磁共振氢谱分析2. 练习解答分析过程和思路核磁共振氢谱的解析步骤最终答案和讨论总结：核磁共振氢谱是一种重要的有机化学分析方法，通过对氢原子的核磁共振现象进行研究，可以得到有机化合物的结构和性质信息。
通过对核磁共振氢谱的基本原理、解析方法和实验操作的学习，可以更好地理解和应用核磁共振氢谱，为有机化学研究和教学提供有力的工具。
科学性：1. 内容准确：课件中的概念、原理和实验操作应基于有机化学和核磁共振氢谱的现有科学知识，确保无误。
2. 信息更新：课件中所引用的文献和数据应是最新的，以保证教学内容的时效性。
核磁共振-氢谱
核磁共振波谱法(NMR)
Nuclear Magnetic Resonance Spectroscopy
一
（1）核磁共振现象的发现
Bloch 等于 1945 年发 现：特定结构中的磁核会
吸收一定波长或频率的电
磁波而实现能级跃迁，从 而开辟了核磁共振分析的 历史，并因此获得1952年
Felix Bloch (布洛赫，瑞士) Edward Mills Purcell
OH NH2 NH
13
12
11
10
9
RCOOH
R H
CR2=CH-R CH2F CH2Cl CH2Br CH2I CH2O CH2NO2
RCHO
CH2Ar CH2NR2 CH2S CCH CH2C=O CH2=CH-CH3
C3CH C2CH2 C-CH3
环烷烃
1)饱和碳上质子的化学位移
甲基的化学位移在0.7~4ppm。亚甲基和次甲基吸收峰较复杂， 亚甲基的化学位移可根据Schoolery经验公式计算。
为磁旋比； 为静磁场强度； 为普朗克常数；
10
在静磁场中，原子核发生能级分裂，能量是量子化 的，相邻能级差与静磁场强度成正比。
4. 核磁共振的产生及条件
(3)辐射能量等于磁核能级差
E E E
12
核磁共振方程：
5. 弛豫过程
受激态高能级磁核，失去能量回到低能级磁核的非辐射过程， 称为“弛豫”。 一组1H核在磁场作用下一分为二，若由低能态吸收能量跃迁
氢键效应
当分子形成氢键后，由于静电场的作用，使 氢核外电子密度降低而去屏蔽，移向低场，δ增加。
在非质子性溶剂中，由于分子间的氢键，羧 酸主要是以二聚体存在，δ值在10~13ppm。
Nuclear Magnetic Resonance Spectroscopy
一
（1）核磁共振现象的发现
Bloch 等于 1945 年发 现：特定结构中的磁核会
吸收一定波长或频率的电
磁波而实现能级跃迁，从 而开辟了核磁共振分析的 历史，并因此获得1952年
Felix Bloch (布洛赫，瑞士) Edward Mills Purcell
OH NH2 NH
13
12
11
10
9
RCOOH
R H
CR2=CH-R CH2F CH2Cl CH2Br CH2I CH2O CH2NO2
RCHO
CH2Ar CH2NR2 CH2S CCH CH2C=O CH2=CH-CH3
C3CH C2CH2 C-CH3
环烷烃
1)饱和碳上质子的化学位移
甲基的化学位移在0.7~4ppm。亚甲基和次甲基吸收峰较复杂， 亚甲基的化学位移可根据Schoolery经验公式计算。
为磁旋比； 为静磁场强度； 为普朗克常数；
10
在静磁场中，原子核发生能级分裂，能量是量子化 的，相邻能级差与静磁场强度成正比。
4. 核磁共振的产生及条件
(3)辐射能量等于磁核能级差
E E E
12
核磁共振方程：
5. 弛豫过程
受激态高能级磁核，失去能量回到低能级磁核的非辐射过程， 称为“弛豫”。 一组1H核在磁场作用下一分为二，若由低能态吸收能量跃迁
氢键效应
当分子形成氢键后，由于静电场的作用，使 氢核外电子密度降低而去屏蔽，移向低场，δ增加。
在非质子性溶剂中，由于分子间的氢键，羧 酸主要是以二聚体存在，δ值在10~13ppm。
核磁共振氢谱
250Hz
J1 31P1H
150~
900Hz
1）s-p杂化 CH3-: -12.4Hz, CH2=: +2.3Hz
2）取代基的影响 吸电子基团使2J往正方向变化
3）构象
4）邻位键的影响 2J往负方向变化
O
CH4
H3C
CN
H
H2C
CN
H
(-12.4Hz)
(-14.4Hz)
(-20.3Hz)
O (-21.5Hz)
苯环上氢值的计算公式： 7.26 Zi
2.2 耦合常数J
2.2.1 耦合的矢量模型
H
H
H
C
C
核自旋 电子自旋
H
H
两个氢核相距奇数根键时，自旋相反，J > 0
两个氢核相距偶数根键时，自旋相同，J < 0
耦合作用随键的数目的增加而迅速下降
2.2.2 1J与2J 影响2J的因素
J1 13C1H
125~
团（或质子）互换，则它们为对映异位（enantiotopic)在 非手性溶剂中为化学等价，是等频的；但在手性溶剂中为
化学不等价，是异频的。
• 没有对称操作能使分子中的两基团（或质子）互换，则
它们为化学不等价，是异频的。非对映异位(diastereotopic)。
2. 分子内的快速运动
• 分子的内旋转 例：RCH2—CXYZ
隔离H因无3J耦合，经常显示粗略的单峰。
5）多取代苯环
五取代：单峰 四取代：A2，AX，AB体系 三取代：AMX，ABX，ABC，AB2体系。
60MHz
2.5.2 取代的杂芳环
由于电负性杂原子的存在，杂芳环上不同位置氢的已 拉开一定距离，取代基使之进一步拉开，因此经常可按一 级谱分析。
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
四个基团相互不等同,则是一手性中心,如
果连有一对相同基团时,该碳原子则是前
手性中心.一般来说前手性中心与手性中心相连,那么这一对相同的基团肯定是化学不等价.如果不与手性中心相连则用对
称面原则来判断,若存在对称面,两个基团
则是对映异位的.反之则是非对映异位.O
H
H3C
CH(CH3)2CH34.同一碳相同二基团a).固定在环上CH2两个氢不是化学等价
如2.分子内存在着快速运动R4R5R1R2R3
R6常见的分子内存在有链的旋转,环的翻转.由于分子内的快速运动,一些不能通过对称操作而交换的基团有可能为化学等价,但也不是两个
相同的基团就一定成为化学等价基团. RCH2-CXYZY
X
R Ha
Z
Y
X
Hb R
Z
X
Ha HbY
R
Hb
Z
Ha从分子旋转的角度,分子总是处于1,2,3 三种构象之一,当温度升高,链的旋转速度加大,三种构象的分子逐步
接近,当无论如何,Ha与Hb也不能是化学等价的.如果把R=H,三个氢是完全等价的.所以甲基的三个氢总是在同一位置.3.前手性(prochirality)在有机化合物中,如果与某碳原子相连的
=5.25+0.8+0.11+0=6.16(实际测定6.10Hb=5.25+Z同CH2Br)+Z顺CO2R)+Z反H)=5.25+0.70+1.18+0=7.13(实际测定7.10)苯环质子化学位移的计算取代苯环的氢化学位移可按照下式计算:δ=7.26+Σ Zi 7.26是未取代的苯环的δ值, Zi是取代参
的核相互偶合但不与体系外任何一个核
偶合.在体系内部不要求一个核和它以外所有的核都偶合.例如CH3COOC2H5分别存在A3和A3X2两个自旋体系.2.谱图分类的原则1).分子中化学位移相同而且对外偶合常数也相同(磁等价),用一个大写英文字母表示,如A1,A2,A3….,下标为核的数目.
2).分子中化学位移不同的核用不同的大写英文字母表示.如果核之间的化学位移之差Δν与J数值相当,用AB,ABC,ABCD….表示,如果Δν比J大许多(Δν/J>6),用AX,AMX,AMPX…表示.3).化学等价但磁不等价的核用AA’,BB’表示表2.3 一些分子自旋体系和波谱类型F
2-4 1,4-
1,9 2.3自旋偶合体系(spin system)2.3.1化学等价(chemical equivalence)化学等价是立体化学中的一个重要观念.
如果分子中两个相同原子(或两相同基团)
处于相同化学环境时,它们是化学等价.化学不等价的两个基团,在化学反应中,可以反映出不同的反应速度,在光谱,波谱的测量中,可能有不同的测量结果,因而可用谱学方法来研究化学等价性.1。考察分子各原子核相对静止状态可用对称操作分析两个基团能否相互交
分子中氢的种类和数目就可以非常容易地推断出有机物的分子结构。2.1 化学位移化学位移是核磁共振最重要参数之一.前
面我们已经讨论了影响化学位移的因素.这里不再讨论.根据上述各种影响氢核化学位移的因素和多年核磁共振测定有机物结构的经验同样总结出了不同有机基团氢核的化学位移δ值。根据δ值可
以进行相应有机基团的推断常见的一些有机基团的氢核的化学位移总结于表2.1中。常见基团化学位移H
用经验公式计算.这些经验公式是根据取代基对化学位移地影响具有加和性(additivity)的原理由大量实验数据归纳总结出来的.某些情况下估算具有较高准确度,具有实用价值,而在某些场合下,虽
然误差较大,但依然有参考价值.化学位移计算主要目的是:1).对谱线进行归属;2).为测定分子结构提供理论依据.亚甲基与次甲基的δ计算对于亚甲基可以用Shoolery公式加以计
CH4Cl2CHCHO
CH3CH2OH
Ph-CH=CH23.核磁共振的谱图的分类核磁谱图可分为一级谱图和二级谱图.一级谱图表现满足两个条件:Δν/J>6同一核组的核必须是磁等价.一级谱图有以下特点:峰的数目可用n +1 规律描述.峰的强度可用二项式展开系数表示.从谱图中可以直接读出δ,J.峰的中心位置为δ,相邻两峰之间的距离为J.1.5
换来判断两个基团(核)是否化学等价.可分为三种情况.两个取代基完全相同,Ha,Hb可以用二次
对称轴C2和对称平面相互交换.具有相同的化学位移,它们是化学等价的. CHa
X
XHbO
H
H3C
CH(CH3)2CH3两个取代基不同,但可以用对称平面,或
者二次旋转对称轴联系起来,具有相同的化学位移,它们是化学等价的.反之则是化学不等价.例
苯6.08.5
醛RCHO 9.010.0
羧酸RCOOH 10.512.0酚4.012.0对于大部分有机化合物来说氢谱的化学位移值在0-13 ppm. 大致可分以下几个区0-0.8 ppm 很少见典型化合物; 环丙烷硅烷以及金属有机化合物。0.8-1.5 ppm烷烃区域. 氢直接与脂肪碳相连没有强电
负性取代基。化学位移地次序
CH>CH2>CH3.。如果有更多的取代基化学位移移向低场。1.5-2.5 ppm 羰基区域质子相邻羰基C=O, C=C or 苯环。3.0-4.5 ppm 醚区域. (同样醇酯有CH-O group.) 质子直接邻氧如果有更多的电负性取代基化学位移移向低场。5.0-7.0 ppm 双键区域. 氢直接与C=C 双键相连. 7.0-8.0 ppm 芳环质子区域. 磁各向异性作用导致芳环质子处于去屏蔽区。同样现象发生在醛由于羰基地磁各向异性醛质子化学位移在
9-10 ppm
-OH 可以出现在任何位置谱线的性质由多重
因此影响H的交换pH.浓度温度溶剂等。
一般芳环酚羟基更趋于低场。
大多数的-NHR, -NH2和醇一样可被交换在
2-3 ppm 区域显示宽峰。
-CO2H 可交换,象醇(>11 ppm) 化学位移的计算某些基团或化合物的质子化学位移可以
R顺
R反
H
同RδC=C-H=5.25 + Z同+Z顺+Z反Z同,Z顺,Z反分别代表相应取代基的取代参数.参阅宁永成P40`41C C
Cl
HCl
Fδ=5.25 +1.08 +0.18 -1.02 =5.49 (5.56)Hb
CH2Br
H3COOC
HaHa=5.25+Z同CO2R)+Z顺CH2Br)+Z反H)
的.例如O
Ha
Hb
H
HΔδ=0.39ppmb).单键不能快速旋转,同碳上两个基团是不等价的.由于C-N单键具有双键性质,不能自由旋转,氮上两个甲基是化学不等价的.
N
CH3CH3
O
H
3CC).与手性碳相连的CH2的两个氢是不等价的.2.3.2磁等价(magnetic equivalence)两个核磁等价必须满足下列两个条件:它们是化学等价的它们对任意另外一个核的偶合常数相同
炔 C≡CH 2.03.0
苯基取代2.23.0
醚基取代ROCH33.34.0溴取代CH3Br 2.54.0氯取代CH3Cl 3.04.0
羟基取代CH3OH 4.04.3氟取代CH3F 4.04.5
酰氧基取代RCOOCH33.74.1胺RNH21.05.0醇ROH 1.05.5烯CCH 4.65.9
J (Hz)
类型
J ( Hz)
12-15 2-9
0 6,5- 7,5
5,5-
7,0
aa 5-8
ae 2-4
ee 2-4 0,5- 3 7-1213-18 4-10
0,5-
2,5
0
9- 13 2- 3
1- 3 2- 4
o 6-
-COR
-COOH0.8
0.9
1.32.01.9
1.4
1.7
1.5
2.3
2.7
2.9
1.0
1.0
3.01.01.2
1.2
0.8
0.7
1.2
C C对于次甲基的δ值依然可以用Shoolery
经验公式计算,但常数项改为1.5. δ=1.50 +Σσ烯烃的化学位移计算C C
图中横坐标为化学位移,图上有三个峰则表明该有机物分子中的氢有三种类型
峰面积的积分比为952表明该化合物的三种不同氢的数目分别是9、5和2化学位移δ 7.2处的峰表示苯环上5个相同的氢δ2.5处的峰表示亚甲基上的2个相同氢而δ0.9处的峰则表示三个甲基上的9个相同的氢。这样能够判断出有机物
Δν/J
6.5
5.5
4.5
2.5
算δ=1.25 +Σσ (2-1)式中σ为取代基的经验屏蔽常数.表中给出其数值.表2.2 Shoolery 公式中的经验屏蔽常数(σ)取代基
σ
RC=C-Ph
Cl
Br
I
OH
-OR-OPh-OCOR
-OCOPh
NH2
NR2
NO2SR-CHO
9
m 1-
3
p 0-
1
1-2 1,6-
2,0
1-3 0,6-
1,0
1-4 1,3-
1,8
2-3 3,2-典型nJH,H-偶合常数1-2 2,0-
2,6
1-3 1,5-2,2 1-4 1,8-
2,3
2-3 2,8-
HCH3HOH氢核类型
果连有一对相同基团时,该碳原子则是前
手性中心.一般来说前手性中心与手性中心相连,那么这一对相同的基团肯定是化学不等价.如果不与手性中心相连则用对
称面原则来判断,若存在对称面,两个基团
则是对映异位的.反之则是非对映异位.O
H
H3C
CH(CH3)2CH34.同一碳相同二基团a).固定在环上CH2两个氢不是化学等价
如2.分子内存在着快速运动R4R5R1R2R3
R6常见的分子内存在有链的旋转,环的翻转.由于分子内的快速运动,一些不能通过对称操作而交换的基团有可能为化学等价,但也不是两个
相同的基团就一定成为化学等价基团. RCH2-CXYZY
X
R Ha
Z
Y
X
Hb R
Z
X
Ha HbY
R
Hb
Z
Ha从分子旋转的角度,分子总是处于1,2,3 三种构象之一,当温度升高,链的旋转速度加大,三种构象的分子逐步
接近,当无论如何,Ha与Hb也不能是化学等价的.如果把R=H,三个氢是完全等价的.所以甲基的三个氢总是在同一位置.3.前手性(prochirality)在有机化合物中,如果与某碳原子相连的
=5.25+0.8+0.11+0=6.16(实际测定6.10Hb=5.25+Z同CH2Br)+Z顺CO2R)+Z反H)=5.25+0.70+1.18+0=7.13(实际测定7.10)苯环质子化学位移的计算取代苯环的氢化学位移可按照下式计算:δ=7.26+Σ Zi 7.26是未取代的苯环的δ值, Zi是取代参
的核相互偶合但不与体系外任何一个核
偶合.在体系内部不要求一个核和它以外所有的核都偶合.例如CH3COOC2H5分别存在A3和A3X2两个自旋体系.2.谱图分类的原则1).分子中化学位移相同而且对外偶合常数也相同(磁等价),用一个大写英文字母表示,如A1,A2,A3….,下标为核的数目.
2).分子中化学位移不同的核用不同的大写英文字母表示.如果核之间的化学位移之差Δν与J数值相当,用AB,ABC,ABCD….表示,如果Δν比J大许多(Δν/J>6),用AX,AMX,AMPX…表示.3).化学等价但磁不等价的核用AA’,BB’表示表2.3 一些分子自旋体系和波谱类型F
2-4 1,4-
1,9 2.3自旋偶合体系(spin system)2.3.1化学等价(chemical equivalence)化学等价是立体化学中的一个重要观念.
如果分子中两个相同原子(或两相同基团)
处于相同化学环境时,它们是化学等价.化学不等价的两个基团,在化学反应中,可以反映出不同的反应速度,在光谱,波谱的测量中,可能有不同的测量结果,因而可用谱学方法来研究化学等价性.1。考察分子各原子核相对静止状态可用对称操作分析两个基团能否相互交
分子中氢的种类和数目就可以非常容易地推断出有机物的分子结构。2.1 化学位移化学位移是核磁共振最重要参数之一.前
面我们已经讨论了影响化学位移的因素.这里不再讨论.根据上述各种影响氢核化学位移的因素和多年核磁共振测定有机物结构的经验同样总结出了不同有机基团氢核的化学位移δ值。根据δ值可
以进行相应有机基团的推断常见的一些有机基团的氢核的化学位移总结于表2.1中。常见基团化学位移H
用经验公式计算.这些经验公式是根据取代基对化学位移地影响具有加和性(additivity)的原理由大量实验数据归纳总结出来的.某些情况下估算具有较高准确度,具有实用价值,而在某些场合下,虽
然误差较大,但依然有参考价值.化学位移计算主要目的是:1).对谱线进行归属;2).为测定分子结构提供理论依据.亚甲基与次甲基的δ计算对于亚甲基可以用Shoolery公式加以计
CH4Cl2CHCHO
CH3CH2OH
Ph-CH=CH23.核磁共振的谱图的分类核磁谱图可分为一级谱图和二级谱图.一级谱图表现满足两个条件:Δν/J>6同一核组的核必须是磁等价.一级谱图有以下特点:峰的数目可用n +1 规律描述.峰的强度可用二项式展开系数表示.从谱图中可以直接读出δ,J.峰的中心位置为δ,相邻两峰之间的距离为J.1.5
换来判断两个基团(核)是否化学等价.可分为三种情况.两个取代基完全相同,Ha,Hb可以用二次
对称轴C2和对称平面相互交换.具有相同的化学位移,它们是化学等价的. CHa
X
XHbO
H
H3C
CH(CH3)2CH3两个取代基不同,但可以用对称平面,或
者二次旋转对称轴联系起来,具有相同的化学位移,它们是化学等价的.反之则是化学不等价.例
苯6.08.5
醛RCHO 9.010.0
羧酸RCOOH 10.512.0酚4.012.0对于大部分有机化合物来说氢谱的化学位移值在0-13 ppm. 大致可分以下几个区0-0.8 ppm 很少见典型化合物; 环丙烷硅烷以及金属有机化合物。0.8-1.5 ppm烷烃区域. 氢直接与脂肪碳相连没有强电
负性取代基。化学位移地次序
CH>CH2>CH3.。如果有更多的取代基化学位移移向低场。1.5-2.5 ppm 羰基区域质子相邻羰基C=O, C=C or 苯环。3.0-4.5 ppm 醚区域. (同样醇酯有CH-O group.) 质子直接邻氧如果有更多的电负性取代基化学位移移向低场。5.0-7.0 ppm 双键区域. 氢直接与C=C 双键相连. 7.0-8.0 ppm 芳环质子区域. 磁各向异性作用导致芳环质子处于去屏蔽区。同样现象发生在醛由于羰基地磁各向异性醛质子化学位移在
9-10 ppm
-OH 可以出现在任何位置谱线的性质由多重
因此影响H的交换pH.浓度温度溶剂等。
一般芳环酚羟基更趋于低场。
大多数的-NHR, -NH2和醇一样可被交换在
2-3 ppm 区域显示宽峰。
-CO2H 可交换,象醇(>11 ppm) 化学位移的计算某些基团或化合物的质子化学位移可以
R顺
R反
H
同RδC=C-H=5.25 + Z同+Z顺+Z反Z同,Z顺,Z反分别代表相应取代基的取代参数.参阅宁永成P40`41C C
Cl
HCl
Fδ=5.25 +1.08 +0.18 -1.02 =5.49 (5.56)Hb
CH2Br
H3COOC
HaHa=5.25+Z同CO2R)+Z顺CH2Br)+Z反H)
的.例如O
Ha
Hb
H
HΔδ=0.39ppmb).单键不能快速旋转,同碳上两个基团是不等价的.由于C-N单键具有双键性质,不能自由旋转,氮上两个甲基是化学不等价的.
N
CH3CH3
O
H
3CC).与手性碳相连的CH2的两个氢是不等价的.2.3.2磁等价(magnetic equivalence)两个核磁等价必须满足下列两个条件:它们是化学等价的它们对任意另外一个核的偶合常数相同
炔 C≡CH 2.03.0
苯基取代2.23.0
醚基取代ROCH33.34.0溴取代CH3Br 2.54.0氯取代CH3Cl 3.04.0
羟基取代CH3OH 4.04.3氟取代CH3F 4.04.5
酰氧基取代RCOOCH33.74.1胺RNH21.05.0醇ROH 1.05.5烯CCH 4.65.9
J (Hz)
类型
J ( Hz)
12-15 2-9
0 6,5- 7,5
5,5-
7,0
aa 5-8
ae 2-4
ee 2-4 0,5- 3 7-1213-18 4-10
0,5-
2,5
0
9- 13 2- 3
1- 3 2- 4
o 6-
-COR
-COOH0.8
0.9
1.32.01.9
1.4
1.7
1.5
2.3
2.7
2.9
1.0
1.0
3.01.01.2
1.2
0.8
0.7
1.2
C C对于次甲基的δ值依然可以用Shoolery
经验公式计算,但常数项改为1.5. δ=1.50 +Σσ烯烃的化学位移计算C C
图中横坐标为化学位移,图上有三个峰则表明该有机物分子中的氢有三种类型
峰面积的积分比为952表明该化合物的三种不同氢的数目分别是9、5和2化学位移δ 7.2处的峰表示苯环上5个相同的氢δ2.5处的峰表示亚甲基上的2个相同氢而δ0.9处的峰则表示三个甲基上的9个相同的氢。这样能够判断出有机物
Δν/J
6.5
5.5
4.5
2.5
算δ=1.25 +Σσ (2-1)式中σ为取代基的经验屏蔽常数.表中给出其数值.表2.2 Shoolery 公式中的经验屏蔽常数(σ)取代基
σ
RC=C-Ph
Cl
Br
I
OH
-OR-OPh-OCOR
-OCOPh
NH2
NR2
NO2SR-CHO
9
m 1-
3
p 0-
1
1-2 1,6-
2,0
1-3 0,6-
1,0
1-4 1,3-
1,8
2-3 3,2-典型nJH,H-偶合常数1-2 2,0-
2,6
1-3 1,5-2,2 1-4 1,8-
2,3
2-3 2,8-
HCH3HOH氢核类型