运筹学第六章网络计划
运筹学-6网络计划精品PPT课件

图2
14
图3
5)网络图中不能有缺口和回路 在网络图中,除始点和终点外,其它各个结点的前后都
应有弧相连接,即图中不能有缺口,使网络图从始点经 任何路线都可到达终点。否则,将使某些工序失去与其 紧后(或紧前)工序应有的联系。
在本章讨论的网络图中不能有回路,即不能有循环现 象。否则将使组成回路的子工程永远不能完工。在如下 网络图4中出现的情况是错误的。
EFTj= ESTj+ tj
一项工作的结束时间应等于其开始时间加
12
1) 方向、时序与结点编号
网络图是有向图,按照工艺流程的顺序,规定工序从左向右排列。 网络图中的各个结点都有一个时间(某一个或若干个工序开始或结 束的时间),一般按各个结点的时间顺序编号。为了便于修改编号及 调整计划,可以在编号过程中留出一些编号
2)紧前工序与紧后工序
例如,在图1中,只有在a 工序结束以后,b、c、d、e工序才能开始。a 工序是b、c、d、e 等工序的紧前工序,而b、c、d、e等工序则是工 序a 的紧后工序
这种计划借助于网络表示各项工作与所需要的时间,以 及各项工作的相互关系。通过网络分析研究工程费用与 工期的相互关系。并找出在编制计划时及计划执行过程 中的关键路线。这种方法称为关键路线法(Critical Path Method)简称CPM。
• 工程计划与甘特图
不易表现工程全貌 不便于对各项工作的安排进行筹划和推敲 不能识别影响进度的关键工作 不能反映一项工作不能按进度完成时对工程进度的影
99-7-5
2 拟拟拟拟拟拟拟拟拟拟拟拟拟
99-7-12
3 拟拟拟拟
99-7-13
99-7-22
4 拟拟拟拟拟拟拟
99-7-23
运筹学网络计划
A
拆迁
/
2
B
工程设计
/
3
C
土建工程设计
B
2.5
D
采购设备
B
6
E
厂房土建
C、A
20
F
设备安装
D、E
4
G
设备调试
F
2
A(2)
1
B (3)
2
C (2.5)
3
D (6)
E (20)
G (2)
F (4)
4
5
6
用箭秆删除法标号(保证箭尾号大于箭头号)
工序
A
B
C
D
EFGHIJKL
M
N
紧前工序
_
_
_
_
D
E
A
F
G
B
由本例可见:关键工序 头尾皆有
=
关键工序时间之和=工期T。
,但反之未必。
二、工程完工期的概率分析
(计划评审技术PERT)
1、PERT与 CPM的区别:
CPM工序时间是确定的
工程工期的概率分析是是时间不确定情况下PERT
的主要工作
确定平均工序时间的三点估计法:
设工序最乐观时间为aij,最悲观时间为bij,最可能时间为m ij ,
t ij
a ij 4m ij bij
- 给任意点 i 标 Li ,
Li=Min{以 i 为箭尾的各箭之 “箭头
- 箭长tij”}
16
(3)求关键路(用标号法)
6
2
8
0
0 1
3
B '(0)
3
2)计算各工序 i
管理运筹学 易错判断题整理

2 网络图的线路与关键路线。 3 最早时间,最迟时间,作业的最早开始,最早结束,最迟开始, 最迟结束时间,作业的总时差,自由时差的概念及计算方法。
判断题: 1 在任一图G中,当点集V确定后,树图是G中边数最少的连通图。 √ 2 一个具有多个发点和多个收点的求网络最大流问题一定可以转化为 求具有单个发点和单个收点的求网络最大流问题。
√ 6. 任何线性规划总可用大M单纯形法求解。
√ 7. 凡能用大M法求解也一定可用两阶段法求解。
√ 8. 两阶段法中第一阶段问题必有最优解。
√ 9. 两阶段法中第一阶段问题最优解中基变量全部非人工变量,则原问题有最优 解。
× 10. 人工变量一旦出基就不会再进基。
√ 11. 当最优解中存在为零的基变量时,则线性规划具有多重最优解。 ×
× 5 如果运输问题或者转运问题模型中,Cij 都是产地i到销地j的最小 运输费用,则运输问题同转运问题将得到相同的最优解。
√
第三章:目标规划
主要内容: 1 描述目标规划建模的思路以及他的数学模型同一般线性 数学模型的相同和不同点。 2 解释下列变量:1正负偏差变量 2绝对约束和目标约束 3 优先因子与权系数。 3 目标规划图解法的步骤。 4 目标规划 目标函数特点。 判断题: 1 目标规划模型中,可以不含有绝对约束但是必须含有目 标约束。
1 最优对策中,如果最优解要求一个人呢采取纯策略,则另一个人也必须采取纯策 ×
2 在两人零和对策支付矩阵的某一行或某一列上加上常数k 将不影响双方各自的最优 ×
3 博弈的纳什均衡是博弈双方达到均势平衡的解,也是使博弈双方得到最好结果的 ×
《运筹学》第六章网络计划方法
关键路径分析
什么是关键路径?
是需要在规定时限内完成的,不 能被延误的最长任务序列。
为什么重要?
因为这条路径上的任何延误都会 导致整个项目的延误。
如何确定?
通过计算出每个任务的最早开始 时间和最晚结束时间,从而找出 关键路径。
项目进度管理
1
制订进度计划
确定任务的完成时间,为项目进度的管
进度监控
2
理提供基础。
风险管理的好处?
有助于降低项目失败风险,增强 规划的稳健性,避免额外成本损 失和延迟。
关键路径法和PERT/CPM方法的比较
相似点
都是用来解决项目延误问题、进行进度计划、任务分析等。
不同点-PERT/CPM
适合单一的大规模计划,对时间的估计更加准确,适合波动较大的工作。
不同点-关键路径法
更适合复杂的工作计划,可以快速有效地过滤重要的任务,以使项目进度良好地推进。
运筹学网络计划方法
运筹学网络计划是一个强大的项目管理工具,能够帮助团队更好地理解项目, 并更好地规划工作。
定义
1 网络计划
是指通过图形化的方式,展现了项目中各项 任务的工作量、执行时间以及任务间的依赖 关系。
2 网络计划方法
是利用网络图形的结构,为项目管理提供项 目的计划、实施、控制和组织,以确保项目 的顺利开展。
网络计划在实际项目中的应用
1
建筑
对建筑贸易来说,它是一种标准的工具,用于确定工作任务,减少延误、提早完 成。
2
IT 项目
在软件和硬件开发过程中,它被广泛使用,以便跟踪任务、减少重叠和缺陷,并 计划偏差管理方法。
3
制造业
网络计划可帮助管理、确定生产期、调度工作、支持制造商的计划和进度控制。
运筹学第六章网络计划

工序(i,j)的总时差=(j)最迟开始时间-t(i,j) -(i)最早开始时间
工序(i,j)的自由时差=(j)最早开始时间- (i)最早完成时间
所有时间参数
例3(P136)某项课题研究工作分解的作业表如下。根据此表绘制此项科研工作的网络图,计算时间参数,并确定关键路线。
工序代号
工序
紧前工序
工序时间
(3)按照工作的新工时,重新计算网络计划的关键 路线及关键工序。
(4)再比较关键工序的直接费用率与间接费用率。
不断重复,直到使总费用上升为止。 (直接费用率>间接费用率)
注:若压缩引起出现多于一条新的关键路线时,需同时压缩各关键路线.
(因为不同时压,则工期不能缩短, 工期=关键工序上工时之和)
表示相邻工序时间分界点,称为事 项,
用 表示
(3)相邻弧:
表示工序的前后衔接关系,称为紧前 (或紧后)关系。
如
A
B
A是B的紧前工序,B是A的紧后工序。
A
(4)虚工序(虚箭线)
为表示工序前后衔接关系的需要而增加的。
6.1 网络计划图的绘制 6.2 时间参数计算与关键路线确定 6.3 网络图的调整及优化
CLICK HERE TO ADD A TITLE
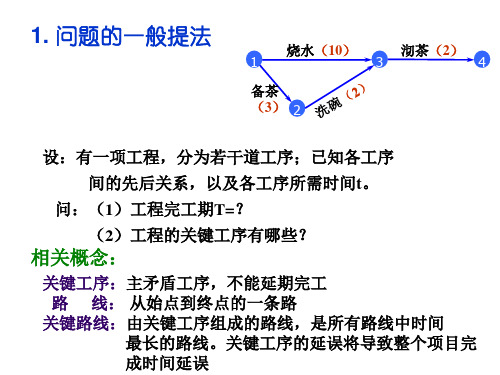
1.问题的一般提法:
设有一项工程,可分为若干道工序,已知各工序间 的先后关系以及各工序所需时间t。
问:
(1)工程完工期T?
(2)工程的关键工序有哪些?
若再各压缩1天
则应压缩B、C(同时压)
此时的直接费用率将是3+4=7>5
故最低成本工期为10天。
注:
(1)有时资料未给可压缩时间,但给了正常工作时间及最短工作时间。则压缩时间=正常工作时间-最短工作时间。
《运筹学》教案(6)—网络计划技术

❖ 图中不能出现平行工序
❖ 图中箭线画成水平线或折线,少画斜线或交叉线 ❖ 图的简化与合并
第五页,共49页。
网络图的绘制规则示例
a 2c 1b 3 d 4f 6
e5
只能有一个始点事项和一个终点事项
a
1
c
2
3
b
1a 2
返回
a 2c 4
i
e
1b
3d
g
5
6
7j
9
继续
f
工序 a b c d e f 紧前工序 — — a b b b
8h
ghi j d f,g c e,g
第十一页,共49页。
网络图的绘制方法示例⑸
❖ 检查是否存在多余的紧前工序时,只需对于“紧前工序” 栏内的组合工序中的各道工序进行检查,判别其中某道工 序的紧前工序中是否包含该组合中的其他工序,如果包含, 则从该组合中将其去除。
2
洗茶杯1 分钟
3
放茶叶 0.5分钟
4
沏茶 0.5 分钟
5
焖制 5 分钟
6
共 需 22分 钟
烧水 15分钟
1 洗茶杯1
放茶叶
3
沏茶 0.5 分钟
4
焖制 5 分钟
5
分钟 2 0.5分钟
共需 20.5分钟
第三页,共49页。
网络图
❖ 网络图的基本概念
工程、工序(活动)
活动—消耗资源、占用时间;用箭线表示,箭线可长可短。
《运筹学》教案(6)—网络计划技术
第一页,共49页。
网络计划技术
❖ 网络计划技术概况 ❖ 网络图及其绘制 ❖ 确定型网络时间的计算
运筹学——网络计划

OR3
3
i 工作名称或代号 持续时间
j
例: 景泰蓝的制作工序:
制胎、掐丝、点蓝、烧蓝、打磨、镀金。
制胎 掐丝 点蓝 烧蓝
打磨
镀金
1 0.5 2 1 3 1 4 2
52
627
注意:网络计划图是有向、有序的赋权图,应按项目的工作 流程从左向右编制。在时序上反应各项工作的先后顺序。 节点编号必须是箭尾编号小于箭头编号。
S-每人或每台设备每工作班能完成的工作量。
n-每天正常工作班次。
OR3
18
(2)三时估计法。先估计三种时间值, 然后求其平均数。
乐观时间,记为a
最可能时间,记为m
悲观时间,记为b
工作持续时间:D a 4m b
6
2
(
ba
2
)
6
OR3
19
2)其它时间的计算公式
OR3
2
1、基本概念
网络图(有向赋权图)的构成:节点和 箭线
节点:每个节点称为事件,是箭线两端 的连接点。表示工序的开始或结束。
剪线:代表工序。剪尾表示该工序的开 始,箭头表示该工序的结束。
工序:是组成整个任务的局部任务,需 要消耗一定资源或占用一定时间。
注意:与工序相比,节点不需要时间或 所需要时间少到可以忽略不计。
可增加此种资源量;某资源对偶解为0,则不 增加此种资源量。 情况② 直接用影子价格与市场价格相比较, 进行决策,决定是否买入该资源。
即:影子价格所含有的信息:1、资源紧 缺状况;2、确定资源转让基价;3、取 得紧缺资源的代价。
OR3
29
Cj
C1 C2 … Cn
管理运筹学讲义第6章_网络计划(6学时)PPT课件

②
sfsf 18
④ 错误的画法
⑤
⑦
缺口 ⑥
OM:SM
第二节 绘制网络图
二、绘制网络图的规则
5、尽量避免箭线交叉,做到美观清晰
②
④
⑧
⑥ ⑩
①
③
⑤
⑦
⑨
④
⑧
①
②
⑤
⑦
⑩
sfsf 19
③
⑥
调整后
⑨
OM:SM
第二节 网络图的绘制
三、网络图的绘制步骤
1、先绘制网络草图
绘制网络草图的方法是顺推法,即以始结点开始,首先确定由始结点引出 的作业,然后根据作业间的逻辑关系,确定每项作业的紧后作业。
sfsf 9
OM:SM
第一节 网络图的基本概念
二、网络图相关的概念
2、基本概念
在下图中,A是D、E的紧前工序,D、E是A的紧后工序,F是A的后 续工序但不是A的紧后工序;A是D、E、F的前道工序但不是 F 的紧前 工序。注意紧前工序、紧后工序、前道工序和后续工序之间的关系。
②
2天
3天
A
E
①
B 3天
sfsf 4
OM:SM
第一节 网络图的基本概念
一、引言
2、网络计划的基本原理
网络计划的基本原理:从需要管理的任务总进度着眼,以任务 中各工作所需要的工时为时间因素,按照工作的先后顺序和相互关 系做出网络图,以反映任务全貌,实现管理过程的模型化。然后计 算时间参数,找出计划中的关键工作和关键线路,以对任务的各项 工作所需的人、财、物通过改善网络计划做出合理安排,得到最优 方案并付诸实施。
⑥
H 20
⑦
⑤ 20
图(a)箭线图
运筹学网络计划技术

自由时差或单时差FF:
◦ 单代号:FFi=min{ESj}-EFi ◦ 双代号:FFij=min{ESjk}-EFij
48
工作A的TF
工作 A
工作A紧后工作B 工作A的TF
工作A的FF 工作A紧后工作C
总时差为零的工作单时差一定为零,总时差不为零 自由时差也可能是零
49
图上作业法 ◦ 单代号 ◦ 双代号 ◦ 绘制时标网络进度求 时间参数 表上作业法 i
37
工序名 称
紧前工 作
工作时 间
工序名 称
紧前工 作
工作时 间
工序名 称
紧前工 作
工作时 间
A
B C D
-
A A A
60
14 20 30
G
H I J
BC
EF F
7
12 60
M
N O P
JK
IL N M
5
15 2 7
DG 10
E
F
A
A
21
10
K
L
H
JK
25
10
Q
OP
5
38
B A
G M
C
J
P
D E L O H I K N Q
21
A
B Finish
Start
C
D
E
22
优点:
◦ 工序之间关系明确 ◦ 易于绘制 ◦ 国外常用软件采用
缺点:
◦ 无法带时标 ◦ 不够直观,所以国内工程师习惯双代号
23
基本概念:
◦ 以结点表示事件,即一项活动的开始或结束 ◦ 以箭线表示一项活动 ◦ 箭首和箭尾事件:一项工作的开始通常称为箭尾事件; 一项工作的结束通常称为箭首事件。
运筹学第六章 网络规划与网络分析

与无向图和有向图相对应,网络又分为无向网络 和有向网络。
图的矩阵表示方法: 关联矩阵:在图G=(V,E) 中,V=(v1,v2,…,vp),E=(e1,e2 ,…,eq), 构造一个矩阵 A (aij ) pq ,其中
1 当点vi与边e j 关联 aij 否则 0
则称A为G的关联矩阵。关联指顶点与边的关系。
vit
的一条链,简记为
v , v
i1
i2
,, vit 。其中 eik (eik , ei ( k 1) ), k 1, 2,..., t 1 。称 vi1和
1 2 3 2 4 5 1 2 4 5
vit 为链的两个端点。图6-3 中的 v , v , v ,v , v , v ,v , v , v , v
为区别起见,把两点间不带箭头的连线称为边, 带箭头的连线称为弧。 由此看出,用图来描述事物间的联系,不仅 直观清晰,便于统观全局,而且网络图的画法简 便,不必拘泥于比例和曲直。总之,这里所讲的 图是反映对象之间关系的一种工具。这样的例子 也很多,电路网络、城市规划、信息传递、物质 结构、物资调配等也都可以用点和线连接起来的 图进行模拟。
都是链。 两个端点重合的链,称为圈。在一个图中,如果任何两个 顶点之间都有一条链,该图称为连通图。
二、有向图
(1)有向图
有向图是一个有序二元组(V,A),记为D(V,A),其中
V (v1 , v2 ,..., vp ) 是p个顶点的集合,A (a1 , a2 ,..., aq ) 是q条弧
ait vi ( t 1) , vit ,则称P是一条链接 vi1 和 vit 的有向路。
三、网络
实际问题中,往往只用图来描述所研究对象之间的 关系还不够,如果在图中赋予边一定的数量指标,我们 常称之为“权”。依据研究问题的需要,权可以代表距 离,也可以代表时间、费用、容量、可靠性等。通常把 这种赋权图称为网络。
运筹学基础-网络计划(2012修正)

不正确的画法
可引入虚作业。
虚作业
虚作业是为了表达相邻作业之间的逻辑关系而虚设的作业。 它不消耗时间、费用和资源,一般用虚箭线表示。 虚作业的引进原因(1) 两个事件之间的工作过程只能代表一项作业,当两个或两 个以上的作业具有同一个始点和终点时,需要引入虚作业,予 以区别。
分解任务的原则
工作的性质不同或由不同单位执行的工作应分开; 如产品设计与工装设计,铸造、锻、机械加工、装配要分开
同一单位进行的工作,时间先后不衔接的要分开; 如技术设计与工作图设计,材料采购与外协件采购要分开
占用时间不消耗资源,但影响工程完工日期的工作应作为分任务;
如油漆后的干燥,热处理后的冷却,方案的审批等
网络图中只能有一个始点和一个终点,使得自网络图的始点 经由任何路径都可以到达终点。
编号的规定
编号应从始事件开始,按照时序依次从小到大对事件编号,直到终 事件。 编号时不允许箭头编号小于箭尾编号。 事件的编号原则 箭尾事件(i)小于箭头事件(j);一般采用非连续编号,即可空留 出几个号,跳着编,将来有变化时,不致打乱全局。
分解任务的要求
编制计划要熟悉业务,了解工程项目的各个组成部分,深入调查。
例:下表是某一工程的作业明细表
任务经过分解以后,可以列出作业明细表。
某一工程的作业时细表 作业 紧接的前项作业 作业时间(周) A 2 无 B 3 无 C A,B 4 D B 1 E A 5 F C 3 G E,F 2 H D,F 7 I G,H 6 J I 5
答案
作业名称 A 紧前作业 无
B 无
C 无
D A
E B
F B、C
A
1
管理运筹学讲义:网络计划

资源分级
02
03
资源租赁与购买
Hale Waihona Puke 根据资源的重要性和稀缺性,对 资源进行分级管理,优先满足关 键资源的供给。
在项目资源不足时,考虑租赁或 购买外部资源,以满足项目需求。
调整关键路径
压缩关键路径
通过优化关键路径上的工作,缩短项目总工 期。
增加人力与物力
在关键路径上增加资源投入,提高工作效率。
任务并行化
通过合理安排任务顺序,使非关键路径上的 工作与关键路径上的工作并行进行。
THANKS FOR WATCHING
感谢您的观看
确定活动之间的逻辑关系
根据确定的活动先后关系,确定各个活动之间的逻辑关系,如并行关系、串行关系等。
确定活动的持续时间
根据历史数据、经验或实际情况,为每个活动分配合理的持续时间。
绘制网络图
使用合适的绘图工具
选择合适的绘图工具,如Visio、 Draw.io等,用于绘制网络图。
绘制网络图
根据确定的活动和关系,绘制出项目 的网络图,清晰地展示各个活动之间 的关系和顺序。
优化项目进度
进度计划优化
根据项目目标和资源状况,制定合理的进度计划,确 保项目按时完成。
进度控制
通过监控项目进度,及时发现偏差并采取措施进行调 整,确保项目按计划进行。
风险管理
识别项目中的潜在风险,制定应对措施,降低进度延 误的风险。
05 网络计划的评价与控制
评价网络计划的可行性
资源可行性
评估项目所需资源是否充足,是否符合 实际资源条件,避免资源浪费和短缺。
成本控制
制定项目成本预算,监控项目成本,及时发现和解决成本超支问题,确保项目成本控制 在预算范围内。
西交《运筹学》重要知识点解析和例题分析第六部分

《运筹学》重要知识点解析和例题分析第六部分一.图的基本概念 定义一个图G 是指一个二元组(V(G),E(G)).即图是由点及点之间的联线所组成。
其中: 1)图中的点称为图的顶点(vertex).记为:v2)图中的连线称为图的边(edge).记为:,i j e v v ⎡⎤=⎣⎦.,i j v v 是边 e 的端点。
3)图中带箭头的连线称为图的弧(arc).记为:(),i j a v v =.,i j v v 是弧 a 的端点。
—— 要研究某些对象间的二元关系时.就可以借助于图进行研究 分类▪ 无向图:点集V 和边集E 构成的图称为无向图(undirected graph).记为: G(V.E)—— 若这种二元关系是对称的.则可以用无向图进行研究▪ 有向图:点集V 和弧集A 构成的图称为有向图(directed graph) .记为:D(V.A)—— 若这种二元关系是非对称的.则可以用有向图进行研究▪ 有限图: 若一个图的顶点集和边集都是有限集.则称为有限图.只有一个顶点的图称为平凡图.其他的所有图都称为非平凡图.图的特点:1 图反映对象之间关系的一种工具.与几何图形不同。
2 图中任何两条边只可能在顶点交叉.在别的地方是立体交叉.不是图的顶点。
3 图的连线不用按比例画.线段不代表真正的长度.点和线的位置有任意性。
4 图的表示不唯一。
如:以下两个图都可以描述“七桥问题”。
点(vertex)的概念1 端点:若e =[u.v] ∈E.则称u.v 是 e 的端点。
2 点的次:以点 v 为端点的边的个数称为点 v 的次.记为:()d v 。
在无向图G 中.与顶点v 关联的边的数目(环算两次),称为顶点v 的度或次数.记为()d v 或 dG(v).在有向图中.从顶点v 引出的边的数目称为顶点v 的出度.记为d+(v).从顶点v 引入的边的数目称为v 的入度.记为d -(v). 称()d v = d+(v)+d -(v)为顶点v 的度或次数. 3 奇点:次为奇数的点。
运筹学基础课后练习答案(项目四 图与网络分析)
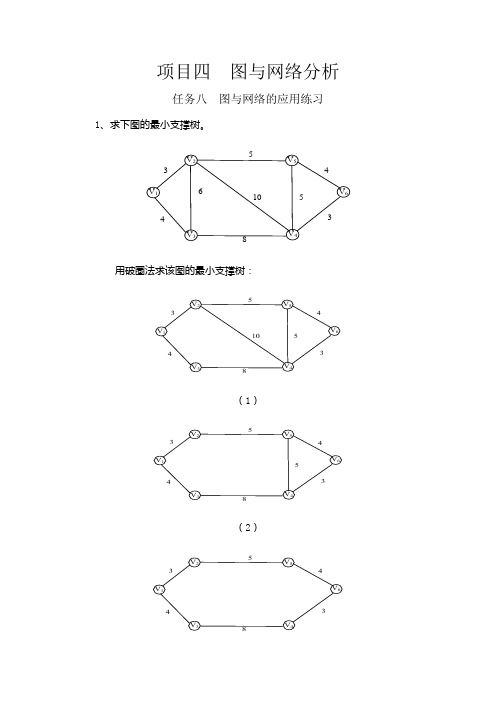
项目四图与网络分析任务八图与网络的应用练习1、求下图的最小支撑树。
用破圈法求该图的最小支撑树:(1)(2)(3)(4)2、分别用破圈法和避圈法求下列各个图的最小支撑树。
a-1:用破圈法求图a的最小支撑树:a-2:用避圈法求图a的最小支撑树:b-1:用破圈法求图b 的最小支撑树:b-2:用避圈法求图b 的最小支撑树:3、用标号法求下图中1v 至7v 的最短路。
1)标号过程(1)初始化;令起点v 1的标号为P ,记做P(1) =0;令其余各点的标号为T ,记做T(i)=∞;(2)计算T标号:刚得到P标号的点为v1,考虑所有与v1相邻的T标号点v 2、v3、v5,修改v2、v3、v5的T标号为:T(2)=min[T(2),P(1)+d12]=min[+∞,0+4]=4T(3)=min[T(3),P(1)+d13]=min[+∞,0+3]=3T(5)=min[T(5),P(1)+d15]=min[+∞,0+5]=5 (3)确定P标号:在所有的T标号点中,找出标号值最小的点标上P标号。
T(2)= 4 T(3) =3 T(4) =+∞T(5)=5 T(6)= +∞ T(7)= +∞令P(3)=3。
(4)计算T标号:刚得到P标号的点为v3,考虑所有与v3相邻的T标号点v 6,修改v6的T标号为:T(6)=min[T(6),P(3)+d36]=min[+∞,3+2]=5 (5)确定P标号:在所有的T标号点中,找出标号值最小的点标上P标号。
T(2)= 4 T(4) =+∞ T(5)=5 T(6)= 5 T(7)= +∞令P(2)=4。
(6)计算T标号:刚得到P标号的点为v2,考虑所有与v2相邻的T标号点v 5,修改v5的T标号为:T(5)=min[T(5),P(2)+d25]=min[5,4+1]=5(7)确定P标号:在所有的T标号点中,找出标号值最小的点标上P标号。
T(4) =+∞ T(5)=5 T(6)= 5 T(7)= +∞令P(5)=5。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例1(P132例)某工厂进行技术改造的工作表如下:
工序代号
A B
C
D E F G
工序名称 紧前工序
拆迁
/
工程设计
/
土建工程
设计
B
采购设备
B
厂房土建 C,A
设备安装 D,E
设备调试
F
运筹学第六章网络计划
工作时间 (周)
2 3
2.5
6 20 4 2B(3)
2
4
D(6)
第六章 网络计划(工程计划问题)
6.1 网络计划图的绘制 6.2 时间参数计算与关键路线确定 6.3 网络图的调整及优化
运筹学第六章网络计划
1.问题的一般提法:
设有一项工程,可分为若干道工序,已知各工序间 的先后关系以及各工序所需时间t。 问: (1)工程完工期T?
(2)工程的关键工序有哪些?
(3)若工序时间T具有随机性,则期望完工期TE=? 完工期为某天的可能性多大?
=max{以 j 为箭头(终点)的各箭的箭尾
+ 箭长 tij }
25
8 K(6)
10
5 L(3) 31
17
31=max{25+6,17+3} 表示第10个事项最早在第31天开始。 之所以取最大,因为在第20天,L工序 已完成,但k工序未完成。
(3)终点 n 的 运tE筹(n学)第即六章为网完络计工划期T(最快的完工期)
(多重边:两点之间有多于一条边) 处理方法:增加虚工序.
A B
C
(回路:工序循环进行,永远不能完成.不允
许)
运筹学第六章网络计划
(2)网络图中的事项要从左至右统一编号,每道工序 的箭尾事项号应小于箭头事项号。
1
2
正确
2
1
错误
(3)尽量避免箭杆交叉。
6 2
1 3
5
7
4
6 3
1
57
2 4
处理方法:先画草图,再整理。
关键工序:B-C-E-F-G
关键路: 1 2 3 4 5
6
(不一定唯一)
总工期: T=31.5(周)
注:1.关键工序
箭头箭尾均有 =
反之不成立。
2.关键工序时间之和=完工期T
运筹学第六章网络计划
所有时间参数
• (j)最早完成时间=(i)最早开始时间-t(i,j) • (i)最迟完成时间=(j)最迟开始时间-t(i,j) • 工序(i,j)的总时差=(j)最迟开始时间-t(i,j) -(i)
K(6) 7
5
10
4 L(3) 6
4=min{10-6,8-3} 表示第5个事项最晚第4天开始。之所以
8 取最小,保证时间最长的工序K能完工 。
2.计算各工序 i j 的时差
R(i,j)= j 的 - tij- i 的 表示这道工序的松弛时间。
如
A(3)
i
j
21
25
R(i,j)=25-3-21=1
1.绘图顺序:按工序先后从左至右
2.网络图的组成要素
A
(1)弧(实箭线)表示工序, 用 i
j 表示。
(2)顶点(结点):表示相邻工序时间分界点,称为事 项,用 i 表示
(3)相邻弧:表示工序的前后衔接关系,称为紧前 (或紧后)关系。如 i A j B k A是B的紧运筹前学第工六序章网,络B计是划 A的紧后工序。
运筹学第六章网络计划
4.绘图准备工作
(1)确定目标
(以谁为主)
时间 资源 费用
(2)工程任务的分解和分析; 分析工程由哪些工序组成并列出全部工序及代号清单。
(3)确定各工序之间先后顺序及衔接关系; 要确定每道工序开工之前有哪些工序必须先期完成。
(4)确定各工序时间。 要确定每道工序运的筹完学第成六所章网需络时计划间。
最早开始时间 • 工序(i,j)的自由时差=(j)最早开始时间- (i)
最早完成时间
运筹学第六章网络计划
例3(P136)某项课题研究工作分解的作业表如下。根 据此表绘制此项科研工作的网络图,计算时间参数, 并确定关键路线。
工序代号 A B C D E F G H I
工序 系统提出和研究问题
研究选点问题 准备调研方案 收集资料工作安排 挑实地训练工作人员 准备收集资料用表格
(4)虚工序(虚箭线)
为表示工序前后衔接关系的需要而增加的。
用 i A’
j 表示。
3.绘图规则: (1)图中不能有缺口,多重边和回路。
1
2
4
5
起点
3
6
终点
(缺口:有几个总开工事项或几个总完工事项)
处理方法:在5、运筹6学之第间六章加网道络计虚划工序
A(3)
1
2
B(2)
A(3) 2
1
A‘(0)
B(2) 3
表示A工序最晚结束时间在第25天,最早 开工时间在第21天,工时为3天,故有1天 的松弛运筹量学。第六章网络计划
3.关键工序
工序时差为0的工序(R(i,j)=0)
如:
A(3)
i
j
22
25
25-3-22=0
表示A工序的开工和结束时间不能 延后,否则整个工期延后一关键 工序。
4.关键路
由关键工序组成的由起点到终点的路。
运筹学第六章网络计划
例2 求例1的关键工序及关键路。
A(2) 1
0 B(3)
0
5.5 5.5 3 E(20) C(2.5)
2 D(6) 4
3
25.5
F(4) 5 G(2) 6
29.5
31.5
3
25.5
29.5
31.5
RA=3.5,RB=0,RC=0,RD=16.5, RE=0,RF=0,RG=0
运筹学第六章网络计划
二、求关键路(关键工序)(标号从后往前) 1.标出各事项的最迟开始时间 tL( i ) (1)给终点 n 标号 T
(2)给任一事项 i 标号 tL( i )
tL(i)= min{tL(j)-t(i,j)}
=min{以 i 为箭尾(起点)的各箭的箭头 箭长tij}
(3)给始点 0 标运号筹学第六0章网络计划
(4)费用优化和资源平衡。
运筹学第六章网络计划
2.解法 关键路径法(CPM方法) 计划评审法(PERT方法)
相同点: 均是用网络表示工程项目,以确定关键路线。
不同点: CPM方法:注重于时间、成本和资源的优化; PERT法:注重于对工程安排的评价与审查。
运筹学第六章网络计划
6.1 网络计划图的绘制
实地调查 分析准备调查报告
任务结束
运筹学第六章网络计划
紧前工序 无 A A B
B,C C
F(4)
5
6
G(2)
运筹学第六章网络计划
6.2 时间参数计算与关键路线确定
—CPM方法
一、求完工期T(标号从前往后)
1.标出各事项的最早开始时间 tE(i)
i
表示第i个事项最早在第20天才开始。
20
(1)给始点 1 标 0
(2)给任意事项 j 标 tE(j)
运筹学第六章网络计划
tE ( j) m tE ( a i) t x ( i,j)
