信号与线性系统分析习题答案
信号与线性系统分析_(吴大正_第四版)习题答案12264精编版
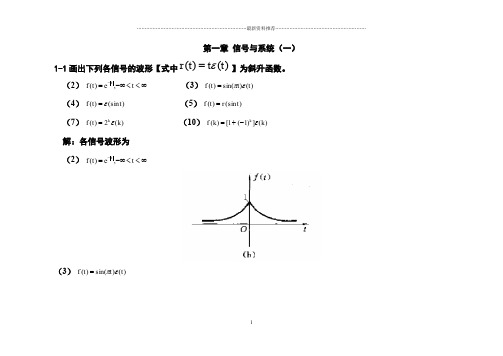
第一章 信号与系统(一)1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ= (4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+= 解:各信号波形为 (2)∞<<-∞=-t e t f t ,)((3))()sin()(t t t f επ=(4))fεt=(sin)(t(5))trf=(sin)(t(7))t(kf kε=)(2(10))f kεk-=(k+(])1(1[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k---=εε 解:各信号波形为 (1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t rt rt rtf(5))2()2()(ttrtf-=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f (5))sin(2cos 3)(5t t t f π+=解:1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
信号与线性系统分析-(吴大正-第四版)第三章习题答案

第三章习题3.1、试求序列k01(k)=2f ⎧⎪⎛⎫⎨ ⎪⎪⎝⎭⎩, 的差分(k)f ∆、(k)f ∇和i=-(i)kf ∞∑。
3.6、求下列差分方程所描述的LTI 离散系统的零输入相应、零状态响应和全响应。
1)()-2(-1)(),()2(),(-1)-1y k y k f k f k k y ε===3)()2(-1)(),()(34)(),(-1)-1y k y k f k f k k k y ε+==+= 5)1()2(-1)(-2)(),()3()(),(-1)3,(-2)-52k y k y k y k f k f k k y y ε++====3.8、求下列差分方程所描述的离散系统的单位序列响应。
2)()-(-2)()=y k y k f k5)()-4(-1)8(-2)()+=y k y k y k f k3.9、求图所示各系统的单位序列响应。
(a)(c)3.10、求图所示系统的单位序列响应。
3.11、各序列的图形如图所示,求下列卷积和。
(1)12()()f k f k *(2)23()()f k f k *(3)34()()f k f k *(4)[]213()-()()f k f k f k *3.13、求题3.9图所示各系统的阶跃响应。
3.14、求图所示系统的单位序列响应和阶跃响应。
3.15、若LTI 离散系统的阶跃响应()()()0.5k g k k ε=,求其单位序列响应。
3.16、如图所示系统,试求当激励分别为(1)()()f k k ε= (2)()()0.5()kf k k ε=时的零状态响应。
3.18、如图所示的离散系统由两个子系统级联组成,已知()1=2cos4k h k π,()()2=k h k k a ε,激励()()()=--1f k k a k δδ,求该系统的零状态响应()zs k y 。
(提示:利用卷积和的结合律和交换律,可以简化运算。
)3.22、如图所示的复合系统有三个子系统组成,它们的单位序列响应分别为()()1=h k k ε,()()2=-5h k k ε,求复合系统的单位序列响应。
信号与线性系统分析吴大正习题答案1_2

1-1画出下列各信号的波形【式中r(t) t (t)】为斜升函数。
(2) f(t) e N, t (4) f(t) (si nt) (7) f(t) 2k (k) 解:各信号波形为(2) f(t) e N, t (3) f(t) sin( t) (t) (5) f (t) r(sint) (10) f(k) [1 ( 1)k] (k)(hl(3) f(t) sin( t) (t)(4) f(t) (si nt)(d)(5) f(t) r(si nt)(7) f(t) 2k (k)(10) f(k) [1 ( 1)k] (k)2卜〔■■ 4* *0::2 3 4 5( 5 21-2画出下列各信号的波形[式中r(t)t (t)为斜升函数]。
(1) f(t) 2 (t 1) 3 (t1) (t 2)(2) f (t) r(t)2r(t1) r(t 2)(5) f(t)r(2t) (2 t)(8) f(k)k[ (k)(k 5)](11) f(k)k(k 7)](12) f(k)2k[ (3k) ( k)] sin( )[ (k)6解:各信号波形为⑴ f(t) 2 (t 1) 3 (t 1) (t 2)(5)f(t) r(2t) (2 t)r(t) 2r(t 1)r(t 2)j/O)Z\1 a7(b)⑵ f(t)4P -OF ■"■(8)f(k) k[ (k) (k 5)]O3)2 13,2<k(11)f(k) sin(~6)[ (k) (k 7)]fa)■MB -»r1.4 1 L_ K _o! 2 3 4 5 6(k)(12)f(k) 2k[ (3k) ( k)]g 8.I~o| 1 2 3 k(I)1-3写出图仁3所示各波形的表达式解图示各波形的表示式分别为:(a) /(f) — 2e(z — 1)—€(『一1) — F (t — 2.) (b)/ (t ) — (t —1)e (r — 1)—2(/—1)c ( f —1) — (t — 3)c ( / 一3)(= 10sint7rZ )_£(?) 一 M — 1 丿_= 1 — 2(r + 2) £(? + 2) — £(r + l)] + (r — 1) c(t H-l) —— 1)12.Ar>1.LIo i tb/(r)正菠函數—1 O l 23(b) I AO(d)1-4写出图1-4所示各序列的闭合形式表达式解图示各序列的闭台形式表示式分别为:(a)/(A)=讥+ 2) (b)/(A) = —3)——7)(c)/«) =e(-^+2) (d)f(k)= (一1)¥⑷1-5判别下列各序列是否为周期性的。
信号与线性系统分析习题答案
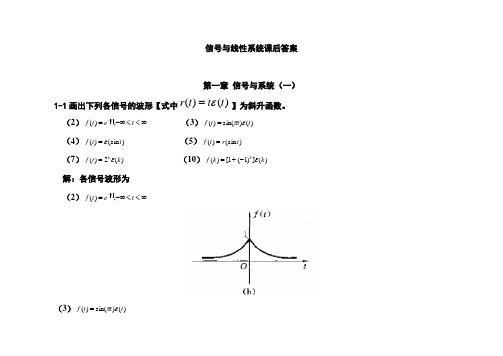
信号与线性系统课后答案第一章 信号与系统(一)1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ= (4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+= 解:各信号波形为 (2)∞<<-∞=-t e t f t ,)((3))()sin()(t t t f επ=(4))fεt=(sin)(t (5))tf=r(sin)(t(7))tf kε(k=(2)(10))f kεk-=(k+]()1(1[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k---=εε 解:各信号波形为 (1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t rt rt rtf(5))2()2()(ttrtf-=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
信号与线性系统分析 (吴大正 第四版)第七章习题答案

7.3 如图7-5的RC 带通滤波电路,求其电压比函数)()()(12s U s U s H 及其零、极点。
7.7 连续系统a 和b ,其系统函数)(s H 的零点、极点分布如图7-12所示,且已知当∞→s 时,1)(=∞H 。
(1)求出系统函数)(s H 的表达式。
(2)写出幅频响应)(ωj H 的表达式。
7.10 图7-17所示电路的输入阻抗函数)()()(11s I s U s Z =的零点在-2,极点在31j ±-,且21)0(=Z ,求R 、L 、C 的值。
7.14 如图7-27所示的离散系统,已知其系统函数的零点在2,极点在-0.6,求各系数a,b。
7.18 图7-29所示连续系统的系数如下,判断该系统是否稳定。
(1)3,210==a a ; (2)3,210-=-=a a ; (3)3,210-==a a 。
7.19 图7-30所示离散系统的系数如下,判断该系统是否稳定。
(1)1,2110-==a a ; (2)1,2110==a a ;(3)1,2110=-=a a 。
7.20 图7-31所示为反馈系统,已知44)(2++=s s ss G ,K 为常数。
为使系统稳定,试确定K 值的范围。
7.26 已知某离散系统的差分方程为)1()2()1(5.1)(-=---+k f k y k y k y(1) 若该系统为因果系统,求系统的单位序列响应h(k)。
(2) 若该系统为稳定系统,求系统的单位序列响应h(k),并计算输入)()5.0()(k k f k ε-=时的零状态响应)(k y zs 。
7.28 求图7-36所示连续系统的系统函数)(sH。
7.30 画出图7-40所示的信号流图,求出其系统函数)(sH。
解(a)由s域系统框图可得系统的信号流图如图7-41(a)。
流图中有一个回路。
其增益为(b)由s 域系统框图可得系统的信号流图如图7-41(b)。
流图中有一个回路。
自考信号与线性系统分析内部题库含答案

单项选择题。
1. 已知序列3()cos()5f k k π=为周期序列,其周期为 () A . 2 B. 5 C. 10 D. 122. 题2图所示()f t 的数学表达式为 ( )图题2A .()10sin()[()(1)]f t t t t πεε=+- B. ()10sin()[()(1)]f t t t t πεε=-- C. ()10sin()[()(2)]f t t t t πεε=-- D. ()10sin()[()(2)]f t t t t πεε=+- 3.已知sin()()()t f t t dt tπδ∞-∞=⎰,其值是 ()A .π B. 2π C. 3π D. 4π4.冲激函数()t δ的拉普拉斯变换为 ( ) A . 1 B. 2 C. 3 D. 45.为了使信号无失真传输,系统的频率响应函数应为 ( ) A . ()djwt H jw e= B. ()djwt H jw e-= C. ()djwt H jw Ke= D. ()djwt H jw Ke-=6.已知序列1()()()3kf k k ε=,其z 变换为 ()A .13z z + B.13z z - C.14z z + D.14z z -7.离散因果系统的充分必要条件是 ( A ) A .0,0)(<=k k h B. 0,0)(>=k k h C. 0,0)(<<k k h D. 0,0)(>>k k h8.已知()f t 的傅里叶变换为()F jw ,那么(3)f t +的傅里叶变换为 ( ) A .()jwF jw e B. 2()j wF jw eC. 3()j wF jw eD. 4()j wF jw e9.已知)()(k k f k εα=,)2()(-=k k h δ,那么()()f k h k *的值为( ) A .)1(1--k k εα B.)2(2--k k εα C. )3(3--k k εα D. )4(4--k k εα10.持续系统的零输入响应的“零”是指( A ) A. 鼓励为零 B. 系统的初始状态为零 C. 系统的冲激响应为零 D. 系统的阶跃响应为零 11. 已知序列k j ek f 3)(π=为周期序列,其周期为 ( )A . 2 B. 4 C. 6 D. 812. 题2图所示()f t 的数学表达式为 ( )A .)1()1()(--+=t t t f εε B.)1()1()(-++=t t t f εε C. )1()()(--=t t t f εε D. )1()()(-+=t t t f εε13.已知)2()(),1()(21-=-=t t f t t f εδ,那么 12()()f t f t *的值是 ( ) A .)(t ε B. )1(-t ε C. )2(-t ε D. )3(-t ε14.已知ωωj j F =)(,那么其对应的原函数为 ( ) A .)(t δ B.)('t δ C. )(''t δ D. )('''t δ15.持续因果系统的充分必要条件是 ( ) A . 0,0)(==t t h B. 0,0)(<=t t h C. 0,0)(>=t t h D. 0,0)(≠=t t h16.单位阶跃序列)(k ε的z 变换为 ( )A .1,1<+z z z B. 1,1>+z z z C. 1,1<-z z z D. 1,1>-z z z 17.已知系统函数ss H 1)(=,那么其单位冲激响应()h t 为 ( )A .)(t ε B. )(t t ε C. )(2t t ε D. )(3t t ε18.已知()f t 的拉普拉斯变换为()F s ,那么)5(t f 的拉普拉斯变换为 ( ) A .)5(s F B.)5(31s F C. )5(51s F D. )5(71s Ft19.已知)2()(2-=-k k f k εα,)2()(-=k k h δ,那么()()f k h k *的值为( ) A .)1(1--k k εα B. )2(2--k k εαC.)3(3--k k εα D. )4(4--k k εα20.已知)(t f 的傅里叶变换为)(ωj F ,那么)(jt F 的傅里叶变换为( ) A. )(ωπ-fB. )(ωπfC. )(2ωπ-fD. )(2ωπf21. 以下微分或差分方程所描述的系统是时变系统的是 ( ) A . )(2)()(2)(''t f t f t y t y -=+ B. )()(sin )('t f t ty t y =+ C. )()]([)(2't f t y t y =+ D. )()2()1()(k f k y k y k y =--+22. 已知)()(),()(21t t f t t t f εε==,那么)()(21t f t f *的值是 ( ) A .)(1.02t t ε B. )(3.02t t ε C. )(5.02t t ε D. )(7.02t t ε23.符号函数)sgn(t 的频谱函数为 ( )A .ωj 1 B. ωj 2 C. ωj 3 D. ωj 4 24.持续系统是稳固系统的充分必要条件是 ( ) A . M dt t h ≤⎰∞∞-)( B. M dt t h ≥⎰∞∞-)(C.M dt t h ≤⎰∞∞-)( D.M dt t h ≥⎰∞∞-)(25.已知函数)(t f 的象函数)5)(2()6()(+++=s s s s F ,那么原函数)(t f 的初值为 ( )A . 0 B. 1 C. 2 D. 3 26.已知系统函数13)(+=s s H ,那么该系统的单位冲激响应为 ( ) A .)(t etε- B.)(2t e t ε- C.)(3t e t ε- D. )(4t e t ε-27.已知)2()(),1()(1-=-=-k k h k k f k δεα,那么)()(k h k f *的值为 ( )A .)(k kεαB.)1(1--k k εαC.)2(2--k k εαD. )3(3--k k εα28. 系统的零输入响应是指( ) A.系统无鼓励信号 B. 系统的初始状态为零C. 系统的鼓励为零,仅由系统的初始状态引发的响应D. 系统的初始状态为零,仅由系统的鼓励引发的响应 29.偶函数的傅里叶级数展开式中 ( )A .只有正弦项 B.只有余弦项 C. 只有偶次谐波 D. 只有奇次谐波 10. 已知信号()f t 的波形,那么)2(t f 的波形为 ( ) A .将()f t 以原点为基准,沿横轴紧缩到原先的12B. 将()f t 以原点为基准,沿横轴展宽到原先的2倍C. 将()f t 以原点为基准,沿横轴紧缩到原先的14D. 将()f t 以原点为基准,沿横轴展宽到原先的4倍 填空题1. 已知象函数223()(1)s F s s +=+,其原函数的初值(0)f +为___________________。
(完整版)信号与线性系统分析_(吴大正_第四版)习题答案

1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t et f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为 (2)∞<<-∞=-t et f t,)((3))()sin()(t t t f επ=(4))(sin )(t t f ε=(5))f=rt)(sin(t (7))t(k=f kε)(2(10))f kεk=(k+-((])11[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k ---=εε解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f (5))sin(2cos 3)(5t t t f π+=解:1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
信号与线性系统分析 (吴大正 第四版)第三章习题答案精编版

第三章习题3.1、试求序列k01(k)=2f ⎧⎪⎛⎫⎨ ⎪⎪⎝⎭⎩, 的差分(k)f ∆、(k)f ∇和i=-(i)kf ∞∑。
3.6、求下列差分方程所描述的LTI 离散系统的零输入相应、零状态响应和全响应。
1)()-2(-1)(),()2(),(-1)-1y k y k f k f k k y ε===3)()2(-1)(),()(34)(),(-1)-1y k y k f k f k k k y ε+==+= 5)1()2(-1)(-2)(),()3()(),(-1)3,(-2)-52k y k y k y k f k f k k y y ε++====3.8、求下列差分方程所描述的离散系统的单位序列响应。
2)()-(-2)()=y k y k f k5)()-4(-1)8(-2)()+=y k y k y k f k3.9、求图所示各系统的单位序列响应。
(a)(c)3.10、求图所示系统的单位序列响应。
3.11、各序列的图形如图所示,求下列卷积和。
(1)12()()f k f k *(2)23()()f k f k *(3)34()()f k f k *(4)[]213()-()()f k f k f k *3.13、求题3.9图所示各系统的阶跃响应。
3.14、求图所示系统的单位序列响应和阶跃响应。
3.15、若LTI 离散系统的阶跃响应()()()0.5k g k k ε=,求其单位序列响应。
3.16、如图所示系统,试求当激励分别为(1)()()f k k ε= (2)()()0.5()kf k k ε=时的零状态响应。
3.18、如图所示的离散系统由两个子系统级联组成,已知()1=2cos4k h k π,()()2=k h k k a ε,激励()()()=--1f k k a k δδ,求该系统的零状态响应()zs k y 。
(提示:利用卷积和的结合律和交换律,可以简化运算。
)3.22、如图所示的复合系统有三个子系统组成,它们的单位序列响应分别为()()1=h k k ε,()()2=-5h k k ε,求复合系统的单位序列响应。
信号与线性系统分析吴大正习题答案

专业课习题解析课程西安电子科技大学844信号与系统专业课习题解析课程第2讲第一章信号与系统(二)1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t et f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为 (2)∞<<-∞=-t et f t,)((3))()sin()(t t t f επ=(4))fεt=(sin)(t (5))f=t(sin)(tr(7))(2)(k t f k ε=(10))(])1(1[)(k k f k ε-+=1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f (5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε (11))]7()()[6sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k---=εε解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t rt rt rtf(5))2()2()(ttrtf-=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
信号与线性系统分析试题及答案(10套)

标准答案(一)一、填空题(每空1分,共30分)1、无线电通信中,信号是以电磁波形式发射出去的。
它的调制方式有调幅、调频、调相。
2、针对不同的调制方式有三种解调方式,分别是检波、鉴频、和鉴相。
3、在单调谐放大器中,矩形系数越接近于1、其选择性越好;在单调谐的多级放大器中,级数越多,通频带越窄、(宽或窄),其矩形系数越(大或小)小。
4、调幅波的表达式为:uAM(t)= 20(1 +0.2COS100πt)COS107πt(V);调幅波的振幅最大值为24V,调幅度Ma为20℅,带宽fBW为100Hz,载波fc为5*106Hz。
5、在无线电技术中,一个信号的表示方法有三种,分别是数学表达式、波形、频谱。
6、调频电路有直接调频、间接调频两种方式。
7、检波有同步、和非同步检波两种形式。
8、反馈式正弦波振荡器按照选频网络的不同,可分为LC、RC、石英晶振等三种。
9、变频器可由混频器、和带通滤波器两部分组成。
10、列出三个常见的频谱搬移电路调幅、检波、变频。
11、用模拟乘法器非线性器件实现调幅最为理想。
二、选择题(每小题2分、共20分)将一个正确选项前的字母填在括号内1、下列哪种信号携带有调制信号的信息(C )A、载波信号B、本振信号C、已调波信号2、小信号谐振放大器的主要技术指标不包含(B )A、谐振电压增益B、失真系数C、通频带D、选择性3、丙类谐振功放其谐振回路调谐于( A )分量A、基波B、二次谐波C、其它高次谐波D、直流分量4、并联型石英晶振中,石英谐振器相当于(C )元件A、电容B、电阻C、电感D、短路线5、反馈式正弦波振荡器的起振条件为( B )A、|AF|=1,φA+φF= 2nπB、|AF| >1,φA+φF = 2nπC、|AF|>1,φA+φF ≠2nπD、|AF| =1,φA+φF ≠2nπ6、要实现集电极调制特性应使功放工作在(B )状态A、欠压状态B、过压状态C、临界状态D、任意状态7、自动增益控制可简称为( B )A、MGCB、AGCC、AFCD、PLL8、利用非线性器件相乘作用来实现频率变换其有用项为( B )A、一次方项B、二次方项C、高次方项D、全部项9、如右图所示的电路是(D )A、普通调幅电路B、双边带调幅电路C、混频器D、同步检波器10、在大信号包络检波器中,由于检波电容放电时间过长而引起的失真是(B)A、频率失真B、惰性失真C、负峰切割失真D、截止失真三、判断题,对的打“√”,错的打“×”(每空1分,共10分)1、谐振放大器是采用谐振回路作负载的放大器。
信号与线性系统分析课后答案吴大正
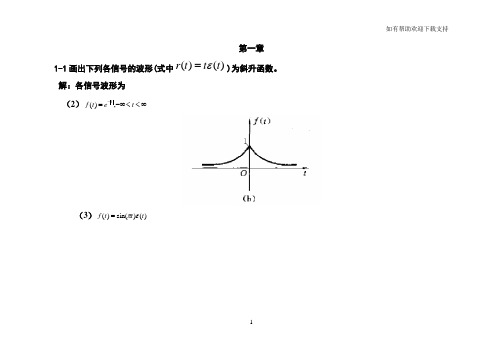
1第一章1-1画出下列各信号的波形(式中)()(t t t r ε=)为斜升函数。
解:各信号波形为 (2)∞<<-∞=-t e t f t ,)((3))()sin()(t t t f επ=(4))fε=t(t(sin)(5))tf=(sinr(t)2(7))tf kε(k=(2)(10))f kεk-=(k+]()1()1[341-2 画出下列各信号的波形[)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k---=εε 解:各信号波形为 (1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t rt rt rtf(5))2()2()(ttrtf-=ε56(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(kkkf k---=εε71-3 写出图1-3所示各波形的表达式。
81-4 写出图1-4所示各序列的闭合形式表达式。
9101-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f (5))sin(2cos 3)(5t t t f π+=解:111-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
(1))()1(t t f ε- (2))1()1(--t t f ε (5))21(t f - (6))25.0(-t f(7)dtt df )( (8)dx x f t ⎰∞-)(解:各信号波形为 (1))()1(t t f ε-12(2))1()1(--t t f ε(5))21(t f -13(6))25.0( t f(7)dt t df )((8)dxxft⎰∞-)(14151-7 已知序列)(k f 的图形如图1-7所示,画出下列各序列的图形。
信号与线性系统分析吴大正习题答案

专业课习题解析课程西安电子科技大学844信号与系统精选专业课习题解析课程第2讲第一章信号与系统(二)精选精选1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t et f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为 (2)∞<<-∞=-t et f t,)((3))()sin()(t t t f επ=(4))fε=t)(sin(t(5))tf=r(t)(sin精选(7))t(kf kε=)(2(10))f kεk-=(k+(])1()1[精选精选1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f (5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε (11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k---=εε 解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t rt rt rtf(5))2()2()(ttrtf-=ε精选精选(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(kkkf k---=εε精选1-3 写出图1-3所示各波形的表达式。
精选1-4 写出图1-4所示各序列的闭合形式表达式。
信号与线性系统分析-(吴大正-第四版)习题答案第二章

第二章2-1已知描述系统的微分方程和初始状态如下,试求其零输入响应。
(1)y''(t) 5y'(t) 6y(t) f (t), y(0) 1, y'(0 ) 1(4)y''(t) y(t) f(t), y(0) 2, y'(0 ) 0解(l)已知方程的特征方程为A2+ 5A + 6 = 0 其特征根为初=-2"? =-36澈分方程的齐次解为央⑴=CL十C代7 由于y(0_) = Kj/70_) =- 1,且激励为零•故有比(0 十〉=y^(0-) = y(O-)= 1 必(0+)=y x(o_)= y(o_)=—i 即并d= G十G = 1 y\(O~) ——2Ci —3G =—1 由上式解得C\ =2,C =-l则系统的零输入响应为y z(n= 2厂孫—色一常d $ 0(4)已知方程的特征方程为A2 -H 1 = 0 其特征根为和=人兀=—人微分方程的齐次解为片(D = Cicos/ + Cg sin/ 由于激励为零,故有>7 (0-r )=力(。
一)=y(0-)= 2 心(0 十)== y(O-)= 0 即划(0_)= Ci = 23/上(0一)= C?2 = 0则系统的零输人响应为几(f)= 2cosz^ 02-2已知描述系统的微分方程和初始状态如下,试求其0值y(0 )和y'(0 )(2)y''(t) 6y'(t) 8y(t) f''(t),y(0 ) 1, y'(0 ) 1, f(t) (t)(4)y''(t) 4y'(t) 5y(t) f'(t),y(0 ) 1,y'(0 ) 2, f (t) e2t (t)解:⑵ y (7)+ 6『⑺一 8了⑺=©"(/) 设/(/> =力一处‘仃)+必(“ +儿(门 则有 丿⑺=必‘(r 〉+处(了)一兀(r )•f/! (r ) = a : (r ) + /0(r )d^同理 y(/) = u (5(z)—人(r) y 2 (r) = /as(r) + 兀(r)dz■ —X 整理得 力"(C + (6u + 6)y (r) + (8a + 6〃 + Cd(r) +L8/2(r)+671(r) + 70(r)]=『⑴<a = 1 = 1・ J 6a 十 Z> = 0=> J )=— 6 丨 8Q + 6〃 + c = 0c = 28r o ・••有 J(O-) - J(O-)= 飞'(r)dr — 6 - Jo. J 0_ =—6 ・:y(0-) = y(0_) — 6 =— 5 (J(r)dr + /i (r)dr J O- ro y Z (0+ ) — y(0_ ) = 8 ( t)dt — 6 8 (/) dz + o_ 0. =28 ■・・y'(0J = 295(/)d/ + Jo. YQ (t)dt(4) /(/) +□></) =-2c_?£(f) + 肮。
信号与线性系统分析(吴大正第四版)第四章习题答案

第四章习题4.6求下列周期信号的基波角频率Ω和周期T O(1) e j100t( 2)cos[^(t—3)](3) cos( 2t) —Sin(4t)( 4)cos( 2nt) +cos(3πt) +cos( 5nt)(5)cosC t) - Sin( t) ( 6)cos(:t)∙ cos( t) cosC t)2 4 23 5亠?Tr 解(I)角频率为Ω= IOO rad∕s.周期T=三=÷⅛SIoU⑵角频率为Ω =rad∕sτ周期= 4 s⑶角频率为Ω = 2 rad厂周期T = ~ = π S(4)角频率为Ω = πrad∕s,周期 T=I^ = 2 sΩ(5)角频率为Ω —rad∕s∙周期T =-^ — 8 S4 £2⑹角频率为C =盒r^d∕s,周期T = = 60 s4.7用直接计算傅里叶系数的方法,求图4-15所示周期函数的傅里叶系数(三角形式或指数形式)。
—4 —IO 1 4图4-15C ¢)解 (1 )周期T = 4 ι∩ ==于F 则有U 4⅛ — 1 ≤ r ≤ 4⅛+ 1 口)=[∣07 4⅛ + 1 < r 〈 4⅛ + 3由此可得。
T *U rt = ~ f TT/(z ) cos (fiΩr) dt = -∣—f /(r )cos(^)drJ ・』—⅛Z ・』—2 乙=£ I sin = 0,?J = 12—ZJ —I 24.10利用奇偶性判断图 4-18示各周期信号的傅里叶系数中 所含有的频率分量。
∕∣∖fΛ -√ 1 √√f /)—rV 1 WZ T "T/1r¥Λlr>/VVVYV NT]/AtJVN*1幷TCOS(^y^)Clr = 2 .——SIn 打Tr窗川=0,12・・ τ f{t)s ∖n(fi∩t)dt = -∣-j ^∕C^)sin(^y^)df (2)周期 T= 2.Ω =■ sin(πf)・0,"≤ r ≤加十1 2⅛ + 1 < r < 2⅛ + 2由此可得=⅛ τ∕(r)^dr = ^J. J —T 艺呢1 + e^pfir ■1r ∣/(t)e"HFFtnidf =SinaCE Or dr—1 Z 」*?! = 0,±1, 土2,…nκ» = O , ± 1. + 2—图4—18=∕1C-z) =—∕l(r⊂ j)/(r)cos(τιΩt) drT n = 0 * 1 * 2 * …du = 盘?= 盘$= *”= 血=久=仏=…・=0 则fΛt)的傅里叶级数中含有的频率分量为奇次余弦波亠(2)由∕2Cr)的波形可知y⅛ (f) =Z-fz(—t)严I J - I J则有丿 4 CT ^ 小=1,2,…I b rt=亍y(f )sιn(^iΩf )df则fz(t>的傅里叶级数中含有的频率分量为正弦波G ¢3)rfl ∕3cn的波形可知人⑺=∕3(-r)则有牛=0Jl 4 「壬・耐=0・1 * 2 *・”*应Ff =〒f(t)co^(ιiΩt )dzJiJG即∕s(r)的傅里叶级数中含有的频率分量为偶次余弦波*⑷ 由Λ(r)的波形可知/⑴ 为奇谐函数,即T.行⑴=—∕√r ± T)则有J = az = a A= = b2= ⅛= ⅛= φ,φ = 0即人(门的博里叶级数中只含有奇次谐波•包拈正弦波和余弦波”4—11某1 Ω电阻两端的电压u(t)如图4-19所示,(1 )求u(t)的三角形式傅里叶系数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章 信号与系统(二)1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f =(7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+=解:各信号波形为(2)∞<<-∞=-t e t f t ,)((3))()sin()(t t t f επ=(4))(sin )(t t f ε=(5))(sin )(t r t f =(7))(2)(k t f k ε=(10))(])1(1[)(k k f k ε-+=1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k ---=εε 解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k ---=εε 1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f (5))sin(2cos 3)(5t t t f π+=解:1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
(1))()1(t t f ε- (2))1()1(--t t f ε (5))21(t f - (6))25.0(-t f (7)dt t df )( (8)dx x f t⎰∞-)(解:各信号波形为(1))()1(t t f ε-(2))1()1(--t t f ε(5))21(t f -(6))25.0(-t f(7)dt t df )((8)dx x f t⎰∞-)(1-7已知序列)(k f 的图形如图1-7所示,画出下列各序列的图形。
(1))()2(k k f ε- (2))2()2(--k k f ε(3))]4()()[2(---k k k f εε (4))2(--k f(5))1()2(+-+-k k f ε (6))3()(--k f k f解: 1-9 已知信号的波形如图1-11所示,分别画出)(t f 和dt t df )(的波形。
解:由图1-11知,)3(t f -的波形如图1-12(a)所示()3(t f -波形是由对)23(t f -的波形展宽为原来的两倍而得)。
将)3(t f -的波形反转而得到)3(+t f 的波形,如图1-12(b)所示。
再将)3(+t f 的波形右移3个单位,就得到了)(t f ,如图1-12(c)所示。
dt t df )(的波形如图1-12(d)所示。
1-10 计算下列各题。
(1)[]{})()2sin(cos 22t t t dtd ε+ (2))]([)1(te dt d t t δ-- (5)dt t t t )2()]4sin([2++⎰∞∞-δπ (8)dx x x t)(')1(δ⎰∞--1-12 如图1-13所示的电路,写出(1)以)(t u C 为响应的微分方程。
(2)以)(t i L 为响应的微分方程。
1-20 写出图1-18各系统的微分或差分方程。
1-23 设系统的初始状态为)0(x ,激励为)(⋅f ,各系统的全响应)(⋅y 与激励和初始状态的关系如下,试分析各系统是否是线性的。
(1)⎰+=-tt dx x xf x e t y 0)(sin )0()( (2)⎰+=t dx x f x t f t y 0)()0()()( (3)⎰+=t dx x f t x t y 0)(])0(sin[)( (4))2()()0()5.0()(-+=k f k f x k y k(5)∑=+=k j j f kx k y 0)()0()( 1-25 设激励为)(⋅f ,下列是各系统的零状态响应)(⋅zs y 。
判断各系统是否是线性的、时不变的、因果的、稳定的?(1)dt t df t y zs )()(=(2))()(t f t y zs = (3))2cos()()(t t f t y zs π= (4))()(t f t y zs -= (5))1()()(-=k f k f k y zs (6))()2()(k f k k y zs -=(7)∑==k j zs j f k y 0)()( (8))1()(k f k y zs -=1-28 某一阶LTI 离散系统,其初始状态为)0(x 。
已知当激励为)()(1k k y ε=时,其全响应为若初始状态不变,当激励为)(k f -时,其全响应为)(]1)5.0(2[)(2k k y k ε-=若初始状态为)0(2x ,当激励为)(4k f 时,求其全响应。
第二章2-1 已知描述系统的微分方程和初始状态如下,试求其零输入响应。
(1)1)0(',1)0(),()(6)('5)(''-===++-y y t f t y t y t y(4)0)0(',2)0(),()()(''===+-y y t f t y t y2-2 已知描述系统的微分方程和初始状态如下,试求其+0值)0(+y 和)0('+y 。
(2))()(,1)0(',1)0(),('')(8)('6)(''t t f y y t f t y t y t y δ====++--(4))()(,2)0(',1)0(),(')(5)('4)(''2t e t f y y t f t y t y t y t ε====++--解:2-4 已知描述系统的微分方程和初始状态如下,试求其零输入响应、零状态响应和全响应。
(2))()(,2)0(',1)0(),(3)(')(4)('4)(''t e t f y y t f t f t y t y t y t ε---===+=++解:2-8 如图2-4所示的电路,若以)(t i S 为输入,)(t u R 为输出,试列出其微分方程,并求出冲激响应和阶跃响应。
2-12 如图2-6所示的电路,以电容电压)(t u C 为响应,试求其冲激响应和阶跃响应。
2-16 各函数波形如图2-8所示,图2-8(b)、(c)、(d)均为单位冲激函数,试求下列卷积,并画出波形图。
(1))(*)(21t f t f (2))(*)(31t f t f (3))(*)(41t f t f (4))(*)(*)(221t f t f t f (5))3()(2[*)(341--t f t f t f波形图如图2-9(a)所示。
波形图如图2-9(b)所示。
波形图如图2-9(c)所示。
波形图如图2-9(d)所示。
波形图如图2-9(e)所示。
2-20 已知)()(1t t t f ε=,)2()()(2--=t t t f εε,求)2('*)1(*)()(21--=t t f t f t y δ2-22 某LTI 系统,其输入)(t f 与输出)(t y 的关系为dx x f e t y t x t )2()(1)(2-=⎰∞---求该系统的冲激响应)(t h 。
2-28 如图2-19所示的系统,试求输入)()(t t f ε=时,系统的零状态响应。
2-29 如图2-20所示的系统,它由几个子系统组合而成,各子系统的冲激响应分别为求复合系统的冲激响应。
第三章习题 、试求序列k 01(k)=2f ⎧⎪⎛⎫⎨ ⎪⎪⎝⎭⎩,的差分(k)f ∆、(k)f ∇和i=-(i)k f ∞∑。
、求下列差分方程所描述的LTI 离散系统的零输入相应、零状态响应和全响应。
1)()-2(-1)(),()2(),(-1)-1y k y k f k f k k y ε===3)()2(-1)(),()(34)(),(-1)-1y k y k f k f k k k y ε+==+=5)1()2(-1)(-2)(),()3()(),(-1)3,(-2)-52k y k y k y k f k f k k y y ε++====、求下列差分方程所描述的离散系统的单位序列响应。
2)()-(-2)()y k y k f k =5)()-4(-1)8(-2)()y k y k y k f k +=、求图所示各系统的单位序列响应。
(a )(c )、求图所示系统的单位序列响应。
、各序列的图形如图所示,求下列卷积和。
(1)12()()f k f k *(2)23()()f k f k *(3)34()()f k f k *(4)[]213()-()()f k f k f k *、求题图所示各系统的阶跃响应。
、求图所示系统的单位序列响应和阶跃响应。
、若LTI 离散系统的阶跃响应()()()0.5k g k k ε=,求其单位序列响应。
、如图所示系统,试求当激励分别为(1)()()f k k ε= (2)()()0.5()k f k k ε=时的零状态响应。
、如图所示的离散系统由两个子系统级联组成,已知()1=2cos 4k h k π,()()2=k h k k a ε,激励()()()=--1f k k a k δδ,求该系统的零状态响应()zs k y 。
(提示:利用卷积和的结合律和交换律,可以简化运算。
)、如图所示的复合系统有三个子系统组成,它们的单位序列响应分别为()()1=h k k ε,()()2=-5h k k ε,求复合系统的单位序列响应。
第四章习题求下列周期信号的基波角频率Ω和周期T 。
(1)t j e 100 (2))]3(2cos[-t π(3))4sin()2cos(t t + (4))5cos()3cos()2cos(t t t πππ++(5))4sin()2cos(t t ππ+ (6))5cos()3cos()2cos(t t t πππ++ 用直接计算傅里叶系数的方法,求图4-15所示周期函数的傅里叶系数(三角形式或指数形式)。
