6第六章-边界层共49页PPT资料
6第六章-边界层

2 y 2 1 y1 y ( c o s ) ( s i n ) 2 0 2 2 4 0
2 2 21 ( ) 0 . 1 3 6 6 4 2
2019/2/13
19
2 y 2 y y ( s i n s i n )( d ) 0 2 2 2
2019/2/13
6
层流边界层与湍流边界层
边界层内的结构
层流 湍流 转捩区 层流底层
边界层内流动状态为层流时,称为层流边界层; 当边界层内流动为湍流时,称为湍流边界层; 从层流变为湍流的过渡段,称为转捩区(或过渡区)。
2019/2/13
7
3、边界层厚度
边界层厚度
2019/2/13
15
【例1】设边界层内速度分布为
y , V x V
1 7
ห้องสมุดไป่ตู้
求: 不可压流体流过平板时位移厚度和动量损失厚度。 解:由定义 * (1 Vx )dy 0 V
y 令
因此
Vx 7 , dy d 则 V
1 1 7
8 7
2019/2/13
10
边界层内由于粘性影响 使质量流量减少的总量为:
V)d y ( V
0 x
理想流体以速度 V 流过 物面时物体表面向外移动 了距离 *所减少的流量
V *
根据质量守恒定理,有
V * ( V V ) d y x 0
2019/2/13
21
分析方程各项数量级,简化方程:
边界层的基本概念课件

边界层的特征
边界层具有很薄的厚度,其厚 度通常远小于流体中的其他尺 度,如流动的长度和速度。
在边界层内,流体的流动状态 从自由流转变为受壁面限制的 流动,流体的速度和方向发生 急剧变化。
边界层内的流体会产生摩擦阻 力,对流体流动产生重要影响 。
边界层的形成
当流体与固体壁面接触时,由于壁面 的限制作用,流体的速度和方向发生 变化,导致流体的切向应力与法向应 力发生突变,形成边界层。
湍流边界层
在流体流动中,靠近固体表面的 薄层,流速较高,流动方向复杂 ,各层速度梯度较大,流动呈现 湍流状态。
热边界层和流动边界层
热边界层
在传热过程中,靠近固体表面的薄层 ,温度梯度较大,热量传递速率较高 。
流动边界层
在流体流动中,靠近固体表面的薄层 ,流速较高或较低,流动方向或湍或 层,与流体主体存在明显的速度梯度 。
边界层的基本概念课件
目 录
• 边界层定义 • 边界层的重要性 • 边界层的分类 • 边界层方程 • 边界层模拟方法 • 边界层的应用
01
边界层定义
边界层的定义
01
边界层是指流体在运动过程中, 流体的切向应力与法向应力发生 突变的位置,通常出现在流体与 固体壁面接触的地方。
02
在边界层内,流体的流动受到壁 面的限制,流体的速度和方向发 生急剧变化,导致流体的物理性 质发生显著变化。
物理边界层和化学边界层
物理边界层
主要涉及流体的物理特性变化,如温度、压力、速度等。
化学边界层
主要涉及流体的化学特性变化,如浓度、组分、化学反应等 。
04
边界层方程
连续性方程
连续性方程是描述流体运动过程中质 量守恒的方程。
高等流体-第六讲,边界层理论

1940年,在第三届国际数学学会上,L.Prandtl在他的
论文中提出,对于像水和空气那样粘性很小的流体,粘性对 流动的影响实际上仅限于贴近固体表面的一个薄层,这一薄 层以外,粘性完全可以忽略,即使应用无粘性流体力学理论 来解释流动也可以达到较高的精确性。 由于不管Re多大,据表面无滑移条件,固体边界上的流速必 为零,所以,在边界的外法线方向流体流动的速度从零迅速 增大。于是,在边界附近的流动区域存在着相当大的流速梯
二.附面层微分方程式
1、基础
dux 1 p 2 x x u x dt duy 1 p 2 N S方程 y u y y dt 1 p duz 2 u z z dt z
2、 假设条件(N-S 方程条件简化) u y u x 0 0 (1)稳定流 t t (2)层流边界层 粘性力与惯性力在同一数量级 (3)质量力不计 X=0 Y=0 (4)不可压缩流体 =c
即为
2
或
0
u u
u 1- u dy
0
2
u u
u 1- u dy
3 C、边界层动量损失厚度 3 其定义与动量损失厚度相似,即理想情况下通过
的流体动
能等于实际情况下整个流场中动能的欠缺量:
3 u2 u2 u 3 u - dy 0 2 2 2
Re
ux
5 6
Rec 3 10 ~ 3 10
3、 边界层的特征综述 a)边界层内,沿厚度方向
du 很大; dy
b)边界层以外,粘性力不计,N-S方程简 Eulerian程; c)附面层内粘性力与惯性力具有相同的量级,均不能忽略; d)附面层的厚度 ,相对于物体特征长度L很小,属于微量;
第6章 边界层流动

6.2 二维平面边界层流动
因为d << L,相对于边界层厚度而言,平板就是无 限长的这样而在边界层流动问题中就找不到一个x方向的 特征长度;因此可以设想在任一x断面流速分布都是相似 的并可作以下变换
微 分 方 程 及 其 精 确 解
将边界层微分方程简化为 边界条件h = 0: f (h) = f '(h) = 0; h = ∞: f '(∞) = 1。 上式是一个非线性三阶常微分方程,有对应于 边界条件的确定解;它由布拉休斯在1908年首次得 出并采用幂级数和渐近方法获得精确解。
微 分 方 程 及 其 精 确 解
6.2 二维平面边界层流动
边界层厚度:
边界层位移厚度:
边界层动量厚度: 壁面切应力系数:
微 分 方 程 及 其 精 确 解
摩擦阻力系数:
t0为壁面切应力、FDf为整个平板受到的力,即
6.2 二维平面边界层流动
以上结果得到试验的证实。图6-5表示顺流放置平 板层流边界层的布拉休斯精确解,以及据此绘制的边 界层厚度的沿程变化和流速分布。
图6-4 平板层流边界层
6.2 二维平面边界层流动
微分方程的精确解 如图6-4所示,取平板前缘为直角坐标系的原点,则 平板前方未受扰动的均匀来流速度U∞与平板平行。由伯努 利方程知,在绕平板流动的势流部分,U = U∞、dp/dx = 0; 而由边界层微分方程知,在边界层中压强沿y方向是均匀 分布的,即边界层内任一点处的压强都与同x坐标处边界 层外势流的压强相等。
微 分 方 程 及 其 精 确 解
g 为另一积分常数。
类似还可得三阶渐近解f = f1 + f2 + f3甚至更高 阶渐近解,本问题中仅考虑到二阶。
传输原理边界层理论PPT

时为层流;Rex>3×10
6
<Rex <3×10 6为层流到湍流的过渡区。
第一节 边界层理论的基本概念
(1)层流区: x<xc (xc为对应于Rex=2×105的流进深度。) ( 2 ) 过 渡 区 : 随 着 流 进 深 度 的 增 长 , 当 x>xc , 使 得 Rex>2×105 , 且 Rex<3×106 时。在这一区 域内,边界层的厚度随着流进尺寸的增加 而迅速增加。 (3)湍流区:随着流进尺寸的进一步增加,使得Rex > 3×106,这时边界层内的流动形态已进入湍 流状态,边界层的厚度随流进长度的增加而 迅速增加。
x x 2x 1 p x y x y x y 2
关于y轴方向上的动量传输方程,因为边界层厚度δ 很 小,第三式中的Vy对x和y的各项偏导数与x轴方向上的
动量传输相比均属无穷小量,可略而不计。因而,第三
式可以简化为
p 0 y
p dp x dx
x
y x
y
y
2 y 2 y 1 p 2 y y y 2 x
因为
x x
是一个无穷小量,所以
是一个高价无穷小,可以略去不计。
第二节
平面层流边界层微分方界层理论
意义:粘性流体流动理论应用于实际问题,明确了研究
理想流体流动的实际意义,在流体力学的发展中起了非
常重要的作用。
第一节 边界层的基本概念
一、边界层的定义 边界层:流体在流经固体壁面时,在固体壁面形成速度 梯度较大的流体薄层。 边界层的厚度:流速相当于主流区速度的 99%处,到固 体壁面的距离称为边界层厚度。 二、边界层的形成与特点 为什么会形成边界层?因为流体内部存在粘附力或粘性 力。 我们已经知道:流体流过管道时,其流动形态是通过雷 诺数来判别的。Re=dυρ /η
边界层理论PPT精选文档

5.1、边界层近似及其特征
普朗特重视观察和分析力学现象,养成了非凡的直观洞察能力,善 于抓住物理本质,概括出数学方程。他曾说:“我只是在相信自己对物 理本质已经有深入了解以后,才想到数学方程。方程的用处是说出量的 大小,这是直观得不到的,同时它也证明结论是否正确。” 普朗特 指导过81名博士生,著名学者Blasius、Von Karman是其学生之一。我 国著名的空气动力学专家、北航流体力学教授陆士嘉先生(女,1911– 1986)是普朗特正式接受的唯一中国学生,唯一的女学生。
粘性流体流经任一物体(例如机翼与机身)的问题,归结 为在相应的边界条件下解N—S方程的问题。由于N—S方程太复 杂,在很多实际问题中,不能不作一些近似假设使其简化,以 求问题得以近似地解决。简化时,必须符合物理事实,因此首 先看看空气流过静止物体(例如翼型)的物理图画:
位流区
边界层
流动分为三个区域:1. 边界层:N-S化简为边界层方程 2. 尾迹区:N-S方程 3. 位流区:理想流方程
EXIT
5.1、边界层近似及其特征
2、边界层的特征
(1)边界层定义 严格而言,边界层区与主流区之间无明显界线,通常
以速度达到主流区速度的0.99倍作为边界层的外缘。由边 界层外缘到物面的垂直距离称为边界层名义厚度,用δ表 示。
(2)边界层的有涡性 粘性流体运动总伴随涡量的产生、扩散、衰减。边界
层就是涡层,当流体绕过物面时,无滑移边界条件相当于 使物面成为具有一定强度的连续分布的涡源。
对于曲率不大的弯曲物面,上述边界层方程也近似成立。 只是要将x和y按上述曲线坐标处理即可。当然如果曲率过大, 则沿法向压强保持不变的条件就很难满足了。
EXIT
5.2、平面不可压缩流体层流边界层方程
流体力学第六章 边界层理论
流体力学第六章
流体力学第六章
Q
v
uv
u dy
udy U
y x 0 0 x
x 0
而
0
uK1
v y
dy
0
uK1
u x
dy
1 K
2
0
x
uK2dy
1 K
2
x
0
uK2dy
U K2
于是第二个积分
vuKudy
v
0
y K10 y
uK1
dyK1(x10u(dyU uK2)U dyK1UK2)
流体力学第六章
u
u x
v
u y
p x
2u y 2
已知普朗特方程组
p y
0
u x
v y
0
0
uk 1
udy x
0
ukv
udy y
p x
0
uk dy
0
uk
2u y2 dy
积分一
积分二
积分三
其中 (x)
(6 2 1)
流体力学第六章
b(x) a(x)
ddxx(x)dx
x 0
0
uk1
u y
2
dy
uk2dy Uk1
udy
k 1 x 0
k 1 x 0
p x
0
uk
dy
k
0
uk1
u y
2 dy
(6-2-3)
流体力学第六章
uk2dyUk1 udy
k1 x 0
k1x0
px0ukdyk0uk1uy2dy
(6-2-3)
上式为哥路别夫积分方程。
边界层的基本概念

5-4 边界层的基本概念
目标
1.绕流现象的主要表现有哪些? 2.什么是附面层(边界层)、边界层分哪几 部分?边界层的特征有哪些? 3边界层流态如何判别,影响因素有哪些?
影响它们们的因素还主要是雷诺数的影响, 影响它们们的因素还主要是雷诺数的影响, 而影响雷诺数的因素有很多,来流紊流度。 而影响雷诺数的因素有很多,来流紊流度。 物体表面的粗糙度等都会影响临界雷诺数 的数值。事实表明, 的数值。事实表明,增加来流紊流度和物 体表面粗糙度都会降低临界雷诺数, 体表面粗糙度都会降低临界雷诺数,是紊 流边界层提前出现。 流边界层提前出现。
边界层的概念
当粘性流体以大雷诺数平滑地绕流静止物 体时, 体时,在壁面附近将出现一个流速由壁面 上的零值迅速增至与来流速度相同数量级 的薄层,称为边界层或者附面层。 的薄层,称为边界层或者附面层。
它的范围:通常把速度与物体表面为零 增大至势流区速度的99%处这一范围定 义为边界层
边界层的基本特征
边界层中也存在着层流区、过渡区 和紊流区,过渡区和紊流区下面也 存在一个层流底层
判别层流边界层和紊流边界层的标准仍然是雷诺数。 判别层流边界层和紊流边界层的标准仍然是雷诺数。 当时Rex≤Recr边界层内时层流状态, Rex>Recr,边 当时 边界层内时层流状态, > , 边界层内时层流状态 界层内时紊流状态。 界层内时紊流状态。
• 1.与被绕物体的长度相比,边界层厚度非常小。 • 2.边界层沿流动方向厚度逐渐增大。 • 3.流体的流速从物体表面为零,沿物体表面法线 方向迅速增加,即速度梯度增。 • 4.边界层内粘性力与惯性力属于同一数量级; • 5.可近似的认为,边界层内沿物面法线方向压力 不变,均等于其外边界处压力值。 • 6.边界层内流体的流动也有层流和紊流两种流动 状态,相对应地分别称之为层流边界层和稳流边 界层。判别边界层内层流和紊流的准则数仍是雷 诺数
流体力学第六章边界层理论(附面层理论)

通过减小边界层的阻力,降低流体机械的能耗,提高运行效率。
流动分离控制
控制边界层的流动分离,防止流体机械中的流动失稳和振动,提 高设备稳定性。
流体动力学中的边界层效应
流动特性的影响
边界层内的流动特性对整体流动行为产生重要影响,如湍流、分离 流等。
流动阻力
边界层内的流动阻力决定了流体动力学的性能,如流体阻力、升力 等。
在推导过程中,需要考虑流体与固体表面之间的相互作用力,如粘性力和压力梯 度等,以及流体内部的动量传递和能量传递过程。
边界层方程的求解方法
边界层方程是一个复杂的偏微分方程,求解难度较大。常用的求解方法包括分离变量法、积分变换法、有限差分法和有限元 法等。
分离变量法是将多维问题简化为多个一维问题,通过求解一维问题得到原问题的解。积分变换法是通过积分变换将偏微分方 程转化为常微分方程,从而简化求解过程。有限差分法和有限元法则是将偏微分方程离散化,通过求解离散化的方程组得到 原问题的近似解。
边界层内的流动可以从层流转变为湍流,或从湍 流转为层流。
边界层内的流动状态
层流边界层
流速在物体表面附近呈现平滑变化的流动状态。
湍流边界层
流速在物体表面附近呈现不规则变化的流动状态。
混合流动状态
边界层内的流动状态可以是层流和湍流的混合状态。
03
边界层方程与求解方法
边界层方程的推导
边界层方程是流体力学中的重要方程,用于描述流体在固体表面附近的流动行为 。其推导基于Navier-Stokes方程,通过引入边界层假设,即认为在靠近固体表 面的薄层内,流体的速度梯度变化剧烈,而远离固体表面的流体则可以视为均匀 流动。
展望
随着科技的不断进步和研究的深入,边界层理论在未来 有望取得以下突破。首先,随着计算能力的提升,更加 精确和可靠的数值模拟方法将得到发展,这有助于更好 地理解和预测复杂流动现象。其次,随着实验技术的进 步,将能够获得更高精度的实验数据,为理论模型的发 展提供有力支持。最后,随着多学科交叉研究的深入, 将能够从不同角度全面揭示流体流动的内在机制,推动 流体力学理论的进一步发展。
流体力学第六章边界层流动5

层流与紊流、雷诺数
在不同的初始和边界条件下,粘性流体质点的运动会出现两种不同
的运动状态,一种是所有流体质点作定向有规则的运动,另一种是
作无规则不定向的混杂运动。前者称为层流状态,后者称为湍流状 态(别称紊流状态)。首先是英国物理学家雷诺在1883年用实验证
明了两种流态的存在,确定了流态的判别方法。
u???????????????????????用量纲分析的方程分析法可得一般二维流动无量纲方程组用量纲分析的方程分析法可得一般二维流动无量纲方程组621平板层流边界层微分方程精确解0??????yuxuyxre12222yuxuxpeuyuuxuuxxxyxx???????????????1121?11?11?11???2?2015112924忽略第二方程最后一项第三方程除压强项的其他项
vc d Re c
Re c
vc d
Re 2320时,管中是层 流; Re 2320时,管中是紊 流。
2018/10/31 13
根据实验结果可知,同管流一样,边界层内也存在着层流和紊流两种 流动状态,若全部边界层内部都是层流,称为层流边界层;若全部边界层 内部都是湍流,称为湍流边界层;若在边界层起始部分内是层流,而在 其余部分内是紊流,称为混合边界层。如图所示,在层流变为紊流之间 有一过渡区。在紊流边界层内紧靠壁面处也有一层极薄的层流底层。
dp dU U dx dx
②第二式右边得到简化(x方向二阶偏导数消失),有利于数值计算。 利用该方程就可计算壁切应力和流动阻力,具有里程碑式意义。
2018/10/31 25
布拉修斯利用相似性解法,引入无量纲坐标:
Rex
*
*
边界层基本介绍

(5) 在边界层内,黏性力与惯性力同一数量级。
(6) 边界层内的流态,也有层流和紊流两种流态。
边界层的基本概念
一、边界层的概念 1904年,在德国举行的第三届国际数学家学会上,德 国著名的力学家普朗特第一次提出了边界层的概念。他认 为对于水和空气等黏度很小的流体,在大雷诺数下绕物体 流动时,黏性对流动的影响仅限于紧贴物体壁面的薄层中, 而在这一薄层外黏性影响很小,完全可以忽略不计,这一 薄层称为边界层。普朗特的这一理论,在流体力学的发展 史上有划时代的意义。 图5-1所示为大雷诺数下黏性流体绕流翼型的二维流动, 根据普朗特边界层理论,把大雷诺数下均匀绕流物体表面 的流场划分为三个区域,即边界层、外部势流和尾涡区。
根据实验结果可知,同管流一样,边界层内也存在着层 流和紊流两种流动状态,若全部边界层内部都是层流,称为 层流边界层,若在边界层起始部分内是层流,而在其余部分 内是紊流,称为混合边界层,如图5-2所示,在层流变为紊流 之间有一过渡区。在紊流边界层内紧靠壁面处也有一层极薄 的层流底层。判别边界层的层流和紊流的准则数仍为雷诺数, 但雷诺数中的特征尺寸用离前缘点的距离x表示之,特征速度 V 取边界层外边界上的速度 ,即
边界层外边界
II尾部流区域 I边界层 边界层外边界
图1 翼型上的边界层
在边界层和尾涡区内,黏性力作用显著,黏性力和惯性力 有相同的数量级,属于黏性流体的有旋流动区;在边界层和尾 涡区外,流体的运动速度几乎相同,速度梯度很小,边界层外 部的流动不受固体壁面的影响,即使黏度较大的流体,黏性力 也很小,主要是惯性力。所以可将这个区域看作是理想流体势 流区,可以利用前面介绍的势流理论和理想流体伯努里方程来 研究流场的速度分布。普朗特边界层理论开辟了用理想流体理 论和黏性流体理论联合研究的一条新途径。实际上边界层内、 外区域并没有明显的分界面,一般将壁面流速为零与流速达到 来流速度的99%处之间的距离定义为边界层厚度。边界层厚度 沿着流体流动方向逐渐增厚,这是由于边界层中流体质点受到 摩擦阻力的作用,沿着流体流动方向速度逐渐减小,因此,只 有离壁面逐渐远些,也就是边界层厚度逐渐大些才能达到来流 速度。
边界层

Chap 5 Planetary Boundary Layer所謂行星邊界層(Planetary Boundary Layer ),就是大氣的近地層因和地面有交互作用(主要是受地表摩擦力的影響),風場和高層不同,如圖5-1,在近地表處存在一垂直風切,圖中的彎曲處為開始受到地面摩擦力的作用。
5.1 Atmospheric Turbulence在大氣中,造成eddy 有兩個原因:1. 地面摩擦:能有效地將動量傳至地面,並將地面的熱(潛熱和可感熱)向上傳遞。
因為摩擦力之故 ♋ 地表面處u = 0 ♋ 垂直風切 ♋ turbulent eddies (mechanically driven )2. 地面加熱:產生convective eddies (thermally driven ) 分子的mean free path 很小(約10-7m ),即分子必頇走很多距離才能和其他分子碰撞,故傳送動量的效率很低;但如果加上亂流的作用,亂流會引起空氣的混合,可以有效地造成動量、質量、熱量和水汽之輸送(但並沒有淨質量的傳送)。
邊界層的高度和大氣環境有關:1. 當大氣非常穩定(即z∂∂θ>0)時,turbulent eddies 無法向上發展地很高,所以邊界層高度低,最低可到數十公尺而已。
2. 若大氣較不穩定或是呈中性,邊界層就會較高,可達3㎞。
一般來說,平均邊界層高度約1㎞。
3. 大氣在夏天因比在冬天較不穩定,所以邊界層較高;同樣地,白天時大氣比晚上時不穩定,因此也有較厚的邊界層。
本章主要討論的是mechanically driven 的eddies 。
在邊界層中,以前所學到的動力方程式必頇做調整,才能包含地面摩擦力造成的turbulence 之作用。
在中緯度的行星邊界層中,主要是氣壓梯度力、科氏力和摩擦力的三力平衡。
5.1.1 The Boussinesq Approximation()'ρρρ+=z在標準大氣中,從地面向上一公里內ρ的變化約只有10﹪,且擾動項'ρ的變動幅度亦僅幾個百分比而已,但這並不表示在此範圍內的流體可假設是同質不 可壓縮的(homogeneous incompressible fluid ),因為ρ的變動對浮力影響甚鉅。
06物体绕流边界层与阻力(教资优择)

的名义厚度。
普朗特理论:边界层内惯性力与粘性力量级相等。
u
u x
~
2u y 2
u2
L
~
u 2
L
~
1 Re
实验表明,对于平板层流边界层
x 5.0 x 5.0x
u
Rex
对于平板湍流边界层
x 0.37x
5 Rex
基础课件
7
§6.2 边界层的特征厚度
一、边界层的排挤厚度δ1 将由不滑移条件造成的质量流量亏损折算成无粘性流体的
C f
pyx b
1 2
ue2
2 d2
dx
称为卡门动量积分方程,适用于无压力梯度的平板定常层流
和湍流边界层流动。
当有压力梯度存在时,方程形式为
d pyx b
ue2 2
dx
1ue
due dx
动量积分方程的特点是建立了阻力与动量损失厚度(及排 挤厚度)的关系。
基础课件
12
§6.3 边界层动量方程
udy 0
ueh
,
由动量方程
h
dy 0 ue
h
x
0
ueue
dy
uudy
0
FD
0
p yx
dx
b
FD ue2h
uudy
0
ue2
0
u ue
1
u ue
dy
ue2 2
对 FD求导可得
dFD
dx
p yx
b
ue2
d2
dx
基础课件
11
§6.3 边界层动量方程
用壁面摩擦系数表示
质量流量相应的厚度δ1 。又称为位移厚度或质量流量亏损厚度。
边界层及其分离

虹吸管正常工作条件 最大真空度 列1-1和最高断面c-c的 能量方程:
pa pc l AC z1 zc g g d 1c v2 2g
第三节 短管出流
l AC p a pc d 1C zc z1 H hv 7 ~ 8mH 2 O l AB g d 1 2
紊流
xE 50 d
9
4.7.3 曲面边界层的分离现象和卡门涡街
一、曲面边界层的分离现象 在实际工程中,物体的边界往往是曲面(流线型或非
流线型物体)。当流体绕流非流线型物体时,一般会出现
下列现象:物面上的边界层在某个位置开始脱离物面, 并在物面附近出现与主流方向相反的回流,流体力学中称 这种现象为边界层分离现象,如下页图所示。流线型物体 在非正常情况下也能发生边界层分离。
10
曲面边界层的分离
11
1、 M M 断面以前,过流断面收缩,流动加速,为顺压梯度区;p 0 x 流体压能向动能转变,不发生边界层分离 2、
p 0 x 在附面层的外边界上, M 具有速度的最小值与压强的最大值 3、S点以后的流体质点在与主流方向相反的压差作用下 ,产生与主流 反方向的回流,但是离物体壁面较远的流体,由于附面层外部流 体对它的带动作用,仍能保持前进的速度。回流和前进这两部分 运动方向相反的流体向接触,就形成旋涡。
hv max p a pc g max l AC d 1C hs H hv 7 ~ 8mH 2 O l AB d 1 2
25
最大安装高度
l AC d 1C hs hv H l AB d 1 2
21
短管淹没出流
边界层
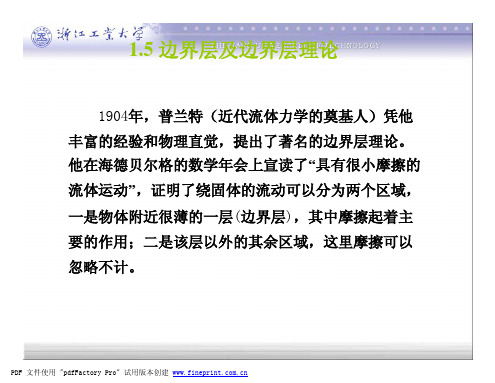
∂ 2v x ∂ 2v x ∂ 2v x ∂v x ∂v x ∂v x ∂v x ∂p N-S方程: ρ ∂t + v x ∂x + v y ∂y + v z ∂z = − ∂x + µ ∂x 2 + ∂y 2 + ∂z 2 ∂ 2v y ∂ 2v y ∂ 2v y ∂v y ∂v y ∂v y ∂v y ∂p ρ ∂t + v x ∂x + v y ∂y + v z ∂z = − ∂y + µ ∂x 2 + ∂y 2 + ∂z 2 ∂ 2vz ∂ 2vz ∂ 2vz ∂v z ∂v z ∂v z ∂v z ∂p ρ ∂t + v x ∂x + v y ∂y + v z ∂z = − ∂z + µ ∂x 2 + ∂y 2 + ∂z 2
PDF 文件使用 "pdfFactory Pro" 试用版本创建
二、边界层的形成和发展
u∞
层流边界层
过渡区
湍流边界层
Re x= ρu∞ x/µ
x流 底 层 层 边界层的发展
流体流过光滑平板时,边界层由层流转变为湍流发生在 Rec=2×105∼3×106
PDF 文件使用 "pdfFactory Pro" 试用版本创建
PDF 文件使用 "pdfFactory Pro" 试用版本创建
1.5 边界层及边界层理论
一、边界层概念及普兰特边界层理论
普兰特边界层理论的主要内容:
边界层

边界层形成与发展
u
层流边
层流底 层
流体沿平壁流动时的边界层示于图1,在边界 层内存在速度梯度,因而必须考虑粘度的影响; 而边界层外,速度梯度可以忽略,则无需考虑 黏性的影响。 边界层按其中的流型可分为层流边界层和湍流 边界层。如图1所示,在壁面的前段,边界层 内的流型为层流,称为层流边界层。离平壁前 缘xc距离后,流型转为湍流,称为湍流边界层。 速度脉动的平均振幅随离壁的距离而变化,越 靠近壁速度脉动越小,因此,即使在高度湍流 条件下,近壁面处仍有一薄层保持着层流特征, 该薄层就称为层流内层,见图1。
边界层
边界层简介
目录
边界层形成与发展
边界层特征 边界层分离
边界层简介
当一个流速均匀的流体与固体界面接触时,由于壁面的阻滞,与壁面直接接触的流 体其速度立即降为零。如果流体不存在黏性,那么第二层流体将仍按原速度u0向前 流动。实际上,由于流体黏性的作用,近壁面 的流体将相继受阻而降速。随着流 体沿壁面向前流动,流速受影响的区域逐渐扩大。通常定义,流速降为未受边壁影 响流速的99%以内的区域为边界层。简而言之,边界层是受边界影响所及的区域。
图2 边界层的分离
边界层分离
在C-C’线一下,流体在逆压强梯度推动下倒流,在 柱体的后部产生大量漩涡,造成机械能损耗,表现 为流体的阻力损失增大,由上述可知: • 流道扩大必造成逆压强梯度; • 逆压强梯度容易造成边界层的分离; • 边界层分离造成大量漩涡,增大机械能消耗。
谢谢
图 1 平壁边界层
边界层特征 层流边界层——速度梯度较均匀地分布于 全层。 湍流边界层——湍流边界层包括湍流核心、 缓冲层、层流底层。在层流底层中具有较 大的速度梯度。
传递过程的阻力主要集中在层流底层。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
– 矛盾:绕流物体阻力为零;达朗贝尔详谬. – 原因:势流理论速度场仅满足固壁不可穿透条件,而不
能满足固壁无滑移条件.
27.04.2020 1
第六章 边界层流动
2、普朗特Prandtl边界层理论(1904) • Prandtl大Re数绕流流动显示实验:
– 即使粘性很小流体(水、空气)绕物体流动时,在贴近 物面处流动速度很慢,
– 在离开物面很小的距离以外流线谱与理想流势流理论计 算结果基本一致。
边界层:物体壁面附近的薄层内存在着很大的速度梯
度和漩涡,粘性影响不能忽略,这一薄层称为边界层。
27.04.2020 2
第六章 边界层流动
Prandtl边界层理论
• Prandtl边界层:流体力学发展的里程碑
– 提出了用粘性理论解决实际问题的途径和方法; – 肯定了势流理论及其解的适用范围; – 奠定了近代流体力学发展的基础。
• 基本概念补充:
– 外流:流体绕物体(如飞行器)的流动,物体外表面构 成流动内边界,外边界理论上一般延伸至无穷远。
– 内流:处于固体壁面边界内部的流动,如管道、发动机 内流动,固体壁面成为外边界。
就是边界层位移厚度δ*。
27.04.2020 9
第六章 边界层流动
边界层内由于粘性影响 使质量流量减少的总量为:
0(VVx)dy
物理面想时流物体体以表速面度向V外
流 移
过 动
了距离 *所减少的流量
V*
根据质量守恒定理,有
可得
V *0 ( VVx)dy
*0(1VVx)dy
27.04.2020 10
27.04.2020 5
第六章 边界层流动
层流边界层与湍流边界层
边界层内的结构
层流 湍流 转捩区 层流底层
边界层内流动状态为层流时,称为层流边界层; 当边界层内流动为湍流时,称为湍流边界层; 从层流变为湍流的过渡段,称为转捩区(或过渡区)。
27.04.2020 6
第六章 边界层流动
~
1
1
L Re
② 边界层内沿物面法向有急剧的速度变化(速度梯度很大)
③ 边界层内惯性力与粘性力具有相同量级;
④ 边界层中流动可以是层流,也可以是湍流,两种流态可同 时存在,通常由层流转变为湍流;即便是湍流区,其下部 贴近壁面的地方也有一个局部的层流底层
⑤ 边界层内压强p与y无关,即p=p(x),故边界层各横截面上的
27.04.2020 11
第六章 边界层流动
2.动量损失厚度 **
边界层对流动的影响之二是使设想中的无粘流体 流过该区域的动量流量亏损了,按单位宽度平板计算
动量流量亏损量,并将其折算成厚度 **,称为动量
损失厚度 .
单位时间内通过边界 层的动量为
0
Vx2dy
同一流量的理想流动 具有的动量为
V
0
Vx
dy
27.04.2020 12
第六章 边界层流动
将粘性引起的动量损
失折算到对应于理想流
动的某一厚度δ**,则
V 2* * V 0
V xd y0
V x 2d y
δ**即为动量损失厚度,由上式可得
不可压流
** Vx (1Vx)dy
0 V V
** Vx (1Vx )dy
0 V V
第六章 边界层流动
§1 边界层概念
粘性流体运动基本方程: N-S方程
•方程非线性,求解困难,极少数简单问题有精确解
1、自然和工程中的大Re数流动
– 飞机:30m, V=100m/s, =1.5*10-5 Re=2*108 – 轮船:30m, V=25m/s, =1.14*10-6 Re=6.6*108
3、边界层厚度
边界层厚度
物面到沿物体表面外法线
上 边界速层度厚达度到,0用.99V表∞的示距。离即称为
y V0.99V
边界层厚度
边界层内的一个重要特点: 边界层内沿物面外法线方
向压强ห้องสมุดไป่ตู้变,即 p 0 y
27.04.2020 7
第六章 边界层流动
4.边界层基本特征
① 与绕流物体长度相比,边界层很薄,厚度沿流动方向逐渐 增厚,随Re数增加而减小:
• 在实际流动中,还包括边界层分离,尾迹区等.
• 边界层假设优点:
– 考虑粘性影响只局限于边界层内,层外则可按理想流体 考虑;
– 建立了理想流体绕流规律与粘性流体绕流规律之间的相 关关系,对近代流体力学发展起了巨大的推动作用;
– 解决了流线型物体摩擦阻力计算的重要问题。
27.04.2020 4
第六章 边界层流动
压强等于同一截面上外边界上压强;
p0 or y
ppa
⑥ 沿曲面边界流动时边界层易出现分离和尾涡。
27.04.2020 8
第六章 边界层流动
§2 边界层位移厚度和动量损失厚度
1.边界层位移厚度*(排挤厚度)
粘性流体通过边界层时,不仅速度大小发生变化, 而且流线被迫向外弯曲。
在任一截面处实际流线相对于理想流线的偏移量,
• 高Re数粘性流动中,物面附近没有发生流动分离 条件下,流动可划分为两个区域,在贴近物面附近 的一个薄层中必须考虑粘性力的作用,则把这个薄 层称为边界层(或附面层)。而在薄层以外,速度梯 度不大,可不计粘性影响,按理想流体考虑。
(1) 边界层区域(y<δ)
– 局限于固体壁面边界附近的一个薄流动层中;紧贴物 面的一层速度为零,由边界向外,速度迅速增大;
– 尽管一般流体粘性系数很小,但在此区域内,法向速 度梯度很大,粘性效应显著,惯性力与粘性力同等重 要。
27.04.2020 3
第六章 边界层流动
(2) 外流区(y >δ)
– 离开壁面很近的地方,流动速度则非常接近理想流体 绕同一物体在该处所能达到的速度了
– 法向速度梯度较小,可略去粘性的作用而近似为理想 流体的有势流动。
δ**表示粘性效应引起动量损失的大小.
27.04.2020 13
第六章 边界层流动
边界层三个特征厚度δ、δ*和δ** 的关系 δ > δ* > δ**
第六章 边界层流动
不可压流
* (1 Vx )dy
0
V
边界层厚度δ取为物面
到 式
中Vx=积0.分99上V∞限处取的∞距与离取,δ上积
分值相差很小,故
* (1 Vx )dy
0
V
当边界层内速度分布确定后,*是一确定值.
位移厚度δ*的物理意义:
位移厚度 *就是由于在边界层内速度降低而要求
通道加宽,即全部粘流所占的通道比无粘(理想流体) 流动应占通道所加宽的部分。
